Transfer-Matrix Method for Calculus of Long Cylinder Tube with Industrial Applications
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Working Assumptions
- Under the action of external forces perpendicular to the average plane, the curvature varies;
- The curvature variation occurs in two planes, forming an elastic surface with double curvature;
- The shape of the elastic surface is characterized by the variation law of the arrow
- f(x, y), in Cartesian coordinates;
- It is assumed that the numerical values of the function f(x, y) are very small in relation to the thickness h;
- The points aligned on the same normal to the average surface before the deformation remain aligned on the same normal to the deformed surface and after deformation;
- The normal stresses in the sections parallel to the median plane are negligible in relation to the bending stresses;
- Normally continue to remain invariable after deformation;
- For a long cylindrical tube, the stresses and the deformations have a revolution’s symmetry;
- The cylinder is defined in a fixed coordinate axis system; the Ox axis is directed according to the generators, the Oy axis is directed according to a radius, and the Oz axis is taken in such a way that the triaxial system Oxyz is directly.
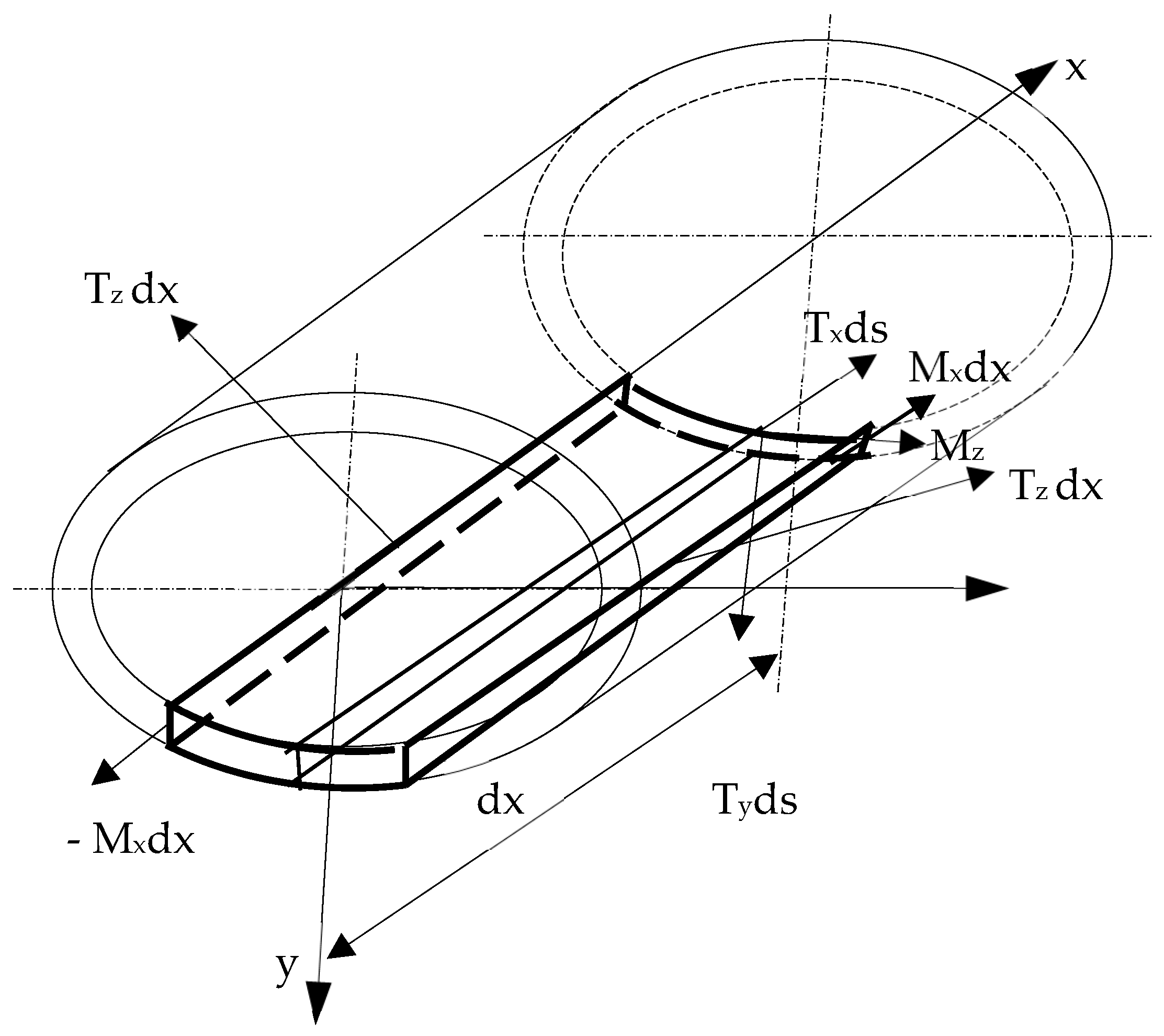
2.2.2. Fundamental Equations for a Long Cylinder
2.2.3. The Transfer-Matrix for a Long Cylindrical Thin Wall Tube
3. Application and Results
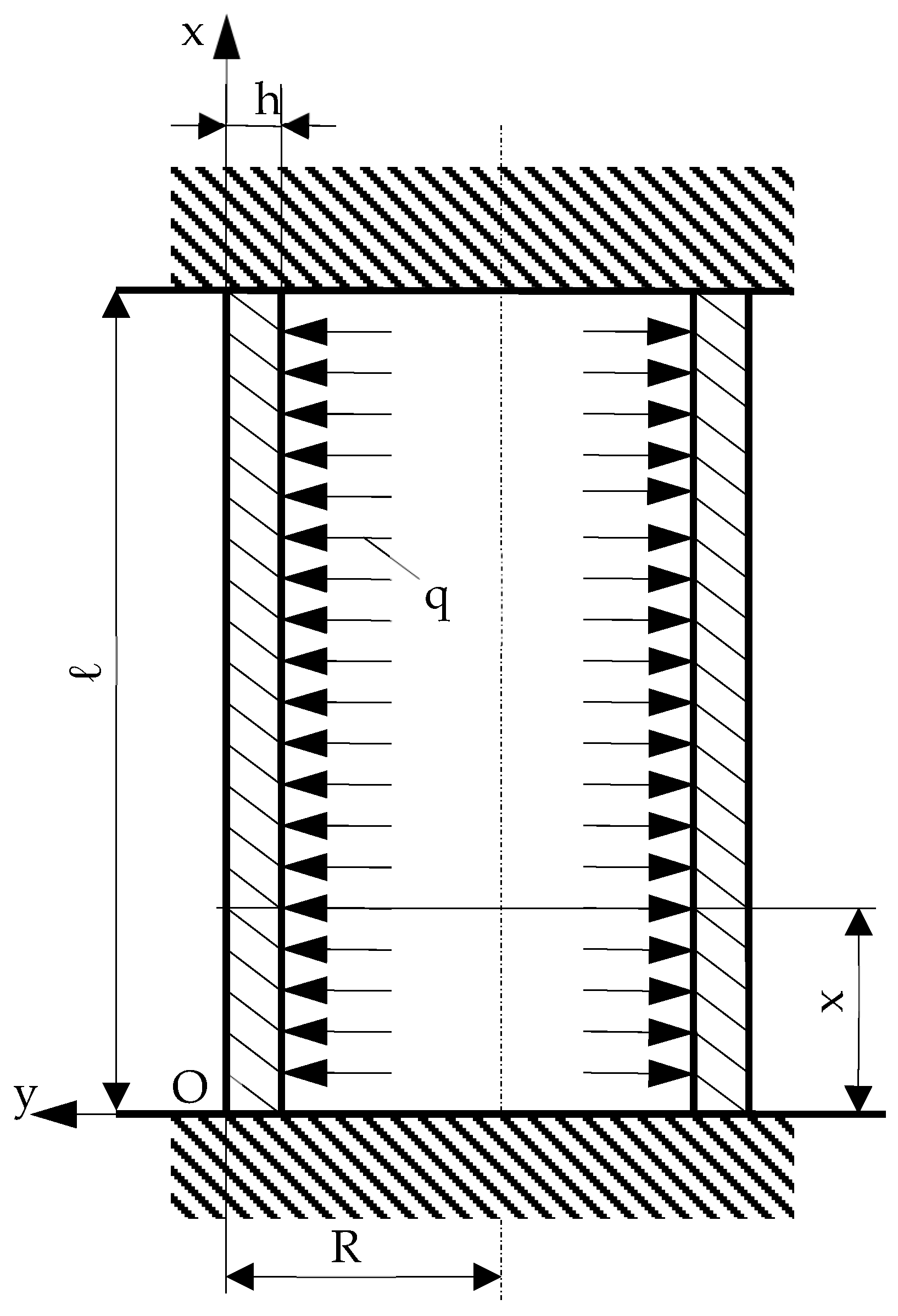
3.1. Long Thin Cylindrical Wall Tube Charged with an Interior Axisymmetric Uniform Distributed Load and Embedded at Both Ends (Figure 4b)
3.2. Long Thin Cylindrical Wall Tube Charged with an Exterior and Interior Axisymmetric Uniform Distributed Load (Figure 4c)
- The calculus of this cylinder under the successive action of the external efforts with the superimposing effects for the successive action of the external efforts on a cylinder;
- The calculus of this cylinder under the simultaneous action of the external efforts.
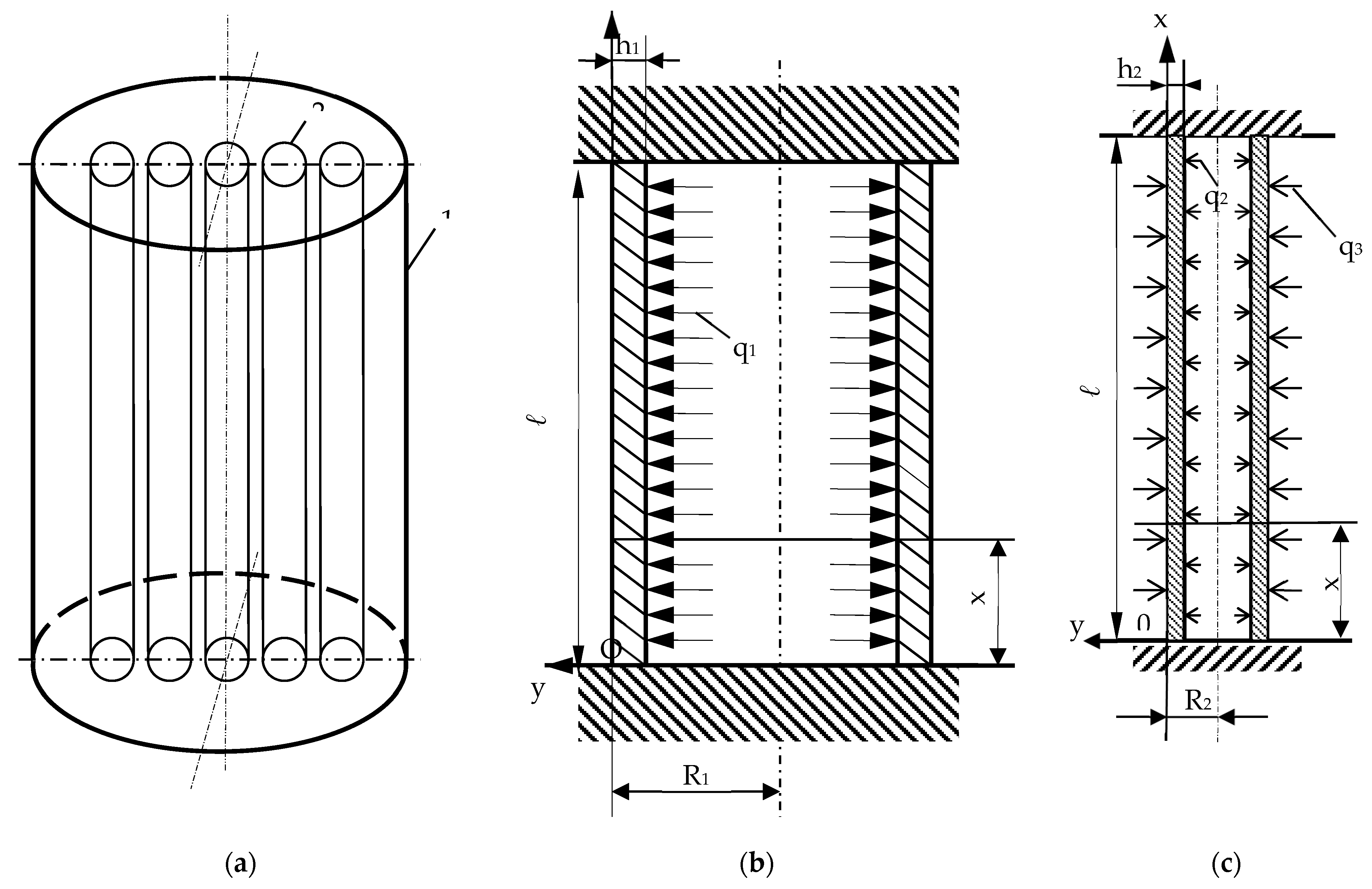
3.2.1. Calculus of Cylinder under Successive Action of External Efforts
Interior Load q2
Exterior Load q3
The Method of the Superimposing Effects for Successive Action of External Efforts on a Cylinder
3.2.2. Calculus of Cylinder under Simultaneous Action of External Efforts
4. Discussion
- –
- The first approach consisted of the successive action of the two loads and the application of the method of overlapping the effects to yield the final results.
- –
- The second approach consisted of the simultaneous action of the two external efforts. Both approaches led to the same results.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gery, P.-M.; Calgaro, J.-A. Les Matrices-Transfert dans le Calcul des Structures; Éditions Eyrolles: Paris, France, 1973. [Google Scholar]
- Suciu, M.; Tripa, M.-S. Strength of Materials; UT Press: Cluj-Napoca, Romania, 2021. [Google Scholar]
- Benamira, A.; Pattanaik, S. Application of the Transfer Matrix Method to Anti-reflective Coating Rendering. In Computer Graphics International Conference; Springer: Berlin/Heidelberg, Germany, 2020; pp. 83–95. [Google Scholar]
- Arsenault, H.H.; Macukow, B.M. Factorization of the transfer matrix for symmetrical optical systems. J. Opt. Soc. Am. 1983, 73, 1350–1359. [Google Scholar] [CrossRef]
- Chen, Y.Z. Study of multiply-layered cylinders made of functionally graded materials using the Transfer-Matrix Method. J. Mech. Mater. Struct. 2011, 6, 641–657. [Google Scholar] [CrossRef]
- Chen, Y.Z. Transfer-Matrix Method for solution of FGMs thick-walled cylinder with arbitrary inhomogeneous response. In Smart Structures and Systems; Techno-Press: Plovdiv, Bulgaria, 2018; Volume 21, pp. 469–477. [Google Scholar]
- Chevillotte, F.; Panneton, R. Coupling transfer matrix method to finite element method for analyzing the acoustics of complex hollow body networks. Appl. Acoust. 2011, 72, 962–968. [Google Scholar] [CrossRef]
- Crețu, N.; Pop, M.I.; Boer, A. Quaternion Formalism for the Intrinsic Transfer Matrix. Phys. Procedia 2015, 70, 262–265. [Google Scholar] [CrossRef]
- Cretu, N.; Pop, M.-I.; Prado, H.S.A. Some Theoretical and Experimental Extensions Based on the Properties of the Intrinsic Transfer Matrix. Materials 2022, 15, 519. [Google Scholar] [CrossRef]
- Dryburgh, P.; Li, W.; Pieris, D.; Fuentes-Domínguez, R.; Patel, R.; Smith, R.J.; Clark, M. Measurement of the single crystal elasticity matrix of polycrystalline materials. Acta Mater. 2021, 225, 117551. [Google Scholar] [CrossRef]
- Eghlidi, M.H.; Mehrany, K.; Rashidian, B. Modified differential transfer matrix method for solution of one dimensional linear inhomogeneous optical structures. J. Opt. Soc. Am. 2005, 22, 1521–1528. [Google Scholar] [CrossRef]
- Eghlidi, M.H.; Mehrany, K.; Rashidian, B. Improved differential transfer matrix method for inhomogeneous one-dimensional photonic crystals. J. Opt. Soc. Am. 2006, 23, 1451–1459. [Google Scholar] [CrossRef]
- Eghlidi, M.H.; Mehrany, K.; Rashidian, B. General solution of linear differential equations by using differential transfer matrix method. In Proceedings of the 2005 European Conference on Circuit Theory and Design, Cork, Ireland, 2 September 2005. [Google Scholar]
- Guo, R.; Tang, W.-B. Transfer matrix methods for sound attenuation in resonators with perforated intruding inlets. Appl. Acoust. 2017, 116, 14–23. [Google Scholar] [CrossRef]
- Kamal, A.; Giurgiutiu, V. Stiffness Transfer Matrix Method (STMM) for Stable Dispersion Curves Solution in Anisotropic Composites. In Health Monitoring of Structural and Biological System; Tribikram, K., Ed.; SPIE: Bellingham, WC, USA, 2014; Volume 9064, p. 906410. [Google Scholar] [CrossRef]
- Khorasani, S.; Adibi, A. Analytical Solution of Linear Ordinary Differential Equations by Differential Transfer Matrix Method. Electron. J. Differ. Equ. 2003, 2003, 1–18. [Google Scholar]
- Khorasani, S.; Mehrany, K. Differential transfer matrix method for solution of one-dimensional linear non-homogeneous optical structures. J. Opt. Soc. Am. 2003, 20, 91–96. [Google Scholar] [CrossRef]
- Knopoff, L.A. Matrix method for elastic wave problems. Bull. Seismol. Soc. Am. 1964, 54, 431–438. [Google Scholar] [CrossRef]
- Laly, Z.; Panneton, R.; Atalla, N. Characterization and development of periodic acoustic metamaterials using a transfer matrix approach. Appl. Acoust. 2022, 185, 108381. [Google Scholar] [CrossRef]
- Lee, C.-M.; Xu, Y. A modified transfer matrix method for prediction of transmission loss of multilayer acoustic materials. J. Sound Vib. 2009, 326, 290–301. [Google Scholar] [CrossRef]
- Lee, M.; Bolton, J.S.; Suh, S. Estimation of the combustion-related noise transfer matrix of a multi-cylinder diesel engine. Mech. Syst. Signal Process. 2020, 136, 106514. [Google Scholar] [CrossRef]
- Liu, X.; Brenner, K.-H. Minimal optical decomposition of ray transfer matrices. Appl. Opt. 2008, 47, E88–E98. [Google Scholar] [CrossRef] [PubMed]
- Lowe, M. Matrix techniques for modeling ultrasonic waves in multilayered media. Ultrason. Ferroelectr. Freq. Control. IEEE Trans. 1995, 42, 525–542. [Google Scholar] [CrossRef]
- Jiani, M.; Khorasani, S.; Rashidian, B.; Mohammadi, S. Formulation of differential transfer matrix method in cylindrical geometry. Proc. SPIE-Int. Soc. Opt. Eng. 2010, 7597, 75971V-2. [Google Scholar] [CrossRef]
- Nicolae, C.; Gelu, N. A simplified modal analysis based on the properties of the transfer matrix. Mech. Mater. 2013, 60, 121–128. [Google Scholar] [CrossRef]
- Parinelleo, A.; Kesour, K.; Ghiringhelli, G.L.; Atalla, N. Diffuse field transmission through multilayered cylinders using a Transfer Matrix Method. Mech. Syst. Signal Process. 2020, 136, 106514. [Google Scholar] [CrossRef]
- Randrianandrasana, J.; Callet, P.; Lucas, L. Transfer matrix based layered materials rendering. ACM Trans. Graph. 2021, 40, 177. [Google Scholar] [CrossRef]
- Sánchez-Soto, L.L.; Monzón, J.J.; Barriuso, A.G.; Cariñena, J.F. The transfer matrix: A geometrical perspective. Phys. Rep. 2012, 513, 191–227. [Google Scholar] [CrossRef]
- Shahsavari, H.; Talebitooti, R.; Kornokar, M. Analysis of wave propagation through functionally graded porous cylindrical structures considering the transfer matrix method. Thin-Walled Struct. 2021, 159, 107212. [Google Scholar] [CrossRef]
- Slettemoen, G.A. Derivation of phase differences of nonsymmetrical interferometers using partitioned transfer matrices. J. Opt. Soc. Am. 1983, 73, 950–958. [Google Scholar] [CrossRef]
- Slovick, B.; Flom, Z.H.; Lucas Zipp, L.; Krishnamurthy, S. Transfer matrix method for four-flux radiative transfer. Appl. Opt. 2017, 56, 5890–5896. [Google Scholar] [CrossRef] [PubMed]
- Song, B.H.; Bolton, J.S. A transfer-matrix approach for estimating the characteristic impedance and wave numbers of limp and rigid porous materials. J. Acoust. Soc. Am. 2000, 107, 1131–1152. [Google Scholar] [CrossRef] [PubMed]
- Suciu, M.; Balc, G.; Paunescu, D.; Bejan, M. Calculus of long cylindrical thin wall tube by the Transfer-Matrix Method. Metal. Int. 2009, 14, 21–28. [Google Scholar]
- Suciu, M. An Approach Using the Transfer-Matrix Method (TMM) for Mandible Body Bone Calculus. Mathematics 2023, 11, 450. [Google Scholar] [CrossRef]
- Verdière, K.; Panneton, R.; Elkoun, S.; Dupont, T.; LeClaire, P. Transfer matrix method applied to the parallel assembly of sound absorbing materials. J. Acoust. Soc. Am. 2013, 134, 4648–4658. [Google Scholar] [CrossRef]
- Vijayasree, N.; Munjal, M. On an Integrated Transfer Matrix method for multiply connected mufflers. J. Sound Vib. 2012, 331, 1926–1938. [Google Scholar] [CrossRef]
- Zariean, N.; Sarrafi, P.; Mehrany, K.; Rashidian, B. Differential-Transfer-Matrix Based on Airy’s Functions in Analysis of Planar Optical Structures With Arbitrary Index Profiles. IEEE J. Quantum Electron. 2008, 44, 324–330. [Google Scholar] [CrossRef]
- Warren, C.Y. ROARK’’S Formulas for Stress & Strain, 6th ed.; McGrawHill Book Company: New York, NY, USA, 1989. [Google Scholar]
- Hernandez-Acosta, M.A.; Martines-Arano, H.; Soto-Ruvalcaba, L.; Martinez-Gonzallez, C.L.; Martinez-Gotierrez, H.; Torres-Torres, C. Fractional thermal transport and twisted light induced by an optical two-wave mixing in single-wall carbon nanotubes. Int. J. Therm. Sci. 2020, 147, 106136. [Google Scholar] [CrossRef]
- Chabassier, J.; Tournemenne, R. About the Transfer Matrix Method in the Context of Acoustical Wave Propagation in Wind Instruments. [Research Report] RR-9254, INRIA Bordeaux, 2019, ffhal-02019515. Available online: https://inria.hal.science/hal-02019515 (accessed on 18 August 2023).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Codrea, L.; Tripa, M.-S.; Opruţa, D.; Gyorbiro, R.; Suciu, M. Transfer-Matrix Method for Calculus of Long Cylinder Tube with Industrial Applications. Mathematics 2023, 11, 3756. https://doi.org/10.3390/math11173756
Codrea L, Tripa M-S, Opruţa D, Gyorbiro R, Suciu M. Transfer-Matrix Method for Calculus of Long Cylinder Tube with Industrial Applications. Mathematics. 2023; 11(17):3756. https://doi.org/10.3390/math11173756
Chicago/Turabian StyleCodrea, Luminita, Mihai-Sorin Tripa, Daniel Opruţa, Robert Gyorbiro, and Mihaela Suciu. 2023. "Transfer-Matrix Method for Calculus of Long Cylinder Tube with Industrial Applications" Mathematics 11, no. 17: 3756. https://doi.org/10.3390/math11173756



