Dynamics of Persistent Epidemic and Optimal Control of Vaccination
Abstract
:1. Introduction
2. An Epidemic Delay Model with Vaccination
3. Epidemic Dynamics without Vaccination
3.1. Integral Equation and Stationary Solutions
3.2. Stability of the Stationary Solution
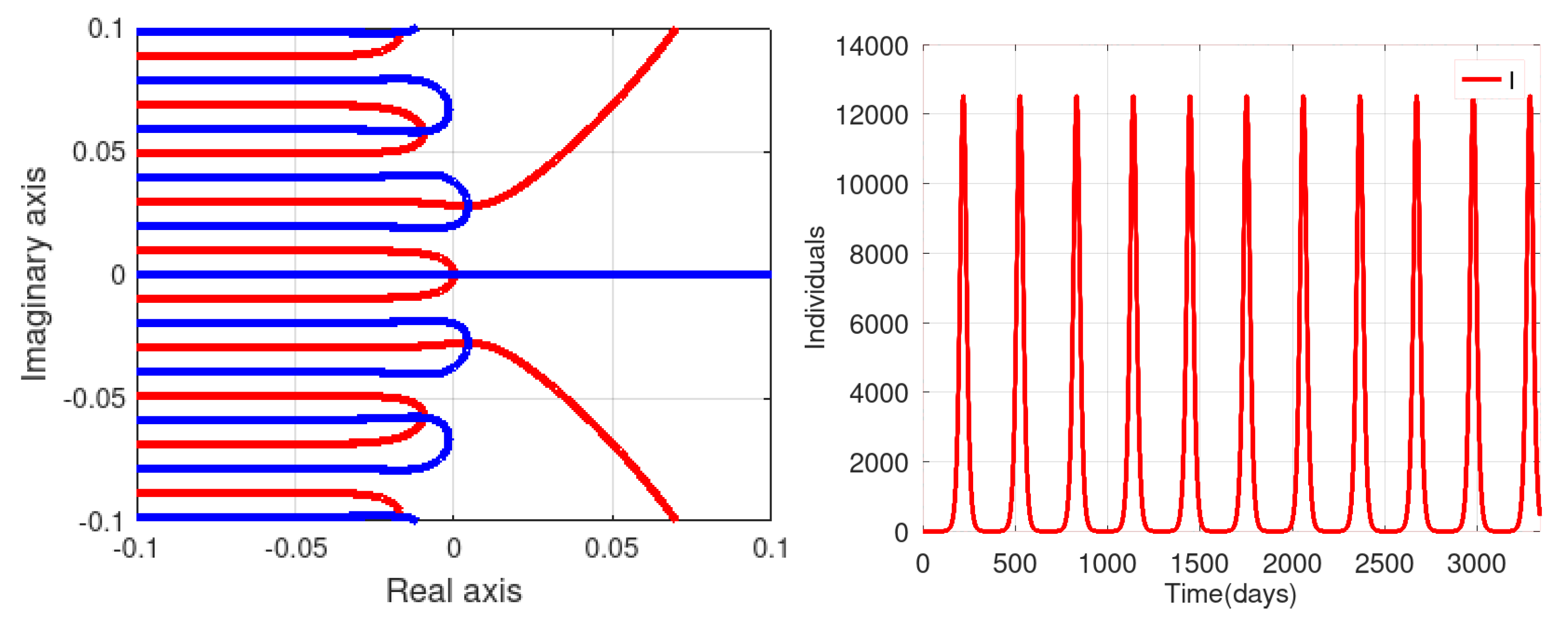
3.3. Numerical Simulations
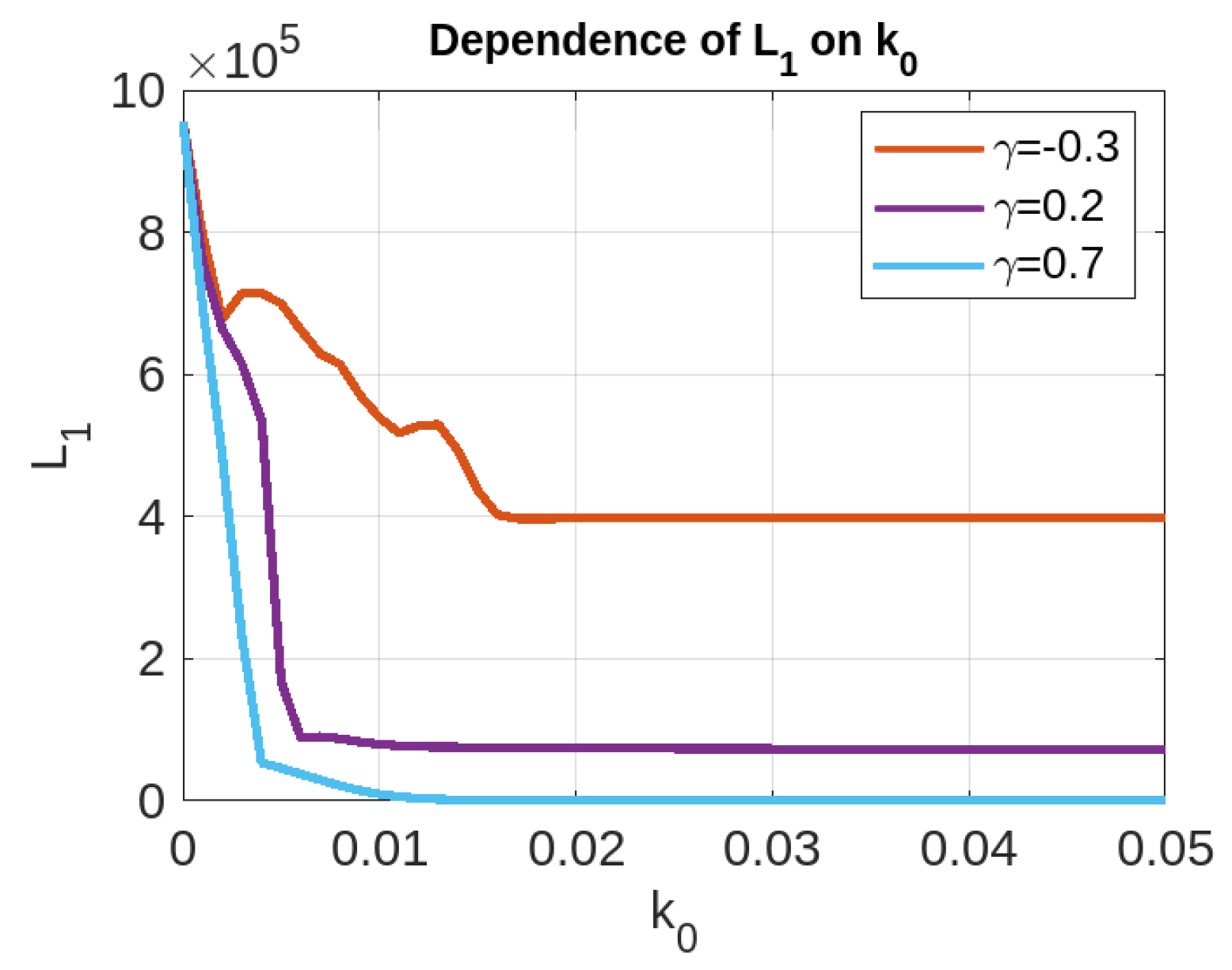
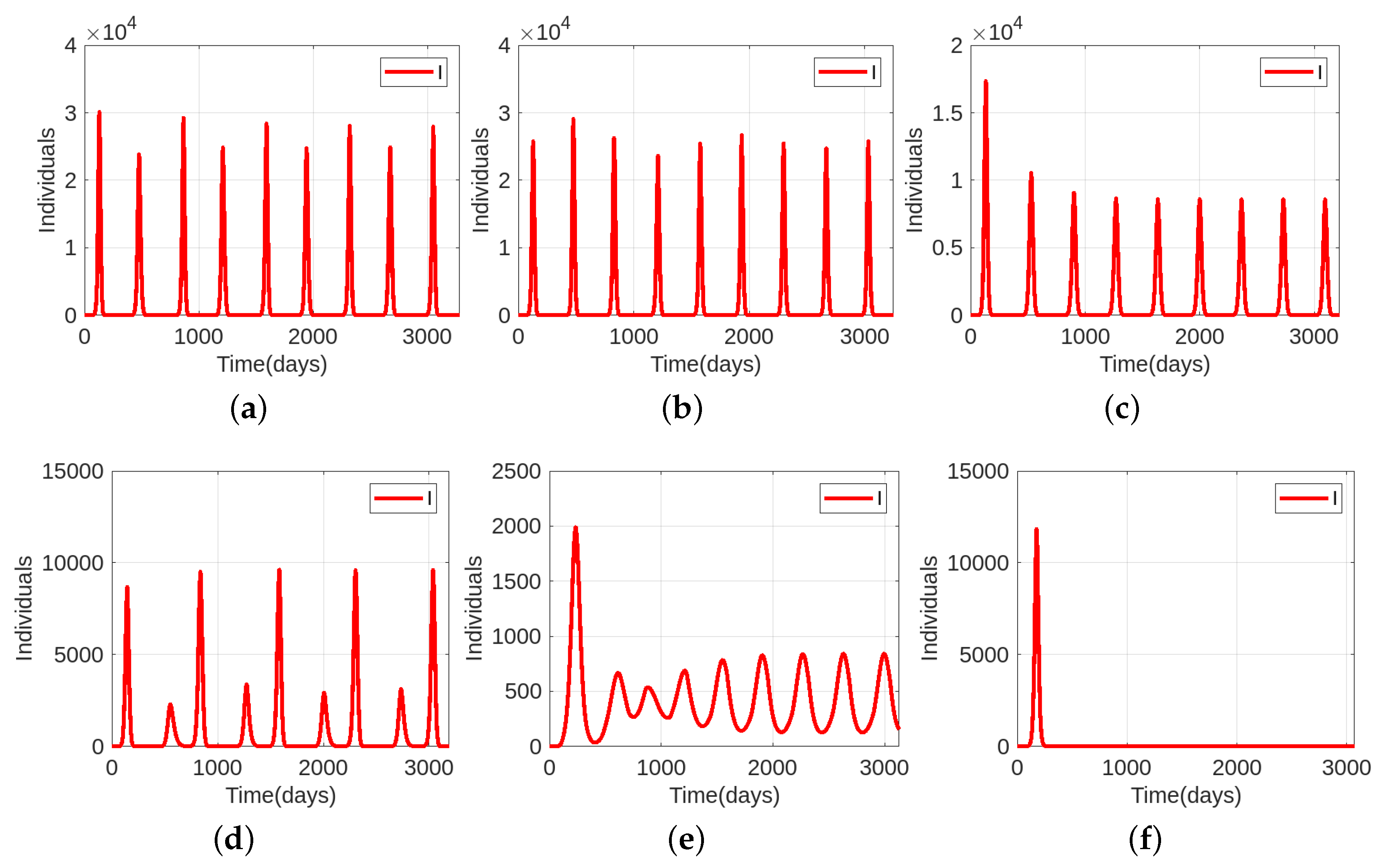
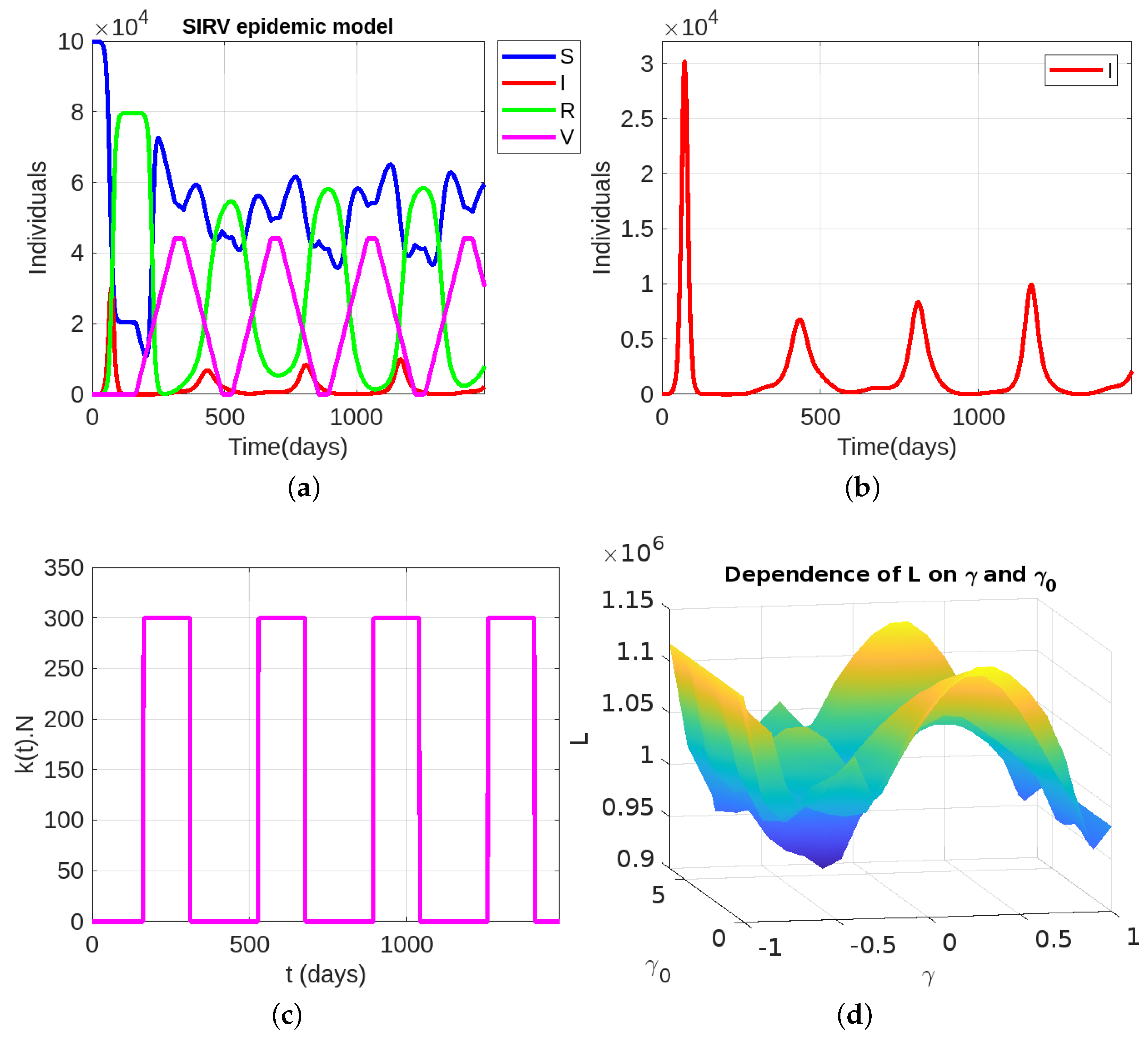
4. Epidemic Dynamics with Vaccination
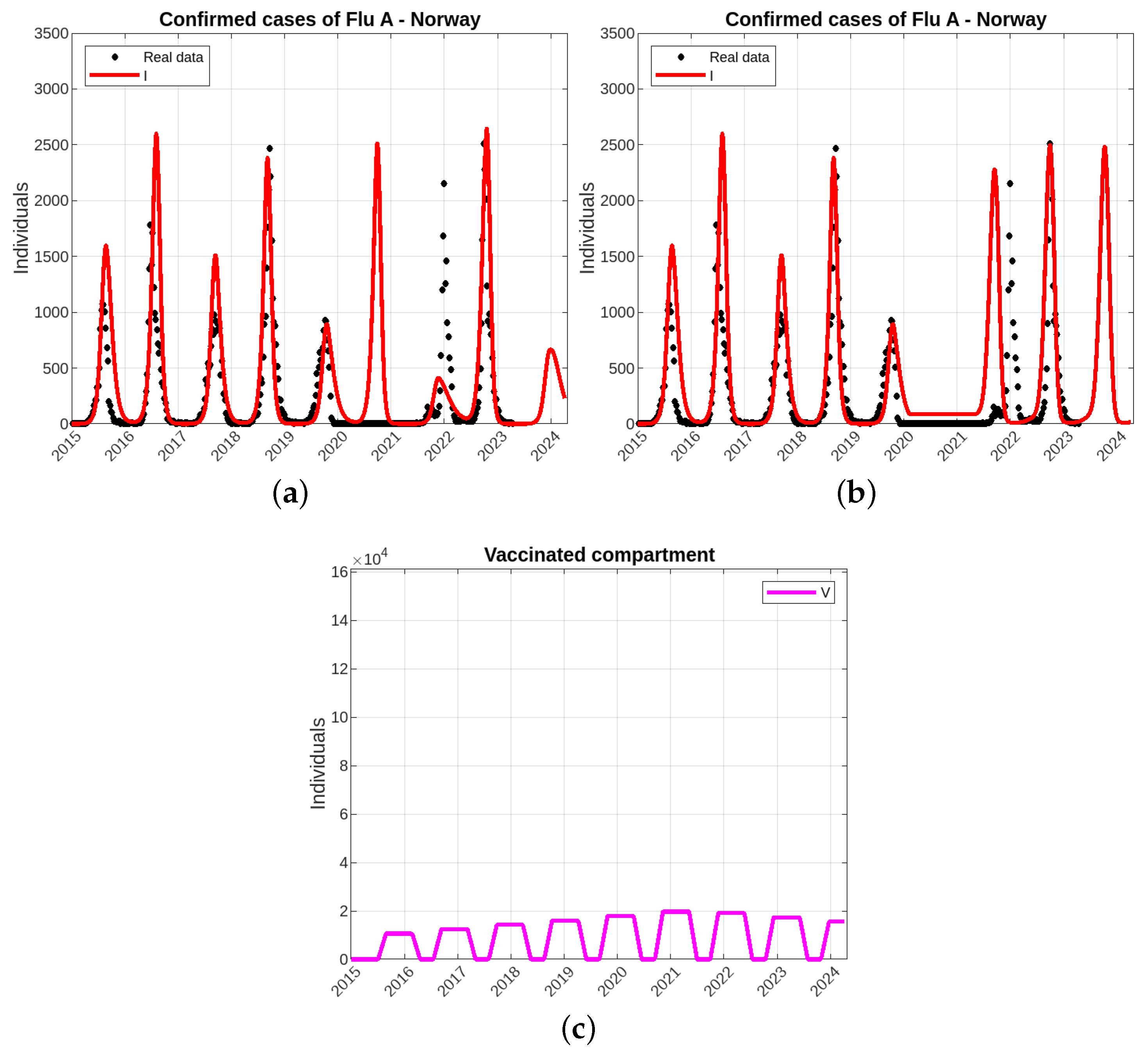
Modeling of Influenza A Epidemics
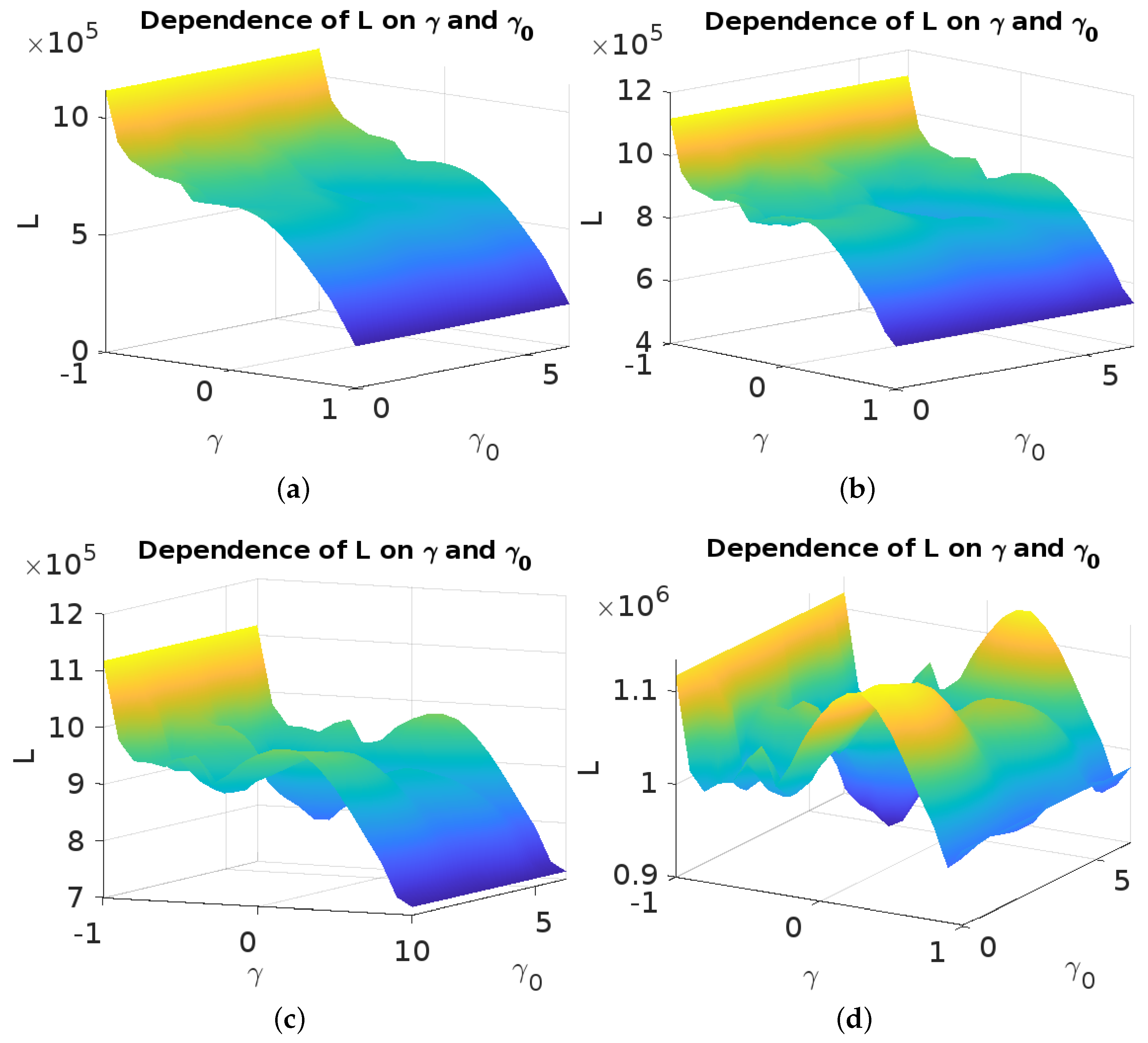
5. Optimal Control Problem
6. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fisher-Hoch, S.; Hutwagner, L. Opportunistic candidiasis: An epidemic of the 1980s. Clin. Infect. Dis. 1995, 21, 897–904. [Google Scholar] [CrossRef] [PubMed]
- Chintu, C.; Athale, U.H.; Patil, P. Childhood cancers in Zambia before and after the HIV epidemic. Arch. Dis. Child. 1995, 73, 100–105. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.M.; Fraser, C.; Ghani, A.C.; Donnelly, C.A.; Riley, S.; Ferguson, N.M.; Leung, G.M.; Lam, T.H.; Hedley, A.J. Epidemiology, transmission dynamics and control of SARS: The 2002–2003 epidemic. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2004, 359, 1091–1105. [Google Scholar] [CrossRef] [PubMed]
- Lam, W.; Zhong, N.; Tan, W. Overview on SARS in Asia and the world. Respirology 2003, 8, S2–S5. [Google Scholar] [CrossRef]
- Chen, S.H.; Mallamace, F.; Mou, C.Y.; Broccio, M.; Corsaro, C.; Faraone, A.; Liu, L. The violation of the Stokes–Einstein relation in supercooled water. Proc. Natl. Acad. Sci. USA 2006, 103, 12974–12978. [Google Scholar] [CrossRef] [PubMed]
- Kilpatrick, A.M.; Chmura, A.A.; Gibbons, D.W.; Fleischer, R.C.; Marra, P.P.; Daszak, P. Predicting the global spread of H5N1 avian influenza. Proc. Natl. Acad. Sci. USA 2006, 103, 19368–19373. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.; Kamimoto, L.; Bramley, A.M.; Schmitz, A.M.; Benoit, S.R.; Louie, J.; Sugerman, D.E.; Druckenmiller, J.K.; Ritger, K.A.; Chugh, R.; et al. Hospitalized patients with 2009 H1N1 influenza in the United States, April–June 2009. N. Engl. J. Med. 2009, 361, 1935–1944. [Google Scholar] [CrossRef]
- Girard, M.P.; Tam, J.S.; Assossou, O.M.; Kieny, M.P. The 2009 A (H1N1) influenza virus pandemic: A review. Vaccine 2010, 28, 4895–4902. [Google Scholar] [CrossRef]
- Briand, S.; Bertherat, E.; Cox, P.; Formenty, P.; Kieny, M.P.; Myhre, J.K.; Roth, C.; Shindo, N.; Dye, C. The international Ebola emergency. N. Engl. J. Med. 2014, 371, 1180–1183. [Google Scholar] [CrossRef]
- Kreuels, B.; Wichmann, D.; Emmerich, P.; Schmidt-Chanasit, J.; de Heer, G.; Kluge, S.; Sow, A.; Renné, T.; Günther, S.; Lohse, A.W.; et al. A case of severe Ebola virus infection complicated by gram-negative septicemia. N. Engl. J. Med. 2014, 371, 2394–2401. [Google Scholar] [CrossRef]
- Kapralov, M.; Khanna, S.; Sudan, M. Approximating matching size from random streams. In Proceedings of the Twenty-Fifth Annual ACM-SIAM Symposium on Discrete Algorithms, SIAM, Portland, OR, USA, 5–7 January 2014; pp. 734–751. [Google Scholar]
- Almeida, R.; Qureshi, S. A fractional measles model having monotonic real statistical data for constant transmission rate of the disease. Fractal Fract. 2019, 3, 53. [Google Scholar] [CrossRef]
- Sharma, S.; Volpert, V.; Banerjee, M. Extended SEIQR type model for COVID-19 epidemic and data analysis. MedRxiv 2020. [Google Scholar] [CrossRef]
- Brauer, F.; Van den Driessche, P.; Wu, J.; Allen, L.J. Mathematical Epidemiology; Springer: Berlin/Heidelberg, Germany, 2008; Volume 1945. [Google Scholar]
- d’Onofrio, A.; Banerjee, M.; Manfredi, P. Spatial behavioural responses to the spread of an infectious disease can suppress Turing and Turing–Hopf patterning of the disease. Phys. A Stat. Mech. Its Appl. 2020, 545, 123773. [Google Scholar] [CrossRef]
- Sun, G.Q.; Jin, Z.; Liu, Q.X.; Li, L. Chaos induced by breakup of waves in a spatial epidemic model with nonlinear incidence rate. J. Stat. Mech. Theory Exp. 2008, 2008, P08011. [Google Scholar] [CrossRef]
- Bichara, D.; Iggidr, A. Multi-patch and multi-group epidemic models: A new framework. J. Math. Biol. 2018, 77, 107–134. [Google Scholar] [CrossRef]
- McCormack, R.K.; Allen, L.J. Multi-patch deterministic and stochastic models for wildlife diseases. J. Biol. Dyn. 2007, 1, 63–85. [Google Scholar] [CrossRef]
- Elbasha, E.H.; Gumel, A.B. Vaccination and herd immunity thresholds in heterogeneous populations. J. Math. Biol. 2021, 83, 73. [Google Scholar] [CrossRef]
- Aniţa, S.; Banerjee, M.; Ghosh, S.; Volpert, V. Vaccination in a two-group epidemic model. Appl. Math. Lett. 2021, 119, 107197. [Google Scholar] [CrossRef]
- Faniran, T.S.; Ali, A.; Al-Hazmi, N.E.; Asamoah, J.K.K.; Nofal, T.A.; Adewole, M.O. New variant of SARS-CoV-2 dynamics with imperfect vaccine. Complexity 2022, 2022, 1062180. [Google Scholar] [CrossRef]
- Ahmed, N.; Wei, Z.; Baleanu, D.; Rafiq, M.; Rehman, M. Spatio-temporal numerical modeling of reaction-diffusion measles epidemic system. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 103101. [Google Scholar] [CrossRef]
- Filipe, J.; Maule, M. Effects of dispersal mechanisms on spatio-temporal development of epidemics. J. Theor. Biol. 2004, 226, 125–141. [Google Scholar] [CrossRef]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Springer: Berlin/Heidelberg, Germany, 2015; Volume 61. [Google Scholar]
- Brauer, F.; Castillo-Chavez, C.; Feng, Z. Mathematical Models in Epidemiology; Springer: Berlin/Heidelberg, Germany, 2019; Volume 32. [Google Scholar]
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Hurd, H.S.; Kaneene, J.B. The application of simulation models and systems analysis in epidemiology: A review. Prev. Vet. Med. 1993, 15, 81–99. [Google Scholar] [CrossRef]
- Volpert, V.; Banerjee, M.; Petrovskii, S. On a quarantine model of coronavirus infection and data analysis. Math. Model. Nat. Phenom. 2020, 15, 24. [Google Scholar] [CrossRef]
- Ghosh, S.; Volpert, V.; Banerjee, M. An epidemic model with time delay determined by the disease duration. Mathematics 2022, 10, 2561. [Google Scholar] [CrossRef]
- Saade, M.; Ghosh, S.; Banerjee, M.; Volpert, V. An epidemic model with time delays determined by the infectivity and disease durations. Math. Biosci. Eng. 2023, 20, 12864–12888. [Google Scholar] [CrossRef]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Schättler, H.; Ledzewicz, U. Optimal control for mathematical models of cancer therapies. In An Application of Geometric Methods; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Bolzoni, L.; Bonacini, E.; Soresina, C.; Groppi, M. Time-optimal control strategies in SIR epidemic models. Math. Biosci. 2017, 292, 86–96. [Google Scholar] [CrossRef]
- Aniţa, S.; Capasso, V.; Scacchi, S. Controlling the spatial spread of a Xylella epidemic. Bull. Math. Biol. 2021, 83, 1–26. [Google Scholar] [CrossRef]
- Aniţa, S.; Capasso, V.; Moşneagu, A.M. Regional control in optimal harvesting of population dynamics. Nonlinear Anal. Theory Methods Appl. 2016, 147, 191–212. [Google Scholar] [CrossRef]
- Aniţa, S.; Capasso, V.; Kunze, H.; La Torre, D. Dynamics and optimal control in a spatially structured economic growth model with pollution diffusion and environmental taxation. Appl. Math. Lett. 2015, 42, 36–40. [Google Scholar] [CrossRef]
- Aniţa, S.; Capasso, V.; Dimitriu, G. Regional control for a spatially structured malaria model. Math. Methods Appl. Sci. 2019, 42, 2909–2933. [Google Scholar] [CrossRef]
- Aniţa, S.; Capasso, V. Reaction-diffusion systems in epidemiology. Ann. Alexandru Ioan Cuza Iaşi Math. 2017, 66, 171–196. [Google Scholar]
- Jang, J.; Kwon, H.D.; Lee, J. Optimal control problem of an SIR reaction–diffusion model with inequality constraints. Math. Comput. Simul. 2020, 171, 136–151. [Google Scholar] [CrossRef]
- Madubueze, C.E.; Dachollom, S.; Onwubuya, I.O. Controlling the spread of COVID-19: Optimal control analysis. Comput. Math. Methods Med. 2020, 2020, 6862516. [Google Scholar] [CrossRef] [PubMed]
- Abbasi, Z.; Zamani, I.; Mehra, A.H.A.; Shafieirad, M.; Ibeas, A. Optimal control design of impulsive SQEIAR epidemic models with application to COVID-19. Chaos Solitons Fractals 2020, 139, 110054. [Google Scholar] [CrossRef]
- Clinical Signs and Symptoms of Influenza. 2022. Available online: https://www.cdc.gov/flu/ (accessed on 28 August 2023).
- Duda, K. How Long Does a Flu Shot Last? 2023. Available online: https://www.verywellhealth.com/ (accessed on 28 August 2023).
- Hungnes, O.; Paulsen, T.H.; Rohringer, A.; Seppälä, E.M.; Tønnessen, R.; Bøås, H.; Dahl, J.; Fossum, E.; Stålcrantz, J.; Klüwer, B.; et al. Interim Influenza Virological and Epidemiological Season Report Prepared for the WHO Consultation on the Composition of Influenza Virus Vaccines for the Northern Hemisphere 2023/2024. 2023. Available online: https://hdl.handle.net/11250/3055881 (accessed on 28 August 2023).
- Dattani, S.; Spooner, F.; Mathieu, E.; Ritchie, H.; Roser, M.; Influenza. Our World in Data 2023. Available online: https://ourworldindata.org/influenza (accessed on 28 August 2023).
- World Health Organization. Respiratory Viruses Surveillance Country, Territory and Area Profiles, 2021; Technical Report; World Health Organization, Regional Office for Europe and European Centre: Geneva, Switzerland, 2022. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saade, M.; Aniţa, S.; Volpert, V. Dynamics of Persistent Epidemic and Optimal Control of Vaccination. Mathematics 2023, 11, 3770. https://doi.org/10.3390/math11173770
Saade M, Aniţa S, Volpert V. Dynamics of Persistent Epidemic and Optimal Control of Vaccination. Mathematics. 2023; 11(17):3770. https://doi.org/10.3390/math11173770
Chicago/Turabian StyleSaade, Masoud, Sebastian Aniţa, and Vitaly Volpert. 2023. "Dynamics of Persistent Epidemic and Optimal Control of Vaccination" Mathematics 11, no. 17: 3770. https://doi.org/10.3390/math11173770
APA StyleSaade, M., Aniţa, S., & Volpert, V. (2023). Dynamics of Persistent Epidemic and Optimal Control of Vaccination. Mathematics, 11(17), 3770. https://doi.org/10.3390/math11173770





