Analytical Solution of Stability Problem of Nanocomposite Cylindrical Shells under Combined Loadings in Thermal Environments
Abstract
:1. Introduction
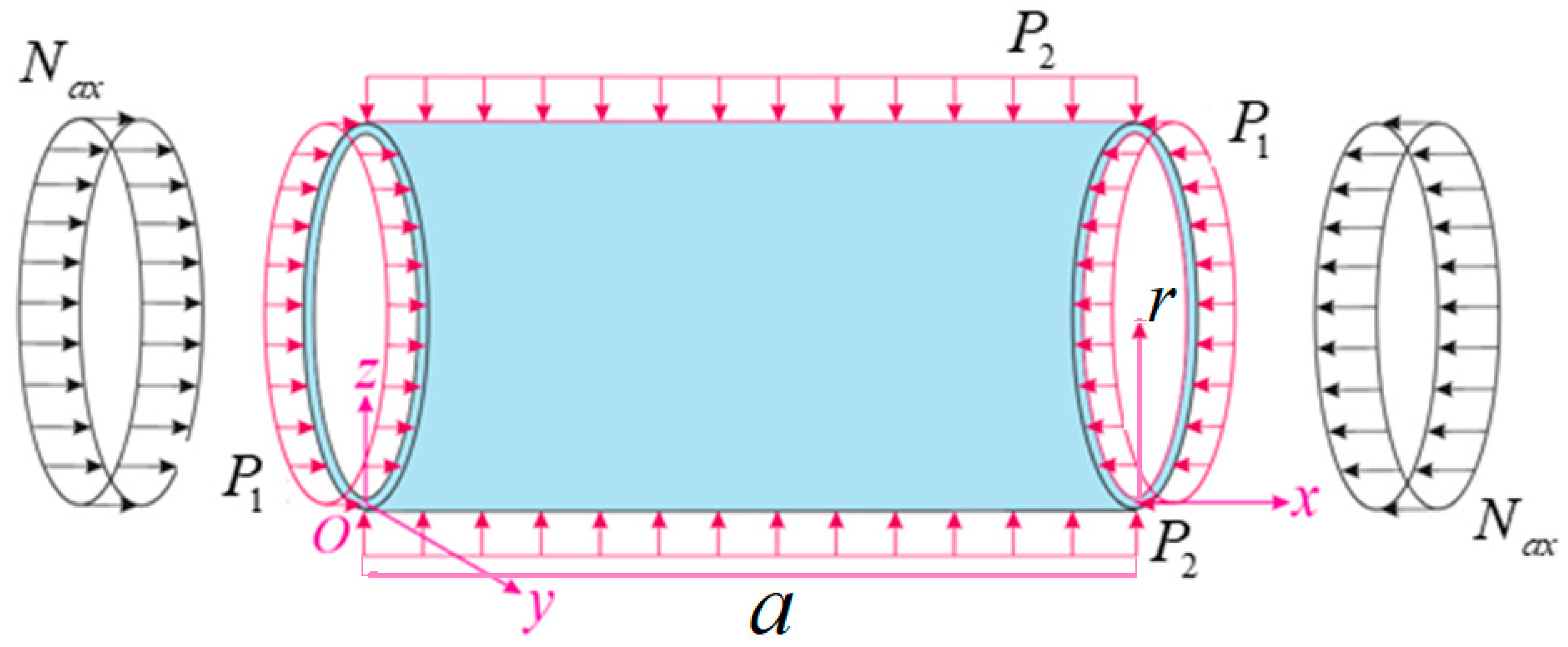
2. Mathematical Modeling of the Problem
2.1. Basic Relationships
2.2. Basic Equations
3. Solution Procedure
4. Results and Discussion
4.1. Initial Data
4.2. Comparative Examples
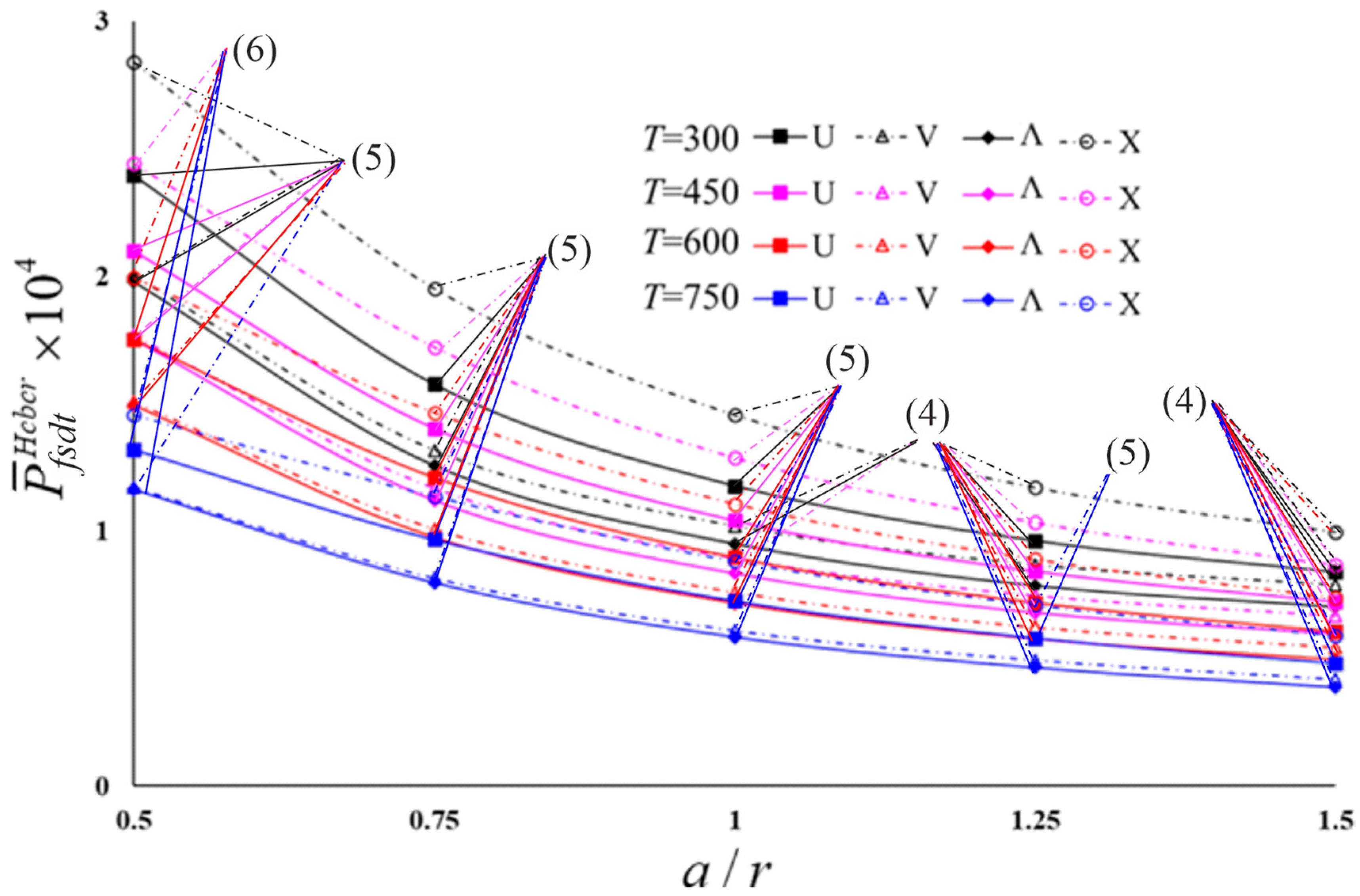
4.3. Parametric Analyses
5. Conclusions
- (a)
- The most significant SDs effect on the critical combined load occurs in the X-model, and the least effect occurs in the Λ- and V-models.
- (b)
- The effect of temperature change on the critical combined load is more pronounced in the FSDT frame compared to the KLT.
- (c)
- While the increase in temperature change increases the effect of inhomogeneity on the critical combined load values in all models, considering the transverse shear strains significantly reduces the effects of the models.
- (d)
- The influence of transverse SDs on the changes irregularly for all models as the nondimensional load-proportional parameter rises.
- (e)
- The magnitudes of the nondimensional critical combined load and the corresponding circumferential wave numbers of four types of CNT-patterned cylindrical shells in thermal environments within two theories reduce as the nondimensional load-proportional parameter rises.
- (f)
- A consideration of the transverse SDs significantly rises the effect of temperature on the critical combined load.
- (g)
- In some cases, the difference of the influence of temperature on the critical combined load within the framework of FSDT and KLT is up to 13%.
- (h)
- Increasing the ratio significantly reduces the values of nondimensional critical combined loads, whereas corresponding wave numbers decrease slightly.
- (i)
- At the small , the influence of transverse SDs on the is quite large and is more likely to damage the structure.
- (j)
- The increase in the significantly reduces the influence of transverse shear strains on the critical combined load at the fixed value of the .
- (k)
- Although the effects of SDs on the for different models decrease when the rises, the model types maintain their sensitivity.
- (l)
- Increasing the temperature significantly rises the SDs effect, as well as decreasing the rate of reduction in the SDs effect, which decreases with the increase in .
- (m)
- The influence of the temperature is quite significant when the ratio is small, the effect within FSDT is quite prominent compared to KLT, and the difference reduces as the ratio increases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols | |
| Length of cylindrical shell | |
| Efficiency parameters for CNTs | |
| Strain components at the mid-surface | |
| Shear stress shape function | |
| Parameters including shear moduli and shear shape function | |
| Parameters depending on nanocomposite shell characteristics | |
| Unknown amplitudes | |
| Differential operators | |
| Longitudinal wave number | |
| Mass of the CNT | |
| , | Moments and thermal moments, respectively |
| Circumferential wave number | |
| Circumferential wave numbers corresponding to critical loads | |
| , | Forces and thermal forces, respectively |
| Membrane forces for the condition with zero initial moments | |
| Axial compressive load | |
| Nondimensional critical axial load within FSDT | |
| Nondimensional axial compressive load | |
| Critical combined load | |
| Nondimensional lateral and hydrostatic pressures, respectively | |
| Uniform external pressures | |
| , | Lateral and hydrostatic pressures, respectively |
| Nondimensional critical lateral pressure within FSDT and KLT | |
| Nondimensional critical hydrostatic pressure within FSDT and KLT | |
| Nondimensional combined loads within FSDT and KLT | |
| Shear forces | |
| Radius of the cylindrical shell | |
| Thickness of the cylindrical shell | |
| Temperature | |
| Reference temperature in which thermal strains are absent | |
| Temperature rise | |
| Displacements in the , directions, respectively | |
| Patterns or CNT distribution in the matrix | |
| Total volume fraction | |
| , | Volume fraction of CNTs and polymer matrix, respectively |
| Normal and shear elastic moduli of nanocomposites | |
| Normal and shear elastic moduli of CNT | |
| Parameter containing elastic properties | |
| Normal and shear elastic moduli of polymer matrix | |
| , | Coordinate axes |
| Thermal expansion coefficients of CNTs | |
| Thermal expansion coefficients of the polymer | |
| Nondimensional load-proportional parameter | |
| Coefficients that depend on the shear stress shape function | |
| , | Strain components |
| Cofactors | |
| Parameters depending on wave numbers and shell properties | |
| Poisson’s ratios of nanocomposites | |
| , | Poisson’s ratios of CNTs and polymer, respectively |
| Density of the nanocomposite | |
| , | Densities of CNT and matrix, respectively |
| Stress components | |
| Average axial compressive load | |
| Parameter including properties of nanocomposite cylindrical shell | |
| Airy stress function | |
| , | Rotations of mid-surface normal about and axes, respectively |
| Abbreviation | |
| CNT | Carbon nanotube |
| KLT | Kirchhoff–Love theory |
| FSDT | First-order shear deformation theory |
| INH-NCCSs | Inhomogeneous nanocomposite cylindrical shells |
| NCs | Nanocomposites |
| Pa | Pascal, unit of Young’s modulus |
| K | Kelvin |
| SDs | Shear deformations |
| SWCNTs | Single-walled carbon nanotubes |
Appendix A
Appendix B
References
- Volmir, A.S. Stability of Elastic Systems; Nauka: Moscow, Russia, 1967. [Google Scholar]
- Shen, H.S.; Chen, T.Y. Buckling and postbuckling behaviour of cylindrical shells under combined external pressure and axial compression. Thin-Walled Struct. 1991, 12, 321–334. [Google Scholar] [CrossRef]
- Anastasiadis, J.S.; Tabiei, A.; Simitses, G.J. Instability of moderately thick, laminated, cylindrical-shells under combined axial-compression and pressure. Compos. Struct. 1994, 27, 367–378. [Google Scholar] [CrossRef]
- Winterstetter, T.A.; Schmidt, H. Stability of circular cylindrical steel shells under combined loading. Thin-Walled Struct. 2002, 40, 893–910. [Google Scholar] [CrossRef]
- Tafresi, A.; Bailey, C.G. Instability of imperfect composite cylindrical shells under combined loading. Compos. Struct. 2007, 80, 49–64. [Google Scholar] [CrossRef]
- Praveen, A.P.; Rajamohan, V.; Mathew, A.T. Recent developments in investigation on buckling and post buckling responses of laminated composite shells. Polymer Compos. 2018, 39, 4231–4242. [Google Scholar] [CrossRef]
- Yang, L.C. Analytical investigation on the buckling of cylindrical shells under combined non-uniform axial compression and external pressure. Proc. Inst. Mech. Eng Part C-J. Mech. Eng. Sci. 2023. [Google Scholar] [CrossRef]
- Iijima, S. Synthesis of carbon nanotubes. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Yu, M.F. Fundamental mechanical properties of carbon nanotubes: Current understanding and the related experimental studies. J. Eng. Mater. Techn. ASME 2004, 126, 271–278. [Google Scholar] [CrossRef]
- Hayashi, T.; Kim, Y.A.; Natsuki, T.; Endo, M. Mechanical properties of carbon nanomaterials. Chemphyschem 2007, 8, 999–1004. [Google Scholar] [CrossRef]
- Suzuki, K.; Nomura, S. On elastic properties of single-walled carbon nanotubes as composite reinforcing fillers. J. Compos. Mater. 2007, 41, 1123–1135. [Google Scholar] [CrossRef]
- Lu, J.Q.; Jiang, H. Theoretical modeling on mechanical-electrical coupling of carbon nanotubes. J. Computat. Theoret. Nanosci. 2008, 5, 449–463. [Google Scholar] [CrossRef]
- Xu, S.; Ray, G.; Abdel-Magid, B. Thermal behavior of single-walled carbon nanotube polymer–matrix composites. Compos. Part A 2006, 37, 114–121. [Google Scholar] [CrossRef]
- Cai, D.Y.; Song, M. Recent advance in functionalized graphene/polymer nanocomposites. J. Mater. Chem. 2010, 20, 7906–7915. [Google Scholar] [CrossRef]
- Su, L.S.; Tsai, J.L. Characterizing the mechanical properties of nanocomposites with aligned graphene. Polym. Compos. 2021, 42, 4005–4014. [Google Scholar] [CrossRef]
- Yadav, A.; Kumar, A.; Sharma, K.; Pandey, A.K. Determination of elastic constants of functionalized graphene-based epoxy nanocomposites: A molecular modeling and MD simulation study. J. Mol. Model. 2022, 8, 143. [Google Scholar] [CrossRef] [PubMed]
- Nurazzi, M.N.; Asyraf, M.R.M.; Khalin, A.; Abdullah, N.; Sabaruddin, F.A.; Kamarudin, S.H.; Ahmad, S.; Mahat, A.M.; Lee, C.L.; Aisyah, H.A.; et al. Fabrication, functionalization, and application of carbon nanotube-reinforced polymer composite: An overview. Polymers 2021, 13, 1047. [Google Scholar] [CrossRef]
- Lim, B.K.; Hwang, J.W.; Lee, D.; Hong, S.H. Fabrication processes and multi-functional applications of carbon nanotube nanocomposites. J. Compos Mater. 2012, 46, 1731–1737. [Google Scholar] [CrossRef]
- Meer, S.; Kausar, A.; Iqbal, T. Trends in conducting polymer and hybrids of conducting polymer/carbon nanotube: A Review. Polym.-Plast. Technol. Eng. 2016, 55, 1416–1440. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Bacciocchi, M.; Agnelli, J.; Benedetti, D. Three-phase homogenization procedure for woven fabric composites reinforced by carbon nanotubes in thermal environment. Compos. Struct. 2020, 254, 112840. [Google Scholar] [CrossRef]
- Vartak, D.A.; Satyanarayana, B.; Munjal, B.S.; Vyas, K.B.; Bhatt, P.; Lal, A.K. Potential applications of advanced nano-composite materials for space payload. Aust. J. Mech. Eng. 2022, 20, 651–659. [Google Scholar] [CrossRef]
- Anashpaul, S.; Drosopoulos, G.A.; Adali, S. Minimum weight design of CNT/fiber reinforced laminates subject to a frequency constraint by optimal distribution of reinforcements across the thickness. Compos. Struct. 2023, 319, 117112. [Google Scholar] [CrossRef]
- Shen, H.-S. Postbuckling of nanotube-reinforced composite cylindrical shells in thermal environments, Part I: Axially-loaded shells. Compos. Struct. 2011, 93, 2096–2108. [Google Scholar] [CrossRef]
- Shen, H.-S. Postbuckling of nanotube-reinforced composite cylindrical shells in thermal environments, Part II: Pressure-loaded shells. Compos. Struct. 2011, 93, 2496–2503. [Google Scholar] [CrossRef]
- Shen, H.-S.; Xiang, Y. Postbuckling of nanotube-reinforced composite cylindrical shells under combined axial and radial mechanical loads in thermal environment. Compos. B Eng. 2013, 52, 311–322. [Google Scholar] [CrossRef]
- Hajlaoui, A.; Chebbi, E.; Dammak, F. Buckling analysis of carbon nanotube reinforced FG shells using an efficient solid-shell element based on a modified FSDT. Thin-Walled Struct. 2019, 144, 106254. [Google Scholar] [CrossRef]
- Hieu, P.T.; Tung, H.V. Postbuckling behavior of CNT-reinforced composite cylindrical shell surrounded by an elastic medium and subjected to combined mechanical loads in thermal environments. J. Thermoplast. Compos. Mater. 2019, 32, 1319–1346. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Tornabene, F.; Dimitri, R.; Kuruoglu, N. Buckling behavior of FG-CNT reinforced composite conical shells subjected to a combined loading. Nanomaterials 2020, 10, 419. [Google Scholar] [CrossRef]
- Monaco, G.T.; Fantuzzi, N.; Fabbrocino, F.; Luciano, R. Trigonometric solution for the bending analysis of magneto-electro-elastic strain gradient nonlocal nanoplates in hygro-thermal environment. Mathematics 2021, 9, 567. [Google Scholar] [CrossRef]
- Monaco, G.T.; Fantuzzi, N.; Fabbrocino, F.; Luciano, R. Critical temperatures for vibrations and buckling of magneto-electro-elastic nonlocal strain gradient plates. Nanomaterials 2021, 11, 87. [Google Scholar] [CrossRef]
- Cornacchia, F.; Fabbrocino, F.; Fantuzzi, N.; Luciano, R.; Penna, R. Analytical solution of cross- and angle-ply nano plates with strain gradient theory for linear vibrations and buckling. Mech. Adv. Mater. Struct. 2021, 28, 1201–1215. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Kuruoglu, N. Buckling analysis of shear deformable composite conical shells reinforced by CNTs subjected to combined loading on the two-parameter elastic foundation. Defence Techn. 2022, 18, 205–218. [Google Scholar] [CrossRef]
- Avey, M.; Fantuzzi, N.; Sofiyev, A.H. Mathematical modeling and analytical solution of thermoelastic stability problem of functionally graded nanocomposite cylinders within different theories. Mathematics 2022, 10, 1081. [Google Scholar] [CrossRef]
- Sun, G.X.; Zhu, S.B.; Teng, R.; Sun, J.; Zhou, Z.; Xu, X.S. Post-buckling analysis of GPLs reinforced porous cylindrical shells under axial compression and hydrostatic pressure. Thin-Walled Struct. 2022, 172, 108834. [Google Scholar] [CrossRef]
- Hieu, D.V.; Phi, B.G.; Sedighi, H.M.; Sofiyev, A.H. Size-dependent nonlinear vibration of functionally graded composite micro-beams reinforced by carbon nanotubes with piezoelectric layers in thermal environments. Acta Mech. 2022, 233, 2249–2270. [Google Scholar]
- Li, C.; Zhu, C.X.; Lim, C.W.; Li, S. Nonlinear in-plane thermal buckling of rotationally restrained functionally graded carbon nanotube reinforced composite shallow arches under uniform radial loading. Appl. Math. Mech. 2022, 43, 1821–1840. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, A.; Kumar, D.R. Buckling response of CNT based hybrid FG plates using finite element method and machine learning method. Compos. Struct. 2023, 319, 117204. [Google Scholar] [CrossRef]
- Kumar, S.; Ramesh, M.R.; Jeyaraj, P.; Doddamani, M. Buckling and dynamic responses of 3D printed nanocomposites and their graded variants. Compos. Struct. 2023, 316, 117031. [Google Scholar] [CrossRef]
- Tomczyk, B.; Bagdasaryan, V.; Gołąbczak, M.; Litawska, A. A new combined asymptotic-tolerance model of thermoelasticity problems for thin biperiodic cylindrical shells. Compos. Struct. 2023, 309, 116708. [Google Scholar] [CrossRef]
- Yang, Z.; Zhao, S.; Yang, J.; Liu, A.; Fu, J. Thermomechanical in-plane dynamic instability of asymmetric restrained functionally graded graphene reinforced composite arches via machine learning-based models. Compos. Struct. 2023, 308, 116709. [Google Scholar] [CrossRef]
- Avey, M.; Fantuzzi, N.; Sofiyev, A.H. Thermoelastic stability of CNT patterned conical shells under thermal loading in the framework of shear deformation theory. Mech. Adv. Mater. Struct. 2023, 30, 1828–1841. [Google Scholar] [CrossRef]
- Chakraborty, S.; Dey, T. Thermomechanical buckling and wrinkling characteristics of softcore sandwich panels with CNT reinforced composite face sheets. Euro. J. Mech. A-Solid. 2023, 98, 104894. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Fantuzzi, N. Stability analysis of shear deformable inhomogeneous nanocomposite cylindrical shells under hydrostatic pressure in thermal environment. Materials 2023, 16, 4887. [Google Scholar] [CrossRef]
- Dong, D.T.; Phuong, N.T.; Nam, V.H.; Ly, L.N.; Tien, N.V.; Duc, V.M.; Minh, T.Q.; Hung, V.T.; Giang, N.T.H. An analytical approach for nonlinear buckling analysis of torsionally loaded sandwich carbon nanotube reinforced cylindrical shells with auxetic Core. Adv. Appl. Math. Mech. 2023, 15, 468–484. [Google Scholar] [CrossRef]
- Shen, H.-S.; Noda, N. Postbuckling of FGM cylindrical shells under combined axial and radial mechanical loads in thermal environments. Int. J. Solid. Struct. 2005, 42, 4641–4662. [Google Scholar] [CrossRef]
- Sofiyev, A.H. Buckling analysis of FGM circular shells under combined loads and resting on the Pasternak type elastic foundation. Mech. Res. Communic. 2010, 37, 539–544. [Google Scholar] [CrossRef]
- Ambartsumian, S.A. Theory of Anisotropic Shells; NASA-TT-F-118; NASA: Washington, DC, USA, 1964.
- Shen, H.-S.; Wang, H.; Yang, D.Q. Vibration of thermally postbuckled sandwich plates with nanotube reinforced composite face sheets resting on elastic foundations. Int. J. Mech. Sci. 2017, 124–125, 253–262. [Google Scholar] [CrossRef]
- Griebel, M.; Hamaekers, J. Molecular dynamics simulations of the elastic moduli of polymer–carbon nanotube composites. Comput. Methods Appl. Mech. Eng. 2004, 193, 1773–1788. [Google Scholar] [CrossRef]
- Han, Y.; Elliott, J. Molecular dynamics simulations of the elastic properties of polymer/carbon nanotube composites. Comput. Mater. Sci. 2007, 39, 315–323. [Google Scholar] [CrossRef]



| Temperature (K) | (TPa) | (TPa) | (TPa) | ||
|---|---|---|---|---|---|
| 300 | 5.6451 | 7.0796 | 2.0665 | 3.4579 | 5.1682 |
| 450 | 5.5461 | 6.9563 | 2.3728 | 4.3758 | 5.0539 |
| 600 | 5.4994 | 6.8984 | 2.9283 | 4.6852 | 4.9535 |
| 750 | 5.4588 | 6.8482 | 3.8325 | 4.6152 | 4.8670 |
| CNT Efficiency Parameters | |||
|---|---|---|---|
| 0.12 | 0.137 | 1.626 | 0.715 |
| 0.17 | 0.142 | 1.626 | 1.138 |
| 0.23 | 0.141 | 1.585 | 1.109 |
| ) for X-Model | ||||||
|---|---|---|---|---|---|---|
| T = 300 (K) | T = 400 (K) | T = 500 (K) | ||||
| Shen and Xiang [25] | ||||||
| 0.12 | 0.112 | 0.218 | 0.098 | 0.191 | 0.084 | 0.166 |
| 0.17 | 0.190 | 0.370 | 0.167 | 0.325 | 0.143 | 0.280 |
| 0.28 | 0.242 | 0.470 | 0.213 | 0.414 | 0.183 | 0.358 |
| Present study | ||||||
| 0.12 | 0.110 | 0.222 | 0.097 | 0.196 | 0.084 | 0.169 |
| 0.17 | 0.187 | 0.379 | 0.165 | 0.333 | 0.142 | 0.286 |
| 0.28 | 0.240 | 0.486 | 0.211 | 0.427 | 0.182 | 0.368 |
| Comparative Studies | U | X | |
|---|---|---|---|
| Present study | 775.23 (5) | 893.46 (5) | |
| Shen [24] | 776.63 (5) | 927.40 (5) | |
| Hajlaoui et al. [26] | 763.46 (5) | 886.32 (5) | |
| Present study | 433.18 (4) | 477.97 (4) | |
| Shen [24] | 433.04 (4) | 484.05 (4) | |
| Hajlaoui et al. [26] | 438.47 (4) | 482.39 (4) | |
| Present study | 344.02 (4) | 379.43 (4) | |
| Shen [24] | 343.81 (4) | 382.59 (4) | |
| Hajlaoui et al. [26] | 346.77 (4) | 381.51 (4) | |
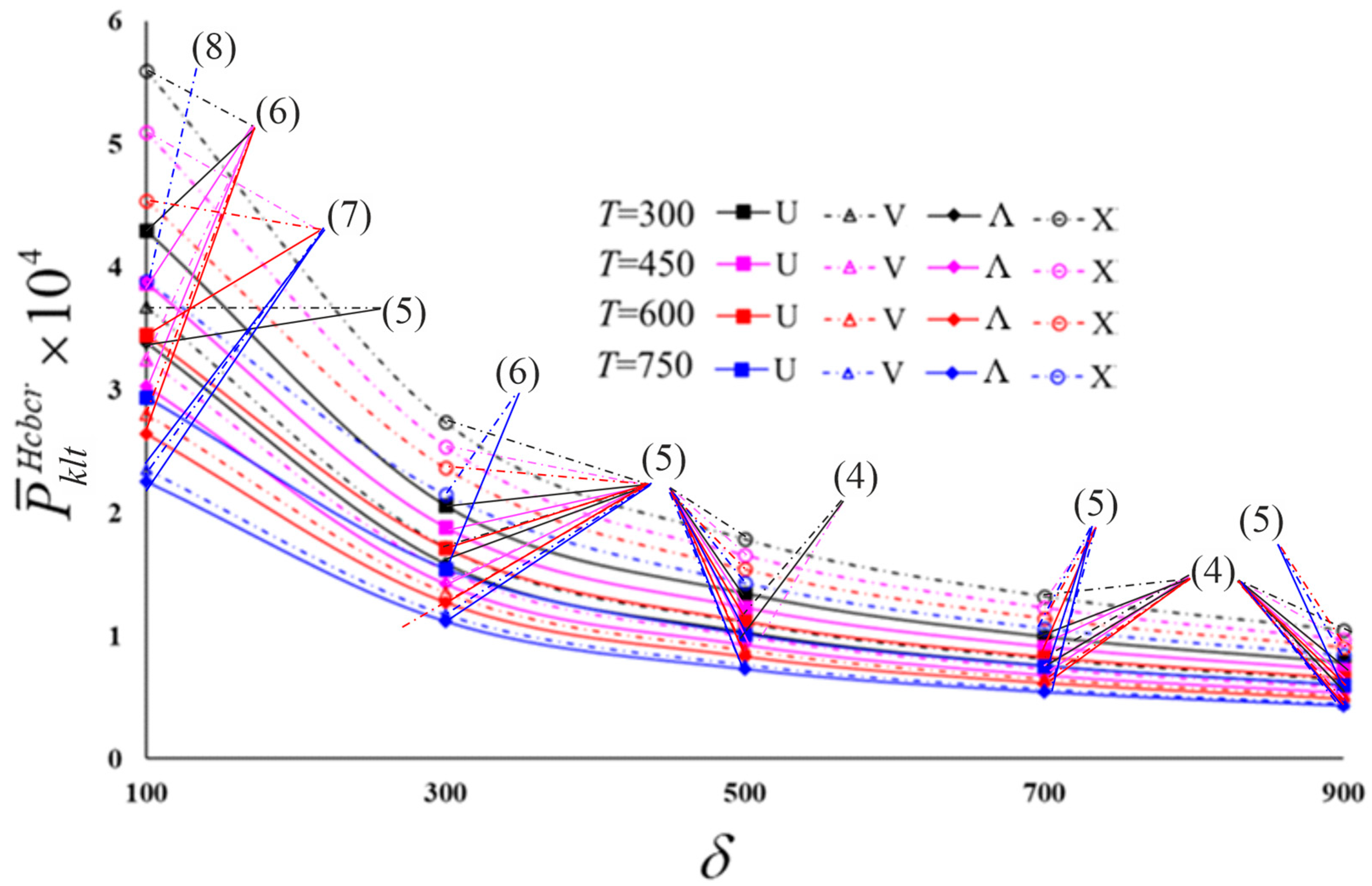
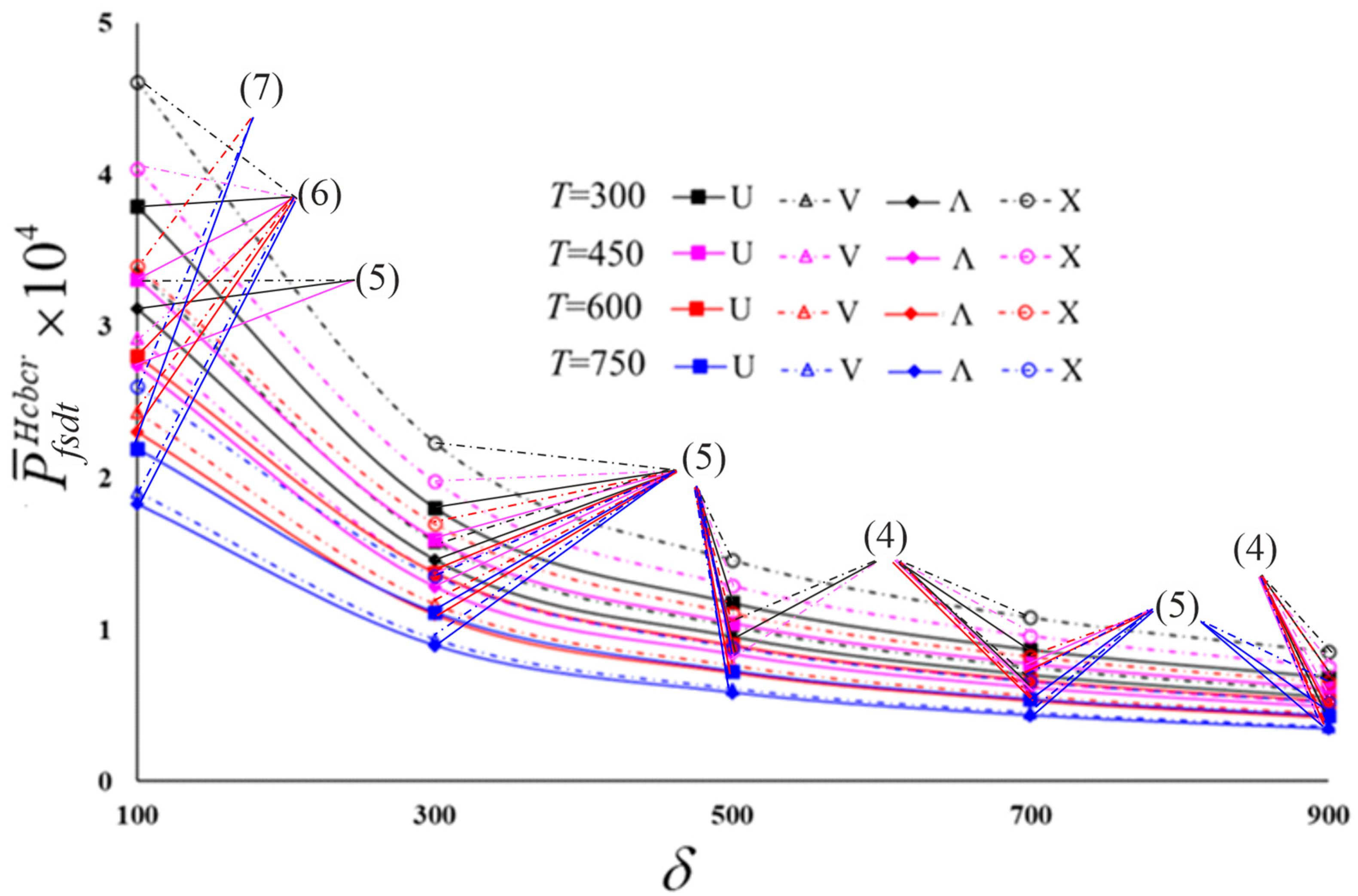
| T = 300 (K) | ||||||||
|---|---|---|---|---|---|---|---|---|
| U | V | Λ | X | |||||
| KLT | FSDT | KLT | FSDT | KLT | FSDT | KLT | FSDT | |
| 100 | 4.303 (6) | 3.792 (6) | 3.677 (5) | 3.367 (5) | 3.388 (5) | 3.116 (5) | 5.599 (6) | 4.612 (6) |
| 300 | 2.059 (5) | 1.804 (5) | 1.720 (5) | 1.575 (5) | 1.585 (5) | 1.458 (5) | 2.737 (5) | 2.231 (5) |
| 500 | 1.344 (5) | 1.177 (5) | 1.109 (4) | 1.020 (4) | 1.030 (4) | 0.951 (4) | 1.786 (5) | 1.456 (5) |
| 700 | 0.991 (4) | 0.870 (4) | 0.815 (4) | 0.749 (4) | 0.756 (4) | 0.698 (4) | 1.322 (4) | 1.079 (4) |
| 900 | 0.783 (4) | 0.688 (4) | 0.644 (4) | 0.592 (4) | 0.598 (4) | 0.552 (4) | 1.044 (4) | 0.853 (4) |
| T = 450 (K) | ||||||||
| 100 | 3.873 (6) | 3.309 (6) | 3.247 (6) | 2.920 (6) | 3.031 (6) | 2.738 (5) | 5.096 (7) | 4.035 (6) |
| 300 | 1.882 (5) | 1.595 (5) | 1.531 (5) | 1.373 (5) | 1.423 (5) | 1.280 (5) | 2.542 (5) | 1.975 (5) |
| 500 | 1.228 (5) | 1.041 (5) | 0.993 (4) | 0.893 (4) | 0.929 (5) | 0.836 (5) | 1.659 (5) | 1.289 (5) |
| 700 | 0.910 (4) | 0.773 (5) | 0.729 (4) | 0.656 (4) | 0.683 (4) | 0.616 (4) | 1.232 (5) | 0.960 (4) |
| 900 | 0.719 (4) | 0.611 (4) | 0.576 (4) | 0.518 (4) | 0.539 (4) | 0.487 (4) | 0.975 (4) | 0.758 (4) |
| T = 600 (K) | ||||||||
| 100 | 3.453 (7) | 2.804 (6) | 2.805 (6) | 2.435 (6) | 2.642 (6) | 2.304 (6) | 4.544 (7) | 3.398 (7) |
| 300 | 1.716 (5) | 1.374 (5) | 1.351 (5) | 1.166 (5) | 1.269 (5) | 1.099 (5) | 2.366 (5) | 1.697 (5) |
| 500 | 1.120 (5) | 0.897 (5) | 0.882 (5) | 0.761 (5) | 0.828 (5) | 0.717 (5) | 1.544 (5) | 1.107 (5) |
| 700 | 0.831 (5) | 0.666 (5) | 0.648 (4) | 0.561 (4) | 0.613 (4) | 0.532 (4) | 1.146 (5) | 0.822 (5) |
| 900 | 0.659 (4) | 0.529 (4) | 0.512 (4) | 0.443 (4) | 0.484 (4) | 0.421 (4) | 0.911 (5) | 0.653 (4) |
| T = 750 (K) | ||||||||
| 100 | 2.941 (7) | 2.195 (7) | 2.351 (7) | 1.908 (6) | 2.253 (7) | 1.828 (6) | 3.887 (8) | 2.602 (7) |
| 300 | 1.544 (6) | 1.113 (5) | 1.171 (5) | 0.935 (5) | 1.116 (5) | 0.895 (5) | 2.148 (6) | 1.352 (5) |
| 500 | 1.013 (5) | 0.726 (5) | 0.764 (5) | 0.610 (5) | 0.728 (5) | 0.584 (5) | 1.430 (5) | 0.883 (5) |
| 700 | 0.752 (5) | 0.539 (5) | 0.567 (5) | 0.453 (5) | 0.541 (5) | 0.433 (5) | 1.062 (5) | 0.656 (5) |
| 900 | 0.598 (5) | 0.429 (5) | 0.448 (4) | 0.359 (4) | 0.430 (4) | 0.345 (5) | 0.844 (5) | 0.521 (5) |
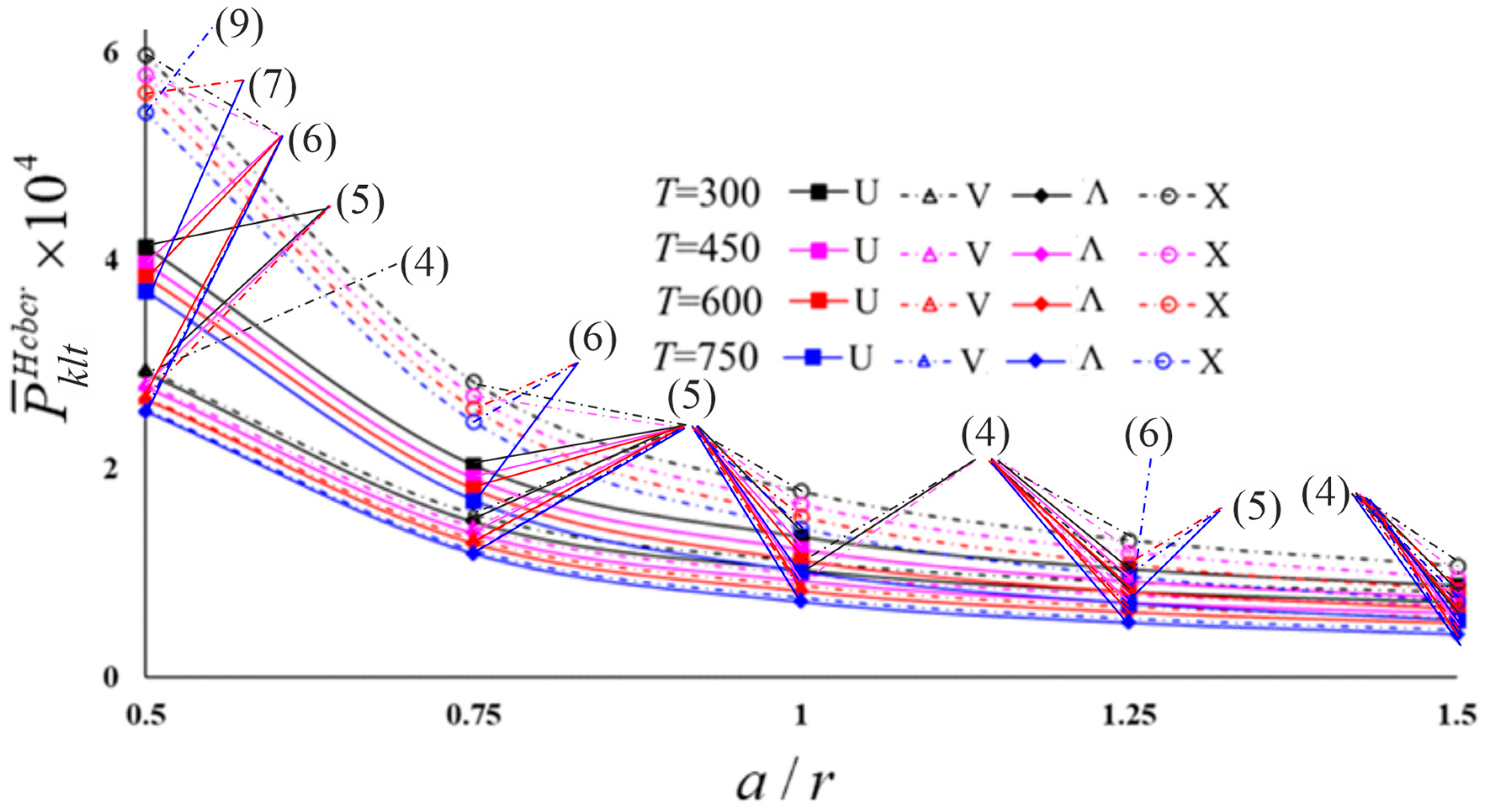
| T = 300 (K) | ||||||||
|---|---|---|---|---|---|---|---|---|
| U | V | O | X | |||||
| KLT | FSDT | KLT | FSDT | KLT | FSDT | KLT | FSDT | |
| 0.50 | 4.131 (5) | 2.397 (5) | 2.958 (4) | 2.001 (5) | 2.923 (5) | 1.978 (5) | 5.977 (6) | 2.839 (5) |
| 0.75 | 2.033 (5) | 1.576 (5) | 1.566 (5) | 1.317 (5) | 1.491 (5) | 1.258 (5) | 2.837 (5) | 1.952 (5) |
| 1.00 | 1.344 (5) | 1.177 (5) | 1.109 (4) | 1.020 (4) | 1.030 (4) | 0.951 (4) | 1.786 (5) | 1.456 (5) |
| 1.25 | 1.034 (4) | 0.961 (4) | 0.909 (4) | 0.867 (4) | 0.821 (4) | 0.787 (4) | 1.318 (4) | 1.171 (4) |
| 1.50 | 0.875 (4) | 0.838 (4) | 0.812 (4) | 0.788 (4) | 0.721 (4) | 0.704 (4) | 1.071 (4) | 0.996 (4) |
| T = 450 (K) | ||||||||
| 0.50 | 3.977 (6) | 2.100 (5) | 2.815 (5) | 1.769 (5) | 2.786 (5) | 1.752 (5) | 5.779 (6) | 2.443 (6) |
| 0.75 | 1.914 (5) | 1.403 (5) | 1.444 (5) | 1.168 (5) | 1.383 (5) | 1.122 (5) | 2.702 (5) | 1.723 (5) |
| 1.00 | 1.228 (5) | 1.041 (5) | 0.993 (4) | 0.893 (4) | 0.929 (5) | 0.836 (5) | 1.659 (5) | 1.289 (5) |
| 1.25 | 0.925 (4) | 0.842 (4) | 0.792 (4) | 0.746 (4) | 0.721 (4) | 0.682 (4) | 1.202 (4) | 1.034 (4) |
| 1.50 | 0.765 (4) | 0.722 (4) | 0.692 (4) | 0.667 (4) | 0.619 (4) | 0.600 (4) | 0.954 (4) | 0.868 (4) |
| T = 600 (K) | ||||||||
| 0.50 | 3.846 (6) | 1.753 (6) | 2.694 (5) | 1.506 (5) | 2.671 (6) | 1.495 (5) | 5.619 (7) | 1.994 (6) |
| 0.75 | 1.809 (5) | 1.211 (5) | 1.331 (5) | 1.009 (5) | 1.286 (5) | 0.976 (5) | 2.585 (6) | 1.465 (5) |
| 1.00 | 1.120 (5) | 0.897 (5) | 0.882 (5) | 0.761 (5) | 0.828 (5) | 0.717 (5) | 1.544 (5) | 1.107 (5) |
| 1.25 | 0.820 (4) | 0.720 (4) | 0.678 (4) | 0.624 (4) | 0.624 (4) | 0.577 (4) | 1.090 (5) | 0.889 (4) |
| 1.50 | 0.657 (4) | 0.606 (4) | 0.574 (4) | 0.545 (4) | 0.519 (4) | 0.496 (4) | 0.842 (4) | 0.738 (4) |
| T = 750 (K) | ||||||||
| 0.50 | 3.709 (7) | 1.321 (6) | 2.573 (6) | 1.173 (5) | 2.550 (6) | 1.163 (6) | 5.427 (9) | 1.455 (6) |
| 0.75 | 1.700 (6) | 0.967 (5) | 1.220 (5) | 0.816 (5) | 1.189 (5) | 0.797 (5) | 2.454 (6) | 1.136 (5) |
| 1.00 | 1.013 (5) | 0.726 (5) | 0.764 (5) | 0.610 (5) | 0.728 (5) | 0.584 (5) | 1.430 (5) | 0.883 (5) |
| 1.25 | 0.710 (5) | 0.580 (5) | 0.564 (6) | 0.494 (4) | 0.528 (4) | 0.464 (4) | 0.967 (5) | 0.711 (5) |
| 1.50 | 0.549 (4) | 0.481 (4) | 0.456 (4) | 0.419 (4) | 0.419 (4) | 0.387 (4) | 0.729 (4) | 0.592 (4) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avey, M.; Fantuzzi, N.; Sofiyev, A.H. Analytical Solution of Stability Problem of Nanocomposite Cylindrical Shells under Combined Loadings in Thermal Environments. Mathematics 2023, 11, 3781. https://doi.org/10.3390/math11173781
Avey M, Fantuzzi N, Sofiyev AH. Analytical Solution of Stability Problem of Nanocomposite Cylindrical Shells under Combined Loadings in Thermal Environments. Mathematics. 2023; 11(17):3781. https://doi.org/10.3390/math11173781
Chicago/Turabian StyleAvey, Mahmure, Nicholas Fantuzzi, and Abdullah H. Sofiyev. 2023. "Analytical Solution of Stability Problem of Nanocomposite Cylindrical Shells under Combined Loadings in Thermal Environments" Mathematics 11, no. 17: 3781. https://doi.org/10.3390/math11173781
APA StyleAvey, M., Fantuzzi, N., & Sofiyev, A. H. (2023). Analytical Solution of Stability Problem of Nanocomposite Cylindrical Shells under Combined Loadings in Thermal Environments. Mathematics, 11(17), 3781. https://doi.org/10.3390/math11173781









