A Hybrid Non-Polynomial Spline Method and Conformable Fractional Continuity Equation
Abstract
:1. Introduction
2. Non-Polynomial Spline Conformable Continuity Construct
3. Application of the NPSCCM to Burgers–Fisher Equations
4. Stability Analysis
5. Numerical Demonstration and Discussion
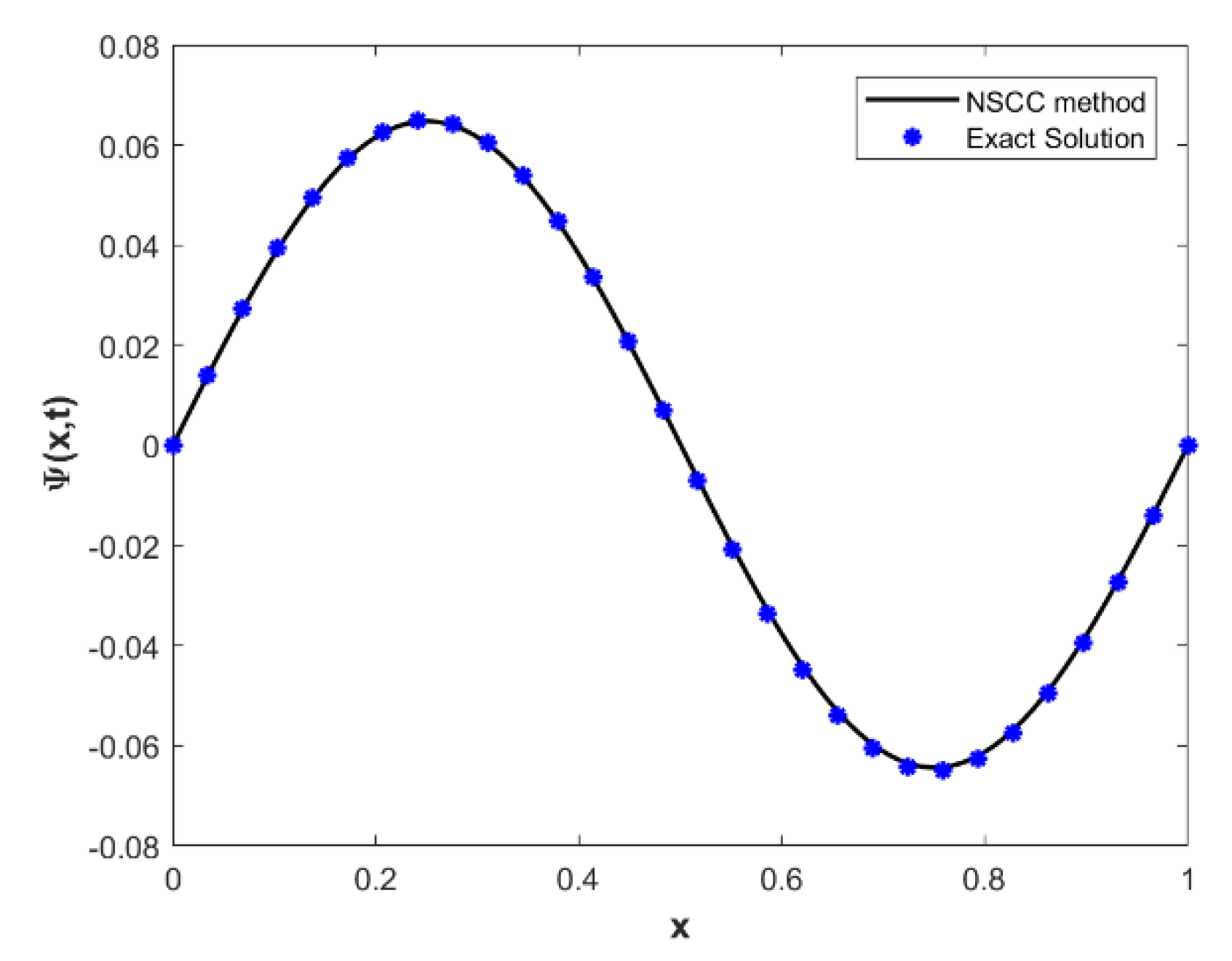
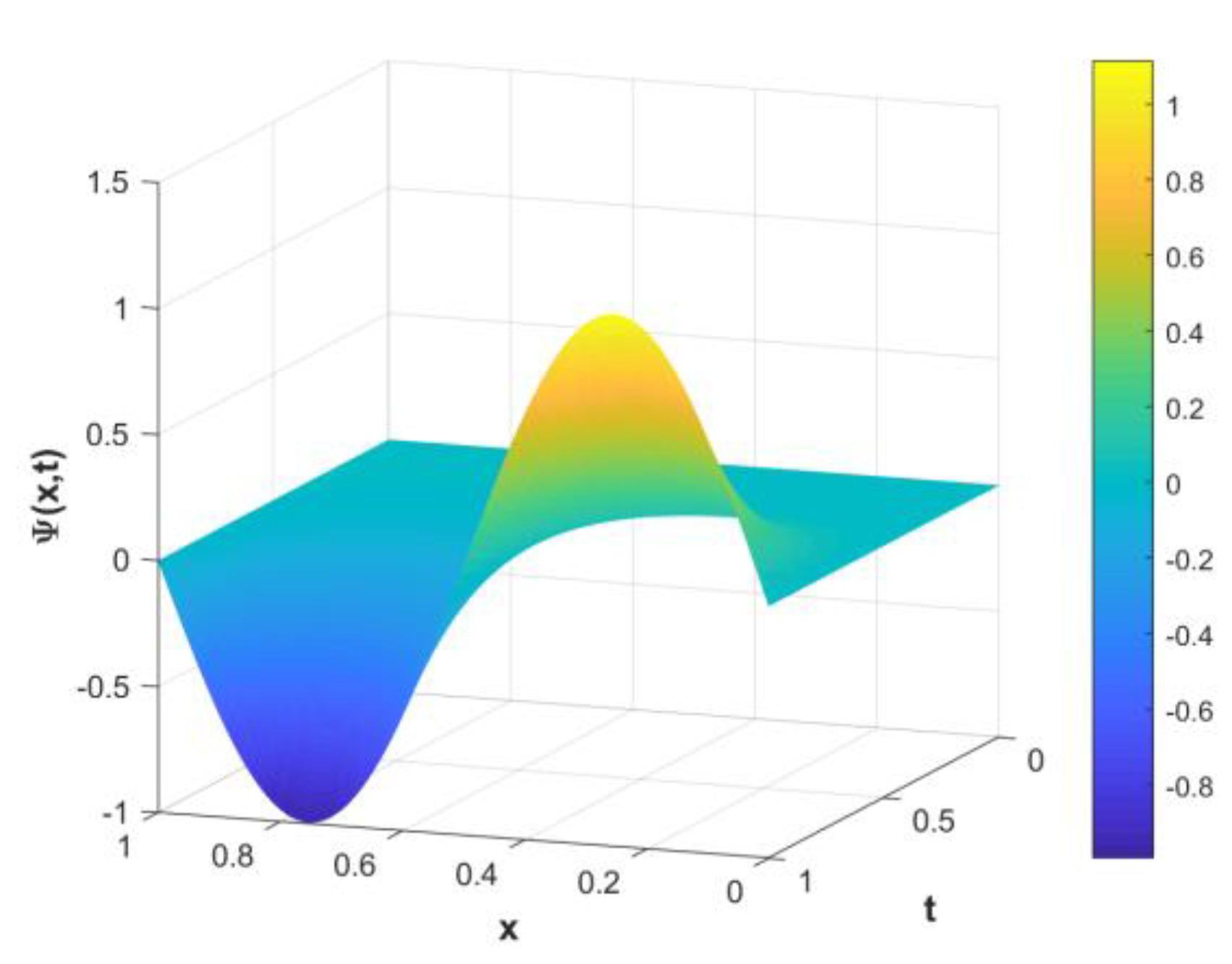
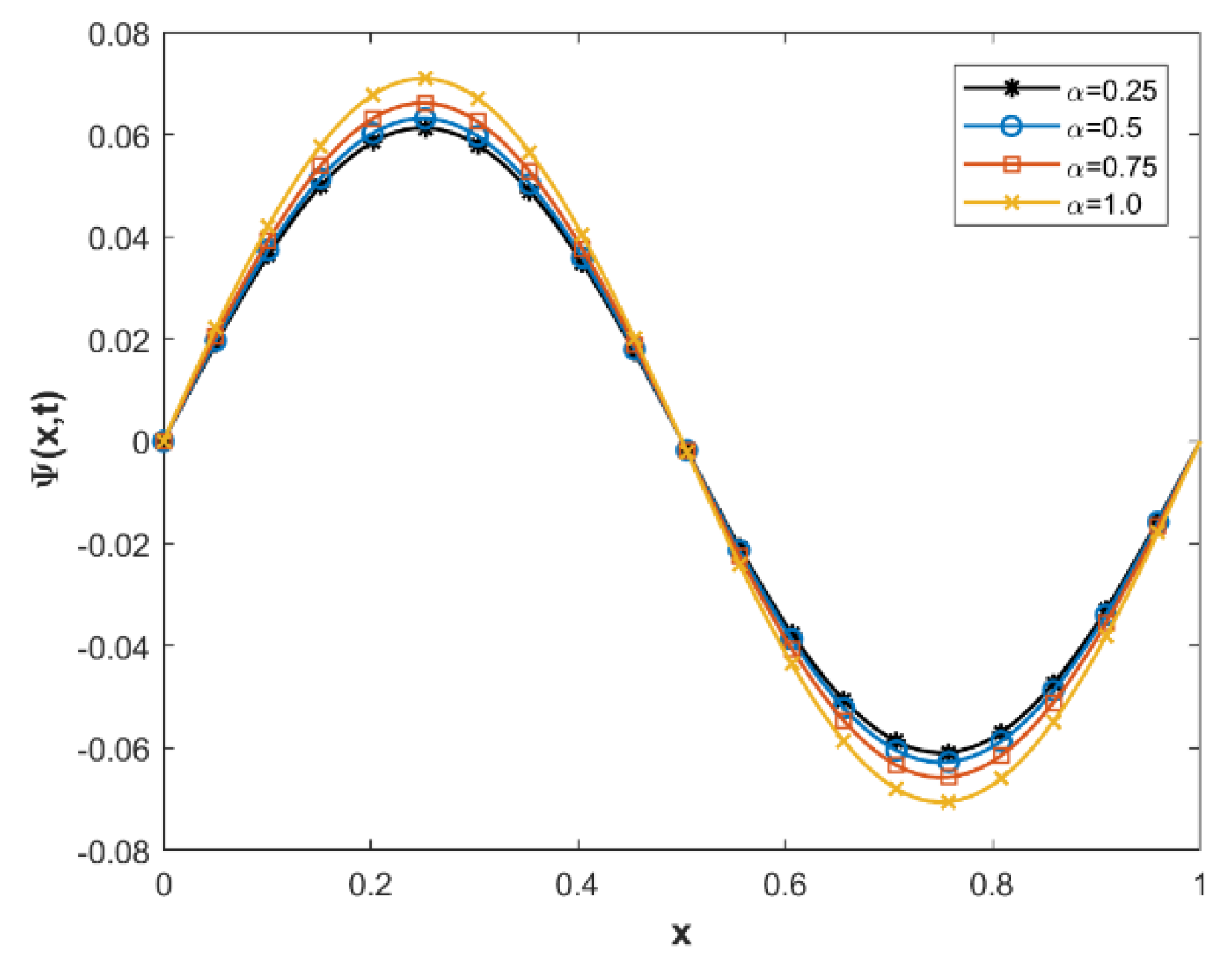
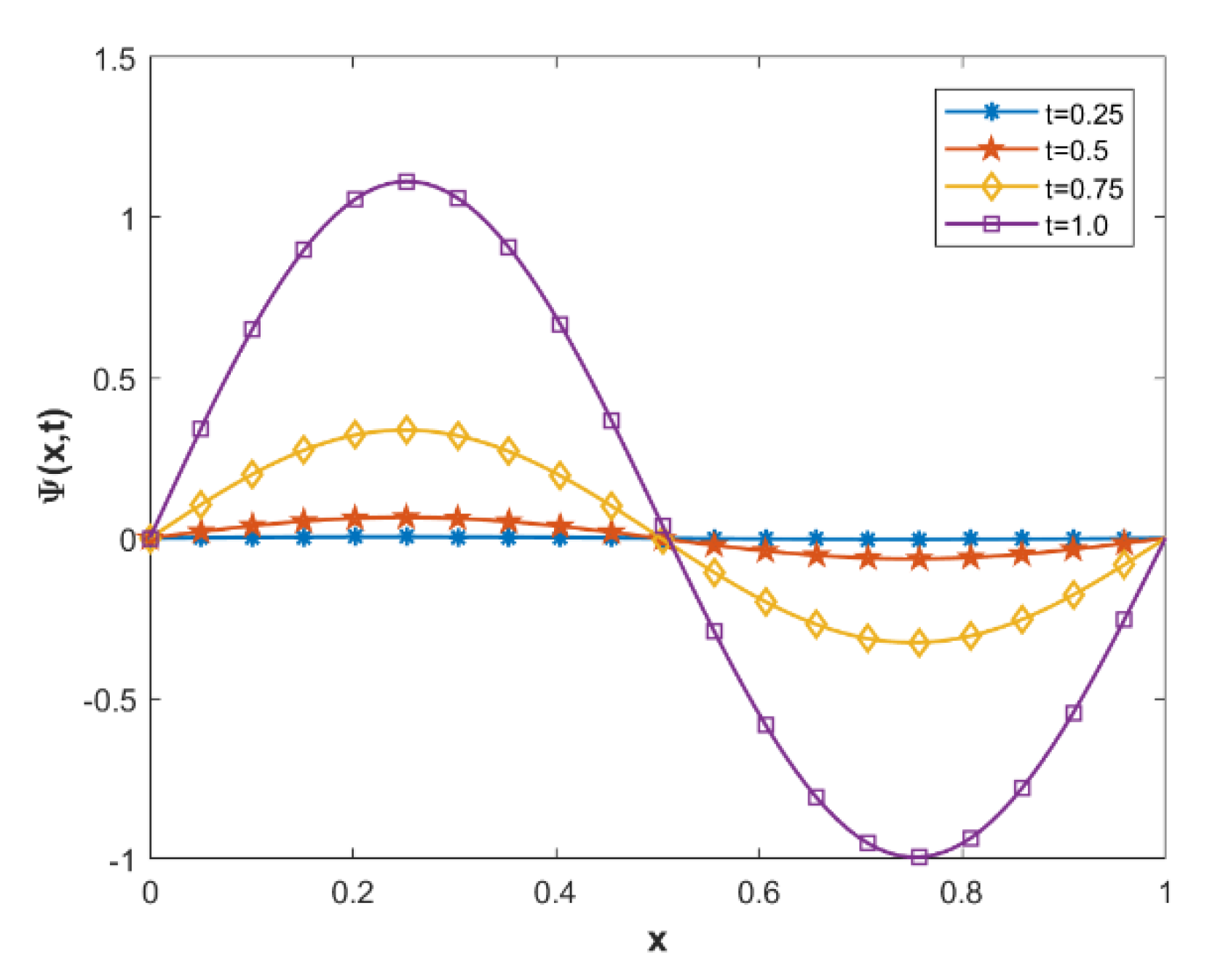
| Non-Polynomial Spline Conformable Continuity Method | Cubic B-Spline Method [52] | |||
|---|---|---|---|---|
| 9.3641 × 10−5 | 3.2539 × 10−6 | 1.9700 × 10−4 | 2.5410 × 10−5 | |
| 1.6212 × 10−5 | 5.5856 × 10−6 | 6.3660 × 10−3 | 6.3710 × 10−4 | |
| 2.4493 × 10−6 | 8.3502 × 10−6 | 3.9000 × 10−4 | 5.3830 × 10−5 | |
| 1.6631 × 10−7 | 5.6903 × 10−8 | 1.8213 × 10−7 | 6.2880 × 10−8 | |
| 1.1006 × 10−7 | 3.7655 × 10−8 | 1.2052 × 10−7 | 4.1610 × 10−8 | |
| 1.0096 × 10−7 | 3.4542 × 10−8 | 1.1056 × 10−7 | 3.8170 × 10−8 | |
| 1.7001 × 10−8 | 5.8167 × 10−8 | 1.8618 × 10−7 | 6.4277 × 10−8 | |
6. Advantage of NPSCCM
- ○
- Enhanced accuracy: incorporates conformable fractional derivatives within the continuity equation framework for improved accuracy in solving fractional order equations.
- ○
- Robustness: handles complex mathematical models effectively by ensuring continuity of fractional derivatives, enhancing robustness.
- ○
- Efficient representation: integrates non-polynomial spline (NPS) interpolation for efficient representation of intricate solutions and complex functional shapes.
- ○
- Stability: demonstrates unconditional stability within specific parameter ranges, ensuring reliable performance across diverse scenarios.
- ○
- Efficiency: shows high efficiency in handling complex mathematical models, making it suitable for a wide range of problems.
- ○
- Broad applicability: superiority is demonstrated across multiple fields like biology, ecology, physics, and more, showcasing its versatility.
- ○
- Validation: offers practical validation through comprehensive numerical examples, reinforcing its applicability and effectiveness.
- ○
- Quantitative accuracy: meticulous evaluations using norm errors ( and ) provide quantitative validation of its accuracy and robustness.
- ○
- Advancement in mathematics: the unique combination of CCE and NPS contributes to the advancement of computational mathematics.
7. Limitation of NPSCCM
- ○
- Smoothness assumption: The proposed technique assumes a certain level of smoothness in the solutions. While it performs well for problems with regular behavior, its performance might be affected when dealing with solutions that exhibit high oscillations or discontinuities.
- ○
- Limited to certain equations: The method is designed particularly for nonlinear time fractional differential equations. Its applicability might be limited when addressing other types of equations or models that do not fit within this framework.
- ○
- Computational resource requirements: The computational efficiency of the method might be influenced by the complexity of the problem. In cases where the problem involves very fine discretization or large computational domains, the method’s resource requirements might increase.
- ○
- Parameter dependence: The method’s effectiveness could be influenced by the choice of parameters, such as the number of spline nodes or the grid resolution. Optimizing these parameters for different problems might be required to achieve the best results.
- ○
- Domain-specific characteristics: While the approach demonstrates superiority across various fields, its performance might be influenced by the specific characteristics of the problem being tackled. The applicability of the technique in certain scenarios could depend on the interplay of the problem’s unique features.
8. Conclusions
- The method’s stability and convergence properties have been thoroughly analyzed and established, ensuring reliable performance across different scenarios.
- The demonstrated superiority over existing approaches in terms of norm errors underscores the competitive edge of the proposed method.
- Future research could explore potential optimizations and refinements to enhance the method’s efficiency and extend its capabilities to address other types of fractional differential equations. Additionally, real-world applications of the technique in specific scientific and engineering domains could be further explored and validated.
- Future research endeavors could explore the extension of our proposed technique to tackle fuzzy differential equations using the conformable continuity equation (CCE) and non-polynomial spline (NPS) interpolation. The integration of these methods holds the potential to provide accurate and robust solutions for systems characterized by imprecision and uncertainty. The challenge lies in adapting the CCE and NPS framework to handle fuzzy dynamics, ensuring the stability of solutions in the presence of fuzziness.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kuramoto, Y. Waves, and Turbulence; Springer Series in Synergetics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA; Tokyo, Japan, 1984. [Google Scholar]
- Glass, L.; Murray, J.D. Interdisciplinary Applied Mathematics: Mathematical Biology I; Springer: New York, NY, USA, 2002. [Google Scholar]
- Jan, M.N.; Zaman, G.; Ali, N.; Ahmad, I.; Shah, Z. Optimal control application to the epidemiology of HBV and HCV co-infection. Int. J. Biomath. 2022, 15, 2150101. [Google Scholar] [CrossRef]
- Zada, I.; Jan, M.N.; Ali, N.; Alrowail, D.; Nisar, K.S.; Zaman, G. Mathematical analysis of hepatitis B epidemic model with optimal control. Adv. Differ. Equ. 2021, 2021, 451. [Google Scholar] [CrossRef]
- Constantin, M.; Gheorghe, D.; Tenreiro, J. Introduction to Fractional Differential Equations; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Wilhelmsson, H.; Lazzaro, E. Reaction-Diffusion Problems in the Physics of Hot Plasmas, 1st ed.; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Zafar, Z.U.A.; Ali, N.; Shah, Z.; Zaman, G.; Roy, P.; Deebani, W. Hopf bifurcation and global dynamics of time delayed Dengue model. Comput. Methods Programs Biomed. 2020, 195, 105530. [Google Scholar] [CrossRef] [PubMed]
- Khalid, A.; Ghaffar, A.; Naeem, M.N.; Nisar, K.S.; Baleanu, D. Solutions of BVPs arising in hydrodynamic and magnetohydro-dynamic stability theory using polynomial and non-polynomial splines. Alex. Eng. J. 2021, 60, 941–953. [Google Scholar] [CrossRef]
- Yousif, M.A.; Hamasalh, F.K. A new numerical scheme non-polynomial spline for solving generalized time fractional Fisher equation. J. Intell. Fuzzy Syst. 2023, 44, 7379–7389. [Google Scholar] [CrossRef]
- Mirzaee, F.; Sayevand, K.; Rezaei, S.; Samadyar, N. Finite Difference and Spline Approximation for Solving Fractional Stochastic Advection-Diffusion Equation. Iran. J. Sci. Technol. Trans. A Sci. 2021, 45, 607–617. [Google Scholar] [CrossRef]
- Gupta, A.K.; Ray, S.S. On the Solutions of Fractional Burgers-Fisher and Generalized Fisher’s Equations Using Two Reliable Methods. Int. J. Math. Math. Sci. 2014, 2014, 682910. [Google Scholar] [CrossRef]
- Tamsir, M.; Dhiman, N.; Nigam, D.; Chauhan, A. Approximation of Caputo time-fractional diffusion equation using redefined cubic exponential B-spline collocation technique. AIMS Math. 2021, 6, 3805–3820. [Google Scholar] [CrossRef]
- Roul, P.; Rohil, V. A high order numerical technique and its analysis for nonlinear generalized Fisher’s equation. J. Comput. Appl. Math. 2022, 406, 114047. [Google Scholar] [CrossRef]
- Mirzaee, F.; Alipour, S. Quintic B-spline collocation method to solve n-dimensional stochastic Itô-Volterra integral equations. J. Comput. Appl. Math. 2021, 384, 113153. [Google Scholar] [CrossRef]
- Mirzaee, F.; Alipour, S. Cubic B-spline approximation for linear stochastic integro-differential equation of fractional order. J. Comput. Appl. Math. 2020, 366, 112440. [Google Scholar] [CrossRef]
- Płociniczak, Ł.; Świtała, M. Numerical scheme for Erdélyi–Kober fractional diffusion equation using Galerkin–Hermite method. Fract. Calc. Appl. Anal. 2022, 25, 1651–1687. [Google Scholar] [CrossRef]
- Alipour, S.; Mirzaee, F. An iterative algorithm for solving two dimensional nonlinear stochastic integral equations: A combined successive approximations method with bilinear spline interpolation. Appl. Math. Comput. 2020, 371, 124947. [Google Scholar] [CrossRef]
- Mirzaee, F.; Alipour, S. Bicubic B-Spline Functions to Solve Linear Two-Dimensional Weakly Singular Stochastic Integral Equation. Iran. J. Sci. Technol. Trans. A Sci. 2021, 45, 965–972. [Google Scholar] [CrossRef]
- Moghaddam, B.; Mostaghim, Z.; Pantelous, A.; Machado, J.T. An integro quadratic spline-based scheme for solving nonlinear fractional stochastic differential equations with constant time delay. Commun. Nonlinear Sci. Numer. Simul. 2021, 92, 105475. [Google Scholar] [CrossRef]
- Yousif, M.A.; Hamasalh, F.K. Novel simulation of the time fractional Burgers–Fisher equations using a non-polynomial spline fractional continuity method. AIP Adv. 2022, 12, 115018. [Google Scholar] [CrossRef]
- Hamasalh, F.K.; Muhammed, P.O. Computational Non-Polynomial Spline Function for Solving Fractional Bagely-Torvik Equation. Math. Sci. Lett. 2017, 6, 83–87. [Google Scholar] [CrossRef]
- Akgül, A.; Akgül, E.K. A Novel Method for Solutions of Fourth-Order Fractional Boundary Value Problems. Fractal Fract. 2019, 3, 33. [Google Scholar] [CrossRef]
- Hammad, D.; Semary, M.S.; Khattab, A.G. Ten non-polynomial cubic splines for some classes of Fredholm integral equations. Ain Shams Eng. J. 2022, 13, 101666. [Google Scholar] [CrossRef]
- Tahernezhad, T.; Jalilian, R. Exponential spline for the numerical solutions of linear Fredholm integro-differential equations. Adv. Differ. Equ. 2020, 2020, 141. [Google Scholar] [CrossRef]
- Rashidinia, J.; Jalilian, R. Non-polynomial spline for solution of boundary-value problems in plate deflection theory. Int. J. Comput. Math. 2007, 84, 1483–1494. [Google Scholar] [CrossRef]
- Chekole, A.T.; Duresssa, G.F.; Kiltu, G.G. Non-polynomial septic spline method for singularly perturbed two point boundary value problems of order three. J. Taibah Univ. Sci. 2019, 13, 651–660. [Google Scholar] [CrossRef]
- Justine, H.; Chew, J.V.L.; Sulaiman, J. Quartic non-polynomial spline solution for solving two-point boundary value problems by using Conjugate Gradient Iterative Method. J. Appl. Math. Comput. Mech. 2017, 16, 41–50. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Ghaffari, R. Polynomial and nonpolynomial spline methods for fractional sub-diffusion equations. Appl. Math. Model. 2014, 38, 3554–3566. [Google Scholar] [CrossRef]
- Chegini, N.G.; Salaripanah, A.; Mokhtari, R.; Isvand, D. Numerical solution of the regularized long wave equation using nonpolynomial splines. Nonlinear Dyn. 2012, 69, 459–471. [Google Scholar] [CrossRef]
- Li, X.; Wong, P.J.Y. Numerical solutions of fourth-order fractional sub-diffusion problems via parametric quintic spline. ZAMM-J. Appl. Math. Mech./Z. Für Angew. Math. Und Mech. 2019, 99, e201800094. [Google Scholar] [CrossRef]
- Belyakova, O.V. On Implementation of Non-Polynomial Spline Approximation. Comput. Math. Math. Phys. 2019, 59, 689–695. [Google Scholar] [CrossRef]
- Ding, Q.; Wong, P.J.Y. Mid-knot cubic non-polynomial spline for a system of second-order boundary value problems. Bound. Value Probl. 2018, 2018, 156. [Google Scholar] [CrossRef]
- Khan, T.U.; Khan, M.A. Generalized conformable fractional operators. J. Comput. Appl. Math. 2019, 346, 378–389. [Google Scholar] [CrossRef]
- Abdelhakim, A.A.; Machado, J.A.T. A critical analysis of the conformable derivative. Nonlinear Dyn. 2019, 95, 3063–3073. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Chung, W.S. Fractional Newton mechanics with conformable fractional derivative. J. Comput. Appl. Math. 2015, 290, 150–158. [Google Scholar] [CrossRef]
- Mitra, S.; Poddar, S.; Ghose-Choudhury, A.; Garai, S. Solitary wave characteristics in nonlinear dispersive media: A conformable fractional derivative approach. Nonlinear Dyn. 2022, 110, 1777–1788. [Google Scholar] [CrossRef]
- Dun, M.; Xu, Z.; Wu, L.; Chen, Y. The information priority of conformable fractional grey model. J. Comput. Appl. Math. 2022, 415, 114460. [Google Scholar] [CrossRef]
- Mohamed, M.Z.; Hamza, A.E.; Sedeeg, A.K.H. Conformable double Sumudu transformations an efficient approximation solutions to the fractional coupled Burger’s equation. Ain Shams Eng. J. 2023, 14, 101879. [Google Scholar] [CrossRef]
- Jhangeer, A.; Muddassar, M.; Kousar, M.; Infal, B. Multistability and Dynamics of Fractional Regularized Long Wave equation with Conformable Fractional Derivatives. Ain Shams Eng. J. 2021, 12, 2153–2169. [Google Scholar] [CrossRef]
- El-Ajou, A.; Al-Smadi, M.; Oqielat, M.N.; Momani, S.; Hadid, S. Smooth expansion to solve high-order linear conformable fractional PDEs via residual power series method: Applications to physical and engineering equations. Ain Shams Eng. J. 2020, 11, 1243–1254. [Google Scholar] [CrossRef]
- Fisher, R.A. The Wave of Advance of Advantageous Genes. Ann. Eugen. 1937, 7, 353–369. [Google Scholar] [CrossRef]
- Ross, J.; Villaverde, A.F.; Banga, J.R.; Vázquez, S.; Morán, F. A generalized Fisher equation and its utility in chemical kinetics. Proc. Natl. Acad. Sci. USA 2010, 107, 12777–12781. [Google Scholar] [CrossRef] [PubMed]
- Merdan, M. Solutions of time-fractional reaction-diffusion equation with modified Riemann-Liouville derivative. Int. J. Phys. Sci. 2012, 7, 2317–2326. [Google Scholar] [CrossRef]
- Kenkre, V. Results from variants of the Fisher equation in the study of epidemics and bacteria. Phys. A Stat. Mech. Its Appl. 2004, 342, 242–248. [Google Scholar] [CrossRef]
- Majeed, A.; Kamran, M.; Iqbal, M.K.; Baleanu, D. Solving time fractional Burgers’ and Fisher’s equations using cubic B-spline approximation method. Adv. Differ. Equ. 2020, 2020, 175. [Google Scholar] [CrossRef]
- Yadav, O.P.; Jiwari, R. Finite element analysis and approximation of Burgers’-Fisher equation. Numer. Methods Partial. Differ. Equ. 2017, 33, 1652–1677. [Google Scholar] [CrossRef]
- Akinfe, T.K.; Loyinmi, A.C. A solitary wave solution to the generalized Burgers-Fisher’s equation using an improved differential transform method: A hybrid scheme approach. Heliyon 2021, 7, e07001. [Google Scholar] [CrossRef]
- Arora, S.; Jain, R.; Kukreja, V. A robust Hermite spline collocation technique to study generalized Burgers-Huxley equation, generalized Burgers-Fisher equation and Modified Burgers’ equation. J. Ocean Eng. Sci. 2022, in press. [CrossRef]
- Lipschutz, S.; Lipson, M. Linear Algebra; McGraw-Hill: New York, NY, USA, 2009. [Google Scholar]
- Majeed, A.; Kamran, M.; Abbas, M.; Singh, J. An Efficient Numerical Technique for Solving Time-Fractional Generalized Fisher’s Equation. Front. Phys. 2020, 8, 293. [Google Scholar] [CrossRef]
- Esen, A.; Tasbozan, O. Numerical solution of time fractional Burgers equation. Acta Univ. Sapientiae Math. 2015, 7, 167–185. [Google Scholar] [CrossRef]
- Singh, A.; Dahiya, S.; Singh, S.P. A fourth-order B-spline collocation method for nonlinear Burgers–Fisher equation. Math. Sci. 2020, 14, 75–85. [Google Scholar] [CrossRef]
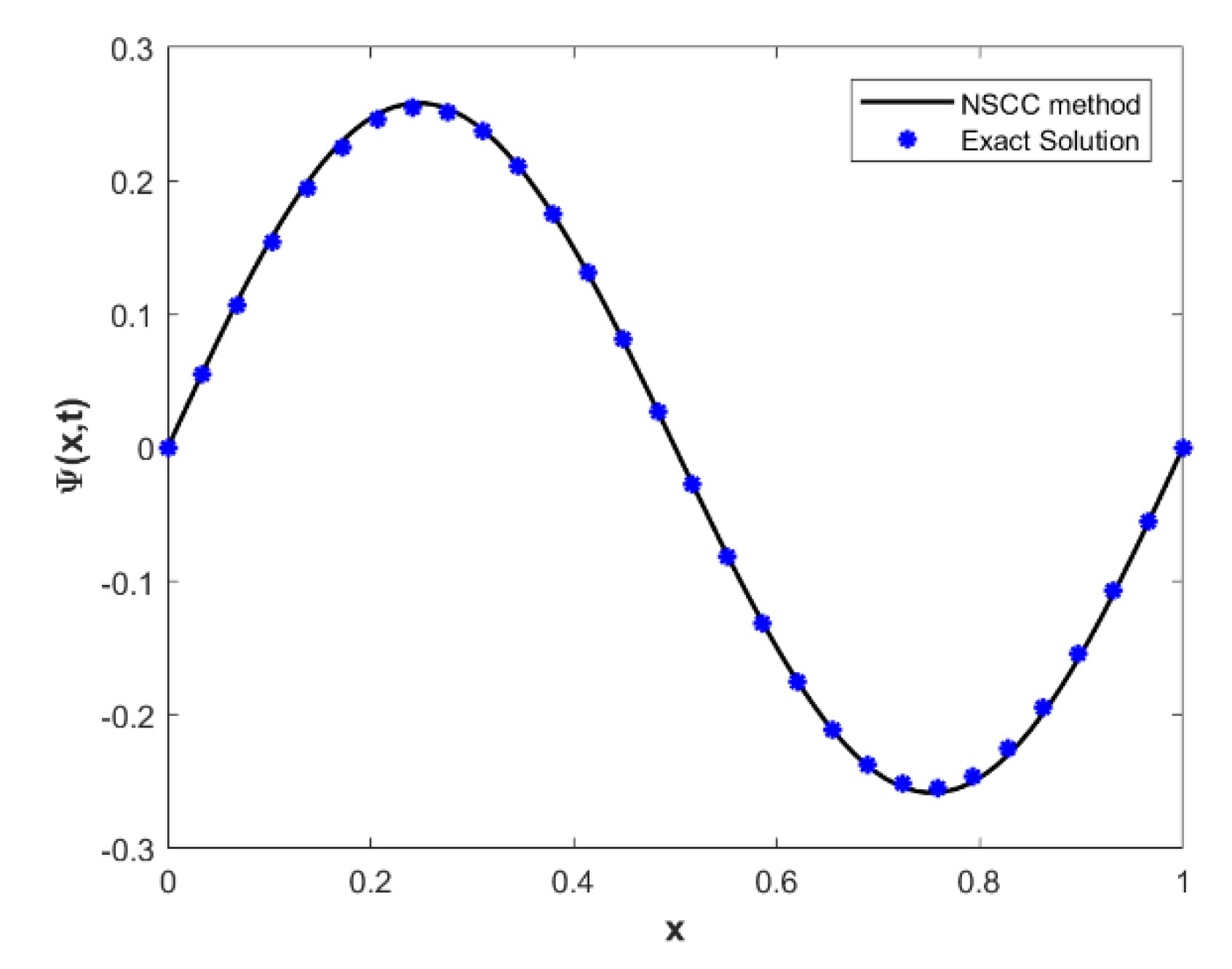
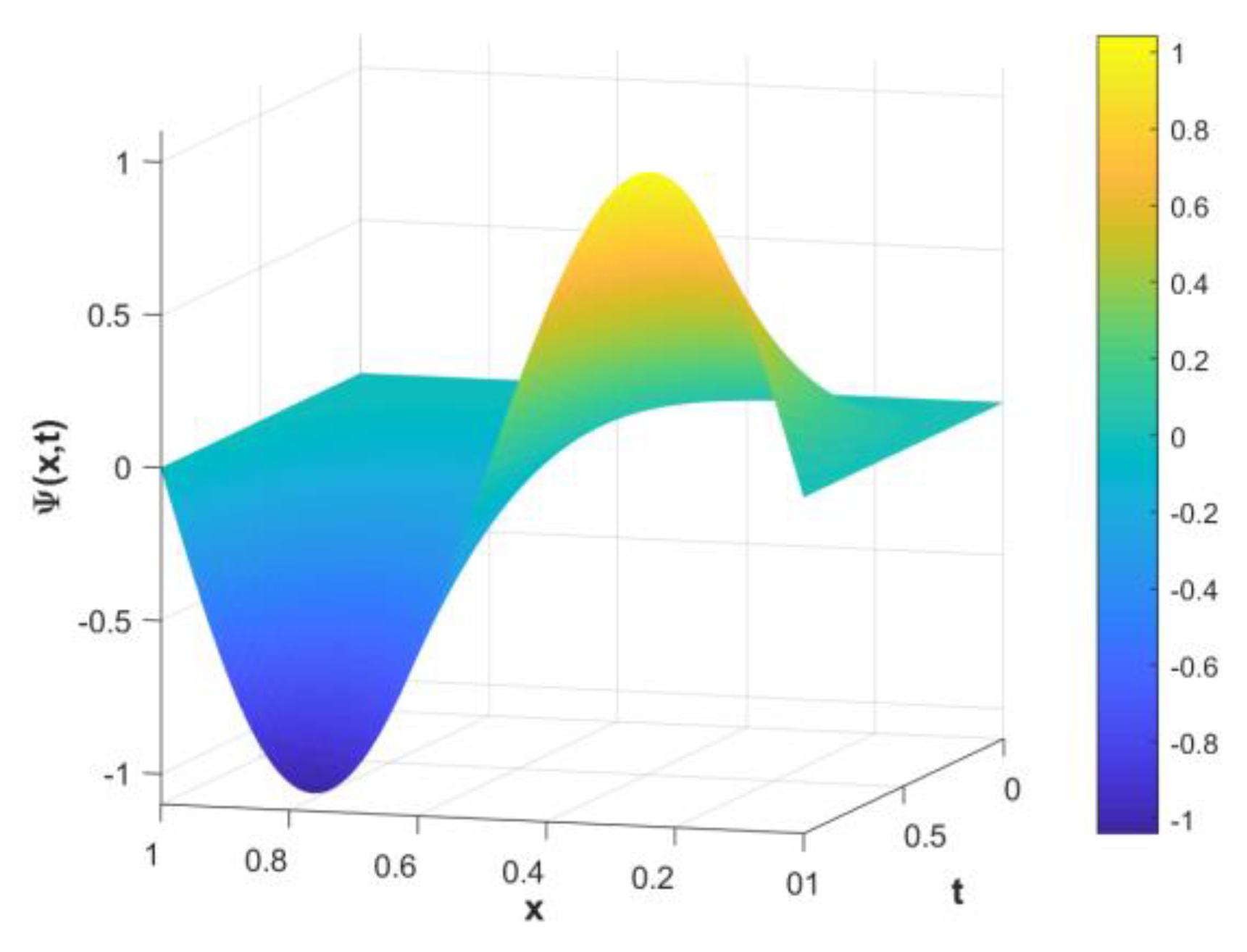
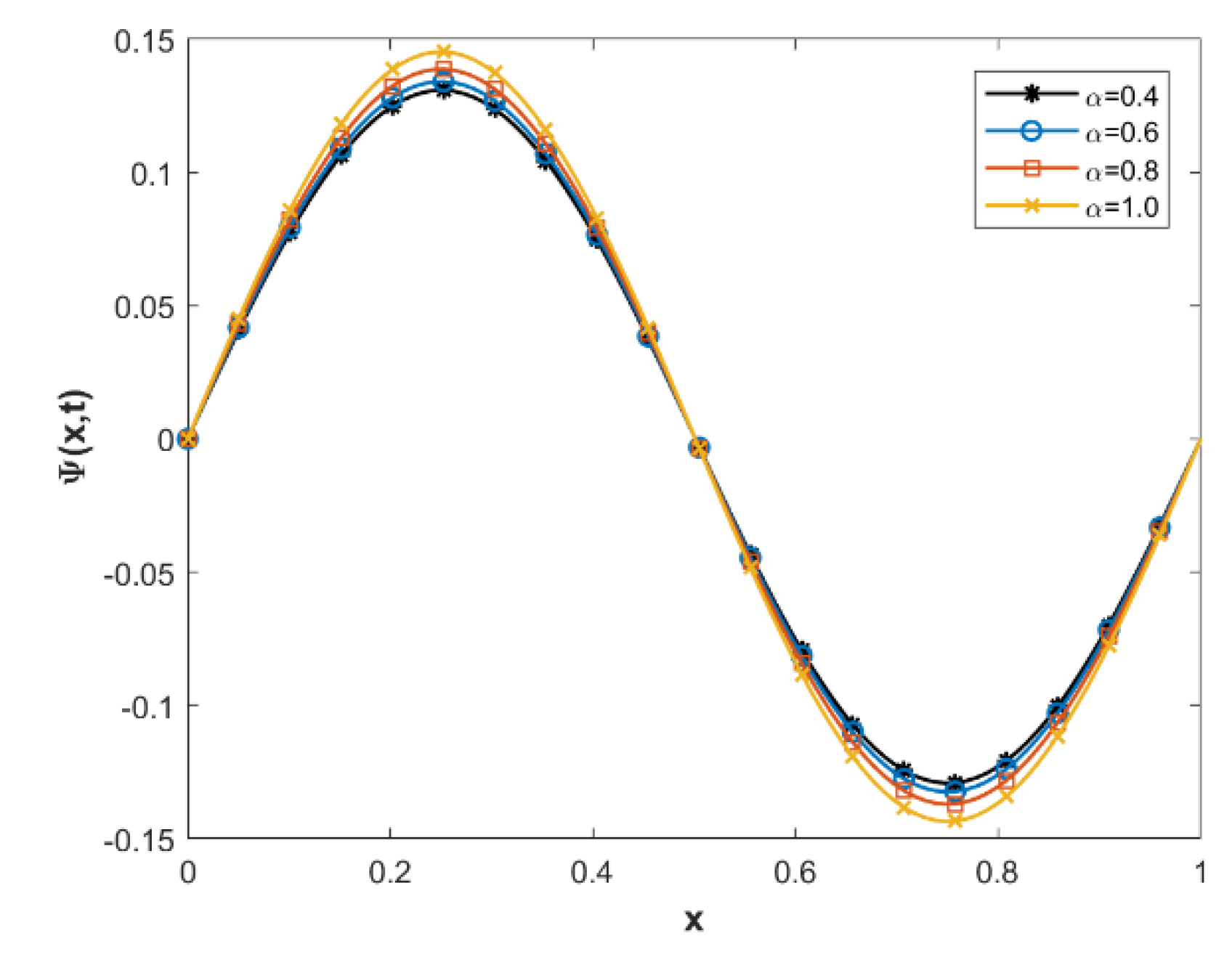
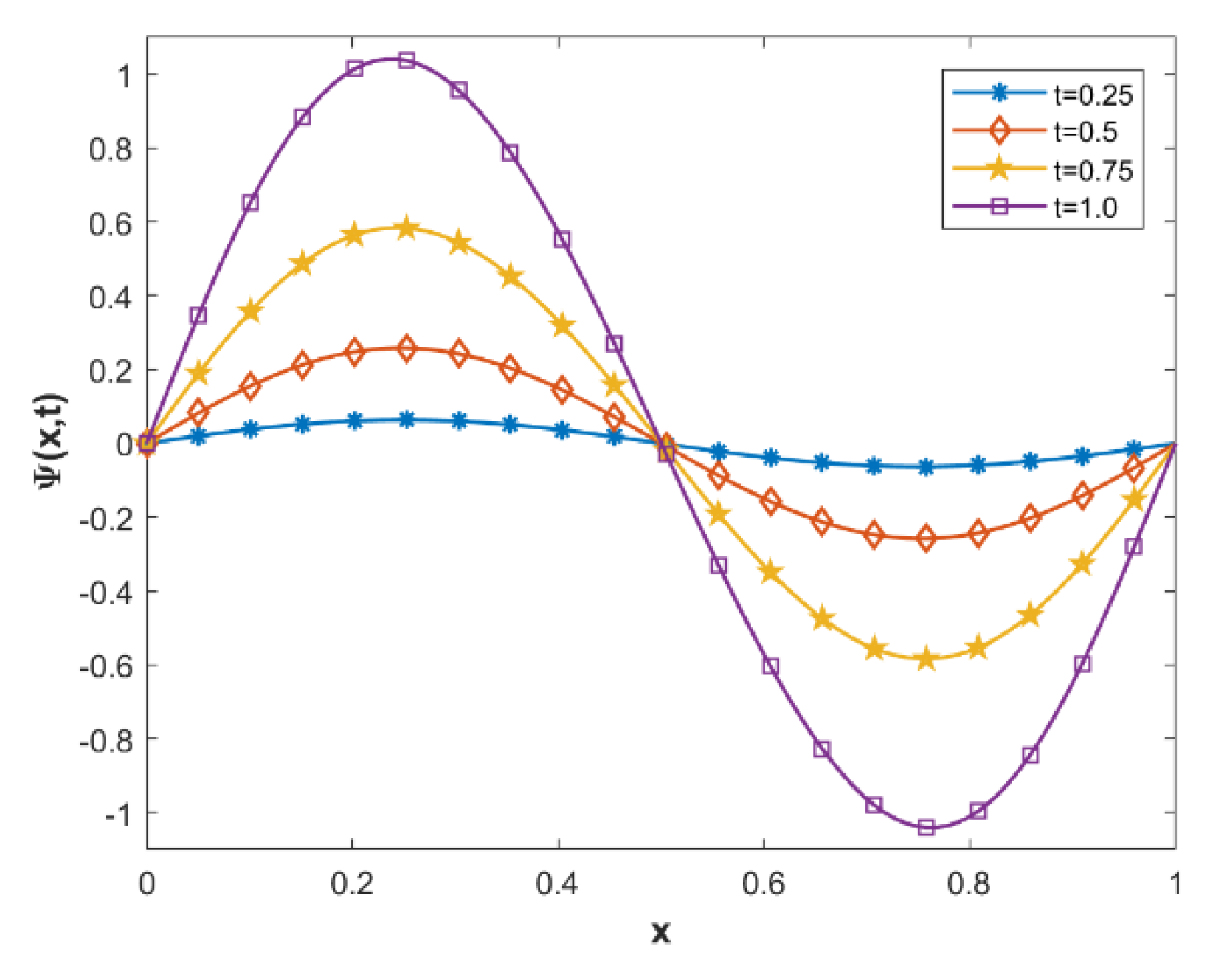
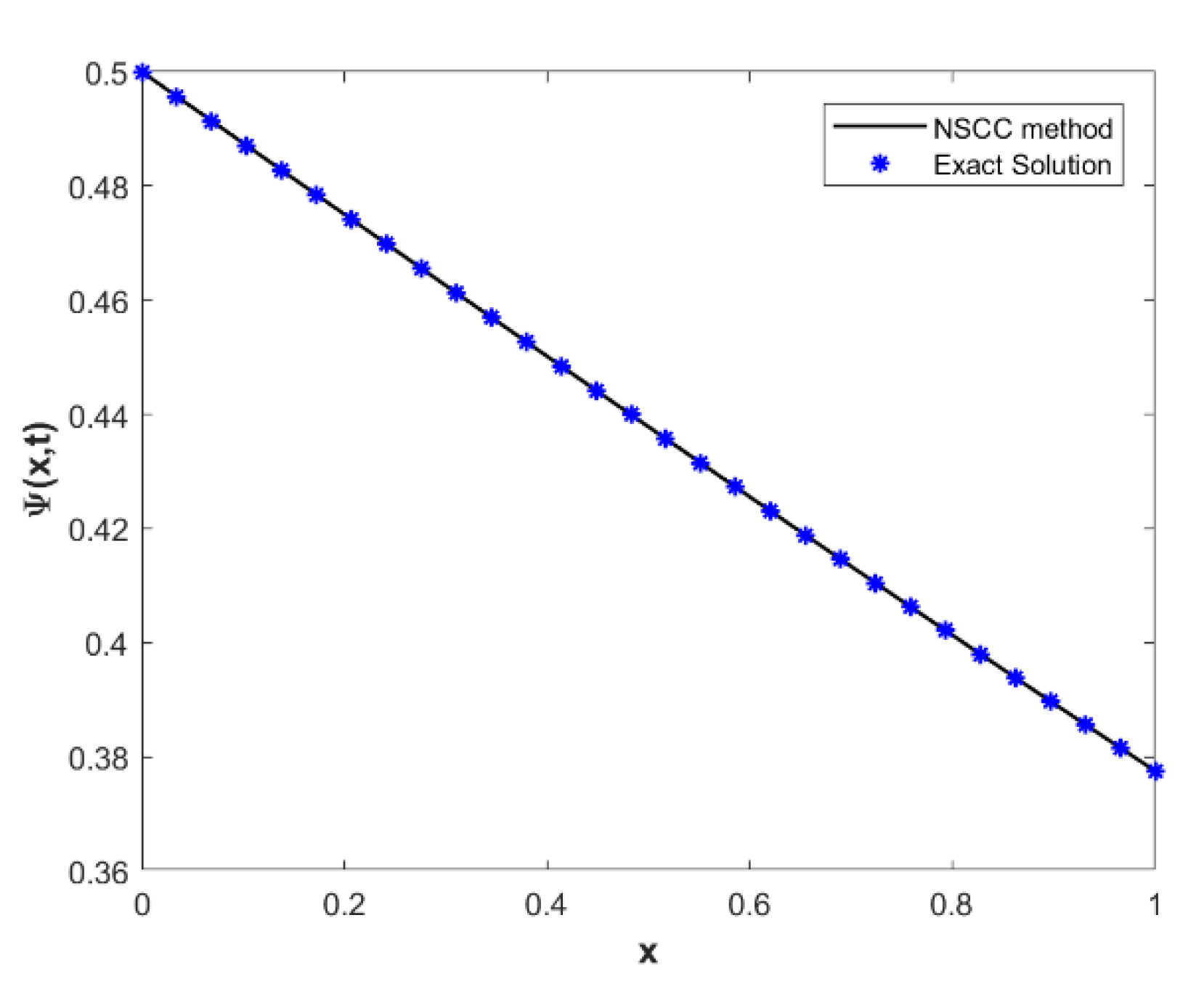
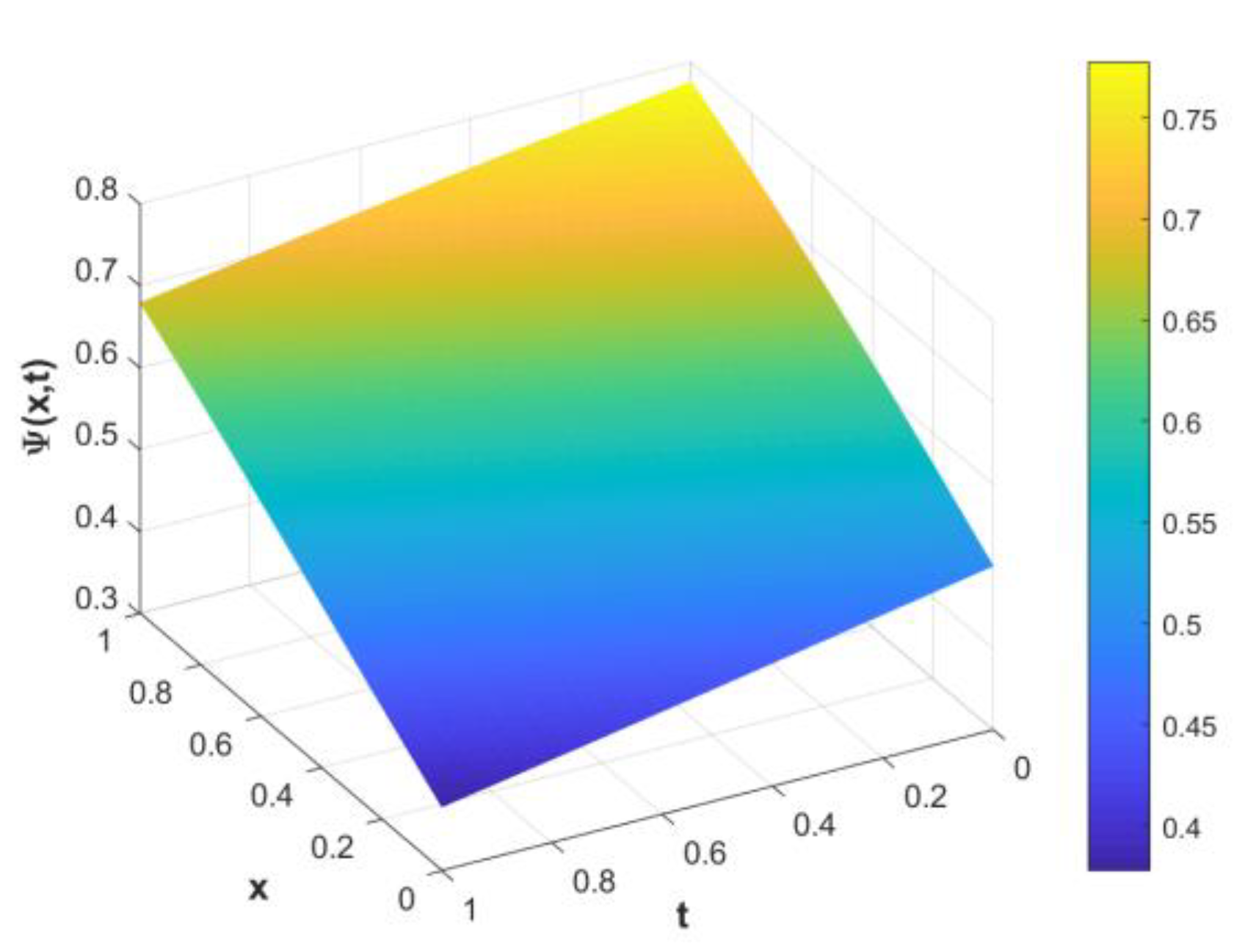
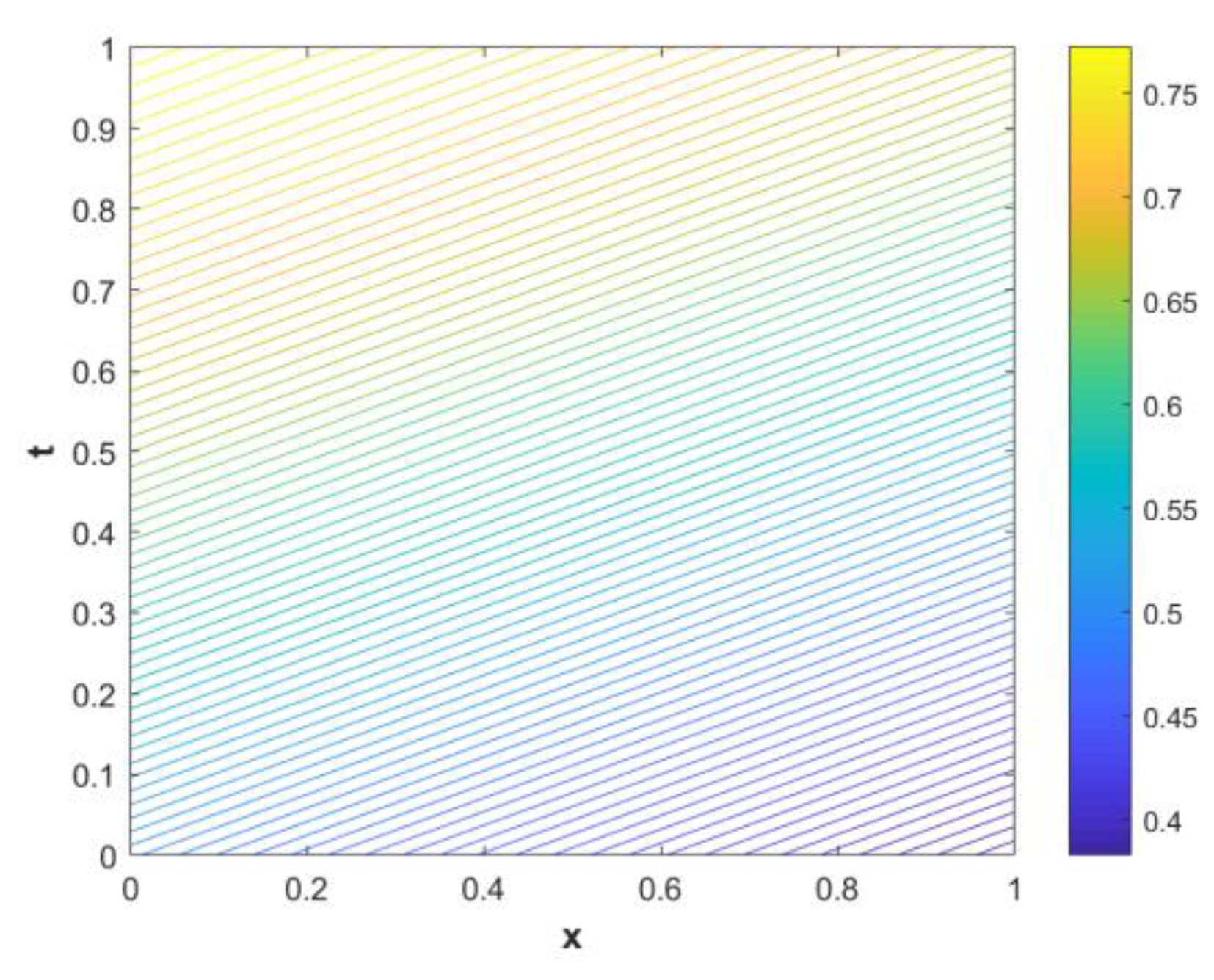
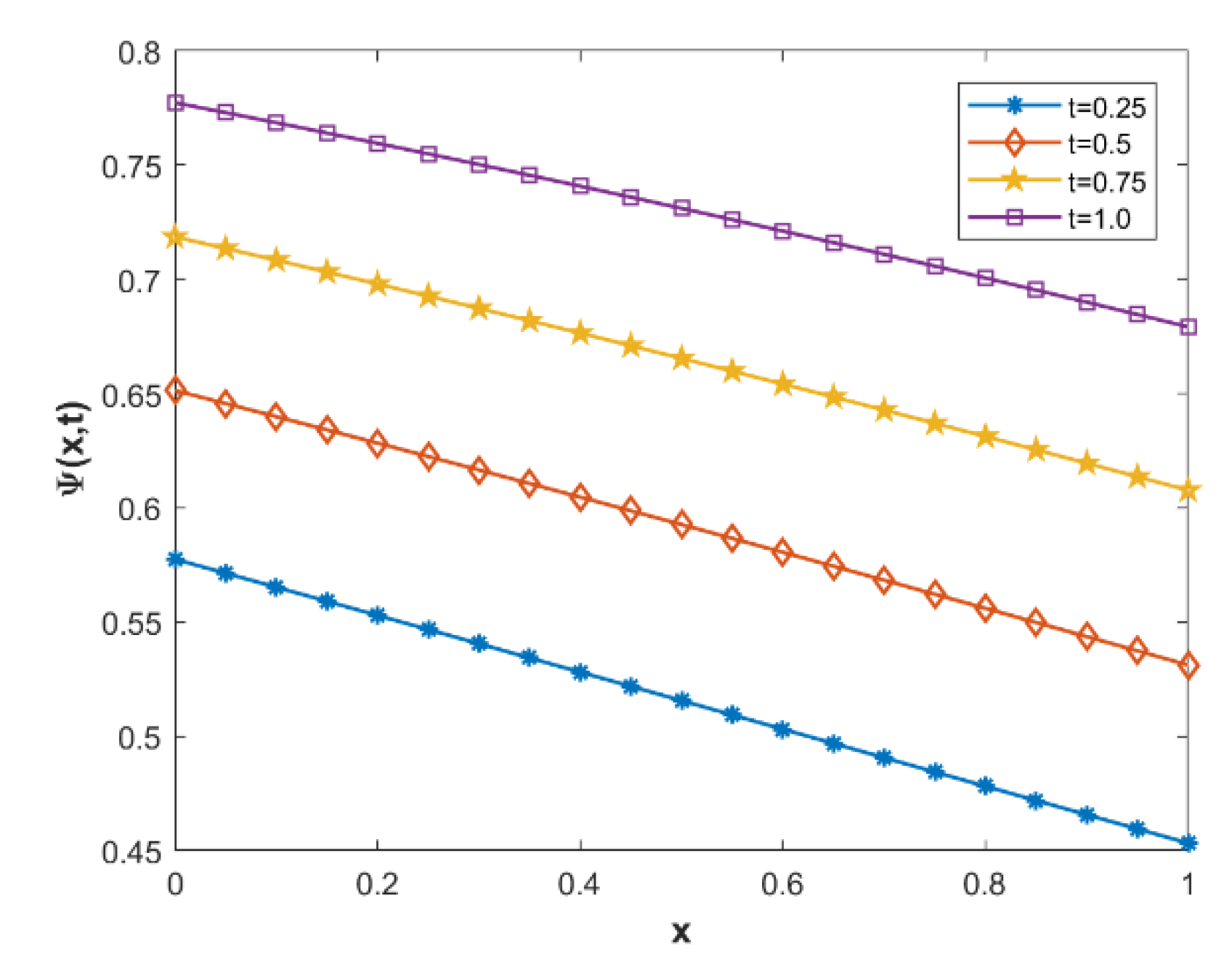
| NPSCCM | QBSGM [53] | NPSCCM | QBSGM [53] | |
|---|---|---|---|---|
| 6.2067 × 10−7 | 0.0322 × 10−3 | 2.9121 × 10−7 | 0.0178 × 10−3 | |
| 1.3361 × 10−6 | 0.5121 × 10−3 | 6.2687 × 10−7 | 0.3595 × 10−3 | |
| 2.3086 × 10−6 | 1.4878 × 10−3 | 1.0831 × 10−6 | 1.0486 × 10−3 | |
| 2.4685 × 10−6 | 1.9744 × 10−3 | 1.1582 × 10−6 | 1.3924 × 10−3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yousif, M.A.; Hamasalh, F.K. A Hybrid Non-Polynomial Spline Method and Conformable Fractional Continuity Equation. Mathematics 2023, 11, 3799. https://doi.org/10.3390/math11173799
Yousif MA, Hamasalh FK. A Hybrid Non-Polynomial Spline Method and Conformable Fractional Continuity Equation. Mathematics. 2023; 11(17):3799. https://doi.org/10.3390/math11173799
Chicago/Turabian StyleYousif, Majeed A., and Faraidun K. Hamasalh. 2023. "A Hybrid Non-Polynomial Spline Method and Conformable Fractional Continuity Equation" Mathematics 11, no. 17: 3799. https://doi.org/10.3390/math11173799
APA StyleYousif, M. A., & Hamasalh, F. K. (2023). A Hybrid Non-Polynomial Spline Method and Conformable Fractional Continuity Equation. Mathematics, 11(17), 3799. https://doi.org/10.3390/math11173799







