Abstract
This article presents a study on forecasting silver prices using the extreme gradient boosting (XGBoost) machine learning method with hyperparameter tuning. Silver, a valuable precious metal used in various industries and medicine, experiences significant price fluctuations. XGBoost, known for its computational efficiency and parallel processing capabilities, proves suitable for predicting silver prices. The research focuses on identifying optimal hyperparameter combinations to improve model performance. The study forecasts silver prices for the next six days, evaluating models based on mean absolute percentage error (MAPE) and root mean square error (RMSE). Model A (the best model based on MAPE value) suggests silver prices decline on the first and second days, rise on the third, decline again on the fourth, and stabilize with an increase on the fifth and sixth days. Model A achieves a MAPE of 5.98% and an RMSE of 1.6998, utilizing specific hyperparameters. Conversely, model B (the best model based on RMSE value) indicates a price decrease until the third day, followed by an upward trend until the sixth day. Model B achieves a MAPE of 6.06% and an RMSE of 1.6967, employing distinct hyperparameters. The study also compared the proposed models with several other ensemble models (CatBoost and random forest). The model comparison was carried out by incorporating 2 additional metrics (MAE and SI), and it was found that the proposed models exhibited the best performance. These findings provide valuable insights for forecasting silver prices using XGBoost.
MSC:
68T99; 62M10; 62P20
1. Introduction
Silver, denoted by the symbol Ag and originating from the Latin term ‘argentum’, stands as a metallic element with an atomic number of 47. Its distinct properties and traits render it a sought-after resource across diverse industries. Renowned for its remarkable electrical and thermal conductivity, silver frequently assumes a crucial role in the production of electronic devices within the manufacturing sector [1]. Furthermore, within the realm of medicine, the utilization of silver nanoparticles has wielded a substantial influence on the progression of treatments in the past few decades [2]. Silver’s antimicrobial properties empower the application of silver nanoparticles as coatings for medical instruments and treatments. Beyond this, silver assumes a pivotal function in the realm of solar energy capture, with a standard solar panel necessitating around 20 g of silver for its production [3]. Year by year, the manufacturing of solar panels demonstrates a consistent rise, driving an escalating need for silver. Additionally, classified as a precious metal, silver maintains a relatively high value and demand in the market [4].
Precious metals such as gold, silver, and platinum have correlations that influence their respective prices [5]. The price correlation among these precious metals can be influenced by various factors, including politics, the value of the US dollar, market demand, and others [6]. For example, in a gold price forecasting study conducted by Jabeur, Mefteh–Wali, and Viviani, supplementary variables including platinum prices, iron ore rates, and the dollar-to-euro exchange rate were incorporated [7]. By incorporating these variables, the forecasting results were more accurate compared to using only one variable [8]. Many investors choose to invest in precious metals (such as silver, gold, and platinum) as valuable assets [9]. The time series data for international silver prices, sourced from investing.com (accessed on 21 February 2023) [10], reveals notable volatility in silver price trends. Considering this challenge, there emerges a necessity for a predictive model capable of forecasting silver prices—a tool that holds value for investors when making informed decisions.
Forecasting is a discipline that involves studying the available data to predict the future [11]. The forecasting process typically involves using time series data with target categories that align with the research objectives. There are many traditional methods available, such as statistical analysis, regression, smoothing, and exponential smoothing, to perform forecasting [12]. However, these traditional methods are often deemed less effective in addressing complex problems. Therefore, machine-learning approaches have been developed to tackle more complex problems.
Machine learning involves a system capable of learning from targeted training data, and automating the creation of analytical models to adeptly tackle various problems [13]. Machine learning finds its common classification in three principal types: supervised learning (involving labeled output), unsupervised learning (operating without labeled output), and reinforcement learning. These categories house an array of evolving methodologies. In particular, supervised learning plays a significant role in forecasting, especially when dealing with time series data containing inherently desired outputs. Amid the plethora of techniques within supervised learning, prominent forecasting methods comprise gradient boosting, LSTM, CatBoost, extreme gradient boosting, and several others.
Extreme gradient boosting, popularly referred to as XGBoost, stands out as one of the most prevalent techniques in the realm of machine learning, employed extensively for tasks like forecasting and classification. XGBoost was first introduced by Friedman as an enhancement of decision tree and gradient boost methods [14]. XGBoost has several advantages, including relatively high computational speed, parallel computing capability, and high scalability [15]. In the process of creating and training an XGBoost model, there are several aspects to consider. Notably, XGBoost entails hyperparameters that require careful tuning to achieve optimal model performance [16]. Researchers must delve into hyperparameter combinations, a process referred to as hyperparameter tuning, to attain an XGBoost model performance that optimally suits the specific problem. In the realm of machine learning, mean absolute error (MAE) and root mean square Error (RMSE) stand as prevalent metrics, employed to gauge the effectiveness of the model [17].
Several previous studies use machine learning in forecasting. One example is the research conducted by Nasiri and Ebadzadeh [18] where they predicted time series data using a multi-functional recurrent fuzzy neural network (MFRFNN). It was found that the proposed method performed better than the second-best method in the Lorenz time series. Luo et al. [19] conducted a study using the ensemble learning method where they compared several methods to estimate the aboveground biomass and found the CatBoost method has the best performance. In addition, there are also several previous studies that use the XGBoost method in forecasting. Li et al. employed XGBoost to forecast solar radiation and discovered that XGBoost outperformed previous research with the lowest RMSE value [20]. Fang et al. conducted forecasting of COVID-19 cases in the USA by comparing the ARIMA and XGBoost methods. It was found that the XGBoost method had better performance based on the metrics used in the study [14]. Jabeur et al. predicted gold prices using XGBoost and compared it with other machine learning methods such as CatBoost, random forest, LightGBM, neural networks, and linear regression. They found that XGBoost demonstrated the best performance [7]. However, it is worth noting that Jabeur et al. conducted their research without hyperparameter tuning, as their focus was on comparing the performance of different machine learning methods.
Based on the background presented, this study aims to forecast silver prices using the XGBoost method, similar to the approach employed by Jabeur et al. [7], but with the addition of hyperparameter tuning using grid search. The novelty offered in this research focuses on the hyperparameter tuning process before grid search. Generally, a random value is selected for each hyperparameter for grid search, but this research proposes to perform hyperparameter tuning for each hyperparameter first by plotting the MAPE and RMSE evaluation values to determine the value to be selected. The study incorporates gold and platinum prices, as well as the euro-to-dollar exchange rate, as additional variables. To attain the best XGBoost model, the performance of the model was evaluated using the MAPE and RMSE. In addition, this research also compares models by adding two evaluation metrics, namely MAE and SI, to obtain a more comprehensive conclusion.
2. Materials and Methods
2.1. Data Collection
This research aims to analyze a time series dataset encompassing silver prices, as well as supplementary variables including gold prices, platinum prices, and the dollar-to-euro exchange rate. This analysis serves as a foundation for conducting forecasting, utilizing a comprehensive dataset comprising 2566 data points. The dataset comprises a daily timeframe obtained from investing.com [10], covering the period from 20 February 2013 to 20 February 2023. Notably, the prices of silver, gold, and platinum are denominated in USD per troy ounce. Captured as a daily time series, the data span a decade.
This dataset is partitioned into training and testing subsets, accounting for 80% and 20%, respectively. The training data encompasses the period from 20 February 2013 to 11 February 2021, while the testing data spans from 12 February 2021 to 20 February 2023. Employing the Python programming language, the data are randomly divided, resulting in 2052 data points for training and 514 for testing. Table 1 presents the descriptive statistics of the time series data used. Figure 1 displays data visualization in graphical form. Figure 2 presents the correlation matrix between variables.

Table 1.
Descriptive statistics.
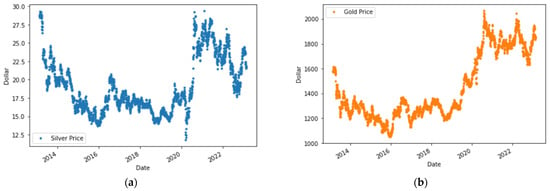
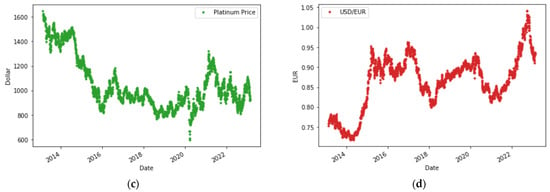
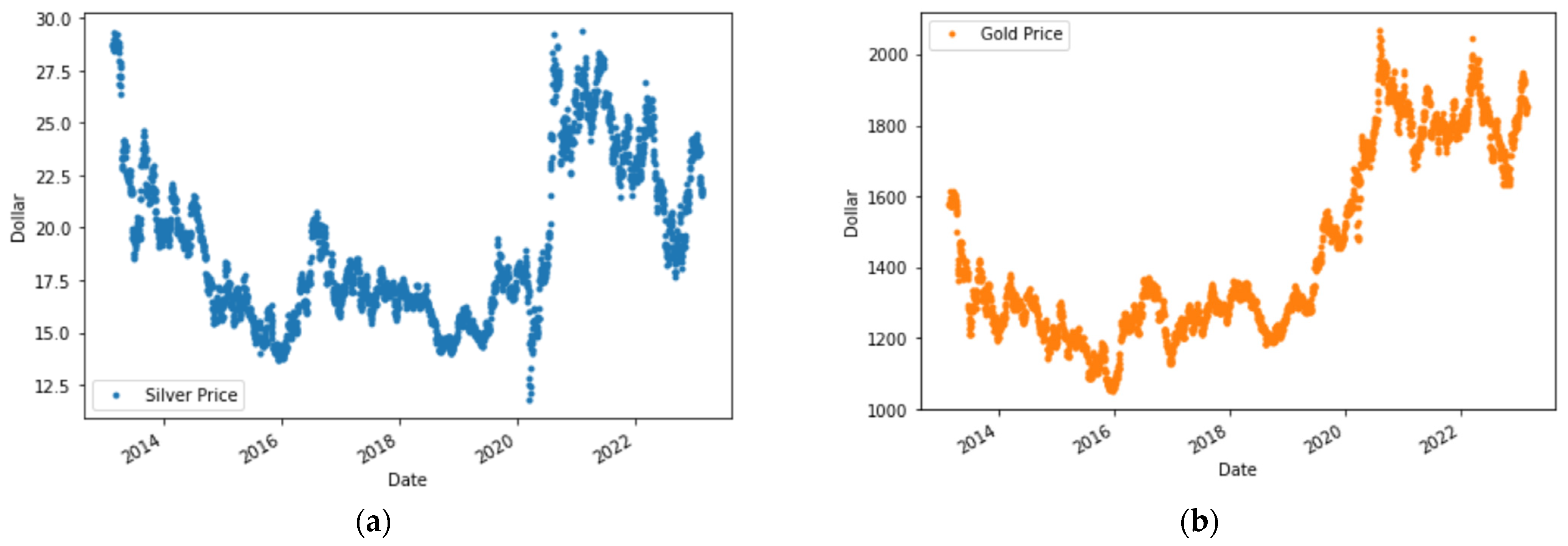
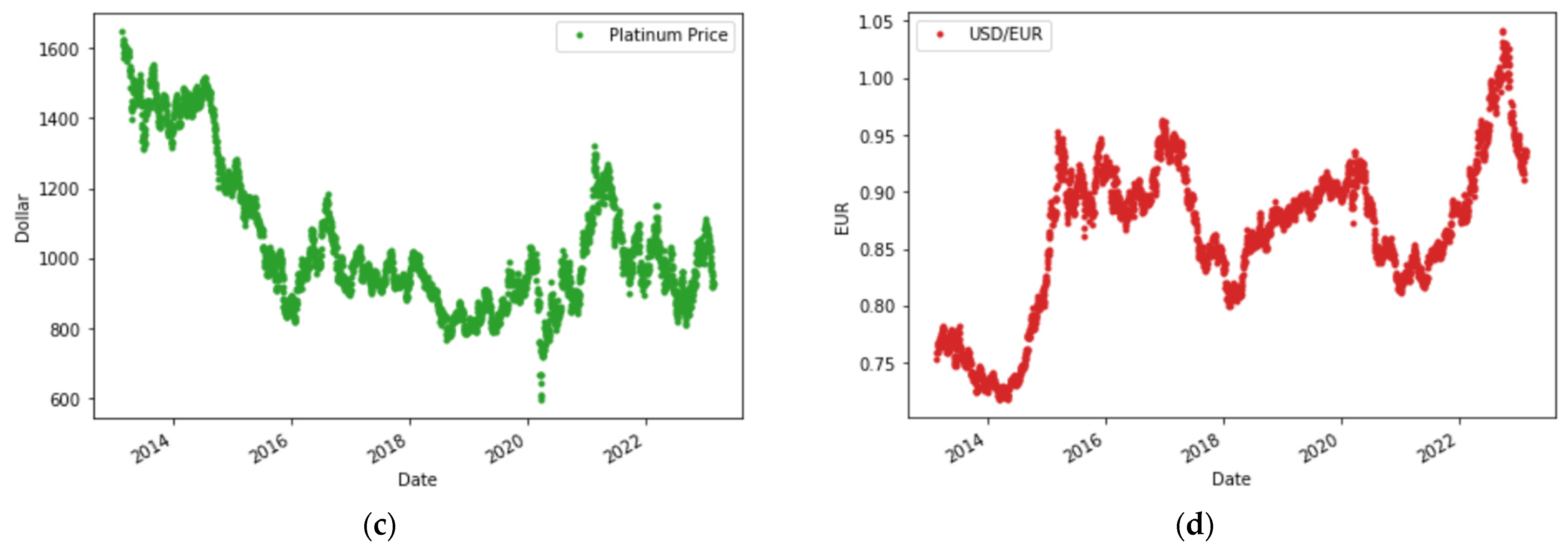
Figure 1.
Graphical plots of each variable. (a) Silver price; (b) gold price; (c) platinum price; (d) USD in EUR.
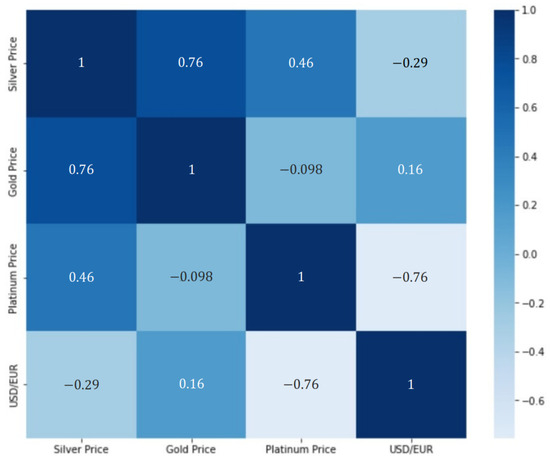
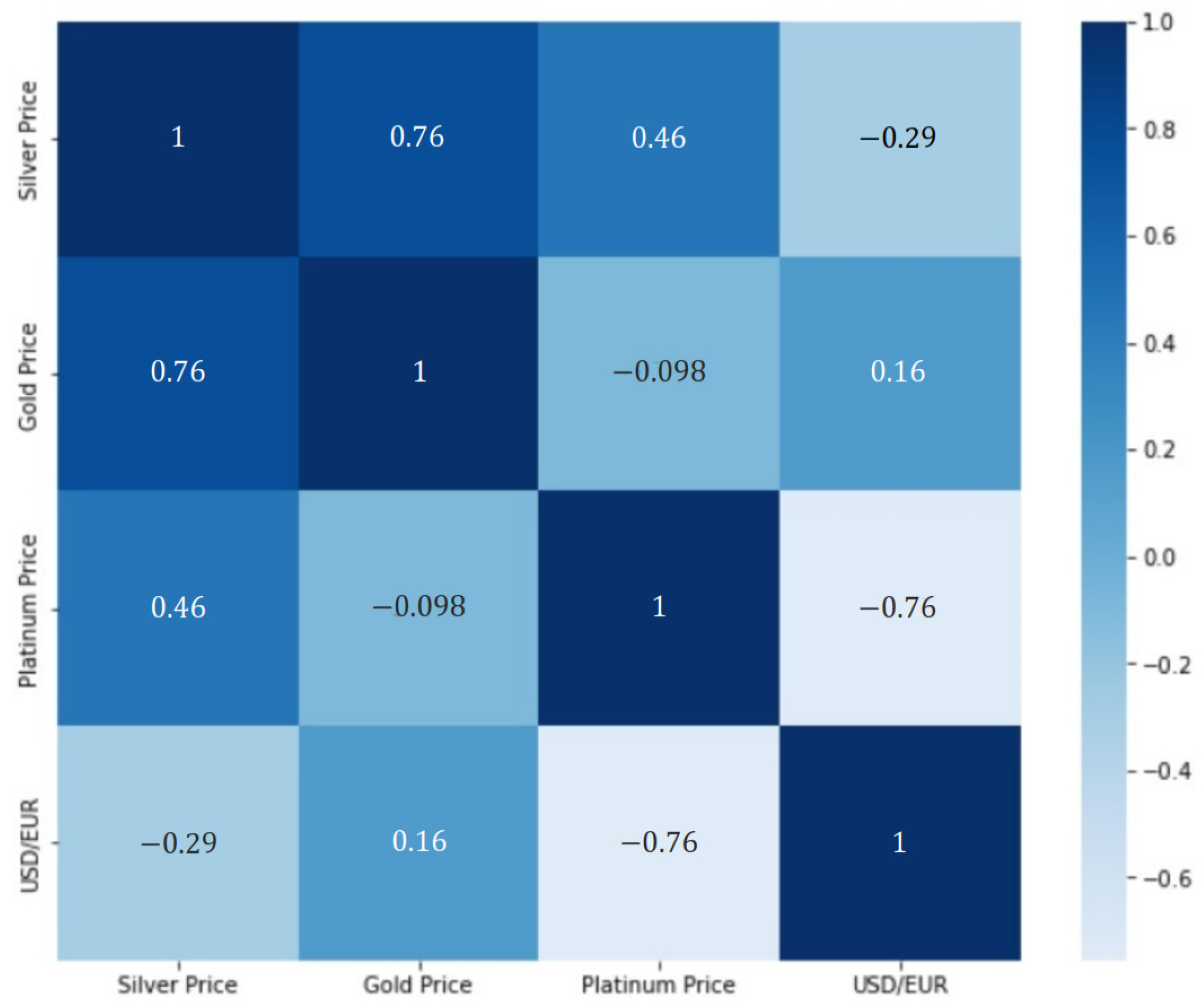
Figure 2.
Correlation heatmap.
2.2. Random Forest
Random forest (RF) is an ensemble learning algorithm commonly used to perform classification or regression processes. RF models are often used as base models to assess the performance of more complex models and are known for their good performance in performing a variety of tasks. The RF method offers better generalizations and valid estimates because it includes random sampling and improved properties of techniques in ensemble methods [21]. The predicted value, , in the RF algorithm can be expressed as follows:
where is a set of -th learner random tree learners and is the number of samples/tree.
2.3. CatBoost
CatBoost or “Categorical Boosting” is one of the machine learning algorithms developed from gradient boosting. CatBoost modifies the standard gradient boosting algorithm called the ordering principle, which avoids target leakage, and a new algorithm for processing categorical features [22]. CatBoost is commonly used on datasets with a mix of categorical and numerical features, which are commonly used in real-world applications. The function of decision tree can be written as:
where is the random vector of input variables, is the outcome, and function is a least squares approximation by the Newton method.
2.4. Extreme Gradient Boosting
Extreme gradient boosting, commonly known as XGBoost, is a method that further enhances or optimizes the gradient boosting technique. XGBoost is a robust and widely used machine learning technique that has swept the data science world [23]. In the boosting method, models are trained sequentially, where the results from each weak learner’s training influence the next model to be trained [24]. This method was developed by Chen and Guestrin [15] to propose an algorithm that exhibits sparsity awareness (identifying data that has little impact on calculations) for tree learning predictions. XGBoost utilizes the output values from each constructed tree to obtain the final output value, as shown in the following equation:
where is the predicted value, is the predicted value at the previous iteration, is the input vector, is the number of regression trees, represents the set of all regression trees, is the output of the th tree, and is the th regression trees. The objective in XGBoost modeling is to minimize the value of the loss function using the following equation:
where is the loss function and is the regularization term. The equation can be expanded as follows:
where indicates the number of iterations.
The equation can be rewritten by applying the second-order Taylor series [25] and eliminating the constant variable as follows:
where and .
2.5. Hyperparameter Tuning
Each machine learning method typically has more than one hyperparameter. The values of these hyperparameters need to be initialized by the model creator before building the model, and they are independent of the data or model used [26]. Hyperparameter tuning is an optimization process performed by the model creator to improve the constructed model by modifying the parameter values that influence the model’s training process [27]. This research uses the grid search method [26] in performing the hyperparameter tuning process. Grid search is an approach in machine learning for systematically exploring a predetermined set of hyperparameter values to find the combination that yields the optimal performance for a model [28]. Here are several hyperparameters of the XGBoost method that were tuned in this research using the Python programming language. More detailed information about the hyperparameters can be found in Table 2.

Table 2.
List of hyperparameters that are tuned.
2.6. Model Evaluation
2.6.1. Mean Absolute Percentage Error
MAPE (mean absolute percentage error) is a metric used as an indicator of model accuracy. Suppose there are samples with forecasted values (forecasted data for the -th sample) and actual values (actual data for the -th sample). The formula for MAPE is as follows [29]:
2.6.2. Root Mean Square Error
RMSE (root mean square error) is commonly used to measure the difference (error) between actual and forecasted data. It calculates the square root of the average squared differences between the actual and forecasted values [30]. The RMSE is given by:
2.6.3. Mean Absolute Error
MAE (mean absolute error) is a commonly used metric to evaluate models for regression or classification. It quantifies the average magnitude of errors between predicted values and actual (observed) values. The formula for MAE is as follows [31]:
2.6.4. Scatter Index
SI (scatter index) is a normalized metric of RMSE. The range of the SI for the classification of the models is “excellent” if SI < 0.1, “good” if 0.1 < SI < 0.2, “fair” if 0.2 < SI < 0.3, and “poor” if SI > 0.3 [32]. The SI formula is given by:
2.6.5. K-Fold Cross Validation
K-fold cross-validation is a commonly used evaluation technique in machine learning [33]. This technique divides the data into segments without repetition to calculate the average metric for each training. In each training process, the model is trained on segments and then validated using the remaining segment [34]. This process continues times until each segment is used exactly once as validation data.
3. Methodology
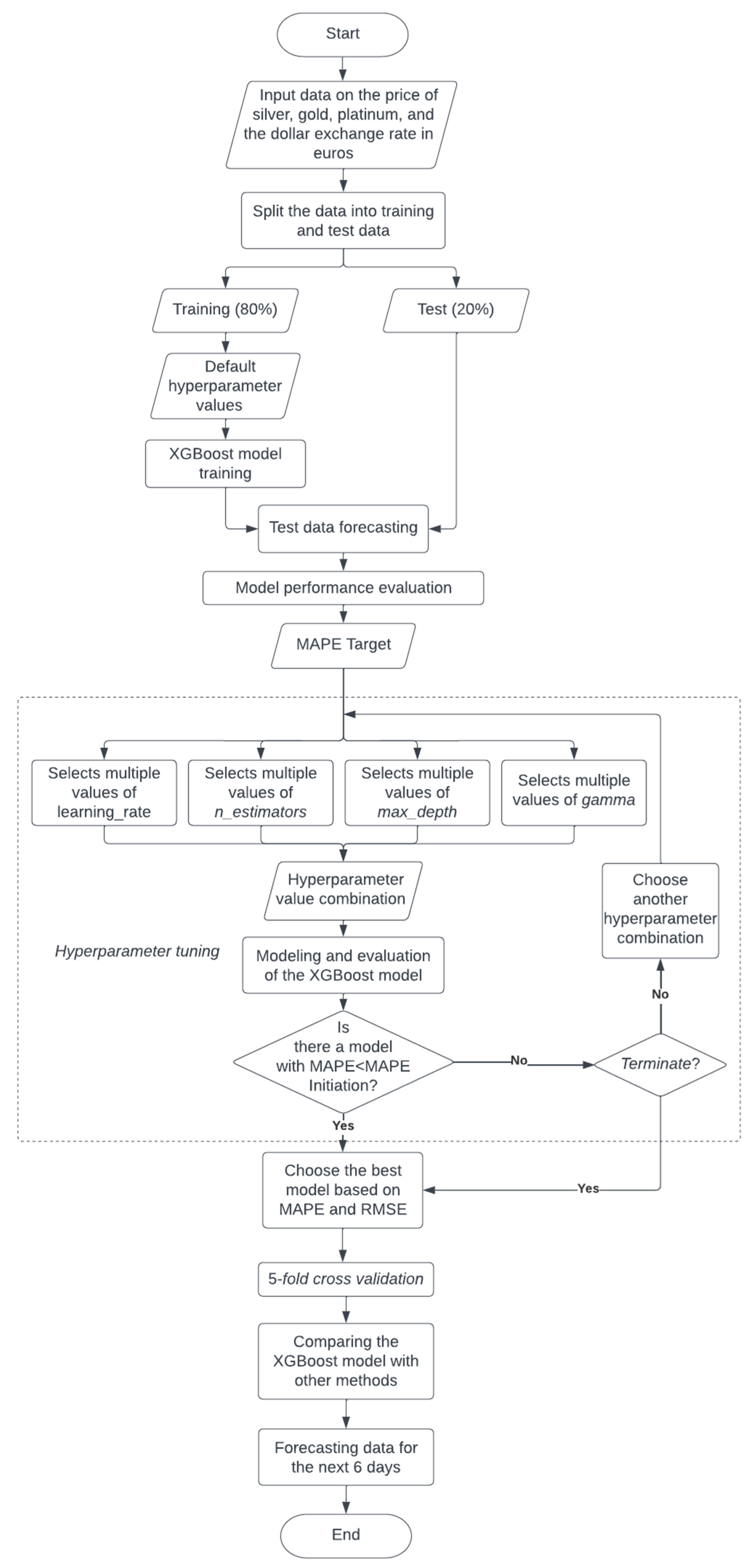
This research uses the XGBoost method to forecast the price of silver with additional variables of platinum price data, gold, and the dollar exchange rate in euros. This research uses the Python programming language. The research process includes the data input process, model building, and hyperparameter tuning which can be seen in full in Figure 3.
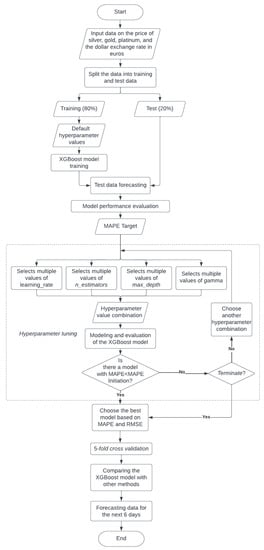
Figure 3.
Research flowchart.
In the hyperparameter tuning process, the values for each hyperparameter are selected first. For example, to select the gamma value, several XGBoost models are built with different gamma values (default values are used for hyperparameters other than gamma). Then each model is evaluated and the MAPE and RMSE values are plotted into a graph. Then from the graph, some hyperparameter values with the best performance are selected. Then the process is carried out for other hyperparameters. After selecting several values for each hyperparameter, GridSearch is performed to build XGBoost models for all possible hyperparameter combinations. Finally, the model with the best MAPE and RMSE values is selected as the final model.
4. Results and Discussion
4.1. Initial Model
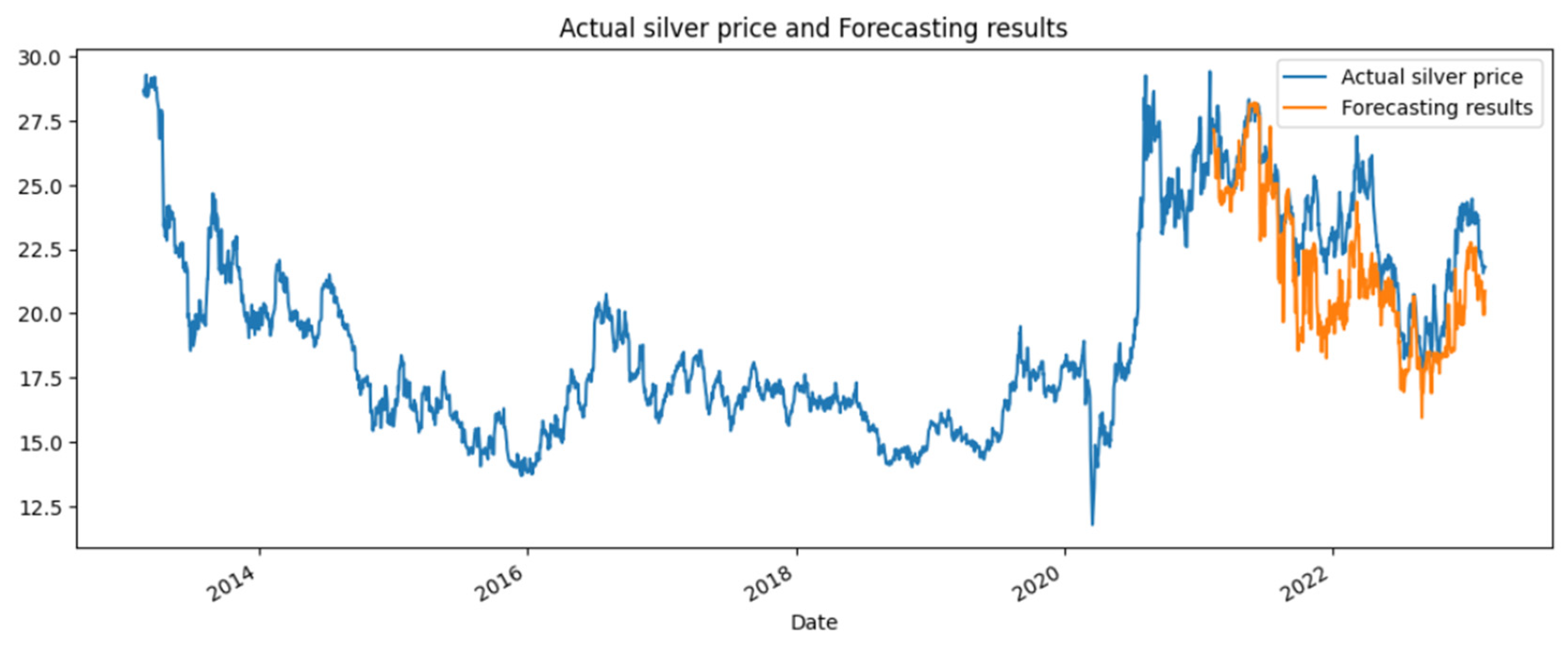
First, an initial baseline model was constructed before performing hyperparameter tuning using the Python programming language. The initial model utilized default values for its hyperparameters (Table 1), which were pre-defined in the xgboost package, leading to the creation of 100 trees. The initial model was built using the training data, and then forecasting was conducted on the testing data, followed by evaluation. The comparison between the forecasted results of the initial model and the actual data can be seen in Figure 4.
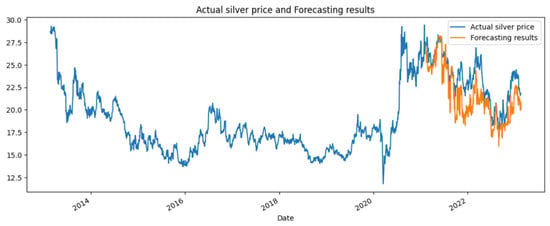
Figure 4.
The forecasted results of the initial model and the actual silver prices.
The evaluation results of the initial model yielded an MAPE value of 7.77% (highly accurate) and an RMSE value of 2.16. Subsequently, the hyperparameter tuning process was conducted with the aim of finding hyperparameter values that could optimize the model to achieve a MAPE value smaller than that of the initial model.
4.2. Hyperparameter Tuning
In order to optimize the model’s performance, a hyperparameter tuning process was conducted to identify the optimal combination of hyperparameters for silver price forecasting. The hyperparameters considered for tuning were max_depth, gamma, learning_rate, and n_estimators. Initially, different values were tested for each hyperparameter using Python programming, aiming to determine suitable value ranges. During each experiment, default values were used for the remaining hyperparameters. MAPE and RMSE were employed as evaluation metrics to assess the performance of each experiment.
4.2.1. Max_Depth
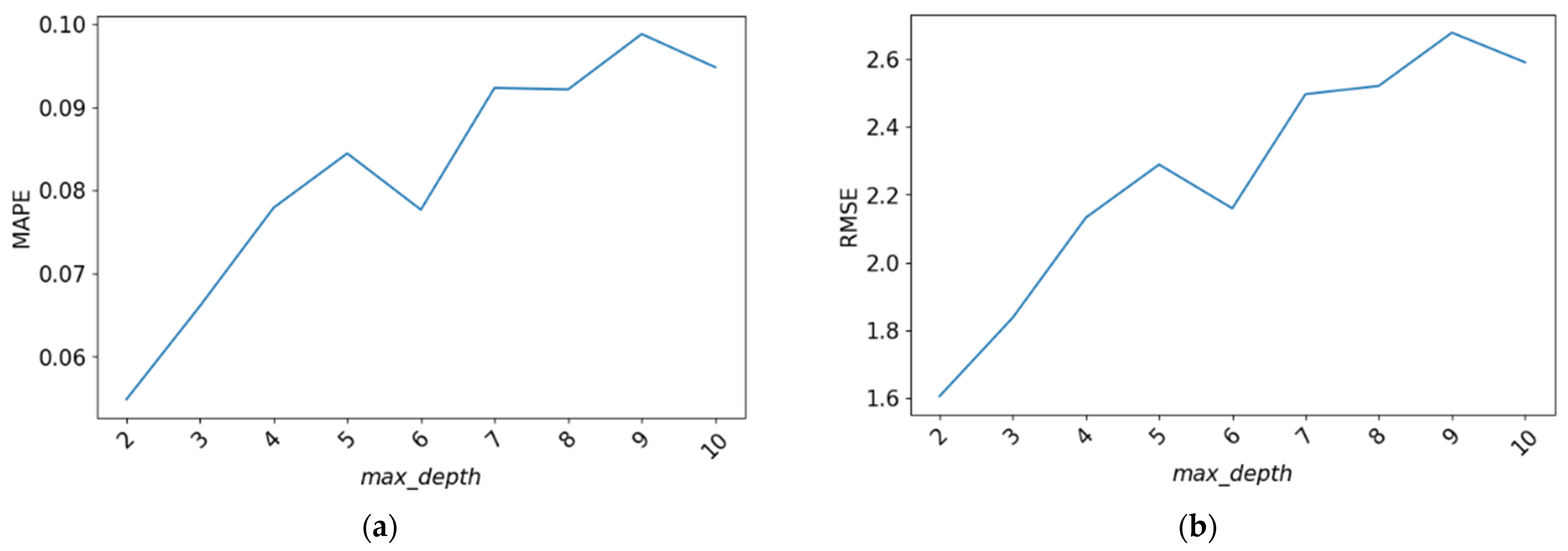
Several values of the hyperparameter max_depth was tested, including 2, 3, 4, 5, 6, 7, 8, 9, and 10. The evaluation results for the RMSE and MAPE values of each model can be observed in Figure 5.
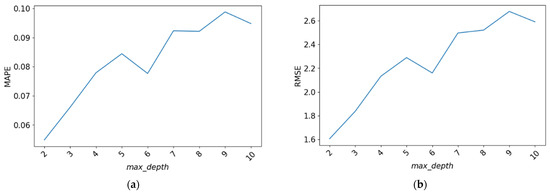
Figure 5.
The evaluation scores for the hyperparameter max_depth. (a) MAPE values obtained from hyperparameter tuning; (b) RMSE values obtained from hyperparameter tuning.
From Figure 5, it can be observed that the MAPE and RMSE values tend to increase as the max_depth value increases. Therefore, the values 2, 3, 4, and 6 were selected for the max_depth parameter.
4.2.2. Gamma
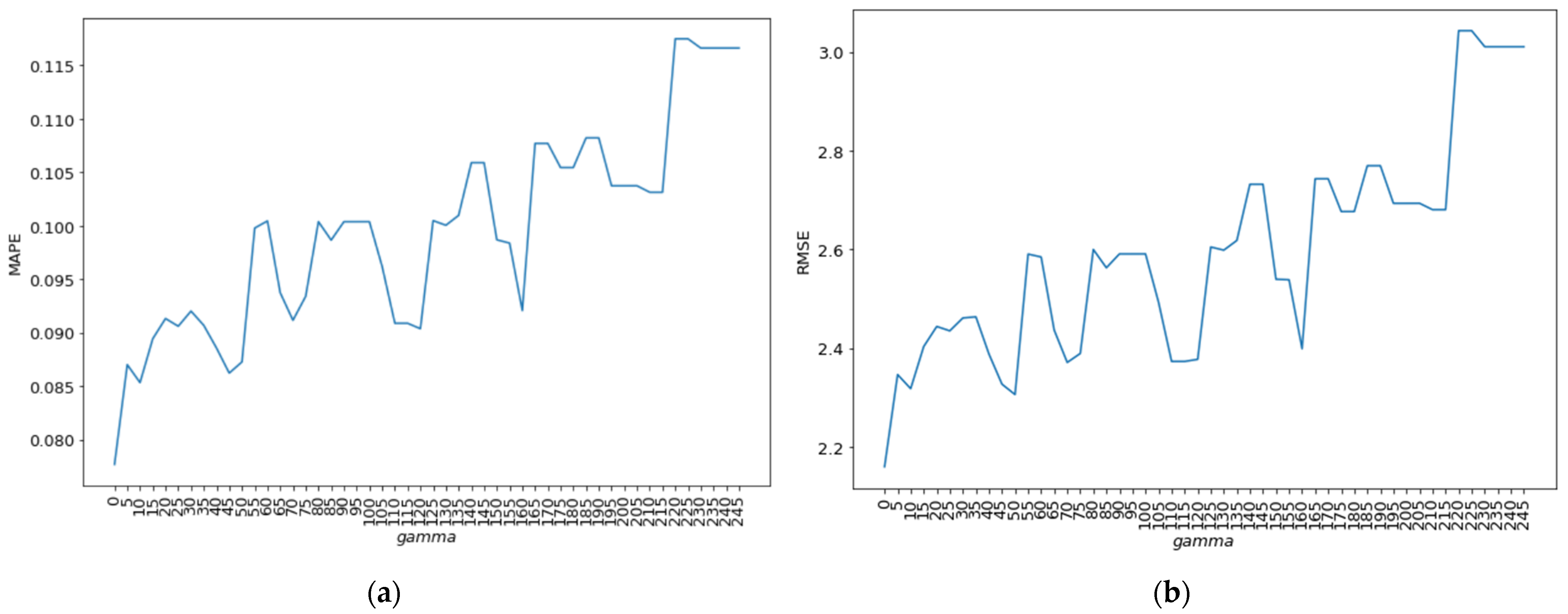
Next, an estimation of the optimal gamma value was attempted. Several values were tested, including 10, 15, 20, 25, 30, 35, 40, 45, …, 250, 255. The RMSE and MAPE values for each gamma value experiment can be observed in Figure 3 in graphical form.
In Figure 6, it can be observed that the MAPE and RMSE values exhibit fluctuations and display an upward trend as the gamma value increases. Consequently, the gamma values of 0, 45, and 70 were chosen based on these observations.
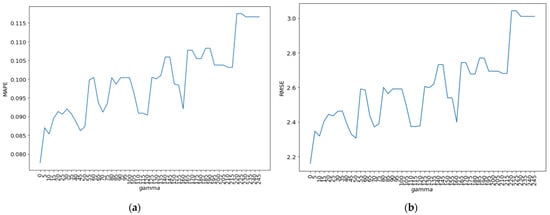
Figure 6.
The evaluation scores for the hyperparameter gamma. (a) MAPE values obtained from hyperparameter tuning; (b) RMSE values obtained from hyperparameter tuning.
4.2.3. Learning_Rate
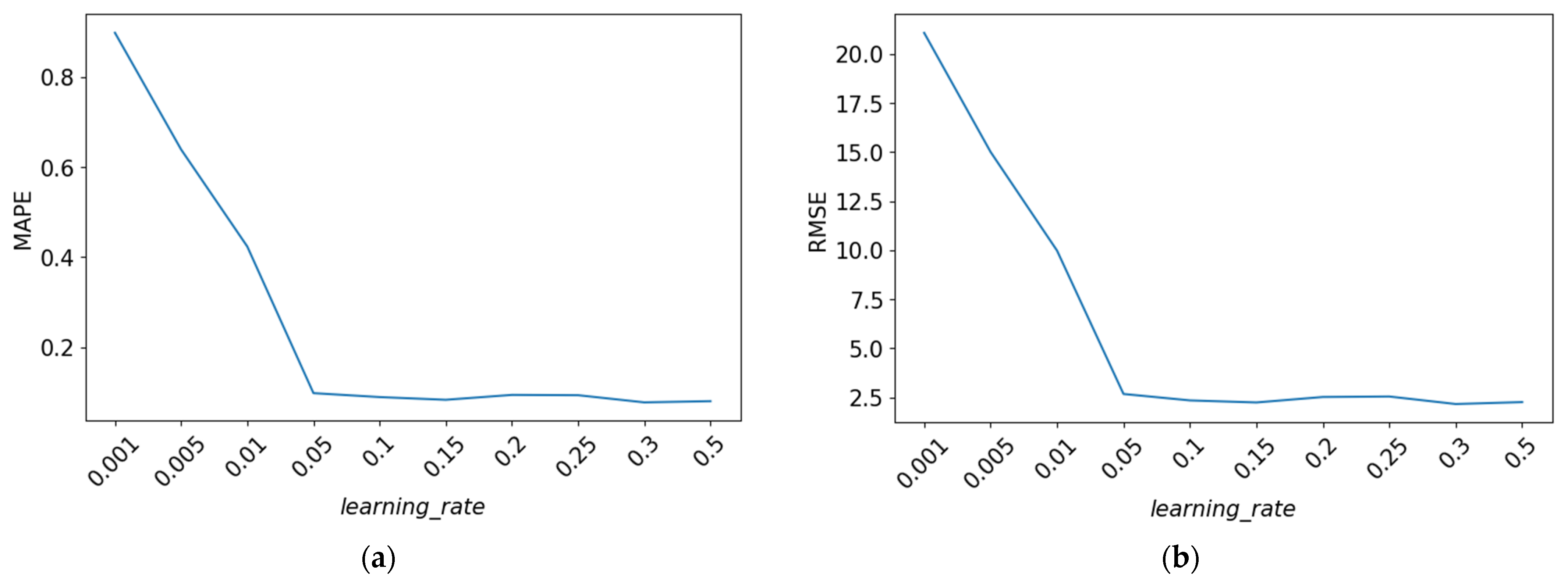
Next, various values were tested for the learning_rate parameter. The tested values included 0.001, 0.005, 0.01, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, and 0.5. The RMSE and MAPE values for each learning_rate experiment can be observed in Figure 4 in graphical form.
From Figure 7, it can be observed that after the learning_rate reaches 0.05, the MAPE and RMSE values do not experience significant changes. Therefore, the learning_rate values of 0.05, 0.1, and 0.15 were chosen.
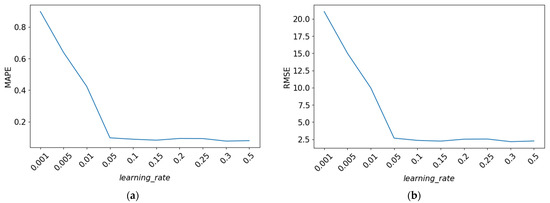
Figure 7.
The evaluation scores for the hyperparameter learning_rate. (a) MAPE values obtained from hyperparameter tuning; (b) RMSE values obtained from hyperparameter tuning.
4.2.4. N_Estimators
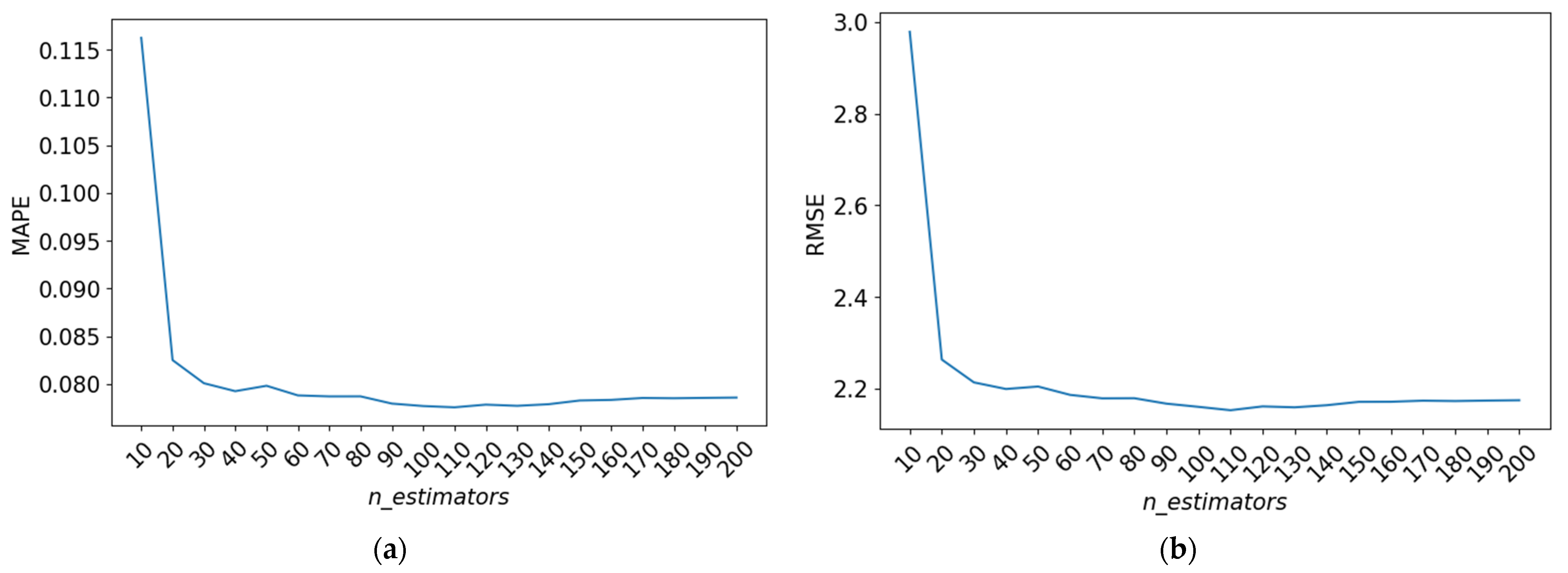
Next, different values were experimented with for the parameter n_estimators. Several values, including 50, 70, 90, 110, 130, ..., 410, and 430, were tested. The resulting RMSE and MAPE values for each n_estimators trial are visualized in Figure 8, depicted in the form of a graph.
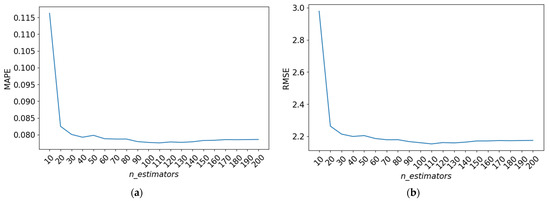
Figure 8.
The evaluation scores for the hyperparameter n_estimators. (a) MAPE values obtained from hyperparameter tuning; (b) RMSE values obtained from hyperparameter tuning.
Figure 8 illustrates that the performance of the model is not significantly affected by the value of n_estimators when it exceeds 20. Therefore, the values of 20, 100, and 130 are chosen for the n_estimators parameter.
4.2.5. Best Hyperparameter Combination
Once the values for each hyperparameter were selected, experiments were conducted for every possible combination of hyperparameters using the grid search method. There was a total of 108 possible combinations of hyperparameters. The process of hyperparameter tuning was stopped as there were already models with better MAPE values than the initial model. From 108 models of hyperparameter tuning results, the average MAPE value is 13.99% and the average RMSE value is 3.5173. Subsequently, the top three models were selected based on the smallest MAPE and RMSE values. In this study, the top three models based on MAPE and RMSE values can be seen in Table 3 and Table 4, respectively.

Table 3.
Three hyperparameter combinations with the best MAPE values.

Table 4.
Three hyperparameter combinations with the best RMSE values.
From Table 3, the combination of learning_rate = 0.15, max_depth = 2, n_estimators = 130, and gamma = 0 is the best hyperparameter combination based on the MAPE value (model A). Meanwhile, from Table 4, the combination of learning_rate = 0.1, max_depth = 3, n_estimators = 130, and gamma = 0 is the best hyperparameter combination based on the RMSE value (model B).
To assess the significance of the model results using improved tuning parameters compared to the initial model, we employed Welch’s t-test (one-tailed). The hypothesis testing of the MAPE value is outlined as follows:
H0:
: this indicating that the performance of the model achieved through hyperparameter tuning is equivalent to that of the initial model.
H1:
: this indicating that the model’s performance, stemming from hyperparameter tuning, surpasses that of the initial model.
Utilizing a significance level (), analysis reveals a p-value = 2.1764 < 0.05, leading to the rejection of . Analogous to the performance of the model resulting from parameter tuning based on RMSE, the p-value = 7.1873 < 0.05. This underscores that the model’s performance, as a result of hyperparameter tuning, significantly surpasses that of the initial model.
4.3. Forecasting Result
Next, we forecast the silver price using model A and model B. The forecasted silver prices for the next 6 days can be seen in Table 5.

Table 5.
The six days ahead forecast results of silver price.
According to the data in Table 5, the forecasted silver prices show a mix of upward and downward trends over the forecast period in model A. However, in model B, the silver prices initially decrease until the third day and then steadily increase until the sixth day.
4.4. K-Fold Cross Validation
Next, an evaluation was conducted using 5-fold cross-validation using the model A and model B that have been obtained. The data partitioning was performed in a non-random manner, but instead sequentially based on the data index. The MAPE and RMSE values from each iteration can be found in Table 6 and the ranking of the two best models can be seen in Table 7.

Table 6.
The result of 5-fold cross-validation.

Table 7.
Ranking of the two best models.
Model A has an average MAPE value of 8% from five iterations and an average RMSE value of 1.9151. Model A has a difference of 2.09% in MAPE and a difference of 0.2153 in RMSE compared to the average result of 5-fold cross-validation. Model B has an average MAPE value of 7.67% from five iterations and an average RMSE value of 1.8394. Model B has a difference of 1.61% in MAPE and a difference of 0.1427 in RMSE compared to the average result of 5-fold cross-validation. From these differences, it can be concluded that both model A and model B are capable of accurately forecasting silver prices.
4.5. Comparison with Other Models
The final models (A and B) obtained from the hyperparameter tuning results are then compared with other machine learning models. CatBoost and random forest models are built which belong to the ensemble learning type with the same basic concept as XGBoost, namely building regression trees. In the process of comparing, it becomes necessary to incorporate extra evaluation measures for a more all-encompassing inference. Supplementary metrics such as MAE and SI are introduced. The results of the model comparison with the evaluation metric value can be seen in Table 8.

Table 8.
Model comparison result.
The results of Table 8 further convince us that XGBoost models A and B with the tuning process are better compared to random forest and CatBoost based on those four metrics.
5. Conclusions
This study builds and optimizes an XGBoost model by conducting hyperparameter tuning to forecast silver prices. The research explores 108 hyperparameter combinations and identifies the top two models based on the evaluation metrics of MAPE and RMSE. The best model based on MAPE has a MAPE value of 5.98% and an RMSE of 1.6998, with a hyperparameter combination of learning_rate = 0.15 and max_depth = 2. The forecasted silver prices for the next six days show a decline on the first and second days, followed by an increase on the third day, another decline on the fourth day, and then a subsequent rise on the fifth and sixth days. The best model based on RMSE has a MAPE value of 6.06% and an RMSE of 1.6967, with a hyperparameter combination of learning_rate = 0.1, max_depth = 3, n_estimators = 130, and gamma = 0. The forecasted silver prices for the next six days indicate a decrease until the third day, followed by a continuous increase until the sixth day. Based on the model evaluation results in Table 8, the MAPE, RMSE, MAE, and SI metrics of the proposed model perform better than other ensemble models (CatBoost and random forest).
6. Recommendations
This study aims to optimize the XGBoost model through hyperparameter tuning, specifically focusing on four hyperparameters. It is suggested for future research to explore additional hyperparameters, including eta, lambda, alpha, and min_child_weight, and to increase the number of hyperparameter variations based on research capacity. Furthermore, incorporating data preprocessing techniques to address missing or messy data can improve the forecasting performance [35]. Additionally, future studies can consider incorporating additional variables such as inflation data, oil prices, or other relevant factors to enhance the accuracy of silver price forecasting.
Author Contributions
Conceptualization, D.N.G., H.N. and F.; methodology, D.N.G.; software, D.N.G.; validation, D.N.G., H.N. and F.; formal analysis, D.N.G.; investigation, D.N.G.; resources, D.N.G.; data curation, D.N.G.; writing—original draft preparation, D.N.G.; writing—review and editing, D.N.G., H.N. and F.; visualization, D.N.G.; supervision, H.N. and F.; project administration, D.N.G.; funding acquisition, H.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Universitas Padjadjaran through Riset Percepatan Lektor Kepala (RPLK), contract number 1549/UN6.3.1/PT.00/2023.
Data Availability Statement
The data in this paper are accessible at the following link: https://github.com/DylanNorbert/SilverPriceForecast-Dylan (accessed on 7 July 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ciner, C. On the Long Run Relationship between Gold and Silver Prices A Note. Glob. Financ. J. 2001, 12, 299–303. [Google Scholar] [CrossRef]
- Lee, S.H.; Jun, B.-H. Silver Nanoparticles: Synthesis and Application for Nanomedicine. Int. J. Mol. Sci. 2019, 20, 865. [Google Scholar] [CrossRef] [PubMed]
- Dutta, A. Impact of Silver Price Uncertainty on Solar Energy Firms. J. Clean. Prod. 2019, 225, 1044–1051. [Google Scholar] [CrossRef]
- Al-Yahyaee, K.H.; Mensi, W.; Sensoy, A.; Kang, S.H. Energy, Precious Metals, and GCC Stock Markets: Is There Any Risk Spillover? Pac.-Basin Financ. J. 2019, 56, 45–70. [Google Scholar] [CrossRef]
- Hillier, D.; Draper, P.; Faff, R. Do Precious Metals Shine? An Investment Perspective. Financ. Anal. J. 2006, 62, 98–106. [Google Scholar] [CrossRef]
- O’Connor, F.A.; Lucey, B.M.; Batten, J.A.; Baur, D.G. The Financial Economics of Gold—A Survey. Int. Rev. Financ. Anal. 2015, 41, 186–205. [Google Scholar] [CrossRef]
- Jabeur, S.B.; Mefteh-Wali, S.; Viviani, J.L. Forecasting Gold Price with the XGBoost Algorithm and SHAP Interaction Values. Ann. Oper. Res. 2021. [Google Scholar] [CrossRef]
- Pierdzioch, C.; Risse, M. Forecasting Precious Metal Returns with Multivariate Random Forests. Empir. Econ. 2020, 58, 1167–1184. [Google Scholar] [CrossRef]
- Shaikh, I. On the Relation between Pandemic Disease Outbreak News and Crude Oil, Gold, Gold Mining, Silver and Energy Markets. Resour. Policy 2021, 72, 102025. [Google Scholar] [CrossRef]
- Investing.Com—Stock Market Quotes & Financial News. Available online: https://www.investing.com/ (accessed on 26 August 2023).
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts, 2018. [Google Scholar]
- Divina, F.; García Torres, M.; Goméz Vela, F.A.; Vázquez Noguera, J.L. A Comparative Study of Time Series Forecasting Methods for Short Term Electric Energy Consumption Prediction in Smart Buildings. Energies 2019, 12, 1934. [Google Scholar] [CrossRef]
- Janiesch, C.; Zschech, P.; Heinrich, K. Machine Learning and Deep Learning. Electron. Mark. 2021, 31, 685–695. [Google Scholar] [CrossRef]
- Fang, Z.G.; Yang, S.Q.; Lv, C.X.; An, S.Y.; Wu, W. Application of a Data-Driven XGBoost Model for the Prediction of COVID-19 in the USA: A Time-Series Study. BMJ Open 2022, 12, e056685. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Qin, C.; Zhang, Y.; Bao, F.; Zhang, C.; Liu, P.; Liu, P. XGBoost Optimized by Adaptive Particle Swarm Optimization for Credit Scoring. Math. Probl. Eng. 2021, 2021, 6655510. [Google Scholar] [CrossRef]
- Srinivasan, A.R.; Lin, Y.-S.; Antonello, M.; Knittel, A.; Hasan, M.; Hawasly, M.; Redford, J.; Ramamoorthy, S.; Leonetti, M.; Billington, J.; et al. Beyond RMSE: Do Machine-Learned Models of Road User Interaction Produce Human-like Behavior? IEEE Trans. Intell. Transp. Syst. 2023, 24, 7166–7177. [Google Scholar] [CrossRef]
- Nasiri, H.; Ebadzadeh, M.M. MFRFNN: Multi-Functional Recurrent Fuzzy Neural Network for Chaotic Time Series Prediction. Neurocomputing 2022, 507, 292–310. [Google Scholar] [CrossRef]
- Luo, M.; Wang, Y.; Xie, Y.; Zhou, L.; Qiao, J.; Qiu, S.; Sun, Y. Combination of Feature Selection and Catboost for Prediction: The First Application to the Estimation of Aboveground Biomass. Forests 2021, 12, 216. [Google Scholar] [CrossRef]
- Li, X.; Ma, L.; Chen, P.; Xu, H.; Xing, Q.; Yan, J.; Lu, S.; Fan, H.; Yang, L.; Cheng, Y. Probabilistic Solar Irradiance Forecasting Based on XGBoost. Energy Rep. 2022, 8, 1087–1095. [Google Scholar] [CrossRef]
- Qi, Y. Random Forest for Bioinformatics. Ensemble Mach. Learn. Methods Appl. 2012, 8, 307–323. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. Adv. Neural Inf. Process. Syst. 2018, 31, 6638–6648. [Google Scholar]
- Alruqi, M.; Hanafi, H.A.; Sharma, P. Prognostic Metamodel Development for Waste-Derived Biogas-Powered Dual-Fuel Engines Using Modern Machine Learning with K-Cross Fold Validation. Fermentation 2023, 9, 598. [Google Scholar] [CrossRef]
- Feng, D.-C.; Liu, Z.-T.; Wang, X.-D.; Chen, Y.; Chang, J.-Q.; Wei, D.-F.; Jiang, Z.-M. Machine Learning-Based Compressive Strength Prediction for Concrete: An Adaptive Boosting Approach. Constr. Build. Mater. 2020, 230, 117000. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Liao, L. Input Delay Estimation for Input-Affine Dynamical Systems Based on Taylor Expansion. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 1298–1302. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On Hyperparameter Optimization of Machine Learning Algorithms: Theory and Practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Probst, P.; Boulesteix, A.-L.; Bischl, B. Tunability: Importance of Hyperparameters of Machine Learning Algorithms. J. Mach. Learn. Res. 2019, 20, 1934–1965. [Google Scholar]
- Ma, Y.; Pan, H.; Qian, G.; Zhou, F.; Ma, Y.; Wen, G.; Zhao, M.; Li, T. Prediction of Transmission Line Icing Using Machine Learning Based on GS-XGBoost. J. Sens. 2022, 2022, 2753583. [Google Scholar] [CrossRef]
- Vivas, E.; Allende-Cid, H.; Salas, R. A Systematic Review of Statistical and Machine Learning Methods for Electrical Power Forecasting with Reported MAPE Score. Entropy 2020, 22, 1412. [Google Scholar] [CrossRef]
- Wang, W.; Lu, Y. Analysis of the Mean Absolute Error (MAE) and the Root Mean Square Error (RMSE) in Assessing Rounding Model. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Kuala Lumpur, Malaysia, 15–16 December 2017; Volume 324, p. 12049. [Google Scholar]
- Chai, T.; Draxler, R.R. Root Mean Square Error (RMSE) or Mean Absolute Error (MAE). Geosci. Model Dev. Discuss. 2014, 7, 1525–1534. [Google Scholar]
- Mokhtar, A.; El-Ssawy, W.; He, H.; Al-Anasari, N.; Sammen, S.S.; Gyasi-Agyei, Y.; Abuarab, M. Using Machine Learning Models to Predict Hydroponically Grown Lettuce Yield. Front. Plant Sci. 2022, 13, 706042. [Google Scholar] [CrossRef]
- Gareth, J.; Daniela, W.; Trevor, H.; Robert, T. An Introduction to Statistical Learning: With Applications in R; Spinger: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Marzban, C.; Liu, J.; Tissot, P. On Variability Due to Local Minima and K-Fold Cross Validation. Artif. Intell. Earth Syst. 2022, 1, e210004. [Google Scholar] [CrossRef]
- Elasra, A. Multiple Imputation of Missing Data in Educational Production Functions. Computation 2022, 10, 49. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).