Dynamical Optimal Values of Parameters in the SSOR, AOR, and SAOR Testing Using Poisson Linear Equations

Abstract

This paper proposes a dynamical approach to determine the optimal values of the parameters used in each iteration of the symmetric successive over-relaxation (SSOR), accelerated over-relaxation (AOR), and symmetric accelerated over-relaxation (SAOR) methods for solving linear equation systems. When the optimal values of the parameters in the SSOR, AOR, and SAOR are hard to determine as some fixed values, they are obtained by minimizing the merit functions, which are based on the maximal projection technique between the left- and right-hand-side vectors, which involves the input vector, the previous step values of the variables, and the parameters. The novelty is a new concept of the dynamical optimal values of the parameters, instead of the fixed values and the maximal projection technique. In a preferred range, the optimal values of the parameters can be quickly determined by using the golden section search algorithm with a loose convergence criterion. Without knowing and having the theoretical optimal values in general, the new methods might provide an alternative and proper choice of the values of the parameters for accelerating the convergence speed. Numerical testings of the linear Poisson equation discretized to a matrix–vector form and a Lyapunov equation form were used to assess the performance of the DOSSOR, DOAOR, and DOSAOR dynamical optimal methods.

1. Introduction

Better dynamical realizations of the symmetric successive over-relaxation (SSOR), the accelerated over-relaxation (AOR), and the symmetric accelerated over-relaxation (SAOR) methods [1,2,3,4] are offered in the paper to solve the following:

$$\mathbf{A}\mathbf{x}=\mathbf{b},$$

(1)

where $\mathbf{A}\in {\mathbb{R}}^{n\times n}$ is a given non-singular coefficient matrix with its diagonal elements being non-zeros, $\mathbf{b}\in {\mathbb{R}}^n$ is a given input vector, and $\mathbf{x}\in {\mathbb{R}}^n$ are unknown variables.

For a numerical solution $\mathbf{x}$ of Equation (1), $\parallel \mathbf{b}-\mathbf{A}\mathbf{x}\parallel$ is the residual norm. Many numerical methods are minimized for the following:

$$\underset{\mathbf{x}}{min}{\parallel \mathbf{b}-\mathbf{A}\mathbf{x}\parallel }^2$$

(2)

to develop the numerical techniques in the Krylov sub-space. For example, the GMRES was developed in [5,6,7,8].

Let

$$\mathbf{y}:=\mathbf{A}\mathbf{x}.$$

(3)

Equation (1) can be viewed as a balance of the unknown vector $\mathbf{y}$ to the input vector $\mathbf{b}$:

$$\mathbf{y}=\mathbf{b}.$$

(4)

In order to solve Equation (1), we maximize the following:

$$\underset{\mathbf{x}}{max}\frac{{(\mathbf{b}·\mathbf{y})}^2}{{\parallel \mathbf{b}\parallel }^2{\parallel \mathbf{y}\parallel }^2}\le 1,$$

(5)

to render $\mathbf{y}$ close to $\mathbf{b}$. Equation (5) signifies the maximum projection of the $\mathbf{y}$ direction onto the direction of $\mathbf{b}$, and, indeed, the maximum value of one is obtained when $\mathbf{y}=\mathbf{b}$. Equation (5) is equivalent to the following:

$$\underset{\mathbf{x}}{min}\left\{f=\frac{{\parallel \mathbf{b}\parallel }^2{\parallel \mathbf{y}\parallel }^2}{{(\mathbf{b}·\mathbf{y})}^2}\right\}\ge 1,$$

(6)

from which some methods [9,10] were developed to solve Equation (1) in an affine Krylov sub-space.

Only for some limited cases, the theoretical value of the optimal relaxation parameter in the method of successive over-relaxation (SOR) is known. When $\mathbf{A}$ is a positive definite matrix, the following w is the optimal value for the SOR [1]:

$$w_{opt}=\frac{2}{1+\sqrt{1-{\rho }^2({\mathbf{I}}_n-{\mathbf{D}}^{-1}\mathbf{A})}},$$

(7)

where $\mathbf{D}$ consists of the diagonal elements of $\mathbf{A}$, and $\rho$ is the spectral radius of ${\mathbf{I}}_n-{\mathbf{D}}^{-1}\mathbf{A}$. An adaptive method based on the Wolfe condition to search for the optimal relaxation parameter in the SOR was proposed in [11].

For a system (1) having a non-square coefficient matrix with dimension $m\times n$, Darvishi and Khosro-Aghdam [12] decomposed $\mathbf{A}$ to obtain the following:

$$\mathbf{A}=\left[\begin{array}{cc}{\mathbf{A}}_{11}& {\mathbf{A}}_{12}\\ {\mathbf{A}}_{21}& {\mathbf{A}}_{22}\end{array}\right],$$

(8)

where the rank of ${\mathbf{A}}_{11}$ is r, and ${\mathbf{A}}_{11}\in {\mathbb{R}}^{r\times r}$, ${\mathbf{A}}_{12}\in {\mathbb{R}}^{r\times (n-r)}$, ${\mathbf{A}}_{21}\in {\mathbb{R}}^{(m-r)\times r}$, and ${\mathbf{A}}_{22}\in {\mathbb{R}}^{(m-r)\times (n-r)}$. Suppose that $\mathbf{B}={\mathbf{A}}_{21}{\mathbf{A}}_{11}^{-1}$. It is remarkable that Darvishi and Khosro-Aghdam [12] derived the following optimal value of the relaxation parameter for the symmetric SOR:

$$w_{opt}=\frac{1}{2}\left[1-\frac{\sqrt{2+{\parallel \mathbf{B}\parallel }^2}}{\parallel \mathbf{B}\parallel }+\sqrt{2}\sqrt{\frac{1}{{\parallel \mathbf{B}\parallel }^2}-1+\frac{2}{\parallel \mathbf{B}\parallel \sqrt{2+{\parallel \mathbf{B}\parallel }^2}}+\frac{\parallel \mathbf{B}\parallel }{\sqrt{2+{\parallel \mathbf{B}\parallel }^2}}}\right].$$

(9)

Tian [13] developed the AOR method for non-square linear systems. Many works were developed for the better convergence behavior analyses of the SSOR, AOR, and SAOR methods [2,3,14]. Liu [15] applied the minimization technique in Equation (6) to search for the optimal value of the relaxation parameter used in the SOR at each iteration step. For dealing with the different extensions of the SOR and AOR for different kinds of linear systems, there are many papers such as the symmetric SOR method for the augmented systems [16,17,18,19,20], the generalized AOR method for the linear complementarity problem [21], the generalized least-square problems [22], and a class of generalized saddle point problems [23], as well as the symmetric successive over-relaxation method for the rank-deficient linear systems [24], the symmetric block SOR methods for the rank-deficient least-squares problems [25].

In general, the aforementioned methods involve one, two, or more parameters. By changing the values of the parameters in these iterative methods, the speed of their convergence changes. Hence, one of the important works in the area of such iterative methods is finding the optimal values for their parameters. That is not an easy task. The theoretical optimal values such as those in Equations (7) and (9) are hard to achieve for the SSOR, AOR, and SAOR methods. In the present paper, we extend this new idea to search for the optimal values of parameters used in the SSOR, AOR, and SAOR. No matter whether using Equation (7) for the SOR or Equation (9) for the SSOR of rectangular systems, $w_{opt}$ is a fixed value when the coefficient matrix $\mathbf{A}$ is given. Rather than the fixed values, we seek the optimal values in each iteration step as dynamical values. The novelty of the present paper is the new dynamical optimal values of the parameters, instead of the fixed values, and a simple idea of the maximal projection technique is derived to determine the dynamical optimal values.

2. Symmetric Successive Overrelaxation (SSOR) Method

It is known that $\mathbf{A}$ can be uniquely decomposed into the following:

$$\mathbf{A}=\mathbf{D}-\mathbf{U}-\mathbf{L},$$

(10)

where $\mathbf{D}$ is a diagonal matrix of $\mathbf{A}$ having non-zero elements, and $\mathbf{U}$ is a strictly upper-triangular matrix of $\mathbf{A}$, while $\mathbf{L}$ is a strictly lower-triangular matrix of $\mathbf{A}$.

It follows from Equations (1) and (10) that an equivalent linear system is formed:

$$\mathbf{D}\mathbf{x}-\mathbf{U}\mathbf{x}-\mathbf{L}\mathbf{x}=\mathbf{b}.$$

(11)

Multiplying Equation (11) by w and adding a term $\mathbf{D}\mathbf{x}$ on both sides generates the following:

$$\mathbf{D}\mathbf{x}+w\mathbf{D}\mathbf{x}-w\mathbf{U}\mathbf{x}-w\mathbf{L}\mathbf{x}=w\mathbf{b}+\mathbf{D}\mathbf{x},$$

(12)

whose iterative form is known as the successive over-relaxation (SOR) method [4]:

$$(\mathbf{D}-w\mathbf{L}){\mathbf{x}}^{(k+1)}=w\mathbf{b}+(1-w)\mathbf{D}{\mathbf{x}}^{\left(k\right)}+w\mathbf{U}{\mathbf{x}}^{\left(k\right)},$$

(13)

of which $0<w<2$ is a relaxation parameter. By using the forward substitution method for Equation (13), it is easy to find the solution of Equation (1) upon ${\mathbf{x}}^{\left(k\right)}$ satisfying the prescribed convergence criterion.

Instead of the SOR, the symmetric successive over-relaxation (SSOR) method reads as follows [26]:

$$\begin{array}{ccc}\hfill & & (\mathbf{D}-w\mathbf{L}){\mathbf{x}}^{(k+1/2)}=w\mathbf{b}+(1-w)\mathbf{D}{\mathbf{x}}^{\left(k\right)}+w\mathbf{U}{\mathbf{x}}^{\left(k\right)},\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill & & (\mathbf{D}-w\mathbf{U}){\mathbf{x}}^{(k+1)}=w\mathbf{b}+(1-w)\mathbf{D}{\mathbf{x}}^{(k+1/2)}+w\mathbf{L}{\mathbf{x}}^{(k+1/2)},\hfill \end{array}$$

(15)

where ${\mathbf{x}}^{(k+1/2)}$ is a tentative vector between ${\mathbf{x}}^{\left(k\right)}$ and ${\mathbf{x}}^{(k+1)}$. It follows from Equations (14) and (15) that the following is obtained:

$$\begin{array}{ccc}\hfill & & {\mathbf{x}}^{(k+1)}={(\mathbf{D}-w\mathbf{U})}^{-1}[(1-w)\mathbf{D}+w\mathbf{L}]{(\mathbf{D}-w\mathbf{L})}^{-1}[(1-w)\mathbf{D}+w\mathbf{U}]{\mathbf{x}}^{\left(k\right)}\hfill \\ & & +w{(\mathbf{D}-w\mathbf{U})}^{-1}\{\mathbf{b}+[(1-w)\mathbf{D}+w\mathbf{L}]{(\mathbf{D}-w\mathbf{L})}^{-1}\mathbf{b}\}.\hfill \end{array}$$

(16)

Determining the optimal value w in Equation (16) is a great challenge.

3. A New Merit Function

We temporarily take ${\mathbf{x}}^{(k+1)}$ in the left-hand side of Equation (15) to be ${\mathbf{x}}^{(k+1/2)}$, and then, at each iterative step, we have a vector equation with $w_k$ to be given as follows:

$$(\mathbf{D}-w_k\mathbf{U}){\mathbf{x}}^{(k+1/2)}=w_k\mathbf{b}+(1-w_k)\mathbf{D}{\mathbf{x}}^{(k+1/2)}+w_k\mathbf{L}{\mathbf{x}}^{(k+1/2)},$$

(17)

where ${\mathbf{x}}^{(k+1/2)}$ is calculated from Equation (14).

The f in Equation (6) consists of two vectors—$\mathbf{y}$ and $\mathbf{b}$—in Equation (4). Similarly, Equation (17) is a balance equation of two vectors with

$${\mathbf{F}}_1={\mathbf{F}}_2,$$

(18)

where

$${\mathbf{F}}_1:=(\mathbf{D}-w_k\mathbf{U}){\mathbf{x}}^{(k+1/2)},{\mathbf{F}}_2:=w_k\mathbf{b}+(1-w_k)\mathbf{D}{\mathbf{x}}^{(k+1/2)}+w_k\mathbf{L}{\mathbf{x}}^{(k+1/2)}.$$

(19)

By inserting values, such as $\mathbf{y}$ and $\mathbf{b}$ in Equation (4), into Equation (6), we can derive the merit function as follows:

$$\begin{array}{ccc}\hfill & & f=\frac{f_1\left(w_k\right)f_2\left(w_k\right)}{f_3^2\left(w_k\right)},\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill & & f_1\left(w_k\right):=\parallel {\mathbf{F}}_1{\parallel }^2,f_2\left(w_k\right):={\parallel {\mathbf{F}}_2\parallel }^2,f_3\left(w_k\right):={\mathbf{F}}_1·{\mathbf{F}}_2.\hfill \end{array}$$

(21)

We can seek the optimal value of $w_k$ to minimize f at each iteration step:

$$\underset{w_k\in (a,b)}{min}\left\{f=\frac{f_1\left(w_k\right)f_2\left(w_k\right)}{f_3^2\left(w_k\right)}\right\}.$$

(22)

In a given interval $(a,b)\subset (0,2)$, the minimization in Equation (22) can be performed by the one-dimensional golden section search algorithm that is shown in Appendix A.

In accordance with Equation (22), the optimal value is available, and the resulting iterative algorithm is named a dynamical optimal SSOR (DOSSOR) method, which provides the dynamical optimal values of $w_k$ in the iterations. Because we are not interested in a very precise value of $w_k$ at each iteration step, and to speed up the computation in Equation (22), the convergence criterion used in the golden section search algorithm is quite loose, say ${10}^{-1}$ or ${10}^{-2}$, such that only a few steps are spent to seek $w_k$.

4. Accelerated Over-Relaxation (AOR) Method and Its Symmetrization

Hadjidimos [2] derived an accelerated over-relaxation (AOR) method to solve Equation (1), which can be realized from Equation (12) by adding another parameter $\sigma$ that preceeds $\mathbf{L}\mathbf{x}$:

$$\mathbf{D}\mathbf{x}+w\mathbf{D}\mathbf{x}-w\mathbf{U}\mathbf{x}-(w-\sigma +\sigma )\mathbf{L}\mathbf{x}=w\mathbf{b}+\mathbf{D}\mathbf{x}.$$

(23)

Then, we remove $w\mathbf{D}\mathbf{x}$, $-w\mathbf{U}\mathbf{x}$, and $-(w-\sigma )\mathbf{L}\mathbf{x}$ to the right-hand side and take the value of $\mathbf{x}$ on the the right-hand side to be ${\mathbf{x}}^{\left(k\right)}$, while on the left-hand side, we take the value of $\mathbf{x}$ to be ${\mathbf{x}}^{(k+1)}$:

$$(\mathbf{D}-\sigma \mathbf{L}){\mathbf{x}}^{(k+1)}=w\mathbf{b}+(1-w)\mathbf{D}{\mathbf{x}}^{\left(k\right)}+w\mathbf{U}{\mathbf{x}}^{\left(k\right)}+(w-\sigma )\mathbf{L}{\mathbf{x}}^{\left(k\right)}.$$

(24)

We temporarily set ${\mathbf{x}}^{(k+1)}$ equal to ${\mathbf{x}}^{\left(k\right)}$ on the left-hand side. By inserting

$${\mathbf{G}}_1=(\mathbf{D}-\sigma \mathbf{L}){\mathbf{x}}^{\left(k\right)},{\mathbf{G}}_2=w\mathbf{b}+(1-w)\mathbf{D}{\mathbf{x}}^{\left(k\right)}+w\mathbf{U}{\mathbf{x}}^{\left(k\right)}+(w-\sigma )\mathbf{L}{\mathbf{x}}^{\left(k\right)}$$

(25)

into Equation (6), we can derive

$$\underset{(w_k,{\sigma }_k)\in (a,b)\times (c,d)}{min}\left\{f=\frac{\parallel {\mathbf{G}}_1{\parallel }^2{\parallel {\mathbf{G}}_2\parallel }^2}{{({\mathbf{G}}_1·{\mathbf{G}}_2)}^2}\right\}.$$

(26)

At each iterative step, we can search for the optimal values of $(w_k,{\sigma }_k)$ to minimize f, which can be performed by the two-dimensional golden section search algorithm that is shown in Appendix B. By using the minimization procedure in Equation (26), we can obtain the dynamical optimal AOR (DOAOR).

As with the modification from the SOR to SSOR, we can modify Equation (24) to become a symmetric AOR (SAOR) [3]:

$$\begin{array}{ccc}\hfill & & (\mathbf{D}-\sigma \mathbf{L}){\mathbf{x}}^{(k+1/2)}=w\mathbf{b}+(1-w)\mathbf{D}{\mathbf{x}}^{\left(k\right)}+w\mathbf{U}{\mathbf{x}}^{\left(k\right)}+(w-\sigma )\mathbf{L}{\mathbf{x}}^{\left(k\right)},\hfill \\ & & (\mathbf{D}-\sigma \mathbf{U}){\mathbf{x}}^{(k+1)}=w\mathbf{b}+(1-w)\mathbf{D}{\mathbf{x}}^{(k+1/2)}+w\mathbf{L}{\mathbf{x}}^{(k+1/2)}+(w-\sigma )\mathbf{U}{\mathbf{x}}^{(k+1/2)}.\hfill \end{array}$$

(27)

In the minimization of Equation (26), we utilize the following:

$${\mathbf{G}}_1=(\mathbf{D}-\sigma \mathbf{U}){\mathbf{x}}^{(k+1/2)},{\mathbf{G}}_2=w\mathbf{b}+(1-w)\mathbf{D}{\mathbf{x}}^{(k+1/2)}+w\mathbf{L}{\mathbf{x}}^{(k+1/2)}+(w-\sigma )\mathbf{U}{\mathbf{x}}^{(k+1/2)}.$$

(28)

Therefore, the optimal values of $(w_k,{\sigma }_k)$ can be found in the rectangle $(a,b)\times (c,d)$ for a faster convergence of the so-called dynamical optimal SAOR (DOSAOR).

5. Numerical Verifications

In order to assess the performance of the DOSSOR, DOAOR, and DOSAOR, we test the following 2D boundary value problem of the Poisson equation:

$$\begin{array}{ccc}\hfill & & \Delta u(x,y)=p(x,y),0<x<1,0<y<1,\hfill \\ & & u(0,y)=g_1\left(y\right),u(x,0)=g_2\left(x\right),u(1,y)=g_3\left(y\right),u(x,1)=g_4\left(x\right),\hfill \end{array}$$

(29)

where $p(x,y)$, $g_1\left(y\right)$, $g_2\left(x\right)$, $g_3\left(y\right)$, and $g_4\left(x\right)$ are given functions.

5.1. Matrix–Vector Form of Equations

The process of constructing the matrix–vector form of Equation (1) from Equation (29) using the finite difference was described by Liu [27]. By using a standard five-point finite difference method that is applied to Equation (29), one can obtain a system of matrix–vector-type linear equations:

$$\begin{array}{ccc}\hfill & & F_{i,j}=\frac{1}{{(\Delta x)}^2}[u_{i+1,j}-2u_{i,j}+u_{i-1,j}]+\frac{1}{{(\Delta y)}^2}[u_{i,j+1}-2u_{i,j}+u_{i,j-1}]-p(x_i,y_j)=0,\hfill \\ & & 1\le i\le n_1,1\le j\le n_2,\hfill \end{array}$$

(30)

where $\Delta x=1/(n_1+1)$, $\Delta y=1/(n_2+1)$, and $u_{i,j}:=u(x_i,y_j)$ are numerical values of $u(x,y)$ at the grid point $(x_i,y_j)=(i\Delta x,j\Delta y)$, in which $u_{0,j}$, $u_{n_1+1,j}$, $u_{i,0}$, and $u_{i,n_2+1}$ are determined by the given boundary values.

By letting $K=n_2(i-1)+j$, running i from 1 to $n_1$, and running j from 1 to $n_2$, we can, respectively, set $x_K$ in Equation (1) and the algebraic equations $F_K$ as the following:

$$\begin{array}{ccc}\hfill & & \mathrm{Do}i=1,n_1\hfill \\ & & \mathrm{Do}j=1,n_2\hfill \\ & & K=n_2(i-1)+j\hfill \\ & & x_K=u_{i,j}\hfill \\ & & F_K=F_{i,j}.\hfill \end{array}$$

(31)

At the same time, the components of the input vector $\mathbf{b}$ and the coefficient matrix $\mathbf{A}$ are constructed as follows:

$$\begin{array}{ccc}\hfill & & \mathrm{Do}i=1,n_1\hfill \\ & & \mathrm{Do}j=1,n_2\hfill \\ & & K=n_2(i-1)+j\hfill \\ & & b_K=p(x_i,y_j)\hfill \\ & & \mathrm{If}i=1\mathrm{and}j=1,\mathrm{then}{b}_K=p(x_i,y_j)-\frac{g_1\left(y_j\right)}{{(\Delta x)}^2}-\frac{g_2\left(x_i\right)}{{(\Delta y)}^2}\hfill \\ & & \mathrm{If}i=1\mathrm{and}j=n_2,\mathrm{then}{b}_K=p(x_i,y_j)-\frac{g_1\left(y_j\right)}{{(\Delta x)}^2}-\frac{g_4\left(x_i\right)}{{(\Delta y)}^2}\hfill \\ & & \mathrm{If}i=n_1\mathrm{and}j=1,\mathrm{then}{b}_K=p(x_i,y_j)-\frac{g_3\left(y_j\right)}{{(\Delta x)}^2}-\frac{g_2\left(x_i\right)}{{(\Delta y)}^2}\hfill \\ & & \mathrm{If}i=n_1\mathrm{and}j=n_2,\mathrm{then}{b}_K=p(x_i,y_j)-\frac{g_3\left(y_j\right)}{{(\Delta x)}^2}-\frac{g_4\left(x_i\right)}{{(\Delta y)}^2}\hfill \\ & & \mathrm{If}i=1\mathrm{and}1<j<n_2,\mathrm{then}{b}_K=p(x_i,y_j)-\frac{g_1\left(y_j\right)}{{(\Delta x)}^2}\hfill \\ & & \mathrm{If}j=n_2\mathrm{and}1<i<n_1,\mathrm{then}{b}_K=p(x_i,y_j)-\frac{g_4\left(x_i\right)}{{(\Delta y)}^2}\hfill \\ & & \mathrm{If}i=n_1\mathrm{and}1<j<n_2,\mathrm{then}{b}_K=p(x_i,y_j)-\frac{g_3\left(y_j\right)}{{(\Delta x)}^2}\hfill \\ & & \mathrm{If}j=1\mathrm{and}1<i<n_1,\mathrm{then}{b}_K=p(x_i,y_j)-\frac{g_2(x_i,0)}{{(\Delta y)}^2}\hfill \\ & & L_1=n_2(i-2)+j,L_2=n_2(i-1)+j-1,L_3=n_2(i-1)+j,\hfill \\ & & L_4=n_2(i-1)+j+1,L_5=n_{2}i+j\hfill \\ & & A_{K,L_1}=A_{K,L_5}=\frac{1}{{(\Delta x)}^2},A_{K,L_2}=A_{K,L_4}=\frac{1}{{(\Delta y)}^2},A_{K,L_3}=-\frac{2}{{(\Delta x)}^2}-\frac{2}{{(\Delta y)}^2}.\hfill \end{array}$$

(32)

Here, we have $n=n_1\times n_2$ linear equations.

First, we consider the following:

$$u(x,y)=(x^2-x)(y^2-y),$$

(33)

which renders $p(x,y)=2(x^2-x)+2(y^2-y)$ and $g_1\left(y\right)=g_2\left(x\right)=g_3\left(y\right)=g_4\left(x\right)=0$.

In the numerical tests, we took $\epsilon ={10}^{-5}$ as a convergence criterion; as a result, $n_1=n_2=29$, $h:=\Delta x=\Delta y=1/30$, and the usual SSOR with $w=1.5$ converged at 221 steps; additionally, the accuracy was measured by the maximum error (ME) = $3.31\times {10}^{-8}$, and the root mean square error (RMSE) = $1.71\times {10}^{-8}$. For the SOR with $w=1.5$, it converged at 414 steps, the accuracy was ME = $3.16\times {10}^{-8}$, and the RMSE = $1.52\times {10}^{-8}$. Obviously, the SSOR converged faster than the SOR by about a factor of two.

By using the DOSSOR, we took $a=1.85$ and $b=1.9$, and, through 105 steps, it converged, as shown in Figure 1a, to satisfy the convergence criterion $\epsilon ={10}^{-5}$, where the residual is defined as $\parallel \mathbf{F}\parallel$. The convergence speed of the DOSSOR was improved by about a factor of two compared to the SSOR. An ME = $1.69\times {10}^{-8}$ and a RMSE = $7.88\times {10}^{-9}$ were obtained by the DOSSOR, which were more accurate values than those obtained by the SSOR. The accuracy and convergence speeds of the presented method DOSSOR were enhanced owing to the use of the merit function (22). As shown in Figure 1b, f quickly tended to 1, and the optimal values of w varied between 1.8527 and 1.8836, as are shown in Figure 1c. It is amazing that when $\epsilon ={10}^{-13}$ was taken, we could obtain an ME = $4.86\times {10}^{-17}$ and a RMSE = $1.49\times {10}^{-17}$, although the DOSSOR did not converge within 300 steps. The numerical solution obtained was almost equal to the exact one.

Table 1. Comparing NI, ME, and RMSE for different $\epsilon$ using the DOSSOR.

$\mathit{\epsilon }$	${10}^{-6}$	${10}^{-7}$	${10}^{-8}$	${10}^{-9}$	${10}^{-10}$	${10}^{-11}$
NI	122	141	159	177	195	213
ME	$1.79\times {10}^{-9}$	$1.51\times {10}^{-10}$	$1.51\times {10}^{-11}$	$1.54\times {10}^{-12}$	$1.55\times {10}^{-13}$	$1.54\times {10}^{-14}$
RMSE	$8.19\times {10}^{-10}$	$6.78\times {10}^{-11}$	$6.64\times {10}^{-12}$	$6.68\times {10}^{-13}$	$6.65\times {10}^{-14}$	$6.55\times {10}^{-15}$

lists the number of iterations (NI), the ME, and the RMSE for different $\epsilon$ using the DOSSOR with a fixed $h=1/30$.

By using the DOAOR, we took $(a,b)=(1.85,1.9)$, $(c,d)=(1.8,1.9)$, and through 119 steps, it converged, as shown in Figure 2a, to satisfy the convergence criterion $\epsilon ={10}^{-5}$. The convergence speed of the DOAOR was improved by about two times more than the ad hoc AOR with $w=1.9$ and $\sigma =1.6$, which spent 257 steps. An ME = $1.07\times {10}^{-9}$ and a RMSE = $1.13\times {10}^{-10}$ obtained by the DOAOR were more accurate than those obtained by the AOR with ME = $3.03\times {10}^{-8}$ and RMSE = $1.54\times {10}^{-8}$. The optimal values of w and $\sigma$ are shown in Figure 2b,c.

Table 2. Comparing NI, ME, and RMSE for different $\epsilon$ using the DOAOR.

$\mathit{\epsilon }$	${10}^{-8}$	${10}^{-9}$	${10}^{-10}$	${10}^{-11}$	${10}^{-12}$
NI	176	185	188	214	245
ME	$4.89\times {10}^{-13}$	$6.64\times {10}^{-13}$	$8.84\times {10}^{-14}$	$2.43\times {10}^{-16}$	$1.48\times {10}^{-16}$
RMSE	$6.67\times {10}^{-14}$	$4.63\times {10}^{-14}$	$9.46\times {10}^{-15}$	$6.21\times {10}^{-17}$	$5.62\times {10}^{-17}$

lists the NI, ME, and RMSE for different $\epsilon$ using the DOAOR with a fixed $h=1/30$. Upon comparing the values to those in Table 1 with the same $\epsilon ={10}^{-8},{10}^{-9},{10}^{-10},{10}^{-11}$, the DOAOR converged slightly slower than the DOSSOR, but the accuracy was raised by one or two orders.

In

Table 3. Comparing NI, ME, and RMSE for different mesh size h using the DOAOR.

h	$1/5$	$1/10$	$1/15$	$1/20$
NI	202	224	235	>300
ME	$5.46\times {10}^{-15}$	$2.59\times {10}^{-16}$	$4.16\times {10}^{-17}$	$1.67\times {10}^{-16}$
RMSE	$1.74\times {10}^{-15}$	$4.19\times {10}^{-17}$	$1.27\times {10}^{-17}$	$7.45\times {10}^{-17}$

, we list the NI, ME, and RMSE for different mesh size h using the algorithm DOAOR with a fixed $\epsilon ={10}^{-13}$. It is interesting that the accuracy was very good, even for a larger mesh size. When $h<1/15$, the accuracy was decreased and did not converge within 300 steps under a stringent convergence criterion of $\epsilon ={10}^{-13}$.

Using the DOSAOR, we took $n_1=n_2=15$, $(a,b)=(1.55,1.65)$, and $(c,d)=(1.55,1.65)$, and, through 125 steps, it converged as shown in Figure 3a to satisfy the convergence criterion $\epsilon ={10}^{-13}$. An ME = $4.03\times {10}^{-16}$ and a RMSE = $2.15\times {10}^{-16}$ were more accurate than those values obtained by the AOR with ad hoc values of $w=1.9$ and $\sigma =1.6$, whose ME = $3.03\times {10}^{-8}$ and RMSE = $1.44\times {10}^{-8}$. The optimal values of w and $\sigma$ are shown in Figure 3b,c. By comparing the values to those in Table 3, it can be seen that the DOSAOR converged faster than the DOAOR, as is shown in

Table 4. Comparing NI, ME, and RMSE for different mesh size h using the DOSAOR.

h	$1/5$	$1/10$	$1/15$	$1/20$
NI	53	74	125	>300
ME	$4.65\times {10}^{-16}$	$5.62\times {10}^{-16}$	$4.03\times {10}^{-16}$	$1.87\times {10}^{-16}$
RMSE	$2.72\times {10}^{-16}$	$2.72\times {10}^{-16}$	$2.15\times {10}^{-16}$	$8.87\times {10}^{-17}$

, with a competitive accuracy.

5.2. Lyapunov Equation

In addition, we can derive a Lyapunov equation for Equation (29):

$$\mathbf{P}\mathbf{U}+\mathbf{U}{\mathbf{P}}^T=\mathbf{Q},$$

(34)

where $\mathbf{U}=\left[u_{ij}\right]$ denotes the numerical solution of $u(x,y)$ at a grid point $(x_i,y_j)$.

$$\mathbf{P}=\left[\begin{array}{cccc}2& -1& 0& \dots \\ -1& 2& \ddots & 0\\ 0& \ddots & \ddots & -1\\ 0& \dots & -1& 2\end{array}\right]$$

(35)

is an $n_1\times n_1$-dimensional tridiagonal matrix, and

$$\tilde{\mathbf{Q}}=-h^2\left[\begin{array}{cccc}p(x_1,y_1)& p(x_1,y_2)& \dots & p(x_1,y_{n_1})\\ ⋮& ⋮& ⋮& ⋮\\ p(x_{n_1},y_1)& p(x_{n_1},y_2)& \dots & p(x_{n_1},y_{n_1})\end{array}\right].$$

(36)

Here, $(x_i,y_j)=(ih,jh),i,j=1,\dots ,n_1$, and $h=1/(n_1+1)$. Hence, we have $n=n_1^2$.

At $(x_i,y_j),i,j=2,\dots ,n_1-1$, we take $Q_{ij}={\tilde{Q}}_{ij}$. However, for other nodal points, the $Q_{ij}$ are constructed according to the following:

$$\begin{array}{ccc}\hfill & & \mathrm{If}i=1\mathrm{and}j=1,\mathrm{then}{Q}_{11}={\tilde{Q}}_{11}+g_1\left(y_1\right)+g_2\left(x_1\right)\hfill \\ & & \mathrm{If}i=1\mathrm{and}j=n_1,\mathrm{then}{Q}_{1,n_1}={\tilde{Q}}_{1,n_1}+g_1\left(y_{n_1}\right)+g_4\left(x_1\right)\hfill \\ & & \mathrm{If}i=n_1\mathrm{and}j=1,\mathrm{then}{Q}_{n_1,1}={\tilde{Q}}_{n_1,1}+g_3\left(y_1\right)+g_2\left(x_{n_1}\right)\hfill \\ & & \mathrm{If}i=n_1\mathrm{and}j=n_1,\mathrm{then}{Q}_{n_1,n_1}={\tilde{Q}}_{n_1,n_1}+g_3(1,y_{n_1})+g_4\left(x_{n_1}\right)\hfill \\ & & \mathrm{If}i=1\mathrm{and}1<j<n_1,\mathrm{then}{Q}_{1,j}={\tilde{Q}}_{1,j}+g_1\left(y_j\right)\hfill \\ & & \mathrm{If}j=n_1\mathrm{and}1<i<n_1,\mathrm{then}{Q}_{i,n_1}={\tilde{Q}}_{i,n_1}+g_4\left(x_i\right)\hfill \\ & & \mathrm{If}i=n_1\mathrm{and}1<j<n_1,\mathrm{then}{Q}_{n_1,j}={\tilde{Q}}_{n_1,j}+g_3\left(y_j\right)\hfill \\ & & \mathrm{If}j=1\mathrm{and}1<i<n_1,\mathrm{then}{Q}_{i,1}={\tilde{Q}}_{i,1}+g_2\left(x_i\right).\hfill \end{array}$$

(37)

We can transform Equation (34) into a vectorized linear equation system with dimension n:

$$({\mathbf{I}}_{n_1}\otimes \mathbf{P}+\mathbf{P}\otimes {\mathbf{I}}_{n_1})vec\left(\mathbf{U}\right)=vec\left(\mathbf{Q}\right),$$

(38)

where ⊗ is the Kronecker product, and $vec\left(\mathbf{U}\right)$ is an n-dimensional vector that consists of all rows of the matrix $\mathbf{U}$.

Using the DOSSOR, we took $a=1.8$ and $b=1.85$, and, through 204 steps, it converged as shown in Figure 4a to satisfy $\epsilon ={10}^{-14}$, where the residual is defined by $\parallel \mathbf{A}{\mathbf{x}}^{\left(k\right)}-\mathbf{b}\parallel$. An ME = $2.22\times {10}^{-14}$ and a RMSE = $1.09\times {10}^{-14}$ were obtained, which were more accurate and faster than those values shown in Table 1. As seen in Figure 4b, f quickly tended to 1, and the optimal values of w varied between 1.821 and 1.845, as are shown in Figure 4c.

Using the DOAOR, we took $(a,b)=(1.8,1.9)$ and $(c,d)=(1.8,1.9)$, and, through 184 steps, it converged as shown in Figure 5a to satisfy the convergence criterion $\epsilon ={10}^{-14}$. An ME = $2.98\times {10}^{-15}$ and a RMSE = $1.09\times {10}^{-15}$ were more accurate and faster than those values obtained by the DOSSOR. The optimal values of w and $\sigma$ are shown in Figure 5b,c.

In

Table 5. Comparing NI, ME, and RMSE for different mesh size h using the DOAOR.

h	$1/10$	$1/15$	$1/20$	$1/25$	$1/30$
NI	160	161	162	164	179
ME	$1.94\times {10}^{-14}$	$4.07\times {10}^{-14}$	$2.42\times {10}^{-14}$	$4.5\times {10}^{-14}$	$1.8\times {10}^{-14}$
RMSE	$9.06\times {10}^{-15}$	$1.55\times {10}^{-14}$	$1.12\times {10}^{-14}$	$1.03\times {10}^{-14}$	$1.66\times {10}^{-15}$

, we list the NI, ME, and RMSE for different mesh size h using the algorithm DOAOR to solve the Lyapunov equation with a fixed $\epsilon ={10}^{-13}$. It is interesting that the accuracy was very good, even for a larger mesh size. By comparing these values to Table 3 with the same $h=1/10,1/15$, the convergence of the DOAOR for the Lyapunov equation has been shown to be faster than that for the matrix–vector equation in Section 5.1; however, the accuracy was worse by about two and three orders, respectively.

Using the DOSAOR, we took $(a,b)=(1.65,1.1.75)$ and $(c,d)=(1.65,1.75)$. In

Table 6. Comparing NI, ME, and RMSE for different mesh size h using the DOSAOR with $\epsilon ={10}^{-13}$.

h	$1/5$	$1/10$	$1/15$	$1/20$
NI	64	78	104	148
ME	$1.54\times {10}^{-13}$	$4.96\times {10}^{-14}$	$1.27\times {10}^{-13}$	$2.16\times {10}^{-13}$
RMSE	$7.4\times {10}^{-14}$	$2.03\times {10}^{-14}$	$6.27\times {10}^{-14}$	$1.11\times {10}^{-13}$

, we list the NI, ME, and RMSE for different mesh size h using the algorithm DOSAOR to solve the Lyapunov equation with a fixed $\epsilon ={10}^{-13}$. Upon comparing those values to Table 4, it can be seen that the convergence of the DOSAOR for the Lyapunov equation was faster, but the accuracy was decreased by about two orders.

To improve the accuracy shown in

Table 7. Comparing NI, ME, and RMSE for different mesh size h using the DOSAOR with $\epsilon ={10}^{-15}$.

h	$1/5$	$1/10$	$1/15$	$1/20$
NI	83	91	120	172
ME	$1.18\times {10}^{-16}$	$4.3\times {10}^{-16}$	$1.35\times {10}^{-15}$	$1.83\times {10}^{-15}$
RMSE	$5.53\times {10}^{-17}$	$1.76\times {10}^{-16}$	$6.68\times {10}^{-16}$	$9.38\times {10}^{-16}$

, the convergence criterion for the DOSAOR with the Lyapunov equation was raised to $\epsilon ={10}^{-15}$. It is interesting that the accuracy was very good, even for a larger mesh size. By comparing those values to Table 4, the convergence of the DOSAOR for the Lyapunov equation has been shown to be faster than that for the matrix–vector equation in Section 5.1, where for $h=1/20$ did not converge within 300 iterations under a larger $\epsilon ={10}^{-13}$.

Next, we consider a a non-homogeneous boundary value problem of the Poisson equation with

$$u(x,y)=x{e}^{xy},$$

(39)

which renders $p(x,y)=(x^3+x{y}^2+2y)e^{xy}$, $g_1\left(y\right)=0$, $g_2\left(x\right)=x$, $g_3\left(y\right)=e^y$, and $g_4\left(x\right)=x{e}^x$.

Using the DOSSOR in Section 5.1, we took $h=1/20$ and $(a,b)=(1.7,1.9)$, and, through 82 steps, it converged to satisfy the convergence criterion $\epsilon ={10}^{-5}$. An ME = $2.72\times {10}^{-5}$ and a RMSE = $1.4\times {10}^{-5}$ were obtained.

Using the DOAOR, we took $h=1/20$, $(a,b)=(1.6,1.9)$, and $(c,d)=(1.7,1.9)$, and, through 64 steps, it converged as shown in Figure 6a to satisfy the convergence criterion $\epsilon ={10}^{-5}$. An ME = $2.5\times {10}^{-5}$ and a RMSE = $1.13\times {10}^{-5}$ were obtained. The optimal values of w and $\sigma$ are shown in Figure 6b,c.

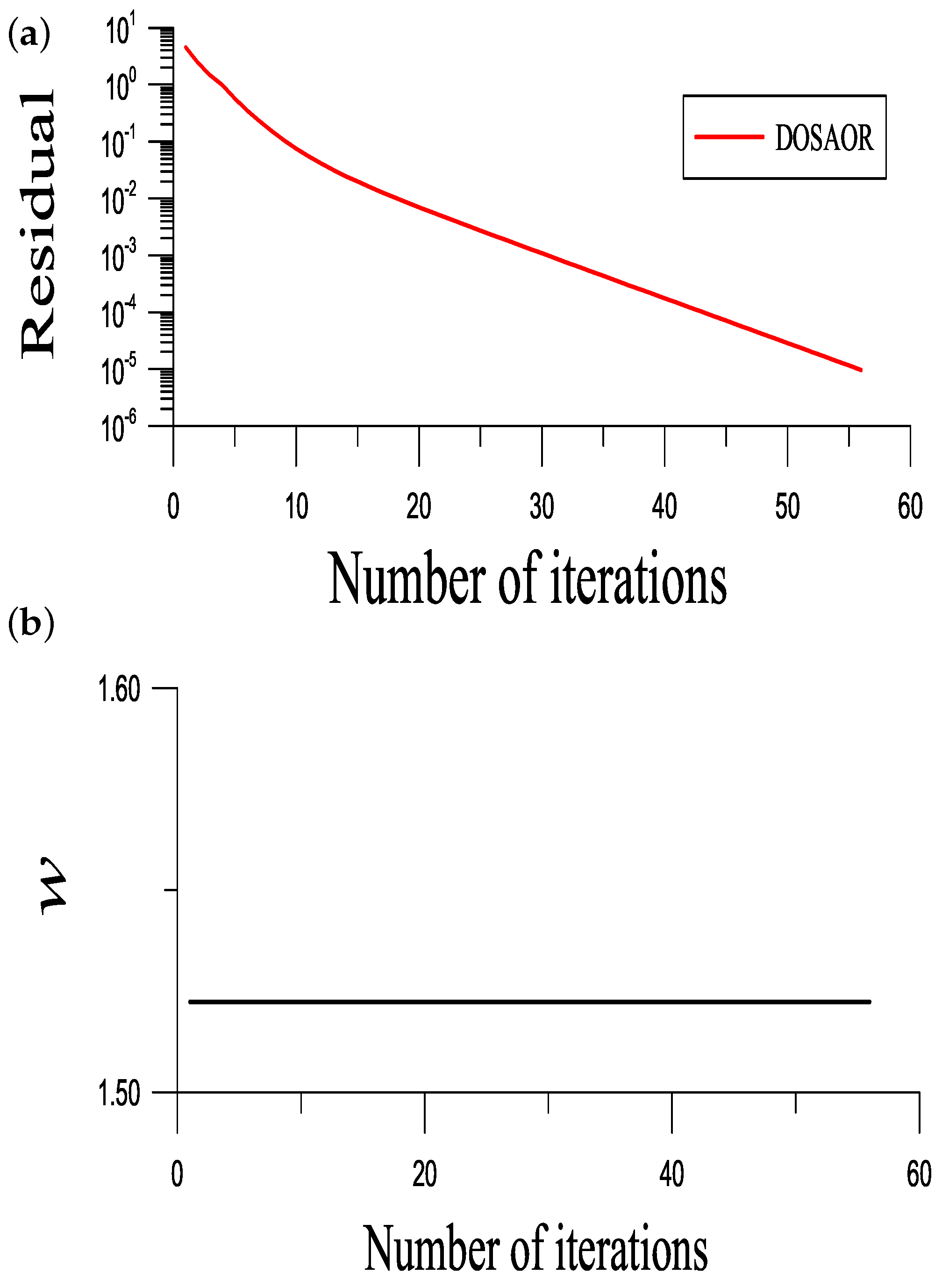
Using the DOSAOR, we took $h=1/20$, $(a,b)=(1.5,1.6)$, and $(c,d)=(1.7,1.9)$, and, through 56 steps, it converged as shown in Figure 7a to satisfy the convergence criterion $\epsilon ={10}^{-5}$. An ME = $1.91\times {10}^{-5}$ and a RMSE = $6.85\times {10}^{-6}$ were obtained. The optimal values of w and $\sigma$ are shown in Figure 7b,c.

5.3. Other Linear System

The proposed iterative methods can be used to solve the general linear system. We cannot exhaust all linear systems; however, we consider a Hilbert problem:

$$\sum _{j=1}^n\frac{x_j}{i+j-1}=b_i,i=1,\dots ,n.$$

(40)

We suppose that $x_j=1,j=1,\dots ,n$ are exact solutions, and $b_i$ can be computed exactly. The Hilbert problem is a highly ill-posed linear equations system. We fix $n=20$. Using the DOSSOR, we took $a=0.1$ and $b=0.5$, and, through NI = 281 steps, it converged as shown in Figure 8a to satisfy the convergence criterion $\epsilon ={10}^{-5}$. An ME = $9.63\times {10}^{-3}$ was obtained by the DOSSOR. w quickly tended to 0.1032522475, as is shown in Figure 8b, which is the optimal value of w for the Hilbert problem with $n=20$. By adopting an ad hoc value $w=0.7$ in the SSOR, NI was raised to NI = 463 under the same convergence criterion $\epsilon ={10}^{-5}$, and more worse is that the ME increased to ME = $1.53\times {10}^{-1}$. Therefore, the presented DOSSOR outperformed the SSOR with an ad hoc value for the parameter w.

We consider a least-square linear system [12]:

$$\left[\begin{array}{ccc}2& 3& -5\\ 4& 5& 3\\ 7& 6& -9\\ 6& 8& -2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}0\\ 12\\ 4\\ 12\end{array}\right].$$

(41)

We suppose that $x_j=1$ and $j=1,2,3$ are exact solutions. We transform it to a normal system:

$$\left[\begin{array}{ccc}105& 116& -73\\ 116& 134& -70\\ -73& -70& 119\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}148\\ 180\\ -24\end{array}\right].$$

(42)

Using the DOSSOR, we took $a=0.45$ and $b=1$, and, through NI = 12 steps, it converged as shown in Figure 9a to satisfy the convergence criterion $\epsilon ={10}^{-2}$. An ME = $1.2\times {10}^{-3}$ was obtained by the DOSSOR. w tended to 0.4527637493 as shown in Figure 9b, which was close to the optimal value $w=0.46898994354$ for the original least-square problem obtained in [12].

6. Conclusions

The accuracy and convergence speed are two main factors to access the performance of an iterative scheme. In this paper, we have performed dynamical realizations in the DOSSOR, DOAOR, and DOSAOR to seek the proper parametric values to improve the convergence speed and accuracy with respect to the original SSOR, AOR and SAOR methods in the solutions of linear systems. Instead of the fixed values of the parameters, the concept of dynamical optimal values of the parameters is novel, and using the maximal projection technique to determine the optimal values of the parameters is highly original. A model problem of the linear Poisson equation in a unit square was formulated with a matrix–vector form and a Lyapunov form of the finite difference equations. In summary, the key outcomes are pointed out here:

• According to the maximal projection technique between two vectors, which is equivalent to the minimization in Equation (6), different merit functions were derived in the DOSSOR, DOAOR and DOSAOR.
• Searching for the minimization was easily performed in a preferred range by the golden section search algorithms with loose convergence criteria.
• In the matrix–vector form equations, the accuracy and convergence speed of the DOAOR were better than the DOSSOR; however, the two-parameter DOAOR required more time to seek the optimal values of the parameters than the single-parameter DOSSOR.
• In the matrix–vector form equations, the convergence speed of the DOSAOR was better than the DOAOR with a competitive accuracy.
• In the matrix–vector form equations, the accuracy obtained by the DOSSOR, DOAOR, and DOSAOR with acceptable iteration numbers were all very good up to the orders ${10}^{-15}$ to ${10}^{-17}$.
• When the DOSSOR, DOAOR, and DOSAOR were applied to the Lyapunov form of finite difference equations, the convergence speeds under the same convergence criterion ${10}^{-13}$ were raised significantly; however, the accuracy was lost by about one or two orders.
• In the Lyapuov form equations, the accuracy of the DOSAOR could be enhanced by using a stringent convergence criterion ${10}^{-15}$, which yielded a highly accurate solution to the order of ${10}^{-16}$ with a smaller number of iterations.
• Instead of the theoretical values of the fixed optimal values of the parameters, which, in general, are not available, the new methods provided an alternative and feasible choice of the optimal values of the parameters at each iteration.
• No matter which form of linear equations was used, the proposed DOSSOR, DOAOR, and DOSAOR could provide almost the exact solution of the Poisson equation within a reasonable number of iterations that was smaller than 300 for 900 discretized linear equations. Even for larger mesh size, the accuracy was also very good.
• The presented methodologies for the DOSSOR, DOAOR, and DOSAOR were quite simple, which, in the near future, may be extended to obtain the optimal values of other versions of SSOR/SAOR methods, such as generalized or modified SSOR/SAOR ones and other types of linear systems.