The Fuzzy Differential Transform Method for the Solution of the System of Fuzzy Integro-Differential Equations Arising in Biological Model
Abstract
:1. Introduction
2. Preliminaries
- 1.
- is a left continuous monotonic bounded increasing function.
- 2.
- is a is a left continuous monotonic bounded decreasing function.
- 3.
- .
- a.
- b.
- c.
- ,
- a.
- ;
- b.
- c.
- d.
- is a complete metric space.
3. Fuzzy Differential Transform Method
- If , then ,
- If , then .
- If , then .
- .
- .
4. Main Results
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wazwaz, A.M. Linear and Nonlinear Integral Equations: Methods and Applications; Springer: Beijing, China, 2011. [Google Scholar]
- Wang, H.; Fu, H.M.; Zhang, H.F.; Hu, Z.Q. A practical thermodynamic method to calculate the best glass-forming composition for bulk metallic glasses. Int. J. Nonlinear Sci. Numer. Simul. 2007, 8, 171–178. [Google Scholar] [CrossRef]
- Xu, L.; He, J.H.; Liu, Y. Electrospun nanoporous spheres with Chinese drug. Int. J. Nonlinear Sci. Numer. Simul. 2007, 8, 199–202. [Google Scholar] [CrossRef]
- Sun, F.Z.; Gao, M.; Lei, S.H.; Zhao, Y.B.; Wang, K.; Shi, Y.T.; Wang, N.H. The fractal dimension of the fractal model of dropwise condensation and its experimental study. Int. J. Nonlinear Sci. Numer. Simul. 2007, 8, 211–222. [Google Scholar] [CrossRef]
- Bo, T.L.; Xie, L.; Zheng, X.J. Numerical approach to wind ripple in desert. Int. J. Nonlinear Sci. Numer. Simul. 2007, 8, 223–228. [Google Scholar] [CrossRef]
- Shakeri, F.; Dehghan, M. Solution of a model describing biological species living together using the variational iteration method. Math. Comput. Model. 2008, 48, 685–699. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning. Inform. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Chang, S.S.L.; Zadeh, L. On fuzzy mapping and control. IEEE Trans. Syst. Man Cybernet. 1972, 2, 30–34. [Google Scholar] [CrossRef]
- Kaleva, O. Fuzzy differential equations. Fuzzy Sets Syst. 1987, 24, 301–317. [Google Scholar] [CrossRef]
- Seikkala, S. On the fuzzy initial value problem. Fuzzy Sets Syst. 1987, 24, 319–330. [Google Scholar] [CrossRef]
- Salahshour, S.; Allahviranloo, T. Application of fuzzy differential transform method for solving fuzzy Volterra integral equations. Appl. Math. Model. 2013, 37, 1016–1024. [Google Scholar] [CrossRef]
- Babolian, E.; Goghary, H.S.; Abbasbandy, S. Numerical solution of linear Fredholm fuzzy integral equations of the second kind by Adomian method. Appl. Math.Comput. 2005, 161, 733–744. [Google Scholar] [CrossRef]
- Younis, M.T.; Al-Hayani, W. Solving fuzzy system of Volterra integro-diofferential equations by using Adomian decomposition method. Eur. J. Pure Appl. Math. 2022, 15, 290–313. [Google Scholar] [CrossRef]
- Molabahrami, A.; Shidfar, A.; Ghyasi, A. An analytical method for solving linear Fredholm fuzzy integral equations of the second kind. Comput. Math. Appl. 2011, 61, 2754–2761. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Hashemzehi, S. The homotopy perturbation method for fuzzy Fredholm integral equations. J. Appl. Math. Islam. Azad Univ. Lahijan 2008, 5, 1–12. [Google Scholar]
- Haq, M.U.; Ullah, A.; Ahmad, S.; Akgul, A. A quantitative approach to nth-order nonlinear fuzzy integro-differential equation. Int. J. Appl. Comput. Math. 2022, 8, 92. [Google Scholar] [CrossRef]
- Kang, S.M.; Iqbal, Z.; Habib, M.; Nazeer, W. Sumudu decomposition method for solving fuzzy integro-differential equations. Axioms 2019, 8, 74. [Google Scholar] [CrossRef]
- Jafarian, A.; Rostami, F.; Golmankhaneh, A.K.; Baleanu, D. Using ANNs Approach for Solving Fractional Order Volterra Integro-differential Equations. Int. J. Comput. Intell. Syst. 2017, 10, 470–480. [Google Scholar] [CrossRef]
- Sahu, P.K.; Ray, S.S. Two dimensional Legendre wavelet method for the numerical solutions of fuzzy integro-differential equations. J. Intell. Fuzzy Syst. 2015, 28, 1271–1279. [Google Scholar] [CrossRef]
- Sahu, P.K.; Ray, S.S. A new Bernoulli wavelet method for accurate solutions of nonlinear fuzzy Hammerstein–Volterra delay integral equations. Fuzzy Sets Syst. 2017, 309, 131–144. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Kiani, N.A.; Motamedi, N. Solving fuzzy differential equations by differential transformation method. Inf. Sci. 2009, 179, 956–966. [Google Scholar] [CrossRef]
- Tang, T.; Xu, X.; Cheng, J. On the spectral methods for Volterra integral equations and the convergence analysis. J. Comput. Math. 2008, 26, 825–837. [Google Scholar]
- Samadi, O.R.N.; Tohodi, E. The spectral method for solving systems of Volterra integral equations. J. Appl. Math. Comput. 2012, 40, 477–497. [Google Scholar] [CrossRef]
- Chen, Y.P.; Tang, T. Spectral methods for weakly singular Volterra integral equations with smooth solutions. J. Comput. Appl. Math. 2009, 233, 938–950. [Google Scholar] [CrossRef]
- Puri, M.L.; Ralescu, D. Differential for fuzzy function. J. Math. Anal. Appl. 1983, 91, 552–558. [Google Scholar] [CrossRef]
- Chalco-Cano, Y.; Román-Flores, H. On new solutions of fuzzy differential equations. Chaos Solitons Fractals 2008, 38, 552–558. [Google Scholar] [CrossRef]
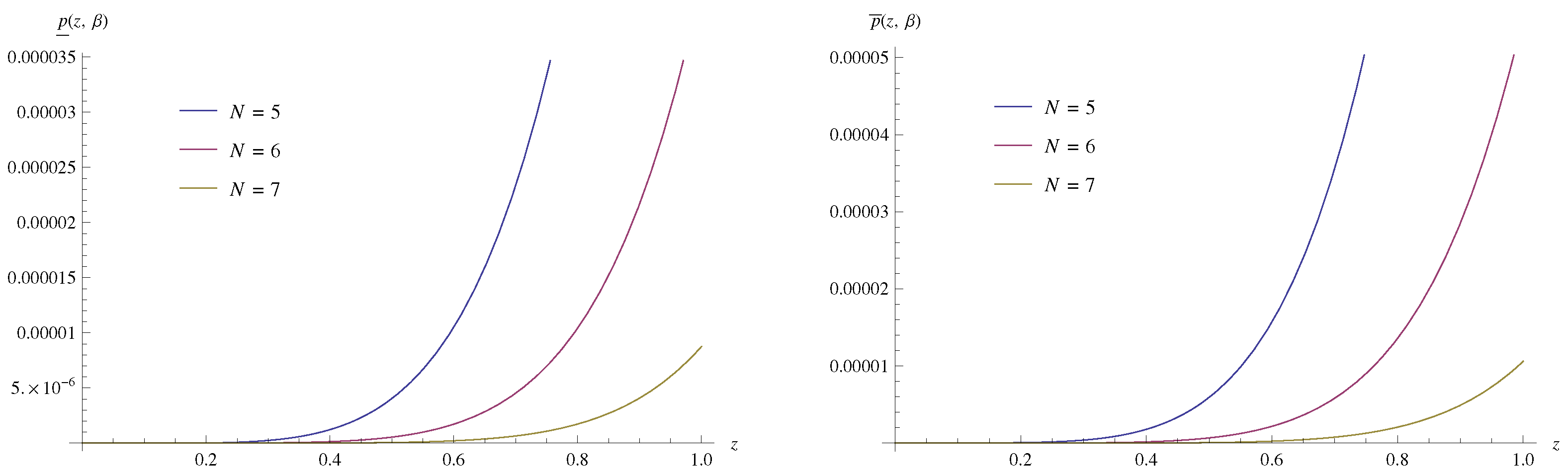
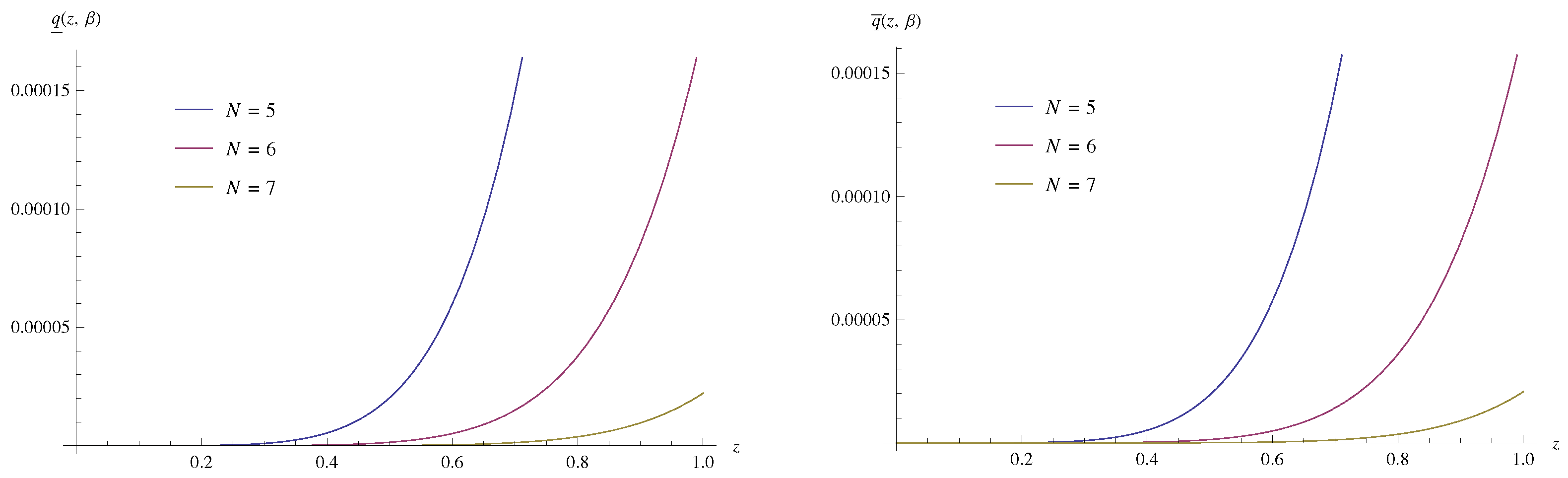
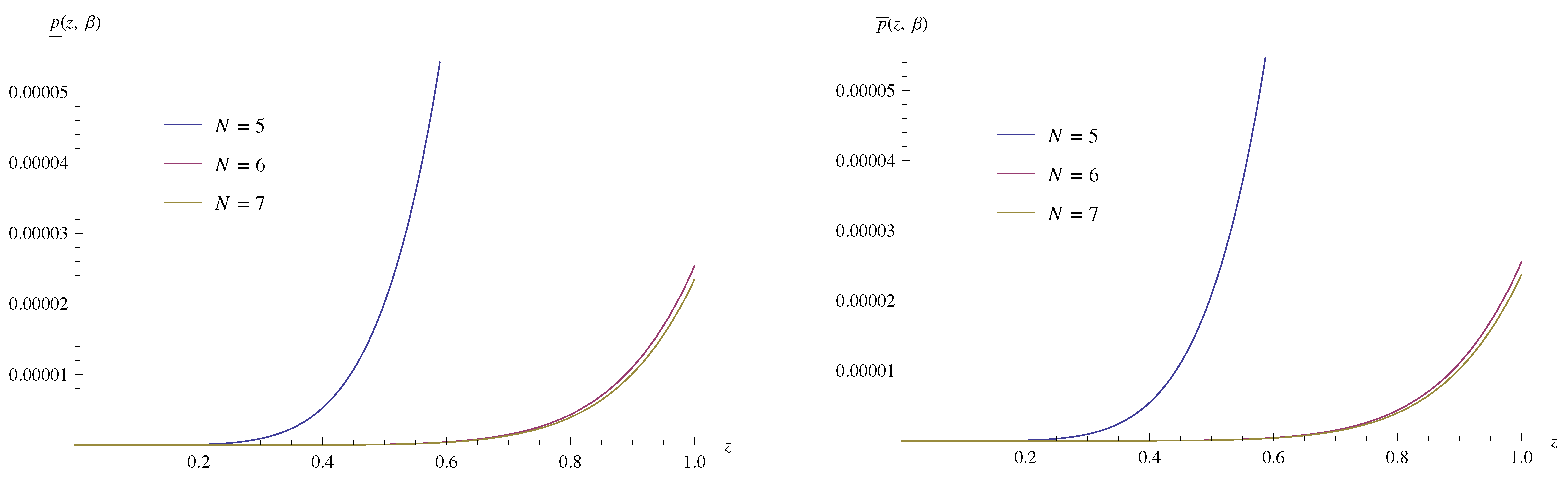

| z | ||||||||
|---|---|---|---|---|---|---|---|---|
| Appx | Exact | Appx | Exact | Appx | Exact | Appx | Exact | |
| 0.1 | −0.03 | −0.03 | 0.05 | 0.05 | −0.15 | −0.15 | 0.17 | 0.17 |
| 0.2 | 0 | 0.0799999 | 0.08 | −0.12 | −0.12 | 0.20 | 0.20 | |
| 0.3 | 0.0499998 | 0.05 | 0.13 | 0.13 | −0.07 | −0.07 | 0.249999 | 0.25 |
| 0.4 | 0.119999 | 0.12 | 0.199998 | 0.20 | 0 | 0.319997 | 0.32 | |
| 0.5 | 0.209996 | 0.21 | 0.289994 | 0.29 | 0.0899987 | 0.09 | 0.409991 | 0.41 |
| 0.6 | 0.319989 | 0.32 | 0.399984 | 0.40 | 0.199997 | 0.20 | 0.519977 | 0.52 |
| 0.7 | 0.449977 | 0.45 | 0.529964 | 0.53 | 0.329995 | 0.33 | 0.649946 | 0.65 |
| 0.8 | 0.599954 | 0.60 | 0.679928 | 0.68 | 0.479992 | 0.48 | 0.79989 | 0.80 |
| 0.9 | 0.769915 | 0.77 | 0.849866 | 0.85 | 0.649988 | 0.65 | 0.969794 | 0.97 |
| z | ||||||||
|---|---|---|---|---|---|---|---|---|
| Appx | Exact | Appx | Exact | Appx | Exact | Appx | Exact | |
| 0.1 | 0.104837 | 0.104837 | 1.70484 | 1.70484 | 0.704837 | 0.704837 | 1.10484 | 1.10484 |
| 0.2 | 0.0187307 | 0.0187308 | 1.61873 | 1.61873 | 0.618731 | 0.618731 | 1.01873 | 1.01873 |
| 0.3 | −0.0591828 | −0.0591818 | 1.54082 | 1.54082 | 0.540817 | 0.540818 | 0.940817 | 0.940818 |
| 0.4 | −0.129685 | −0.12968 | 1.47031 | 1.47032 | 0.470314 | 0.47032 | 0.870315 | 0.87032 |
| 0.5 | −0.19349 | −0.193469 | 1.40651 | 1.40653 | 0.40651 | 0.406531 | 0.806512 | 0.806531 |
| 0.6 | −0.251248 | −0.251188 | 1.34875 | 1.34881 | 0.34875 | 0.348812 | 0.748756 | 0.748812 |
| 0.7 | −0.303563 | −0.303415 | 1.29644 | 1.29659 | 0.296433 | 0.296585 | 0.696446 | 0.696585 |
| 0.8 | −0.350998 | −0.350671 | 1.24901 | 1.24933 | 0.248994 | 0.249329 | 0.64902 | 0.649329 |
| 0.9 | −0.394085 | −0.39343 | 1.20593 | 1.20657 | 0.2059 | 0.20657 | 0.60595 | 0.60657 |
| z | ||||||||
|---|---|---|---|---|---|---|---|---|
| FDTM | ADM | FDTM | ADM | FDTM | ADM | FDTM | ADM | |
| 0.1 | ||||||||
| 0.2 | ||||||||
| 0.3 | ||||||||
| 0.4 | ||||||||
| 0.5 | ||||||||
| 0.6 | ||||||||
| 0.7 | ||||||||
| 0.8 | ||||||||
| 0.9 | ||||||||
| z | ||||||||
|---|---|---|---|---|---|---|---|---|
| Appx | Exact | Appx | Exact | Appx | Exact | Appx | Exact | |
| 0.1 | 1.095 | 1.095 | 0.895004 | 0.895004 | 1.895 | 1.895 | 0.0950042 | 0.0950042 |
| 0.2 | 1.08007 | 1.08007 | 0.880067 | 0.880067 | 1.88007 | 1.88007 | 0.0800667 | 0.0800666 |
| 0.3 | 1.05534 | 1.05534 | 0.855337 | 0.855336 | 1.85534 | 1.85534 | 0.0553375 | 0.0553365 |
| 0.4 | 1.02107 | 1.02106 | 0.821066 | 0.821061 | 1.82106 | 1.82106 | 0.0210667 | 0.021061 |
| 0.5 | 0.977603 | 0.977583 | 0.777603 | 0.777583 | 1.77759 | 1.77758 | −0.0223958 | −0.0224174 |
| 0.6 | 0.925396 | 0.925336 | 0.725398 | 0.725336 | 1.72537 | 1.72534 | −0.0746 | −0.0746644 |
| 0.7 | 0.864995 | 0.864842 | 0.664999 | 0.664842 | 1.66493 | 1.66484 | −0.134996 | −0.135158 |
| 0.8 | 0.797047 | 0.796707 | 0.597057 | 0.596707 | 1.59690 | 1.59671 | −0.202933 | −0.203293 |
| 0.9 | 0.7223 | 0.72161 | 0.522318 | 0.52161 | 1.52203 | 1.52161 | −0.277663 | −0.27839 |
| z | ||||||||
|---|---|---|---|---|---|---|---|---|
| Appx | Exact | Appx | Exact | Appx | Exact | Appx | Exact | |
| 0.1 | 0.224958 | 0.224958 | −0.175042 | −0.175042 | 1.82496 | 1.82496 | −1.77504 | −1.77504 |
| 0.2 | 0.249667 | 0.249667 | −0.150333 | −0.150333 | 1.84967 | 1.84967 | −1.75033 | −1.75033 |
| 0.3 | 0.27388 | 0.27388 | −0.12612 | −0.12612 | 1.87388 | 1.87388 | −1.72612 | −1.72612 |
| 0.4 | 0.297355 | 0.297355 | −0.102645 | −0.102645 | 1.89735 | 1.89735 | −1.70265 | −1.70265 |
| 0.5 | 0.319857 | 0.319856 | −0.0801420 | −0.0801436 | 1.91985 | 1.91986 | −1.68014 | −1.68014 |
| 0.6 | 0.341161 | 0.341161 | −0.0588345 | −0.0588394 | 1.94113 | 1.94116 | −1.65884 | −1.65884 |
| 0.7 | 0.361057 | 0.361054 | −0.0389333 | −0.0389456 | 1.96099 | 1.96105 | −1.63894 | −1.63895 |
| 0.8 | 0.379345 | 0.379339 | −0.0206337 | −0.020661 | 1.9792 | 1.97934 | −1.62065 | −1.62066 |
| 0.9 | 0.395847 | 0.395832 | −0.0041126 | −0.00416827 | 1.99558 | 1.99583 | −1.60414 | −1.60417 |
| z | ||||||||
|---|---|---|---|---|---|---|---|---|
| FDTM | ADM | FDTM | ADM | FDTM | ADM | FDTM | ADM | |
| 0.1 | ||||||||
| 0.2 | ||||||||
| 0.3 | ||||||||
| 0.4 | ||||||||
| 0.5 | ||||||||
| 0.6 | ||||||||
| 0.7 | ||||||||
| 0.8 | ||||||||
| 0.9 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Routaray, M.; Sahu, P.K.; Chalishajar, D.N. The Fuzzy Differential Transform Method for the Solution of the System of Fuzzy Integro-Differential Equations Arising in Biological Model. Mathematics 2023, 11, 3840. https://doi.org/10.3390/math11183840
Routaray M, Sahu PK, Chalishajar DN. The Fuzzy Differential Transform Method for the Solution of the System of Fuzzy Integro-Differential Equations Arising in Biological Model. Mathematics. 2023; 11(18):3840. https://doi.org/10.3390/math11183840
Chicago/Turabian StyleRoutaray, Mitali, Prakash Kumar Sahu, and Dimplekumar Navinchandra Chalishajar. 2023. "The Fuzzy Differential Transform Method for the Solution of the System of Fuzzy Integro-Differential Equations Arising in Biological Model" Mathematics 11, no. 18: 3840. https://doi.org/10.3390/math11183840
APA StyleRoutaray, M., Sahu, P. K., & Chalishajar, D. N. (2023). The Fuzzy Differential Transform Method for the Solution of the System of Fuzzy Integro-Differential Equations Arising in Biological Model. Mathematics, 11(18), 3840. https://doi.org/10.3390/math11183840








