An Efficient Hybrid Multi-Objective Optimization Method Coupling Global Evolutionary and Local Gradient Searches for Solving Aerodynamic Optimization Problems
Abstract
:1. Introduction
- (1)
- As the number of design variables and objectives increases, the multi-objective evolutionary algorithm (MOEA) requires a larger population size and more iterations to approach the optimal Pareto front (PF), resulting in a significant decrease in optimization efficiency and accuracy.
- (2)
- Although the existing gradient-based multi-objective optimization algorithms are efficient, they can only obtain local optimal solutions and cannot solve MOPs with arbitrary PF.
- (3)
- High-fidelity aerodynamic shape optimization is usually calculated using a computational fluid dynamics (CFD) solver based on the Reynolds-Averaged Navier–Stokes (RANS) equations, which makes the aerodynamic analysis very computationally costly.
2. Related Work and Motivation
2.1. Difficulties of Multi-Objective Optimization Problems
2.2. Multi-Objective Gradient Algorithm Based on Dynamic Stochastic Weights
- The new MOGBA assigns stochastic weights to each individual. In addition, the stochastic weights are dynamically updated during iterations.
- In each iteration, the solutions can diffuse in different directions, which makes it possible to generate arbitrary PFs by scanning the weight space. The MOGBA effectively solves the issue of inequivalence between the fixed weight vectors and the solutions in objective space.
- A combined gradient descent direction based on multiple objective functions can be provided for each individual so that a uniformly distributed Pareto optimal solution can be obtained. However, the convergence speed may be slightly reduced compared to the traditional gradient weighting method due to the constantly changing search directions.
| Algorithm 1 Multi-Objective Gradient-Based Algorithm | |
| Input: N (population size), M (number of objectives) T (maximum iteration number) Output: P (final population) | |
| 1: | |
| 2: | for do |
| 3: | for do |
| 4: | // generate random weights |
| 5: | //weight sum methods |
| 6: | compute from the L-BFGS-B procedures |
| 7: | |
| 8: | end for |
| 9: | |
| 10: | end for |
2.3. Gradient-Enhanced Kriging with Partial Least Squares Approach
2.4. Motivation
3. Hybrid Multi-Objective Algorithm Coupling Global Evolution and Local Gradient Search
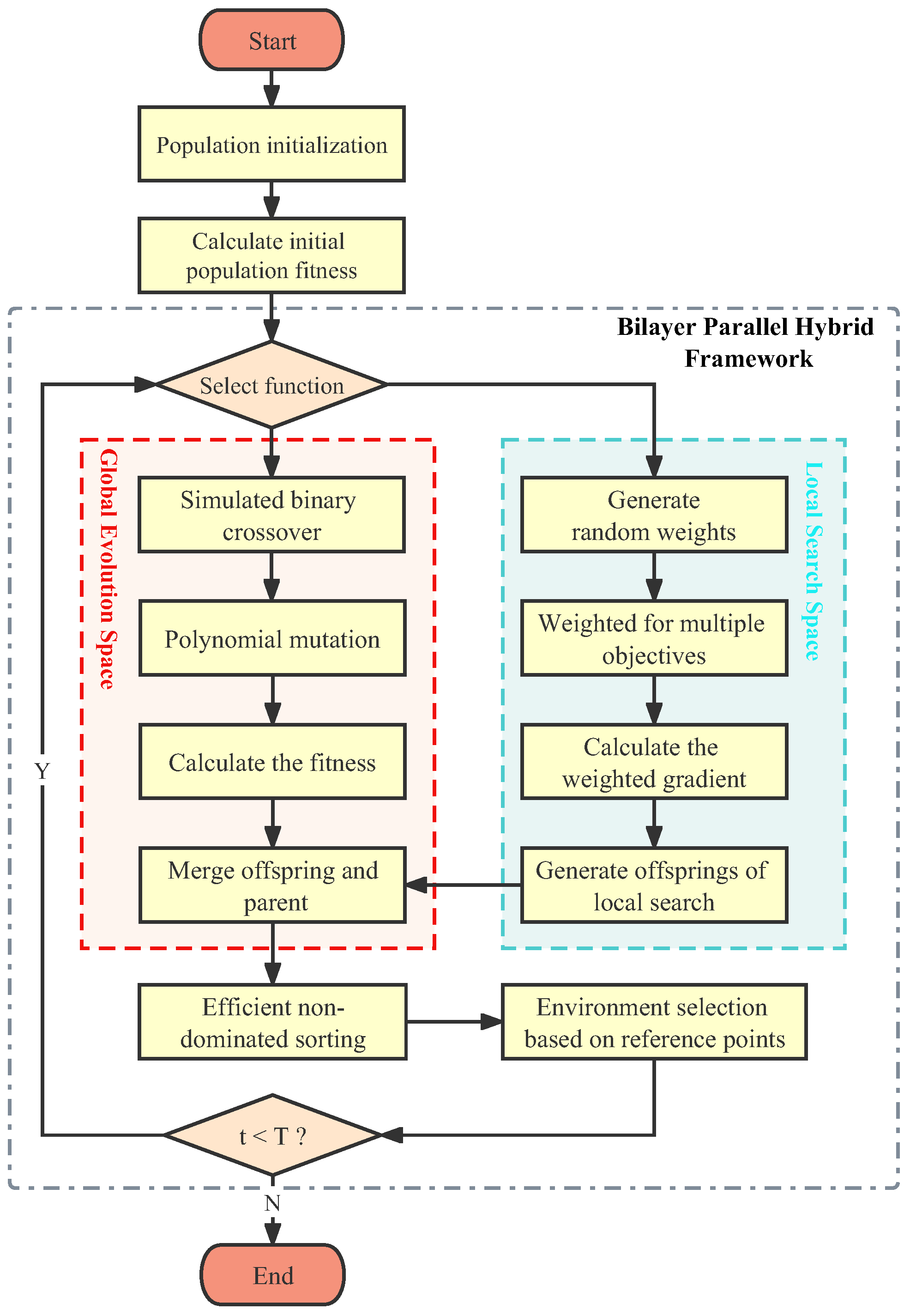
3.1. Hybrid Multi-Objective Algorithm Framework
| Algorithm 2 MOHA Procedure | |
| Input: N (population size), (crossover probability), (mutation probability), T (maximum iteration number), P (acceptance probability), M (number of objectives) Output: (next population) | |
| 1: | t ← 0; |
| 2: | Z ← |
| 3: | ← |
| 4: | ← |
| 5: | while do |
| 6: | ← |
| 7: | if Local search then |
| 8: | for do |
| 9: | ← ; //Local search based on gradient information |
| 10: | end for |
| 11: | ← (∪); |
| 12: | else |
| 13: | ← (,,);//Global search |
| 14: | end if |
| 15: | ← ∪; |
| 16: | () ← (); |
| 17: | ← Ø, i ← 1; |
| 18: | repeat |
| 19: | ← ∪ and i ← i + 1 |
| 20: | until |
| 21: | Last front to be included: = ; |
| 22: | if then |
| 23: | =, break |
| 24: | else |
| 25: | = ; |
| 26: | //:reference points on normalized hyperplane |
| 27: | Points to be chosen from : ; |
| 28: | [] ← (); // :closest reference point, d:distance between s and |
| 29: | ← ();//:niche count for the jth reference point |
| 30: | end if |
| 31: | t ← |
| 32: | end while |
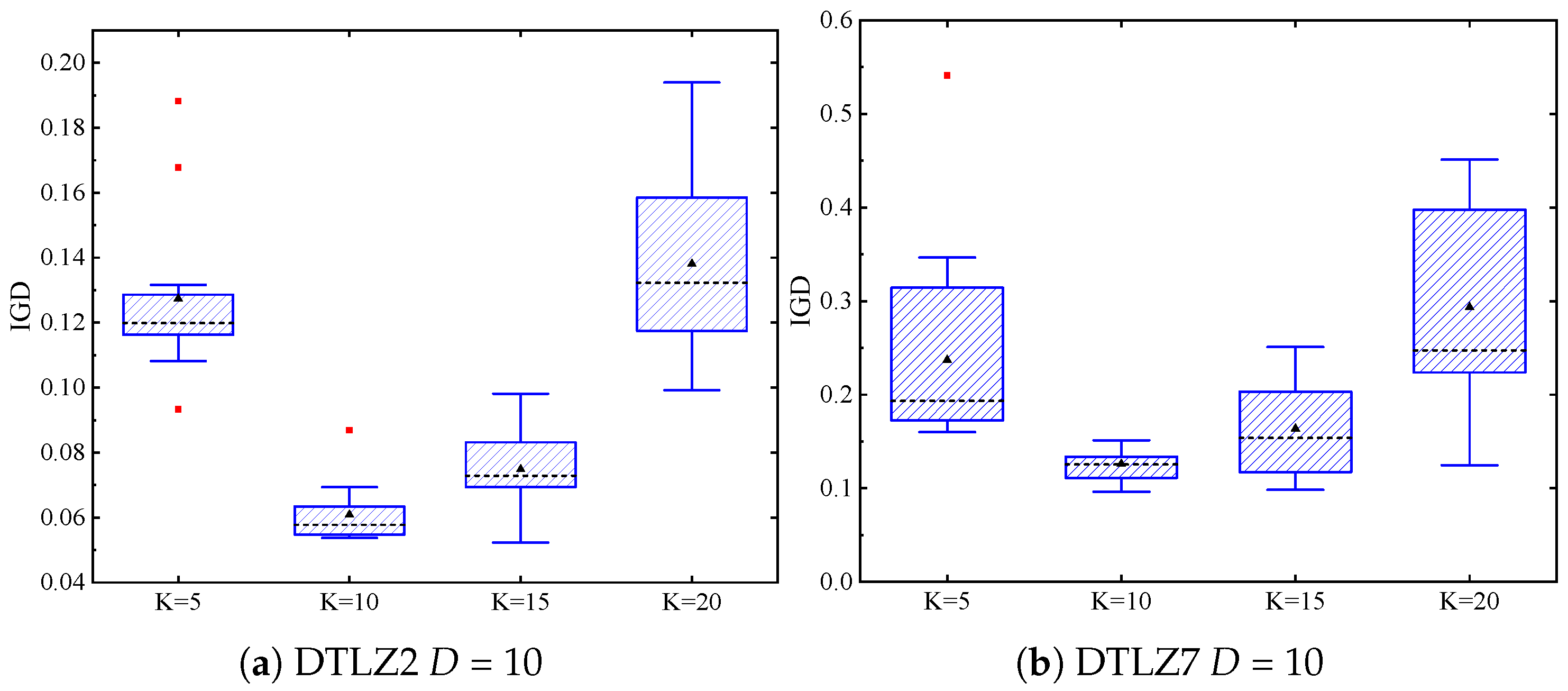
3.2. Sensitivity Analysis of the Local Search Parameter P
3.3. Population Evolution and Acceleration Mechanism Analysis of Multi-Objective Hybrid Algorithm
- In the hybrid framework, elite individuals are selected into the local space. These elite individuals are generated by MOEA and carry the vast majority of useful information. A multi-objective gradient search on this basis not only amplifies this advantage but also increases population diversity.
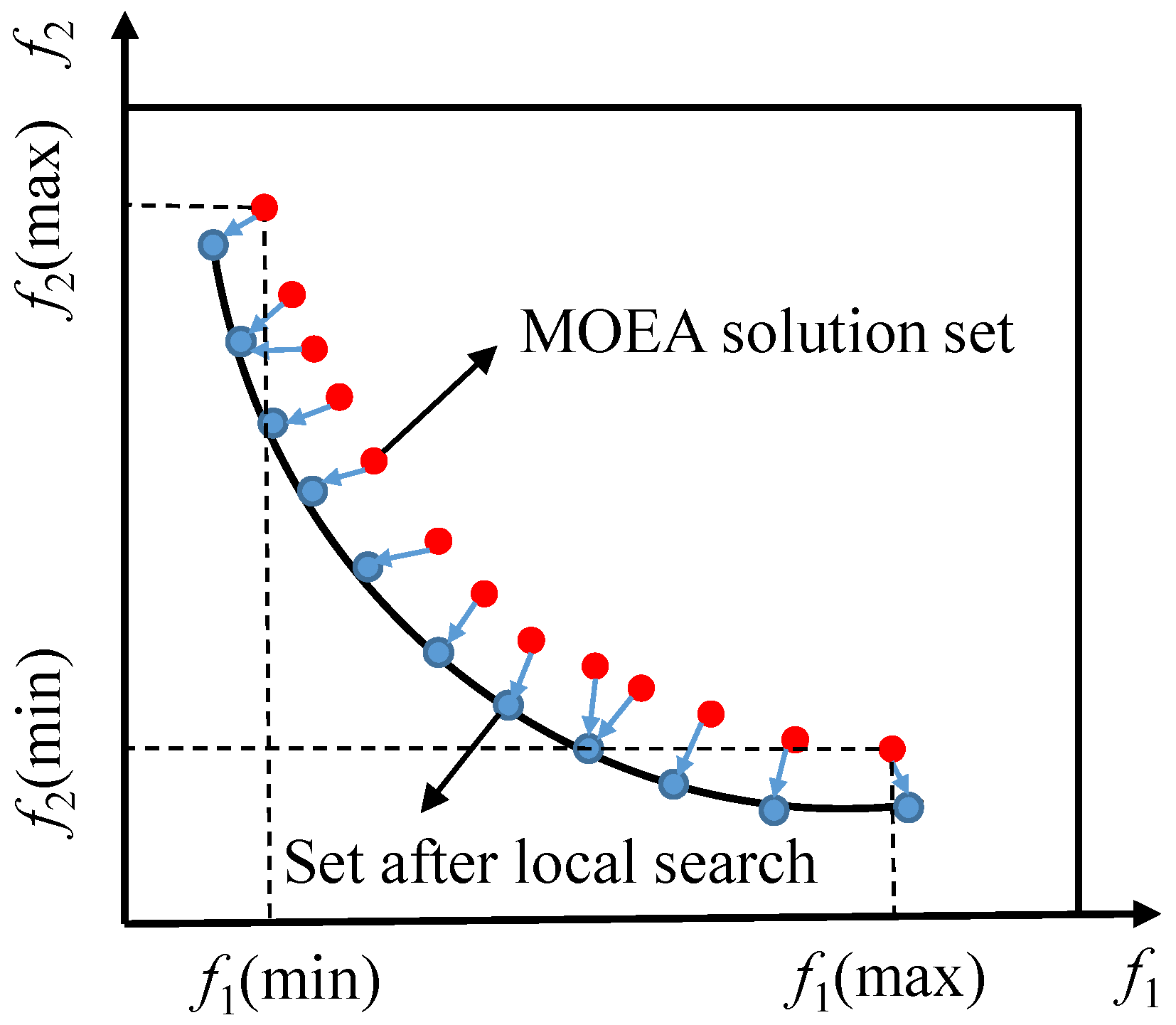
- The quality of most offspring solutions generated by local search is always better than that of global search as shown by the red dots in Figure 10c. They carry a great number of excellent genes and a great deal of knowledge and are therefore able to guide the evolutionary direction of other individuals. This information exchange substantially improves the speed of the algorithm in finding the global optimal solution.
- The proposed algorithm can quickly approximate the global optimal PF, mainly due to its good global exploration and local search capabilities. When MOEA approaches the true Pareto front, it tends to slow down and the solutions generated may oscillate. This phenomenon can be eliminated by using hybridization.
4. Hybrid Optimization Algorithm Based on GEKPLS Surrogate Model
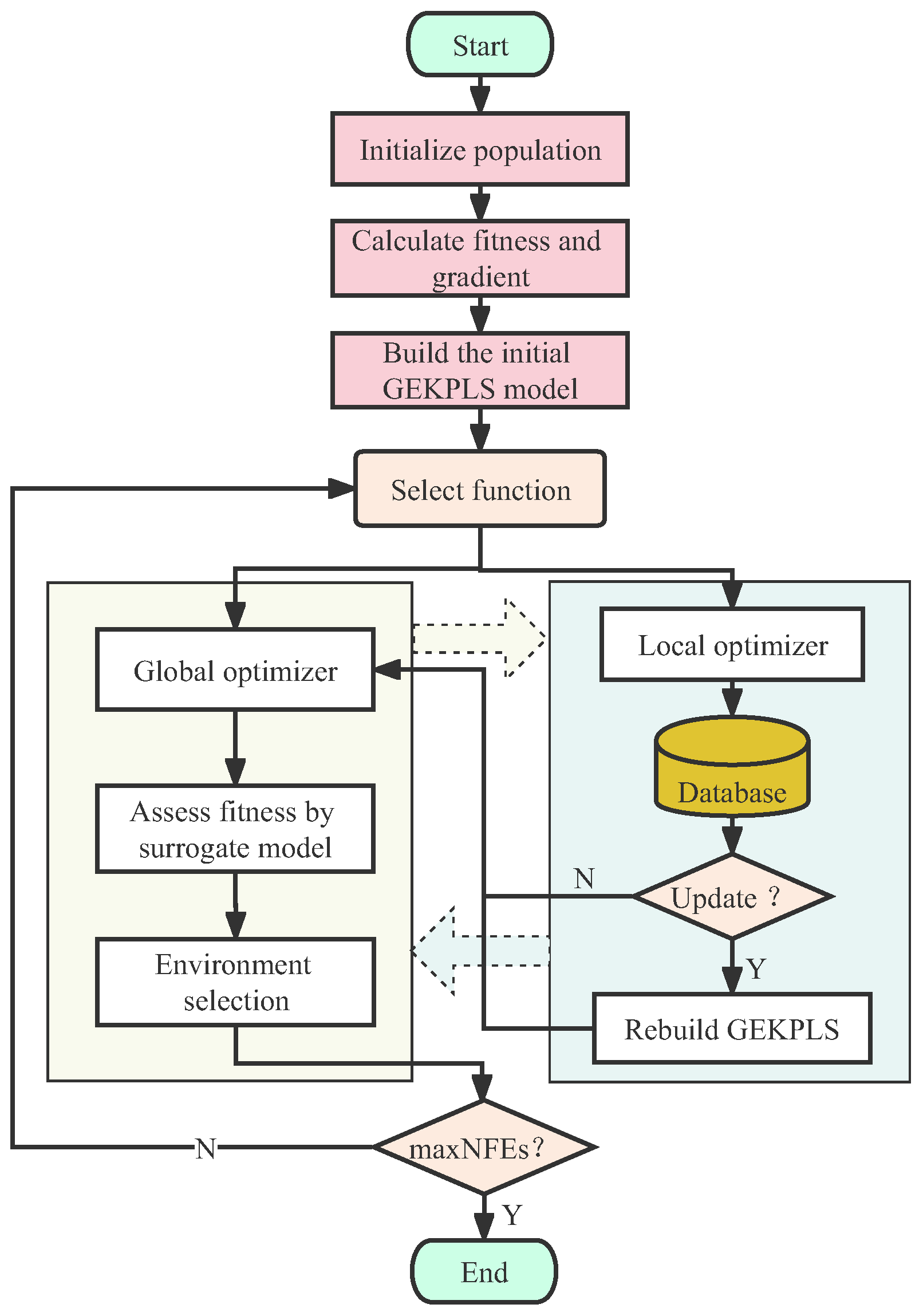
4.1. Surrogate-Assisted Hybrid Multi-Objective Algorithm Framework
- Step 1: Generate random populations and evaluate their objective function values and gradient values. After that, the initial surrogate model of GEKPLS is built.
- Step 2: Control the global evolution and local search behaviors of individuals using selection functions. The global optimizer uses a surrogate model for fitness calculation. The global search of the surrogate model is performed using polynomial mutation (PM) and simulated binary crossover (SBX) operators. Meanwhile, the real fitness and gradient of individuals entering the local optimizer are calculated.
- Step 3: An external database is created to store the real fitness and gradient information generated by the local optimizer in each iteration. Here, the gradient is calculated using the finite difference method, but the adjoint method is used in aerodynamic optimization.
- Step 4: Decide whether the GEKPLS model needs to be updated. If the surrogate model is updated, the GEKPLS model is rebuilt with the individual information from the external archive set. Otherwise, the original model is used for function evaluation.
- Step 5: Merging the offspring generated by the global and local optimizers. Then, the next generation population is selected through the environmental selection mechanism.
- Step 6: Stop the algorithm if the stopping criterion is satisfied. Otherwise, go to Step 2.
- (1)
- With MOHA as the main driving engine, GS-MOHA inherits all the advantages of the hybrid algorithm and has a faster convergence speed.
- (2)
- Combining fitness values and gradient values at each sampling point has the potential to enrich the surrogate model. This means that GS-MOHA runs faster and with higher accuracy for the same number of sampling points. The local search technique based on gradient information not only facilitates the evolution of the population but also enhances the quality of the surrogate model.
- (3)
- GS-MOHA uses a multi-point infill strategy. The number of filling points is related to the number of elite solutions in local search. This infill strategy makes reasonable and efficient use of the hybrid algorithm framework.
- (4)
- GS-MOHA is capable of solving expensive MOPs with decision variable dimensions greater than 10. Due to the adoption of the GEKPLS and hybrid algorithm framework, the search efficiency and modeling accuracy in high-dimensional design spaces are better than traditional methods. This fulfills our primary purpose of pursuing efficiency in engineering optimization.
4.2. Model Update Management and Validation
| Algorithm 3 The Surrogate-Assisted Model Update Strategy | |
| Input: P (current population), M (number of objectives), V (decision variables), K (update frequency), T (maximum number of iterations) Output: (offspring population of MOEA), (offspring population of MOGBA), Q (next population) | |
| 1: | Y ← ; |
| 2: | G ← ; |
| 3: | for do |
| 4: | ← the ith column of Y; |
| 5: | ← the ith column of G; |
| 6: | GEKPLS ← ; |
| 7: | end for |
| 8: | for do |
| 9: | if and then |
| 10: | Update GEKPLS with the solutions generated by Algorithm 1; |
| 11: | else |
| 12: | ← Predicted objective values by the ith GEKPLS model; |
| 13: | ← Algorithm 1; |
| 14: | Q ← ∪; |
| 15: | ← ; |
| 16: | end if |
| 17: | end for |
5. Numerical Experiments and Discussion
5.1. Performance Comparison between MOHA and Existing MOEAs
5.1.1. Experimental Setting
- (1)
- Population Sizing: The population size of NSGA-III and MOEA/D is not arbitrarily specified but depends on the number of reference points or weight vectors. As recommended in [55], the population size is set at 105 when and 126 for the corresponding .
- (2)
- Termination Conditions: An increase in the number of decision variables and objective functions will increase the optimization difficulty. For the three-objective test problems, with 30 and 50 decision variables, the maximum number of evaluations is set to 50,000 and 100,000. Similarly, when , the evaluations are set to 100,000 and 150,000, respectively. Statistical results of all test problems were obtained by 20 independent experiments for each algorithm.
- (3)
- Performance Metrics: The performances of the algorithms are evaluated with IGD [37] and hypervolume (HV) [46]. In principle, both IGD and HV can evaluate the convergence and diversity of the obtained non-dominated solutions. A smaller value of IGD indicates a better quality of the obtained solution set, while HV is just the opposite: a larger value indicates better solution quality.
- (4)
- Control parameters: For the MOHA, the acceptance probability is set to . And the gradient is estimated using a 2-point finite difference estimation with an absolute step size. The number of local gradient searches is set to one. All of the algorithms adopt the same evolutionary operators such as PM and SBX. The parameters of the evolutionary operator are consistent with the literature [55].
5.1.2. Discussion of Results
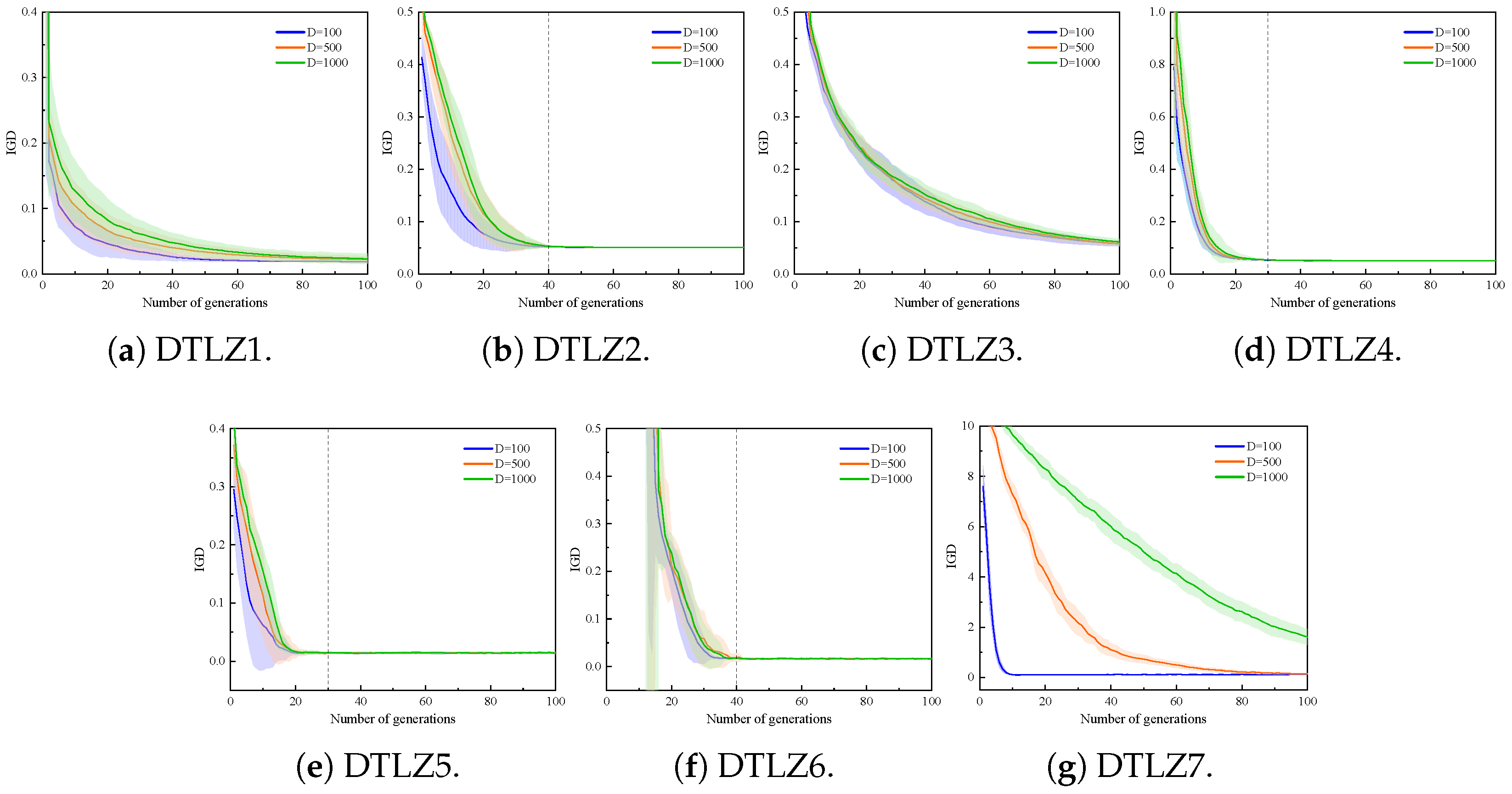
5.1.3. Performance of MOHA on Large-Scale MOPs with 1000 Decision Variables
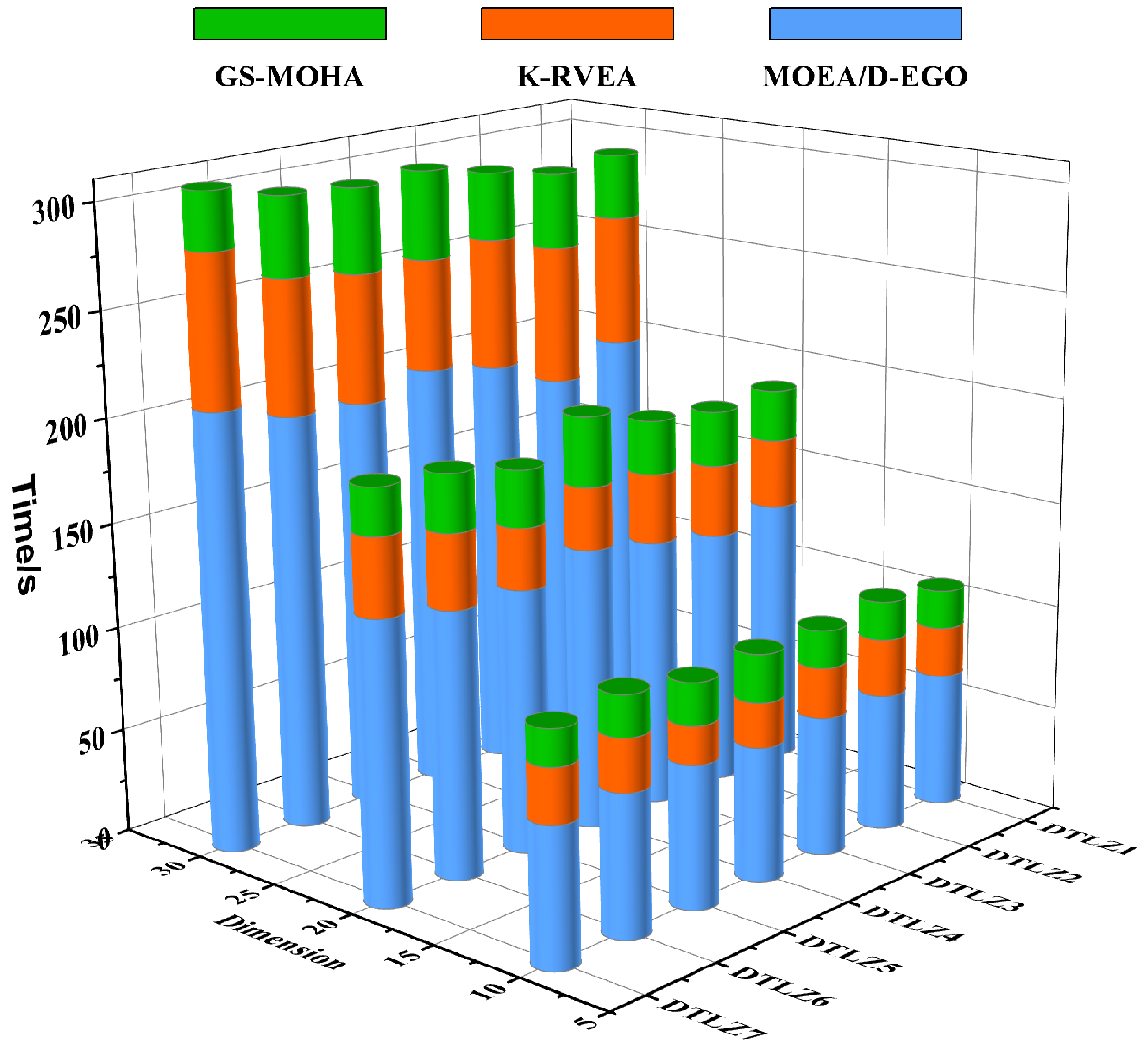
5.1.4. Efficiency Analysis of MOHA
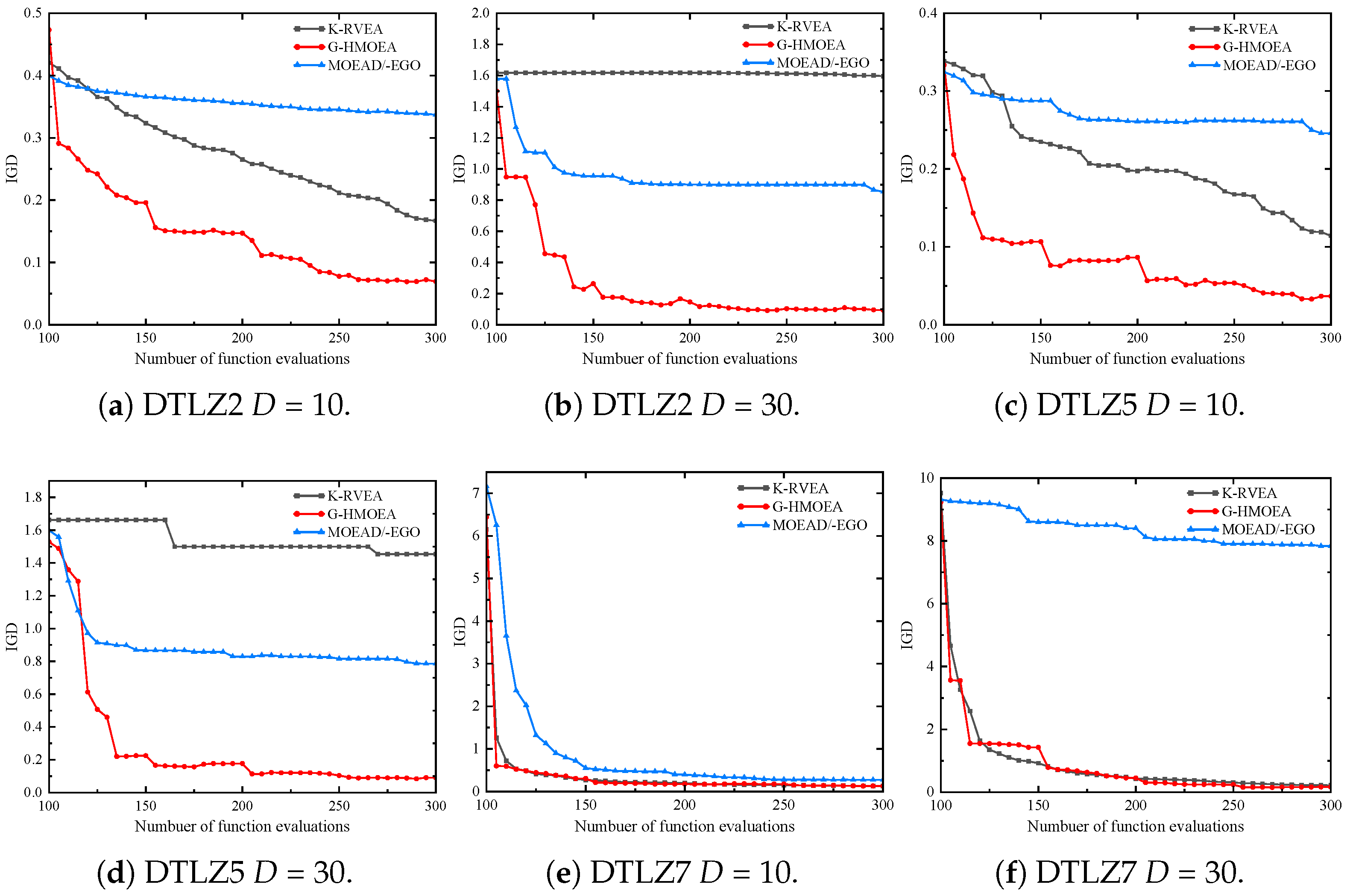
5.2. Performance Comparison between GS-MOHA and Existing SAEAs
5.2.1. Experimental Results of Algorithms in Different Dimensions
5.2.2. Efficiency Analysis of GS-MOHA
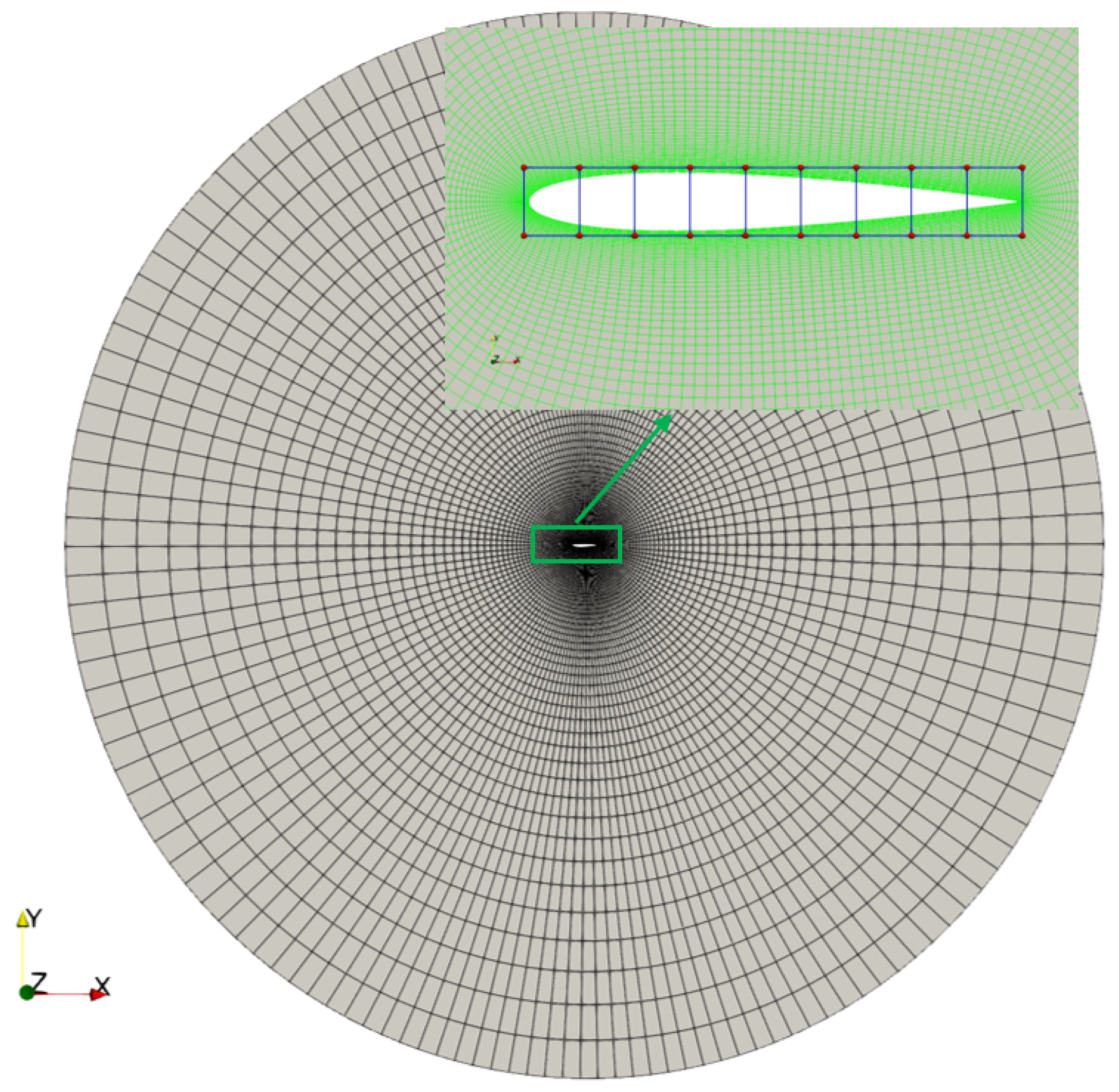
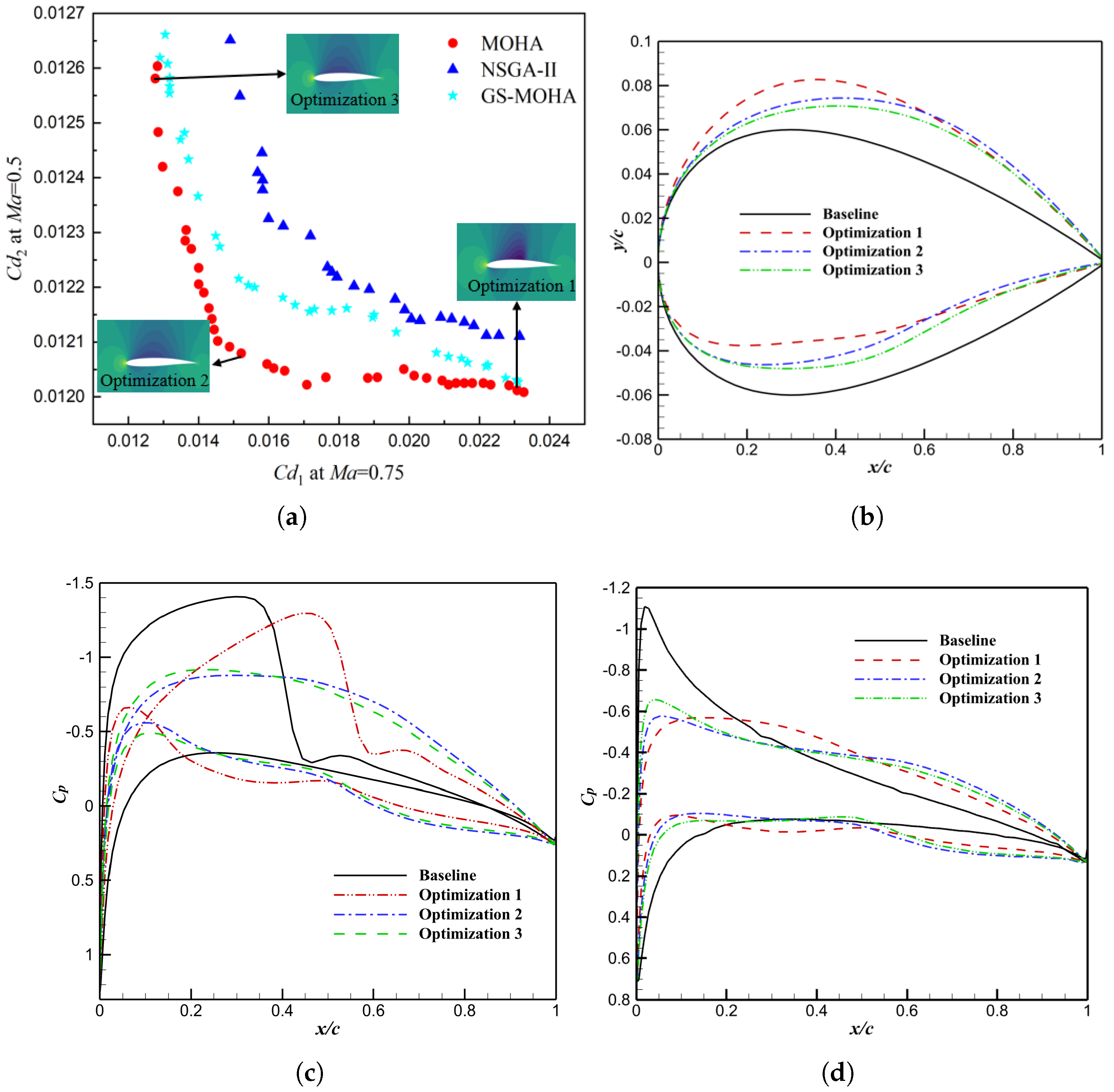
6. Multi-Objective Aerodynamic Shape Optimization of Airfoil
7. Conclusions
- (1)
- The proposed MOHA is insensitive to the dimension of MOPs. For benchmark test functions with different numbers of decision variables (30, 50) and objectives (3, 5), the convergence and diversity of MOHA are significantly better than the comparison algorithms (i.e., MOEA/D, NSGA-III, RVEA, and VaEA) and the computational efficiency is increased by about 5–10 times. Furthermore, MOHA still illustrates good stability and efficiency for large-scale MOPs with decision variables up to 1000 dimensions. This demonstrates that MOHA is an efficient optimization algorithm capable of solving large-scale MOPs.
- (2)
- GS-MOHA could solve expensive MOPs efficiently in high dimensions (). GEKPLS utilizes the PLS method to accelerate Kriging construction. The higher the dimensionality of the decision variables, the more significant the efficiency improvement of the algorithm. For the 30-dimensional DTLZ problems, the runtime of GS-MOHA is about half that of K-RVEA and one-fifth that of MOEA/D-EGO.
- (3)
- The rational use of low-cost gradient information is a very promising approach in the framework of hybrid algorithms. We can not only promote the evolution of MOEA and maintain population diversity through multi-objective gradient search but also use this low-cost gradient information to improve the accuracy of Kriging.
- (4)
- Computing gradients in local search can use the adjoint method, which does not impose an additional huge computational burden, because the cost of computing gradients using the adjoint method is roughly equivalent to that of fitness evaluation. Moreover, unlike the finite-difference approximation, the computational cost of the adjoint method is independent of the dimensionality of the decision variables. This makes it easy to apply our proposed two hybrid algorithms to the high-dimensional aerodynamic shape optimization design.
- (5)
- In this work, the optimization efficiency of MOHA and GS-MOHA was preliminarily validated on a multi-objective optimization problem of NACA0012 with 22 design variables. The results demonstrated promising engineering application potential. The proposed algorithms will be applied to the multi-objective aerodynamic optimization of complex aircraft shapes in the future.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tang, Z.; Zhang, L. A new Nash optimization method based on alternate elitist information exchange for multi-objective aerodynamic shape design. Appl. Math. Model. 2019, 68, 244–266. [Google Scholar] [CrossRef]
- Jing, S.; Zhao, Q.; Zhao, G.; Wang, Q. Multi-Objective Airfoil Optimization Under Unsteady-Freestream Dynamic Stall Conditions. J. Aircr. 2023, 60, 293–309. [Google Scholar] [CrossRef]
- Anosri, S.; Panagant, N.; Champasak, P.; Bureerat, S.; Thipyopas, C.; Kumar, S.; Pholdee, N.; Yıldız, B.S.; Yildiz, A.R. A Comparative Study of State-of-the-art Metaheuristics for Solving Many-objective Optimization Problems of Fixed Wing Unmanned Aerial Vehicle Conceptual Design. Arch. Comput. Methods Eng. 2023, 30, 3657–3671. [Google Scholar] [CrossRef]
- Yu, Y.; Lyu, Z.; Xu, Z.; Martins, J.R. On the influence of optimization algorithm and initial design on wing aerodynamic shape optimization. Aerosp. Sci. Technol. 2018, 75, 183–199. [Google Scholar] [CrossRef]
- Dai, Y.H. Convergence properties of the BFGS algoritm. Siam J. Optim. 2002, 13, 693–701. [Google Scholar] [CrossRef]
- Zhu, C.; Byrd, R.H.; Lu, P.; Nocedal, J. Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. ACM Trans. Math. Softw. (TOMS) 1997, 23, 550–560. [Google Scholar] [CrossRef]
- Yuan, G.; Hu, W. A conjugate gradient algorithm for large-scale unconstrained optimization problems and nonlinear equations. J. Inequal. Appl. 2018, 2018, 1–19. [Google Scholar] [CrossRef]
- Bomze, I.M.; Demyanov, V.F.; Fletcher, R.; Terlaky, T.; Fletcher, R. Nonlinear Optimization; Springer: Berlin, Germany, 2010. [Google Scholar]
- Jameson, A. Optimum aerodynamic design using CFD and control theory. In Proceedings of the 12th Computational Fluid Dynamics Conference, San Diego, CA, USA, 19–22 June 1995; p. 1729. [Google Scholar]
- Wang, Z.; Pei, Y.; Li, J. A Survey on Search Strategy of Evolutionary Multi-Objective Optimization Algorithms. Appl. Sci. 2023, 13, 4643. [Google Scholar] [CrossRef]
- Lyu, Z.; Martins, J.R. Aerodynamic design optimization studies of a blended-wing-body aircraft. J. Aircr. 2014, 51, 1604–1617. [Google Scholar] [CrossRef]
- Lyu, Z.; Kenway, G.K.; Martins, J.R. Aerodynamic shape optimization investigations of the common research model wing benchmark. AIAA J. 2015, 53, 968–985. [Google Scholar] [CrossRef]
- Gao, W.; Wang, Y.; Liu, L.; Huang, L. A gradient-based search method for multi-objective optimization problems. Inf. Sci. 2021, 578, 129–146. [Google Scholar] [CrossRef]
- Zhao, X.; Tang, Z.; Cao, F.; Zhu, C.; Periaux, J. An Efficient Hybrid Evolutionary Optimization Method Coupling Cultural Algorithm with Genetic Algorithms and Its Application to Aerodynamic Shape Design. Appl. Sci. 2022, 12, 3482. [Google Scholar] [CrossRef]
- Kiani, F.; Nematzadeh, S.; Anka, F.A.; Findikli, M.A. Chaotic Sand Cat Swarm Optimization. Mathematics 2023, 11, 2340. [Google Scholar] [CrossRef]
- He, C.; Zhang, Y.; Gong, D.; Ji, X. A review of surrogate-assisted evolutionary algorithms for expensive optimization problems. Expert Syst. Appl. 2023, 217, 119495. [Google Scholar] [CrossRef]
- Li, J.; Cai, J.; Qu, K. Surrogate-based aerodynamic shape optimization with the active subspace method. Struct. Multidiscip. Optim. 2019, 59, 403–419. [Google Scholar] [CrossRef]
- He, Y.; Sun, J.; Song, P.; Wang, X.; Usmani, A.S. Preference-driven Kriging-based multiobjective optimization method with a novel multipoint infill criterion and application to airfoil shape design. Aerosp. Sci. Technol. 2020, 96, 105555. [Google Scholar] [CrossRef]
- Yang, Z.; Qiu, H.; Gao, L.; Chen, L.; Liu, J. Surrogate-assisted MOEA/D for expensive constrained multi-objective optimization. Inf. Sci. 2023, 639, 119016. [Google Scholar] [CrossRef]
- Khuri, A.I.; Mukhopadhyay, S. Response surface methodology. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 128–149. [Google Scholar] [CrossRef]
- Martin, J.D.; Simpson, T.W. Use of Kriging models to approximate deterministic computer models. AIAA J. 2005, 43, 853–863. [Google Scholar] [CrossRef]
- Dongare, A.; Kharde, R.; Kachare, A.D. Introduction to artificial neural network. Int. J. Eng. Innov. Technol. (IJEIT) 2012, 2, 189–194. [Google Scholar]
- Buhmann, M.D. Radial basis functions. Acta Numer. 2000, 9, 1–38. [Google Scholar] [CrossRef]
- Zhong, L.; Liu, R.; Miao, X.; Chen, Y.; Li, S.; Ji, H. Compressor Performance Prediction Based on the Interpolation Method and Support Vector Machine. Aerospace 2023, 10, 558. [Google Scholar] [CrossRef]
- Knowles, J. ParEGO: A hybrid algorithm with on-line landscape approximation for expensive multiobjective optimization problems. IEEE Trans. Evol. Comput. 2006, 10, 50–66. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, W.; Tsang, E.; Virginas, B. Expensive multiobjective optimization by MOEA/D with Gaussian process model. IEEE Trans. Evol. Comput. 2009, 14, 456–474. [Google Scholar] [CrossRef]
- Chugh, T.; Jin, Y.; Miettinen, K.; Hakanen, J.; Sindhya, K. A surrogate-assisted reference vector guided evolutionary algorithm for computationally expensive many-objective optimization. IEEE Trans. Evol. Comput. 2016, 22, 129–142. [Google Scholar] [CrossRef]
- Cai, X.; Ruan, G.; Yuan, B.; Gao, L. Complementary surrogate-assisted differential evolution algorithm for expensive multi-objective problems under a limited computational budget. Inf. Sci. 2023, 632, 791–814. [Google Scholar] [CrossRef]
- Bouhlel, M.A.; Martins, J.R.R.A. Gradient-enhanced Kriging for high-dimensional problems. Eng. Comput. 2019, 35, 157–173. [Google Scholar] [CrossRef]
- Hong, W.J.; Yang, P.; Tang, K. Evolutionary Computation for Large-scale Multi-objective Optimization: A Decade of Progresses. Int. J. Autom. Comput. 2021, 18, 155–169. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, H.; Huang, L.; Qu, R.; Nojima, Y. A Pareto Front grid guided multi-objective evolutionary algorithm. Appl. Soft Comput. 2023, 136, 110095. [Google Scholar] [CrossRef]
- Cao, B.; Zhao, J.; Gu, Y.; Ling, Y.; Ma, X. Applying graph-based differential grouping for multiobjective large-scale optimization. Swarm Evol. Comput. 2020, 53, 100626. [Google Scholar] [CrossRef]
- Huband, S.; Hingston, P.; Barone, L.; While, L. A review of multiobjective test problems and a scalable test problem toolkit. IEEE Trans. Evol. Comput. 2006, 10, 477–506. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. The weighted sum method for multi-objective optimization: New insights. Struct. Multidiscip. Optim. 2010, 41, 853–862. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; Da Fonseca, V.G. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Zuhal, L.R.; Zakaria, K.; Palar, P.S.; Shimoyama, K.; Liem, R.P. Polynomial-chaos–Kriging with gradient information for surrogate modeling in aerodynamic design. AIAA J. 2021, 59, 2950–2967. [Google Scholar] [CrossRef]
- Han, Z.H.; Zhang, Y.; Song, C.X.; Zhang, K.S. Weighted gradient-enhanced Kriging for high-dimensional surrogate modeling and design optimization. Aiaa J. 2017, 55, 4330–4346. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, Q.; Han, Z. MOEA/D with gradient-enhanced Kriging for expensive multiobjective optimization. Nat. Comput. 2022, 22, 329–339. [Google Scholar] [CrossRef]
- Bouhlel, M.A.; Bartoli, N.; Otsmane, A.; Morlier, J. Improving Kriging surrogates of high-dimensional design models by Partial Least Squares dimension reduction. Struct. Multidiscip. Optim. 2016, 53, 935–952. [Google Scholar] [CrossRef]
- Tang, Z.; Hu, X.; Périaux, J. Multi-level Hybridized Optimization Methods Coupling Local Search Deterministic and Global Search Evolutionary Algorithms. Arch. Comput. Methods Eng. 2020, 27, 939–975. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, G.; Wang, H. NSGA-II/SDR-OLS: A Novel Large-Scale Many-Objective Optimization Method Using Opposition-Based Learning and Local Search. Mathematics 2023, 11, 1911. [Google Scholar] [CrossRef]
- Bouaziz, H.; Bardou, D.; Berghida, M.; Chouali, S.; Lemouari, A. A novel hybrid multi-objective algorithm to solve the generalized cubic cell formation problem. Comput. Oper. Res. 2023, 150, 106069. [Google Scholar] [CrossRef]
- Nayyef, H.M.; Ibrahim, A.A.; Mohd Zainuri, M.A.A.; Zulkifley, M.A.; Shareef, H. A Novel Hybrid Algorithm Based on Jellyfish Search and Particle Swarm Optimization. Mathematics 2023, 11, 3210. [Google Scholar] [CrossRef]
- Cao, B.; Zhang, W.; Wang, X.; Zhao, J.; Gu, Y.; Zhang, Y. A memetic algorithm based on two_Arch2 for multi-depot heterogeneous-vehicle capacitated arc routing problem. Swarm Evol. Comput. 2021, 63, 100864. [Google Scholar] [CrossRef]
- Deb, K.; Goel, T. A Hybrid Multi-objective Evolutionary Approach to Engineering Shape Design. In Proceedings of the Evolutionary Multi-Criterion Optimization, Zurich, Switzerland, 7–9 March 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 385–399. [Google Scholar]
- Sun, Y.; Zhang, L.; Gu, X. A hybrid co-evolutionary cultural algorithm based on particle swarm optimization for solving global optimization problems. Neurocomputing 2012, 98, 76–89. [Google Scholar] [CrossRef]
- Forrester, A.I.J.; Keane, A.J. Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Parr, J.M.; Keane, A.J.; Forrester, A.I.; Holden, C.M. Infill sampling criteria for surrogate-based optimization with constraint handling. Eng. Optim. 2012, 44, 1147–1166. [Google Scholar] [CrossRef]
- Han, Z.H. SurroOpt: A generic surrogate-based optimization code for aerodynamic and multidisciplinary design. In Proceedings of the 30th Congress of the International Council of the Aeronautical Sciences—ICAS 2016, Daejeon, Republic of Korea, 25–30 September 2016. [Google Scholar]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y.; Olhofer, M.; Sendhoff, B. A Reference Vector Guided Evolutionary Algorithm for Many-Objective Optimization. IEEE Trans. Evol. Comput. 2016, 20, 773–791. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhou, Y.; Li, M.; Chen, Z. A Vector Angle-Based Evolutionary Algorithm for Unconstrained Many-Objective Optimization. IEEE Trans. Evol. Comput. 2017, 21, 131–152. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, Y.; Cheng, R.; Jin, Y. A Decision Variable Clustering-Based Evolutionary Algorithm for Large-Scale Many-Objective Optimization. IEEE Trans. Evol. Comput. 2018, 22, 97–112. [Google Scholar] [CrossRef]
- Areias, P.; Correia, R.; Melicio, R. Airfoil Analysis and Optimization Using a Petrov–Galerkin Finite Element and Machine Learning. Aerospace 2023, 10, 638. [Google Scholar] [CrossRef]
- He, P.; Mader, C.A.; Martins, J.R.; Maki, K.J. Dafoam: An open-source adjoint framework for multidisciplinary design optimization with openfoam. AIAA J. 2020, 58, 1304–1319. [Google Scholar] [CrossRef]
- Kenway, G.; Kennedy, G.; Martins, J.R. A CAD-free approach to high-fidelity aerostructural optimization. In Proceedings of the 13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference, Ft. Worth, TX, USA, 13–15 September 2010; p. 9231. [Google Scholar]
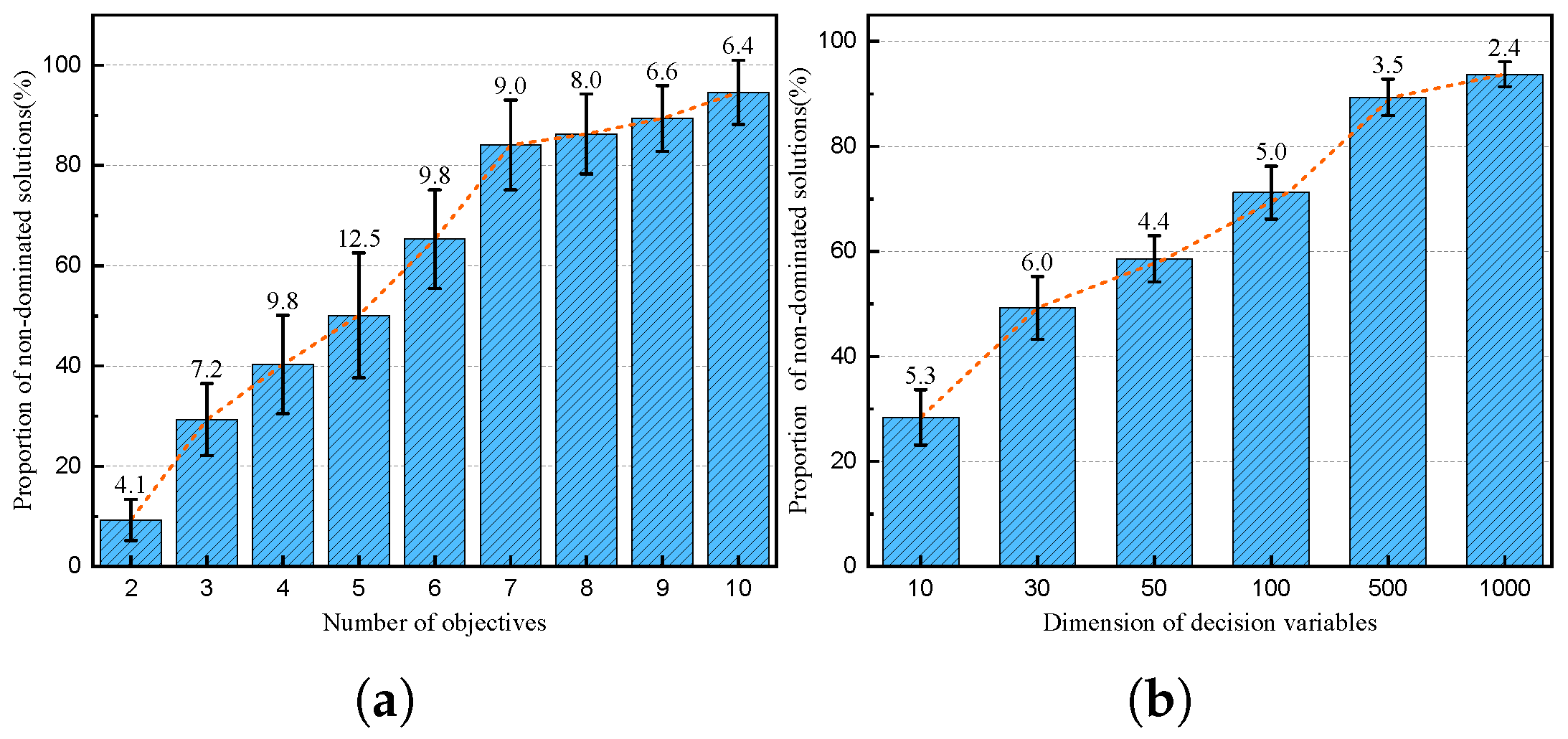


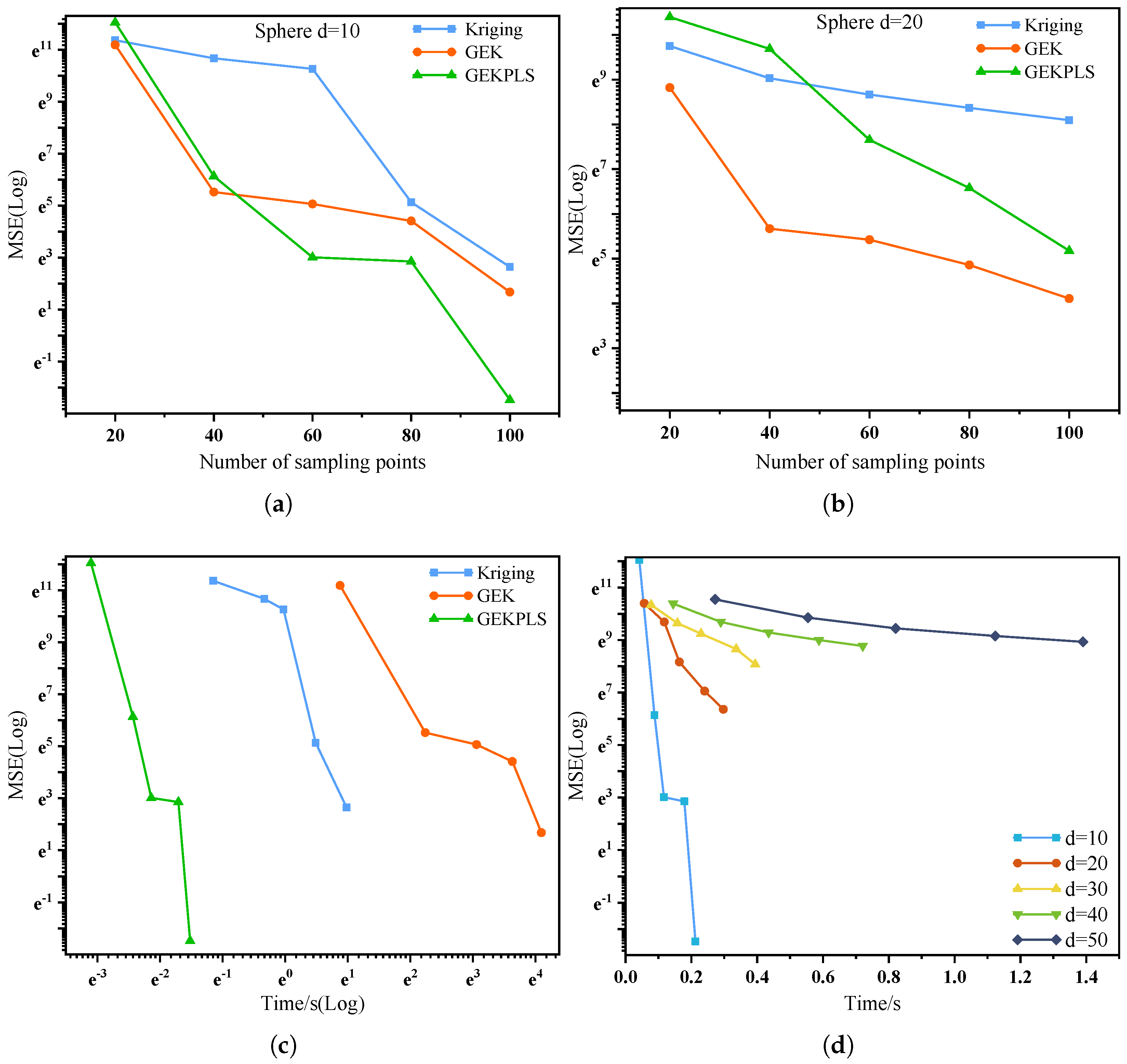
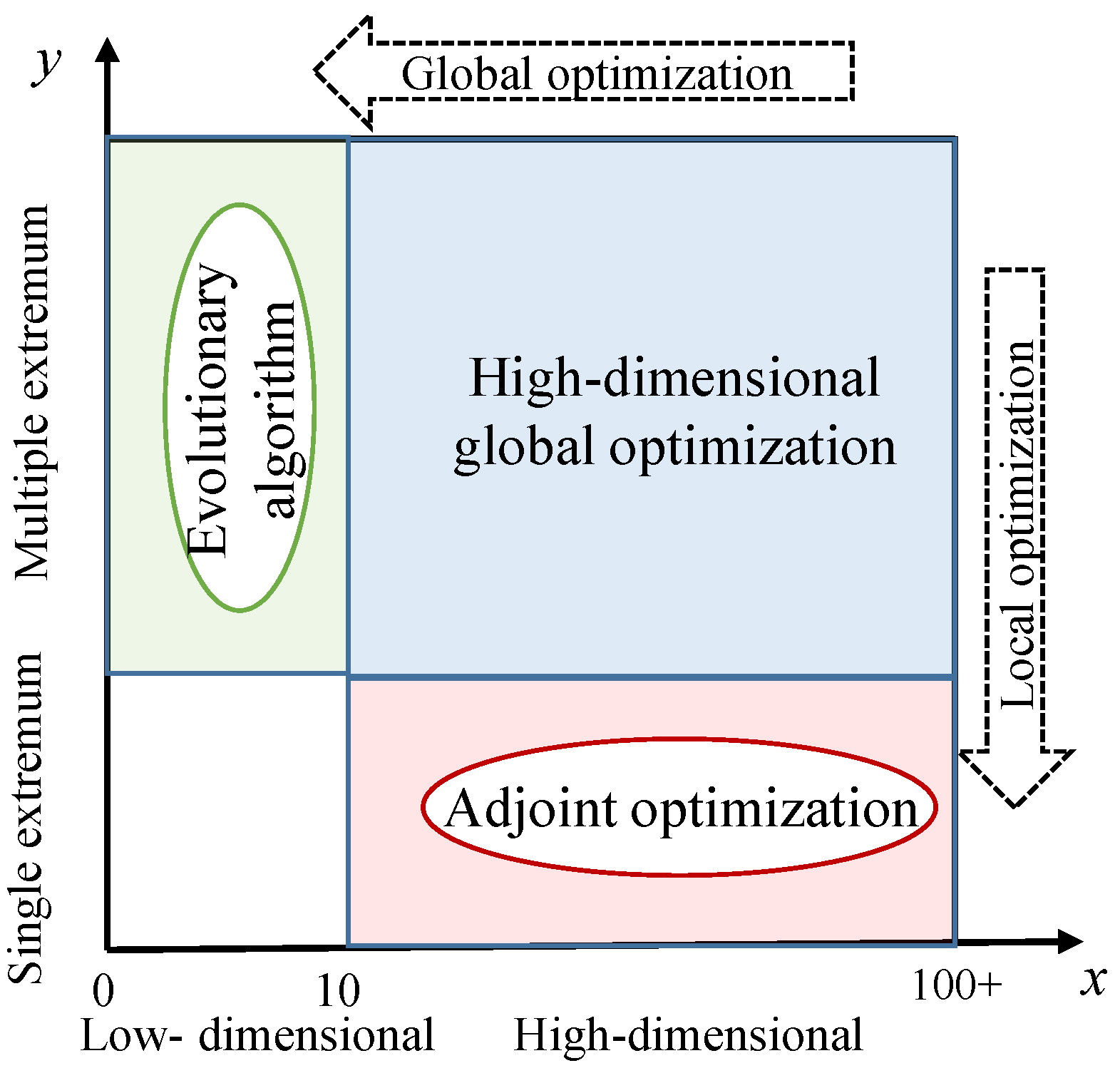
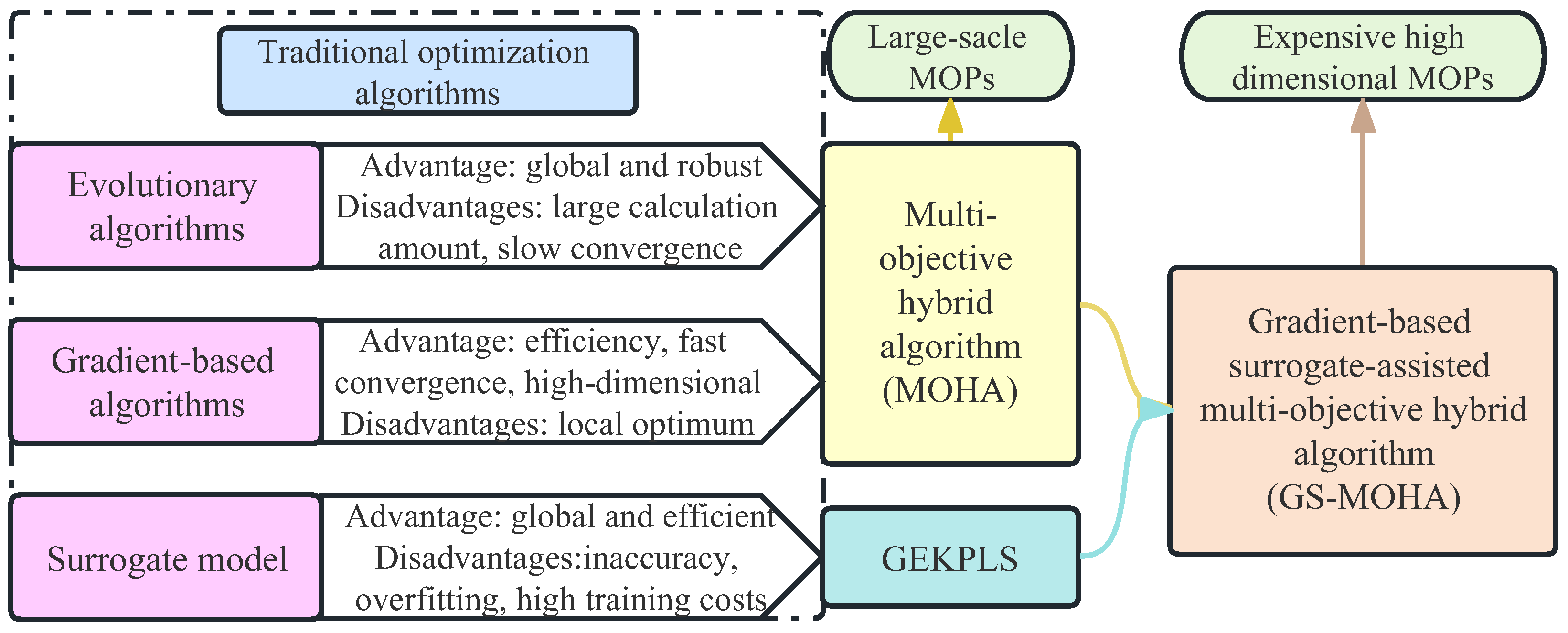


| Problems | Features |
|---|---|
| DTLZ1 | Linear, multi-modal |
| DTLZ3 | Non-convex, multi-modal |
| DTLZ2,4 | Non-convex, unimodal |
| DTLZ5,6 | Non-convex, degenerate PF |
| DTLZ7 | Mixed, disconnected, and multi-modal |
| Problem | M | D | MOEA/D | NSGA-III | RVEA | VaEA | MOHA |
|---|---|---|---|---|---|---|---|
| DTLZ1 | 3 | 30 | () − | () − | () − | () − | |
| 3 | 50 | () − | () − | () − | () − | ||
| 5 | 30 | () − | () − | () − | () − | ||
| 5 | 50 | () − | () − | () − | () − | ||
| DTLZ2 | 3 | 30 | () = | () − | () − | () − | |
| 3 | 50 | () − | () − | () − | () − | ||
| 5 | 30 | () − | () − | () − | () | ||
| 5 | 50 | () − | () − | () − | () | ||
| DTLZ3 | 3 | 30 | () − | () − | () − | () − | |
| 3 | 50 | () − | () − | () − | () − | ||
| 5 | 30 | () − | () − | () − | () − | ||
| 5 | 50 | − | − | − | − | ||
| DTLZ4 | 3 | 30 | − | − | − | ||
| 3 | 50 | − | |||||
| 5 | 30 | ||||||
| 5 | 50 | ||||||
| DTLZ5 | 3 | 30 | |||||
| 3 | 50 | ||||||
| 5 | 30 | ||||||
| 5 | 50 | ||||||
| DTLZ6 | 3 | 30 | |||||
| 3 | 50 | ||||||
| 5 | 30 | ||||||
| 5 | 50 | ||||||
| DTLZ7 | 3 | 30 | |||||
| 3 | 50 | ||||||
| 5 | 30 | ||||||
| 5 | 50 | ||||||
| +/−/= | 2/25/1 | 1/27/0 | 1/26/1 | 3/23/2 | N/A | ||
| Problem | M | D | MOEA/D | NSGA-III | RVEA | VaEA | MOHA |
|---|---|---|---|---|---|---|---|
| DTLZ1 | 3 | 30 | |||||
| 3 | 50 | ||||||
| 5 | 30 | ||||||
| 5 | 50 | ||||||
| DTLZ2 | 3 | 30 | |||||
| 3 | 50 | ||||||
| 5 | 30 | ||||||
| 5 | 50 | ||||||
| DTLZ3 | 3 | 30 | |||||
| 3 | 50 | ||||||
| 5 | 30 | ||||||
| 5 | 50 | ||||||
| DTLZ4 | 3 | 30 | |||||
| 3 | 50 | ||||||
| 5 | 30 | ||||||
| 5 | 50 | ||||||
| DTLZ5 | 3 | 30 | |||||
| 3 | 50 | ||||||
| 5 | 30 | ||||||
| 5 | 50 | ||||||
| DTLZ6 | 3 | 30 | |||||
| 3 | 50 | ||||||
| 5 | 30 | ||||||
| 5 | 50 | ||||||
| DTLZ7 | 3 | 30 | |||||
| 3 | 50 | ||||||
| 5 | 30 | ||||||
| 5 | 50 | ||||||
| +/−/= | 3/25/0 | 3/24/1 | 1/26/1 | 5/21/2 | N/A | ||
| Problem | M | D | MOHA | NSGA-III |
|---|---|---|---|---|
| DTLZ1 | 3 | 30 | 112 | >1000 |
| 3 | 50 | 130 | >1000 | |
| 5 | 30 | 165 | >1000 | |
| 5 | 50 | 188 | >1000 | |
| DTLZ2 | 3 | 30 | 35 | 116 |
| 3 | 50 | 40 | 158 | |
| 5 | 30 | 42 | 170 | |
| 5 | 50 | 48 | 293 | |
| DTLZ3 | 3 | 30 | 168 | >1000 |
| 3 | 50 | 195 | >1000 | |
| 5 | 30 | 175 | >1000 | |
| 5 | 50 | 210 | >1000 | |
| DTLZ4 | 3 | 30 | 30 | 96 |
| 3 | 50 | 35 | 184 | |
| 5 | 30 | 45 | 152 | |
| 5 | 50 | 48 | 283 | |
| DTLZ5 | 3 | 30 | 25 | 123 |
| 3 | 50 | 30 | 195 | |
| 5 | 30 | 104 | 454 | |
| 5 | 50 | 115 | 611 | |
| DTLZ6 | 3 | 30 | 36 | 248 |
| 3 | 50 | 55 | 692 | |
| 5 | 30 | 126 | 967 | |
| 5 | 50 | 144 | >1000 | |
| DTLZ7 | 3 | 30 | 33 | 150 |
| 3 | 50 | 35 | 216 | |
| 5 | 30 | 40 | 265 | |
| 5 | 50 | 48 | 352 |
| Problem | M | D | MOEA/D-EGO | K-RVEA | GS-MOHA |
|---|---|---|---|---|---|
| DTLZ1 | 3 | 10 | |||
| 3 | 20 | ||||
| 3 | 30 | ||||
| DTLZ2 | 3 | 10 | |||
| 3 | 20 | ||||
| 3 | 30 | ||||
| DTLZ3 | 3 | 10 | |||
| 3 | 20 | ||||
| 3 | 30 | ||||
| DTLZ4 | 3 | 10 | |||
| 3 | 20 | ||||
| 3 | 30 | ||||
| DTLZ5 | 3 | 10 | |||
| 3 | 20 | ||||
| 3 | 30 | ||||
| DTLZ6 | 3 | 10 | − | ||
| 3 | 20 | ||||
| 3 | 30 | ||||
| DTLZ7 | 3 | 10 | |||
| 3 | 20 | ||||
| 3 | 30 | ||||
| +/−/= | 2/18/1 | 2/17/2 | N/A | ||
| Problem | M | D | MOEA/D-EGO | KRVEA | GS-MOHA |
|---|---|---|---|---|---|
| DTLZ1 | 3 | 10 | |||
| 3 | 20 | ||||
| 3 | 30 | ||||
| DTLZ2 | 3 | 10 | |||
| 3 | 20 | ||||
| 3 | 30 | ||||
| DTLZ3 | 3 | 10 | |||
| 3 | 20 | ||||
| 3 | 30 | ||||
| DTLZ4 | 3 | 10 | |||
| 3 | 20 | ||||
| 3 | 30 | ||||
| DTLZ5 | 3 | 10 | |||
| 3 | 20 | ||||
| 3 | 30 | ||||
| DTLZ6 | 3 | 10 | |||
| 3 | 20 | ||||
| 3 | 30 | ||||
| DTLZ7 | 3 | 10 | |||
| 3 | 20 | ||||
| 3 | 30 | ||||
| +/−/= | 0/12/9 | 1/10/10 | N/A | ||
| NSGA-II | MOHA | GS-MOHA | |
|---|---|---|---|
| Population size | 50 | 50 | 50 |
| Number of design variables | 22 | 22 | 22 |
| Number of CFD evaluations | 4000 | 2000 | 1000 |
| Number of gradient evaluations | - | 115 | 1000 |
| Number of CPU | 16 | 16 | 16 |
| Number of non-dominated solutions | 25 | 37 | 33 |
| CPU cost (h) | ≈133 | ≈71 | ≈26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, F.; Tang, Z.; Zhu, C.; Zhao, X. An Efficient Hybrid Multi-Objective Optimization Method Coupling Global Evolutionary and Local Gradient Searches for Solving Aerodynamic Optimization Problems. Mathematics 2023, 11, 3844. https://doi.org/10.3390/math11183844
Cao F, Tang Z, Zhu C, Zhao X. An Efficient Hybrid Multi-Objective Optimization Method Coupling Global Evolutionary and Local Gradient Searches for Solving Aerodynamic Optimization Problems. Mathematics. 2023; 11(18):3844. https://doi.org/10.3390/math11183844
Chicago/Turabian StyleCao, Fan, Zhili Tang, Caicheng Zhu, and Xin Zhao. 2023. "An Efficient Hybrid Multi-Objective Optimization Method Coupling Global Evolutionary and Local Gradient Searches for Solving Aerodynamic Optimization Problems" Mathematics 11, no. 18: 3844. https://doi.org/10.3390/math11183844
APA StyleCao, F., Tang, Z., Zhu, C., & Zhao, X. (2023). An Efficient Hybrid Multi-Objective Optimization Method Coupling Global Evolutionary and Local Gradient Searches for Solving Aerodynamic Optimization Problems. Mathematics, 11(18), 3844. https://doi.org/10.3390/math11183844






