Abstract
We consider an unstructured neuron network model composed of excitatory and inhibitory neurons. The synaptic connections are supplied with spike timing-dependent plasticity (STDP). We take the STDP model implemented using a memristor. In normal conditions, the network forms so-called bursting discharges typical of unstructured living networks in dissociated neuronal cultures. Incorporating a biologically inspired model, we demonstrate how memristive plasticity emulates spike timing-dependent plasticity, which is crucial for regulating synchronous brain activity. We have found that, when the memristor-based STDP for inhibitory connections is activated, the bursting dynamics are suppressed and the network turns to a random spiking mode. The dependence of bursting properties on the degree of the memristor-based STDP plasticity is analyzed. These findings hold implications for advancing invasive neurointerfaces and for the identification and management of epileptiform activity.
MSC:
92C05; 92B20; 3A30
1. Introduction
Network bursting is a phenomenon observed in various neural systems, where groups of neurons exhibit synchronized spiking activity, leading to bursts of spikes [1]. Bursting activity is commonly seen in neural circuits, aiding neuron communication [2,3]. Unlike single spike firing, burst firing involves multiple spikes followed by quiet periods [4]. Bursts enhance synaptic transmission reliability, also enabling selective neuron communication [5]. Bursting neurons synchronize more easily, which is vital for information transfer [6]. This behavior holds significant implications within the context of spiking neuron networks (SNNs), impacting network dynamics and computational efficiency. Spiking neuron networks use spike timing for computation, capturing biological dynamics [7]. The spiking neuron model mimics real neurons’ firing patterns. Effectively controlling network bursting is pivotal for ensuring precise information processing and maintaining the stability of SNNs.
Bursting dynamics play a pivotal role in information encoding and processing. The precise timing and sequence of spikes within bursts can carry specific information, enabling neurons to encode complex patterns and temporal relationships [8]. Bursting neurons can also enhance the reliability of information transmission by exploiting the multiplexing of information within bursts [9].
Exploring the mechanisms that give rise to bursting behavior provides insights into the intrinsic properties of neurons and their interactions within networks. Bursting can emerge due to a variety of factors, including the interplay between excitatory and inhibitory synaptic connections, network topology, and individual neuron properties [10]. Research into the mechanisms driving network bursting has revealed the interplay of excitatory and inhibitory connections within neuron networks. In particular, the balance between excitatory and inhibitory influences is crucial for the generation and termination of bursts. Investigations by van Vreeswijk and Sompolinsky [11] highlight the role of inhibitory interneurons in modulating network excitability and preventing runaway synchronization.
The temporal dynamics of network bursting have implications for learning and plasticity. The precise timing of spikes within bursts can carry specific information, enabling neurons to communicate and learn in a highly time-sensitive manner. Studies by Buzsáki [12] and Abeles [13] emphasize how burst synchronization can facilitate Hebbian learning mechanisms, enabling neurons to wire together based on their temporal firing patterns.
Studies have shown that burst-based patterns can facilitate learning and plasticity processes within neuron networks. Burst timing-dependent plasticity (BTDP) mechanisms, akin to spike timing-dependent plasticity (STDP), emphasize the significance of spike sequences during bursts for synaptic weight modifications [14,15]. This underscores the relevance of bursting in shaping network connectivity.
The regulation of network bursting often revolves around the manipulation of synaptic plasticity, the ability of synapses to adjust their strengths based on the spiking activities of connected neurons. Researchers have explored various plasticity mechanisms to control network bursting. One prominent example is spike timing-dependent plasticity (STDP), a rule where the timing of pre-synaptic and post-synaptic spikes determines the synaptic weight change. STDP has been demonstrated to influence network bursting tendencies [16,17,18].
An emerging avenue for controlling bursting involves the use of memristor-based plasticity. Memristors, nanoscale devices with tunable resistance, offer the potential to emulate synaptic plasticity in hardware. These devices, with their ability to mimic certain aspects of biological synaptic plasticity, can be harnessed to regulate network dynamics, including bursting behavior [19,20].
Memristive plasticity, as explored in studies [21,22], represents a promising avenue in the field of information processing and computational systems. The memristor, a fundamental element of memristive systems, exhibits unique electrical behavior, allowing it to modify its resistance in response to applied electrical signals. This characteristic endows memristors with the ability to store and process information, akin to synaptic plasticity observed in biological systems [23].
The utilization of memristive devices in computing architectures has garnered significant attention in recent years [21]. By leveraging the memristor’s ability to modulate its resistance, these devices can be employed as memory elements, logic gates, and even synapse-like components in neuromorphic systems [24]. This memristor-based approach holds promise for achieving efficient and scalable computing platforms that mimic the functionalities of biological neuron networks [25].
The foundation of memristive plasticity lies in the ability of memristors to modify their conductance in response to electrical stimuli [21]. This alteration in conductance can occur through various mechanisms, such as the migration of charged defects or the restructuring of the memristive material. These changes in conductance enable the adaptive adjustment of synaptic weights and the establishment of long-term potentiation (LTP) and long-term depression (LTD)-like processes, crucial for learning and memory functions in biological neuron networks [23].
The potential of memristive plasticity in computational systems is vast. These devices offer the opportunity to develop novel computing architectures that exploit their parallelism, non-volatility, and low energy consumption [21]. By integrating memristors into neuron network models, researchers aim to replicate key characteristics of synaptic plasticity and explore the potential of hardware implementations for neuromorphic computing [25].
The phenomenon of bursts is widely studied across various fields, including neuroscience [26], chemical systems [27], and fluid mechanics [28]. Currently, active research focuses on controlling dynamic modes in various systems, including those utilizing memristive devices. Thermoacoustic research reveals that burst behavior primarily results from the interaction of slow and fast oscillations in laminar and low-turbulence systems, while turbulence plays a predominant role in high-turbulence systems [29]. A model of an unstructured neural network, based on the Hindmarsh–Rose neuron and memristive connections, demonstrates synchronization among neurons with different connection types [30]. The formation of mixed-mode oscillations (MMOs) is observed in a system of three coupled non-autonomous LCR oscillators with shared nonlinearity, achieved using memristive devices [31]. Additionally, a memristor-based Shimizu–Morioka system model, illustrating burst dynamics, is proposed and studied [32]. In our work, we focus on burst dynamics, a well-established concept in neuroscience, as defined in the works of Izhikevich [1,5,26]. Using a biologically functional model of cortical circuitry, we demonstrate that memristive plasticity, mimicking spike timing-dependent plasticity, can replicate the homeostatic regulation of synchronous brain activity observed in real brain structures [18]. These findings hold potential significance for the development of invasive neurointerfaces [33].
In this paper, we propose a new model for balancing the processes of excitation and inhibition in a spiking neuron network using memristive plasticity. The memristive plasticity plays the role of inhibitory spike timing-dependent plasticity (iSTDP) [18,34]. In the model, memristive plasticity is introduced into inhibitory synapses to regulate the impact of inhibitory neurons on network activity. Such regulation demonstrates the possibility of switching the dynamics of a spiking neuron network from bursting to asynchronous.
This work is organized as follows. Section 1, Introduction, provides a brief description of the relevance of the research and the current state of the research. Section 2, The Model, discusses the neuron model, memristive plasticity, and the structure of the neuron network, as well as the methods and libraries used to obtain the results. In Section 3, Results, the main results of the study are presented, demonstrating the observed effect. In Section 4 and Section 5, possible directions of research are presented, as well as brief results of the research.
2. The Model
2.1. Neuron Model
Neuron dynamics were defined by a simple leaky integrate-and-fire (LIF) neuron model with excitatory and inhibitory conduction-based synapses, and a constant input current [18,35,36], as follows:
where is the membrane potential, is the leakage potential, is the leaky conductance, —excitatory and inhibitory, respectively, is the reverse potential for excitatory and inhibitory conduction, is the direct input current, is the membrane capacity, is the time constants of excitatory and inhibitory synaptic inputs, is the weight of the synapse from neuron i, is the time of spike occurrence in neuron i, and the summation term on the right accounts for synaptic activations due to presynaptic spikes. The weight, , can vary as either plastic or fixed, determined by the synapse’s identity.
The leaky integrate-and-fire (LIF) neuron model is a widely used mathematical model in computational neuroscience that simplifies the behavior of individual neurons. This model describes the dynamics of a neuron’s membrane potential as it receives synaptic inputs and generates action potentials, or spikes. The model is defined by a differential equation, Equation (1), that governs the membrane potential’s evolution in response to synaptic currents. When the membrane potential, , crosses the threshold voltage,, the neuron generates a spike and resets its membrane potential to the value .
The computational efficiency of the leaky integrate-and-fire (LIF) neuron model is one of its key advantages, making it a popular choice in computational neuroscience and neural network simulations. The efficiency of the LIF model arises from its simplicity and low computational cost, which allow for the simulation of large networks of neurons in real-time or near-real-time. Here are some reasons why the LIF neuron model is computationally efficient:
- Low Computational Complexity: The LIF model employs a straightforward differential equation, minimizing computational complexity [7].
- Deterministic Spike Timing: Spike generation in the LIF model is deterministic, eliminating the need for complex stochastic processes [10].
- Event-Driven Simulation: Simulations can be event-driven, conserving computational resources by updating neurons only when spikes occur [10].
- Parallelization: Its simplicity allows for efficient parallel computing, speeding up simulations [7].
- Spike Timing Approximations: For instance, the exponential decay of the membrane potential can be approximated as a linear decay over small time intervals, simplifying the numerical integration process [7].
2.2. Memristive Plasticity
Plasticity model for nanocomposite memristors [37] was used to describe the plasticity in synapses between inhibitory and excitatory neurons, as follows:
The constants remain unchanged, consistent with the original study [37]: , , .
Hence, a modification in the synaptic weight of an inhibitory synapse connecting inhibitory and excitatory neurons can be described as follows:
The spike timing dependence curves, illustrating various conductance values, are presented in Figure 1.
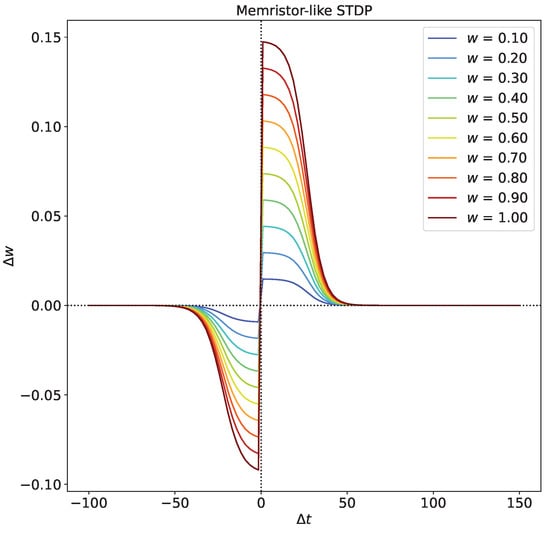
Figure 1.
Spike timing dependence curves: the dependence of the change in synaptic conductance on the interval between a presynaptic spike and a postsynaptic spike for different current synaptic conductance values w.
2.3. Neuron Network
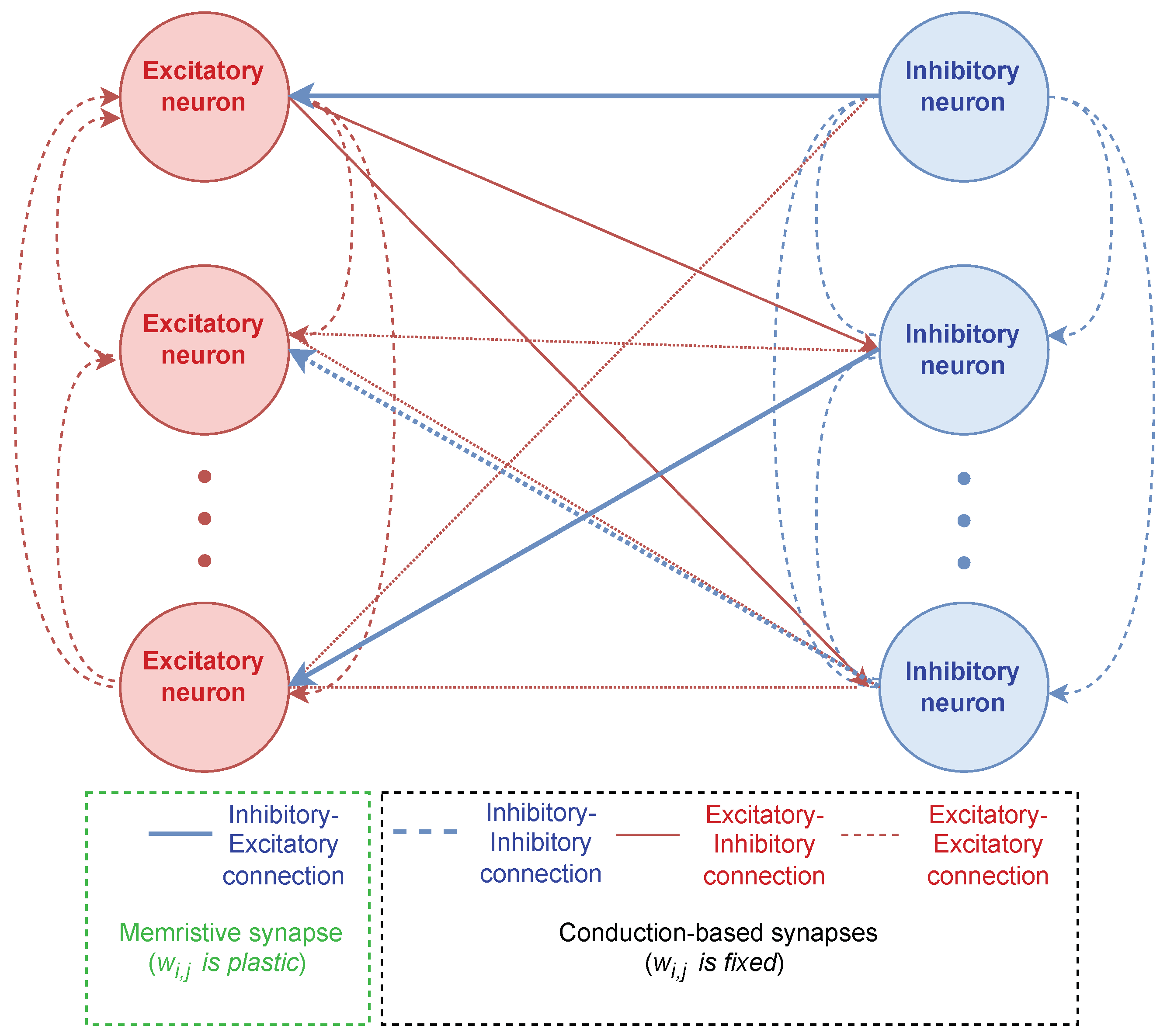
The spiking neuron network’s schematic is presented in Figure 2. The neuron network consists of 8000 excitatory neurons (depicted in red) and 2000 inhibitory neurons (depicted in blue). Neurons are interconnected in an “all-to-all” manner, with a connection probability of 2 percent. In the neuron network, inhibitory–excitatory connections (represented by bold blue arrows) are established using synapses with memristive plasticity, Equations (2) and (3). The remaining connections, namely excitatory–excitatory, excitatory–inhibitory, and inhibitory–inhibitory, are formed using simple conduction-based synapses [36] whose dynamics are determined by Equation (1).
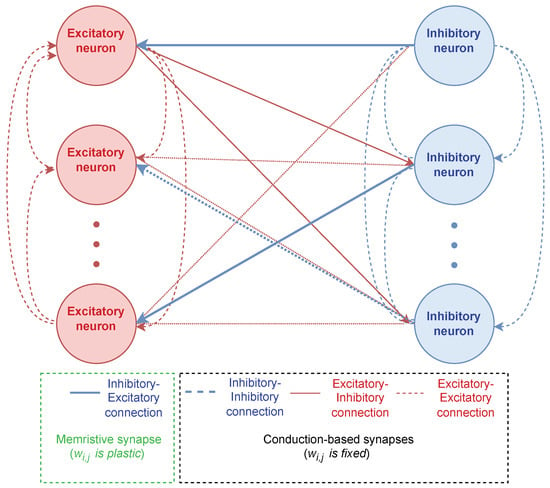
Figure 2.
Diagram of a spiking neuron network with memristive plasticity. All synapses in the neuron network are depicted as conduction-based synapses with varying synaptic weights, , which can be adaptable for memristive synapses (inhibitory–excitatory connection in the green block) and fixed for others (black block).
It should be noted that the bursting activity of the neuron network is formed as a result of the collective synchronization mechanism, which involves both excitatory and inhibitory neurons [7], rather than the dynamics of an individual neuron as observed in the Izhikevich neuron model [10] or the Hindmarsh–Rose model [38]. Excitatory neurons drive the network toward increased activity, while inhibitory neurons provide feedback inhibition, preventing overexcitation. The interplay between excitation and inhibition can lead to synchronized bursts of activity. Such dynamics are particularly observed in many experimental studies using dissociated cultures of brain neurons [39,40] and theoretical studies [5,7,41,42,43].
2.4. Numerical Simulation and Data Analysis Methods
Numerical calculations were performed using the Euler method with an integration step of 0.01. The model’s numerical computation program was implemented in Python [44], utilizing the Pandas library [45] for data processing and analysis. Model simulation was carried out with Brian2 [46], while data visualization and analysis employed the Matplotlib, Seaborn [47], and Scipy [48] libraries. All calculations were conducted on a personal computer with an Intel i7 processor.
The population activity rate was computed by summing the number of neuron spikes per second, with averaging performed using a sliding Gaussian window over time. The width parameter of the Gaussian window determines the standard deviation, which in our case is set to 0.5 ms.
3. Results
To demonstrate the impact of memristive plasticity regulation on excitation and inhibition processes in a spiking neuron network, the following sequence of model simulations was employed:
- During the first second, the spiking neuron network model was computed without memristive plasticity.
- After the initial second, memristive plasticity was enabled in the synapses connecting inhibitory and excitatory neurons.
The total simulation duration of the model was 10 s.
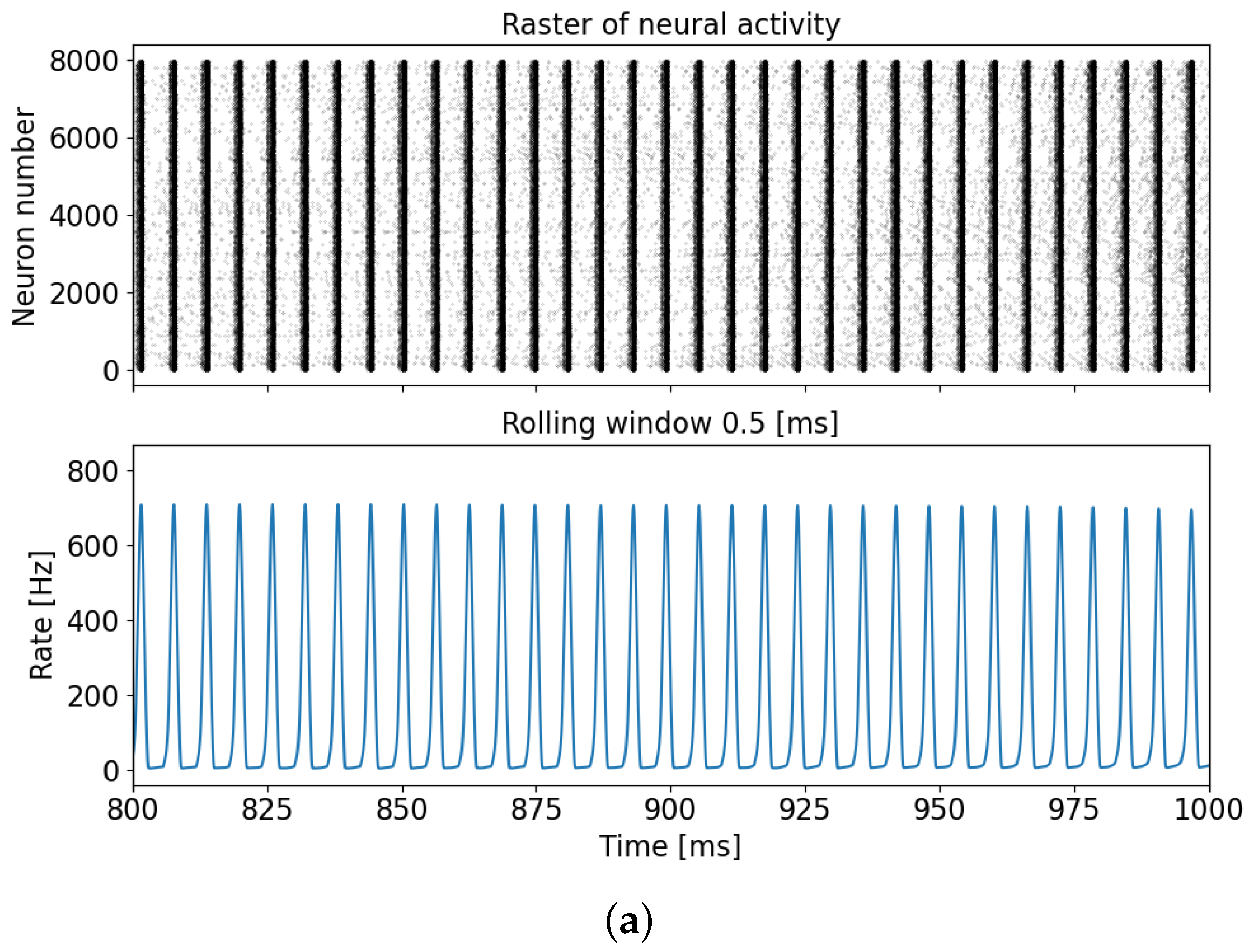
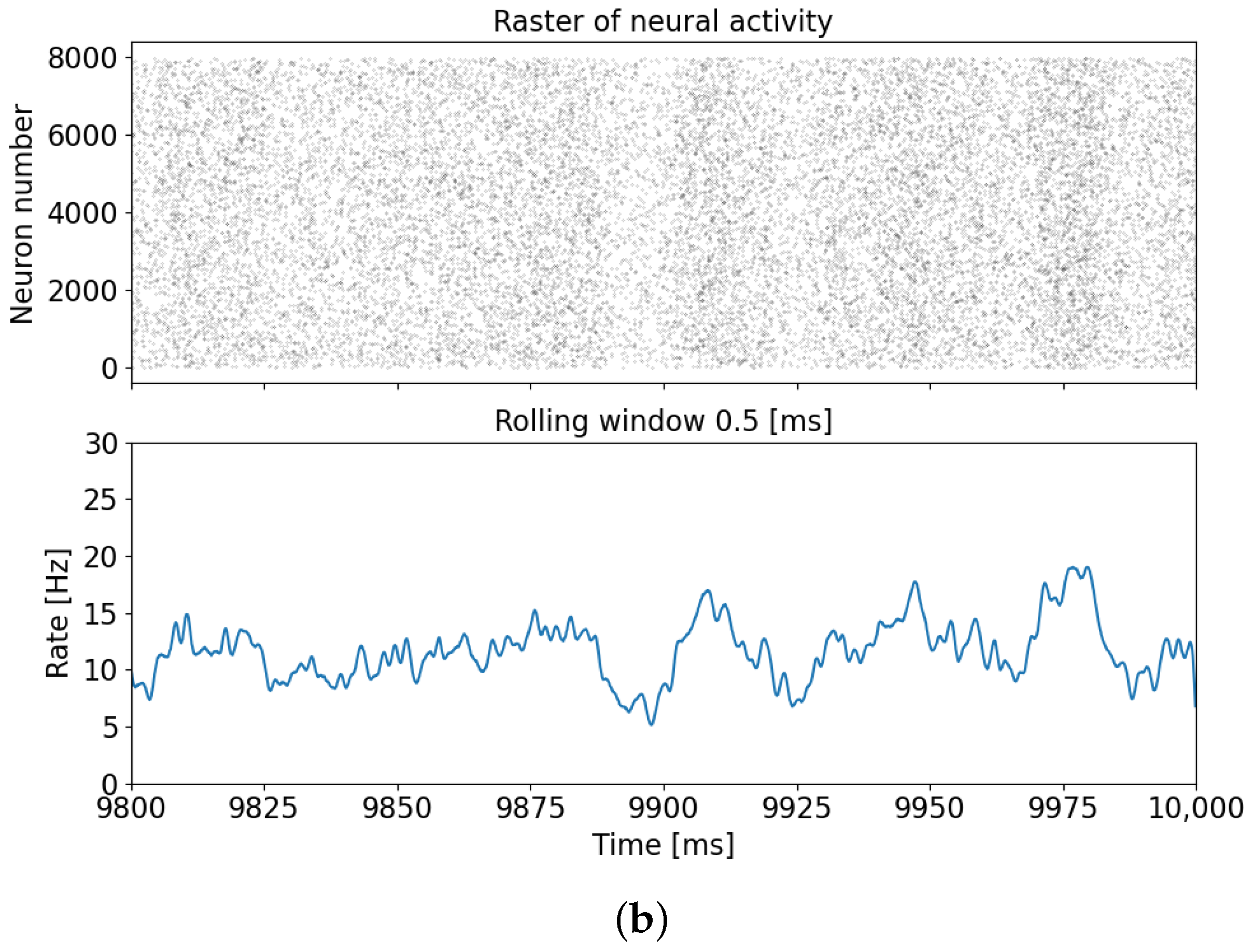
In the absence of memristive plasticity, during the simulation period of up to 1 s, the neuron network exhibits neuron synchronization and the emergence of a burst mode, as depicted in Figure 3a. Conversely, when memristive plasticity is present, the bursting dynamics of the neuron network vanishes, as illustrated in Figure 3b.
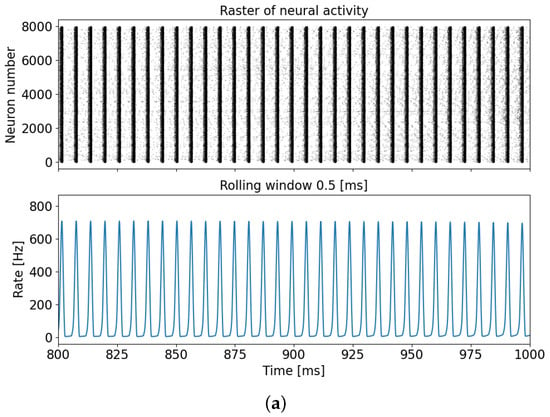
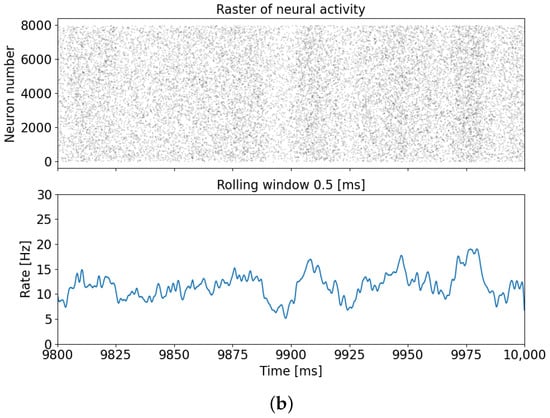
Figure 3.
Raster diagram of neuronal activity and the population activity rate for cases without memristive plasticity (a) and with memristive plasticity (b).
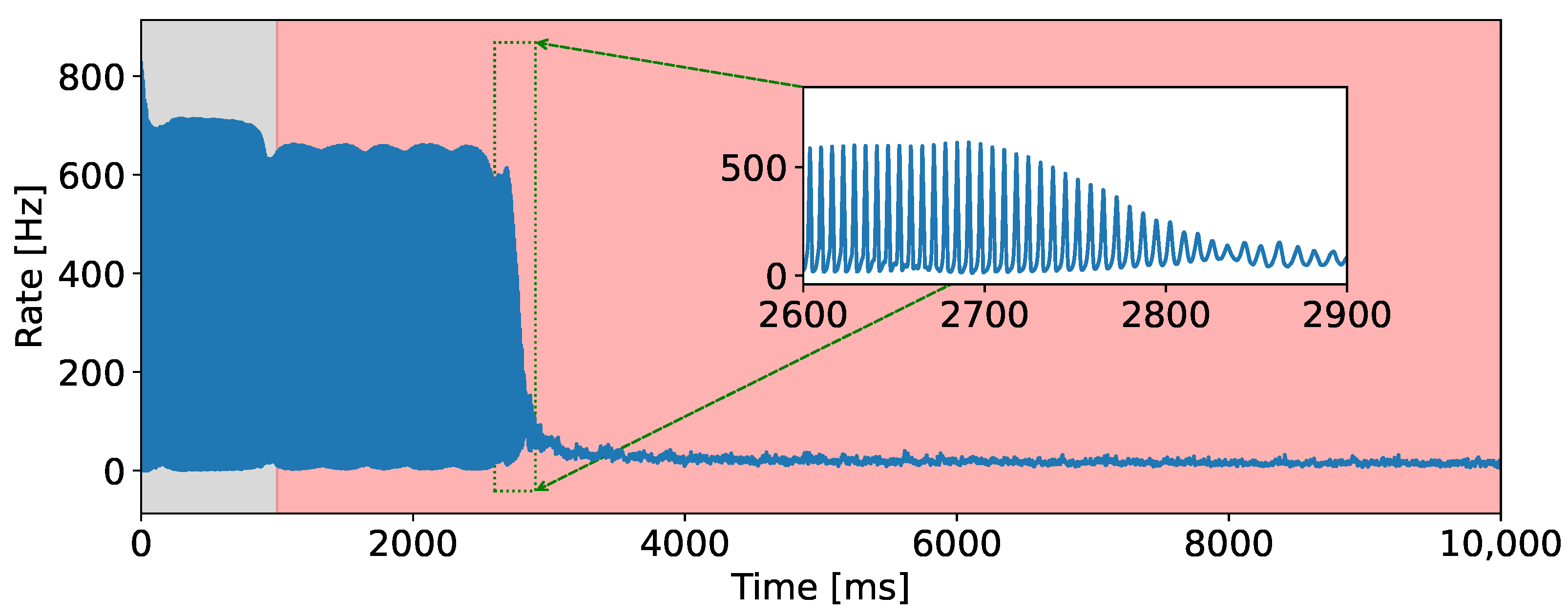
Throughout the complete simulation of the model (approximately 10 s), comprising both periods without memristive plasticity (gray area in Figure 4) and periods with memristive plasticity (red area in Figure 4), there is a gradual shift in the dynamics of the neuron network. Within the red region, one can observe both heterogeneous dynamics and a lack of neuronal synchronization. Moreover, the amplitude of bursts will progressively diminish and alter over time (Figure 4). The decrease in burst amplitude to complete disappearance is depicted in Figure 4 by the blue region, representing the rate of population activity for 10 s. Furthermore, the area highlighted with green dots has been magnified in the figure, illustrating the decline in burst amplitude over a 300 ms duration.
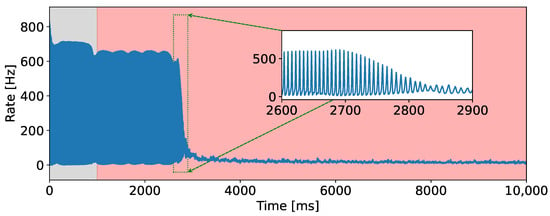
Figure 4.
Rate of population activity for 10 s. The gray area corresponds to the absence of memristive plasticity, while the red area corresponds to its presence.
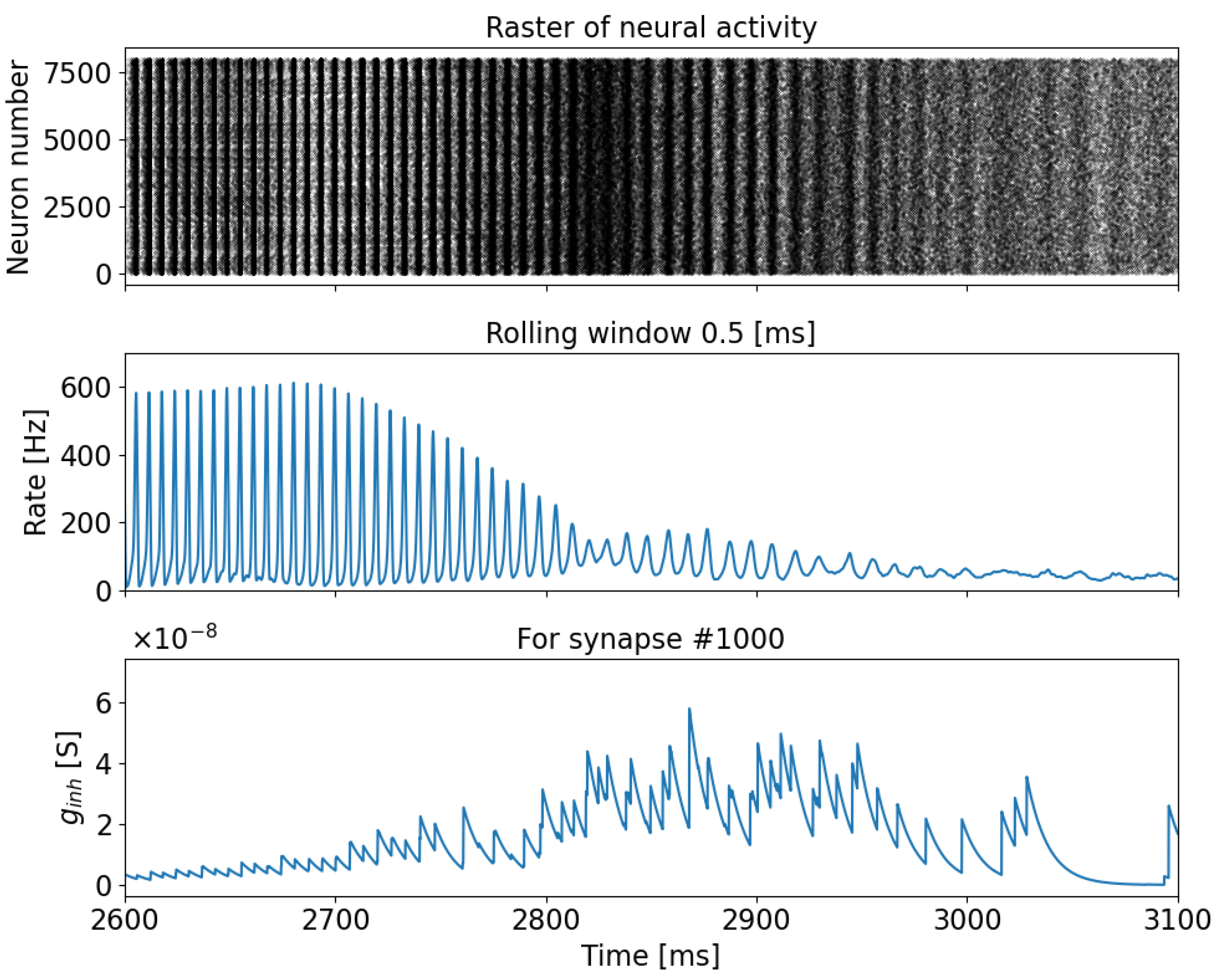
If we carefully examine the simulation period of the model with memristive plasticity from 2.6 s to 3.1 s (Figure 5), we can observe a gradual transition from burst dynamics to asynchronous neuronal dynamics as the synaptic conduction between inhibitory and excitatory neurons () with memristive plasticity evolves. During this transition, both the amplitude of the bursts and the period of their repetition undergo changes, which are evident in the time interval from 2.8 s to 2.9 s (Figure 5).
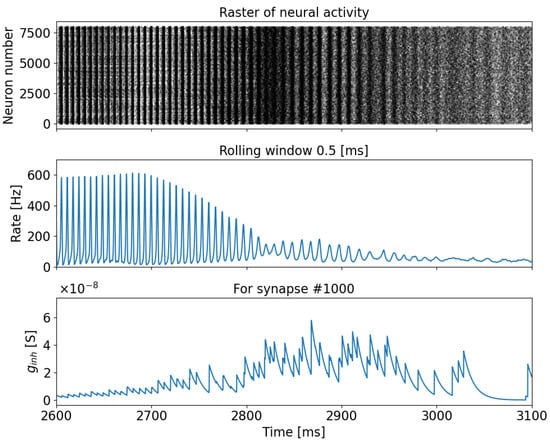
Figure 5.
Raster diagram of neuronal activity (upper panel), the population activity rate (middle panel), and the change in synapse conductance, , between inhibitory and excitatory neurons for a single synapse (bottom panel).
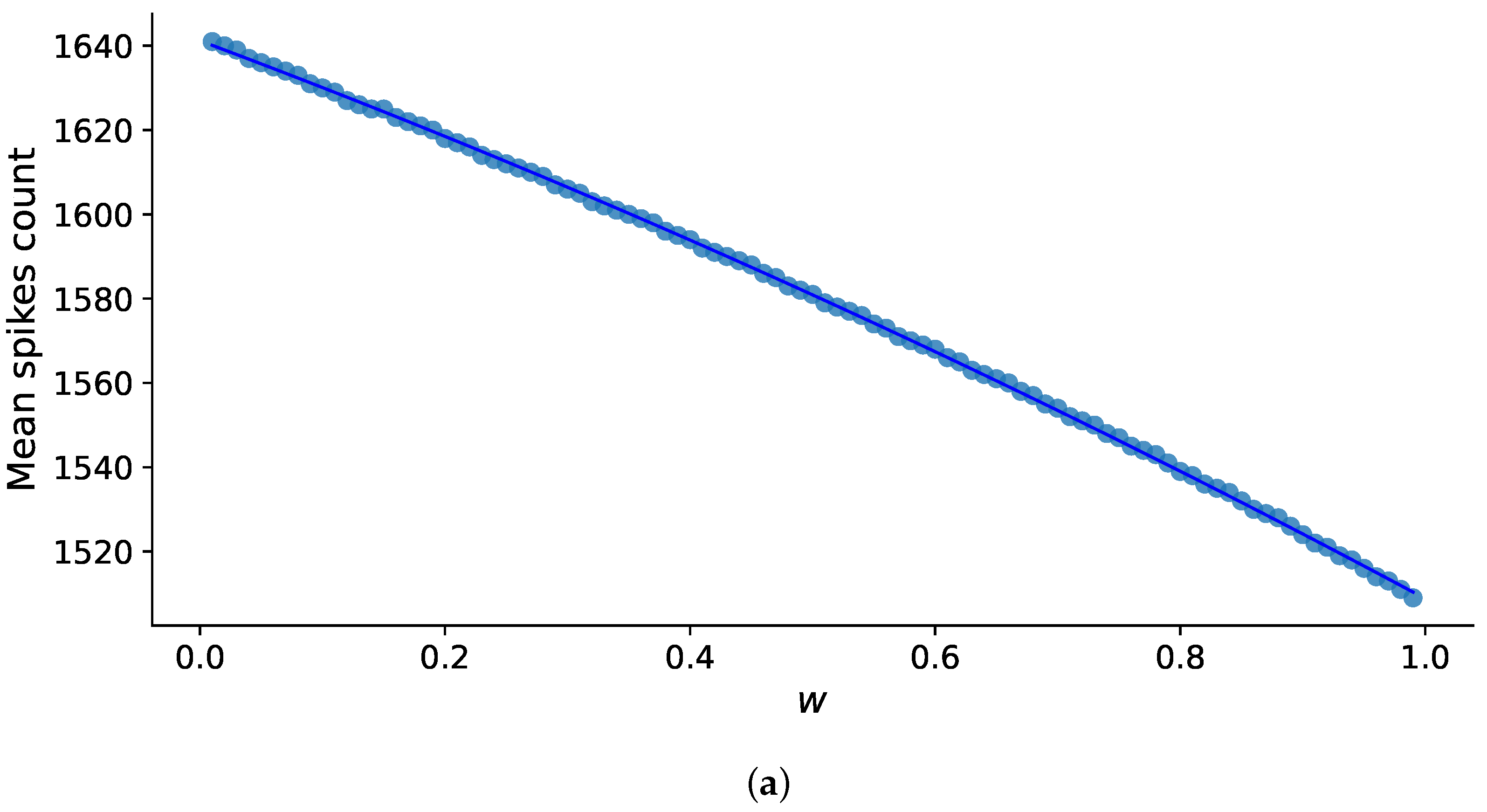
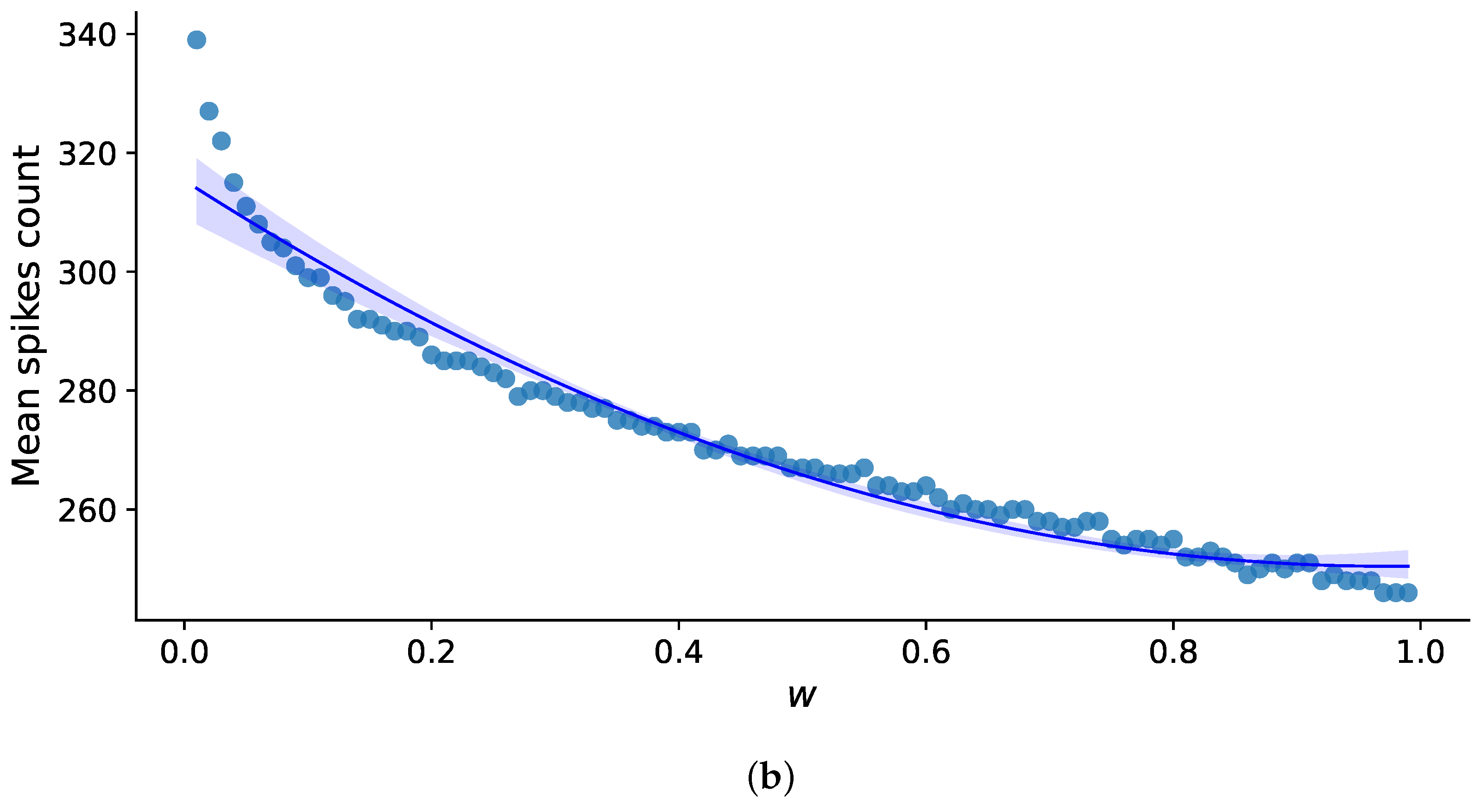
Next, we investigated the impact of memristive plasticity on the average number of spikes (Figure 6) per instance and the average frequency of burst generation (Figure 7) per instance, considering the synaptic weight values of the corresponding synapses, . Each point’s values were derived by averaging across five instances, each lasting 10 s, for both the mean number of spikes in the instance and the mean frequency of burst generation per instance.
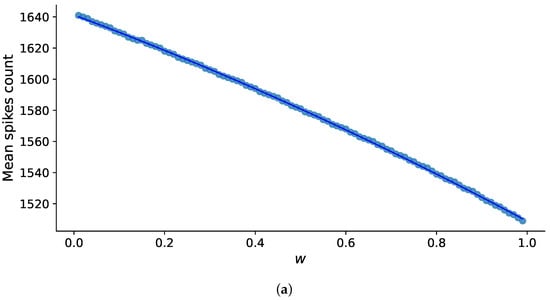
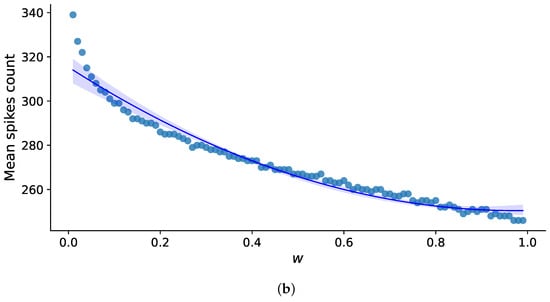
Figure 6.
The relationship between the mean number of spikes per 10-s realization and the value of synaptic weight, w, in the absence of memristive plasticity (a) and the presence of memristive plasticity (b).
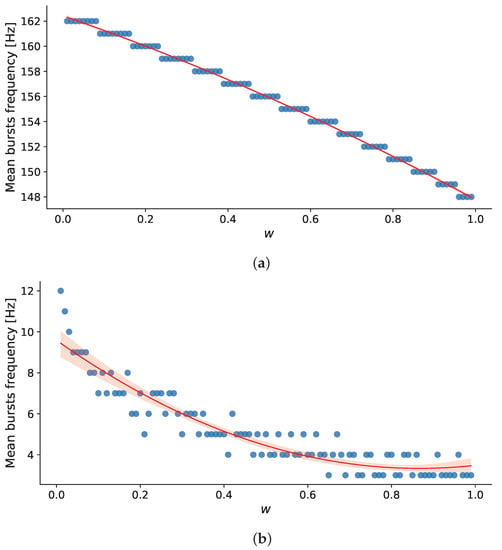
Figure 7.
The relationship between the mean burst frequency per 10-s realization and the value of synaptic weight, w, in the absence of memristive plasticity (a) and the presence of memristive plasticity (b).
4. Discussion
Network bursting phenomena have implications beyond fundamental neuroscience. They play a role in various neurological disorders and are often associated with abnormal synchronization patterns observed in conditions such as epilepsy [49]. Additionally, bursting dynamics are relevant to the field of artificial neural networks, where mimicking burst patterns could enhance information processing in neuromorphic computing systems.
Burst phenomena are extensively studied in neuroscience, chemical systems, and fluid mechanics [26,27,28]. Current research focuses on controlling dynamic modes, including the use of memristive devices. In thermoacoustics, bursts result from slow–fast oscillations in calm systems and turbulence in turbulent ones [29]. Models utilizing Hindmarsh–Rose neurons and memristive connections demonstrate neuron synchronization [30]. Memristive devices induce mixed-mode oscillations in coupled LCR oscillators [31] and a memristor-based Shimizu–Morioka system illustrates burst dynamics [32]. We compared our model with existing analogs (see Table A1).
Using a biologically inspired model, we demonstrate how memristive plasticity emulates spike timing-dependent plasticity, which is crucial for regulating synchronous brain activity [18]. These findings carry implications for the development of invasive neurointerfaces [33]. Another actively developing application of memristive devices is in the identification and control of epileptiform activity [50,51,52].
The insights gained from studying bursting dynamics in SNNs hold implications beyond neuroscience. Bursting-inspired computational models have been proposed for neuromorphic computing applications [20]. Harnessing the computational power of bursting can lead to energy-efficient and biologically plausible computing paradigms.
In a recent study, detailed comparisons between spiking and bursting dynamics in the context of liquid computing have been investigated [53]. The findings revealed that neuron networks characterized by bursting activity exhibited significantly superior computational performance compared to those reliant on spike firings. Bursting, with its higher probability and larger size, effectively expanded the liquid’s information capacity. Further analysis unveiled that the rapid firing pattern inherent in bursting dynamics markedly improved the efficiency of synaptic integration from pre-neurons, both temporally and spatially. Additionally, bursting dynamics heightened activity complexity and stochastic resonance, reflecting their proficiency in information processing. As such, bursting activity emerged as an efficient mechanism for signal processing and computations.
The intricate interplay between synaptic plasticity mechanisms, inhibitory circuits, and memristor-based plasticity presents a multidimensional approach to controlling network bursting in spiking neuron networks. By leveraging these mechanisms, researchers aim to unlock the full potential of SNNs for efficient information processing and cognitive applications.
Memristive devices show promise in achieving efficient and scalable computing systems that mimic neuron network functionalities [21]. Their ability to modify conductance enables adaptive synaptic weight adjustments [23], making them valuable for neuromorphic computing [25] and neuromorphic applications [54,55,56,57].
There is existing work on the implementation of LIF neurons, Equation (1), and networks of them in hardware using CMOS technology [58], as well as a memristive-like STDP model, Equation (2), in the form of a nanocomposite memristor [37]. This suggests the potential to realize the proposed model in hardware in the near future.
Further advancement of the model can be linked to the utilization of memristive regulation to shape the dynamics of a spiking neuron network during the implementation of cognitive functions, such as image recognition.
5. Conclusions
In conclusion, we have introduced a new model for controlling network bursting in a spiking network, utilizing memristor-implemented plasticity. By incorporating memristive plasticity into inhibitory synapses, we successfully regulated the impact of inhibitory neurons on network activity. This regulatory approach showcased the potential to transition the dynamics of a spiking neuron network from bursting to asynchronous behavior. Our findings demonstrate the viability of our model in achieving a more balanced and efficient neuron network operation. Using a biologically inspired model, we illustrate how memristive plasticity emulates spike timing-dependent plasticity, a crucial element in regulating synchronous brain activity [18]. These findings hold implications for the advancement of invasive neurointerfaces [33], and for the identification and management of epileptiform activity [50,51,52].
Author Contributions
Conceptualization, S.V.S.; methodology, S.V.S.; software, S.V.S.; validation, S.V.S.; formal analysis, S.V.S.; investigation, S.V.S.; resources, S.V.S.; data curation, S.V.S.; writing—original draft preparation, S.V.S., A.N.M., and V.B.K.; writing—review and editing, S.V.S., A.N.M., and V.B.K.; visualization, S.V.S.; supervision, S.V.S.; project administration, S.V.S. and V.B.K.; funding acquisition, S.V.S. and V.B.K. All authors have read and agreed to the published version of the manuscript.
Funding
The work regarding the development of a mathematical model of a spiking neural network and the implementation of computational experiments was supported by a grant from the Russian Federation Government (Agreement No. 075-15-2022-1123); the work regarding the implementation of the memristive plasticity model and the selection of its parameters was supported by the scientific program of the National Center for Physics and Mathematics, section No. 9 “Artificial intelligence and big data in technical, industrial, natural and social systems”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Model Comparison

Table A1.
Comparison between models.
Table A1.
Comparison between models.
| Proposed Model | Tandon’s Model [29] | Kanagaraj’s Model [30] | Asir’s Model [31] | Wen’s Model [32] | |
|---|---|---|---|---|---|
| Simulation object | Biologically functional cortical circuitry | Thermoacoustic system (the horizontal Rijke tube) | Unstructured neuron network | System of three coupled non-autonomous LCR oscillators | Shimizu–Morioka system |
| Observed effect | Homeostatic mechanism that leads to asynchronous irregular network states | Interactions between subsystems with different timescales lead to regular amplitude-modulated bursting, while noise induces irregular modulations | The transition to synchronization occurs for all network connectivities depending on the memristive coupling strength | Mixed-mode oscillations (MMOs) in a system of three coupled non-autonomous LCR oscillators sharing a common nonlinearity | The behavior of the system is investigated when there is an ordinal gap between the excitation frequency and the natural frequency |
| Element model | Leaky integrate-and-fire, fixed voltage threshold, fixed absolute refractory time | Balasubrama- nian’s model | Hindmarsh–Rose neuron | Linear LCR oscillator | Novel memristor-based chaotic system |
| Model structure | 2 layers of excitatory and inhibitory neurons | 1 item | Layer of similar neurons | n/a | 1 item |
| Communication type | Random all-to-all connections | n/a | Regular, small-world, and random | n/a | n/a |
| Number of network elements | 10,000 | n/a | 100 | 3 | n/a |
| Synapse model | Conductance-based inputs (exponentially decaying PSC) | n/a | Li’s model | n/a | n/a |
| Synaptic plasticity | Memristive-like STDP | n/a | n/a | n/a | n/a |
References
- Izhikevich, E. Bursting. Scholarpedia 2006, 1, 1300. [Google Scholar] [CrossRef]
- Sohal, V.; Huguenard, J. It takes T to tango. Neuron 2001, 31, 3–4. [Google Scholar] [CrossRef] [PubMed]
- Llinás, R.; Steriade, M. Bursting of thalamic neurons and states of vigilance. J. Neurophysiol. 2006, 95, 3297–3308. [Google Scholar] [CrossRef] [PubMed]
- Izhikevich, E. Which model to use for cortical spiking neurons? IEEE Trans. Neural Netw. 2004, 15, 1063–1070. [Google Scholar] [CrossRef]
- Izhikevich, E.; Desai, N.; Walcott, E.; Hoppensteadt, F. Bursts as a unit of neural information: Selective communication via resonance. Trends Neurosci. 2003, 26, 161–167. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Wang, Q.; Lu, Q. Firing synchronization and temporal order in noisy neuronal networks. Cogn. Neurodyn. 2008, 2, 195–206. [Google Scholar] [CrossRef]
- Gerstner, W.; Kistler, W. Spiking Neuron Models: Single Neurons, Populations, Plasticity; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar] [CrossRef]
- Sjöström, P.; Häusser, M. A cooperative switch determines the sign of synaptic plasticity in distal dendrites of neocortical pyramidal neurons. Neuron 2006, 51, 227–238. [Google Scholar] [CrossRef]
- Izhikevich, E. Polychronization: Computation with spikes. Neural Comput. 2006, 18, 245–282. [Google Scholar] [CrossRef]
- Izhikevich, E. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. Dyn. Syst. 2007, 441. [Google Scholar] [CrossRef]
- Van Vreeswijk, C.; Sompolinsky, H. Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science 1996, 274, 1724–1726. [Google Scholar] [CrossRef]
- Buzsáki, G. Feed-forward inhibition in the hippocampal formation. Prog. Neurobiol. 1984, 22, 131–153. [Google Scholar] [CrossRef] [PubMed]
- Abeles, M. Corticonics: Neural Circuits of the Cerebral Cortex; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar] [CrossRef]
- Silveira, J.; Protachevicz, P.; Viana, R.; Batista, A. Effects of burst-timing-dependent plasticity on synchronous behaviour in neuronal network. Neurocomputing 2021, 436, 126–135. [Google Scholar] [CrossRef]
- Pfister, J.; Gerstner, W. Triplets of spikes in a model of spike timing-dependent plasticity. J. Neurosci. 2006, 26, 9673–9682. [Google Scholar] [CrossRef] [PubMed]
- Markram, H.; Gerstner, W.; Sjöström, P. A history of spike-timing-dependent plasticity. Front. Synaptic Neurosci. 2011, 3, 4. [Google Scholar] [CrossRef] [PubMed]
- Song, S.; Miller, K.; Abbott, L. Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 2000, 3, 919–926. [Google Scholar] [CrossRef]
- Vogels, T.; Sprekeler, H.; Zenke, F.; Clopath, C.; Gerstner, W. Inhibitory plasticity balances excitation and inhibition in sensory pathways and memory networks. Science 2011, 334, 1569–1573. [Google Scholar] [CrossRef]
- Chua, L. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Indiveri, G.; Stefanini, F.; Chicca, E. Spike-based learning with a generalized integrate and fire silicon neuron. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 1951–1954. [Google Scholar]
- Yang, J.; Strukov, D.; Stewart, D. Memristive devices for computing. Nat. Nanotechnol. 2013, 8, 13–24. [Google Scholar] [CrossRef]
- Kipelkin, I.; Gerasimova, S.; Guseinov, D.; Pavlov, D.; Vorontsov, V.; Mikhaylov, A.; Kazantsev, V. Mathematical and Experimental Model of Neuronal Oscillator Based on Memristor-Based Nonlinearity. Mathematics 2023, 11, 1268. [Google Scholar] [CrossRef]
- Pershin, Y.; Di Ventra, M. Memory effects in complex materials and nanoscale systems. Adv. Phys. 2011, 60, 145–227. [Google Scholar] [CrossRef]
- Jo, S.; Chang, T.; Ebong, I.; Bhadviya, B.; Mazumder, P.; Lu, W. Nanoscale memristor device as synapse in neuromorphic systems. Nano Lett. 2010, 10, 1297–1301. [Google Scholar] [CrossRef] [PubMed]
- Indiveri, G.; Linares-Barranco, B.; Hamilton, T.; Schaik, A.; Etienne-Cummings, R.; Delbruck, T.; Liu, S.; Dudek, P.; Häfliger, P.; Renaud, S. Others Neuromorphic silicon neuron circuits. Front. Neurosci. 2011, 5, 73. [Google Scholar] [CrossRef] [PubMed]
- Izhikevich, E. Neural excitability, spiking and bursting. Int. J. Bifurc. Chaos 2000, 10, 1171–1266. [Google Scholar] [CrossRef]
- Bi, Q. The mechanism of bursting phenomena in Belousov-Zhabotinsky (BZ) chemical reaction with multiple time scales. Sci. China Technol. Sci. 2010, 53, 748–760. [Google Scholar] [CrossRef]
- Yalin, M. River Mechanics; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar] [CrossRef]
- Tandon, S.; Pawar, S.; Banerjee, S.; Varghese, A.; Durairaj, P.; Sujith, R. Bursting during intermittency route to thermoacoustic instability: Effects of slow–fast dynamics. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 103112. [Google Scholar] [CrossRef]
- Kanagaraj, S.; Durairaj, P.; Sampath, S.; Karthikeyan, A.; Rajagopal, K. Collective dynamics of a coupled Hindmarsh–Rose neurons with locally active memristor. Biosystems 2023, 232, 105010. [Google Scholar] [CrossRef]
- Asir, M.; Premraj, D.; Sathiyadevi, K. Complex mixed-mode oscillations in oscillators sharing nonlinearity. Eur. Phys. J. Plus 2022, 137, 282. [Google Scholar] [CrossRef]
- Wen, Z.; Li, Z.; Li, X. Bursting oscillations and bifurcation mechanism in memristor-based Shimizu–Morioka system with two time scales. Chaos Solitons Fractals 2019, 128, 58–70. [Google Scholar] [CrossRef]
- Mikhaylov, A.; Pimashkin, A.; Pigareva, Y.; Gerasimova, S.; Gryaznov, E.; Shchanikov, S.; Zuev, A.; Talanov, M.; Lavrov, I.; Demin, V. Others Neurohybrid memristive CMOS-integrated systems for biosensors and neuroprosthetics. Front. Neurosci. 2020, 14, 358. [Google Scholar] [CrossRef]
- Vogels, T.; Froemke, R.; Doyon, N.; Gilson, M.; Haas, J.; Liu, R.; Maffei, A.; Miller, P.; Wierenga, C.; Woodin, M. Others Inhibitory synaptic plasticity: Spike timing-dependence and putative network function. Front. Neural Circuits 2013, 7, 119. [Google Scholar] [CrossRef]
- Dayan, P.; Abbott, L. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Brunel, N. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci. 2000, 8, 183–208. [Google Scholar] [CrossRef] [PubMed]
- Demin, V.; Nekhaev, D.; Surazhevsky, I.; Nikiruy, K.; Emelyanov, A.; Nikolaev, S.; Rylkov, V.; Kovalchuk, M. Necessary conditions for STDP-based pattern recognition learning in a memristive spiking neural network. Neural Netw. 2021, 134, 64–75. [Google Scholar] [CrossRef]
- Hindmarsh, J.; Rose, R. A model of neuronal bursting using three coupled first order differential equations. Proc. R. Soc. London. Ser. B. Biol. Sci. 1984, 221, 87–102. [Google Scholar] [CrossRef]
- Wagenaar, D.; Pine, J.; Potter, S. An extremely rich repertoire of bursting patterns during the development of cortical cultures. BMC Neurosci. 2006, 7, 11. [Google Scholar] [CrossRef] [PubMed]
- Pimashkin, A.; Kastalskiy, I.; Simonov, A.; Koryagina, E.; Mukhina, I.; Kazantsev, V. Spiking signatures of spontaneous activity bursts in hippocampal cultures. Front. Comput. Neurosci. 2011, 5, 46. [Google Scholar] [CrossRef] [PubMed]
- Lazarevich, I.; Stasenko, S.; Kazantsev, V. Synaptic multistability and network synchronization induced by the neuron–glial interaction in the brain. J. Exp. Theor. Phys. Lett. JETP Lett. 2017, 105, 210–213. [Google Scholar] [CrossRef]
- Stasenko, S.; Kazantsev, V. Bursting Dynamics of Spiking Neural Network Induced by Active Extracellular Medium. Mathematics 2023, 11, 2109. [Google Scholar] [CrossRef]
- Stasenko, S.; Kazantsev, V. Information Encoding in Bursting Spiking Neural Network Modulated by Astrocytes. Entropy 2023, 25, 745. [Google Scholar] [CrossRef]
- Van Rossum, G.; Drake, F., Jr. Python Tutorial; Centrum voor Wiskunde en Informatica: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Nelli, F.; Nelli, F. The Pandas Library—An Introduction. In Python Data Analytics: Data Analysis and Science Using Pandas, Matplotlib, and the Python Programming Language; Apress: Berkeley, CA, USA, 2015; pp. 63–101. [Google Scholar]
- Stimberg, M.; Brette, R.; Goodman, D. Brian 2, an intuitive and efficient neural simulator. Elife 2019, 8, e47314. [Google Scholar] [CrossRef]
- Bisong, E.; Bisong, E. Matplotlib and seaborn. In Building Machine Learning and Deep Learning Models on Google Cloud Platform: A Comprehensive Guide for Beginners; Springer: Berlin/Heidelberg, Germany, 2019; pp. 151–165. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J. Others SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Wendling, F.; Bartolomei, F.; Bellanger, J.; Bourien, J.; Chauvel, P. Epileptic fast intracerebral EEG activity: Evidence for spatial decorrelation at seizure onset. Brain 2003, 126, 1449–1459. [Google Scholar] [CrossRef] [PubMed]
- Bessa, W.; Lima, G. Intelligent Control of Seizure-Like Activity in a Memristive Neuromorphic Circuit Based on the Hodgkin–Huxley Model. J. Low Power Electron. Appl. 2022, 12, 54. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, L.; Li, X.; Wu, Y.; Liu, S.; Wang, J.; Hu, S.; Yu, Q.; Chen, T.; Liu, Y. Epilepsy detection with artificial neural network based on as-fabricated neuromorphic chip platform. AIP Adv. 2022, 12, 035106. [Google Scholar] [CrossRef]
- Liu, Z.; Tang, J.; Gao, B.; Yao, P.; Li, X.; Liu, D.; Zhou, Y.; Qian, H.; Hong, B.; Wu, H. Neural signal analysis with memristor arrays towards high-efficiency brain–machine interfaces. Nat. Commun. 2020, 11, 4234. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Chen, Q.; Xue, F. Bursting dynamics remarkably improve the performance of neural networks on liquid computing. Cogn. Neurodynamics 2016, 10, 415–421. [Google Scholar] [CrossRef] [PubMed]
- Stasenko, S.; Mikhaylov, A.; Kazantsev, V. Model of Neuromorphic Odorant-Recognition Network. Biomimetics 2023, 8, 277. [Google Scholar] [CrossRef] [PubMed]
- Snider, G.; Amerson, R.; Carter, D.; Abdalla, H.; Qureshi, M.; Léveillé, J.; Versace, M.; Ames, H.; Patrick, S.; Chandler, B. Others From synapses to circuitry: Using memristive memory to explore the electronic brain. Computer 2011, 44, 21–28. [Google Scholar] [CrossRef]
- Zafar, I.; Cui, Y.; Bai, Q.; Yang, Y. Classifying Beers with Memristor Neural Network Algorithm in a Portable Electronic Nose System. Front. Phys. 2022, 10, 403. [Google Scholar] [CrossRef]
- Wang, T.; Huang, H.; Wang, X.; Guo, X. An artificial olfactory inference system based on memristive devices. InfoMat 2021, 3, 804–813. [Google Scholar] [CrossRef]
- Asghar, M.; Arslan, S.; Kim, H. A low-power spiking neural network chip based on a compact LIF neuron and binary exponential charge injector synapse circuits. Sensors 2021, 21, 4462. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).