Numerical Investigation of Cavitating Jet Flow Field with Different Turbulence Models
Abstract
:1. Introduction
2. Numerical Methods
2.1. Geometry of Organ Pipe Nozzle
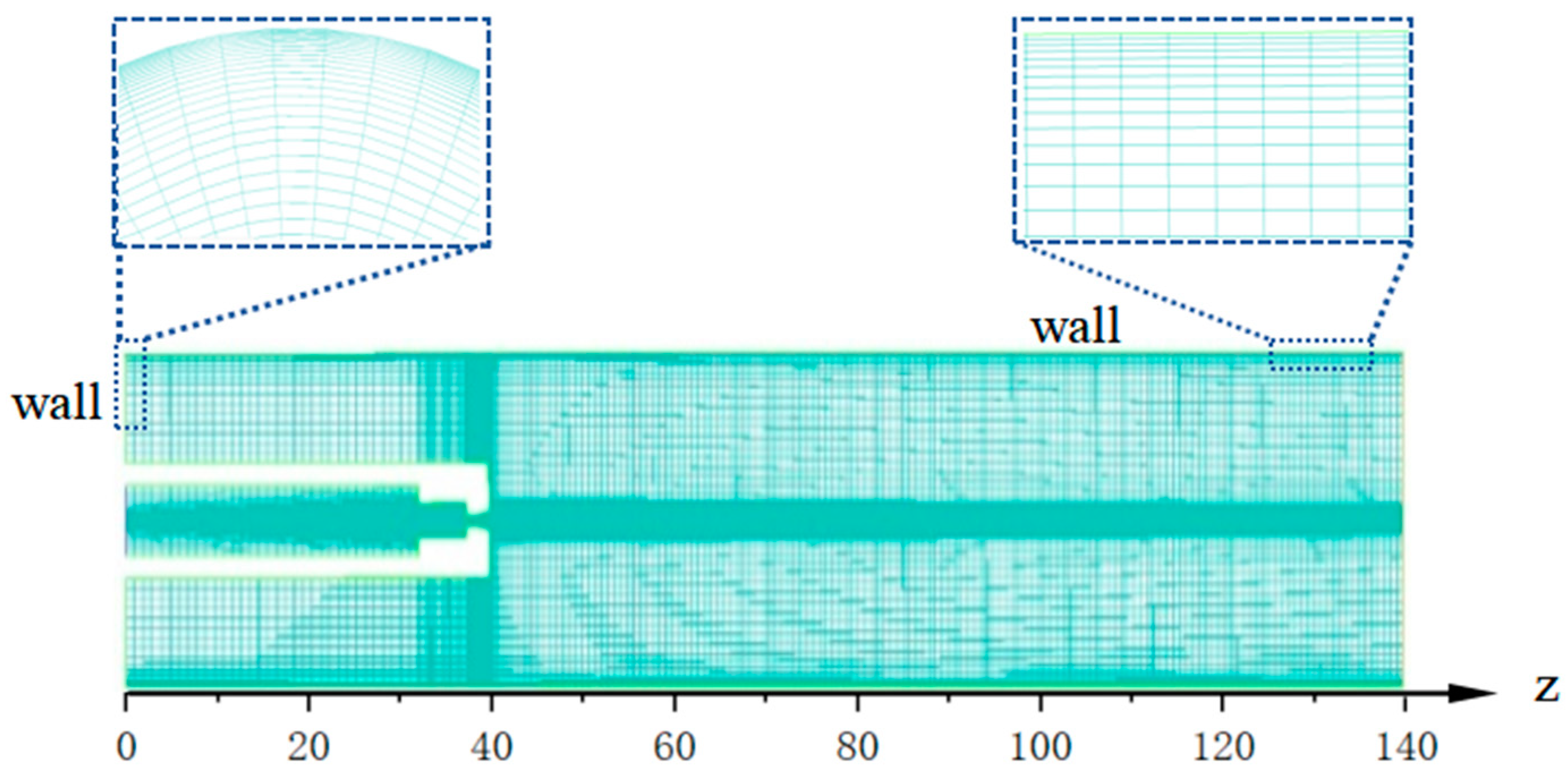
2.2. Grid and Independence Validation
2.2.1. Mesh Generation
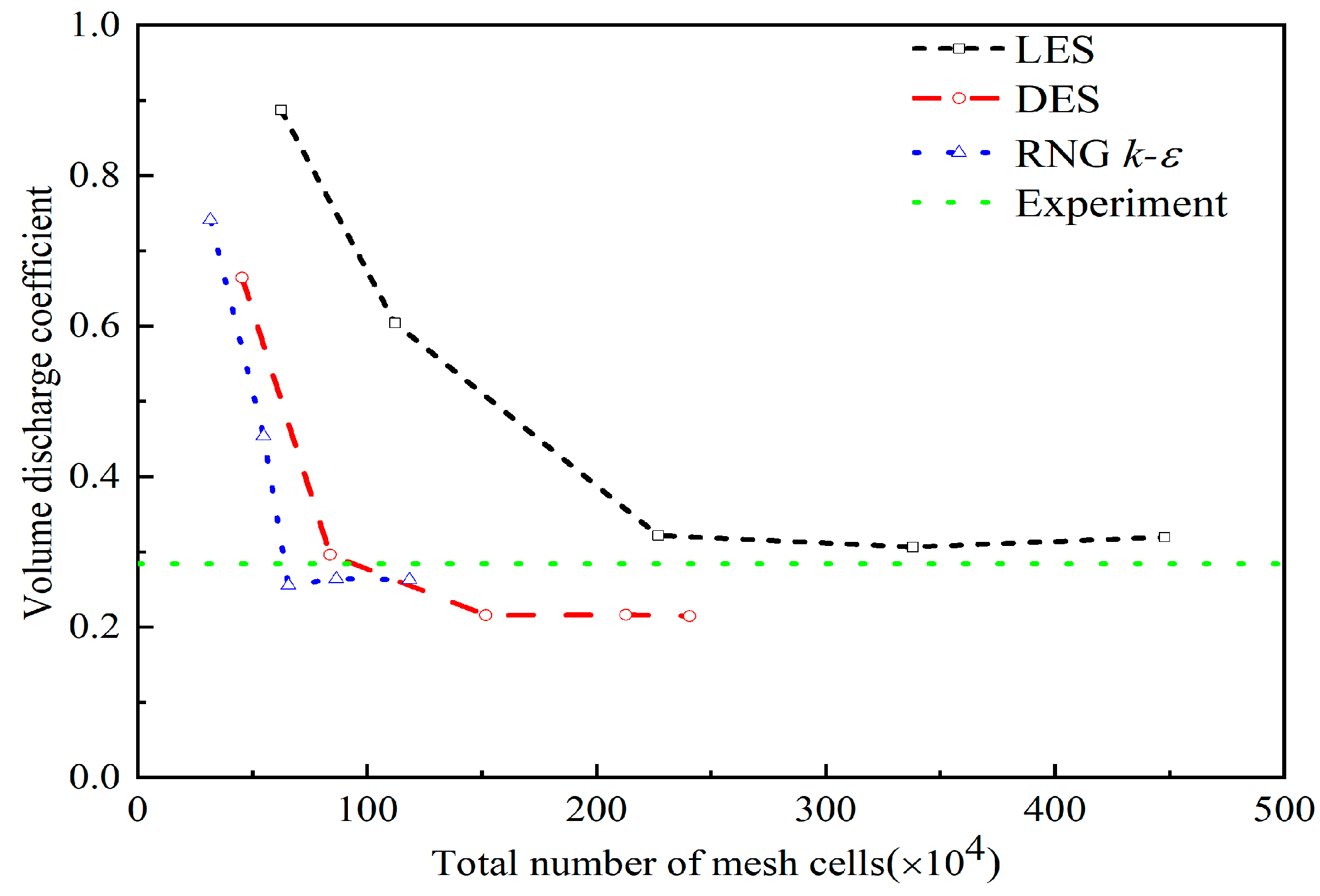
2.2.2. Mesh Independence and Numerical Uncertainty Analysis
2.3. Boundary Conditions and Discretization Methods
2.4. Control Equations of Mixture Model
2.4.1. Continuity Equation
2.4.2. Momentum Equation
2.5. Zwart–Gerber–Belamri (ZGB) Cavitating Model
2.6. Turbulent Model
2.6.1. RNG k−ε Model
2.6.2. LES with the WALE Model
2.6.3. DES with the SST k−ω Model
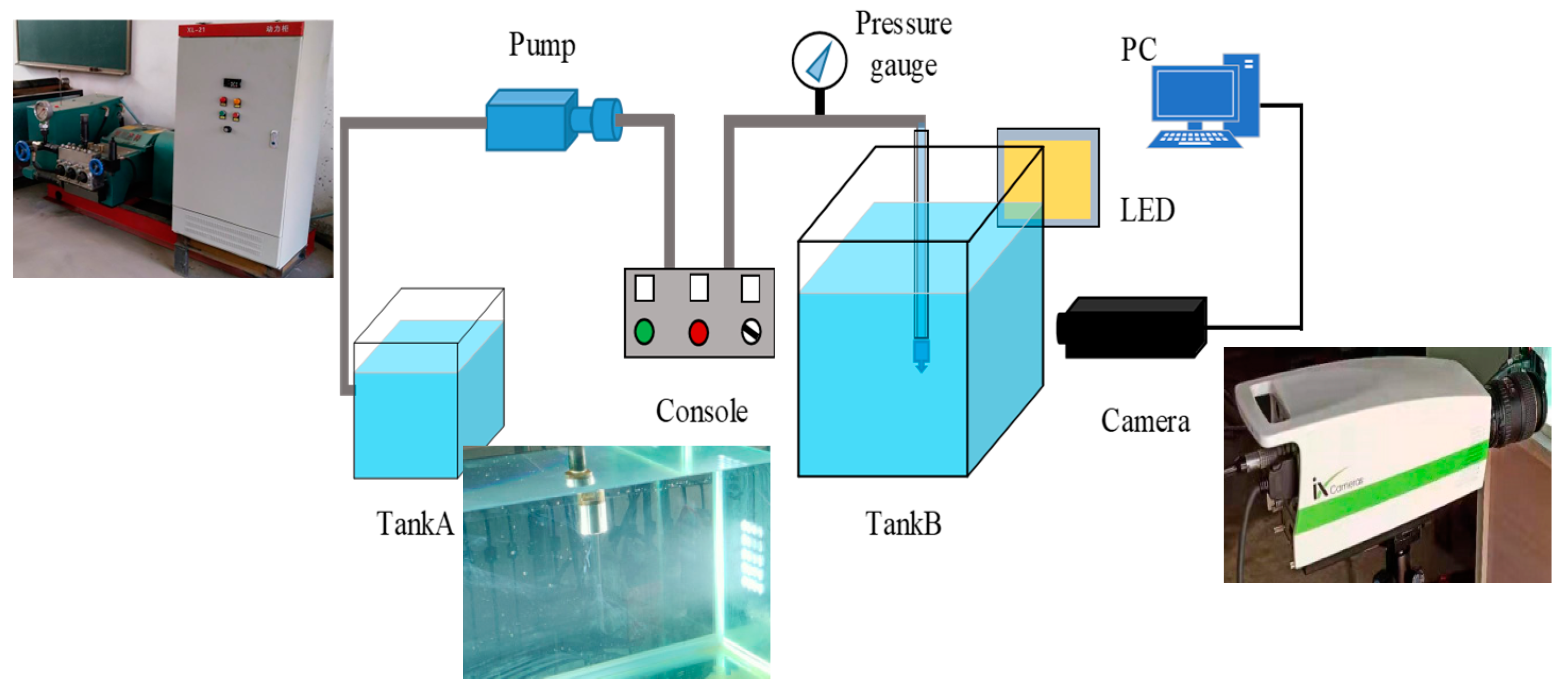
3. Experimental Methods
4. Results and Discussion
4.1. Comparison of the Simulation and Experiments Results
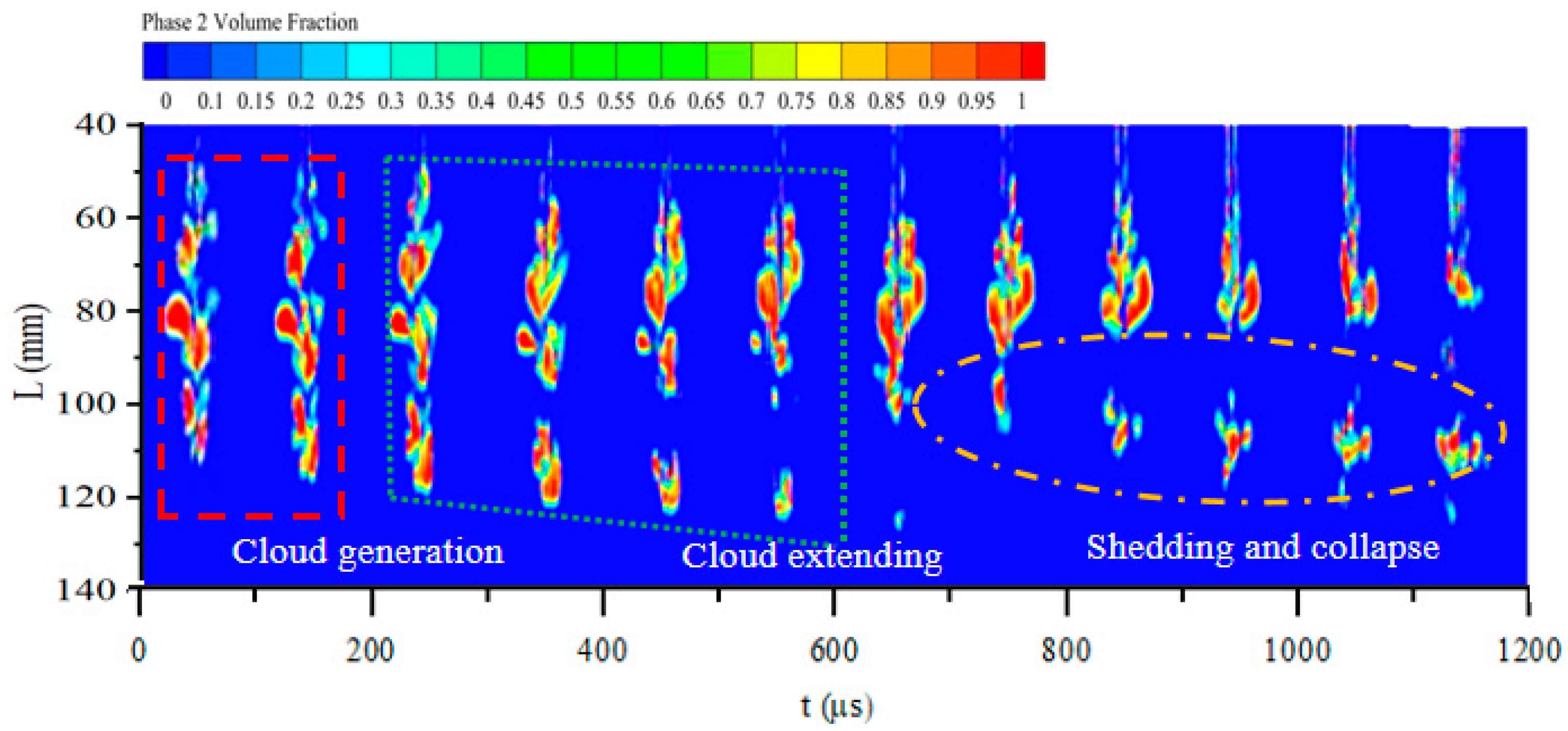
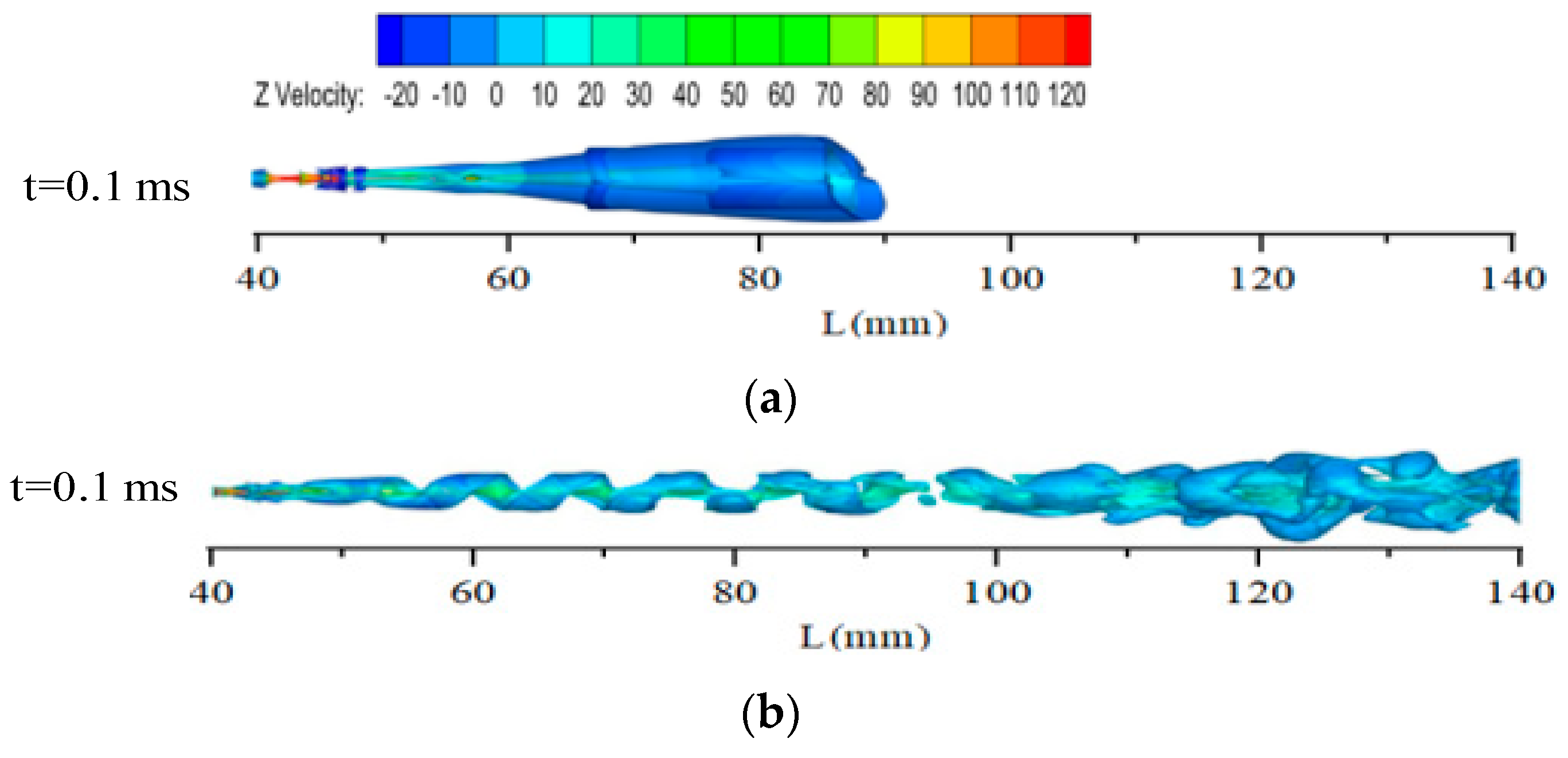
4.1.1. LES Simulation Results for Cavitating Cloud Evolution
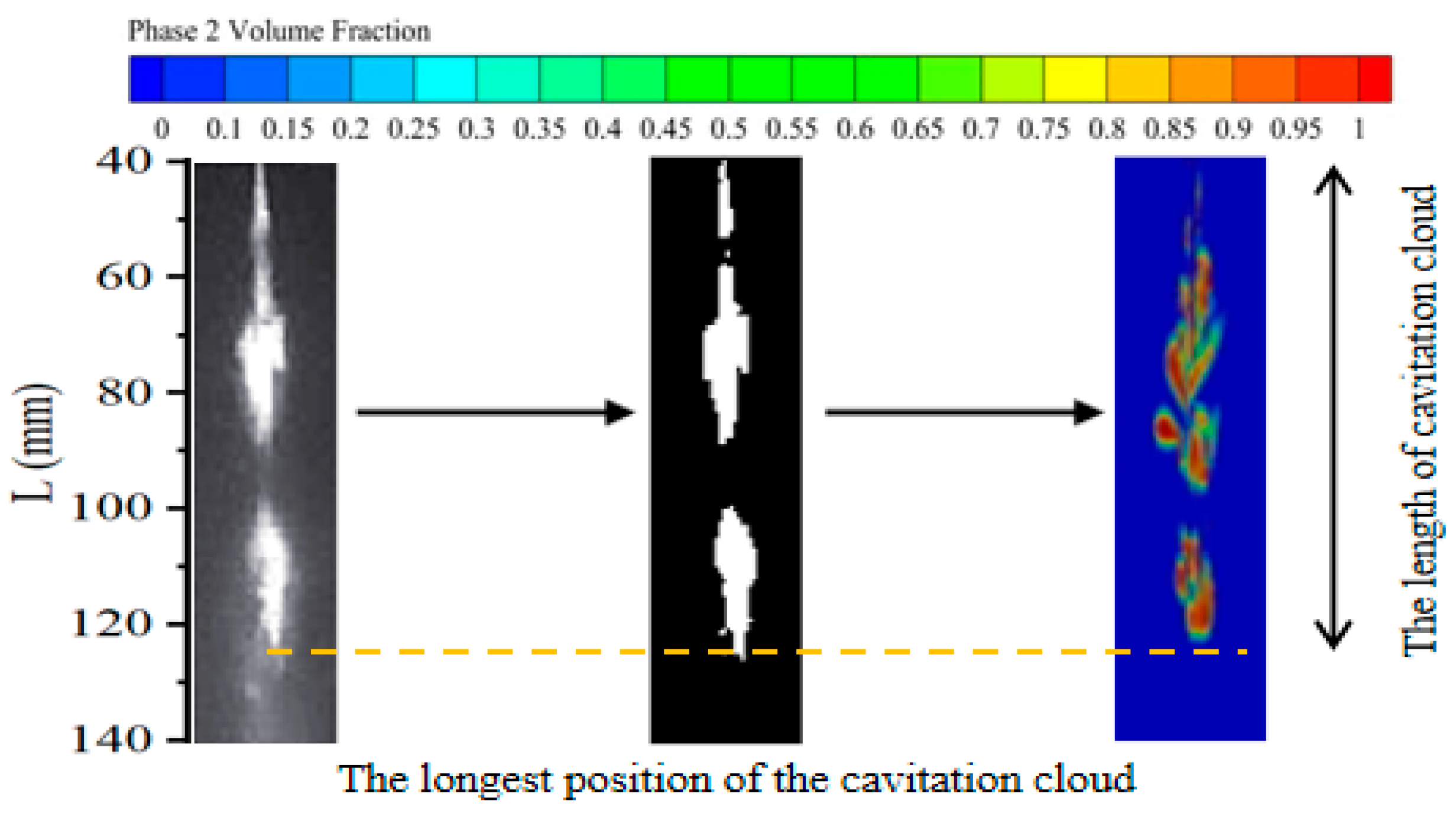
4.1.2. The Experiment Results
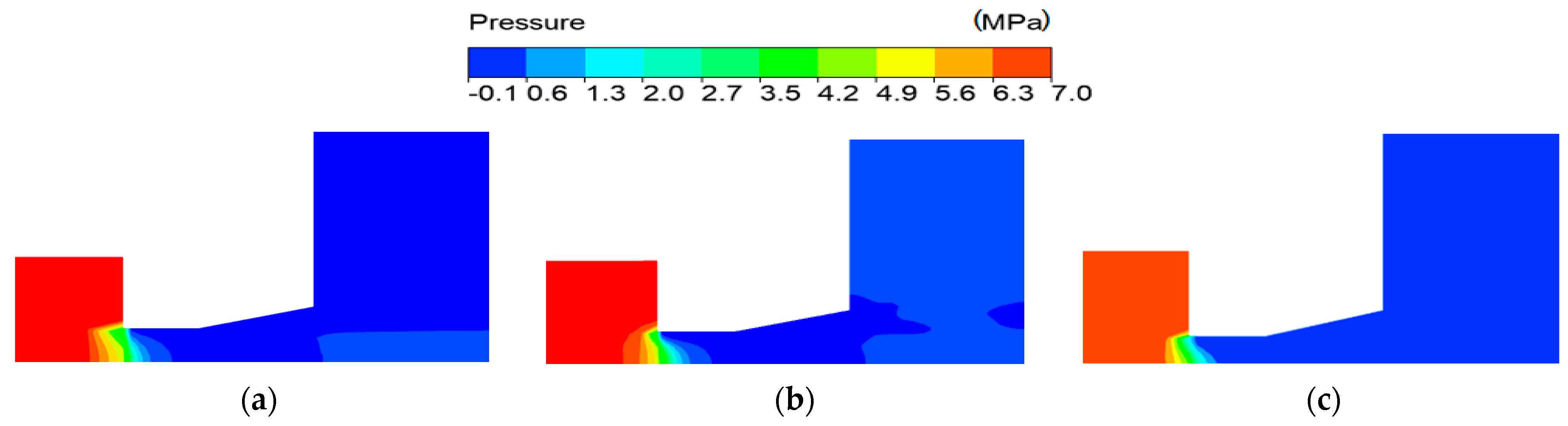
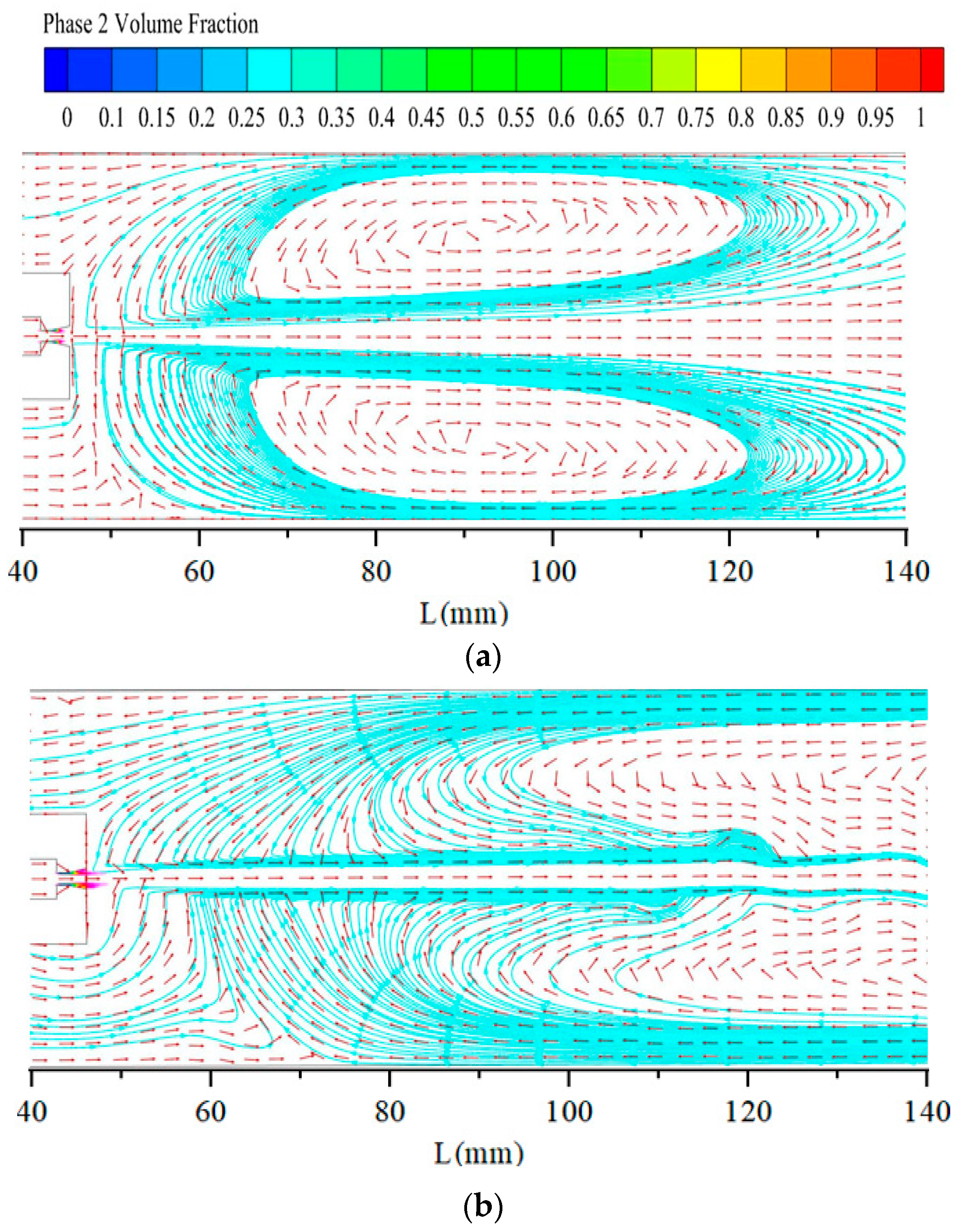
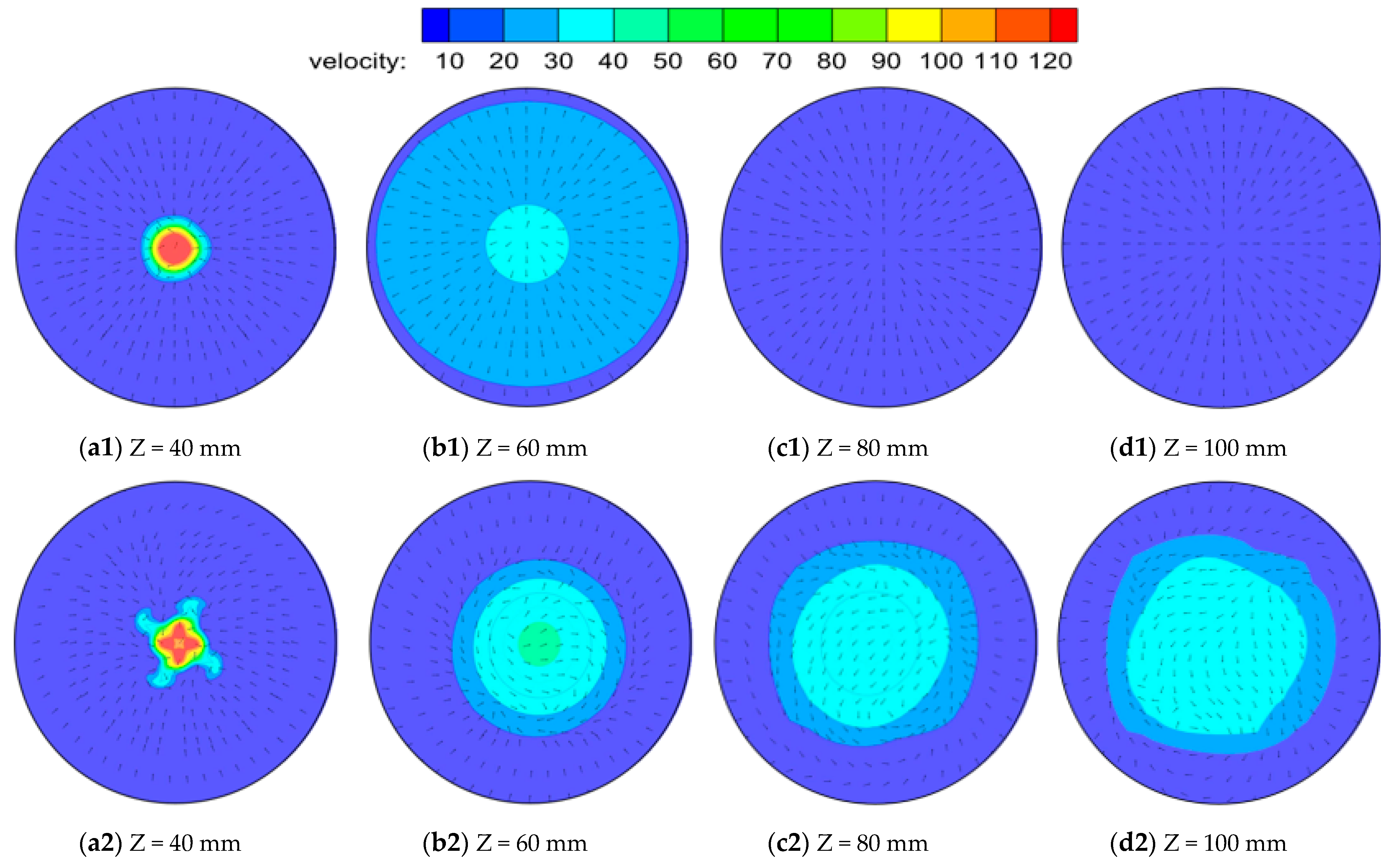
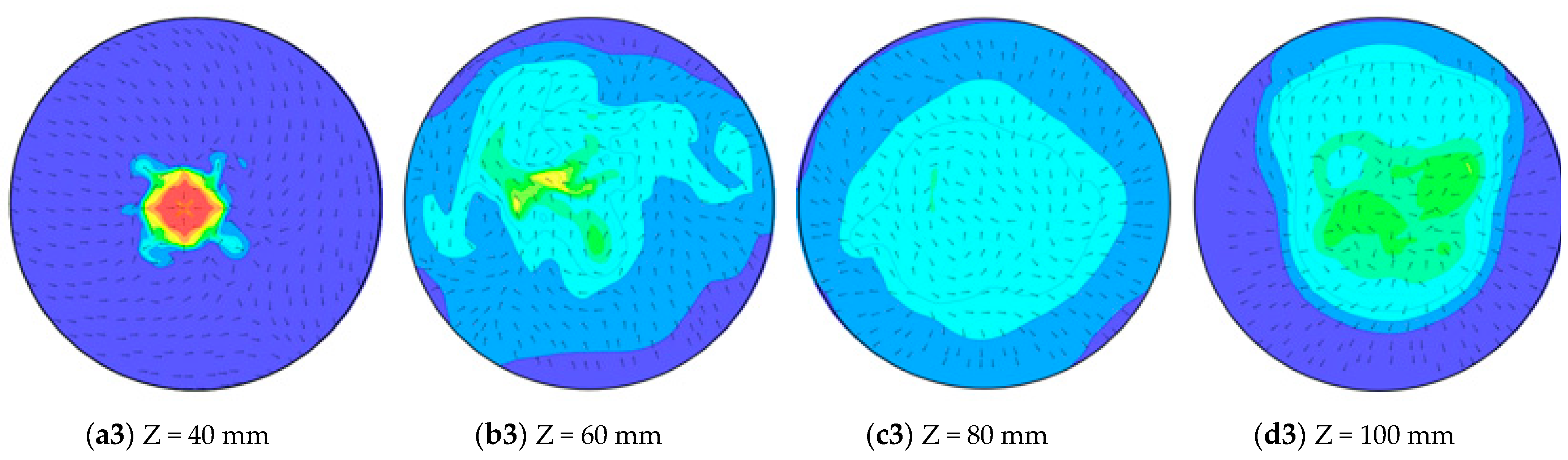
4.2. The Cavitating Jet Flow Field with Different Turbulence Models
4.3. The Flow Field Outside Nozzles with Different Turbulence Models
5. Conclusions
- (1)
- The numerical simulation of the cavitating flow in the organ pipe nozzle was conducted using the mixture model, the ZGB cavitation model, and three turbulence models, namely the RNG k−ε, DES, and LES models. The findings from three turbulence models indicate that the static pressure in both the cylindrical and diffusion sections is below the saturation vapor pressure of water. The velocity streamlines of the RNG k−ε and DES models exhibit a separation flow, whereas the velocity streamlines of the LES model demonstrate the presence of vortex rings in close proximity to the cylindrical and diffusion sections. These vortex rings contribute to the formation of cavitation. The LES model demonstrates effective simulation capabilities for accurately representing the cavitating flow phenomena in an organ pipe nozzle.
- (2)
- The cavitating cloud evolutions of an organ pipe nozzle were achieved using high-speed photography. There were periodic developments: the generation, development, shedding and collapse stages for cavitating clouds. The development period of a cavitating cloud is about 1200 µs and the maximum length of a cavitating cloud is about 90 mm at the inlet pressure of 7 MPa. The RNG k−ε and DES models are inadequate in simulating the formation of cavitation clouds outside the nozzle. In contrast, the LES model is capable of accurately simulating the dynamic behavior of cavitating clouds, which aligns well with experimental observations.
- (3)
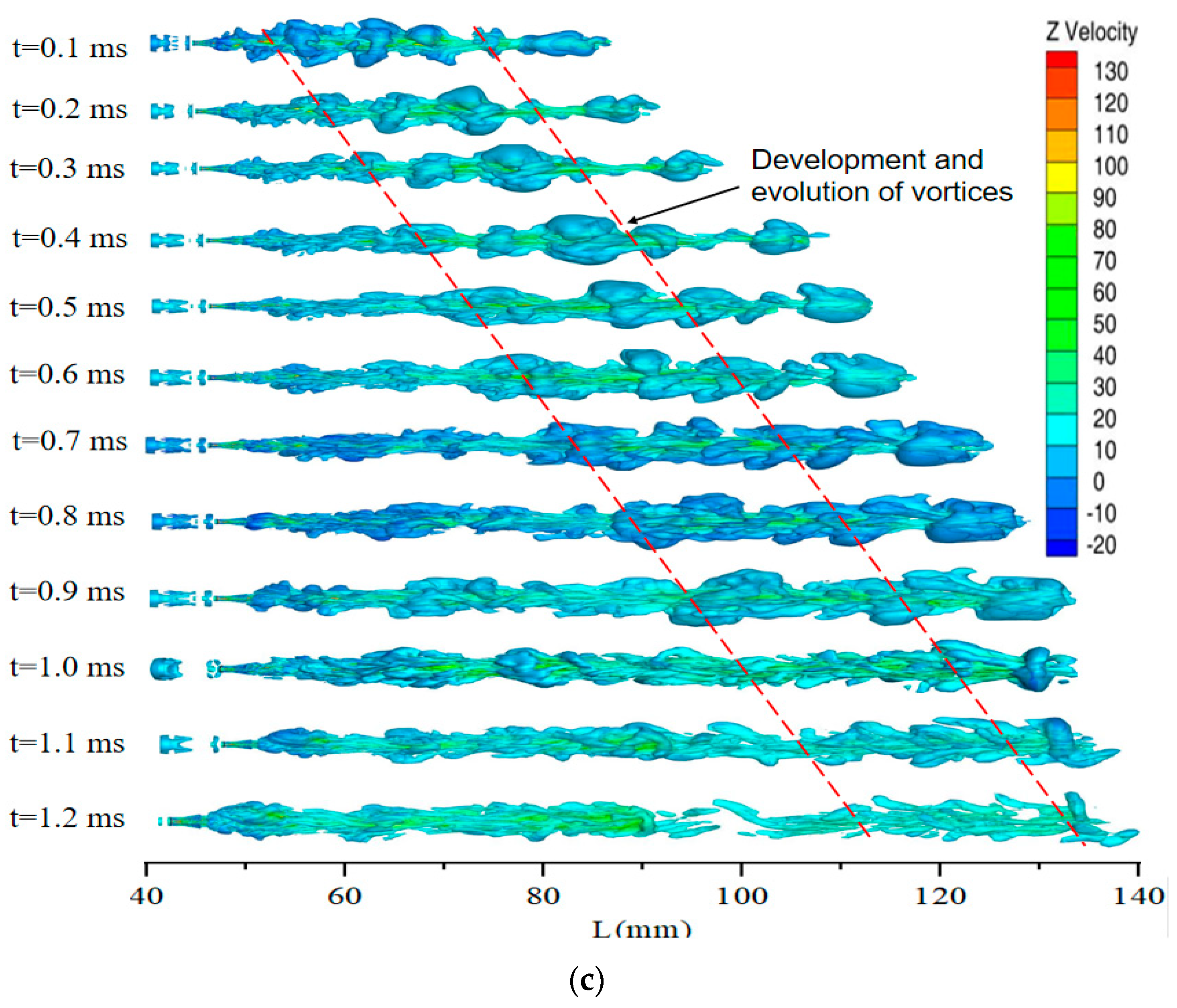
- The LES model accurately replicates the evolution of vorticity, which exhibits a consistent pattern during the periodic formation of a cavitation cloud. The dimensions of the vortex structure expand as the cavitating jet progresses, and the asymmetrical vortexes in the cross-sectional area experience growth during the initial stages of the cavitation jet. The cavitation bubble’s collapse at the termination of the cavitation jet induces perturbations in the adjacent fluid, causing the fragmentation of macroscopic vortexes into smaller-scale vortexes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| volume discharge coefficient | |
| area of the cross-section | |
| inlet pressure | |
| outlet pressure | |
| radial | |
| axial velocity | |
| local far-field pressure | |
| density of the liquid phase | |
| turbulent kinetic energy of the liquid phase | |
| turbulence kinetic energy | |
| strain tensor rate | |
| distance from the wall | |
| mass-averaged velocity | |
| mixture density | |
| volume fraction of phase k | |
| number of phases | |
| body force | |
| drift velocity of secondary phase k | |
| saturation vapor pressure | |
| saturation pressure | |
| constant value | |
| SGS turbulent viscosity | |
| Carmen constant | |
| volume of mesh |
References
- Ge, M.M.; Petkovšek, M.; Zhang, G.J.; Jacobs, D.; Coutier-Delgosha, O. Cavitation dynamics and thermodynamic effects at elevated temperatures in a small Venturi channel. Int. J. Heat Mass Transf. 2021, 170, 120970. [Google Scholar] [CrossRef]
- Soyama, H. Cavitating Jet: A Review. Appl. Sci. 2020, 10, 7280. [Google Scholar] [CrossRef]
- Li, G.S.; Liao, H.L.; Huang, Z.W.; Shen, L.H. Rock Damage Mechanisms under Ultra-high Pressure Water Jet Impact. J. Mech. Eng. 2009, 45, 284–293. [Google Scholar] [CrossRef]
- Cai, S.G.; Liu, P.T.; Zhao, X.J.; Chen, C.H.; Ren, R.M. Water Cavitation Peening-induced Surface Hardening and Cavitation Damage of Pure Titanium. China Surf. Eng. 2014, 27, 100–105. [Google Scholar]
- Shi, F.X.; Zhao, J.; Sun, X.G.; Yin, H.L. Numerical Simulation of Surface Cleaning Flow Field by Gas-Liquid Two-Phase Jet. J. Cent. South Univ. (Nat. Sci. Ed.) 2021, 52, 960–970. [Google Scholar]
- Szolcek, M.; Cassineri, S.; Cioncolini, A.; Scenini, F.; Curioni, M. CRUD Removal via Hydrodynamic Cavitation in Micro-Orifices. Nucl. Eng. Des. 2019, 343, 210–217. [Google Scholar] [CrossRef]
- Ge, M.M.; Sun, C.Y.; Zhang, G.J. Olivier Coutier-Delgosha, Dixia Fan, Combined suppression effects on hydrodynamic cavitation performance in Venturi-type reactor for process intensification. Ultrason. Sonochem. 2022, 86, 106035. [Google Scholar] [CrossRef]
- Han, J.; Cai, T.F.; Pan, Y.; Ma, F. Study on Jet’ s Characteristics of Organ Nozzle and Helmholtz Nozzle. Saf. Coal Mine 2017, 48, 134–137. [Google Scholar]
- Wang, C.H.; Hu, Y.N.; Rao, C.J.; Deng, X.G. Numerical Analysis of Cavitation Effects and Self-excited Oscillation Pulse Nozzle and Jet Forms. China Mech. Eng. 2017, 28, 1535–1541. [Google Scholar]
- Yu, H.T.; Xu, Y.; Wang, J.Y.; Liu, H.S.; Zhang, J.L.; Wang, Z.C. Optimization of Organ Pipe Nozzle Structure Based on CFD. Chem. Eng. Mach. 2021, 48, 883–887. [Google Scholar]
- Cai, T.F.; Pan, Y.; Ma, F.; Qiu, L.B.; Xu, P.P. Effects of Outlet Geometry of Organ-pipe Nozzle on Cavitation Due to Impingement of the Waterjet. J. Mech. Eng. 2019, 55, 150–156. [Google Scholar]
- Dong, W.; Yao, L.; Luo, W. Numerical Simulation of Flow Field of Submerged Angular Cavitation Nozzle. Appl. Sci. 2023, 13, 613. [Google Scholar] [CrossRef]
- Ran, Z.; Ma, W.; Liu, C. 3D Cavitation Shedding Dynamics: Cavitation Flow-Fluid Vortex Formation Interaction in a Hydrodynamic Torque Converter. Appl. Sci. 2021, 11, 2798. [Google Scholar] [CrossRef]
- Yan, C.Y.; Chen, Y. Numerical Investigation on the Water-Entry Cavity Feature and Flow Structure of a Spinning Sphere Based on Large-Eddy Simulation. Chin. J. Theor. Appl. Mech. 2022, 54, 1012–1025. [Google Scholar]
- Cheng, H.Y.; Ji, B.; Long, X.P.; Huai, W.X. LES Invetigation on The Influence of Cavitation on The Evolution and Characteristics of Tip Leakage Vortex. Chin. J. Theor. Appl. Mech. 2021, 53, 1268–1287. [Google Scholar]
- Xue, M.; Pu, Y. Large Eddy Simulation on Cavitation Inception of A Diesel Nozzle. Eng. Mech. 2013, 30, 417–422. [Google Scholar]
- Yang, Y.F. Investigation on Mechanism of Submerged High-Pressure Cavitation Jet and Metal Strength Improvement Using Cavitation Bubble Shock Wave; Jiangsu University: Zhenjiang, China, 2020. [Google Scholar]
- Yang, Y.; Shi, W.D.; Tan, L.W.; Li, W.; Chen, S.P.; Ban, B. Numerical Research of the Submerged High-Pressure Cavitation Water Jet Based on the RANS-LES Hybrid Model. Shock Vib. 2021, 2021, 16718. [Google Scholar] [CrossRef]
- Wang, G.; Yang, Y.; Wang, C.; Shi, W.; Li, W.; Pan, B. Effect of Nozzle Outlet Shape on Cavitation Behavior of Submerged High-Pressure Jet. Machines 2022, 10, 4. [Google Scholar] [CrossRef]
- Sou, A.; Biçer, B.; Tomiyama, A. Numerical Simulation of Incipient Cavitation Flow In a Nozzle of Fuel Injector. Comput. Fluids 2014, 103, 42–48. [Google Scholar] [CrossRef]
- Trummler, T.; Schmidt, S.J.; Adams, N.A. Investigation of Condensation Shocks and Re-entrant Jet Dynamics in a Cavitating Nozzle Flow by Large-Eddy Simulation. Int. J. Multiph. Flow 2020, 125, 103215. [Google Scholar] [CrossRef]
- Ge, M.M.; Zhang, G.J.; Petkovšek, M.; Long, K.P.; Coutier-Delgosha, O. Intensity and regimes changing of hydrodynamic cavitation considering temperature effects. J. Clean. Prod. 2022, 338, 130470. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, H.S.; Wang, Z.C.; Zhang, J.L.; Wang, J.X. Analysis of the Efects of Nozzle Geometry on the Cavitation Water Jet Flow Field Using Orthogonal Decomposition. Iran. J. Sci. Technol. Trans. Mech. Eng. 2023. [Google Scholar] [CrossRef]
- Long, Y.; Long, X.-P.; Ji, B.; Huai, W.-X.; Qian, Z.-D. Verification and validation of URANS simulations of the turbulent cavitating flow around the hydrofoil. J. Hydrodyn. Ser. B 2017, 16, 60774–60776. [Google Scholar] [CrossRef]
- Han, X.D.; Kang, Y.; Li, D.; Zhao, W.G. Effects of surface roughness on self-excited cavitating water jet intensity in the organ-pipe nozzle: Numerical simulations and experimental results. Mod. Phys. Lett. B 2019, 33, 1950324. [Google Scholar] [CrossRef]
- Yang, Y.F.; Li, W.; Shi, W.D.; Zhang, W.Q. Numerical Investigation of a High-Pressure Submerged Jet Using a Cavitation Model Considering Effects of Shear. Processes 2019, 7, 541. [Google Scholar] [CrossRef]
- Tian, C.L.; Chen, T.; Zou, T. Numerical study of unsteady cavitating flows with RANS and DES models. Mod. Phys. Lett. B. Condens. Matter Phys. Stat. Phys. Appl. Phys. 2019, 33, 20. [Google Scholar] [CrossRef]
- Savchenko, Y.N.; Savchenko, G.Y.; Semenov, Y.A. Effect of a Boundary Layer on Cavity Flow. Mathematics 2020, 8, 909. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- He, Z.X.; Chen, Y.H.; Leng, X.Y.; Wang, Q.; Guo, G.M. Experimental visualization and LES investigations on cloud cavitation shedding in a rectangular nozzle orifice. Int. Commun. Heat Mass Transf. Rapid Commun. J. 2016, 76, 108–116. [Google Scholar] [CrossRef]
- Ge, M.M.; Manikkam, P.; Ghossein, J.; Kumar Subramanian, R.; Coutier-Delgosha, O.; Zhang, G.J. Dynamic mode decomposition to classify cavitating flow regimes induced by thermodynamic effects. Energy 2022, 254 Pt C, 124426. [Google Scholar] [CrossRef]
- Ferrari, A. Fluid Dynamics of Acoustic and Hydrodynamic Cavitation in Hydraulic Power Systems. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20160345. [Google Scholar] [CrossRef]
- Zhao, B.J.; Xie, J.T.; Liao, W.Y. Applicability Analysis of the Second Generation Vortex Identification Method in the Internal Flow Field of Mixed-Flow Pump. J. Mech. Eng. 2020, 56, 216–223. [Google Scholar]
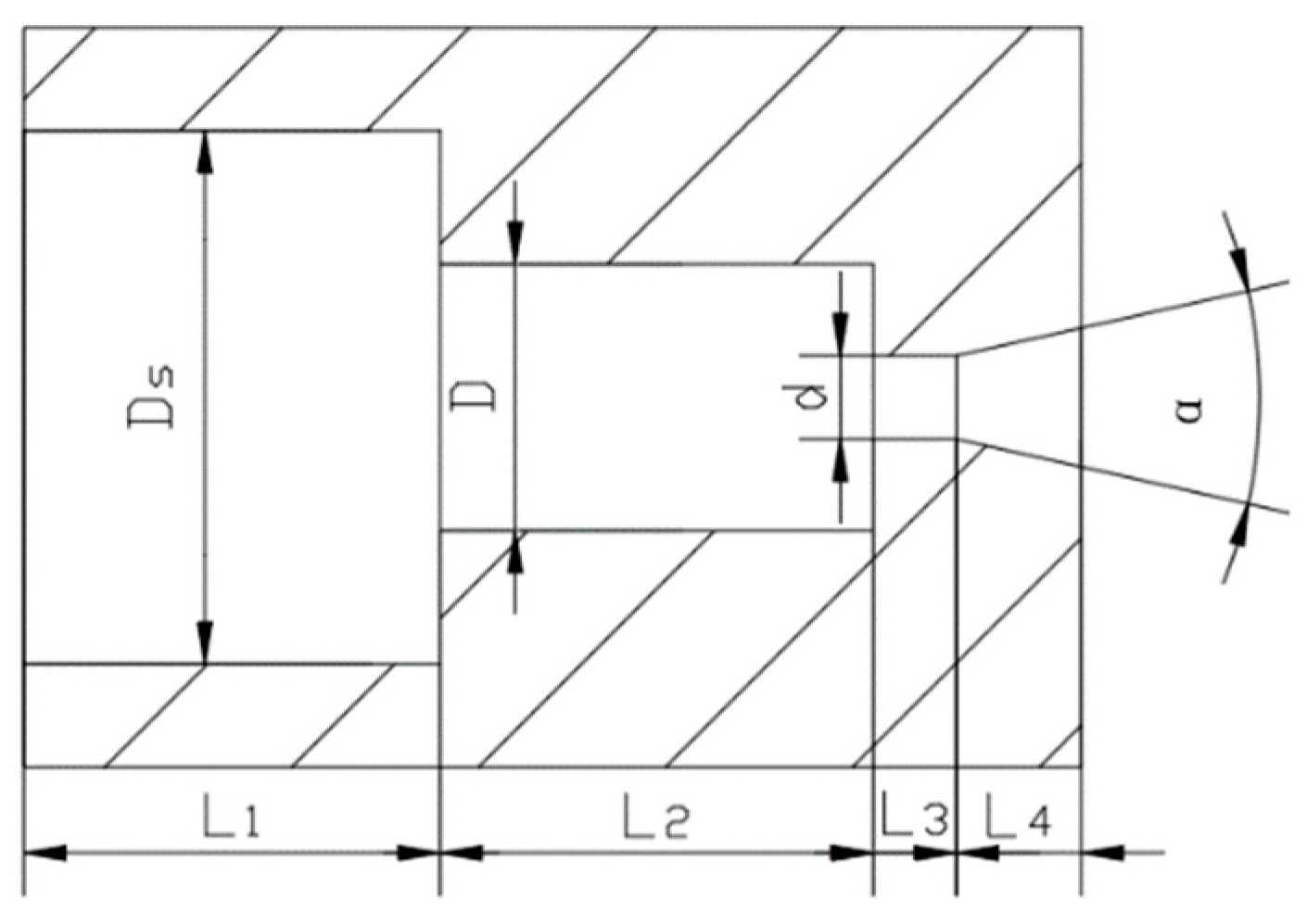






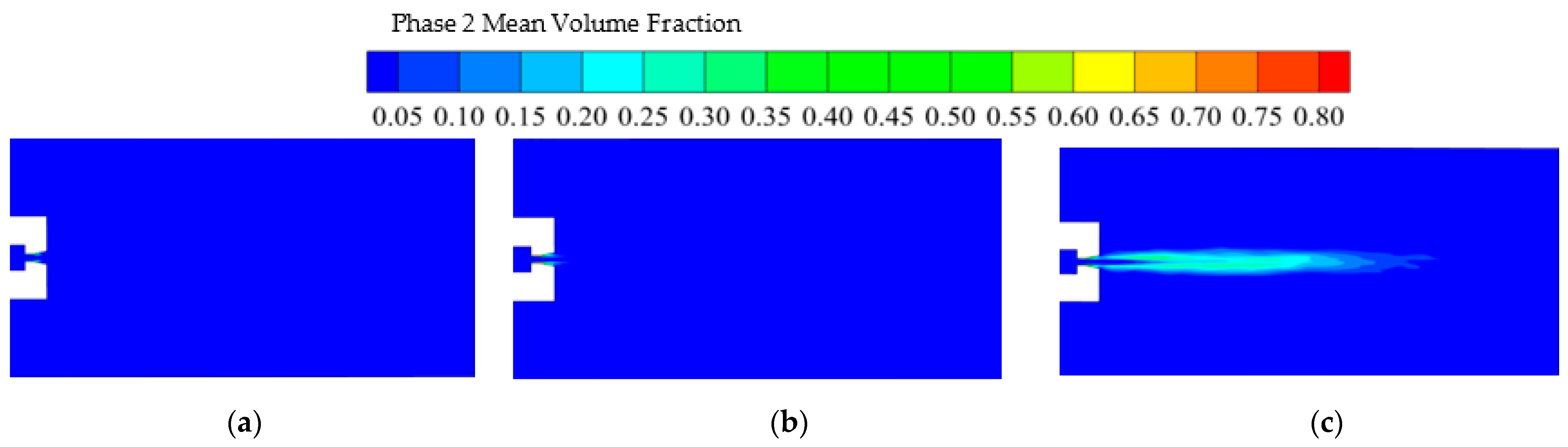
| Ds (mm) | D (mm) | d (mm) | L1 (mm) | L2 (mm) | L3 (mm) | L4 (mm) | α (°) |
|---|---|---|---|---|---|---|---|
| 6.4 | 3.2 | 1 | 5 | 5.2 | 1 | 1.5 | 12.5 |
| Turbulent Model | RNG k−ε Model | LES with WALE Model | DES Model |
|---|---|---|---|
| The coupled pressure–velocity method | Coupled | Coupled | Coupled |
| The interpolation method with gradient | Least squares cell-based | Least squares cell-based | Least squares cell-based |
| The interpolation method with pressure | PRESTO! | PRESTO! | PRESTO! |
| Convection interpolation | 2nd-order upwind | Bounded central differencing | Bounded central differencing |
| Volume fraction interpolation | 1st-order upwind | 1st-order upwind | 1st-order upwind |
| Time step | 1 × 10−5 | 1 × 10−5 | 1 × 10−5 |
| Convergence precision | 1 × 10−4 | 1 × 10−4 | 1 × 10−4 |
| Transient Formulation | Bounded Second-OrderImplicit | First-OrderImplicit | First-OrderImplicit |
| The Thermal | 25 °C | 25 °C | 25 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Xu, Y.; Ge, M.; Wang, Z.; Li, S.; Zhang, J. Numerical Investigation of Cavitating Jet Flow Field with Different Turbulence Models. Mathematics 2023, 11, 3977. https://doi.org/10.3390/math11183977
Li L, Xu Y, Ge M, Wang Z, Li S, Zhang J. Numerical Investigation of Cavitating Jet Flow Field with Different Turbulence Models. Mathematics. 2023; 11(18):3977. https://doi.org/10.3390/math11183977
Chicago/Turabian StyleLi, Lidong, Yan Xu, Mingming Ge, Zunce Wang, Sen Li, and Jinglong Zhang. 2023. "Numerical Investigation of Cavitating Jet Flow Field with Different Turbulence Models" Mathematics 11, no. 18: 3977. https://doi.org/10.3390/math11183977
APA StyleLi, L., Xu, Y., Ge, M., Wang, Z., Li, S., & Zhang, J. (2023). Numerical Investigation of Cavitating Jet Flow Field with Different Turbulence Models. Mathematics, 11(18), 3977. https://doi.org/10.3390/math11183977







