Optimal Fair-Workload Scheduling: A Case Study at Glorytek

Abstract

Taichung is the center of the Taiwanese precision optical industry. Optics companies are modernized and automated, with most running 24 h production lines. With machines running around the clock, production lines must be assigned engineers to handle unexpected situations. The optical lens industry depends on precision technology. For fully automated production lines, each production process requires an engineer to be on call to troubleshoot production problems in real-time. However, shifts are currently scheduled manually, and the staff of each unit are responsible for scheduling the various production processes for each month. Administrative staff for each engineering department must take half a day to one day to complete the shift for a month, with results that usually do not ensure the best average workload, often leading engineers to question its fairness. Considering the manpower requirements for the actual production line shift and the fairness of balancing shifts, the scope of this study is the shift scheduling of engineering staff in the assembly line to perform different duties during a fixed cycle. The research aims to provide a solution for Glorytek to increase the efficiency of engineering shift scheduling and optimize the allocation of engineering staff. We will compare the duty allocation and efficiency of the current manual shift scheduling system with a new automated one. The results show that the efficiency of shift scheduling arrangements increased by more than 96%, and the maximum number of days of staff attendance (5 days) is less than that for manual assignment (6 days) while still satisfying the shift limits stipulated by the company. Two factors remain when implementing the proposed system. First, due to technical concerns, the internal process of the scheduling arrangement would be shifted from administrative staff to the IT department. Another concern is the inevitable investment in off-the-shelf optimization software.

1. Introduction

The Glorytek in this study is a well-known high precision lens company in Taichung, established in 2000, now a leading lens manufacturer of mobile phone lenses with more than 20 years in the optical business, competent in optical/mechanical design, mold design and fabrication, injection molding, and process control for mass production. The company focuses on optics research, creation, and innovation to apply global products in the display, mobile, living, entertainment, and optical communication fields. Moreover, considering the high accuracy of lens performance requirements, Glorytek utilizes automatic processes and equipment to produce its lenses. The optical lens industry generally requires high precision and is technology-intensive. From lens injection molding, coating, and assembly to final performance testing, all steps rely on automated production and inspection equipment (Figure 1). This is a highly automated production industry, mainly because of the high precision and technical thresholds required by the camera end products. Moreover, since high-resolution requirements for image systems necessitate camera designs that combine more than six plastic lens elements, it is imperative to set the equipment’s production parameters in the production line. In particular, for the lens assembly process, each lens is assembled to the inside of the mechanism using CCD alignment to ensure that the optical axis coincides with the mechanical axis. Nevertheless, during the assembly process, the machine displacement tolerance, lens production tolerance, and assembly fixture tolerance all affect the quality and performance of the lens assembly. In view of this, the production parameters of the machine are subject to 24 h production monitoring. Once the machine issues warning signals or the continuous defect rate increases, full-time engineering staff are required to immediately analyze production and adjust the production parameters of the machine to avoid downtime affecting the schedule and capacity of post-production processing. Therefore, on the Glorytek assembly line, operators are responsible for transferring finished and semi-finished products to confirm the progress and output quantity, while engineering members are on-call to handle unexpected situations or urgent issues in real-time. Hence, it is critical for Glorytek’s management supervisors to properly arrange engineers on-call within each process, ensuring that they take place smoothly in the assembly line and manufacture plastic lenses for camera applications.

In practice, engineers are on-call during weekday night shifts (20:00 p.m.–2:00 a.m.), weekday graveyard shifts (2:00 a.m.–8:00 a.m.), holiday day shifts (8:00 a.m.–16:00 p.m.), holiday night shifts (16:00 p.m.–12:00 a.m.), and holiday graveyard shifts (12:00 a.m.–8:00 a.m.). They are not required to be on-site during duty but are required to be on-call at all times. Upon notification of an anomaly in the production line, they must arrive within one hour to eliminate the anomaly. Currently, on-call scheduling is arranged manually based on experience. However, manual assignments do not consider the frequency of each individual’s attendance and whether they are often scheduled to work on weekends, which often causes new engineers to express dissatisfaction with the shifts and question whether senior engineers are on call less often than new engineers. Glorytek’s HR manager has indicated that this issue could lead to a high turnover of new engineers, which would hinder the company from achieving its talent development goals. Therefore, Glorytek’s management team seeks a solution that can fairly arrange engineers’ on-call schedules and improve the efficiency of the schedule arrangement.

Shift-scheduling research began in the 1950s when pioneering researchers, such as [1,2], used mathematical models to construct the most appropriate shift and assign tasks accordingly. Currently, shift-scheduling problems occur in all industries, so it is more efficient and fairer to replace manual assignments with mathematical models to identify the best scheduling pattern.

Manual assignment is also time-consuming and error-prone. In the past, it took half a day to one whole day to complete a monthly shift for an engineering department. Furthermore, when a staff member resigned, schedules needed to be re-arranged. In this study, based on integer programming, we obtain the optimal load-averaging scheduling pattern from workers’ existing shifts and on-duty loads in a fixed cycle. Apart from shift averaging, this study attempts to avoid consecutive working weekends and averages each labor load in an effort to reduce the turnover risk of new employees under fair shift scheduling. Our research findings demonstrate positive results, which show that the efficiency of shift scheduling arrangements increased by more than 96%, and the maximum number of days of staff attendance (5 days) is less than that for manual assignment (6 days) while still satisfying the shift limits stipulated by the company.

2. Literature Review

An early study on staff assignment problems was conducted by [3], who distinguished three types of problems: shift scheduling, days-off scheduling, and tour scheduling. If the shifts were such that every single worker could be scheduled separately, the problems would be simple to solve; in contrast, duty-on-leave or overlapping problems are relatively complex. Shift-scheduling problems were characterized in [4] into six major axes: demand forecasting, days-off scheduling, shift scheduling, line-of-work construction (tour scheduling), task assignment, and staff assignment. Staff assignment problems have been shown to be NP-hard problems that thus cannot be solved optimally in a reasonable computational time. Therefore, a heuristic solution method is generally used to determine an approximate solution in the shortest possible time. In [5], the literature on shift-scheduling problems was identified ten common models for solving staff scheduling problems: (1) manual solution, (2) integer programming, (3) implicit modeling, (4) decomposition, (5) goal programming, (6) working set generation, (7) LP-based solutions, (8) construction/improvement, (9) metaheuristics, and (10) other methods. Shift-scheduling problems occur in all walks of life, among which on-duty issues have been extensively discussed in the nursing industry for many years. In addition to finding the optimal shift through mathematical determinants, also it was also argued by [6] that scheduling nursing staff is relatively complex. When scheduling nursing staff, the immediate needs of emergency cases must also be considered in addition to their regular shifts. Therefore, their schedules must also include off-call and on-call shifts during holidays. In view of this, Stolletz incorporates operational cost and fairness considerations into the scheduling problems of nursing staff to construct a reasonable on-call shift for them. In [7], it was pointed out that creating shift schedules is intricate. While algorithms should assist, it is vital to consider not just the objective quality, such as economic or legal aspects, but also the subjective experiences of those involved. Employee well-being in shift work closely relates to how schedules are determined. They emphasize perceived fairness and propose an inclusive system. The fairness issue should also be considered in the rotation schedules of physicians’ residency programs. Work of [8] was devoted to designing the Automated Internal Medicine Scheduler (AIMS), which improved several metrics of schedule quality, as well as resident satisfaction. They collected preference data through surveys and integrated it into the scheduling system. The results showed that AIMS improved schedule quality by reducing conflicts, aligning with resident preferences, enhancing satisfaction, and improving fairness perception. A reduced set covering formulation was adopted in [6], with results that turned out to be more efficient than using implicit modeling in the computation of an optimal schedule. In [9], goal programming was used to arrange monthly leave shifts for nursing staff in emergency centers. It was shown that nearly 74.7% of nursing staff in Korea are required to perform night shifts, with an average of 6.3 to 6.8 days per month [10]. Lee further indicated that night shifts could be physically and mentally stressful for workers. Failure to arrange proper shift schedules negatively impacts workers’ physical and mental health as well as the turnover rate. The scheduling system must allocate every employee to their designated shifts for each day of the planning cycle. In addition to addressing shift coverage and organizational factors, effective schedules also take into account elements like fairness and employee contentment. Employee discontentment with the shift schedule can lead to higher employee turnover and reduced work efficiency [11]. Therefore, it is necessary to consider a reasonable number of days on call and rotate the shifts. As suggested in [12], consecutive night shifts should be avoided when scheduling shifts to protect the physical and mental health of the workers. Indicated by [13], the worst shift is consecutive night shifts followed by consecutive morning shifts, which has a serious impact on the physical and mental health of the workers; in contrast, a short alternation between morning and evening shifts (one evening shift plus one morning shift, or two consecutive evening shifts followed by two consecutive morning shifts) is more desirable. Therefore, in scheduling shifts, apart from arranging them as evenly as possible, it is also important to note that different shift patterns are also a concern to workers. It was found in [14] that apart from shift averaging and different shift patterns, shift scheduling preferences vary according to age, gender, and the marital status of the workers, so a resilient shift must meet their flexible needs.

From the above literature, it is understood that staff scheduling is more frequently explored in the healthcare industry, where the main issues are discussed. It also provides the researcher with an understanding of the factors which must be considered to come up with an appropriate schedule to avoid adverse impacts on workers’ physical, mental, and sleep health. Furthermore, in practical situations, on-call or standby assignments are regularly utilized to maintain service quality; however, the literature has not given as much consideration to the planning of on-call duties [11], and no studies have been conducted on on-call duties scheduling in the optical industry. Therefore, in this study, we conduct a case study in the optical industry to design a fair shift schedule considering employee leave and minimizing average on-call duties in an effort to prevent employees’ health from being affected by consecutive shifts, which in turn leads to a brain drain in the company. We also expect to replace traditional manual assignments with systematic and automatic scheduling. On one hand, we take into account the scheduling fairness, and on the other, we help the company arrange shifts for engineering staff in a more efficient way to ensure continuous production.

3. Problem Description and Model Construction

3.1. Problem Description

At Glorytek, production lines are highly automated due to precision requirements. All components are assembled and arranged by automatic aligners, after which all optical components are assembled by automatic assembly machines. The final product specifications are examined by automatic optical inspection machines, after which the product is packed and shipped. It is thus essential to maintain production accuracy in the machines. Due to continuous production, machines are subject to wear and tear of assembly tools or displacement of moving optical stages. Even slight changes can affect the performance and production yield of the finished lens. In view of this, assembly line machines are subject to 24 h production monitoring. Upon notification of an anomaly in the machines, engineering personnel are required to arrive within one hour to resolve the anomaly. The lens assembly line resembles a pipeline with interlocked production processes. Once a process stops, it affects the efficiency of all subsequent processes. Therefore, each production station in the lens assembly line must be equipped with full-time engineering staff to troubleshoot problems with the machine at any time to ensure assembly accuracy and output efficiency. Generally, the lens assembly line produces 24 h a day for 365 days. The OP of the production line is responsible for the transfer of finished and semi-finished products from each production station and the inspection of the production machines, whereas the engineers are responsible for machine parameter settings, parameter correction, and anomaly resolution. Therefore, on weekdays, engineers are on call for two shifts (lunch shift and night shift; there is no morning shift because it is a regular shift, so if any problem occurs with the machine, the project engineer of the finished product is responsible for it), whereas on holidays, they must be on-call for three shifts: morning, afternoon, and evening.

Currently, the shift schedule is arranged by the administrative staff of each unit. The scheduling of the shifts for the next month is completed on the 25th of each month. It takes an average of half a day to one day for the staff to finish planning (depending on the number of staff on call in the department and the number of shifts required by each department). After the shifts are scheduled, they are to be confirmed by the manager of each unit. If there is no problem, the schedule is implemented on the first day of the following month. However, there are several problems:

• Staff scheduling is time-consuming.
• The scheduler must manually check to ensure a 12 h interval between a shift and the following shift, which often fails to be fully carried out. Hence, when consecutive shifts occur, workers must be temporarily transferred to another shift.
• If an employee joins or leaves during the month, the scheduler must manually adjust the shifts again, which leads to a lack of timeliness in scheduling.
• Shifts are not averaged fairly: some workers have a greater number of shifts than others in a given month.

3.2. Model Constructions

In view of the problems of manual assignment, we develop an optimal model based on the actual shift-scheduling demand of the lens assembly line through several planning methods and use it to plan a fair schedule. The objective is to achieve load balancing of fairness among all participants, subject to practical constraints. The fairness is measured through the minimization of the maximum attendance of the individuals.

• Manpower of assembly line engineers: The total number of personnel for the assembly line is 17, including 2 section managers and 15 engineers. All personnel are equipped with the necessary professional knowledge to adjust the parameters of the assembly machine and troubleshoot anomalies and have passed the pre-service training provided by the unit. Therefore, all engineers are fit to perform their duties.
• All personnel can meet the shift demands of all assembly machines in the production line. There is no problem with matching machines and engineering staff.
• In terms of scheduling, the engineering staff are on call during weekday night shifts (16:00 p.m.–12:00 a.m.) and weekday graveyard shifts (12:00 a.m.–8:00 a.m.) because the normal working hours for all engineers are 8:00 a.m.–5:00 p.m. Therefore, after working hours, there are only two shifts on weekdays. However, on weekends, three shifts are required: holiday day shifts (8:00 a.m.–16:00 p.m.), holiday night shifts (16:00 p.m.–12:00 a.m.), and holiday graveyard shifts (12:00 a.m.–8:00 a.m.). They must stay on call at all times. When notified by the production line, the staff must arrive at the site within one hour to troubleshoot the problems. To protect employees’ physical and mental health and balance their labor, no employees are allowed to work two consecutive shifts in a day, and a 12 h interval should separate two shifts.
• Taking into account employees’ living conditions of rest and labor balance, the scheduling condition that employees shall not be on call for two consecutive weeks during holidays shall be met, given sufficient manpower for shifting.
• This study model does not consider personnel salary costs. In the future, if each unit considers labor costs, this can be included in the input cost factor of the model. The shift allocation and adjustment for scheduling can be carried out according to the model’s output.
• At the same time, the scheduling model established in this study is based on the assumption that all staff members are available and present. Special leave, sick leave, and so on are unanticipated conditions and are thus not included in the scope of this study.

3.3. Mathematical Model

• Parameter settings

P	Number of employees	(P = 17)
D	Number of days in a month	(D = 30)
Cj	The set of all shift numbers for each day
Z	Maximum number of attendances per month
k	Shift index k (Morning shift: 1/night shift: 2/graveyard shift: 3)	k = 1, 2, 3
xijk	i-th worker on date j and k shift on call or not	xijk = 1 or 0
i	i-th worker on call	i = 1, …, 17
j	Day j of each month	j = 1, …, 30

• Objective Function

• $\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}Z$

  $$\sum _{j=1}^D\sum _{k=1}^{C_j}{x}_{ijk}\le Z1\le i\le P.$$

  (1)
  Constraints:

  $$\sum _{k=1}^{C_j}{x}_{ijk}\le 1,1\le i\le P,1\le j\le D,$$

  (2)

  $$\sum _{i=1}^P{x}_{ijk}=1,1\le j\le D,1\le k\le C_j,$$

  (3)

  $$x_{ijk}+x_{i,j+1,k}+x_{i,j+7,k}+x_{i,j+8,k}\le 1,1\le i\le P,1\le j\le D-8$$

  (4)

  $$x_{ij2}+x_{i,j+\mathrm{1,1}}+x_{i,j+\mathrm{1,2}}\le 1,1\le i\le P,1\le j\le D-1,$$

  (5)

  $$x_{ij1}+x_{i,j+\mathrm{1,1}}\le 1,\forall 1\le i\le P,1\le j\le D-1.$$

  (6)

3.4. Model Description

Equation (1) is for the objective function of Z, which represents minimizing the maximum number of attendances per month for each engineer. Five categories of constraints follow to confine the required characteristics of feasible schedules. Constraints (2) require that each person can only take a maximum of one shift per day. Constraints (3) confine that for each shift of each day, there is exactly one engineer who stays on call. Constraints (4) consider employees’ work schedules and labor balance, stating that shift workers should not be on call for two consecutive weekends. Constraints (5) and (6) both stipulate that the interval between employee shifts be 12 h or more. This means that employees who work the graveyard shifts on Friday cannot work the day or night shift on Saturday, and employees who work the night shift on Fridays are not allowed to work the day shift on Saturdays. These conditions are in place to ensure that employees have sufficient rest time.

3.5. Solution

We conducted a case study of the assembly lines of Glorytek. The engineers required for the assembly come from the product technology department. The case company has a total of 17 engineers in the said department who can be scheduled for shifts.

The scheduling model of this study can be optimized by adjusting its constraints and parameters according to the factors of manpower, day requirements specified by the unit, and the limitations of rotating adjustment in order to devise the best shift for engineering personnel. If there is an adjustment in the demand for duty or the amount of manpower, the relevant parameters, constraints, and mathematical models may be modified using mathematical planning software to plan the fairest schedule. Therefore, this model helps complete scheduling in the shortest time and attain fairness in workload allocation.

In this study, Gurobi Optimizer 9.0, a mathematical programming software package combined with Microsoft Excel 2010, was used to optimize the scheduling model. The process assists enterprise units in rotating shifts, which shortens the time spent on manual scheduling and inspection.

4. Case Validation

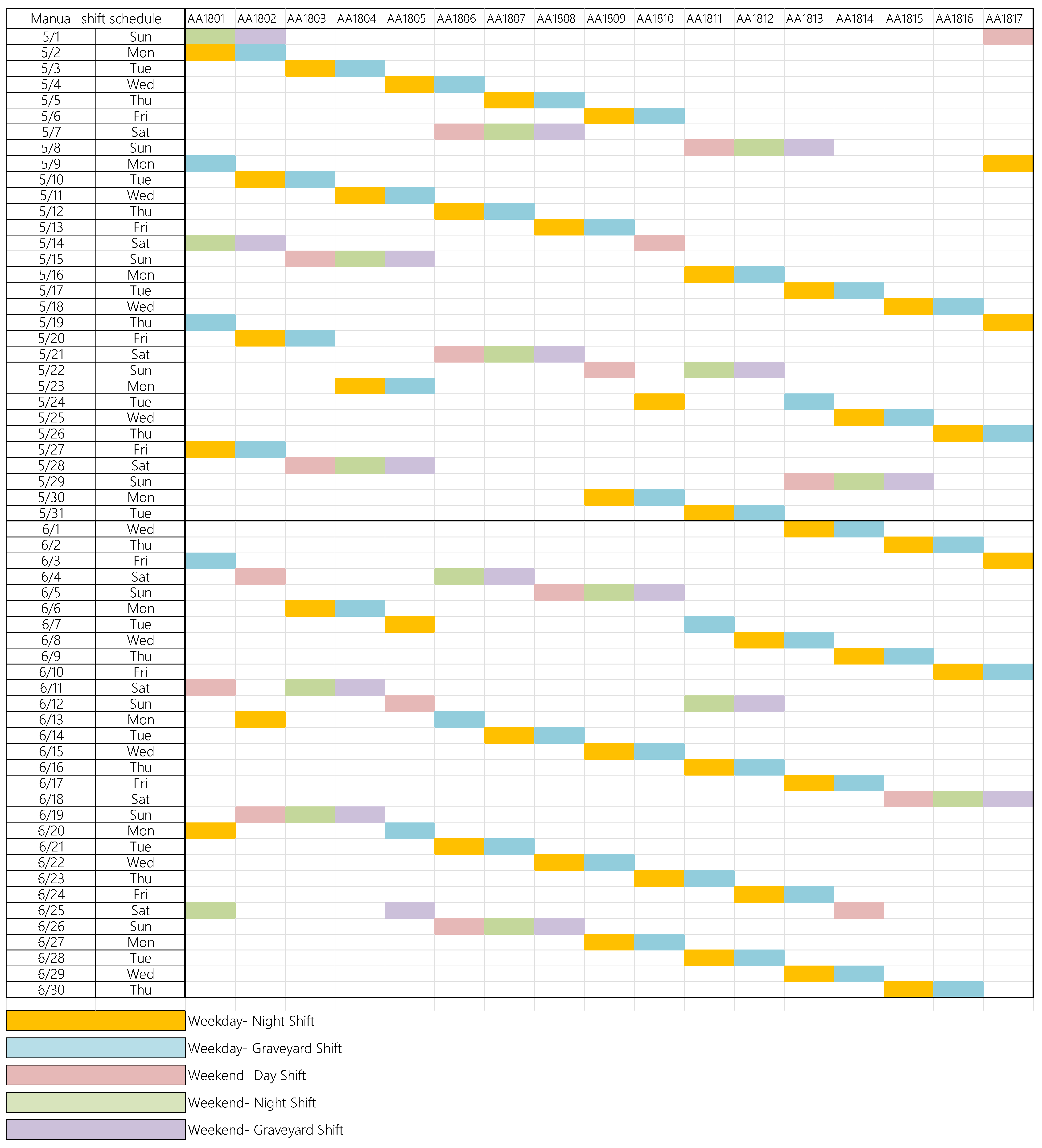
4.1. Real Case Example

To verify the practicality and correctness of this study model, the actual manpower and scheduling requirements of the production technology unit of Glorytek were used to plan the 2022/05 schedule for the engineering staff. We based the test on an integer programming model and proved that the optimized model in this study is more efficient and fairer than manual assignments.

The following are the basic parameters of the sample test:

X_ijk: Shift k of the i-th person on the j-th day. In this study, there were 17 people in the production technology, k is the shift (k = 1 day shift/k = 2 night shift/k = 3 graveyard shift), and the number of days of attendance in May was 31 days.

The study used Gurobi 9.0, Microsoft Windows 11, and an Intel(R) Core(TM) i5-1035G1 CPU at 1.00 GHz with 8 GB RAM. The output results are described below and compared with manual assignments for analyzing different plans.

4.1.1. Model Outcome

The minimum Z value reported by the Gurobi solution session is 5 days, and the elapsed computation time is 0.04 s.

4.1.2. Comparison of Results and Benefits of Automatic Scheduling and Manual Assignment

• Duty Allocation

Gurobi found the optimal solution: the maximum number of shifts in 2022/05 was five days. Compared with manual assignment’s maximum value of six days, automatic scheduling yielded a more balanced distribution of engineering staff. Additionally, with automatic optimal scheduling, every employee on call had the opportunity to be scheduled on weekends (

Table 1. Automatic l shift schedule_Real case example.

Auto shift schedule	AA1801	AA1802	AA1803	AA1804	AA1805	AA1806	AA1807	AA1808	AA1809	AA1810	AA1811	AA1812	AA1813	AA1814	AA1815	AA1816	AA1817
Weekday—Night Shift	2	1	4	1	2	2	0	2	1	0	2	0	2	0	0	2	1
Weekday—Graveyard Shift	1	1	0	2	0	2	2	0	1	3	1	2	1	2	2	1	1
Weekend—Day Shift	0	3	0	1	0	1	0	2	0	0	1	0	0	0	0	0	1
Weekend—Night Shift	0	0	1	0	2	0	0	0	1	1	0	1	0	2	0	1	0
Weekend—Graveyard Shift	2	0	0	1	0	0	2	0	1	0	0	1	1	0	1	0	0
On Call on Weekdays	3	2	4	3	2	4	2	2	2	3	3	2	3	2	2	3	2
On Call on Weekends	2	3	1	2	2	1	2	2	2	1	1	2	1	2	1	1	1
Total On Call Days	5	5	5	5	4	5	4	4	4	4	4	4	4	4	3	4	3

). However, manual assignment missed some employees, failing to schedule them on weekends (

Table 2. Manual shift schedule_Real case example.

Manual shift schedule	AA1801	AA1802	AA1803	AA1804	AA1805	AA1806	AA1807	AA1808	AA1809	AA1810	AA1811	AA1812	AA1813	AA1814	AA1815	AA1816	AA1817
Weekday—Night Shift	2	2	1	2	1	1	1	1	2	1	2	0	1	1	1	1	2
Weekday—Graveyard Shift	2	2	2	1	2	1	1	1	1	2	0	2	1	1	1	1	1
Weekend—Day Shift	0	0	2	0	0	2	0	0	1	1	1	0	1	0	0	0	1
Weekend—Night Shift	2	0	0	2	0	0	2	0	0	0	1	1	0	1	0	0	0
Weekend—Graveyard Shift	0	2	0	0	2	0	0	2	0	0	0	1	1	0	1	0	0
On Call on Weekdays	4	4	3	3	3	2	2	2	3	3	2	2	2	2	2	2	3
On Call on Weekends	2	2	2	2	2	2	2	2	1	1	2	2	2	1	1	0	1
Total On Call Days	6	6	5	5	5	4	4	4	4	4	4	4	4	3	3	2	4

). Therefore, automatic scheduling achieved a relatively balanced rotation in shift scheduling.

• Scheduling Efficiency

In terms of the efficiency of scheduling a monthly shift, the average time required for manual assignment in the past was four hours, from staff scheduling to completion of checking whether the shifts complied with the company’s regulations and then adjusting non-compliant shifts. In comparison, the scheduling model proposed in this study allows new monthly shifts to be completed in approximately ten minutes, from the adjustment of model parameters (confirming the number of personnel and duty days for the month) to the generation and checking of the shifts (automatic scheduling by computer takes only 0.04 s). This greatly improves the efficiency of staff scheduling and reduces the overall scheduling time by roughly 96%. As a result, systematic imports not only eliminate errors in personnel schedules but also help the administrative staff of each unit complete their rosters quickly.

• Achievement of Shift Restrictions

In Figure 2 and Figure 3, both of the models meet the requirements of the company’s shift regulations, namely, a 12 h interval between shifts and two non-consecutive weekends. The only difference is that manual assignment requires a post-scheduling constraint check and then micro-adjustment. However, automatic scheduling can be directly planned by adding restrictions, eliminating human error and the need for additional staff to check the conditions, which helps enhance efficiency.

• Fairness

In terms of computer software scheduling, the distribution of duty and duty frequency on weekdays and holidays is planned in an overall way by the system. It is acceptable that there may be a difference of one to two times due to the difference of 30 or 31 days per month. Compared with manual assignment, negligence on the part of the scheduler may result in more shifts for some employees or more shifts for them on weekends, thus causing junior officers to question the fairness of the scheduling. In contrast, software scheduling can be more balanced, and it can reduce the occurrence of unfair scheduling caused by human factors, consecutive shifts, or even two consecutive weekend shifts caused by human negligence. On the whole, automatic shift arrangement improves labor distribution and employee fairness.

• Rotation Flexibility

Automatic scheduling allows for more flexible adjustment. For example, when a new employee joins the team, to produce a new shift, only the personnel count parameter needs to be adjusted. In contrast, manual assignment requires four hours of rescheduling and inspection. Automatic scheduling can be extended or modified according to the company’s needs or employee preferences. Manual assignment, however, is less flexible and less comprehensive. Increasing the number of constraints on shift scheduling complicates scheduling and also increases the elapsed composition time and potentioal errors. Therefore, in terms of efficiency, fairness, and flexibility, automatic scheduling is indeed more favorable than manual assignment.

4.2. Large-Size Problem Scenarios

To verify whether the automatic scheduling system can work on a larger scale to minimize the value of Z, our study includes two additional scenarios to compare the outcomes of automatic and manual shift schedule assignments. The first scenario involves arranging schedules for two consecutive months, while the second scenario involves increasing the number of engineers from 17 to 36, with the updated restriction that each shift requires two engineers on call.

4.2.1. Schedule for Two Consecutive Months

All the restrictive conditions and objective functions are the same as those in the real case test sample. The only difference is arranging the schedule for May and June 2022 and then comparing the results.

4.2.2. Schedule for Increasing the Number of Engineers

The objective function is the same as that in the real case test sample, but two restriction conditions differ from the real case test sample.

X_ijk: Shift k of the i-th person on the j-th day. In this scenario, there are 36 people in the production technology department.

4.2.3. Model Outcome

Gurobi has solved both scenarios for the minimum Z value and met all restriction conditions.

To automatically arrange two consecutive months, both models in Figure 4 and Figure 5 meet the company’s shift regulations, which require a 12 h interval between shifts and two non-consecutive weekends. The minimum Z value of automatically arranging achieved is 9 days (

Table 3. Shift details for two consecutive months.

Auto shift schedule	AA1801	AA1802	AA1803	AA1804	AA1805	AA1806	AA1807	AA1808	AA1809	AA1810	AA1811	AA1812	AA1813	AA1814	AA1815	AA1816	AA1817
Weekday—Night Shift	3	4	2	3	2	5	2	1	1	6	1	2	4	1	2	5	0
Weekday—Graveyard Shift	2	3	2	4	2	1	4	4	3	0	2	4	2	3	4	1	3
Weekend—Day Shift	2	1	0	1	1	1	1	2	0	1	1	1	0	2	1	1	1
Weekend—Night Shift	0	1	3	0	1	2	2	1	3	0	1	0	1	1	1	0	0
Weekend—Graveyard Shift	2	0	1	1	2	0	0	0	1	0	2	1	1	1	0	2	3
On Call on Weekdays	5	7	4	7	4	6	6	5	4	6	3	6	6	4	6	6	3
On Call on Weekends	4	2	4	2	4	3	3	3	4	1	4	2	2	4	2	3	4
Total On Call Days	9	9	8	9	8	9	9	8	8	7	7	8	8	8	8	9	7

), compared to 10 days for manual arrangement (

Table 4. Shift details manually generated for two consecutive months.

Manual shift schedule	AA1801	AA1802	AA1803	AA1804	AA1805	AA1806	AA1807	AA1808	AA1809	AA1810	AA1811	AA1812	AA1813	AA1814	AA1815	AA1816	AA1817
Weekday—Night Shift	3	3	2	2	2	2	2	2	4	2	4	2	4	2	3	2	3
Weekday—Graveyard Shift	3	2	2	2	3	2	2	2	2	4	2	4	3	4	2	3	2
Weekend—Day Shift	1	2	2	0	1	3	0	1	1	1	1	0	1	1	1	0	1
Weekend—Night Shift	3	0	2	2	0	1	3	0	1	0	2	1	0	1	0	1	0
Weekend—Graveyard Shift	0	2	0	2	3	0	1	3	0	1	0	2	1	0	1	0	1
On Call on Weekdays	6	5	4	4	5	4	4	4	6	6	6	6	7	6	5	5	5
On Call on Weekends	4	4	4	4	4	4	4	4	2	2	3	3	2	2	2	1	2
Total On Call Days	10	9	8	8	9	8	8	8	8	8	9	9	9	8	7	6	7

). The computation time required for automatic arrangement was only 0.04 s.

In another scenario with a larger number of engineers, both models in Figure 6 and Figure 7 also meet the shift regulations. The objective function Z values were also satisfied, with the automatic arrangement system achieving a minimum Z value of 2 days (

Table 5. Shift details generated for a larger number of engineers.

Auto shift schedule	AA1801	AA1802	AA1803	AA1804	AA1805	AA1806	AA1807	AA1808	AA1809	AA1810	AA1811	AA1812	AA1813	AA1814	AA1815	AA1816	AA1817	AA1818	AA1819	AA1820	AA1821	AA1822	AA1823	AA1824	AA1825	AA1826	AA1827	AA1828	AA1829	AA1830	AA1831	AA1832	AA1833	AA1834	AA1835	AA1836
Weekday—Night Shift	0	1	1	0	1	1	2	0	1	0	1	0	1	1	2	0	0	1	0	0	0	1	0	0	1	0	1	0	0	2	0	0	2	1	1	0
Weekday—Graveyard Shift	0	0	0	0	1	0	0	2	0	1	1	1	0	1	0	1	1	0	0	2	1	0	2	1	0	1	1	2	1	0	0	1	0	0	0	1
Weekend—Day Shift	1	1	0	0	0	0	0	0	1	1	0	0	0	0	0	0	1	0	1	0	0	1	0	0	0	0	0	0	0	0	1	1	0	0	0	0
Weekend—Night Shift	1	0	1	0	0	0	0	0	0	0	0	1	1	0	0	1	0	1	0	0	1	0	0	1	0	0	0	0	0	0	0	0	0	1	0	0
Weekend—Graveyard Shift	0	0	0	2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	1	0	0	1	0	1	0	0	0	1	1
On Call on Weekdays	0	1	1	0	2	1	2	2	1	1	2	1	1	2	2	1	1	1	0	2	1	1	2	1	1	1	2	2	1	2	0	1	2	1	1	1
On Call on Weekends	2	1	1	2	0	0	0	0	1	1	0	1	1	0	0	1	1	1	2	0	1	1	0	1	1	1	0	0	1	0	2	1	0	1	1	1
Total On Call Days	2	2	2	2	2	1	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2

) and only one staff member attending work for 1 day. However, when compared to manual arrangement (

Table 6. Shift details manually generated for a larger number of engineers.

Manual shift schedule	AA1801	AA1802	AA1803	AA1804	AA1805	AA1806	AA1807	AA1808	AA1809	AA1810	AA1811	AA1812	AA1813	AA1814	AA1815	AA1816	AA1817	AA1818	AA1819	AA1820	AA1821	AA1822	AA1823	AA1824	AA1825	AA1826	AA1827	AA1828	AA1829	AA1830	AA1831	AA1832	AA1833	AA1834	AA1835	AA1836
Weekday—Night Shift	2	0	1	0	2	0	2	0	2	0	1	0	1	0	1	0	0	0	1	0	0	0	1	0	0	0	2	0	1	0	1	0	1	0	3	0
Weekday—Graveyard Shift	0	2	0	1	0	2	0	2	0	2	0	1	0	1	0	1	0	0	0	1	0	0	0	1	0	0	0	2	0	1	0	1	0	1	0	3
Weekend—Day Shift	0	0	0	0	0	0	0	0	1	0	0	0	1	0	0	0	1	1	0	0	0	1	1	1	0	0	0	0	0	1	0	1	0	0	0	0
Weekend—Night Shift	0	0	0	0	0	0	0	0	0	1	0	0	0	1	0	0	0	1	1	0	0	0	0	0	2	0	1	0	0	0	1	0	1	0	0	0
Weekend—Graveyard Shift	0	0	0	0	0	0	0	0	0	0	1	0	0	0	1	0	0	0	1	1	0	0	0	1	0	1	0	1	0	0	0	1	0	1	0	0
On Call on Weekdays	2	2	1	1	2	2	2	2	2	2	1	1	1	1	1	1	0	0	1	1	0	0	1	1	0	0	2	2	1	1	1	1	1	1	3	3
On Call on Weekends	0	0	0	0	0	0	0	0	1	1	1	0	1	1	1	0	1	2	2	1	0	1	1	2	2	1	1	1	0	1	1	2	1	1	0	0
Total On Call Days	2	2	1	1	2	2	2	2	3	3	2	1	2	2	2	1	1	2	3	2	0	1	2	3	2	1	3	3	1	2	2	3	2	2	3	3

), the minimum Z value is 3 days, with more than one staff member attending work for only 1 day.

Based on the results of both scenarios, it is evident that the automatic arrangement system can achieve a minimum Z value and provide a fairer shift schedule result because the number of shifts worked by engineers is relatively balanced (

Table 7. Results comparison.

	Results Comparison	Duty Allocation (Z Auto < Z Manual)	Scheduling Efficiency	Achievement of Shift Restrictions	Fairness (Minimum Number of Shifts Worked)		Rotation Flexibility
Case
Real Case Example		✓ Z Auto: 5 < Z Manual: 6	✓	✓	✓	Auto: 3 days Manual: 2 days	✓
Scenarios 1—Schedule for consecutive two months		✓ Z Auto: 9 < Z Manual: 10	✓	✓	✓	Auto: 7 days Manual: 6 days	✓
Scenarios 2—Schedule for consecutive two months		✓ Z Auto: 2 < Z Manual: 3	✓	✓	✓	Auto: 1 days (one staff) Manual: 1 days (eight staff)	✓

).

5. Conclusions and Recommendations

In this study, we developed an optimal model using integer programming. Our design can be automated to present the scheduling results for decision-makers to use it more flexibly and effectively in scheduling shifts for engineering staff. Compared with manual assignment, the model shaves 96% of the time to complete shift scheduling, and the maximum number of days of staff attendance (5 days) is less than that for manual assignment (6 days) while satisfying the shift limits stipulated by the company. Moreover, in our study, we also added two larger number problems to verify if our model is compatible with those scenarios. As a result, we demonstrated from Table 7 that even with a larger number of problems, our system can achieve fair outcomes and meet our minimum Z value. Therefore, overall, the scheduling model proposed in this study is more efficient and fairer. This model can be adjusted in the future by incorporating employee satisfaction feedback into the settings. Employee satisfaction surveys can be conducted according to the results of shift scheduling. In case of poor satisfaction levels, the model and parameters can be adjusted according to the employee’s preferred scheduling method. This study attempts to achieve balanced demand in shift arrangements for both employers and shift workers to facilitate the company’s talent retention. However, costs are not considered in this study.

For practical adoption of the research work, there are two issues which the company may need to take into consideration. The first is that they need to change the internal process of scheduling arrangements. If they decide to implement the automated scheduling system, then the system and schedule arrangement should be controlled by the IT department, instead of the administrative staff of each unit, because they may need to go through Python to change the parameters. Their internal process will be at the beginning of each month, and IT engineers are required to provide a preliminary shift schedule to each department for review based on their rotating shift needs, then engineer lead for final approval. Secondly, they need to consider investment in the off-the-shelf optimization solver for adopting the automated scheduling system.

A follow-up study could improve the reflection of operational conditions and decision-making needs by including real salary cost factors. For instance, future studies could account for the cost factor by considering Labor Standards Law regulations. According to this law, employers must pay overtime rates if employees work more than 8 h. Therefore, two factors can be considered in future studies: first, how to design the shift schedule interval, as different overtime hours lead to different overtime pay rates based on labor law regulations. Second, engineers’ job grades lead to different costs, which future studies can consider. Moreover, if fairness and cost are to be considered simultaneously, then a multi-objective programming approach should be considered. The current model minimizes the frequency of on-call attendance, but if cost is considered, then minimizing cost would be another objective. The end goal of the engineering schedule system, in this case, would be to strike a balance between fairness and low cost.