Blood Gas Parameters and Acid–Base Balance during Extracorporeal Lung Support with Oxygenators: Semi-Empirical Evaluation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Estimation of Oxygen and Carbon Dioxide Content from Their Partial Pressure
2.2. Estimation of Blood Gas Parameters Based on the Empirical Equations and Initial Conditions
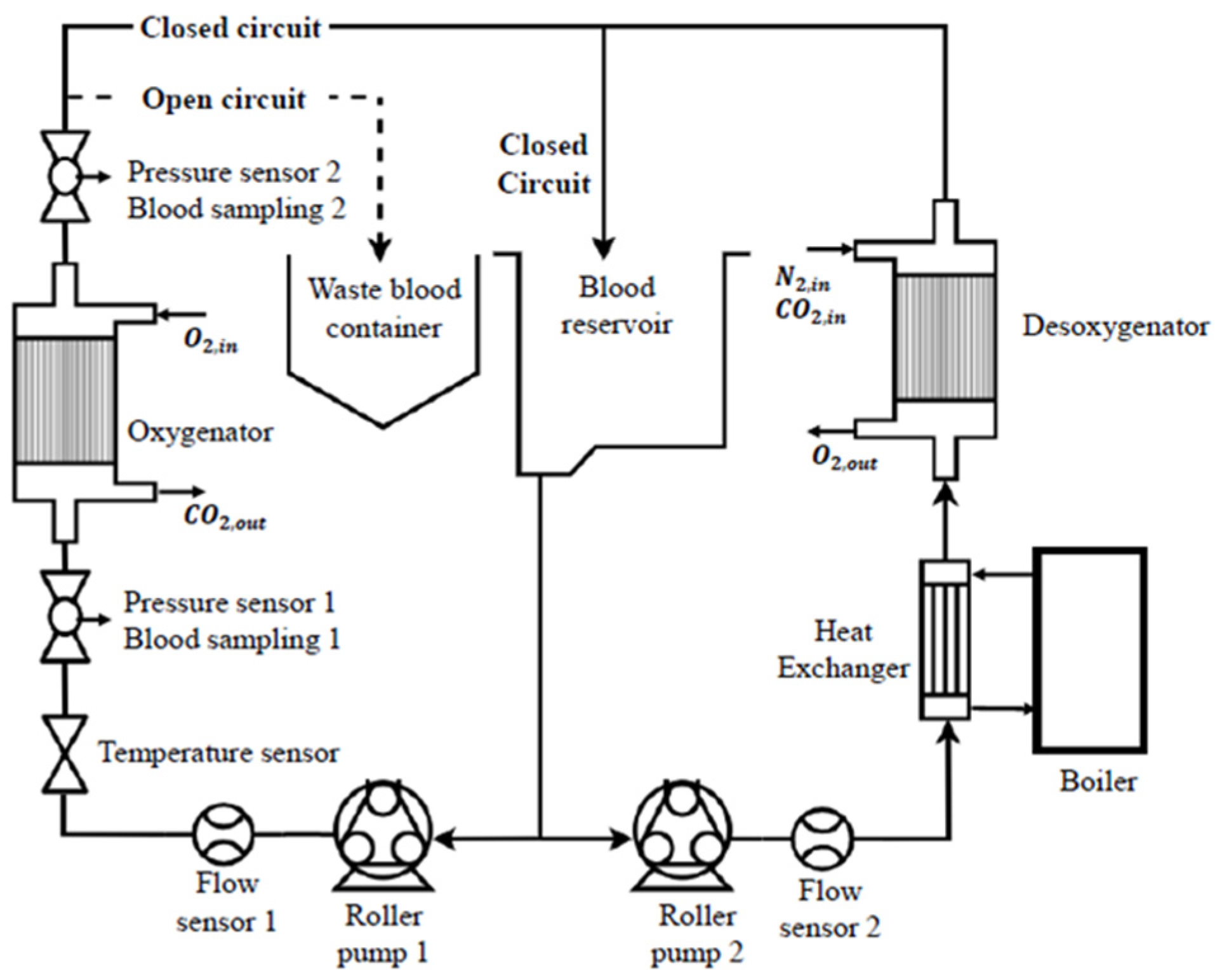
2.3. Experimental Circuit
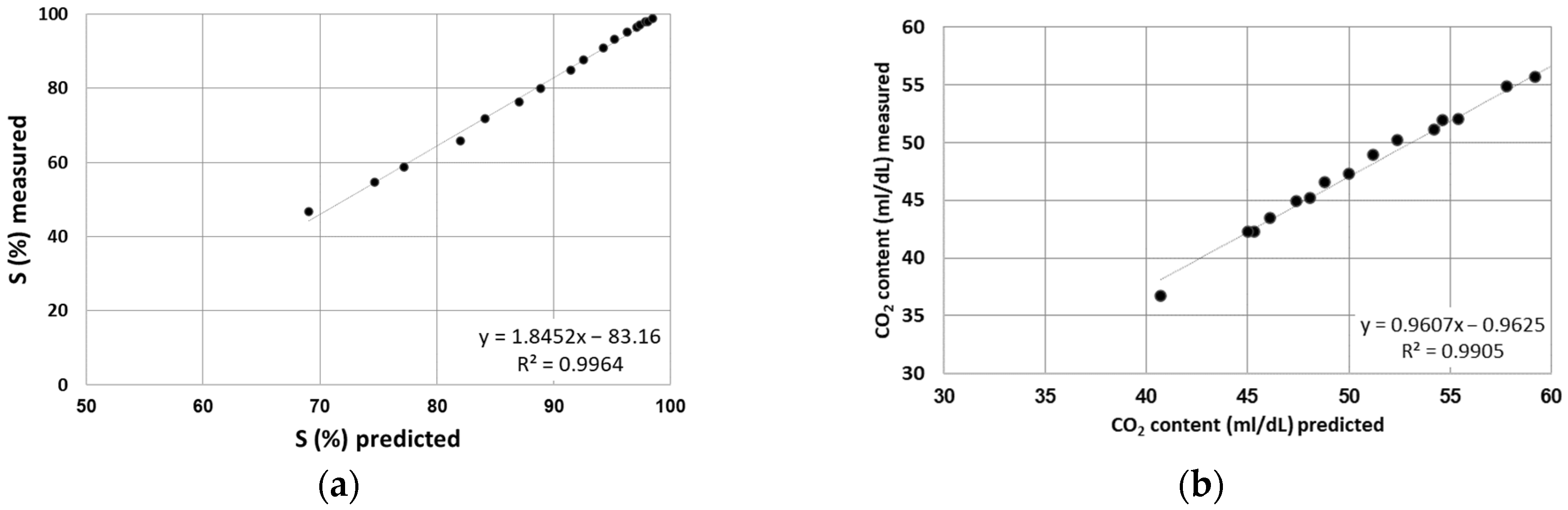
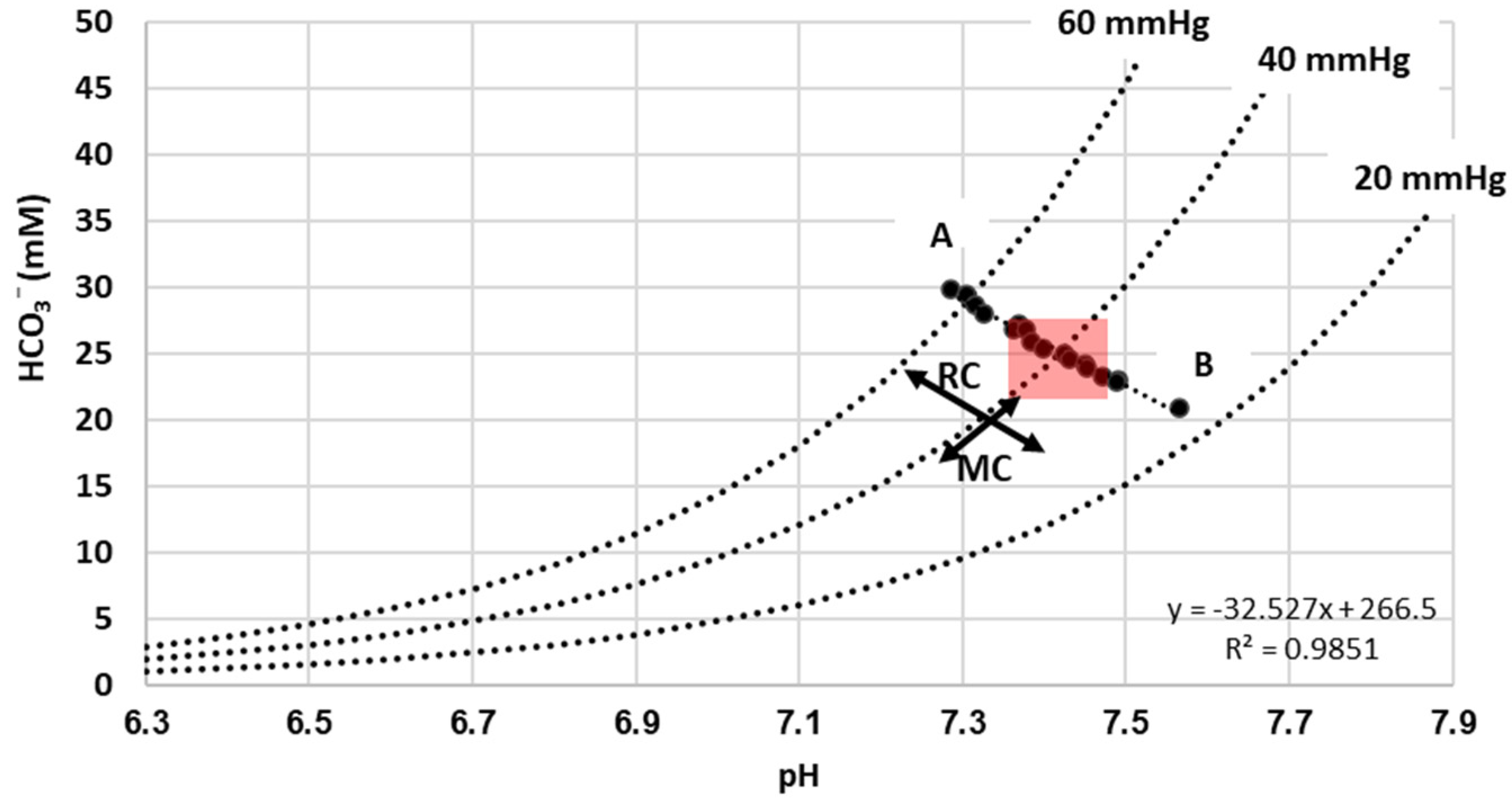
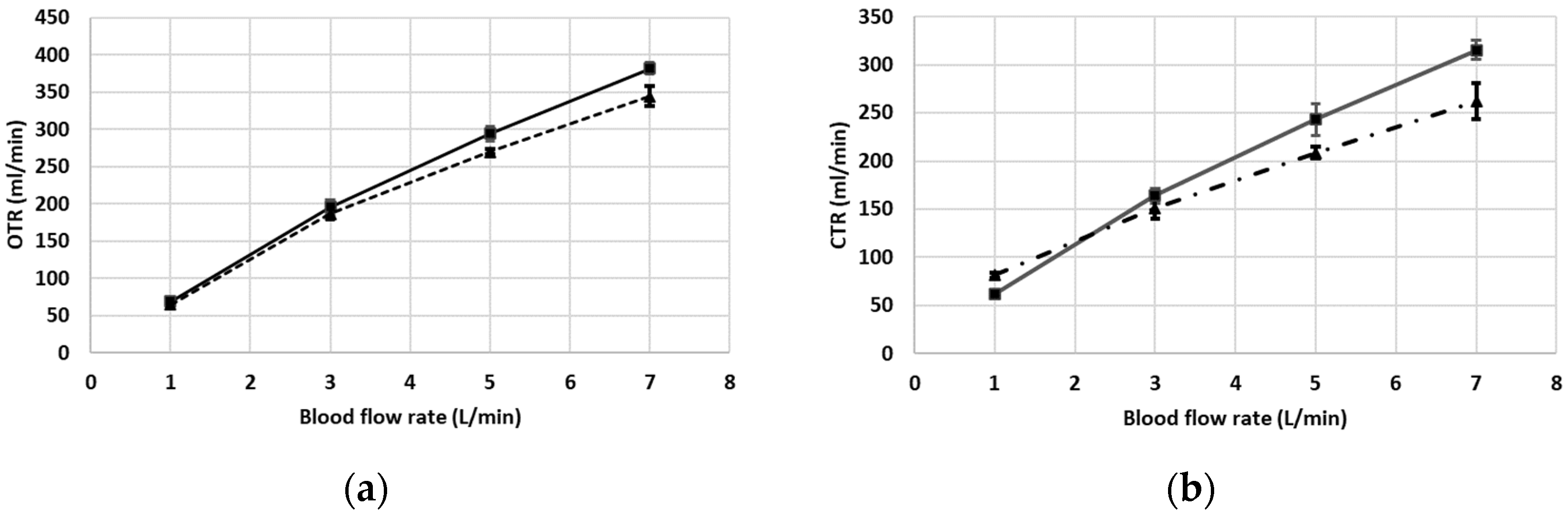
3. Results
Description of Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nosé, Y. Manual on Artificial Organs; The oxygenator; Mosby: St. Louis, MO, USA, 1973; Volume II. [Google Scholar]
- Iwahashi, H.; Yuri, K.; Nosé, Y. Development of the oxygenator: Past, present, and future. J. Artif. Organs 2004, 7, 111–120. [Google Scholar] [CrossRef] [PubMed]
- Mottaghy, K.; Bey, R.; Oedekoven, B.; Schaich-Lester, D.; Schmid-Schonbein, H. Extracorporeal CO2-removal: Pulmonary and extracorporeal equilibria in dogs and sheep. Eur. J. Appl. Physiol. Occup. Physiol. 1985, 54, 546–553. [Google Scholar] [CrossRef] [PubMed]
- Mottaghy, K.; Steyrer, K.; Freund, E.; Dringenberg, I. Eine standardisierte Methode zur Bestimmung der Gasaustauschkapazität der Oxygenatoren am Beispiel eines Bubble -und Liquid- Oxygenators. Biomed. Tech. 1978, 23, 126. [Google Scholar] [CrossRef]
- ISO 7199:2016; Cardiovascular Implants, and Artificial Organs—Blood-Gas Exchangers (Oxygenators). ISO: Geneva, Switzerland, 2016.
- Sander, R. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmos. Chem. Phys. 2015, 15, 4399–4981. [Google Scholar] [CrossRef]
- Fehler, J. Acid base physiology I: The bicarbonate buffer system and respiratory compensation. In Quantitative Human Physiology an Introduction, 2nd ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Kelman, G.R. Digital computer subroutine for the conversion of oxygen tension into saturation. J. Appl. Physiol. 1966, 21, 1375–1376. [Google Scholar] [CrossRef] [PubMed]
- Bain, B.J.; Lewis, M.; Bates, I. Basic haematological techniques. In Dacie and Lewis Practical Haematology, 10th ed.; Churchill Livingstone: London, UK, 2006; pp. 25–57. [Google Scholar]
- Douglas, A.R.; Jones, N.L.; Reed, J.W. Calculation of whole blood CO2 content. J. Appl. Physiol. 1988, 65, 473–477. [Google Scholar] [CrossRef] [PubMed]
- Austin, W.H.; Lacombe, E.; Rand, P.W.; Chatterjee, M. Solubility of carbon dioxide in serum from 15 to 38 C. J. Appl. Physiol. 1963, 18, 301–304. [Google Scholar] [CrossRef] [PubMed]
- Siggaard-Andersen, O.; Garby, L. The Bohr Effect and the Haldane Effect. Scand. J. Clin. Lab. Investig. 1973, 31, 1–8. [Google Scholar] [CrossRef] [PubMed]
| Blood Flow Rate (L/min) | Inlet | Outlet | ||
|---|---|---|---|---|
| pO2 (mmHg) | pCO2 (mmHg) | pO2 (mmHg) | pCO2 (mmHg) | |
| 1 | 36.05 (0.51) | 43.8 (0.67) | 518 (4.89) | 29.53 (0.17) |
| 3 | 35.83 (0.7) | 43.63 (0.83) | 367.73 (18.05) | 34.27 (0.09) |
| 5 | 37.7 (0.16) | 46.97 (0.42) | 210.33 (8.65) | 38.53 (0.33) |
| 7 | 37.81 (0.83) | 45.97 (0.33) | 122.04 (5.83) | 38.47 (0.24) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khadka, L.B.; Mouzakis, F.L.; Kashefi, A.; Hima, F.; Spillner, J.W.; Mottaghy, K. Blood Gas Parameters and Acid–Base Balance during Extracorporeal Lung Support with Oxygenators: Semi-Empirical Evaluation. Mathematics 2023, 11, 4088. https://doi.org/10.3390/math11194088
Khadka LB, Mouzakis FL, Kashefi A, Hima F, Spillner JW, Mottaghy K. Blood Gas Parameters and Acid–Base Balance during Extracorporeal Lung Support with Oxygenators: Semi-Empirical Evaluation. Mathematics. 2023; 11(19):4088. https://doi.org/10.3390/math11194088
Chicago/Turabian StyleKhadka, Lal Babu, Foivos Leonidas Mouzakis, Ali Kashefi, Flutura Hima, Jan Wilhelm Spillner, and Khosrow Mottaghy. 2023. "Blood Gas Parameters and Acid–Base Balance during Extracorporeal Lung Support with Oxygenators: Semi-Empirical Evaluation" Mathematics 11, no. 19: 4088. https://doi.org/10.3390/math11194088
APA StyleKhadka, L. B., Mouzakis, F. L., Kashefi, A., Hima, F., Spillner, J. W., & Mottaghy, K. (2023). Blood Gas Parameters and Acid–Base Balance during Extracorporeal Lung Support with Oxygenators: Semi-Empirical Evaluation. Mathematics, 11(19), 4088. https://doi.org/10.3390/math11194088






