Numerical Modeling of Elastic Wave Propagation in Porous Soils with Vertically Inhomogeneous Fluid Contents Due to Infiltration

Abstract

The structure of soils is often heterogeneous with layered strata having distinct permeabilities. An advanced mathematical and numerical coupled model of elastic wave propagation in poroelastic multi-layered soils subjected to subsoil water infiltration is proposed in this study. The coupled model was based on the introduction of an inhomogeneous functionally graded fluid-saturation of the considered soil depending on the infiltration time, which was evaluated employing Richards’ equation. The time-harmonic solution was formulated in terms of the Fourier transform of Green’s matrix and the surface load that excites the vibration. The convergence and efficiency of the proposed approach are demonstrated. An example of dispersion curves for partially saturated porous strata made of loam, sand, and rock at different infiltration times is provided, and it is shown that the characteristics of the surface acoustic waves change with time, which can be further used for inverse problems’ solution.

1. Introduction

Controlling fluid transport within subsurface porous media is crucial to many environmental and industrial studies from agriculture to geophysics. Therefore, efficient mathematical and computer models accurately simulating their behavior are required. Complex engineering problems currently can be solved using robust numerical methods such as the finite element method, as well as the spectral element method, the boundary element method, the finite volume method, and meshless methods. Various coupling procedures (hybrid and coupled numerical methods) have been proposed incorporating different numerical methods in order to take advantage of their respective benefits [1,2,3].

The structure of real porous media is often heterogeneous with layered strata with distinct permeabilities causing uneven flow partitioning across the strata. Developing more-advanced interpretation tools is hindered by the lack of open-source and semi-analytical numerical techniques for simulating partially saturated porous media [4]. Thus, the aim of this study was to develop an advanced mathematical and numerical coupled model of elastic wave propagation in poroelastic multi-layered soil subjected to subsoil water infiltration.

Sufficient soil water content, which is a key requirement for good agricultural yields, depends on numerous factors. First of all, there are the temperature and humidity of the environment leading either to the evaporation of moisture from the soil or, vice versa, contributing to the saturation of the soil with water [5,6]. The soil hydrology is also a significant factor, which depends on the soil texture and structure [7,8].

The water infiltration process in variably saturated soil pores as described by Richards’ equation demonstrates the complex nonlinear distributions of porous water content with soil depth and is dependent on the material parameters of the composite (solid and complex fluid as a combination of air and water), initial water saturation, and time of infiltration [9]. Soil water dynamics are simulated using various numerical methods from the finite element method [10,11,12] and Bayesian inverse modeling using Markov chain Monte Carlo [13,14] to machine learning-based methods. For instance, Yang and Mei [15], Jana et al. [16] employed physics-informed neural-network-based numerical approaches for studying soil water vertical infiltration. Other approaches include using pore-scale simulations with X-ray tomography [17] and continuum approaches using volumetric averaging [18]. A comparison of some different traditionally used models for soil water infiltration such as the Philip model, Kostiakov model, Mezencev model, USDA-NRCS model, and Horton model can be found in [19]. The latest techniques in field estimation of soil water infiltration include the use of electrical resistivity tomography (ERT) and ground-penetrating radar (GPR) [20].

The theoretical study of elastic wave propagation in fluid-saturated porous media is based on the boundary-value problem for Biot’s equation [21,22,23]. To solve the wave problems for poroelastic structures with complex irregular boundaries and obstacles, the following numerical methods have been developed: the boundary element method (BEM) [24,25], the finite element method [26,27,28], and its modifications as the spectral element method [29,30], extended finite elements [31,32], or particle finite elements [33,34], as well as meshless methods [35,36]. Waves in poroelastic structures with traditional regular boundaries are usually investigated by analytical and semi-analytical methods. The description of such methods to analyze waves excited in poroelastic isotropic structures with plane-parallel boundaries such as half-spaces or layered spaces and the analysis of guided waves in the layered media can be found in [37,38,39,40,41,42]. The matrix iteration methods for modeling waves in multilayered porous media were developed in [43,44]. The wave propagation in functionally graded poroelastic fluid-saturated media have also been actively studying recently [45,46,47,48] by semi-analytical approaches. Dudarev et al. [45] also developed and studied the method for the reconstruction of Biot’s modulus as spatial function using elastic waves measured on the surface of a poroelastic functionally graded cylinder. The analytical solution of a multi-layered structure satisfies the conditions at infinity and allows studying guided waves, as well as can be used as a basis for boundary integral equation methods and the BEM for layered structures with irregularities [49,50,51].

Chen et al. [52] investigated the correlation between soil moisture changes and deformations at slope surfaces by means of elastic wave propagation in soils. Their analysis of longitudinal and shear wave velocities in homogeneous media showed that the elastic wave velocity continuously decreases in response to moisture content and deformation. Chen et al. [53] estimated the elastic wave velocity of an unsaturated soil slope, and they showed that the effects of rainfall duration/initial water content, density, slope angle, and surface layer thickness on the decrease rate of the normalized wave velocity with the volumetric water content and the tilt angle are relatively small in homogeneous media. Solazzi et al. [54] assumed a one-dimensional unconsolidated porous half-space under steady-state saturation conditions and considered the influence of the capillary suction effects on the longitudinal and shear wave dispersion characteristics for different water table depths and overlying soil textures. Recently, Deng et al. [55] presented Biot’s model with two fluid phases and also studied body waves in vertically inhomogeneous saturated porous media resulting from porous water infiltration. To the authors’ knowledge, the surface wave propagation problem was not considered taking into account the infiltration effect.

Therefore, we propose here a semi-analytical two-stage numerical method for modeling wave propagation in multi-layered porous media with properties varying across the strata and taking into account the infiltration effect. In the first stage, the depth and time-dependent saturation were evaluated employing Richards’ equation. Then, an inhomogeneous functionally graded fluid saturation was transferred into Biot’s equations, which were solved via the semi-analytical boundary integral equation method at various infiltration times. The algorithm for Green’s matrix of multi-layered porous solids [41] was improved in this investigation in terms of numerically stable matrix iterations for the considered vertically stratified (functionally graded) medium [56]. The convergence and efficiency of the method are demonstrated. Examples of dispersion curves for partially saturated porous strata made of loam, sand, and bedrock at different infiltration times are provided, and it is shown that the characteristics of surface acoustic waves change with time, which can be further used for inverse problems’ solution. The model also assists in the investigation of the influence of infiltration time on wave propagation in porous media.

2. Mathematical Models

2.1. Elastic Waves in a Layered Poroelastic Soil

The wave propagation generated by the surface load of an inhomogeneous soil modeled by a three-layered half-space was considered (Figure 1). Further, we used the designation for a layer as $\mathbb{L}\left(\mathcal{M},z_1,z_2\right)$, where $\mathcal{M}$ is the set of material properties and $z_1$ and $z_2$ are the z-coordinates in the Cartesian coordinate system $(x,y,z)$ (or $(x_1,x_2,x_3)$ as the same) of the planes bounding the layer. The layered half-space $\mathbb{HS}={\mathbb{L}}_{loam}\cup {\mathbb{L}}_{sand}\cup {\mathbb{L}}_{rock}$ consists of two poroelastic layers ${\mathbb{L}}_{loam}=\mathbb{L}({\mathcal{M}}_{loam},0,z_1)$, ${\mathbb{L}}_{sand}=\mathbb{L}({\mathcal{M}}_{sand},z_1,z_2)$ with thicknesses $a_1$ and $a_2$, $z_1=-a_1$ and $z_2=-a_1-a_2$, consequently, and the bottom pure elastic homogeneous half-space ${\mathbb{L}}_{rock}=\mathbb{L}({\mathcal{M}}_{rock},z_2,-\infty )$. The first poroelastic layer ${\mathbb{L}}_{loam}$ models the loam with vertically inhomogeneous fluid contents due to water infiltration and air saturation of the vacated pore space. The infiltration is a dynamical process; however, its speed is much less than the speed of the elastic waves; therefore, the properties of the first layer are considered to be fixed during the measurements of elastic waves.

The steady-state harmonic waves with frequency $\omega$ were considered further ($u(t)=u(\omega )exp(-\mathrm{i}\omega t)$). The displacements in a poroelastic medium according to Biot [21] are expressed in terms of two complex-valued displacement vectors ${\mathit{u}}_s$ and ${\mathit{u}}_f$ in the solid skeleton and porous fluid, respectively. The displacements are governed by Biot’s equations in the frequency domain:

$$\begin{array}{c}\nabla [(\lambda +\mu )\nabla ·{\mathit{u}}_s+Q\nabla ·{\mathit{u}}_f]+\mu {\nabla }^2{\mathit{u}}_s+{\widehat{\rho }}_{11}{\omega }^2{\mathit{u}}_s+{\widehat{\rho }}_{12}{\omega }^2{\mathit{u}}_f=0,\hfill \\ \nabla [Q\nabla ·{\mathit{u}}_s+R\nabla ·{\mathit{u}}_f]+{\widehat{\rho }}_{12}{\omega }^2{\mathit{u}}_s+{\widehat{\rho }}_{22}{\omega }^2{\mathit{u}}_f=0.\hfill \end{array}$$

(1)

The complex amplitudes of the traction vector ${\mathit{\tau }}_n$ at a surface element with normal $\mathit{n}$ are given as

$$\begin{array}{c}{\mathit{\tau }}_n={\mathit{\tau }}_{s;n}-\varphi p_f\mathit{n}\hfill \\ {\mathit{\tau }}_{s;n}=\left[\lambda \nabla ·{\mathbf{u}}_s+Q\nabla ·{\mathbf{u}}_f\right]\mathit{n}+2\mu \nabla {\mathit{u}}_s·\mathit{n}+\mu (\mathit{n}\times \nabla \times {\mathit{u}}_s)\hfill \\ p_f=-\frac{1}{\varphi }\left[Q\nabla ·{\mathit{u}}_s+R\nabla ·{\mathit{u}}_f\right].\hfill \end{array}$$

(2)

Here, ${\mathit{\tau }}_{s;n}$ is the traction (stress) of the solid skeleton, $p_f$ is the pore fluid pressure, ∇ is the nabla operator, “·” and “×” are operators of the dot and cross products, respectively, and $\lambda ,\mu ,Q,R$ are Biot’s poroelastic constants. The coefficients ${\widehat{\rho }}_{mn}={\rho }_{mn}-\mathrm{i}{(-1)}^{m+n}b/\omega$ are expressed in terms of the effective mass densities ${\rho }_{11},{\rho }_{22}$, and ${\rho }_{12}={\rho }_{21}$ and the dissipation factor b. The relative displacements of the fluid as $\mathit{w}=\varphi ({\mathit{u}}_s-{\mathit{u}}_f)$ needs further for analysis.

In practice, the parameters of poroelastic materials (${\mathcal{M}}_{loam}$ and ${\mathcal{M}}_{sand}$) are presented by the specific porosity $\varphi$, shear modulus $\mu$, the bulk modulus of dried porous material $K_d$, the bulk modulus $K_s$, $K_f$, and the mass densities ${\rho }_s$, ${\rho }_f$ of the solid skeleton and porous fluid, consequently, as well as the tortuosity parameter ${\alpha }_s$, the intrinsic permeability ${\kappa }_s$, and the dynamic viscosity of the fluid ${\eta }_f$. The parameters of Equations (1) and (2) are expressed as

$$\begin{array}{c}Q=\varphi (1-\varphi -K_d/K_s)\Lambda ,R={\varphi }^2\Lambda ,\hfill \\ \lambda =K_d+Q^2/R-2/3\mu ,\Lambda =K_s/(1-\varphi -K_d/K_s+\varphi K_s/K_f);\hfill \\ {\rho }_{12}=\varphi {\rho }_f(1-{\alpha }_s),{\rho }_{11}={\rho }_s(1-\varphi )+{\rho }_{12},\hfill \\ {\rho }_{22}={\rho }_f\varphi -{\rho }_{12},b={\eta }_f{\varphi }^2/{\kappa }_s.\hfill \end{array}$$

(3)

The pore fluid in the top layer ${\mathbb{L}}_{loam}$ is vertically functionally graded due to infiltration, which leads to homogeneous water saturation $\varsigma (z)$. Let ${\rho }_{\mathtt{w}},K_{\mathtt{w}},{\eta }_{\mathtt{w}}$ and ${\rho }_{\mathtt{a}},K_{\mathtt{a}},{\eta }_{\mathtt{a}}$ be the mass densities, the bulk modulus, and the viscosities of water and air, respectively. One of the conventional approaches is to consider a homogenized fluid. Applying the mixing theory to water and air, the effective bulk modulus $K_f$, mass density ${\rho }_f$, and viscosity ${\eta }_f$ are taken as [23,57]

$${\displaystyle \frac{1}{K_f}}={\displaystyle \frac{\varsigma }{K_{\mathtt{w}}}}+{\displaystyle \frac{1-\varsigma }{K_{\mathtt{a}}}},{\rho }_f={\rho }_{\mathtt{w}}\varsigma +{\rho }_{\mathtt{a}}(1-\varsigma ),{\eta }_f={\eta }_{\mathtt{w}}^{\varsigma }{\eta }_{\mathtt{a}}^{1-\varsigma },$$

(4)

The displacements ${\mathit{u}}_s$ and tensions ${\mathit{\tau }}_n$ in the pure elastic bottom half-space obey the Lame equations and Hooke’s law as follows:

$$\begin{array}{c}\nabla [(\lambda +\mu )\nabla ·{\mathit{u}}_s]+\mu {\nabla }^2{\mathit{u}}_s+{\rho }_s{\omega }^2{\mathit{u}}_s=0,\hfill \\ {\mathit{\tau }}_n=\lambda \nabla ·{\mathit{u}}_s\mathbf{n}+2\mu \nabla {\mathit{u}}_s·\mathit{n}+\mu (\mathit{n}\times \nabla \times {\mathbf{u}}_s)\hfill \end{array}$$

(5)

The excitation of elastic waves is caused by the surface load given by axisymmetric traction $\mathit{q}(x,y)=\mathit{q}(r)$, $r^2=x^2+y^2$, at some finite circular region $\Omega$ as

$${\mathit{\tau }}_3=\mathit{q},p_f=q_3,\mathrm{at}z=0,(x,y)\in \Omega .$$

(6)

The displacement ${\mathbf{u}}_s$ and tension ${\mathit{\tau }}_3$ vectors are continuous at the interfaces between layers. The continuity of the normal component of the relative phase displacements $w_3$ and porous fluid pressure $p_f$ are additionally imposed at the porous–porous interface as

$$\left[{\mathit{u}}_s\right]=0,\left[{\mathit{\tau }}_3\right]=0,\left[w_3\right]=0,\left[p_f\right]=0\mathrm{at}z=z_1.$$

(7)

At the interface between the porous layer and elastic half-space, the relative phase displacements $w_3$ is eliminated:

$$\left[{\mathit{u}}_s\right]=0,\left[{\mathit{\tau }}_3\right]=0,\left[w_3\right]=0\mathrm{at}z=z_2.$$

(8)

Describing correctly waves at infinity, such radiation conditions as the limiting absorption principle [58] were used.

2.2. Mathematical Model of Water Infiltration into Porous Soil

The water flow in porous media is governed by Richards’ equation:

$$\frac{\partial \theta }{\partial t}=\frac{\partial }{\partial x_i}\left[\mathcal{K}\left({\mathcal{K}}_{ij}^A\frac{\partial h}{\partial x_j}+{\mathcal{K}}_{iz}^A\right)\right]-\mathcal{S}$$

(9)

written in terms of the volumetric water content $\theta$, the pressure head h, and the unsaturated hydraulic conductivity:

$$\mathcal{K}(h,x_1,x_2,x_3)={\mathcal{K}}_s(x_1,x_2,x_3){\mathcal{K}}_r(h,x_1,x_2,x_3)$$

(10)

which is the function of the saturated hydraulic conductivity ${\mathcal{K}}_s$ and the relative hydraulic conductivity ${\mathcal{K}}_r$. Here, Cartesian coordinates $x_i$$(i=1,2,3)$ were considered; as before, t is the time of water infiltration, ${\mathcal{K}}_{}^A$ is an anisotropy tensor, and $\mathcal{S}$ is a sink term.

The water content $\theta (h)$ and hydraulic conductivity $\mathcal{K}(h)$ are unsaturated soil hydraulic properties that are highly non-linear functions of the pressure head h. Different analytical models exist to compute these quantities. However, the formulation of Van Genuchten [9] offers a reasonable balance between accuracy and model complexity. Hence, this formulation is used in this study. According to the van Genuchten model, water content and hydraulic conductivity are expressed in terms of the residual water content ${\theta }_r$, the saturation water content ${\theta }_s$, the inverse of the air-entry pressure ${\alpha }_h$, the pore-size distribution index $\mathfrak{n}$, and the effective water content:

$${\mathcal{S}}_e=\frac{\theta -{\theta }_r}{{\theta }_s-{\theta }_r}$$

(11)

The pore connectivity parameter l is as follows:

$$\theta (h)=\left\{\begin{array}{cc}\hfill {\theta }_r+{\displaystyle \frac{{\theta }_s-{\theta }_r}{{\left[1+|{\alpha }_h{h|}^{\mathfrak{n}}\right]}^{\mathfrak{m}}}},& \hfill h<0\\ \hfill {\theta }_s,& \hfill h\ge 0\end{array}\right.$$

(12)

$$\mathcal{K}(h)={\mathcal{K}}_s{\mathcal{S}}_e^l{\left[1-{\left(1-{\mathcal{S}}_e^{\frac{1}{\mathfrak{m}}}\right)}^{\mathfrak{m}}\right]}^2$$

(13)

Here,

$$\mathfrak{m}=1-\frac{1}{\mathfrak{n}},\mathfrak{n}>1.$$

The parameters $\alpha$ and $\mathfrak{n}$ are considered empirical shape-fitting parameters, and l has been estimated to be equal to 0.5 on average for a wide range of soils.

2.3. Numerical Solution of Richards’ Equation

Richards’ Equation (9) does not have an analytical solution and is limited to numerical solutions only. In this study, we used the commercially available HYDRUS-3D software package from PC-Progress [59]. HYDRUS uses Galerkin-type linear finite element schemes to numerically solve the water flow equation. The solution to matrix equations derived from the discretization of the governing equations varies based on the problem’s magnitude. For banded matrices, Gaussian elimination is employed, while symmetric matrices utilize the conjugate gradient method, and asymmetric matrices use the ORTHOMIN method. The software can examine the movement of water and solutes in porous media that are unsaturated, partially saturated, or fully saturated. Flow and transport can take place in the vertical or horizontal plane, a three-dimensional area with radial symmetry around the vertical axis, or a fully three-dimensional space. HYDRUS can handle water flow computation for domains having boundaries with a prescribed head and flux, boundaries influenced by atmospheric conditions, free drainage boundary conditions, or more-intricate combinations.

In this study, the soil domain was discretized with three different boundary conditions (BCs). The top surface was assigned an “Atmospheric” BC, while the bottom layer was assigned a “Free Drainage” BC. The side walls of the domain were assigned a “No Flow” BC, resulting in a flow regime that is purely vertical. The first two BCs are described below.

2.3.1. Atmospheric BC

The Atmospheric BC is a system-dependent BC that exists at the interface between the air and the soil that is exposed to atmospheric conditions. The fluid flux at this boundary is driven by external conditions (such as precipitation) and also due to existing soil water content conditions that can be time-dependent. The application of this BC imposes that the numerical solution of (9) is obtained by limiting the absolute water flux in a manner that satisfies the following two conditions:

$$|\mathcal{K}({\mathcal{K}}_{ij}^A{\displaystyle \frac{\partial h}{\partial x_j}}+{\mathcal{K}}_{iz}^A)n_i|\le E$$

(14)

and

$$h_a\le h\le h_s$$

(15)

where $n_i$ are components of the outward unit vector normal to the boundary, E is the maximum potential flux rate (infiltration or evaporation), h is the pressure head at the soil surface, $h_a$ is the minimum allowed pressure head determined from the equilibrium between the soil water and the atmospheric water vapor pressure, and $h_s$ is the maximum allowed pressure head, which is generally the condition of complete saturation where the value can be set to zero.

This BC allows for the direction of the water flux at the interface to switch directions depending on the prevailing internal and external conditions. For example, the application of water (by precipitation or irrigation) at the boundary to the soil domain with water content below saturation results in the infiltration (or the downward movement) of the water. On the other hand, the introduction of the effect of temperature allows for the evaporation of water through the boundary (upward movement). In this study, the Atmospheric BC was assigned to ensure the free flow of water through the domain with no upward suction due to the creation of vacuum pockets.

2.3.2. Free Drainage BC

This is a gradient type BC of the form

$$\left({\mathcal{K}}_{ij}^A{\displaystyle \frac{\partial h}{\partial x_j}}+{\mathcal{K}}_{iz}^A\right)n_i=f(x,y,z,t)$$

(16)

Here, HYDRUS implements a unit vertical hydraulic gradient that mimics free water flow through the boundary. Such scenarios are very commonly encountered in field studies where the soil profile is deep and the water table is much below the study domain.

3. Simulation of Wave Propagation in Functionally Graded Poroelastic Media

3.1. Wavefield Representation in a Homogeneous Poroelastic Layer

Let us consider a poroelastic layer $\mathbb{L}({\mathcal{M}}_p,z_1,z_2)$, where ${\mathcal{M}}_p$ is a set of poroelastic parameters. The solution of Biot’s Equation (1) ${\mathit{u}}_s$ and ${\mathit{u}}_f$ in a homogeneous media can be determined in terms of two scalar potentials ${\phi }_1$, ${\phi }_2$ and the curl potential $\mathit{\psi }$ as follows:

$$\begin{array}{c}{\mathit{u}}_s=\nabla {\phi }_1+{\eta }_2\nabla {\phi }_2+\nabla \times \mathit{\psi },\hfill \\ {\mathit{u}}_f={\eta }_1\nabla {\phi }_1+\nabla {\phi }_2+{\eta }_3\nabla \times \mathit{\psi }.\hfill \end{array}$$

(17)

Here, the potentials ${\phi }_k$ ($k=1,2$) and $\mathit{\psi }=\{\partial {\psi }_1/\partial y,-\partial {\psi }_1/\partial x,{\psi }_2\}$ obey the Helmholtz equations:

$$\begin{array}{ccc}\hfill {\nabla }^2{\phi }_k+{\varkappa }_{\mathrm{p}k}^2{\phi }_k& =& 0,{\varkappa }_{\mathrm{p}k}=\omega /v_{\mathrm{p}k};k=1,2\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill {\nabla }^2{\mathit{\psi }}_j+{\varkappa }_{\mathrm{s}}^2{\mathit{\psi }}_j& =& 0,{\varkappa }_s=\omega /v_{\mathrm{s}};j=1,2\hfill \end{array}$$

(19)

The fast and slow longitudinal wave velocities $v_{\mathrm{p}i}$, coefficients $m_i$, and shear velocity $v_{\mathrm{s}}$ in decomposition (17) are determined by the formulas:

$$\begin{array}{c}{v}_{\mathrm{p}k}^2=\left[b-{(-1)}^k\sqrt{b^2-4\Delta C\Delta B}\right]/(2\Delta B),v_{\mathrm{s}}^2=\mu {\widehat{\rho }}_{22}/\Delta B;\hfill \\ {\eta }_1=-(P-v_{p1}^2{\widehat{\rho }}_{11})/(Q-v_{\mathrm{p}1}^2{\widehat{\rho }}_{12}),{\eta }_2=-(R-v_{\mathrm{p}2}^2{\widehat{\rho }}_{22})/(Q-v_{p2}^2{\widehat{\rho }}_{12}),\hfill \\ b=R{\widehat{\rho }}_{11}-2Q{\widehat{\rho }}_{12}+P{\widehat{\rho }}_{22},\Delta B={\widehat{\rho }}_{11}{\widehat{\rho }}_{22}-{\widehat{\rho }}_{12}^2,\hfill \\ \Delta C=PR-Q^2,P=\lambda +2\mu \hfill \end{array}$$

(20)

and ${\eta }_3=-{\displaystyle \frac{{\widehat{\rho }}_{12}}{{\widehat{\rho }}_{22}}}$ in Equation (17).

Applying the Fourier transform,

$$\begin{array}{c}{\displaystyle G({\alpha }_1,{\alpha }_2)={\mathfrak{F}}_{x,y}\left[g\right]=\underset{-\infty }{\overset{\infty }{\int \int }}g(x,y){\mathrm{e}}^{\mathrm{i}({\alpha }_{1}x+{\alpha }_{2}y)}\mathrm{d}x\mathrm{d}y,}\hfill \end{array}$$

with respect to coordinates $x_1$ and $x_2$ allows us to write the potentials in terms of relations (20) as the general solutions of Equations (18) and (19):

$$\begin{array}{c}{\Phi }_k(\alpha ,z)={\mathfrak{F}}_{x,y}\left[{\phi }_k\right]=t_k^{+}{\mathrm{e}}^{-{\sigma }_{\mathrm{p}k}(z_1-z)}+t_k^{-}{\mathrm{e}}^{-{\sigma }_{\mathrm{p}k}(z-z_2)},k=1,2\hfill \\ {\Psi }_m(\alpha ,z)={\mathfrak{F}}_{x,y}\left[{\psi }_m\right]=t_{2+m}^{+}{\mathrm{e}}^{-{\sigma }_{\mathrm{s}}(z_1-z)}+t_{2+m}^{-}{\mathrm{e}}^{-{\sigma }_{\mathrm{s}}(z-z_2)},m=1,2.\hfill \end{array}$$

(21)

where

$$\alpha =\sqrt{{\alpha }_1^2+{\alpha }_2^2},{\sigma }_{\mathrm{p}k}=\sqrt{{\alpha }^2-{\varkappa }_{\mathrm{p}k}^2},(k=1,2),{\sigma }_{\mathrm{s}}=\sqrt{{\alpha }^2-{\varkappa }_s^2}.$$

The branches of the square roots for $\sigma$ were chosen so that

$$\mathrm{Re}\sigma ⩾0,\mathrm{Im}\sigma ⩽0$$

for real $\alpha$ in accordance with the limiting absorption principle [60]. Meanwhile, the relations (21) are expressed via exponentially decaying terms ($z_2⩽z⩽z_1⩽0$), which provide numerical stability.

Due to the isotropic property of the materials considered in this investigation, axisymmetric terms can be extracted from the displacement and stress fields. Therefore, applying the Fourier transform and the linear transformation:

$$\mathbf{B}=\left(\begin{array}{ccc}0& 0& 1\\ i{\alpha }_1/{\alpha }^2& i{\alpha }_2/{\alpha }^2& 0\\ i{\alpha }_2/{\alpha }^2& -i{\alpha }_1/{\alpha }^2& 0\end{array}\right),$$

The Fourier transforms ${\tilde{\mathit{U}}}_s(\alpha ,z)=B{\mathfrak{F}}_{x,y}\left[{\mathit{u}}_s\right]$, ${\tilde{\mathit{U}}}_f(\alpha ,z)=B{\mathfrak{F}}_{x,y}\left[{\mathit{u}}_f\right]$, $\tilde{\mathit{T}}(\alpha ,z)=B{\mathfrak{F}}_{x,y}\left[{\mathit{\tau }}_3\right]$, and $P_f(\alpha ,z)={\mathfrak{F}}_{x,y}\left[p_f\right]$ are also axisymmetric with respect to the Fourier transform parameters $({\alpha }_1,{\alpha }_2)$:

$$\begin{array}{c}{\tilde{\mathit{U}}}_{\gamma }={\{{\Phi }_{\gamma }^{\prime }+{\alpha }^2{\Psi }_{\gamma 1},{\Phi }_{\gamma }+{\Psi }_{\gamma 1}^{\prime },{\Psi }_{\gamma 2}\}}^T,\gamma =s,f,\hfill \\ \tilde{\mathit{T}}={\{{\xi }_1{\Phi }_1+{\xi }_2{\Phi }_2+2\mu {\alpha }^2{\Psi }_1^{\prime },2\mu {\Phi }_s^{\prime }+\mu (2{\alpha }^2-{\varkappa }_3^2){\Psi }_1,\mu {\Psi }_2^{\prime }\}}^T,\hfill \\ P_f=\frac{1}{\varphi }[(Q+R{\eta }_1){\varkappa }_{\mathrm{p}1}^2{\Phi }_1+(Q{\eta }_2+R){\varkappa }_{\mathrm{p}2}^2{\Phi }_2].\hfill \end{array}$$

(22)

Here,

$${\Phi }_{\gamma }={\eta }_{\gamma 1}{\Phi }_1+{\eta }_{\gamma 2}{\Phi }_2,$$

$${\Psi }_{sk}={\Psi }_k,{\Psi }_{fk}={\eta }_3{\Psi }_k$$

are the linear combinations of the potentials, whereas

$${\xi }_k=2\mu {\alpha }^2{\eta }_{sk}-((P+Q){\eta }_{sk}+(R+Q){\eta }_{fk}){\varkappa }_{\mathrm{p}k}^2,$$

$${\eta }_{s1}={\eta }_{f2}=1,{\eta }_{s2}={\eta }_2,{\eta }_{f1}={\eta }_1.$$

Satisfying the boundary conditions (7), the generalized state vector $\mathit{V}(\alpha ,z)=\{{\tilde{\mathit{U}}}_s,W_3,\tilde{\mathit{T}},P_f\}$, where $W_3=\varphi ({\tilde{U}}_{s1}-{\tilde{U}}_{f1})$, must be continuous at the interfaces between two dissimilar poroelastic layers. Employing Equations (21) and (22), the generalized state vector is written in matrix form as follows:

$$\begin{array}{c}\mathit{V}={\mathbf{C}}^{+}(z){\mathit{t}}^{+}+{\mathbf{C}}^{-}(z){\mathit{t}}^{-};\hfill \\ {\mathbf{C}}^{+}={\mathbf{M}}^{+}(\alpha )\mathbf{G}(\alpha ,z_1-z),{\mathbf{C}}^{-}={\mathbf{M}}^{-}(\alpha )\mathbf{G}(\alpha ,z-z_2).\hfill \end{array}$$

(23)

Here, the amplitude coefficient vectors ${\mathit{t}}^{\pm }=\{t_1^{\pm },t_2^{\pm },t_3^{\pm },t_4^{\pm }\}$ obey appropriate boundary conditions at the interfaces,

$$\mathbf{G}=exp(-\mathbf{diag}\{{\sigma }_{\mathrm{p}1},{\sigma }_{\mathrm{p}2},{\sigma }_{\mathrm{s}}\}z)$$

is the diagonal exponential matrix,

$$\begin{array}{c}{\mathbf{M}}^{\pm }=\mathbf{M}(\alpha ,\pm {\sigma }_{\mathrm{p}1},\pm {\sigma }_{\mathrm{p}2},\pm {\sigma }_{\mathrm{s}}),\hfill \\ \mathbf{M}(\alpha ,{\sigma }_1,{\sigma }_2,{\sigma }_3)=\left(\begin{array}{ccc}{\sigma }_1& {\eta }_2{\sigma }_2& {\alpha }^2\\ 1& {\eta }_2& {\sigma }_3\\ d_{11}& d_{12}& d_{13}\\ d_{21}& d_{22}& d_{23}\\ d_{31}& d_{32}& d_{33}\\ d_{41}& d_{42}& d_{43}\end{array}\right)\hfill \end{array}$$

and

$$\begin{array}{cc}{d}_{1k}=\varphi ({\eta }_{fk}-{\eta }_{sk}){\sigma }_k,(k=1,2),\hfill & d_{13}=\varphi ({\eta }_3-1){\alpha }^2;\hfill \\ d_{2k}={\xi }_k,\hfill & d_{23}=2\mu {\alpha }^2{\sigma }_3;\hfill \\ d_{3k}=2\mu {\eta }_{sk}{\sigma }_k,\hfill & d_{33}=\mu (2{\alpha }^2-{\varkappa }_s^2);\hfill \\ d_{4k}=-({\eta }_{sk}Q+{\eta }_{fk}R){\varkappa }_k^2/\varphi .\hfill \end{array}$$

For the case of a pure elastic isotropic layer, the solution is also of the form (23), where the generalized state vector $\mathit{V}=\{{\tilde{\mathit{U}}}_s,\tilde{\mathit{T}}\}$ and matrices $\mathbf{M}(\alpha ,{\sigma }_{\mathrm{p}},{\sigma }_{\mathrm{s}})$, and $\mathbf{G}=exp(-\mathbf{diag}\{{\sigma }_{\mathrm{p}},{\sigma }_{\mathrm{s}}\}z)$ is $6\times 2$-dimensional now. Here,

$${\sigma }_{\mathrm{p}}=\sqrt{{\alpha }^2-{\varkappa }_{\mathrm{p}}^2},{\sigma }_{\mathrm{s}}=\sqrt{{\alpha }^2-{\varkappa }_s^2}$$

and ${\varkappa }_{\mathrm{p}}$, ${\varkappa }_{\mathrm{s}}$ are wavenumbers of P- and S-waves in the elastic medium.

3.2. ES-Matrix Method for a Layered and Functionally Graded Poroelastic Structure

The generalized state vector $\mathit{V}(\alpha ,z)$ can be found in the form of Equation (23) for a layered poroelastic structure $\mathbb{S}$ as

$$\mathit{V}={\mathbf{E}}_{\mathbb{S}}^{+}{\mathit{c}}^{+}+{\mathbf{E}}_{\mathbb{S}}^{-}{\mathit{c}}^{-},$$

(24)

where ${\mathbf{E}}_{\mathbb{S}}^{\pm }(\alpha ,z)$ and their horizontal concatenation ${\mathbf{E}}_{\mathbb{S}}=[{\mathbf{E}}_{\mathbb{S}}^{+},{\mathbf{E}}_{\mathbb{S}}^{-}]$ are stepwise matrix functions, the so-called matrices of the eigensolutions of the layered structure (ES-matrices), which were introduced in [51] for layered piezoelectric materials. The vector of the amplitude coefficients ${\mathit{c}}^{+}$ has the same size as the vector ${\mathit{t}}^{+}$ for the first layer of $\mathbb{S}$, while the vector ${\mathit{c}}^{-}$ is of the same size as the vector ${\mathit{t}}^{-}$ for the last layer of the structure in the representation (23) for the corresponding layers.

The ES-matrices’ construction algorithm is recurrent. The ES-matrix ${\mathbf{E}}_n$ of the layered structure ${\mathbb{S}}_n={\mathbb{S}}_{n-1}\cup {\mathbb{L}}_n$ is obtained from the known ES-matrix ${\mathbf{E}}_{n-1}$ of the laminate ${\mathbb{S}}_{n-1}={\bigcup }_{j=1}^{n-1}{\mathbb{L}}_j$ and the ES-matrix ${\mathbf{E}}_{{\mathbb{L}}_n}=[{\mathbf{C}}_n^{+},{\mathbf{C}}_n^{-}]$ of the layer ${\mathbb{L}}_n$ as follows:

$$\begin{array}{c}{\mathbf{E}}_n^{+}=\left\{\begin{array}{cc}{\mathbf{E}}_{n-1}^{+}+{\mathbf{E}}_{n-1}^{-}{\mathit{T}}^{-},\hfill & z\in {\mathbb{S}}_{n-1},\hfill \\ {\mathbf{C}}_n^{+}{\mathit{T}}^{+},\hfill & z\in {\mathbb{L}}_n\hfill \end{array}\right.,{\mathbf{E}}_n^{-}=\left\{\begin{array}{cc}{\mathbf{E}}_{n-1}^{-}{\mathbf{R}}^{-},\hfill & z\in {\mathbb{S}}_{n-1},\hfill \\ {\mathbf{C}}_n^{+}{\mathbf{R}}^{+}+{\mathbf{C}}_n^{-},\hfill & z\in {\mathbb{L}}_n.\hfill \end{array}\right.\hfill \end{array}$$

(25)

Here, the matrices ${\mathbf{C}}_n^{\pm }$ are constructed like the matrices ${\mathbf{C}}^{\pm }$ in Equation (23) just for appropriate material parameters of the layer ${\mathbb{L}}_n$. Constant matrices ${\mathbf{T}}^{\pm }$ and ${\mathbf{R}}^{\pm }$ should be determined from the boundary condition at the interface $x_3=z_n$ between ${\mathbb{S}}_{n-1}$ and ${\mathbb{L}}_n$:

$${\mathbf{\Lambda }}_{n-1,n}{\mathbf{E}}_n^{\pm }(z_n+\epsilon )={\mathbf{\Lambda }}_{n,n-1}{\mathbf{E}}_n^{\pm }(z_n-\epsilon )\mathrm{at}\epsilon \to +0,$$

(26)

where matrices ${\mathbf{\Lambda }}_{n-1,n}$ and ${\mathbf{\Lambda }}_{n,n-1}$ are employed to determine the quantities for the boundary conditions (7) or (8). Therefore, if the contacting layers are of the same type, then these matrices are identity matrices, but if the contacting layers ${\mathbb{L}}_{n-1}$ and ${\mathbb{L}}_n$ are porous and pure elastic, respectively, then ${\mathbf{\Lambda }}_{n-1,n}={\mathbf{\Lambda }}_{p,s}$ and ${\mathbf{\Lambda }}_{n,n-1}={\mathbf{\Lambda }}_{s,p}$, where

$${\mathbf{\Lambda }}_{p,s}\mathit{V}=\{{\tilde{\mathit{U}}}_s,W_3,\tilde{\mathit{T}}\},{\mathbf{\Lambda }}_{s,p}\mathit{V}=\{{\tilde{\mathit{U}}}_s,0,\tilde{\mathit{T}}\}.$$

Satisfying the boundary condition (26), ${\mathbf{T}}^{\pm }$ and ${\mathbf{R}}^{\pm }$ in (25) can be obtained as blocks of the following matrix:

$$\left(\begin{array}{cc}{\mathbf{T}}^{+}\hfill & {\mathbf{R}}^{+}\hfill \\ {\mathbf{T}}^{-}\hfill & {\mathbf{R}}^{-}\hfill \end{array}\right)={\mathbf{W}}^{-1}\mathbf{Z},$$

(27)

where $\mathbf{W}$ and $\mathbf{Z}$ are expressed using horizontal concatenations of ${\mathbf{C}}_n^{\pm }$ and ${\mathbf{E}}_{n-1}^{\pm }$ as

$$\mathbf{W}=[{\Lambda }_{n-1,n}{\mathbf{C}}_n^{+}(z_n),-{\Lambda }_{n,n-1}{\mathbf{E}}_{n-1}^{-}(z_n)],$$

$$\mathbf{Z}=[{\Lambda }_{n-1,n}{\mathbf{E}}_{n-1}^{+}(z_n),-{\Lambda }_{n,n-1}{\mathbf{C}}_n^{-}(z_m)].$$

The functionally graded porous layer ${\mathbb{L}}_{loam}$ is simulated as a layered structure ${\mathbb{L}}_{loam}^a$ with M homogeneous sublayers:

$${\mathbb{L}}_{loam}\approx {\mathbb{L}}_{loam}^a(M)=\bigcup _{k=1}^M\mathbb{L}({\mathbb{M}}_{loam}({\overline{d}}_k),d_{k-1},d_k),$$

(28)

where ${\mathbb{M}}_{loam}({\overline{d}}_k)$ is the set of poroelastic properties of the loam slice calculated according to Equations (3) and (4) for fixed water saturation $\varsigma ({\overline{d}}_k)$, ${\overline{d}}_k=\frac{1}{2}(d_{k-1}+d_k)$ and $d_k=z_{1}k/M$.

For the known ES-matrix $E_{\mathbb{HS}}(\alpha ,z)$ of the considered half-space $\mathbb{HS}$, the displacements ${\mathit{u}}_s(\mathbf{x},\omega )$ and ${\mathit{u}}_f(\mathbf{x},\omega )$ are expressed in terms of the inverse Hankel transform as

$${\displaystyle {\mathit{u}}_{\gamma }(\mathbf{x},\omega )={\displaystyle \frac{1}{2\pi }}\underset{\Gamma }{\int }{\mathbf{K}}_{\gamma }(\alpha ,-i\frac{\partial }{\partial x},-i\frac{\partial }{\partial y},z)\mathit{Q}(\alpha )J_0(\alpha r)\alpha d\alpha ,\gamma \in \{s,f\},}$$

(29)

where $\mathit{Q}={\mathfrak{F}}_{x,y}\left[\mathit{q}\right]$ and ${\mathbf{K}}_{\gamma }(\alpha ,{\alpha }_1,{\alpha }_2,z)={\mathfrak{F}}_{x,y}\left[{\mathbf{k}}_{\gamma }(x,y,z)\right]$ are the Fourier transforms of the surface load and Green’s matrix ${\mathbf{k}}_{\gamma }$, respectively, while $J_0(z)$ is the Bessel function of the first kind of zero order. The infinite path $\Gamma$ goes along the real axis and surrounds the real poles $\alpha =\zeta$ of matrix ${\mathbf{K}}_{\gamma }$ in accordance with the limiting absorption principle [41,61]. Green’s matrices have the following form:

$${\mathbf{K}}_{\gamma }={\mathbf{B}}^{-1}{\tilde{\mathbf{K}}}_{\gamma }\mathbf{B}=\left(\begin{array}{ccc}-i({\alpha }_1^2{M}_{\gamma }+{\alpha }_2^2{N}_{\gamma })/{\alpha }^2& -i{\alpha }_1{\alpha }_2(M_{\gamma }-N_{\gamma })/{\alpha }^2& -i{\alpha }_1{P}_{\gamma }\\ -i{\alpha }_1{\alpha }_2(M_{\gamma }-N_{\gamma })/{\alpha }^2& -i({\alpha }_2^2{M}_{\gamma }+{\alpha }_1^2{N}_{\gamma })/{\alpha }^2& -i{\alpha }_2{P}_{\gamma }\\ {\alpha }_1{S}_{\gamma }/{\alpha }^2& {\alpha }_2{S}_{\gamma }/{\alpha }^2& R_{\gamma }\end{array}\right),$$

(30)

where the matrix:

$${\tilde{\mathbf{K}}}_{\gamma }={\mathbf{\Lambda }}_{u\gamma }{\mathbf{E}}_{\mathbb{HS}}^{+}(\alpha ,z){\left({\mathbf{\Lambda }}_{load}{\mathbf{E}}_{\mathbb{HS}}^{+}(\alpha ,0)\right)}^{-1}$$

(31)

can be simplified and rewritten as the matrix of the axisymmetric solutions for unitary axisymmetric loads as follows:

$${\tilde{\mathbf{K}}}_{\gamma }(\alpha ,z)=\left(\begin{array}{ccc}{R}_{\gamma }& S_{\gamma }& 0\\ P_{\gamma }& M_{\gamma }& 0\\ 0& 0& N_{\gamma }\end{array}\right).$$

The linear operators ${\mathbf{\Lambda }}_{load}$ and ${\mathbf{\Lambda }}_{u\gamma }$ applied to the wavefield $\mathit{V}$ are defined as

$${\mathbf{\Lambda }}_{load}\mathit{V}=\{\tilde{\mathit{T}},P_f\},{\mathbf{\Lambda }}_{u\gamma }\mathit{V}={\tilde{\mathit{U}}}_{\gamma }.$$

Matrix ${\mathbf{K}}_{\gamma }$ in integral representation (29) obtained after substituting the derivatives with respect to the spatial coordinates x and y for ${\alpha }_1$ and ${\alpha }_2$, respectively, becomes a differential operator applied to $J_0(\alpha r)$ [61].

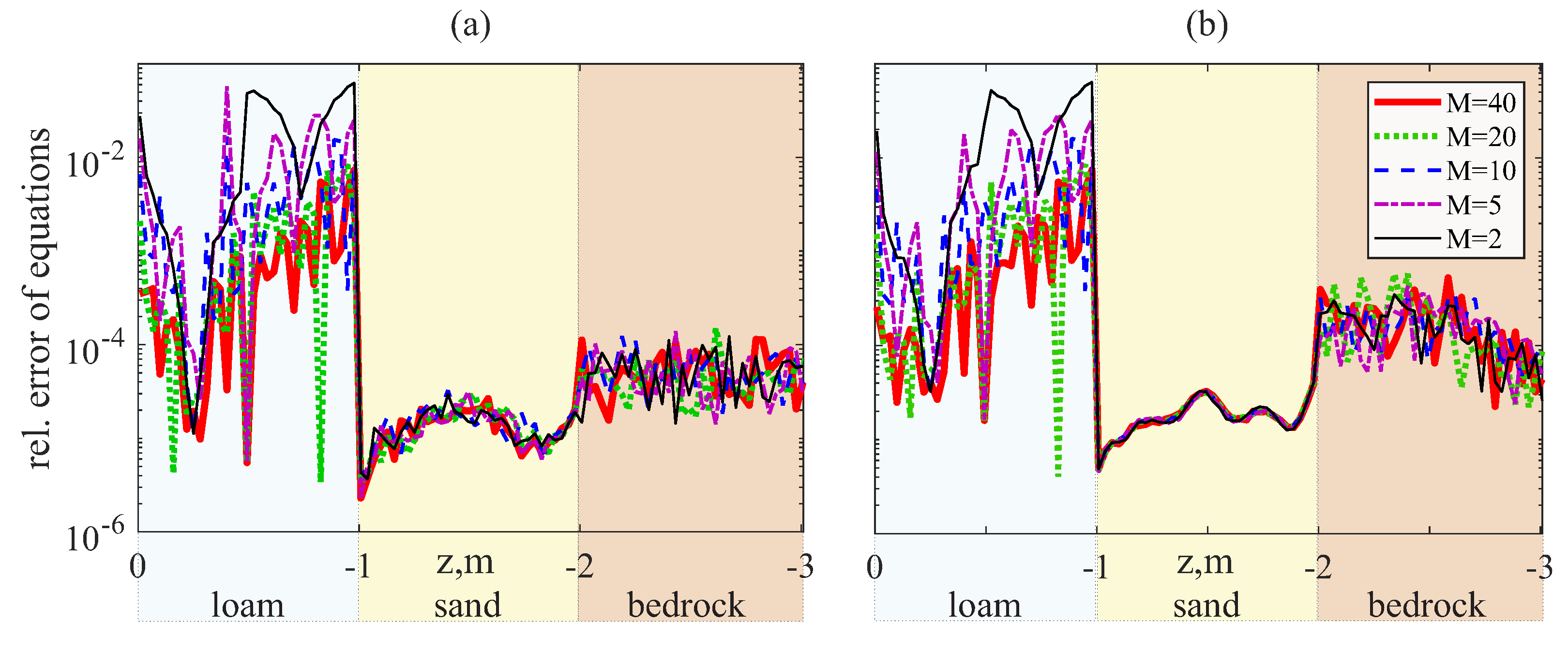
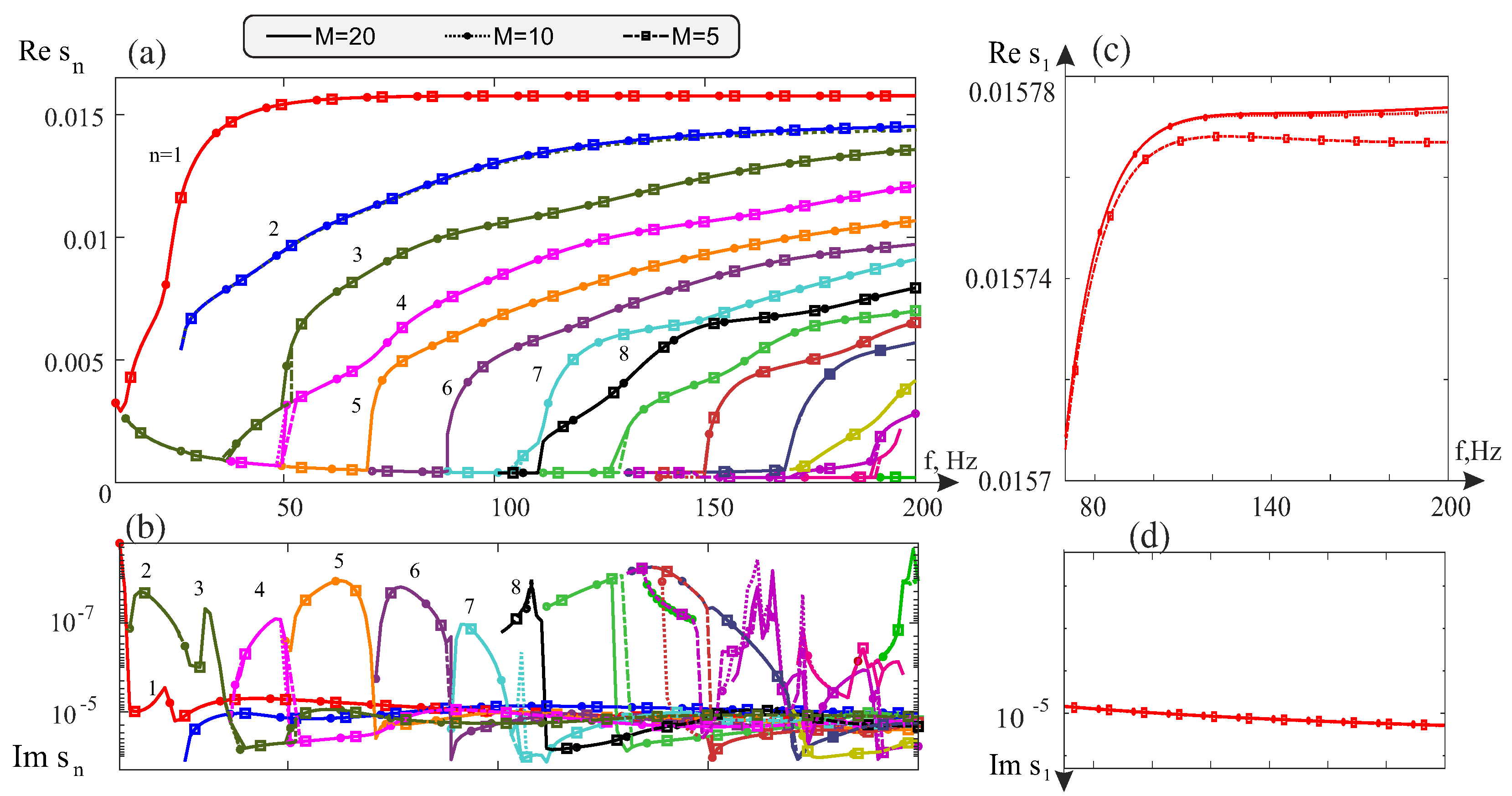
4. Results

Let us consider three-layered strata: the poroelastic loam layer of thickness $a_1=1$ m subjected to the process of water infiltration, the poroelastic fully water saturated sand layer of thickness $a_2=1$ m, and the pure elastic bedrock. The elastic parameters of the considered materials taken in [62] are shown in

Table 1. Material poroelastic parameters.

Material	${\mathit{\rho }}_{\mathit{s}}$	${\mathit{K}}_{\mathit{s}}$	$\mathit{\mu }$	$\mathit{\varphi }$	${\mathit{\rho }}_{\mathit{f}}$	${\mathit{K}}_{\mathit{f}}$	${\mathit{K}}_{\mathit{d}}$	${\mathit{\alpha }}_{\mathit{s}}$	${\mathit{\kappa }}_{\mathit{s}}·{10}^{13}$	${\mathit{\eta }}_{\mathit{f}}{10}^6$
	kg/m ${}^{\mathbf{3}}$	GPa	MPa		kg/m ${}^{\mathbf{3}}$	MPa	MPa		m ${}^{\mathbf{2}}$	N s/m ${}^{\mathbf{2}}$
water-saturated loam	2650	35	$6.3$	$0.463$	997	$2.25·{10}^3$	$17.6$	$1.58$	$3.74$	100
air-saturated loam	2650	35	$6.3$	$0.463$	$1.1$	$0.145$	$17.6$	$1.58$	$3.74$	18
water-saturated sand	2650	35	$13.3$	$0.437$	997	$2.25·{10}^3$	$35.3$	$1.64$	$3.74$	100
bedrock	2600	$52.7$	15,600	0	–	–	–	–	–	–

. The loam hydrological parameters are the following:

$${\theta }_r=0,{\theta }_s=0.463,\mathfrak{n}=1.56,l=0.5,{\alpha }_h=3.5(1/\mathrm{m}),{\mathcal{K}}_s=0.2496(\mathrm{m}/\mathrm{day}).$$

4.1. Infiltration in Loam

The soil simulation domain was initialized with the water content $\theta$ varying linearly with depth. The water content at the top surface had an initial condition (IC) at just below the porosity value (0.463) and linearly reduced with depth to reach an IC value of 0.001 (just above the residual water content) at the bottom layer of the domain. This is an IC scenario that well represents a dry soil domain being wetted from the top down and is encountered in reality during experiments to determine the hydraulic conductivity of the soil in the field using disk infiltrometers. Values just under ${\theta }_s$ and just above ${\theta }_r$ were used in order to not encounter computational errors in the numerical solution.

The finite element solution of Richards’ equation for the representative volume of the loam ($1\times 1\times 1$ m${}^3$) provides the water saturation parameter $\varsigma (t,x_3)=\overline{\theta }(t,x_3)/\varphi$, where $\overline{\theta }(t,x_3)$ is the mean value of $\theta (t,x_1,x_2,x_3)$ over the plane coordinate $(x_1,x_2)$. The obtained saturation $\varsigma$ is depicted in Figure 2 for times $t\in [0,45]$ days. A significant deviation from the initial linear distribution of porous water content is observed. The water content decreases gradually in the upper part of the loam layer, while the water content increases in the second (bottom) part of the layer. Thus, the water saturation gradually levels off, reaching an almost constant value $\varsigma =0.47$ throughout the thickness of the layer at $t=45$ days of the infiltration process. During infiltration, water partially and freely penetrates the layer of sand. It was further assumed that there is some runoff of water in the sand; therefore, the sand layer was assumed to be fully saturated.

4.2. Validation. Influence of Water Saturation on Surface Waves

To validate the developed method, let us consider the layered soil at $t=1$ day of infiltration and excite the wave fields by a constant vertical load in a circle of radius $a=1$ m:

$$\mathit{q}(\mathbf{x})=\left\{\begin{array}{cc}\{0,0,1\},& r⩽a\\ \{0,0,0\},& r>a\end{array}\right..$$

The numerical satisfaction of displacements ${\mathit{u}}_s$, ${\mathit{u}}_f$ by the governing Equations (1) and (5) in the layers of the structure is presented in Figure 3 for two frequencies: $f=100$ Hz (Subplot a) and $f=200$ Hz (Subplot b) at points $(1,0,z)$ (m). The displacements are calculated using the numerical integration of the representation (29) with the relative error $\epsilon =1\times {10}^{-5}$. Therefore, the derivatives for the governing Equations (1) and (5) are calculated numerically as well with the second-order-accurate formula with the relative error $\epsilon =1\times {10}^{-5}$. Then, the obtained residuals for the governing equations are divided by the norm of the inertial part of the equations. The functionally graded loam is simulated as an M-layered medium described by the relations (28). To check the accuracy, the continuous properties $\mathbb{M}(z)$ are substituted into the governing Equations (1) and (2). Therefore, the relative error in the functionally graded loam is decaying with M, while it is stable in the homogeneous media (sand and bedrock).

The convergence of the developed method for functionally graded strata is demonstrated in Figure 4 by means of the vertical component of the Umov–Poynting vector $e_z$. For the case of a poroelastic medium, this component has the following representation [63]:

$$e_z=-\frac{\omega }{2}\mathtt{Im}({\mathit{u}}_s·{\mathit{\tau }}_3-w_3{p}_f^{*}).$$

Here, $p_f^{*}$ is the complex conjugation of the water pressure $p_f$. Due to continuity boundary conditions at the interfaces, the vertical component $e_z$ is also continuous at interfaces $z_k$, which can be observed in Figure 4 for frequencies $f=100$ and $f=200$ Hz at points $(1,0,z)$. Sufficient accuracy is already achieved at $M=20$ for the considered frequency range (frequencies up to $f=1000$ Hz).

The slownesses $s_n$ for the n-th guided wave are related to the wavenumber ${\zeta }_n$ as $s_n={\zeta }_n/\omega$, where the magnitudes of ${\zeta }_n$ are the poles of the Fourier transform of Green’s matrix ${\mathbf{K}}_{\gamma }$. The rather fast convergence of the slownesses with the number of sublayers of loam M increase is observed. As an example, the dispersion curves, namely the real and imaginary parts of the slownesses–frequency relation $s_n(f)$, are shown in Figure 5 for the considered poroelastic three-layer strata. Here, the convergence with the variation of the number of sublayers M is also clearly demonstrated considering $M=5,10$, and 20. All traveling waves determined here numerically have an attenuation due to pore fluid viscosity (see Figure 5b). The smallest attenuation ($\mathtt{Im}{s}_n$) is observed with the smallest slownesses ($\mathtt{Re}{s}_n$). Here, we can also observe the relay transmission of guided waves due to the osculation or repulsion of modes, which was studied earlier for purely elastic laminates [64,65].

As the provided analysis has shown, the effect of infiltration on the guided waves’ slowness can be observed. The most-significant effect is observed for the slowest guided wave ($n=1$) at higher frequencies, as demonstrated in Figure 6. The real part of $s_1$ increases, while the attenuation ($\mathtt{Im}{s}_1$) decreases with increasing infiltration time t. The most-significant changes in $s_1$ are observed during the first day of infiltration ($t\le 1$).

5. Discussion

The determination of the structure and water saturation of porous media is still a challenging task requiring extensive and time-consuming calculations since complex interactions in inhomogeneous and stratified media are to be accurately simulated. This study presented a two-stage poroelastic dynamic model for modeling wave propagation in partially saturated layered strata with the fluid saturation of the media depending on the infiltration time. The semi-analytical method based on the boundary integral equation method employed in the second stage of the simulations does not demand sufficient computational resources and provides accurate results quickly.

Sensors located at the surface of soil can register the characteristics of guided waves as the reciprocal of phase velocities [66]. Therefore, the proposed two-stage method can be further employed for the inverse problem solution, where the saturation can be determined, e.g., from the experimentally determined wavenumber–frequency relations for the propagating surface acoustic waves using the techniques for material properties’ identification in an elastic waveguide [67,68,69]. The latter should rely on information about the dispersion characteristics of guided waves, which are extracted by applying the matrix pencil method, for instance.

The developed mathematical model is applicable to fast parametric analysis of surface acoustic wave propagation in various porous media due to its semi-analytical nature. It should also be noted that other relations for homogenization or explicit two-fluid model of poroelasticity [70,71] can be used to adjust the model to the experimental data.