Abstract
The article is devoted to a review of bistability and quadro-stability phenomena found in a certain class of mathematical models of population numbers and allele frequency dynamics. The purpose is to generalize the results of studying the transition from bi- to quadro-stability in such models. This transition explains the causes and mechanisms for the appearance and maintenance of significant differences in numbers and allele frequencies (genetic divergence) in neighboring sites within a homogeneous habitat or between adjacent generations. Using qualitative methods of differential equations and numerical analysis, we consider bifurcations that lead to bi- and quadro-stability in models of the following biological objects: a system of two coupled populations subject to natural selection; a system of two connected limited populations described by the Bazykin or Ricker model; a population with two age stages and density-dependent regulation. The bistability in these models is caused by the nonlinear growth of a local homogeneous population or the phase bistability of the 2-cycle in populations structured by space or age. We show that there is a series of similar bifurcations of equilibrium states or fixed or periodic points that precede quadro-stability (pitchfork, period-doubling, or saddle-node bifurcation).
Keywords:
population; dynamics; age structure; migration; genetic divergence; bistability; bifurcations PACS:
87.23.-n; 87.10.Ed
MSC:
92Dxx; 92D25; 37N25; 34C23
1. Introduction
In theoretical population biology, there are many interesting dynamic mathematical models that show bistability, such as the existence of two alternative asymptotically stable regimes (in particular, equilibrium states) where the selection between them is determined by the value of the initial conditions [1,2,3,4,5,6,7,8,9,10]. For example, for structured populations represented by two interacting subpopulations with bistability, the extinction of one or their coexistence with similar sizes is possible under different initial conditions. Intermediate states of populations with significant differences in adjacent sites, not related to the extinction, arise when several additional equilibrium states are born, at least two of which are stable. Here, the biological system goes from bistable to quadro-stable. The properties of a population as a nonlinear dynamic system often lead to the birth of two or more alternative stable states, which frequently follow similar scenarios. This scenario occurs in different mathematical models and content problems and, as a rule, leads to interesting, often counterintuitive conclusions [2,10,11,12,13,14,15].
This paper reviews well-known nonlinear dynamic mathematical models with a similar scenario for the birth of the bi- and quadro-stability of equilibrium states. Although this scenario is directly explained by the choice of the models used (matrix models with quadratic or cubic dependence of demographic transition coefficients on population size), we can argue that this scenario is quite universal. It allows one to show the mechanisms leading to spatio-temporal heterogeneity in genetically structured populations (primary genetic divergence). Some results are already familiar (Section 1, Section 2, Section 3 and Section 5), but we present them here using modern methods for analyzing dynamical systems and visualizing the behavior of dynamic regimes. We present some results for the first time (Section 4).
2. Reduced Fitness of Heterozygotes
2.1. Microevolution. Allele Frequency Dynamics
To understand the main patterns of microevolution for a population of diploid organisms subject to natural selection, we consider a simple model situation in which the adaptive diversity of a population is determined by one diallelic locus with the allelomorphs A and a. The phenotype of the individuals is rigidly determined by their genotype; the population is panmictic and Mendelian rules of inheritance apply. Then, the action of natural selection can be described quantitatively by assigning one coefficient to each of the genotypic classes of individuals , and . For different models, the selection is characterized either by the values , and , called the fitnesses of individuals with the genotype , and , or by the values , and , called the selection coefficients. For a population of continuously reproducing organisms, the fitness of individuals with the genotype () is equal to the sum of the average number of surviving offspring produced by one individual of a given genotypic class and the proportion of survived individuals per unit of time.
These assumptions are sufficient to obtain the following differential equation for the dynamics of allele A’s frequency [1,16,17,18]:
Let us consider the types of changes in the frequency of allele A, determined by Equation (1). There are three cases here.
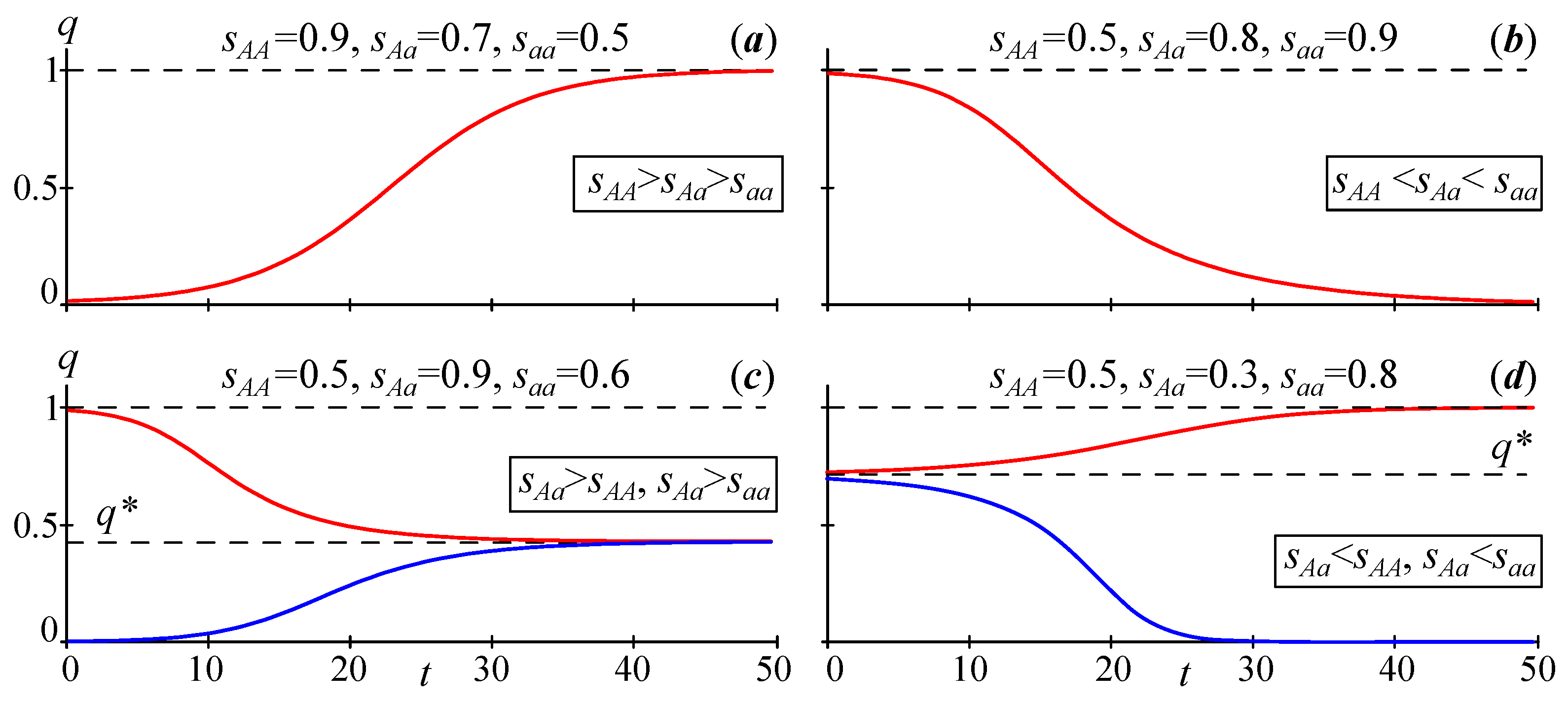
1. Intermediate fitness of heterozygotes: (a) and (b) . With such ratios for the selection coefficients, Equation (1) has two equilibrium states: and . In case (a), the equilibrium is unstable, and the equilibrium is stable. The frequency of allele A monotonically increases from any initial state , tending to the equilibrium , i.e., allele A is fixed, and allele a is expelled from the population (Figure 1a). In case (b), the equilibrium is stable, and the equilibrium is unstable. The frequency of allele A decreases monotonically from any initial state , tending to the equilibrium , i.e., allele A is expelled, and allele a is fixed (Figure 1b).
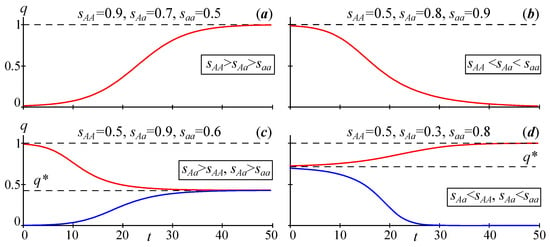
Figure 1.
Three types of solutions to Equation (1) with different ratios of fitness of homo- and heterozygotes.
2. Increased fitness of heterozygotes: and . Here, Equation (1) has three equilibriums: , and . Equilibriums and are unstable, and equilibrium is stable. The frequency of allele A monotonically increases from any initial state or decreases monotonically from any initial state , tending to the equilibrium (Figure 1c). Then, a stable polymorphism arises in the population—the coexistence of all three genotypes (homozygotes and heterozygotes).
3. Reduced fitness of heterozygotes: and . Here, Equation (1) again has three stationary solutions , and . However, the equilibrium is unstable, while the equilibriums and are stable. The frequency of allele A monotonically decreases from any initial state , tending to the equilibrium , and monotonically increases from any initial state , tending to the other equilibrium (Figure 1d). This is where bistability comes in; under some initial conditions (), allele A is expelled, and the population becomes monomorphic consisting only of individuals with the genotype, while, under other initial conditions (), allele a is expelled, and the monomorphic population includes only individuals with the genotype.
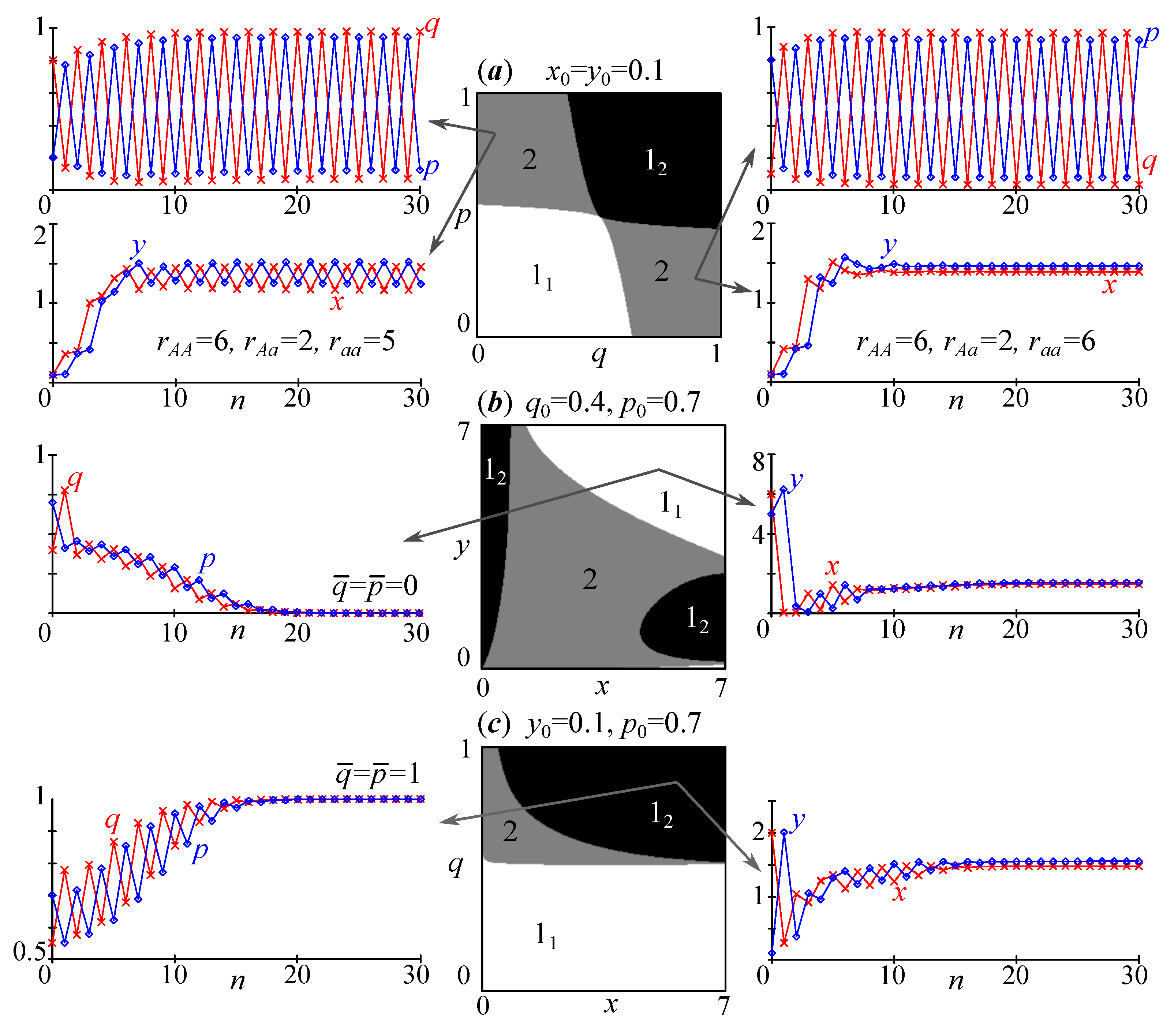
Let us consider two identical panmictic Mendelian single-locus diallel populations inhabiting two adjacent local sites (territories) of a homogeneous range. Assume that the individuals of each local population with the same genotype do not differ in fitness, but the allele frequencies in populations may initially vary. Suppose that the populations exchange individuals (migrants) and the intensities of the migration flows are proportional to the size of the population from which this flow comes. Denote the migration coefficient (the fraction of migrants per unit of time) as .
Describe the evolution of such a population system using the following dynamic variables: and are the concentrations (frequencies) of allele A in the first and second populations (, ), respectively; is the weight of the first population to the total size, where and are the numbers of the first and second populations ().
These assumptions allow us to write the following system of differential equations, which describes the evolution process of two populations living in a selection-homogeneous area and coupled by migrations:
where and are the average values of the selection coefficient of the first and second populations, respectively. A more detailed process for constructing Equation (2) can be found in [1,10].
Consider a situation in which the fitness of a heterozygote lies outside the range of fitness of the homozygotes. We confine ourselves to considering the “symmetric” case and assume that and .
Substituting these selection coefficients into system (2), we obtain:
System (3) has the following equilibrium states:
(1) —both populations consist only of individuals with the genotype, and there are no or genotypes (monomorphic population);
(2) —both populations include individuals of the three genotypes, with an equal concentration of each allele (polymorphic population);
(3) —both populations consist only of individuals with the genotype (monomorphic population);
(4–5) A couple of equilibriums that exist at and or at and . However, only in part of these two parameter ranges do these points have biologically significant coordinates (lying within a single cube). It is easy to show that this pair, , is born (or disappears) on the line during the pitchfork bifurcation. Here, the point “splits” into two additional points, and . Each of these points corresponds to a divergence between populations: in one of the polymorphic populations, one allele predominates over the other. For example, there is a high concentration of allele A and a low concentration of allele a, while the other allele predominates in the second population (a high concentration of allele a and a low concentration of allele A).
Note that many of the cited researchers do not use population size or the weight of one population relative to the total size as a model variable to describe the dynamics of allele frequencies or use them infrequently. Some researchers conventionally suppose that there are quite a lot of individuals and that natural selection does not significantly change the population size, and only the ratio of the genotypes changes (values and ). For example, the articles [2,3,9] dealt with a similar problem in which the population number is a parameter and its variation changes the values of the fitness at which monomorphism and polymorphism occur in adjacent populations.
2.2. A Special Case of System (3) with p = 1/2
It is easy to see that in the nondegenerate case, any of the equilibrium states have the weight , i.e., both populations in the asymptotic case are equal in number, regardless of the frequencies of alleles A and a. Let us analyze how the concentration of alleles will change in populations with constant numbers or with constant ratios of numbers, i.e., with . First, let us consider the simplest case: –-the size of two populations is equal in both territories. Then, system (3) has the form:
A.D. Bazykin [12,13] proposed and studied a similar system of equations (up to notation) when analyzing the conditions for the emergence and maintenance of primary genetic divergence.
The equilibrium points of system (4) satisfy the following algebraic equations:
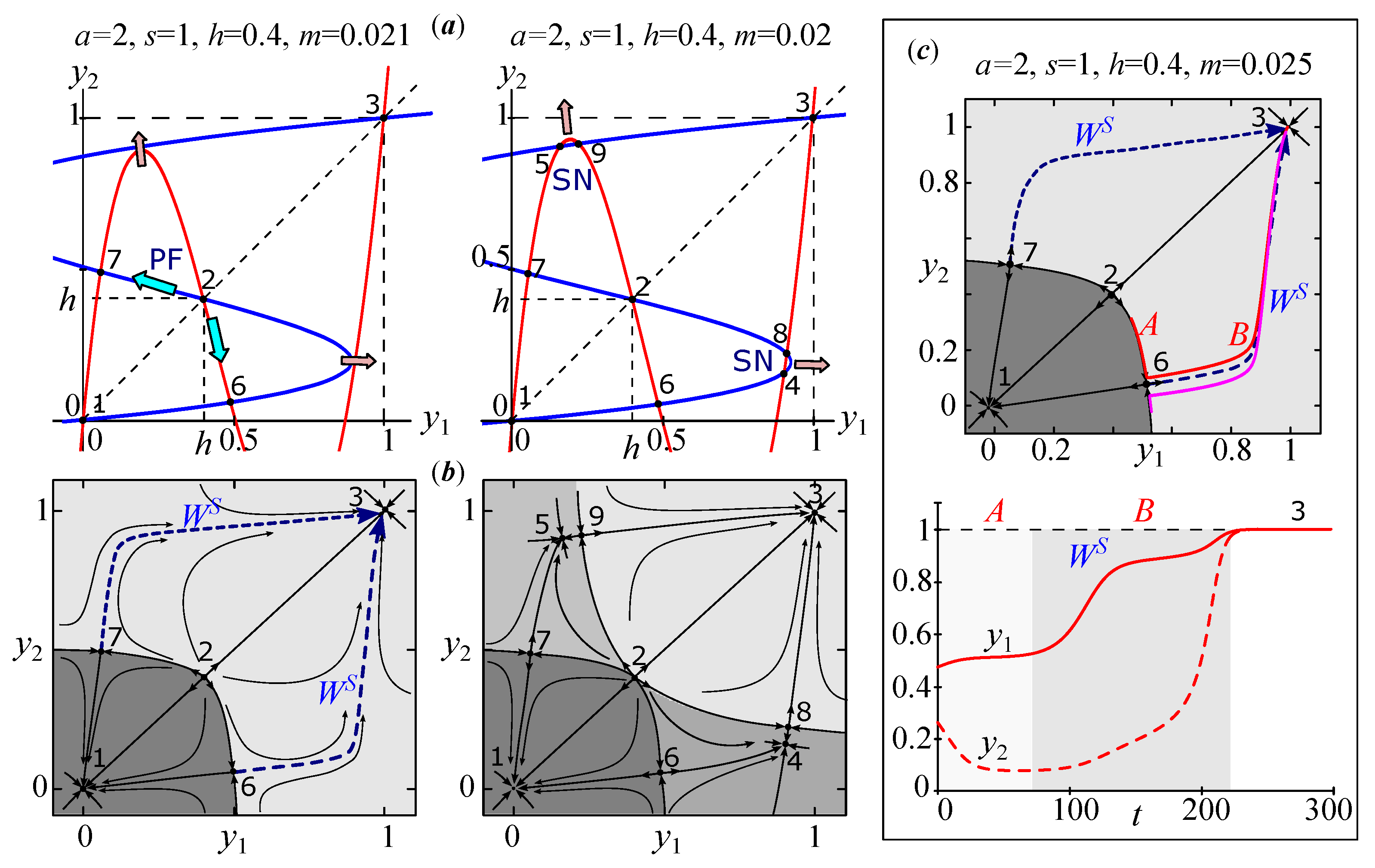
The bottom of Figure 2 shows the graphs of the functions and corresponding to system (5) for small values of the coefficient m. Each equilibrium state of system (4) corresponds to one of the intersection points of these graphs.
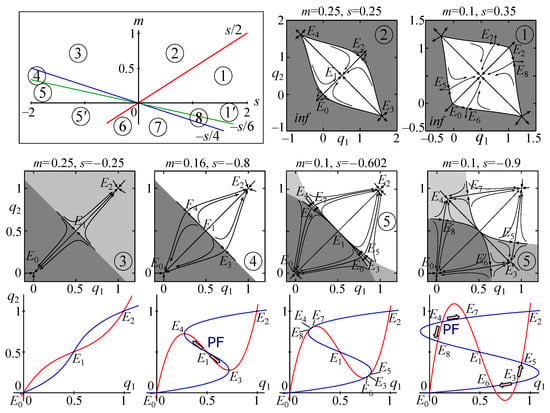
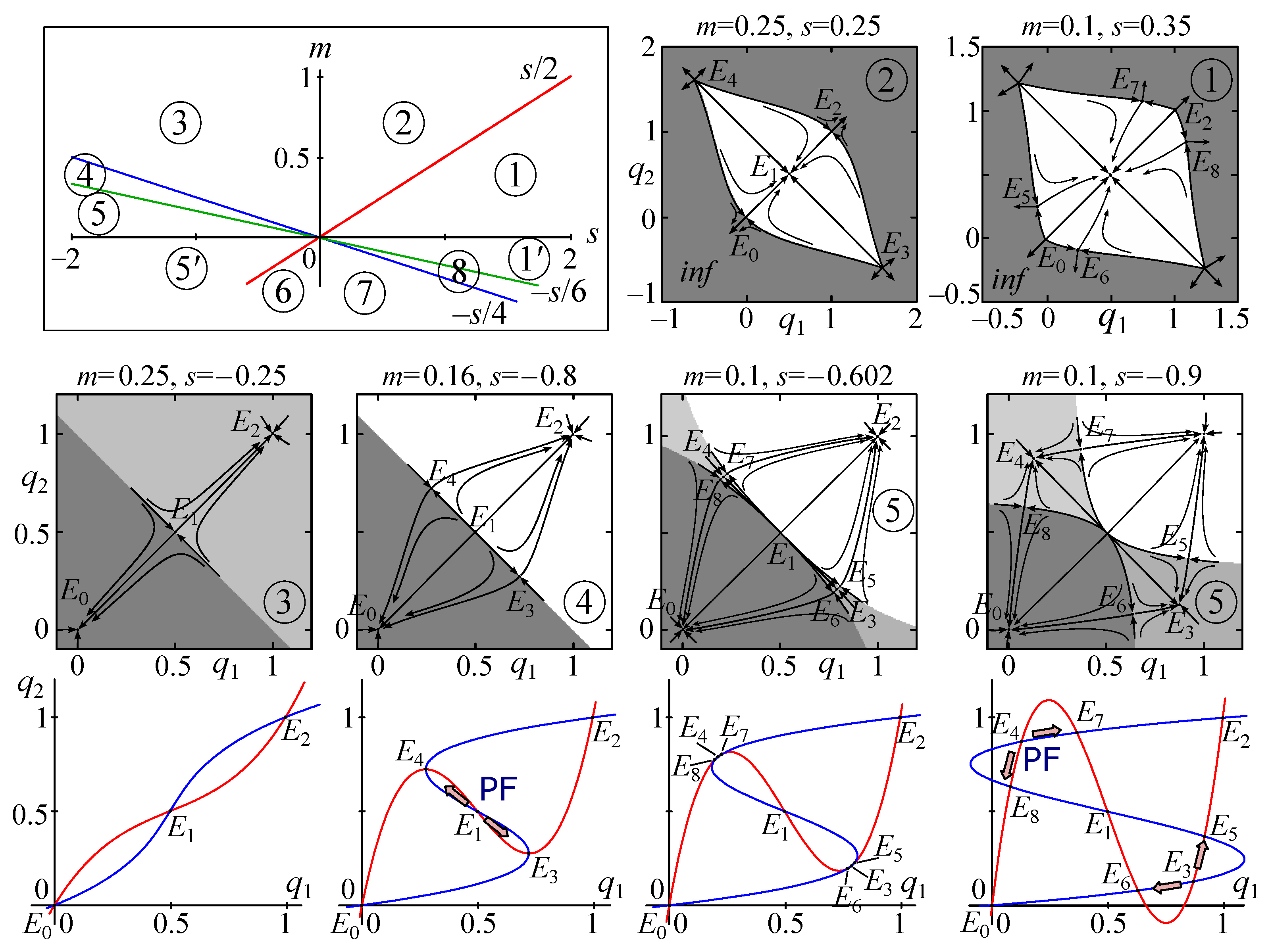
Figure 2.
Parametric portrait of system (4), phase portraits combined with basins of attraction of steady states, and the nullclines of system (4), demonstrating the formation of points . The gray area (inf) on basins 1 and 2 corresponds to unbounded model trajectories. In other cases, white and gray areas are basins of coexisting stable equilibriums.
System (4) has the same set of equilibriums as (3): . However, four additional points, , appear, which are defined as the roots of the equation:
The value of can be found by the formula:
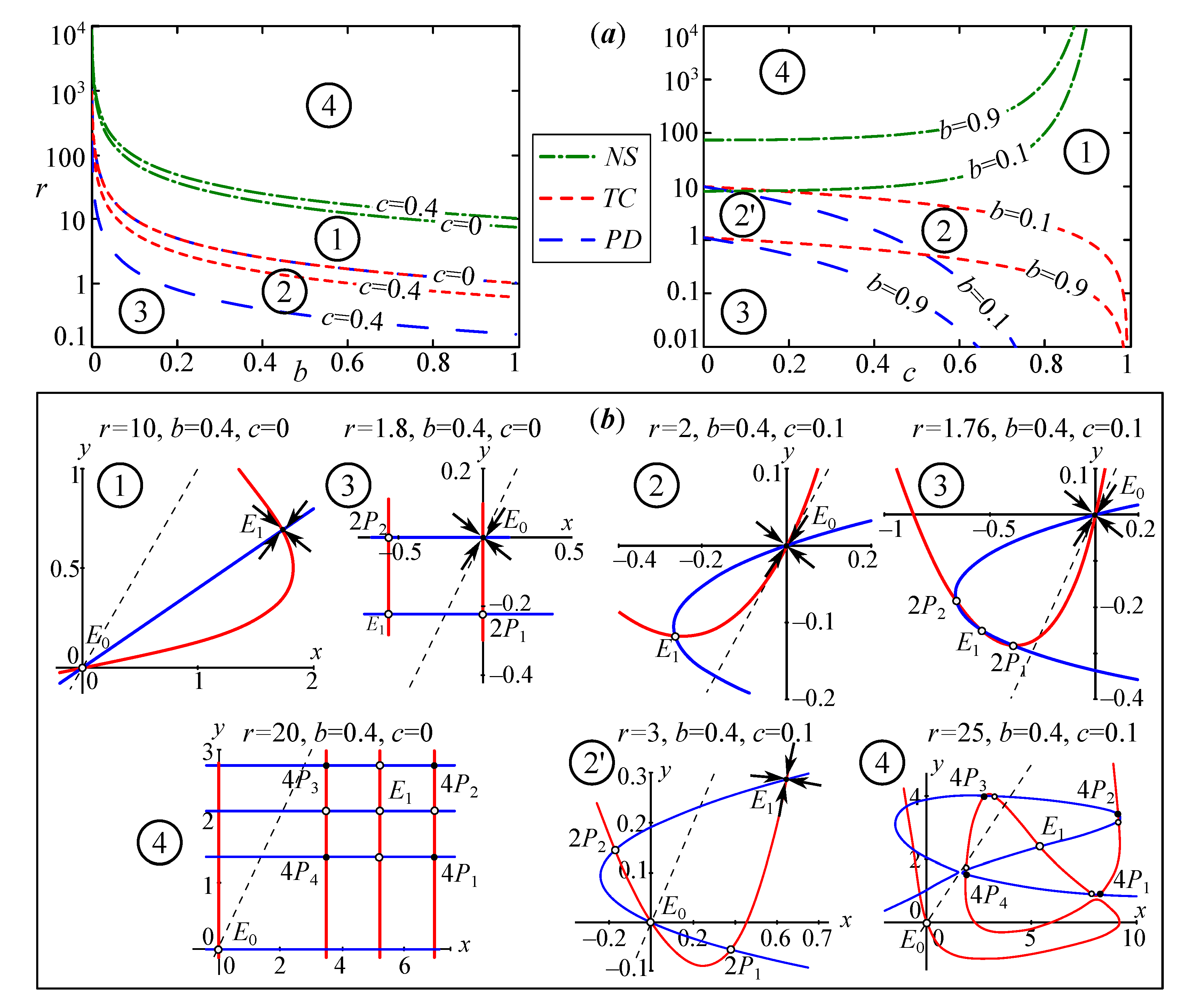
The form of these equilibriums is rather cumbersome, so we will not present them here. However, it is easy to show that this polynomial has exactly four real roots for if (domain 5 and in Figure 2) and for if (domain 1 and ). At the boundaries of this interval, i.e., at or , the polynomial has only two roots of the second multiplicity, coinciding with points and at or with and at . Accordingly, within these ranges of parameters, points exist and are born because of the pitchfork bifurcation from pair or .
The domains of existence and stability of points coincide with those of system (3), and, for points , they are “embedded” within them. The upper left corner of Figure 2 shows these regions in the parameter plane. Let us consider them in more detail.
In area 1, there are nine equilibriums, . In area 2, there are five points, . The stable equilibrium is a polymorphic state . It is noteworthy that for positive values of the migration coefficient m, part of the equilibriums is located outside the first quadrant, so the basin of the polymorphic point includes both the entire unit square and the zones located outside it.
In area 3, the dynamics of system (4) become bistable where there are two steady states—the monomorphic and with attraction basins, separated by a line . In area 4, the pair appears, which does not fundamentally affect the attraction basins of monomorphic equilibrium states but introduces peculiar features into the dynamics. Here, the model trajectories include nonmonotonic segments of the dynamics. If the sum of the starting concentrations is equal to one (or close enough to one), then the trajectory first moves along the separatrix until it reaches the vicinity of point or (corresponding to the divergence, where it can “stay” for a while), and then, because of small perturbations, it rushes to point or . As a result, the value of will initially increase, and will fall, or contrariwise. After, and will simultaneously increase when moving towards or fall when moving towards .
Finally, in area 5, two pairs, and , split off from points and , and the polymorphic points and become stable. As a result, in these parameter areas, in addition to the stable monomorphic states, the stable equilibriums appear, corresponding to polymorphic populations with a high concentration of allele A and a low concentration of allele a, or contrariwise. Thus, the dynamics of system (4) become quadro-stable, i.e., depending on the initial conditions, the concentrations and tend toward four fundamentally different values over time (for a sufficiently large t): either monomorphic states with a zero concentration of the allele A or a or polymorphic states with unequal concentrations (with a predominance of one or another allele).
2.3. Generalization of Model (4) for Any p
Let us now assume that the population sizes in adjacent sites are different, but the size ratio remains constant: (). We will consider the value of p as a parameter, which, if it changes, will change quite slowly [10]:
As before, system (6) has from three to nine equilibriums, which depend on the parameter p, except for points , and . The form of the other six equilibriums is very cumbersome, and it makes no sense to present them. Obviously, for , they coincide with the points from the previous paragraph. Model (6) is a three-parameter one, so, when analyzing the change in stability, we change all three parameters.
Equilibriums , and exist for any value of the coefficients. As in the previous case, for , point at the center of the unit square is always stable. For , points and are stable. The pair of points , corresponding to the genetic divergence, is generated by splitting the polymorphic state into two because of the pitchfork bifurcation. However, for , equilibriums and become stable in a slightly different way than in the previous case.
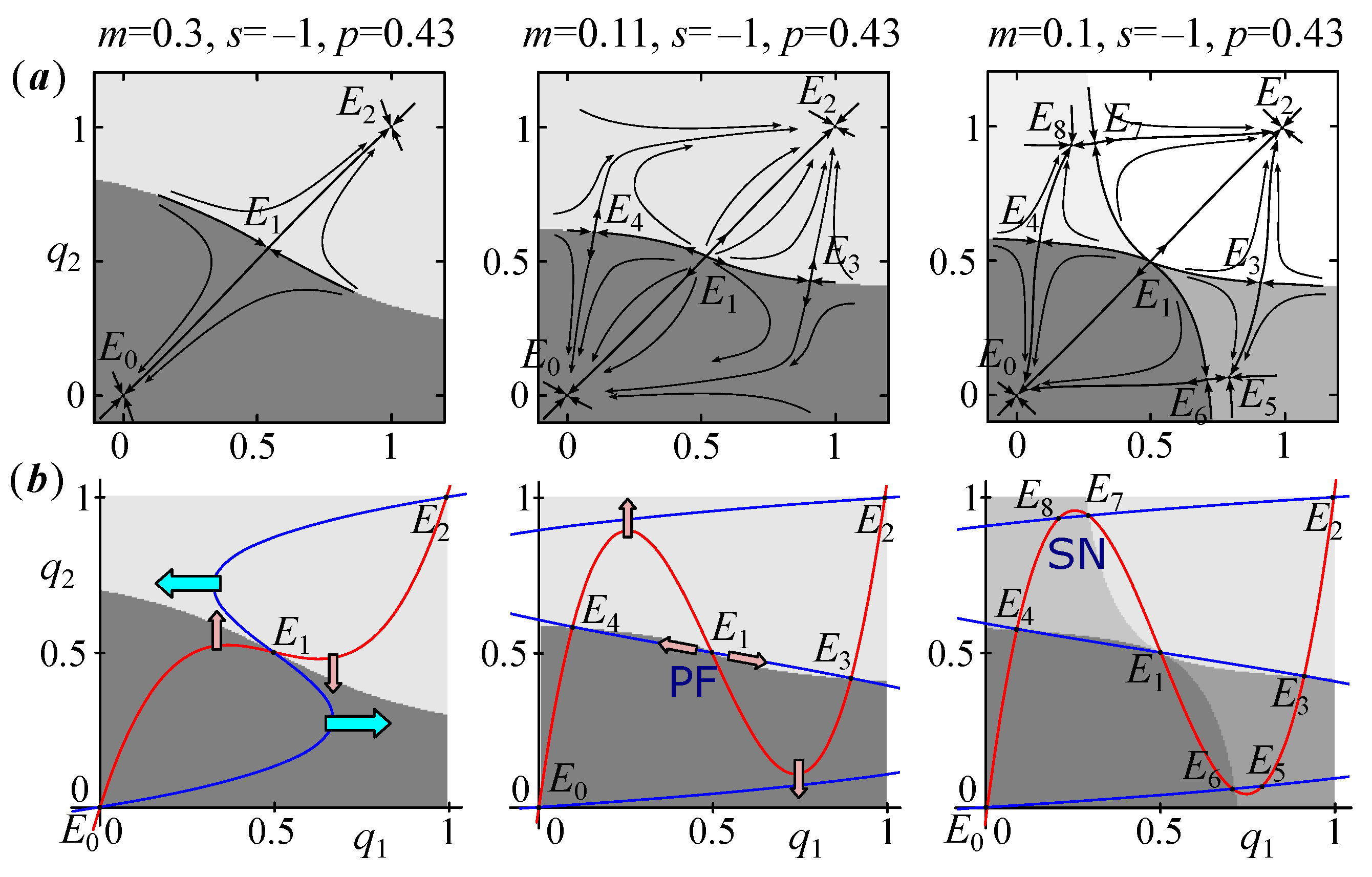
Strictly for and , additional pairs of points, and , are the result of a subcritical pitchfork bifurcation (PF). This means that before this bifurcation, the unstable states and are saddles. After splitting, the pairs of points and , located symmetrically to and , are born around them, and points and acquire stability. As a result, the dynamics are quadro-stable. Figure 3,a allows us to trace the changes in the phase space before and after this bifurcation.
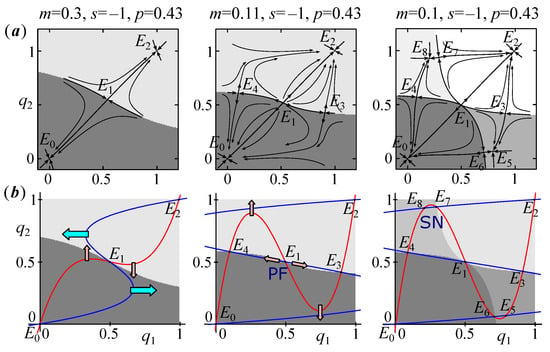
When the value of the parameter p even slightly deviates from , the type of bifurcation in the system (6) changes (Figure 3b). On the one hand, at and , pairs or lie on the phase plane to the left (or to the right) of or (Figure 3d) and are not on both sides of them, as for (Figure 2). As a result, the phase portraits and the basins of attraction are not so symmetrical (Figure 3). On the other hand, the birth of pairs and does not change the type of stability of and ; they were saddles and stay saddles, unlike in the earlier case. Here, each of the pairs and contains a stable node ( and ) and a saddle point ( and ). This means that, for , these pairs of points appear because of a saddle-node bifurcation (SN) and not a pitchfork bifurcation. As a result, at low values of s (, ), system (6) is quadro-stable (there are four stable points).
The size of the attraction basins of the equilibrium states corresponding to the divergence is practically independent of the weight p. Changing p shifts only the boundaries of the basins (separatrixes), as follows. If (the first population is larger), then the boundary shifts toward monomorphism by genotype A, i.e., to point If (the first population is smaller), then it shifts toward monomorphism by genotype a, i.e., to the point .
The study of models (2), (4) and (6) demonstrates that genetic divergence can occur in populations that keep the ratio (weight) of their numbers (), including the populations of different sizes (). In any case, a constant weight is possible with their synchronous growth or fall. In reality, synchronization of the dynamics of coupled elements, as a rule, is observed with a sufficiently strong migration, or if their starting states are close enough. However, our study shows that divergence is observed only at small values of the migration coefficient m (in addition to reduced fitness of the heterozygotes, i.e., ). At (area 4 in Figure 2), the divergence is asymptotically unstable and is observed only as part of the transitional dynamics but for specially selected initial conditions. Divergence is stable only if the migration rate is low enough, namely at (area 5 in Figure 2). Then, the population demonstrates quadro-stability, whereby both monomorphism and divergence are possible, depending on the initial ratio of the concentrations of zygotes with the A or a genome on different sites. For one set of initial conditions, the same type of monomorphism by allele A or a is formed in adjacent sites. For another set, in adjacent sites, polymorphism occurs with a predominance of different alleles—the frequency of allele A is higher in the first one, and the frequency of allele a is higher in the second one, or contrariwise.
3. Population Dynamics. Bazykin Model
A.D. Bazykin, in the article [11], built the model of dynamics of the isolated population, in which the ability of individuals to reproduce significantly depends on the population density. The following differential equation was proposed to describe the change in the size of the local population:
where a is a constant with a dimension of numbers; b is the natural mortality rate; c is the coefficient of intraspecific competition; and k is the coefficient of proportionality.
The value in model (7), characterizing the growth of individuals, has a clear biological meaning, and its inclusion into the equation of dynamics was justified by A.D. Bazykin [11,19]. We emphasize that, for large numbers, when , the value is close to the traditional form . For small numbers, when , this value is approximately proportional to the square of the number of individuals . Indeed, in small populations with a sexual structure, the chance of having a calf depends on the number of encounters between individuals, while, in large populations, this probability linearly depends on the number of females.
For , Equation (7) has three real non-negative equilibrium points , and , where
It is clear that . It is easy to show that is an unstable equilibrium, and and is a stable one. If , then the population size will increase monotonically up to the maximum possible stationary population size B. If , then the population dies out, and its number drops to zero. This trigger character of population dynamics is described more than once for real populations.
Consider a situation in which there are two identical populations in the area, coupled by migration, and the migration intensities are proportional to the size of the population from which these migrants come. Let us denote the migration coefficient (the fraction of migrants per unit of time) as . Here, we obtain two coupled equations [20]:
Below, we will use as variables not absolute, but relative population sizes, i.e., we will use the change in variables . Then, system (8) can be represented as:
where , and .
The equilibriums of system (8) satisfy the following algebraic equations:
Figure 4a shows the graphs of the functions and corresponding to these equations for small values of the coefficient m. Each equilibrium (stationary point) of system (9) corresponds to one of the intersection points of these graphs.
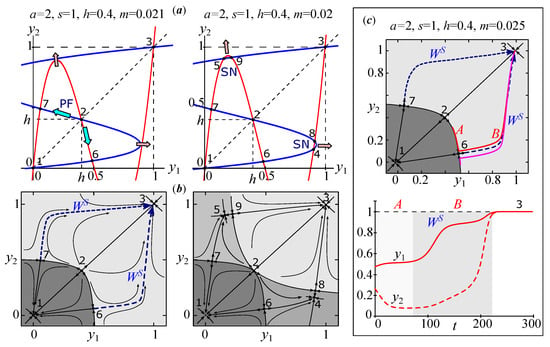
Figure 4.
(a) Plots of functions and (nullclines of system (9)); (b) phase portraits for small migration coefficients; (c) an example of dynamics containing long-term sections with significant differences in numbers at different sites, as part of the transition dynamics. A is the motion along the separatrix, and B is along the manifold .
System (9) can have nine equilibrium points. Three of these correspond to equal values of variables, i.e., equal to the numbers of both populations:
1. ; 2. ; 3. .
We will not give precise values for the remaining six equilibrium points but instead show their approximate values without terms beyond :
4. , ; 5. , ;
6. , ; 7. , ;
8. , ; 9. , .
The approximate coordinates of these equilibriums do not fully describe the behavior of solutions to system (9). In frequency, they exist for any admissible values of the coefficients (), while the number of “true” stationary points changes in a nontrivial way as the coefficients change. Some points merge and disappear, or, on the contrary, are born, splitting off from each other. On the whole, these bifurcations are similar to those studied for model (6). The criteria for the existence and stability of the equilibriums are rather cumbersome, so we will focus on the most significant of them.
Among the nine equilibriums, the fourth and fifth are of the greatest interest to us. They correspond to situations when, in the first site, the stationary population size is close to the maximum, and, in the second, it is close to zero and is supported only by migration. Figure 4a,b show that the pair of points 7–6 appears because of the splitting of the central point 2 (pitchfork bifurcation), and pairs 5–9 and 4–8 appear because of the saddle-node bifurcation away from point 7 or 6. When these points are born, the dynamics go from bistable to quadro-stable.
In the stability study of the equilibriums, we obtained the following results. The first and second points are always stable, and the third point is always unstable. The fourth and fifth stationary points are stable only if the following inequality holds:
Meanwhile, inequality (10) is the necessary condition for existence of the four other stationary points (six-nine) that are unstable within the entire range of coefficients.
Thus, for a small m (), system (9) has four stable equilibrium points, and the phase space must have at least four basins of attraction. From each basin, the trajectories will converge to the corresponding steady states. In addition to the “central” unstable stationary point , for , there are four unstable points that lie on the boundary of the attraction regions. The phase portrait of system (9) for is shown in Figure 4b and is combined with the attraction basins of the bi- and quadro-stable regimes for clarity. These basins look similar to the attraction regions for model (6) with quadro-stability, which describes the dynamics of two alleles at different sites. However, they are weakly similar in the case of bistability. In particular, if system (9) has only three stationary points, 1–3, then the phase space is divided in half by the basins, as in model (6) with . For , the basin of point 3 is smaller than those of point 1 and on the contrary for . The birth of a pair of points, 7 and 6, on the boundary of the basins leads to further narrowing of the corresponding basins (Figure 4b on the right). In model (6), such division of the phase space is not observed because its center point is always .
After the birth of saddle-node pairs 5, 9 and 4, 8, the basins of attraction of steady states 5 and 4 are always formed from a larger basin; which of them will be large depends on the value of h (Figure 4b on the left). The shape of the basins of points 5 and 4 is quite symmetrical and similar to the basins of system (6). The difference is that changing the value h shifts the central point, 2, higher or lower on the phase plane.
Thus, in the system of two coupled identical populations with a small migration rate m, a stable difference in abundance is possible when model (9) has stable states with a low, but not zero, number of the first subpopulation and a high number in the second that does not reach the maximum value. This solution is very interesting because such heterogeneity in density is the result of the reproduction processes in the population and not the result of area heterogeneity or environmental conditions. Apparently, the reproduction mechanism (described, for example, by Equation (7)) leads to a difference in population density in some real populations living in a homogeneous area, a phenomenon widely known to population biologists. Note that the fundamental possibility of the regime containing long sections of dynamics with significant differences in population abundance occurs “long before” the birth of stable points 5 and 4, i.e., before a saddle-node bifurcation. However, such a regime exists only as part of the transient dynamics, when the trajectory, starting from certain initial conditions (far enough from points 1, 2 and 3), tends toward point 1 or 3 intricately. The left side of Figure 4c shows two such trajectories marked in red and pink, and the right side shows the dynamics of and , corresponding to this type of dynamic behavior. A sufficient condition for such a solution is the presence of saddle points 7 and 6. An unstable eigenspace of saddle points produces a stable manifold , which goes around one of the nullclines and ends at points 1 and 3. As a result, the trajectory cannot monotonically reach stable point 1 or 3 for a sufficiently wide range of initial conditions. Apparently, a similar solution exists in the model of two alleles in the system (6).
4. Population Dynamics. Discrete-Time Models
4.1. Local Population
R. May and A.P. Shapiro proposed the use of mathematical models based on fairly simple first-order difference equations to describe the dynamics of populations [21,22,23]:
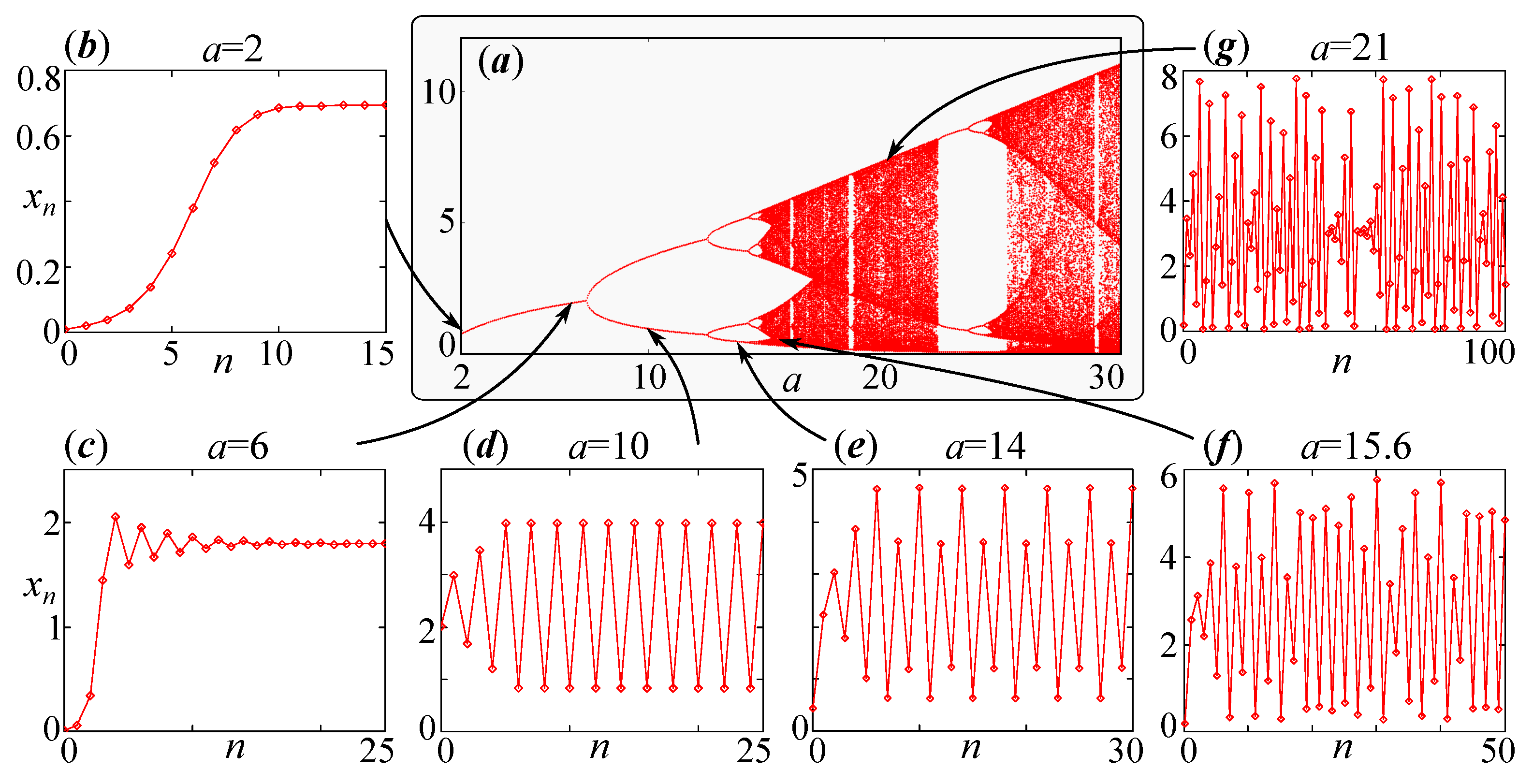
For model (11), it is usually assumed that the function satisfies and at . By selecting a particular function , for model (11), we can numerically construct a bifurcation diagram that characterizes the limiting (asymptotic) regimes depending on the value of the coefficient a determining the rate of population growth. The discrete analog of the Verhulst logistic growth model, for which , and the model proposed by the Canadian ichthyologist W. Ricker [24], for which , are well studied. In order to study model (11), the scaling parameter k usually excludes and passes the dimensionless variables—the “relative” numbers . Then, the discrete analog of the Verhulst model has the form of , and the Ricker model has the form of . Figure 5 shows the dynamics of the Ricker model and the bifurcation diagram.
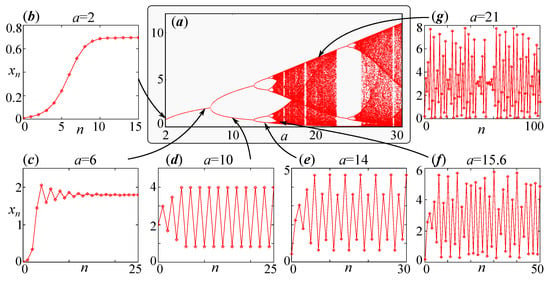
Figure 5.
(a) Bifurcation diagram and (b–f) solutions to difference equation for various values of the reproductive potential a: (b) monotonous convergence to equilibrium, (c) damped oscillations, (d) 2-cycle, (e) 4-cycle, (f,g) irregular (chaotic) dynamics.
Let us briefly consider the type of dynamic regime shown in Figure 5. For , the trivial equilibrium (fixed point) is stable. Further, at , a transcritical bifurcation occurs, the trivial point loses stability and the nontrivial one, , becomes stable up to . At , the period-doubling bifurcation occurs, and, for , a stable 2-cycle is born. The limiting points of the 2-cycle at (periodic points) lie on the “fork” on both sides of the unstable nontrivial fixed point. When the coefficient a increases further, there is a cascade of the period-doubling bifurcation that follows the Feigenbaum universality [25].
Note that in the domain of coefficients with a stable 2-cycle, in fact, there are two stable 2-cycles that differ in the order of transition between the periodic points. In other words, these cycles differ in the phases of oscillations. From some initial conditions, the solutions tend toward one 2-cycle (for example, with maxima for an even n and minima for an odd n), and from other initial conditions, they tend toward the second one (with maxima for an odd n and minima for an even n). Thus, for values of the coefficient a, which corresponds to a stable 2-cycle, model (11) is the phase bistability.
4.2. The System of Two Populations Coupled by Migration
Let us describe the dynamics of coupled populations (metapopulation). Of all of the possible types of coupling between local populations, consider the migration that occurs right after reproduction. If both subpopulations have equal reproductive potential () and equal migration rates (), the equations of the population dynamics look similar to this:
For system (12), in particular, the similarity relations are established based on the Feigenbaum universality, the bifurcation mechanisms of the synchronization of the dynamic variables are described, etc. [26,27,28,29].
We will consider the features of the dynamics of system (12) with the admissible values of the reproductive potential a and the fraction of migration m for a non-symmetric map f based on the Ricker stock-replenishment model:
At , system (13) has the form:
and describes the dynamics of symmetrically coupled local populations with reproduction according to the Ricker model [30,31]. As in the single difference Equation (map) (13), system (14) has the unique nontrivial fixed point . We will further call the in-phase solutions (cycles) of the system (14), for which the following is true: ( is small enough) for . If the maximum closeness of the variables occurs at a certain shift in the season number n of one variable relative to another, i.e., for , (T is the cycle period), then this solution to the system (14) will be called out-of-phase. Accordingly, if and , then the values of the phase variables are asymptotically equal, i.e., for , and the dynamics of the two coupled populations are complete or fully synchronous.
As is known, for systems of the form of (12) with a unimodal reproduction function f, its completely synchronous in-phase solutions can be described by a single map . In-phase regimes lie on the bisector of the first coordinate angle around a nontrivial fixed point, which obviously holds for system (14). Out-of-phase regimes of (14), are located symmetrically around the segment , .
Considering that, for the Ricker model , it is easy to calculate the characteristic polynomial of system (14) in the nontrivial fixed point:
which has the roots and , whence it is easy to understand that the fixed point of system (14) is stable in the same place as the analogous point of map (13), i.e., for , and further evolution of the in-phase regimes follows the classical scenario of the transition to chaos through the period-doubling bifurcation.
The simulation shows that the out-of-phase regimes ( for ) are possible outside the region defined by the inequality . Moreover, on the lines for and for , the multiplier of system (14) is equal to . When the coefficients pass through these lines, in addition to the in-phase ones, various stable out-of-phase attractors may appear in system (14). Which one is implemented depends on the starting point . This property is related to multistability, which comprises the existence the several stable solutions to system (14) for one set of the coefficients—several attractors with different degrees of synchronization (in-, out-of- or anti-phase cycles with different periods) arise depending on the initial conditions.
4.3. Features of the Formation of In-Phase and Out-of-Phase Two-Cycles
The most interesting are the mechanisms of formation of in-phase and out-of-phase regimes in the model (14). Consider these using the example of 2-cycles.
To determine the periodic points with a period of two, we apply map (12) twice for points and :
where , . Then, the periodic points can be calculated from the system:
Solving numerically Equation (16) for each variable, we obtain two curves on the phase plane, symmetric to the bisector of the first coordinate angle. The intersections of these curves correspond to the periodic points with a period of two (Figure 6). On the other hand, the solution to system (14), corresponding to the out-of-phase cycle with a period of two (), satisfies the relations: , and , , whence, with (12) and (15), the elements of the out-of-phase cycle can be found from the following system:
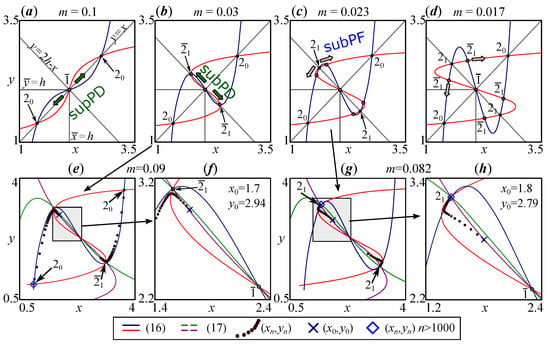
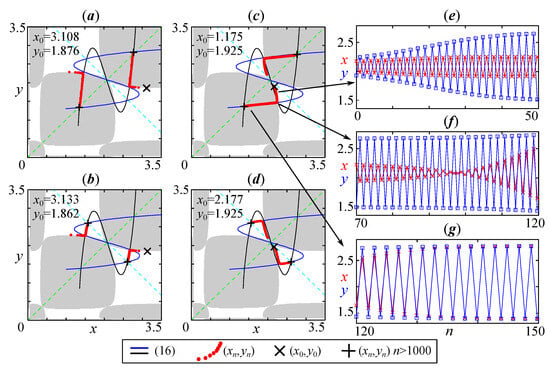
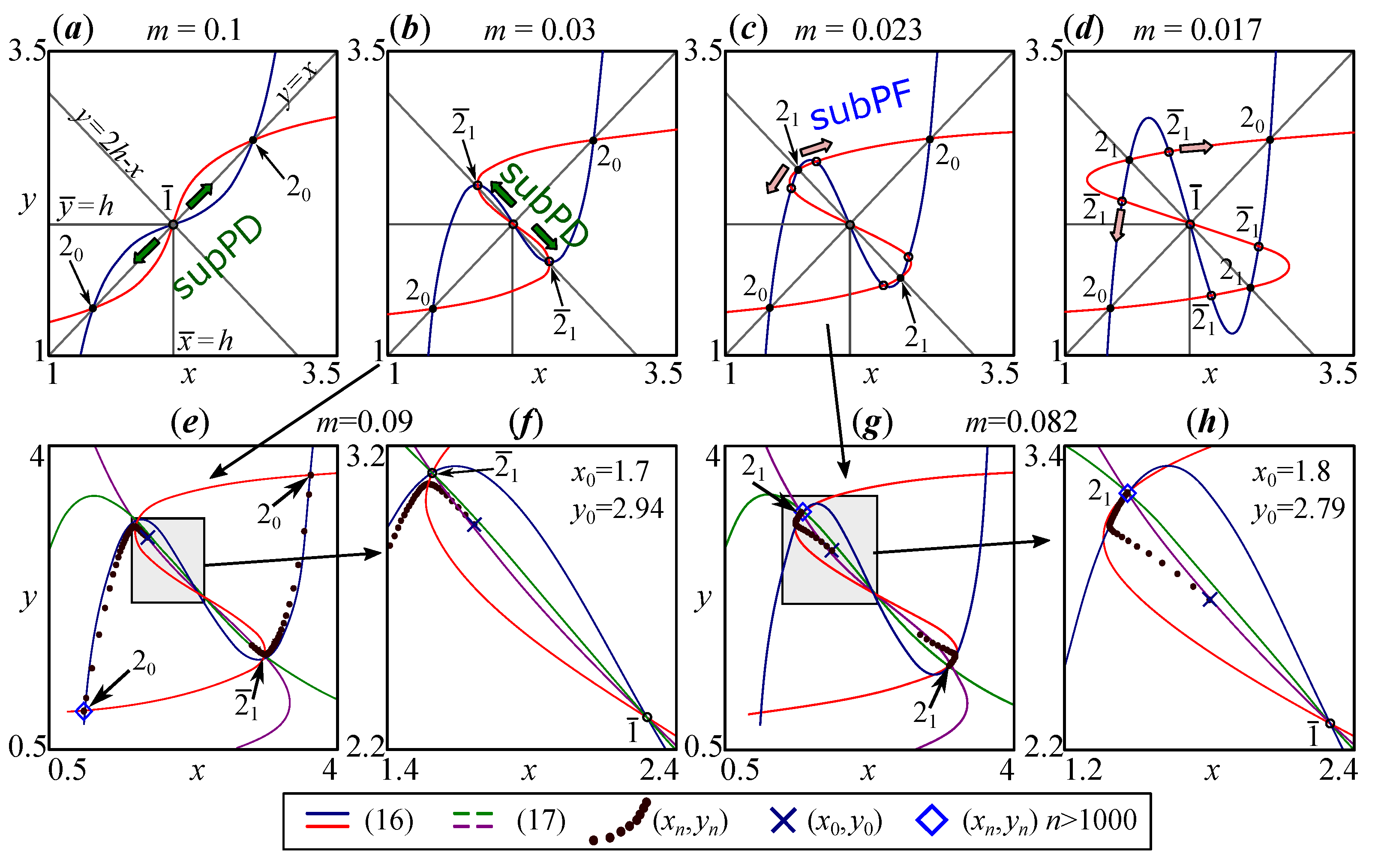
Figure 6.
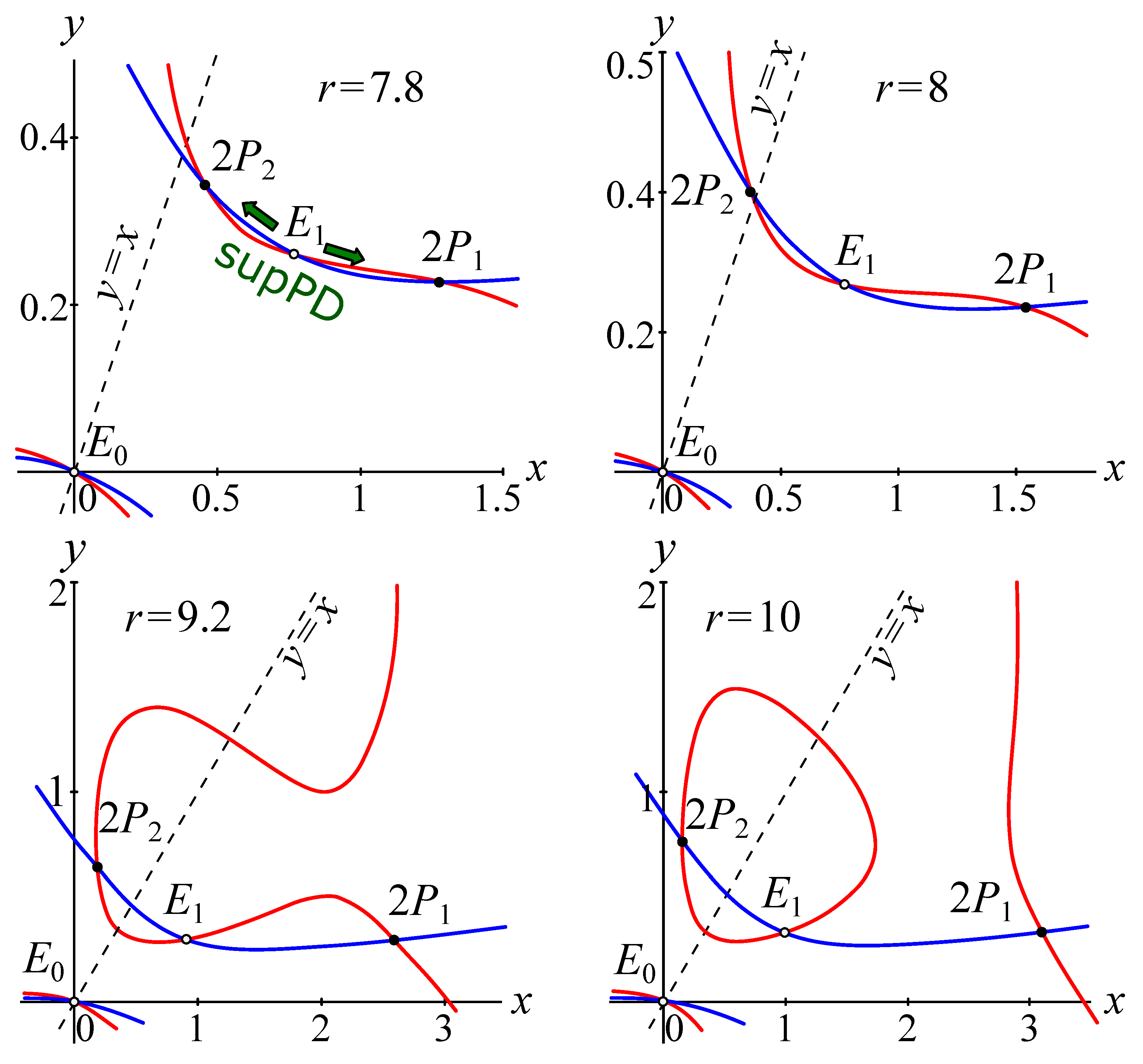
(a–d) Evolution of non-zero periodic points of system (16) because of super- and subcritical period-doubling and pitchfork bifurcations (supPD, subPD and subPF) with a decreasing coupling coefficient m at and . The unstable fixed and all periodic points of the 2-cycle correspond to the intersection points of the curves for (16) (nullclines); the points of precisely the out-of-phase 2-cycle correspond to the intersection points of the curves for (17). Transition from (e,f) the unstable out-of-phase 2-cycle () to (g,h) the stable one () at .
It is easy to see that system (17) satisfies the trivial and nontrivial fixed points, as well as the desired pair of periodic points, , which corresponds to the out-of-phase cycle of system (12), but not the points of the in-phase cycle . For , this also applies to system (14). It is easy to show that (16) and (17) have points as their solution if and only if (), i.e., outside the stability domain.
Let us follow how solutions (16) and (17) change with . For , i.e., in the stability domain, the curves constructed from (16) and (17) intersect only at points corresponding to the fixed points and . With the growth of the reproductive potential a, the number of solutions to (16) expands significantly. Figure 6a–d show the curves given by (16) after eliminating the trivial solution.
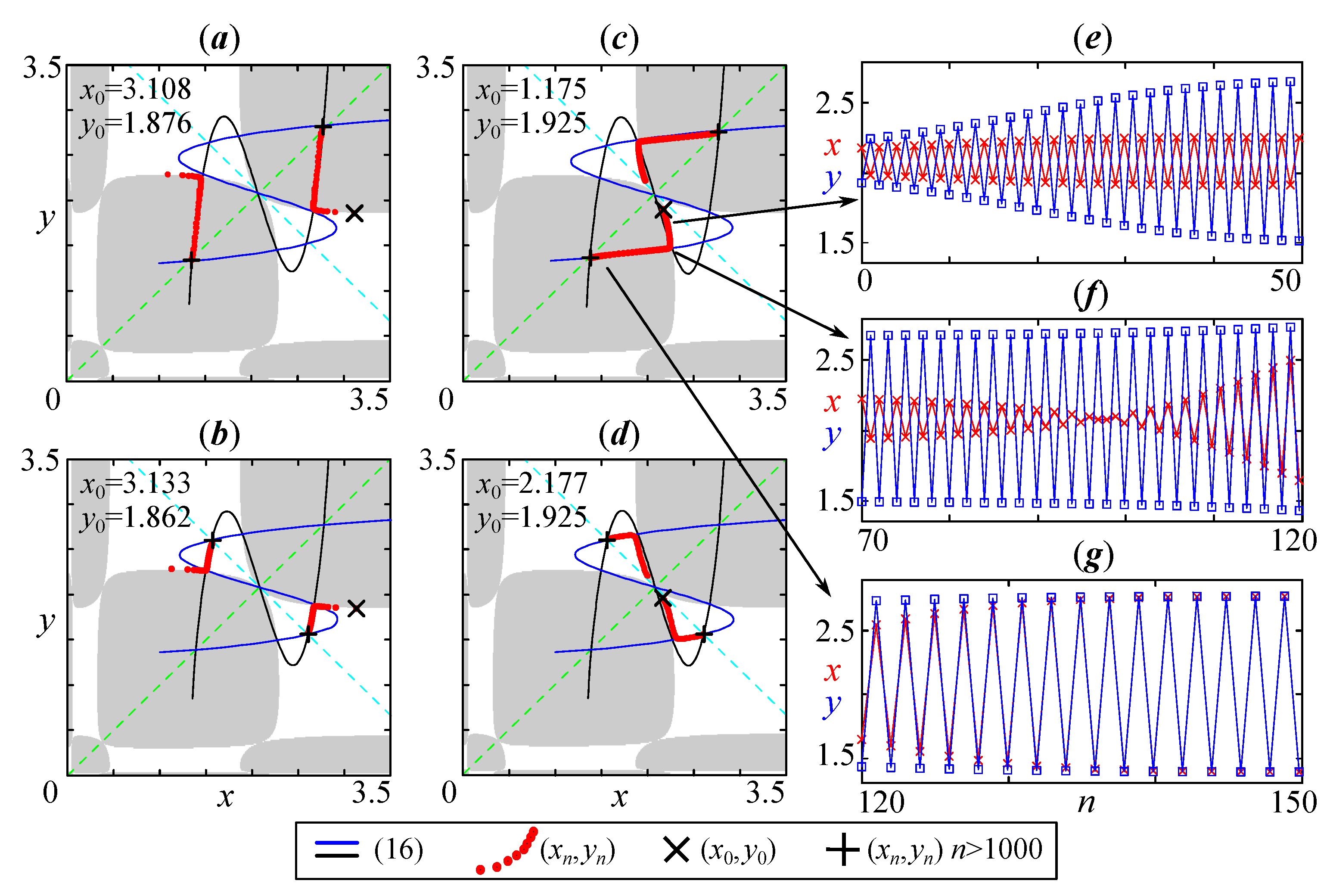
After the first bifurcation (passing through ), the solutions to the system (16) are three points with positive coordinates—the unstable fixed point and the stable periodic point corresponding to an in-phase 2-cycle (Figure 6a). With a decrease in the coupling coefficient m, when the coefficients fall into the region , among the roots of (16), another pair of solutions appears, corresponding to the periodic point of an unstable anti-phase 2-cycle (Figure 6b). With a further decrease in the coefficient m, this anti-phase 2-cycle becomes stable. This occurs during the subcritical pitchfork bifurcation (subPF), at which two additional pairs of solutions appear (Figure 6b–d). These roots of (16) correspond to unstable out-of-phase 2-cycles with partial out-of-phase synchronization (unequal oscillation amplitudes). The birth of these unstable cycles ( in Figure 6d) leads to the possibility of stable out-of-phase dynamics ( in Figure 6d). Figure 6e–h, in addition to the curves of systems (16) and (17), show the trajectory of the model (14) (Figure 6e,g) and the enlarged fragment of the phase plane (Figure 6f–h), including the stable periodic point and the unstable fixed point . Figure 6e–h illustrate the process of the full in-phase and out-of-phase synchronization of population dynamics described in (14) for a case when the out-of-phase cycle exists but is unstable (Figure 6e,f) and when it becomes stable (Figure 6c,d).
Let us now consider the formation mechanism of cycles and . Figure 7 shows the relative position of the basins of attraction, the curves of (16) and the trajectory of system (14). The gray area is the attraction basin of the in-phase synchronous regimes, and the white area is that of the anti-phase ones. Converging to one of the stable cyclic states, the trajectory of the system can pass in the vicinity of an unstable point (a state with partial synchronization). Part of the trajectory before reaching this unstable point lies on the boundary of two synchronization basins (gray areas). Figure 7 shows two ways to achieve full synchronous and anti-phase regimes when the trajectory passes near an unstable pair of points. As a result, the synchronization here will take a long time due to the proximity of the initial states and the basin boundary. So, in the neighborhood of the unstable point, the capture of phase (order of transition between periodic points) occurs. In this moment, one oscillator (subpopulation) “stops” for two iterations, which is shown in the time realizations in Figure 7e–g.
5. The Characteristics of Population Cycles with Two Age Stages
Consider a population with an age structure that can be described by a set of two overlapped generations: the younger one, which includes immature individuals, and the adult one involved in reproduction. Denote by the size of the younger age class in the nth breeding season, and is the size of the reproductive part of the population. The breeding season ends with the birth of newborn individuals of the next generation. We assume that the time between two adjacent seasons is enough for the maturation of the youngest class of individuals to the sexually mature state and the newborns (or larvae) to the young immature age. Let us assume that the survival and reproductive capacity of mature individuals do not depend on their chronological age. This is true for organisms with a short lifespan, including two or three mating seasons, as numerous insects, fish, small mammals, two- and three-year-old plants, etc. We can write the following system of difference equations describing the relative numbers of the considered age groups in adjacent generations:
where A is the birth rate, and B and C are the survival rates of the younger and older age classes, respectively.
Regulation of population growth by density-dependent birth control is observed in many animals, especially small mammals, for which the birth rate decreases as the population size increases. Basically, density-dependent regulation of fertility is expressed through the stress syndrome, leading to a decrease in sexual activity and a decrease in fertility, up to the resorption of part of the embryos. In particular, this is typical for species subject to strong population fluctuations, such as lemmings and voles [32]. To model the dynamics of such populations, the survival rates can be considered the constants , and fertility, by analogy with the Ricker model, can be written as , where r is the reproductive potential and and are coefficients describing the intensity of the impact of the numbers (densities) of the immature and mature age class on the decrease in fertility. Considering this and passing to dimensionless variables or relative values of the numbers and , we can rewrite model (18) in the form:
where the coefficient characterizes the influence of the younger age class on the reproduction limitation.
Papers [33,34,35] studied the dynamics of the two-age population described by model (19). It was shown that the more effective mechanism for regulating population growth is a decrease in the birth rate with an increase in the number of individuals. However, with large reproductive potentials and high survival rates of individuals, a decline in the birth rate with an increase in the number of individuals can lead to a loss of stability and complex population fluctuations.
In particular, it was shown that when birth control is performed mainly by the younger age class, i.e., for relatively large values of the coefficient , a loss of stability leads to the two-year oscillations as in the original one-dimensional Ricker model. Further, with such a birth regulation, only a period-doubling bifurcation is observed, and the larger the value of , the lower the values of the reproductive potential r, at which fluctuations occur.
Figure 8 shows that a pair of periodic points is split off from the nontrivial fixed point , corresponding to population fluctuations with a period of two (2-cycle). Immediately after period doubling, points become stable, while point , on the contrary, loses stability. The main feature of the generated periodic regime based on points is that right after the period-doubling bifurcation, the periodic and nontrivial fixed points lie below the bisector of the first coordinate angle. This shows that, in the asymptotic case, the amount of the younger age class always exceeds the amount of the older one. However, the subsequent increase in the reproductive potential r leads to the fact that at certain points in time, n, the number of mature individuals is several times greater than the number of immature individuals. Figure 8 shows that as r increases, point moves to the right along the phase plane, while point moves to the left, pressing against the y-axis. As a result, the dynamics of the immature and mature individuals are anti-phase: for even seasons, n, the number of mature individuals exceeds the number of immature ones; for odd seasons, n, the number of immature individuals is greater than the number of mature ones. Apparently, synchronous regimes of dynamics are not possible in the system (19).
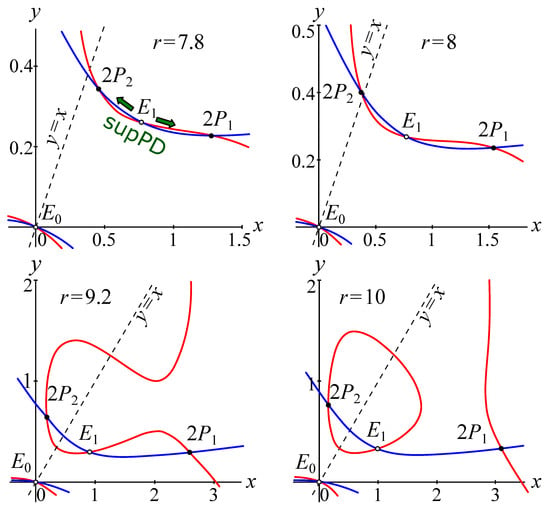
Figure 8.
Nullclines (color lines) of system (19), showing the birth and location of the periodic point (2-cycle) on the phase plane at , and (the value of r is shown in the figure).
At , a two-aged population can be described as two groups of individuals (subpopulations) that keep non-zero sizes only due to flows of individuals from one group to another. Here, the conditions for the period doubling and the existence of a stable periodic point for system (19) coincide with the conditions for transcritical bifurcation, when the nontrivial fixed point and the trivial point merge. As a result, for in the asymptotic case, the 2-cycle lies entirely on the coordinate axes: for an even n, the number of immature and the number of mature (for ); for an odd n, on the contrary, and . The dynamics are obviously out-of-phase.
If birth control is performed mainly by the number of adult mature individuals, i.e., for a small (), then a loss of stability can occur only with the complex conjugate roots of the characteristic equation leading to the birth of the limit invariant curves in model (19). Accordingly, a decrease in the birth rate with an increase in the number of adults can lead to complex population fluctuations. It appears that this mechanism determines the dynamic behavior of small mammals, such as lemmings and voles [36].
An interesting dynamic behavior of system (19) is observed at , i.e., without birth control by the younger age class. With the growth of the reproductive potential r, the loss of stability of the nontrivial equilibrium follows Neimark–Sacker bifurcation (line in Figure 9a), or, with a decrease in r, according to the transcritical bifurcation, when the nontrivial fixed point changes in stability with the trivial one (line in Figure 9a). In addition, at low values of r, a subcritical period-doubling bifurcation occurs. However, the periodic points of the 2-cycle have negative coordinates (domain 3 in Figure 9). Figure 9a shows how the bifurcation lines of model (19) move as the coefficients c and s vary. At , the and coincide. These lines go down and move away from each other as the coefficients c and s increase. The line, on the contrary, goes up in the parameter space. As a result, as the values of c and s increase, the domain of stability expands.
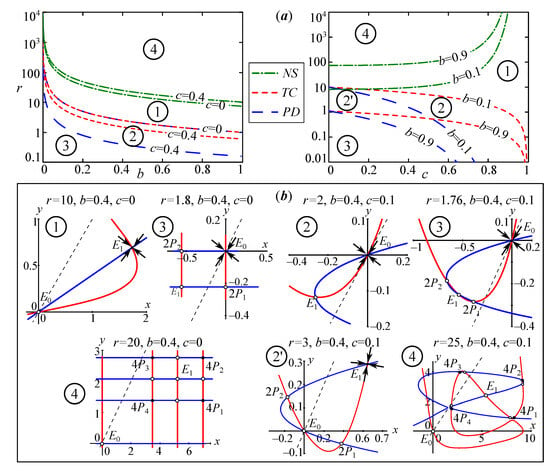
Figure 9.
(a) Parametric portraits of system (19) at and variations of the coefficients c and s. The lines , and are the Neimark–Sacker, period-doubling and transcritical bifurcations, respectively. (b) The nullcline on the phase plane for simple dynamics, when a trivial (domain 2–3) or nontrivial point (domain 1) is stable, and the others are saddles.
In domain 4 in Figure 9 for and a small c, what is most interesting and important is a strong resonance 1:4 (Arnold tongue), which can be described as a periodic point with a period of four designated as (). It is easy to show that strictly at and system (19) has the form of the Ricker stock-recruitment model:
which describes the dynamics of every second element of the sequence . The second variable y of the model (19) depends linearly on x: . As a result, the birth of a strong 1:4 resonance in the complete system (19) corresponds to period doubling of the fixed point of Equation (20), which occurs at . Then, the cascade of period doubling in map (20) corresponds to the birth of resonances of 1:8, 1:16, etc. in system (19). In the -plane, these resonant cycles lie on nullclines that are parallel to the coordinate axes (Figure 10a and Figure 11a). Figure 8, Figure 9 and Figure 10 show the nullclines constructed for Equation (19), which were iterated four or eight times.
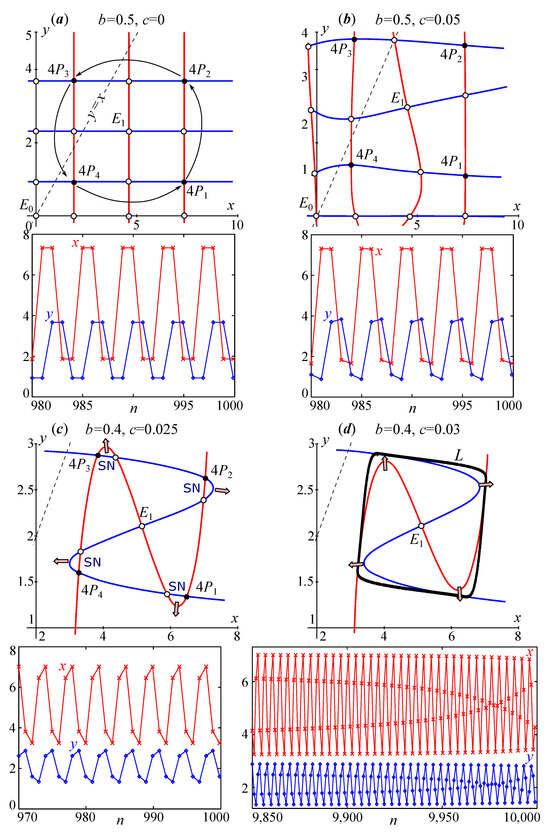
Figure 10.
The nullclines and examples of dynamics of system (19) with and .
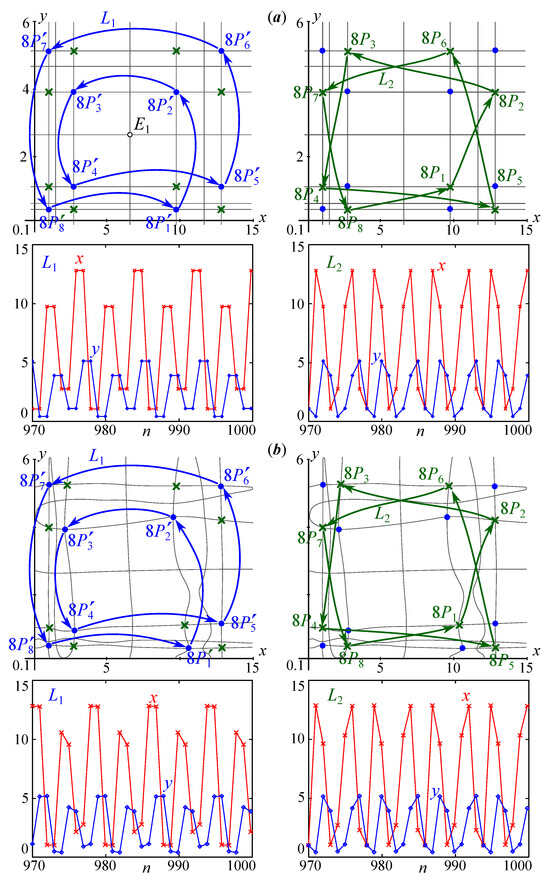
Figure 11.
(a) Two between points. It’s all in the caption. types of 8-cycles of Equation (20) or system (19) with , , and , (b) and their changes at small . The blue dots () and green crosses () are the points of different cycles ( and ); the arrows between them show the order of transitions between points.
It is interesting to follow how the cycles of the reduced Equation (20) change in the complete system (19) with a small variation in the coefficients c and and to see what the features of the dynamics are.
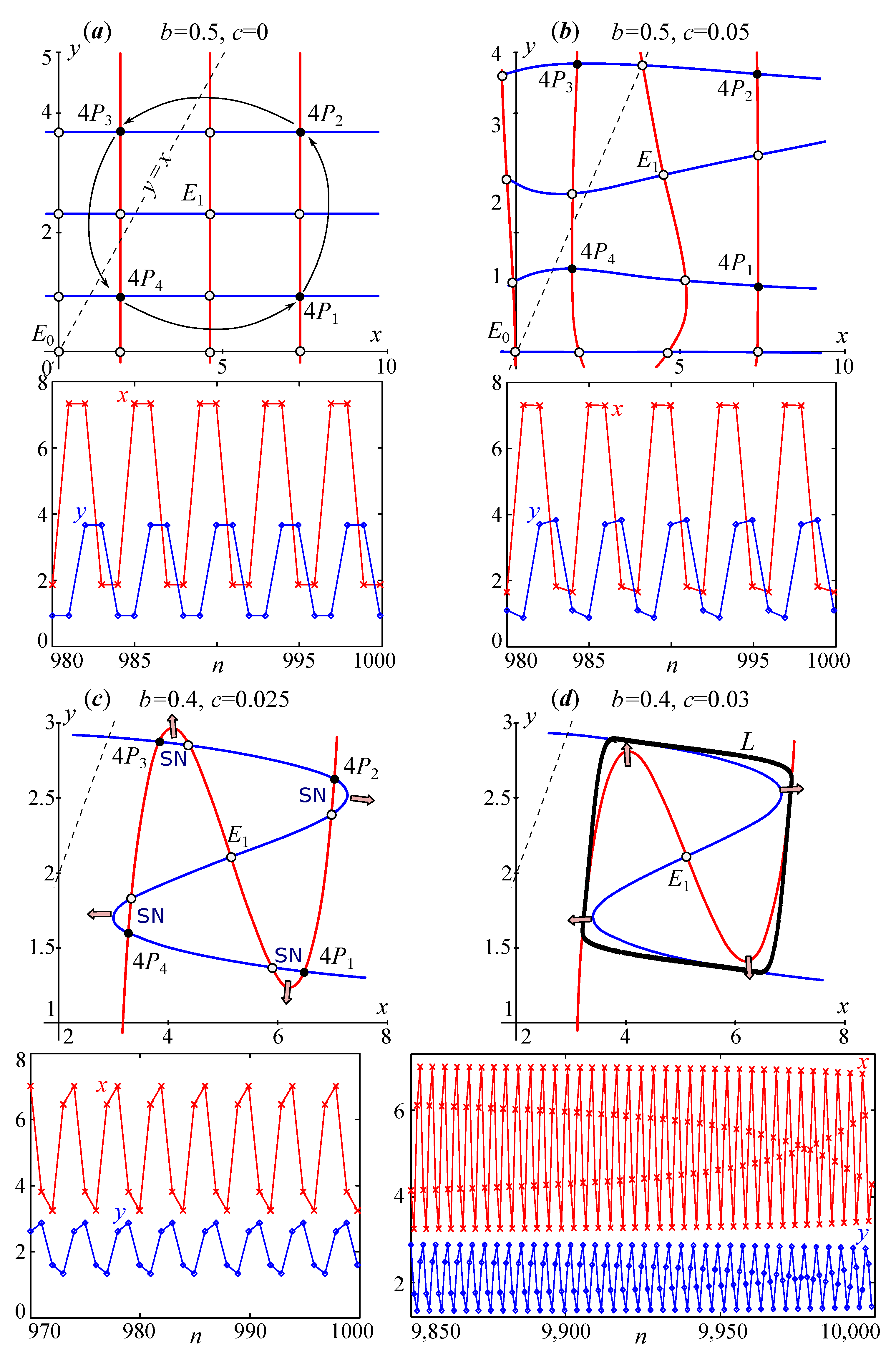
Figure 10 shows the breaking of the resonant 4-cycle as the coefficient c increases. From Figure 10b,c, it can be concluded that the nullclines twist but still have intersections at points () and adjacent saddles. However, at the critical values of c or b, these points disappear, and a limiting invariant curve is formed. As a result, the breaking of the resonance of 1:4 corresponds to the saddle-node bifurcation in the four-times iterated map (19).
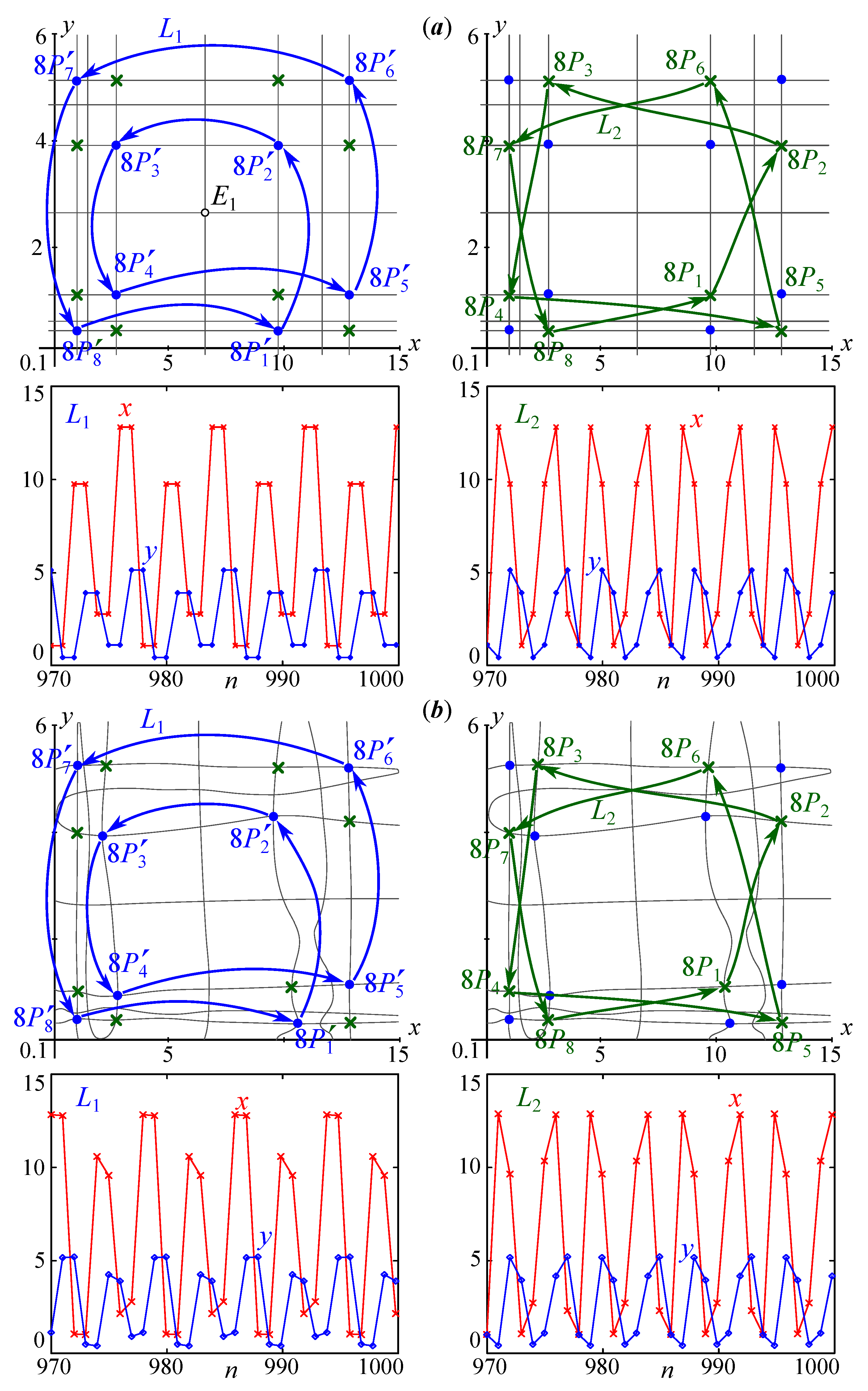
Figure 11a shows the 8-cycle, which, for the complete system (19), results from the period-doubling bifurcation of the resonant 4-cycle (but not the 1:8 resonance). Unlike the 4-cycle, it has at least two versions depending on the initial conditions. These two 8-cycles, first of all, differ in the sequence of jumps between the periodic points , as well as in the phase shift in the variables x and y relative to each other (phase multistability). However, for and , the set of values of the phase variables in the asymptotic case is limited, and the values of x and y lie at the nodes of a rectangular lattice formed by the nullclines of the four-times iterated map (19). Therefore, the 8-cycles from Figure 11 have exactly four, not eight, values for x and y, which alternate in a different order depending on the initial conditions.
For a small , the complete system (19) keeps these two types of cycles of Equation (20), although the values of the phase variables no longer lie at the nodes of the rectangular lattice, since the nullclines, here, are deformed (Figure 11b). As a result, the number of values of the variables x and y in the asymptotic case is exactly eight. The second cycle, marked in Figure 11b as , collapses as c grows, i.e., the growth in the survival of the second subpopulation (mature individuals), because of the saddle-node bifurcation. Therefore, system (19) for a sufficiently large c has a unique 8-cycle.
6. Reduced Fitness of Heterozygotes in a Population with Two Age Stages
When the reproductive potential r is genetically determined by one adaptive autosomal diallelic locus, the equations of the dynamics for the two-aged population are transformed in an obvious way. They are supplemented by the equations of the gene frequency dynamics, which characterize the change in the genetic structure during the evolution [37]. With density-dependent birth control, as in the previous section, the model equations have the form [15]:
With density-dependent control of the younger age class’s survival, the equations have the form:
where and are the frequency of allele A in the older and younger age classes. The coefficients , and characterize the reproductive potentials of the genotypes , and , and is the average reproductive potential.
For models (21) and (22), there are three types of natural selection, as for model (1). The existence and stability of these genetic states (fixed points) depend on the ratio of the reproductive potentials of genotypes. Let us consider the most important phenomenon, in which the genetic divergence occurs between adjacent generations, as well as new dynamic effects caused by the age structure of the population.
With reduced fitness of the heterozygotes (), both monomorphic population states can be stable, and the system tends toward one of them, depending on the initial conditions. Moreover, in a population without an age structure (for example, described by model (1)), the dependence of the asymptotic genetic structure on the initial conditions looks extremely simple: for , it tends toward equilibrium and, for , toward . While in an age-structured population, there is a very complex sequence of attraction basins of monomorphic states. Consequently, the result of natural selection in a limited population depends not only on the initial allele frequency but also on the abundance and age structure of the population.
In addition to the well-studied bistability associated with the stability of two monomorphic states, we somewhat unexpectedly found a completely new solution to the models for the dynamics of age-structured populations with reduced fitness of the heterozygotes. This regime occurs at low values of the survival coefficient of mature individuals and consists of the asymptotically stable cycle in the genetic structure. For this cycle, the predominance in the population of one allele in even years and the other in odd years is typical (Figure 12). This periodic regime, arising under certain initial conditions, means the possibility of the stable primary genetic divergence (differentiation) of individuals of adjacent generations. The size of its attraction basin grows as isolation increases between generations, i.e., with a decrease in the survival of mature individuals. As an example of such a regime of the dynamics with complete isolation between generations, we can note a pronounced allozyme differentiation of Pacific pink salmon populations (Oncorhynchus gorbuscha), which spawns in its second year of life. Because of this particular peculiarity of salmon, individuals of even and odd generations breed and grow in the same river but with strict reproductive isolation. As a result, the even and the odd years’ subpopulations produce a two-year cycle of numbers. Using the data on the genetic variability of pink salmon, it was shown that there are significant genetic differences between the generations of even and odd years [38,39,40]. Thus, along with the known and expected regimes of evolutionary dynamics in the simplest models of natural selection, new and interesting effects appear that require further research and conceptualization.
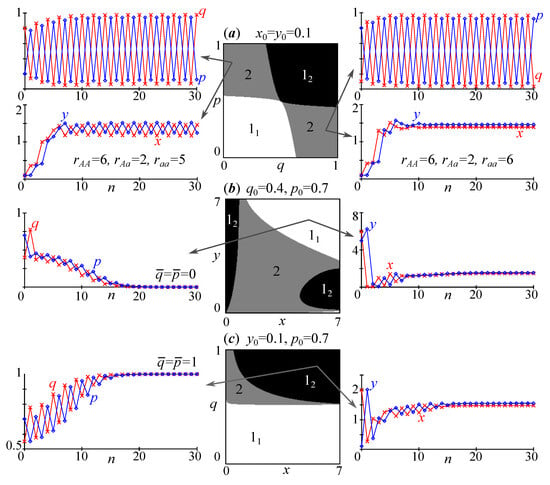
Figure 12.
Attraction basins and examples of the dynamics of gene frequencies and population sizes by model (21) with reduced fitness of the heterozygotes with , , and . (a) In the gray basins, there are the stable fluctuations of the gene frequencies of adjacent generations with a period of two. With a small difference in the reproductive capabilities of homozygotes (), the gene fluctuations cause the population fluctuations (the example on the left). The white basin corresponds to a monomorphism with (b) ; the black basin corresponds to (c) .
7. Discussion
Let us sum up and list the scenarios for the transition from bistability to quadro-stability in the population models and compare the results of the simulation with real biological systems.
The first class of models with the studied scenario describes the evolution in a system of identical panmictic Mendelian single-locus diallel populations connected by migration and under the influence of natural selection directed against heterozygotes (disruptive selection). In these models (systems (3) and (4)), the transition from bi- to quadro-stability occurs as follows. For sufficiently large values of the migration rate (), the system of the populations is bistable and has two stable monomorphic states with no allele A or a in the whole system and a state with equal concentrations of both alleles (saddle point). As the migration coefficient decreases, a pair of unstable saddle points, corresponding to the genetic divergence, splits from the central saddle point. Then, these states become stable nodes after pairs of new saddles split from them. As a result, for , the dynamics of system (4) become quadro-stable, i.e., depending on the initial conditions, over time, the populations tend toward four fundamentally different genetic states—a monomorphic state with a zero concentration of allele A or a or a polymorphic state with unequal allele concentrations with a predominance of one allele or another.
For different-sized populations (system (6)), the scenario of the transition from bi- to quadro-stability is somewhat different. As the migration coefficient decreases, pairs of additional points do not divide from unstable saddle points by pitchfork bifurcation but are born from saddle-node bifurcation when one point from the pair is a saddle, and the other is a stable node. As a result, system (6) becomes quadro-stable and has dynamic regimes similar to those of (4).
Let us consider how the simulation results correspond to the observations of genetic divergence in real population systems. Generally speaking, there are very few reports of stable primary genetic divergence of natural populations living in a homogeneous area. Richard Lewontin, for example, explained this because researchers usually rarely report their attempts to find a correlation between geographic variability and the action of any natural factors, if they obtained a negative result [41]. Nevertheless, examples of such studies can be found. Interesting cases of stable spatial heterogeneity of the genetic structures of natural populations are shown in the work of Yu.N. Novozhenova with co-authors [42]. In this work, in particular, for three populations (two adjacent and one spatially distant) of the May chafer (Melolontha hippocastani), they studied strong color dimorphism. Moreover, one morph significantly predominated in one of the adjacent populations, while the alternative morph predominated in the other. These differences in morph concentrations persisted throughout the 5-year study period. The authors did not find differences in soils, forest types, or vegetation cover in the study territories occupied by the of beetle populations. They proved an attempt to explain the beetle color differences by the time of forest felling also unpromising. Thus, there are good reasons to believe that we are dealing with genetic divergence in a homogeneous area. It is possible to show more strictly the possibility of genetic divergence in a homogeneous area and minimize the influence of environmental heterogeneity only in laboratory conditions.
In the late 1970s, the team led by Yu.P. Altukhov performed a large-scale experiment for modeling genetic processes in the Drosophila population system (Drosophila melanogaster) [43,44,45]. They studied the dynamics of allelic concentrations in a system of 30 box populations connected by migration into a ring structure. The average number of individuals in the box population was 135 individuals. They defined the average migration coefficient m as approximately . As the genetic markers for identifying differences between populations, they chose a co-dominantly inherited autosomal locus, encoding the synthesis of -Glycerophosphate Dehydrogenase (-GDH), the variants of which are easily identified electrophoretically.
A total of 150 pairs of heterozygous males and females of D. melanogaster were placed in one box. They were given the opportunity to breed freely and settle in the ring range. After the colonization of the boxes and stabilization of the fly’s population dynamics, they created a local panmictic population with the same abundance and almost completely repeated the gene pool of the ring system. Every few successive, non-overlapping generations, approximately 30% of each subpopulation was examined, averaging 40 flies, to estimate the -GDH allele concentration. The distribution of the allele frequencies over the subpopulations of the ring system quickly gained the form of several peaks, at which one form of the allele was fixed in several neighboring populations, and the alternative allele was fixed in others. This spatio-temporal structure has been preserved in time. At the same time, the average concentration of one form of the -GDH alleles in the ring system slightly increased over 60 generations, while in the panmictic population, this allele was completely replaced by the allele of the alternative form. Based on the dynamics of alleles in the panmictic population, the selection coefficients were estimated, showing the presence of a disruptive type of selection with reduced fitness of the heterozygotes [46]. Comparison of the experimental data with the simulation results allows us to conclude with great certainty that this laboratory population system is characterized by a disruptive selection, which provided the primary genetic divergence of fly subpopulations.
In molecular genetic studies of natural populations devoted to genetic divergence and speciation, two or more isolated populations that split some time ago are most often compared. There are enough examples of consanguineous populations with significant phylogenetic differences. For example, these include populations of char of the genus Salvelinus in the lake and lake–river systems of the Kamchatka Peninsula [47]; the northern slimy salamander (Plethodon glutinosus), living in several southern states of the United States [48]; Jenynsia lineata, which is a small viviparous fish from South America [49]; and the black-throated blue warbler (Dendroica caerulescens), living in North America with northern and southern subpopulations [50]. With the variety of reasons for the disjoining of these populations, it can be assumed that they are characterized by disruptive selection of certain traits and reproductive isolation between extreme forms. Because of the spread over long distances, spatial isolation arose with small zones of hybridization.
The results of the mathematical models of evolution, shown in this review, allow us to look differently at the causes and mechanisms of speciation. In particular, the reasons are clear that even minimal differences in the initial numbers or ratio of genotypes, caused by small perturbations, eventually lead to the accumulation of genetic differences and the separation of populations. The described transition from bi- to quadro-stability seems to play a key role in genetic divergence.
On the other hand, in the system of two populations coupled by migration functioning according to the Bazykin Equation (model (9)) there is a scenario of a transition from bi- to quadro-stability, such as in system (6). A minor difference between models (6) and (9) is observed in the change in the symmetry of the attraction basins of different stable states with a variation in the model coefficients.
In models of population dynamics based on difference equations (maps), there is a transition of a slightly different kind. There is a transition from the phase bistability of the 2-cycle to the phase quadro-stability, which occurs at the birth of anti-phase 2-cycles and without bifurcations of the equilibriums (fixed points). Despite this, for a system of two identical populations coupled by migration (system (14)), the transition scenario is actually similar to the scenario for the birth of quadro-stability of the allele frequencies with reduced fitness of the heterozygotes (models (4) and (6)), in terms of similar phase portraits, nullclines and bifurcations. Here, we see the following bifurcations. The first period doubling leads to the birth of an in-phase 2-cycle corresponding to the phase bistability. Further, a pair of saddle periodic points, corresponding to an unstable anti-phase 2-cycle, separates from the unstable fixed point. Each of these saddle points later splits into a pair of unstable out-of-phase periodic points, and the out-of-phase 2-cycle becomes stable. As a result, the dynamics of two coupled populations is phase-quadro-stable, when, depending on the initial population sizes, the trajectory tends toward one of the four stable periodic regimes that differs in its degree of synchronization. As for model (4), in this system, the additional points divide symmetrically from the elements of the anti-phase -cycle according to transcritical bifurcation. We can assume that, for non-equal-sized populations, the scenario of the transition to quadro-stability has a more general form (as in model (6)), according to saddle-node bifurcation. It probably occurs for populations that have ecological niches of different sizes, different birth rates or different intensities of migration flows. This is typical for populations whose reproductive capabilities change during evolution [51]. This definitely requires further research.
The transition to fluctuating dynamics (movement between periodic points), rather than to a single equilibrium state, is a typical behavior of real population systems. There is still no single frame of mind on the causes of population fluctuations. Short cycles are well known, for example, for populations of small mammals such as voles, lemmings, hares, etc. As a rule, the population cycles do not have exactly the same values in the population peaks of the time series. However, the intervals between the peaks can be constant, i.e., the phase of the cycles is unchanged. Random external influences perturb the absolute values of the numbers. At the same time, for the noted species, a certain variability in the lengths (periods) of the cycles is described. These shifts in the cycle lengths were found both over long periods of observation (changes in time) and from one territory to another (changes in space). For example, in the structure of the dynamics of the Fennoscandian populations of bank voles (Clethrionomys glareolus), the geographical gradient in the cycle length is well known, associated with the transition from non-cyclic dynamics in the southern regions to cycles with a period of two, three, five or more years in the north [52]. Such shifts between cycles of different lengths are followed by a change in the coherence (degree of phase synchronization) between the dynamics of rodents and the predators that feed on them (foxes, arctic foxes and birds) in distant sites [53,54]. Interestingly, as the cycle length increases from south to north, fluctuations in vole and predator populations are quite synchronous at large distances and less synchronous in the south. In other words, there is a phase synchronization of the distant uncoupled populations, and there is no phase synchronization of the adjacent populations that can exchange migrants.
The results of theoretical studies of coupled populations (metapopulation), including those presented in this article, show the essential role of synchronization in the conservation and sustainable development of populations over a vast area. In particular, it was found that a complete synchronization of population dynamics is an alarm sign in the simplest models of metapopulation dynamics [55,56]. It was shown that a catastrophic decline in numbers in just one site increases the risk of extinction throughout the entire area, particularly with completely synchronous dynamics in all sites [56]. In works devoted to model (14), it was shown that the transition from complete synchronization to anti-phase synchronization globally stabilizes the dynamics of equal-sized and symmetrically coupled populations due to enlargement of the attraction basins of the out-of-phase regimes [27,28,30,31]. However, this happens for weak coupling, and, for strongly coupling populations, only complete synchronization occurs. The coupling strength (migration rate) can be interpreted as the distance between sites when neighboring sites are strongly connected and intensively exchange migrants, while far distant sites are weakly connected. On the other hand, real populations are usually, unequal, non-identical and coupled asymmetrically, and so they can only be phase-synchronized with each other. A simulation of the coupled populations shows that phase synchronization can lead to the stability of the entire population system, but it also causes the spatial patterns with traveling waves, especially with complex (chaotic) dynamics of local populations [57]. For example, for vole populations in the north of England, statistical methods revealed a spatial wave of the abundance concentration and a decrease in synchronization with distance [58]. Similar results were obtained for laboratory Drosophila metapopulations (D. melanogaster) living in a ring box system, in which flies live and freely migrate [59,60]. Apparently, in the above examples, the transition from the phase bistability to quadro-stability plays an important role in the formation of these types of spatio-temporal dynamics.
In other discrete-time population models, the general asymmetric scenario of the transition to quadro-stability often arises. For example, in the Ricker equation with a periodic population growth rate, there is a transition from the phase bistability of the 2-cycle to the quadro-stability [61,62], which leads to anti-phase 2-cycles. However, this scenario is more similar to the scenario of the formation of quadro-stability in the model of the dynamics of two populations coupled by migration, functioning according to the Bazykin Equation (model (9)). Indeed, as the growth rate increases, the elements of the out-of-phase cycles do not divide from an unstable fixed point but are born because of saddle-node bifurcation. Apparently, this is due to the asymmetric order of the bifurcation values of the Ricker model, according to the Feigenbaum universality, and the model trajectory falls into the regions of different cycles with each change in the periodic growth rate. For these cycles, the size of the basins of attraction varies not only for in-phase and out-of-phase solutions but also for different phases of the same cycle.
The phase bistability of the Ricker model for the 2-cycle transforms into the phase quadro-stability in the model of two-age populations (19). The major feature of the regimes of dynamics for system (19) in the domain of the 2-cycle of the Ricker model is the birth of a strong resonance 1:4 (Arnold tongue) with a weak connection between adjacent generations (small survival rates). This resonance in the simplest case corresponds to the existence of a stable periodic point of a period of four. In fact, with zero survival of the older age group and no influence of younger age on the birth rate (or older age on the juveniles’ survival), two disconnected subpopulations are simultaneously living in one site. Indeed, the current number of juveniles is determined only by the number of older ages of the previous generation and will only affect the number of older ages in the next breeding season. On the contrary, the current abundance of older age depends only on the abundance of younger ages of the previous season and will only affect the number of younger ages in the next generation. The phase bistability of the 2-cycles for each such local population naturally leads to the phase quadro-stability of the entire system, which is preserved at a small non-zero survival rate and is realized as a strong resonance.
If a single-gene genetic diversity in terms of reproductive potential is included in the models of an age-structured population, then a very interesting superposition of the considered models appears. It is found that along with the two stable monomorphic states of the two-aged population, a third stable state is somewhat unexpectedly found. This state leads to periodic fluctuations in the genetic structure, in which during even years (in the first subpopulation) one allele predominates, and, during odd years (in the second subpopulation), the other predominates. This happens with a weak connection between adjacent generations (small survival rates), relatively low fitness of homozygotes (providing stability of the monomorphic state) and reduced fitness of the heterozygotes. As already noted, an example of such a regime is a pronounced allozyme differentiation between generations of even and odd years in different populations of Pacific pink salmon (O. gorbuscha) [38,39,40,63].
8. Conclusions
The above review of very different population studies allows us to conclude that bistability in simple local models can lead to quadro-stability, for example, when models become more complex and describe processes in space. In other words, spatio-temporal and genetic inhomogeneity are often the result of local bistability. This is found in different models and very different content problems but occurs according to similar scenarios, leading, as a rule, to very interesting, and often counterintuitive, conclusions.
Author Contributions
E.F. Corresponding member of RAS (Conceptualization: Lead; Supervision: Lead; Investigation: Equal; Writing—original draft: Equal). M.K. (Investigation: Equal; Software: Lead; Writing—original draft: Equal). All authors have read and agreed to the published version of the manuscript.
Funding
This work was carried out within the framework of the state targets of the Institute for Complex Analysis of Regional Problems of the Far Eastern Branch of the Russian Academy of Sciences.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Frisman, E.Y. Primary Genetic Divergence (Theoretical Analysis and Modeling); DVNTS AN SSSR: Vladivostok, Russia, 1986. (In Russian) [Google Scholar]
- Altrock, P.M.; Traulsen, A.; Reeves, R.G.; Reed, F.A. Using underdominance to bi-stably transform local populations. J. Theor. Biol. 2010, 267, 62–75. [Google Scholar] [CrossRef]
- Bürger, R.A. Survey of migration-selection models in population genetics. Discret. Contin. Dyn. Syst. 2014, 19, 883–959. [Google Scholar] [CrossRef]
- Banerjee, M.; Mukherjee, N.; Volpert, V. Prey-predator model with a nonlocal bistable dynamics of prey. Mathematics 2018, 6, 41. [Google Scholar] [CrossRef]
- Goldbeter, A. Dissipative structures in biological systems: Bistability, oscillations, spatial patterns and waves. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376, 20170376. [Google Scholar] [CrossRef] [PubMed]
- Láruson, Á.J.; Reed, F.A. Stability of underdominant genetic polymorphisms in population networks. J. Theor. Biol. 2016, 390, 156–163. [Google Scholar] [CrossRef] [PubMed]
- Lin, G.; Ji, J.; Wang, L.; Yu, J. Multitype bistability and long transients in a delayed spruce budworm population model. J. Differ. Equ. 2021, 283, 263–289. [Google Scholar] [CrossRef]
- Sadhu, S.; Thakur, S.C. Uncertainty and predictability in population dynamics of a bitrophic ecological model: Mixed-mode oscillations, bistability and sensitivity to parameters. Ecol. Complex. 2017, 32, 196–208. [Google Scholar] [CrossRef]
- Yeaman, S.; Otto, S.P. Establishment and maintenance of adaptive genetic divergence under migration, selection, and drift. Evolution 2011, 65, 2123–2129. [Google Scholar] [CrossRef]
- Frisman, E.Y.; Kulakov, M.P. On the genetic divergence of two adjacent populations living in a homogeneous habitat. Izv. VUZ. Appl. Nonlinear Dyn. 2021, 29, 706–726. (In Russian) [Google Scholar] [CrossRef]
- Bazykin, A.D. Model of population dynamics and problem of coexistence of related species. Zhurnal Obs. Biol. 1969, 30, 259–264. (In Russian) [Google Scholar]
- Bazykin, A.D. Selection and genetic divergence in systems of local populations and populations with a continuous range (mathematical model). Probl. Evolyutsii 1973, 231–241. (In Russian) [Google Scholar]
- Bazykin, A.D. Disadvantages of heterozygotes in a system of two adjacent populations. Sov. Genet. 1974, 8, 1453–1457. (In Russian) [Google Scholar] [PubMed]
- Bertram, J.; Masel, J. Different mechanisms drive the maintenance of polymorphism at loci subject to strong versus weak fluctuating selection. Evolution 2019, 73, 883–896. [Google Scholar] [CrossRef]
- Frisman, E.Y.; Zhdanova, O.L.; Neverova, G.P. Ecological and genetic models in population biophysics. Biophysics 2020, 65, 810–825. [Google Scholar] [CrossRef]
- Wright, S. Evolution in Mendelian populations. Genetics 1931, 16, 97–159. [Google Scholar] [CrossRef]
- Svirezhev, Y.M.; Pasekov, V.P. Basics of Mathematical Genetics; Nauka: Moscow, Russia, 1982. (In Russian) [Google Scholar]
- Nagylaki, T.; Lou, Y. The dynamics of migration-selection models. Tutor. Math. Biosci. IV Lect. Notes Math. Ed. Friedman A 2008, 1922, 117–170. [Google Scholar] [CrossRef]
- Bazykin, A.D. Nonlinear Dynamics of Interacting Populations; World Scientific: Singapore, 1998. [Google Scholar] [CrossRef]
- Frisman, E.Y. Differences in densities of individuals in population with uniform range. Ecol. Model. 1980, 8, 345–354. [Google Scholar] [CrossRef]
- Shapiro, A.P. On the issue of cycles in return sequences. Upr. I Informatsiya 1972, 3, 96–118. (In Russian) [Google Scholar]
- May, R.M. Biological population obeying difference equations: Stable points, stable cycles, and chaos. J. Theor. Biol. 1975, 51, 511–524. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef]
- Ricker, W.E. Stock and recruitment. J. Fish. Board Can. 1954, 11, 559–623. [Google Scholar] [CrossRef]
- Feigenbaum, M.J. Universal behavior in nonlinear systems. Physica. D Nonlinear Phenom. 1983, 7, 16–39. [Google Scholar] [CrossRef]
- Kuznetsov, A.P.; Kuznetsov, S.P. Critical dynamics of coupled-map lattices at onset of chaos (review). Radiophys. Quantum. Electron. 1991, 34, 845–868. (In Russian) [Google Scholar] [CrossRef]
- Gyllenberg, M.; Söderbacka, G.; Ericson, S. Does migration stabilize local population dynamics? Analysis of a discrete matapopulation model. Math. Biosci. 1993, 118, 25–49. [Google Scholar] [CrossRef]
- Udwadia, F.E.; Raju, N. Dynamics of Coupled Nonlinear Maps and Its Application to Ecological Modeling. Appl. Math. Comput. 1997, 82, 137–179. [Google Scholar] [CrossRef]
- Bezruchko, B.P.; Prokhorov, M.D.; Seleznev, Y.P. Oscillation types, multistability, and basins of attractors in symmetrically coupled period-doubling systems. Chaos Solitons Fractals 2003, 15, 695–711. [Google Scholar] [CrossRef]
- Wysham, D.B.; Hastings, A. Sudden Shift Ecological Systems: Intermittency and Transients in the Coupled Riker Population Model. Bull. Math. Biol. 2008, 70, 1013–1031. [Google Scholar] [CrossRef]
- Kulakov, M.P.; Frisman, E.Y. Synchronizing the period-2 cycle in the system of symmetrical coupled populations with stock-recruitment based on the Ricker population model. Izv. VUZ. Appl. Nonlinear Dyn. 2010, 18, 25–41. (In Russian) [Google Scholar] [CrossRef]
- Dazho, R.; Nazarov, V.I. Fundamentals of Ecology; Progress: Moscow, Russia, 1975. (In Russian) [Google Scholar]
- Frisman, E.Y.; Neverova, G.P.; Revutskaya, O.L.; Kulakov, M.P. Dynamic modes of two-age population model. Izv. VUZ. Appl. Nonlinear Dyn. 2010, 18, 111–130. (In Russian) [Google Scholar] [CrossRef]
- Frisman, E.Y.; Neverova, G.P.; Revutskaya, O.L. Complex dynamics of the population with a simple age structure. Ecol. Model. 2011, 222, 1943–1950. [Google Scholar] [CrossRef]
- Neverova, G.P.; Kulakov, M.P.; Frisman, E.Y. Changes in population dynamics regimes as a result of both multistability and climatic fluctuation. Nonlinear Dyn. 2019, 97, 107–122. [Google Scholar] [CrossRef]
- Chernyavsky, F.B.; Lazutkin, A.N. Cycles of Lemmings and Voles in the North; IBPS DVO RAN: Magadan, Russia, 2004. (In Russian) [Google Scholar]
- Frisman, E.Y.; Zhdanova, O.L. Evolutionary transition to complex population dynamic patterns in a two-age population. Russ. J. Genet. 2009, 45, 1124–1133. [Google Scholar] [CrossRef]
- Pustovoyt, S.P. Main results of genetic monitoring of the North Sea of Okhotsk pink salmon (Oncorhynchus gorbuscha) populations. Vavilovskiy Zhurnal Genet. I Sel. 2011, 15, 475–484. (In Russian) [Google Scholar]
- Pustovoyt, S.P. Thirty years of the hypothesis of fluctuating stocks of pink salmon Oncorhynchus gorbuscha (Walbaum). Izv. TINRO 2017, 188, 162–172. (In Russian) [Google Scholar] [CrossRef]
- Podlesnykh, A.V.; Kukhlevsky, A.D.; Brykov, V.A. The genetic variability and demographic history of a population of the even-year broodline pink salmon Oncorhynchus gorbuscha (Walbaum, 1792) (Bakhura River, Sakhalin Island) inferred from the polymorphism of two mitochondrial genes. Russ. J. Mar. Biol. 2017, 45, 47–55. [Google Scholar] [CrossRef]
- Lewontin, R.C. The Genetic Base of Evolutionary Change; Columbian University Press: New York, NY, USA, 1974. [Google Scholar]
- Novozhenov, Y.I.; Beregovoy, V.E.; Khokhotkin, M.I. Detection of the boundaries of elementary populations in polymorphic species by the frequency of occurrence of forms. Probl. Evol. 1973, 3, 252–260. (In Russian) [Google Scholar]
- Novozhenov, Y.I.; Altukhov, Y.P.; Bemashevskaya, A.G. Experimental modeling of gene frequency dynamics in a system of semi-isolated populations. Dokl. Biol. Sci. 1978, 238, 712–714. (In Russian) [Google Scholar]
- Altukhov, Y.P.; Bemashevskaya, A.G.; Milishnikov, A.N. Experimental modeling of genetic processes in the population system of Drosophila melanogaster corresponding to the ring step model. Dokl. Biol. Sci. 1979, 4, 646–655. (In Russian) [Google Scholar]
- Novozhenov, Y.I.; Altukhov, Y.P.; Bemashevskaya, A.G. Experimmental modelling of genetic processes in a population system of drosophila melanogaster corresponding to a circular stepping-stone model: 2. Stability of allelic composition and periodic relationship of allele frequency with distance. Sov. Genet. 1981, 6, 1052–1059. (In Russian) [Google Scholar]
- Zhdanova, O.L.; Frisman, E.Y. About the genetic divergence of populations coupled by migrations: Modern modeling based on experimental results of Yu.P. Altukhov and coauthors. Genetika 2023, 59, 708–717. (In Russian) [Google Scholar] [CrossRef]
- Salmenkova, E.A.; Omel’chenko, V.T.; Radchenko, O.A.; Gordeeva, N.V.; Rubtsova, G.A.; Romanov, N.S. Genetic divergence of chars of the genus Salvelinus from Kronotsky Lake (Kamchatka Peninsula). Russ. J. Genet. 2005, 41, 897–906. [Google Scholar] [CrossRef]
- Smith, W.H.; Wooten, J.A.; Camp, C.D.; Stevenson, D.J.; Jensen, J.B.; Turner, M.; Reed, N.A. Genetic divergence correlates with the contemporary landscape in populations of Slimy Salamander (Plethodon glutinosus) species complex across the lower Piedmont and Coastal Plain of the southeastern United States. Can. J. Zool. 2018, 96, 1244–1254. [Google Scholar] [CrossRef]
- Briñoccoli, Y.F.; de Queiroz, L.J.; Bogan, S.; Paracampo, A.; Posadas, P.E.; Somoza, G.M.; Montoya-Burgos, J.I.; Cardoso, Y.P. Processes that drive the population structuring of Jenynsia lineata (Cyprinidontiformes, Anablepidae) in the La Plata Basin. Ecol. Evol. 2021, 11, 6119–6132. [Google Scholar] [CrossRef] [PubMed]
- Davis, L.A.; Roalson, E.H.; Cornell, K.L.; McClanahan, K.D.; Webster, M.S. Genetic divergence and migration patterns in a North American passerine bird: Implications for evolution and conservation. Mol. Ecol. 2006, 15, 2141–2152. [Google Scholar] [CrossRef]
- Kulakov, M.P.; Frisman, E.Y. Genetic divergence in the system of adjacent populations with density-dependent limitation of gamete production. Reg. Probl. 2023, 26, 12–27. (In Russian) [Google Scholar] [CrossRef]
- Steen, H.; Ims, R.A.; Sonerud, G.A. Spatial and temporal patterns of small-rodent population dynamics at a regional scale. Ecology 1996, 77, 2365–2372. [Google Scholar] [CrossRef]
- Sundell, J.; Huitu, O.; Henttonen, H.; Kaikusalo, A.; Korpimäki, E.; Pietiainen, H.; Saurola, P.; Hanski, I. Large-scale spatial dynamics of vole populations in Finland revealed by the breeding success of vole-eating avian predators. J. Anim. Ecol. 2004, 73, 167–178. [Google Scholar] [CrossRef]
- Henden, J.A.; Ims, R.A.; Yoccoz, N.G. Nonstationary spatio-temporal small rodent dynamics: Evidence from long-term Norwegian fox bounty data. J. Anim. Ecol. 2009, 78, 636–645. [Google Scholar] [CrossRef]
- Earn, D.J.D.; Rohani, P.; Grenfell, B.T. Persistence, chaos and synchrony in ecology and epidemiology. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1998, 265, 7–10. [Google Scholar] [CrossRef]
- Earn, D.J.D.; Levin, S.A.; Rohani, P. Coherence and Conservation. Science 2000, 290, 1360–1364. [Google Scholar] [CrossRef]
- Blasius, B.; Huppert, A.; Stone, L. Complex dynamics and phase synchronization in spatially extended ecological systems. Nature 1999, 399, 354–359. [Google Scholar] [CrossRef]
- Mackinnon, J.L.; Petty, S.J.; Elston, D.A.; Thomas, C.J.; Sherratt, T.N.; Lambin, X. Scale invariant spatio-temporal patterns of field vole density. J. Anim. Ecol. 2001, 70, 101–111. [Google Scholar] [CrossRef]
- Mueller, L.D.; Joshi, A.; Borash, D.J. Does population stability evolve? Ecology 2000, 81, 1273–1285. [Google Scholar] [CrossRef]
- Dey, S.; Joshi, A. Chapter 7—Two decades of drosophila population dynamics: Modeling, experiments, and implications, integrated population biology and modeling. In Handbook of Statistics; Part A; Arni, S.R., Srinivasa Rao, C.R., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 39, pp. 275–312. [Google Scholar] [CrossRef]
- Sacker, R.J. A note on periodic Ricker maps. J. Differ. Equ. Appl. 2007, 13, 89–92. [Google Scholar] [CrossRef]
- Shlufman, K.V.; Neverova, G.P.; Frisman, E.Y. Dynamic modes of the Ricker model with periodic Malthusian parameter. Russ. J. Nonlinear Dyn. 2017, 13, 363–380. (In Russian) [Google Scholar] [CrossRef]
- Sato, S.; Urawa, S. Genetic variation of Japanese pink salmon populations inferred from nucleotide sequence analysis of the mitochondrial DNA control region. Environ. Biol. Fishes 2017, 100, 1355–1372. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).