Numerical Investigation on the Performance of Horizontal Helical-Coil-Type Backfill Heat Exchangers with Different Configurations in Mine Stopes

Abstract

The application of ground heat exchanger technology in backfill mines can actualize subterranean heat storage, which is one of the most effective solutions for addressing solar energy faults such as intermittence and fluctuation. This paper provides a 3D unsteady heat transfer numerical model for full-size horizontal backfill heat exchangers (BFHEs) with five configurations in a mining layer of a metal mine by using a COMSOL environment. In order to ensure the fairness of the comparative analysis, the pipes of BFHEs studied have the same heat exchange surface area. By comparing and evaluating the heat storage/release characteristics of BFHEs in continuous operation for three years, it was discovered that the helical pipe with serpentine layout may effectively enhance the performance of BFHEs. Compared with the traditional SS BFHEs, the heat storage capacity of the S-FH type is significantly increased by 21.7%, followed by the SA-FH type, which is increased by 11.1%, while the performances of U-DH and SH type are considerably lowered. Also, the impact of the critical structural factors (pitch length and pitch diameter) was further studied using the normalized parameters C₁ and C₂ based on the inner diameter of the pipe. It is discovered that BFHEs should be distributed in a pipe with a lower C₁, and increasing C₂ encourages BFHEs to increase the storaged/released heat of BFHEs. By comparatively analysing the effect of thermal conductivity, it is found that the positive effects of thermal conductivity on the performance of SH, U-DH, SA-FH, and S-FH type BFHEs are found to decrease successively. This work proposes a strategy for improving the heat storage and release potential of BFHEs in terms of optimal pipe arrangement.

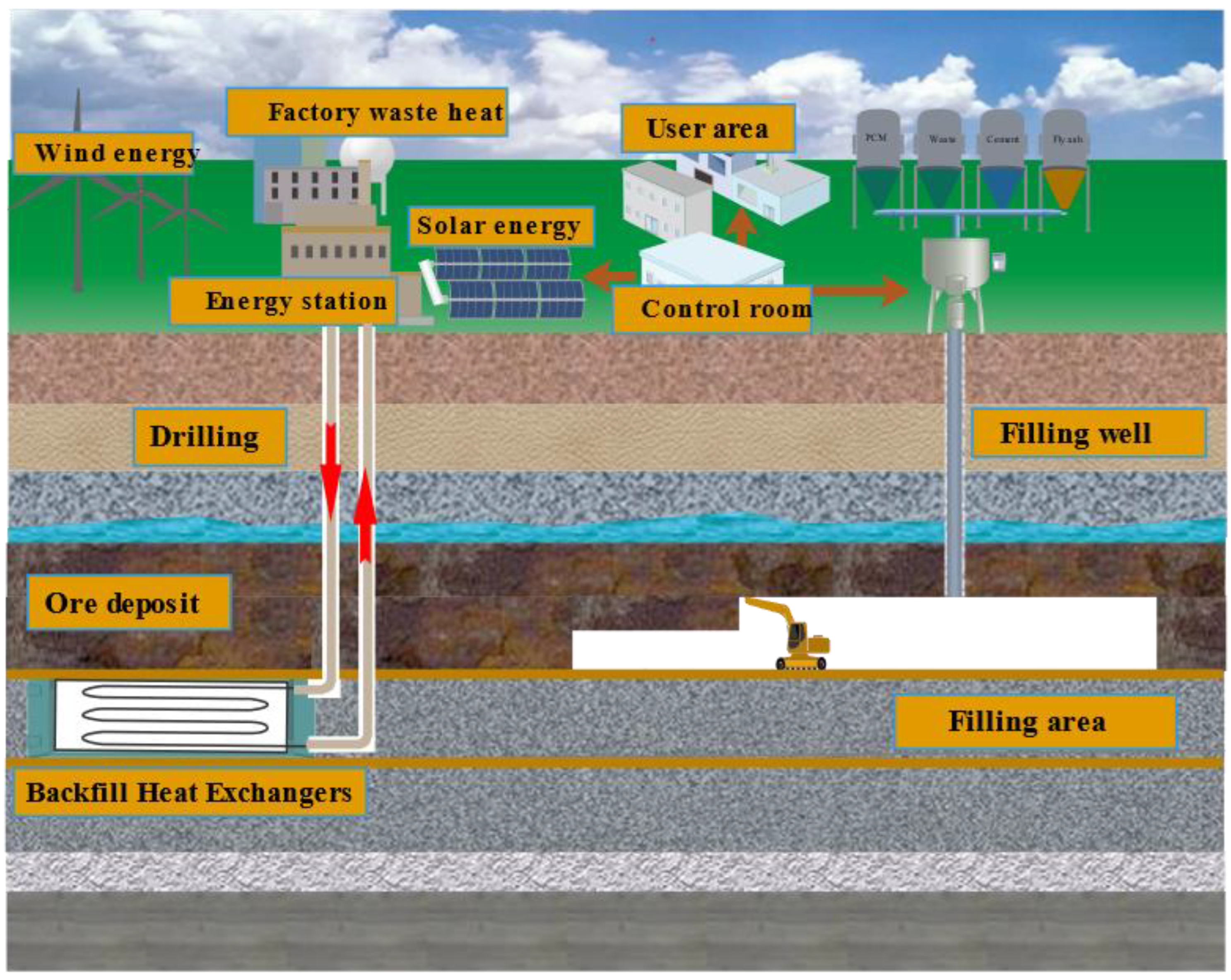
1. Introduction

The rapid growth increase in the world’s energy demand has led to the development of solar energy as it is a sustainable and clean source of energy, and it is expected that solar technology will provide about 70% of the world’s energy consumption by the year 2100 [1]. However, the biggest dilemma of solar energy is that it is unstable and cannot be matched in real-time with user demand, which severely limits its utilization efficiency. Thermal energy storage (TES, thermal energy storage) is an effective technological solution that stores solar energy and extracts it for utilization at the time of need, thus considering both the demand side and the supply side at different time scales [2,3].

The hollow area formed after mining provides a huge, utilizable space for underground heat storage and energy storage. Some researchers have combined geothermal exploitation with underground space in order to realize the secondary usage of underground space, in addition to doing research on the stability of subterranean space, rock damage, and rock-burst suppression ect. [4,5,6]. Ghoreishi et al. [7] first applied the underground pipe heat transfer technology to the backfilling mine to exploit the deep mine geothermal energy by using the backfilling body as the heat storage medium, and the results of the study elucidated its feasibility and good economic benefits. Guo Pingye et al. [8] concluded that the use of underground space for anti-seasonal cyclic energy storage can realize efficient heating and cooling in winter and summer seasons, significantly reduce the carbon dioxide emission coefficient, and enhance economic benefits. Li et al. [9] used numerical methods to evaluate the thermal storage performance of the backfilling quarry with pre-buried heat exchanger pipes, and the results showed that a 3 km long underground backfilling quarry of a typical coal mine could provide 23 GWh of thermal energy per year. Therefore, based on the academic theoretical foundation of functional mine backfilling, the process method of deposit-geothermal synergistic mining [10] can be adopted, and the heat exchanger pipelines can be buried into the backfilling body during the back backfilling process of the mine to construct the BFHEs, and then form the underground heat storage and energy storage system of the backfilling mine (as shown in Figure 1) to storage the solar energy, etc., in the form of thermal energy. Solar energy is stored in the form of thermal energy in the underground backfilling body, realizing cross-seasonal storage and solving the contradiction of imbalance between the supply and demand of thermal energy.

BFHEs, as the core component of downhole thermal energy storage, whose heat exchanger pipe arrangement is reasonable or not, will inevitably have a great impact on the performance of downhole thermal energy storage systems. Sivasakthivel et al. [11] experimentally compared the heat transfer performance of single U and double U buried pipes and found that the latter has higher heat transfer performance in both heat storage/release modes. Zhao et al. [12] experimentally investigated and comparatively analyzed the effect of heat transfer performance of serpentine, single U, and double U-shaped buried pipes based on a similar theory, and the results showed that the serpentine arrangement has the highest performance with the total efficiency of 46.1%. Liang Pu et al. [13] simulated the heat transfer performance of double-layer serpentine buried pipe and found that when the relative offset displacement (D/S) is greater than 1/3, the heat transfer performance of the staggered arrangement is better than that of the down-row arrangement.

In the design of buried pipes, their geometrical structure is also continuously innovated and developed, and helix pipe is widely used due to its advantages of large heat exchange area, small occupied space, and easy assembly [14,15]. Zhao et al. [16] comprehensively analyzed the transient heat transfer process of U,W-type, and helix pipe-type heat exchangers and found that helix pipes have better heat transfer performance in both the long- and short-term. Saeidi et al. [17] constructed a 1D–3D unsteady state model of helix buried pipes heat exchangers by using COMSOL simulation software, and the study found that the pitch length of screws has a great influence on the heat transfer performance. Kim et al. [18] investigated the heat transfer performance of helix and slink-type buried pipes heat exchangers through thermal response experiments (TPTs), and the results showed that the form of heat exchanger pipe arrangement is one of the main influencing factors of buried pipes heat exchangers, and the heat transfer performance of helix type is better than slink type. Javadi et al. [19] compared eight types of buried pipes heat exchangers with a helix arrangement and single U type and found that single U-type has the worst heat transfer performance, although the pressure drop is small. Serageldin et al. [20] used numerical simulation to compare the heat transfer performance of single U-type and double helix-type buried pipes heat exchangers at two different flow rates and found that the thermal efficiency and heat transfer power of the double helix-type increased by 40.8% and 44.1%, respectively, compared with that of single U-type, and that the effect of helix pitch diameter in the structural parameters was the most significant. Jalaluddin et al. [21] comparatively studied the heat transfer power and pressure drop per meter drilled for different pitch lengths of the helix GHE and U-type GHE with different pitch lengths in terms of heat transfer power and pressure drop per meter of drilled holes and analyzed from the point of view of energy efficiency, the use of helix pipe in ground source heat pump system has a better performance than the use of U-type pipe. Shi et al. [22] compared and analyzed the heat transfer performance of four arrangements of GHE, namely, Slinky, helix, tandem U-type, and tiled, and concluded that the tandem U-type has the best performance and that the performance of tandem U-type is the best for the helix pipe increasing the center diameter and decreasing the pitch length reduces its economic efficiency. Dinh et al. [23] investigated two types of pipes, Horizontal U-pipe and Horizontal helix pipe, in terms of economic and heat transfer performance, and the results showed that although the total initial installation cost of helix type of GHE is 30% higher, its high annual heat exchange leads to shorter payback period and higher internal rate of return.

Helix-buried pipes heat exchanger is very popular for their advantages of small footprint, simple installation, and high concentration of heat exchanger pipes, and extensive research has been carried out in the technical evaluation and optimization of its heat transfer performance [24], but the heat storage carriers are mostly soils and sandy soils, and there are fewer researches on the performance of helix heat exchanger with mine backfiller as the heat storage medium. Therefore, this paper constructs four arrangement forms of helix and traditional U-type filled body buried pipes heat exchangers and numerically simulates their heat storage/release performance using COMSOL simulation software to provide a theoretical basis for the optimal design of inter-seasonal heat storage and energy storage system based on the backfilling mine.

2. Numerical Modeling

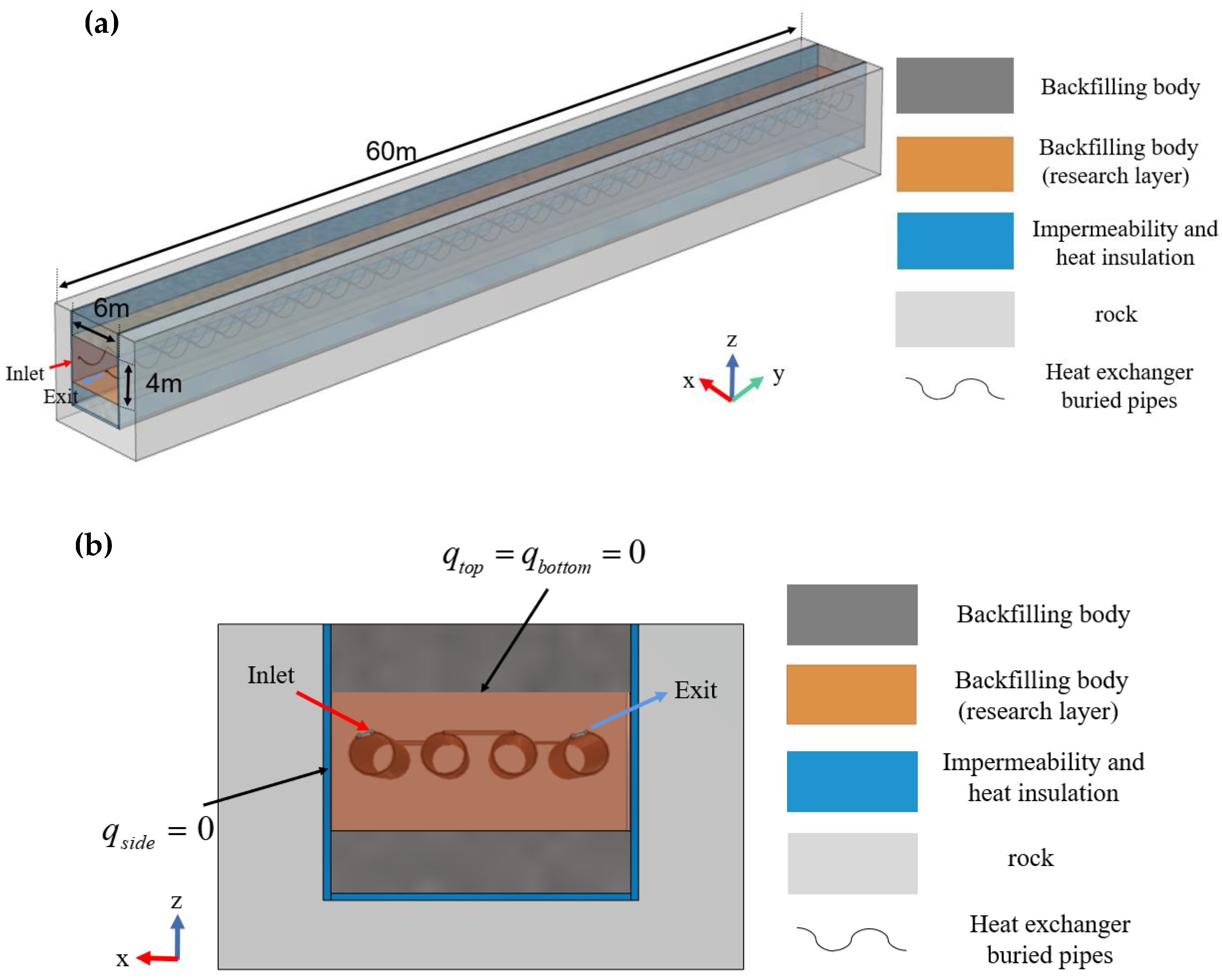
2.1. Physical Model

In this paper, with reference to the quarry dimensions of the Jinchuan II mine in Jinchang City, Gansu Province, China [25], BFHEs are constructed in a backfill sublayer (4 m × 6 m × 60 m) as shown in Figure 2. The buried pipes are arranged in the form of traditional Serpentine Straight-pipes (SS), Single Helix-pipes (SH), U-type Double Helix-pipes (U-DH), Serpentine-type four helix-pipes (S-FH), and Square Array-type four helix-pipes (SA-FH), as shown in Figure 3.

The heat exchange surface area of buried pipe is the key factor in determining the heat exchange capacity of BFHEs; in order to ensure the fairness of the comparative analysis, the studied BFHEs with different buried pipe arrangement forms and structural parameters keep the same heat exchange internal surface area of the buried pipe. The inner diameter of the buried pipes, the pitch diameter, and the pitch length of the helix buried pipes are selected with reference to the relevant literature and combined with the actual size of the backfilling body [26,27,28] and the geometrical parameters of the BFHEs with different forms of pipe arrangement and the related material thermo-physical parameters are shown in

Table 1. Geometric parameters of BFHEs with different configurations.

Pipe Distribution Form	Pipe Inner Diameter /m	Pipe Length /m	Total Surface Area of Pipe Inner Wall /m2	Pitch Diameter /m	Helix Pitch /m
SH	0.038	183.7	21.75	0.8	1.4
U-DH	0.028	248.0	21.80
S-FH/SA-FH	0.016	433.4	21.77
SS *	0.038	182.3	21.75	/

* Note: Pipe spacing is 2 m [9].

and

Table 2. Thermophysical properties of BFHEs materials [29].

Material	Density (m3/kg)	Thermal Conductivity W/(m·K)	Specific Heat Capacity J/(kg·K)
Backfill body	1709	0.6	1235
Copper	8500	110	393.6
Rock	2400	2.5	2000

, respectively.

2.2. Mathematical Model

In BFHEs, the process of storing and releasing heat is a complicated three-dimensional unstable heat transfer. The thermophysical parameters of the heat transfer fluid are listed in

Table 3. Thermophysical parameters of heat transfer fluids.

Type	Parameter	Value
Heat transfer fluid (water)	Qf,in (inlet volume flow rate)	3.5 × 10−4 m3/s
	ρ (density of water)	998 m3/kg
	λ (thermal conductivity of water)	0.6 W/(m·k)
	cp (specific heat of water)	4182 J/(kg·K)

. The following hypotheses are used in the numerical simulation process to make the calculation simpler [20,30]:

(1)

The backfilling body is homogeneous and isotropic;

(2)

Neglect the contact thermal resistance between the buried pipe wall and the backfilling body and the contact thermal resistance between the backfilling body and the surrounding rock;

(3)

The influence of underground seepage is not considered;

(4)

The heat transfer fluid is an incompressible fluid, and the temperature and velocity are uniform in any radial section;

(5)

The thermo-physical properties of materials are temperature-independent.

2.2.1. Governing Equation

(1)

Backfill body region

Energy equation:

$$\frac{\partial \mathrm{T}}{\partial \tau }=\frac{{\lambda }_{\mathrm{b}}}{{\rho }_{\mathrm{b}}{c}_{\mathrm{p},\mathrm{b}}}(\frac{{\partial }^{2}T}{\partial {\mathrm{x}}^2}+\frac{{\partial }^{2}T}{\partial {\mathrm{y}}^2}+\frac{{\partial }^{2}T}{\partial {\mathrm{z}}^2})$$

(1)

(2)

Backfill Heat Exchangers region

The energy equation for the heat transfer fluid inside a heat exchanger buried pipes [31]:

$${\rho }_{\mathrm{f}}{A}_{\mathrm{p}}{c}_{\mathrm{f}}\frac{\partial T_{\mathrm{f}}}{\partial \tau }+{\rho }_{\mathrm{f}}{A}_{\mathrm{p}}{c}_{\mathrm{f}}u\cdot \nabla T_{\mathrm{f}}=\nabla \cdot \left(A_{\mathrm{p}}{k}_{\mathrm{f}}\nabla T_{\mathrm{f}}\right)\frac{1}{2}{f}_{\mathrm{D}}\frac{{\rho }_{\mathrm{f}}{A}_{\mathrm{p}}}{d_{\mathrm{h}}}{\left|u\right|}^3+Q+Q_{\mathrm{wall}}$$

(2)

$$Q_{\mathrm{wall}}={\left(hZ\right)}_{\mathrm{eff}}\left(T_{\mathrm{ext}}-T_{\mathrm{f}}\right)$$

(3)

$${\left(hZ\right)}_{\mathrm{eff}}=\frac{2\pi }{\frac{1}{r_0{h}_{\mathrm{int}}}+\frac{\ln \frac{r_1}{r_0}}{\lambda }}$$

(4)

Momentum equation:

$${\rho }_{\mathrm{f}}\frac{\partial u}{\partial \tau }+{\rho }_{\mathrm{f}}u\cdot \nabla u=-\nabla p_{\mathrm{f}}-f_{\mathrm{D}}\frac{{\rho }_{\mathrm{f}}}{2d_{\mathrm{h}}}u\left|u\right|$$

(5)

The continuity equation:

$$\frac{\partial {\rho }_{\mathrm{f}}}{\partial \tau }+\nabla \cdot \left({\rho }_{\mathrm{f}}{u}_{\mathrm{f}}\right)=0$$

(6)

2.2.2. Boundary Condition

The heat transfer fluid, the backfilling body, and the heat transfer buried pipe are the main components of the model under consideration. During the simulation, the relevant boundary conditions are set as follows:

(1)

BFHEs are provided with impermeable and thermal insulation on both sides of the backfilling body (as shown in Figure 2), so both sides are set to be adiabatic in the simulation:

$$q_{\mathrm{side}}=0$$

(7)

(2)

Based on geometric symmetry, the top and bottom of the backfilling of BFHEs are adiabatic surfaces:

$$q_{\mathrm{top}}=q_{\mathrm{bottom}}=0$$

(8)

(3)

Inlet temperature of heat exchanger buried pipe:

$${T_{\mathrm{f}}(x,\tau )|}_{x=0}=T_{\mathrm{f},\mathrm{in}}$$

(9)

where T_f,in is the temperature of the heat transfer fluid at the inlet of the heat transfer buried pipes, the heat storage phase is taken as 90 °C, and the heat release phase is taken as 20 °C [9].

(4)

Buried pipe inlet volume flow rate:

$${Q_{\mathrm{f}}(x,\tau )|}_{x=0}=Q_{\mathrm{f},\mathrm{in}}=A_{\mathrm{p}}\times \frac{\pi d_{\mathrm{h}}^2}{4}$$

(10)

In the formula, Q_f,in for the heat transfer fluid in the buried pipe inlet volume flow rate to the pipe inner diameter of 38 mm, the flow rate of 0.3 m/s as the basis for the calculation of the default value of 3.5 × 10⁻⁴ m³/s, and to ensure that all the conditions of the inlet volume flow rate are the same.

2.2.3. Initial Conditions

Heat storage phase:

$$T_{\mathrm{f}}=T_{\mathrm{b}}=T_{\mathrm{p}}=T_0$$

(11)

Heat release phase:

$$T_{\mathrm{f}}=T_{\mathrm{b}}=T_{\mathrm{p}}=T_{\mathrm{e}}$$

(12)

where T₀ is the initial temperature of BFHEs, which is taken as 45 °C [32,33]; T_e is the initial temperature of BFHEs in the heat release phase, which is the same as the temperature distribution at the moment of the end of heat storage.

3. Numerical Simulation and Verification

3.1. Geometric Modeling and Meshing

Due to the intricacy of the heat transfer mechanism at the intersection of the backfilling body and the underground pipe, geometric modeling and meshing of the BFHEs are performed using COMSOL software prior to numerical simulation computations. The grid is locally encrypted in the vicinity of the heat transfer buried pipe (As shown in the red box), as shown in Figure 4, to increase calculation accuracy.

3.2. Grid and Time-Step Independence Verification

It is vital to select a reasonable number of grids and time steps in order to guarantee the correctness of the calculations while also reducing the cost of computational time. For the 240th day of thermal storage for S-FH type BFHEs, the variation of the body-averaged temperature with the number of grids is shown in Figure 5a. As can be observed, there are more grids overall (from 375,105 to 866,340), yet the change in body temperature is only 0.2 °C. Figure 5b shows the variation of the outlet temperature of the heat transfer fluid of the S-FH type BFHEs for 240 d of heat storage at different time steps. It can be seen that the temperature difference between time steps 1 d and 0.5 d is tiny, with a change value of less than 0.1%, but the temperature difference with 5 d is greater than 5%. The number of grids is selected as 375,105 with a time step of 1 d for comprehensive consideration.

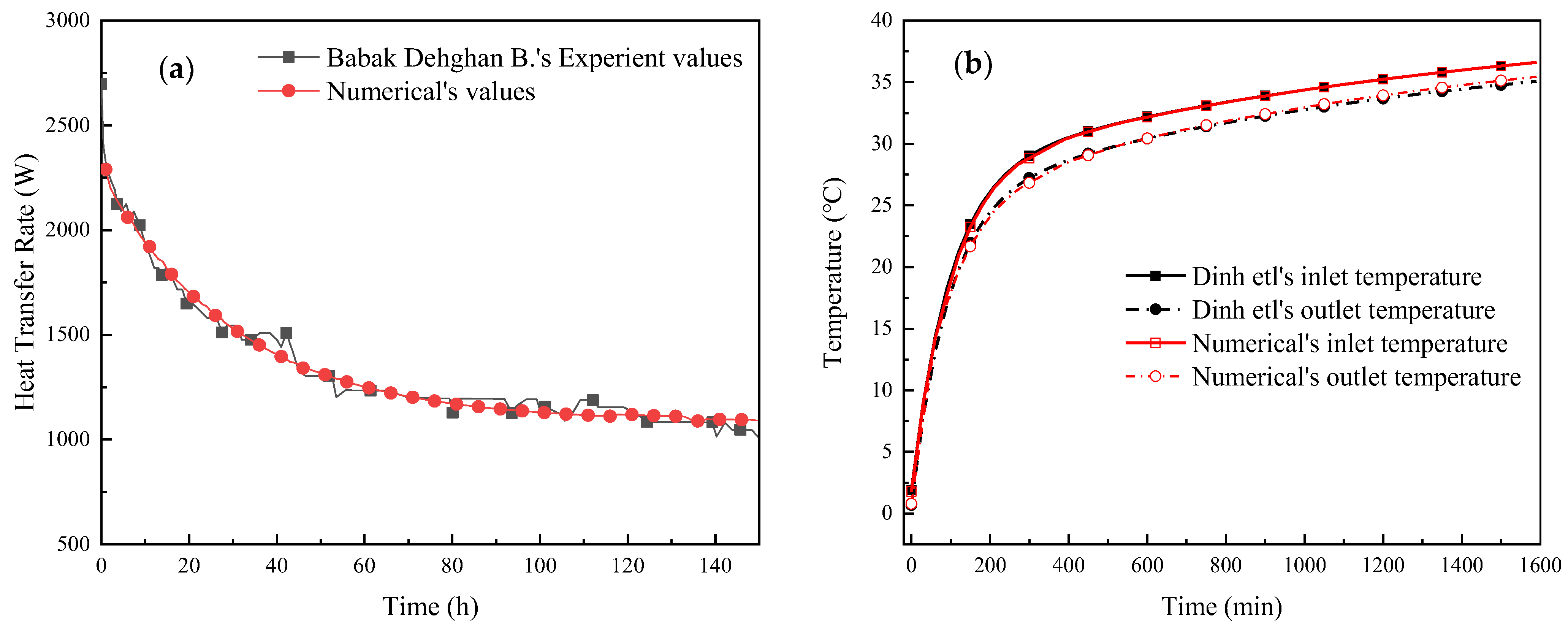
3.3. Model Validation

In this paper, the experimental data of Dehghan B.B. [34] and Dinh B.H. et al. [23] are used to confirm the precision of the established mathematical model. The validation model’s geometrical parameters, boundary conditions, beginning circumstances, and operational conditions are maintained in accordance with previous research, details of the parameters are shown in

Table 4. Model parameters for Dinh B.H. [23] and Dehghan B.B. [34].

Model		Dinh B.H.	Dehghan B.B.
Geometric dimensions of models		5 × 1 × 1 m	6 × 6 × 4 m
Backfill materials	Density	1782 m3/kg	2100 m3/kg
	Thermal conductivity	1.62 W/(m·k)	1.8 W/(m·k)
	Specific heat	860 J/(kg·K)	900 J/(kg·K)
Heat transfer fluid (water)	Volume flow rate	4 L/min	15 L/min
	Inlet temperature	change over time	50 °C
Operation time		1600 min	150 h

. According to Figure 6, the difference between the simulated value of the inlet and outlet temperatures of the heat transfer fluid and the experimental value of Dinh et al. is less than 10%, and the error between the simulated value of the heat transfer rate and the experimental value of Dehghan B. is within 10%. It demonstrates that the numerical model developed in this publication has good accuracy and can be used moving forward for additional research.

4. Evaluation Indicators

4.1. Accumulated Heat Storage/Release and Heat Storage/Release Rate

Accumulated heat storage/release refers to the cumulative heat stored or released by BFHEs after a τ time period, calculated from the initial moment of the heat storage or release phase, respectively, reflecting their overall heat storage/release capacity.

The heat storage/release rate, which reflects the BFHEs’ actual heat storage/release capacity, is the amount of heat that they store and release per unit of time. The equations are as follows:

$$Q={\displaystyle {\int }_0^{\tau }{m}_{\mathrm{f}}{c}_{\mathrm{pf}}\left(T_{\mathrm{i},\mathrm{f}}-T_{\mathrm{o},\mathrm{f}}\right)}d\tau$$

(13)

$$\Phi =\frac{dQ}{d\tau }=m_{\mathrm{f}}{c}_{\mathrm{pf}}\left(T_{\mathrm{i},\mathrm{f}}-T_{\mathrm{o},\mathrm{f}}\right)$$

(14)

4.2. Total Heat Storage and Release Efficiency

The total heat storage-release efficiency is the ratio of the effective cumulative heat release to the cumulative heat storage of the BFHEs in a heat storage-release cycle and is calculated as follows [35]:

$${\eta }_{\mathrm{BFHEs}}=\frac{\left|Q_r\right|}{\left|Q_s\right|}=\frac{{\displaystyle {\int }_0^{{\tau }_2}{m}_{\mathrm{f}}{c}_{\mathrm{pf}}\left(T_{\mathrm{o},\mathrm{f}}-T_{\mathrm{i},\mathrm{f}}\right)}d\tau }{{\displaystyle {\int }_0^{{\tau }_1}{m}_{\mathrm{f}}{c}_{\mathrm{pf}}\left(T_{\mathrm{i},\mathrm{f}}-T_{\mathrm{o},\mathrm{f}}\right)}d\tau }$$

(15)

where τ₁ and τ₂ are the heat storage time and heat release time of a heat storage-release cycle, s.

4.3. Comprehensive Heat Transfer Performance

A comprehensive evaluation of the thermal performance of BFHEs needs to consider its heat transfer efficiency and flow resistance, this paper takes the SS-type BFHEs with the same buried pipe heat transfer area as the reference and introduces the comprehensive heat transfer performance TPC for evaluation and the specific calculation formula is as follows [20]:

$$TPC=\frac{\phi /{\phi }_0}{f/f_0}$$

(16)

The average combined heat transfer performance of a heat storage and release cycle is calculated by the following equation:

$$TP{C}_{\mathrm{ave}}=\frac{{\displaystyle {\int }_0^{\tau }TPCd\tau }}{\tau }$$

(17)

where φ₀ and f₀ are the heat transfer efficacy and friction coefficient of SS-type BFHEs, respectively; φ and f are the heat transfer efficacy and friction coefficient of helix BFHEs, respectively;

The heat transfer efficiencies of the BFHEs are calculated as follows:

$$\phi =\frac{T_{\mathrm{i},\mathrm{f}}-T_{\mathrm{o},\mathrm{f}}}{T_{\mathrm{i},\mathrm{f}}-T_{\mathrm{ave},\mathrm{b}}}$$

(18)

where T_ave,b is the average temperature of the filled body storage/release initial body. The heat storage is T₀ and the heat release is T_e, °C.

The friction coefficient f is calculated as follows [20]:

$$f=\frac{\mathsf{\Delta }P}{\frac{1}{2}{\rho }_{\mathrm{f}}{u}^2}\cdot \frac{d_{\mathrm{h}}}{L_{\mathrm{T}}}=\frac{2d_h\mathsf{\Delta }P}{{\rho }_{\mathrm{f}}{u}^2{L}_{\mathrm{T}}}$$

(19)

where d_h is the diameter of heat transfer buried pipe, m; ∆P is the pressure drop between the inlet and outlet of the heat transfer buried pipe, Pa; ρ_f is the density of heat transfer fluid, kg/m³;

The formula for calculating the pipe length of helix pipe is as follows [20]:

$$L_T=\frac{H_{\mathrm{h}}}{P_{\mathrm{h}}}\sqrt{{\left(\pi D_{\mathrm{h}}\right)}^2+P_{\mathrm{h}}{}^2}$$

(20)

5. Simulation Results and Analysis

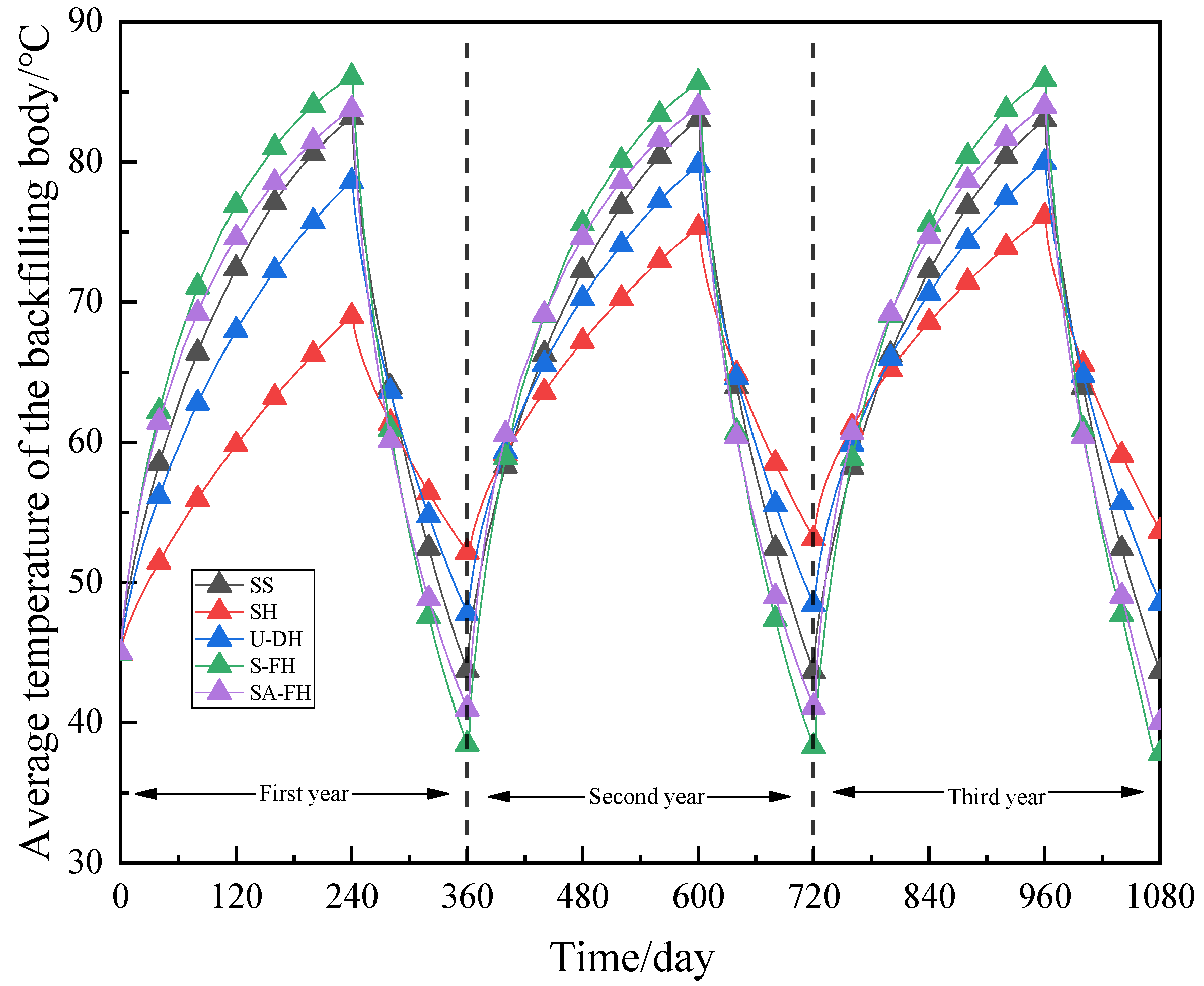
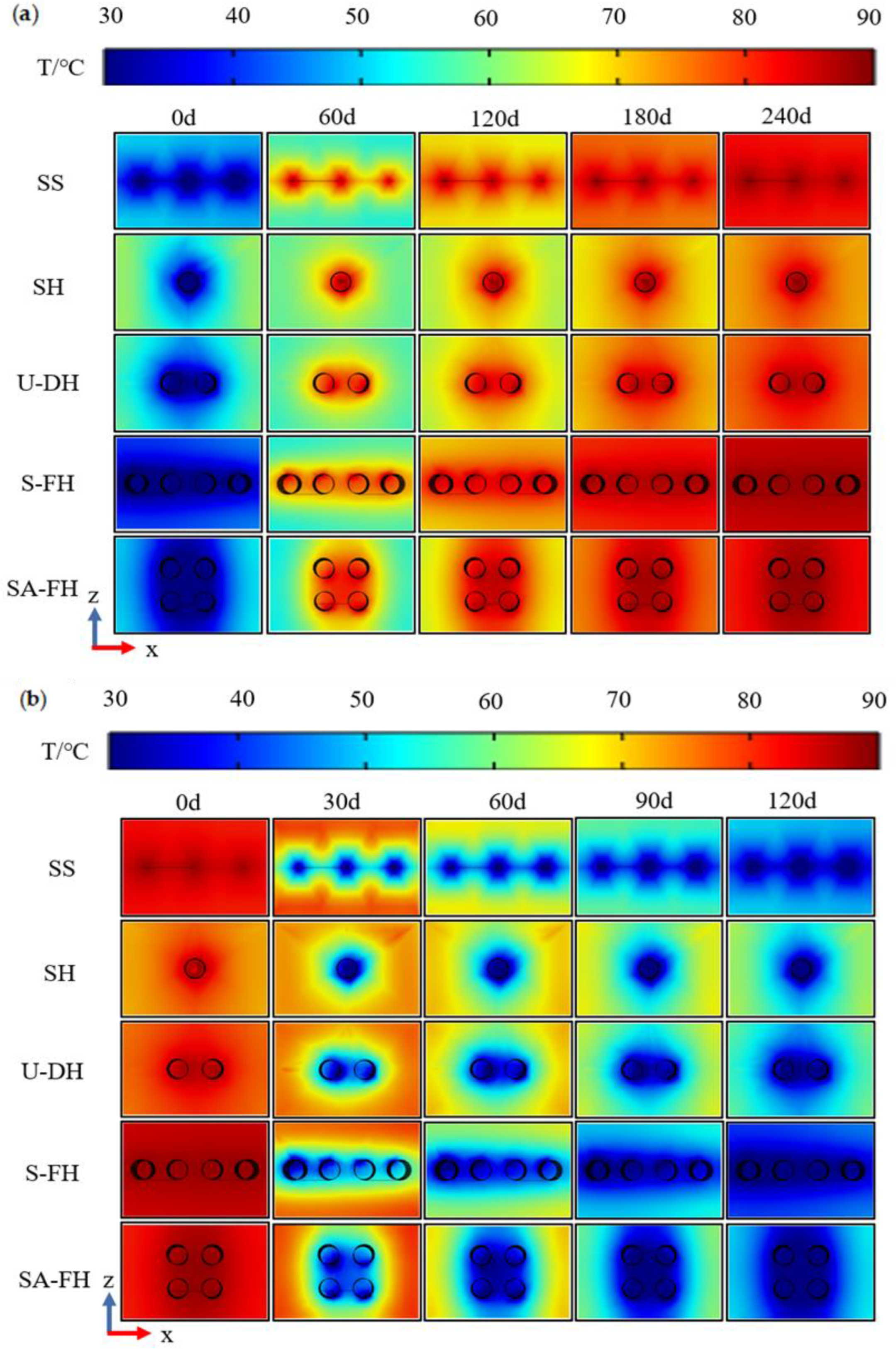
5.1. Comparative Analysis of the Heat Storage/Release Characteristics of BFHEs in Five Arrangement Forms

The capacity of BFHEs to storage and release heat can be readily observed in the backfilling body’s average body temperature change. Figure 7 displays the average temperature variation for traditional serpentine BFHEs and helix pipe BFHEs over a period of three years. As seen in Figure 7, the average body temperature of the S-FH type reached 85.9 °C and 37.7 °C at the end of heat storage/release, respectively. The temperature change range is the largest, reaching 48.2 °C, which was 21.7% higher than that of the SS type. The average body temperature change range of the SA-FH type is second, increased by 11.1%. This suggests that when the heat exchange area of the buried pipe is the same, the heat storage/release capacity of S-FH BFHEs is greatly increased. The SA-FH type’s heat storage/release capability is lower than that of the S-FH type as a result of the pipe group’s interlayer thermal interference. The thermal resistance of the backfilling body affects the SH type, so it has the lowest capacity for heat storage/release.

Figure 8 shows the change in heat storage/release rate between helix BFHEs and traditional serpentine BFHEs with different arrangements for 3 years of continuous operation. It can be seen from the figure that BFHEs have a high rate of heat storage/release at the beginning of the heat storage/release phase, which then decreases rapidly and gradually slows down. It is found that at the beginning of heat storage/release, the heat storage/release rate of SA-FH type and S-FH type is slightly higher than that of SS type by 3~6%, while the U-DH type and SH type are significantly lower than that of SS type, about 43% and 35%, respectively. In the early phase of the heat storage/release phase, the heat storage rate of Ss-type decreases faster, and the heat storage/release rates of both SA-FH-type and S-FH-type are significantly higher than those of SS-type, with the maximum difference reaching about 15 kW, while in the late phase, they are slightly lower than those of SS-type, with the maximum difference not exceeding 0.4 kW. Due to the initial low rate of heat storage/release, the U-DH and SH types are essentially lower than the SS type throughout the storage/release period. The rate of heat storage/heat release of BFHEs organized in five varied greatly at the beginning of heat storage/release but only slightly at the end, between 1.5 and 2.5 kW and 4.0 and 7.5 kW, respectively. The rate of heat storage/release of BFHEs arranged by S-FH, SA-FH, SS, U-DH, and SH decreases consecutively throughout the entire storage/release period.

Figure 9 displays the cumulative heat storage/release variance for three years of continuous operation for helix BFHEs with various arrangements. The S-FH type of the four-helix BFHEs has the highest cumulative heat storage/release, which is much higher than that of the SS type, as can be seen from the figure. This demonstrates how the serpentine-shaped helix buried pipe may effectively increase the heat storage/release capacity of BFHEs by better matching the backfilling body’s internal heat transfer. The heat transfer between the helix buried pipe and the backfilling body is too concentrated in the SH type, resulting in a decrease in the heat storage/release capacity of BFHEs, which is much lower than that of the SS type, and the U-DH type has a significant improvement over the SH type. The SA-FH type is affected by the thickness of the backfilling body, the smaller spacing of the pipe rows, and the intensification of thermal interference, resulting in a poorer heat storage/release capacity than the S-FH type, although it is much improved over the U-DH type.

The total efficiency of SS-type storage/release heat fluctuates around 0.95, according to Figure 9’s variation in the total efficiency of storage-heat release, while the total efficiency of U-DH type in the second year is 0.94, which is comparable to that of SS-type. The total efficiency of the S-FH type and SA-FH type in the second year of operation has reached 0.99, and the storage/release of heat has basically reached equilibrium, reflecting a good storage-release of heat stabilization, while the SH type is 0.87 storage-release of heat stabilization of the worst ability.

Figure 10 displays the TPCs of variously arranged helix BFHEs in their third year of operation. TPC larger than 1 denotes that the overall heat transfer performance of this helix BFHEs is superior to that of the SS type and vice versa. The figure shows that the TPC of the SA-FH type decreases rapidly in the early phase of heat storage, and the TPC of the S-FH type starts to be less than 1 on the 96th and 50th days, respectively. The TPC of the S-FH type is 1.63 and 1.67 at the beginning of heat storage and decreases to 0.30 and 0.40 at the end as the heat storage progressed, which demonstrates that the S-FH type and SA-FH type have better overall heat transfer performance than the SS type in the early phases of heat storage. However, as heat storage capacity decreases, the negative effects of increased resistance brought on by the reduction in heat exchange pipe diameter gradually become apparent. As a result, the comprehensive heat transfer performance is lower than the SS type in the middle and late phases of heat storage, and the gap widens. At the start and end of heat storage, the TPC of SH type and U-DH type is comparable to that of SS type, and the TPC is lower than 1 while heat storage is taking place, indicating that their overall heat transfer performance is inferior to that of SS type. It can also be found from the figure that the comprehensive heat transfer performance of SH type and U-DH type is also lower than that of SS type in the heat release phase, but S-FH and SA-FH type are significantly improved, and they are better than SS type in the whole heat release phase.

The average TPC variation of helix BFHEs over three years of operation in various configurations is shown in Figure 11. The average comprehensive heat transfer performance of heat storage is marginally better than that of SS type, but the average comprehensive heat transfer performance of heat release is significantly better compared with that of SS type, as can be seen from the fact that in the second and third years of the storage-release cycle, the S-FH type heat storage TPC_ave is about 1.10, and the heat release TPC_ave is about 1.51. The average comprehensive heat transfer performance of the heat storage phase is slightly worse than that of the SS type, but the heat release phase is significantly stronger, according to the TPC_ave of the SA-FH type in the heat storage and release phases, which are about 0.96 and 1.39, respectively. The average complete heat transfer performance is the worst, with the TPC_ave of the storage/release phase of U-DH ranking third at about 0.85 and the TPC_ave value of the SH type being around 0.64.

Figure 12 depicts the change in the BFHEs cross-sectional temperature cloud at y = 30 m during heat storage/heat release in five pipe shapes. The cloud diagram shows that the temperature distribution of SS-type BFHEs is relatively uniform along the X-direction at the end of the heat storage/release process and close to the temperature around the buried pipe. However, the distribution along the Z direction is less uniform and has a larger temperature gradient, which reduces the heat storage/release capacity of SS-type BFHEs, thus affecting its performance. The combination of serpentine and helix S-FH inherits the advantages of uniform temperature distribution in the X direction of SS and improves the temperature distribution in the Z direction significantly, and the temperature at the boundary of the backfilling body at the end of heat storage/release is very close to that of the peripheral area of the heat exchanger pipe, so its heat storage/release capacity is most significantly improved. SA-FH further improves the temperature distribution in the Z-direction, but the rectangular cross-section of backfilling body, the difference in the temperature distribution along the X-direction increases, so its heat storage/release capacity is reduced compared with that of S-FH. The heat transfer surface of the SH type is too concentrated in the center of the cross-section of the backfilling body, and the temperature distribution uniformity is the worst, and the temperature distribution of U-DH is still inferior to that of the SS type, although it has a more obvious improvement than that of SH type, resulting in the heat storage/release capacity of both SH type and U-DH type being lower than that of SS type.

5.2. The Influence of Helix Pitch Length and Pitch Diameter

The helix pitch length, pitch diameter, and inner diameter of the buried pipe have important effects on the heat transfer performance of the helix buried pipe [7,20,36]. In this paper, five commonly used buried pipes (with inner diameters of 20 mm, 25 mm, 32 mm, 38 mm, and 48 mm, respectively) are selected, and the four-helix BFHEs in the paper are arranged by varying the helix pitch length and pitch diameter, respectively, with the pitch diameter of 0.8 m and the pitch length of 1.4 m as the default dimensions. The arrangement process ensured that the total internal surface of the buried pipe was 21.75 m² (as shown in Table 1), with a maximum of 1.5% inaccuracy.

In order to facilitate the study of the effect of pitch length and pitch diameter on the heat transfer performance of these four helical buried pipes BFHEs, in this paper, the pitch length and pitch diameter are normalized with the diameter of the buried pipes to form two dimensionless parameters:

$$C_1=\frac{P_{\mathrm{h}}}{d_{\mathrm{h}}}$$

(21)

$$C_2=\frac{D_{\mathrm{h}}}{d_{\mathrm{h}}}$$

(22)

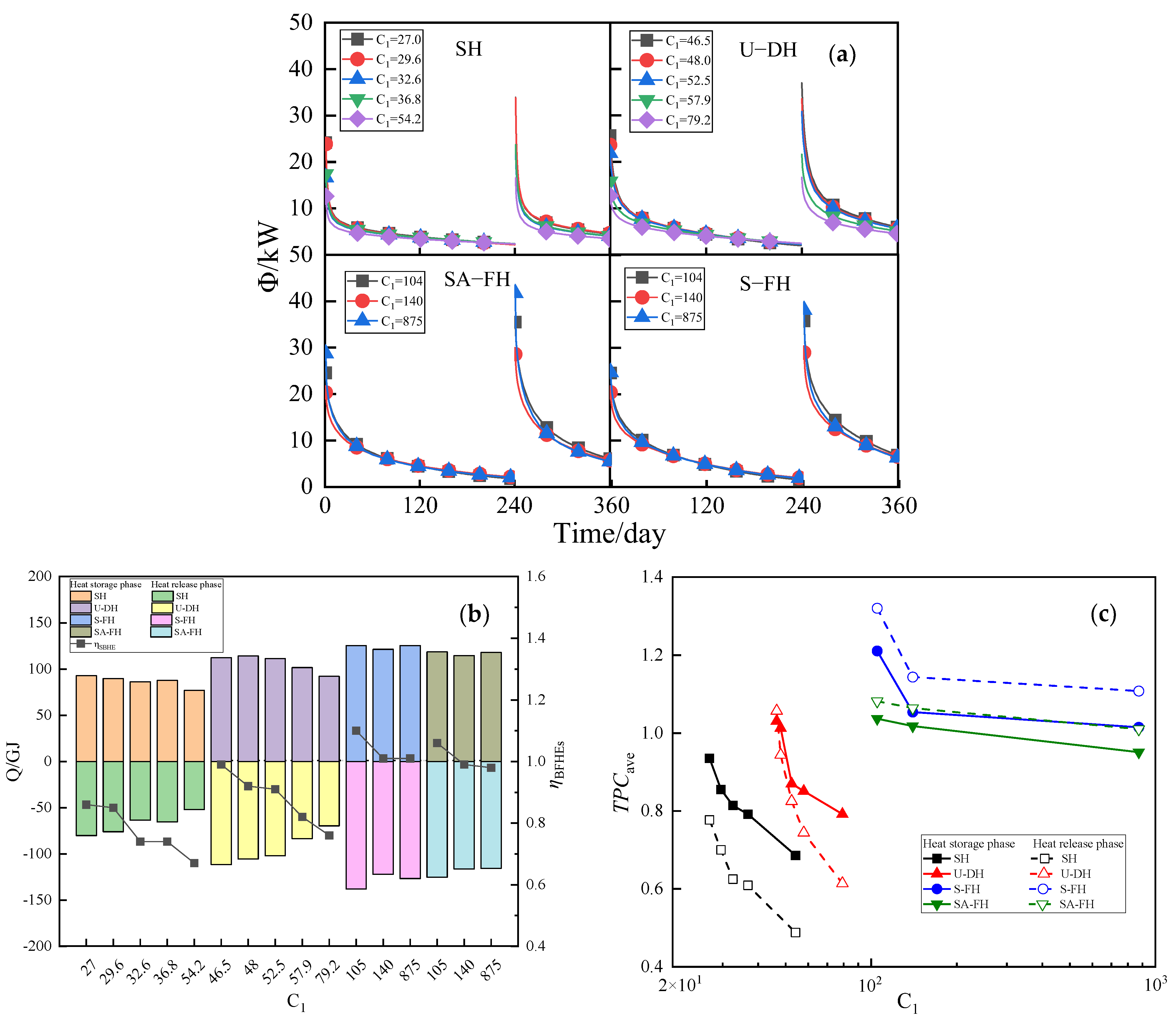
5.2.1. The Influence of Helix Pitch Length

Figure 13 shows the heat storage/release characteristics of the four-helix pipe forms of BFHEs at different C₁. Figure 13a shows that the initial storage/release rates of BFHEs with different C₁ differ significantly, but the difference is very small at the end of the storage/release period. The larger the C₁ is, the lower the initial storage/release rates of SH-type and U-DH-type, which results in lower storage/release rates in most phases of the storage/release period. The initial heat storage rate of SA-FH and S-FH BFHEs do not exhibit a monotonic trend with C₁. As seen in Figure 13a, the SA-FH and S-FH types’ initial heat storage/release rates are not the greatest at a C₁ value of 875. However, they rise rather than decrease as heat is stored/released, and the average heat storage/release rate is not the highest.

According to Figure 13b, the cumulative heat storage/release of BFHEs of the SH and U-DH types is significantly lowering with respect to C₁. The cumulative heat storage-release of S-FH and SA-FH types is comparatively stable, with the same amount of heat storage/release for larger values of C₁, and the total efficiency of heat storage-release near 1, which is essentially in a stable state. In contrast, the cumulative heat storage-release of SH and U-DH types decreases more than the cumulative heat release with an increase in C₁, leading to a decreasing trend of the total heat storage-release efficiency of BFHEs in the first year.

The average integrated heat transfer performance of BFHEs degrades monotonically with C₁, with the TPC_ave for SH and U-DH types degrading more noticeably. This is seen in Figure 13c. Therefore, when the flow resistance and heat transfer capacity are thoroughly taken into account, the BFHEs should be selected with a smaller C₁ in the form of piping. The sequential decline in TPC_ave of the S-FH, SA-FH, U-DH, and SH types is also evident in Figure 13c. It is not advised to choose the SH type because, in the range of C₁ values examined, all of its TPC_ave are smaller than 1, reflecting its less effective overall heat transmission than the SS type. U-DH type, which is superior to SS type, is only marginally over 1.0 at smaller C₁. The improvement in overall heat transfer performance is particularly pronounced in S-FH and SA-FH types, where the TPC_ave is essentially more than 1.0.

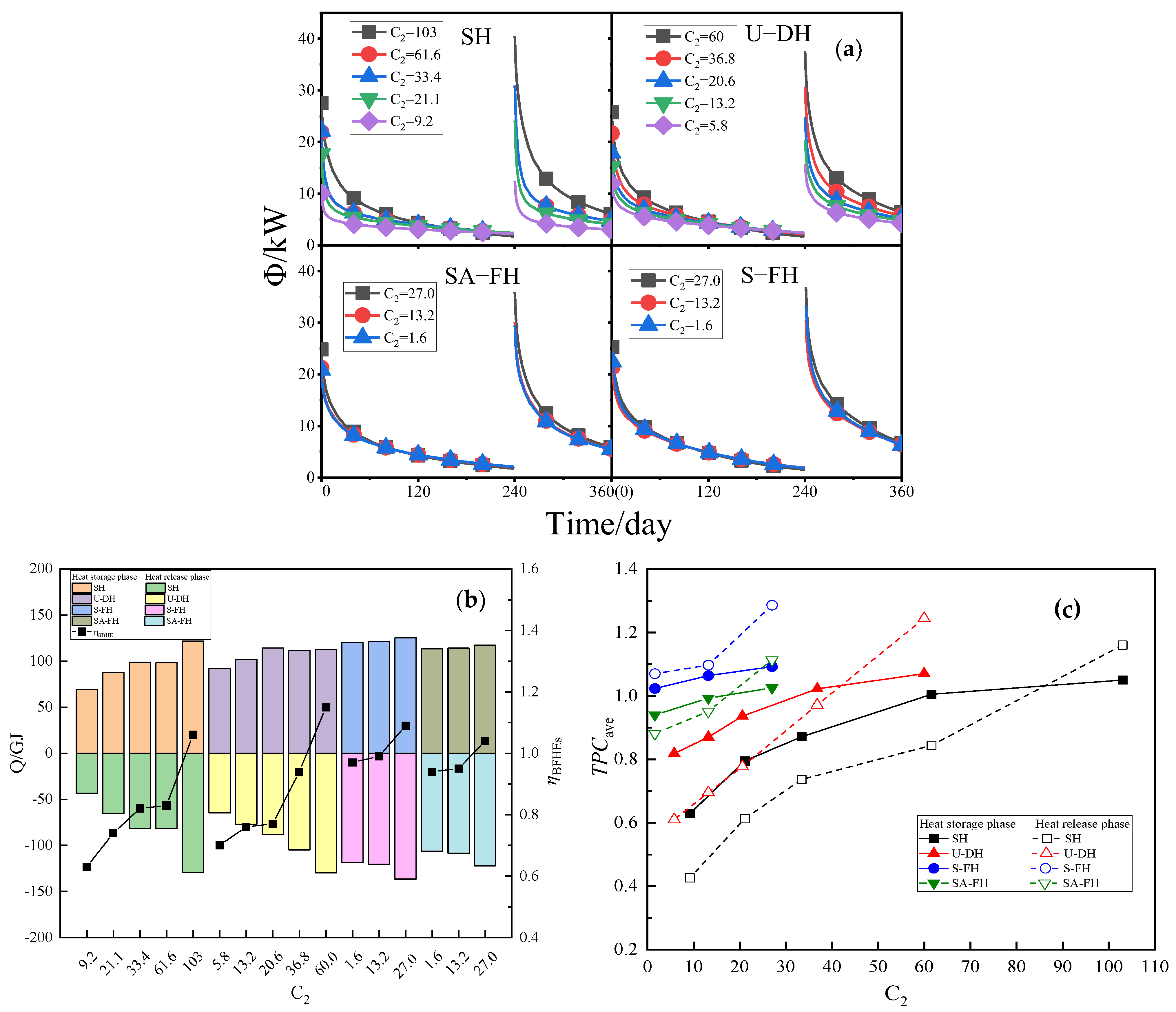
5.2.2. The Influence of Pitch Diameter

Figure 14 shows the heat storage/release characteristics of the four helical BFHEs at different C₂. Figure 14a shows that the differences in the storage/release heat rates of BFHEs at different C₂ are very obvious. Increasing the C₂, the initial storage/release rates of SH and U-DH types are elevated, and therefore, the overall higher storage/release rates were observed. However, the change of C₂ has a relatively small effect on the storage/release rates of SA-FH and S-FH BFHEs, and the smaller the C₂, the smaller the difference in storage/release rates.

As shown in Figure 14b, increasing C₂ is beneficial to improving the cumulative heat storage/release of BFHEs, especially for SH and U-DH types. In addition, it can be found from Figure 14b that the total accumulation-release heat efficiency increases significantly with C₂, indicating that increasing C₂ can enhance the heat release capacity of BFHEs more effectively.

Figure 14c shows that the average integrated heat transfer efficiency TPC_ave of the four helix BFHEs monotonically increases with C₂, where the TPC_ave increase is more pronounced in the heat release phase. Therefore, the BFHEs should be selected with a larger C₂ in the form of piping when the flow resistance and heat exchange capacity are considered comprehensively. It is found that the TPC_ave of the S-FH BFHEs is better than that of the other three helix pipe arrangements and is always greater than 1 within the range of C₂ studied, which further indicates that the serpentine and helix pipe arrangement combination is the best option.

5.3. The Influence of Thermal Conductivity

Figure 15 illustrates the changes in the thermal storage/release performance of the four-helix BFHEs with different thermal conductivity of the backfilling body. From Figure 15a, it can be seen that increasing the thermal conductivity of the backfilling body can effectively strengthen the heat storage/release rate of the BFHEs, but for the U-DH, SA-FH, and S-FH types, at the later phase of the heat storage phase, due to the small temperature difference between the heat transfer fluid in the pipe and the backfilling body, the heat storage rate will instead be reduced, which leads to differences in the degree of strengthening. The thermal conductivity of the backfilling body is enhanced from 0.4 W/(m·k) to 0.8 W/(m·k), and the thermal storage rate of BFHEs of SH, U-DH, SA-FH, and S-FH types is enhanced by 46%, 34%, 25%, and 22% on average. Due to the short duration of the heat release phase, the heat release rate enhancement was even more pronounced, with average enhancements of 78%, 67%, 40%, and 39%.

Figure 15b demonstrates that the total heat storage-release efficiency and cumulative heat storage/release efficiency of the four helical BFHEs increase linearly with the backfilling body’s thermal conductivity, with the increase in total heat storage-release efficiency indicating that the backfilling body’s improved thermal conductivity results in better utilization of the total heat stored there.

The average TPC of the four helical BFHEs increases with an increase in thermal conductivity, as shown in Figure 15c because an increase in thermal conductivity improves the heat storage/release rate of BFHEs. The figure shows that the TPC_ave of the SH, U-DH, SA-FH, and S-FH type BFHEs decreases in line with the increase in thermal conductivity. This is mostly caused by the variable impact of the backfilling body’s thermal conductivity resistance on the heat transfer of BFHEs. Since the SH type’s buried pipes arrangement is highly centralized and the backfilling body’s thermal conductivity resistance has the greatest impact on heat transfer performance, improving thermal conductivity has the most obvious positive impact on the SH type’s storage/release capacity. The backfilling body’s influence on the S-FH type buried pipes arrangement’s thermal conductivity resistance is minimized by optimal dispersion and matching, and the improvement brought about by an increase in thermal conductivity occurs naturally, thermal conductivity naturally reduces as it gets better.

6. Conclusions

The numerical simulation of the performance of the full-size horizontal BFHEs used in metal backfilling mines is performed in this work. A three-dimensional unsteady heat transfer model of BFHEs is established by COMSOL software, and its accuracy is validated. Considering the same inner surface of the heat exchange pipe, the helical pipe BFHEs with four different arrangements are compared with the traditional SS-type BFHEs for the three years of continuous operation and the influence of main parameters (pitch length, pipe diameter and thermal conductivity of backfill body) on the heat storage/release performance of the helical pipe BFHEs is analyzed, and the following conclusions can be reached:

(1)

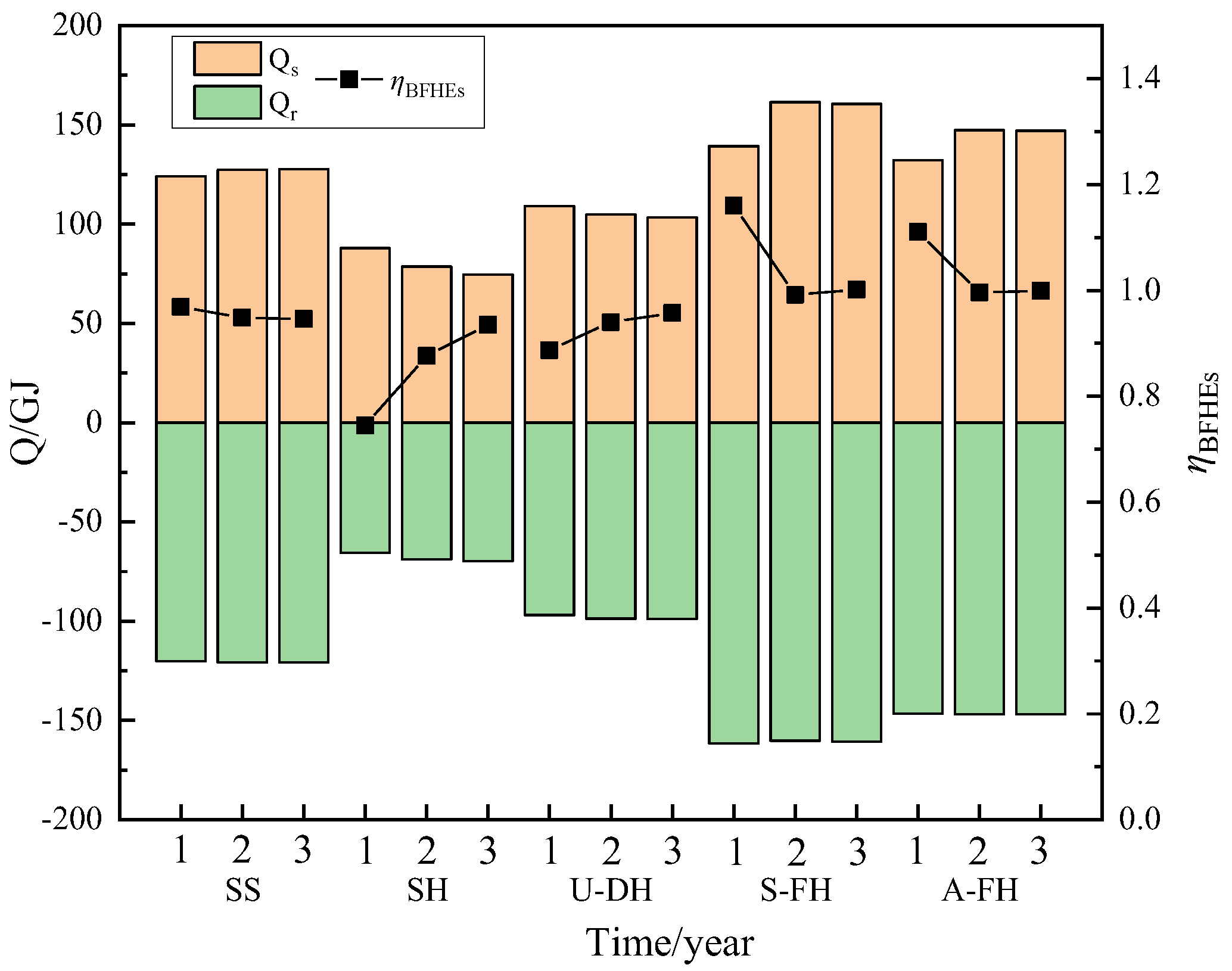
Compared with the conventional Serpentine Straight-pipes (SS), the Serpentine-type four helix-pipes (S-FH) have the best fit with the internal heat transfer of the backfill body in the mining layer of the metal mine, and the internal temperature distribution of the backfill body is the most uniform throughout the processes of heat storage/release. And it can increase the capacity of heat storage/release of BFHEs by a large amount of 21.7%. The next best configuration, with an improvement of 11.1%, is the Square Array-type four helix-pipes (SA-FH). The Single Helix-pipes (SH) and U-type Double Helix-pipes (U-DH) layouts, which have fallen by 19.9% and 42.7%, respectively, are both subpar.

(2)

The pipe configuration significantly affects the change in the heat storage/release rate of BFHEs, especially in the early phase of the heat storage/release processes. With a maximum increase of roughly 15 kW, S-FH and SA-FH have much higher heat storage/release rates than SS, but U-DH and SH have significantly lower rates.

(3)

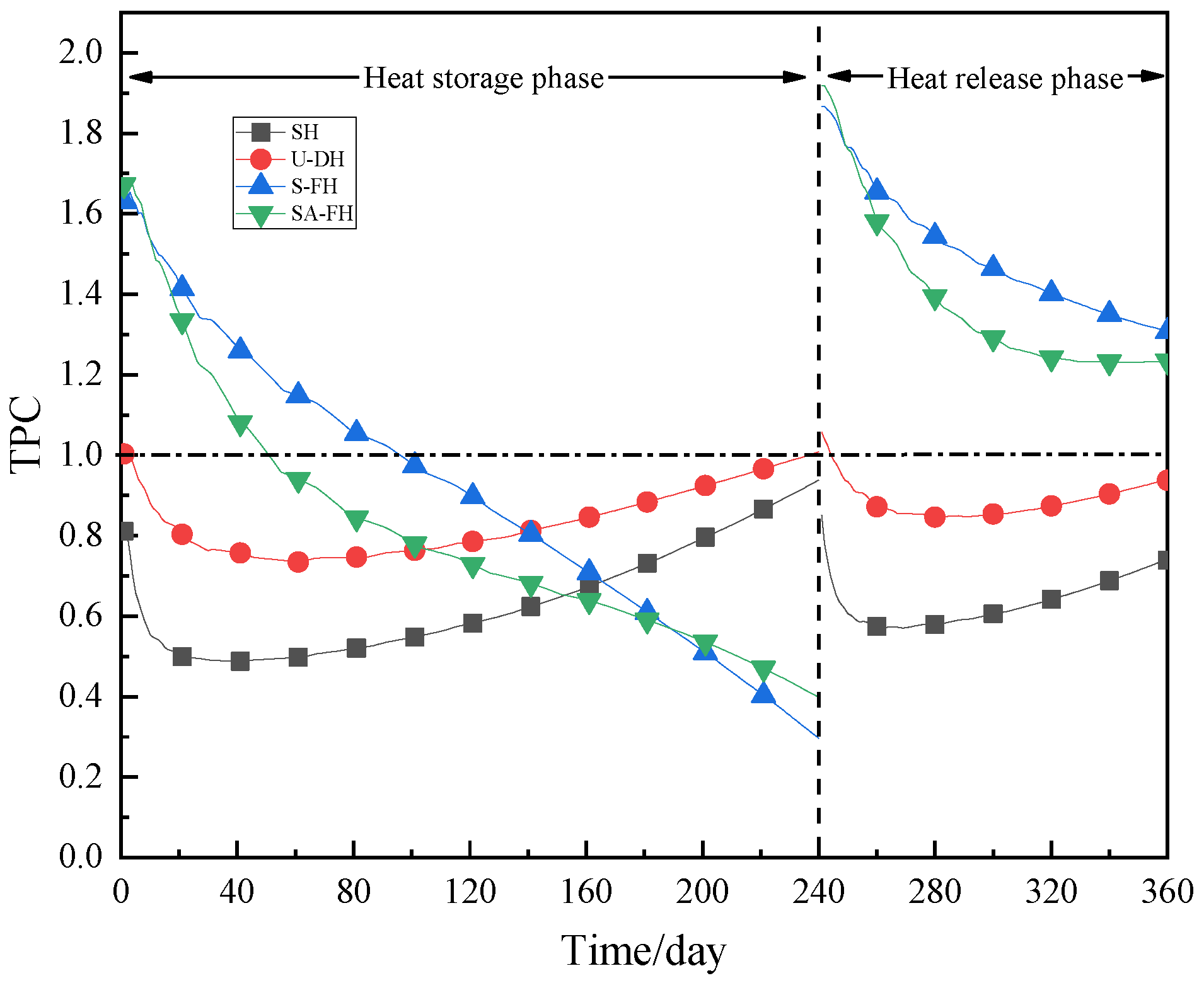
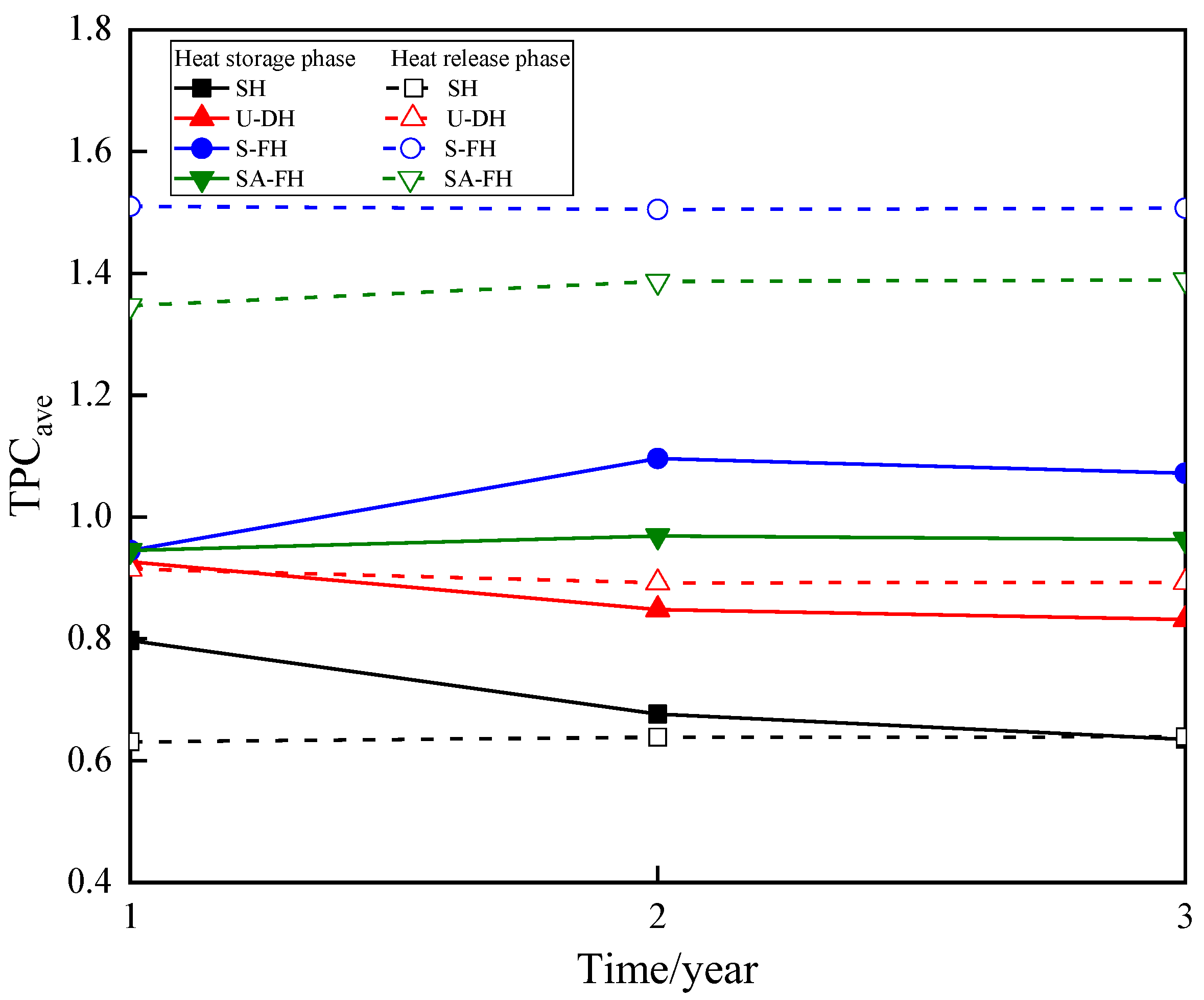
Given the flow resistance, the pipe configuration distinctly influences the thermal performance capability of helical BFHEs. When BFHEs are operating steadily, S-FH and SA-FH have TPC_ave in the heat storage phase that is similar to that of SS at roughly 1.10 and 0.96 and in the heat release phase that is substantially higher at 1.51 and 1.39. The TPC_ave of U-DH and SH, at roughly 0.85 and 0.64, respectively, is significantly lower than that of SS during the heat storage/release phase.

(4)

To enhance the thermal performance and heat storage/release capacity of helical BFHEs, it is advantageous to decrease the pitch length to pipe diameter ratio (C₁) and increase the pitch diameter to pipe diameter ratio (C₂).

(5)

The thermal performance of helical BFHEs can be effectively improved by increasing the backfill body’s thermal conductivity, with SH experiencing the greatest improvement and S-FH experiencing the least improvement. The average increases in the heat storage/release rates of SH, U-DH, SA-FH, and S-FH are 46%/78%, 34%/67%, 25%/40%, and 22%/39%, respectively, when the thermal conductivity is raised from 0.4 W/(m·k) to 0.8 W/(m·k).