On Λ-Fractional Wave Propagation in Solids

Abstract

Wave propagation in solids is discussed, based upon inherently non-local Λ-fractional analysis. Following the governing equations of Λ-fractional continuum mechanics, the Λ-fractional wave equations are derived. Since the variational procedures are only global, in the present Λ-fractional analysis, various jumpings, either in the strain or the stress, may be shown. The proposed theory is applied to impact-induced transitions in two-phase elastic materials and viscoelastic materials.

1. Introduction

Lately, mechanics have adapted various fractional calculus models to describe viscoelastic behavior and simulating experiments, Bagley et al. [1,2]. Atanackovic [3] and Mainardi [4] have presented various viscoelastic and wave propagation models in mechanics. The fundamental characteristic of fractional calculus is its global dependence. Lazopoulos [5], based upon fractional calculus, proposed the deformation of a non-homogeneous bar with possible voids. In that case, Noll’s axiom of local action, Truesdell [6], fails to be valid. According to Eringen [7], micro- and nanomaterials should be based on the axiom of non-local action. In fact, the strains in the neighborhood of that point define the stress.

Introducing non-local derivatives, fractional calculus has recently been applied to physics advances, engineering, mechanics, bioengineering, physics, biology, etc. In fact, Leibniz [8] foresaw the importance of fractional derivatives because they acquire properties quite different from common derivatives. Their strikingly different property is the non-locality they inherently possess, contrary to the common derivatives expressing locality. Many famous mathematicians like Liouville [9], Lagrange, Poincare, and Riemann [10] have worked on fractional derivatives. Information concerning fractional calculus may be found in various texts, like Miller et al. [11], Poldubny [12], Samko et al. [13], and Oldham et al. [14]. Nevertheless, fractional derivatives are not mathematical derivatives according to differential topology, which Chillingworth [15] satisfies:

• Linearity $\mathrm{D}\left(\mathrm{a}\mathrm{f}\left(\mathrm{x}\right)+\mathrm{b}\mathrm{g}\left(\mathrm{x}\right)\right)=\mathrm{a}\mathrm{D}\mathrm{f}\left(\mathrm{x}\right)+bDg\left(x\right)$.
• Leibniz rule $D\left(f\left(x\right)\bullet g\left(x\right)\right)=Df\left(x\right)\bullet g\left(x\right)+f\left(x\right)Dg\left(x\right).$
• Chain rule $D\left(g\left(f\right)\right)\left(x\right)=Dg\left(f\right(x)\bullet Df(x)$.

Although fractional calculus is considered necessary when studying various problems in physics, engineering, biology, etc., fractional geometry does not exist. Hence the mathematical analysis of the presented problems does not possess the accuracy demanded by mathematics.

Nevertheless, the application of fractional calculus is considered quite important in various scientific areas requiring the consideration of non-local procedures. Lazopoulos [16,17,18,19,20] introduced the Λ-fractional derivative, because it is a unique fractional derivative satisfying all the prerequisites of differential topology for being a mathematical derivative. Hence it is a unique fractional differential procedure formulating fractional differential geometry and correct differential equations with the existence and uniqueness theorem applied in physics and mechanics. Another essential feature of fractional calculus is the necessity for the consideration of global variational procedures with the additional Weierstrass–Erdmann corner conditions, Lazopoulos [21]. Hence, the co-existence of phases phenomena, Ericksen in [22], may be revealed.

Wave propagation is studied in the context of Λ-fractional analysis. Due to global variation procedures, jumps in the strain and stress may be revealed. Jumping in strain or stress with non-linear elasticity has already been discussed in [23]. In fact, the evolution of phase transitions is present in the wave propagation of strains in non-local Λ-fractional mechanics. The Λ-fractional impact-induced transitions in two-phase elastic materials are discussed. Further, the Λ-fractional wave propagation with possible jumping is discussed in the context of viscoelastic materials.

2. The Λ-Fractional Analysis

The importance of fractional derivatives was suggested by Leibnitz in 1695. The main characteristic of fractional calculus is non-locality. Non-local properties are exhibited mainly by micro and nanomaterials [7].

For a fractional order 0 < γ $\le$ 1, the left and right fractional integrals are expressed by

$${}_{\mathrm{a}}I_x^{\gamma }f(x)=\frac{1}{\Gamma (\gamma )}{\displaystyle \underset{\mathrm{a}}{\overset{x}{\int }}\frac{f(s)}{{(x-s)}^{1-\gamma }}ds}$$

(1)

$${}_{x}I_b^{\gamma }f(x)=\frac{1}{\Gamma (\gamma )}{\displaystyle \underset{x}{\overset{b}{\int }}\frac{f(s)}{{(s-x)}^{1-\gamma }}ds}$$

(2)

where Γ(γ) denotes Euler’s Gamma function. There exist many fractional derivatives. However, there is only one fractional integral. The Riemann–Liouville (RL) fractional derivative (FR) is the most common fractional derivative. In fact, the left RL fractional derivative is defined by

$${}_a{}^{RL}D_x^{\gamma }f(x)=\frac{d}{dx}\left({}_{\alpha }I_x^{1-\gamma }\left(f(x)\right)\right)=\frac{1}{\Gamma (1-\gamma )}\frac{d}{dx}{\displaystyle \underset{a}{\overset{x}{\int }}\frac{f(s)}{{(x-s)}^{\gamma }}ds},$$

(3)

whereas, the right RL fractional derivative (RL) is expressed by

$${}_x{}^{RL}D_b^{\gamma }f(x)=\frac{d}{dx}\left({}_{x}I_b^{1-\gamma }\left(f(x)\right)\right)=-\frac{1}{\Gamma (1-\gamma )}\frac{d}{dx}{\displaystyle \underset{x}{\overset{b}{\int }}\frac{f(s)}{{(s-x)}^{\gamma }}ds}$$

(4)

Fractional integrals and derivatives are connected through the relation

$${}_x{}^{\mathit{RL}}D_x^{\gamma }\left({}_{a}I_x^{\gamma }f\left(x\right)\right)=f\left(x\right)$$

(5)

It is well known that fractional derivatives fail to satisfy the differential topology prerequisites, Chillingworth [15], for creating the differential geometry necessary for describing physical problems. Nevertheless, well-known fractional derivatives have been used in physics, mechanics, biomechanics, etc., without being able to generate the geometry necessary for the study of the physical problems.

The Λ-fractional analysis, proposed by Lazopoulos [16], is consistent with the prerequisites of differential topology, and Λ-fractional derivatives may correctly generate differential geometry. Λ-fractional analysis has already been applied to geometry, physics, mechanics, differential equations, etc., Lazopoulos [16,17,18,19,20].

The Λ-fractional derivative (Λ-FD) is defined as

$${}_a{}^{\Lambda }D{}_x^{\gamma }f(x)=\frac{{}_{\alpha }{}^{RL}D{}_x^{\gamma }f(x)}{{}_a{}^{RL}D{}_x^{\gamma }x}.$$

(6)

In addition, the Λ-FD becomes

$${}_a{}^{\Lambda }D{}_x^{\gamma }f\left(x\right)=\frac{\frac{d{}_{a}I_x^{1-\gamma }f(x)}{dx}}{\frac{d{}_{a}I_x^{1-\gamma }x}{dx}}=\frac{d_a{I}_x{}^{1-\gamma }f(x)}{d_a{I}_x{}^{1-\gamma }x},$$

(7)

with the help of Equation (3). Moreover, the Λ-fractional space is constructed using (X,F(X)) with

$$\hspace{1em}X{=}_a{I}_x{}^{1-\gamma }x,\hspace{1em}\hspace{1em}F(X){=}_a{I}_x{}^{1-\gamma }f(x(X)).$$

(8)

Taking into consideration Equation (5), the results generated by analysis in the Λ-fractional space may be transferred into the original space. Hence,

$$f\left(x\right)={{}_a{}^{RL}{D}_x^{1-\gamma }}^{}F\left(X\left(x\right)\right)={{{}_{\alpha }{}^{RL}D}_x^{1-\gamma }}^{}\left(I^{1-\gamma }f\left(x\right)\right).$$

(9)

The Λ-fractional procedure presents similarities to Laplace’s transformation applied to fractional calculus. However, Λ-fractional transformation applies only to functions, not to derivatives, and the corresponding functions in the Λ-fractional space form various derivatives. Applying analysis in the Λ-fractional space, the various results may be transferred back into the initial space as simple functions only.

Another essential feature of Λ-fractional analysis is the global stable features of the various fractional problems. The defect was pointed out in [18], and the governing continuum mechanics laws were corrected in a recent work by Lazopoulos [24]. Following Ericksen [22], the various globally stable states in the introduced Λ-fractional space should satisfy the conditions of Erdmann–Weierstrass, Gelfand, and Fomin [25]. Those ideas have already been applied to biological balloons under pressure. The same procedures will employed in the present study of Λ-fractional waves.

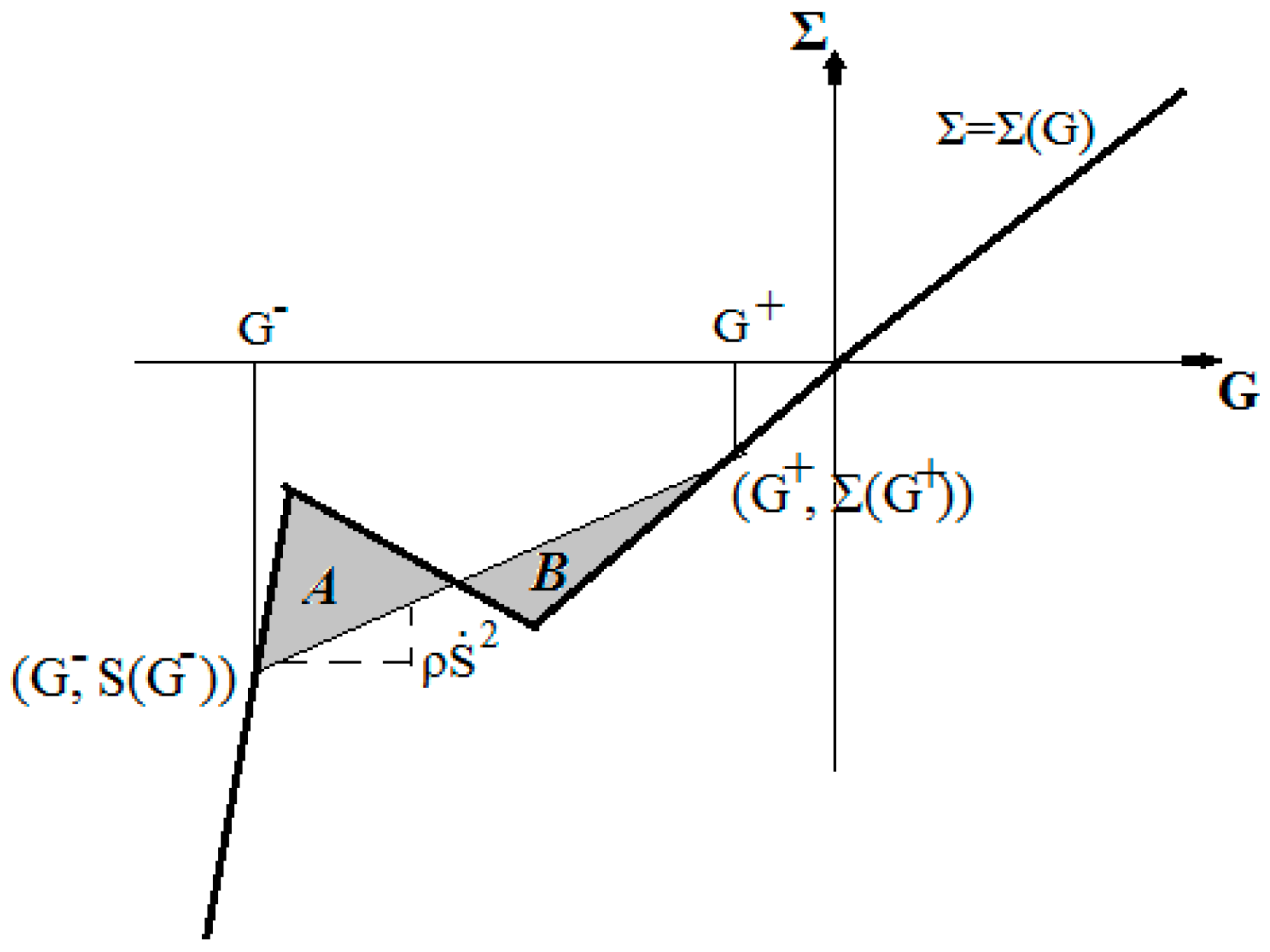
3. Waves with Shocks in Λ-Fractional Non-Linear Elasticity

Consider a one-dimensional bar in the interval 0 $\le X\le L$ in Λ-fractional space. That is considered the reference placement of the bar in the Λ-fractional space. During its motion, the particle at X is transferred into its current placement Y, with

Y(X,T) = X + U(X,T),

(10)

where, U(X,T) is the continuous displacement. The displacement might accept first and second piecewise continuous derivatives with respect to space and time. The assumed smoothness for the displacement U(X,T) allows for jump discontinuities in the strain G = U_X(X,T) and velocity V = U_T(X,T). Considering the portion of the bar lying in the interval [X₁, X₂], in the absence of body force, the balance of momentum in the sub-bar [X₁, X₂] is expressed by

$$\Sigma X_2,T-\Sigma X_1,T = \frac{D}{DT}{\int }_{X_1}^{X_2}\rho V\left(X,T\right)dX,$$

(11)

where ρ denotes the constant mass per unit referential volume.

For smooth fields, the momentum balance law yields

Σ_Χ(X,T) = ρV_T (X,T).

(12)

Moreover,

V_X(X,T) = G_T(X,T)

(13)

$$\mathrm{with} G(X,T) = \frac{\partial U(X,T)}{\partial X}.$$

(14)

If the motion exhibits a single strain discontinuity point between [X₁, X₂] with a location in the reference configuration X = S(T), then the momentum balance equation, Equation (11), and the assumed smoothness of the displacement yield the jump conditions

$$⟦\mathit{\Sigma }⟧=-\rho \dot{\mathit{S}}⟦V⟧,$$

(15)

$$⟦V⟧=-\dot{S}⟦G⟧.$$

(16)

Further, the constitutive law

Σ = Σ(G),

(17)

with the jumping conditions, Equations (15) and (16), yield the expression of the velocity of the discontinuity and the strains $G^{\pm }$ on either side.

$$\rho {\dot{S}}^2=\frac{\Sigma \left(G^{+}\right)-\Sigma \left(G^{-}\right)}{G^{+}-G^{-}}.$$

(18)

Transferring the velocity of the jump discontinuities, as a function, into the initial space with the help of Equation (9), considering the space fractional order ${\gamma }_1$ and time fractional order ${\gamma }_2$, yields

$$\dot{\mathrm{s}}\left(x\right)={{}_0{}^{RL}D}_t^{1-{\gamma }_2}{{{}_{\alpha }{}^{RL}D}_x^{1-{\gamma }_1}}^{}\dot{\mathrm{S}}\left(X\left(x\right),T\left(t\right)\right)={{}_0{}^{RL}D}_t^{1-{\gamma }_2}{{{}_{\alpha }{}^{RL}D}_x^{1-{\gamma }_1}}^{}\left(I^{1-{\gamma }_2}{I}^{1-{\gamma }_1}\dot{S}\left(x,t\right)\right).$$

(19)

Equation (19) includes both effects of the fractional space and the time distributions.

4. The Fractional Impact Problem for Two-Phase Materials

Let us consider a one-dimensional rod in the Λ-fractional space in its reference configuration with the strains G(X,0) = 0 and velocities V(X,0) = 0. Further, a constant velocity V(0,T) = V₀ is applied at time T = 0 and remains constant at all times T at the initial point X = 0. Therefore, the dynamical problem of the bar is defined by the equations

$${\Sigma }^{\prime }\left(G\right)G_{X }=\rho V_T \mathrm{for} \mathrm{X} \ge 0, \mathrm{T} \ge 0$$

(20)

V_X = G_T

(21)

and the initial conditions,

$$G(X,0) = V(X,0) = 0, \mathit{for} X \ge 0$$

(22)

and the boundary conditions,

$$V(0,T) = V_0 \mathit{for} T\ge 0.$$

(23)

Let us consider W(G) the strain energy density per unit reference volume concerning the uniaxial deformation of the rod. The stress is defined through

Σ = W^′ (G) = Σ(G).

(24)

The diagram of Figure 1 is the most straightforward stress–strain diagram for developing two-phase deformation in compression.

For the material presented in Figure 1, the stress is defined by

$$\Sigma \left(G\right)={\mu }_{L}G \mathit{for}>-G_m,$$

(25)

$$\Sigma \left(G\right)={\mu }_H(G+G_T) \mathit{for} -1 < G<-G_m,$$

(26)

Hence, two branches exist: the low-pressure stress–strain deformation section with G > −G_m and the high-pressure deformation with −1 < G < −G_M.

Therefore, Equation (25) yields for low-pressure shock the velocity

$$\dot{{\mathrm{S}}_{\mathrm{L}}}=\sqrt{\frac{{\mathsf{\mu }}_{\mathrm{L}}}{\mathsf{\rho }}}$$

(27)

Further, the velocity of the shock wave for the high-pressure phase is defined by

$$\dot{ S_H}=\sqrt{\frac{{\mu }_H}{\rho }}$$

(28)

Moreover, Figure 2 denotes the stress-strain diagram with jumping of strains. For the transition from the low-pressure phase to the high-pressure phase, Equation (18) will be recalled.

Therefore, Equation (18) yields

$$\rho {\dot{S}}^2=\frac{\Sigma \left(G^{+}\right)-\Sigma \left(G^{-}\right)}{G^{+}-G^{-}}$$

(29)

Therefore, three separate cases are pointed out, corresponding to the impact problem:

i.

The low-pressure phase shock wave case.

ii.

The low-pressure phase shock wave followed by a low-pressure phase followed by a high-pressure phase boundary.

iii.

A phase boundary from the low-pressure phase to the high-pressure phase. No shock wave is involved.

For further information see Abeyaratne and Knowles [23]. The results gathered in the Λ-fractional space may be transferred into the initial space through the transformation Equation (19).

5. Waves with Shocks in Λ-Fractional Viscoelasticity

There is a result concerning the shock front in viscoelastic fractal media calculated by Demnie et al. [26], who point out that the fractality of the rod does not affect the jumping solution of the stress. Of course, there exist two comments concerning that result. The first is that fractional calculus, adhered to in that reference, fails to exhibit fractional derivatives acquiring the properties of a derivative, and secondly, the fractional time behavior has not been taken into consideration in the viscoelastic response.

Following [26], the stress Σ and the displacement U(X) in the Λ-fractional space are connected through the governing equation

$${\Sigma ,}_X=\rho {U,}_{TT}$$

(30)

with ρ the constant mass density and the boundary conditions

U(0,T) = U,_T(X,0) = 0.

(31)

Furthermore, the initial conditions are expressed by

Σ(0,Τ) = −Σ₀H(Τ).

(32)

where H is the Heaviside function.

Following [26], the jumping of the stress Σ in the Λ-Fractional space is connected with the jumping of the wave velocity U,_T through the relation

$$⟦\Sigma ⟧=-\rho C⟦{U,}_T⟧,$$

(33)

where $⟦\Phi ⟧$ denotes the jumping in Φ.

Moreover, the linear viscoelastic process in the Λ-fractional space starting at time T = $T_0^{+}$ is defined by

$$\Sigma \left(T\right)=E\left(0\right){U,}_X\left(T\right)+{\int }_{T_0^{+}}^T{E,}_T\left(T-S\right){U,}_{S}dS,$$

(34)

where, E(T) is the relaxation function.

Recalling the conservation of the governing linear momentum equation,

$$⟦{\Sigma ,}_x⟧=\rho ⟦{U,}_{TT}⟧,$$

(35)

the solution for the jumping of $⟦\Sigma ⟧$ in the Λ-fractional space is defined by, see [26],

$$⟦\Sigma \left(T\right)⟧={\Sigma }_{0}exp\left\{\frac{1}{2}\frac{{E,}_T\left(0\right)}{E\left(0\right)}T\right\}.$$

(36)

As it has been pointed out, the fractality of the space does not enter into the jumping distribution of the stress Σ in the Λ-fractional space. However, transferring the jumping distribution from the Λ-space to the initial one, the fractional order of the space ${\gamma }_1$ and the time ${\gamma }_2$ should be taken into consideration. Indeed, taking into consideration Equations (8) and (9) transforms the initial space (x,t) into the Λ-fractional space (X,T) with

$$X=\frac{x^{2-{\gamma }_1}}{\Gamma (3-{\gamma }_1)}$$

(37)

$$T=\frac{t^{2-{\gamma }_2}}{\Gamma (3-{\gamma }_2)}.$$

(38)

Indeed, the transformation of Equation (36) into the initial space demands the following steps:

a.

Substitution of the T variable by the equivalent of T in Equation (36). Hence,

$$⟦\Sigma \left(T\right)⟧=⟦\Sigma (\frac{t^{2-{\gamma }_2}}{\Gamma (3-{\gamma }_2)})⟧ = Y(t)$$

(39)

b.

Transferring the jumping function of the stress into the initial space just to yield the function

$$⟦\sigma (\mathrm{x},\mathrm{t})⟧=\frac{1}{\Gamma \left(1-{\gamma }_1\right)\Gamma (1-{\gamma }_2)}\frac{d}{\mathrm{d}\mathrm{x}}{\int }_0^{\mathrm{x}}\frac{1}{{\left(\mathrm{x}-\mathrm{s}\right)}^{{\gamma }_1}}ds\frac{d}{\mathrm{d}\mathrm{t}}{\int }_0^t\frac{\mathsf{{\rm Y}}\left(\mathsf{\tau }\right)}{{\left(\mathrm{t}-\tau \right)}^{{\gamma }_2}}d\tau$$

(40)

Simplifying Equation (41), the jumping function of the stress into the initial space is defined by

$$⟦\sigma (\mathrm{x},\mathrm{t})⟧=\frac{x^{-{\gamma }_1}}{\Gamma \left(1-{\gamma }_1\right)\Gamma (1-{\gamma }_2)}\frac{d}{\mathrm{d}\mathrm{t}}{\int }_0^t\frac{{\rm Y}\left(\tau \right)}{{\left(\mathrm{t}-\tau \right)}^{{\gamma }_2}}d\tau$$

(41)

6. Conclusions—Further Results

The present analysis concerns Λ-fractional wave propagation into elastic and viscoelastic media. The main characteristic of the present analysis is the development of various jumpings, either in strain or stress, due to the globally stable conditions derived from the Erdmann–Weierstrass conditions. The wave propagation with strain jumping in a two-phase material, due to the trilinear stress–strain diagram, and the propagation of stress jumping in viscoelastic media is discussed. The present analysis will be transferred into fractional fluids, where the various shocks will be studied. Further information concerning the fractional propagation of waves in solids may be found in [27,28,29,30,31]. In fact, fractional derivatives are non-local, contrary to the fractal waves that access local derivatives [32]. Nevertheless, there exists the influence of fractional order calculus upon the fractal dimensions [33,34,35,36].