Categorical Variable Mapping Considerations in Classification Problems: Protein Application

Abstract

The mapping of categorical variables into numerical values is common in machine learning classification problems. This type of mapping is frequently performed in a relatively arbitrary manner. We present a series of four assumptions (tested numerically) regarding these mappings in the context of protein classification using amino acid information. This assumption involves the mapping of categorical variables into protein classification problems without the need to use approaches such as natural language process (NLP). The first three assumptions relate to equivalent mappings, and the fourth involves a comparable mapping using a proposed eigenvalue-based matrix representation of the amino acid chain. These assumptions were tested across a range of 23 different machine learning algorithms. It is shown that the numerical simulations are consistent with the presented assumptions, such as translation and permutations, and that the eigenvalue approach generates classifications that are statistically not different from the base case or that have higher mean values while at the same time providing some advantages such as having a fixed predetermined dimensions regardless of the size of the analyzed protein. This approach generated an accuracy of 83.25%. An optimization algorithm is also presented that selects an appropriate number of neurons in an artificial neural network applied to the above-mentioned protein classification problem, achieving an accuracy of 85.02%. The model includes a quadratic penalty function to decrease the chances of overfitting.

1. Introduction

Machine learning applications have been successful in different classification tasks in areas such as physics [1,2,3], chemistry [4,5,6,7,8,9], and engineering [10,11,12], and many different algorithms currently exist, such as Trees [13,14,15], K-Nearest Neighbors (KNNs) [16,17,18], or Support Vector Machines (SVMs) [19,20,21]. The internal logic of these machine learning algorithms can substantially vary among the different types of models. A machine learning approach might be advantageous in a situation in which more traditional models do not exist or when these models are too complex to be efficiently implemented. Typically, machine learning models do not require a detailed understanding of the underlying problem that they are trying to model (requiring only some input and output data) or when such detailed modeling is too costly from a computational (or economic) point of view. Therefore, machine learning techniques might be suitable for modeling some complex processes [22,23,24,25] such as protein classification. In this article, we focused on the classification task of small proteins and numerical simulations regarding some assumptions regarding the mapping of categorical values, which is an issue directly related to protein modeling, as the input is typically a chain of amino acids, with each amino acid designated with a given letter. A frequently mentioned drawback of this type of approach is that machine learning techniques tend to be black boxes [26,27,28]. In other words, even if the classification estimations are accurate, the underlying logic is not easily explainable. In this type of modeling, some categorical variables are commonly mapped into numerical values, as it is frequently more convenient to use numerical data in the simulations [29,30]. In this paper, we present a series of four mapping assumptions in the context of protein classification [31,32]. There is a relatively high degree of arbitrariness in the way in which these categorical variables are mapped into numerical values, and it appears interesting to test a series of assumptions about these mapping with numerical simulations. This, in fact, is one of the motivations of this article, as the issue of categorical mapping in the context of protein classification could have some modeling implications.

An algorithm is also presented for the optimization of artificial neural networks [33,34,35] for the classification problem, including a penalty function [36,37]. The objective of the penalty function is to favor simpler models among classification models that have similar precision. Simpler models, for example, neural networks with fewer neurons, have the advantage of being less prone to overfitting [38,39]. Overfitting is a relatively common issue in which the selected model fits rather accurately to the training data but is not properly generalized when faced with new data. Optimization approaches are commonly used in many diverse fields, such as machine learning applications in the context of ambient music in gyms [40]. There are many different proteins and many different classifications of proteins, thus making this type of analysis challenging, which is a potential limitation of the analysis. In order to minimize this risk, a well-known database of proteins (Protein Data Bank (PDB)) was selected, and we used its standard classification of proteins.

This paper is structured into five sections. An introduction in which some of the basic concepts and the main theme of the article are presented, a literature review in which related works are reported, a materials and methods section in which the four mathematical assumptions about the categorical mapping are stated, as well as the optimization algorithm, data, and general procedures. The last two sections are the results and the conclusions and recommendations, in which we analyze the results, propose potential areas of future research, and suggest some recommendations in this type of analysis.

2. Literature Review

The field of protein modeling using machine learning techniques is rapidly expanding [41]. For instance, Xu et al. used machine learning techniques to describe sequence/activity relationship [42]. This article also focused on mutations, which is an area out of the scope of our analysis. Another interesting article in the field is that of Salau and Jain [43]. In this article, the authors used machine learning techniques for the classification of cell decisions for AKT proteins. The authors used, among other techniques, neural networks such as radial basis functions (RBFs) and multi-layer perceptron (MLP). The importance of feature extraction in this context is frequently mentioned in the literature [44], and it is not exclusive to neural networks, as other popular machine learning techniques such as KNN and SVMs are also mentioned in the literature [45]. There are also some articles such as Hancock et al. [46], highlighting the importance of categorical information in machine learning techniques. More precisely, this article is a survey of categorical information in neural network applications. Some authors, such as Ofer et al. [47], followed a different approach by using natural language processing (NLP) for this type of protein classification task, which avoids the issue of categorical classification (mapping from a categorical value to a numerical value). This, however, remains an approach not followed by the majority of researchers. A potential reason for this is that a numerical approach facilitates the application of some well-known machine learning techniques, and there is so far no indication that this type of NLP approach can generate more accurate results than more traditional machine learning approaches.

Many authors, such as McDowall and Hunter [48] and Nanni et al. [49], revealed the complexity of manually performing protein classification, which is probably one of the reasons for the increasing number of applications of machine learning techniques in this field. Diplaris et al. [50] explicitly mentioned the need for automated tools that can classify new proteins. Data availability has also increased [31]. Using SVMs, Cai et al. managed to achieve an accuracy ranging from 69.1% to 99.6% [51]. Another related field in protein classification that has raised interest from a machine learning approach is the field of protein–protein interaction. In this type of research, the objective is not to identify the type of protein but to forecast the protein–protein interaction. To some degree, the classification of the type of protein could have some impact on the interaction, but it is likely not the determining factor. Bock et al. [52] achieved an 80% success rate in this type of protein–protein interaction analysis. More recently, Das and Chakrabarti [53] followed a similar approach, achieving comparable results. For the special case of G-protein-coupled receptors, Karchin et al. [54] also followed a machine learning approach, using several techniques and obtaining an error ranging from 13.7% to 49%.

In this article, we focus on the analysis of small proteins, which is an area of increasing medical interest [55,56,57]. We also focus on the analysis of the classification of categorical variables, i.e., amino acids (in different representations), without the need to use NLP approaches. As previously mentioned, the importance of the process of categorical mapping into numerical values has been frequently mentioned in the existing literature. There are some articles using machine learning applications in the field of small proteins. For example, Ernest et al. [58] used this approach to study antimicrobial peptides. This research in antimicrobial peptides is actually one of the subfields that have received more interest among researchers [59,60], but there is some existing research in other areas as well, for example, regarding antifungal peptides [61].

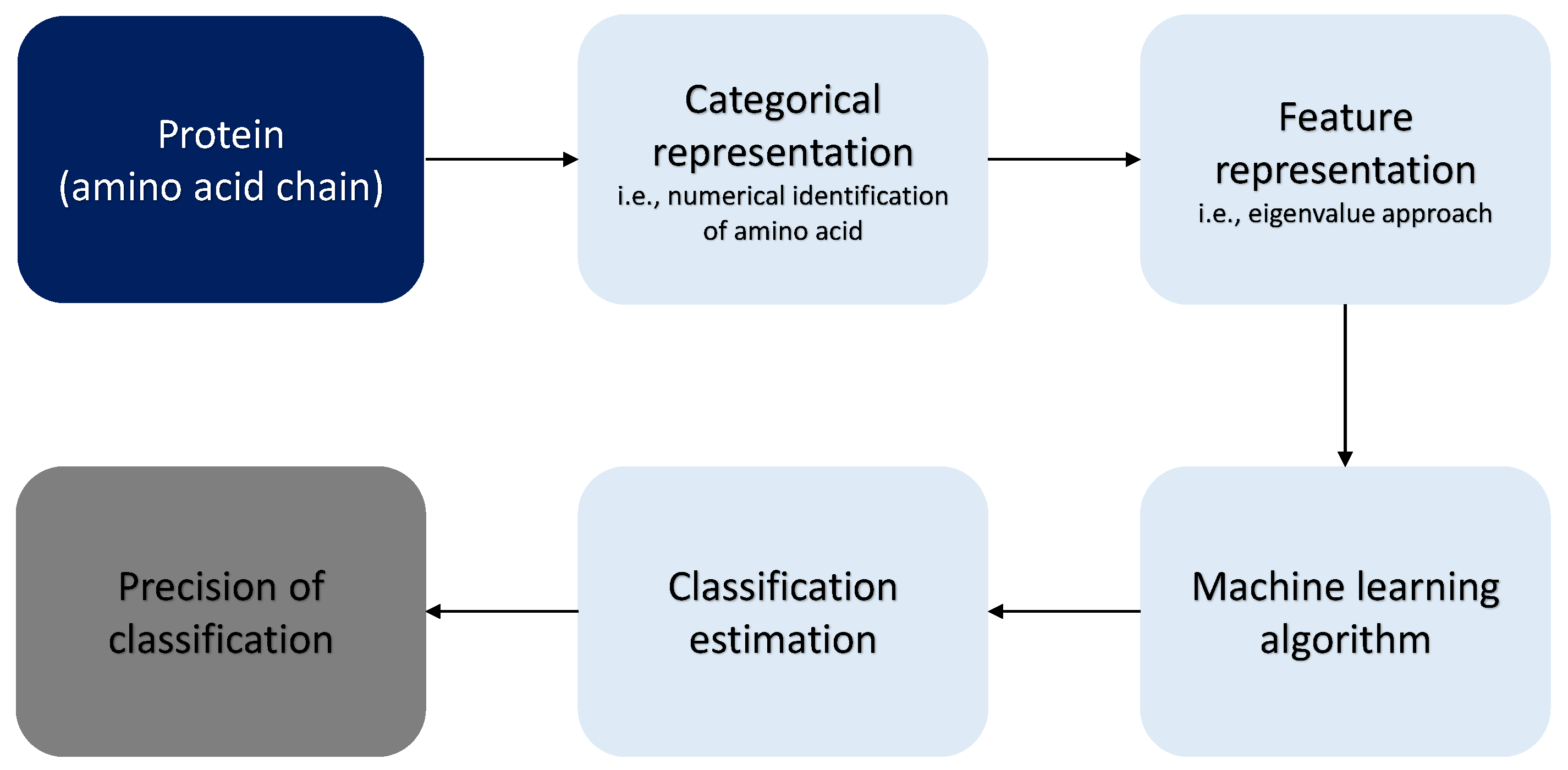
3. Materials and Methods

Mapping variables is a common practice in machine learning applications such as classification problems [62], particularly in situations in which it is necessary to model a process using categorical variables, for example, a protein classification task using their amino acid chains. There is a certain degree of arbitrariness in this process. A protein P can be described by its amino acid chain. This can be seen with an example, as illustrated in Equation (1).

$$P=\{AC\dots A\}$$

(1)

where each amino acid is defined with its standard letter. Note that the letter B is not typically associated with an amino acid. It is usually more convenient in machine learning applications to map into numerical values. A common practice is to map it using alphabetical order and increasing numbers (Equation (2)).

$$\{A,C,\dots \}\to f_1\{A,C,\dots .\}=\{1,2,\dots \}$$

(2)

As previously mentioned, this type of mapping is a bit arbitrary, as other numbers could have been used. For example, this should be equivalent to a mapping function that is identical to the previous, but a constant $\alpha$ is added to all the values.

$$f_2\{A,C,\dots \}=\{1+\alpha ,2+\alpha ,\dots \}$$

(3)

This could be noted as (Equation (4))

$$f_1\leftrightarrow f_2$$

(4)

Assumption 1

(translation). A mapping function (Equation (5))

$$f_1\{C_1,C_2,\dots .\}=\{a_1,a_2,\dots \}$$

(5)

where $\{C_1,C_2,\dots \}$ are categorical values, and $\{a_1,a_2,\dots \}$ are numerical values, should be equivalent $(f_1\leftrightarrow f_2)$ to a mapping function $f_2$ such that (Equation (6))

$$f_2\{C_1,C_2,\dots .\}=\{a_1+\alpha ,a_2+\alpha ,\dots \}$$

(6)

with $\alpha \ge 0$ as a constant.

Assumption 1 could be understood as a translation of mapping with a constant $\alpha$. Similarly, there is no reason in principle to assume that the numerical values shown in Equation (2) are specifically representative of the related amino acid; hence, a permutation of these values (assigned to each amino acid) should generate another equivalent mapping. For example, mapping according to Equation (7)

$$\{A,C,\dots \}\to f_3\{A,C,\dots .\}=\{2,1,\dots \}$$

(7)

should be equivalent to $f_1$$(f_1\leftrightarrow f_3)$. In this example, the amino acids A and C are mapped into the values 1 and 2, respectively, in mapping $f_1$, and to the values 2 and 1 in mapping $f_3$. This change should have no effect on the output of a machine learning classification analysis.

Assumption 2

(permutation). A mapping function (Equation (8))

$$f_1\{C_1,C_2,\dots \}=\{a_1,a_2,\dots \}$$

(8)

with $\{C_1,C_2,\dots \}$ as categorical values and $\{a_1,a_2,\dots \}$ as numerical values should be equivalent to mapping according to $f_3$, as described in Equation (9).

$$f_3\{C_1,C_2,\dots \}=\{a_1,a_2,\dots ,a_j,a_{j-1},\dots .\}$$

(9)

where we have a permutation of the numerical values of $f_1$ in $f_3$.

Another common situation in machine learning classification analysis is having data vectors of different lengths, for example, a group of proteins with different numbers of amino acids. These types of data are frequently stored in a matrix for easy use. It is more practical to use a square matrix, and hence a common practice is to add additional zeros (or other numerical values) to the amino acid chains to make them all of the same dimensions. We can define an operator $L\left(\right)$ such that (Equation (10))

$$L\left(P^i\right)=L\left(\{a_1,a_2,\dots \}\right)=l$$

(10)

where $P^i$ is a given protein, and l is the length of the vector (number of amino acids) in this protein. Given a set of k proteins, the maximum size $\left(\overline{l}\right)$ can be defined as Equation (11):

$$\overline{l}=sup(L\left(P^1\right),\dots ,L\left(P^k\right))$$

(11)

Hence, $\forall P^i$, $L\left(P^i\right)\le \overline{l}$. The set of these proteins can be represented as Equation (12):

$$X=(P^1,P^2,\dots .P^l)=\left(\begin{array}{cccc}{a}_1^1& a_1^2& \cdots & a_1^k\\ a_2^1& a_2^2& \cdots & a_2^k\\ ⋮& ⋮& ⋮& ⋮\\ \beta & \beta & \cdots & a_{\overline{l}}^k\end{array}\right)$$

(12)

where $\beta$ is a constant (usually set equal to zero or to a positive value) added in order to make the dimensions of the data vector containing each protein the same. Through this process, we ordered the proteins for clarity purposes (Equation (13)), but this is not a requirement.

$$L\left(P^1\right)\le L\left(P^1\right)\le \cdots \le L\left(P^k\right)$$

(13)

As previously mentioned, the constant $(\beta \ge 0)$ added to the data is arbitrary, and hence it should not impact the output of a machine learning classification estimation.

Assumption 3

(constant). A mapping function (Equation (14))

$$f_1\{C_1,C_2,\dots \}=\{a_1,a_2,\dots ,{\beta }_1\}$$

(14)

where ${\beta }_1\ge 0$ is an added constant to fit the required dimensions is equivalent to a mapping function $f_4$ (Equation (15)).

$$f_4\{C_1,C_2,\dots \}=\{a_1,a_2,\dots ,{\beta }_2\}$$

(15)

$\forall {\beta }_2\ge {\beta }_1\ge 0.$

3.1. Comparable Mappings

In Assumptions 1–3, the mappings are presumed to be equivalents. A less strict requirement (comparable mapping) can be also assumed on similar (but not strictly equivalent) mapping representations. For example, a protein can be described by the number of each type of amino acid and some other indicators such as the length of the chain. In this case, the mapping function would be (Equation (16)):

$$f_5\{C_1,C_2,\dots \}=\{n{a}_1,n{a}_2,\dots ,n{a}_{20},\dots \}$$

(16)

where $n{a}_i$ is the number of amino acids of type $a_i$ contained in the chain. It should be noted that the information contained in this mapping is less than in $f_1$, as it is typically assumed that the order in which the amino acids appear is an important factor in determining the shape and function of the protein [63,64,65]. Therefore, it cannot be claimed that $f_1$ and $f_5$ are equivalent. We denote this as a comparable (but not equivalent) mapping, as expressed in Equation (17).

$$f_1\leftrightsquigarrow f_5$$

(17)

Note that in $f_5$, some additional terms, such as the length of the chain, are not explicitly shown for simplicity. A potential full depiction of $f_5$ could be (Equation (18)).

$$f_5\{C_1,C_2,\dots \}=\{l^{*},n{a}_1,n{a}_2,\dots ,n{a}_{20},\overline{M},\underline{M},(\overline{M}-\underline{M}),l^{*}(\overline{M}-\underline{M})\}$$

(18)

with the terms $l^{*}$, $\overline{M}$, and $\underline{M}$ defined in Equations (19)–(21).

$$l^{*}=card\{C_1,C_2,\dots \}$$

(19)

$$\overline{M}=sup\{n{a}_1,n{a}_2,\dots ,n{a}_{20}\}$$

(20)

$$\underline{M}=inf\{n{a}_1,n{a}_2,\dots ,n{a}_{20}\}$$

(21)

with this mapping, the information for each protein is represented with a vector of length 25. This information can be also represented by a $5x5$ matrix.

$$A=\left(\begin{array}{ccccc}{l}^{*}& n{a}_1& n{a}_2& n{a}_3& n{a}_4\\ n{a}_5& n{a}_6& n{a}_7& n{a}_8& n{a}_9\\ n{a}_{10}& n{a}_{11}& n{a}_{12}& n{a}_{13}& n{a}_{14}\\ n{a}_{15}& n{a}_{16}& n{a}_{17}& n{a}_{18}& n{a}_{19}\\ n{a}_{20}& \overline{M}& \underline{M}& (\overline{M}-\underline{M})& l^{*}(\overline{M}-\underline{M})\end{array}\right)$$

(22)

A comparable representation (Equation (23)) would be the eigenvalues of this matrix $|A-\lambda I|=0$.

$$f_6\{C_1,C_2,\dots \}=\{{\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4,{\lambda }_5\}$$

(23)

Hence, k proteins could be represented as (Equation (24)):

$$\left(\begin{array}{cccc}{\lambda }_1^1& {\lambda }_1^2& \cdots & {\lambda }_1^k\\ {\lambda }_2^1& {\lambda }_2^2& \cdots & {\lambda }_2^k\\ {\lambda }_3^1& {\lambda }_3^2& \cdots & {\lambda }_3^k\\ {\lambda }_4^1& {\lambda }_4^2& \cdots & {\lambda }_4^k\\ {\lambda }_5^1& {\lambda }_5^2& \cdots & {\lambda }_5^k\end{array}\right)$$

(24)

Assumption 4

(eigenvalues). For some applications, mappings $f_1$ and $f_6$ are comparable $(f_1\leftrightsquigarrow f_6)$.

When using only five variables per protein, $f_6$ is more compact than $f_1$ compared with an arbitrary, large amount for $f_1$ (depending on the length of the amino acid chain). Assumptions 1–4 will be tested in a later section.

The eigenvalue approach could be considered a feature selection approach. Feature selection is an important component in machine learning approaches [66]. A simplified flowchart can be seen in Figure 1.

3.2. Optimization

In this section, we present an algorithm for the optimization of the structure of an artificial neural network. The steps are as follows:

1.

Chose the number of simulations $\left(k\right)$, the required accuracy $C_m$, the maximum number of iterations $\left(j_m\right)$, and the maximum number of neurons $\overline{a}$.

2.

Define a penalty function P. For example,

$$P=\omega a^2$$

(25)

where a is the number of neurons, and $\omega$ is a constant.

3.

Obtain a randomly generated number of neurons $\left(a\right)$, with $1\le a\le \overline{a}\in I$.

4.

Store a classification vector $Y=\{y_1,y_2,\dots .\}$ (target vector) with $y_i=\{0,1\}$ and the mapping into a matrix X.

5.

Divide the data into a training dataset $\{X_T,Y_T\}$ and a testing dataset $\{X_E,Y_E\}$ [67,68,69].

6.

Train the network $\left(\varphi \right)$ with the training dataset $\left(\varphi (X_T,Y_T)\right)$.

7.

Estimate the classification estimations $(Y_T^F=Y_T^F\left(\varphi (X_T,Y_T)\right))$.

8.

Estimate $b_i$ as follows:

$$If\left\{\begin{array}{c}{Y}_{T,i}^F=Y_{T,i}\Rightarrow b_i=0\hfill \\ Y_{T,i}^F\ne Y_{T,i}\Rightarrow b_i=1\hfill \end{array}\right.$$

(26)

9.

Estimate the accuracy $Ac$ (Equation (27)) and calculate the additional metrics of precision (Pr), recall (Rec), and F1-score (F1) using Equations (28)–(30), respectively.

$$Ac=\frac{\sum b_i}{i}$$

(27)

$$Pr=\frac{TP}{TP+FP}$$

(28)

$$Rec=\frac{TP}{TP+FN}$$

(29)

$$F1=\frac{2·Precision·Recall}{Precision+Recall}$$

(30)

In this notation, TP, FP, and FN are the true-positive, false-positive, and false-negative values, respectively.

10.

The estimated adjusted accuracy $A{c}^{*}$ is expressed in Equation (31):

$$A{c}^{*}=Ac-P\left(a\right)$$

(31)

This term penalizes an overly complex model with too many neurons.

11.

Compare the results of iterations and choose the model.

• $j=0\Rightarrow MN\left(j\right)=A{c}^{*}$
• $j\ne 0$

  $$If\left\{\begin{array}{c}A{c}^{*}>MN(j-1)\Rightarrow MN\left(j\right)=A{c}^{*}\hfill \\ A{c}^{*}\le MN(j-1)\Rightarrow MN\left(j\right)=MN(j-1)\hfill \end{array}\right.$$

  (32)

12.

Iterate until $(j=j_m)$ or $MN\left(j\right)\ge C_m$.

13.

Repeat k times generating $MN$={ $M{N}^1,M{N}^2,\dots ,M{N}^k$ }.

14.

Select $\overline{MN}=sup\{M{N}^1,M{N}^2,\dots ,M{N}^k\}$.

15.

Calculate the classification estimations (Equation (33)) with the testing dataset for the mode $\overline{MN}$.

$$Y_E^F=Y_E^F\left(\varphi (x_E,Y_E)\right)$$

(33)

16.

Repeat step 7 with $Y_E^F$ to obtain the testing dataset accuracy.

3.3. Data

A total of 307 small proteins were analyzed using their amino acid sequence. The data were obtained from the Protein Data Bank (PDB) [70,71,72]. This database is a frequently used database for protein information [73,74,75,76,77]. For the numerical simulations, we used the protein classification used in PDB. All the analyzed molecules were either classified as asymmetric or cyclic. A categorical variable was assigned to these two types of proteins. The dataset was composed of 254 asymmetric and 53 symmetric small proteins. The median and average number of amino acids were 84 and 81, respectively, and the amino acid chain ranged from 26 to 225 amino acids.

$$Y=Y\{0,1\}=\left(\begin{array}{c}Asymmetric\\ Cyclic\end{array}\right)=\left(\begin{array}{c}0\\ 1\end{array}\right)$$

(34)

The full list of the analyzed molecules can be seen in the Supplementary Material file. All the results shown were estimated using only the testing dataset. In machine learning, it is often not difficult to create a model that accurately describes the training dataset but fails to generalize when faced with new (unseen) data. The training dataset contains approximately 66.6% of the proteins, and the testing dataset contains the remainder 33.3%. Examples of cyclic (Figure 2) and asymmetric (Figure 3) are shown below.

3.4. Numerical Simulations

Numerical simulations were carried out to test Assumptions 1 to 4. There could be a sizeable difference in accuracy in classification results when using different machine learning algorithms. In order to account for this, a relatively large number (23) of classification algorithms were used. The list of the algorithms used in this study can be found in

Table 1. List of classification algorithms (and related Matlab libraries).

N.	Algorithm	N.	Algorithm
1	Complex Tree (fitctree)	13	Fine KNN (fitcknn)
2	Medium Tree (fitctree)	14	Medium KNN (fitcknn)
3	Simple Tree (fitctree)	15	Coarse KNN (fitcknn)
4	Linear Discriminant (fitcdiscr)	16	Cosine KNN (fitcknn)
5	Quadratic Discriminant (fitcdiscr)	17	Cubic KNN (fitcknn)
6	Logistic Regression (fitglm)	18	Weighted KNN (fitcknn)
7	Linear SVM (fitcsvm)	19	Boosted Trees (fitctree)
8	Quadratic SVM (fitcsvm)	20	Bagged Tress (fitctree)
9	Cubic SVM (fitcsvm)	21	Subspace Discriminant (fitcdiscr)
10	Fine Gaussian SVM (fitcsvm)	22	Subspace KNN (fitcknn)
11	Medium Gaussian SVM (fitcsvm)	23	RUSBoosted Trees (fitctree)
12	Coarse Gaussian SVM (fitcsvm)

. Each model was simulated q times in order to obtain a mean value for accuracy.

The optimization algorithm was applied to neural networks. The training algorithm selected was the scaled conjugate gradient with the number of neurons selected in an automated way using the optimization algorithm. The optimization algorithm was run for one million iterations, with a constant $\omega$ in the penalty function equal to 0.0001.

4. Results

4.1. Assumption 1

In addition to the base case, 4 different models, each with 23 algorithms, were used to test Assumption 1 The difference between these four models resides in the value of the translation constant $\alpha$ ranging from 1000 to 1,000,000 $(\{{\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_5\}$ = 0, 1000, 10,000, 100,000, 1,000,000). Model 1 was the base case with $\alpha =0$. The results showing the accuracy can be seen in Figure 4, while the results showing the precision, recall, and F1-score can be seen in Appendix A in Figure A1, Figure A2, Figure A3. A Kolmogorov–Smirnov test [78] was carried out comparing the base model (Model 1 with $\alpha =0$) with the other models for each of the 23 algorithms (see

Table A1. p-values of the Kolmogorov–Smirnov test Assumption 1 (translation).

M1–M2	M1–M3	M1–M4	M1–M5
0.97479	0.97479	0.31285	0.67508
0.97479	0.97479	0.031047	0.67508
1.00000	0.67508	0.67508	0.97479
1.00000	0.67508	0.11084	0.11084
1.00000	0.31285	1.89 × 10${}^{-5}$	1.89 × 10${}^{-5}$
0.97479	0.31285	0.97479	0.67508
1.00000	0.67508	0.31285	0.97479
0.97479	0.97479	0.11084	0.31285
0.97479	0.97479	0.67508	0.67508
1.00000	0.97479	0.97479	1.00000
0.97479	0.97479	0.97479	0.97479
1.00000	1.00000	1.00000	1.00000
1.00000	0.31285	0.67508	0.11084
1.00000	0.97479	1.00000	0.67508
1.00000	1.00000	1.00000	1.00000
1.00000	0.97479	0.67508	0.97479
1.00000	0.67508	0.97479	0.97479
0.97479	0.67508	0.67508	0.67508
1.00000	0.67508	0.031047	0.67508
1.00000	0.97479	0.11084	0.31285
1.00000	0.97479	0.11084	0.03105
0.67508	0.67508	0.31285	0.67508
0.97479	0.67508	0.11084	0.67508

in Appendix A). The test shows that, for the majority of models and algorithms, it cannot be concluded that there is a statistically significant difference between these distributions (accuracy value).

4.2. Assumption 2

Five models with different permutations of the numerical values were created for all twenty-three algorithms. The number of permutations for each model was selected randomly. No additional restrictions were introduced in the permutations. The results showing the accuracy can be seen in Figure 5, while the results showing the precision, recall, and F1-score can be seen in Appendix A in Figure A4, Figure A5, Figure A6. As in the previous assumption, the results for the majority of cases suggest no statistically significant difference among the majority of models and algorithms. This was also the result when using a Kolmogorov–Smirnov test comparing Model 1 with Models 6 to 9 (see

Table A2. p-values of the Kolmogorov–Smirnov test Assumption 2 (permutation).

M1–M6	M1–M7	M1–M8	M1–M9	M1–M10
0.67508	0.67508	0.67508	0.67508	0.31285
0.97479	0.67508	0.67508	0.67508	0.31285
1.00000	0.97479	0.67508	0.31285	0.31285
0.31285	0.11084	0.67508	0.31285	0.31285
1.00000	0.67508	1.00000	1.00000	0.67508
0.67508	0.031047	0.97479	0.67508	0.31285
0.67508	0.97479	1.00000	0.97479	0.11084
0.31285	0.67508	0.67508	0.67508	0.67508
0.31285	0.11084	0.31285	0.31285	0.67508
1.00000	0.97479	0.67508	1.00000	0.97479
0.97479	0.97479	0.97479	0.97479	0.97479
1.00000	1.00000	1.00000	1.00000	1.00000
0.97479	0.97479	0.67508	0.31285	0.97479
0.67508	0.67508	0.97479	1.00000	0.67508
1.00000	1.00000	1.00000	1.00000	1.00000
0.31285	1.00000	0.67508	0.97479	0.97479
0.31285	0.97479	0.67508	0.97479	0.97479
0.67508	0.97479	1.00000	0.97479	0.67508
0.11084	0.0068986	0.11084	0.031047	0.31285
1.00000	0.67508	0.31285	0.31285	0.97479
1.00000	1.00000	0.31285	0.67508	0.67508

in Appendix A).

4.3. Assumption 3

In this section, a variable $\beta$ was added to each vector to make their length equal. The base case continued to be Model 1 with a $\beta =0$. Four models were tested with four different betas $(\{{\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4\}$ = {1000, 10000, 100,000, 1,000,000}). It is worth noting that, in this case, the constant $\beta$ was added in order to make the dimensions equal, and hence the existing data were not altered as in the case of Assumption 1, in which all data increased by a certain amount $\alpha$. Figure 6 shows the results (accuracy) of the numerical simulations, indicating, as in the previous cases, that for most of the models and algorithms, there are no statistically significant differences. The results showing the precision, recall, and F1-Score can be seen in Appendix A in Figure A7, Figure A8, Figure A9. Kolmogorov–Smirnov test comparing Model 1 with Models 11 to 14 (see

Table A3. p-values of the Kolmogorov–Smirnov test Assumption 3 (constant).

M1–M11	M1–M12	M1–M13	M1–M14
1.00000	0.67508	0.11084	0.67508
1.00000	0.67508	0.31285	0.97479
0.67508	0.67508	0.31285	0.67508
1.00000	0.0012162	0.67508	0.0068986
0.97479	0.0068986	0.97479	1.89 × 10${}^{-5}$
0.67508	0.31285	0.97479	0.31285
0.97479	0.67508	0.97479	0.31285
0.67508	0.0068986	0.11084	0.031047
0.97479	0.00017012	0.67508	0.0068986
0.97479	0.31285	0.67508	0.97479
0.97479	0.97479	0.97479	1.00000
1.00000	1.00000	1.00000	1.00000
0.97479	0.67508	0.67508	0.31285
0.97479	1.00000	1.00000	0.97479
1.00000	1.00000	1.00000	1.00000
0.97479	0.67508	0.97479	0.97479
0.97479	0.97479	1.00000	0.97479
0.67508	0.31285	0.67508	1.00000
1.00000	0.67508	0.67508	0.97479
0.31285	0.11084	0.97479	0.67508
0.97479	0.31285	0.97479	0.031047
0.67508	0.67508	0.67508	0.31285
0.31285	0.67508	0.67508	0.67508

in Appendix A) generated similar results.

4.4. Assumption 4

In Model 15, rather than the full sequence of amino acids, the input for the classification models was the number of times that a given amino acid appeared in the amino acid chain. Hence, the information about the order of the amino acids was lost. The length of the amino acid chain was also included $\left(\{l^{*},n{a}_1,n{a}_2,\dots n{a}_{20}\}\right)$. Model 16 was similar to Model 15 but without the length $\left(l^{*}\right)$ of the protein $\left(\{n{a}_1,n{a}_2,\dots n{a}_{20}\}\right)$, see the results (accuracy) in Figure 7 and Figure 8. The results for the precision, recall, and F1-score are shown in Appendix A in Figure A10, Figure A11, Figure A12, Figure A13, Figure A14, Figure A15. The results of the Kolmogorov–Smirnov tests, comparing the base model (Model 1) with Models 15 and 16, showed that for the majority of the algorithms, there is no statistically significant difference, as shown in

Table A4. p-values of the Kolmogorov–Smirnov test Models 15 and 16.

M1–M15	M1–M16
0.31285	0.67508
0.031047	0.67508
0.11084	0.31285
0.0012162	0.00017012
1.89 × 10${}^{-5}$	1.89 × 10${}^{-5}$
1.89 × 10${}^{-5}$	1.89 × 10${}^{-5}$
0.31285	0.31285
0.67508	0.31285
0.97479	0.11084
0.97479	0.97479
0.97479	0.31285
1.00000	1.00000
0.31285	0.0012162
0.67508	0.67508
1.00000	1.00000
0.67508	0.67508
0.67508	0.97479
0.97479	1.00000
0.031047	0.67508
0.97479	0.11084
0.00017012	0.00017012
0.11084	0.67508
0.31285	0.97479

in Appendix A.

The next step entailed using the eigenvalues and some additional terms such as the $l^{*}$, as defined in expression (22). In many numerical simulations, SVM failed to generate an estimation, and they were thus excluded from the analysis. Interestingly, the rest of the models were accurate or led to better results than the base case (Model 1). The only exception to this trend was the case of the linear discriminant, in which the eigenvalue approach was statistically significantly less accurate. For all the other cases, there was no statistically significant difference, or the mean accuracy of the eigenvalue approach was higher than the value obtained in the base case. Most of the models achieved a mean accuracy above 80%. In

Table 2. Mean values of the accuracy for the eigenvalue approach and Model 1 as well as p-values of the Kolmogorov–Smirnov test comparing these two approaches. T refers to the average computational time required to train the algorithm.

Algorithm	Eig. Acc.	M1 Acc.	p-Value (ks)	T (s)
Complex Tree	82.89	72.04	0.0001	1.34
Medium Tree	82.83	72.13	0.0001	1.79
Simple Tree	82.75	78.11	0.0002	0.60
Linear Discriminant	17.08	54.44	0.0001	1.70
Quadratic Discriminant	30.37	17.47	0.6751	1.82
Logistic regression	82.95	61.87	0.0001	4.32
Fine KNN	79.88	76.53	0.0002	7.96
Medium KNN	81.59	83.18	0.6751	7.85
Coarse KNN	80.65	82.88	1.0000	7.69
Cosine KNN	81.83	82.95	0.6751	8.52
Cubic KNN	81.75	83.14	0.6751	7.10
Weighted KNN	83.25	81.83	0.0069	6.90
Boosted Trees	80.65	75.64	0.0001	7.64
Bagged Trees	82.83	81.6	0.0069	9.71
Subspace Discriminant	81.91	77.03	0.0001	10.98
Subspace KNN	82.59	78.91	0.0002	11.84
RUSBoosted Trees	81.55	54.74	0.0001	13.32

, the mean accuracy values are shown for the eigenvalue approach and Model 1, as well as the p-values for the Kolmogorov–Smirnov test comparing these two approaches. In this table, it can be seen that the best model is the Weighted KNN model, with a mean accuracy of 83.25%, closely followed by the Subspace KNN, Simple Tree, Medium Tree, Complex Tree, and Logistic Regression, with an accuracy of 82.59%, 82.75%, 82.83%, 82.89%, and 82.95% respectively.

4.5. Optimization

We also used an algorithm for the optimization of the classification using neural networks, as described in Section 3.2. The algorithm was the scale conjugate gradient, and the process involved one million iterations. This model achieved an 85.02% out-of-sample classification accuracy with 215 neurons, suggesting that model parameter optimization plays an important role in improving classification accuracy. In the context of protein classification, it is important to carry out parameter optimization in a consistent way to improve the chances of the model to generalize (classify new data) with a reasonable level of accuracy. Randomly selecting the parameter could potentially lead to biases in the model or poor generalization. Figure 9 shows that the classification accuracy improves as the number of iterations increase, initially very rapidly and then more slowly as the model approaches its upper limit. There are several potential ways of performing data validation [79]. In this article, we performed cross-validation of the data in the training dataset 10 times, and then the results were tested with the testing dataset (not used during the training phase).

A limitation in this article, and a potential area of future work, is increasing the number of analyzed proteins. In this article, we analyzed 307 proteins for classification purposes, but this number could be further increased. This type of analysis could also be parallelized, which could enable a larger number of simulations to be performed while potentially not substantially increasing computational time.

5. Conclusions and Recommendations

Mapping categorical variables into numerical variables is a common practice in many machine learning classification tasks, and it is frequently carried out in an arbitrary matter. In this paper, we proposed four different assumptions related to this topic in the context of protein classification: (1) translation, (2) permutation, (3) constant, and (4) eigenvalues. Assumptions 1–3 are related to the concept of equivalent mappings in which changes to the mapping should, in principle, not alter the results of a classification analysis (for instance, adding a constant to all the input parameters). Assumption 4 relates to a less strict requirement in which the mappings are not in principle strictly equivalent, but they are comparable. An example is the eigenvalue mapping approach in which the information about the order of the amino acids (present in the initial mapping $f_1$) is not contained in this new mapping $\left(f_6\right)$. The results for Assumptions 1–3 showed that, in the majority of the cases, no statistically significant difference exists between the mappings when we compared their mean accuracy. The case of Assumption 4 is different, and we see that using the eigenvalue approach generates similar or more accurate classifications than the base case model. All these numerical simulations were carried out for 23 different classification algorithms, including KNN, Tress, and SVMs. As previously mentioned, the eigenvalue approach (related to Assumption 4) generated accurate estimations for most algorithms. One noticeable exception was SVM, which, in many cases, failed to generate a classification estimation and was, therefore, excluded from the analysis. For the majority of the other algorithms, the eigenvalue approach generated results that were not statistically significantly different from the base case or that had higher mean accuracy than the base case. The best model obtained a mean classification accuracy of 83.25%. While direct comparisons are challenging, this result is 14.15% better than the lower-bound result obtained by Cai et al. [51] but lower than the upper bound. This is consistent with the idea of focusing the analysis on the stability of results rather than only focusing on increasing accuracy. This result is also substantially higher than the lower bound achieved by Karchin et al. [54], in which the authors focused on a specific subset of proteins (G-protein-coupled receptors).

An optimization analysis algorithm was also presented for the automated selection of the number of neurons in a classification model using only the frequency of the occurrence of amino acid in the amino acid chain as input (no order information), as well as the length of the chain. The model included a quadratic penalty function to try to decrease the chance of overfitting. This approach generated an accuracy of 85.02% percent. This result is even closer to the upper bound (and substantially higher than the lower bound) of Cai et al. [51] even after accounting for the penalty function introduced to avoid an overly complex model, which potentially could impact the generalization capabilities of the model, i.e., the accuracy of the classification when faced with new data. Furthermore, this approach does not require the use of techniques such as NLP [47], which could be beneficial from an implementation point of view, as there is a large number of machine learning applications that can be easily and accurately applied to numerical values, and there is no indication that an NLP approach will generate more accurate results.

It should be noted that this accuracy is not directly comparable with the accuracy obtained in the previous sections, as there was no additional algorithm optimization. The focus of the previous section was on the comparability of the models, and hence it did not appear appropriate to add additional optimization techniques that differ in the different algorithms. For instance, an optimization process based on finding an appropriate number of neurons, as shown in the optimization section, cannot be performed for other classification techniques such as KNN, SVM, or Trees, as they do not use artificial neurons.

This type of big data analysis is challenging and can be computationally expensive, depending on the type of machine learning applied and/or the optimization algorithm followed. As an area of future research, it would be interesting to use genetic algorithms or particle algorithms as potential optimization strategies. There is a wide range of options to optimize this type of analysis. There is, however, the risk of overfitting the model, and some measures should be taken to minimize that risk, such as using a penalty function, as we used in this article, to penalize the accuracy of overly complex models. Arguably, an overly complex model is more likely to result in an overfitting issue than a simpler model.