Numerical Simulation and Structure Optimization of Multilayer Metamaterial Plus-Shaped Solar Absorber Design Based on Graphene and SiO2 Substrate for Renewable Energy Generation
Abstract
:1. Introduction
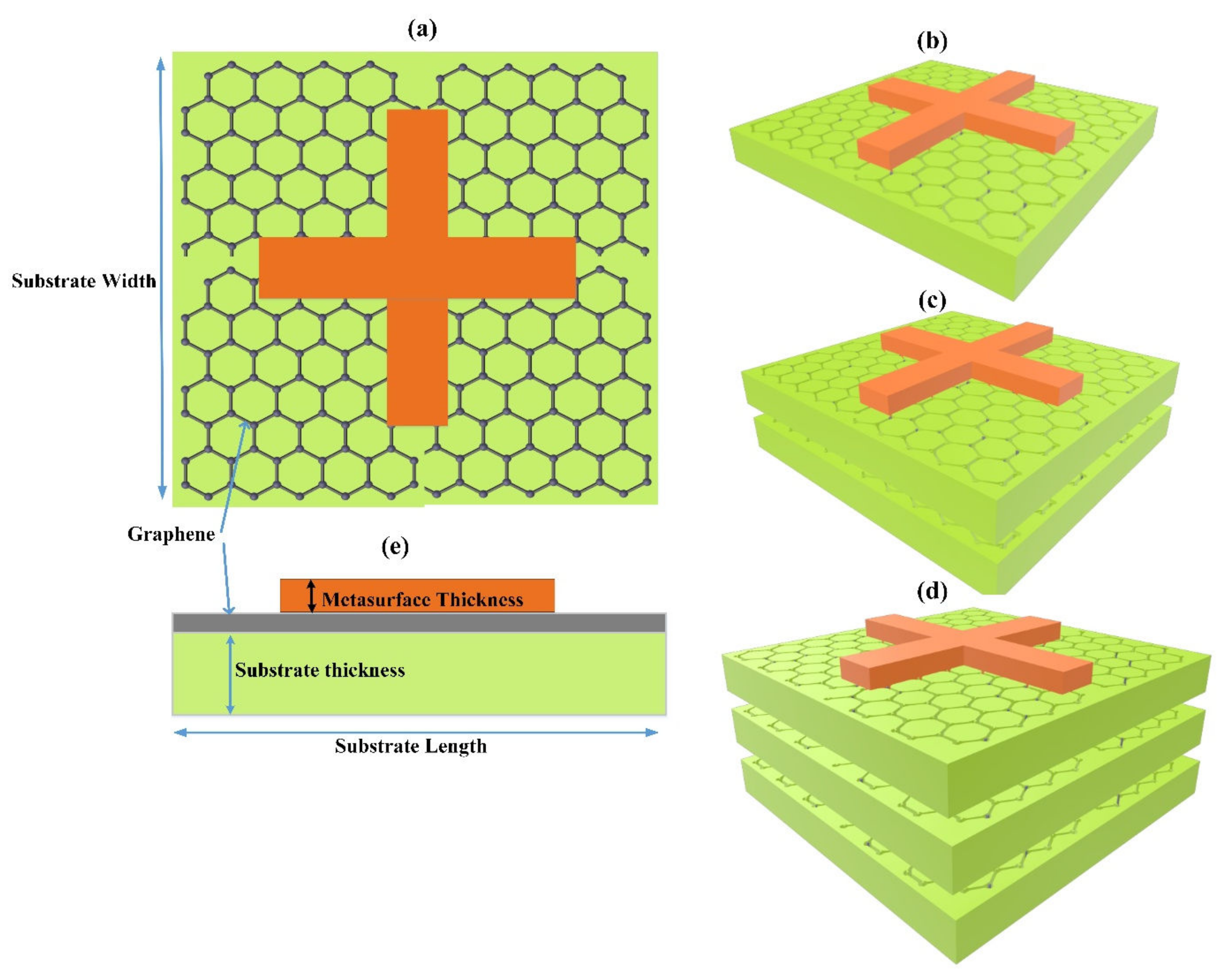
2. Multilayer Design
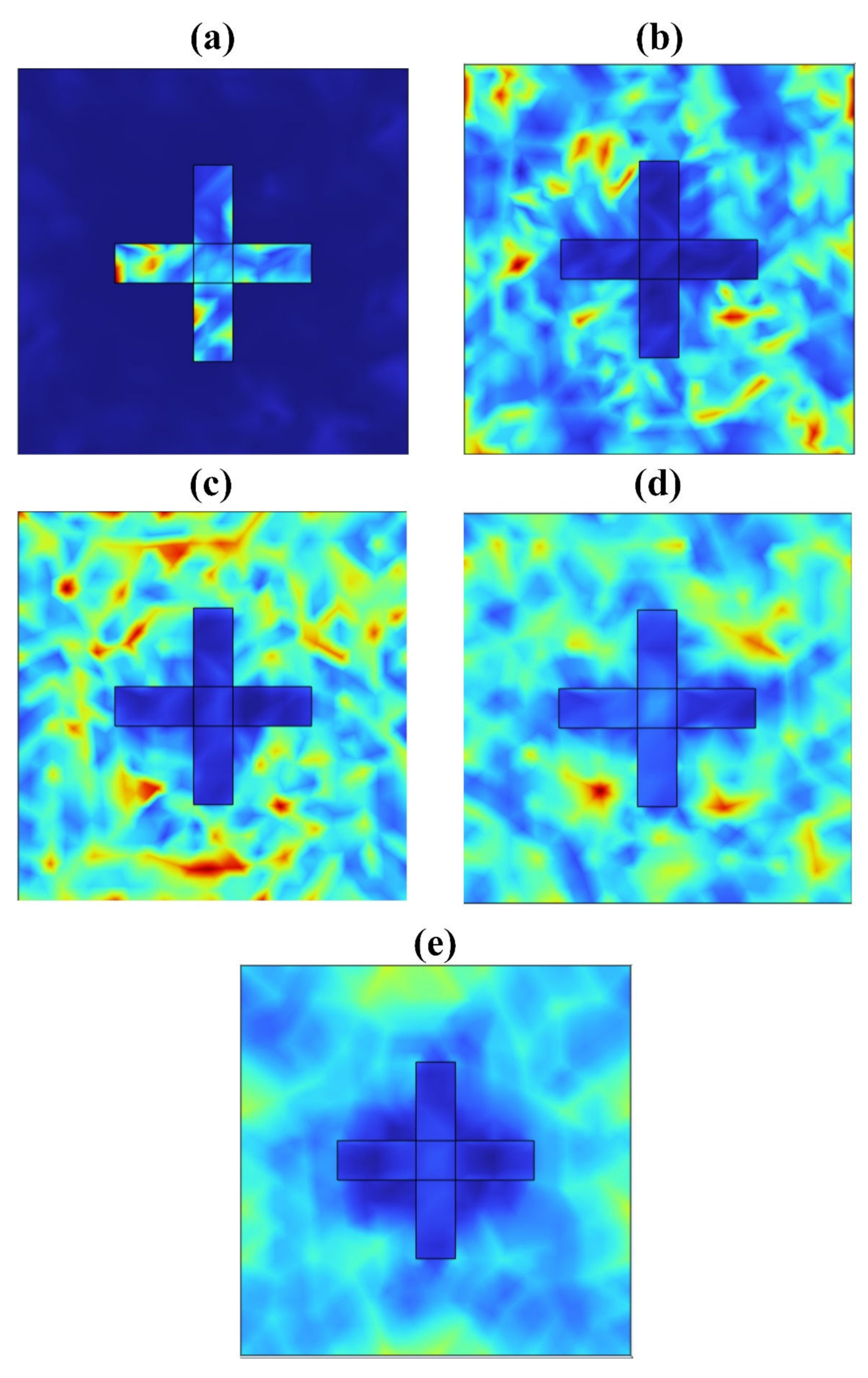
3. Multilayer Absorber Results
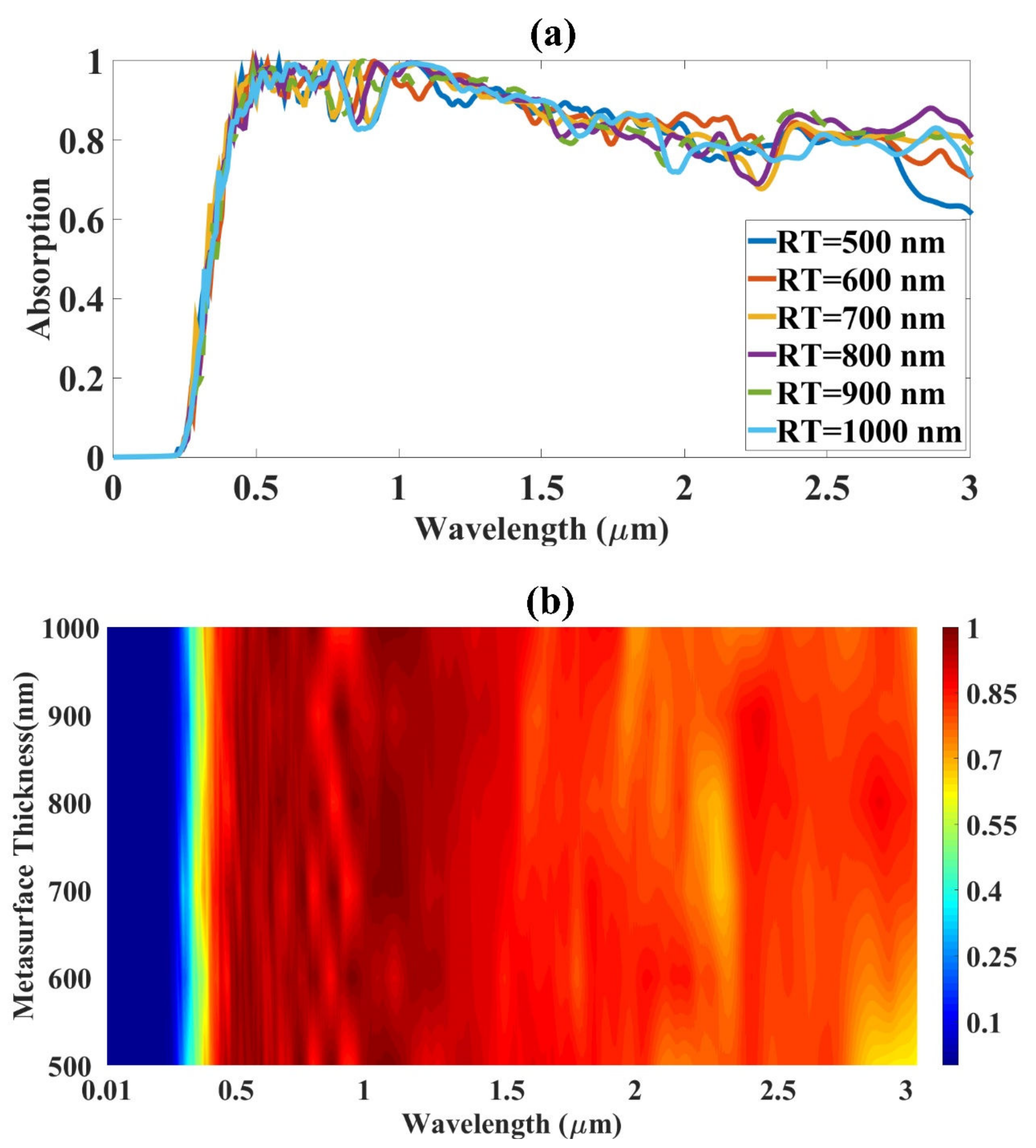
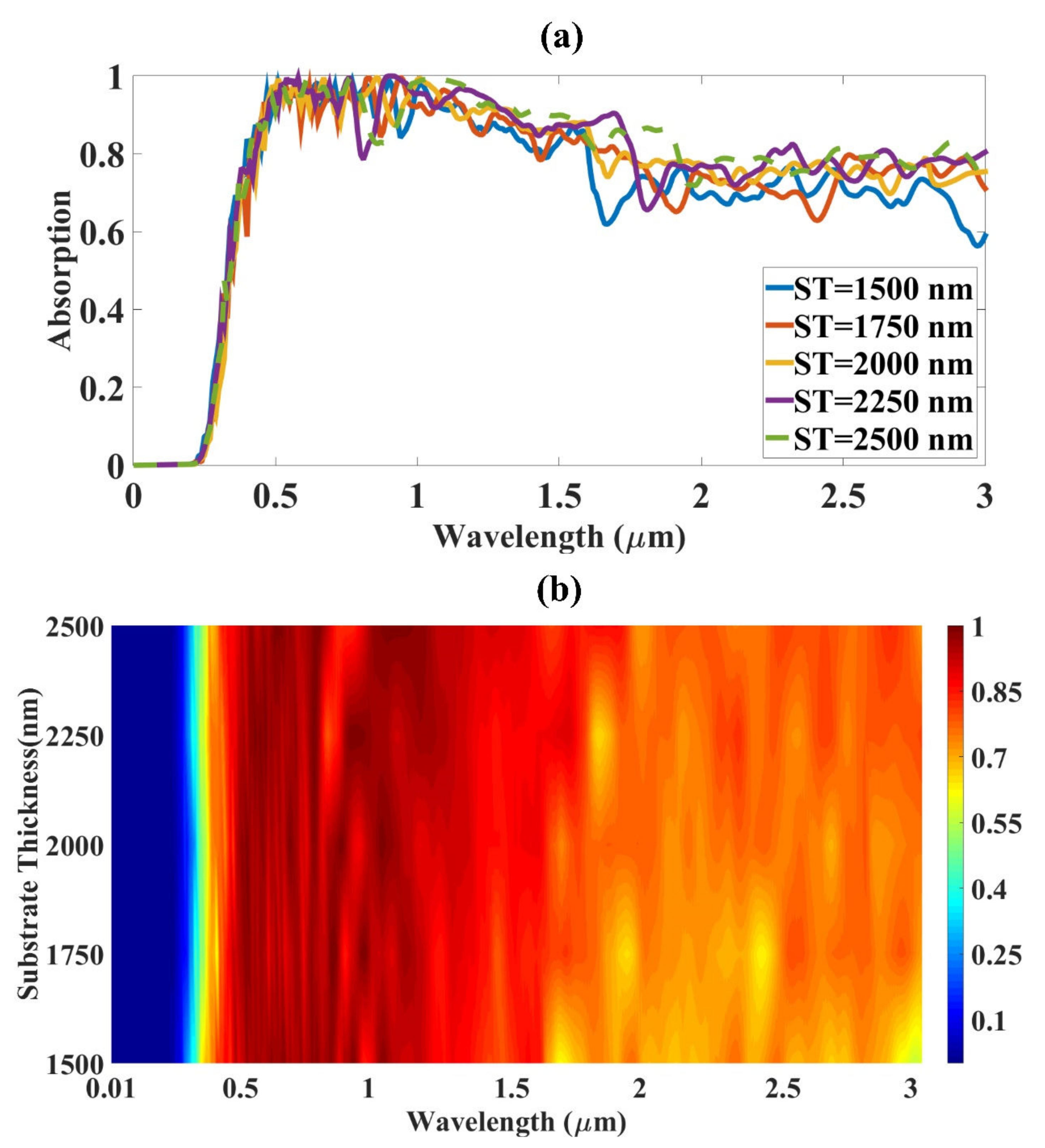
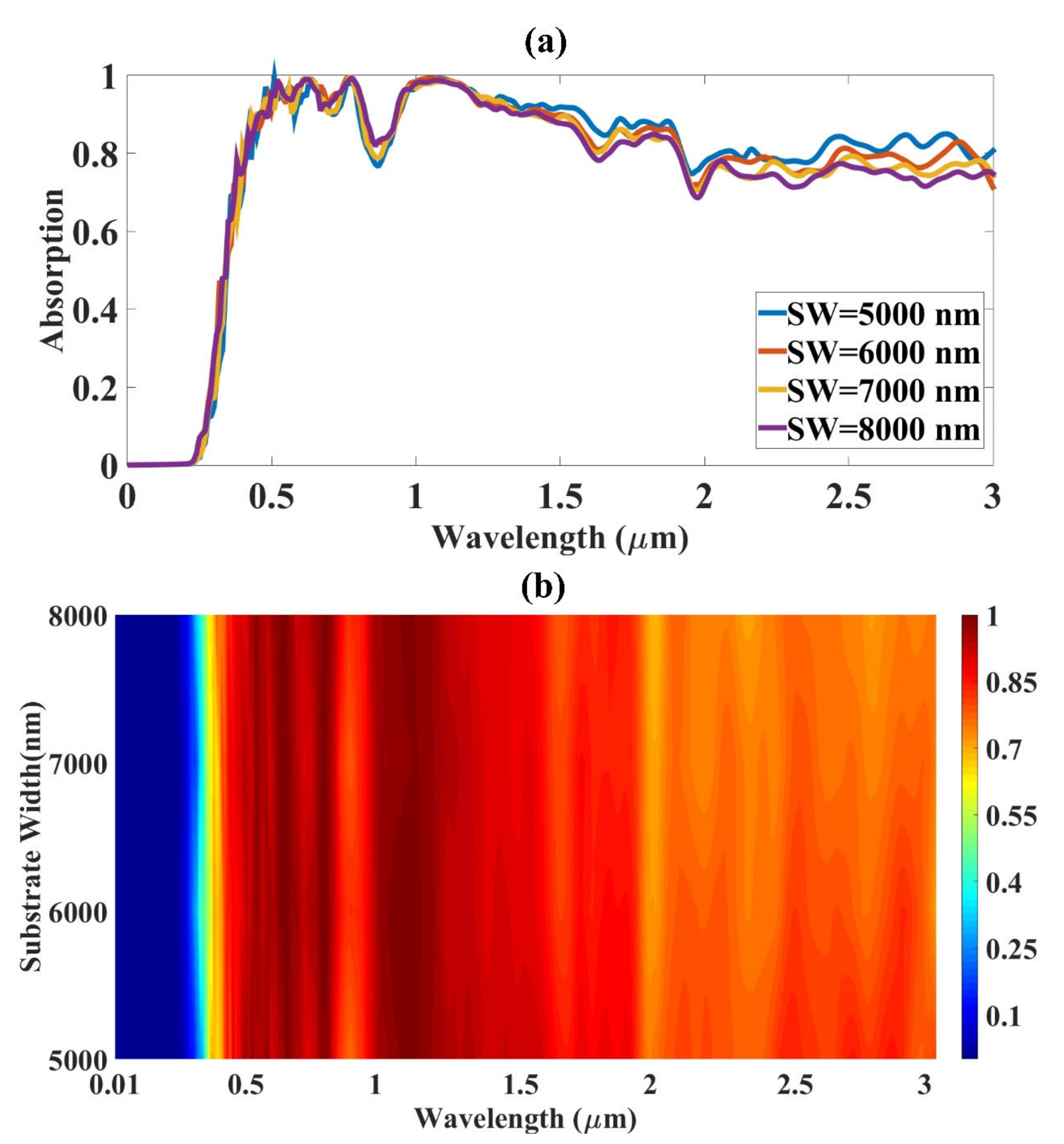
4. Structure Optimization of the Design
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hoque, A.; Islam, M.T.; Almutairi, A.F.; Faruque, M.R.I. Design of Split Hexagonal Patch Array Shaped Nano-metaabsorber with Ultra-wideband Absorption for Visible and UV Spectrum Application. Nanoscale Res. Lett. 2019, 14, 393. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chang, C.-C.; Kort-Kamp, W.J.M.; Nogan, J.; Luk, T.S.; Azad, A.K.; Taylor, A.J.; Dalvit, D.A.R.; Sykora, M.; Chen, H.-T. High-Temperature Refractory Metasurfaces for Solar Thermophotovoltaic Energy Harvesting. Nano Lett. 2018, 18, 7665–7673. [Google Scholar] [CrossRef]
- Nguyen, D.M.; Lee, D.; Rho, J. Control of light absorbance using plasmonic grating based perfect absorber at visible and near-infrared wavelengths. Sci. Rep. 2017, 7, 2611. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patel, S.K.; Parmar, J.; Katrodiya, D.; Nguyen, T.K.; Holdengreber, E.; Dhasarathan, V. Broadband metamaterial-based near-infrared absorber using an array of uniformly placed gold resonators. J. Opt. Soc. Am. B 2020, 37, 2163–2170. [Google Scholar] [CrossRef]
- Hoque, A.; Islam, M.T. Numerical Analysis of Single Negative Broadband Metamaterial Absorber Based on Tri Thin Layer Material in Visible Spectrum for Solar Cell Energy Harvesting. Plasmonics 2020, 15, 1061–1069. [Google Scholar] [CrossRef]
- Feng, H.; Xu, Z.; Li, K.; Wang, M.; Xie, W.; Luo, Q.; Chen, B.; Kong, W.; Yun, M. Tunable polarization-independent and angle-insensitive broadband terahertz absorber with graphene metamaterials. Opt. Express 2021, 29, 7158–7167. [Google Scholar] [CrossRef]
- Lin, K.-T.; Lin, H.; Yang, T.; Jia, B. Structured graphene metamaterial selective absorbers for high efficiency and omnidirectional solar thermal energy conversion. Nat. Commun. 2020, 11, 904–909. [Google Scholar] [CrossRef] [Green Version]
- Sekhi, S.Z.; Shokooh-Saremi, M.; Mirsalehi, M.M. Ultra-broadband, wide-angle, and polarization-insensitive metamaterial perfect absorber for solar energy harvesting. J. Nanophotonics 2020, 14, 046014. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, X.; Zhang, H.; Liu, M.; Yi, Q.; Liu, Z.; Wang, J. Cross-Shaped Titanium Resonators Based Metasurface for Ultra-Broadband Solar Absorption. IEEE Photon. J. 2021, 13, 1–8. [Google Scholar] [CrossRef]
- Cheng, Y.; Du, C. Broadband plasmonic absorber based on all silicon nanostructure resonators in visible region. Opt. Mater. 2019, 98, 109441. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhao, J. Simple design of a six-band terahertz perfect metasurface absorber based on a single resonator structure. Phys. Scr. 2022, 97, 95508. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, Y.; Luo, H.; Chen, F.; Li, X. Dual-Band Tunable Terahertz Perfect Absorber Based on All-Dielectric InSb Resonator Structure for Sensing Application. J. Alloys Compd. 2022, 925, 166617. [Google Scholar] [CrossRef]
- Zhao, J.; Cheng, Y. Temperature-Tunable Terahertz Perfect Absorber Based on All-Dielectric Strontium Titanate (STO) Resonator Structure. Adv. Theory Simul. 2022, 5, 2200520. [Google Scholar] [CrossRef]
- Cheng, Y.; Qian, Y.; Luo, H.; Chen, F.; Cheng, Z. Terahertz Narrowband Perfect Metasurface Absorber Based on Micro-Ring-Shaped GaAs Array for Enhanced Refractive Index Sensing. Phys. E LowDimens. Syst. Nanostruct. 2023, 146, 115527. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, G.; Ming, X.; Liu, X.; Hou, B.; Mei, T.; Li, J.; Wang, J.; Wang, X. Oxygen plasma treated graphene aerogel as a solar absorber for rapid and efficient solar steam generation. Carbon 2018, 130, 250–256. [Google Scholar] [CrossRef]
- Šest, E.; Dražič, G.; Genorio, B.; Jerman, I. Graphene nanoplatelets as an anticorrosion additive for solar absorber coatings. Sol. Energy Mater. Sol. Cells 2018, 176, 19–29. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Şirin, C.; Öztop, H.F. Improving the performance of an active greenhouse dryer by integrating a solar absorber north wall coated with graphene nanoplatelet-embedded black paint. Sol. Energy 2022, 231, 140–148. [Google Scholar] [CrossRef]
- Huang, H.; Xia, H.; Xie, W.; Guo, Z.; Li, H.; Xie, D. Design of broadband graphene-metamaterial absorbers for permittivity sensing at mid-infrared regions. Sci. Rep. 2018, 8, 4183. [Google Scholar] [CrossRef] [Green Version]
- Safaei, M.R.; Goshayeshi, H.R.; Chaer, I. Solar Still Efficiency Enhancement by Using Graphene Oxide/Paraffin Nano-PCM. Energies 2019, 12, 2002. [Google Scholar] [CrossRef] [Green Version]
- Cen, C.; Chen, Z.; Xu, D.; Jiang, L.; Chen, X.; Yi, Z.; Wu, P.; Li, G.; Yi, Y. High Quality Factor, High Sensitivity Metamaterial Graphene—Perfect Absorber Based on Critical Coupling Theory and Impedance Matching. Nanomaterials 2020, 10, 95. [Google Scholar] [CrossRef]
- Ogawa, S.; Shimatani, M.; Fukushima, S.; Okuda, S.; Matsumoto, K. Graphene on metal-insulator-metal-based plasmonic metamaterials at infrared wavelengths. Optics Express 2018, 26, 5665–5674. [Google Scholar] [CrossRef] [PubMed]
- Lakshmiprabha, K.E.; Govindaraju, C.; Mahendran, G. Broadband plus-Shaped Metasurface Absorber Based on Graphene for Visible and Ultraviolet Regions. Opt. Quantum Electron. 2022, 54, 774. [Google Scholar] [CrossRef]
- Rezk, H.; Ali, Z.M.; Abdalla, O.; Younis, O.; Gomaa, M.R.; Hashim, M. Hybrid Moth-Flame Optimization Algorithm and Incremental Conductance for Tracking Maximum Power of Solar PV/Thermoelectric System under Different Conditions. Mathematics 2019, 7, 875. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Wu, C.; Ren, Y. Broadband terahertz metamaterial absorber based on graphene resonators with perfect absorption. Results Phys. 2021, 26, 104466. [Google Scholar] [CrossRef]
- Patel, S.K.; Surve, J.; Parmar, J.; Nguyen, T.K. Review on Graphene-Based Absorbers for Infrared to Ultraviolet Frequencies. J. Adv. Eng. Comput. 2021, 5, 214. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-inspired optimization algorithms: Challenges and open problems. J. Comput. Sci. 2020, 46, 101104. [Google Scholar] [CrossRef] [Green Version]
- Shuai, H.; Fang, J.; Ai, X.; Wen, J.; He, H. Optimal Real-Time Operation Strategy for Microgrid: An ADP-Based Stochastic Nonlinear Optimization Approach. IEEE Trans. Sustain. Energy 2018, 10, 931–942. [Google Scholar] [CrossRef] [Green Version]
- Jiang, T.; Zhang, C.; Zhu, H.; Gu, J.; Deng, G. Energy-Efficient Scheduling for a Job Shop Using an Improved Whale Optimization Algorithm. Mathematics 2018, 6, 220. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.-S. How to Deal with Constraints. In Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2021; pp. 207–220. [Google Scholar]
- Aragón, F.J.; Goberna, M.A.; López, M.A.; Rodríguez, M.M.L. Nonlinear Optimization (Springer Undergraduate Texts in Mathematics and Technology); Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Yu, P.; Chen, X.; Yi, Z.; Tang, Y.; Yang, H.; Zhou, Z.; Duan, T.; Cheng, S.; Zhang, J.; Yi, Y. A numerical research of wideband solar absorber based on refractory metal from visible to near infrared. Opt. Mater. 2019, 97, 109400. [Google Scholar] [CrossRef]
- Patel, S.K.; Charola, S.; Parmar, J.; Ladumor, M.; Ngo, Q.M.; Dhasarathan, V. Broadband and Efficient Graphene Solar Absorber Using Periodical Array of C-Shaped Metasurface. Opt. Quantum Electron. 2020, 52, 250. [Google Scholar] [CrossRef]
- Lin, H.; Sturmberg, B.C.P.; Lin, K.-T.; Yang, Y.; Zheng, X.; Chong, T.K.; de Sterke, C.M.; Jia, B. A 90-nm-thick graphene metamaterial for strong and extremely broadband absorption of unpolarized light. Nat. Photonics 2019, 13, 270–276. [Google Scholar] [CrossRef]
- Azad, A.K.; Kort-Kamp, W.J.M.; Sykora, M.; Weisse-Bernstein, N.R.; Luk, T.S.; Taylor, A.J.; Dalvit, D.A.R.; Chen, H.-T. Metasurface Broadband Solar Absorber. Sci. Rep. 2016, 6, 20347. [Google Scholar] [CrossRef]
- Liu, B.; Tang, C.; Chen, J.; Xie, N.; Tang, H.; Zhu, X.; Park, G.-S. Multiband and Broadband Absorption Enhancement of Monolayer Graphene at Optical Frequencies from Multiple Magnetic Dipole Resonances in Metamaterials. Nanoscale Res. Lett. 2018, 13, 153. [Google Scholar] [CrossRef] [Green Version]
- Sang, T.; Gao, J.; Yin, X.; Qi, H.; Wang, L.; Jiao, H. Angle-Insensitive Broadband Absorption Enhancement of Graphene Using a Multi-Grooved Metasurface. Nanoscale Res. Lett. 2019, 14, 105. [Google Scholar] [CrossRef] [Green Version]
- Rufangura, P.; Sabah, C. Graphene-Based Wideband Metamaterial Absorber for Solar Cells Application. J. Nanophotonics 2017, 11, 036008. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Chen, Y.; Li, J.; Hung, T.-C.; Li, J. Study of energy absorption on solar cell using metamaterials. Sol. Energy 2012, 86, 1586–1599. [Google Scholar] [CrossRef]
- Patel, S.K.; Charola, S.; Parmar, J.; Ladumor, M. Broadband metasurface solar absorber in the visible and near-infrared region. Mater. Res. Express 2019, 6, 086213. [Google Scholar] [CrossRef]
- Katrodiya, D.; Jani, C.; Sorathiya, V.; Patel, S.K. Metasurface based broadband solar absorber. Opt. Mater. 2019, 89, 34–41. [Google Scholar] [CrossRef]



| Design | Visible Band (400 to 700 nm) Absorption (%) | Infrared Band (701 to 2000 nm) Absorption (%) |
|---|---|---|
| Single-layer design | 93 | 69 |
| Two-layer design | 92.6 | 82 |
| Three-layer design | 93.8 | 90 |
| Design | Visible Band (400 to 700 nm) Absorption (%) | Infrared Band (701 to 2000 nm) Absorption (%) |
|---|---|---|
| Single-layer design | 93 | 69 |
| Two-layer design | 92.6 | 82 |
| Three-layer design | 93.8 | 90 |
| [31] | 90 | - |
| [32] | 86.5 | - |
| [33] | 93 | - |
| [34] | 90 | - |
| [34] | 90 | - |
| [35] | 80 | - |
| [36] | 71.1 | - |
| [37] | 70 | - |
| [38] | 84 | 77 |
| [39] | 93.7 | - |
| [40] | 92 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsaif, H.; Patel, S.K.; Ali, N.B.; Armghan, A.; Aliqab, K. Numerical Simulation and Structure Optimization of Multilayer Metamaterial Plus-Shaped Solar Absorber Design Based on Graphene and SiO2 Substrate for Renewable Energy Generation. Mathematics 2023, 11, 282. https://doi.org/10.3390/math11020282
Alsaif H, Patel SK, Ali NB, Armghan A, Aliqab K. Numerical Simulation and Structure Optimization of Multilayer Metamaterial Plus-Shaped Solar Absorber Design Based on Graphene and SiO2 Substrate for Renewable Energy Generation. Mathematics. 2023; 11(2):282. https://doi.org/10.3390/math11020282
Chicago/Turabian StyleAlsaif, Haitham, Shobhit K. Patel, Naim Ben Ali, Ammar Armghan, and Khaled Aliqab. 2023. "Numerical Simulation and Structure Optimization of Multilayer Metamaterial Plus-Shaped Solar Absorber Design Based on Graphene and SiO2 Substrate for Renewable Energy Generation" Mathematics 11, no. 2: 282. https://doi.org/10.3390/math11020282
APA StyleAlsaif, H., Patel, S. K., Ali, N. B., Armghan, A., & Aliqab, K. (2023). Numerical Simulation and Structure Optimization of Multilayer Metamaterial Plus-Shaped Solar Absorber Design Based on Graphene and SiO2 Substrate for Renewable Energy Generation. Mathematics, 11(2), 282. https://doi.org/10.3390/math11020282










