Order-Restricted Inference for Generalized Inverted Exponential Distribution under Balanced Joint Progressive Type-II Censored Data and Its Application on the Breaking Strength of Jute Fibers

Abstract

This article considers a new improved balanced joint progressive type-II censoring scheme based on two different populations, where the lifetime distributions of two populations follow the generalized inverted exponential distribution with different shape parameters but a common scale parameter. The maximum likelihood estimates of all unknown parameters are obtained and their asymptotic confidence intervals are constructed by the observed Fisher information matrix. Furthermore, the existence and uniqueness of solutions are proved. In the Bayesian framework, the common scale parameter follows an independent Gamma prior and the different shape parameters jointly follow a Beta-Gamma prior. Based on whether the order restriction is imposed on the shape parameters, the Bayesian estimates of all parameters concerning the squared error loss function along with the associated highest posterior density credible intervals are derived by using the importance sampling technique. Then, we use Monte Carlo simulations to study the performance of the various estimators and a real dataset is discussed to illustrate all of the estimation techniques. Finally, we seek an optimum censoring scheme through different optimality criteria.

1. Introduction

In real lifetime testing, progressive censoring schemes have been widely mentioned in the statistical literature during the past couple of decades. The purpose of introducing different progressive censoring schemes is to accelerate the experimental process and reduce the experimental cost because a pre-fixed number of functioning units can be removed intentionally and ensure that a certain number of failures are observed during the process of lifetime experiments to make it more efficient. For example, in the process of life testing, the longer lifetime or accidental damage of equipment makes it difficult for the experimenter to collect complete lifetime data, thus affecting the experiment results. Therefore, research on progressive censoring schemes is applied to deal with these problems. In recent years, a great quantity of work has been done on the different progressive censoring schemes; relevant content can be found in Ref. [1].

Nearly all conventional censoring schemes, for instance, hybrid censoring, progressive type-I censoring, progressive first-failure censoring, etc (see Refs. [2,3,4]), are based on a single population. However, to carry out comparative lifetime testing on products, which are from two or more populations under the same survival conditions, more censoring schemes are proposed. For example, in the joint progressive type-II censoring scheme (JPC), the lifetime testing of two samples from different populations will be carried out simultaneously and when a certain number of failures are observed, the experiment is terminated. In the background of the JPC scheme, Ref. [5] first considered the exact statistical inference for two exponential populations, while Ref. [6] extended similar research contents to k-sample exponential populations. Ref. [7] discussed the interval estimation, which was constructed by three methods, and the conditional maximum likelihood of two Weibull distributions. Furthermore, Ref. [8] considered the classical and Bayesian inference when the order restriction was imposed on the scale parameters. Ref. [9] employed the EM algorithm to calculate the maximum likelihood estimates of all parameters and the order restriction of the shape parameters were considered in the Bayesian inference. Here, Ref. [10] computed the Bayesian estimates of unknown parameters under the generalized entropy loss function and discussed the criteria for obtaining the optimal censoring scheme.

Recently, Ref. [11] proposed a new censoring scheme based on two samples from exponential distributions, which is considered to be a balanced joint progressive censoring scheme (B-JPC). Compared with the JPC scheme, the B-JPC scheme has more advantages. For example, at each failure, a pre-fixed number of the functioning units will be removed from the products of two populations simultaneously, which makes the analysis process more flexible and the calculation more simple. In practice, under different stress levels, we use the B-JPC scheme to accelerate the life testing of products. When it comes to an acceptable sampling scheme, this scheme is employed to make acceptance decisions for products from different batches. Hence, we can decide on diversified products in a single experiment. According to the B-JPC scheme, Ref. [12] proposed a new criterion that depends on the precise joint confidence region volume of parameters to find the optimum censoring scheme, and Ref. [13] developed the Bayesian inference under the condition that the order restriction is imposed on scale parameters and employed precision criteria to obtain the optimum censoring scheme. Ref. [14] used the research content discussed by Ref. [13] for flexible prior assumptions, and different design criteria, along with the variable neighborhood search algorithm proposed in Ref. [15], are employed to obtain the optimum censoring scheme. Ref. [16] studied the statistical inferences for the Lindley distribution and the optimum censoring scheme is obtained by using the Bayesian and classical design criteria.

Compared with the generalized inverse exponential distribution under the JPC scheme, discussed in Ref. [17], we have a flexible censoring process and consider whether the scale parameter is known in this article. Here, we suppose that the lifetimes of experimental units from two different populations follow a two-parameter generalized inverse exponential distribution with different shape parameters but the same scale parameter. Furthermore, we discuss the Bayesian inference based on the order restriction between the two shape parameters as well as the likelihood estimation of all parameters. Under these circumstances, suppose that the same scale parameter follows a Gamma prior, and the shape parameters jointly follow an ordered Beta-Gamma distribution. Furthermore, we compare the different censoring schemes under precision criteria to find the optimum censoring scheme.

In order to overcome these disadvantages, which contain the non-closed form or constant hazard rates of some distributions, such as the gamma and exponential distribution, the generalized inverted exponential distribution is proposed. According to Ref. [18], some properties and characteristics of this distribution are provided. Based on the existing research about the hazard rate function, the shape of the generalized inverted exponential distribution is non-monotone unimodal and it is suitable to analyze the data from the distribution of the non-monotone failure rate function.

The rest of this article is arranged as follows. We provide the notations and brief introduction to the B-JPC scheme in Section 2. The maximum likelihood estimations and coverage probabilities of model parameters are discussed in Section 3. Using the observed Fisher information matrix, the asymptotic confidence intervals of all parameters are constructed. Furthermore, proof of the existence and uniqueness of maximum likelihood estimation is provided. The order restriction on the shape parameters, the highest posterior density credible intervals, and the Bayesian estimates of all unknown parameters concerning the importance sampling method are discussed in Section 4. Section 5 contains the simulation study and analysis results for real datasets. Then, we obtain the optimum censoring scheme through five precision criteria in Section 6. Finally, we draw the conclusions of this article in Section 7.

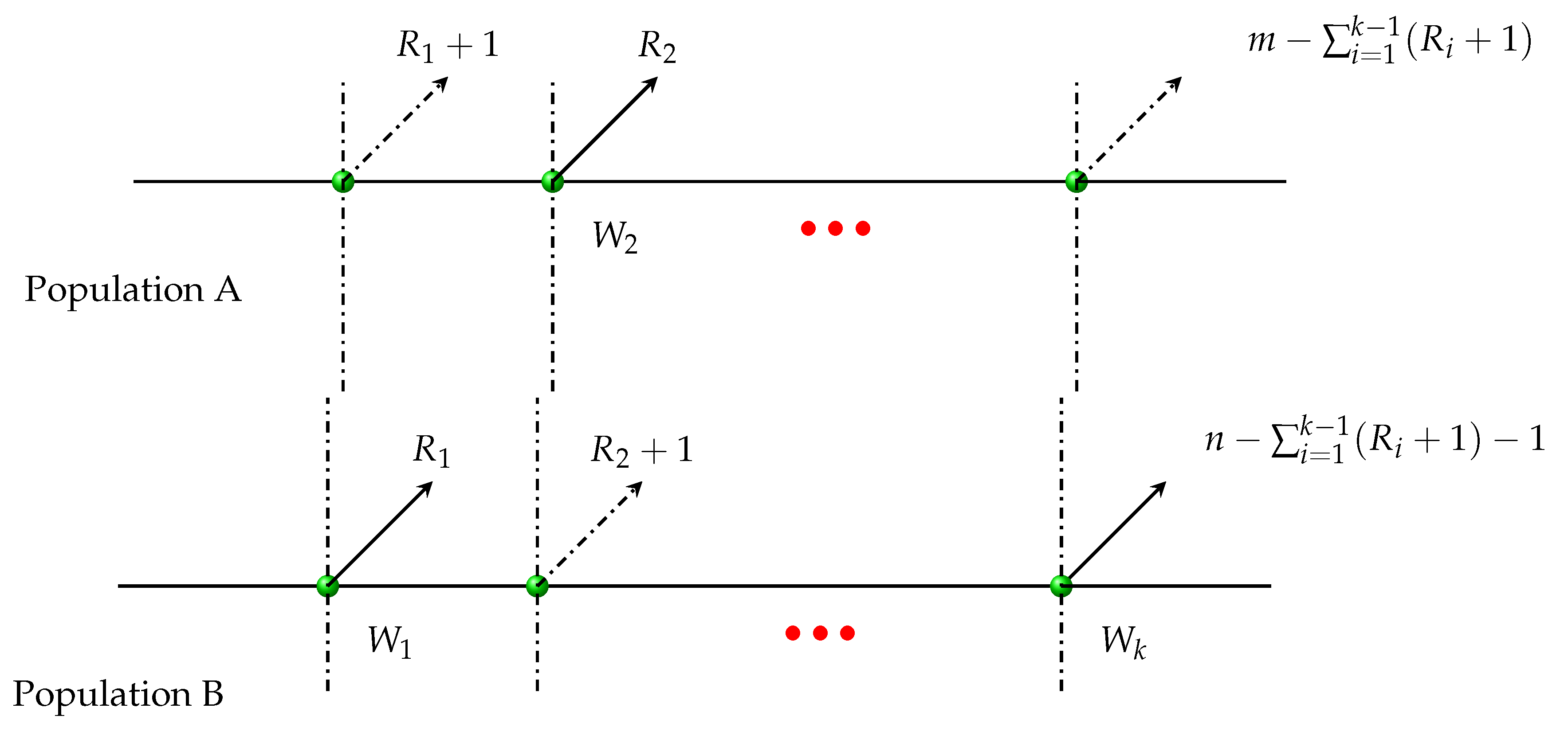
2. Notations, Model Description and Assumption

2.1. Notations

$$\begin{array}{cc}\mathrm{CI}:\hfill & \mathrm{Confidence}/\mathrm{credible}\mathrm{interval}\hfill \\ \mathrm{IP}/\mathrm{NIP}:\hfill & \mathrm{Informative}\mathrm{prior}/\mathrm{non-informative}\mathrm{prior}\hfill \\ \mathrm{AV}/\mathrm{AL}:\hfill & \mathrm{Average}\mathrm{estimate}/\mathrm{length}\hfill \\ \mathrm{MSE}:\hfill & \mathrm{Mean}\mathrm{squared}\mathrm{error}\hfill \\ \mathrm{CP}:\hfill & \mathrm{Coverage}\mathrm{percentage}\hfill \\ \mathrm{BG}/\mathrm{OBG}:\hfill & \mathrm{Beta-Gamma}/\mathrm{Ordered}\mathrm{Beta-Gamma}\hfill \\ \mathrm{BE}:\hfill & \mathrm{Bayesian}\mathrm{estimate}\hfill \\ \mathrm{CDF}:\hfill & \mathrm{Cumulative}\mathrm{distribution}\mathrm{function}\hfill \\ \mathrm{GIED}:\hfill & \mathrm{Generalized}\mathrm{inverted}\mathrm{exponential}\mathrm{distribution}\hfill \\ \mathrm{PDF}:\hfill & \mathrm{Probability}\mathrm{density}\mathrm{function}\hfill \\ \mathrm{SELF}:\hfill & \mathrm{Squared}\mathrm{error}\mathrm{loss}\mathrm{function}\hfill \\ \mathrm{MLE}:\hfill & \mathrm{Maximum}\mathrm{likelihood}\mathrm{estimator}\hfill \\ \mathrm{i}.\mathrm{i}.\mathrm{d}.:\hfill & \mathrm{Independent}\mathrm{and}\mathrm{identically}\mathrm{distributed}\hfill \\ k:\hfill & \mathrm{Total}\mathrm{count}\mathrm{of}\mathrm{failures}\hfill \\ \mathrm{HPD}:\hfill & \mathrm{Highest}\mathrm{posterior}\mathrm{density}\hfill \\ k_1:\hfill & \mathrm{Total}\mathrm{count}\mathrm{of}\mathrm{failures}\mathrm{from}\mathrm{population}\mathrm{A}\hfill \\ \mathrm{CS}:\hfill & \mathrm{Censoring}\mathrm{scheme}\hfill \\ GA(\alpha ,\lambda ):\hfill & \mathrm{PDF}\mathrm{of}\mathrm{Gamma}\mathrm{distribution}:\hfill \\ & f_{GA}\left(x;\alpha ,\lambda \right)=\frac{{\lambda }^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}{x}^{\alpha -1}{e}^{-\lambda x},x>0;\alpha ,\lambda >0.\hfill \\ k_2:\hfill & \mathrm{Total}\mathrm{count}\mathrm{of}\mathrm{failures}\mathrm{from}\mathrm{population}\mathrm{B}\hfill \\ Beta(a,b):\hfill & \mathrm{PDF}\mathrm{of}\mathrm{Beta}\mathrm{distribution}:\hfill \\ & f_{Beta}\left(y;a,b\right)=\frac{\mathrm{\Gamma }\left(a+b\right)}{\mathrm{\Gamma }\left(a\right)\mathrm{\Gamma }\left(b\right)}{y}^{a-1}{\left(1-y\right)}^{b-1},0<y<1;a,b>0.\hfill \end{array}$$

2.2. Model Description and Assumption

We introduce the B-JPC scheme as follows: suppose a random sample of size m units is taken from population A, while another random sample of size n is drawn from population B. Then, the two samples will be conducted in the lifetime experiment at the same time. During the B-JPC process, suppose only $k\left(k<min\left(m,n\right)\right)$ failures are observed in the life testing experiment and the censoring scheme $R=\left(R_1,R_2,\cdots ,R_{k-1}\right)$ are pre-fixed positive integers satisfying $R_1+R_2+\cdots +R_{k-1}+k-1<min\left(m,n\right)$. Here, we record the time of the first failure as $W_1$, which is from the sample of population B. At $W_1$, $\left(R_1+1\right)$ units are removed from the m units of population A at random and $R_1$ units are removed from population B, whose remaining surviving units are $n-1$. Next, it is assumed that the next failure belongs to population A and we record the failure time point as $W_2$. At $W_2$, $R_2$ units are removed randomly from the $m-\left(R_1+1\right)-1$ units of population A, and $\left(R_2+1\right)$ experimental units are randomly chosen to drop from the remaining $n-R_1-1$ surviving units of population B simultaneously. Furthermore, when the i-th failure occurs $\left(i=1,2,\cdots ,k-1\right)$, we record the time of occurrence as $W_i$. $R_i$ units are dropped randomly from one sample where the i-th failure occurs and $R_i+1$ units are dropped randomly from another sample. The experiment is continued until the k-th (from population B or A) failure occurs, and the whole remaining surviving units from both populations A and B are removed at the k-th failure. The experimental process of the B-JPC scheme is shown in Figure 1 and Figure 2.

In this life testing experiment, $\left(Z_1,Z_2,\cdots ,Z_k\right)$ represents a series of indicator variables. Here, when i-th failure belongs to population A, $Z_i$ = 1. Otherwise, the i-th failure belongs to the sample of population B. Hence, the data consist of $\left(\mathbf{W},\mathbf{Z},R\right)$ based on the B-JPC scheme.

It is assumed that the lifetimes of size m experimental units from population A, here, the random variables $X_1$, $X_2$, ⋯, $X_m$, are independently and identically distributed across GIED with the parameters $\lambda$ and ${\alpha }_1$. Then, the probability density function $f\left(x\right)$, the corresponding cumulative distribution function $F\left(x\right)$, and the survival function $\overline{F}\left(x\right)$ are defined as

$$\begin{array}{c}\hfill \left.\begin{array}{c}f\left(x;{\alpha }_1,\lambda \right)=\frac{{\alpha }_1\lambda }{x^2}{e}^{-\frac{\lambda }{x}}{\left(1-e^{-\frac{\lambda }{x}}\right)}^{{\alpha }_1-1},x>0;\lambda ,{\alpha }_1>0\\ F\left(x;{\alpha }_1,\lambda \right)=1-{\left(1-e^{-\frac{\lambda }{x}}\right)}^{{\alpha }_1},x>0;\lambda ,{\alpha }_1\\ \overline{F}\left(x;{\alpha }_1,\lambda \right)={\left(1-e^{-\frac{\lambda }{x}}\right)}^{{\alpha }_1},x>0;\lambda ,{\alpha }_1>0,\end{array}\right\}\end{array}$$

(1)

In the same way, suppose that the lifetimes of size n units from population B, $Y_1$, $Y_2$, ⋯, $Y_m$ are iid GIED with parameters $\lambda$ and ${\alpha }_2$. The probability density function $g\left(y\right)$ as well as the corresponding cumulative distribution function $G\left(y\right)$, and the survival function $\overline{G}\left(y\right)$ are given by

$$\begin{array}{c}\hfill \left.\begin{array}{c}g\left(y;{\alpha }_2,\lambda \right)=\frac{{\alpha }_2\lambda }{y^2}{e}^{-\frac{\lambda }{y}}{\left(1-e^{-\frac{\lambda }{y}}\right)}^{{\alpha }_2-1},y>0;\lambda ,{\alpha }_2>0\\ G\left(y;{\alpha }_2,\lambda \right)=1-{\left(1-e^{-\frac{\lambda }{y}}\right)}^{{\alpha }_2},y>0;\lambda ,{\alpha }_2>0\\ \overline{G}\left(y;{\alpha }_2,\lambda \right)={\left(1-e^{-\frac{\lambda }{y}}\right)}^{{\alpha }_2},y>0;\lambda ,{\alpha }_2>0\end{array}\right\}\end{array}$$

(2)

where $\lambda$, ${\alpha }_1$, and ${\alpha }_2$ are the common scale parameter and different shape parameters, where they are both positive. Figure 3 and Figure 4 show the PDFs and CDFs for different $\alpha$ and fixed $\lambda$ of GIED. According to Figure 3, we find that the PDF of GIED is nonmonotone and when $\lambda$ is fixed, the more sharp the decreases and increases in PDF are with the bigger $\alpha$. As for the CDF of the distribution in Figure 4, a smaller $\alpha$ results in a lower rising rate.

3. Maximum Likelihood Estimation

3.1. Point Estimation

Based on the progressive censoring scheme R, let ${\omega }_1$, ${\omega }_2$, …, ${\omega }_k$ be a B-JPC sample, which is from population A with PDF f(.) and CDF F(.) and population B with PDF g(.) and CDF G(.). Here, the following Algorithm 1 is applied to generate the B-JPC sample. Under the B-JPC sample, the likelihood function $L\left({\alpha }_1,{\alpha }_2,\lambda |w,z,R\right)$ is given by    

$$\begin{array}{ccc}\hfill L& =& c\prod _{i=1}^{k-1}\left[{\left\{f\left(w_i\right){\left(\overline{G}\left(w_i\right)\right)}^{R_i+1}{\left(\overline{F}\left(w_i\right)\right)}^{R_i}\right\}}^{z_i}{\left\{g\left(w_i\right){\left(\overline{G}\left(w_i\right)\right)}^{R_i}{\left(\overline{F}\left(w_i\right)\right)}^{R_i+1}\right\}}^{1-z_i}\right]\hfill \\ & & \times {\left\{f\left(w_k\right){\left(\overline{G}\left(w_k\right)\right)}^{n-{\sum }_{i=1}^{k-1}\left(R_i+1\right)}{\left(\overline{F}\left(w_k\right)\right)}^{m-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-1}\right\}}^{z_k}\hfill \\ & & \times {\left\{g\left(w_k\right){\left(\overline{F}\left(w_k\right)\right)}^{m-{\sum }_{i=1}^{k-1}\left(R_i+1\right)}{\left(\overline{G}\left(w_k\right)\right)}^{n-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-1}\right\}}^{\left(1-z_k\right)}.\hfill \end{array}$$

(3)

here, $c={\prod }_{i=1}^k\left[\left(n-{\sum }_{j=1}^{i-1}\left(R_j+1\right)\right)\left(1-z_i\right)+\left(m-{\sum }_{j=1}^{i-1}\left(R_j+1\right)\right)z_i\right].$

Algorithm 1: Generate the B-JPC sample from GIED.

Step 1: Given the initial values of k, m, n, R, $\lambda$, ${\alpha }_1$ and ${\alpha }_2$. Step 2: Generate $X_1$, ⋯, $X_m$ from GIED ($\lambda$, ${\alpha }_1$) and sort them as $X_{\left(1\right)}$, ⋯, $X_{\left(m\right)}$. Step 3: Generate $Y_1$, ⋯, $Y_n$ from GIED ($\lambda$, ${\alpha }_2$) and sort them as $Y_{\left(1\right)}$, ⋯, $Y_{\left(n\right)}$. Step 4: Calculate $W_1$ = min($X_{\left(1\right)},Y_{\left(1\right)}$), if $X_{\left(1\right)}\le Y_{\left(1\right)}$, $Z_1$ = 1, otherwise $Z_1$ = 0. Step 5: Calculate $W_i$ = min($X_{\left({\eta }_i\right)},Y_{\left({\eta }_i\right)}$). Similarly, if $X_{\left({\eta }_i\right)}\le Y_{\left({\eta }_i\right)}$, $Z_i$ = 1, otherwise             $Z_i$ = 0 (i = 2, 3, ⋯, k), here ${\eta }_i=i-1+{\sum }_{j=1}^{i-1}{R}_j$. Step 6: Here ($W_1,Z_1$), ⋯, ($W_k,Z_k$) are the B-JPC sample from GIED that we need.

In this case, the likelihood function of the unknown parameters ($\lambda$, ${\alpha }_1$, ${\alpha }_2$) with respect to the observed data $\left(w,z\right)$ is defined as

$$\begin{array}{ccc}\hfill L\left(\lambda ,{\alpha }_1,{\alpha }_2|w,z,R\right)& =& c{\alpha }_1^{k_1}{\alpha }_2^{k_2}{\lambda }^k\prod _{i=1}^k\frac{1}{{\omega }_i^2}{e}^{-\frac{\lambda }{{\omega }_i}}\hfill \\ & & \times \prod _{i=1}^{k-1}{\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)}^{{\alpha }_1{R}_i+{\alpha }_1-z_i}{\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}^{{\alpha }_1\left(m-{\sum }_{i=1}^{k-1}\left(R_i+1\right)\right)-z_k}\hfill \\ & & \times \prod _{i=1}^{k-1}{\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)}^{{\alpha }_2-1+z_i+{\alpha }_2{R}_i}{\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}^{{\alpha }_2\left(n-{\sum }_{i=1}^{k-1}\left(R_i+1\right)\right)+z_k-1}.\hfill \end{array}$$

(4)

Here, $k_1={\sum }_{i=1}^k{z}_i$ and $A_1\left(\lambda \right)={\sum }_{i=1}^k{z}_{i}ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)$, $k_2=k-k_1={\sum }_{i=1}^k\left(1-z_i\right)$ and $A_2\left(\lambda \right)={\sum }_{i=1}^k\left(1-z_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)$.

Thus, ignoring the normalizing constant, the log-likelihood function is given by

$$\begin{array}{ccc}\hfill l\left(\lambda ,{\alpha }_1,{\alpha }_2|w,z,R\right)& =& k_{1}ln\left({\alpha }_1\right)+k_{2}ln\left({\alpha }_2\right)-2\sum _{i=1}^{k}ln\left({\omega }_i\right)-\sum _{i=1}^k\frac{\lambda }{{\omega }_i}+kln\left(\lambda \right)\hfill \\ & & +\sum _{i=1}^{k-1}\left({\alpha }_1{R}_i+{\alpha }_1-z_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)\hfill \\ & & +\left[{\alpha }_1\left(m-\sum _{i=1}^{k-1}\left(R_i+1\right)\right)-z_k\right]ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)\hfill \\ & & +\sum _{i=1}^{k-1}\left({\alpha }_2-1+z_i+{\alpha }_2{R}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)\hfill \\ & & +\left[{\alpha }_2\left(n-\sum _{i=1}^{k-1}\left(R_i+1\right)\right)+z_k-1\right]ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right).\hfill \end{array}$$

(5)

Then, the partial derivatives involving ${\alpha }_1$, ${\alpha }_2$, and $\lambda$ are taken and equated to zero. The calculation results are as follows:

$$\begin{array}{ccc}\hfill \frac{\partial l}{\partial \lambda }& =& \frac{k}{\lambda }-\sum _{i=1}^k\frac{1}{{\omega }_i}+\sum _{i=1}^{k-1}\left({\alpha }_1{R}_i+{\alpha }_1-z_i\right)\frac{e^{-\frac{\lambda }{{\omega }_i}}\frac{1}{{\omega }_i}}{1-e^{-\frac{\lambda }{{\omega }_i}}}\hfill \\ & & +\left[{\alpha }_1\left(m-\sum _{i=1}^{k-1}\left(R_i+1\right)\right)-z_k\right]\frac{e^{-\frac{\lambda }{{\omega }_k}}\frac{1}{{\omega }_k}}{1-e^{-\frac{\lambda }{{\omega }_k}}}\hfill \\ & & +\sum _{i=1}^{k-1}\left({\alpha }_2-1+z_i+{\alpha }_2{R}_i\right)\frac{e^{-\frac{\lambda }{{\omega }_i}}\frac{1}{{\omega }_i}}{1-e^{-\frac{\lambda }{{\omega }_i}}}\hfill \\ & & +\left[{\alpha }_2\left(n-\sum _{i=1}^{k-1}\left(R_i+1\right)\right)+z_k-1\right]\frac{e^{-\frac{\lambda }{{\omega }_k}}\frac{1}{{\omega }_k}}{1-e^{-\frac{\lambda }{{\omega }_k}}}=0,\hfill \end{array}$$

(6)

$$\begin{array}{c}\hfill \frac{\partial l}{\partial {\alpha }_1}=\frac{k_1}{{\alpha }_1}+\sum _{i=1}^{k-1}\left(R_i+1\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+\left(m-\sum _{i=1}^{k-1}\left(R_i+1\right)\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)=0,\end{array}$$

(7)

$$\begin{array}{c}\hfill \frac{\partial l}{\partial {\alpha }_2}=\frac{k_2}{{\alpha }_2}+\sum _{i=1}^{k-1}\left(R_i+1\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+\left(n-\sum _{i=1}^{k-1}\left(R_i+1\right)\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)=0.\end{array}$$

(8)

However, owing to the nonlinearity of the equations, it is hard to obtain the closed-form solutions of the above equations; hence, the Newton–Raphson method is considered to compute the roots of equations. Here, we employ the Newton–Raphson method to solve this problem and calculate the MLEs for unknown parameters. After solving Equations (6)–(8), $\widehat{{\alpha }_1}$, $\widehat{{\alpha }_2}$, and $\lambda$ are acquired.

Theorem 1.

The uniqueness and existence of maximum likelihood estimation.

Let ${\xi }_1\left(\lambda \right)=\frac{\partial l}{\partial \lambda }$, ${\xi }_2\left({\alpha }_1\right)=\frac{\partial l}{\partial {\alpha }_1}$ and ${\xi }_3\left({\alpha }_2\right)=\frac{\partial l}{\partial {\alpha }_2}$, which are defined in Equations (6)–(8). The above functions attain unique MLEs at $0<\lambda ,{\alpha }_1,{\alpha }_2<\infty$ in which $\widehat{\lambda }$, $\widehat{{\alpha }_1}$ and $\widehat{{\alpha }_2}$ are the solutions of ${\xi }_1\left(\lambda \right)=0$, ${\xi }_2\left({\alpha }_1\right)=0$ and ${\xi }_3\left({\alpha }_2\right)=0$ if $k_1>0$ and $k_2>0$, where $k_1={\sum }_{i=1}^k{z}_i$ and $k_2=k-k_1={\sum }_{i=1}^k\left(1-z_i\right)$.

Proof. 

From Equations (6)–(8)

$${lim}_{\lambda \to 0}{\xi }_1\left(\lambda \right)\to +\infty , {lim}_{{\alpha }_1\to 0}{\xi }_2\left({\alpha }_1\right)\to +\infty \mathrm{and} {lim}_{{\alpha }_2\to 0}{\xi }_3\left({\alpha }_2\right)\to +\infty ;$$

$${lim}_{\lambda \to \infty }{\xi }_1\left(\lambda \right)=-{\sum }_{i=1}^k\frac{1}{{\omega }_i}<0, {lim}_{{\alpha }_1\to \infty }{\xi }_2\left({\alpha }_1\right)<0 and {lim}_{{\alpha }_2\to \infty }{\xi }_3\left({\alpha }_2\right)<0;$$

$${\xi }_1^{\prime }\left(\lambda \right)=\frac{{\partial }^{2}l}{\partial {\lambda }^2}<0, {\xi }_2^{\prime }\left({\alpha }_1\right)=\frac{{\partial }^{2}l}{\partial {\alpha }_1^2}<0 and {\xi }_3^{\prime }\left({\alpha }_2\right)=\frac{{\partial }^{2}l}{\partial {\alpha }_2^2}<0.$$

Hence, ${\xi }_1\left(\lambda \right)$, ${\xi }_2\left({\alpha }_1\right)$, and ${\xi }_3\left({\alpha }_2\right)$ are continuous and monotonically decreasing functions on $\left(0,\infty \right)$, and they reduce from $+\infty$ to a negative number. Therefore, we prove the existence of MLEs of $\lambda$, ${\alpha }_1$, and ${\alpha }_2$ and show that they are unique solutions of the equation ${\xi }_1\left(\lambda \right)=0$, ${\xi }_2\left({\alpha }_1\right)=0$, and ${\xi }_3\left({\alpha }_2\right)=0$ if $k_1>0$ and $k_2>0$.    □

3.2. Asymptotic Confidence Interval

Applying the asymptotic theory, the asymptotic confidence intervals for $\lambda$, ${\alpha }_1$, and ${\alpha }_2$ are obtained from the variance–covariance matrix, which is also regarded as the inverse Fisher information matrix. Supposing that $\theta$ = $\left(\lambda ,{\alpha }_1,{\alpha }_2\right)$, the Fisher information matrix of the parameters $\theta$ is expressed as follows:

$$I\left(\theta \right)=-E\left[\begin{array}{ccc}\frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\lambda }^2}& \frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial \lambda \partial {\alpha }_1}& \frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial \lambda \partial {\alpha }_2}\\ \frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_1\partial \lambda }& \frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_1^2}& \frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_1\partial {\alpha }_2}\\ \frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_2\partial \lambda }& \frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_2\partial {\alpha }_1}& \frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_2^2}\end{array}\right].$$

(9)

Here,

$$\begin{array}{ccc}\hfill \frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\lambda }^2}& =& -\frac{k}{{\lambda }^2}-\sum _{i=1}^{k-1}\left({\alpha }_1{R}_i+{\alpha }_1-z_i\right){\left(\frac{1}{{\omega }_i}\right)}^2\frac{e^{-\frac{\lambda }{{\omega }_i}}}{{\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)}^2}\hfill \\ & & -\left[{\alpha }_1\left(m-\sum _{i=1}^{k-1}\left(R_i+1\right)\right)-z_k\right]{\left(\frac{1}{{\omega }_k}\right)}^2\frac{e^{-\frac{\lambda }{{\omega }_k}}}{{\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}^2}\hfill \\ & & -\sum _{i=1}^{k-1}\left({\alpha }_2-1+z_i+{\alpha }_2{R}_i\right){\left(\frac{1}{{\omega }_i}\right)}^2\frac{e^{-\frac{\lambda }{{\omega }_i}}}{{\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)}^2}\hfill \\ & & -\left[{\alpha }_2\left(n-\sum _{i=1}^{k-1}\left(R_i+1\right)\right)+z_k-1\right]{\left(\frac{1}{{\omega }_k}\right)}^2\frac{e^{-\frac{\lambda }{{\omega }_k}}}{{\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}^2},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial \lambda \partial {\alpha }_1}=\frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_1\partial \lambda }& =& \sum _{i=1}^{k-1}\left(R_i+1\right)\frac{e^{-\frac{\lambda }{{\omega }_i}}\frac{1}{{\omega }_i}}{1-e^{-\frac{\lambda }{{\omega }_i}}}+\left(m-\sum _{i=1}^{k-1}\left(R_i+1\right)\right)\frac{e^{-\frac{\lambda }{{\omega }_k}}\frac{1}{{\omega }_k}}{1-e^{-\frac{\lambda }{{\omega }_k}}},\hfill \\ \hfill \frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial \lambda \partial {\alpha }_2}=\frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_2\partial \lambda }& =& \sum _{i=1}^{k-1}\left(R_i+1\right)\frac{e^{-\frac{\lambda }{{\omega }_i}}\frac{1}{{\omega }_i}}{1-e^{-\frac{\lambda }{{\omega }_i}}}+\left(n-\sum _{i=1}^{k-1}\left(R_i+1\right)\right)\frac{e^{-\frac{\lambda }{{\omega }_k}}\frac{1}{{\omega }_k}}{1-e^{-\frac{\lambda }{{\omega }_k}}},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_1\partial {\alpha }_2}& =& \frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_2\partial {\alpha }_1}=0,\frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_1^2}=-\frac{k_1}{{\alpha }_1^2},\frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_2^2}=-\frac{k_2}{{\alpha }_2^2}.\hfill \end{array}$$

For the above expressions, the expected values are not easy to obtain. Thus, in order to obtain an approximate expected Fisher information matrix, we apply the observed Fisher information matrix. Suppose the MLE of the parameter $\theta =\left(\lambda ,{\alpha }_1,{\alpha }_2\right)$ is $\widehat{\theta }=\left(\widehat{\lambda },\widehat{{\alpha }_1},\widehat{{\alpha }_2}\right)$. Here, the observed Fisher information matrix I$\left(\widehat{\theta }\right)$ turns out to be

$$\begin{array}{c}\hfill I\left(\widehat{\theta }\right)={\left[\begin{array}{ccc}-\frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\lambda }^2}& -\frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial \lambda \partial {\alpha }_1}& -\frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial \lambda \partial {\alpha }_2}\\ -\frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_1\partial \lambda }& -\frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_1^2}& -\frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_1\partial {\alpha }_2}\\ -\frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_2\partial \lambda }& -\frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_2\partial {\alpha }_1}& -\frac{{\partial }^{2}l\left(\lambda ,{\alpha }_1,{\alpha }_2\right)}{\partial {\alpha }_2^2}\end{array}\right]}_{\theta =\widehat{\theta }}.\end{array}$$

(10)

Furthermore, through inverting the observed Fisher information matrix, we obtain the observed variance–covariance matrix $I^{-1}\left(\widehat{\theta }\right)$ of MLEs $\left(\widehat{\lambda },\widehat{{\alpha }_1},\widehat{{\alpha }_2}\right)$, which is given by

$$I^{-1}\left(\widehat{\theta }\right)=\left[\begin{array}{ccc}Var\left(\widehat{\lambda }\right)& Cov\left(\widehat{\lambda },\widehat{{\alpha }_1}\right)& Cov\left(\widehat{\lambda },\widehat{{\alpha }_2}\right)\\ Cov\left(\widehat{{\alpha }_1},\widehat{\lambda }\right)& Var\left(\widehat{{\alpha }_1}\right)& Cov\left(\widehat{{\alpha }_1},\widehat{{\alpha }_2}\right)\\ Cov\left(\widehat{{\alpha }_2},\widehat{\lambda }\right)& Cov\left(\widehat{{\alpha }_2},\widehat{{\alpha }_1}\right)& Var\left(\widehat{{\alpha }_2}\right)\end{array}\right].$$

(11)

Here, we know that the asymptotic distribution of $\widehat{\theta }$ is $N\left(\theta ,I^{-1}\left(\widehat{\theta }\right)\right)$. Therefore, the $100(1-\gamma )\%$ ACI of the parameter ${\theta }_j$ for a significance level $0<\gamma <1$ is constructed as $\widehat{{\theta }_j}\pm z_{\frac{\gamma }{2}}\sqrt{Var\left(\widehat{{\theta }_j}\right)}$ ($j=1,2,3$), where $z_{\frac{\gamma }{2}}$ represents the upper $z_{\frac{\gamma }{2}}$-th percentile of the standard normal distribution. Furthermore, the coverage probabilities of parameters $\lambda$, ${\alpha }_1$ and ${\alpha }_2$ are given by  

$$C{P}_{\lambda }=P\left[\left|\frac{(\widehat{\lambda }-\lambda )}{\sqrt{Var\left(\widehat{\lambda }\right)}}\right|\le z_{\gamma /2}\right],C{P}_{{\alpha }_1}=P\left[\left|\frac{(\widehat{{\alpha }_1}-{\alpha }_1)}{\sqrt{Var\left(\widehat{{\alpha }_1}\right)}}\right|\le z_{\gamma /2}\right],C{P}_{{\alpha }_2}=P\left[\left|\frac{(\widehat{{\alpha }_2}-{\alpha }_2)}{\sqrt{Var\left(\widehat{{\alpha }_2}\right)}}\right|\le z_{\gamma /2}\right].$$

4. Bayesian Estimation

4.1. Without Order Restriction of Shape Parameters

Before studying Bayesian inference, we discuss the assumptions of the unknown parameters. Here, we assume a very flexible prior on the shape parameters. Meanwhile, when we find that one population is superior to another in reliability, the order restriction between shape parameters is reasonable. Hence, when the order-restricted condition is discussed between shape parameters, a prior is considered for them. In this article, $\lambda$ is the common scale parameter, while ${\alpha }_1$ and ${\alpha }_2$ are two shape parameters. Suppose $\alpha$ = ${\alpha }_1$ + ${\alpha }_2$, then

$$\begin{array}{c}\hfill {\alpha }_1+{\alpha }_2=\alpha \sim GA\left(b_1,b_2\right),\frac{{\alpha }_1}{\alpha }\sim Beta\left(b_3,b_4\right),\end{array}$$

where they are independent, and the hyper-parameters $b_1,b_2,b_3,b_4$ are positive numbers. The transformation of variables method can be easily used to obtain the joint PDF of $\left({\alpha }_1,{\alpha }_2\right)$, derived as follows:

$$\begin{array}{c}\hfill \pi \left({\alpha }_1,{\alpha }_2|b_1,b_2,b_3,b_4\right)=\frac{\mathrm{\Gamma }\left(b_3+b_4\right)}{\mathrm{\Gamma }\left(b_3\right)\mathrm{\Gamma }\left(b_4\right)\mathrm{\Gamma }\left(b_1\right)}{b_2}^{b_1}{\alpha }_1^{b_3-1}{\alpha }_2^{b_4-1}{\left({\alpha }_1+{\alpha }_2\right)}^{b_1-b_3-b_4}{e}^{-b_2\left({\alpha }_1+{\alpha }_2\right)},\end{array}$$

(12)

where $0<{\alpha }_1,{\alpha }_2<\infty$. Then, the joint PDF (12), which is a Beta-Gamma distribution (BG), can be expressed as BG($b_1,b_2,b_3,b_4$). It is found that the bivariate BG distribution is fairly flexible and absolutely continuous. Based on the BG distribution, the following Lemma 1 is employed to generate samples.

Lemma 1.

($X,Y$)∼BG($b_1,b_2,b_3,b_4$), if and only if $Z=X+Y\sim GA(b_1,b_2)$, $V=\frac{X}{X+Y}\sim Beta\left(b_3,b_4\right)$, and Z and V are independently distributed.

Proof. 

Using the transformation method of variables, the above results are easy to prove

$$\begin{array}{ccc}\hfill E\left({\alpha }_1\right)& =& \frac{b_1}{b_2}\frac{b_3}{b_3+b_4},E\left({\alpha }_2\right)=\frac{b_1}{b_2}\frac{b_4}{b_3+b_4},\hfill \\ \hfill E\left({\alpha }_1^2\right)& =& \frac{b_1\left(b_1+1\right)}{b_2^2}\frac{b_3\left(b_3+1\right)}{\left(b_3+b_4\right)\left(b_3+b_4+1\right)},E\left({\alpha }_2^2\right)=\frac{b_1\left(b_1+1\right)}{b_2^2}\frac{b_4\left(b_4+1\right)}{\left(b_3+b_4\right)\left(b_3+b_4+1\right)},\hfill \\ \hfill E\left({\alpha }_1,{\alpha }_2\right)& =& \frac{b_1\left(b_1+1\right)}{b_2^2}\frac{b_3{b}_4}{\left(b_3+b_4\right)\left(b_3+b_4+1\right)},Cov\left({\alpha }_1,{\alpha }_2\right)=\frac{b_1{b}_3{b}_4\left(b_3+b_4-b_1\right)}{b_2^2{\left(b_3+b_4\right)}^2\left(b_3+b_4+1\right)}.\hfill \end{array}$$

   □

Between the two shape parameters, the Beta-Gamma prior is included in distinct dependency structures, and the correlation between ${\alpha }_1$ and ${\alpha }_2$ is determined by the values of $b_1$, $b_3$, and $b_4$. When $b_3+b_4>b_1$, ${\alpha }_1$ and ${\alpha }_2$ are positively correlated, while for $b_3+b_4<b_1$, they are negatively correlated. If $b_3+b_4=b_1$, ${\alpha }_1$ and ${\alpha }_2$ are independent.

Owing to the flexibility and wide application of the Gamma distribution in statistical inference, we suppose that the scale parameter

$$\begin{array}{c}\hfill \lambda \sim GA\left(a_0,b_0\right)=\pi \left(\lambda |a_0,b_0\right),\end{array}$$

where the hyper-parameters are $a_0>0$ and $b_0>0$. In addition, the scale parameter $\lambda$ and shape parameters $\left({\alpha }_1,{\alpha }_2\right)$ are independent.

Based on the prior assumptions discussed previously and the squared error loss function, the Bayesian estimators are considered for all parameters of the generalized inverted exponential distribution in this section. Then, we also obtain the associated credible intervals under different situations. Here, the likelihood function (4) is also denoted as

$$\begin{array}{ccc}\hfill L\left(\lambda ,{\alpha }_1,{\alpha }_2|\mathbf{w},\mathbf{z},R\right)& =& c{\alpha }_1^{k_1}{\alpha }_2^{k_2}{\lambda }^k{e}^{-2{\sum }_{i=1}^{k}ln\left({\omega }_i\right)}{e}^{-\lambda {\sum }_{i=1}^k\frac{1}{{\omega }_i}}{e}^{\left({\alpha }_1-1\right)A_1\left(\lambda \right)}{e}^{\left({\alpha }_2-1\right)A_2\left(\lambda \right)}\hfill \\ & & \times \prod _{i=1}^{k-1}{\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)}^{{\alpha }_1{R}_i+{\alpha }_1-{\alpha }_1{z}_i}{\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}^{{\alpha }_1\left(m-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-z_k\right)}\hfill \\ & & \times \prod _{i=1}^{k-1}{\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)}^{{\alpha }_2{z}_i+{\alpha }_2{R}_i}{\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}^{{\alpha }_2\left(n-{\sum }_{i=1}^{k-1}\left(R_i+1\right)+z_k-1\right)}.\hfill \end{array}$$

(13)

4.1.1. Posterior Analysis: Scale Parameter$\lambda$ Is known

In this section, when we know the scale parameter$\lambda$ and the order restriction on ${\alpha }_1$ and ${\alpha }_2$ is not considered, the Bayesian estimates and the corresponding credible intervals are constructed. Ignoring the constants, the joint posterior distribution of parameters ${\alpha }_1$ and ${\alpha }_2$ is given by

$$\begin{array}{ccc}\hfill {\pi }^{\ast }\left({\alpha }_1,{\alpha }_2|\lambda ,data\right)& \propto & e^{-{\alpha }_1\left(A\left(\lambda \right)-A_1\left(\lambda \right)\right)}{\left({\alpha }_1+{\alpha }_2\right)}^{b_1-b_3-b_4}{e}^{-\left({\alpha }_1+{\alpha }_2\right)\left(b_2-A\left(\lambda \right)\right)}{\alpha }_1^{k_1+b_3-1}{\alpha }_2^{b_4+k_2-1}\hfill \\ & & \times e^{-{\alpha }_2\left(A\left(\lambda \right)-A_2\left(\lambda \right)\right)}{e}^{{\sum }_{i=1}^{k-1}\left({\alpha }_1{R}_i+{\alpha }_1-{\alpha }_1{z}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_1\left(m-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ & & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_2{z}_i+{\alpha }_2{R}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_2\left(n-{\sum }_{i=1}^{k-1}\left(R_i+1\right)+z_k-1\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)},\hfill \end{array}$$

(14)

for $0<{\alpha }_1<{\alpha }_2<\infty$, where $A\left(\lambda \right)=min\left(A_1\left(\lambda \right),A_2\left(\lambda \right)\right)$, and the $A_1\left(\lambda \right)$, $A_2\left(\lambda \right)$ are the same as described in function (4). Therefore, ${\pi }^{\ast }\left({\alpha }_1,{\alpha }_2|\lambda ,data\right)$ can also be expressed as

$${\pi }^{\ast }\left({\alpha }_1,{\alpha }_2|\lambda ,data\right)\propto h_0\left({\alpha }_1,{\alpha }_2\right)\times {\pi }_0\left({\alpha }_1,{\alpha }_2|\lambda ,data\right),$$

where

$$\begin{array}{cc}\hfill {\pi }_0\left({\alpha }_1,{\alpha }_2|\lambda ,data\right)& \sim BG\left(k+b_1,b_2-A\left(\lambda \right),k_1+b_3,k_2+b_4\right),\hfill \\ \hfill h_0\left({\alpha }_1,{\alpha }_2\right)& =e^{{\sum }_{i=1}^{k-1}\left({\alpha }_1{R}_i+{\alpha }_1-{\alpha }_1{z}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_1\left(m-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ \hfill & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_2{z}_i+{\alpha }_2{R}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_2\left(n-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-1+z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}.\hfill \\ \hfill & \times e^{-{\alpha }_2\left(A\left(\lambda \right)-A_2\left(\lambda \right)\right)}{e}^{-{\alpha }_1\left(A\left(\lambda \right)-A_1\left(\lambda \right)\right)}\hfill \end{array}$$

Therefore, we regard the Beta-Gamma prior as a conjugate prior for the known scale parameter $\lambda$. From Lemma 1, the corresponding posterior means are the Bayesian estimates of ${\alpha }_1$ and ${\alpha }_2$ concerning the SELF. Hence, they are directly calculated as

$$\widehat{{\alpha }_1}=E\left({\alpha }_1\right)=\frac{b_1+k}{b_2-A\left(\lambda \right)}\times \frac{b_3+k_1}{b_3+b_4+k} \mathrm{and} \widehat{{\alpha }_2}=E\left({\alpha }_2\right)=\frac{b_1+k}{b_2-A\left(\lambda \right)}\times \frac{b_4+k_2}{b_3+b_4+k}$$

4.1.2. Posterior Analysis: Scale Parameter $\lambda$ Is Not Known

Furthermore, we analyze the situation based on the unknown scale parameter $\lambda$. On this condition, the joint posterior distribution of parameters $\lambda$, ${\alpha }_1$, and ${\alpha }_2$ is derived as follows:

$$\begin{array}{ccc}\hfill {\pi }^{\ast }\left(\lambda ,{\alpha }_1,{\alpha }_2|data\right)& \propto & e^{-{\alpha }_1\left(A\left(\lambda \right)-A_1\left(\lambda \right)\right)}{\left({\alpha }_1+{\alpha }_2\right)}^{b_1-b_3-b_4}{e}^{-\left({\alpha }_1+{\alpha }_2\right)\left(b_2-A\left(\lambda \right)\right)}{\alpha }_1^{k_1+b_3-1}{\alpha }_2^{b_4+k_2-1}\hfill \\ & & \times e^{-{\alpha }_2\left(A\left(\lambda \right)-A_2\left(\lambda \right)\right)}{e}^{{\sum }_{i=1}^{k-1}\left({\alpha }_1{R}_i+{\alpha }_1-{\alpha }_1{z}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_1\left(m-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ & & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_2{z}_i+{\alpha }_2{R}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_2\left(n-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-1+z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ & & \times {\lambda }^{a_0+k-1}{e}^{-\lambda \left(b_0+{\sum }_{i=1}^k\frac{1}{{\omega }_i}\right)}{e}^{-2{\sum }_{i=1}^{k}ln\left({\omega }_i\right)-{\sum }_{i=1}^{k}ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)}\hfill \\ & & \times \frac{1}{{\left(b_2-A\left(\lambda \right)\right)}^{b_1+k}}.\hfill \end{array}$$

(15)

Hence, the Bayesian estimate of $g\left(\lambda ,{\alpha }_1,{\alpha }_2\right)$ regarding the SELF is expressed as

$$\begin{array}{c}\hfill E\left(g\left(\lambda ,{\alpha }_1,{\alpha }_2\right)|data\right)={\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }g\left(\lambda ,{\alpha }_1,{\alpha }_2\right){\pi }^{\ast }\left(\lambda ,{\alpha }_1,{\alpha }_2|data\right)d\lambda d{\alpha }_{1}d{\alpha }_2.\end{array}$$

(16)

However, an explicit form of (16) may not be easy to obtain under general situations. Therefore, the importance sampling technique (IS) is applied to obtain the Bayesian estimates, and the HPD credible intervals are also constructed; these results can be acquired as follows.

For further development, ${\pi }^{\ast }\left(\lambda ,{\alpha }_1,{\alpha }_2|data\right)$ is expressed again as

$$\begin{array}{c}\hfill \pi \ast \left(\lambda ,{\alpha }_1,{\alpha }_2|data\right)\propto h_0\left(\lambda ,{\alpha }_1,{\alpha }_2\right)\times {\pi }_0\left({\alpha }_1,{\alpha }_2|\lambda ,data\right)\times {\pi }_1\left(\lambda |data\right),\end{array}$$

where

$$\begin{array}{cc}\hfill {\pi }_0\left({\alpha }_1,{\alpha }_2|\lambda ,data\right)& \sim BG\left(k+b_1,b_2-A\left(\lambda \right),k_1+b_3,k_2+b_4\right),\hfill \\ \hfill {\pi }_1\left(\lambda |data\right)& \sim GA\left(k+a_0,b_0+\sum _{i=1}^k\frac{1}{{\omega }_i}\right),\hfill \\ \hfill h_0\left(\lambda ,{\alpha }_1,{\alpha }_2\right)& =e^{-{\alpha }_2\left(A\left(\lambda \right)-A_2\left(\lambda \right)\right)}{e}^{-2{\sum }_{i=1}^{k}ln\left({\omega }_i\right)-{\sum }_{i=1}^{k}ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)}{e}^{-{\alpha }_1\left(A\left(\lambda \right)-A_1\left(\lambda \right)\right)}\hfill \\ \hfill & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_1{R}_i+{\alpha }_1-{\alpha }_1{z}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_1\left(m-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ \hfill & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_2{z}_i+{\alpha }_2{R}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_2\left(n-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-1+z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ \hfill & \times \frac{1}{{\left(b_2-A\left(\lambda \right)\right)}^{b_1+k}}.\hfill \end{array}$$

Therefore, the Bayesian estimate of $g\left(\lambda ,{\alpha }_1,{\alpha }_2\right)$ regarding the SELF is expressed as

$$\begin{array}{c}\hfill E\left(g\left(\lambda ,{\alpha }_1,{\alpha }_2\right)|data\right)=\frac{{\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }g\left(\lambda ,{\alpha }_1,{\alpha }_2\right){\pi }_0\left({\alpha }_1,{\alpha }_2|\lambda ,data\right){\pi }_1\left(\lambda |data\right)h_0\left(\lambda ,{\alpha }_1,{\alpha }_2\right)d\lambda d{\alpha }_{1}d{\alpha }_2}{{\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }{\pi }_0\left({\alpha }_1,{\alpha }_2|\lambda ,data\right){\pi }_1\left(\lambda |data\right)h_0\left({\alpha }_1,{\alpha }_2,\lambda \right)d\lambda d{\alpha }_{1}d{\alpha }_2}.\end{array}$$

We employ the following Algorithm 2 to obtain the Bayesian estimate and corresponding HPD credible interval of $g\left(\lambda ,{\alpha }_1,{\alpha }_2\right)$.

Algorithm 2: The application of the importance sampling technique in Bayesian estimates.

Step 1: Under the given observed data, generate $\lambda$ from ${\pi }_1\left(\lambda |data\right)$. Step 2: Generate ${\alpha }_1$ and ${\alpha }_2$ from ${\pi }_0\left({\alpha }_1,{\alpha }_2|\lambda ,data\right)$ for the given $\lambda$. Step 3: Repeat step 1 and 2 M times to acquire $\left(\left({\lambda }_1,{\alpha }_{11},{\alpha }_{21}\right),\cdots ,\left({\lambda }_M,{\alpha }_{1M},{\alpha }_{2M}\right)\right)$. Step 4: In order to calculate the Bayesian estimates of $g\left(\lambda ,{\alpha }_1,{\alpha }_2\right)$, the $\left(h_{01},\cdots h_{0M}\right)$             and $(g_1,\cdots ,g_M)$ are computed. Here, $$h_{0i}=h_0\left({\lambda }_i,{\alpha }_{1i},{\alpha }_{2i}\right) \mathrm{and} g_i=g\left({\lambda }_i,{\alpha }_{1i},{\alpha }_{2i}\right).$$ Step 5: The approximate Bayesian estimates of $g\left(\lambda ,{\alpha }_1,{\alpha }_2\right)$ are given by $$\widehat{g_{IS}}\left(\lambda ,{\alpha }_1,{\alpha }_2\right)=\frac{{\sum }_{i=1}^M{g}_i{h}_{0i}}{{\sum }_{i=1}^M{h}_{0i}}.$$

Here, the Bayesian estimates of all unknown parameters $\lambda$, ${\alpha }_1$, ${\alpha }_2$ under SELF are obtained as

$${\widehat{{\alpha }_1}}_{IS}=\frac{{\sum }_{i=1}^M{\alpha }_{1i}{h}_0\left({\alpha }_{1i},{\lambda }_i\right)}{{\sum }_{i=1}^M{h}_0\left({\alpha }_{1i},{\lambda }_i\right)},{\widehat{{\alpha }_2}}_{IS}=\frac{{\sum }_{i=1}^M{\alpha }_{2i}{h}_0\left({\alpha }_{2i},{\lambda }_i\right)}{{\sum }_{i=1}^M{h}_0\left({\alpha }_{2i},{\lambda }_i\right)},{\widehat{\lambda }}_{IS}=\frac{{\sum }_{i=1}^M{\lambda }_i{h}_0\left({\alpha }_i,{\lambda }_i\right)}{{\sum }_{i=1}^M{h}_0\left({\alpha }_i,{\lambda }_i\right).}$$

4.2. With Order Restriction of Shape Parameters

We suppose ${\alpha }_2>{\alpha }_1$ when we consider the order restriction on the shape parameters ${\alpha }_1$ and ${\alpha }_2$. Then, the joint prior distribution of parameters ${\alpha }_1$ and ${\alpha }_2$ is written as

$$\begin{array}{ccc}\hfill \pi \left({\alpha }_1,{\alpha }_2|b_1,b_2,b_3,b_4\right)& =& \frac{\mathrm{\Gamma }\left(b_3+b_4\right)}{\mathrm{\Gamma }\left(b_3\right)\mathrm{\Gamma }\left(b_4\right)\mathrm{\Gamma }\left(b_1\right)}{b_2}^{b_1}{\left({\alpha }_1+{\alpha }_2\right)}^{b_1-b_3-b_4}{e}^{-b_2\left({\alpha }_1+{\alpha }_2\right)}\hfill \\ & & \times \left({\alpha }_1^{b_3-1}{\alpha }_2^{b_4-1}+{\alpha }_1^{b_4-1}{\alpha }_2^{b_3-1}\right).0<{\alpha }_1<{\alpha }_2<\infty ,\hfill \end{array}$$

(17)

Moreover, the joint prior (17) mentioned above is the joint PDF of $\left({\alpha }_{\left(1\right)},{\alpha }_{\left(2\right)}\right)$, and the $\left({\alpha }_{\left(1\right)},{\alpha }_{\left(2\right)}\right)$ are ordered random variables. Here,

$$\begin{array}{c}\hfill \left({\alpha }_{\left(1\right)},{\alpha }_{\left(2\right)}\right)=\left\{\begin{array}{cc}\left({\alpha }_1,{\alpha }_2\right)\hfill & \mathrm{if}{\alpha }_1<{\alpha }_2\hfill \\ \left({\alpha }_2,{\alpha }_1\right)\hfill & \mathrm{if}{\alpha }_1\ge {\alpha }_2\hfill \end{array}\right.\end{array}$$

and $\left({\alpha }_1,{\alpha }_2\right)$ follows BG ($b_1,b_2,b_3,b_4$). The joint prior (17) is referred to as an ordered Beta-Gamma prior distribution, which is denoted as OBG ($b_1,b_2,b_3,b_4$). Simultaneously, the common scale parameter $\lambda$ follows $\pi \left(\alpha |a_0,b_0\right)$ defined previously, which is independent of $\left({\alpha }_1,{\alpha }_2\right)$.

4.2.1. Posterior Analysis: Scale Parameter $\lambda$ Is Known

In this section, the Bayesian estimate is discussed concerning the order restriction ${\alpha }_1<{\alpha }_2$. The joint posterior distribution of parameters ${\alpha }_1$ and ${\alpha }_2$ can be expressed as

$$\begin{array}{ccc}\hfill {\pi }^{\ast }\left({\alpha }_1,{\alpha }_2|\lambda ,data\right)& \propto & \left({\alpha }_1^{b_3+J-1}{\alpha }_2^{b_4+J-1}+{\alpha }_1^{b_4+J-1}{\alpha }_2^{b_3+J-1}\right){\left({\alpha }_1+{\alpha }_2\right)}^{b_1-b_3-b_4}{e}^{-b_2\left({\alpha }_1+{\alpha }_2\right)}\hfill \\ & & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_1{R}_i+{\alpha }_1-{\alpha }_1{z}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_1\left(m-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ & & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_2{z}_i+{\alpha }_2{R}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_2\left(n-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-1+z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ & & \times e^{\left({\alpha }_1-1\right)A_1\left(\lambda \right)}{e}^{\left({\alpha }_2-1\right)A_2\left(\lambda \right)}.\hfill \end{array}$$

(18)

The function (18) is also expressed as

$$\begin{array}{ccc}\hfill {\pi }^{\ast }\left({\alpha }_1,{\alpha }_2|\lambda ,data\right)& \propto & \left({\alpha }_1^{b_3+J-1}{\alpha }_2^{b_4+J-1}+{\alpha }_1^{b_4+J-1}{\alpha }_2^{b_3+J-1}\right){\left({\alpha }_1+{\alpha }_2\right)}^{b_1-b_3-b_4}{e}^{-\left({\alpha }_1+{\alpha }_2\right)\left(b_2-A\left(\lambda \right)\right)}\hfill \\ & & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_1{R}_i+{\alpha }_1-{\alpha }_1{z}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_1\left(m-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ & & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_2{z}_i+{\alpha }_2{R}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_2\left(n-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-1+z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ & & \times {\alpha }_1^{K_1-J}{e}^{-{\alpha }_2\left(A\left(\lambda \right)-A_2\left(\lambda \right)\right)}{\alpha }_2^{K_2-J}{e}^{-{\alpha }_1\left(A\left(\lambda \right)-A_1\left(\lambda \right)\right)},\hfill \\ \hfill \end{array}$$

(19)

where $A\left(\lambda \right)$ = min$\left(A_1\left(\lambda \right),A_2\left(\lambda \right)\right)$, and $J=min\left(k_1,k_2\right)$.

Then, the joint posterior distribution of parameters ${\alpha }_1$ and ${\alpha }_2$ given in function (19) is written as follows

$${\pi }^{\ast }\left({\alpha }_1,{\alpha }_2|\lambda ,data\right)\propto h_0\left({\alpha }_1,{\alpha }_2\right)\times {\pi }_0\left({\alpha }_1,{\alpha }_2|\lambda ,data\right),$$

where

$$\begin{array}{cc}\hfill {\pi }_0\left({\alpha }_1,{\alpha }_2|\lambda ,data\right)& \sim OBG\left(b_1+2J,b_2-A\left(\lambda \right),b_3+J,b_4+J\right),\hfill \\ \hfill h_0\left({\alpha }_1,{\alpha }_2\right)& =e^{-{\alpha }_1\left(A\left(\lambda \right)-A_1\left(\lambda \right)\right)}{\alpha }_1^{K_1-J}{\alpha }_2^{K_2-J}{e}^{-{\alpha }_2\left(A\left(\lambda \right)-A_2\left(\lambda \right)\right)}\hfill \\ \hfill & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_1{R}_i+{\alpha }_1-{\alpha }_1{z}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_1\left(m-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ \hfill & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_2{z}_i+{\alpha }_2{R}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_2\left(n-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-1+z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}.\hfill \end{array}$$

Therefore, Algorithm A1 (see Appendix A.1 for details) is used for obtaining the Bayesian estimates along with the CIs of the parameters ${\alpha }_1$ and ${\alpha }_2$.

4.2.2. Posterior Analysis: Scale Parameter $\lambda$ Is Not Known

Based on the order restriction ${\alpha }_1<{\alpha }_2$ and the unknown scale parameter $\lambda$, the posterior distribution of all parameters ${\alpha }_1$, ${\alpha }_2$ and $\lambda$ can be expressed as

$$\begin{array}{ccc}\hfill {\pi }^{\ast }\left(\lambda ,{\alpha }_1,{\alpha }_2|data\right)& \propto & \left({\alpha }_1^{b_3+J-1}{\alpha }_2^{b_4+J-1}+{\alpha }_1^{b_4+J-1}{\alpha }_2^{b_3+J-1}\right){\left({\alpha }_1+{\alpha }_2\right)}^{b_1-b_3-b_4}{e}^{-b_2\left({\alpha }_1+{\alpha }_2\right)}\hfill \\ & & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_1{R}_i+{\alpha }_1-{\alpha }_1{z}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_1\left(m-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ & & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_2{z}_i+{\alpha }_2{R}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_2\left(n-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-1+z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ & & \times e^{\left({\alpha }_1-1\right)A_1\left(\lambda \right)}{e}^{-2{\sum }_{i=1}^{k}ln\left({\omega }_i\right)-\lambda {\sum }_{i=1}^k\frac{1}{{\omega }_i}}{\lambda }^{a_0+k-1}{e}^{-b_0\lambda }{e}^{\left({\alpha }_2-1\right)A_2\left(\lambda \right)}\hfill \\ & & \times \frac{1}{{\left(b_2-A\left(\lambda \right)\right)}^{b_1+2J}}.\hfill \end{array}$$

(20)

Here, function (20) is rewritten as

$$\begin{array}{ccc}\hfill {\pi }^{\ast }\left(\lambda ,{\alpha }_1,{\alpha }_2|data\right)& \propto & e^{-\left({\alpha }_1+{\alpha }_2\right)\left(b_2-A\left(\lambda \right)\right)}{\left({\alpha }_1+{\alpha }_2\right)}^{b_1-b_3-b_4}\left({\alpha }_1^{b_3+J-1}{\alpha }_2^{b_4+J-1}+{\alpha }_1^{b_4+J-1}{\alpha }_2^{b_3+J-1}\right)\hfill \\ & & \times {\alpha }_1^{K_1-J}{\alpha }_2^{K_2-J}{e}^{-{\alpha }_1\left(A\left(\lambda \right)-A_1\left(\lambda \right)\right)}{e}^{-2{\sum }_{i=1}^{k}ln\left({\omega }_i\right)-{\sum }_{i=1}^{k}ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)}{e}^{-{\alpha }_2\left(A\left(\lambda \right)-A_2\left(\lambda \right)\right)}\hfill \\ & & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_1{R}_i+{\alpha }_1-{\alpha }_1{z}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_1\left(m-z_k-{\sum }_{i=1}^{k-1}\left(R_i+1\right)\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ & & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_2{z}_i+{\alpha }_2{R}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_2\left(n-{\sum }_{i=1}^{k-1}\left(R_i+1\right)+z_k-1\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ & & \times {\lambda }^{a_0+k-1}{e}^{-\lambda \left(b_0+{\sum }_{i=1}^k\frac{1}{{\omega }_i}\right)}\hfill \\ & & \times \frac{1}{{\left(b_2-A\left(\lambda \right)\right)}^{b_1+2J}},\hfill \end{array}$$

(21)

where $A\left(\lambda \right)=min\left(A_1\left(\lambda \right),A_2\left(\lambda \right)\right)$ and $J=min\left(k_1,k_2\right)$. According to the function (21), we observe that the joint posterior distribution of parameters ${\alpha }_1$, ${\alpha }_2$, and $\lambda$ in this situation is given by

$${\pi }^{\ast }\left(\lambda ,{\alpha }_1,{\alpha }_2|data\right)\propto h_0\left(\lambda ,{\alpha }_1,{\alpha }_2\right)\times {\pi }_0\left({\alpha }_1,{\alpha }_2|\lambda ,data\right)\times {\pi }_1\left(\lambda |data\right),$$

where

$$\begin{array}{cc}\hfill {\pi }_0\left({\alpha }_1,{\alpha }_2|\lambda ,data\right)& \sim OBG\left(b_1+2J,b_2-A\left(\lambda \right),b_3+J,b_4+J\right),\hfill \\ \hfill {\pi }_1\left(\lambda |data\right)& \sim GA\left(a_0+k,b_0+\sum _{i=1}^k\frac{1}{{\omega }_i}\right),\hfill \\ \hfill h_0\left(\lambda ,{\alpha }_1,{\alpha }_2\right)& ={\alpha }_1^{K_1-J}{\alpha }_2^{K_2-J}{e}^{-{\alpha }_1\left(A\left(\lambda \right)-A_1\left(\lambda \right)\right)}{e}^{-2{\sum }_{i=1}^{k}ln\left({\omega }_i\right)-{\sum }_{i=1}^{k}ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)}{e}^{-{\alpha }_2\left(A\left(\lambda \right)-A_2\left(\lambda \right)\right)}\hfill \\ \hfill & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_1{R}_i+{\alpha }_1-{\alpha }_1{z}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_1\left(m-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ \hfill & \times e^{{\sum }_{i=1}^{k-1}\left({\alpha }_2{z}_i+{\alpha }_2{R}_i\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_i}}\right)+{\alpha }_2\left(n-{\sum }_{i=1}^{k-1}\left(R_i+1\right)-1+z_k\right)ln\left(1-e^{-\frac{\lambda }{{\omega }_k}}\right)}\hfill \\ \hfill & \times \frac{1}{{\left(b_2-A\left(\lambda \right)\right)}^{b_1+2J}}.\hfill \end{array}$$

Then, Algorithm A2 (see Appendix A.2) is applied to obtain the Bayesian estimates and CIs of all parameters $\lambda$, ${\alpha }_1$, and ${\alpha }_2$.

4.3. HPD Credible Interval

In this section, the generated importance samples are applied to construct the highest posterior density CIs of ${\alpha }_1$, ${\alpha }_2$, and $\lambda$. We arrange ${\alpha }_{1\left(1\right)}<\cdots <{\alpha }_{1\left(M\right)}$ and ${\alpha }_{2\left(1\right)}<\cdots <{\alpha }_{2\left(M\right)}$ as the ordered value of ${\alpha }_{i1},{\alpha }_{i2},\cdots ,{\alpha }_{iM}$ $\left(i=1,2\right)$. Then, employing the algorithm provided in [19], the $100\times (1-\gamma )\%$ HPD credible intervals for $0<\gamma <1$ of the parameters $\lambda$, ${\alpha }_1$ and ${\alpha }_2$ are obtained as $\left({\lambda }_{\left(j\right)},{\lambda }_{(j+[(1-\gamma )M\left]\right)}\right)$, $\left({\alpha }_{1\left(j\right)},{\alpha }_{1(j+[(1-\gamma )M\left]\right)}\right)$ and $\left({\alpha }_{2\left(j\right)},{\alpha }_{2(j+[(1-\gamma )M\left]\right)}\right)$, where j satisfies that

$${\lambda }_{(j+[M(1-\gamma )\left]\right)}-{\lambda }_{\left(j\right)}=\underset{1\le i\le M\gamma }{min}\left({\lambda }_{(i+[M(1-\gamma )\left]\right)}-{\lambda }_{\left(i\right)}\right),j=1,2,\dots ,M,$$

$${\alpha }_{1(j+[M(1-\gamma )\left]\right)}-{\alpha }_{1\left(j\right)}=\underset{1\le i\le M\gamma }{min}\left({\alpha }_{1(i+[M(1-\gamma )\left]\right)}-{\alpha }_{1\left(i\right)}\right),j=1,2,\dots ,M,$$

$${\alpha }_{2(j+[M(1-\gamma )\left]\right)}-{\alpha }_{2\left(j\right)}=\underset{1\le i\le M\gamma }{min}\left({\alpha }_{2(i+[M(1-\gamma )\left]\right)}-{\alpha }_{2\left(i\right)}\right),j=1,2,\dots ,M,$$

where $\left[y\right]$ is the integer part of y.

5. Simulation Study and Data Analysis

5.1. Simulation Study

We conduct some simulation experiments to analyze the effects and performance of various estimators in this section. B-JPC samples are obtained from the combinations of various sample sizes, effective sample sizes, different true values of all parameters $\left(\lambda ,{\alpha }_1,{\alpha }_2\right)$, and censoring schemes $(m,n,k)$ for GIED $\left(\lambda ,{\alpha }_1,{\alpha }_2\right)$. Here, the R software is employed for all the calculations. Based on the true values of all parameters, we consider the same scale parameter $\lambda$ = 0.5 and the different shape parameters $\left({\alpha }_1,{\alpha }_2\right)$ are taken as (0.4, 0.8) and (0.4, 0.3). Here, the shape parameters jointly follow a Beta-Gamma prior and the scale parameter follows a Gamma prior; these parameters are proposed to compute Bayesian estimates concerning SELF.

In the process of Bayesian estimation, a simulation study is first performed based on the informative priors (IP). Here, in order to match the true expected values of the two different populations with their prior expectations, the hyper-parameters are selected as $\left(b_1,b_2,b_3,b_4,a_0,b_0\right)=\left(1.3,1,1.3,2,0.25,0.5\right)\mathrm{and}\left(1.4,2,2.6,2,0.25,0.5\right)$. Meanwhile, for the non-informative prior (NIP), the hyper-parameters are chosen as $b_1=b_2=b_3=b_4=a_0=b_0={10}^{-5}$, which are close to zero to avoid improper posterior density. Here, the notation R = $\left(3,2,2_{\left(5\right)}\right)$ means $R_1$ = 3, $R_2$ = 2, $R_3=R_4=\cdots =R_7$ = 2.

Based on the various B-JPC censoring schemes, the MLEs and Bayesian estimates of all parameters are discussed. The whole process is repeated 1000 times for each case of MLEs, and we obtain the average estimates (AV), variance estimates, and associated mean squared errors (MSE). Here, the corresponding results are recorded in

Table 1. MSEs and AVs of the MLEs of the model parameters with $\lambda$ = 0.5, ${\alpha }_1$ = 0.4, ${\alpha }_2$ = 0.8 based on different CSs.

	$\widehat{\mathit{\lambda }}$			$\widehat{{\mathit{\alpha }}_1}$			$\widehat{{\mathit{\alpha }}_2}$
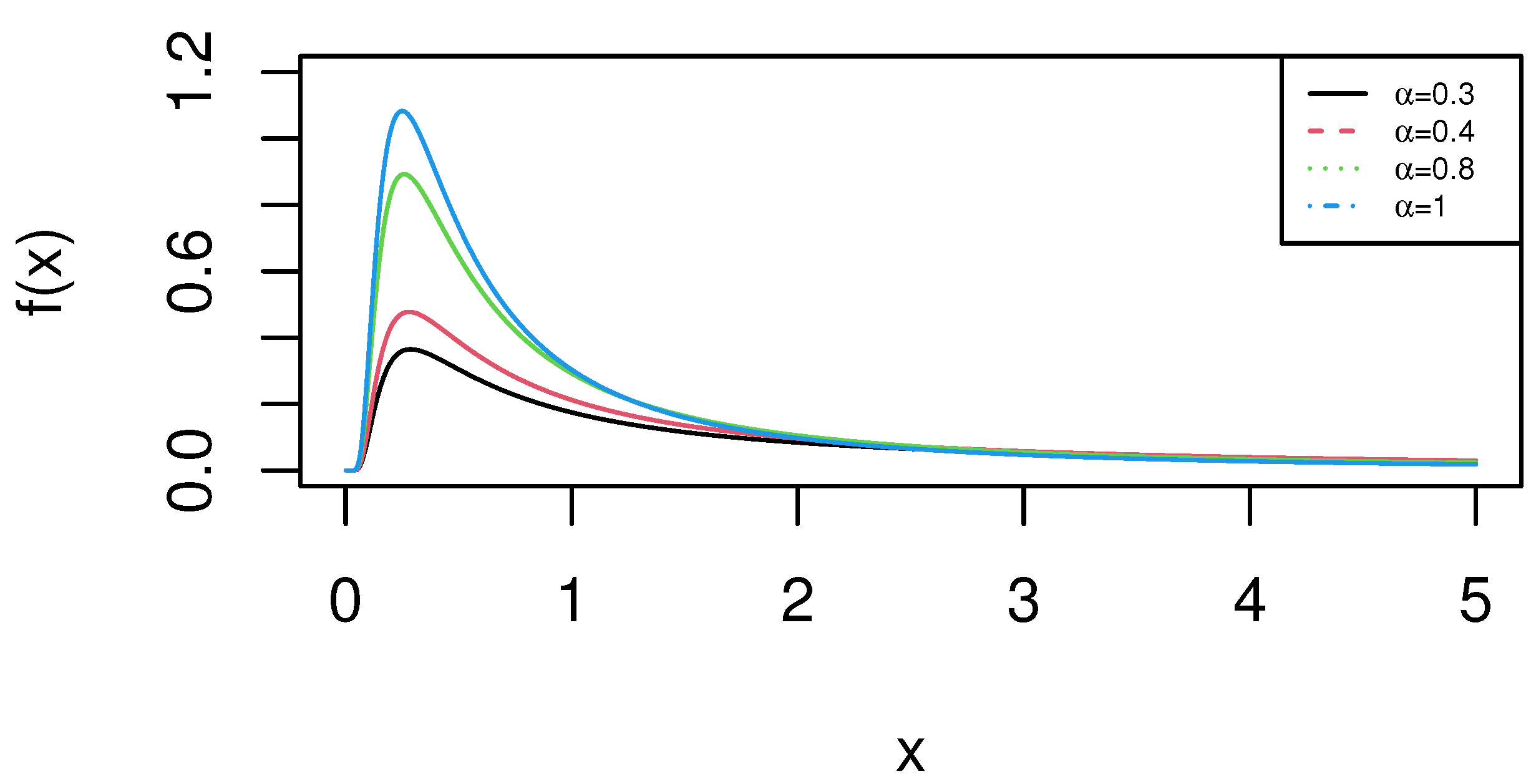
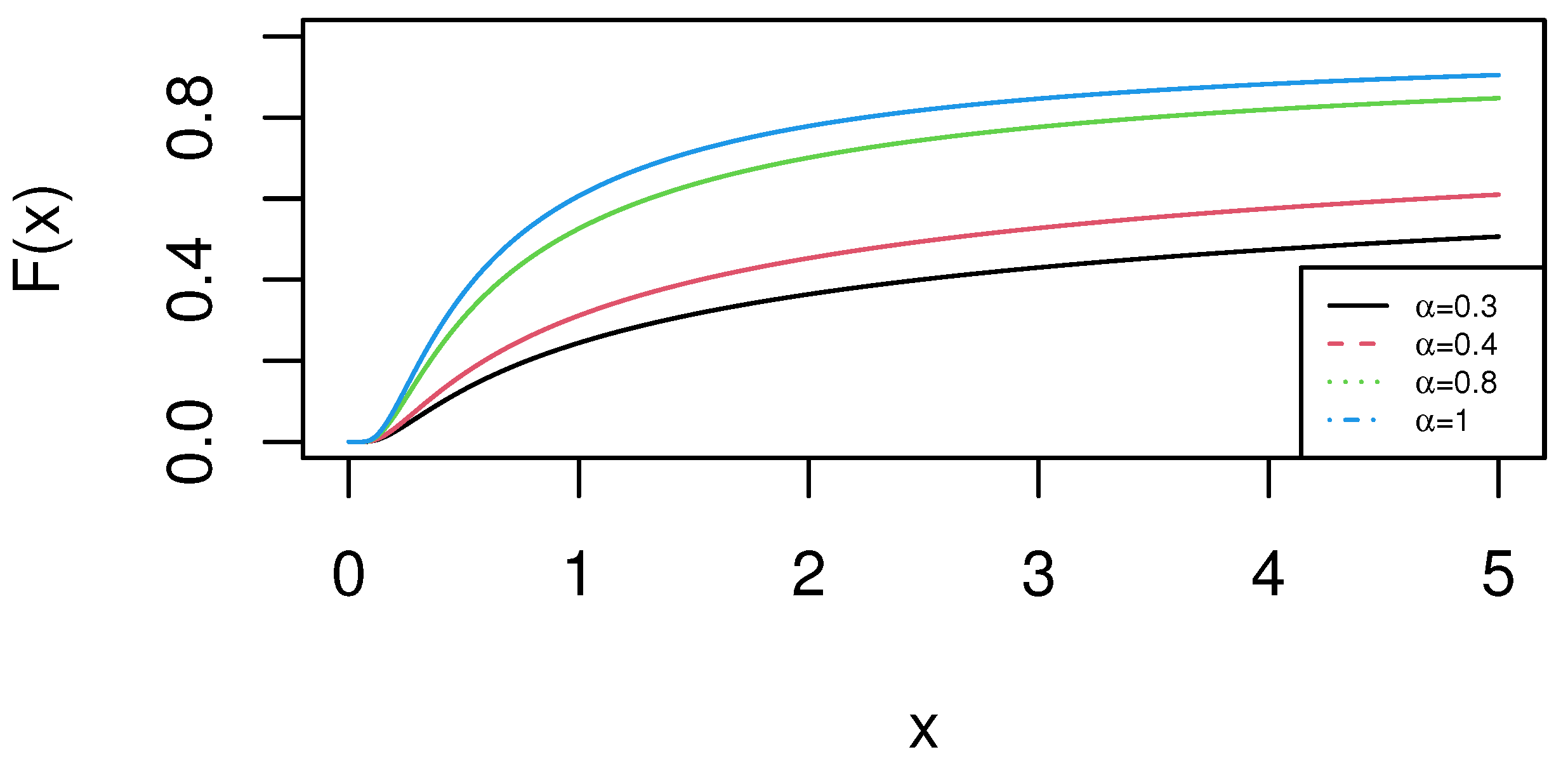
Censoring Scheme	AV	MSE	Variance Estimate	AV	MSE	Variance Estimate	AV	MSE	Variance Estimate
k = 8, R = (2, $2_{\left(6\right)}$)	0.573	0.040	0.035	0.272	0.070	0.053	0.572	0.218	0.166
k = 8, R = ($2_{\left(4\right)}$, 3, $2_{\left(2\right)}$)	0.588	0.049	0.041	0.287	0.111	0.099	0.635	0.455	0.427
k = 8, R = ($2_{\left(7\right)}$)	0.580	0.044	0.038	0.285	0.072	0.059	0.596	0.404	0.362
k = 8, R = (3, 2, $2_{\left(5\right)}$)	0.612	0.057	0.044	0.303	0.084	0.075	0.702	0.433	0.423
k = 8, R = (5, 4, $1_{\left(5\right)}$)	0.658	0.071	0.046	0.373	0.131	0.130	0.904	0.562	0.551
k = 8, R = ($2_{\left(5\right)}$, 3, 4)	0.610	0.055	0.043	0.314	0.108	0.101	0.675	0.360	0.345
k = 10, R = (7, $1_{\left(8\right)}$)	0.712	0.098	0.053	0.445	0.125	0.123	1.106	1.386	1.292
k = 10, R = ($2_{\left(5\right)}$, 2, $1_{\left(3\right)}$)	0.667	0.072	0.044	0.353	0.066	0.064	0.790	0.362	0.361
k = 10, R = ($2_{\left(6\right)}$, $1_{\left(3\right)}$)	0.663	0.073	0.046	0.352	0.078	0.076	0.792	0.441	0.440
k = 10, R = ($4_{\left(2\right)}$, $1_{\left(7\right)}$)	0.714	0.098	0.051	0.426	0.113	0.112	1.018	0.583	0.536
k = 10, R = (5, 3, $1_{\left(7\right)}$)	0.719	0.097	0.049	0.435	0.132	0.130	1.055	0.639	0.574
k = 10, R = ($2_{\left(7\right)}$, $1_{\left(2\right)}$)	0.757	0.143	0.077	0.483	0.126	0.119	0.424	0.132	0.117

Abbreviations: AV—average estimate. MSE—mean square error.

and

Table 2. MSEs and AVs of the MLEs of the model parameters with $\lambda$ = 0.5, ${\alpha }_1$ = 0.4, and ${\alpha }_2$ = 0.3 based on different CSs.

	$\widehat{\mathit{\lambda }}$			$\widehat{{\mathit{\alpha }}_1}$			$\widehat{{\mathit{\alpha }}_2}$
Censoring Scheme	AV	MSE	Variance Estimate	AV	MSE	Variance Estimate	AV	MSE	Variance Estimate
k = 8, R = (2, $2_{\left(6\right)}$)	0.629	0.084	0.067	0.350	0.080	0.078	0.304	0.113	0.113
k = 8, R = ($2_{\left(4\right)}$, 3, $2_{\left(2\right)}$)	0.657	0.098	0.073	0.377	0.083	0.083	0.318	0.073	0.072
k = 8, R = ($2_{\left(7\right)}$)	0.634	0.086	0.068	0.362	0.090	0.089	0.304	0.092	0.092
k = 8, R = (3, 2, $2_{\left(5\right)}$)	0.671	0.103	0.074	0.393	0.104	0.104	0.328	0.073	0.073
k = 8, R = (5, 4, $1_{\left(5\right)}$)	0.732	0.136	0.083	0.477	0.189	0.183	0.395	0.132	0.123
k = 8, R = ($2_{\left(5\right)}$, 3, 4)	0.669	0.107	0.078	0.391	0.081	0.081	0.340	0.101	0.099
k = 10, R = (7, $1_{\left(8\right)}$)	0.810	0.190	0.094	0.592	0.226	0.189	0.511	0.243	0.198
k = 10, R = ($2_{\left(5\right)}$, 2, $1_{\left(3\right)}$)	0.726	0.124	0.073	0.448	0.073	0.071	0.390	0.103	0.094
k = 10, R = ($2_{\left(6\right)}$, $1_{\left(3\right)}$)	0.739	0.134	0.077	0.447	0.068	0.066	0.393	0.088	0.077
k = 10, R = ($4_{\left(2\right)}$, $1_{\left(7\right)}$)	0.801	0.183	0.092	0.554	0.173	0.150	0.476	0.180	0.149
k = 10, R = (5, 3, $1_{\left(7\right)}$)	0.792	0.169	0.083	0.541	0.138	0.118	0.462	0.153	0.126
k = 10, R = ($2_{\left(7\right)}$, $1_{\left(2\right)}$)	0.757	0.143	0.077	0.483	0.126	0.119	0.424	0.132	0.117

Abbreviations: AV—average estimate; MSE—mean square error.

. Moreover, the standard errors are computed by squaring the root of the variance estimates. In

Table 3. CPs and ALs of 95% asymptotic confidence intervals of the model parameters with $\lambda$ = 0.5, ${\alpha }_1$ = 0.4, and ${\alpha }_2$ = 0.8 based on different CSs.

	$\widehat{\mathit{\lambda }}$		$\widehat{{\mathit{\alpha }}_1}$		$\widehat{{\mathit{\alpha }}_2}$
	AL	CP	AL	CP	AL	CP
k = 8, R = (2, $2_{\left(6\right)}$)	0.902	98.6%	0.834	68.3%	1.680	71.6%
k = 8, R = ($2_{\left(4\right)}$, 3, $2_{\left(2\right)}$)	0.905	98.7%	0.873	72.8%	1.705	71.4%
k = 8, R = ($2_{\left(7\right)}$)	0.885	97.9%	0.835	68.2%	1.524	68.8%
k = 8, R = (3, 2, $2_{\left(5\right)}$)	0.923	98.6%	0.913	74.0%	1.837	75.7%
k = 8, R = (5, 4, $1_{\left(5\right)}$)	0.954	97.4%	1.262	83.2%	2.670	88.1%
k = 8, R = ($2_{\left(5\right)}$, 3, 4)	0.925	98.3%	0.961	73.2%	1.898	75.0%
k = 10, R = (7, $1_{\left(8\right)}$)	0.937	96.2%	1.205	86.1%	2.746	92.6%
k = 10, R = ($2_{\left(5\right)}$, 2, $1_{\left(3\right)}$)	0.886	98.4%	0.901	79.2%	1.817	83.8%
k = 10, R = ($2_{\left(6\right)}$, $1_{\left(3\right)}$)	0.900	97.1%	0.940	82.6%	1.880	83.0%
k = 10, R = ($4_{\left(2\right)}$, $1_{\left(7\right)}$)	0.939	96.5%	1.116	86.0%	2.578	92.4%
k = 10, R = (5, 3, $1_{\left(7\right)}$)	0.943	95.8%	1.215	88.4%	2.675	93.0%
k = 10, R = ($2_{\left(7\right)}$, $1_{\left(2\right)}$)	0.937	96.7%	1.044	86.0%	2.276	87.8%

and

Table 4. CPs and ALs of 95% asymptotic confidence intervals of the model parameters with $\lambda$ = 0.5, ${\alpha }_1$ = 0.4, and ${\alpha }_2$ = 0.3 based on different CSs.

	$\widehat{\mathit{\lambda }}$		$\widehat{{\mathit{\alpha }}_1}$		$\widehat{{\mathit{\alpha }}_2}$
	AL	CP	AL	CP	AL	CP
k = 8, R = (2, $2_{\left(6\right)}$)	1.021	97.9%	0.966	81.0%	0.877	85.4%
k = 8, R = ($2_{\left(4\right)}$, 3, $2_{\left(2\right)}$)	1.029	98.0%	0.948	83.3%	0.872	85.4%
k = 8, R = ($2_{\left(7\right)}$)	1.022	98.6%	0.944	83.0%	0.849	85.5%
k = 8, R = (3, 2, $2_{\left(5\right)}$)	1.055	98.9%	0.977	86.2%	0.908	88.6%
k = 8, R = (5, 4, $1_{\left(5\right)}$)	1.107	98.5%	1.237	91.6%	1.124	91.2%
k = 8, R = ($2_{\left(5\right)}$, 3, 4)	1.040	98.2%	0.957	86.5%	0.940	86.9%
k = 10, R = (7, $1_{\left(8\right)}$)	1.082	94.9%	1.322	96.8%	1.314	96.0%
k = 10, R = ($2_{\left(5\right)}$, 2, $1_{\left(3\right)}$)	1.031	96.9%	1.071	93.0%	1.046	94.3%
k = 10, R = ($2_{\left(6\right)}$, $1_{\left(3\right)}$)	1.024	96.1%	1.014	93.6%	0.980	92.9%
k = 10, R = ($4_{\left(2\right)}$, $1_{\left(7\right)}$)	1.093	95.0%	1.235	95.3%	1.216	95.9%
k = 10, R = (5, 3, $1_{\left(7\right)}$)	1.104	94.7%	1.243	96.4%	1.239	96.8%
k = 10, R = ($2_{\left(7\right)}$, $1_{\left(2\right)}$)	1.077	95.1%	1.106	94.8%	1.148	94.6%

, we also record the average lengths (AL) of 95% asymptotic CIs and the corresponding 95% coverage percentages (CP) of all parameters based on 1000 samples. In different cases of Bayesian estimation, when the order-restricted condition between two shape parameters is discussed, the average values of the Bayesian estimates (BE) and corresponding MSEs both for the NIP and IP are recorded in

Table 5. MSEs and BEs of the Bayesian estimates of the model parameters with $\lambda$ = 0.5, ${\alpha }_1$ = 0.4, and ${\alpha }_2$ = 0.3 based on the importance sampling procedure and different CSs.

		Without Order Restriction				With Order Restriction
		IP		NIP		IP		NIP
Censoring Scheme	Parameter	BE	MSE	BE	MSE	BE	MSE	BE	MSE
k = 8, R = (2, $2_{\left(6\right)}$)	$\lambda$	0.575	0.045	0.485	0.034	0.565	0.039	0.533	0.043
	${\alpha }_1$	0.370	0.023	0.374	0.050	0.337	0.022	0.311	0.040
	${\alpha }_2$	0.289	0.018	0.302	0.053	0.265	0.019	0.277	0.036
k = 8, R = ($2_{\left(4\right)}$, 3, $2_{\left(2\right)}$)	$\lambda$	0.580	0.047	0.494	0.040	0.594	0.044	0.541	0.038
	${\alpha }_1$	0.378	0.027	0.387	0.056	0.356	0.023	0.324	0.043
	${\alpha }_2$	0.298	0.019	0.300	0.059	0.286	0.018	0.279	0.042
k = 8, R = ($2_{\left(7\right)}$)	$\lambda$	0.576	0.044	0.494	0.039	0.595	0.049	0.530	0.045
	${\alpha }_1$	0.386	0.024	0.377	0.054	0.349	0.027	0.324	0.046
	${\alpha }_2$	0.303	0.020	0.313	0.056	0.286	0.018	0.276	0.036
k = 8, R = (3, 2, $2_{\left(5\right)}$)	$\lambda$	0.565	0.045	0.518	0.040	0.617	0.056	0.536	0.037
	${\alpha }_1$	0.377	0.030	0.410	0.104	0.365	0.020	0.355	0.043
	${\alpha }_2$	0.290	0.020	0.318	0.051	0.280	0.016	0.283	0.036
k = 8, R = (5, 4, $1_{\left(5\right)}$)	$\lambda$	0.631	0.071	0.539	0.038	0.653	0.070	0.604	0.058
	${\alpha }_1$	0.417	0.027	0.433	0.065	0.407	0.029	0.424	0.077
	${\alpha }_2$	0.337	0.029	0.339	0.084	0.305	0.016	0.347	0.065
k = 8, R = ($2_{\left(5\right)}$, 3, 4)	$\lambda$	0.576	0.058	0.518	0.037	0.600	0.053	0.534	0.039
	${\alpha }_1$	0.389	0.023	0.368	0.048	0.354	0.022	0.337	0.041
	${\alpha }_2$	0.306	0.024	0.333	0.071	0.299	0.024	0.290	0.052
k = 10, R = (7, $1_{\left(8\right)}$)	$\lambda$	0.666	0.071	0.673	0.085	0.699	0.084	0.722	0.106
	${\alpha }_1$	0.487	0.035	0.559	0.116	0.467	0.030	0.527	0.087
	${\alpha }_2$	0.403	0.044	0.370	0.071	0.385	0.033	0.452	0.118
k = 10, R = ($2_{\left(5\right)}$, 2, $1_{\left(3\right)}$)	$\lambda$	0.641	0.056	0.629	0.064	0.658	0.064	0.642	0.072
	${\alpha }_1$	0.419	0.022	0.466	0.068	0.408	0.021	0.397	0.033
	${\alpha }_2$	0.337	0.018	0.370	0.071	0.320	0.018	0.362	0.086
k = 10, R = ($2_{\left(6\right)}$, $1_{\left(3\right)}$)	$\lambda$	0.649	0.069	0.597	0.053	0.662	0.072	0.648	0.073
	${\alpha }_1$	0.443	0.028	0.452	0.062	0.413	0.026	0.432	0.060
	${\alpha }_2$	0.345	0.024	0.409	0.096	0.332	0.025	0.386	0.061
k = 10, R = ($4_{\left(2\right)}$, $1_{\left(7\right)}$)	$\lambda$	0.683	0.075	0.669	0.083	0.680	0.072	0.707	0.098
	${\alpha }_1$	0.472	0.047	0.492	0.084	0.449	0.026	0.507	0.086
	${\alpha }_2$	0.372	0.387	0.427	0.095	0.354	0.026	0.431	0.088
k = 10, R = (5, 3, $1_{\left(7\right)}$)	$\lambda$	0.705	0.096	0.688	0.096	0.679	0.096	0.710	0.102
	${\alpha }_1$	0.465	0.037	0.567	0.131	0.455	0.032	0.489	0.099
	${\alpha }_2$	0.387	0.038	0.450	0.129	0.377	0.032	0.452	0.127
k = 10, R = ($2_{\left(7\right)}$, $1_{\left(2\right)}$)	$\lambda$	0.674	0.082	0.629	0.064	0.670	0.070	0.674	0.090
	${\alpha }_1$	0.457	0.036	0.501	0.084	0.416	0.019	0.469	0.067
	${\alpha }_2$	0.369	0.034	0.415	0.091	0.353	0.021	0.408	0.102

and

Table 6. MSEs and BEs of the Bayesian estimates of the model parameters with $\lambda$ = 0.5, ${\alpha }_1$ = 0.4, and ${\alpha }_2$ = 0.8 based on the importance sampling procedure and different CSs.

		Without Order Restriction				With Order Restriction
		IP		NIP		IP		NIP
Censoring Scheme	Parameter	BE	MSE	BE	MSE	BE	MSE	BE	MSE
k = 8, R = (2, $2_{\left(6\right)}$)	$\lambda$	0.480	0.026	0.437	0.028	0.527	0.027	0.464	0.025
	${\alpha }_1$	0.322	0.059	0.253	0.078	0.275	0.044	0.253	0.056
	${\alpha }_2$	0.604	0.122	0.571	0.222	0.543	0.118	0.428	0.201
k = 8, R = ($2_{\left(4\right)}$, 3, $2_{\left(2\right)}$)	$\lambda$	0.500	0.021	0.433	0.028	0.525	0.021	0.471	0.021
	${\alpha }_1$	0.324	0.054	0.235	0.059	0.305	0.039	0.263	0.068
	${\alpha }_2$	0.646	0.145	0.588	0.137	0.579	0.117	0.507	0.185
k = 8, R = ($2_{\left(7\right)}$)	$\lambda$	0.503	0.025	0.413	0.032	0.520	0.030	0.455	0.024
	${\alpha }_1$	0.320	0.049	0.257	0.081	0.283	0.040	0.232	0.070
	${\alpha }_2$	0.640	0.127	0.524	0.193	0.573	0.191	0.461	0.199
k = 8, R = (3, 2, $2_{\left(5\right)}$)	$\lambda$	0.513	0.027	0.446	0.023	0.525	0.020	0.490	0.030
	${\alpha }_1$	0.310	0.052	0.243	0.065	0.291	0.038	0.290	0.078
	${\alpha }_2$	0.643	0.123	0.615	0.195	0.579	0.117	0.550	0.352
k = 8, R = (5, 4, $1_{\left(5\right)}$)	$\lambda$	0.548	0.029	0.487	0.025	0.565	0.029	0.531	0.032
	${\alpha }_1$	0.342	0.050	0.277	0.098	0.325	0.046	0.298	0.069
	${\alpha }_2$	0.791	0.166	0.829	0.399	0.697	0.089	0.665	0.205
k = 8, R = ($2_{\left(5\right)}$, 3, 4)	$\lambda$	0.506	0.027	0.452	0.027	0.537	0.025	0.475	0.026
	${\alpha }_1$	0.331	0.052	0.262	0.072	0.275	0.042	0.254	0.061
	${\alpha }_2$	0.641	0.134	0.615	0.175	0.591	0.099	0.529	0.198
k = 10, R = (7, $1_{\left(8\right)}$)	$\lambda$	0.604	0.036	0.554	0.030	0.613	0.042	0.566	0.029
	${\alpha }_1$	0.428	0.078	0.353	0.101	0.400	0.047	0.356	0.064
	${\alpha }_2$	0.903	0.139	0.937	0.323	0.832	0.086	0.768	0.151
k = 10, R = ($2_{\left(5\right)}$, 2, $1_{\left(3\right)}$)	$\lambda$	0.582	0.038	0.521	0.024	0.570	0.032	0.549	0.025
	${\alpha }_1$	0.371	0.047	0.310	0.061	0.344	0.032	0.330	0.050
	${\alpha }_2$	0.755	0.101	0.711	0.157	0.628	0.088	0.611	0.145
k = 10, R = ($2_{\left(6\right)}$, $1_{\left(3\right)}$)	$\lambda$	0.583	0.036	0.536	0.030	0.598	0.036	0.551	0.032
	${\alpha }_1$	0.331	0.039	0.324	0.063	0.339	0.037	0.308	0.050
	${\alpha }_2$	0.777	0.121	0.725	0.186	0.653	0.082	0.621	0.162
k = 10, R = ($4_{\left(2\right)}$, $1_{\left(7\right)}$)	$\lambda$	0.626	0.045	0.585	0.038	0.605	0.037	0.589	0.039
	${\alpha }_1$	0.398	0.060	0.352	0.079	0.385	0.042	0.366	0.062
	${\alpha }_2$	0.916	0.202	0.951	0.351	0.777	0.092	0.792	0.206
k = 10, R = (5, 3, $1_{\left(7\right)}$)	$\lambda$	0.595	0.031	0.569	0.033	0.630	0.050	0.600	0.046
	${\alpha }_1$	0.388	0.047	0.337	0.073	0.388	0.045	0.353	0.053
	${\alpha }_2$	0.873	0.168	0.890	0.241	0.803	0.101	0.804	0.188
k = 10, R = ($2_{\left(7\right)}$, $1_{\left(2\right)}$)	$\lambda$	0.582	0.032	0.556	0.031	0.602	0.035	0.595	0.046
	${\alpha }_1$	0.369	0.040	0.343	0.074	0.363	0.044	0.348	0.068
	${\alpha }_2$	0.767	0.112	0.794	0.178	0.709	0.084	0.696	0.169

, and the above processes are repeated 1000 times. According to the importance sampling procedure,

Table 7. CPs and ALs of 95% HPD credible interval of the model parameters with $\lambda$ = 0.5, ${\alpha }_1$ = 0.4, and ${\alpha }_2$ = 0.8 based on different CSs.

		Without Order Restriction				With Order Restriction
		IP		NIP		IP		NIP
Censoring Scheme	Parameter	AL	CP	AL	CP	AL	CP	AL	CP
k = 8, R = (2, $2_{\left(6\right)}$)	$\lambda$	0.382	77.6%	0.370	70.0%	0.453	88.6%	0.448	80.1%
	${\alpha }_1$	0.437	61.6%	0.351	42.8%	0.483	68.7%	0.435	56.7%
	${\alpha }_2$	0.806	65.3%	0.802	61.0%	0.771	57.9%	0.750	52.0%
k = 8, R = ($2_{\left(4\right)}$, 3, $2_{\left(2\right)}$)	$\lambda$	0.394	76.9%	0.345	63.0%	0.469	90.3%	0.470	85.1%
	${\alpha }_1$	0.445	62.4%	0.373	46.4%	0.493	67.4%	0.470	62.7%
	${\alpha }_2$	0.785	61.0%	0.726	52.2%	0.846	67.1%	0.862	61.6%
k = 8, R = ($2_{\left(7\right)}$)	$\lambda$	0.361	74.2%	0.358	62.3%	0.477	91.2%	0.448	76.8%
	${\alpha }_1$	0.415	54.6%	0.363	45.0%	0.496	70.3%	0.433	57.9%
	${\alpha }_2$	0.712	58.4%	0.782	59.2%	0.790	64.3%	0.781	56.5%
k = 8, R = (3, 2, $2_{\left(5\right)}$)	$\lambda$	0.401	80.2%	0.394	74.1%	0.478	87.7%	0.484	84.3%
	${\alpha }_1$	0.465	60.8%	0.364	44.6%	0.524	73.0%	0.509	61.7%
	${\alpha }_2$	0.861	70.0%	0.873	63.3%	0.836	65.3%	0.858	60.2%
k = 8, R = (5, 4, $1_{\left(5\right)}$)	$\lambda$	0.434	84.5%	0.429	80.0%	0.509	92.3%	0.489	88.2%
	${\alpha }_1$	0.521	73.6%	0.492	53.9%	0.608	75.5%	0.606	71.5%
	${\alpha }_2$	1.025	81.4%	1.143	71.5%	0.995	85.2%	1.048	72.3%
k = 8, R = ($2_{\left(5\right)}$, 3, 4)	$\lambda$	0.397	80.4%	0.373	71.1%	0.468	86.2%	0.475	82.2%
	${\alpha }_1$	0.464	67.7%	0.394	48.8%	0.521	71.5%	0.513	65.2%
	${\alpha }_2$	0.878	70.0%	0.831	59.8%	0.815	66.1%	0.913	61.1%
k = 10, R = (7, $1_{\left(8\right)}$)	$\lambda$	0.481	87.3%	0.465	90.3%	0.506	90.3%	0.488	86.4%
	${\alpha }_1$	0.663	84.0%	0.605	69.5%	0.652	87.6%	0.697	79.7%
	${\alpha }_2$	1.250	89.0%	1.438	86.6%	1.083	92.6%	1.180	85.3%
k = 10, R = ($2_{\left(5\right)}$, 2, $1_{\left(3\right)}$)	$\lambda$	0.463	88.6%	0.417	80.6%	0.500	88.0%	0.509	87.2%
	${\alpha }_1$	0.527	76.5%	0.454	59.9%	0.534	82.9%	0.578	69.3%
	${\alpha }_2$	0.971	79.5%	0.977	70.1%	0.886	78.6%	0.965	75.2%
k = 10, R = ($2_{\left(6\right)}$, $1_{\left(3\right)}$)	$\lambda$	0.442	89.9%	0.429	81.2%	0.489	88.6%	0.498	92.0%
	${\alpha }_1$	0.510	73.7%	0.505	60.7%	0.543	77.8%	0.546	74.7%
	${\alpha }_2$	0.928	77.4%	0.900	66.8%	0.884	82.2%	0.944	77.4%
k = 10, R = ($4_{\left(2\right)}$, $1_{\left(7\right)}$)	$\lambda$	0.475	87.3%	0.463	86.9%	0.505	95.0%	0.514	90.1%
	${\alpha }_1$	0.618	78.6%	0.618	67.8%	0.606	84.6%	0.696	79.5%
	${\alpha }_2$	1.186	88.0%	1.318	81.9%	0.986	89.3%	1.154	83.7%
k = 10, R = (5, 3, $1_{\left(7\right)}$)	$\lambda$	0.472	89.0%	0.457	88.1%	0.490	89.0%	0.515	92.0%
	${\alpha }_1$	0.578	83.6%	0.576	71.5%	0.619	81.6%	0.632	78.5%
	${\alpha }_2$	1.149	86.0%	1.398	85.4%	1.009	84.9%	1.137	86.5%
k = 10, R = ($2_{\left(7\right)}$, $1_{\left(2\right)}$)	$\lambda$	0.463	88.6%	0.443	82.2%	0.502	89.3%	0.511	91.0%
	${\alpha }_1$	0.535	79.1%	0.526	67.4%	0.601	84.9%	0.603	74.3%
	${\alpha }_2$	0.980	80.5%	1.138	76.5%	0.941	80.9%	1.013	76.7%

and

Table 8. CPs and ALs of 95% HPD credible interval of the model parameters with $\lambda$ = 0.5, ${\alpha }_1$ = 0.4, and ${\alpha }_2$ = 0.3 based on different CSs.

		Without Order Restriction				With Order Restriction
		IP		NIP		IP		NIP
Censoring Scheme	Parameter	AL	CP	AL	CP	AL	CP	AL	CP
k = 8, R = (2, $2_{\left(6\right)}$)	$\lambda$	0.493	78.3%	0.397	69.7%	0.623	90.7%	0.545	87.9%
	${\alpha }_1$	0.470	78.3%	0.458	66.2%	0.515	87.7%	0.543	72.1%
	${\alpha }_2$	0.414	80.7%	0.397	65.5%	0.450	86.3%	0.507	78.3%
k = 8, R = ($2_{\left(4\right)}$, 3, $2_{\left(2\right)}$)	$\lambda$	0.503	82.2%	0.406	71.5%	0.611	89.6%	0.567	85.6%
	${\alpha }_1$	0.467	84.6%	0.465	64.9%	0.520	86.6%	0.566	77.5%
	${\alpha }_2$	0.413	81.9%	0.407	64.9%	0.467	90.0%	0.501	78.2%
k = 8, R = ($2_{\left(7\right)}$)	$\lambda$	0.500	84.2%	0.394	70.8%	0.621	90.3%	0.557	86.2%
	${\alpha }_1$	0.474	84.5%	0.433	72.2%	0.517	86.3%	0.520	77.3%
	${\alpha }_2$	0.411	85.2%	0.392	65.6%	0.450	85.3%	0.459	70.9%
k = 8, R = (3, 2, $2_{\left(5\right)}$)	$\lambda$	0.541	84.9%	0.459	75.4%	0.654	92.0%	0.572	90.5%
	${\alpha }_1$	0.515	83.2%	0.542	72.7%	0.569	87.3%	0.561	77.5%
	${\alpha }_2$	0.442	85.3%	0.449	68.7%	0.472	90.3%	0.512	79.6%
k = 8, R = (5, 4, $1_{\left(5\right)}$)	$\lambda$	0.583	89.0%	0.513	76.0%	0.687	93.0%	0.635	91.2%
	${\alpha }_1$	0.574	92.0%	0.659	77.0%	0.594	92.0%	0.693	82.5%
	${\alpha }_2$	0.489	90.7%	0.564	66.9%	0.555	92.0%	0.660	89.5%
k = 8, R = ($2_{\left(5\right)}$, 3, 4)	$\lambda$	0.583	85.7%	0.417	75.6%	0.614	90.6%	0.578	87.1%
	${\alpha }_1$	0.500	85.3%	0.472	71.8%	0.539	87.3%	0.578	80.0%
	${\alpha }_2$	0.455	84.0%	0.456	69.3%	0.482	88.6%	0.546	80.7%
k = 10, R = (7, $1_{\left(8\right)}$)	$\lambda$	0.666	86.7%	0.575	78.3%	0.718	84.3%	0.652	80.8%
	${\alpha }_1$	0.647	92.3%	0.797	86.3%	0.698	96.7%	0.826	89.9%
	${\alpha }_2$	0.605	93.0%	0.758	79.0%	0.633	94.0%	0.808	84.2%
k = 10, R = ($2_{\left(5\right)}$, 2, $1_{\left(3\right)}$)	$\lambda$	0.566	83.6%	0.527	81.5%	0.660	91.3%	0.623	87.6%
	${\alpha }_1$	0.537	93.3%	0.605	81.5%	0.580	94.0%	0.663	87.0%
	${\alpha }_2$	0.490	93.3%	0.563	74.0%	0.539	96.3%	0.612	89.3%
k = 10, R = ($2_{\left(6\right)}$, $1_{\left(3\right)}$)	$\lambda$	0.576	81.3%	0.500	80.0%	0.676	86.7%	0.635	86.2%
	${\alpha }_1$	0.521	90.0%	0.614	79.3%	0.577	97.0%	0.661	88.2%
	${\alpha }_2$	0.494	89.0%	0.569	72.3%	0.523	93.7%	0.650	87.6%
k = 10, R = ($4_{\left(2\right)}$, $1_{\left(7\right)}$)	$\lambda$	0.645	85.3%	0.547	79.9%	0.716	86.7%	0.683	81.8%
	${\alpha }_1$	0.611	95.0%	0.711	84.3%	0.665	96.7%	0.767	89.9%
	${\alpha }_2$	0.583	90.0%	0.671	74.6%	0.607	95.3%	0.735	87.5%
k = 10, R = (5, 3, $1_{\left(7\right)}$)	$\lambda$	0.642	80.7%	0.556	80.8%	0.714	88.0%	0.682	81.5%
	${\alpha }_1$	0.653	93.7%	0.698	83.8%	0.660	97.7%	0.736	91.6%
	${\alpha }_2$	0.573	91.0%	0.629	82.1%	0.619	94.3%	0.728	89.9%
k = 10, R = ($2_{\left(7\right)}$, $1_{\left(2\right)}$)	$\lambda$	0.581	85.6%	0.513	80.4%	0.666	89.0%	0.648	83.1%
	${\alpha }_1$	0.563	91.9%	0.628	84.5%	0.584	94.3%	0.699	87.5%
	${\alpha }_2$	0.523	90.6%	0.627	73.3%	0.563	94.0%	0.705	88.1%

present the ALs and CPs of 95% HPD credible intervals, and the value of M in the importance sampling procedure is 1000.

From Table 1 and Table 5, it is observed that the MSEs and standard error of all parameters increase with the increase in effective sample size k. Compared with MLEs, the performance of the Bayesian estimators is better concerning MSEs. Here, in terms of MSEs, the Bayesian estimators also perform better for IP than NIP, as expected. However, when the order restriction is discussed between two shape parameters, the Bayesian estimation of ${\alpha }_1$ and ${\alpha }_2$ under order restriction is slightly better.

From Table 3 and Table 8, we also observe that the average lengths of 95% asymptotic CIs are longer than those of the 95% HPD credible intervals in most cases. Furthermore, with respect to coverage percentage, the performance of the HPD credible intervals is better for IP than NIP, and the above two HPD credible intervals with order restriction perform better than that without order restriction.

Therefore, by comparing the Bayesian estimators and MLEs, we observe that the performance of the Bayesian estimators concerning NIP is better than that of MLEs. Therefore, when there is no prior information imposed on all parameters and the order-restricted condition is considered for different shape parameters, we recommend employing the Bayesian estimators with NIP in this case and obtaining the corresponding CIs for the NIP. Furthermore, if there is some prior knowledge of all unknown parameters, we give priority to the IP.

5.2. Real Data Analysis

In order to illustrate whether these different methods work well in practice, we consider real datasets in this section. Here, the real datasets represent the breaking strength of jute fiber and can be obtained from Ref. [9]. Dataset 1 and dataset 2 show the breaking strength of jute fiber, where the gauge lengths are 10 mm and 20 mm. These data are presented below.

$\mathbf{Dataset}\mathbf{1}$ (10 mm):

43.93, 50.16, 101.15, 123.06, 108.94, 151.48, 163.40, 141.38, 177.25, 212.13, 183.16, 257.44, 291.27, 303.90, 262.90, 353.24, 323.83, 376.42, 422.11, 506.60, 383.43, 530.55, 671.49, 590.48, 693.73, 637.66, 727.23, 700.74, 704.66, 778.17.

$\mathbf{Dataset}\mathbf{2}$ (20 mm):

36.75, 45.58, 71.46, 48.01, 99.72, 83.55, 116.99, 119.86, 113.85, 145.96, 166.49, 187.85, 200.16, 187.13, 284.64, 244.53, 350.7, 375.81, 456.6, 419.02, 578.62, 581.60, 585.57, 547.44, 594.29, 688.16, 662.66, 756.70, 707.36, 765.14.

According to [9], we divide the real data by 1000 without affecting the inference process, and fit a two-parameter GIED for each dataset. Using the Kolmogorov–Smirnov (K-S) distance between the fitted distributions and empirical distribution functions, as well as the corresponding p-values for both datasets, we illustrate the fitting results. Then, the MLEs of all parameters and the above results are recorded in

Table 9. The K-S distance and MLEs of the two datasets.

	MLEs with Complete Samples
Dataset	$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\lambda }}$	K-S Distance	p Value
Dataset 1	1.353	0.188	0.162	0.367
Dataset 2	1.841	0.293	0.141	0.536

. To check whether real datasets have equal scale parameters, supposing $H_0$: ${\lambda }_1$ = ${\lambda }_2$, the likelihood-ratio test is performed, and the associated p-value is obtained as 0.937. Therefore, we confirm the null hypothesis. Based on the assumption, the MLE of the scale parameter is computed as 0.195 and the MLEs of the shape parameters are calculated as 1.394 and 1.270 for dataset 1 and 2, respectively.

For the above datasets, we generate three balanced joint censored samples based on the three different censoring schemes. The third column of

Table 10. Three B-JPC samples from the breaking strength of jute fiber based on different CSs.

(m, n, k)	Scheme	Balanced Joint Progressive Type-II Censored Samples
(30, 30, 10)	R${}_1$ = (9, $1_{\left(8\right)}$)	36.75, 145.96, 187.13, 200.16, 284.64, 375.81, 422.11, 530.55, 585.57, 662.66
	R${}_2$ = ($2_{\left(5\right)}$, 3, $2_{\left(3\right)}$)	36.75, 48.01, 99.72, 119.86, 187.13, 244.53, 383.43, 530.55, 594.29, 704.66
	R${}_3$ = (6, 7, $1_{\left(7\right)}$)	36.75, 113.85, 244.53, 350.70, 383.43, 506.60, 581.60, 594.29, 688.16, 727.23

represents the B-JPC samples, while the second column shows various censoring schemes. We compute the Bayesian estimates and the maximum likelihood estimates of all parameters in the above three cases. For MLEs, the estimated values of unknown parameters and the corresponding 95% CIs are recorded. For Bayesian inference, owing to the lack of prior information on parameters, the non-informative prior is employed to estimate all parameters, and the corresponding 95% HPD credible intervals are also constructed. Here, they are also discussed in the case of whether the shape parameters have order restriction. In the process of the importance sampling procedure, the value of M is taken as 1000. These results are listed in

Table 11. The Bayesian estimates and MLEs of the parameters under order restriction and without order restriction with the real dataset.

Censoring Scheme	R${}_1$	R${}_2$	R${}_3$
${\widehat{{\alpha }_1}}_{ML}$	0.4743 (0.0145, 0.9341)	0.2962 (0.0126, 0.5799)	0.4613 (−0.0046, 0.9271)
${\widehat{{\alpha }_2}}_{ML}$	0.1186 (−0.0644, 0.3015)	0.1270 (−0.0360, 0.2900)	0.1977 (−0.0639, 0.4593)
${\widehat{\lambda }}_{ML}$	0.2111 (0.0429, 0.3794)	0.1389 (0.0302,0.2477)	0.2362 (0.0584, 0.4141)
${\widehat{{\alpha }_1}}_I$	0.1070 (0.0144, 0.2559)	0.1957 (0.1049, 0.4601)	0.2104 (0.1029, 0.5959)
${\widehat{{\alpha }_2}}_I$	0.1670 (0.1122, 0.3040)	0.1395 (0.1041, 0.1705)	0.2300 (0.0976, 0.2960)
${\widehat{\lambda }}_I$	0.3970 (0.2175, 0.7283)	0.7115 (0.3430, 0.9272)	0.6056 (0.3183, 0.8765)
${\widehat{{\alpha }_1}}_{II}$	0.1189 (0.0031, 0.3083)	0.1198 (0.0386, 0.2851)	0.1785 (0.0225, 0.4332)
${\widehat{{\alpha }_2}}_{II}$	0.1980 (0.0721, 0.3211)	0.1223 (0.0573, 0.1819)	0.2077 (0.0586, 0.3309)
${\widehat{\lambda }}_{II}$	0.4587 (0.1031, 0.9138)	0.2704 (0.0359, 0.4962)	0.4088 (0.1311, 0.7794)

Notes: ${\widehat{{\alpha }_1}}_I$, ${\widehat{{\alpha }_2}}_I$, and ${\widehat{\lambda }}_I$—Bayesian estimates without order restriction; ${\widehat{{\alpha }_1}}_{II}$, ${\widehat{{\alpha }_2}}_{II}$, and ${\widehat{\lambda }}_{II}$—Bayesian estimates under order restriction.

.

6. Optimum Censoring Scheme

Here, we discuss the optimal censoring schemes with given values of $\left(m,n,k\right)$. In the previous sections, the process of the interval and point estimation of all parameters based on the B-JPC samples of the GIED was discussed. Furthermore, many methods are considered to solve the problem of selecting an optimum censoring scheme (OCS), which can be found in the literature; for example, see Refs. [20,21]. Here, we use the following classical optimal criteria to obtain the OCS in the case of B-JPC schemes:

Criterion 1: Through this criterion, we obtain the minimum value of the determinant of the inverse of the observed Fisher information matrix $I^{-1}\left(\widehat{\theta }\right)$ for the maximum likelihood estimates of all parameters, where $\widehat{\theta }=\left(\widehat{\lambda },\widehat{{\alpha }_1},\widehat{{\alpha }_2}\right)$.

Criterion 2: This criterion is based on the minimization of the trace of the matrix $I^{-1}\left(\widehat{\theta }\right)$ (the definition is the same as above) of all parameters.

Criterion 3: According to this criterion, we can obtain the minimum of the greatest eigenvalue of the matrix $I^{-1}\left(\widehat{\theta }\right)$ of the MLEs of all parameters.

Criterion 4: This criterion is based on the maximization of the trace of the observed Fisher information matrix $I\left(\widehat{\theta }\right)$.

Criterion 5: This criterion is based on some specific choices of a quantile “q”. For a fixed weight $0\le \omega \le 1$, Criterion 5 is given by

$$C_5\left(q\right)=wVar\left(ln{\widehat{T}}_{q,1}\right)+(1-w)Var\left(ln{\widehat{T}}_{q,2}\right)$$

In this criterion, the qth quantile points of the two generalized inverted exponential distributions are

$$T_{q,1}=-\lambda /ln\left(1-{(1-q)}^{1/{\alpha }_1}\right), T_{q,2}=-\lambda /ln\left(1-{(1-q)}^{1/{\alpha }_2}\right)$$

Hence, the logarithmic forms of the qth quantile of the two generalized inverted exponential distributions are calculated as

$$ln{T}_{q,1}=ln\left[\frac{-\lambda }{ln\left(1-{(1-q)}^{1/{\alpha }_1}\right)}\right], ln{T}_{q,2}=ln\left[\frac{-\lambda }{ln\left(1-{(1-q)}^{1/{\alpha }_2}\right)}\right],$$

where $0<q<1$. Here, we denote ${\mathit{V}}_{\mathbf{1}}=\left(\frac{\partial ln{T}_{q,1}}{\partial \lambda },\frac{\partial ln{T}_{q,1}}{\partial {\alpha }_1}\right)$ and ${\mathit{V}}_{\mathbf{2}}=\left(\frac{\partial ln{T}_{q,2}}{\partial \lambda },\frac{\partial ln{T}_{q,2}}{\partial {\alpha }_2}\right)$, and then $Var\left(ln{\widehat{T}}_{q,1}\right)$ and $Var\left(ln{\widehat{T}}_{q,2}\right)$ can be approximated by the delta method as follows:

$$var\left(ln{T}_{q,1}\right)={\mathit{V}}_{\mathbf{1}}{\mathit{I}}^{-1}\left({\mathbf{\beta }}_{\mathbf{1}}\right){\mathit{V}}_{\mathbf{1}}^T, var\left(ln{T}_{q,2}\right)={\mathit{V}}_{\mathbf{2}}{\mathit{I}}^{-1}\left({\mathbf{\beta }}_{\mathbf{2}}\right){\mathit{V}}_{\mathbf{2}}^T.$$

For further development, $I^{-1}\left({\beta }_1\right)$ and $I^{-1}\left({\beta }_2\right)$ can be given as follows:

$$I^{-1}\left({\beta }_1\right)=\left[\begin{array}{cc}{I}_{11}& I_{12}\\ I_{21}& I_{22}\end{array}\right] \mathrm{and} I^{-1}\left({\beta }_2\right)=\left[\begin{array}{cc}{I}_{11}& I_{13}\\ I_{31}& I_{33}\end{array}\right]$$

and

$$\frac{\partial ln{T}_{q,k}}{\partial {\alpha }_k}=\frac{{\left(1-q\right)}^{\frac{1}{{\alpha }_k}}ln\left(1-q\right)}{\left(-1+{\left(1+q\right)}^{\frac{1}{{\alpha }_k}}\right){{\alpha }_k}^{2}ln\left(1-{\left(1-q\right)}^{\frac{1}{{\alpha }_k}}\right)}, \frac{\partial ln{T}_{q,k}}{\partial \lambda }=\frac{1}{\lambda }, \left(k=1,2\right).$$

Based on the criteria discussed above, we illustrate the content of the optimum censoring scheme, employing the real datasets related to gauge lengths of 10 mm and 20 mm, which are described in the previous section. For $\mathit{Criterion}\mathit{5}$, the $\omega$ and q are taken as 0.5 and 0.05. Then, the values of the greatest eigenvalue $\left(I^{-1}\left(\widehat{\theta }\right)\right)$, $trace\left(I^{-1}\left(\widehat{\theta }\right)\right)$, $det\left(I^{-1}\left(\widehat{\theta }\right)\right)$, and $trace\left(I\left(\widehat{\theta }\right)\right)$, as well as $C_5$, are recorded in

Table 12. Selection of optimum censoring scheme based on different criteria.

Censoring Scheme	Criterion 1	Criterion 2	Criterion 3	Criterion 4	Criterion 5
R${}_1$ = (9, $1_{\left(8\right)}$)	1.456742 × ${10}^{-6}$	0.07111649	0.05996095	475.8505	0.1896620
R${}_2$ = ($2_{\left(5\right)}$, 3, $2_{\left(3\right)}$)	2.072309 × 10${}^{-\mathbf{7}}$	0.02329576	0.05948553	902.4102	0.1402625
R${}_3$ = (6, 7, $1_{\left(7\right)}$)	3.260692 × ${10}^{-6}$	0.08255037	0.06397661	380.0584	0.1001845

. According to Table 12, we conclude that censoring scheme 2 is the optimal scheme in terms of criteria 1, 2, 3, and 4. Furthermore, scheme 3 is the optimal scheme for criterion 5 at $\omega$ = 0.5.

7. Conclusions

Throughout this article, the analysis of the B-JPC scheme for different populations is considered. Suppose that the lifetime distributions of the products from two different populations follow a GIED with different shape parameters but the same scale parameter. Here, the MLEs of parameters along with the corresponding 95% confidence intervals are obtained, and the existence and uniqueness of MLEs are proved. Assuming that the shape parameters jointly follow an ordered Beta-Gamma prior and the common scale parameter follows a Gamma prior, the Bayesian estimates are derived by importance sampling technique and the corresponding 95% HPD credible intervals are also constructed. The above prior assumptions are commonly used in the statistical inference process and the order restriction inference between the different shape parameters is considered.

Through a considerable amount of simulation study, we find that the performance of Bayesian estimators of the IP is significantly superior to that concerning NIP for point estimation based on the MSE and average estimate. Then, the performance of Bayesian estimators concerning NIP performs better than that of MLEs with respect to MSE and standard error. In terms of coverage percentage, the credible intervals for the IP are better than those of the NIP. However, the MLEs have longer ALs and higher CPs of CIs than those of the other two methods. It is also observed that if there is an order restriction considered for two shape parameters, we suggest employing it, because the inference result of this method is much better than that of other methods. Finally, we set some precision criteria to compare the various censoring schemes and obtain an optimum censoring scheme. In this paper, it is found in the derivation that when the order restriction of parameters is considered in the classical framework, the form of the function is complex and it is difficult to prove the existence and uniqueness of MLEs. On the contrary, the above content is easier to calculate in the Bayesian framework. Of course, all inference processes can be extended to a classical framework in future research, and there is more work to be done in that direction.