Constructal Optimizations of Liquid-Cooled Channels with Triangle or Square Sections in a Cylindrical Heating Body
Abstract
:1. Introduction
2. Mathematical and Physical Model
2.1. Geometric Model
2.2. Heat Transfer Model
3. Result Analyses
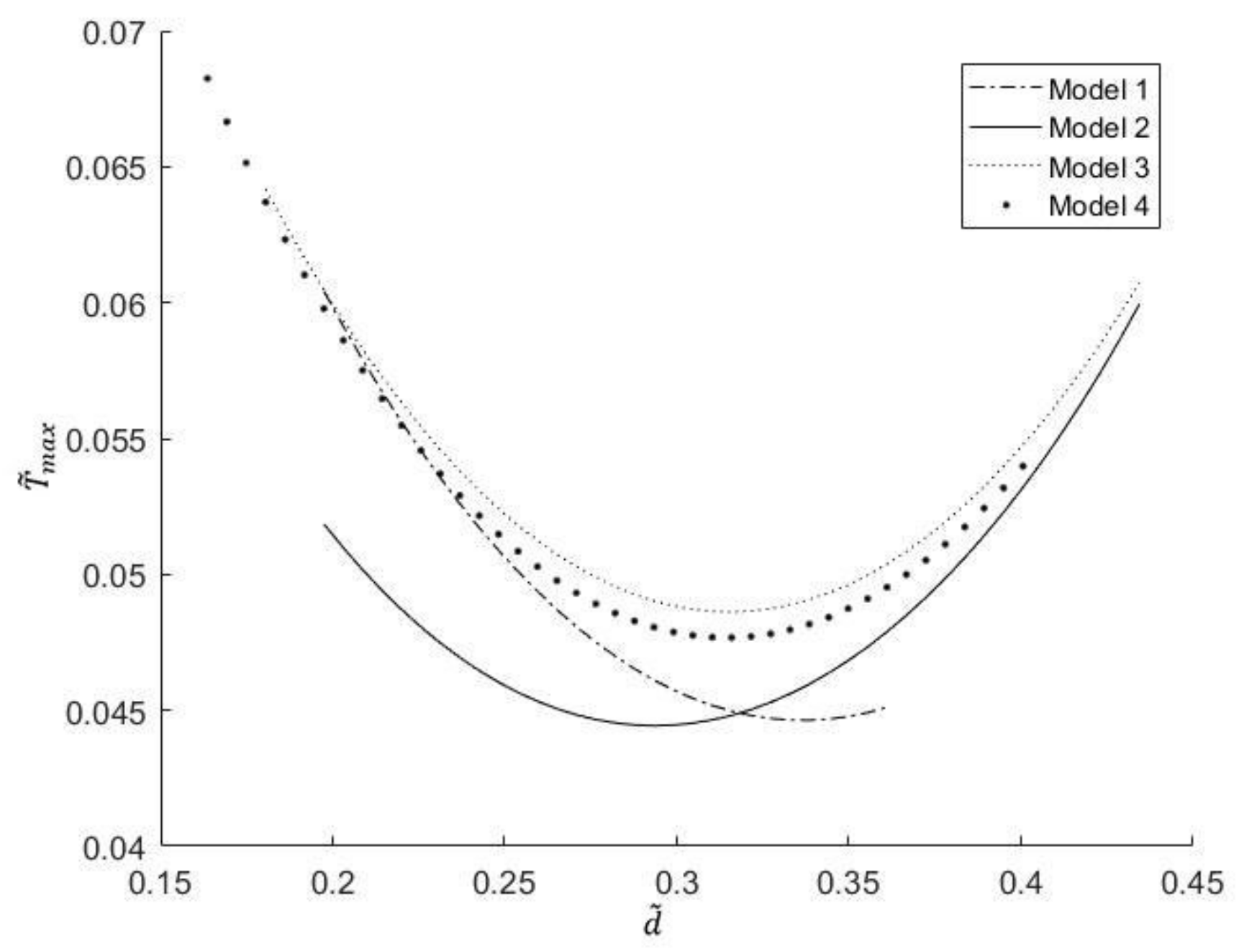
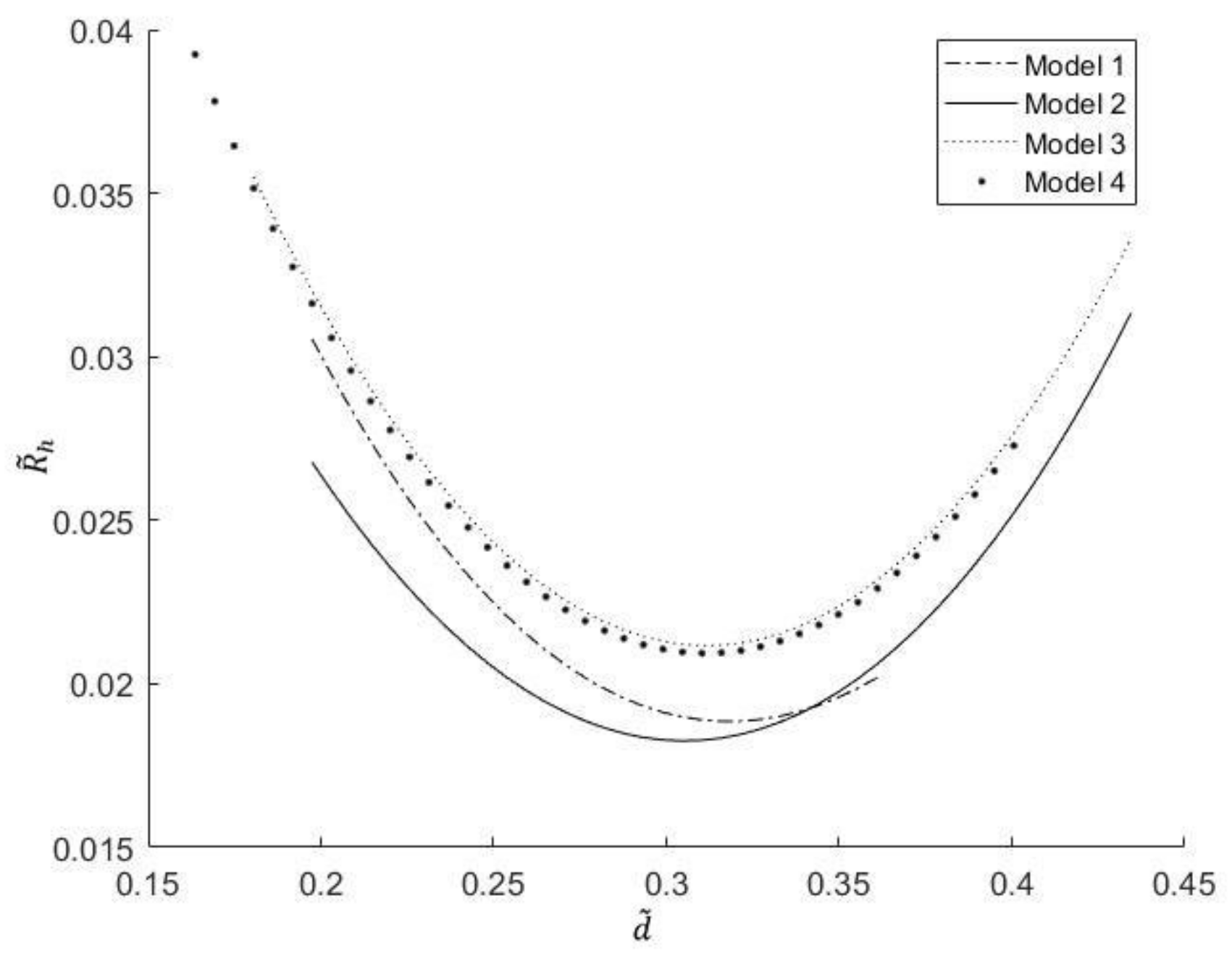
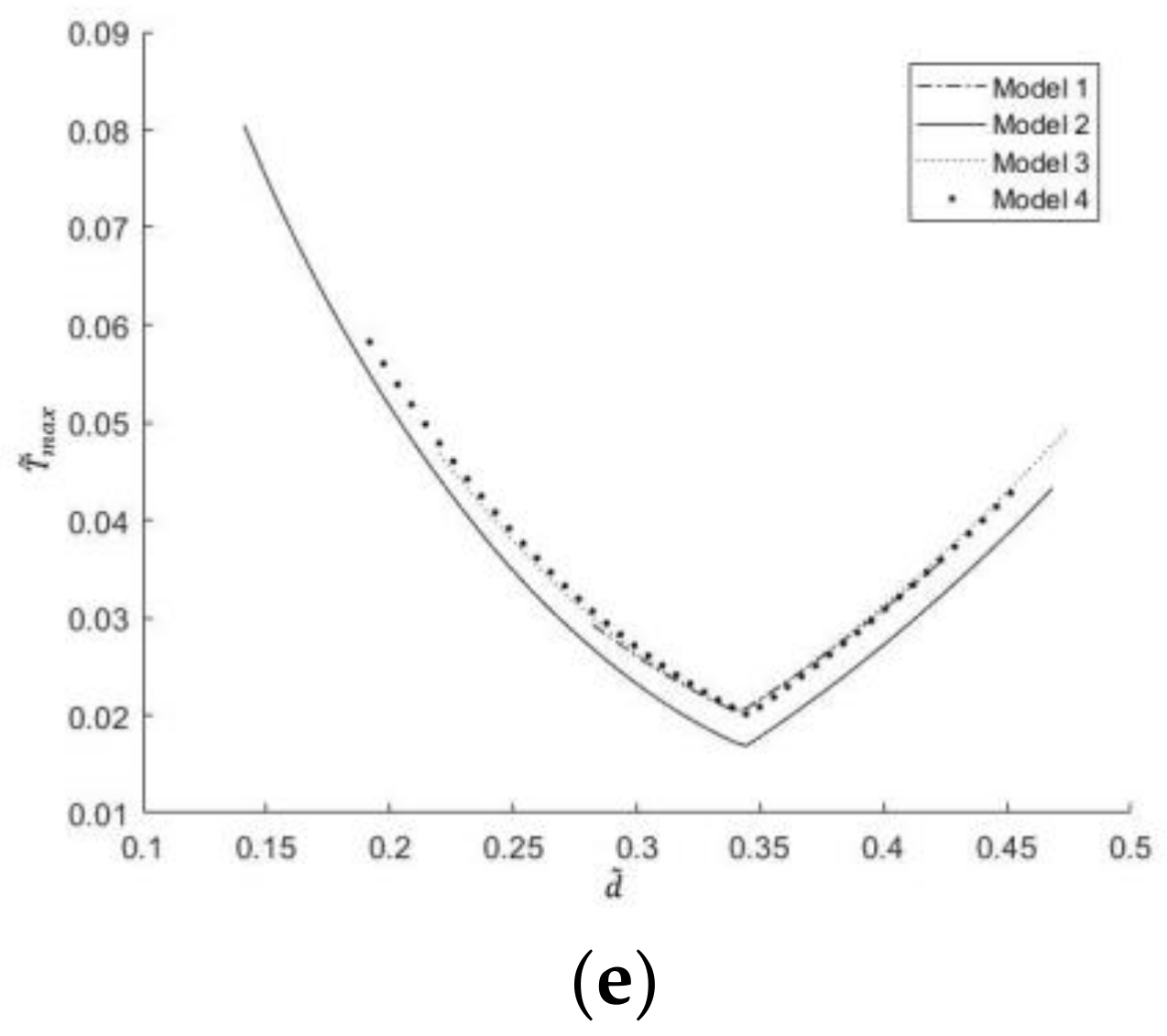
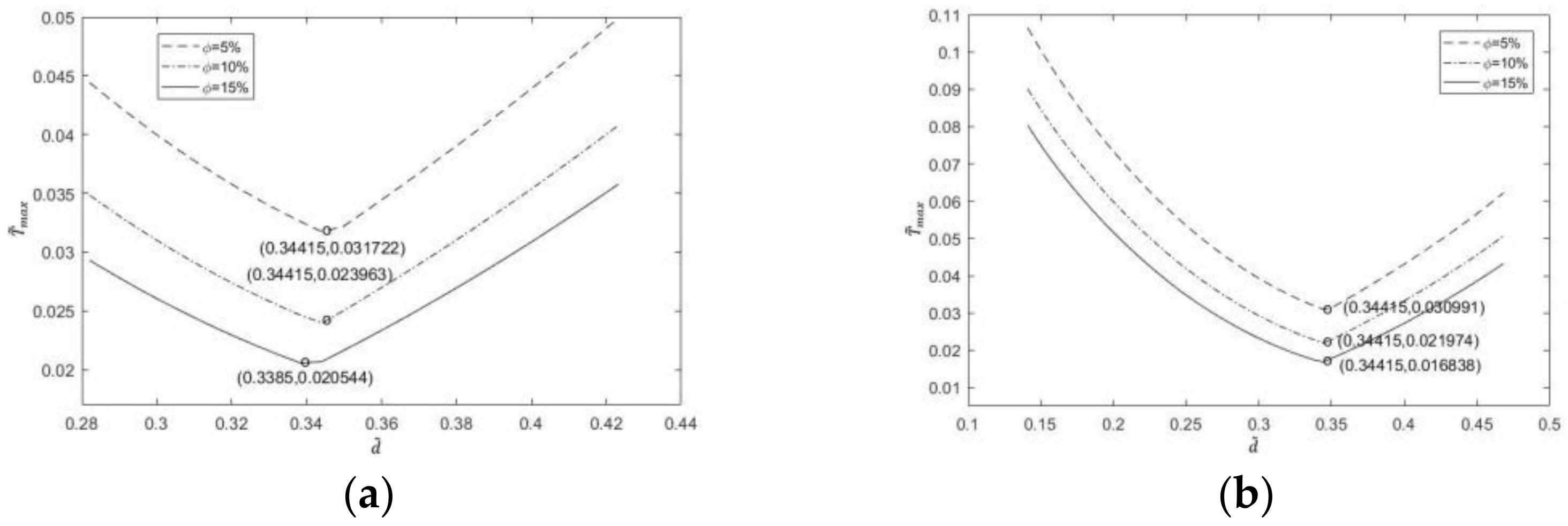
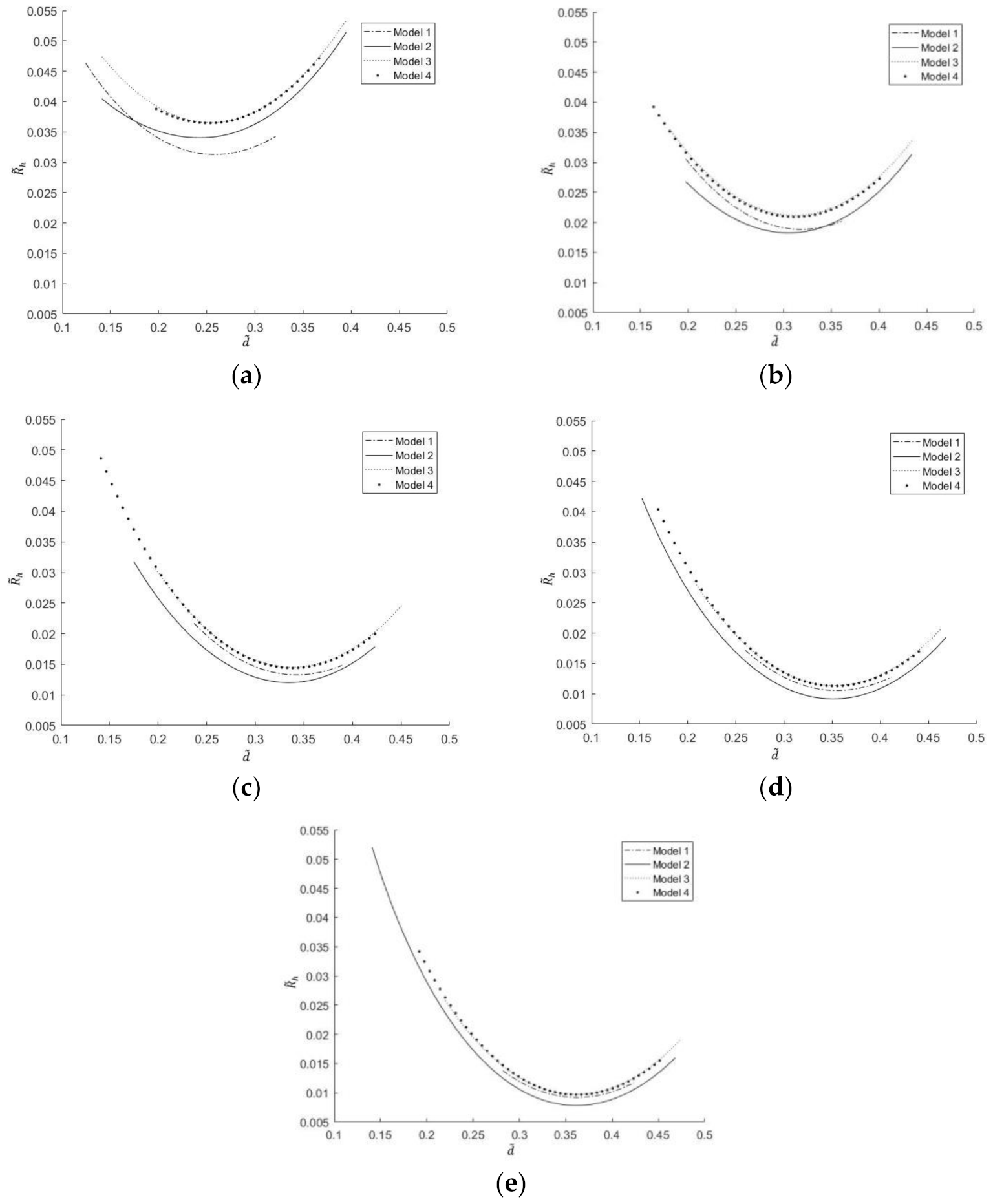
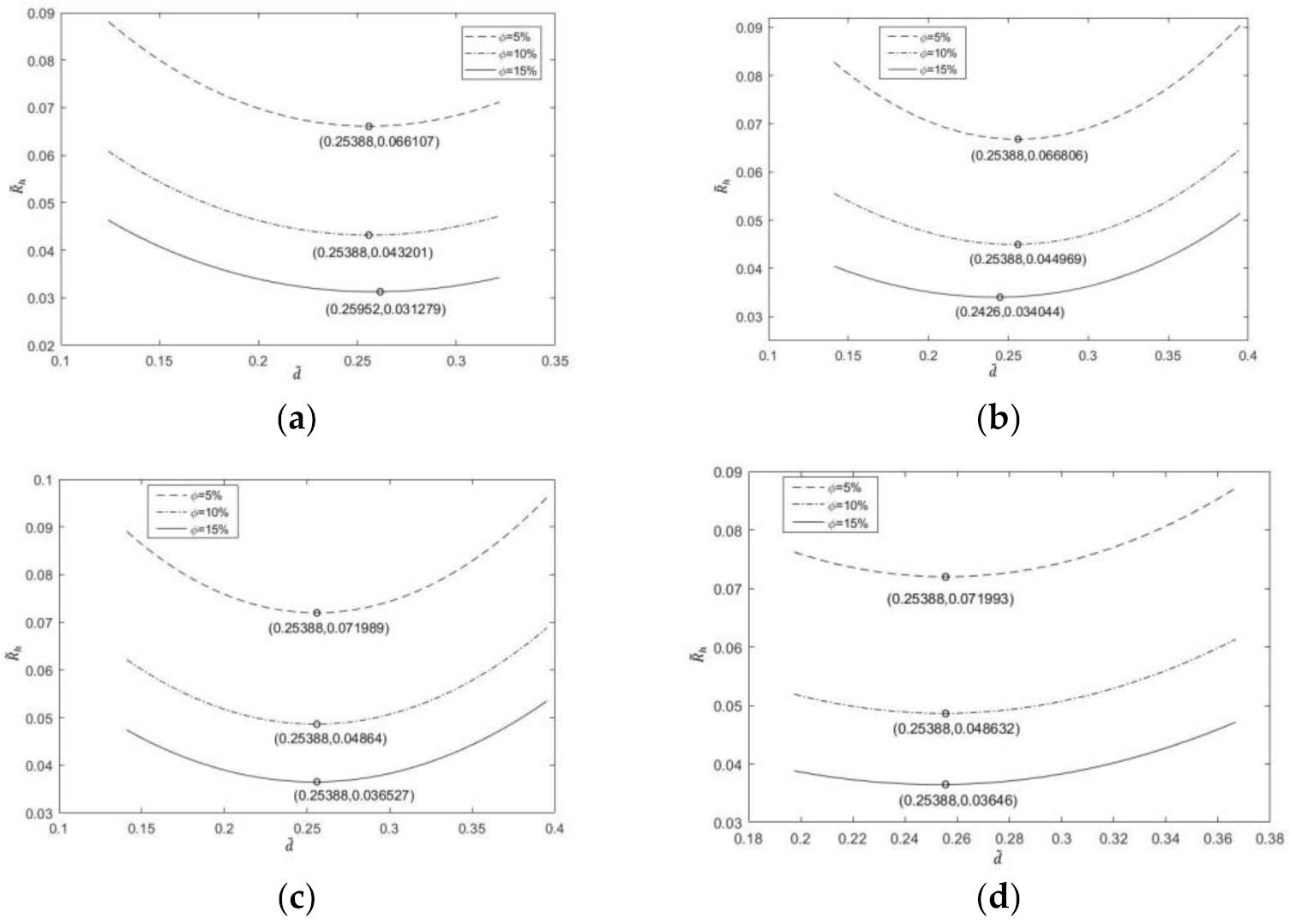
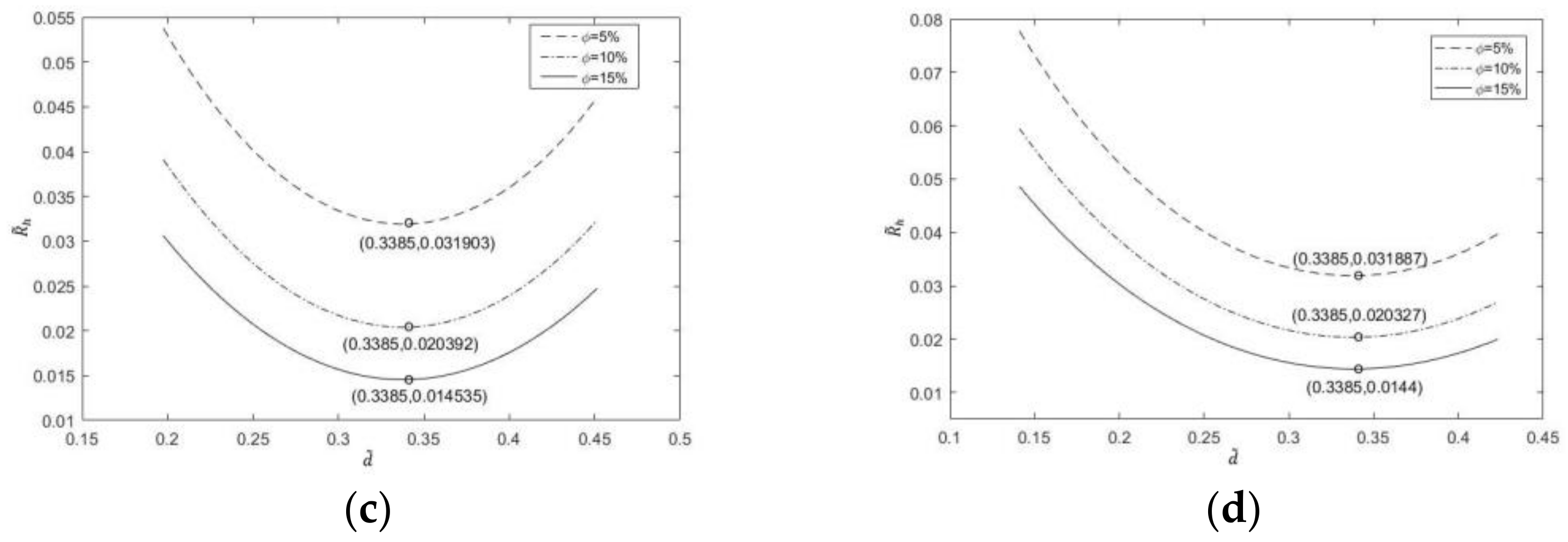
3.1. One-Time Optimization with Single Freedom Degree
- (1)
- Minimization of dimensionless maximum temperature
- (2)
- Minimization of dimensionless EETR
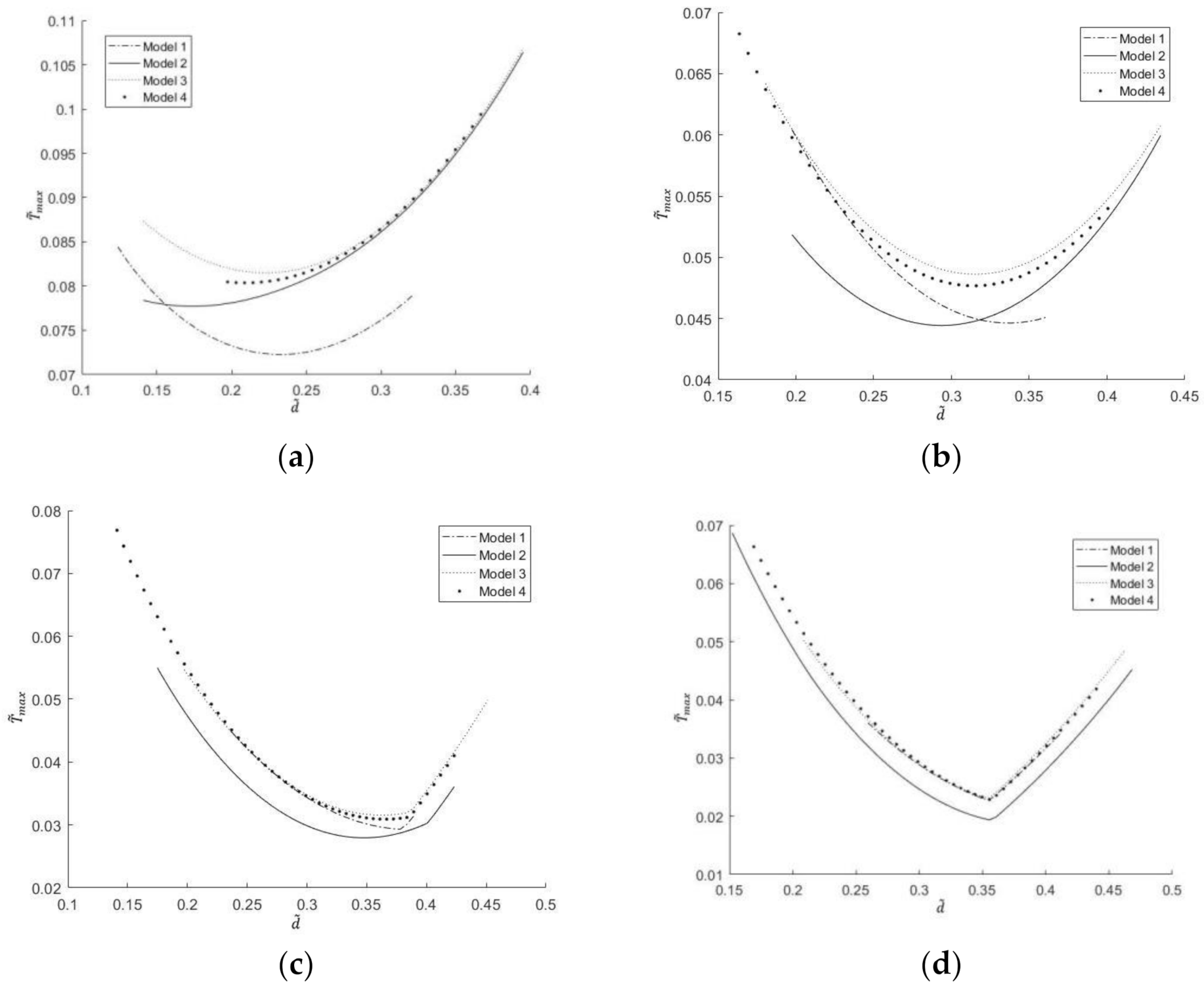
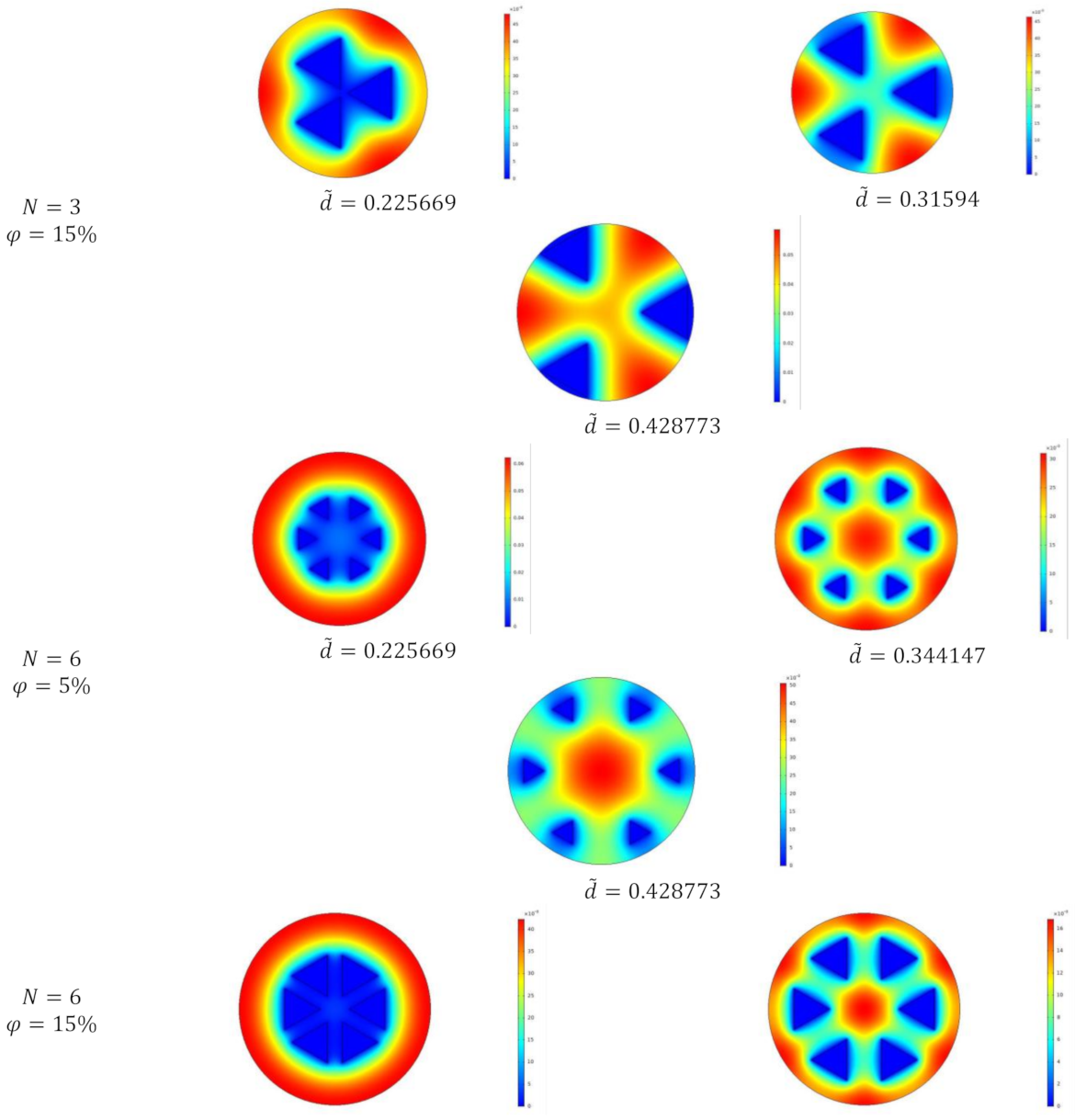
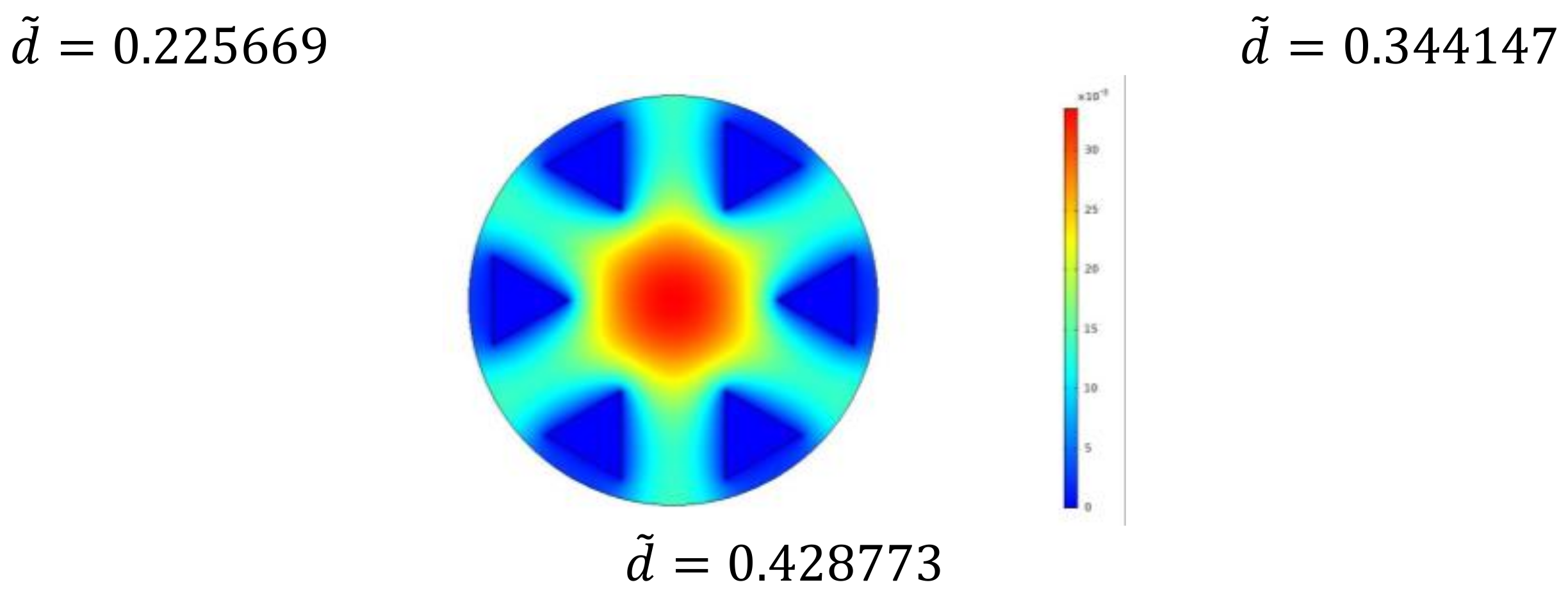
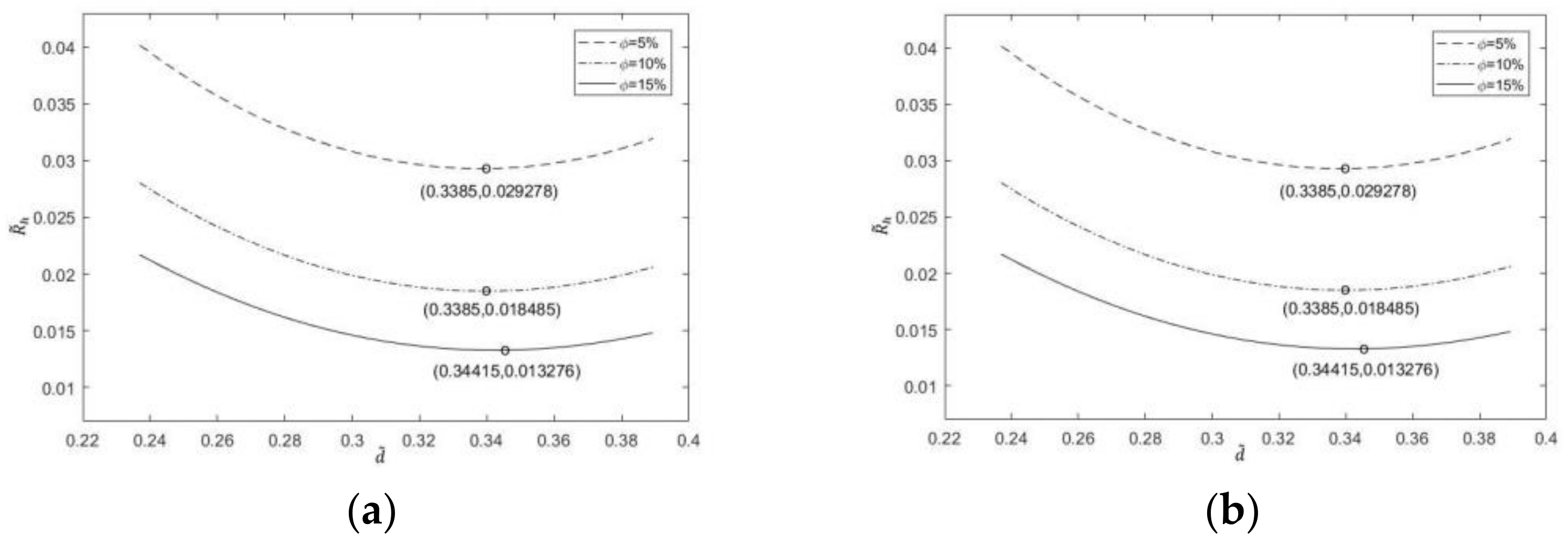
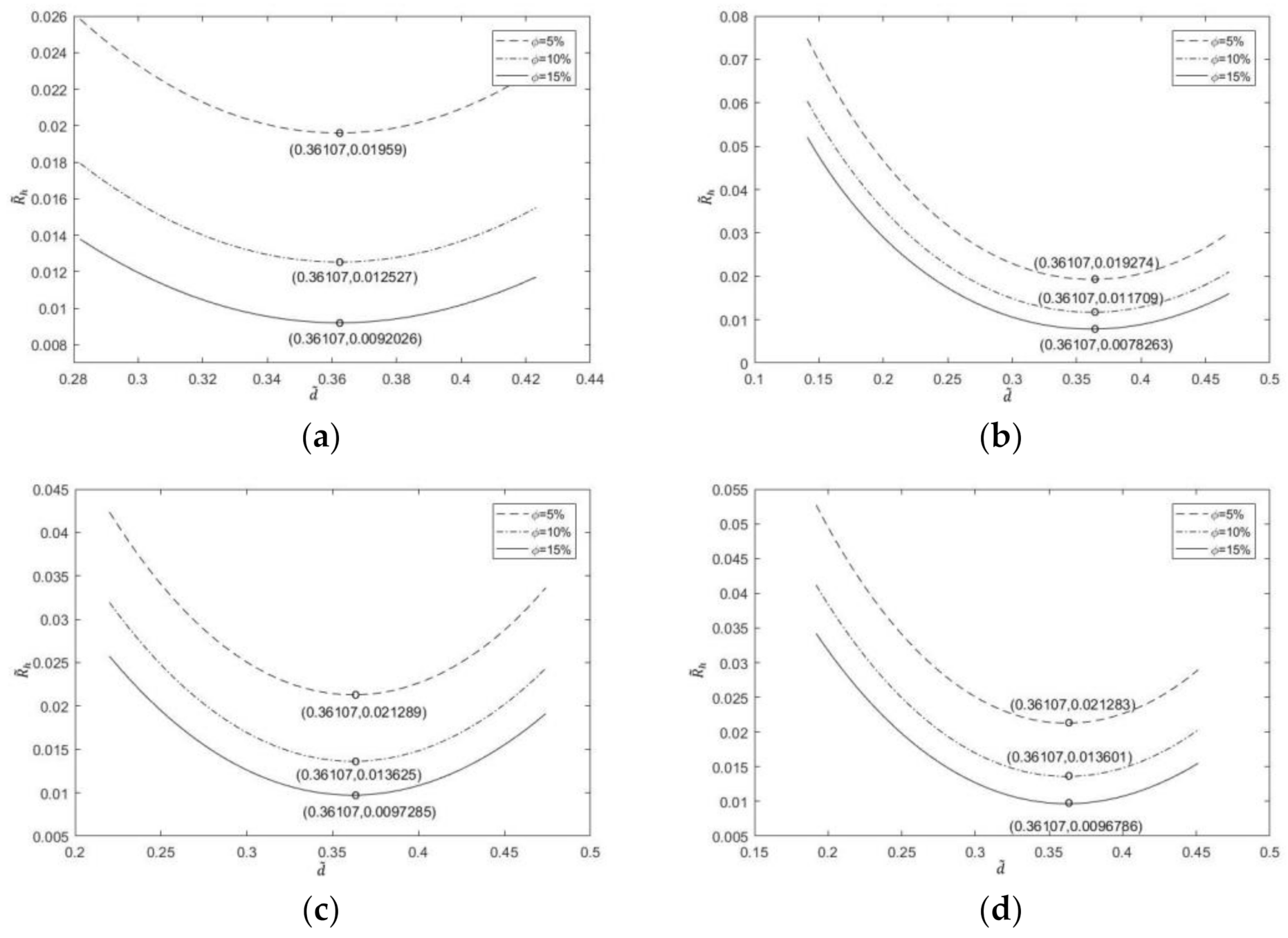
3.2. Double Optimization with Double Freedom Degree
- (1)
- Minimization of dimensionless maximum temperature
- (2)
- Minimization of dimensionless EETR
4. Conclusions
- (1)
- Corresponding to different proportions of channels, channel section and number of liquid cooling channels, the dimensionless maximum temperature and the dimensionless EETR change from monotonically decreasing to monotonically increasing with the increase in the dimensionless center distance. There are different optimal center distances of the dimensionless circle, which make the dimensionless maximum temperature and the dimensionless EETR reach the respective minima.
- (2)
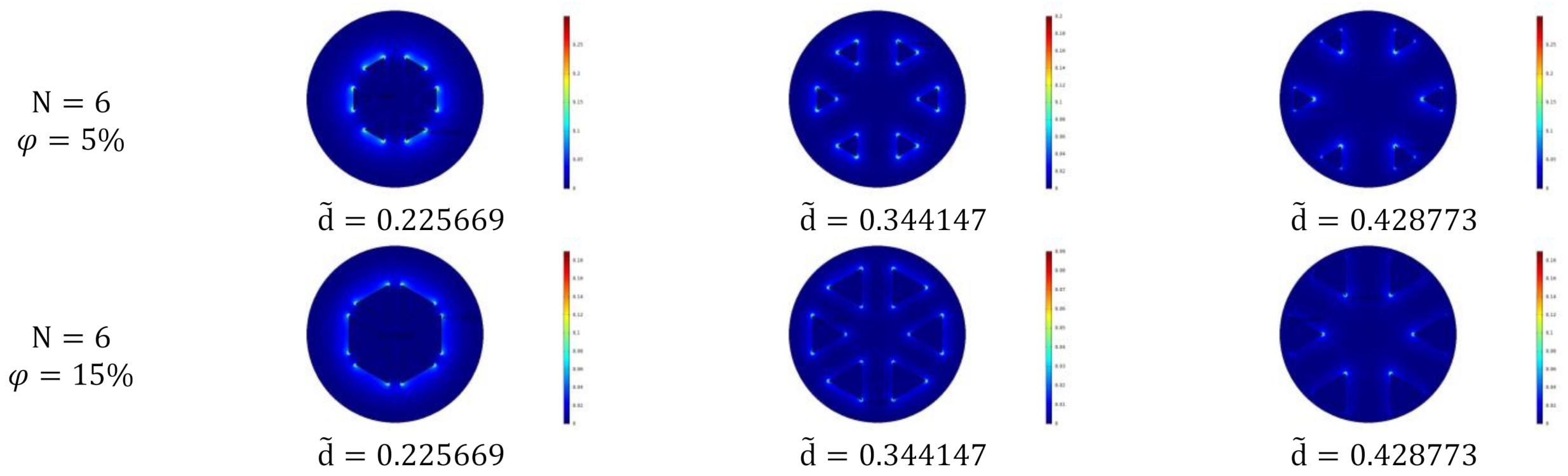
- The dimensionless maximum temperature and dimensionless EETR decrease with the increase in the number of liquid cooling channels. With the increase in the number of liquid cooling channels, the optimal dimensionless center distance of dimensionless maximum temperature first increases and then decreases, while the optimal dimensionless center distance of dimensionless EETR gradually increases.
- (3)
- The results reveal that the dimensionless maximum temperature and the dimensionless EETR decrease when the proportion of channels increases, but the optimal dimensionless center distances is almost the same for different proportions of channels.
- (4)
- For the same proportion of channels and number of liquid cooling channels, the dimensionless maximum temperature and dimensionless EETR of the triangle section liquid cooling channels are smaller than that of the square section liquid cooling channels, and with the increase in the number of liquid cooling channels, the cooling effect of model 2 (angle to angle in triangle section) is the best.
- (5)
- In engineering applications, the demands are multifaceted, including but not limited to the cost, the thermal stress, the convenience of manufacturing and operating and so on. Therefore, it is necessary to study the effects of cross-section shape of channels on the performances and far more performance indicators should be considered synthetically.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Erp, R.; Soleimanzadeh, R.; Nela, L.; Kampitsis, G.; Matioli, E. Co-Designing Electronics with Microfluidics for More Sustainable Cooling. Nature 2020, 585, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Xiao, H.; Liu, Z.C.; Liu, W. Conjugate heat transfer enhancement in the mini-channel heat sink by realizing the optimized flow pattern. Appl. Therm. Eng. 2021, 182, 116131. [Google Scholar] [CrossRef]
- Zhang, G.H.; Sundén, B.; Xie, G.N. Combined experimental and numerical investigations on heat transfer augmentation in truncated ribbed channels designed by adopting fractal theory. Int. Commun. Heat Mass Transf. 2021, 121, 105080. [Google Scholar] [CrossRef]
- Senn, S.M.; Poulikakos, D. Laminar mixing, heat transfer and pressure drop in tree-like microchannel nets and their application for thermal management in polymer electrolyte fuel cells. J. Power Sources 2004, 130, 178–191. [Google Scholar] [CrossRef]
- Abo-Zahhad, E.M.; Ookawara, S.; Radwan, A.; Elkady, M.F.; El-Shazly, A.H. Optimization of stepwise varying width microchannel heat sink for high heat flux applications. Case Stud. Therm. Eng. 2020, 18, 100587. [Google Scholar] [CrossRef]
- Ahmed, S.S.; Rageb, A.M.A. Thermal performance study of parallel and radial divergence microchannel arrangement using numerical method. Basrah J. Eng. Sci. 2020, 20, 37–43. [Google Scholar] [CrossRef]
- Yang, M.; Cao, B.Y. Multi-objective optimization of a hybrid microchannel heat sink combining manifold concept with secondary channels. Appl. Therm. Eng. 2020, 181, 1155592. [Google Scholar] [CrossRef]
- Bejan, A. Street network theory of organization in nature. J. Adv. Transp. 1996, 30, 85–107. [Google Scholar] [CrossRef]
- Bejan, A. Constructal-theory network of conducting paths for cooling a heat generating volume. Int. J. Heat Mass Transf. 1997, 40, 799–816. [Google Scholar] [CrossRef]
- Chen, L.G. Progress in study on constructal theory and its applications. Sci. China Technol. Sci. 2012, 55, 802–820. [Google Scholar] [CrossRef]
- Chen, L.G.; Feng, H.J.; Xie, Z.H.; Sun, F. Progress of constructal theory in China over the past decade. Int. J. Heat Mass Transf. 2019, 130, 393–419. [Google Scholar] [CrossRef]
- Lorente, S.; Bejan, A. Current trends in constructal law and evolutionary design. Heat Transf. Asian Res. 2019, 48, 357–389. [Google Scholar] [CrossRef]
- Bejan, A.; Gucluer, S. Morphing the design to go with the times. Int. Commun. Heat Mass Transf. 2021, 120, 104837. [Google Scholar] [CrossRef]
- Bejan, A. Heat Transfer: Evolution, Design and Performance; John Wiley & Sons: New York, NY, USA, 2022. [Google Scholar]
- Bello-Ochende, T.; Meyer, J.P. Constructal cooling channels: Application to heat transfer in micro-channel heat sinks. Int. J. Emerg. Multidiscip. Fluid Sci. 2009, 1, 61–83. [Google Scholar] [CrossRef]
- Xie, Z.H.; Chen, L.G.; Sun, F.R. Constructal entropy generation rate minimization of line-to-line vascular networks with convective heat transfer. Int. J. Therm. Sci. 2013, 74, 72–80. [Google Scholar] [CrossRef]
- Adewumi, O.O.; Bello-Ochende, T.; Meyer, J.P. Numerical investigation into the thermal performance of single microchannels with varying axial length and different shapes of micro pin-fin inserts. Heat Transf. Eng. 2017, 38, 1157–1170. [Google Scholar] [CrossRef]
- Farzaneh, M.; Salimpour, M.R.; Tavakoli, M.R. Design of bifurcating microchannels with/without loops for cooling of square-shaped electronic components. Appl. Therm. Eng. 2016, 108, 581–595. [Google Scholar] [CrossRef]
- Farzaneh, M.; Tavakoli, M.R.; Salimpour, M.R. Effect of reverting channels on heat transfer performance of microchannels with different geometries. J. Appl. Fluid Mech. 2017, 10, 41–53. [Google Scholar] [CrossRef]
- Zhang, F.Y.; Feng, H.J.; Chen, L.G.; You, J.; Xie, Z. Constructal design of an arrow-shaped high thermal conductivity channel in a square heat generation body. Entropy 2020, 22, 475. [Google Scholar] [CrossRef]
- You, J.; Feng, H.J.; Chen, L.G.; Xie, Z.; Xia, S. Constructal design and experimental validation of a non-uniform heat generating body with rectangular cross-section and parallel circular cooling channels. Int. J. Heat Mass Transf. 2020, 148, 119028. [Google Scholar] [CrossRef]
- Chen, C.; You, J.; Feng, H.J.; Chen, L. A multi-objective study on the constructal design of non-uniform heat generating disc cooled by radial- and dendritic-pattern cooling channels. Sci. China Technol. Sci. 2021, 64, 729–744. [Google Scholar] [CrossRef]
- Ahmadian-Elmi, M.; Mohammadifar, M.; Rasouli, E.; Hajmohammadi, M. Optimal design and placement of heat sink elements attached on a cylindrical heat-generating body for maximum cooling performance. Thermochim. Acta 2021, 700, 178941. [Google Scholar] [CrossRef]
- Bejan, A.; Almahmoud, H.; Gucluer, S. Evolutionary design of composite structures for thermal conductance and strength. Int. Commun. Heat Mass Transf. 2021, 125, 105293. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Zhu, H.Y.; Liang, X.G. Entransy—A physical quantity describing heat transfer ability. Int. J. Heat Mass Transf. 2007, 50, 2545–2556. [Google Scholar] [CrossRef]
- Chen, L.G. Progress in entransy theory and its applications. Chin. Sci. Bull. 2012, 57, 4404–4426. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Liu, X.H.; Tang, H.D.; Liu, J. Progress of entransy analysis on the air-conditioning system in buildings. Sci. China Technol. Sci. 2016, 59, 1463–1474. [Google Scholar] [CrossRef]
- Cheng, X.T.; Zhao, J.M.; Liang, X.G. Discussion on the extensions of the entransy theory. Sci. China Technol. Sci. 2017, 60, 363–373. [Google Scholar] [CrossRef]
- Anwar, M.K.; Sharqawy, M.H. Entransy effectiveness for analysis of heat exchangers. Glob. J. Res. Eng. 2017, 17, 49–52. [Google Scholar]
- Cheng, X.T.; Liang, X.G. Entransy functions for steady heat transfer. Sci. China Technol. Sci. 2019, 62, 1726–1734. [Google Scholar] [CrossRef]
- Zhao, T.; Liu, D.; Chen, Q. A collaborative optimization method for heat transfer systems based on the heat current method and entransy dissipation extremum principle. Appl. Therm. Eng. 2019, 146, 635–647. [Google Scholar] [CrossRef]
- Xu, S.Z.; Guo, Z.Y. Entransy transfer analysis methodology for energy conversion systems operating with thermodynamic cycles. Energy 2021, 224, 120189. [Google Scholar] [CrossRef]
- Geete, A.; Bhattacharjee, A.; Patwa, A.; Pandey, K. Entropy, exergy and entransy analyses on fabricated shell and spiral tube heat exchanger. J. Inst. Eng. India Ser. C 2021, 102, 897–908. [Google Scholar] [CrossRef]
- Xu, S.Z.; Zhao, T.; Chen, Q.; Liang, X.G.; Guo, Z.Y. State functions/quantities in thermodynamics and heat transfer. Fundam. Res. 2022, 2, 101–107. [Google Scholar] [CrossRef]
- Chen, L.G.; Feng, H.J.; Xie, Z.H. Generalized thermodynamic optimization for iron and steel production processes: A theoretical exploration and application cases. Entropy 2016, 18, 353. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.G.; Xiao, Q.H.; Feng, H.J. Constructal optimizations for heat and mass transfers based on the entransy dissipation extremum principle, performed at the Naval University of Engineering; a review. Entropy 2018, 20, 74. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Xie, Z.H.; Chen, L.G.; Wang, R.; Feng, H. Equivalent thermal resistance minimization for a circular disc heat sink with reverting microchannels based on constructal theory and entransy theory. Sci. China Technol. Sci. 2021, 64, 111–121. [Google Scholar] [CrossRef]
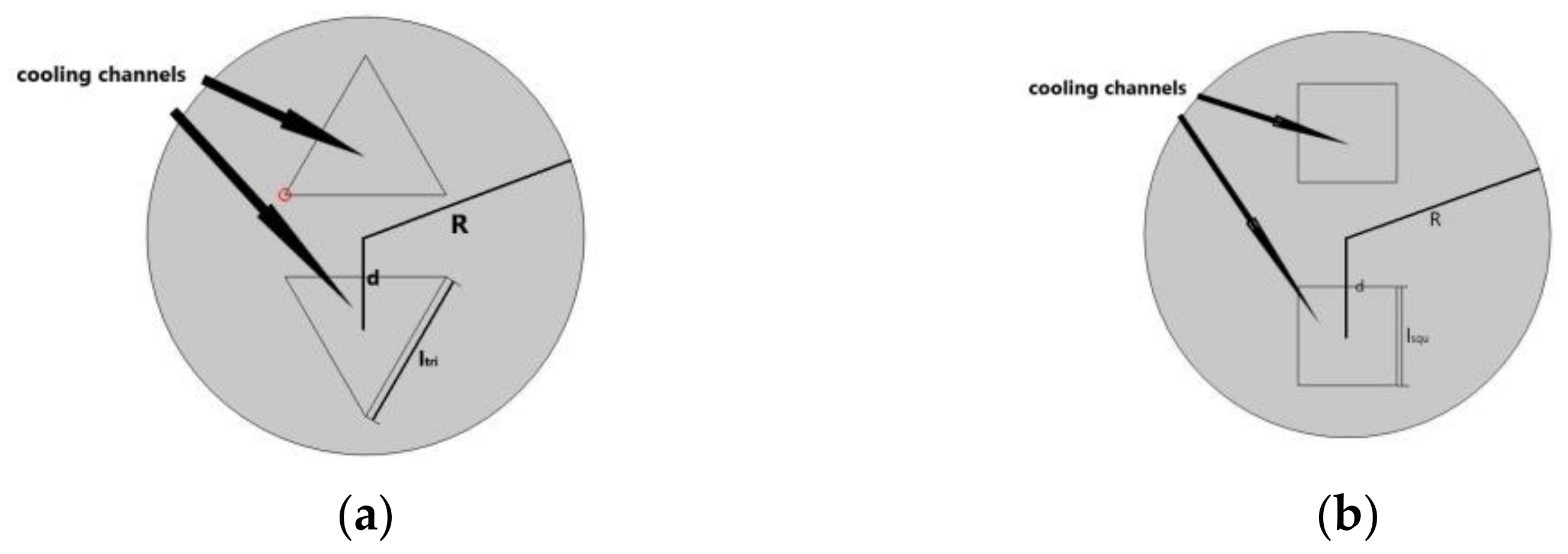





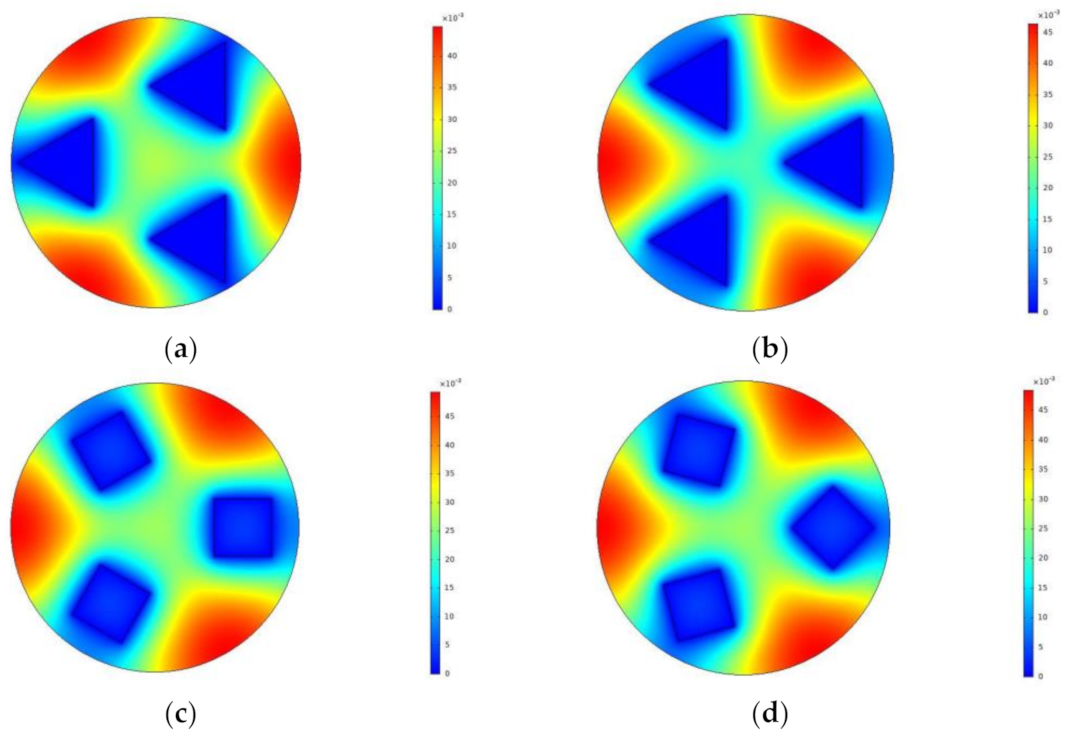

| Cross-Section Shape of Liquid Cooling Channel | Cross-Section Shape of Liquid Cooling Channel | ||||
|---|---|---|---|---|---|
| Edge to edge in triangle section | 0.044637 | 0.33850 | Angle to angle in triangle section | 0.044436 | 0.29337 |
| Edge to edge in Square section | 0.048623 | 0.31594 | Angle to angle in Square section | 0.047677 | 0.31594 |
| Cross-Section Shape of Liquid Cooling Channel | Cross-Section Shape of Liquid Cooling Channel | ||||
|---|---|---|---|---|---|
| Edge to edge in triangle section | 0.018854 | 0.31594 | Angle to angle in triangle section | 0.018259 | 0.30465 |
| Edge to edge in Square section | 0.02117 | 0.3103 | Angle to angle in Square section | 0.020935 | 0.3103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Xie, Z.; Lin, D.; Lu, Z.; Ge, Y. Constructal Optimizations of Liquid-Cooled Channels with Triangle or Square Sections in a Cylindrical Heating Body. Mathematics 2023, 11, 357. https://doi.org/10.3390/math11020357
Li Y, Xie Z, Lin D, Lu Z, Ge Y. Constructal Optimizations of Liquid-Cooled Channels with Triangle or Square Sections in a Cylindrical Heating Body. Mathematics. 2023; 11(2):357. https://doi.org/10.3390/math11020357
Chicago/Turabian StyleLi, Yunfeng, Zhihui Xie, Daoguang Lin, Zhuoqun Lu, and Yanlin Ge. 2023. "Constructal Optimizations of Liquid-Cooled Channels with Triangle or Square Sections in a Cylindrical Heating Body" Mathematics 11, no. 2: 357. https://doi.org/10.3390/math11020357
APA StyleLi, Y., Xie, Z., Lin, D., Lu, Z., & Ge, Y. (2023). Constructal Optimizations of Liquid-Cooled Channels with Triangle or Square Sections in a Cylindrical Heating Body. Mathematics, 11(2), 357. https://doi.org/10.3390/math11020357






