Effect of Learning and Forgetting on Inventory Model under Carbon Emission and Agile Manufacturing
Abstract
1. Introduction
2. Literature Review
2.1. Flexibility in Manufacturing System
2.2. Effect of Learning and Forgetting Process
- (a)
- Learning phenomenon
- (b)
- Forgetting phenomenon
2.3. Carbon Emissions
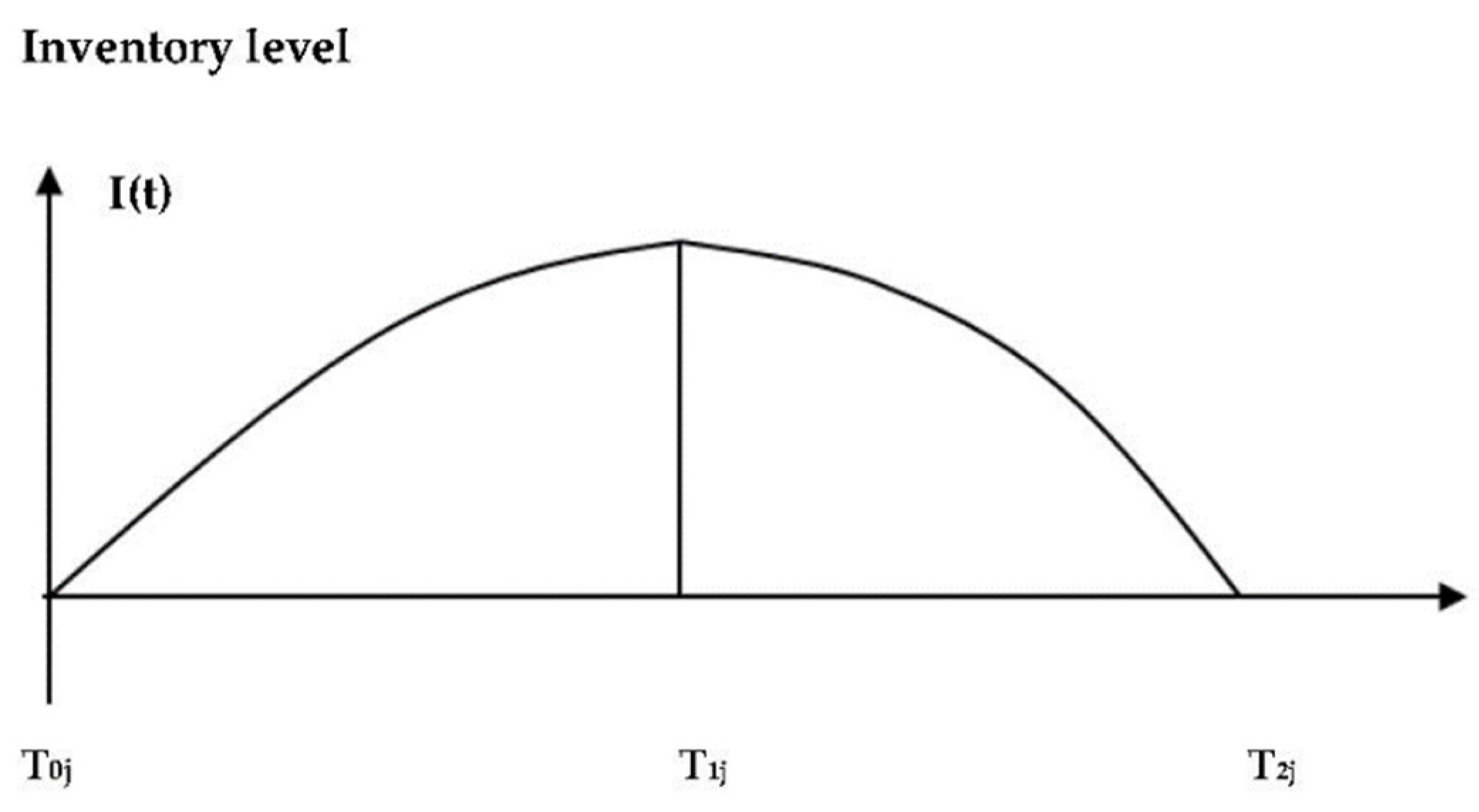
3. Problem Description, Notation, and Assumptions
3.1. Problem Description
3.2. Notation
3.3. Assumptions
4. Mathematical Modeling
4.1. Manufacturer’s Model
4.1.1. Item Cost (this Cost also Includes the Deterioration Cost)
4.1.2. Holding Cost
4.1.3. Setup Cost
4.1.4. Production Cost
4.2. Model Formulation under LFL
4.3. Solution Methodology
5. Numerical Experiments
5.1. Numerical Example
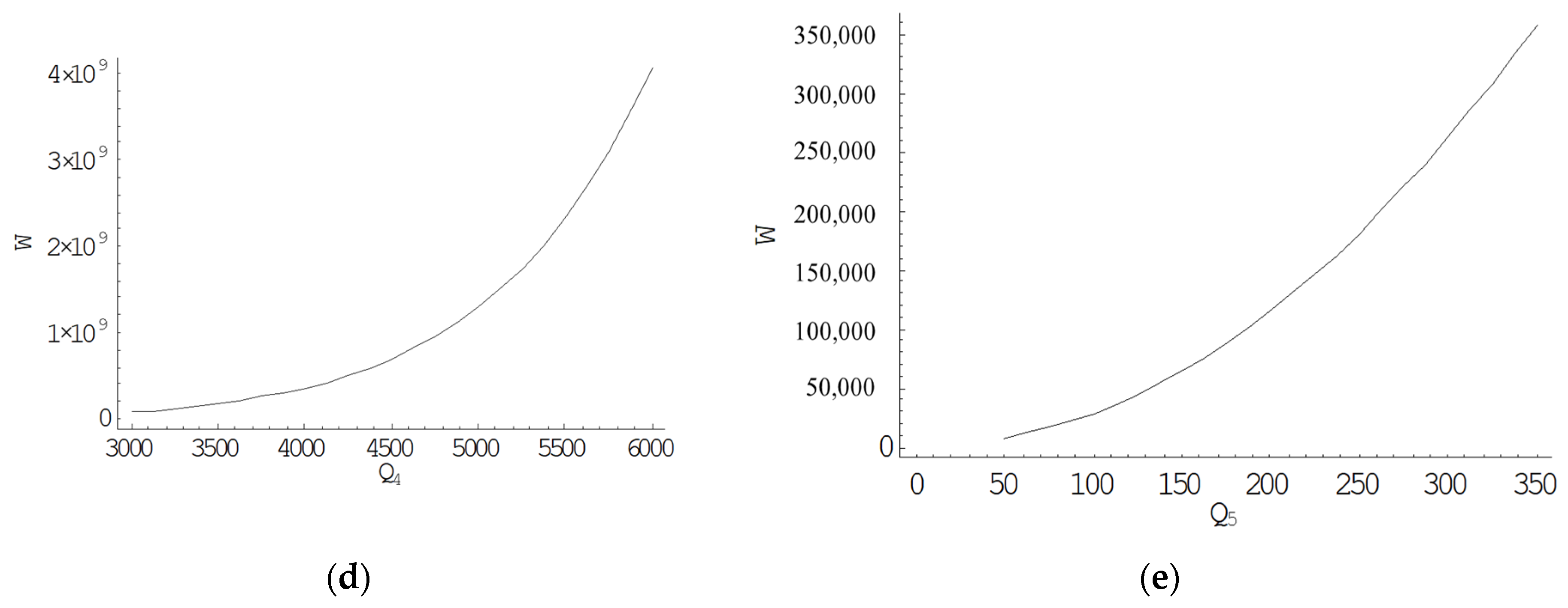
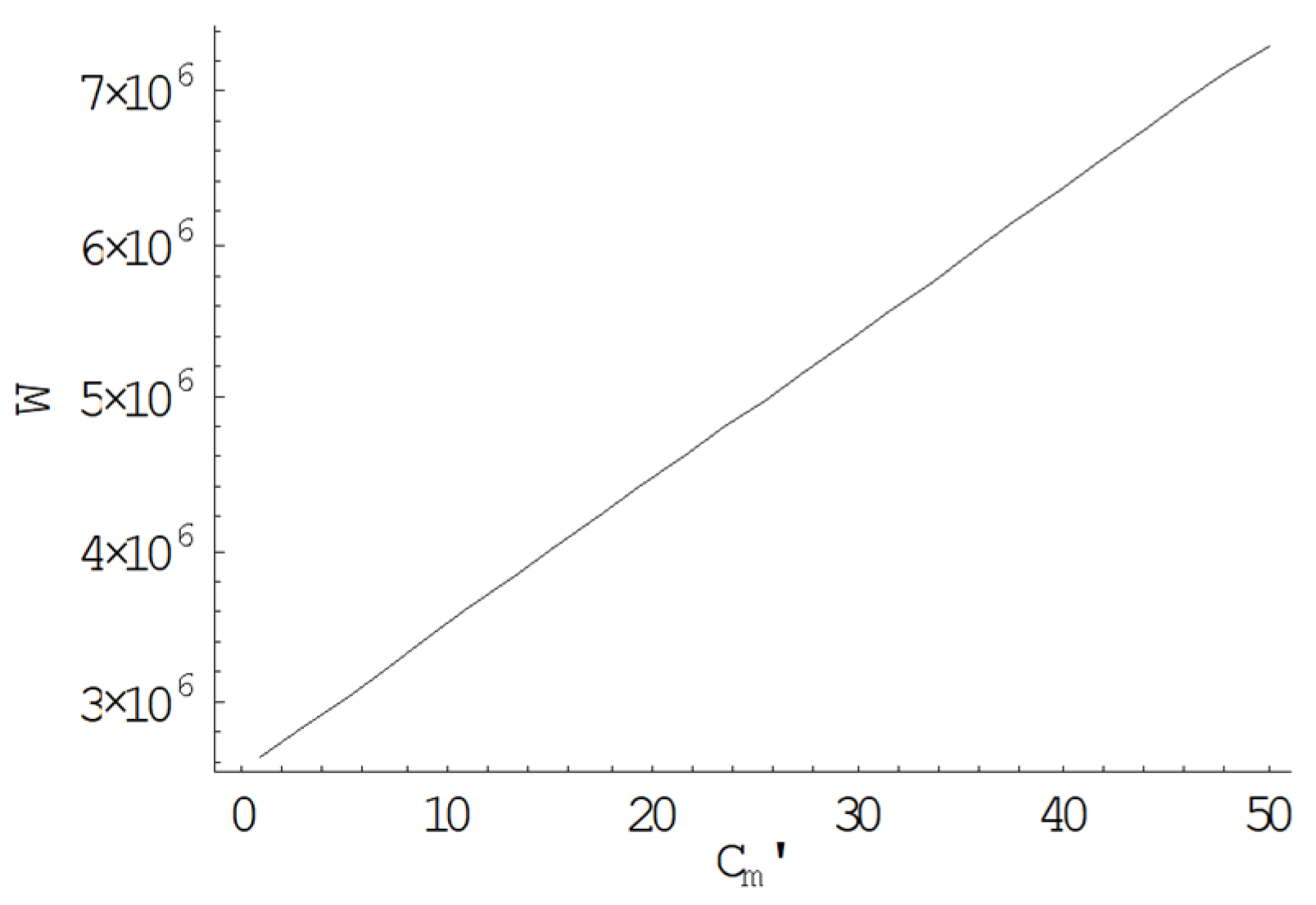
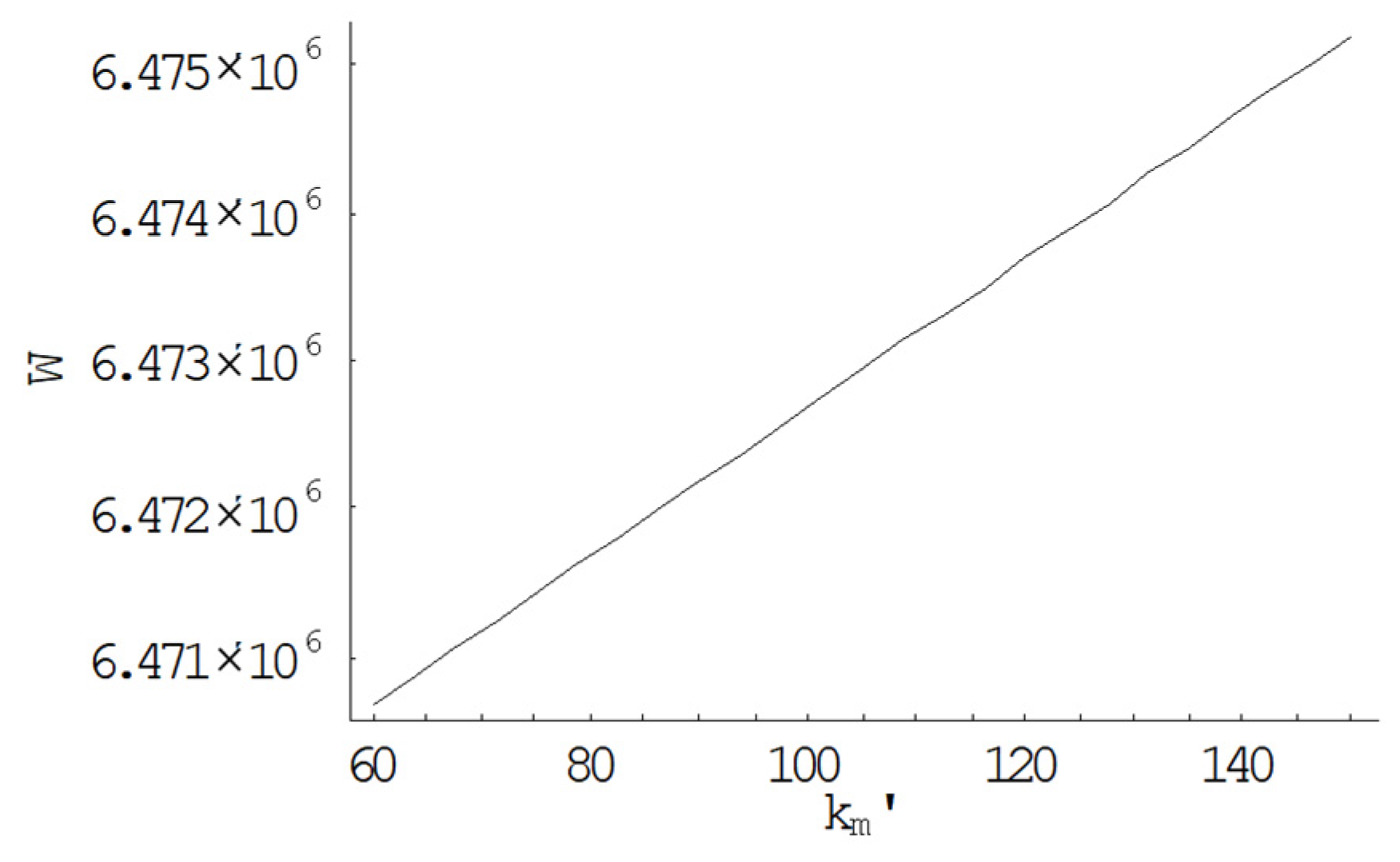
5.2. Sensitivity Analysis
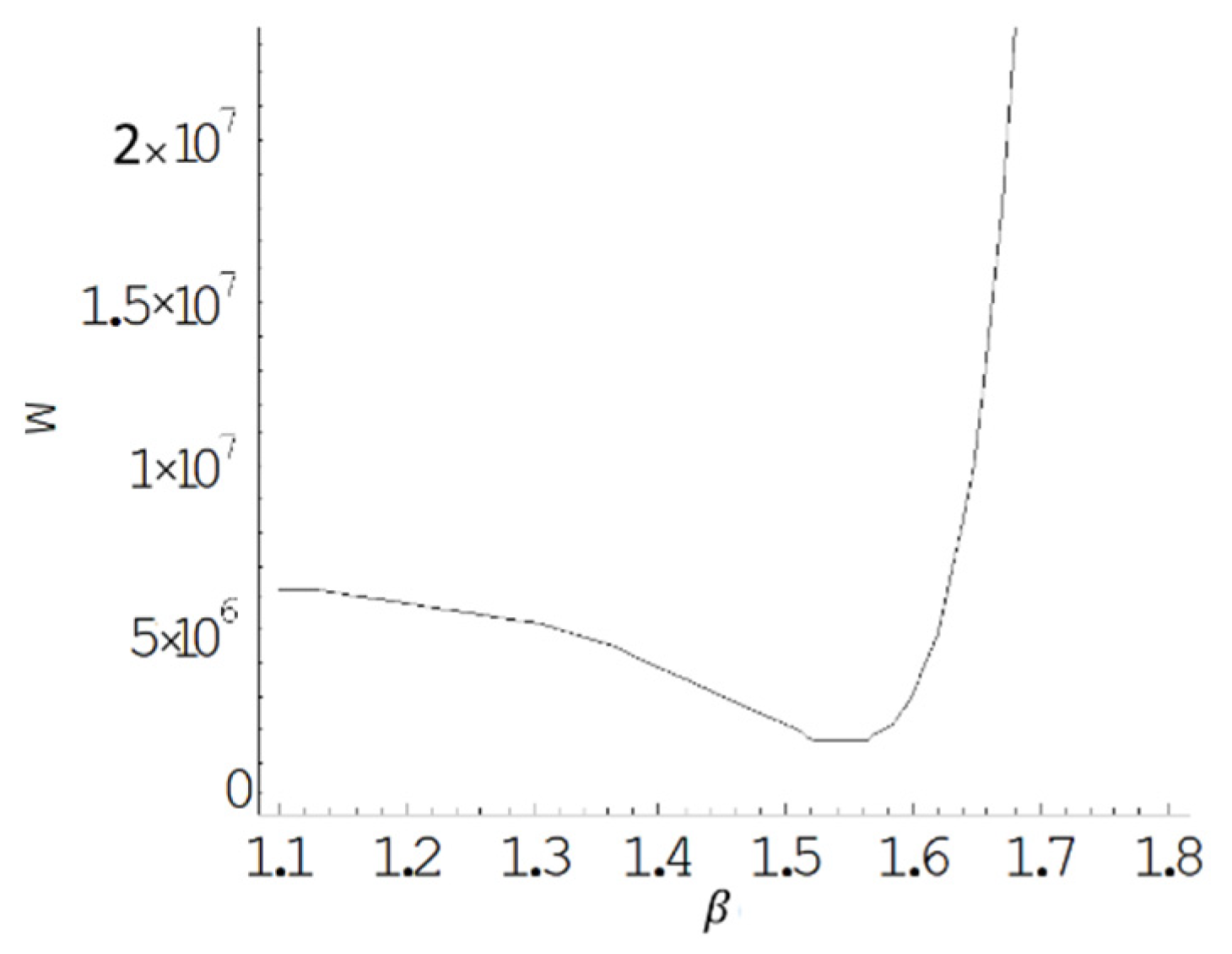
5.2.1. Effect of Slope of Learning Curve
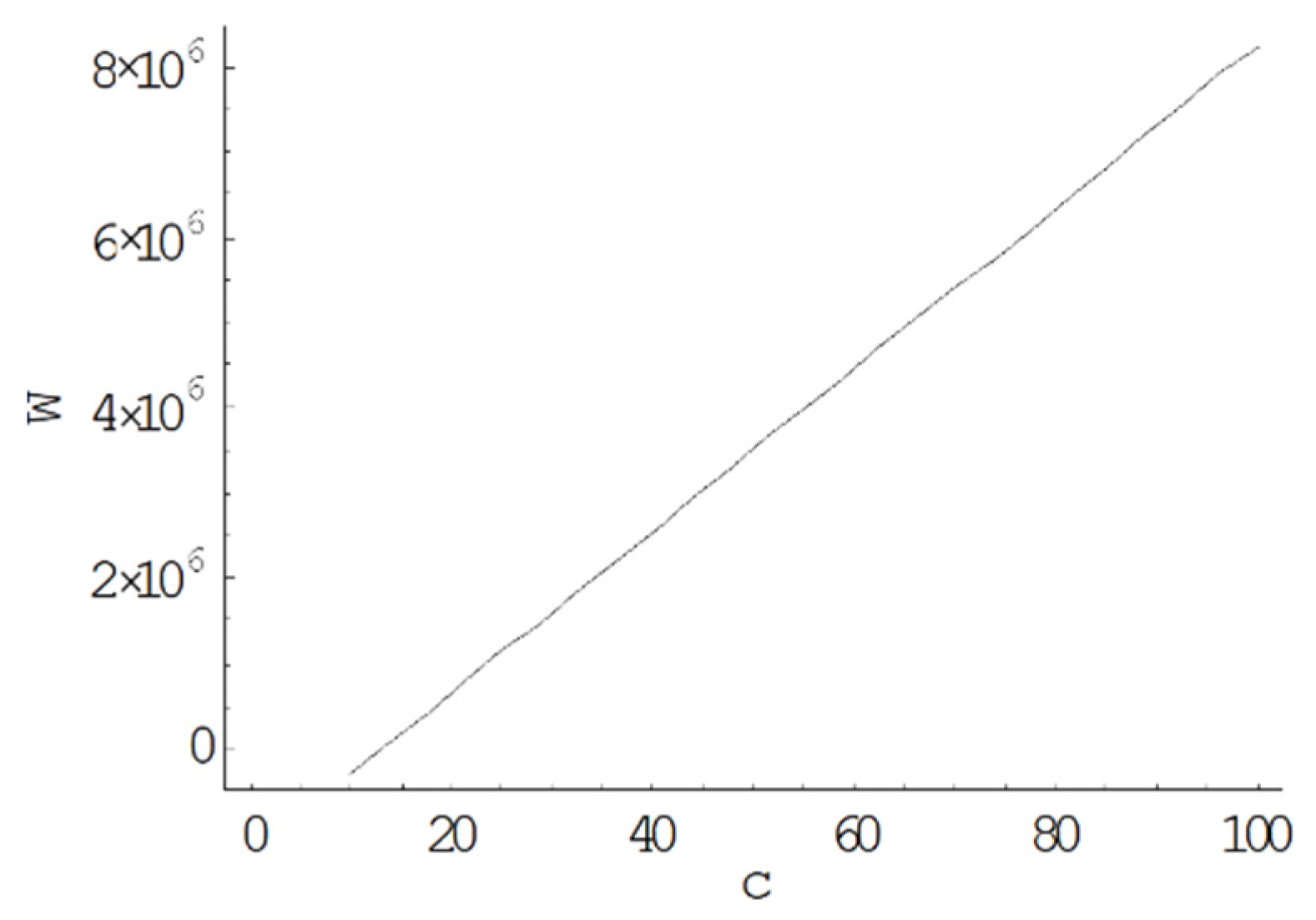
5.2.2. Effect of Carbon Emission Parameters
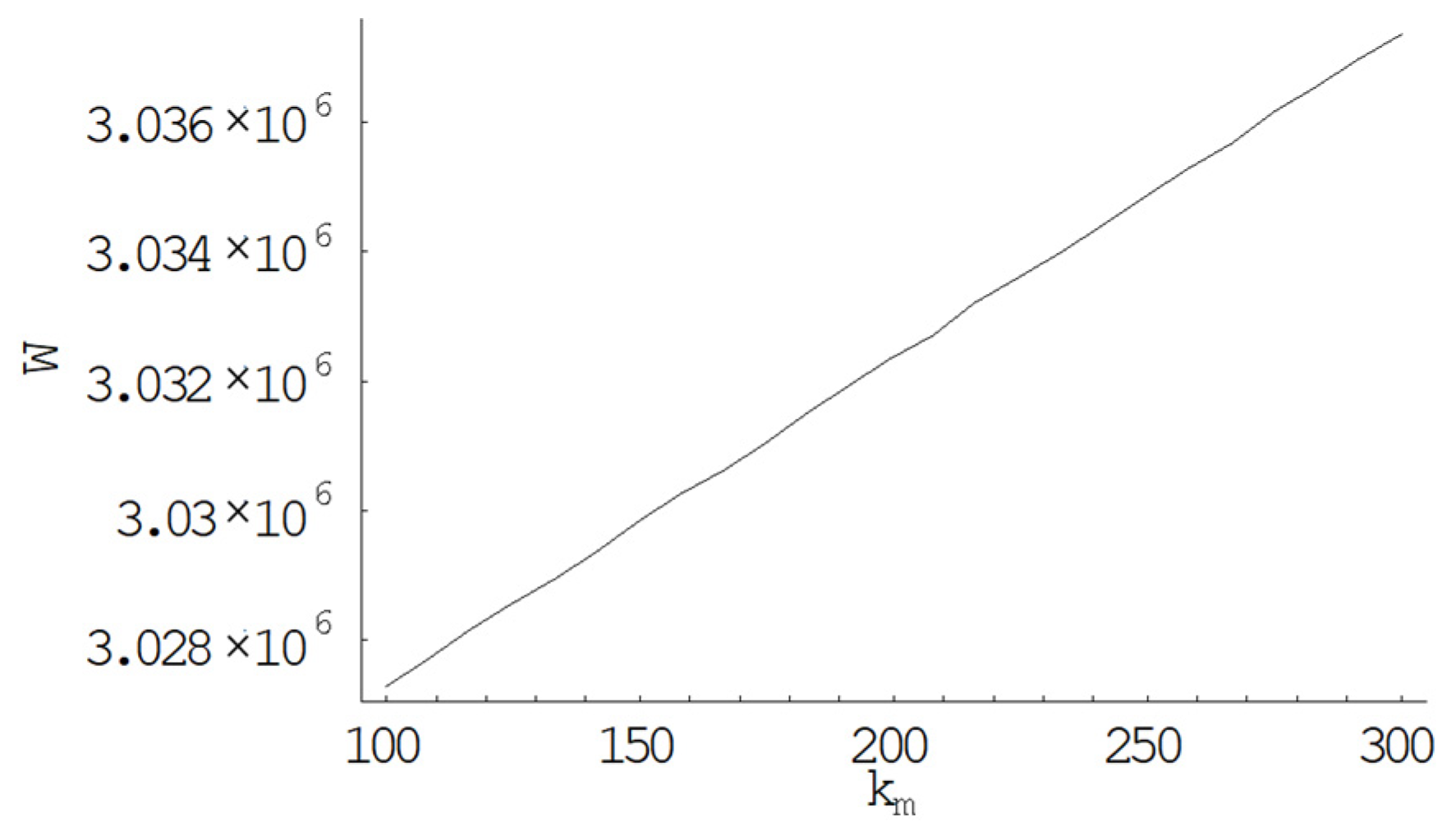
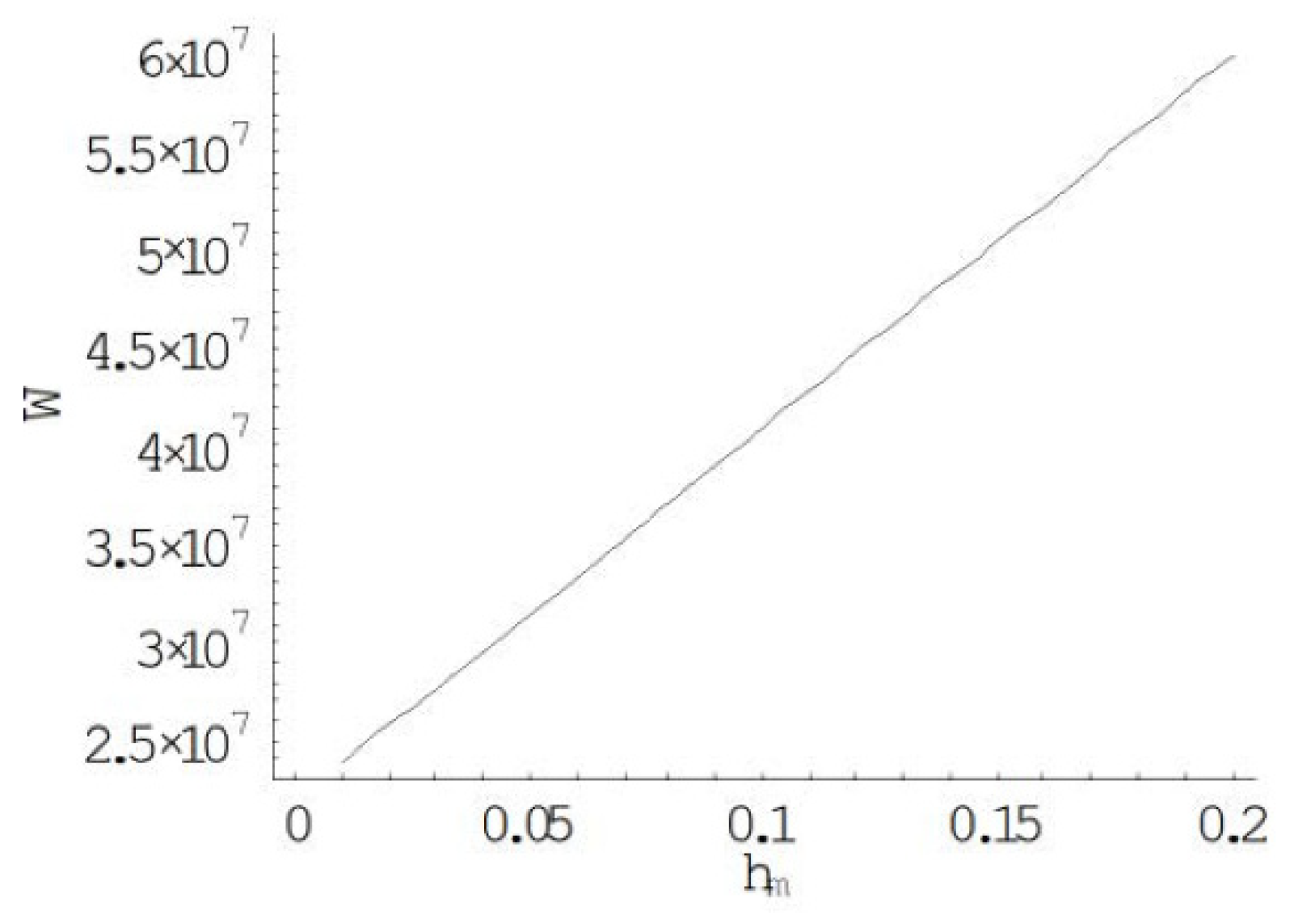
5.2.3. Effect of Cost Parameters
5.2.4. Effect of Parameters Used in Deterioration Rate
5.3. Effect of Parameters Used in Production Cost
5.4. Managerial Insights
6. Observations
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Notation
| r | Slope of the learning curve |
| Q(t) | Number of units produced up to time t (units/cycle) |
| T | Complete cycle time (days) |
| cm | Item cost per unit per unit of time ($/unit) |
| cm’ | Carbon emission cost due to deterioration per unit per unit of time ($/unit) |
| hm | Unit holding cost per unit of time ($/unit/days) |
| hm’ | Carbon emission cost from holding items in the warehouse per unit per unit of time ($/unit/days) |
| km | Setup cost per setup ($/setup) |
| km’ | Carbon emission cost due to transportation per order ($/order) |
| l | Slope of forgetting |
| t11 | Time required to produce the first unit in the first cycle (days) |
| Tij | Production time (days) |
| T2j | Inventory depletion time (days) |
| k | Material cost ($/unit) |
| g | Development cost ($/unit) |
| s | Scaling parameter of tool/die cost ($/unit) |
| a,b | Scaling and shape paramter of demand, a > 0, b > 0, and a > b |
| Scaling and shape paramter of deteriorateion rate |
References
- Khouja, M. The economic production lot size model under volume flexibility. Comput. Oper. Res. 1995, 22, 515–523. [Google Scholar] [CrossRef]
- Khouja, M. The scheduling of economic lot size on volume flexibility production system. Int. J. Prod. Econ. 1997, 48, 73–86. [Google Scholar] [CrossRef]
- Sana, S.; Chaudhuri, K.S. On a volume flexible stock dependent inventory model. Adv. Model. Optim. 2003, 5, 197–210. [Google Scholar]
- Singh, S.R.; Singh, A.P.; Bhatia, D. A supply chain model with variable holding cost for flexible manufacturing system. Int. J. Oper. Res. Optim. 2010, 1, 107–120. [Google Scholar]
- Singh, S.R.; Gupta, V.; Gupta, P. EOQ model with volume agility, variable demand rate, Weibull deterioration rate and inflation. Int. J. Comput. Appl. 2013, 72, 1–6. [Google Scholar]
- Mehrotra, K.; Dem, H.; Singh, S.R.; Sharma, R. A volume flexible inventory model with trapezoidal demand under inflation. Pak. J. Stat. Oper. Res. 2014, 9, 429–442. [Google Scholar] [CrossRef][Green Version]
- Singhal, S.; Singh, S.R. Modeling of an inventory model with multi variate demand under volume flexibility and learning. Uncertain Supply Chain. Manag. 2015, 3, 147–158. [Google Scholar] [CrossRef]
- Singh, S.R.; Gupta, V. Vendor-Buyer model with error in quality inspection and selling price dependent demand rate under the effect of volume agility. Int. J. Oper. Quant. Manag. 2016, 22, 357–371. [Google Scholar]
- Kamna, K.M.; Gautam, P.; Jaggi, C.K. Sustainable inventory policy for an imperfect production system with energy usage and volume agility. Int. J. Syst. Assur. Eng. Manag. 2020, 12, 44–52. [Google Scholar] [CrossRef]
- Sarkar, M.; Sarkar, B.; Dolgui, A. An Automated Smart Production with System Reliability Under a Leader-Follower Strategy of Supply Chain Management. In IFIP International Conference on Advances in Production Management Systems; Springer: Berlin/Heidelberg, Germany, 2022; pp. 459–467. [Google Scholar]
- Jauhari, W.A.; Pujawan, I.N.; Suef, M.; Govindan, K. Low carbon inventory model for vendor–buyer system with hybrid production and adjustable production rate under stochastic demand. Appl. Math. Model. 2022, 108, 840–868. [Google Scholar] [CrossRef]
- Jauhari, W.A.; Pujawan, N.; Suef, M. Sustainable inventory management with hybrid production system and investment to reduce defects. Ann. Oper. Res. 2022. [Google Scholar] [CrossRef]
- Wright, T. Factors affecting the cost of airplanes. J. Aeronaut. Sci. 1936, 3, 122–128. [Google Scholar] [CrossRef]
- Carlson, J.G.; Rowe, R.G. How much does forgetting cost? Ind. Eng. 1976, 8, 40–47. [Google Scholar]
- Elmaghraby, S.E. Economic manufacturing quantities under conditions of learning and forgetting (EMQ/LAF). Prod. Plan. Control 1990, 1, 196–208. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Bonney, M. Production breaks and the learning curve: The forgetting phenomenon. Appl. Math. Model. 1996, 20, 162–169. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Bonney, M. The economic manufacture/order quantity (EMQ/EOQ) and the learning curve: Past, present, and future. Int. J. Prod. Econ. 1999, 59, 93–102. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Kher, H.V. The dual-phase learning–forgetting model. Int. J. Prod. Econ. 2002, 76, 229–242. [Google Scholar] [CrossRef]
- Balkhi, Z.T. The effect of learning on the optimal production lot size for deteriorating and partially backordered items with time varying demand and deterioration rates. Appl. Math. Model. 2003, 22, 763–779. [Google Scholar] [CrossRef][Green Version]
- Alamri, A.A.; Balkhi, Z.T. The effects of learning and forgetting on the optimal production lot size for deteriorating items with time varying demand and deterioration rate. Int. J. Prod. Econ. 2007, 107, 125–138. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Kher, H.V. Variant versus invariant time to total forgetting; the learn–forget curve model revisited. Comput. Ind. Eng. 2004, 46, 697–705. [Google Scholar] [CrossRef]
- Jaber, M.; Bonney, Y.; Moualek, I. Lot sizing with learning, forgetting and entropy. Int. J. Prod. Econ. 2009, 118, 19–25. [Google Scholar] [CrossRef]
- Das, D.; Roy, A.; Kar, S. A production inventory model for a deteriorating item incorporating learning effect using genetic algorithm. Adv. Oper. Res. 2011, 26, 146042. [Google Scholar] [CrossRef]
- Mahapatra, A.S.; Mahapatra, M.S.; Sarkar, B.; Majumder, S.K. Benefit of preservation technology with promotion and time-dependent deterioration under fuzzy learning. Expert Syst. Appl. 2022, 201, 117169. [Google Scholar] [CrossRef]
- Bachar, R.K.; Bhuniya, S.; Ghosh, S.K.; Sarkar, B. Controllable energy consumption in a sustainable smart manufacturing model considering superior service, flexible demand, and partial outsourcing. Mathematics 2022, 10, 4517. [Google Scholar] [CrossRef]
- Kumar, R.S.; Goswami, A. EPQ model with learning consideration, imperfect production and partial backlogging in fuzzy random environment. Int. J. Syst. Sci. 2015, 46, 1486–1497. [Google Scholar] [CrossRef]
- Kazemi, N.; Olugu, E.U.; Abdul-Rashid, S.H.; Ghazilla, R.A.R. A fuzzy EOQ model with backorders and forgetting effect on fuzzy parameters: An empirical study. Comput. Ind. Eng. 2016, 96, 140–148. [Google Scholar] [CrossRef]
- Ahmad, T.; Chen, H. Utility companies strategy for short-term energy demand forecasting using machine learning based models. Sustain. Cities Soc. 2018, 39, 401–417. [Google Scholar] [CrossRef]
- Batarfi, R.; Jaber, M.Y.; Glock, C.H. Pricing and inventory decisions in a dual-channel supply chain with learning and forgetting. Comput. Ind. Eng. 2019, 136, 397–420. [Google Scholar] [CrossRef]
- Marchi, B.; Zanoni, S.; Jaber, M.Y. Economic production quantity model with learning in production, quality, reliability and energy efficiency. Comput. Ind. Eng. 2019, 129, 502–511. [Google Scholar] [CrossRef]
- Marchi, B.; Zanoni, S.; Zavanella, L.E.; Jaber, M.Y. Green supply chain with learning in production and environmental investments. IFAC PapersOnLine 2018, 51, 1738–1743. [Google Scholar] [CrossRef]
- Sarkar, B.; Joo, J.; Kim, Y.; Park, H.; Sarkar, M. Controlling defective items in a complex multi-phase manufacturing system. RAIRO Oper. Res. 2022, 56, 871–889. [Google Scholar] [CrossRef]
- Sarkar, B.; Ganguly, B.; Pareek, S.; Cárdenas-Barrón, L.E. A three-echelon green supply chain management for biodegradable products with three transportation modes. Comput. Ind. Eng. 2022, 174, 108727. [Google Scholar] [CrossRef]
- Padiyar, S.V.S.; Vandana; Bhagat, N.; Singh, S.R.; Sarkar, B. Joint replenishment strategy for deteriorating multi-item through multi-echelon supply chain model with imperfect production under imprecise and inflationary environment. RAIRO Oper. Res. 2022, 56, 3071–3096. [Google Scholar] [CrossRef]
- Habib, M.S.; Omair, M.; Ramzan, M.B.; Chaudhary, T.N.; Farooq, M.; Sarkar, B. A robust possibilistic flexible programming approach toward a resilient and cost-efficient biodiesel supply chain network. J. Clean. Prod. 2022, 366, 132752. [Google Scholar] [CrossRef]
- Hota, S.K.; Ghosh, S.K.; Sarkar, B. Involvement of smart technologies in an advanced supply chain management to solve unreliability under distribution robust approach. AIMS Environ. Sci. 2022, 9, 461–492. [Google Scholar] [CrossRef]
- Yadav, D.; Singh, R.; Kumar, A.; Sarkar, B. Reduction of pollution through sustainable and flexible production by controlling by-products. J. Environ. Inform. 2022, 40, 106–124. [Google Scholar] [CrossRef]
- Moon, I.; Yun, W.Y.; Sarkar, B. Effects of variable setup cost, reliability, and production costs under controlled carbon emissions in a reliable production system. Eur. J. Ind. Eng. 2022, 16, 371–397. [Google Scholar] [CrossRef]
- Sarkar, B.; Kar, S.; Basu, K.; Guchhait, R. A sustainable managerial decision-making problem for a substitutable product in a dual-channel under carbon tax policy. Comput. Ind. Eng. 2022, 172, 108635. [Google Scholar] [CrossRef]
- Wangsa, I.D. Greenhouse gas penalty and incentive policies for a joint economic lot size model with industrial and transport emissions. Int. J. Ind. Eng. Comput. 2017, 8, 453–480. [Google Scholar]
- Marchi, B.; Zanoni, S.; Zavanella, L.E.; Jaber, M.Y. Supply chain models with greenhouse gases emissions, energy usage, imperfect process under different coordination decisions. Int. J. Prod. Econ. 2019, 211, 145–153. [Google Scholar] [CrossRef]
- Castellano, D.; Gallo, M.; Grassi, A.; Santillo, L.C. The effect of GHG emissions on production, inventory replenishment and routing decisions in a single vendor-multiple buyers supply chain. Int. J. Prod. Econ. 2019, 218, 30–42. [Google Scholar] [CrossRef]
- Daryanto, Y.; Wee, H.M.; Astanti, R.D. Three-echelon supply chain model considering carbon emission and item deterioration. Transp. Res. Part E: Logist. Transp. Rev. 2019, 122, 368–383. [Google Scholar] [CrossRef]
- Hariga, M.A.; Benkherouf, L. Optimal and heuristic inventory replenishment models for deteriorating items with exponential time-varying demand. Eur. J. Oper. Res. 1994, 79, 123–137. [Google Scholar] [CrossRef]
- Hota, S.K.; Ghosh, S.K.; Sarkar, B. A solution to the transportation hazard problem in a supply chain with an unreliable manufacturer. AIMS Environ. Sci. 2022, 9, 354–380. [Google Scholar] [CrossRef]
- Oryani, B.; Moridian, A.; Sarkar, B.; Rezania, S.; Kamyab, H.; Khan, M.K. Assessing the financial rеsоurсе curse hypothesis in Iran: Thе nоvеl dynаmiс АRDL approach. Resour. Policy 2022, 78, 102899. [Google Scholar] [CrossRef]
- Mukherjee, T.; Sangal, I.; Sarkar, B.; Alkadash, T.M. Mathematical estimation for maximum flow of goods within a cross-dock to reduce inventory. Math. Biosci. Eng. 2022, 19, 13710–13731. [Google Scholar] [CrossRef]
- Mishra, M.; Ghosh, S.K.; Sarkar, B. Maintaining energy efficiencies and reducing carbon emissions under a sustainable supply chain management. AIMS Environ. Sci. 2022, 9, 603–635. [Google Scholar] [CrossRef]






| Researchers | Model | Manufacturing Type | Policy | Demand Pattern | Environment |
|---|---|---|---|---|---|
| Khouja [1,2] | EPQ | Volume flexibility | Not applicable | Constant | Not applicable |
| Singh et al. [5] | EPQ | Volume agility | Not applicable | Variable | Inflation |
| Singhal and Singh [7] | EPQ | Volume agility | Not applicable | Variable | Not applicable |
| Kamna et al. [9] | EPQ | Volume agility | Sustainable | Variable | Energy usage |
| Elmaghraby [15] | EPQ | Traditional | LFCM | Variable | Not applicable |
| Jaber and Boney [16] | EOQ | Not applicable | LFCM | Constant | Not applicable |
| Jaber and Kher [18] | EOQ | Not applicable | Dual Phase LFCM | Constant | Not applicable |
| Balkhi [19] | EPQ | Traditional | Learning | Variable | Not applicable |
| Alamri and Balkhi [20] | EPQ | Traditional | LFCM | Variable | Not applicable |
| Das et al. [23] | EPQ | Traditional | Learning, genetic algorithm | Constant | Not applicable |
| Mahapatra et al. [24] | EPQ | Not applicable | Learning | Uncertain | Fuzzy |
| Bachar et al. [25] | EPQ | Smart | Not applicable | Variable | Not applicable |
| Kumar and Goswami [26] | EPQ | Traditional | Learning | Uncertain | Fuzzy |
| Batarfi et al. [29] | SCM | Traditional | LFCM | Variable | Not applicable |
| Sarkar et al. [33] | SCM | Traditional | Not applicable | Variable | Carbon emission |
| This paper | EPQ | Volume agility | LFCM | Variable | Carbon emission and Weibull deterioration rate |
| Cycle no. j | Required Time to Produce First Unit t1j (Days) | Produced Units in [T0j, T1j] Qj (Units/Cycle) | No. of Units Remembered in [T0j, T2j] ηj+1 | Production Period T1j (Days) | Production Rate by Time T1j is P(T1j) (Units) | Consumption Period T2j (Days) | Qj + Rj | Intercept of the Forgetting Curve | Forgetting Slo pe lj | Minimum Total Cost W ($/Cycle) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.065 | 1888 | 1896.82 | 61.66 | 34.02 | 80.29 | 2529 | 0.0296 | 0.0025 | 3.0325 × 106 |
| 2 | 0.029 | 8382 | 8143.12 | 109 | 85.1 | 402 | 35,578 | 0.0115 | 0.0024 | 2.89 × 1012 |
| 3 | 0.0117 | 6557.24 | 6366.3 | 35 | 25.8 | 133.6 | 28,683 | 0.0048 | 0.0023 | 1.631 × 1010 |
| 4 | 0.0049 | 3181.19 | 3067 | 7.73 | 457.1 | 39.73 | 19,590 | 0.0022 | 0.0022 | 1.136 × 108 |
| 5 | 0.0021 | 155.778 | 148.94 | 0.23 | 753.041 | 1.733 | 1,470.12 | 0.0013 | 0.0021 | 69,532.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vandana; Singh, S.R.; Sarkar, M.; Sarkar, B. Effect of Learning and Forgetting on Inventory Model under Carbon Emission and Agile Manufacturing. Mathematics 2023, 11, 368. https://doi.org/10.3390/math11020368
Vandana, Singh SR, Sarkar M, Sarkar B. Effect of Learning and Forgetting on Inventory Model under Carbon Emission and Agile Manufacturing. Mathematics. 2023; 11(2):368. https://doi.org/10.3390/math11020368
Chicago/Turabian StyleVandana, Shiv Raj Singh, Mitali Sarkar, and Biswajit Sarkar. 2023. "Effect of Learning and Forgetting on Inventory Model under Carbon Emission and Agile Manufacturing" Mathematics 11, no. 2: 368. https://doi.org/10.3390/math11020368
APA StyleVandana, Singh, S. R., Sarkar, M., & Sarkar, B. (2023). Effect of Learning and Forgetting on Inventory Model under Carbon Emission and Agile Manufacturing. Mathematics, 11(2), 368. https://doi.org/10.3390/math11020368







