High Resolution Spatio-Temporal Model for Room-Level Airborne Pandemic Spread
Abstract
:1. Background
2. Model Definition
2.1. The Environment E
2.2. The Population
2.3. Model Implementation
3. Simulations and Results
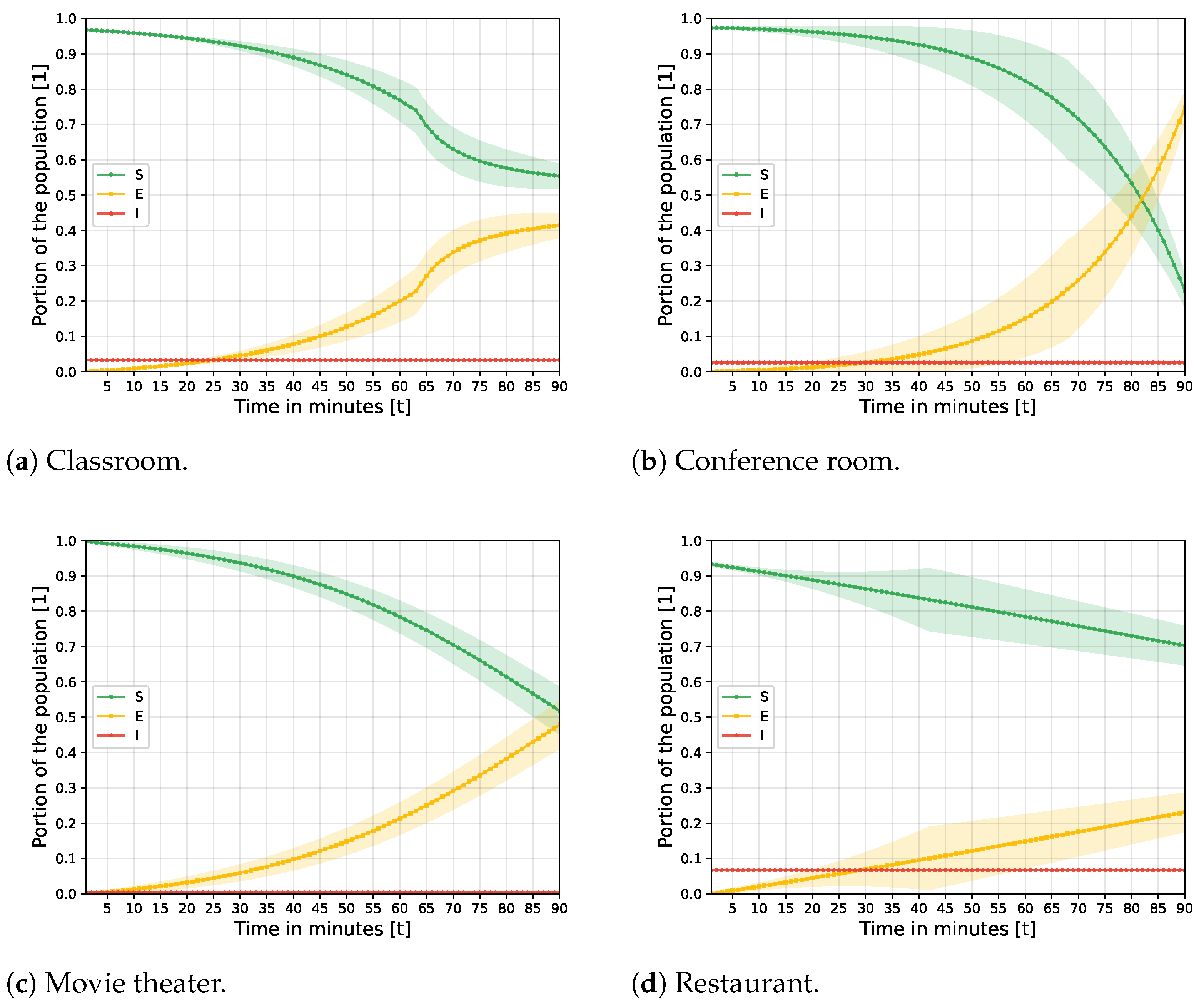
3.1. Baseline Model Dynamics
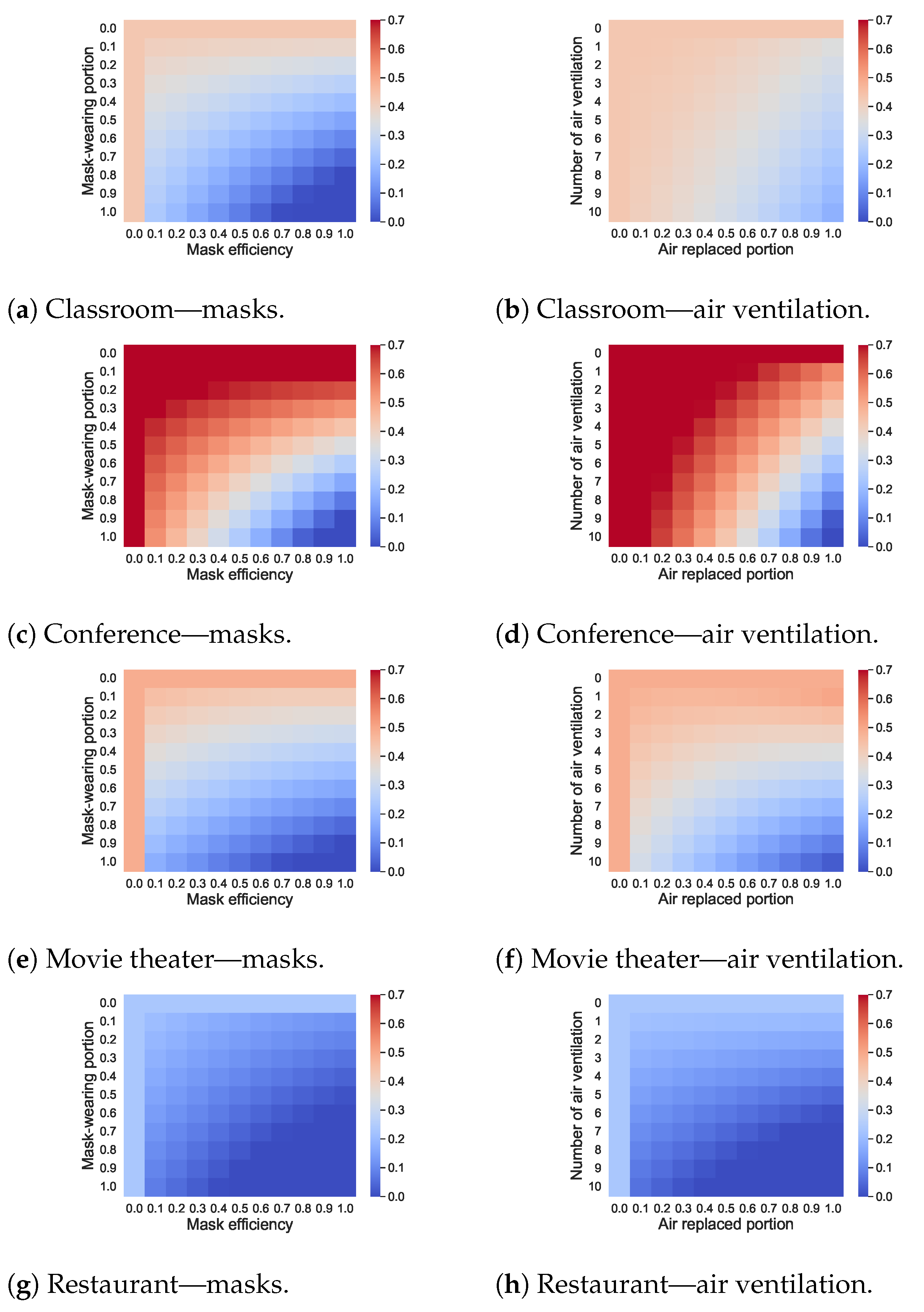
3.2. Pandemic Intervention Policies
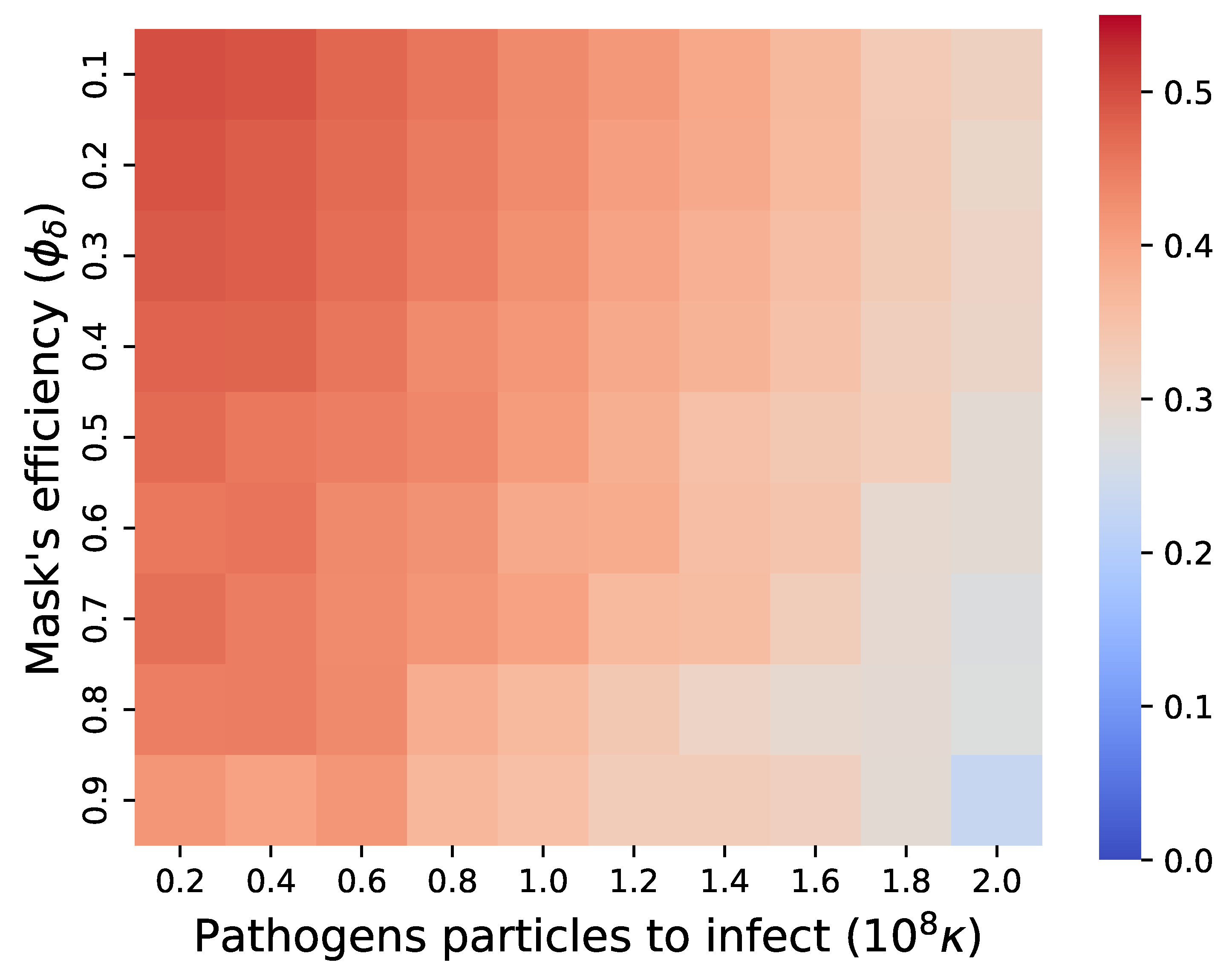
3.3. Model Sensitivity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brodeur, A.; Gray, D.; Islam, A.; Bhuiyan, S. A Literature Review of the Economics of COVID-19. IZA Discussion Paper No. 13411, 2020. Available online: https://ssrn.com/abstract=3636640 (accessed on 1 August 2022).
- Conti, A.A. Historical and methodological highlights of quarantine measures: From ancient plague epidemics to current coronavirus disease (COVID-19) pandemic. Acta Bio Medica Atenei Parm. 2020, 91, 226–229. [Google Scholar]
- Eurosurveillance Editorial Team. Note from the editors: World Health Organization declares novel coronavirus (2019-nCoV) sixth public health emergency of international concern. Eurosurveillance 2020, 25, 200131e. [Google Scholar]
- Lederberg, J. Medical Science, Infectious Disease, and the Unity of Humankind. JAMA 1988, 260, 684–685. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Perrings, C.; Kinzig, A.; Collins, J.P.; Minteer, B.A.; Daszak, P. Economic growth, urbanization, globalization, and the risks of emerging infectious diseases in China: A review. Ambio 2017, 46, 18–29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Quinn, T.C. Global burden of the HIV pandemic. Lancet 1996, 348, 99–106. [Google Scholar] [CrossRef]
- Genuis, S.J.; Dabog, F.; Genuis, S.K. Managing the sexually transmitted disease pandemic: A time for reevaluation. Am. J. Obstet. Gynecol. 2004, 191, 1103–1112. [Google Scholar] [CrossRef]
- Djillali, S.; Bentout, S.; Touaoula, T.M.; Tridane, A. Global dynamics of alcoholism epidemic model with distributed delays. Math. Biosci. Eng. 2021, 18, 8245–8256. [Google Scholar] [CrossRef]
- Djillali, S.; Bentout, S.; Touaoula, T.M.; Tridane, A.; Kumar, S. Global behavior of Heroin epidemic model with time distributed delay and nonlinear incidence function. Results Phys. 2021, 31, 104953. [Google Scholar] [CrossRef]
- Ferguson, N.M.; Cummings, D.A.T.; Fraser, C.; Cajka, J.C.; Cooley, P.C.; Burke, D.S. Strategies for mitigating an influenza pandemic. Nature 2006, 442, 448–452. [Google Scholar] [CrossRef]
- Domingo, J.L.; Marques, M.; Rovira, J. Influence of airborne transmission of SARS-CoV-2 on COVID-19 pandemic. A review. Environ. Res. 2020, 188, 109861. [Google Scholar] [CrossRef]
- Fernandez-Montero, J.V.; Soriano, V.; Barreiro, P.; de Mendoza, C.; Artacho, M. Coronavirus and other airborne agents with pandemic potential. Curr. Opin. Environ. Sci. Health 2020, 17, 41–48. [Google Scholar] [CrossRef] [PubMed]
- Araz, O.M.; Damien, P.; Paltiel, D.A.; Burke, S.; van de Geijn, B.; Galvani, A.; MEyers, L.A. Simulating school closure policies for cost effective pandemic decision making. BMC Public Health 2012, 12, 449. [Google Scholar] [CrossRef] [PubMed]
- Meltzer, M.I.; Cox, N.J.; Fukuda, K. The economic impact of pandemic influenza in the United States: Priorities for intervention. Emerg. Infect. Dis. 1999, 5, 659–671. [Google Scholar] [CrossRef] [PubMed]
- Kabir, M.; Afzai, M.S.; Khan, A.; Ahmed, H. COVID-19 pandemic and economic cost; impact on forcibly displaced people. Travel Med. Infect. Dis. 2020, 35, 101661. [Google Scholar] [CrossRef]
- Perrin, P.; McCabe, O.; Everly, G.; Links, J. Preparing for an Influenza Pandemic: Mental Health Considerations. Prehospital Disaster Med. 2009, 24, 223–230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taylor, M.R.; Agho, K.E.; Stevens, G.J.; Raphael, B. Factors influencing psychological distress during a disease epidemic: Data from Australia’s first outbreak of equine influenza. BMC Public Health 2008, 8, 347. [Google Scholar] [CrossRef] [Green Version]
- Miller, J.C. Mathematical models of SIR disease spread with combined non-sexual and sexual transmission routes. Infect. Dis. Model. 2017, 2, 35–55. [Google Scholar] [CrossRef] [PubMed]
- Tuite, A.R.; Fisman, D.N.; Greer, A.L. Mathematical modelling of COVID-19 transmission and mitigation strategies in the population of Ontario, Canada. CMAJ 2020, 192, E497–E505. [Google Scholar] [CrossRef] [Green Version]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. 1927, 115, 700–721. [Google Scholar]
- Lazebnik, T.; Bunimovich-Mendrazitsky, S. The Signature Features of COVID-19 Pandemic in a Hybrid Mathematical Model—Implications for Optimal Work–School Lockdown Policy. Adv. Theory Simul. 2021, 4, e2000298. [Google Scholar] [CrossRef]
- Ivorra, B.; Ferrandez, M.R.; Vela-Perez, M.; Ramos, A.M. Mathematical modeling of the spread of the coronavirus disease 2019 (COVID-19) taking into account the undetected infections. The case of China. Commun. Nonlinear Sci. Numer. Simulat. 2020, 88, 105303. [Google Scholar] [CrossRef] [PubMed]
- Long, J.B.; Ehrenfeld, J.M. The Role of Augmented Intelligence (AI) in Detecting and Preventing the Spread of Novel Coronavirus. J. Med Syst. 2020, 44, 59. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nesteruk, L. Statistics-based Predictions of Coronavirus Epidemic Spreading in Mainland China. Innov. Biosyst. Bioeng. 2020, 4, 13–18. [Google Scholar] [CrossRef]
- Lazebnik, T.; Shami, L.; Bunimovich-Mendrazitsky, S. Spatio-Temporal Influence of Non-Pharmaceutical Interventions Policies on Pandemic Dynamics and the Economy: The Case of COVID-19. Res. Econ. 2021, 35, 1833–1861. [Google Scholar] [CrossRef]
- Acemoglu, D.; Chernozhukov, V.; Werning, I.; Whinston, M.D. Optimal Targeted Lockdowns in a Multigroup SIR model. Am. Econ. Rev. Insights 2021, 3, 487–502. [Google Scholar] [CrossRef]
- Agarwal, M.; Bhadauria, A.S. Modeling Spread of Polio with the Role of Vaccination. Appl. Appl. Math. 2011, 6, 552–571. [Google Scholar]
- Bunimovich-Mendrazitsky, S.; Stone, L. Modeling polio as a disease of development. J. Theor. Biol. 2005, 237, 302–315. [Google Scholar] [CrossRef]
- Dang, Y.X.; Li, X.Z.; Martcheva, M. Competitive exclusion in a multi-strain immuno-epidemiological influenza model with environmental transmission. J. Biol. Dyn. 2016, 10, 416–456. [Google Scholar] [CrossRef] [Green Version]
- Marquioni, V.M.; de Aguiar, M.A.M. Modeling neutral viral mutations in the spread of SARS-CoV-2 epidemics. PLoS ONE 2021, 16, e0255438. [Google Scholar] [CrossRef]
- Lazebnik, T.; Alexi, A. Comparison of pandemic intervention policies in several building types using heterogeneous population model. Commun. Nonlinear Sci. Numer. Simul. 2022, 107, 106176. [Google Scholar] [CrossRef]
- Edmunds, W.J.; O’Callaghan, C.J.; Nokes, D.J. Who mixes with whom? A method to determine the contact patterns of adults that may lead to the spread of airborne infections. Proc. Biol. Sci. 1997, 264, 949–957. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keeling, M.J. The implications of network structure for epidemic dynamics. Theor. Popul. Biol. 2005, 67, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Klovdahl, A.S.; Potterat, J.J.; Woodhouse, D.E.; Muth, J.B.; Muth, S.Q.; Darrow, W.W. Social networks and infectious disease: The Colorado Springs study. Soc. Sci. Med. 1994, 38, 79–88. [Google Scholar] [CrossRef] [PubMed]
- Keeling, M.J.; Eames, K.T.D. Networks and epidemic models. J. R. Soc. Interface 2005, 2, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Bearman, P.S.; Moody, J.; Stovel, K. Chains of affection: The structure of adolescent romantic and sexual networks. Am. J. Sociol. 2004, 110, 44–91. [Google Scholar] [CrossRef] [Green Version]
- Cooper, I.; Mondal, A.; Antonopoulos, C.G. A SIR model assumption for the spread of COVID-19 in different communities. Chaos Solitons Fractals 2020, 139, 110057. [Google Scholar] [CrossRef]
- Lazebnik, T.; Bunimovich-Mendrazitsky, S.; Shami, L. Pandemic management by a spatio–temporal mathematical model. Int. J. Nonlinear Sci. Numer. Simul. 2021, 107, 106176. [Google Scholar] [CrossRef]
- Moore, C.; Newman, M.E.J. Epidemics and percolation in small-world networks. Phys. Rev. E 2000, 61, 5678. [Google Scholar] [CrossRef] [Green Version]
- Milner, F.A.; Zhao, R. S-I-R Model with Directed Spatial Diffusion. Math. Popul. Stud. 2008, 15, 160–181. [Google Scholar] [CrossRef]
- Fabricius, G.; Maltz, A. Exploring the threshold of epidemic spreading for a stochastic SIR model with local and global contacts. Phys. Stat. Mech. Its Appl. 2020, 540, 123208. [Google Scholar] [CrossRef] [Green Version]
- Paeng, S.H.; Lee, J. Continuous and discrete SIR-models with spatial distributions. J. Math. Biol. 2017, 74, 1709–1727. [Google Scholar] [CrossRef] [PubMed]
- Samaresh, S.; Vaishali, V.; Abhay, V.R.; Aditya, S.; Abhishek, K.; Shail, V.A. Real-time imaging of airflow patterns and impact of infection control measures in ophthalmic practice: A pandemic perspective. J. Cataract. Refract. Surg. 2021, 47, 842–846. [Google Scholar]
- Wei, J.; Li, Y. Airborne spread of infectious agents in the indoor environment. Am. J. Infect. Control 2016, 44, S102–S108. [Google Scholar] [CrossRef] [PubMed]
- Segal, R.A.; Guan, X.; Shearer, M.; Martonen, T.B. Mathematical model of airflow in the lungs of children I; effects of tumor sizes and locations. J. Theor. Med. 2000, 2, 199–213. [Google Scholar] [CrossRef]
- Ammari, H. A mathematical model of thermal performance of a solar air heater with slats. Renew. Energy 2003, 28, 1597–1615. [Google Scholar] [CrossRef]
- Rossello, C.; Canellas, J.; Simal, S.; Berna, A. Simple Mathematical Model To Predict the Drying Rates of Potatoes. J. Agrie. Food Chem. 1992, 40, 2374–2378. [Google Scholar] [CrossRef]
- Peng, Z.; Rogas, P.A.L.; Kropff, E.; Bahnfleth, W.; Buonanno, G.; Dancer, S.J.; Kurnitski, J.; Li, Y.; Loomans, M.G.L.C.; Marr, L.C.; et al. Practical Indicators for Risk of Airborne Transmission in Shared Indoor Environments and Their Application to COVID-19 Outbreaks. Environ. Sci. Technol. 2020, 56, 1125–1137. [Google Scholar] [CrossRef]
- Riley, E.C.; Murphy, G.; Riley, R.L. Airborne Spread of Measles in a Suburban Elementary School. Am. J. Epidemiol. 1978, 107, 421–432. [Google Scholar] [CrossRef]
- Yu, Y.; Megri, A.C.; Jiang, S. A review of the development of airflow models used in building load calculation and energy simulation. Build. Simul. 2019, 12, 347–363. [Google Scholar] [CrossRef]
- Fariborz, H.; Li, H. Building Airflow Movement - Validation of Three Airflow Models. J. Archit. Plan. Res. 2004, 21, 331–349. [Google Scholar]
- Cao, C. Sufficient Conditions for the Regularity to the 3D Navier–Stokes. Discret. Contin. Dyn. Syst. 2016, 26, 1141–1151. [Google Scholar] [CrossRef]
- Smyth, T.A.G. A review of Computational Fluid Dynamics (CFD) airflow modelling over aeolian landforms. Aeolian Res. 2016, 22, 153–164. [Google Scholar] [CrossRef]
- Versteeg, H.; Malalasekra, W. An Introduction to Computational Fluid Dynamics—The Finite Volume Method; Pearson Education: New York, NY, USA, 2007. [Google Scholar]
- Su, F.; Kinnas, S.A.; Jukola, H. Application of a BEM/RANS Interactive Method to Contra-Rotating Propellers. In Proceedings of the Fifth International Symposium on Marine Propulsion, Espoo, Finland, 12–15 June 2017. [Google Scholar]
- Zhiyin, Y. Large-eddy simulation: Past, present and the future. Chin. J. Aeronaut. 2015, 28, 11–24. [Google Scholar] [CrossRef] [Green Version]
- Kato, S. Review of airflow and transport analysis in building using CFD and network model. Jpn. Archit. Rev. 2018, 1, 299–309. [Google Scholar] [CrossRef]
- Nahor, H.B.; Hoang, M.L.; Verboven, P.; Baelmans, M.; Nicolai, B.M. CFD model of the airflow, heat and mass transfer in cool stores. Int. J. Refrig. 2005, 28, 368–380. [Google Scholar] [CrossRef]
- Smale, N.J.; Moureh, J.; Cortella, G. A review of numerical models of airflow in refrigerated food applications. Int. J. Refrig. 2006, 29, 911–930. [Google Scholar] [CrossRef]
- Cravero, C.; Marsano, D. Simulation of COVID-19 indoor emissions from coughing and breathing with air conditioning and mask protection effects. Indoor Built Environ. 2021, 31, 1242–1261. [Google Scholar] [CrossRef]
- Fefferman, C.L. Existence and Smoothness Of The Navier–Stokes Equation. Comput. Fluids 2013, 7, 86–92. [Google Scholar]
- Zheng, J.; Wu, X.; Fang, F.; Li, J.; Wang, Z.; Xiao, H.; Zhu, J.; Pain, C.; Linden, P.; Xiang, B. Numerical study of COVID-19 spatial–temporal spreading in London. Phys. Fluids 2021, 33, E10. [Google Scholar] [CrossRef]
- Chin, A.W.H.; Chu, J.T.S.; Perera, M.R.A.; Hui, K.P.Y.; Yen, H.L.; Chan, M.C.W.; Peiris, M.; Poon, L.L.M. Stability of SARS-CoV-2 in different environmental conditions. Lancet Microbe 2020, 1, E10. [Google Scholar] [CrossRef]
- Ciatto, G.; Schumacher, M.I.; Omicini, A.; Calvaresi, D. Agent-based explanations in AI: Towards an abstract framework. In Proceedings of the International Workshop on Explainable, Transparent Autonomous Agents and Multi-Agent Systems; Springer; Cham, Switzerland, 2020; pp. 3–20. [Google Scholar]
- Tesfatsion, L. Agent-Based Computational Economics: Growing Economies From the Bottom Up. Artif. Life 2002, 8, 55–82. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raberto, M.; Cincotti, S.; Focardi, S.M.; Marchesi, M. Agent-based simulation of a financial market. Phys. A Stat. Mech. Its Appl. 2001, 299, 319–327. [Google Scholar] [CrossRef] [Green Version]
- Peng, C.; Yan, D.; Wu, R.; Wang, C.; Zhou, X.; Jiang, Y. Quantitative description and simulation of human behavior in residential buildings. Build. Simul. 2012, 5, 85–94. [Google Scholar] [CrossRef]
- Kwon, K.S.; Park, J.I.; Park, Y.J.; Jung, D.M.; Ryu, K.W.; Lee, J.H. Evidence of Long-Distance Droplet Transmission of SARS-CoV-2 by Direct Air Flow in a Restaurant in Korea. J. Korean Med Sci. 2020, 35, e415. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Jimenez, J.L. Exhaled CO2 as a COVID-19 Infection Risk Proxy for Different Indoor Environments and Activities. Environ. Sci. Technol. Lett. 2021, 8, 392–397. [Google Scholar] [CrossRef]
- Shen, Y.; Li, C.; Dong, H.; Wang, Z.; Martinez, L.; Sun, Z.; Handel, A.; Chen, Z.; Chen, E.; Ebell, M.H.; et al. Community Outbreak Investigation of SARS-CoV-2 Transmission Among Bus Riders in Eastern China. JAMA Intern. Med. 2020, 180, 1665–1671. [Google Scholar] [CrossRef]
- Jang, S.; Han, S.; Rhee, J. Cluster of Coronavirus Disease Associated with Fitness Dance Classes, South Korea. Emerg. Infect. Dis. 2020, 26, 1917–1920. [Google Scholar] [CrossRef]
- Jie, S.; Sampath, A. Urban DEM Generation from Raw Lidar Data. Photogramm. Eng. Remote Sens. 2005, 71, 217–226. [Google Scholar]
- Douillard, B.; Underwood, J.; Kuntz, N.; Vlaskine, V.; Quadros, A.; Morton, P.; Frenkel, A. On the segmentation of 3D LIDAR point clouds. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2798–2805. [Google Scholar]
- Zheng, J.; Zhu, J.; Wang, Z.; Fang, F.; Pain, C.C.; Xiang, J. Towards a new multiscale air quality transport model using the fully unstructured anisotropic adaptive mesh technology of fluidity. Geosci. Model Dev. 2015, 8, 3421–3440. [Google Scholar] [CrossRef]
- Hutchinson, J. Breathing pattern in humans: Diversity and individuality. J. Appl. Physiol 1850. [Google Scholar]
- Perez, W.; Tobim, M.J. Separation of factors responsible for change in breathing pattern induced by instrumentation. J. Appl. Physiol. 1985, 59, 1515–1520. [Google Scholar] [CrossRef] [PubMed]
- Quetelet, M.A. A treatise on man and the development of his faculties. J. Appl. Physiol 1842. [Google Scholar]
- Benchetrit, G. Breathing pattern in humans: Diversity and individuality. Respir. Physiol. 2000, 122, 123–129. [Google Scholar] [CrossRef] [PubMed]
- Hernandez-Vargas, E.A.; Velasco-Hernandez1, J.X. In-host Modelling of COVID-19 Kinetics in Humans. medRxiv 2021. [Google Scholar]
- Sender, R.; Bar-On, Y.M.; Gleizer, S.; Bernshtein, B.; Flamholz, A.; Phillips, R.; Milo, R. The total number and mass of SARS-CoV-2 virions. Proc. Natl. Acad. Sci. USA 2021, 118, e2024815118. [Google Scholar] [CrossRef]
- Oruc, B.E.; Baxter, A.; Keskinocak, P.; Asplund, J.; Serban, N. Homebound by COVID19: The Benets and Consequences of Non-pharmaceutical Intervention Strategies. BMC Public Health 2020, 21, 655. [Google Scholar] [CrossRef]
- Li, T.; Liu, Y.; Li, M.; Qian, X.; Dai, S.Y. Mask or no mask for COVID-19: A public health and market study. PLoS ONE 2020, 15, e0237691. [Google Scholar] [CrossRef]
- Brienen, N.C.J.; Timen, A.; Wallinga, J.; Van Steenbergen, J.E.; Teunis, P.F.M. The Effect of Mask Use on the Spread of Influenza During a Pandemic. Risk Anal. 2010, 30, 1210–1218. [Google Scholar] [CrossRef]
- O’Dowd, K.; Nair, K.M.; Forouzanadeh, P.; Mathew, S.; Grant, J.; Moran, R.; Bartlett, J.; Bird, J.; Pillai, S.C. Face Masks and Respirators in the Fight Against the COVID-19 Pandemic: A Review of Current Materials, Advances and Future Perspectives. Materials 2020, 13, 3363. [Google Scholar] [CrossRef]
- Alexi, A.; Rosenfeld, A.; Lazebnik, T. The Trade-Off between Airborne Pandemic Control and Energy Consumption Using Air Ventilation Solutions. Sensors 2022, 22, 8594. [Google Scholar] [CrossRef]
- Simon, L.; Liberzon, A.; Lazebnik, T. SciMED: A Computational Framework For Physics-Informed Symbolic Regression with Scientist-In-The-Loop. arXiv 2022, arXiv:2209.06257. [Google Scholar]
- Loh, W.Y. Some modifications of levene’s test of variance homogeneity. J. Stat. Comput. Simul. 1987, 28, 213–226. [Google Scholar] [CrossRef]
- West, R.M. Best practice in statistics: Use the Welch t-test when testing the difference between two groups. Ann. Clin. Biochem. 2021, 58, 267–269. [Google Scholar] [CrossRef] [PubMed]
- Khavarian-Garmsir, A.R.; Sharifi, A.; Moradpour, N. Are high-density districts more vulnerable to the COVID-19 pandemic? Sustain. Cities Soc. 2021, 70, 102911. [Google Scholar] [CrossRef]
- Hamidi, S.; Sabouri, S.; Ewing, R. Does Density Aggravate the COVID-19 Pandemic? Early Findings and Lessons for Planners. J. Am. Plan. Assoc. 2020, 84, 495–509. [Google Scholar] [CrossRef]
- Fukuoka, T.; Ito, K. Exposure Risk Assessment by Coupled Analysis of CFD and SIR model in Enclosed Space. In Proceedings of the AIVC International Conference, Seoul, Republic of Korea, 26–28 October 2010; pp. 44–60. [Google Scholar]
- Chen, Y.; Liang, X.; Hong, T.; Luo, X. Simulation and visualization of energy-related occupant behavior in office buildings. Build. Simul. 2017, 10, 785–798. [Google Scholar] [CrossRef]
- Rieger, M.O. To wear or not to wear? Factors influencing wearing face masks in Germany during the COVID-19 pandemic. Soc. Health Behav. 2020, 3, 50–54. [Google Scholar] [CrossRef]
- Flaskrud, J.H. Masks, Politics, Culture and Health. Issues Ment. Health Nurs. 2020, 41, 846–849. [Google Scholar] [CrossRef]
- Martinelli, L.; Kopilas, V.; Vidmar, M.; Heavin, C.; Machado, H.; Todorovic, Z.; Buzas, N.; Pot, M.; Prainsack, B.; Gajovic, S. Face Masks During the COVID-19 Pandemic: A Simple Protection Tool With Many Meanings. Front. Public Health 2021, 8, 846–849. [Google Scholar] [CrossRef]
- Dai, H.; Zhao, B. Association of the infection probability of COVID-19 with ventilation rates in confined spaces. Build. Simul. 2020, 13, 1321–1327. [Google Scholar] [CrossRef]
- Levine, H.; Stein-Zamir, C. The measles outbreak in Israel in 2018–2019: Lessons for COVID-19 pandemic. Hum. Vaccines Immunother. 2021, 7, 2085–2089. [Google Scholar]
- Roberts, L. Why measles deaths are surging – and coronavirus could make it worse. Nature 2020, 580, 446–447. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunuba, Z.; Cuomo-Dannenburg, G.; et al. Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. Imp. Coll. 2020, 20, 77482. [Google Scholar]
- Lemaitre, J.C.; Grantz, K.H.; Kaminsky, J.; Meredith, H.R.; Truelove, S.A.; Lauer, S.A.; Keegan, L.T.; Shah, S.; Wills, J.; Kaminsky, K.; et al. A scenario modeling pipeline for COVID-19 emergency planning. Sci. Rep. 2021, 11, 7534. [Google Scholar] [CrossRef] [PubMed]
- Lazebnik, T.; Blumrosen, G. Advanced Multi-Mutation With Intervention Policies Pandemic Model. IEEE Access 2022, 10, 22769–22781. [Google Scholar] [CrossRef]
- Fudolig, M.; Howard, R. The local stability of a modified multi-strain SIR model for emerging viral strains. PLoS ONE 2020, 15, e0243408. [Google Scholar] [CrossRef] [PubMed]
- Khyar, O.; Allali, K. Global dynamics of a multi-strain SEIR epidemic model with general incidence rates: Application to COVID-19 pandemic. Nonlinear Dyn. 2020, 102, 489–509. [Google Scholar] [CrossRef]
- Lazebnik, T.; Bunimovich-Mendrazitsky, S. Generic approach for mathematical model of multi-strain pandemics. PLoS ONE 2022, 17, 1–20. [Google Scholar] [CrossRef]
- Minayev, P.; Ferguson, N. Improving the realism of deterministic multi-strain models: Implications for modelling influenza A. J. R. Soc. Interface 2009, 6, 509–518. [Google Scholar] [CrossRef]


| Parameter | Notation | Value | Source |
|---|---|---|---|
| Population size [1] | N | DPS | - |
| Exposed to infected transformation rate in minutes [] | [31] | ||
| Simulation’s step in time (in seconds) [t] | 0.02 | [50] | |
| Number of simulation steps [1] | T | 270,000 | - |
| Average decay rate of the pathogen particles in air in minutes [] | D | [62] | |
| CFD’s mesh’s single volume element size in cubic centimeters [m] | 1 | [74] | |
| Inhaling duration in seconds [t] | [75,76] | ||
| Exhaling duration in seconds [t] | [76,77] | ||
| No breathing duration in seconds [t] | - | [76,78] | |
| Inhaling volume in cubic centimeter [m] | [76] | ||
| Exhaling volume in cubic centimeter [m] | [76] | ||
| Average distance of pathogen particle influenced by inhaling in meters [m] | 0.34 | [79] | |
| Average decay rate of pathogen particles in host in minutes [] | [79] | ||
| Average number of pathogens particles needed to infected a susceptible individual [1] | [80] | ||
| Average number of pathogens particles generated by infected individual at each exhaling [1] | [80] |
| Name | Population Size | Room Size [m] | Density [1/m] |
|---|---|---|---|
| Classroom 1 | |||
| Classroom 2 | |||
| Classroom 3 | |||
| Classroom 4 | |||
| Classroom 5 | |||
| Restaurant 1 | |||
| Restaurant 2 | |||
| Restaurant 3 | |||
| Restaurant 4 | |||
| Restaurant 5 | |||
| Movie theater 1 | |||
| Movie theater 2 | |||
| Movie theater 3 | |||
| Movie theater 4 | |||
| Movie theater 5 | |||
| Conference 1 | |||
| Conference 2 | |||
| Conference 3 | |||
| Conference 4 | |||
| Conference 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lazebnik, T.; Alexi, A. High Resolution Spatio-Temporal Model for Room-Level Airborne Pandemic Spread. Mathematics 2023, 11, 426. https://doi.org/10.3390/math11020426
Lazebnik T, Alexi A. High Resolution Spatio-Temporal Model for Room-Level Airborne Pandemic Spread. Mathematics. 2023; 11(2):426. https://doi.org/10.3390/math11020426
Chicago/Turabian StyleLazebnik, Teddy, and Ariel Alexi. 2023. "High Resolution Spatio-Temporal Model for Room-Level Airborne Pandemic Spread" Mathematics 11, no. 2: 426. https://doi.org/10.3390/math11020426
APA StyleLazebnik, T., & Alexi, A. (2023). High Resolution Spatio-Temporal Model for Room-Level Airborne Pandemic Spread. Mathematics, 11(2), 426. https://doi.org/10.3390/math11020426







