Peristalsis of Nanofluids via an Inclined Asymmetric Channel with Hall Effects and Entropy Generation Analysis
Abstract
:1. Introduction
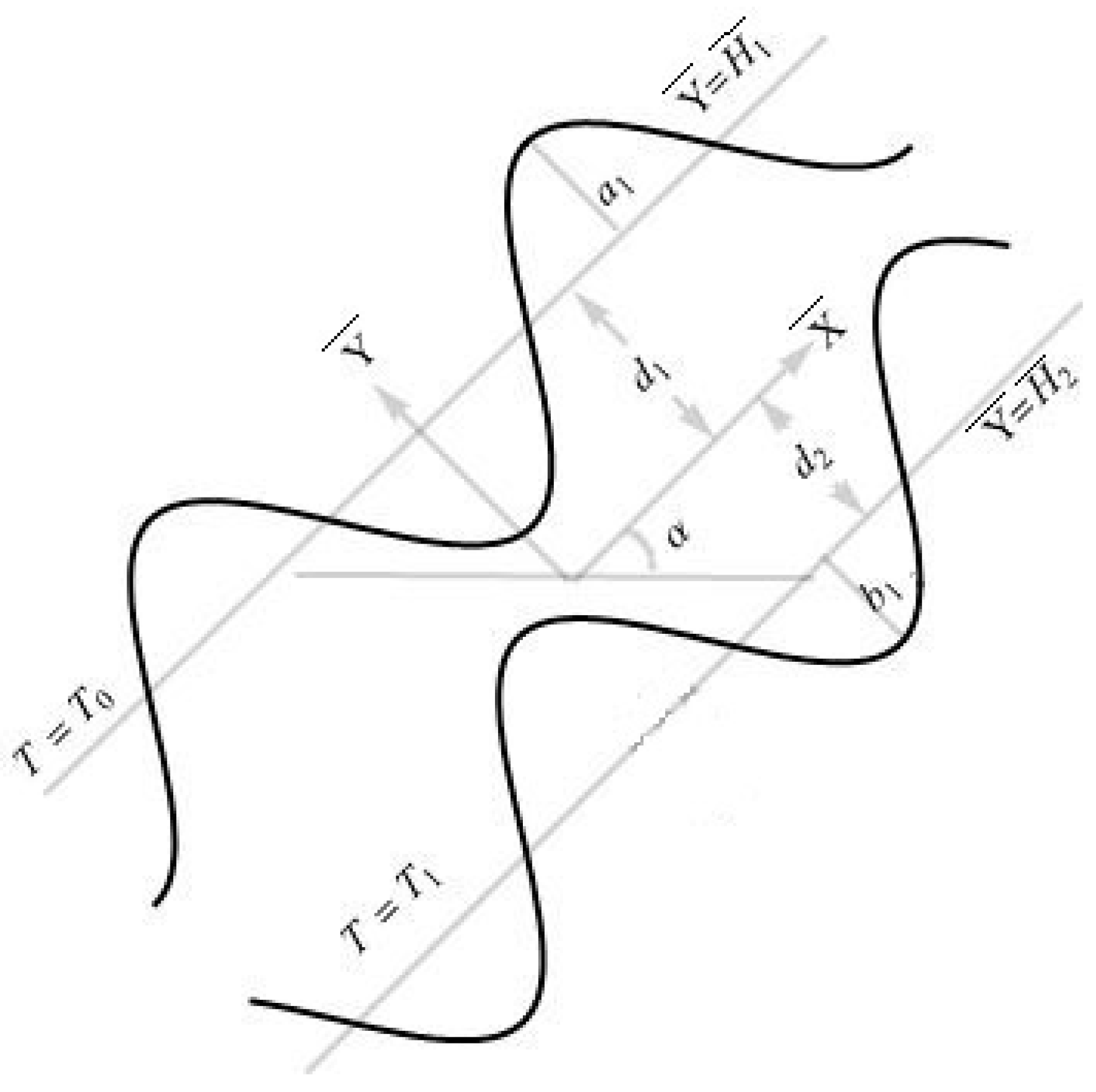
2. Governing Equations
3. Non-Dimensionalization Process
4. Entropy Generation
5. Solution Methodology
5.1. Construction of Homotopy
5.2. Zeroth-Order System
5.3. First-Order System
5.4. Second-Order System
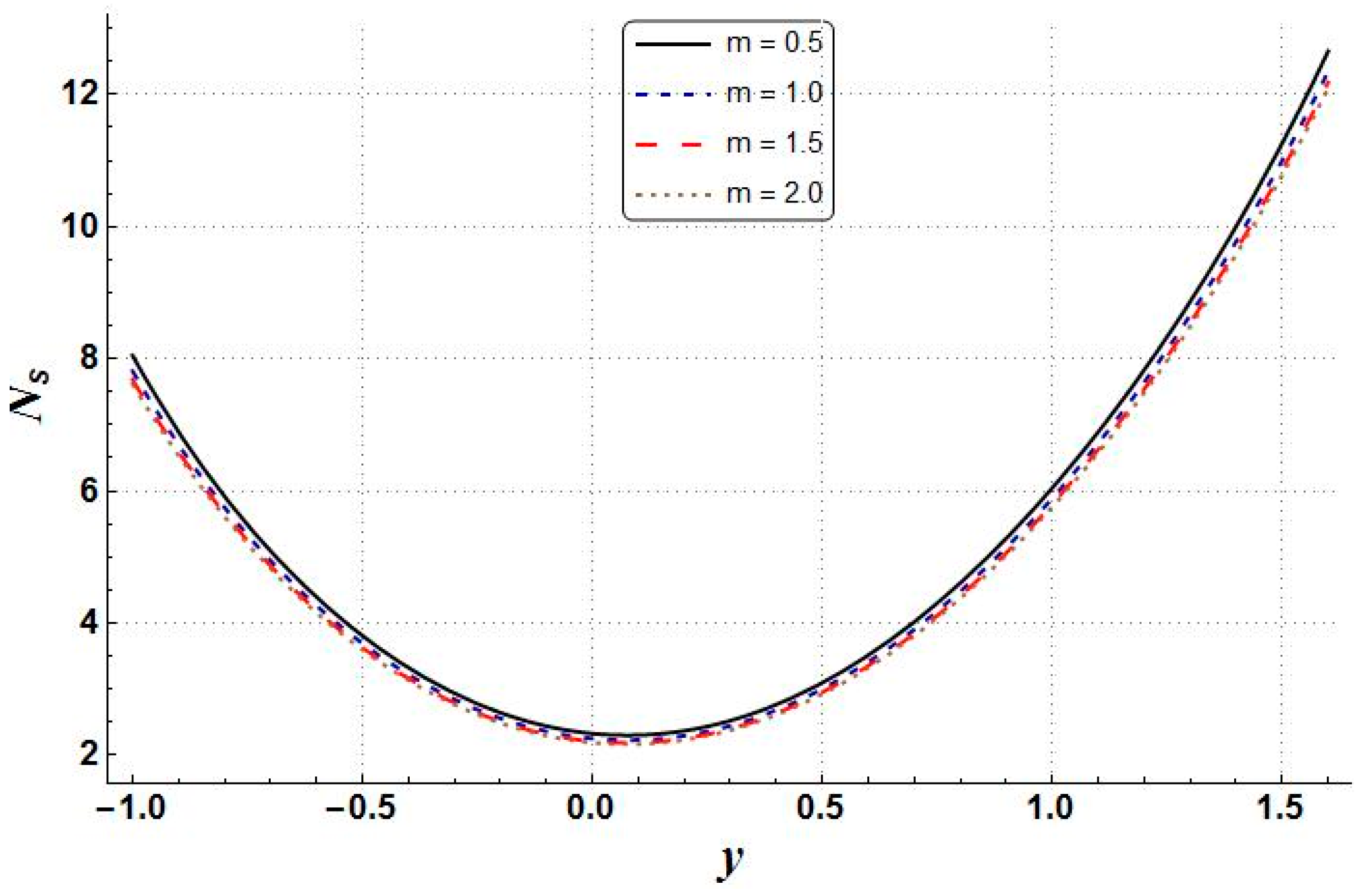
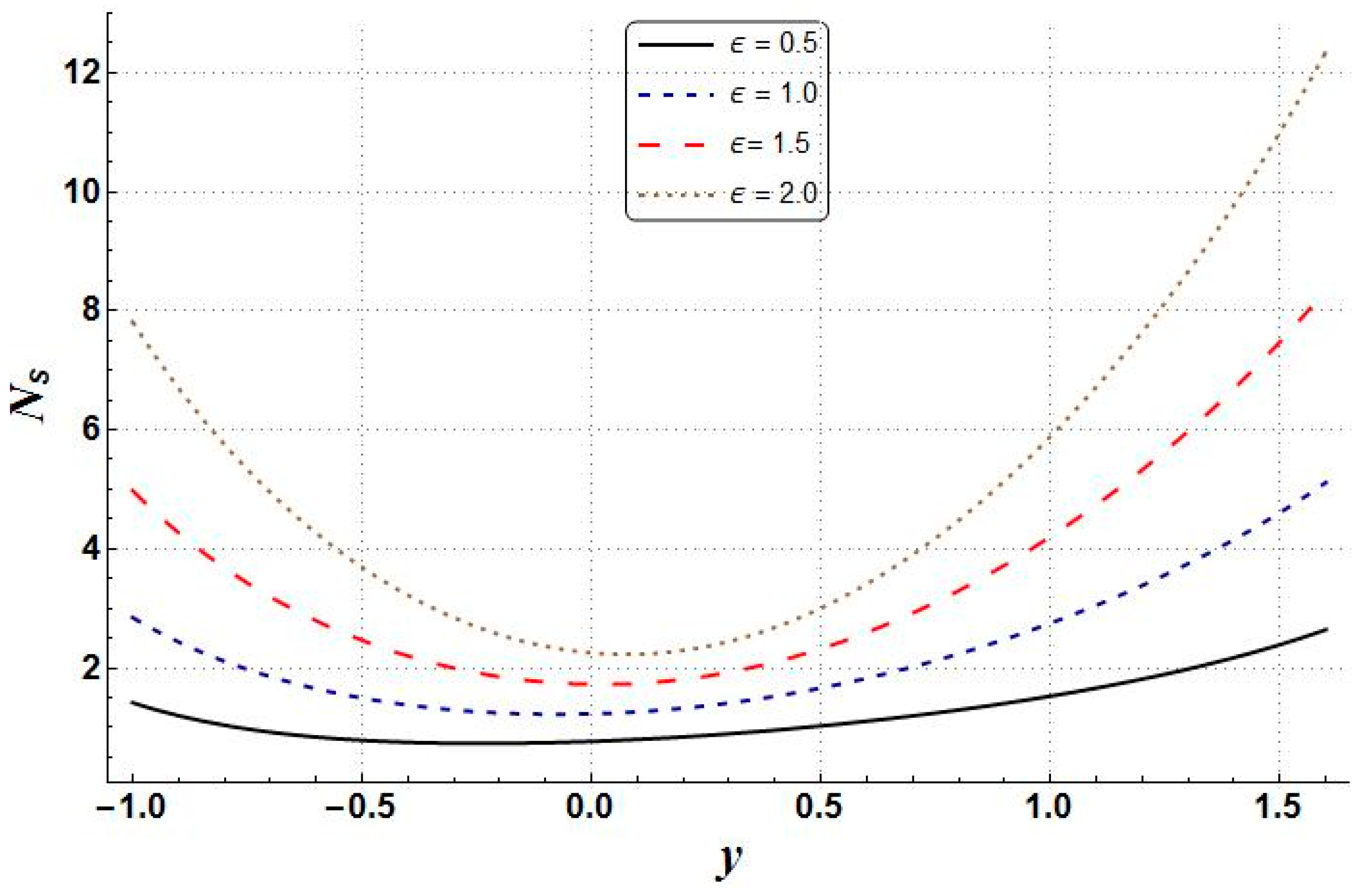
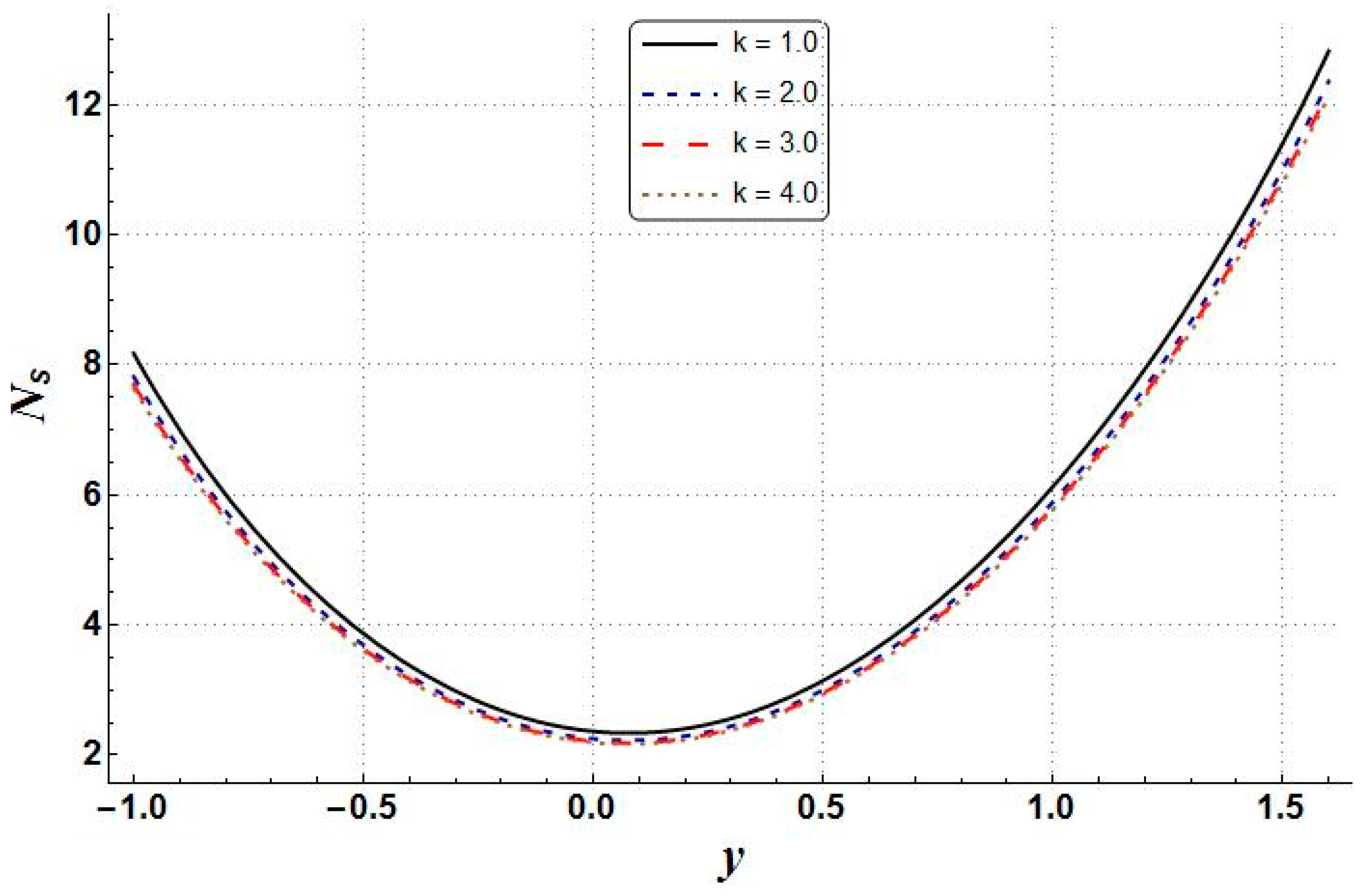
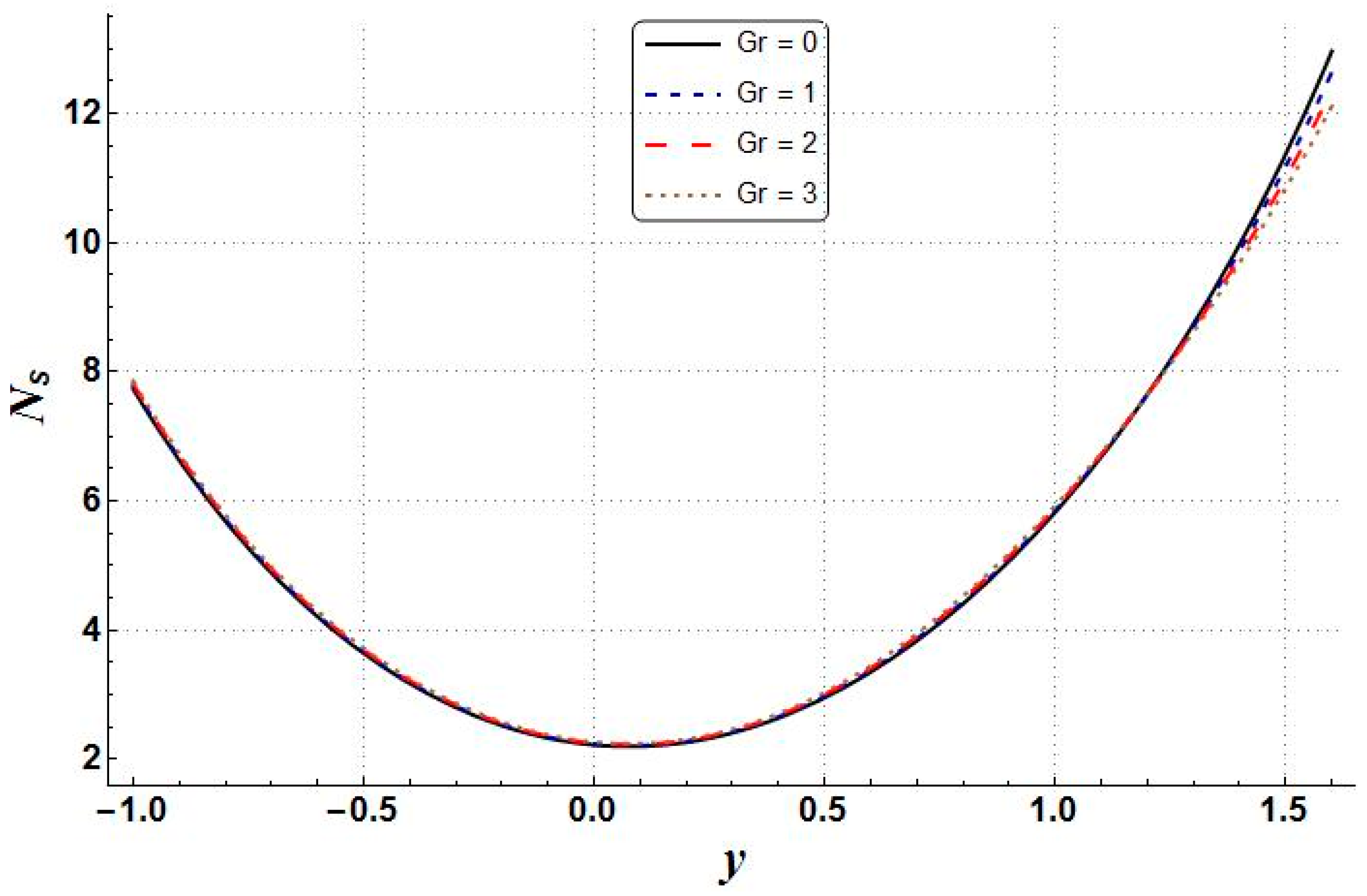
6. Results and Discussion
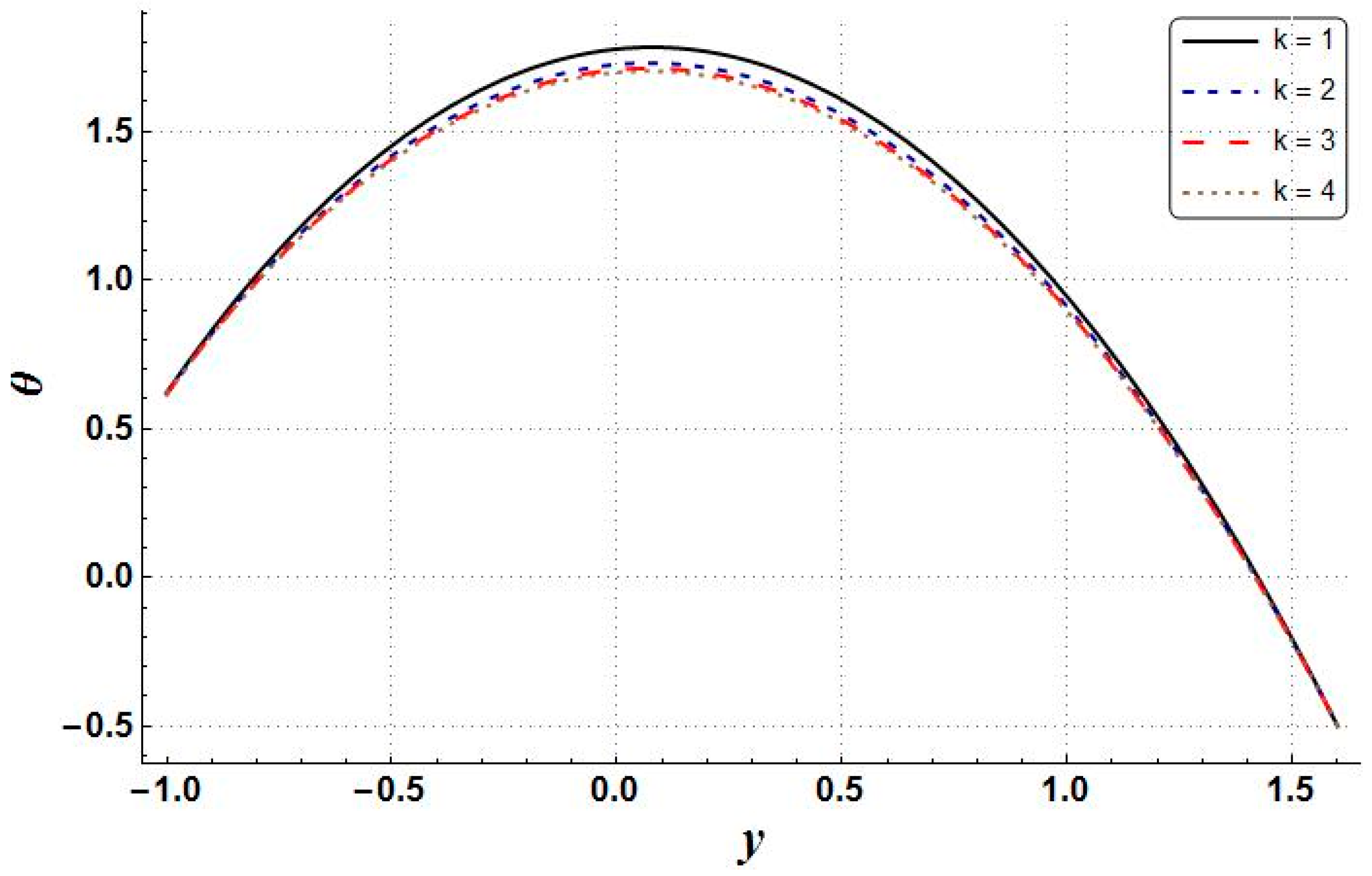
Validation of the Results
7. Conclusions
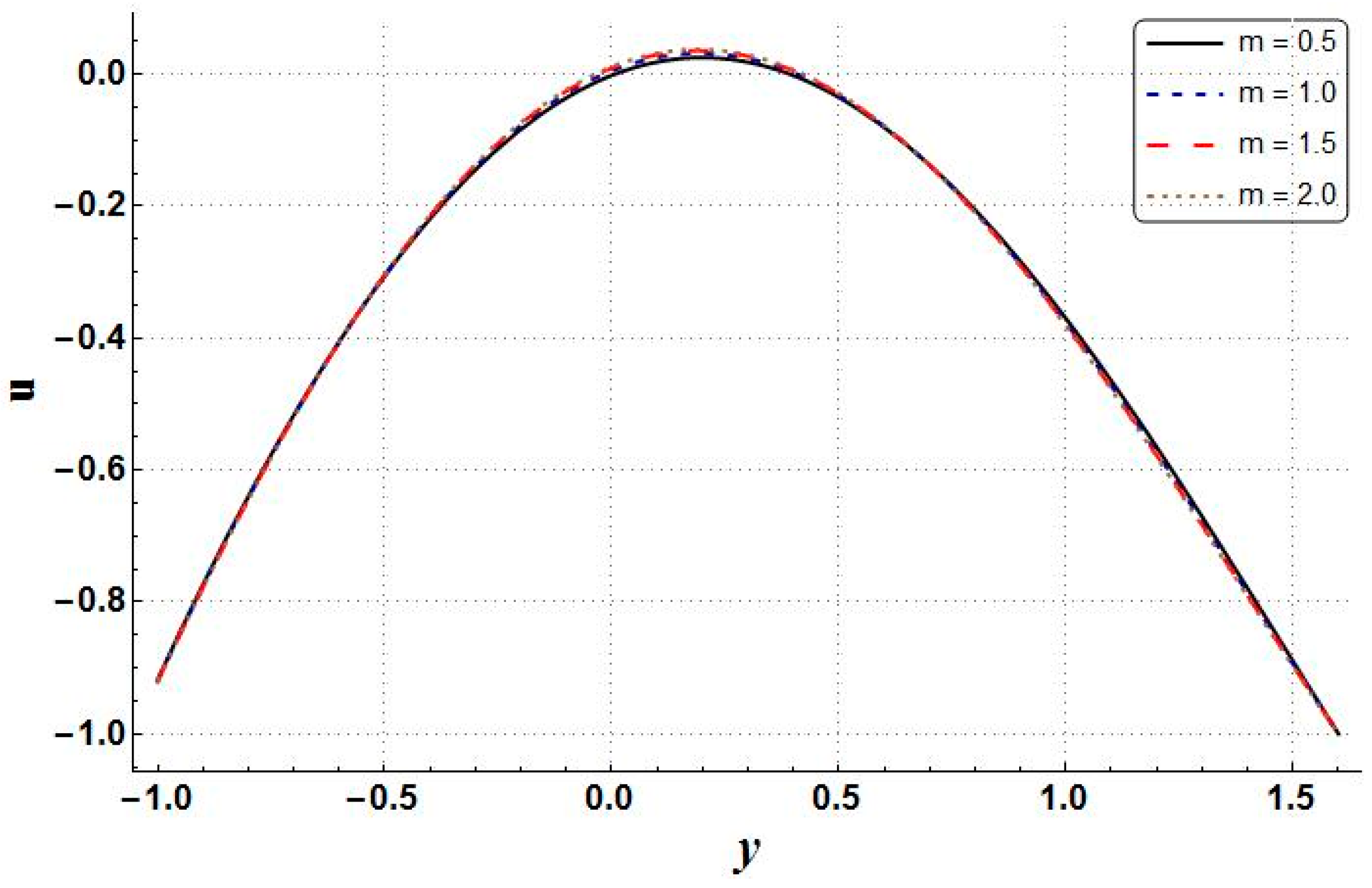
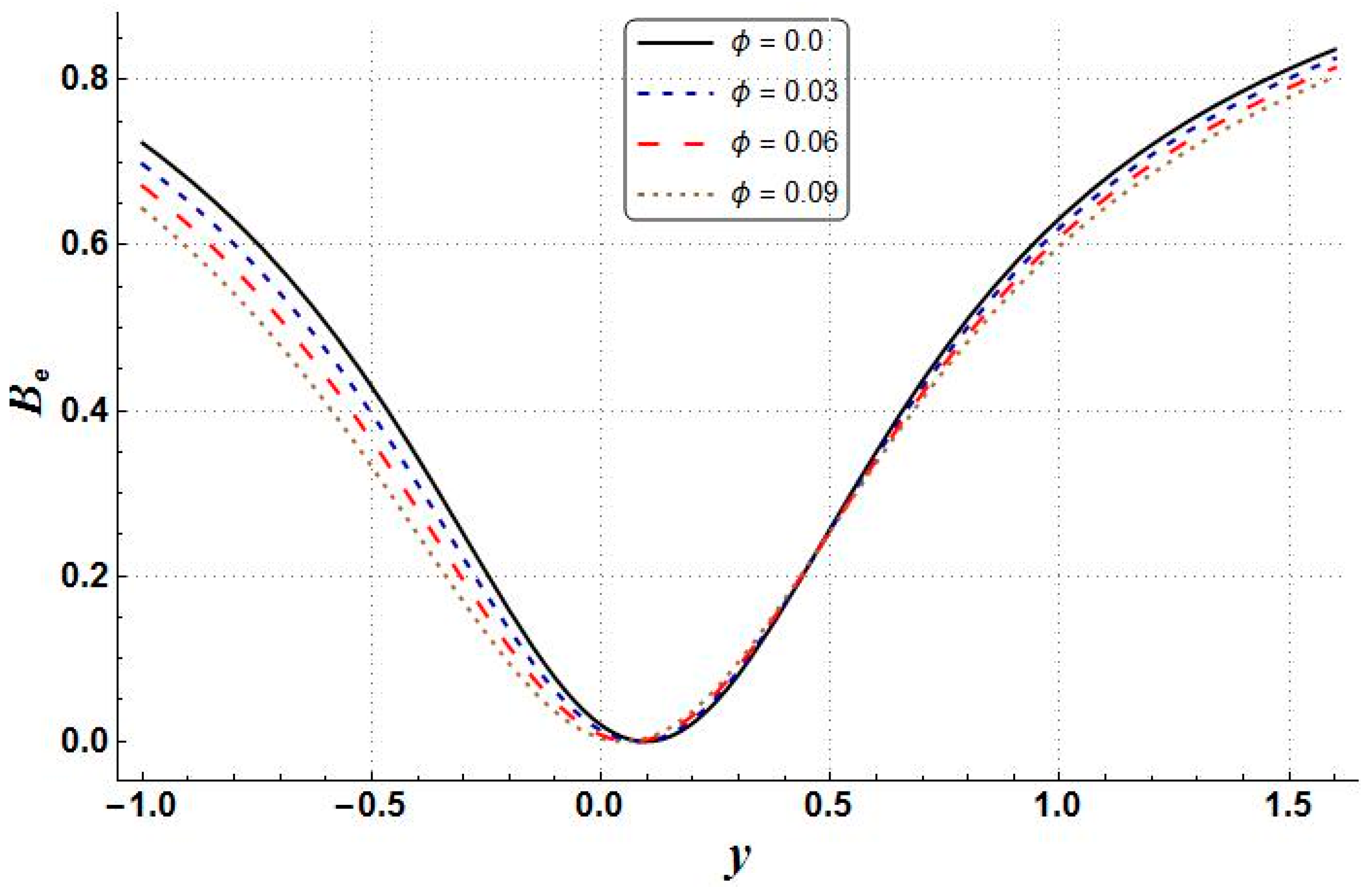
- The growth of nanoparticle volume fraction resulted in the reduction of temperature, entropy generation, velocity, pressure gradient, and Bejan number;
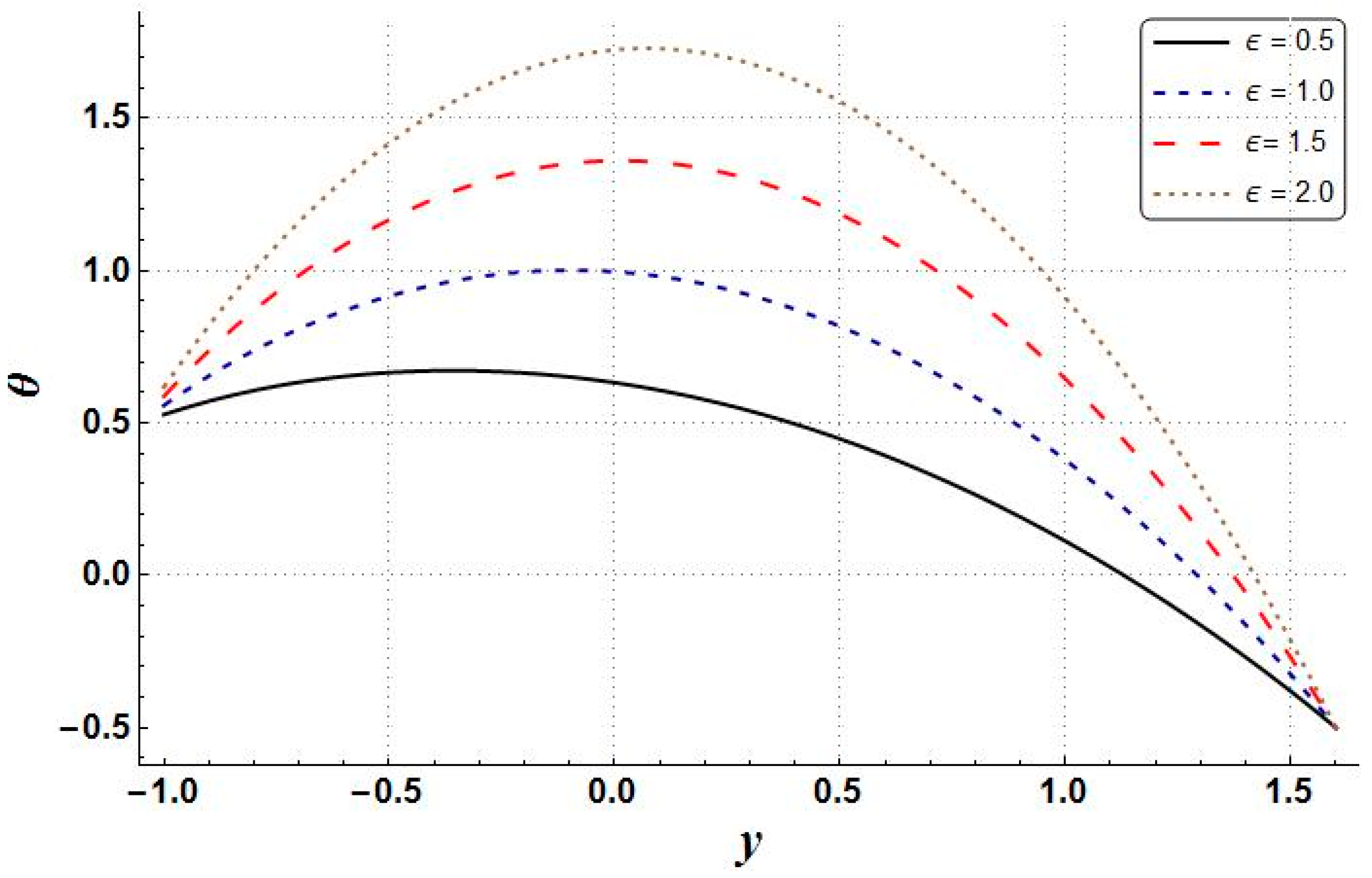
- Increases in the values of entropy generation, Bejan number, and temperature have been noted as being due to increasing values of Hartman number, whereas the velocity profile and pressure gradient behaved in quite the opposite way;
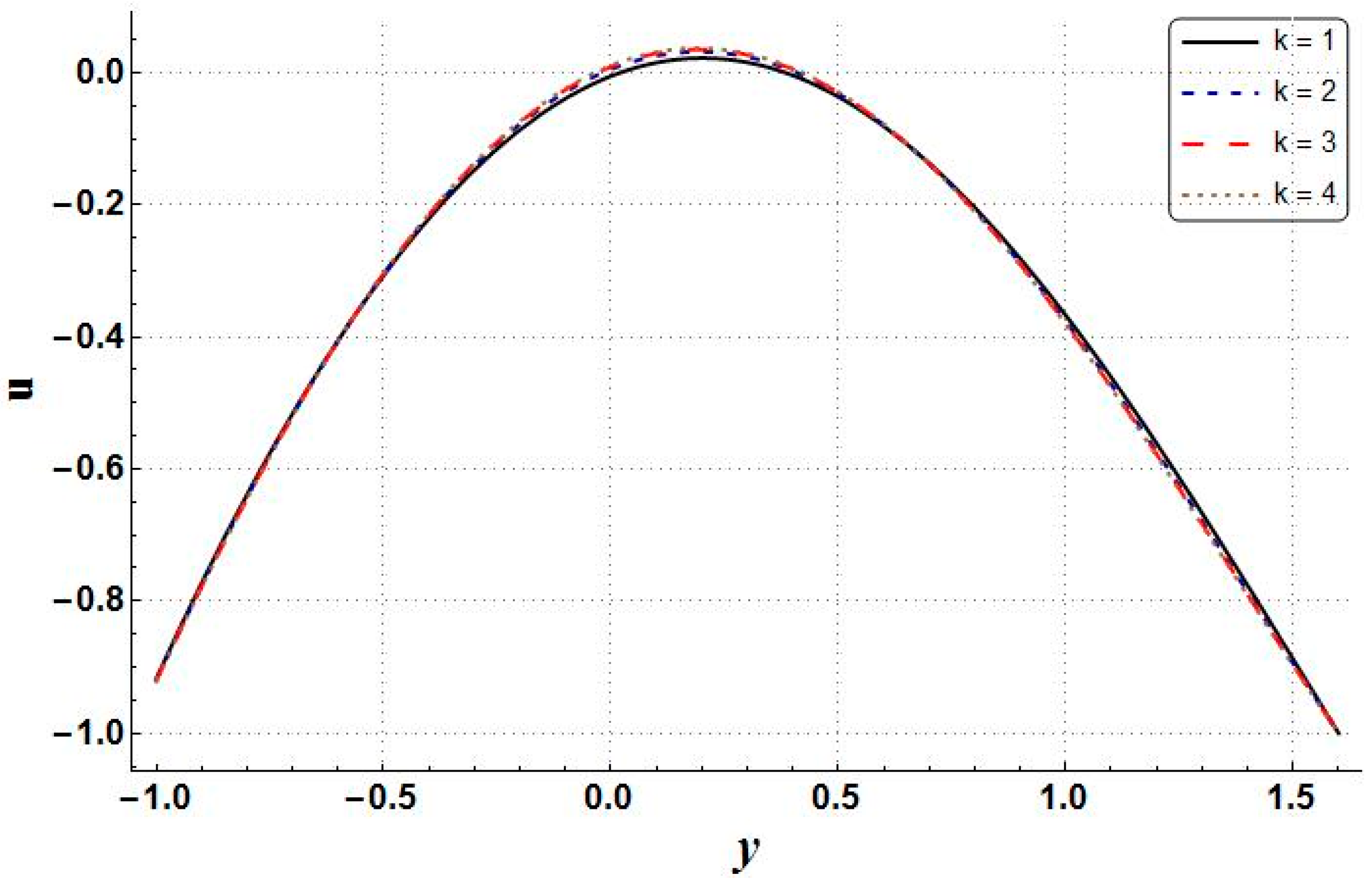
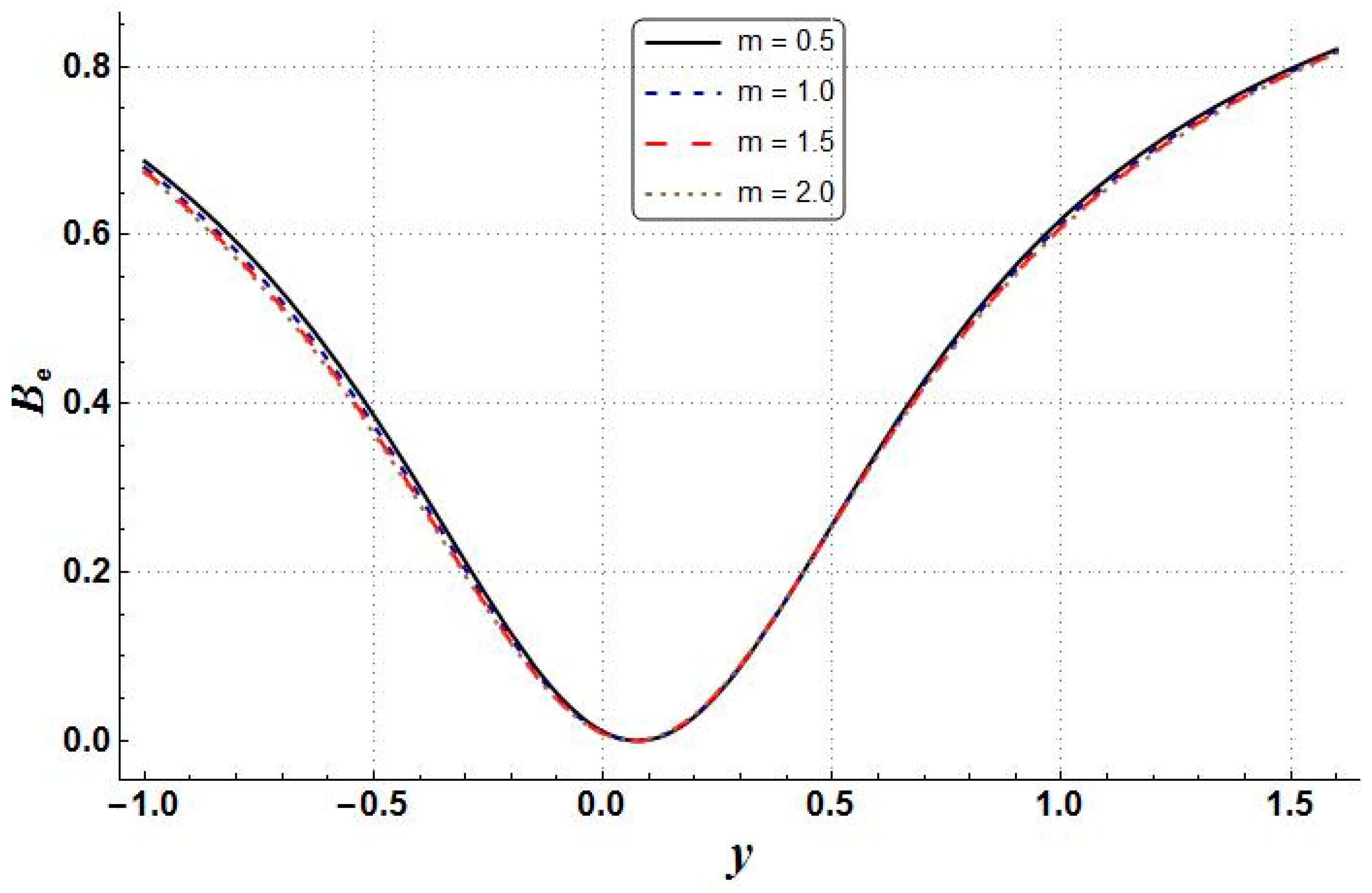
- Reductions in the entropy generation, temperature, and Bejan number were shown to be due to an increase in the Hall parameter, as shown by the relevant figures. However, the velocity of the nanofluid and pressure gradient increased;
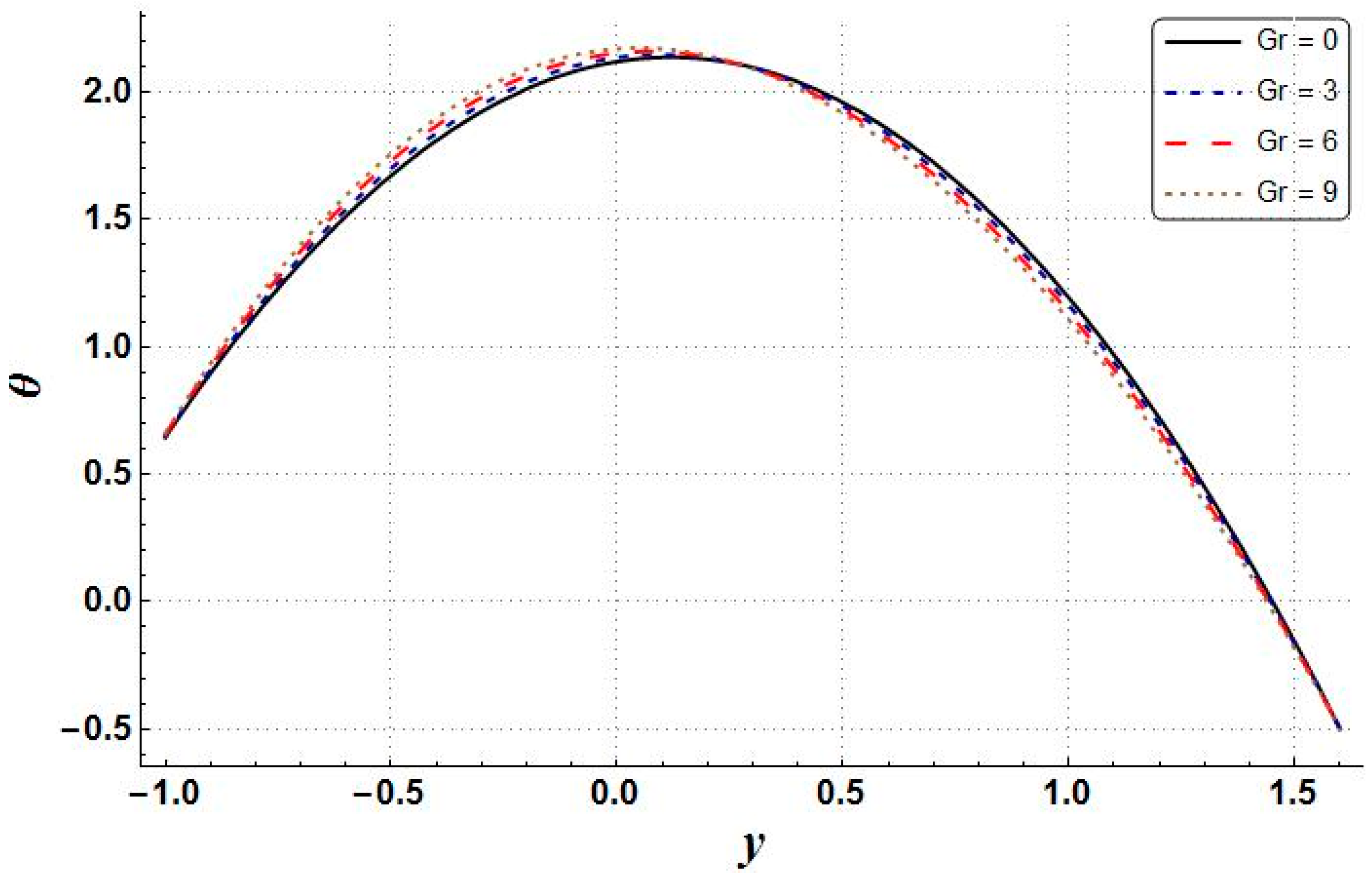
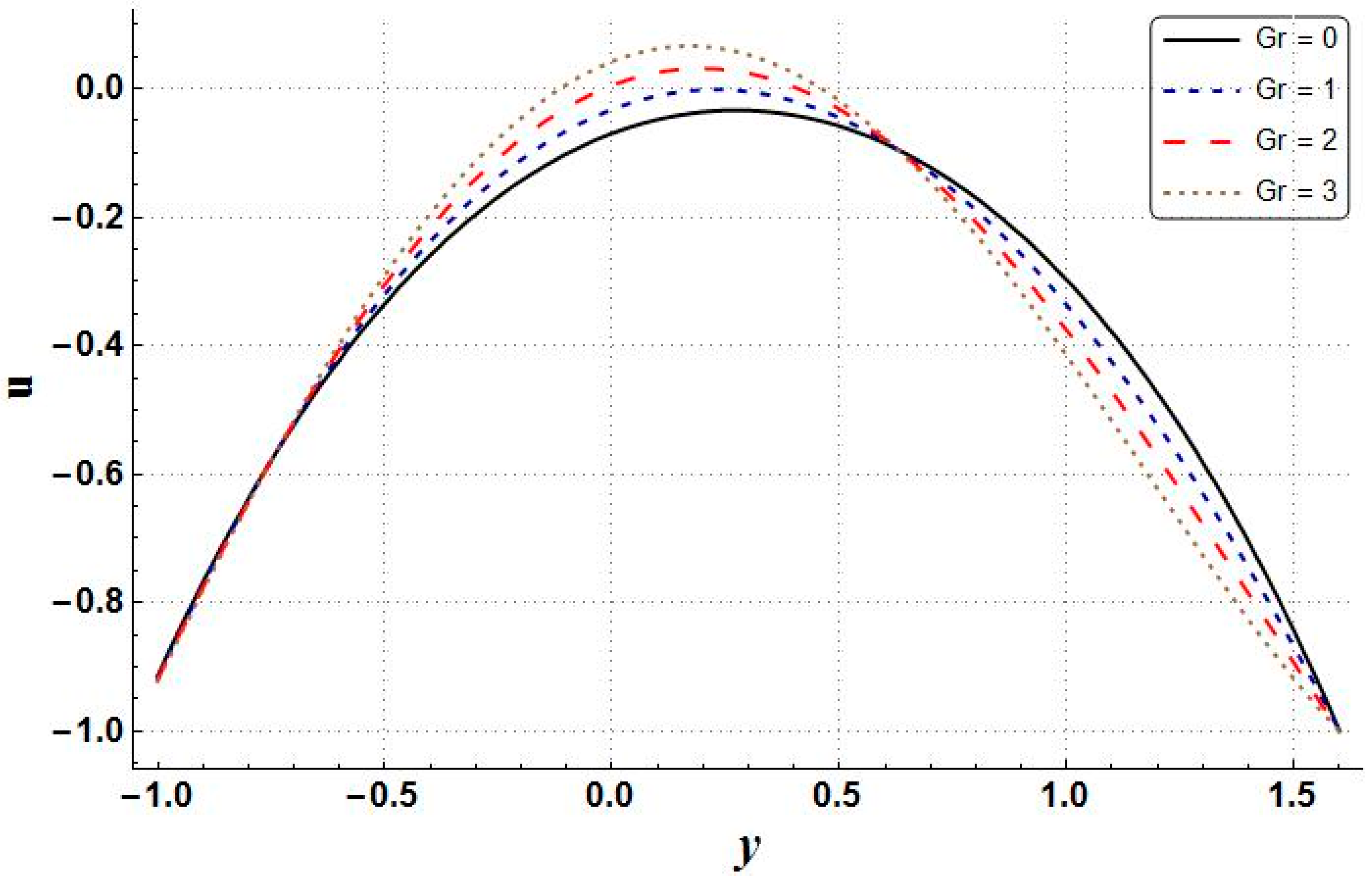
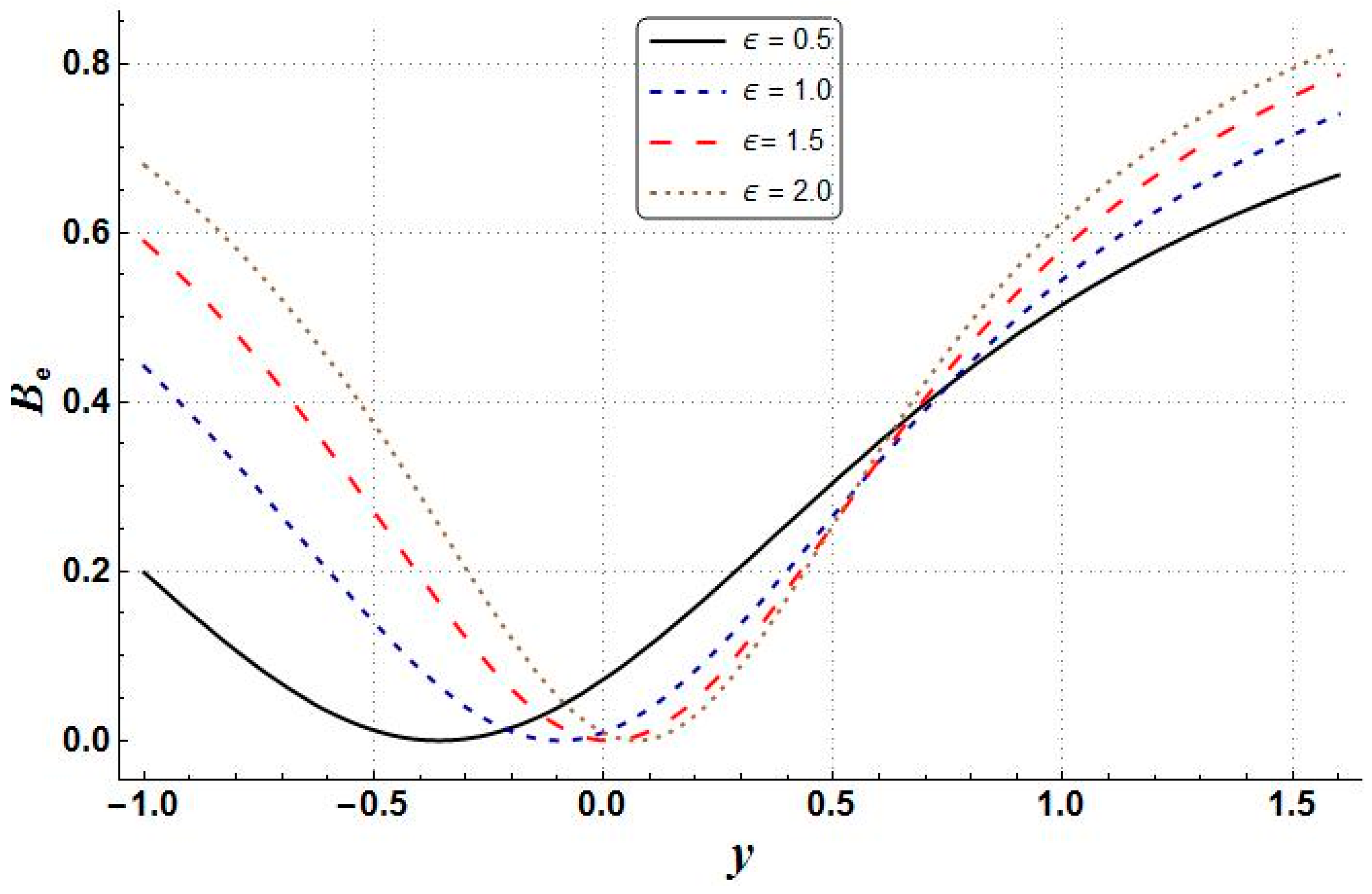
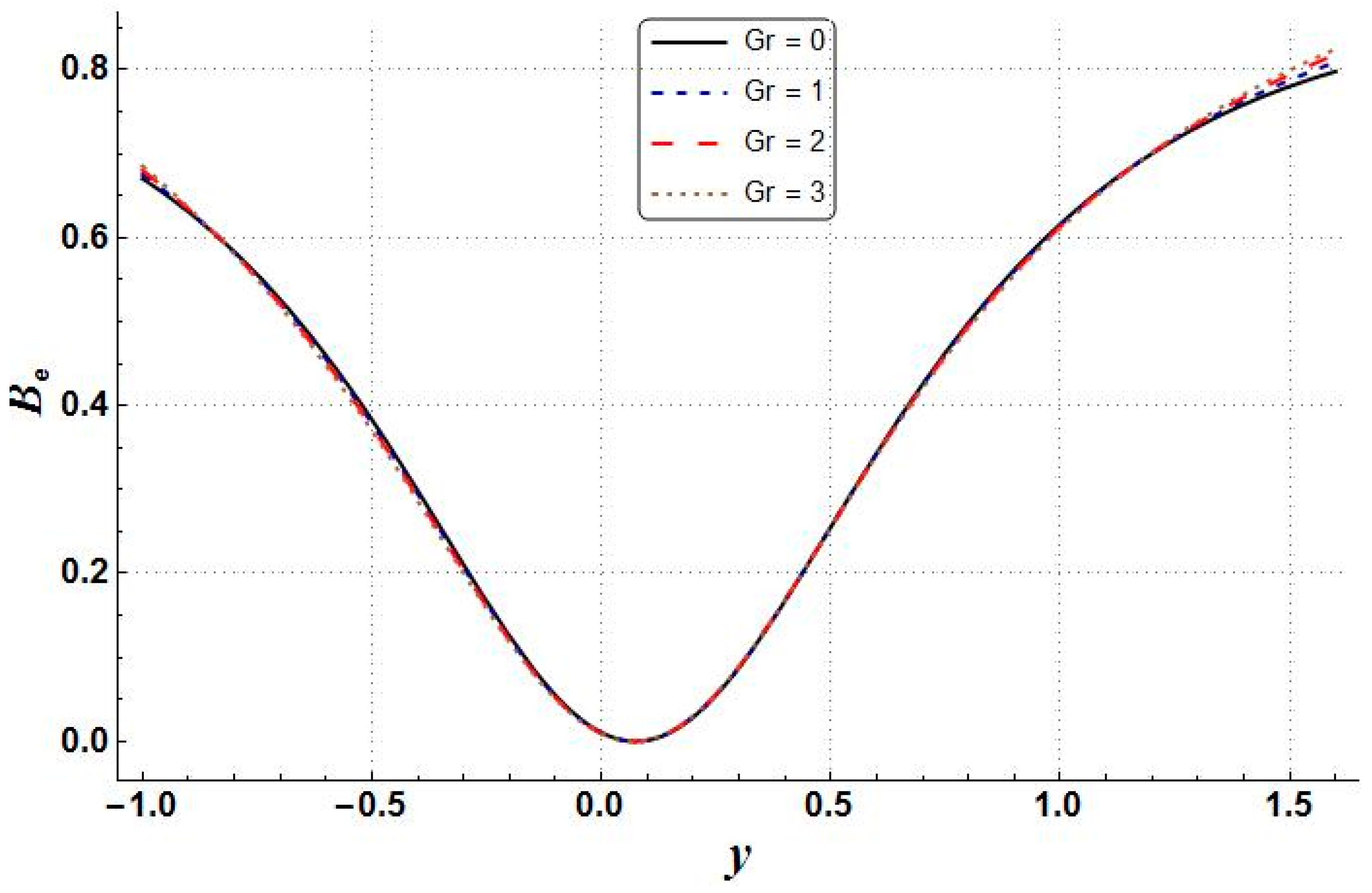
- The velocity, pressure gradient, and Bejan number showed an increasing trend with the increasing values of Grashof number;
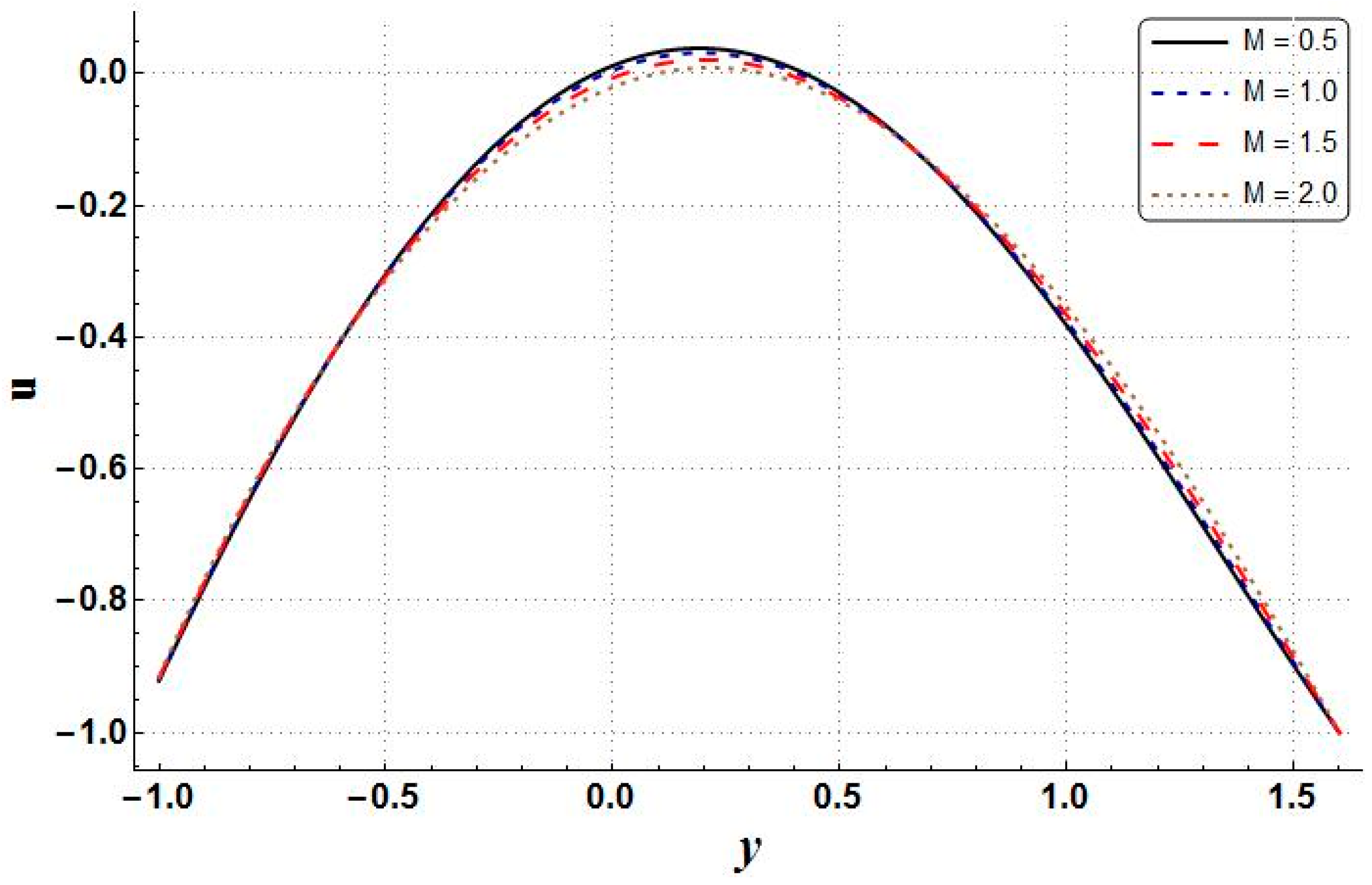
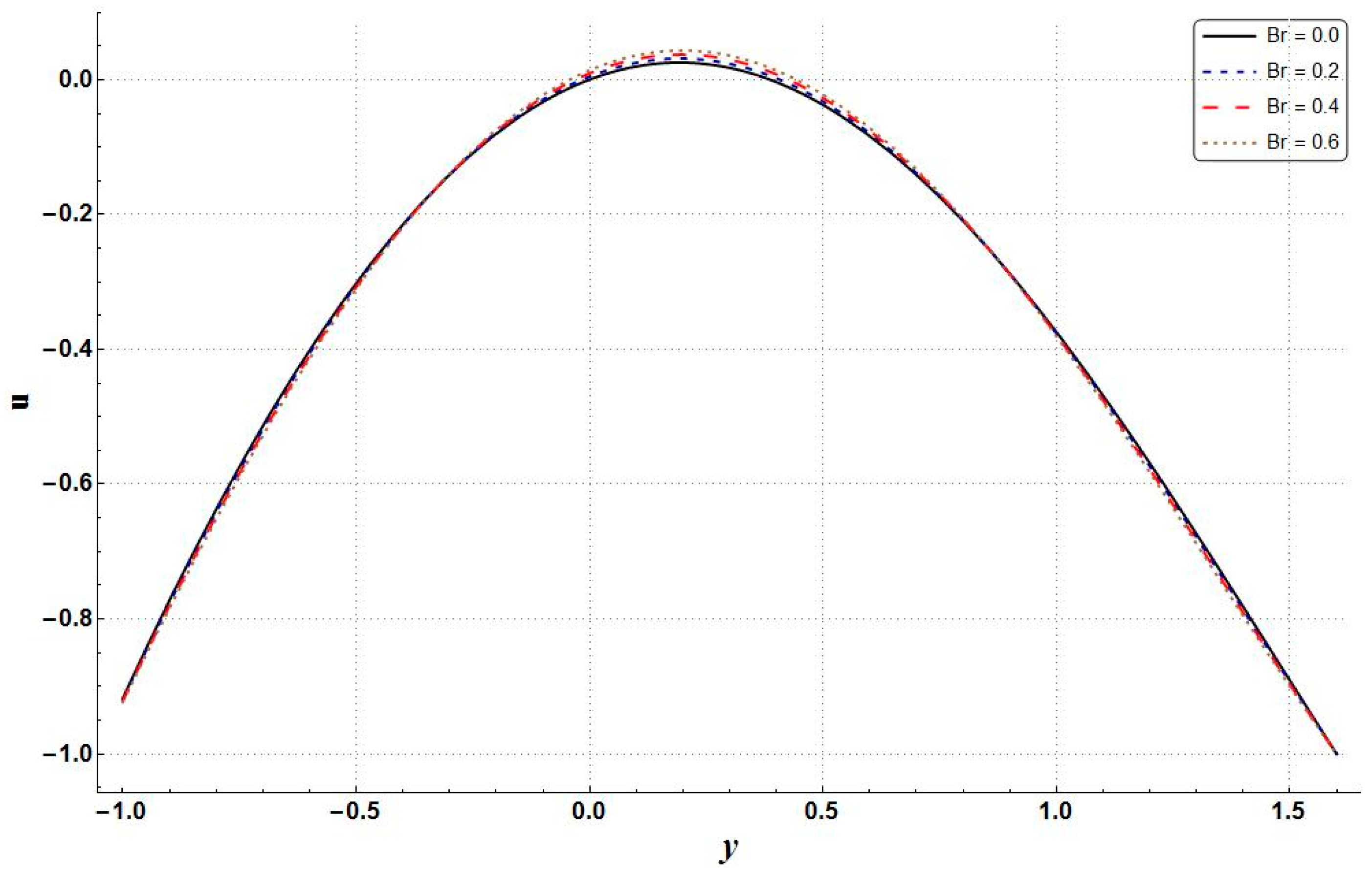
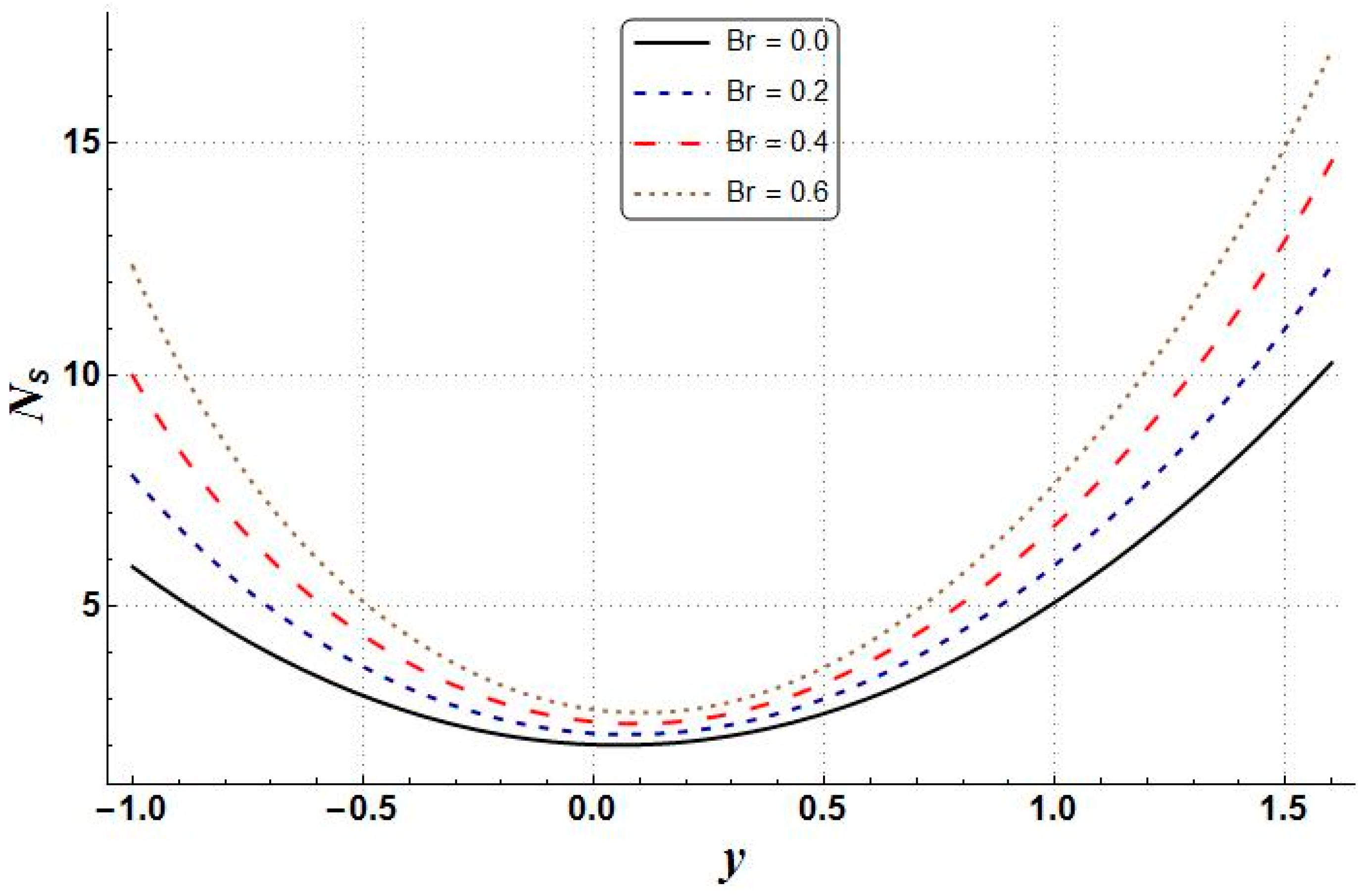
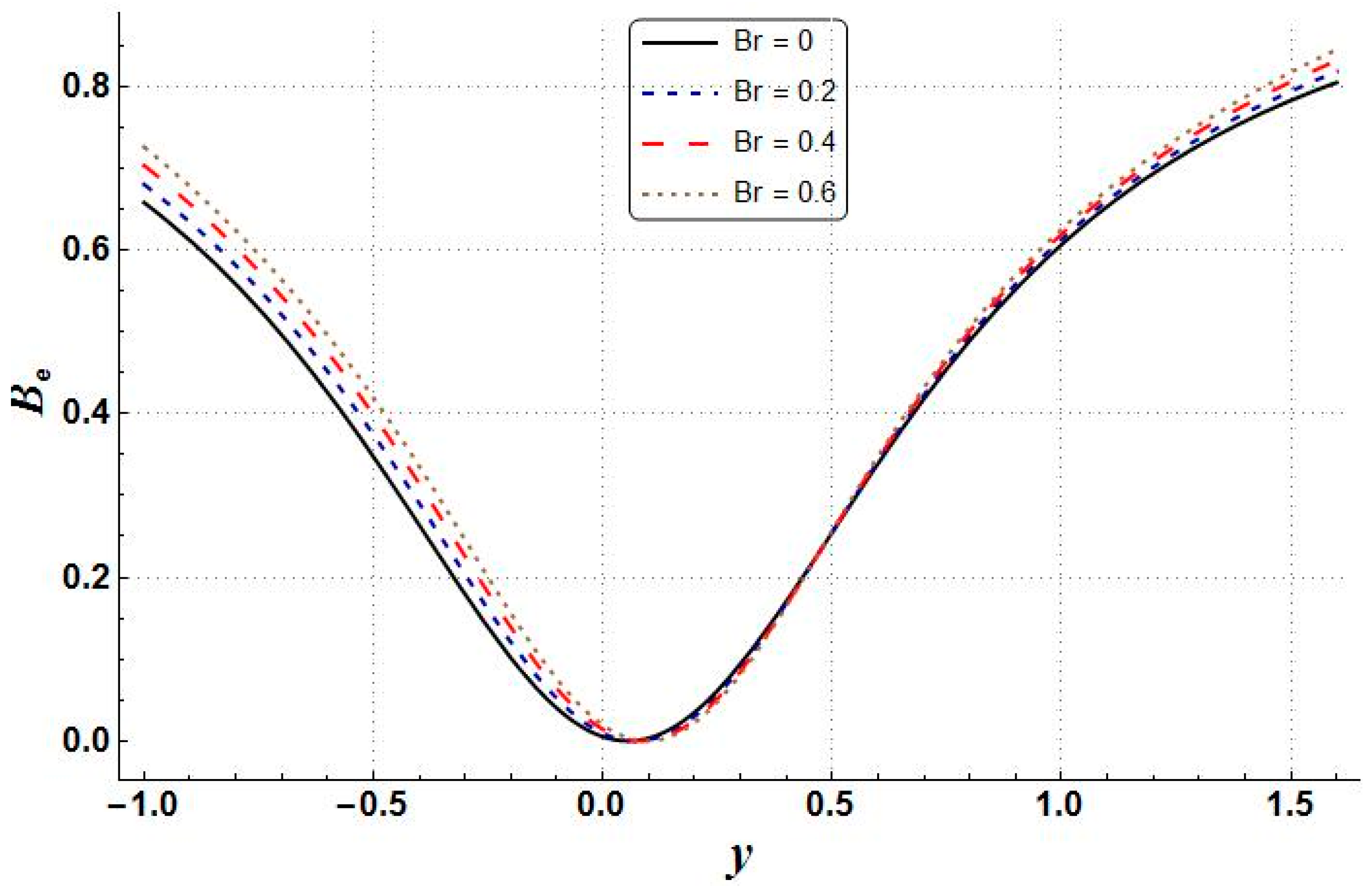
- The entropy generation, temperature, velocity, pressure gradient, and Bejan numbers increased with higher values of Brinkman number.
Funding
Data Availability Statement
Conflicts of Interest
References
- Latham, T.W. Fluid Motion in a Peristaltic Pump. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1966. [Google Scholar]
- Shapiro, A.H.; Jaffrin, M.Y.; Weinberg, S.L. Peristaltic pumping with long wavelengths at low Reynolds number. J. Fluid Mech. 1969, 37, 799–825. [Google Scholar] [CrossRef]
- Lew, S.H.; Fung, Y.C.; Lowenstein, C.B. Peristaltic carrying and mixing of chyme. J. Biomech. 1971, 4, 297–315. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S. Augmentation of peristaltic micro-flows through electro-osmotic mechanisms. J. Phys. D 2006, 39, 5356–5363. [Google Scholar] [CrossRef]
- Riaz, A.; Ellahi, R.; Nadeem, S. Peristaltic transport of a Carreau fluid in a compliant rectangular duct. Alex. Eng. J. 2014, 53, 475–484. [Google Scholar] [CrossRef] [Green Version]
- Abbasi, F.M.; Saba; Shehzad, S. A. Heat transfer analysis for peristaltic flow of Carreau-Yasuda fluid through a curved channel with radial magnetic field. Int. J. Heat Mass Transf. 2017, 115, 777–783. [Google Scholar] [CrossRef]
- Hayat, T.; Ahmed, B.; Abbasi, F.M.; Alsaedi, A. Peristalsis of nanofluid through curved channel with Hall and Ohmic heating effects. J. Cent. South Univ. 2019, 26, 2543–2553. [Google Scholar] [CrossRef]
- Rafiq, M.; Yasmin, H.; Hayat, T.; Alsaadi, F. Effect of Hall and ion-slip on the peristaltic transport of nanofluid: A biomedical application. Chin. J. Phys. 2019, 60, 208–227. [Google Scholar] [CrossRef]
- Eldabe, N.T.; Moatimid, G.M.; Abouzeid, M.Y.; ElShekhipy, A.A.; Abdallah, N.F. A semianalytical technique for MHD peristalsis of pseudo plastic nanofluid with temperature-dependent viscosity: Application in drug delivery system. Heat Transf.-Asian Res. 2020, 49, 424–440. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the 1995 International mechanical engineering congress and exhibition, San Francisco, CA, USA, 12–17 November 1995; Argonne National Lab.: Argonne, IL, USA, 1995; pp. 12–17. [Google Scholar]
- Choi, S.U.S. Enhancing thermal conductivity of fluid with nanofluids. In Developments and Applications of Non-Newtonian Flows; Siginer, D.A., Wang, H., Eds.; Argonne National Lab.: Argonne, IL, USA, 1995; Volume 66, pp. 99–105. [Google Scholar]
- Xue, Q.Z. Model for thermal conductivity of carbon nanotube-based composites. Phys. B Condens. Matter 2005, 368, 302–307. [Google Scholar] [CrossRef]
- Pankhurst, Q.A.; Connolly, J.; Jones, S.K.; Dobson, J. Applications of magnetic nanoparticles in biomedicine. J. Phy. D Appl. Phys. 2003, 36, R167–R181. [Google Scholar] [CrossRef]
- Habibi, M.R.; Ghassemi, M.; Hamedi, M.H. Analysis of high gradient magnetic field effects on distribution of nanoparticles injected into pulsatile blood stream. J. Magn. Magn. Mater. 2012, 324, 1473–1482. [Google Scholar] [CrossRef]
- Hayat, T.; Nisar, Z.; Ahmad, B.; Yasmin, H. Simultaneous effects of slip and wall properties on MHD peristaltic motion of nanofluid with Joule heating. J. Magn. Magn. Mater. 2015, 395, 48–58. [Google Scholar] [CrossRef]
- Ebaid, A. Effects of magnetic field and wall slip conditions on the peristaltic transport of a Newtonian fluid in an asymmetric channel. Phys. Lett. A 2008, 372, 4493–4499. [Google Scholar] [CrossRef]
- Abbasi, F.M.; Hayat, T.; Ahmad, B. Peristalsis of silver-water nanofluid in the presence of Hall and Ohmic heating effects: Application in drug delivery. J. Mol. Liq. 2015, 207, 248–255. [Google Scholar] [CrossRef]
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. ASME J. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization; CRC Press: New York, NY, USA, 1996. [Google Scholar]
- Hijleh, B.A.; Abu-Qudais, M.; Abu-Nada, E. Numerical prediction of entropy generation due to natural convection from a horizontal cylinder. Energy 1999, 24, 327–333. [Google Scholar] [CrossRef]
- Ranjit, N.K.; Shit, G.C. Entropy generation on electro-osmotic flow pumping by a uniform peristaltic wave under magnetic environment. Energy 2017, 128, 649–660. [Google Scholar] [CrossRef]
- Al-Hadhrami, A.K.; Elliott, L.; Ingham, D.B. A new model for viscous dissipation in porous media across a range of permeability values. Transp. Porous Media 2003, 53, 117–122. [Google Scholar] [CrossRef]
- Hayat, T.; Abbasi, F.M.; Ahmad, B.; Chen, G.-Q. Slip effects on mixed convective peristaltic transport of copper-water nanofluid in an inclined channel. PLoS ONE 2014, 9, e105440. [Google Scholar] [CrossRef] [PubMed]
- Bazdar, H.; Toghraie, D.; Pourfattah, F.; Akbari, O.A.; Nguyen, H.M.; Asadi, A. Numerical investigation of turbulent flow and heat transfer of nanofluid inside a wavy microchannel with different wavelengths. J. Therm. Anal. Calorim. 2020, 139, 2365–2380. [Google Scholar] [CrossRef]
- Arasteh, H.; Mashayekhi, R.; Goodarzi, M.; Motaharpour, S.H.; Dahari, M.; Toghraie, D. Heat and fluid flow analysis of metal foam embedded in a double-layered sinusoidal heat sink under local thermal non-equilibrium condition using nanofluid. J. Therm. Anal. Calorim. 2019, 138, 1461–1476. [Google Scholar] [CrossRef]
- Khodabandeh, E.; Rozati, S.A.; Joshaghani, M.; Akbari, O.A.; Akbari, S.; Toghraie, D. Thermal performance improvement in water nanofluid/GNP–SDBS in novel design of double-layer microchannel heat sink with sinusoidal cavities and rectangular ribs. J. Therm. Anal. Calorim. 2019, 136, 1333–1345. [Google Scholar] [CrossRef]
- Boroomandpour, A.; Toghraie, D.; Hashemian, M. A comprehensive experimental investigation of thermal conductivity of a ternary hybrid nanofluid containing MWCNTs-titania-zinc oxide/water-ethylene glycol (80:20). Synth. Met. 2020, 268, 116501. [Google Scholar] [CrossRef]
- Akbari, S.; Faghiri, S.; Poureslami, P.; Hosseinzadeh, K.; Shafii, M.B. Analytical solution of non-Fourier heat conduction in a 3-D hollow sphere under time-space varying boundary conditions. Heliyon 2022, 8, e12496. [Google Scholar] [CrossRef]
- Faghiri, S.; Akbari, S.; Shafii, M.B.; Hosseinzadeh, K. Hydrothermal analysis of non-Newtonian fluid flow (blood) through the circular tube under prescribed non-uniform wall heat flux. Theor. Appl. Mech. Lett. 2022, 12, 100360. [Google Scholar] [CrossRef]
- Gulzar, M.M.; Aslam, A.; Waqas, M.; Javed, M.A.; Hosseinzadeh, K. A nonlinear mathematical analysis for magneto-hyperbolic-tangent liquid featuring simultaneous aspects of magnetic field, heat source and thermal stratification. Appl. Nanosci. 2020, 10, 4513–4518. [Google Scholar] [CrossRef]
- Ramesh, K. Influence of heat and mass transfer on peristaltic flow of a couple stress fluid through porous medium in the presence of inclined magnetic field in an inclined asymmetric channel. J. Mol. Liq. 2016, 71, 219–256. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Nanofluid flow and heat transfer due to a rotating disk. Comput. Fluids 2014, 94, 139–146. [Google Scholar] [CrossRef]
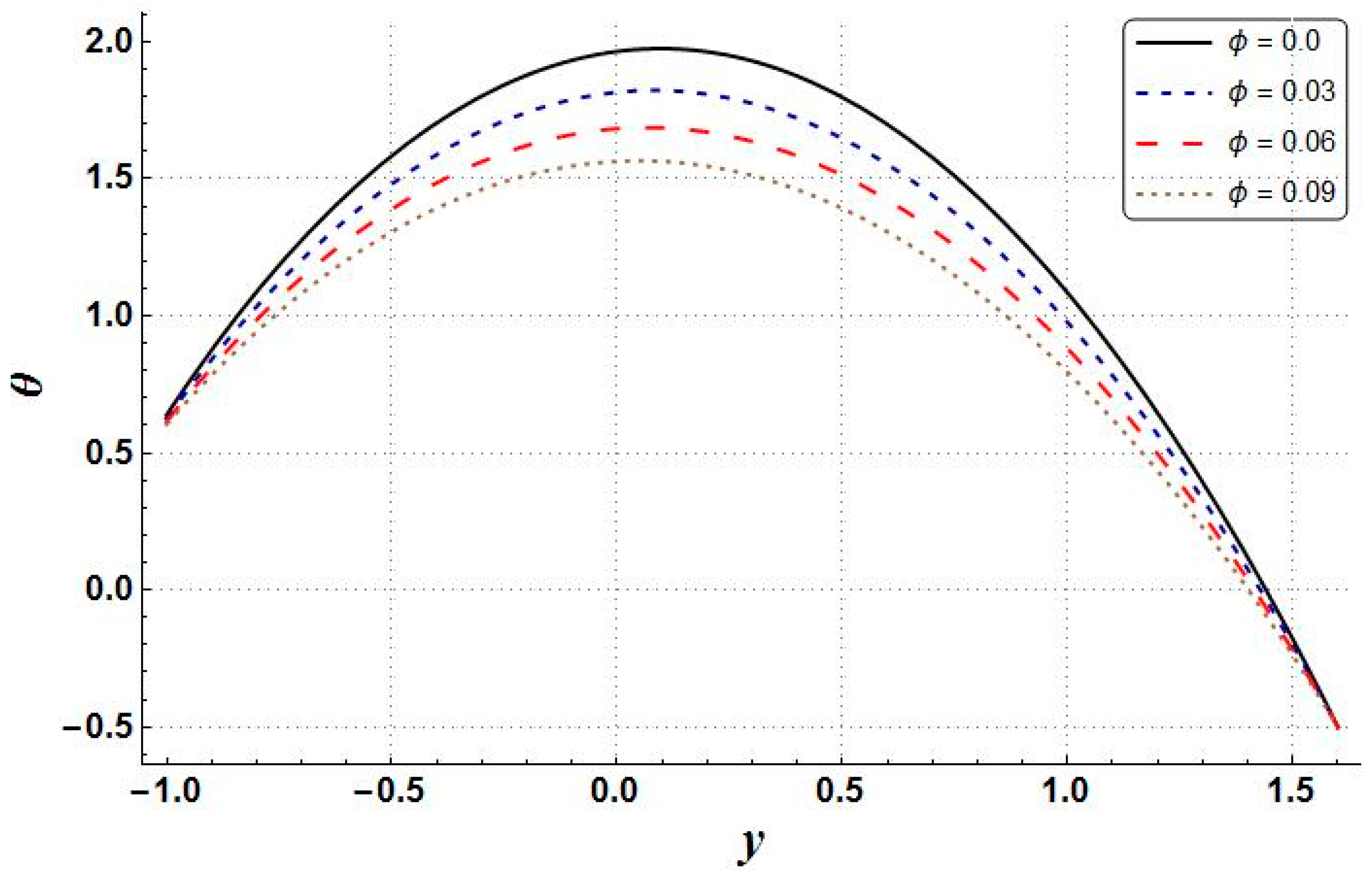
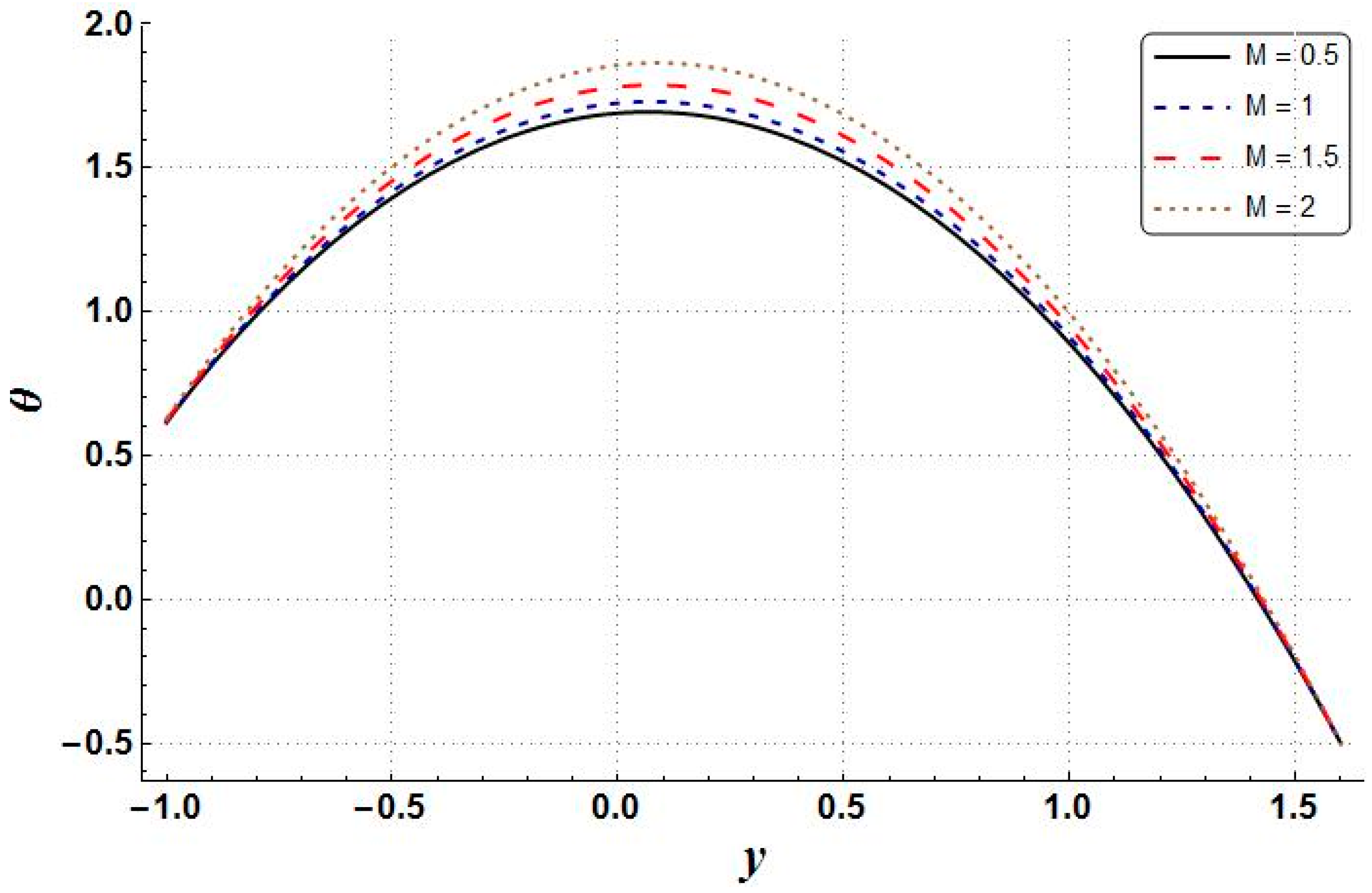
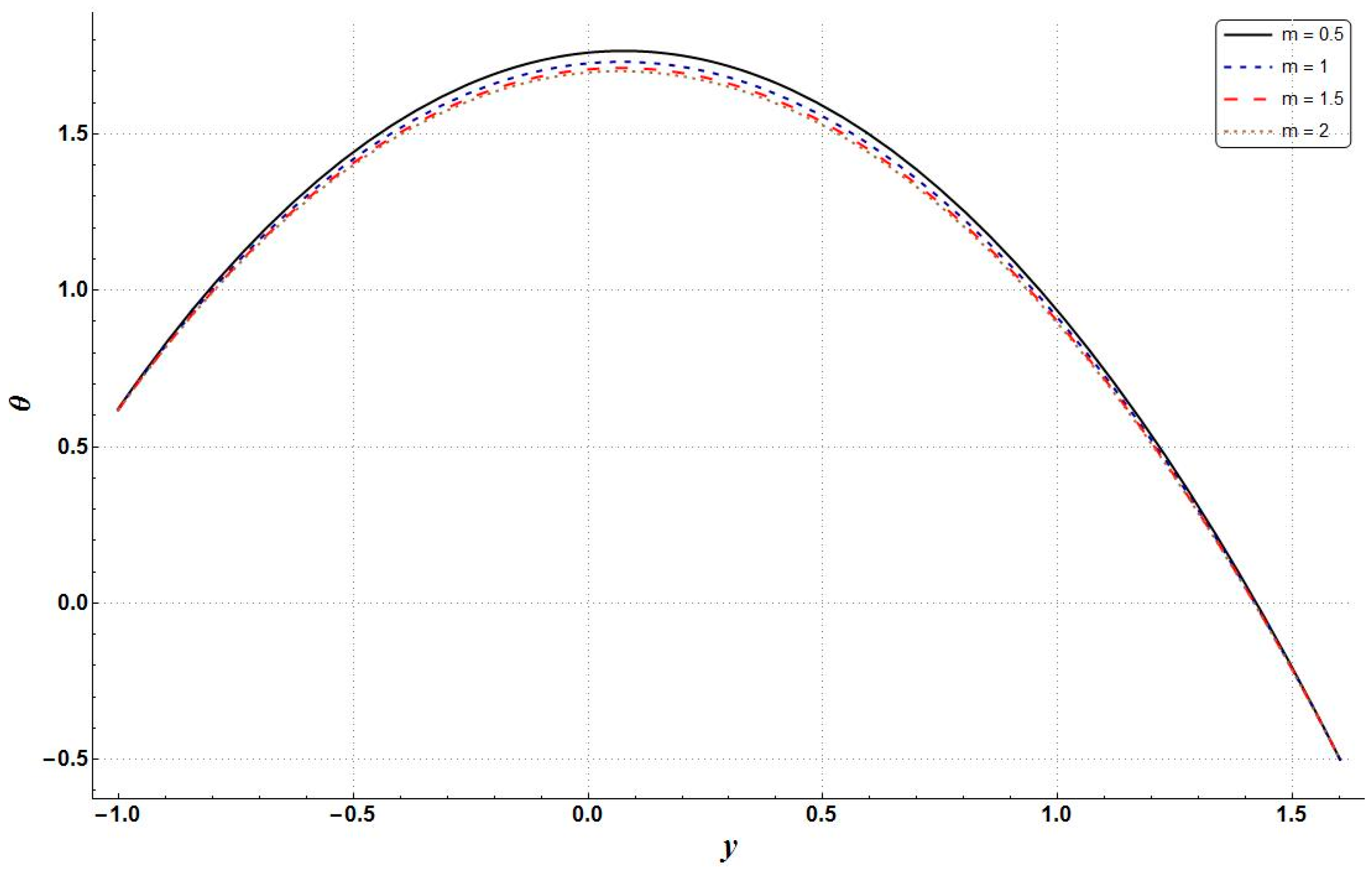



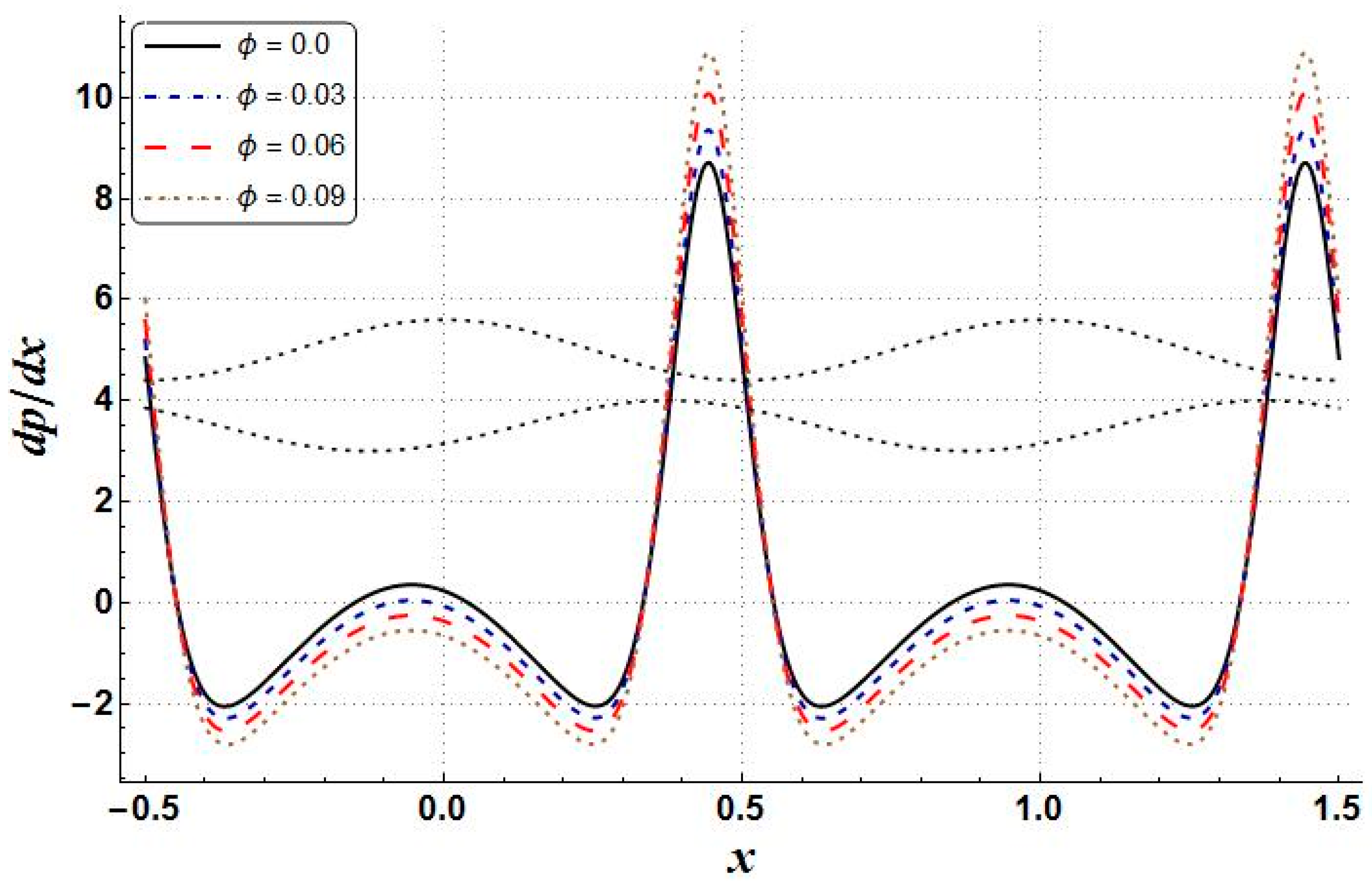
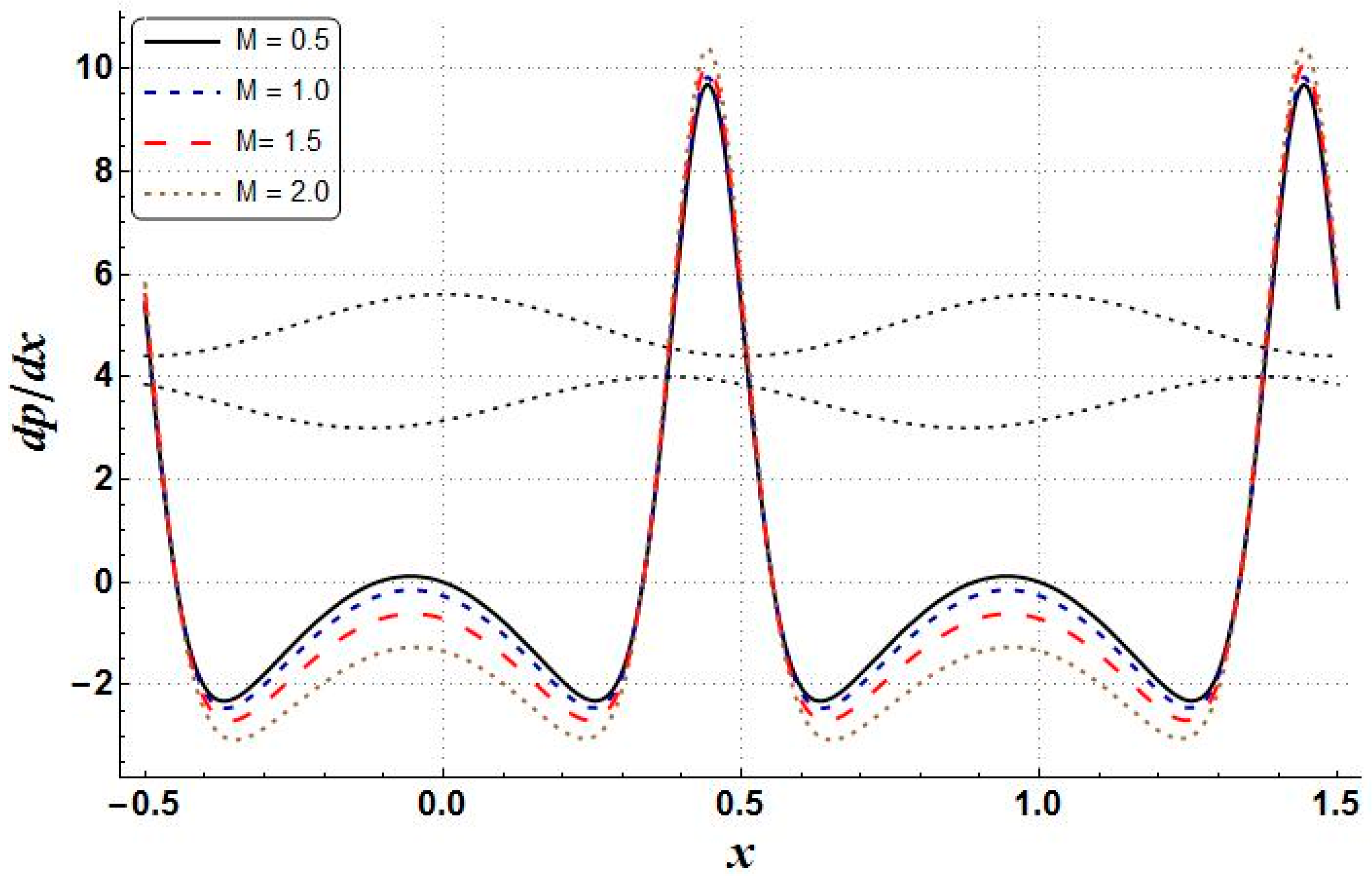
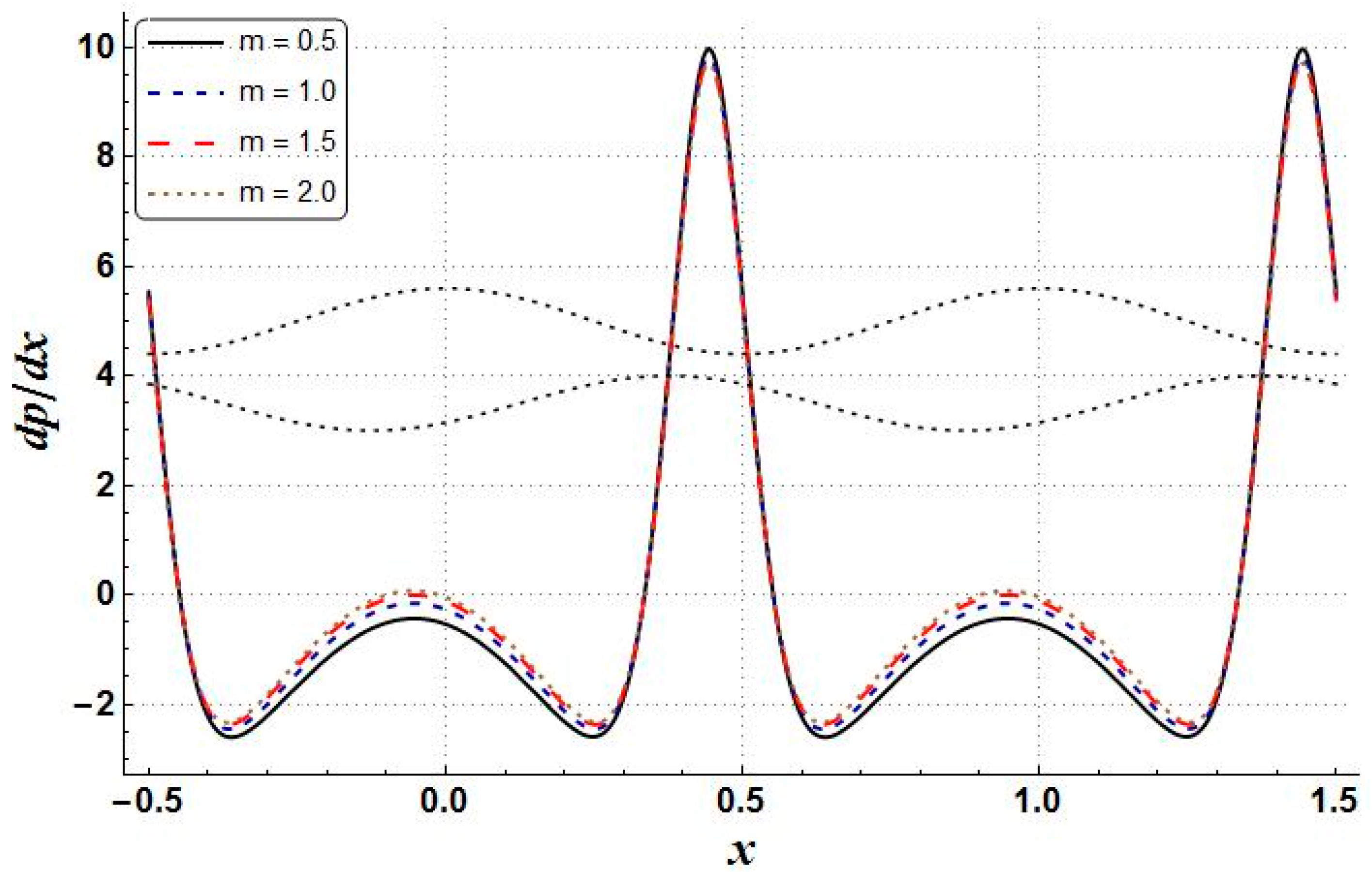




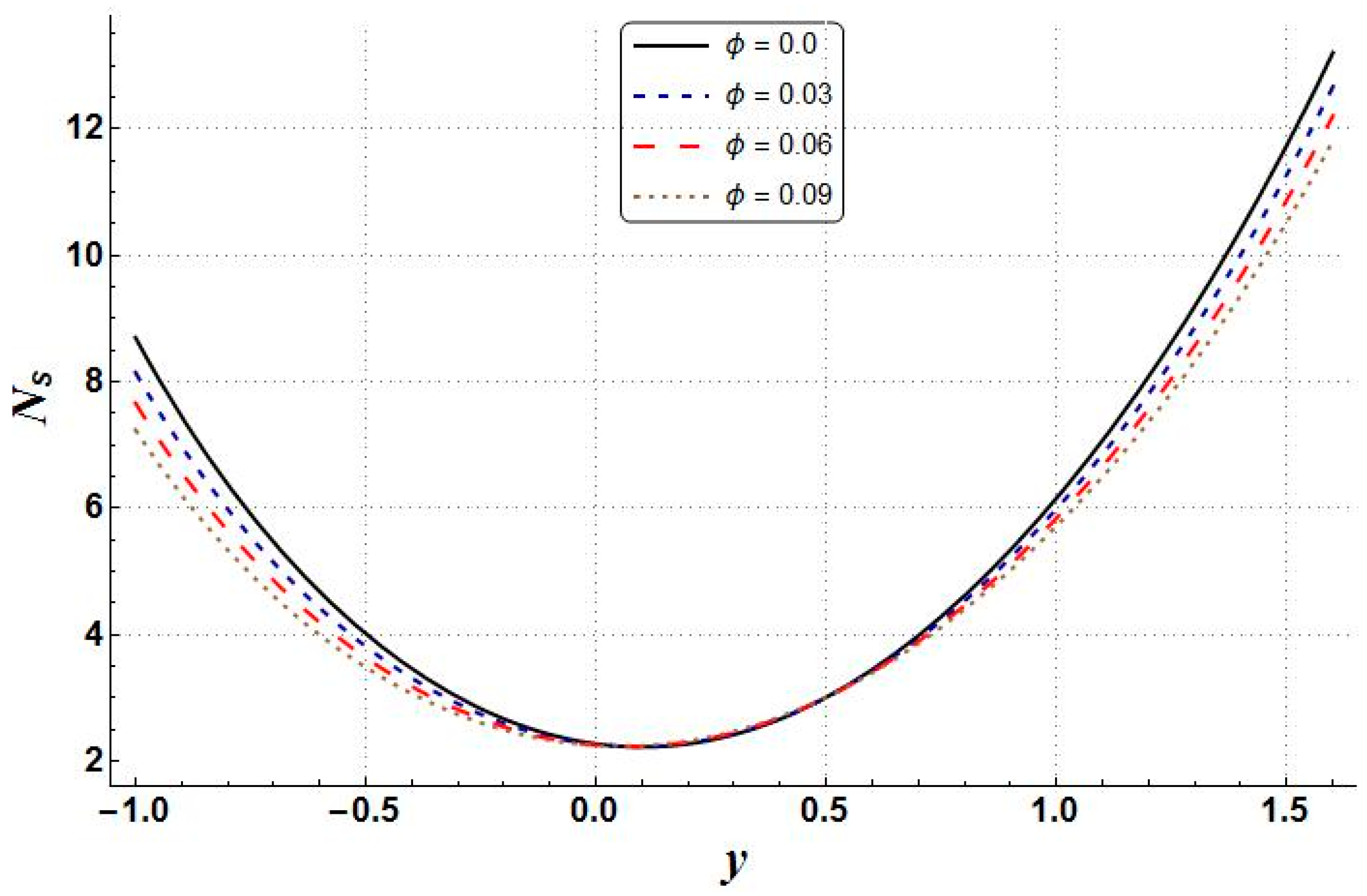



| Property | Base Fluid (Water) | Copper |
|---|---|---|
| 997.1 | 8933 | |
| 0.613 | 401 | |
| 4179 | 385 | |
| 210 | 16.65 | |
| 0.05 | 5.96 × 107 |
| Difference % | |||
|---|---|---|---|
| 0.0 | 3.3471 | 3.34155 | 0.55 |
| 0.03 | 3.3999058 | 3.39625 | 0.36 |
| 0.06 | 3.4574883 | 3.45552 | 0.19 |
| 0.09 | 3.5203507 | 3.51908 | 0.12 |
| m | Difference % | ||
|---|---|---|---|
| 0.5 | 3.48729 | 3.487743 | 0.045 |
| 1.0 | 3.43773 | 3.435047 | 0.4 |
| 1.5 | 3.41023 | 3.405980 | 0.42 |
| 2.0 | 3.39607 | 3.391042 | 0.52 |
| Br | Difference % | ||
|---|---|---|---|
| 0.0 | 3.089619 | 3.089619 | 0.00000 |
| 0.2 | 3.437732 | 3.435047 | 0.26 |
| 0.4 | 3.789015 | 3.781528 | 0.74 |
| 0.6 | 4.144163 | 4.129062 | 1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alrashdi, A.M.A. Peristalsis of Nanofluids via an Inclined Asymmetric Channel with Hall Effects and Entropy Generation Analysis. Mathematics 2023, 11, 458. https://doi.org/10.3390/math11020458
Alrashdi AMA. Peristalsis of Nanofluids via an Inclined Asymmetric Channel with Hall Effects and Entropy Generation Analysis. Mathematics. 2023; 11(2):458. https://doi.org/10.3390/math11020458
Chicago/Turabian StyleAlrashdi, Abdulwahed Muaybid A. 2023. "Peristalsis of Nanofluids via an Inclined Asymmetric Channel with Hall Effects and Entropy Generation Analysis" Mathematics 11, no. 2: 458. https://doi.org/10.3390/math11020458




