Global Asymptotic Stability and Synchronization of Fractional-Order Reaction–Diffusion Fuzzy BAM Neural Networks with Distributed Delays via Hybrid Feedback Controllers
Abstract
:1. Introduction
2. Preliminaries and Problem Definition
3. Global Asymptotic Stability via State Feedback Control
4. Global Mittag–Leffler Synchronization
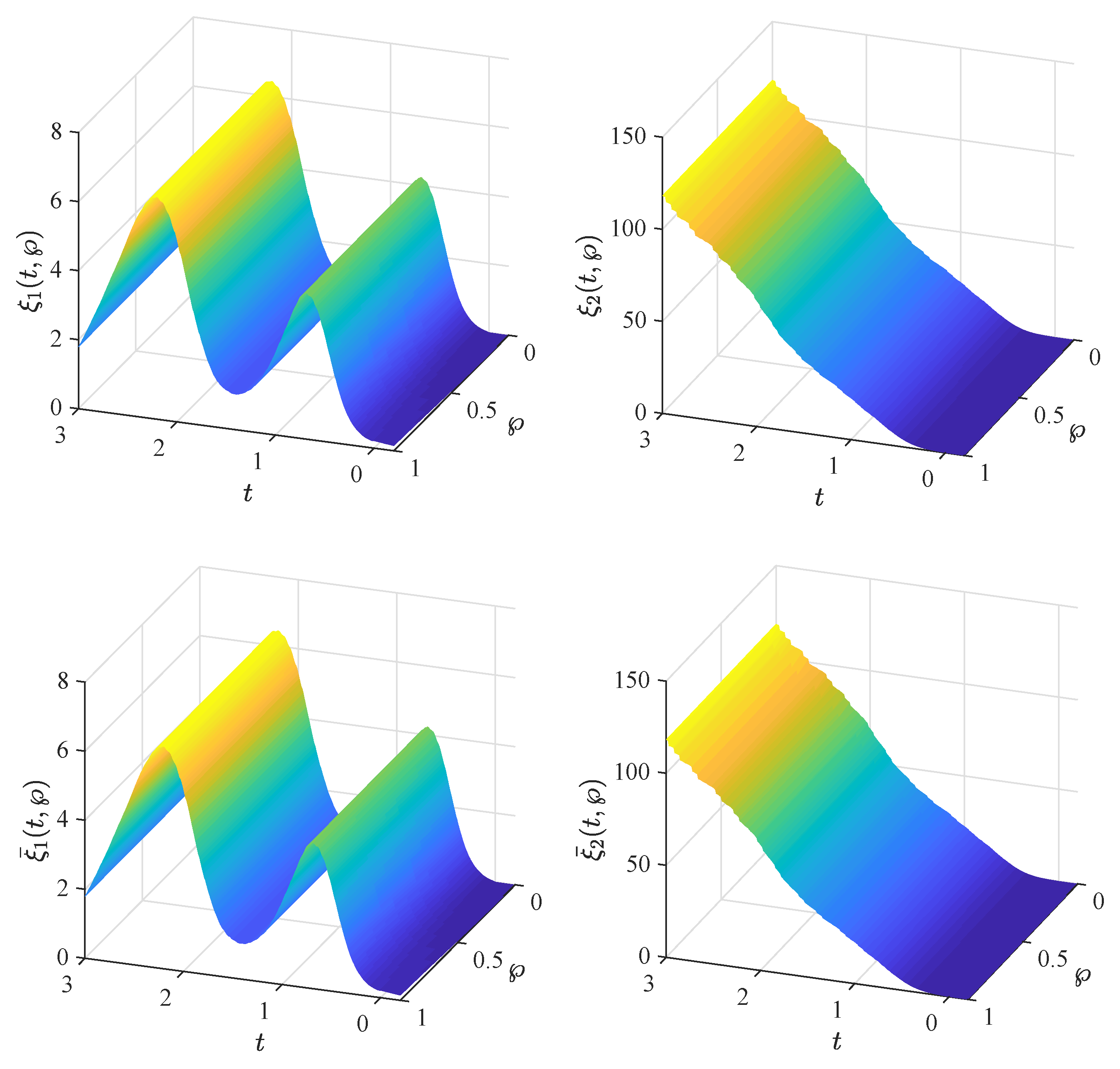
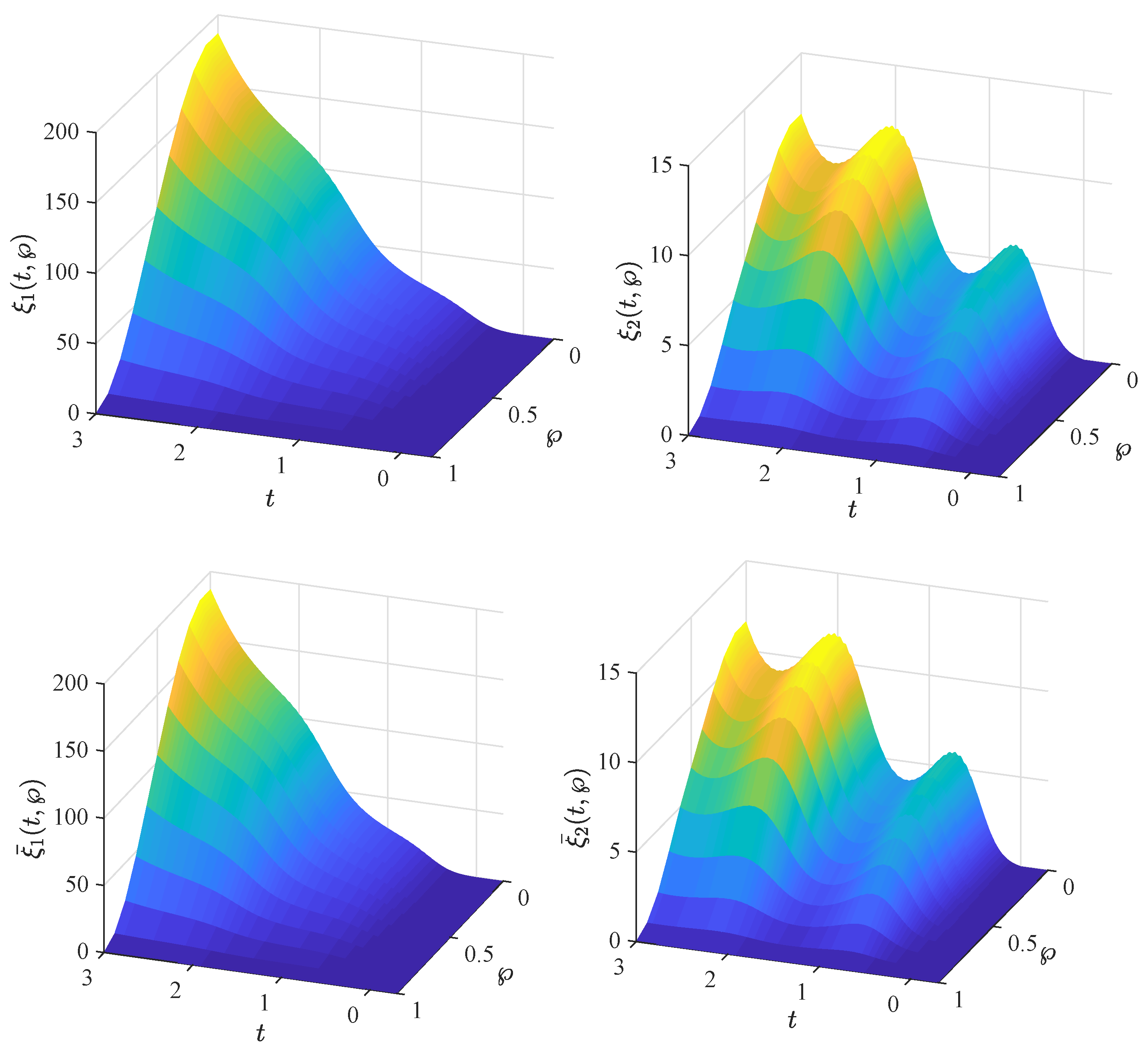
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Syed Ali, M.; Hymavathi, M.; Saroha, S.; Krishna Moorthy, R. Global asymptotic stability of neutral type fractional-order memristor-based neural networks with leakage term, discrete and distributed delays. Math. Methods Appl. Sci. 2021, 44, 5953–5973. [Google Scholar] [CrossRef]
- Syed Ali, M.; Hymavathi, M.; Rajchakit, G.; Saroha, S.; Palanisamy, L.; Hammachukiattikul, P. Synchronization of fractional order fuzzy BAM neural networks with time varying delays and reaction diffusion terms. IEEE Access 2020, 8, 186551–186571. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods, 1st ed.; World Scientific: Singapore, 2012; ISBN 978-981-4355-20-9. [Google Scholar]
- Bao, H.; Park, J.H.; Cao, J. Non-fragile state estimation for fractional-order delayed memristive BAM neural networks. Neural Netw. 2019, 119, 190–199. [Google Scholar] [CrossRef]
- Bohner, M.; Jonnalagadda, J.M. Discrete fractional cobweb models. Chaos Solit. Fract. 2022, 162, 112451. [Google Scholar] [CrossRef]
- Magin, R. Fractional Calculus in Bioengineering, 1st ed.; Begell House: Redding, CA, USA, 2006; ISBN 978-1567002157. [Google Scholar]
- Podlubny, I. Fractional Differential Equations, 1st ed.; Academic Press: San Diego, CA, USA, 1999; ISBN 558840-2. [Google Scholar]
- Singh, H.; Srivastava, H.M.; Nieto, J.J. (Eds.) Handbook of Fractional Calculus for Engineering and Science, 1st ed.; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2022; ISBN 9781003263517. [Google Scholar]
- Wang, Z.; Huang, X.; Shi, G. Analysis of nonlinear dynamics and chaos in a fractional order financial system with time delay. Comput. Math. Appl. 2011, 62, 1531–1539. [Google Scholar] [CrossRef]
- Wang, L.; Song, Q.; Liu, Y.; Zhao, Z.; Alsaadi, F. Finite-time stability analysis of fractional order complex-valued memristor-based neural networks with both leakage and time-varying delays. Neurocomputing 2017, 245, 86–101. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Y.; Wang, F. Synchronization analysis of fractional-order neural networks with time-varying delays via discontinuous neuron activations. Neurocomputing 2017, 275, 40–49. [Google Scholar] [CrossRef]
- Abdurahman, A.; Jiang, H.; Teng, Z. Finite-time synchronization for fuzzy cellular neural networks with time-varying delays. Fuzzy Sets Syst. 2016, 297, 96–111. [Google Scholar] [CrossRef]
- Li, X.; Rakkiyappan, R.; Balasubramaniam, P. Existence and global stability analysis of equilibrium of fuzzy cellular neural networks with time delay in the leakage term under impulsive perturbations. J. Franklin Inst. 2011, 348, 135–155. [Google Scholar] [CrossRef]
- Kumar, A.; Das, S.; Yadav, V.K.; Jinde Cao, J.; Huang, C. Synchronizations of fuzzy cellular neural networks with proportional time-delay. AIMS Math. 2021, 6, 10620–10641. [Google Scholar] [CrossRef]
- Du, F.; Lu, J.G. Finite-time stability of fractional-order fuzzy cellular neural networks with time delays. Fuzzy Sets Syst. 2022, 438, 107–120. [Google Scholar] [CrossRef]
- Singh, A.; Rai, J.N. Stability of fractional order fuzzy cellular neural networks with distributed delays via hybrid feedback controllers. Neural Process. Lett. 2021, 53, 1469–1499. [Google Scholar] [CrossRef]
- Kosko, B. Adpative bidirecctional associative memoreis. Appl. Opt. 1987, 26, 4947–4960. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Wang, J.; Chen, X.; Cao, J. Bifurcations in a fractional-order BAM neural network with four different delays. Neural Netw. 2021, 141, 344–354. [Google Scholar] [CrossRef] [PubMed]
- Syed Ali, M.; Hymavathi, M.; Kauser, S.A.; Boonsatit, N.; Hammachukiattikul, P.; Rajchakit, G. Synchronization of fractional order uncertain BAM competitive neural networks. Fractal Fract. 2022, 6, 14. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C. Existence and global exponential stability of equilibrium for discrete-time fuzzy BAM neural networks with variable delays and impulses. Fuzzy Sets Syst. 2013, 217, 62–79. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Jiang, W.; Liu, W. The stability of anti-periodic solutions for fractional-order inertial BAM neural networks with time-delays. AIMS Math. 2023, 8, 6176–6190. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, X.; Yang, X. Exponential stability for stochastic reaction–diffusion BAM neural networks with time-varying and distributed delays. Appl. Math. Comput. 2011, 217, 6078–6091. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Comput. Math. Appl. 2010, 24, 1429–1468. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.Y.; Jiang, W.; Zhou, X.F. Mittag–Leffler stability of nonlinear fractional neutral singular systems. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3961–3966. [Google Scholar] [CrossRef]
- Stamov, T.; Stamova, I. Design of impulsive controllers and impulsive control strategy for the Mittag–Leffler stability behavior of fractional gene regulatory networks. Neurocomputing 2021, 424, 54–62. [Google Scholar] [CrossRef]
- Wu, A.; Liu, L.; Huang, T.; Zeng, Z. Mittag–Leffler stability of fractional-order neural networks in the presence of generalized piecewise constant arguments. Neural Netw. 2017, 85, 118–127. [Google Scholar] [CrossRef] [PubMed]
- Wu, A.; Zeng, Z. Global Mittag–Leffler stabilization of fractional-order memristive neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2015, 28, 206–217. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Zhong, S.; Li, Y.; Xu, F. Finite-time Mittag–Leffler synchronization of fractional-order memristive BAM neural networks with time delays. Neurocomputing 2017, 219, 431–439. [Google Scholar] [CrossRef]
- Yan, H.; Qiao, Y.; Duan, L.; Zhang, L. Global Mittag–Leffler stabilization of fractional-order BAM neural networks with linear state feedback controllers. Math. Probl. Eng. 2020, 2020, 6398208. [Google Scholar] [CrossRef]
- Li, X.; Caraballo, T.; Rakkiyappan, R.; Han, X. On the stability of impulsive functional differential equations with infinite delays. Math. Methods Appl. Sci. 2015, 38, 3130–3140. [Google Scholar] [CrossRef]
- Song, Q.; Wang, Z. Neural networks with discrete and distributed time-varying delays: A general stability analysis. Neural Netw. 2008, 37, 1538–1547. [Google Scholar] [CrossRef]
- Syed Ali, M.; Saravanan, S. Robust finite-time H∞ control for a class of uncertain switched neural networks of neutral-type with distributed time varying delays. Neurocomputing 2016, 177, 454–468. [Google Scholar]
- Zhang, G.; Zeng, Z.; Hu, J. New results on global exponential dissipativity analysis of memristive inertial neural networks with distributed time-varying delays. Neural Netw. 2018, 97, 183–191. [Google Scholar] [CrossRef]
- Stamova, I.; Stamov, G. Mittag–Leffler synchronization of fractional neural networks with time-varying delays and reaction-diffusion terms using impulsive and linear controllers. Neural Netw. 2017, 96, 22–32. [Google Scholar] [CrossRef]
- Li, R.; Cao, J.; Alsaedi, A.; Alsaadi, F. Exponential and fixed-time synchronization of Cohen–Grossberg neural networks with time-varying delays and reaction-diffusion terms. Appl. Math. Comput. 2017, 313, 37–51. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, H.; Stamova, I.; Cao, J. Global synchronization for BAM delayed reaction-diffusion neural networks with fractional partial differential operator. J. Franklin Inst. 2023, 360, 635–656. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, Q. Global exponential stability of BAM neural networks with time-varying delays and reaction-diffusion terms. Phys. Lett. A 2007, 371, 83–89. [Google Scholar]
- Wei, T.; Li, X.; Stojanovic, V. Input-to-state stability of impulsive reaction–diffusion neural networks with infinite distributed delays. Nonlinear Dyn. 2021, 103, 1733–1755. [Google Scholar] [CrossRef]
- Wu, X.; Liu, S.; Wang, Y. Stability analysis of Riemann–Liouville fractional-order neural networks with reaction-diffusion terms and mixed time-varying delays. Neurocomputing 2021, 431, 169–178. [Google Scholar] [CrossRef]
- Antsaklis, P.J. Special issue on hybrid systems: Theory and applications-a brief introduction to the theory and applications of hybrid systems. Proc. IEEE 2000, 88, 879–887. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]
- Liang, S.; Wu, R.; Chen, L. Comparision principles and stability of nonlinear fractional-order cellular neural networks with multiple time delays. Neurocomputing 2015, 168, 618–625. [Google Scholar] [CrossRef]
- Kuang, J.C. Applied Inequalities, 3rd ed.; Shandong Science and Technology Press: Jinan, China, 2004; ISBN 9787533136185. (In Chinese) [Google Scholar]
- Wu, H.; Zhang, X.; Xue, S.; Wang, L.; Wang, Y. LMI conditions to global Mittag-Leffler stability of fractional-order neural networks with impulses. Neurocomputing 2016, 193, 148–154. [Google Scholar] [CrossRef]
- Lu, J.G. Global exponential stability and periodicity of reaction-diffusion delayed recurrent neural networks with Dirichlet boundary conditions. Chaos Solitons Fract. 2008, 35, 116–125. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Syed Ali, M.; Stamov, G.; Stamova, I.; Ibrahim, T.F.; Dawood, A.A.; Osman Birkea, F.M. Global Asymptotic Stability and Synchronization of Fractional-Order Reaction–Diffusion Fuzzy BAM Neural Networks with Distributed Delays via Hybrid Feedback Controllers. Mathematics 2023, 11, 4248. https://doi.org/10.3390/math11204248
Syed Ali M, Stamov G, Stamova I, Ibrahim TF, Dawood AA, Osman Birkea FM. Global Asymptotic Stability and Synchronization of Fractional-Order Reaction–Diffusion Fuzzy BAM Neural Networks with Distributed Delays via Hybrid Feedback Controllers. Mathematics. 2023; 11(20):4248. https://doi.org/10.3390/math11204248
Chicago/Turabian StyleSyed Ali, M., Gani Stamov, Ivanka Stamova, Tarek F. Ibrahim, Arafa A. Dawood, and Fathea M. Osman Birkea. 2023. "Global Asymptotic Stability and Synchronization of Fractional-Order Reaction–Diffusion Fuzzy BAM Neural Networks with Distributed Delays via Hybrid Feedback Controllers" Mathematics 11, no. 20: 4248. https://doi.org/10.3390/math11204248






