Estimation and Inference for Spatio-Temporal Single-Index Models
Abstract
:1. Introduction
2. A Brief Description of the rMAVE
- Step 0.
- Give the calculation of the initial value of .
- Step 1.
- Calculate:and:
- Step 2.
- Calculate:where , and is a trimming function.
- Step 3.
- Repeat steps 1–3 with , where denotes the Euclidean distance, until convergence. The vector obtained in the last iteration is defined as the rMAVE estimator of , denoted by .
- Step 4.
- Put into step 1 and obtain the estimators of and , denoted by .
3. Estimation of the Variance Function
3.1. Estimation of the Variance Function with Fully Nonparametric Function
3.2. Estimation of the Variance Function with Dimension Reduction Structure
4. Reweighting Estimation and Asymptotic Properties
4.1. Reweighting Estimation
4.2. Asymptotic Properties
5. Monte Carlo Study
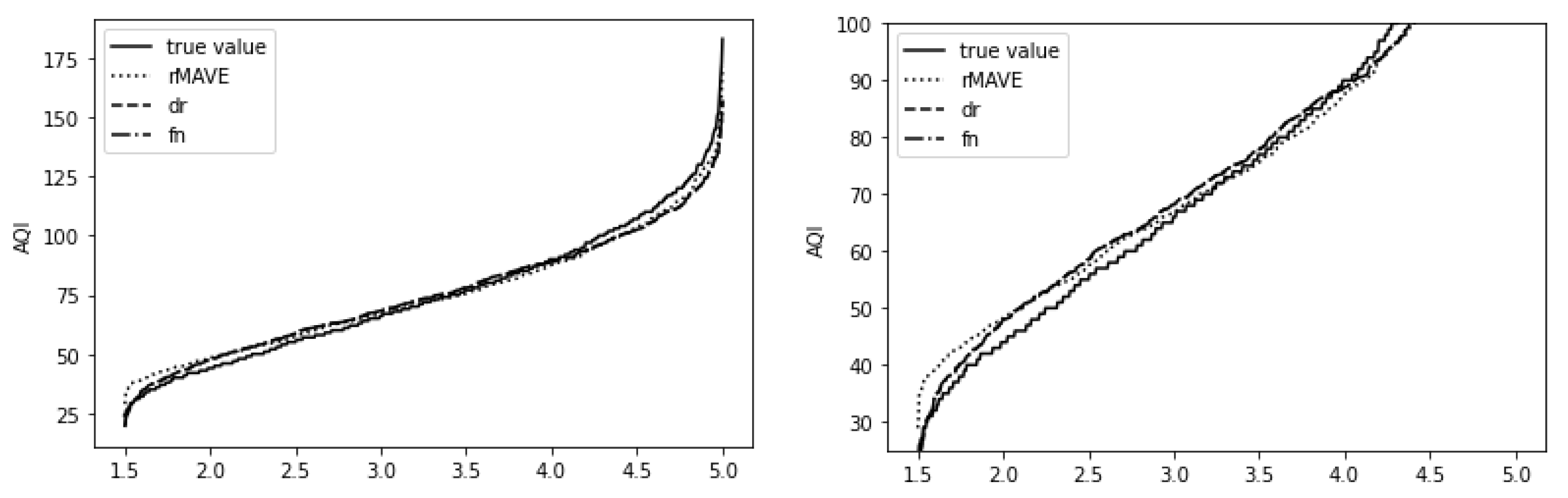
6. Real Data Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Assumptions
- (C1)
- The density function of and its derivatives up to the third order are bounded on R for all : where is a constant, , and .
- (C2)
- The conditional mean and its derivatives up to the third order are bounded for all : where .
- (C3)
- is a symmetric univariate density function with finite moments of all orders and a bounded derivative. Bandwidth and .
- (C4)
- is a symmetric multivariate density function with finite moments and bounded derivatives. Bandwidth and . , such that .
- (C5)
- is a symmetric univariate density function with finite moments and bounded derivatives. Bandwidth and . , such that .
Appendix B. Proof
References
- Fotheringham, A.S.; Yang, W.; Kang, W. Multiscale geographically weighted regression (MGWR). Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
- Wu, C.; Ren, F.; Hu, W.; Du, Q. Multiscale geographically and temporally weighted regression: Exploring the spatio-temporal determinants of housing prices. Int. J. Geogr. Inf. Sci. 2019, 33, 489–511. [Google Scholar] [CrossRef]
- Chu, H.J.; Huang, B.; Lin, C.Y. Modeling the spatio-temporal heterogeneity in the PM10-PM2.5 relationship. Atmos. Environ. 2015, 102, 176–182. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhou, X.; Yang, T. Hetero-ConvLSTM: A deep learning approach to traffic accident prediction on heterogeneous spatio-temporal data. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 984–992. [Google Scholar]
- Wang, H.; Wang, J.; Huang, B. Prediction for spatio-temporal models with autoregression in errors. J. Nonparametric Stat. 2012, 24, 1–28. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Z.; Wu, Y.; Luo, X. B-spline method for spatio-temporal inverse model. J. Syst. Sci. Complex. 2022, 35, 2336–2360. [Google Scholar] [CrossRef]
- Římalovȧ, V.; Fišerováa, E.; Menafogliob, A.; Pinic, A. Inference for spatial regression models with functional response using a permutational approach. J. Multivar. Anal. 2022, 189, 104893. [Google Scholar] [CrossRef]
- Lin, W.; Kulasekera, K.B. Identifiability of single-index models and additive-index models. Biometrika 2007, 94, 496–501. [Google Scholar] [CrossRef]
- Stoker, T.M. Consistent estimation of scaled coefficients. Econometrica 1986, 54, 1461–1481. [Google Scholar] [CrossRef]
- Powell, J.L.; Stock, J.H.; Stoker, T.M. Semiparametric estimation of index coefficients. Econometrica 1989, 57, 1403–1430. [Google Scholar] [CrossRef]
- Xia, Y. Asymptotic distributions for two estimators of the single-index model. Econom. Theory 2006, 22, 1112–1137. [Google Scholar] [CrossRef]
- Xia, Y. A constructive approach to the estimation of dimension reduction directions. Ann. Stat. 2007, 35, 2654–2690. [Google Scholar] [CrossRef]
- Härdle, W.; Hall, H.; Ichimura, H. Optimal smoothing in single-index models. Ann. Stat. 1993, 21, 157–178. [Google Scholar] [CrossRef]
- Li, G.; Peng, H.; Dong, K.; Tong, T. Simultaneous confidence bands and hypothesis testing for single-index models. Stat. Sin. 2014, 24, 937–955. [Google Scholar] [CrossRef]
- Fan, Y.; James, G.M.; Radchenko, P. Functional additive regression. Ann. Stat. 2015, 43, 2296–2325. [Google Scholar] [CrossRef]
- Xue, L. Estimation and empirical likelihood for single-index models with missing data in the covariates. Comput. Stat. Data Anal. 2013, 52, 1458–1476. [Google Scholar] [CrossRef]
- Xue, L.; Zhu, L. Empirical likelihood for single-index model. J. Multivar. Anal. 2006, 97, 1295–1312. [Google Scholar] [CrossRef]
- Cook, R.D.; Li, B. Dimension reduction for conditional mean in regression. Ann. Stat. 2002, 30, 455–474. [Google Scholar] [CrossRef]
- Zhu, L.; Ferré, L.; Wang, T. Sufficient dimension reduction through discretization-expectation estimation. Biometrika 2010, 97, 295–304. [Google Scholar] [CrossRef]
- Ma, Y.; Zhu, L. A review on dimension reduction. Int. Stat. Rev. 2013, 81, 134–150. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, J.; Wang, H.; Zhao, H.; Chen, X. Efficient estimation in heteroscedastic single-index models. J. Nonparametric Stat. 2021, 33, 273–298. [Google Scholar] [CrossRef]
- Horowitz, J.L.; Härdle, W. Direct semiparametric estimation of single-index models with discrete covariates. J. Am. Stat. Assoc. 1996, 91, 1632–1640. [Google Scholar] [CrossRef]
- Ichimura, H. Semiparametric least squares (SLS) and weighted SLS estimation of single-index models. J. Econom. 1993, 58, 71–120. [Google Scholar] [CrossRef]
- Cressie, N.A.C. Statistics for Spatial Data; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Mack, Y.P.; Silverman, B.W. Weak and strong uniform consistency of kernel regression estimates. Zeitschrift für Wahrscheinlichkeitstheorie Und Verwandte Geb. 1982, 61, 405–415. [Google Scholar] [CrossRef]
- Liebscher, E. Strong convergence of sums of α-mixing random variables with applications to density estimation. Stoch. Process. Their Appl. 1996, 65, 69–80. [Google Scholar] [CrossRef]
- Schott, J.R. Matrix Analysis for Statistics; Wiley: Hoboken, NJ, USA, 1997. [Google Scholar]
- Chow, Y.S.; Teicher, H. Probability Theory: Independence, Interchangeability, Martin-Gales; Springer: Berlin/Heidelberg, Germany, 1978; p. 122. [Google Scholar]
- Lu, Z.; Arvid, L.; Dag, T.; Yao, Q. Exploring spatial nonlinearity using additive approximation. Bernoulli 2007, 13, 447–472. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J. Estimation of the trend function for spatio-temporal models. J. Nonparametric Stat. 2009, 21, 567–588. [Google Scholar] [CrossRef]
- Lu, Z.; Linton, O. Local linear fitting under near epoch dependence. Econ. Theory 2007, 23, 37–70. [Google Scholar] [CrossRef]
| Item | Estimator | |||
|---|---|---|---|---|
| Mean | 0.2793 | 0.2745 | 0.2615 | |
| 0.2761 | 0.2772 | 0.2578 | ||
| 0.2779 | 0.2793 | 0.2600 | ||
| 0.5487 | 0.5582 | 0.5291 | ||
| 0.5358 | 0.5390 | 0.5289 | ||
| 0.5420 | 0.5438 | 0.5277 | ||
| 0.7858 | 0.7784 | 0.7933 | ||
| 0.7963 | 0.7941 | 0.7947 | ||
| 0.7916 | 0.7892 | 0.7937 | ||
| −0.007 | −0.0070 | 0.0015 | ||
| −0.0004 | −0.0055 | 0.0009 | ||
| −0.0031 | −0.0036 | 0.0017 | ||
| SSD | 0.0279 | 0.0362 | 0.2145 | |
| 0.0318 | 0.0334 | 0.1653 | ||
| 0.0349 | 0.0421 | 0.1597 | ||
| 0.0430 | 0.0626 | 0.2183 | ||
| 0.0235 | 0.0319 | 0.1642 | ||
| 0.0228 | 0.0283 | 0.1583 | ||
| 0.0255 | 0.0386 | 0.2253 | ||
| 0.0125 | 0.0178 | 0.1633 | ||
| 0.0151 | 0.0190 | 0.1558 | ||
| 0.0144 | 0.0189 | 0.2306 | ||
| 0.0063 | 0.0113 | 0.1668 | ||
| 0.0064 | 0.0081 | 0.1572 | ||
| SRE | 0.6758 | 0.6974 | 2.5971 | |
| 0.7974 | 0.6210 | 1.4813 | ||
| 0.9713 | 0.9779 | 1.3349 | ||
| 4.1839 | 6.5845 | 2.6142 | ||
| 1.1334 | 1.5277 | 1.4925 | ||
| 1.1822 | 1.3079 | 1.3617 | ||
| 3.0887 | 4.7931 | 2.7372 | ||
| 0.6304 | 0.8887 | 1.6809 | ||
| 1.1264 | 1.2255 | 1.6126 | ||
| 4.0594 | 4.0605 | 2.6925 | ||
| 0.6396 | 1.5820 | 1.6784 | ||
| 0.8161 | 0.8023 | 1.6117 |
| Item | Estimator | |||
|---|---|---|---|---|
| Mean | 0.2602 | 0.2558 | 0.2642 | |
| 0.2563 | 0.2587 | 0.2577 | ||
| 0.2516 | 0.2548 | 0.2644 | ||
| 0.5345 | 0.5501 | 0.5096 | ||
| 0.5319 | 0.5423 | 0.5038 | ||
| 0.5391 | 0.5427 | 0.5312 | ||
| 0.8029 | 0.7912 | 0.8169 | ||
| 0.8052 | 0.7998 | 0.8227 | ||
| 0.8032 | 0.7993 | 0.8044 | ||
| −0.0113 | 0.0493 | −0.0018 | ||
| −0.0059 | 0.0161 | −0.0094 | ||
| −0.0039 | 0.0229 | −0.0028 | ||
| SSD | 0.0306 | 0.0446 | 0.0256 | |
| 0.0238 | 0.0186 | 0.0346 | ||
| 0.0185 | 0.0125 | 0.0138 | ||
| 0.0260 | 0.0179 | 0.0323 | ||
| 0.0142 | 0.0133 | 0.0278 | ||
| 0.0148 | 0.0141 | 0.0198 | ||
| 0.0158 | 0.0214 | 0.0226 | ||
| 0.0041 | 0.0090 | 0.0257 | ||
| 0.0088 | 0.0120 | 0.0135 | ||
| 0.0210 | 0.0305 | 0.0219 | ||
| 0.0207 | 0.0252 | 0.0214 | ||
| 0.0224 | 0.0212 | 0.0203 | ||
| SRE | 1.6501 | 9.6640 | 3.6479 | |
| 1.1514 | 1.9198 | 7.0692 | ||
| 0.9846 | 1.4218 | 1.0852 | ||
| 3.3675 | 2.855 | 4.9831 | ||
| 1.0456 | 1.2121 | 5.1506 | ||
| 1.1884 | 1.3611 | 1.2101 | ||
| 3.9555 | 5.358 | 4.8345 | ||
| 0.4494 | 0.7964 | 7.1304 | ||
| 1.2435 | 1.4159 | 1.2323 | ||
| 1.0402 | 4.8466 | 1.1845 | ||
| 0.8493 | 1.2902 | 1.3420 | ||
| 0.9447 | 1.4113 | 1.0247 |
| Item | Estimator | |||
|---|---|---|---|---|
| Mean | 0.3180 | 0.3203 | 0.3091 | |
| 0.3026 | 0.3060 | 0.3146 | ||
| 0.3013 | 0.2936 | 0.3070 | ||
| 0.5422 | 0.5131 | 0.5647 | ||
| 0.5417 | 0.5147 | 0.5581 | ||
| 0.5412 | 0.5152 | 0.5587 | ||
| 0.7760 | 0.7945 | 0.7602 | ||
| 0.7824 | 0.7973 | 0.7681 | ||
| 0.7842 | 0.8022 | 0.7635 | ||
| 0.0114 | −0.0101 | 0.0185 | ||
| 0.0083 | 0.0015 | 0.0301 | ||
| 0.0076 | 0.0014 | 0.0045 | ||
| SSD | 0.0239 | 0.0599 | 0.1064 | |
| 0.0228 | 0.0576 | 0.1007 | ||
| 0.0205 | 0.0317 | 0.0672 | ||
| 0.0127 | 0.0278 | 0.0515 | ||
| 0.0095 | 0.0235 | 0.0421 | ||
| 0.0082 | 0.0202 | 0.0115 | ||
| 0.0081 | 0.0373 | 0.0762 | ||
| 0.0098 | 0.0350 | 0.0632 | ||
| 0.0069 | 0.0308 | 0.0360 | ||
| 0.0509 | 0.0200 | 0.0337 | ||
| 0.0357 | 0.0133 | 0.0337 | ||
| 0.0344 | 0.0055 | 0.0089 | ||
| SRE | 1.8127 | 0.8880 | 0.7741 | |
| 1.0206 | 1.1188 | 1.2239 | ||
| 0.9112 | 0.9941 | 0.9501 | ||
| 0.6660 | 1.5348 | 0.8369 | ||
| 1.2903 | 1.1565 | 1.0343 | ||
| 0.9032 | 0.9960 | 0.9485 | ||
| 1.7353 | 0.8257 | 1.5072 | ||
| 1.0690 | 1.1678 | 1.3741 | ||
| 0.9846 | 1.0108 | 0.9238 | ||
| 1.8545 | 4.6052 | 3.8478 | ||
| 0.8656 | 4.2492 | 1.9594 | ||
| 0.9830 | 0.9644 | 1.3002 |
| Item | Estimator | |||
|---|---|---|---|---|
| Mean | 0.3033 | 0.3071 | 0.3112 | |
| 0.3022 | 0.3011 | 0.3018 | ||
| 0.2986 | 0.2960 | 0.2952 | ||
| 0.5532 | 0.5267 | 0.5474 | ||
| 0.5492 | 0.5288 | 0.5448 | ||
| 0.5449 | 0.5298 | 0.5380 | ||
| 0.7700 | 0.8020 | 0.7742 | ||
| 0.7764 | 0.8017 | 0.7799 | ||
| 0.7781 | 0.8016 | 0.7810 | ||
| 0.0552 | −0.0040 | −0.012 | ||
| 0.0468 | −0.0033 | −0.0089 | ||
| 0.0463 | −0.0031 | -0.0063 | ||
| SSD | 0.0296 | 0.0154 | 0.0150 | |
| 0.0238 | 0.0146 | 0.0117 | ||
| 0.0225 | 0.0100 | 0.0098 | ||
| 0.0209 | 0.0162 | 0.0132 | ||
| 0.0188 | 0.0125 | 0.0098 | ||
| 0.0146 | 0.0102 | 0.0026 | ||
| 0.0088 | 0.0256 | 0.0087 | ||
| 0.0073 | 0.0230 | 0.0033 | ||
| 0.0023 | 0.0160 | 0.0010 | ||
| 0.0582 | 0.0062 | 0.0920 | ||
| 0.0566 | 0.0017 | 0.0832 | ||
| 0.0508 | 0.0009 | 0.0708 | ||
| SRE | 0.9646 | 1.5420 | 1.7484 | |
| 0.9738 | 0.9465 | 0.8725 | ||
| 0.9994 | 1.0162 | 1.1460 | ||
| 1.1077 | 1.8686 | 1.9866 | ||
| 1.0915 | 1.4366 | 0.9473 | ||
| 1.0115 | 0.7647 | 0.9885 | ||
| 1.3524 | 1.3291 | 1.5706 | ||
| 0.8750 | 1.2429 | 0.8803 | ||
| 0.9261 | 1.0108 | 1.1370 | ||
| 1.0374 | 1.4991 | 0.7267 | ||
| 1.0193 | 0.8973 | 0.9798 | ||
| 0.9941 | 0.9644 | 1.1907 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhao, Z.; Hao, H.; Huang, C. Estimation and Inference for Spatio-Temporal Single-Index Models. Mathematics 2023, 11, 4289. https://doi.org/10.3390/math11204289
Wang H, Zhao Z, Hao H, Huang C. Estimation and Inference for Spatio-Temporal Single-Index Models. Mathematics. 2023; 11(20):4289. https://doi.org/10.3390/math11204289
Chicago/Turabian StyleWang, Hongxia, Zihan Zhao, Hongxia Hao, and Chao Huang. 2023. "Estimation and Inference for Spatio-Temporal Single-Index Models" Mathematics 11, no. 20: 4289. https://doi.org/10.3390/math11204289
APA StyleWang, H., Zhao, Z., Hao, H., & Huang, C. (2023). Estimation and Inference for Spatio-Temporal Single-Index Models. Mathematics, 11(20), 4289. https://doi.org/10.3390/math11204289







