Analysis of Noise-Induced Transitions in a Thermo-Kinetic Model of the Autocatalytic Trigger
Abstract
:1. Introduction
2. Deterministic Model
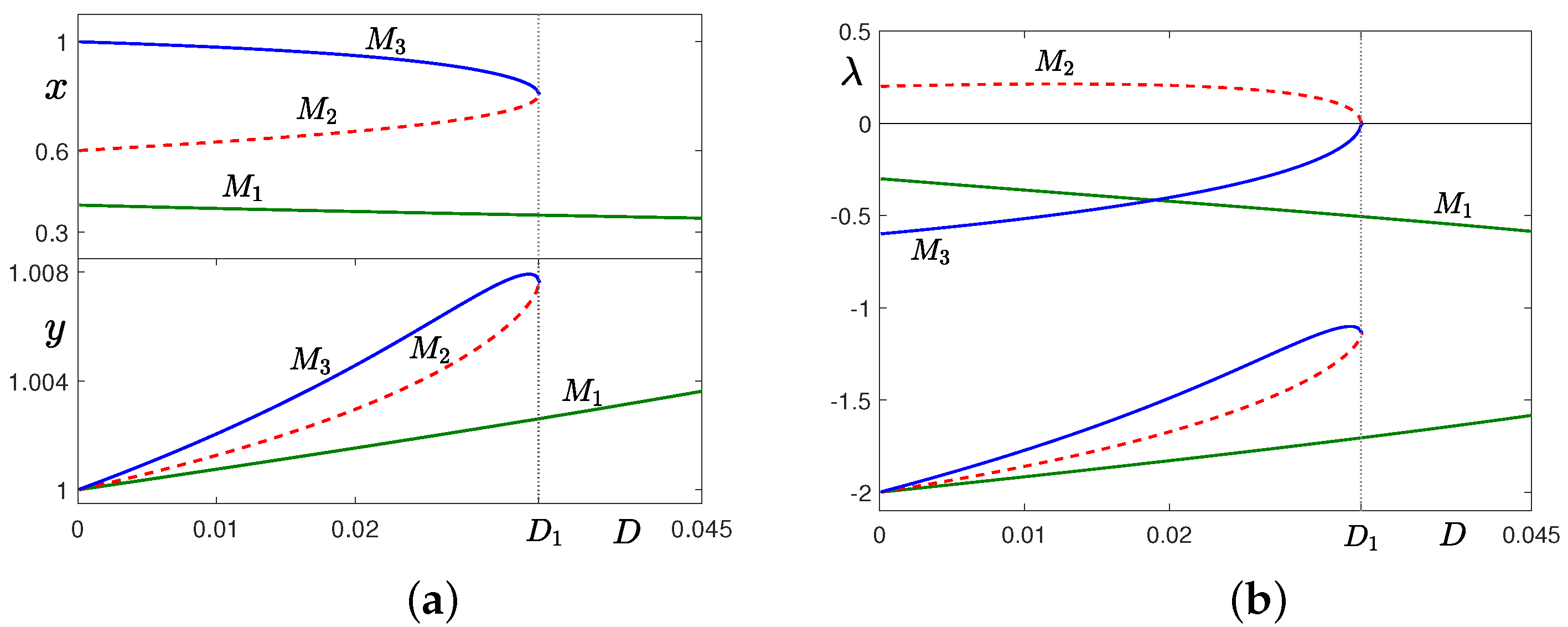
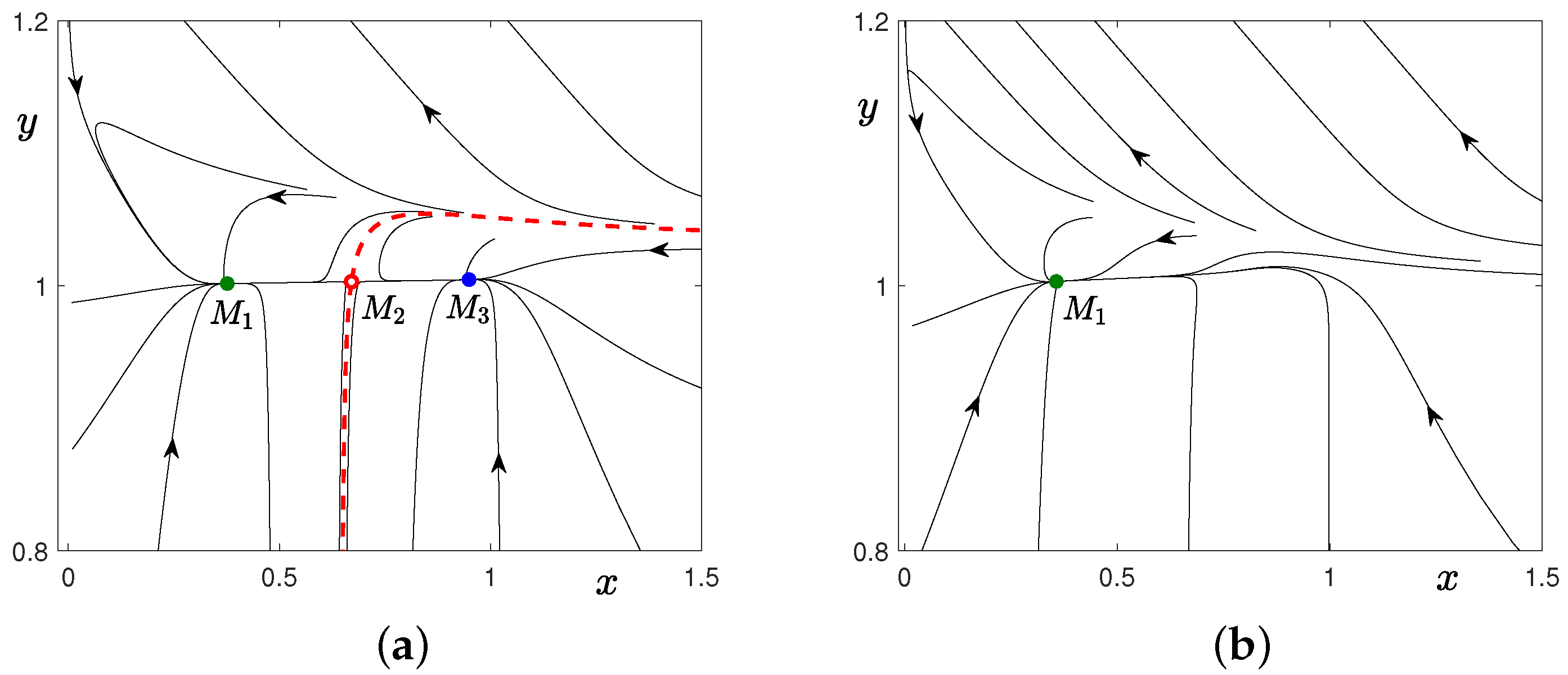
2.1. Case 1: ,
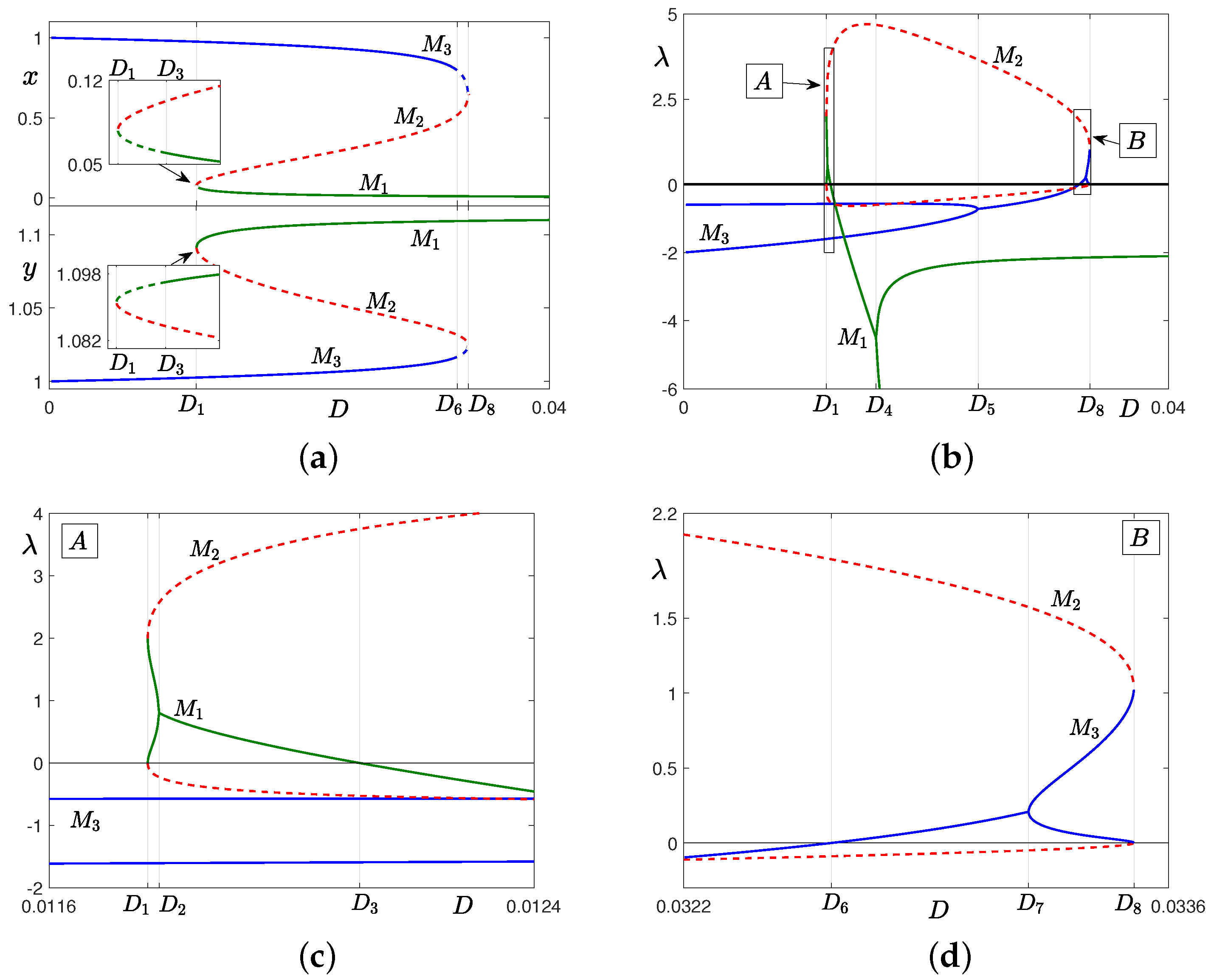
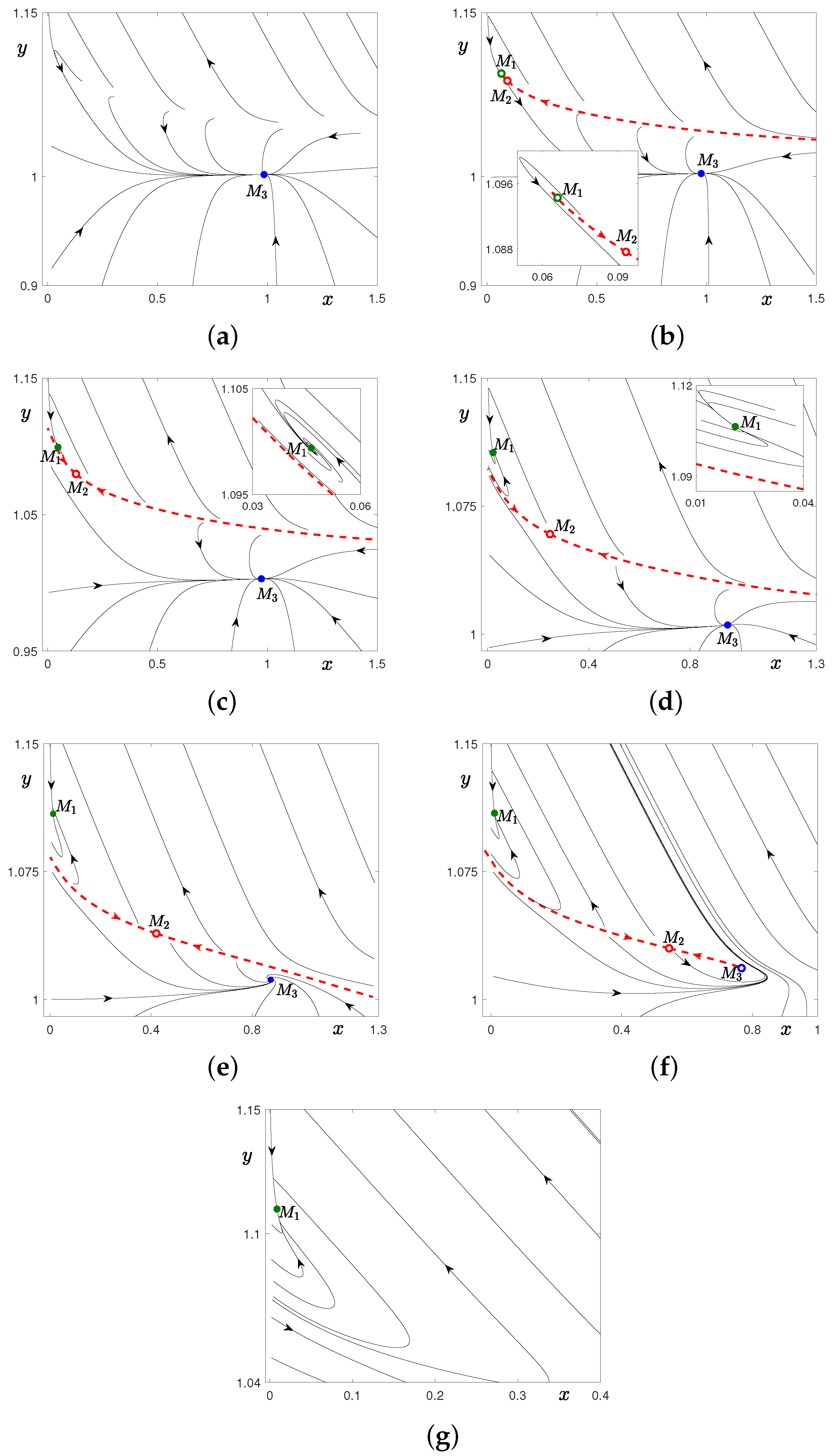
2.2. Case 2: ,
3. Stochastic Model
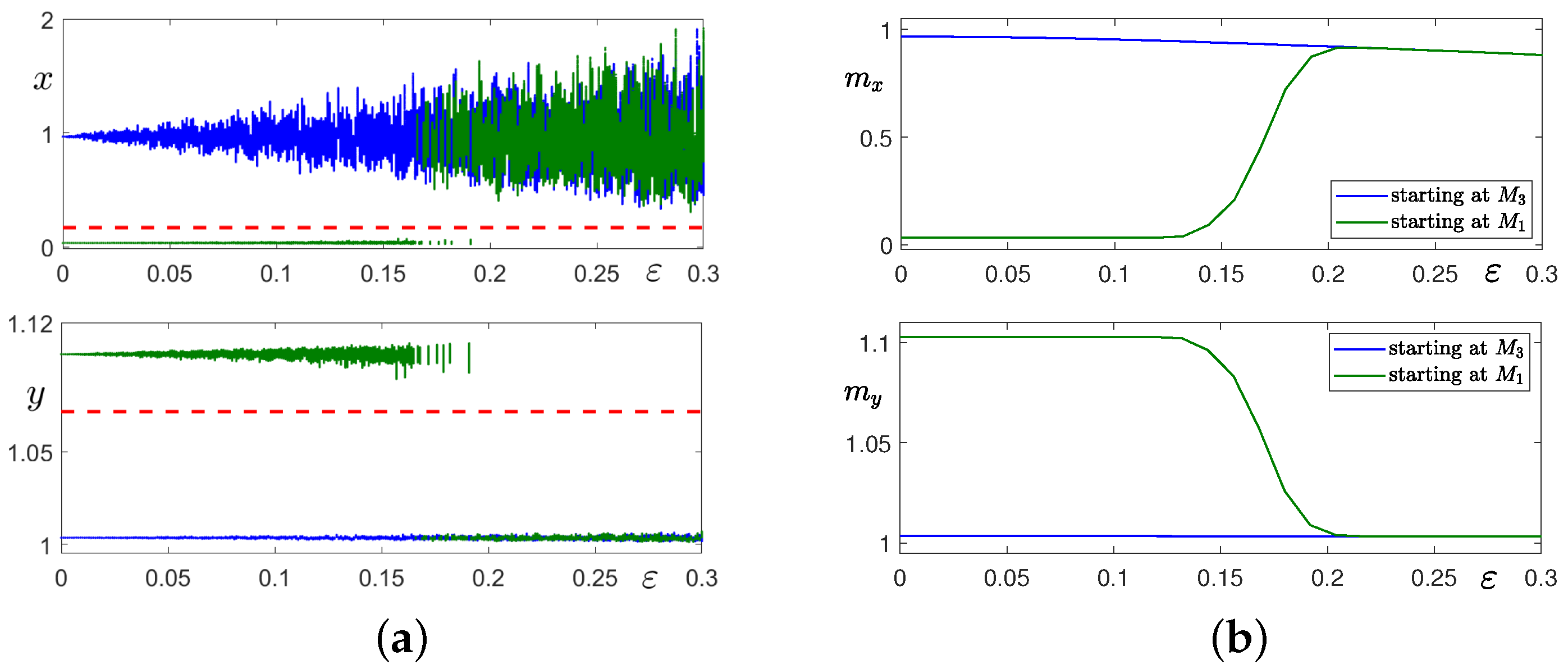
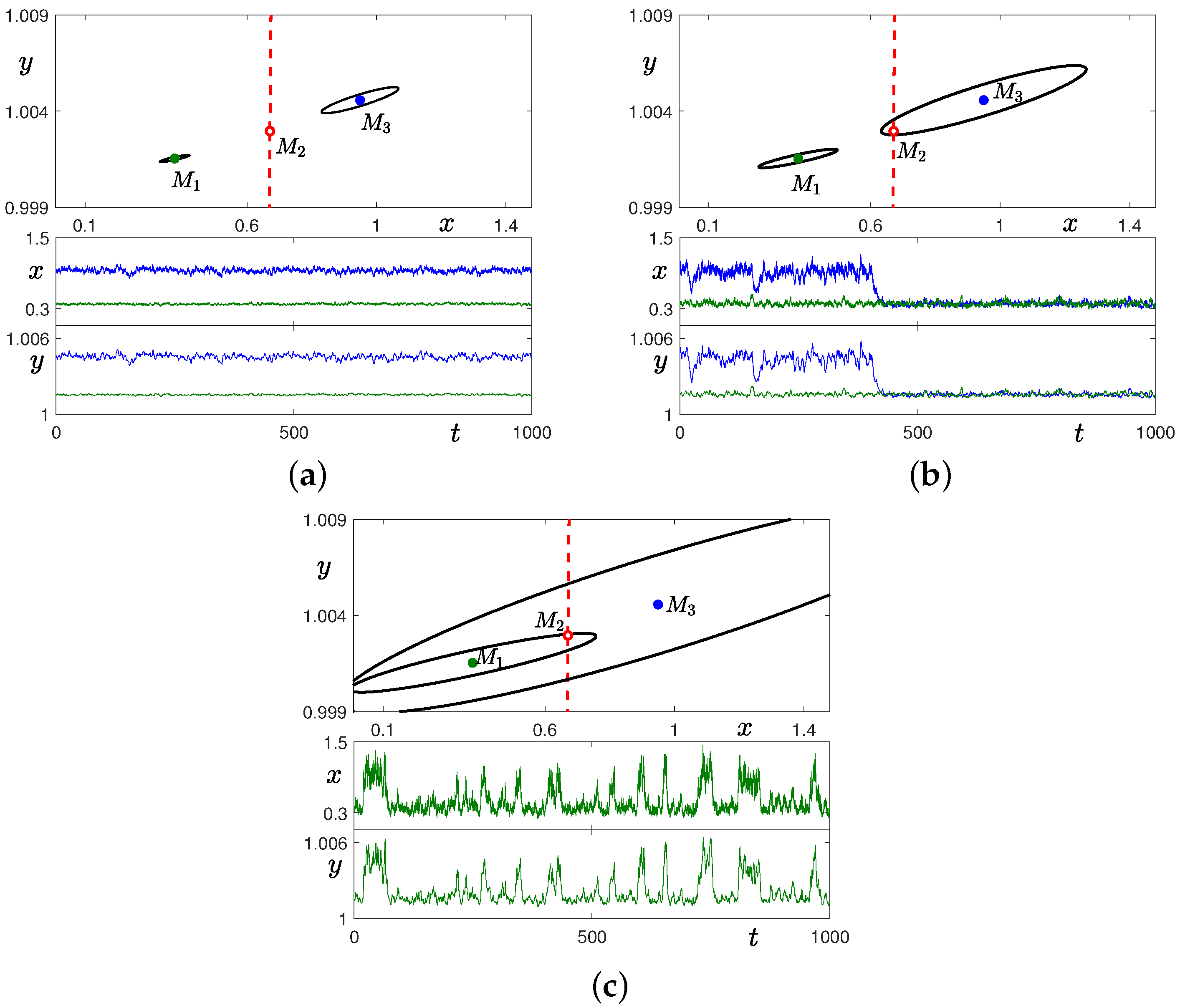
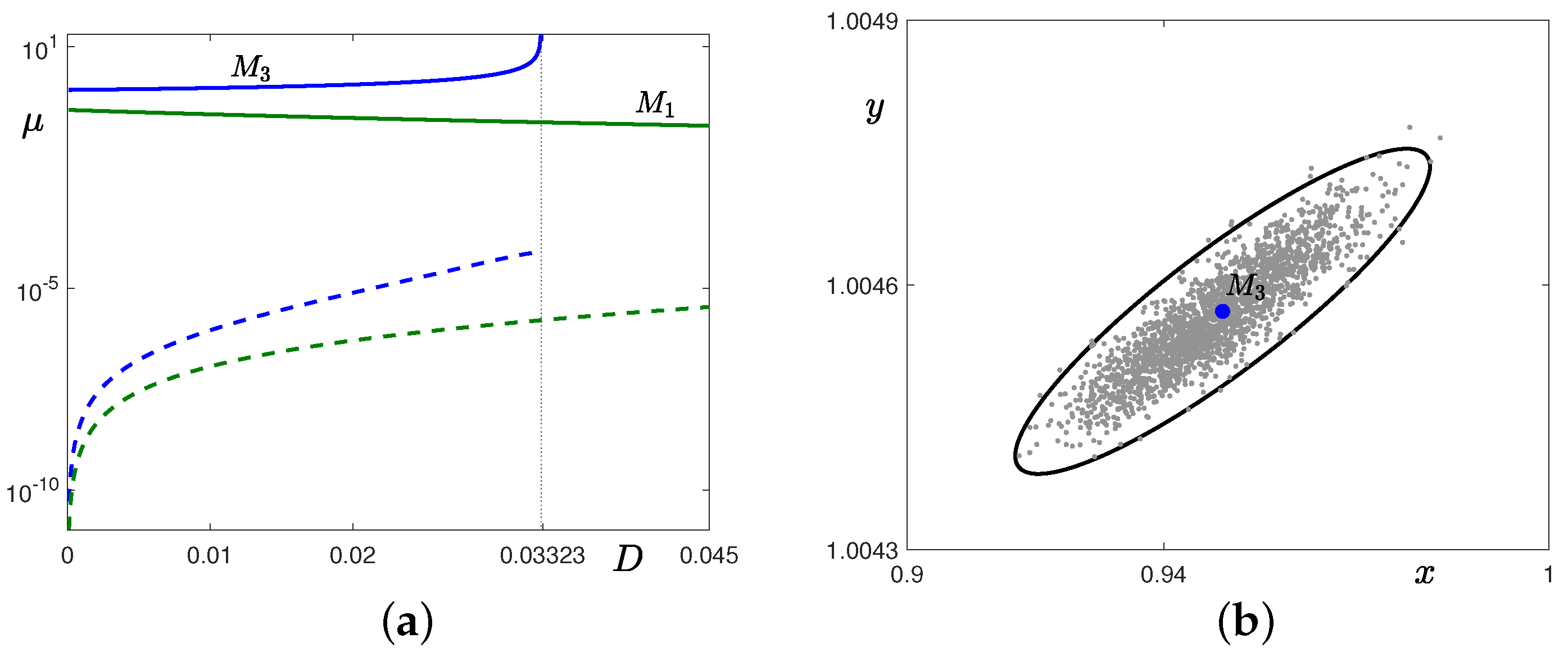
3.1. Stochastic Effects in the Case 1 with ,
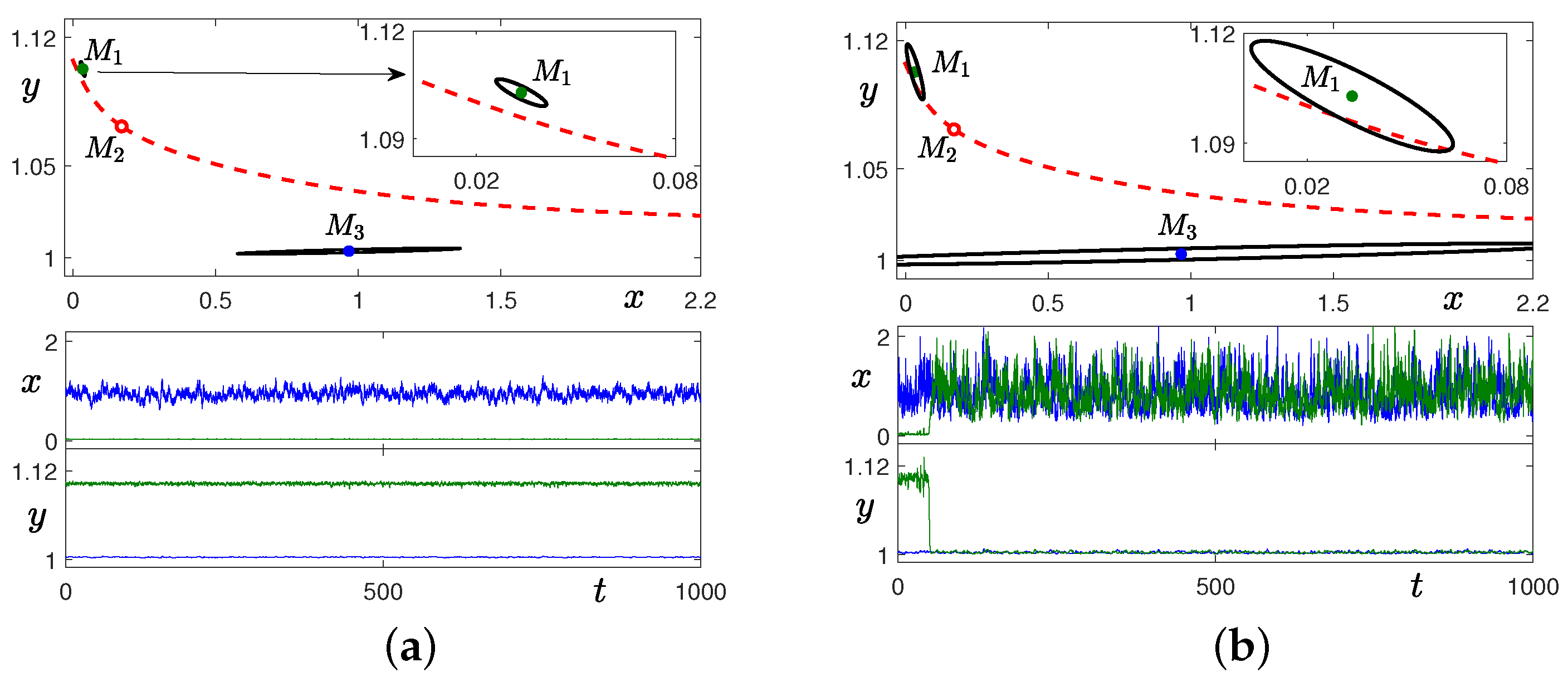
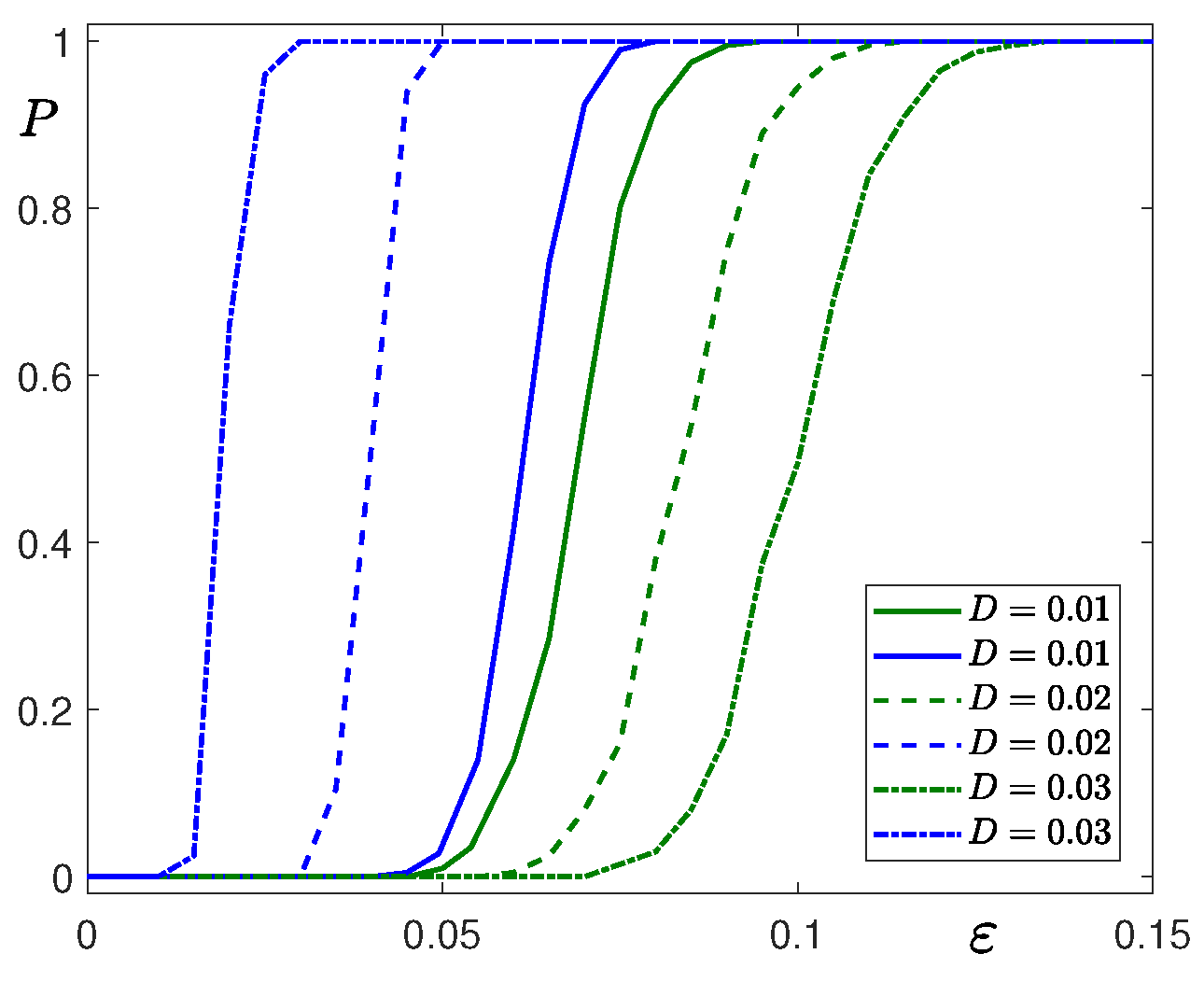
3.2. Stochastic Effects in the Case 2 with ,
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schmidt, L.D. The Engineering of Chemical Reactions; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Davis, M.E. Fundamentals of Chemical Reaction Engineering; McGraw-Hill: Boston, MA, USA, 2003. [Google Scholar]
- Bykov, V.I.; Tsybenova, S.B.; Yablonsky, G. Chemical Complexity via Simple Models; De Gruyter: Berlin, Germany, 2018. [Google Scholar]
- Uppal, A.; Ray, W.H.; Poore, A.B. The classification of the dynamic behavior of continuous stirred tank reactors—Influence of reactor resident time. Chem. Eng. Sci. 1976, 31, 205–214. [Google Scholar] [CrossRef]
- Kawczyński, A.L.; Gorecki, J. Molecular dynamics simulations of sustained oscillations in a thermochemical system. J. Phys. Chem. 1992, 96, 1060–1067. [Google Scholar] [CrossRef]
- Kawczyński, A.L.; Nowakowski, B. Master equation simulations of a model of a thermochemical system. Phys. Rev. E 2003, 68, 036218. [Google Scholar] [CrossRef] [PubMed]
- Bashkirtseva, I.; Ivanenko, G.; Mordovskikh, D.; Ryashko, L. Canards oscillations, noise-induced splitting of cycles and transition to chaos in thermochemical kinetics. Mathematics 2023, 11, 1918. [Google Scholar] [CrossRef]
- Shilnikov, L.P.; Shilnikov, A.L.; Turaev, D.V.; Chua, L.O. Methods of Qualitative Theory in Nonlinear Dynamics; World Scientific: Singapore, 1998; p. 416. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: Berlin/Heidelberg, Germany, 1983; p. 462. [Google Scholar]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Kloeden, P.E.; Platen, E.; Schurz, H. Numerical Solution of SDE Through Computer Experiments; Springer: Berlin/Heidelberg, Germany, 2002; p. 294. [Google Scholar]
- Gautschi, W. Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Awrejcewicz, J. Numerical Simulations of Physical and Engineering Processes; InTech: Rijeka, Croatia, 2011; p. 614. [Google Scholar]
- Butcher, J.C. Numerical Methods for Ordinary Differential Equations; Wiley: Chichester, UK, 2016; p. 544. [Google Scholar]
- Milstein, G.N.; Tretyakov, M.V. Stochastic Numerics for Mathematical Physics; Springer: Berlin/Heidelberg, Germany, 2021; p. 736. [Google Scholar]
- Bykov, V.; Tsybenova, S. A model of thermokinetic oscillations on the surface of a catalyst. Russ. J. Phys. Chem. A 2003, 77, 1402–1405. [Google Scholar]
- Tsybenova, S. The basic thermokinetic models. Phys.-Chem. Kinet. Gas Dyn. 2008, 6, 281. [Google Scholar]
- Bykov, V.; Tsybenova, S. A parametric analysis of the basic nonlinear models of the catalytic reactions. Math. Model. Nat. Phenom. 2015, 10, 68–83. [Google Scholar] [CrossRef]
- Horsthemke, W.; Lefever, R. Noise-Induced Transitions; Springer: Berlin/Heidelberg, Germany, 1984; p. 338. [Google Scholar]
- Anishchenko, V.S.; Astakhov, V.V.; Neiman, A.B.; Vadivasova, T.E.; Schimansky-Geier, L. Nonlinear Dynamics of Chaotic and Stochastic Systems. Tutorial and Modern Development; Springer: Berlin/Heidelberg, Germany, 2007; p. 535. [Google Scholar]
- Arnold, L. Random Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 1998; p. 600. [Google Scholar]
- Lindner, B.; Garcia-Ojalvo, J.; Neiman, A.; Schimansky-Geier, L. Effects of noise in excitable systems. Phys. Rep. 2004, 392, 321–424. [Google Scholar] [CrossRef]
- McDonnell, M.D.; Stocks, N.G.; Pearce, C.E.M.; Abbott, D. Stochastic Resonance: From Suprathreshold Stochastic Resonance to Stochastic Signal Quantization; Cambridge University Press: Cambridge, UK, 2008; p. 446. [Google Scholar]
- Gardiner, C.W. Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Freidlin, M.I.; Wentzell, A.D. Random Perturbations of Dynamical Systems; Springer: New York, NY, USA; Berlin, Germany, 1984. [Google Scholar]
- Mil’shtein, G.N.; Ryashko, L.B. A first approximation of the quasipotential in problems of the stability of systems with random non-degenerate perturbations. J. Appl. Math. Mech. 1995, 59, 47–56. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Ryashko, L. Stochastic sensitivity of 3D-cycles. Math. Comput. Simul. 2004, 66, 55–67. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Ryashko, L. Sensitivity and chaos control for the forced nonlinear oscillations. Chaos Solitons Fractals 2005, 26, 1437–1451. [Google Scholar] [CrossRef]
- Ryashko, L.; Bashkirtseva, I.; Gubkin, A.; Stikhin, P. Confidence tori in the analysis of stochastic 3D-cycles. Math. Comput. Simul. 2009, 80, 256–269. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Ryashko, L. Sensitivity analysis of stochastic attractors and noise-induced transitions for population model with Allee effect. Chaos 2011, 21, 047514. [Google Scholar] [CrossRef]
- Bashkirtseva, I. Stochastic sensitivity analysis: Theory and numerical algorithms. IOP Conf. Ser. Mater. Sci. Eng. 2017, 192, 012024. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, T.; Zhou, Y. Stochastic sensitivity and dynamical complexity of newsvendor models subject to trade credit. Math. Comput. Simul. 2021, 181, 471–486. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Perevalova, T. Analysis of stochastic bifurcations in the eco-epidemiological oscillatory model with weak Allee effect. Int. J. Bifurc. Chaos 2022, 32, 2250124. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Ryashko, L. Sensitivity analysis of stochastically forced quasiperiodic self-oscillations. Electron. J. Differ. Equ. 2016, 2016, 1–12. [Google Scholar]
- Bashkirtseva, I.; Ryashko, L. Stochastic sensitivity of the closed invariant curves for discrete-time systems. Phys. A 2014, 410, 236–243. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Ryashko, L. Stochastic sensitivity of regular and multi-band chaotic attractors in discrete systems with parametric noise. Phys. Lett. A 2017, 381, 3203–3210. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Bashkirtseva, I.A.; Crucifix, M.; Ryashko, L.B. Nonlinear climate dynamics: From deterministic behaviour to stochastic excitability and chaos. Phys. Rep. 2021, 902, 1–60. [Google Scholar] [CrossRef]
- Slepukhina, E.; Bashkirtseva, I.; Ryashko, L.; Kügler, P. Stochastic mixed-mode oscillations in the canards region of a cardiac action potential model. Chaos Solitons Fractals 2022, 164, 112640. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Chukhareva, A.; Ryashko, L. Stochastic dynamics of nonlinear tumor–immune system with chemotherapy. Physica A 2023, 622, 128835. [Google Scholar] [CrossRef]
- Bashkirtseva, I. Method of stochastic sensitivity synthesis in a stabilisation problem for nonlinear discrete systems with incomplete information. Int. J. Control 2017, 90, 1652–1663. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Ryashko, L.; Chen, G. Stochastic sensitivity synthesis in nonlinear systems with incomplete information. J. Frankl. Inst. 2020, 357, 5187–5198. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bashkirtseva, I.; Pavletsov, M.; Perevalova, T.; Ryashko, L. Analysis of Noise-Induced Transitions in a Thermo-Kinetic Model of the Autocatalytic Trigger. Mathematics 2023, 11, 4302. https://doi.org/10.3390/math11204302
Bashkirtseva I, Pavletsov M, Perevalova T, Ryashko L. Analysis of Noise-Induced Transitions in a Thermo-Kinetic Model of the Autocatalytic Trigger. Mathematics. 2023; 11(20):4302. https://doi.org/10.3390/math11204302
Chicago/Turabian StyleBashkirtseva, Irina, Makar Pavletsov, Tatyana Perevalova, and Lev Ryashko. 2023. "Analysis of Noise-Induced Transitions in a Thermo-Kinetic Model of the Autocatalytic Trigger" Mathematics 11, no. 20: 4302. https://doi.org/10.3390/math11204302
APA StyleBashkirtseva, I., Pavletsov, M., Perevalova, T., & Ryashko, L. (2023). Analysis of Noise-Induced Transitions in a Thermo-Kinetic Model of the Autocatalytic Trigger. Mathematics, 11(20), 4302. https://doi.org/10.3390/math11204302







