A Simplified Controller Design for Fixed/Preassigned-Time Synchronization of Stochastic Discontinuous Neural Networks
Abstract
:1. Introduction
- (1)
- The PTS problem for delayed SNNs with DF (DSNNsDF) is solved. Compared with the previous PTS results in [23,25], this paper focuses on effective control design that can eliminate the negative effects caused by time delays, DF, and stochastic perturbations. Thus, our obtained PTS results are more valuable and practical.
- (2)
- Based on a preliminary design of the FxTS controller with simple structure, the criteria of FxTS as well as an estimation time are obtained by the incomplete beta functions. Compared to previous FxTS controllers in [20,21,29], our controller has the simplest structure. Moreover, due to the reduction of criteria and the improvement of estimation method, the obtained estimation for the synchronization time is more accurate and less conservative.
- (3)
- A simple and efficient PTS controller is designed based on the former FxTS result. Compared with the previous PTS controller in [21,27,28], our PTS controller is capable of achieving the ideal synchronization effect with minimal control gains owing to more accurate time estimation and the simplest controller.
2. Preliminaries
- (1)
- is continuous on and absolutely continuous on .
- (2)
- there exists a measurable function such that for almost every , the component satisfies and
- (1)
- Finite-time attractiveness in probability: For any non-zero initial error , the first hitting time , regarded as stochastic settling time, is almost surely finite, i.e., and , a.s., .
- (2)
- Stability in probability: For given values and , there exists a positive value such that the probability of the error being within a specified range in which holds for any and for initial error .
- (1)
- The error system (6) is finite-time stability in probability;
- (2)
- Mathematical expectation for settling time function is bounded with , which is independent of the initial state for . Furthermore, if can be arbitrarily selected as required, error system (6) is said to be preassigned-time stability in probability.
- (1)
- (2)
3. Main Results
3.1. Simplified Controller Design
3.2. FxTS of DSNNsDF
3.3. PTS of DSNNsDF
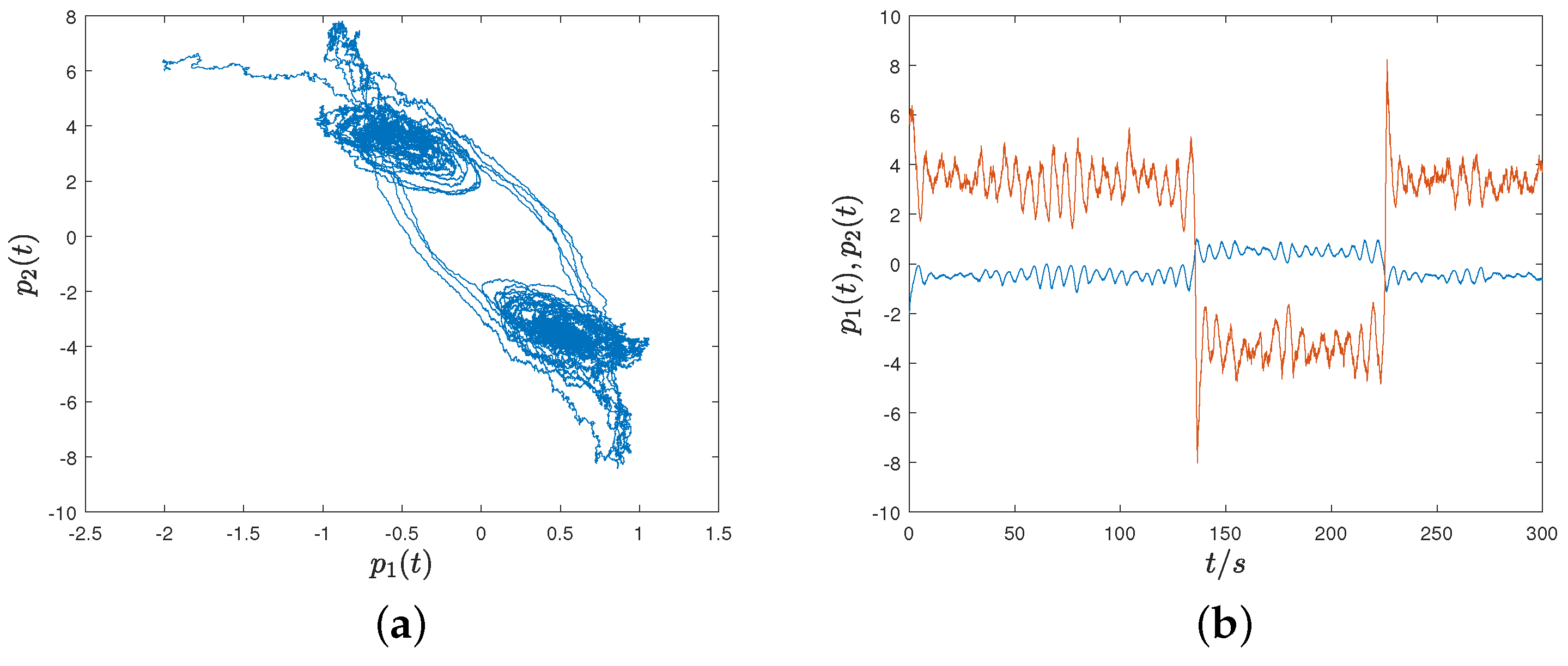
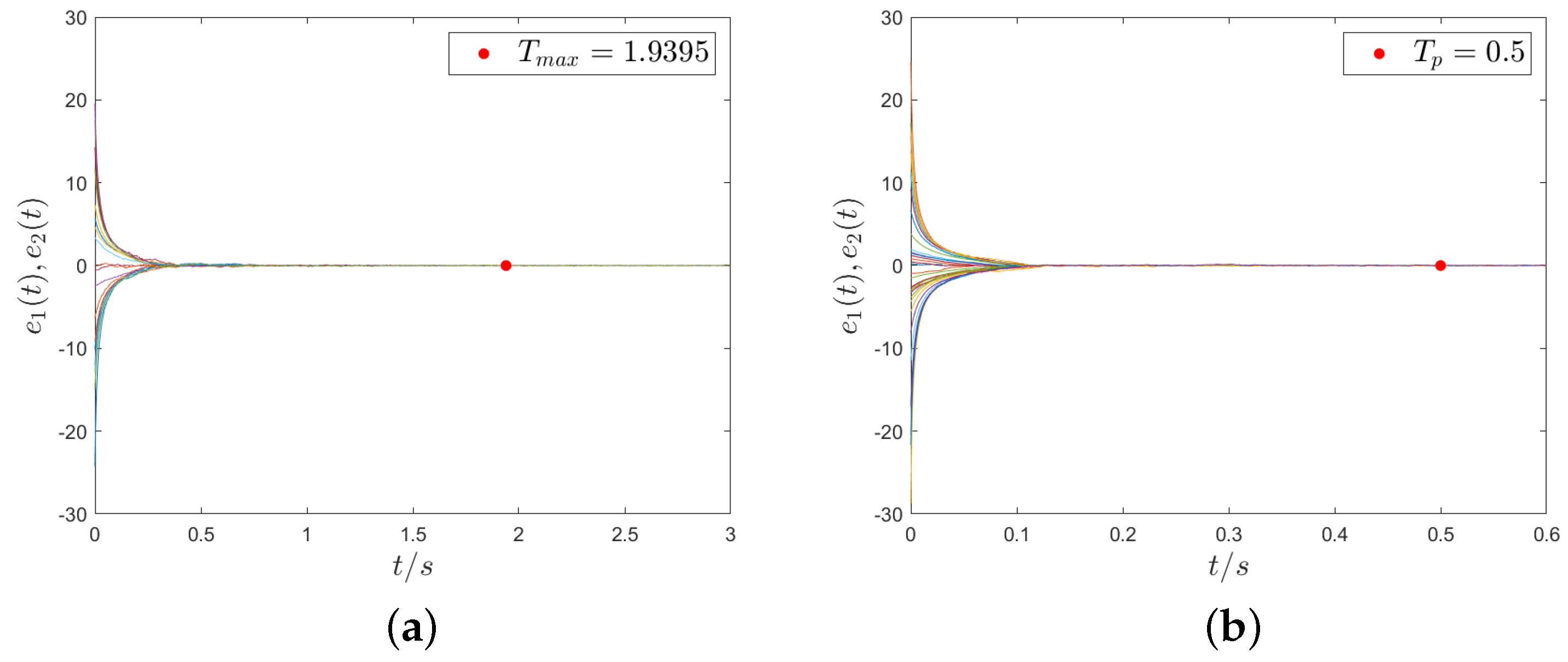
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Abbreviations
| FxTS | fixed-time synchronization |
| PTS | preassigned-time synchronization |
| DSNNsDF | delayed stochastic neural networks with discontinuous activation functions |
References
- Lawrence, S.; Giles, C.L.; Tsoi, A.C.; Back, A.D. Face recognition: A convolutional neural-network approach. IEEE Trans. Neural Netw. 1997, 8, 98–113. [Google Scholar] [CrossRef] [PubMed]
- Cochocki, A.; Unbehauen, R. Neural Networks for Optimization and Signal Processing; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1993. [Google Scholar]
- Tang, Y.; Qian, F.; Gao, H.; Kurths, J. Synchronization in complex networks and its application–a survey of recent advances and challenges. Annu. Rev. Control 2014, 38, 184–198. [Google Scholar] [CrossRef]
- Chung, S.J.; Ahsun, U.; Slotine, J.J.E. Application of synchronization to formation flying spacecraft: Lagrangian approach. J. Guid. Control Dyn. 2009, 32, 512–526. [Google Scholar] [CrossRef]
- Wang, L.; He, H.; Zeng, Z. Global synchronization of fuzzy memristive neural networks with discrete and distributed delays. IEEE Trans. Fuzzy Syst. 2019, 28, 2022–2034. [Google Scholar] [CrossRef]
- Hu, X.; Wang, L.; Zhang, C.K.; Wan, X.; He, Y. Fixed-time stabilization of discontinuous spatiotemporal neural networks with time-varying coefficients via aperiodically switching control. Sci. China Inf. Sci. 2023, 66, 1–14. [Google Scholar] [CrossRef]
- Li, H.; Hu, X.; Wang, Q.; Wang, L. Anti-synchronization in fixed-/preassigned-time of delayed memristive neural networks with discontinuous activation functions. Int. J. Control 2023. accepted. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks; IEEE Computer Society Press: Washington, DC, USA, 1994. [Google Scholar]
- Yao, Y.; Zhang, G.; Li, Y. Fixed/Preassigned-Time Stabilization for Complex-Valued Inertial Neural Networks with Distributed Delays: A Non-Separation Approach. Mathematics 2023, 11, 2275. [Google Scholar] [CrossRef]
- Abudusaimaiti, M.; Abudukeremu, A.; Sabir, A. Fixed/Preassigned-Time Stochastic Synchronization of Complex-Valued Fuzzy Neural Networks with Time Delay. Mathematics 2023, 11, 3769. [Google Scholar] [CrossRef]
- Danca, M.F. Controlling chaos in discontinuous dynamical systems. Chaos Solitons Fractals 2004, 22, 605–612. [Google Scholar] [CrossRef]
- Forti, M.; Grazzini, M.; Nistri, P.; Pancioni, L. Generalized Lyapunov approach for convergence of neural networks with discontinuous or non-Lipschitz activations. Phys. D Nonlinear Phenom. 2006, 214, 88–99. [Google Scholar] [CrossRef]
- Yu, X.; Yin, J.; Khoo, S. Generalized Lyapunov criteria on finite-time stability of stochastic nonlinear systems. Automatica 2019, 107, 183–189. [Google Scholar] [CrossRef]
- Liu, J.; Niu, B.; Zhao, P.; Li, X.; Qi, W. Almost fast finite-time adaptive tracking control for a class of full-state constrained pure-feedback nonlinear systems. Int. J. Robust Nonlinear Control 2020, 30, 7517–7532. [Google Scholar] [CrossRef]
- Su, Y. Global continuous finite-time tracking of robot manipulators. Int. J. Robust Nonlinear Control IFAC-Affil. J. 2009, 19, 1871–1885. [Google Scholar] [CrossRef]
- Du, H.; Li, S.; Qian, C. Finite-time attitude tracking control of spacecraft with application to attitude synchronization. IEEE Trans. Autom. Control 2011, 56, 2711–2717. [Google Scholar] [CrossRef]
- Perruquetti, W.; Floquet, T.; Moulay, E. Finite-time observers: Application to secure communication. IEEE Trans. Autom. Control 2008, 53, 356–360. [Google Scholar] [CrossRef]
- Yu, J.; Yu, S.; Li, J.; Yan, Y. Fixed-time stability theorem of stochastic nonlinear systems. Int. J. Control 2019, 92, 2194–2200. [Google Scholar] [CrossRef]
- Kong, F.; Zhu, Q.; Sakthivel, R. New fixed-time stability in probability lemmas of stochastic discontinuous systems and applications. Nonlinear Dyn. 2022, 110, 2753–2768. [Google Scholar] [CrossRef]
- Cui, W.; Wang, Z.; Jin, W. Fixed-time synchronization of Markovian jump fuzzy cellular neural networks with stochastic disturbance and time-varying delays. Fuzzy Sets Syst. 2021, 411, 68–84. [Google Scholar] [CrossRef]
- Hou, M.; He, Q.; Ma, Y. Preassigned/fixed-time stochastic synchronization of complex networks via simpler nonchattering quantified adaptive control strategies. Neural Comput. Appl. 2022, 34, 19161–19179. [Google Scholar] [CrossRef]
- Hu, C.; He, H.; Jiang, H. Fixed/preassigned-time synchronization of complex networks via improving fixed-time stability. IEEE Trans. Cybern. 2020, 51, 2882–2892. [Google Scholar] [CrossRef]
- Li, H.; Hu, C.; Zhang, G.; Hu, J.; Wang, L. Fixed-/Preassigned-time stabilization of delayed memristive neural networks. Inf. Sci. 2022, 610, 624–636. [Google Scholar] [CrossRef]
- Chen, C.; Mi, L.; Zhao, D.; Guan, H.; Li, L.; Zhao, H. A new judgment theorem for predefined-time stability and its application in the synchronization analysis of neural networks. Int. J. Robust Nonlinear Control 2022, 32, 10072–10086. [Google Scholar] [CrossRef]
- Wei, W.; Yu, J.; Wang, L.; Hu, C.; Jiang, H. Fixed/Preassigned-time synchronization of quaternion-valued neural networks via pure power-law control. Neural Netw. 2022, 146, 341–349. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Wang, X.; Song, Y. Prescribed performance tracking control under uncertain initial conditions: A neuroadaptive output feedback approach. IEEE Trans. Cybern. 2022, 1–11. [Google Scholar] [CrossRef]
- Pal, A.K.; Kamal, S.; Nagar, S.K.; Bandyopadhyay, B.; Fridman, L. Design of controllers with arbitrary convergence time. Automatica 2020, 112, 108710. [Google Scholar] [CrossRef]
- Krishnamurthy, P.; Khorrami, F.; Krstic, M. A dynamic high-gain design for prescribed-time regulation of nonlinear systems. Automatica 2020, 115, 108860. [Google Scholar] [CrossRef]
- Abudusaimaiti, M.; Abdurahman, A.; Jiang, H.; Hu, C. Fixed/predefined-time synchronization of fuzzy neural networks with stochastic perturbations. Chaos Solitons Fractals 2022, 154, 111596. [Google Scholar] [CrossRef]
- Wang, Y.; Li, H.; Guan, Y.; Chen, M. Predefined-time chaos synchronization of memristor chaotic systems by using simplified control inputs. Chaos Solitons Fractals 2022, 161, 112282. [Google Scholar] [CrossRef]
- Clarke, F.H. Optimization and Nonsmooth Analysis; SIAM: Philadelphia, PA, USA, 1990. [Google Scholar]
- Hardy, G.; Littlewood, J.; Polya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Li, N.; Wu, X.; Feng, J.; Lü, J. Fixed-time synchronization of complex dynamical networks: A novel and economical mechanism. IEEE Trans. Cybern. 2020, 52, 4430–4440. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, W.; Ruan, D.; Yang, T.; Li, Y. Fast fixed-time impulsive bipartite synchronization of TS fuzzy complex networks with signed graphs. Nonlinear Anal. Hybrid Syst. 2023, 48, 101325. [Google Scholar] [CrossRef]
- Zhou, L.; Lin, H.; Tan, F. Fixed/predefined-time synchronization of coupled memristor-based neural networks with stochastic disturbance. Chaos Solitons Fractals 2023, 173, 113643. [Google Scholar] [CrossRef]
- He, Q.; Ma, Y. Quantized adaptive pinning control for fixed/preassigned-time cluster synchronization of multi-weighted complex networks with stochastic disturbances. Nonlinear Anal. Hybrid Syst. 2022, 44, 101157. [Google Scholar] [CrossRef]
- Li, N.; Wu, X.; Feng, J.; Xu, Y. Fixed-time synchronization in probability of drive-response networks with discontinuous nodes and noise disturbances. Nonlinear Dyn. 2019, 97, 297–311. [Google Scholar] [CrossRef]
| K = | K = | |||
|---|---|---|---|---|
| this paper | ✓ | ✓ | ||
| [29,33] | ✓ | ✓ | ||
| [21,25,34] | ✓ | ✓ | ||
| [19,20,23,35,36] | ✓ | ✓ | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Wang, L.; Shen, W. A Simplified Controller Design for Fixed/Preassigned-Time Synchronization of Stochastic Discontinuous Neural Networks. Mathematics 2023, 11, 4414. https://doi.org/10.3390/math11214414
Li H, Wang L, Shen W. A Simplified Controller Design for Fixed/Preassigned-Time Synchronization of Stochastic Discontinuous Neural Networks. Mathematics. 2023; 11(21):4414. https://doi.org/10.3390/math11214414
Chicago/Turabian StyleLi, Haoyu, Leimin Wang, and Wenwen Shen. 2023. "A Simplified Controller Design for Fixed/Preassigned-Time Synchronization of Stochastic Discontinuous Neural Networks" Mathematics 11, no. 21: 4414. https://doi.org/10.3390/math11214414
APA StyleLi, H., Wang, L., & Shen, W. (2023). A Simplified Controller Design for Fixed/Preassigned-Time Synchronization of Stochastic Discontinuous Neural Networks. Mathematics, 11(21), 4414. https://doi.org/10.3390/math11214414






