Abstract
In the real world, a nonparametric control chart is a powerful substitute for enhancing outcome quality, although the fundamental procedure characteristic often fails to match the distribution assumptions. This study aims to construct and evaluate an extended exponentially weighted moving average control chart based on signed-rank statistics (EEWMA-SR) for recognizing changes in procedures. According to the study, the proposed chart proves more potent recognition of shifts in the process mean, predominantly small shifts, than the other control charts by the average run length in Monte Carlo simulation. Applying the proposed control chart to an actual dataset yielded events that corroborated the study discoveries.
Keywords:
signed-rank test; extended exponentially weighted moving average control chart; average run length; mean process; detection; nonparametric control chart MSC:
65C60
1. Introduction
Statistical process control (SPC) assists organizations in monitoring and controlling quality. It allows manufacturers to increase efficiency, decrease waste products, and detect concerns early. The monitoring of quality and processes is critical to manufacturing efficiency. A control chart is a statistical instrument used to track and control the performance of a process over a specific time. Control charts aim to detect and prevent irregularities or deviations in operation. Shewhart was the first author to develop a control chart [], which was more effective at detecting significant large shifts. Next, the moving average (MA) [], exponentially weighted moving average (EWMA) [], and cumulative sum (CUSUM) control charts were utilized to identify small to medium-sized shifts []. In terms of rapidly detecting shifts, Naveed et al. developed an extended exponentially weighted moving average (EEWMA) control chart that was expanded from the EWMA structure for effectively tracking the process mean with the result outperforming the Shewhart and EWMA control charts [].
For ordinary purposes, parametric control charts assume that process observations follow a normal distribution. Nevertheless, if the observations are from a non-normal distribution, employing counterparts of these control charts to monitor process shifts is not appropriate. As a result, constructing a nonparametric control chart is a viable option. Nonparametric control charts have many positives, including accessibility, no requirement for assuming a particular parametric distribution for the foundational process, more robustness and resistance to outliers, and no requirement for estimating the variance when creating charts for the location parameter. Many researchers use the sign and signed-rank statistics in conjunction with the other control charts, such as the EWMA-Sign control chart designed by Yang et al. []. Lu developed the generally weighted moving average (GWMA) sign control chart to enhance the ability to detect small process shifts and suggested it as a replacement when process information is lacking []. Sukparungsee demonstrated the robustness of a generally weighted moving average based on a signed-rank (GWMA-SR) control chart for monitoring skew process shifts compared to GWMA-SN and EWMA-SN control charts []. The results show that the GWMA-SR chart is resistant to skew. Abid et al. proposed a new Cumulative Sum–Wilcoxon signed-rank chart for monitoring process location with ranked set sampling []. Depending on the average run length, the proposed chart outperforms some competing counterpart charts in shift detection. Pawar et al. proposed nonparametric moving average control charts that detect shifts in the median of symmetric process distributions using sign and signed-rank statistics []. Their comparison showed that the proposal outperforms its competitors. In 2020, Aslam et al. presented a modified exponentially weighted moving average control chart combined with the sign statistic (MEWMA-Sign) via the average run length serving as an efficiency evaluation []. The results revealed that the MEWMA-Sign chart proved better than the EWMA-Sign chart at recognizing changes. Rasheed et al. designed a nonparametric triple exponentially weighted moving average Wilcoxon signed-rank control chart based on ranked set sampling []. At the same time, their findings showed that the proposed chart was better than existing control charts in identifying small shifts in process location. The effectiveness of a distribution-free double-exponentially weighted moving average chart based on the sign test statistic was compared with the output of existing control charts employing run length tests []. The assessment revealed that the proposed chart outperforms its competitors in detecting small and medium shifts in process location. Taboran and Sukparungsee investigate the MEWMA-Sign control chart for monitoring procedure mean under abnormal distributions [], and the findings show that the chart exceeds EWMA-Sign in detecting tiny shifts. Abbas et al. designed the nonparametric progressive mean control chart based on the Wilcoxon signed-rank statistic (NPPM-SR), and the results show that it is more efficient than the nonparametric EWMA sign (NPEWMA-SN) chart or the nonparametric EWMA based on Wilcoxon signed-rank statistic (NPEWMA-SR) chart using average run length criteria []. Petcharat and Sukparungsee present a new MEWMA-Wilcoxon sign rank chart to detect change in the mean parameter [].
This study aims to design an EEWMA chart based on sign rank statistics (hereafter referred to as EEWMA-SR) that effectively recognizes minor changes in procedure location in normal (0,1), Laplace (1,1) and lognormal (0,1) distributions. The performance of the proposed chart was evaluated and compared with existing control charts using the average run length (ARL) in Monte Carlo simulation analysis. Finally, illustrations of the proposed chart using real data are offered.
2. Materials and Methods
This section describes the control chart design structures and performance evaluation. Section 2.1 depicts the parametric control charts, the Exponentially Weighted Moving Average control chart (EWMA) and the Extended Exponentially Weighted Moving Average control chart (EEWMA), as well as the existing nonparametric control charts, the Exponentially Weighted Moving Average-sign control chart (EWMA-SN), the Exponentially Weighted Moving Average-sign rank control chart (EWMA-SR), the Extended Exponentially Weighted Moving Average-sign control chart (EEWMA-SN), and the proposed Extended Exponentially Weighted Moving Average-sign rank control chart (EEWMA-SR). Section 2.2 defines the performance evaluation method.
2.1. Control Charts
Let be a sample of size n drawn from a process having a continuous distribution with process mean . Then, the difference between the observation and the target value, i.e., within groups, can be denoted as follows:
The Sign statistic can be defined as:
where .
Then, the Sign statistic is the total number of the observations that follow the binomial distribution with a parameter for the control case. The is the process proportion, which is in a controlled process. In contrast, when the process is out of control, .
Let denote the rank of the absolute difference within the subgroup. The sign rank statistics are defined as follows:
where .
2.1.1. Exponentially Weighted Moving Average Control Chart (EWMA)
The EWMA control chart was designed by Roberts and can detect small shifts in the process mean and the EWMA statistic with a smoothing parameter γ (0 < γ ≤ 1) [], as shown in Equation (1):
, independent and identically distributed random variables, are drawn from a normal sample with mean and variance . The initial value is usually given to equal . The mean and asymptotic variance are:
The EWMA control limit boundaries are:
where the average and standard deviation of the processes are , and is the EWMA chart’s coefficient control limit corresponding to the wanted ARL0.
2.1.2. Extended Exponentially Weighted Moving Average (EEWMA) Control Chart
The EEWMA control chart was established by Naveed et al. as highly beneficial for recognizing an abrupt change in the mean with the following EEWMA statistic []:
where and are smoothing parameters that range from 0 to 1, where and . The average and the asymptotic variance of , when , are defined as follows:
The control limits of the EEWMA chart are as follows:
where and represent the average and standard deviation of the processes under consideration, respectively, and is the EEWMA chart’s coefficient control limit corresponding to the wanted ARL0.
2.1.3. Exponentially Weighted Moving Average-Sign Control Chart (EWMA-SN)
Yang et al. created the mixed EWMA chart based on the Sign statistic, known as the EWMA-SN []. The EWMA-SN statistic with a smoothing parameter γ (0 < γ ≤ 1) is shown in Equation (12):
The mean and asymptotic variance are:
The EWMA-SN control limits boundaries are:
where is the EWMA-SN chart’s coefficient control limit corresponding to the wanted ARL0.
2.1.4. Exponentially Weighted Moving Average-Sign Rank Control Chart (EWMA-SR)
Graham et al. presented a nonparametric EWMA combined with a signed-rank statistic control chart []. The EWMA-SR statistic is shown in Equation (16):
The mean and asymptotic variance are:
The EWMA-SR control limit boundaries are:
where is the EWMA-SR chart’s coefficient control limit corresponding to the wanted ARL0.
2.1.5. Extended Exponentially Weighted Moving Average-Sign Control Chart (EEWMA-SN)
The EEWMA-SN control chart was created by combining EEWMA and Sign statistics. The EEWMA-SN control design statistic is described this way in Equation (12):
where and are smoothing parameters that range from 0 to 1, where and . The average and variance of EEWMA-SN are:
The control limits of the EEWMA-SN chart are as follows:
where H5 is the initial value of the EEWMA-SN control chart’s suitable limit.
2.1.6. Extended Exponentially Weighted Moving Average-Sign Rank Control Chart (EEWMA-SR)
The proposed EEWMA-SR control chart was created by combining EEWMA and Sign rank statistics. The EEWMA-SR control design statistic, which has smoothing parameters and ( and ), is described this way in Equation (24):
The average and variance of EEWMA-SR are:
The control limits of the EEWMA-SR chart are as follows:
where H5 is the initial value of the EEWMA-SR control chart’s suitable limit. Finally, the mean and variance formulas are shown in Appendix A.
2.2. Performance Evaluation
Various run length properties are available in statistical process control literature to evaluate a control chart. The average run length (ARL) is instrumental in determining the performance of the control chart and its capacity to shift. The in-control ARL, ARL0, is expected to be large enough to prevent false alarms. The out-of-control ARL, ARL1, should be small enough to detect shifts quickly when the process is out of control. The ARL is described in Equation (28), where indicates the number of samples needed prior to the approach becoming uncontrollable for the first time:
The run-length feature of the control chart can be investigated using Monte Carlo simulation with 100,000 recurrence (N) and the control process set to 370. As a result, the control limits coefficient must be chosen so that the resultant value matches up to or equivalent to the roughly ARL0. The procedure that can be employed to identify a solution is explained in the following step:
- (i)
- Create n random samples from any particular distribution.
- (ii)
- Estimate the proposed tracking statistic and evaluate “H” at .
- (iii)
- The control limit is subsequently determined and the values statistic is operated.
- (iv)
- Continue to iterate 100,000 times (N) to calculate the ARL and assess the control chart effectiveness.
Finally, we determined the average run length value in each of the control charts. The performance of the proposed chart is compared to the EWMA chart, the EEWMA chart, the EWMA-SN chart, the EWMA-SR chart, and the EEWMA-SN chart. A chart with a low ARL1 value at a given shift is considered to be more effective.
3. Results
This section explains the simulation results by comparing the proposed chart to five existing charts in Section 3.1 and presents an application in Section 3.2.
3.1. Simulation
A simulation research investigation is carried out to validate the precision of the proposed chart (EEWMA-SR). In this experiment, we choose the smoothing parameters , in the EWMA, EWMA-SN, and EWMA-SR charts, but employ and in the EEWMA, EEWMA-SN, and proposed charts with 5 and 10 subgroups in Monte Carlo simulations under ARL0 = 370. The smoothing parameter was used in the simulation because it is commonly used and encountered in manufacturing; it can be found in [,,,,]. The distributions employed in this study are normal (0,1), lognormal (0,1), and Laplace (1,1), with specific shifts ranging from 0 to 1.5. Additionally, we compared the effectiveness of the proposed chart (EEWMA-SR) with the outcomes of the existing charts, determining that the chart with the least ARL1 is the most powerful.
From the results, the control limit constants of the nonparametric control charts (EWMA-SN, EWMA-SR, EEWMA-SN, and EEWMA-SR) are relatively high in all distributions when compared to their parametric control charts (EWMA and EEWMA). However, we discovered that as the smoothing parameter value increased, the coefficient control limit of parametric control charts increased while that of nonparametric control charts decreased.
Table 1 and Table 2 display the numerical outcomes for different subgroups, n = 5 and n = 10, while the distribution of the observations is normal (0,1). We discovered that the proposed chart outperforms other existing control charts when shift sizes are small (), the EWMA-SR performs better when , but the EEWMA has slightly better detectability in shifts . Furthermore, the EWMA outperforms in detecting large shifts (). However, when n = 5 and n = 10 with smoothing parameters in parametric control charts and as well as and in nonparametric control charts, an equivalent result is obtained. Figure 1 depicts the performance graphically.

Table 1.
ARL1 performance of the proposed chart and existing control chart in the normal distribution when .

Table 2.
ARL1 performance of the proposed chart and existing control chart in the normal distribution when n = 10.
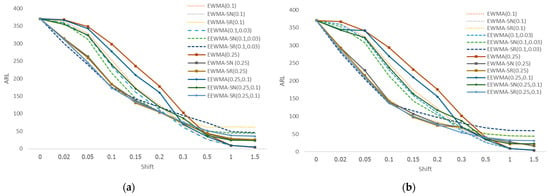
Figure 1.
The shape of the ARL control charts in the normal distribution with (a) n = 5 and (b) n = 10.
We explore the proposed chart’s efficiency with the Laplace (1,1) distribution for distinct subgroups of n = 5 and n = 10, as demonstrated in Table 3 and Table 4. When considering subgroups n = 5, the proposed chart appeared to be the most successful at recognizing changes at . The EWMA-SR chart exceeded various control charts for detecting changes , except for large changes (), where the EWMA chart outperformed. Moreover, the computational results from n = 10 subgroups produce the same result as n = 5 subgroups. Separate smoothing parameters created the same outcomes in both cases. Figure 2 presents the results graphically.

Table 3.
ARL1 performance of the proposed chart and existing control chart in the Laplace distribution when .

Table 4.
ARL1 performance of the proposed chart and existing control chart in the Laplace distribution when .
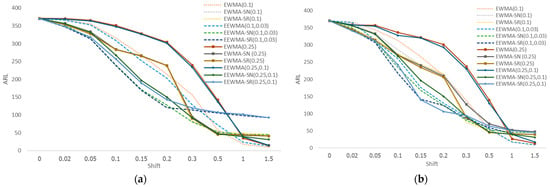
Figure 2.
The shape of the ARL control charts in the Laplace distribution with (a) n = 5 and (b) n = 10.
Table 5 and Table 6 examine the proposed chart to five fighting control charts employing ARL1 values from the lognormal (0,1) distribution. For a slight shift (), the proposed chart performs better than the existing charts. The EWMA-SR and EWMA-SN perform better for moderate and significant shifts, respectively. Additionally, for the two smoothing parameters, the numerical outcomes gained with n = 5 subgroups lead to similar outcomes to n = 10 subgroups. Figure 3 clearly shows the performance.

Table 5.
ARL1 performance of the proposed chart and existing control chart in the lognormal distribution when .

Table 6.
ARL1 performance of the proposed chart and existing control chart in the lognormal distribution when .
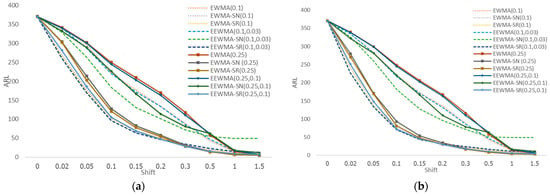
Figure 3.
The shape of the ARL control charts in the lognormal distribution with (a) n = 5 and (b) n = 10.
3.2. Application
We will present rice productivity data below 550 kg generated for the planting year 2021 in 47 provinces of Thailand on the proposed chart [], EWMA, EEWMA, EWMA-SN, EWMA-SR, EEWMA-SN charts via data under the lognormal distribution with mean 5.987, standard deviation = 0.154, and significance estimated as a lognormal distribution with a p-value = 0.062. Figure 4 indicates that the EEWMA-SR control chart can quickly detect changes in the second sample. The EWMA-SR chart eventually identified a change on the fifth sample, the EWMA-SN chart on the twelfth sample, the EEWMA-SR on the seventeenth sample; the parametric control charts (EWMA and EEWMA) did not detect any shifts. As a result, the proposed chart recognizes shifts more quickly than the existing charts. This implies that when the data exceed control limits, the method may improve the planning and strategy of plant rice.
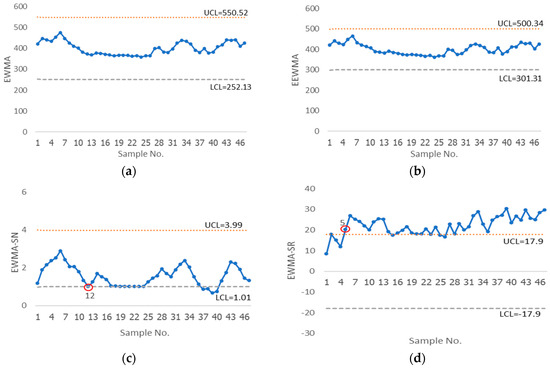
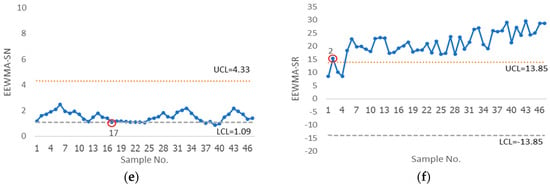
Figure 4.
The capacity of the following charts to identify a change in rice data: (a) the EWMA chart, (b) the EEWMA chart, (c) the EWMA-SN chart, (d) the EWMA-SR chart, (e) the EEWMA-SN chart, and (f) the EEWMA-SR chart.
4. Discussion and Conclusions
In this research, we offer a control chart that employs the ARL to develop more effective mean monitoring systems for symmetric and skewed distributions by combining the EEWMA with the nonparametric sign rank statistic. According to the findings, the proposed chart is the most suitable control chart for small shifts across all distributional settings, with the lowest ARL1 compared to EWMA, EEWMA, EWMA-SN, EWMA-SR, and EEWMA-SN. Nonetheless, the EWMA chart recognizes significant shifts with greater precision than other charts, except for the lognormal distribution, where the EWMA-SN operates most effectively. Alternatively, nonparametric control charts, such as the EWMA-SN, EWMA-SR, and EEWMA-SN control charts, outperform parametric control charts, considering they can overcome the constraints of assuming a known parameter for process observation. When applied to the proposed chart for real data, the results revealed that the chart was successful at recognizing shifts quickly.
Furthermore, we compare the proposed ARL performance to the Modified Exponentially Weighted Moving Average sign control chart (MEWMA-Sign) under the Laplace distribution and ARL0 = 370 with 5 and 10 subgroups []. The simulation results proved that the proposed chart is superior to the MEWMA-Sign charts in all shift dimensions. Therefore, studying more values of smoothing parameters reveals that the results are more robust. The proposed chart offers quality practitioners that are an alternative way of adopting an accurate and efficient control chart. The work described may be developed in future studies to monitor the process mean in skewed distributions, such as Weibull and Gamma, and extended to monitor the variation process. Following that, it can be applied to real-world data with a variety of distributions.
Author Contributions
Conceptualization, S.S.; methodology, K.T.; software, K.T.; validation, K.T., Y.A. and S.S.; formal analysis, K.T.; investigation, K.T. and Y.A.; resources, K.T.; data curation, K.T.; writing—original draft preparation, K.T.; writing—review and editing, S.S.; visualization, S.S.; supervision, S.S.; project administration, S.S.; funding acquisition, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Thailand Science Research and Innovation, Ministry of Higher Education, Science, Research, grant number KMUTNB-FF-67-B-17 and the APC was also funded by KMUTNB-FF-67-B-17.
Data Availability Statement
The data supporting this study’s findings are available from the corresponding author.
Acknowledgments
The authors would like to express thanks to the Department of Applied Statistics for supporting materials and superhigh-performance computer. We would also like to express gratitude to King Mongkut’s University of Technology North Bangkok and Thailand Science Research and Innovation, Ministry of Higher Education, Science, Research for supporting the research fund.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Derivation of the mean and variance of the EEWMA-SN statistics.
Substitute the expression (A1) in (A2).
Let , ,
Continuing to EEWMA, where k= 2, 3, 4, ….
Taking expectation of Equation (A3):
We obtain: ; therefore, .
Taking variance of Equation (A3):
Thus, .
Derivation of the mean and variance of the proposed EEWMA-SR statistics.
Taking expectation of Equation (A4):
We obtain: , let p = 0.5. Therefore, .
Taking variance of Equation (A4):
Let p = 0.5, q = 0.5. Thus, .
References
- Shewhart, W.A. Economic Control of Quality of Manufactured Product; D. Van Nostrand Co.: New York, NY, USA, 1931. [Google Scholar]
- Khoo, M.B.C. A Moving Average Control Chart for Monitoring the Fraction Non-conforming. Qual. Reliab. Eng. Int. 2004, 20, 617–635. [Google Scholar] [CrossRef]
- Roberts, S.W. Control Chart Tests Based on Geometric Moving Averages. Technometrics 1959, 1, 239–250. [Google Scholar] [CrossRef]
- Page, E.S. Continuous Inspection Schemes. Biometrika 1954, 41, 100–115. [Google Scholar] [CrossRef]
- Naveed, M.; Azam, M.; Khan, N.; Aslam, M. Design of a Control Chart Using Extended EWMA Statistic. Technologies 2018, 6, 108. [Google Scholar] [CrossRef]
- Yang, S.F.; Lin, J.S.; Cheng, S.W. A New Nonparametric EWMA Sign Control Chart. Expert Syst. Appl. 2011, 38, 6239–6243. [Google Scholar] [CrossRef]
- Lu, S.L. An Extended Nonparametric Exponentially Weighted Moving Average Sign Control Chart. Qual. Reliab. Eng. Int. 2015, 31, 3–13. [Google Scholar] [CrossRef]
- Sukparungsee, S. Robustness of Generally Weighted Moving Average Signed-rank Control Chart for Monitoring a Shift of Skew Processes. Int. J. Sci. Technol. Res. 2018, 4, 125–137. [Google Scholar] [CrossRef]
- Abid, M.; Nazir, H.Z.; Tahir, M.; Riaz, M. On designing a New Cumulative Sum Wilcoxon Signed Rank Chart for Monitoring Process Location. PLoS ONE 2018, 13, e0195762. [Google Scholar] [CrossRef] [PubMed]
- Pawar, V.Y.; Shirke, D.T.; Khilare, S.K. Nonparametric Moving Average Control Charts Using Sign and Signed-rank Statistics. Int. J. Sci. Res. Math. Stat. Sci. 2018, 5, 171–178. [Google Scholar] [CrossRef]
- Aslam, M.; Raza, M.A.; Azam, M.; Ahmad, L.; Jun, C.-H. Design of a Sign Chart using A New EWMA Statistic. Commun. Stat. 2020, 49, 1299–1310. [Google Scholar] [CrossRef]
- Rasheed, Z.; Zhang, H.; Arslan, M.; Zaman, B.; Anwar, M.S.; Abid, M.; Abbasi, A.S. An Efficient Robust Nonparametric Triple EWMA Wilcoxon Signed-Rank Control Chart for Process Location. Math. Probl. Eng. 2021, 2021, 2570198. [Google Scholar] [CrossRef]
- Ali, S.; Abbas, Z.; Nazir, Z.H.; Riaz, M.; Abid, M. A New Distribution-Free Control Chart for Monitoring Process Median Based on the Statistic of the Sign Test. J. Test. Eval. 2022, 50, 20210135. [Google Scholar] [CrossRef]
- Taboran, R.; Sukparungsee, S. An Enhanced Performance to Monitor Process Mean with Modified Exponentially Weighted Moving Average—Sign Control Chart. Appl. Sci. Eng. Prog. 2022, 15, 5532. [Google Scholar] [CrossRef]
- Abbas, Z.; Nazir, Z.H.; Akhtar, N.; Abid, M.; Riaz, M. Non-Parametric Progressive Signed-Rank Control Chart for Monitoring the Process Location. J. Stat. Comput. Simul. 2022, 92, 2596–2622. [Google Scholar] [CrossRef]
- Petcharat, K.; Sukparungsee, S. Development of a New MEWMA-Wilcoxon Sign Rank Chart for Detection of Change in Mean Parameter. Appl. Sci. Eng. Prog. 2023, 16, 5892. [Google Scholar] [CrossRef]
- Graham, M.A.; Chakraborti, S.; Human, S.W. A Nonparametric Exponentially Weighted Moving Average Signed-rank Chart for Monitoring Location. Comput. Stat. Data Anal. 2011, 55, 2490–2503. [Google Scholar] [CrossRef]
- Alevizakos, V.; Chatterjee, K.; Koukouvinos, C. The Triple Exponentially Weighted Moving Average Control Chart. Qual. Technol. Quant. Manag. 2021, 18, 326–354. [Google Scholar] [CrossRef]
- Ali, S.; Abbas, Z.; Nazir, Z.H.; Riaz, M.; Zhang, X.; Li, Y. On Designing Non-Parametric EWMA Sign Chart under Ranked Set Sampling Scheme with Application to Industrial Process. Mathematics 2020, 8, 1497. [Google Scholar] [CrossRef]
- Office of Agricultural Economics. Available online: https://www.oae.go.th/ (accessed on 30 August 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).