Stretch-Energy-Minimizing B-Spline Interpolation Curves and Their Applications
Abstract
:1. Introduction
2. Cubic B-Spline Interpolation Curves with the Minimum Stretch Energy
3. Experimental Results
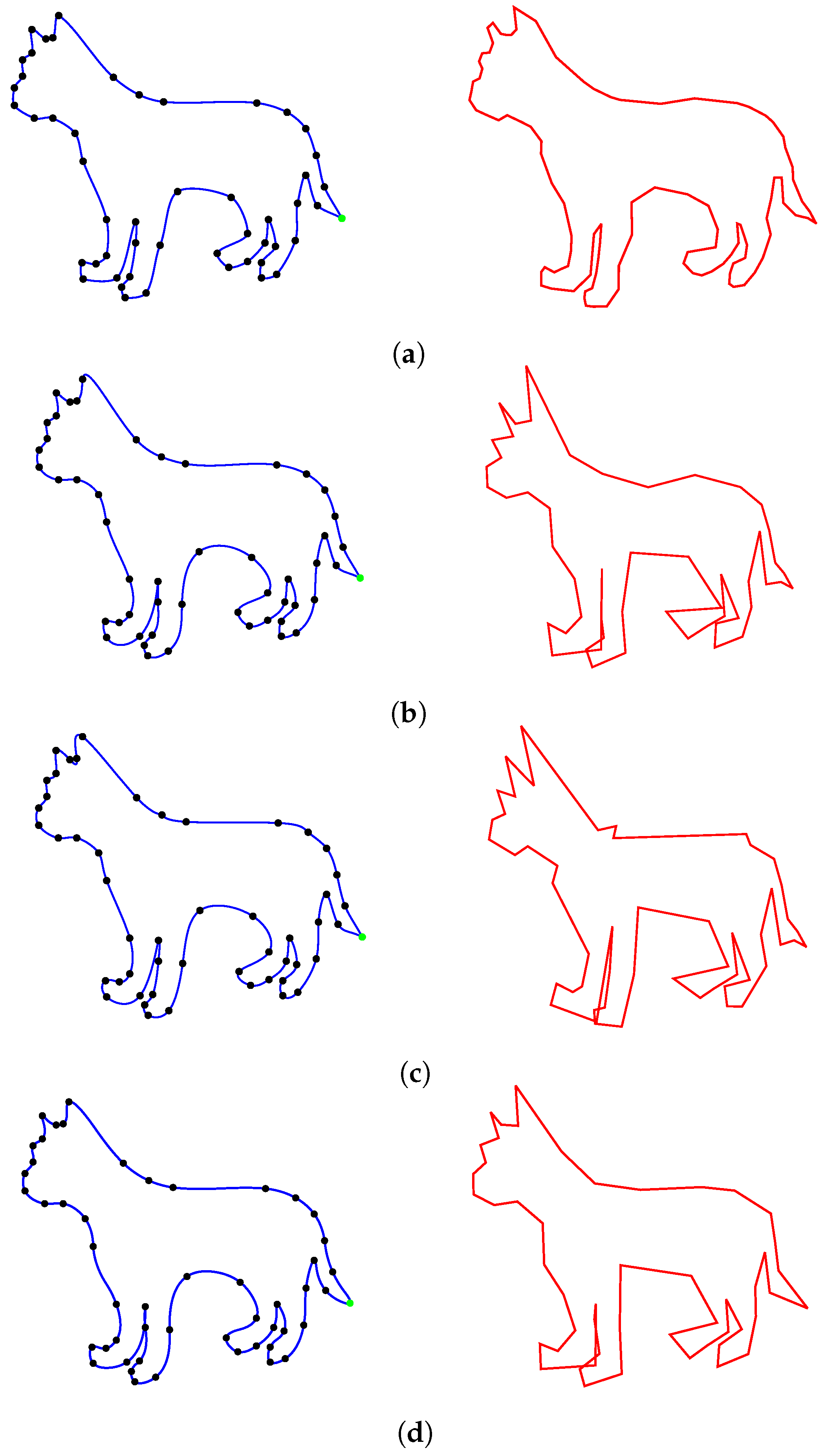
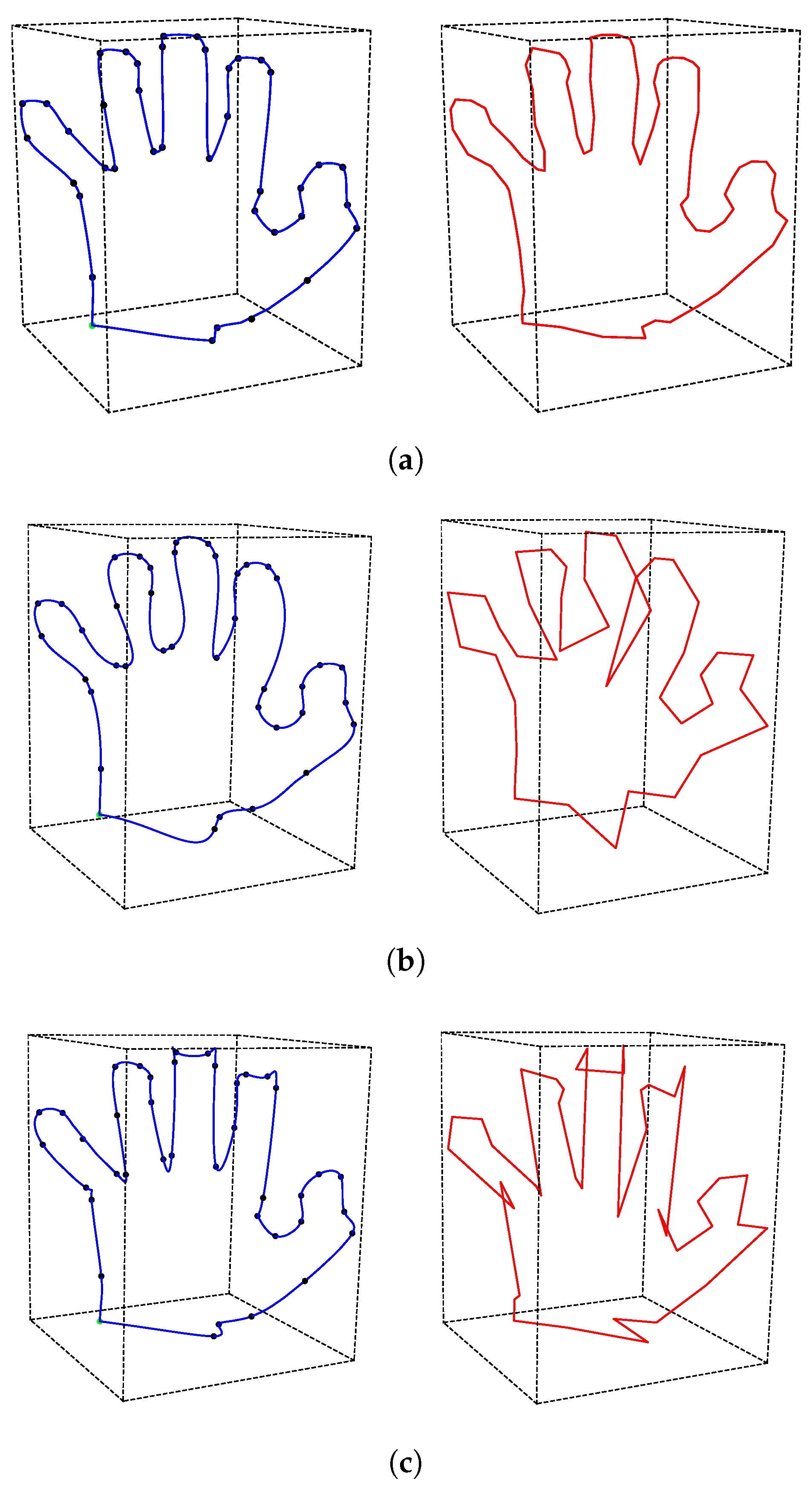
3.1. Energy-Minimizing Interpolation Curves of Planar Graphic Examples
3.2. Energy-Minimizing Interpolation Curves in a Font Modeling Example
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farin, G. Curves and Surfaces for CAGD (Fifth Edition) A Practical Guide; Morgan Kaufmann: Burlington, MA, USA, 2001. [Google Scholar]
- Wang, X.; Cheng, F.F.; Barsky, B.A. Energy and B-spline interproximation. Comput.-Aided Des. 1997, 29, 485–496. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, P.; Cheng, F.F. Fairing spline curves and surfaces by minimizing energy. Comput.-Aided Des. 2001, 33, 913–923. [Google Scholar] [CrossRef]
- Wallner, J. Existence of set-interpolating and energy-minimizing curves. Comput. Aided Geom. Des. 2004, 21, 883–892. [Google Scholar] [CrossRef]
- Hofer, M.; Pottmann, H. Energy-minimizing splines in manifolds. In ACM SIGGRAPH 2004 Papers; Association for Computing Machinery: New York, NY, USA, 2004; pp. 284–293. [Google Scholar]
- Yong, J.H.; Cheng, F.F. Geometric Hermite curves with minimum strain energy. Comput. Aided Geom. Des. 2004, 21, 281–301. [Google Scholar] [CrossRef]
- Li, C.Y.; Wang, R.H.; Zhu, C.G. Designing approximation minimal parametric surfaces with geodesics. Appl. Math. Model. 2013, 37, 6415–6424. [Google Scholar] [CrossRef]
- Johnson, M.J.; Johnson, H.S. A constructive framework for minimal energy planar curves. Appl. Math. Comput. 2016, 276, 172–181. [Google Scholar] [CrossRef]
- Xu, G.; Zhu, Y.; Deng, L.; Wang, G.; Li, B.; Hui, K.C. Efficient construction of B-spline curves with minimal internal energy. Comput. Mater. Contin. 2019, 58, 879–892. [Google Scholar] [CrossRef]
- Jiang, X.; Lin, Y. Reparameterization of B-spline surface and its application in ship hull modeling. Ocean Eng. 2023, 286, 115535. [Google Scholar] [CrossRef]
- Schneider, R.; Kobbelt, L. Discrete fairing of curves and surfaces based on linear curvature distribution. In Curve and Surface Design: Saint-Malo; 1999; pp. 371–380. Available online: https://www.graphics.rwth-aachen.de/media/papers/stmalo.pdf (accessed on 9 April 2015).
- Yan, Z.; Schiller, S.; Wilensky, G.; Carr, N.; Schaefer, S. κ-curves: Interpolation at local maximum curvature. ACM Trans. Graph. 2017, 36, 1–7. [Google Scholar] [CrossRef]
- Miura, K.T.; Gobithaasan, R.; Salvi, P.; Wang, D.; Sekine, T.; Usuki, S.; Inoguchi, J.i.; Kajiwara, K. ϵκ-Curves: Controlled local curvature extrema. Vis. Comput. 2022, 38, 2723–2738. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, B.; Huo, G.; Su, C.; Yan, D.M.; Zheng, Z. Scattered Points Interpolation with Globally Smooth B-Spline Surface using Iterative Knot Insertion. Comput.-Aided Des. 2022, 148, 103244. [Google Scholar] [CrossRef]
- Birk, L.; McCulloch, T.L. Robust generation of constrained B-spline curves based on automatic differentiation and fairness optimization. Comput. Aided Geom. Des. 2018, 59, 49–67. [Google Scholar] [CrossRef]
- Fang, J.J.; Hung, C.L. An improved parameterization method for B-spline curve and surface interpolation. Comput.-Aided Des. 2013, 45, 1005–1028. [Google Scholar] [CrossRef]
- Deng, J.; Chen, F.; Li, X.; Hu, C.; Tong, W.; Yang, Z.; Feng, Y. Polynomial splines over hierarchical T-meshes. Graph. Model. 2008, 70, 76–86. [Google Scholar] [CrossRef]
- Ni, Q.; Wang, X.; Deng, J. Modified PHT-splines. Comput. Aided Geom. Des. 2019, 73, 37–53. [Google Scholar] [CrossRef]
- Ni, Q.; Wang, X.; Deng, J. Modified basis functions for MPHT-splines. J. Comput. Appl. Math. 2020, 375, 112817. [Google Scholar] [CrossRef]
- Chan, C.L.; Anitescu, C.; Rabczuk, T. Volumetric parametrization from a level set boundary representation with PHT-splines. Comput.-Aided Des. 2017, 82, 29–41. [Google Scholar] [CrossRef]
- Nguyen-Thanh, N.; Kiendl, J.; Nguyen-Xuan, H.; Wüchner, R.; Bletzinger, K.U.; Bazilevs, Y.; Rabczuk, T. Rotation free isogeometric thin shell analysis using PHT-splines. Comput. Methods Appl. Mech. Eng. 2011, 200, 3410–3424. [Google Scholar] [CrossRef]
- Pan, M.; Tong, W.; Chen, F. Compact implicit surface reconstruction via low-rank tensor approximation. Comput.-Aided Des. 2016, 78, 158–167. [Google Scholar] [CrossRef]
- Pan, M.; Tong, W.; Chen, F. Phase-field guided surface reconstruction based on implicit hierarchical B-splines. Comput. Aided Geom. Des. 2017, 52, 154–169. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Z.; Jin, L.; Deng, J.; Chen, F. Parallel and adaptive surface reconstruction based on implicit PHT-splines. Comput. Aided Geom. Des. 2011, 28, 463–474. [Google Scholar] [CrossRef]
- Lai, M.J.; Schumaker, L.L. Spline Functions on Triangulations; Cambridge University Press: Cambridge, UK, 2007; Volume 110. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, Q.; Xie, C. Stretch-Energy-Minimizing B-Spline Interpolation Curves and Their Applications. Mathematics 2023, 11, 4534. https://doi.org/10.3390/math11214534
Ni Q, Xie C. Stretch-Energy-Minimizing B-Spline Interpolation Curves and Their Applications. Mathematics. 2023; 11(21):4534. https://doi.org/10.3390/math11214534
Chicago/Turabian StyleNi, Qian, and Chen Xie. 2023. "Stretch-Energy-Minimizing B-Spline Interpolation Curves and Their Applications" Mathematics 11, no. 21: 4534. https://doi.org/10.3390/math11214534
APA StyleNi, Q., & Xie, C. (2023). Stretch-Energy-Minimizing B-Spline Interpolation Curves and Their Applications. Mathematics, 11(21), 4534. https://doi.org/10.3390/math11214534





