Bifurcating Limit Cycles with a Perturbation of Systems Composed of Piecewise Smooth Differential Equations Consisting of Four Regions
Abstract
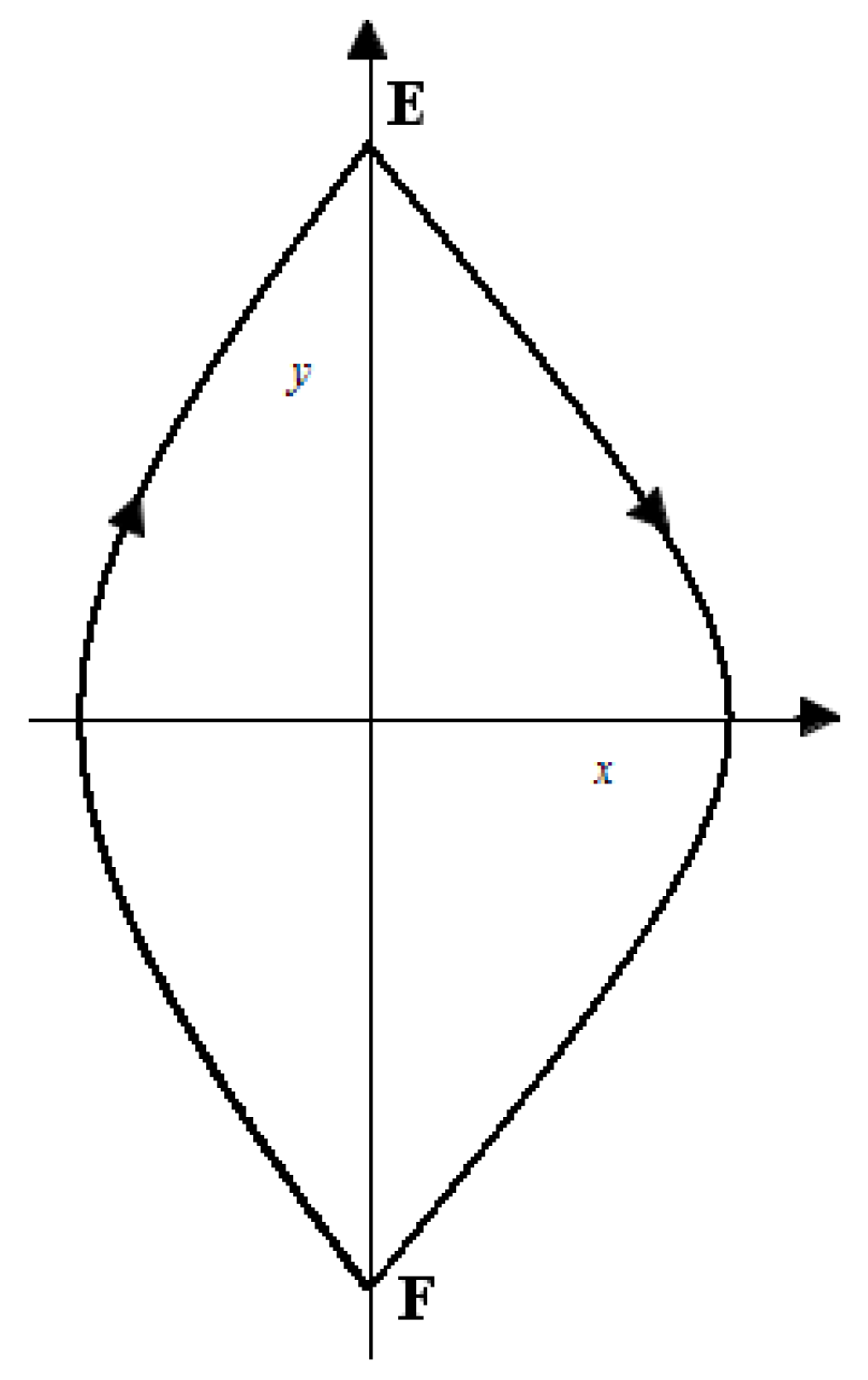
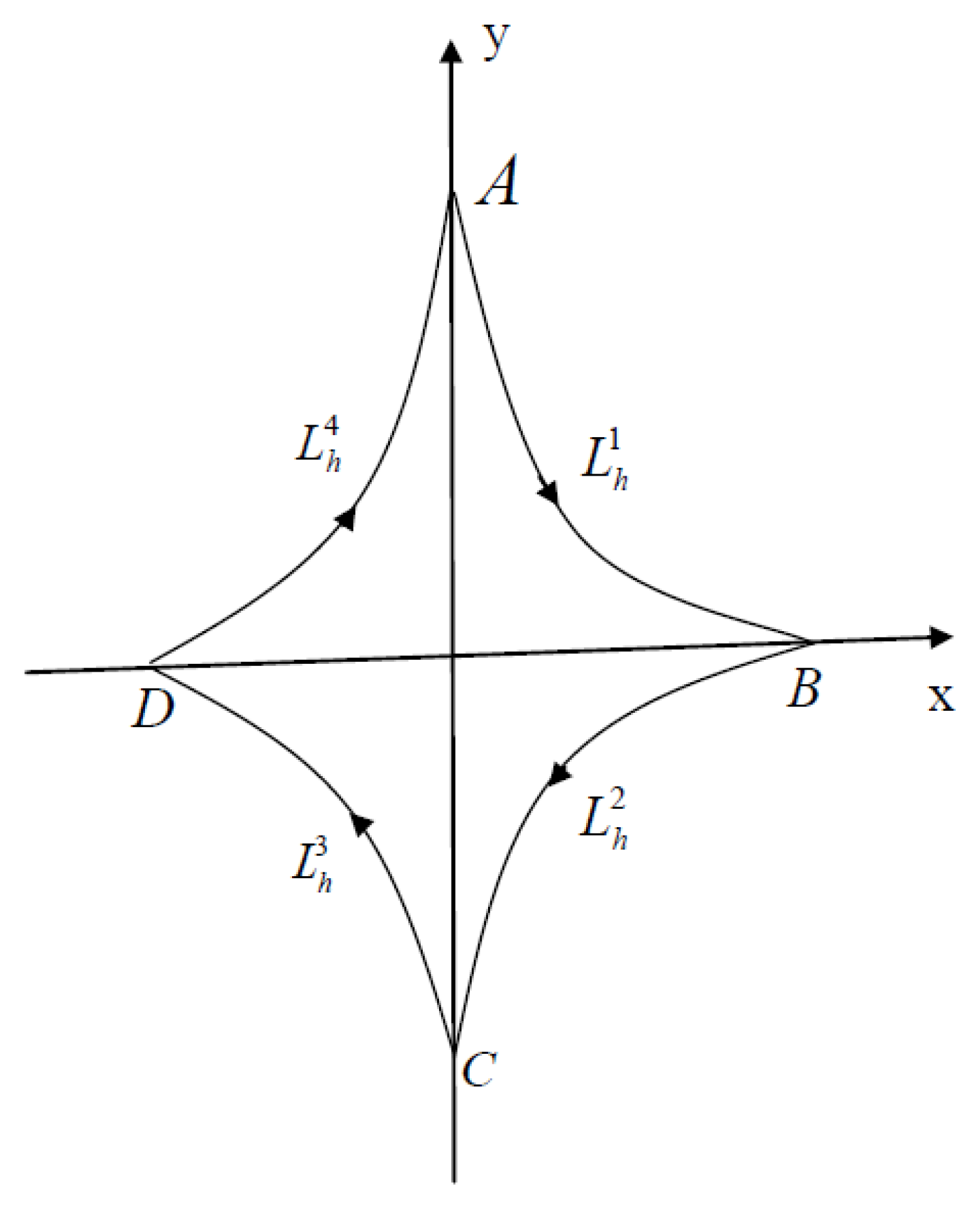
:1. Background and Literature
2. Primary Outcomes
3. M() Represented Algebraically through Mathematical Analysis
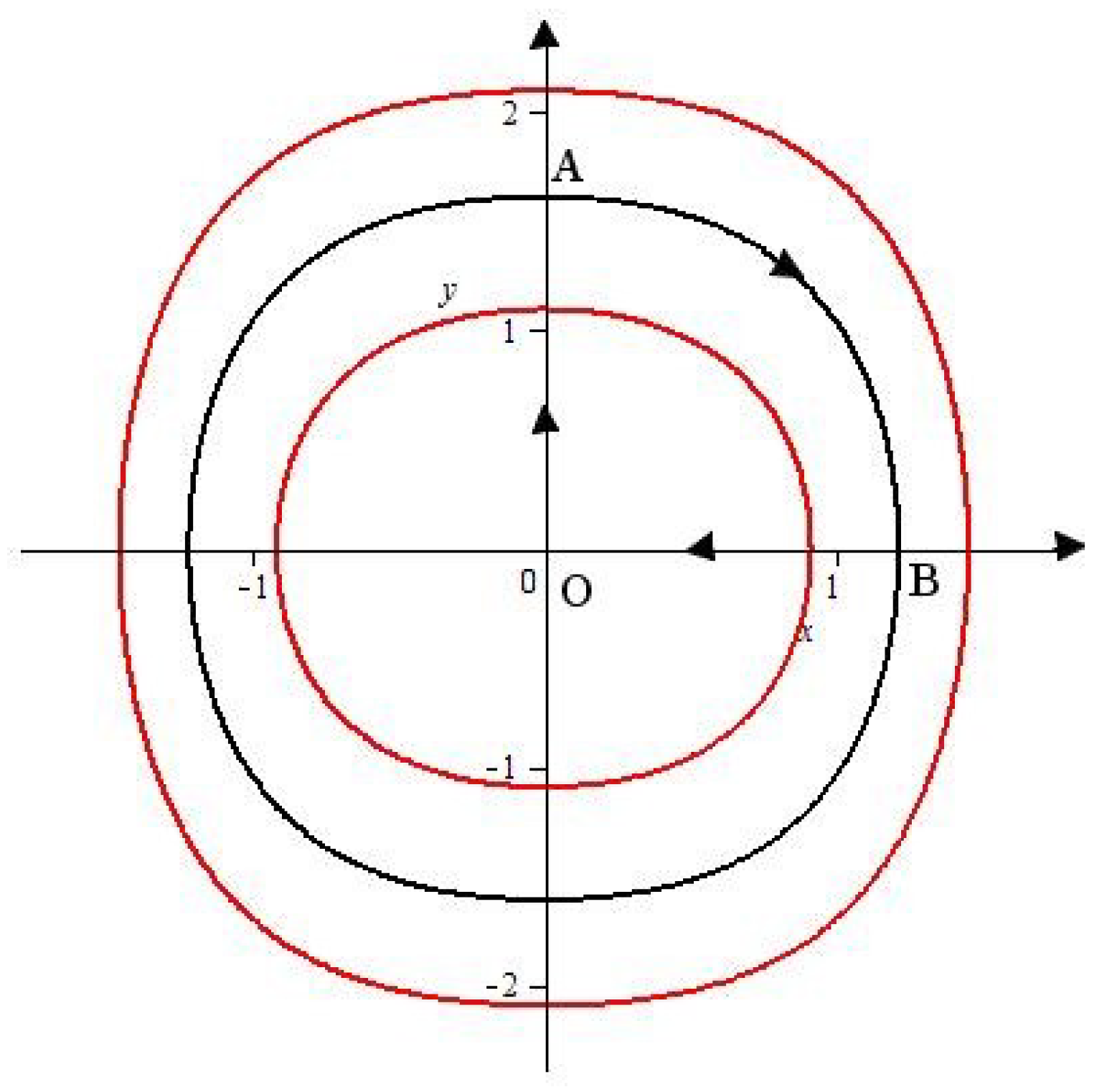
4. Establishing Theorem 1
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hilbert, D. Mathematical problems. Bull. Am. Math. Soc. 1902, 8, 437–479. [Google Scholar] [CrossRef]
- Tian, Y.; Shang, X.; Han, M. Bifurcation of limit cycles in a piecewise smooth near-integrable. J. Math. Anal. Appl. 2021, 504, 125578. [Google Scholar] [CrossRef]
- Gasull, A.; Geyer, A.; Mañosas, F. On the number of limit cycles for perturbed pendulum equations. J. Differ. Equ. 2016, 261, 2141–2167. [Google Scholar] [CrossRef]
- Ramirez, O.; Alves, A.M. Bifurcation of limit cycles by perturbing piecewise non-Hamiltonian systems with nonlinear switching manifold. Nonlinear Anal. Real World Appl. 2021, 57, 103188. [Google Scholar] [CrossRef]
- Tian, Y.; Han, M. Hopf and homoclinic bifurcations for near-Hamiltonian systems. J. Differ. Equ. 2017, 262, 3214–3234. [Google Scholar] [CrossRef]
- Xiong, Y.; Han, M. Limit cycles appearing from a generalized heteroclinic loop with a cusp and a nilpotent saddle. J. Differ. Equ. 2021, 303, 575–607. [Google Scholar] [CrossRef]
- Yu, P.; Li, F. Bifurcation of limit cycles in a cubic-order planar system around a nilpotent critical point. J. Math. Anal. Appl. 2017, 453, 645–667. [Google Scholar] [CrossRef]
- Cen, X.; Li, S.; Zhao, Y. On the number of limit cycles for a class of discontinuous quadratic differential systems. J. Math. Anal. Appl. 2017, 449, 314–342. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Y.; Li, J. On the number of limit cycles of a perturbed cubic polynomial differential center. J. Math. Anal. Appl. 2013, 404, 212–220. [Google Scholar] [CrossRef]
- Llibre, J.; del Rio, J.; Rodriguez, J. Averaging analysis of a perturbated quadratic center. Nonlinear Anal. 2001, 46, 45–51. [Google Scholar] [CrossRef]
- Llibre, J.; Mereu, A.; Novaes, D. Averaging theory for discontinuous piecewise differential systems. J. Differ. Equ. 2015, 258, 4007–4032. [Google Scholar] [CrossRef]
- Horozov, E.; Iliev, I. A Linear estimate for the number of zeros of Abelian integrals with cubic Hamiltonians. Nonlinearity 1998, 11, 1521–1537. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, Z. A Linear estimate of the number of zeros of Abelian integrals for a kind of quartic Hamiltonians. J. Differ. Equ. 1999, 155, 73–88. [Google Scholar] [CrossRef]
- Gasull, A.; Lázaro, J.T.; Torregrosa, J. On the Chebyshev property for a new family of functions. J. Math. Anal. Appl. 2012, 387, 631–644. [Google Scholar] [CrossRef]
- Grau, M.; Ma nosas, F.; Villadelprat, J. A Chebyshev criterion for Abelian integrals. Trans. Amer. Math. Soc. 2011, 363, 109–129. [Google Scholar] [CrossRef]
- Huang, J.; Liu, C.; Wang, J. Abelian integrals in unfoldings of codimension 3 singularities with nilpotent linear parts. J. Math. Anal. Appl. 2017, 449, 884–896. [Google Scholar] [CrossRef]
- Ma nosas, F.; Villadelprat, J. Bounding the number of zeros of certain Abelian integrals. J. Differ. Equ. 2011, 251, 1656–1669. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, L. The perturbation of a class of hyper-elliptic Hamilton system with a double eight figure loop. Qual. Theory Dyn. Syst. 2017, 16, 317–360. [Google Scholar] [CrossRef]
- Gasull, A.; Torregrosa, J. A new approach to the computation of the Lyapunov constants, in The Geometry of Differential Equations and Dynamical Systems. Comput. Appl. Math. 2001, 20, 149–177. [Google Scholar]
- Han, M.; Yu, P. Normal Forms, Melnikov Functions, and Bifurcation of Limit Cycles; Springer: New York, NY, USA, 2012. [Google Scholar]
- Li, F.; Liu, Y.; Yu, P. Bi-center problem and bifurcation of limit cycles from nilpotent singular points in Z2-equivariant cubic vector fields. J. Differ. Equ. 2018, 265, 4965C–4992C. [Google Scholar] [CrossRef]
- Han, M.; Romanovski, V.G.; Zhang, X. Equivalence of the Melnikov function method and the averaging method. Qual. Theory Dyn. Syst. 2016, 15, 471C–479C. [Google Scholar] [CrossRef]
- Yang, J. Picard–Fuchs equation applied to quadratic isochronous systems with two switching lines. Int. J. Bifurc. Chaos 2020, 30, 2050042. [Google Scholar] [CrossRef]
- Krivan, V. On the Gause predator-prey model with a refuge: A fresh look at the history. J. Theoret. Biol. 2011, 274, 67–73. [Google Scholar] [CrossRef]
- Teixeira, M. Perturbation theory for non-smooth systems. In The Encyclopedia of Complexity and Systems Science; Springer: New York, NY, USA, 2009. [Google Scholar]
- Di Bernardo, M.; Budd, C.; Champneys, A.; Kowalczyk, P. Piecewise-Smooth Dynamical Systems, Theory and Applications; Springer: London, UK, 2008. [Google Scholar]
- Leine, R.I.; Van Campen, D.H. Bifurcations in non-smooth dynamic systems. SIAM Rev. 2008, 50, 629–701. [Google Scholar]
- Liu, X.; Han, M. Bifurcation of limit cycles by perturbing piecewise Hamiltonian systems. Int. J. Bifurc. Chaos Appl. Sci. Eng. 2010, 20, 1379–1390. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, L. Bifurcation of limit cycles of a piecewise smooth Hamiltonian system. Qual. Theory Dyn. Syst. 2022, 21, 142. [Google Scholar] [CrossRef]
- Chen, J.; Han, M. Bifurcation of limit cycles by perturbing a piecewise linear Hamiltonian system. Qual. Theory Dyn. Syst. 2022, 21, 34. [Google Scholar] [CrossRef]
- Itikawa, J.; Llibre, J.; Mereu, A.C.; Oliveira, R. Limit cycles in uniform isochronous centers of discontinuous differential systems with four zones. Discret. Contin. Dyn. Syst. Ser. B 2017, 22, 3259–3272. [Google Scholar] [CrossRef]
- Li, S.; Cen, X.; Zhao, Y. Bifurcation of limit cycles by perturbing piecewise smooth integrable non-Hamiltonian systems. Nonlinear Anal. RWA 2017, 34, 140–148. [Google Scholar] [CrossRef]
- Liu, S.; Hana, M.; Li, J. Bifurcation methods of periodic orbits for piecewise smooth systems. J. Differ. Equ. 2021, 275, 204–233. [Google Scholar] [CrossRef]
- Li, J.; Guo, Z.; Zhu, S.; Gao, T. Bifurcation of periodic orbits and its application for high-dimensional piecewise smooth near integrable systems with two switching manifolds. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106840. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, L. Bifurcation of limit cycles by perturbing piecewise smooth integrable differential systems with four zones. arXiv 2017. [Google Scholar] [CrossRef]
- Zhang, Z.-F.; Li, B.Y. High order Melnikov functions and the problem of uniformity in global bifurcations. Ann. Mat. Pura Appl. 1992, 161, 181–212. [Google Scholar]
- Hu, N.; Du, Z. Bifurcation of periodic orbits emanated from a vertex in discontinuous planar systems. Commun. Nonlinear Sci. Numer. Simulat. 2013, 18, 3436–3448. [Google Scholar] [CrossRef]
- Wang, Y.; Han, M.; Constantinescu, D. On the limit cycles of perturbed discontinuous planar systems with 4 switching lines. Chaos Solitons Fractals 2016, 83, 158–177. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, E.; Yang, J.; Shateyi, S. Bifurcating Limit Cycles with a Perturbation of Systems Composed of Piecewise Smooth Differential Equations Consisting of Four Regions. Mathematics 2023, 11, 4555. https://doi.org/10.3390/math11214555
Zhang E, Yang J, Shateyi S. Bifurcating Limit Cycles with a Perturbation of Systems Composed of Piecewise Smooth Differential Equations Consisting of Four Regions. Mathematics. 2023; 11(21):4555. https://doi.org/10.3390/math11214555
Chicago/Turabian StyleZhang, Erli, Jihua Yang, and Stanford Shateyi. 2023. "Bifurcating Limit Cycles with a Perturbation of Systems Composed of Piecewise Smooth Differential Equations Consisting of Four Regions" Mathematics 11, no. 21: 4555. https://doi.org/10.3390/math11214555
APA StyleZhang, E., Yang, J., & Shateyi, S. (2023). Bifurcating Limit Cycles with a Perturbation of Systems Composed of Piecewise Smooth Differential Equations Consisting of Four Regions. Mathematics, 11(21), 4555. https://doi.org/10.3390/math11214555





