Rectangular Cylinder Orientation and Aspect Ratio Impact on the Onset of Vortex Shedding
Abstract
:1. Introduction
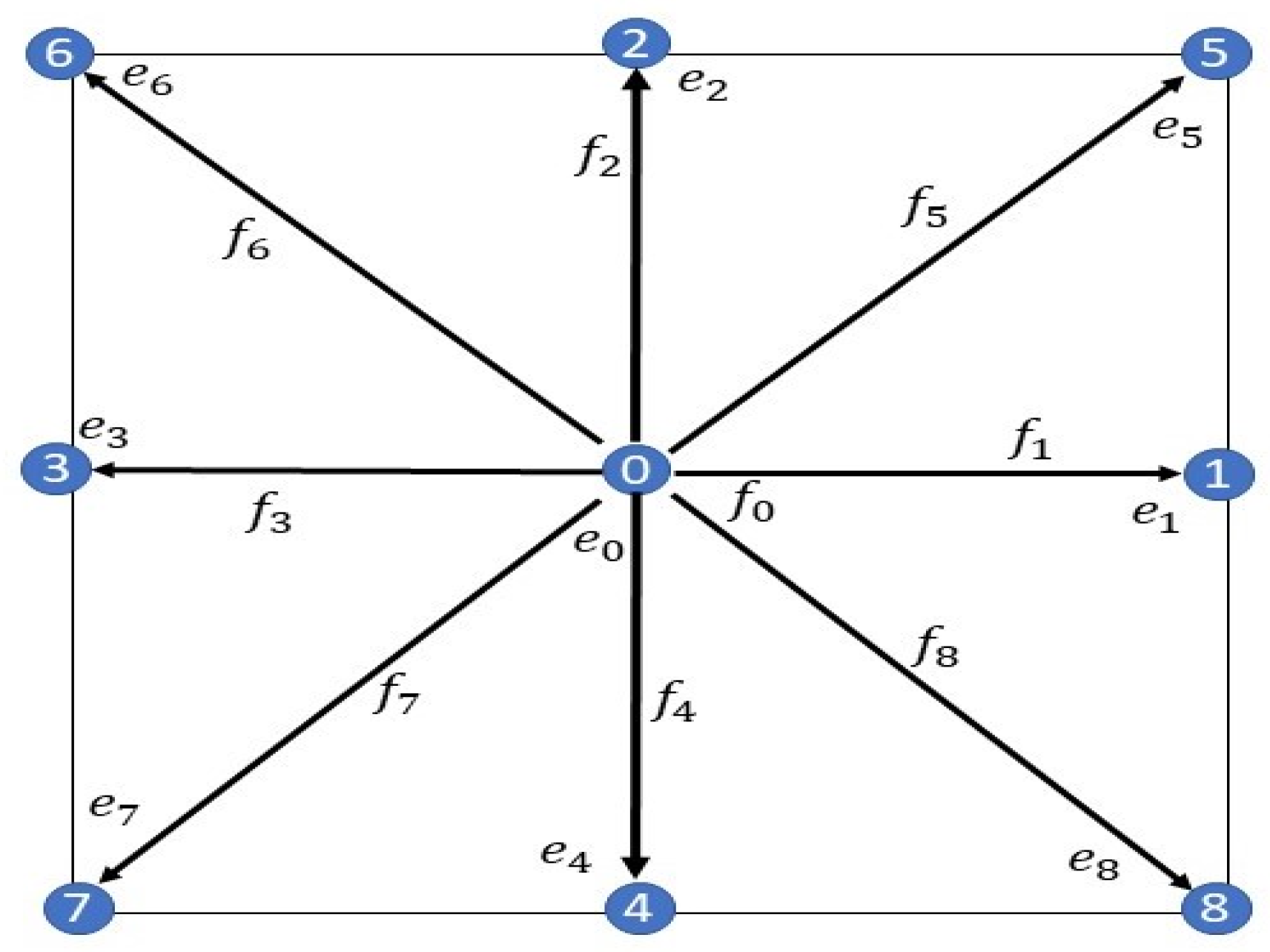
2. Numerical Methodology
3. Problem Description, Grid Independence, and Code Validation
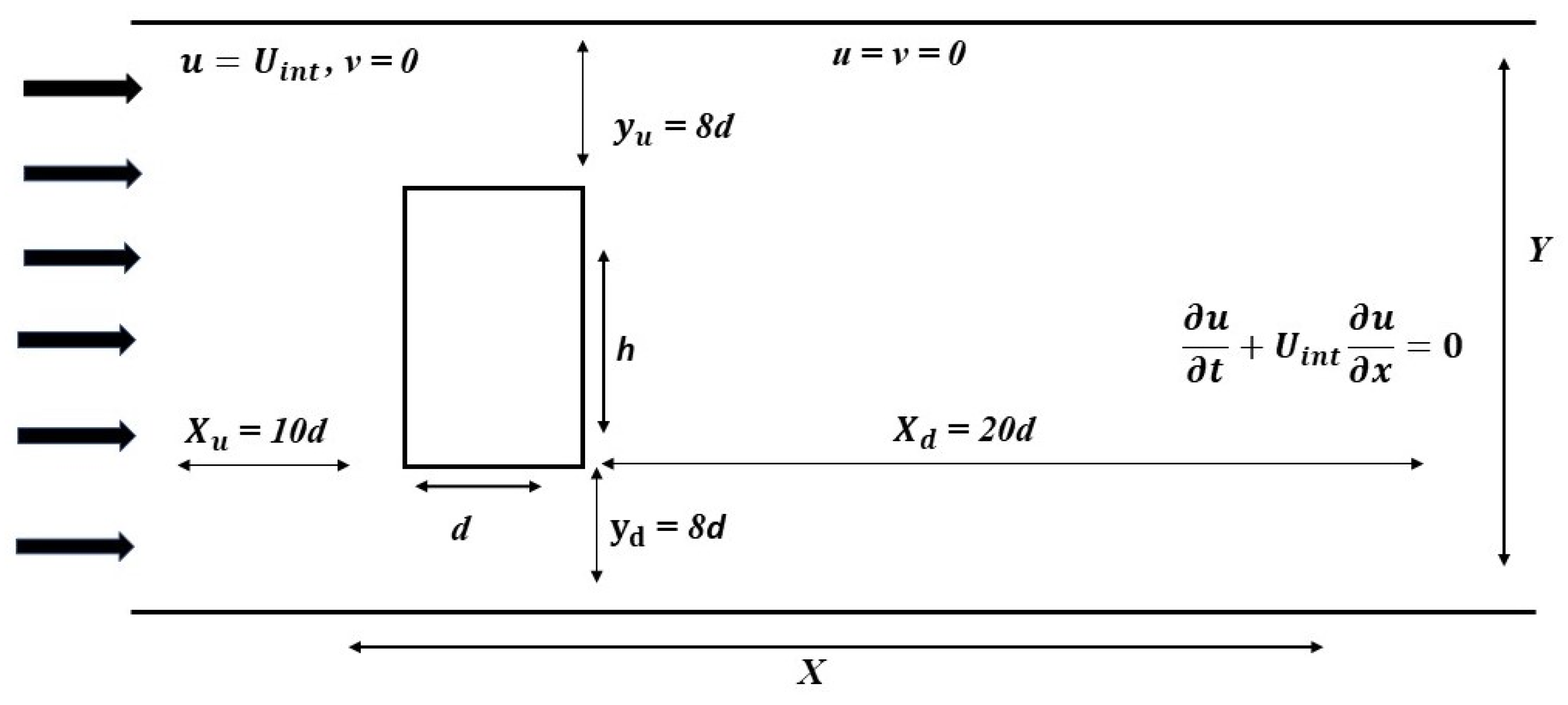
3.1. Boundary Conditions
3.2. Grid Independence
3.3. Code Validation
4. Results and Discussion
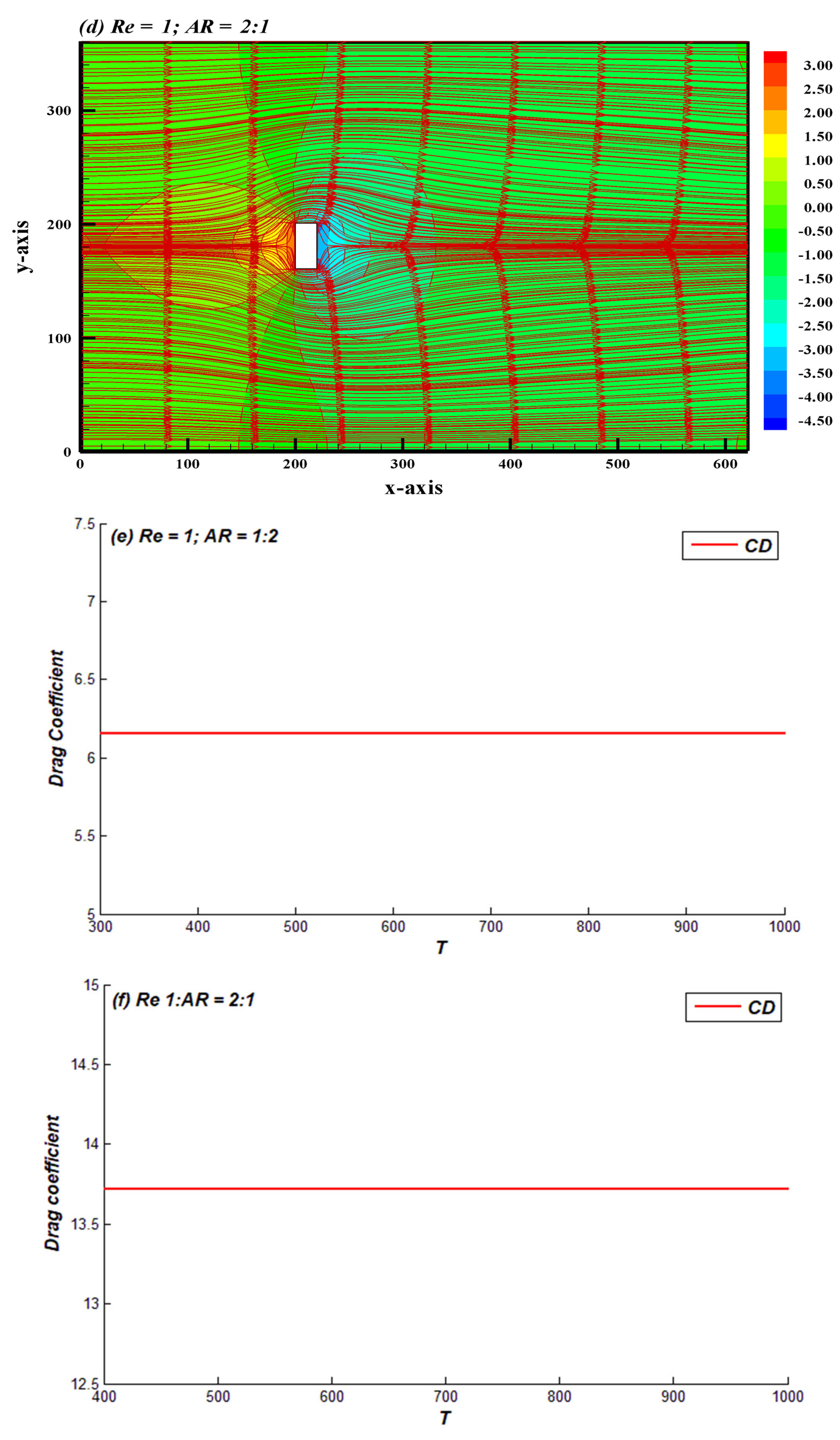
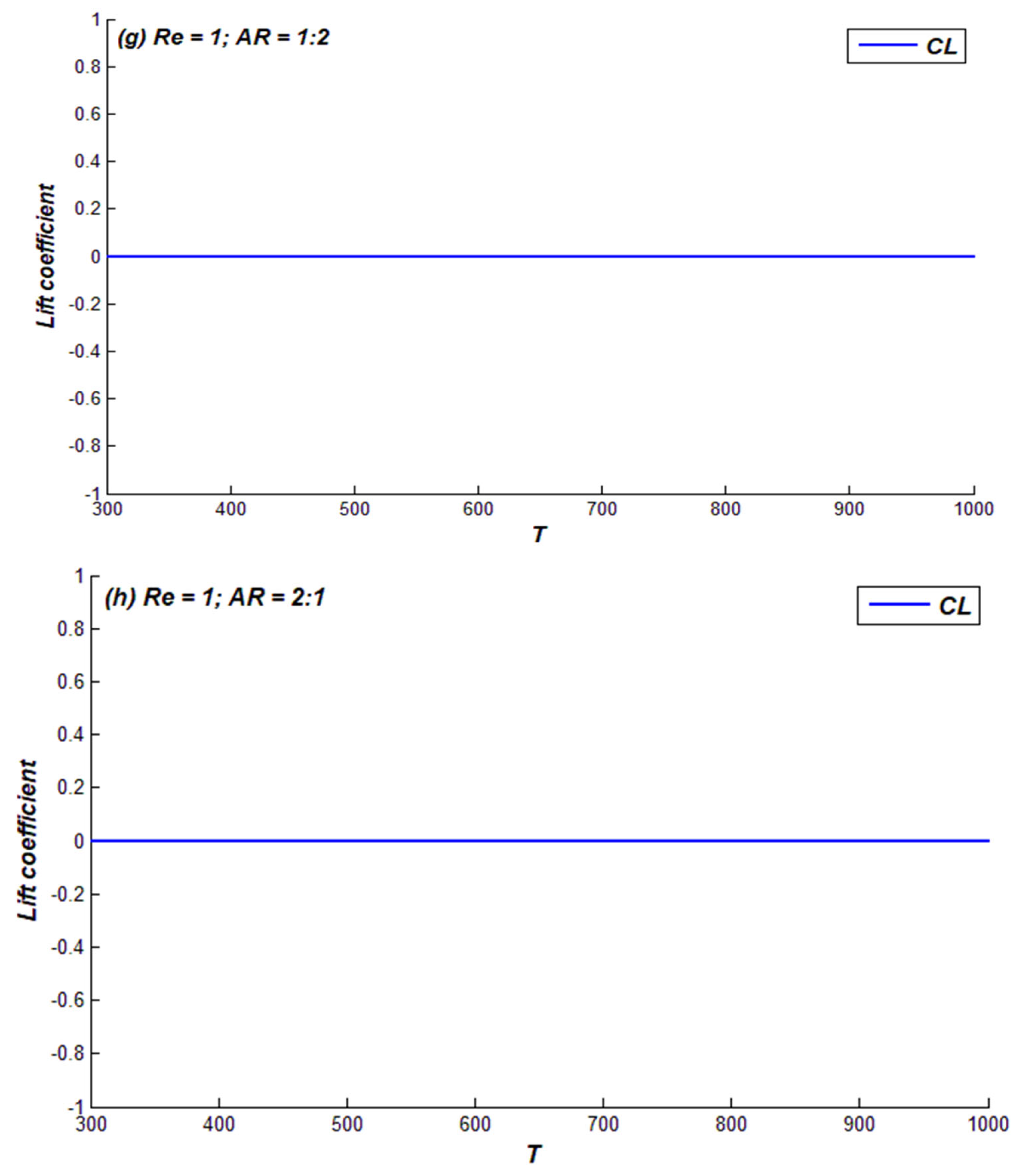
4.1. Regime I
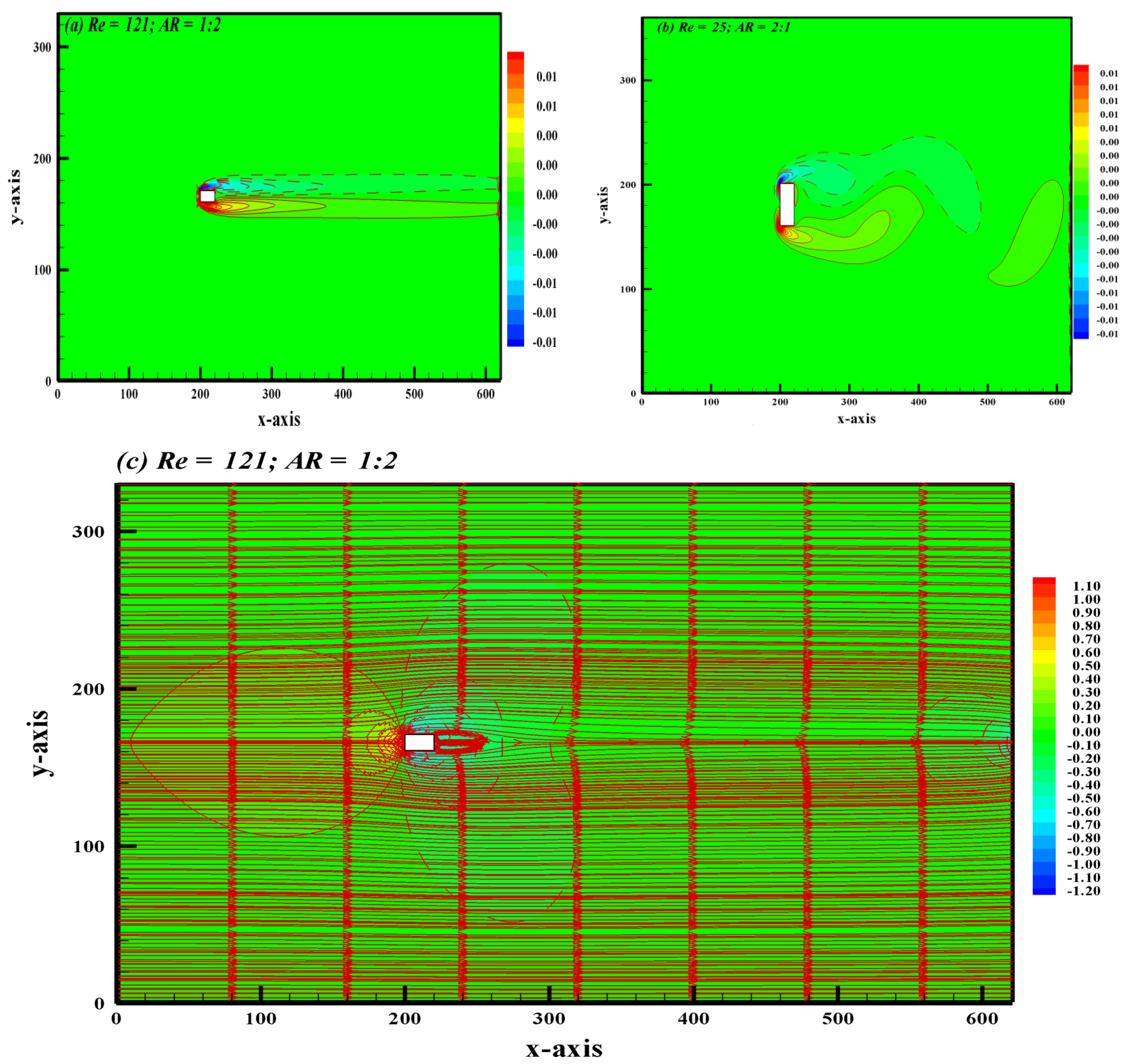
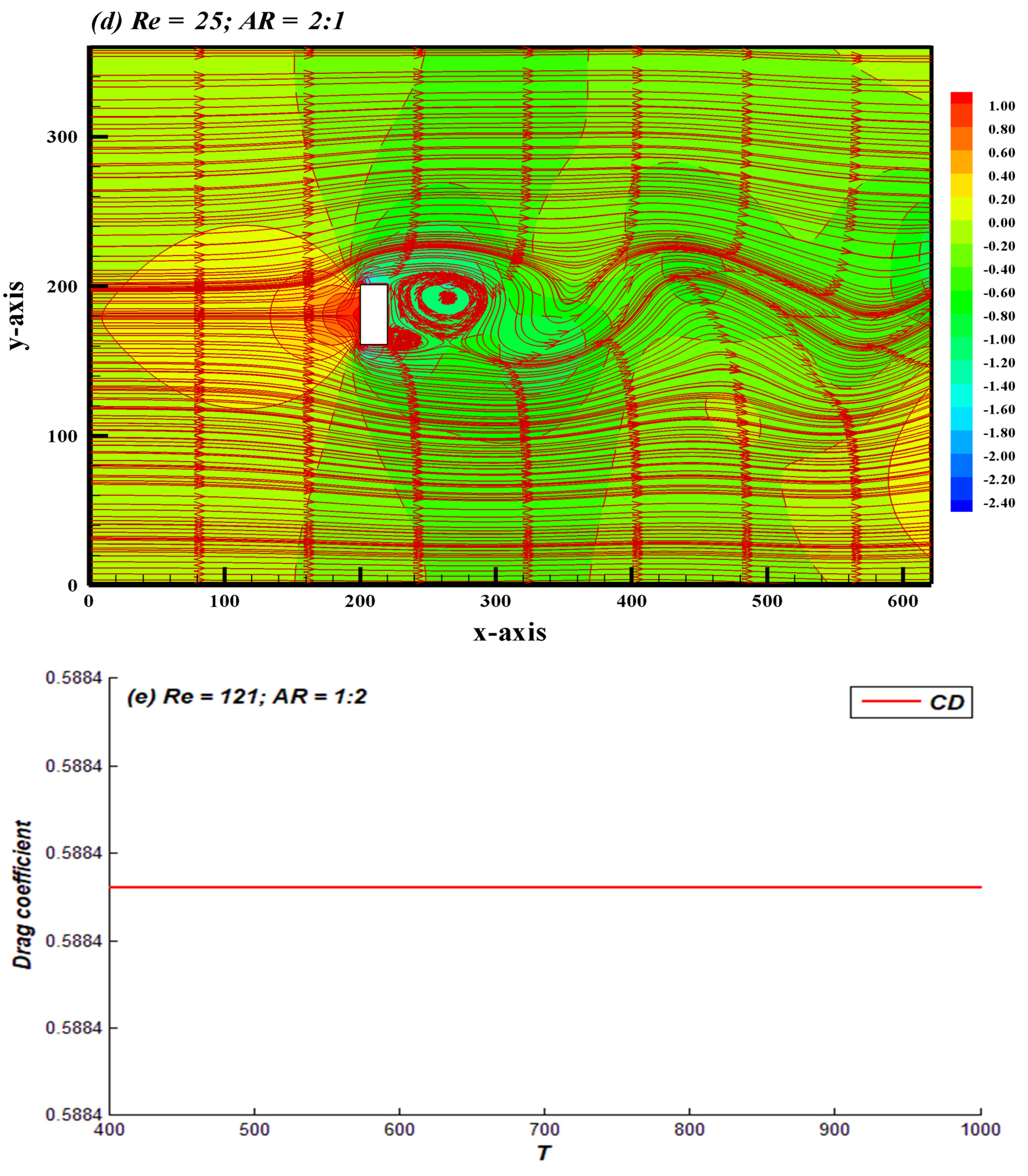
4.2. Regime II
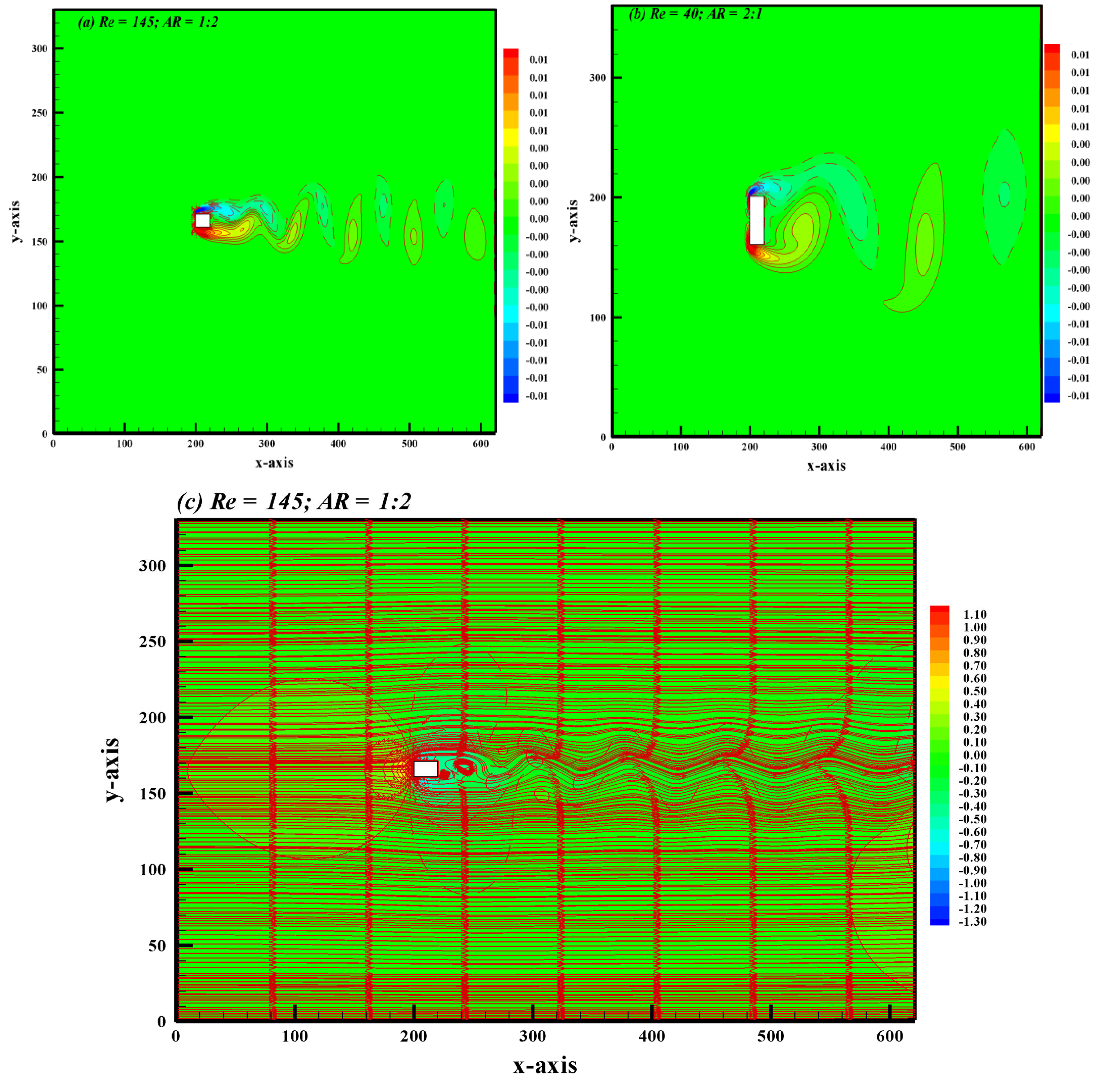
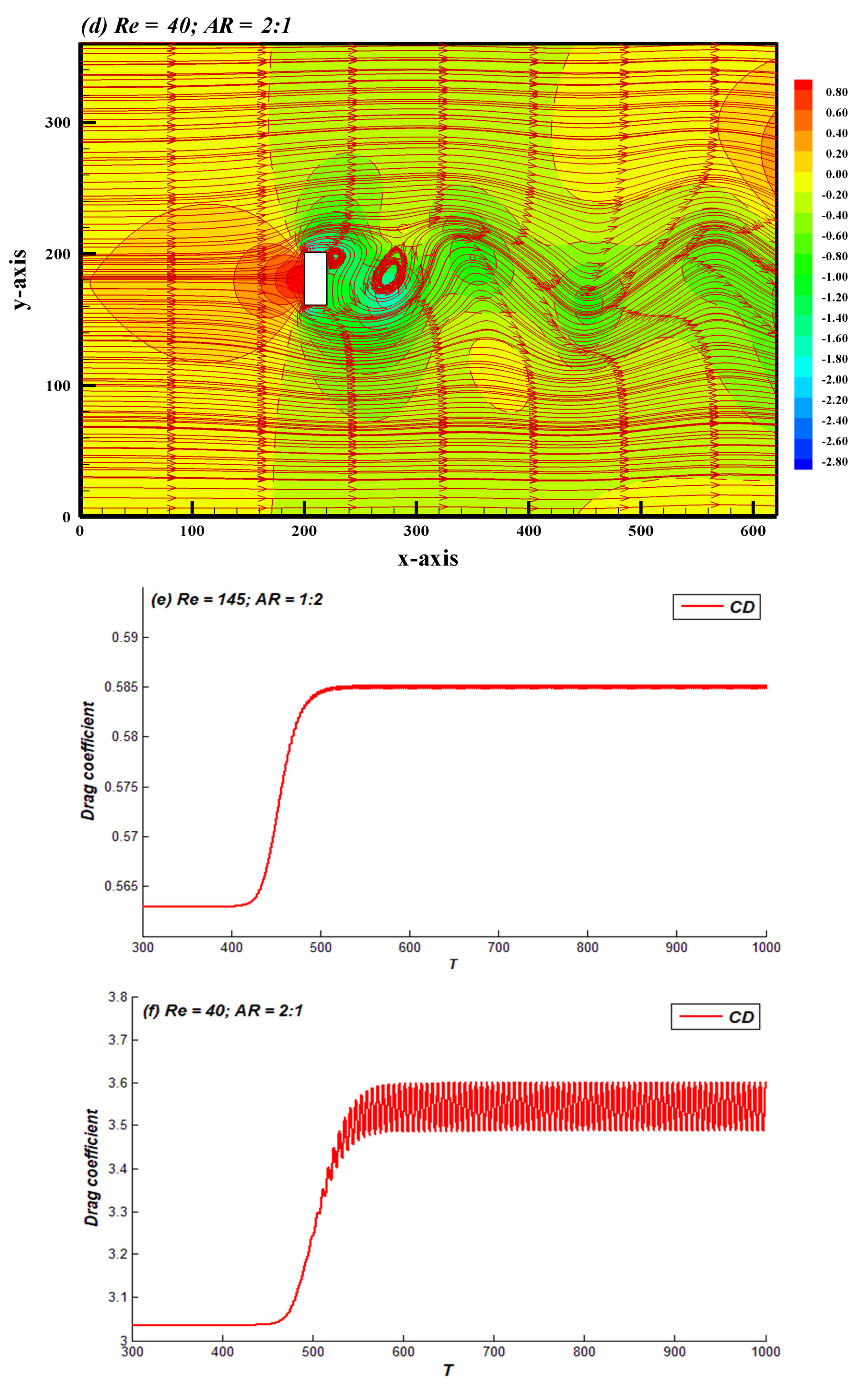
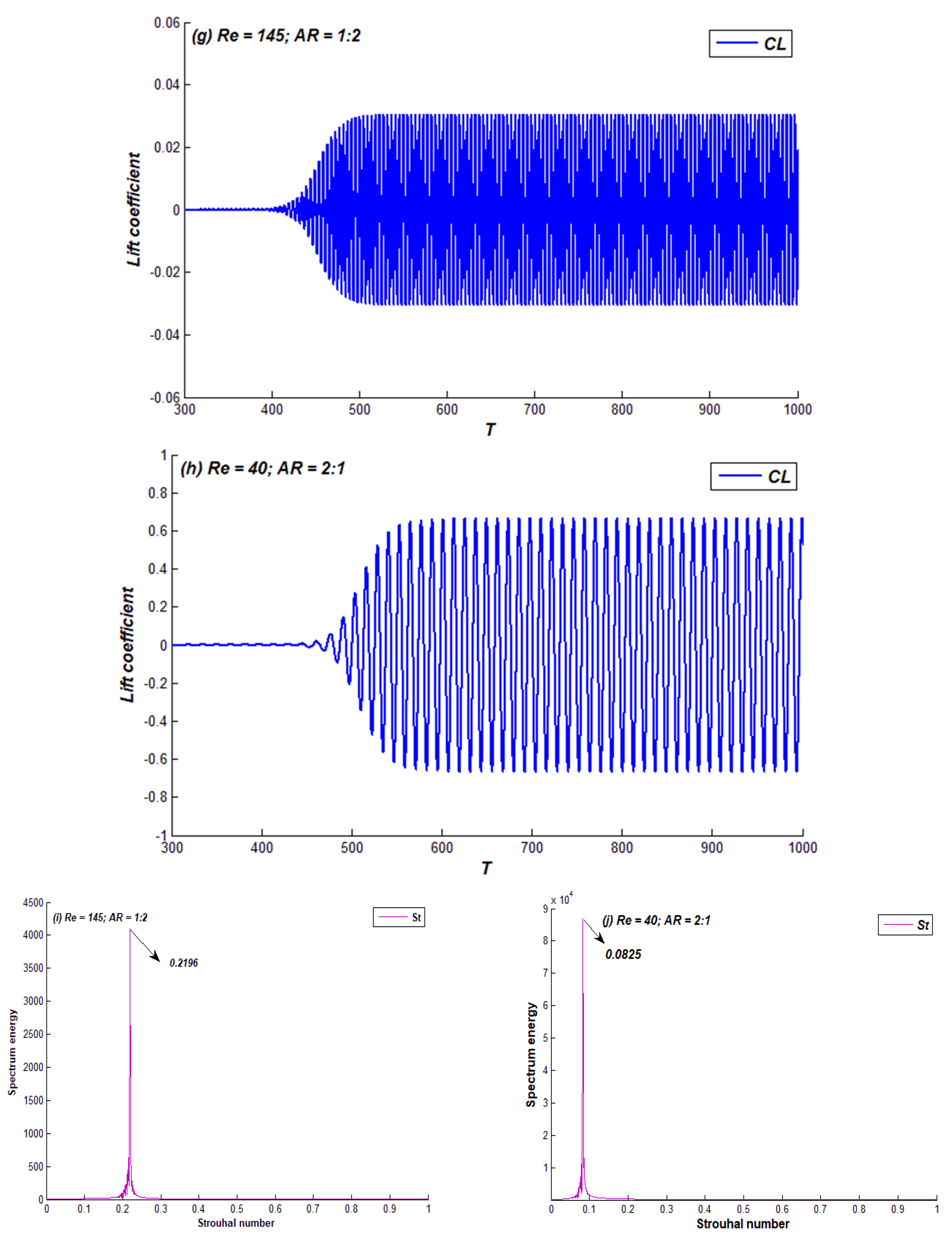
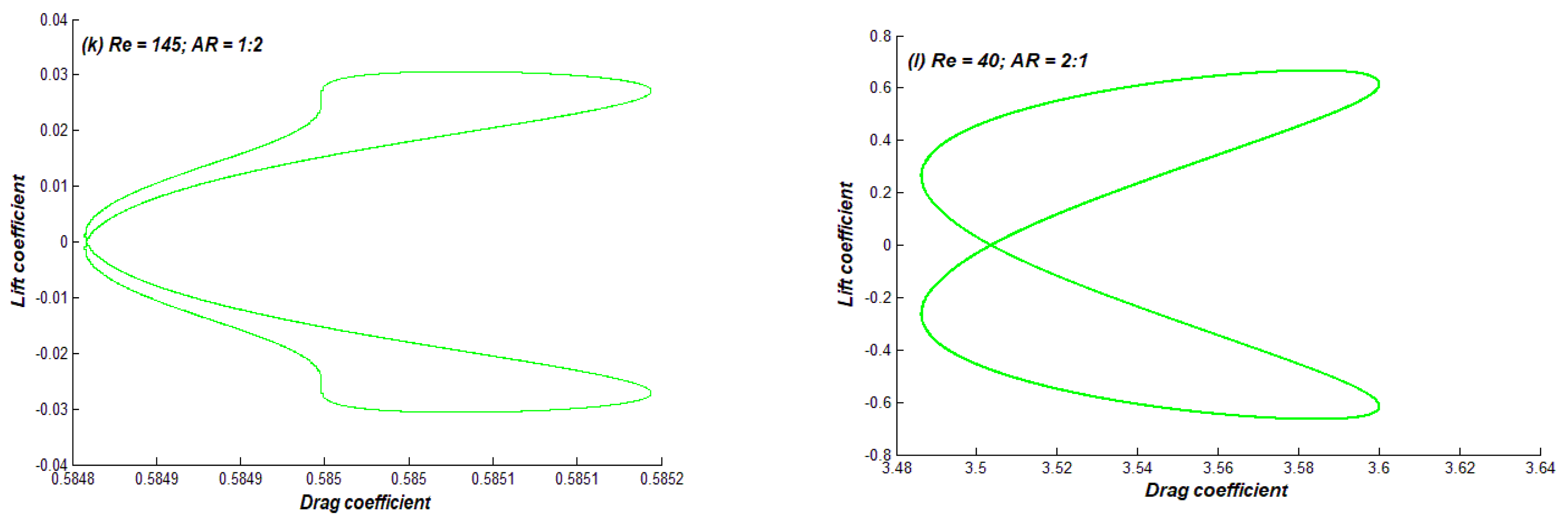
4.3. Regime III
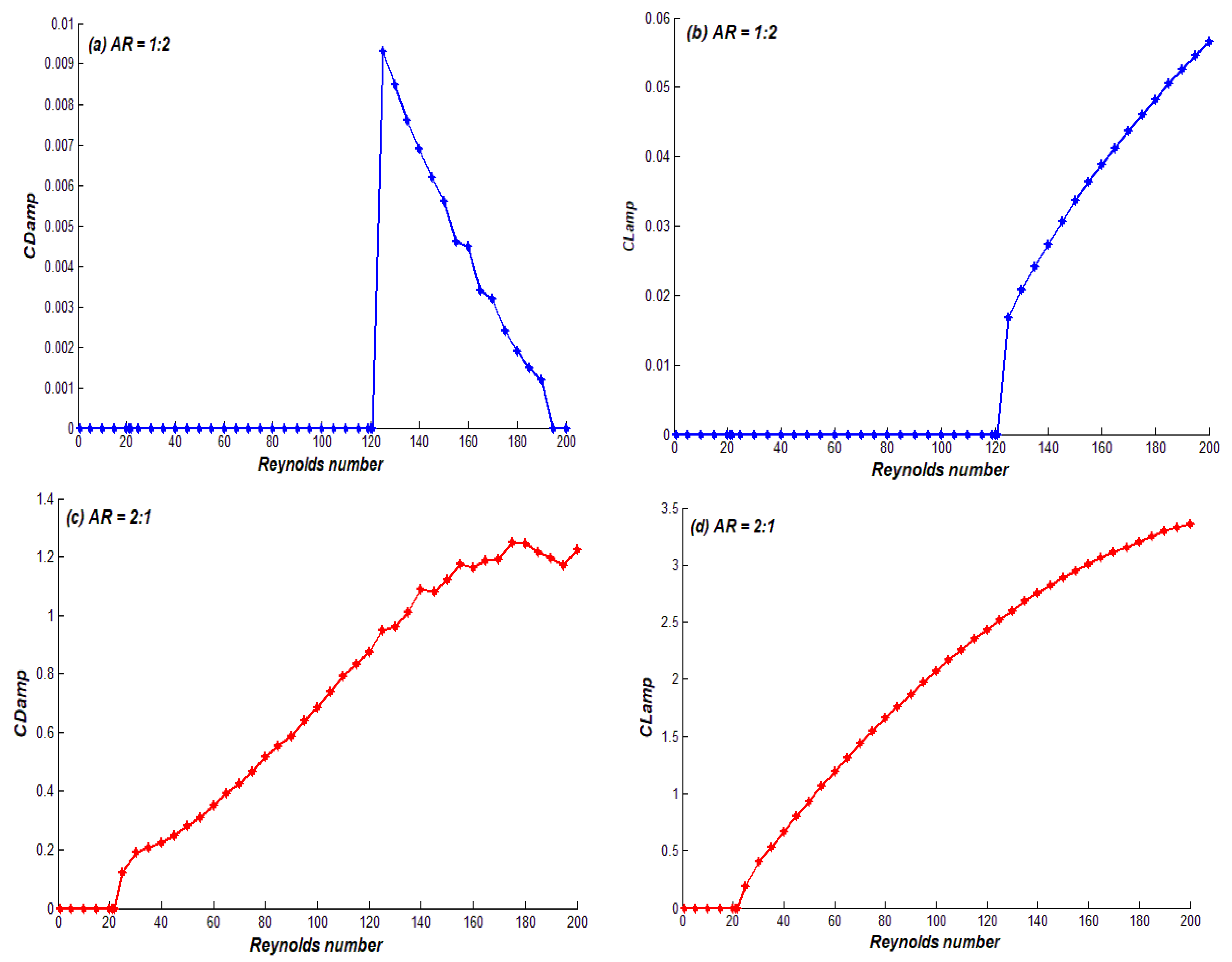
5. Force Statistics: Comparison between AR = 1:2 and 2:1
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AR | Aspect ratio |
| LBM | Lattice Boltzmann method |
| Re | Reynolds number |
| St | Strouhal number |
| CD | Drag coefficient |
| CL | Lift coefficient |
| CDrms | Root mean square values of drag coefficient |
| CLrms | Root mean square values of lift coefficient |
| Pressure drag coefficient | |
| Pressure drag | |
| Angle of incidence | |
| Relaxation time parameter | |
| B | Blockage ratio |
| G | Gap spacing |
| CDamp | Amplitude of drag coefficient |
| CLamp | Amplitude of lift coefficient |
| LGCA | Lattice gas cellular automata |
| BGK | Bhatnagar, Gross, and Krook |
| BE | Boltzmann equation |
| GKS | Gas kinetic scheme |
| Mean drag coefficient | |
| Drag force | |
| 2D | Two dimensional |
| Lift force | |
| NSE | Navier–Stokes equation |
| P | Pressure |
| Coefficient of pressure | |
| Mean pressure coefficient | |
| Base pressure | |
| Force coefficients | |
| FFT | Fast Fourier transform |
| T | Non-dimensional time |
References
- Hamane, D.; Guerri, O.; Larbi, S. Investigation of flow around a circular cylinder in laminar and turbulent flow using the Lattice Boltzmann method. AIP Conf. Proc. 2015, 1648, 850094. [Google Scholar]
- Park, J.; Kwon, K.; Choi, H. Numerical solutions of flow past a circular cylinder at Reynolds numbers up to 160. KSME Int. J. 1998, 12, 1200–1205. [Google Scholar] [CrossRef]
- Mehdi, H.; Namdev, V.; Kumar, P.; Tyagi, A. Numerical Analysis of Fluid Flow around a Circular Cylinder at Low Reynolds Number. IOSR J. Mech. Civ. Eng. 2016, 13, 94–101. [Google Scholar]
- Behr, M.; Hastreiter, D.; Mittal, S.; Tezduyar, T. Incompressible flow past a circular cylinder: Dependence of the computed flow field on the location of the lateral boundaries. Comput. Methods Appl. Mech. Eng. 1995, 123, 309–316. [Google Scholar] [CrossRef]
- Yoon, D.; Yang, K.; Choi, C. Flow past a square cylinder with an angle of incidence. Phys. Fluids 2010, 22, 043603. [Google Scholar] [CrossRef]
- Jiang, H.; Cheng, L. Flow separation around a square cylinder at low to moderate Reynolds numbers. Phys. Fluids 2020, 32, 044103. [Google Scholar] [CrossRef]
- Islam, S.; Zhou, C. Characteristics of flow past of square cylinder using the lattice Boltzmann method. Inf. Technol. J. 2009, 8, 1094–1114. [Google Scholar] [CrossRef]
- Breuer, M.; Bernsdorf, J.; Zeiser, T.; Durst, F. Accurate computations of the laminar flow past a square cylinder based on two different methods: Lattice-Boltzmann and finite-volume method. Int. J. Heat Fluid Flow 2000, 21, 186–196. [Google Scholar] [CrossRef]
- Kelkar, K.M.; Patankar, S. Numerical prediction of vortex shedding behind a square cylinder. Int. J. Numer. Methods Fluids 1992, 14, 327–341. [Google Scholar] [CrossRef]
- Sohankar, A.; Norberg, C.; Davidson, L. Low-Reynolds-number flow around a square cylinder at incidence: Study of blockage, onset of vortex shedding and outlet boundary condition. Int. J. Numer. Methods Fluids 1998, 26, 39–56. [Google Scholar] [CrossRef]
- Islam, S.U.; Zhou, C.Y.; Shah, A.; Xie, P. Numerical simulation of flow past rectangular cylinders with different aspect ratios using the incompressible lattice Boltzmann method. J. Mech. Sci. Technol. 2012, 26, 1027–1041. [Google Scholar] [CrossRef]
- Ahmed, S.; Islam, S.; Nazeer, G.; Zhou, C.Y. Numerical Investigation of Strouhal number discontinuity and flow characteristics around single rectangular cylinder at low aspect ratios and Reynolds numbers. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 1–26. [Google Scholar] [CrossRef]
- Sohankar, A.; Norberg, C.; Davidson, L. Numerical simulation of unsteady low-Reynolds number flow around rectangular cylinders at incidence. J. Wind Eng. Ind. Aerodyn. 1997, 69–71, 189–201. [Google Scholar] [CrossRef]
- Ohya, Y. Note on a discontinuous change in wake pattern for a rectangular cylinder. J. Fluid Struct. 1994, 8, 325–330. [Google Scholar] [CrossRef]
- Bearman, P.W.; Trueman, D.M. An investigation of the flow around rectangular cylinders. Aeronaut. Q. 1972, 23, 229–237. [Google Scholar] [CrossRef]
- Sohankar, A. Large eddy simulation of flow past rectangular-section cylinders: Side ratio effects. J. Wind Eng. Ind. Aerodyn. 2008, 96, 640–655. [Google Scholar] [CrossRef]
- Islam, Z.; Islam, S.; Zhou, C.Y. The wake and force statistics of flow past tandem rectangles. Ocean Eng. 2021, 236, 109476. [Google Scholar] [CrossRef]
- Islam, S.; Rahman, H.; Zhou, C. Effect of gap spacings on flow past row of rectangular cylinders with aspect ratio 1.5. Ocean Eng. 2016, 119, 1–15. [Google Scholar] [CrossRef]
- Rahman, H.; Islam, S.; Abbasi, W.S.; Manzoor, R.; Amin, F.; Alam, Z. Numerical computations for flow patterns and force statistics of three rectangular cylinders. Math. Probl. Eng. 2021, 2021, 9991132. [Google Scholar] [CrossRef]
- Islam, S.; Manzoor, R.; Ying, Z.C.; Islam, Z. Numerical investigation of different aspect ratios for flow past three inline rectangular cylinders. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 410. [Google Scholar] [CrossRef]
- Islam, S.; Manzoor, R.; Zahid, M.; Kulsoom, S.; Kausar, U. Numerical study of flow past three rectangular rods at unequal gap spacing. Indian J. Sci. Technol. 2019, 12, 32. [Google Scholar] [CrossRef]
- Salvador, G.; Stoesser, T.; Rodi, W. LES of the flow around two cylinders in tandem. J. Fluids Struct. 2008, 24, 1304–1312. [Google Scholar] [CrossRef]
- Islam, S.U.; Zhou, C.Y. Numerical Simulation of flow around a row of circular cylinders using Lattice Boltzmann Method. Inf. Technol. J. 2009, 8, 513–520. [Google Scholar] [CrossRef]
- Agrawal, A.; Djenidi, L.; Antonia, R.A. Investigation of flow around a pair of side-by-side square cylinders using the lattice Boltzmann method. Comput. Fluids 2006, 35, 1093–1107. [Google Scholar] [CrossRef]
- Adeeb, E.; Haider, B.A.; Sohn, C.H. Flow interference of two side-by-side square cylinders using IB-LBM—Effect of corner radius. Results Phys. 2018, 10, 256–263. [Google Scholar] [CrossRef]
- Manzoor, R.; Islam, S.U.; Abbasi, W.S.; Parveen, S. Variation of wake patterns and force coefficients of the flow past square bodies aligned inline. J. Mech. Sci. Technol. 2016, 30, 1691–1704. [Google Scholar] [CrossRef]
- McNamara, G.R.; Zanetti, G. Use of the Boltzmann equation to simulate lattice-gas automata. Phys. Rev. Lett. 1988, 61, 1–4. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, B.; Wang, N. Lattice BGK Model for Incompressible Navier–Stokes Equation. J. Comput. Phys. 2000, 165, 288–298. [Google Scholar] [CrossRef]
- Mohamad, A.A. Lattice Boltzmann Method: Fundamentals and Engineering Applications with Computer Codes, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Kruger, K.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method: Principles and Practice; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Ma, Y.; Mohebbi, R.; Rashidi, M.M.; Yang, Z. Numerical simulation of flow over a square cylinder with upstream and downstream circular bar using lattice Boltzmann method. Int. J. Mod. Phys. C 2018, 29, 28. [Google Scholar] [CrossRef]
- Saha, A.K.; Muralidhar, K.; Biswas, G. Transition and Chaos in two-Dimensional flow past a square cylinder. J. Eng. Mech. 2000, 126, 523–532. [Google Scholar] [CrossRef]
- Okajima, A. Strouhal numbers of rectangular cylinders. J. Fluid Mech. 1982, 123, 379–398. [Google Scholar] [CrossRef]
- Norberg, C. Flow around rectangular cylinders: Pressure forces and wake frequencies. J. Wind Eng. Ind. Aerodyn. 1993, 49, 187–196. [Google Scholar] [CrossRef]
- Abograis, A.S.; Alshayji, A.E. Reduction of fluid forces on a square cylinder in a laminar flow using passive control methods. In Proceedings of the COMSOL Conference, Boston, MA, USA, 9–11 October 2013. [Google Scholar]
- Guo, F.; Wu, G.; Du, X.; Mason, M.S. Numerical investigation of flow around a square cylinder in accelerated flow. Phys. Fluids 2021, 33, 104105. [Google Scholar] [CrossRef]
- Abbasi, W.S.; Islam, S.U.; Faiz, L.; Rahman, H. Numerical investigation of transitions in flow states and variation in aerodynamic forces for flow around square cylinders arranged inline. Chin. J. Aeronaut. 2018, 31, 2111–2123. [Google Scholar] [CrossRef]
- Rastan, M.R.; Alam, M.M.; Zhu, H.; Ji, C. Onset of vortex shedding from a bluff body modified from square cylinder to normal flat plate. Ocean Eng. 2022, 244, 110393. [Google Scholar] [CrossRef]




| = 100 | 10-Points | 20-Points | 40-Points |
|---|---|---|---|
| 1.4630 (1.34%) | 1.4434 (0.2%) | 1.4414 | |
| 0.1498 (0.5%) | 0.1491 (0%) | 0.1491 | |
| 0.1798 (3.1%) | 0.1742 (1.2%) | 0.1762 |
| St | ||
|---|---|---|
| Saha et al. [32] | 1.510 | 0.159 |
| Sohankar et al. [10] | 1.444 | 0.145 |
| Okajima [33] | 1.600 | 0.141 |
| Norberg [34] | … | 0.140 |
| Abograis and Alshayji [35] | 1.480 | 0.140 |
| Present | 1.443 | 0.151 |
| Regimes | AR = 1:2 | AR = 2:1 |
|---|---|---|
| Regime I | 1 Re 120 | 1 Re 24 |
| Regimes II | 121 Re 144 | 25 Re 39 |
| Regimes III | 145 Re 200 | 40 Re 200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tahir, N.; Abbasi, W.S.; Rahman, H.; Alrashoud, M.; Ghoneim, A.; Alelaiwi, A. Rectangular Cylinder Orientation and Aspect Ratio Impact on the Onset of Vortex Shedding. Mathematics 2023, 11, 4571. https://doi.org/10.3390/math11224571
Tahir N, Abbasi WS, Rahman H, Alrashoud M, Ghoneim A, Alelaiwi A. Rectangular Cylinder Orientation and Aspect Ratio Impact on the Onset of Vortex Shedding. Mathematics. 2023; 11(22):4571. https://doi.org/10.3390/math11224571
Chicago/Turabian StyleTahir, Neelam, Waqas Sarwar Abbasi, Hamid Rahman, Mubarak Alrashoud, Ahmed Ghoneim, and Abdulhameed Alelaiwi. 2023. "Rectangular Cylinder Orientation and Aspect Ratio Impact on the Onset of Vortex Shedding" Mathematics 11, no. 22: 4571. https://doi.org/10.3390/math11224571
APA StyleTahir, N., Abbasi, W. S., Rahman, H., Alrashoud, M., Ghoneim, A., & Alelaiwi, A. (2023). Rectangular Cylinder Orientation and Aspect Ratio Impact on the Onset of Vortex Shedding. Mathematics, 11(22), 4571. https://doi.org/10.3390/math11224571





