Abstract
In this paper, the classification of crisis states and their dynamics is carried out. The asset crisis model is approximated and formalized. Invariant stationary components and the boundaries of crisis fluctuations are determined, which allows for predictions of the course of a crisis. The hypothesis of the phase invariance of crises is statistically confirmed, and four main phases and five marker points in the development of an investment asset crisis are distinguished. A statistical study of the changes in the value of 620 investment assets over 7 years (1,584,720 values) was conducted, including 710 crisis asset states (9940 values), which allowed us to formulate a mathematical model of crisis variability that makes it possible to detect the onset of crisis phases or the passage of marker points via the values of the first- and second-order derivatives of the model. This model has not only evaluative properties, but also predictive properties relative to the risk of a crisis asset, which is also confirmed experimentally. An experiment is conducted to assess the quality of the econometric crisis model, which is based on real historical data. The results of the experiment showed the high quality of the model as a crisis detection tool. A method of early detection of the initial crisis phase is developed, in which it is seen that a statistically unpredictable state causes such a change in the indicator that it violates the valid bound constraints.
MSC:
62B15; 62D05; 62E99; 62G32
1. Introduction
Over the years, a great deal of scientific effort has been dedicated to researching economic crises. There are many contributions that are worth mentioning: Karl Marx [1] asserted the inevitability of crises; John Maynard Keynes [2] believed that an economy without crises was possible; Israel Krizner [3] criticized the models suggested by the above authors; Paul Krugman [4] came up with a model that was accepted as conventional; Albert Aftalion [5] considered crises a periodic phenomena; Nikolai Kondratieff [6] discovered the periodicity of crises; Wesley Clair Mitchell [7] examined the nature of economic cycles; Murray Rothbard [8] investigated historical and economic aspects of the Great Depression; and Hernando De Soto [9] revealed the economic nature of social crises.
Let us turn to the study of crisis processes in the economy, and we will investigate this by considering the economic theories that address the issues of crisis processes in the economy.
1.1. Theory of Overproduction
There are several directions in the theory of overproduction. According to the first one, crises of overproduction in the economy occur due to a disproportion in the structure of production, which in turn is caused by the overaccumulation of capital. This direction is represented by A. Spiethoff [10] and J. Schumpeter [11]. According to the second direction, the cause of crises is the overaccumulation of capital, the means of production, and equipment in conditions of insufficient demand. The founders of this position are the authors of A. Aftalion [12], J. M. Clark [13], and R. F. Harrod [14].
1.2. Keynesian Business Cycle Theory
John Keynes [2,15], when he published his work, produced—in actuality—a revolution, and he predetermined the course of development of the future economy. It was he who laid the foundation for theoretical developments on the prevention of crisis situations in the world economy. In his study, he focused on the issue of “effective demand”, namely its insufficiency, which is a key problem of the economy. He also showed that the crisis issue cannot be considered a microeconomic phenomenon, since it is a problem at the macroeconomic scale. To analyze this phenomenon, he investigated the relationship between income, capital accumulation, and household savings. The founders of the Keynesian theory of cycles are the authors of J. Keynes [16], R. Harrod [17], P. Samuelson [18], J. Clark [13], J. Hicks [19], and A. Hansen [20].
1.3. The Theory of Economic Long Waves
N. D. Kondratiev put forward the theory of the existence of long waves— periodic cycles of boom and bust in the economy [21]. He highlighted the following cycles:
- Seasonal—lasts up to a year;
- Small—has a duration of 2 to 4 years;
- Commercial and industrial—lasts from 7 to 11 years;
- Large cycles—lasts from 50 to 60 years.
1.4. Review of Modern Works in the Field of Crisis Research in the Economy
The most essential step in the evolution of crisis management was made with modeling; through conducting this, Paul Krugman developed his Nobel-Prize-winning model in 2008 [4,22]. Krugman suggested that crises were caused by an inadequacy of monetary and foreign exchange policy. P. Cumperayot and R. Kouwenberg [23] developed an econometric model of crisis, which is based on the readings of financial indicators of monthly exchange rates. P. Jutasompakorn et al. [24] proposed an econometric model of the banking crisis. The model describes three market states: growth, decline, and crisis. A. Korobeinikov [25] describes a crisis as an epidemic of corporate bankruptcies. The authors Bocola L., Bornstein G., and Dovis A. [26], using the case of the European debt crisis, proposed a concretized quantitative model of the crisis, which requires calibration for each specific crisis and is based on the ratio of sovereign debt to the budget revenue. The authors Osiyevskyy O. and Dewald J. [27] argued that economic crises have not only a negative, but also a healing effect on the economy, thereby increasing competition and motivating companies to develop, innovate, and reduce costs. The authors Rhee K. J. and Park K. S. [28], based on the data of the Korean market from 2000–2015, argued that financial crises motivate market participants to reduce dividend payments and invest in their own companies. The authors Wegener C., Kruse R., and Basse T. [29], based on an analysis of the stock exchange bubbles of the European Union and the United States in the period of 2007–2009, concluded that the main cause of the financial crises in the US and the European Union was due to the poor quality of the fiscal system, which allowed the state or companies to hide the true state of affairs in a particular sector of the economy. The authors Hlaing S. W. and Kakinaka M. [30] linked the main causes of the 2008 crisis to the financial liberalization that took place in the world from 1975 to 2005. The authors name insufficient state regulation and the easing of financial legislation as the main causes of the crisis. The authors Gao H. L. and Mei D. C. [31] argued that, during economic crises, the inter-market correlation of the main indices (for example, the Dow Jones, Nasdaq, etc.) decreases significantly, which gives greater opportunities for arbitrage trading (the development of which occurs during these periods).
Many modern authors have found a relationship between increased volatility and crises. As such, Moshirian F. and Wu Q. [32] conducted an empirical analysis on this topic, and they found that increased volatility in the financial market can lead to the onset of a banking crisis. D. Kenurgios [33] empirically showed that there was an increase in the contagion between the volatility indices (VIX, VFTSE, VDAX, VSMI, and VCAC) during the crisis period in various markets, and they attributed this to behavioral factors. S. Ross [34] showed that return volatility can be influenced by the rate of information flows. That is, a strong increase in volatility in one market can lead to an increase in volatility in another market (provided it has related information flows). Ozer-Imer I. and Ozkan I. [35] concluded that there is a relationship between the duration of the crisis and the level of volatility. Thus, according to the results of the study, it was found that—following the outbreak of the crisis—the volatilities increased at least twofold, and that the volatility was negatively correlated with the crisis duration. Sergio M. Garcia-Carranco et al. [36] studied the bubbling phenomenon and its connection with volatility.
The analysis of the contributions to crisis modeling leads us to the conclusion that many authors have put a great deal of emphasis on practical implications and specification, which is evident from the varying values of such indicators as volatility, reduction in asset value, etc. It should be noted that these works are generally not statistically sound. At the same time, due attention was not paid to abstract theories that could be statistically justified. In empirical works, a crisis is described in the context of an already accomplished fact; meanwhile, in abstract theories, it can be described as a process.
2. Crisis Dynamics in the Modern Economy
According to L. von Bertalanffy [37], in view of the axiomatics of the persistency of the laws of nature, a system-wide isomorphism is extended to the economy as part of the noosphere. As a consequence, it can be represented in a form of an open, self-organizing adaptive system that consists of multiple non-additive factorial components that have a multipolar direction with different phase and frequency characteristics [38].
Such a system is adaptive. The adaptivity of the system in this respect is aimed at correcting the internal energy imbalance and achieving the state of optimum entropy. The system can be considered in terms of two counterpolar factors. The amplitude ratio and frequency response of such a system will then depend solely on the initial store of energy and the interference degree of the counterpolar parameters. Figure 1 shows an example of such a system in dynamics that are based on a case of agricultural production.
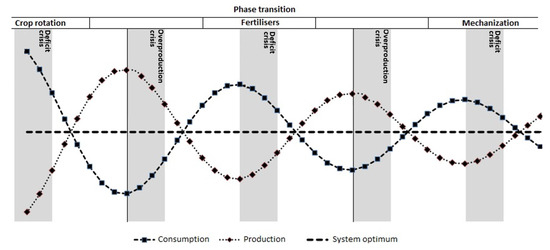
Figure 1.
An example of the development of an open system (agricultural production).
The simplest mathematical description of such a system is Equation (1):
where and are the counterdirectional factors (the sum of the interaction of which tends to result in the optimum entropy in time); A is the total energy expended on the interaction; and is the periodic function.
In the process, both the supply of external energy and the adaptation of the system can lead to a change in amplitudes, phases, and frequencies . However, the main tendency of the aggregate system energy to a minimum remains unchanged. In this case, any energy supply into the system from the outside can be only presented as the amplitude variation of one of the system components with a simultaneous displacement of optimum entropy.
From a systemic point of view, the above model undergoes the phases of convergence and divergence. The boundaries of the transitions from a state of convergence to a state of divergence can be considered a crisis (from the Greek , which means turning point). The general definition of crisis implies that the beginning of this process corresponds to the extremum points at which the derivative of the first order equals zero. According to I. R. Prigogine, phase transitions of the system are inevitable.
Given the fact that the economy is an open system, we can formulate a conclusion about the possibility of changes in the optimum entropy, phase, amplitude, and frequency of counterpolar factors in view of the inevitability of systemic crises (phase transitions). An example of an emerging systemic crisis can be found in the upcoming crisis of the world monetary system, a coming crisis that will be associated with the status transition of money from a substitute for exchange to a substitute for trust. This example is presented in Figure 2.
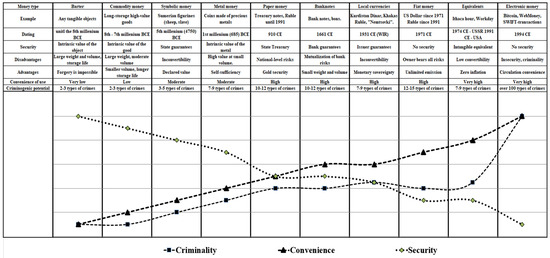
Figure 2.
The monetary crisis divergence.
The above graph shows the criteria of the monetary system, such as the security, convenience, and criminality of money over the last three thousand years; these criteria are expressed on the normalized, ranking and evaluative scale that was designed by the authors based on historical data. As such, the convenience of use was evaluated in terms of the protective and accumulative properties of money. Criminality was assessed by the number of economic crimes that are possible with this type of money, and it was reflected in the remaining legislative sources. The security of money was estimated as a factor of guaranteed liquidity, and this was determined with regard to the source of guarantee and its possibilities.
The graph shows a reduction in the liquidity of currencies, while criminality and convenience of use are increasing. Thus, we observe a continuously growing gap between the security of money and its degree of criminality—in other words, a divergence of the monetary system that will sooner or later lead to a global crisis.
The crisis trends were found to be most pronounced in the financial sector of the economy, where the frequency of overheating and stock market crashes was particularly high.
Results of World Economic System Development
Starting from the middle of the last century, intensification processes have occurred in the economy. These process have entailed the development of data transmission facilities, an increase in transmission speed, as well as the enhancement of frequency and the velocity of transactions, thus leading to an overall economic advancement that has been achieved to the point of its overheating. Figure 3 and Figure 4 show summary diagrams of the economic crises that we know about from over the past 800 years.
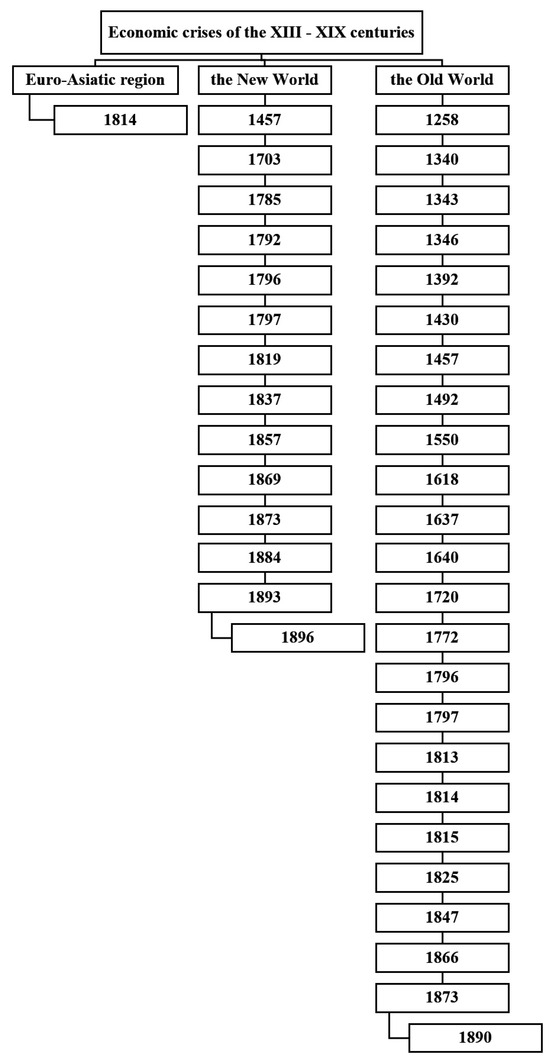
Figure 3.
Summary graph of the economic crises of the XIII–XIX centuries (see Table A1).
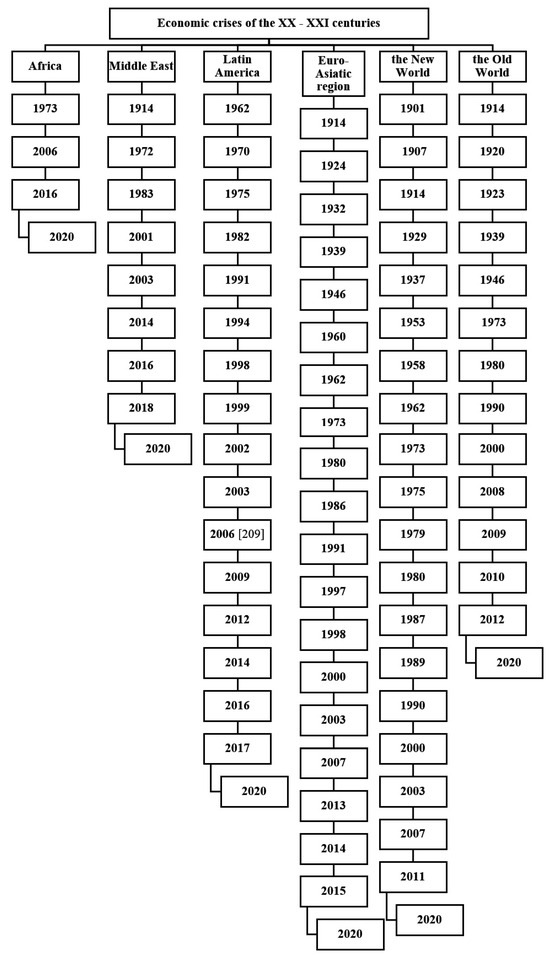
Figure 4.
Summary graph of the economic crises of the XX–XXIV centuries (see Table A1).
Electronic trading, which has existed since 1867, has contributed to the expansion in the number and velocity of transactions in the financial market. Meanwhile, the nine orders of magnitude gain that we have seen over 145 years in the intensity and rate of data exchange (Figure 5) has been determined as being a fundamental factor in the increase in average economic crises frequency (Figure 6).
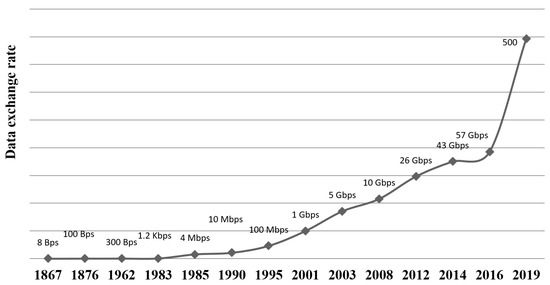
Figure 5.
Data exchange rate in the XIX–XXI centuries.
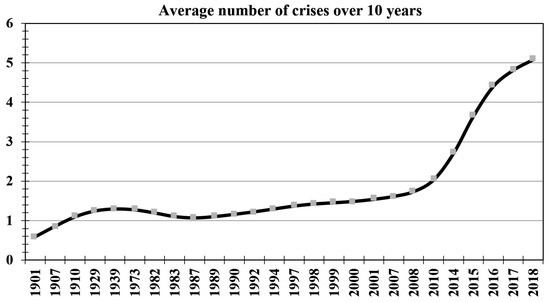
Figure 6.
Crises frequency over the period of 1901 to 2018.
Based on the facts described above, there is a need to create an econometric model of crises.
In the first stage, we introduce the concept of an asset crisis indicator.
3. Asset Crisis Indicator
This paper presents the authors’ explanation of a crisis seen from the perspective of the ratio of market demand and supply with interchanging states of stability and imbalance. This series of states has definite stages of decline, plateau, and growth, as well as intermediate reversal states that also feature equilibrium and bifurcation points. As opposed to conventional models, where crises are often considered as a non-recurrent state (for instance, K. Marx’s market saturation point or P. Krugman’s bifurcation point), the authors of this paper choose to analyze it as an ongoing process. Based on statistical indicators, we propose a classification of the major crisis stages. We also develop a methodology through which to identify a crisis at its early stage, where it is detectable as a statistically unpredictable state that causes such a change in the indicator that it violates the valid bound constraints.
Thus, we argue that a crisis should be viewed not as a spontaneous and abrupt failure, but, contrarily, as a natural characteristic of the economy; one that has a particular development pattern.
However, after a crisis has started, it is possible to register its initial stage. This means that the next stages of the crisis may be projected accordingly.
The biggest problem in making managerial decisions is ignorance and incompleteness of information regarding the current situation as it develops. The ability to anticipate further developments is the most important factor when making managerial decisions. Therefore, the main task of this study was to create a model based on which it is possible not only to detect the beginning of the crisis process, but to also anticipate its further development and end. Solving this problem will bring practical benefits to managers at all levels, thereby helping them to make management decisions in a timely manner and to mitigate the consequences of crisis processes.
According to standard statistical representations, the short-term standard deviation of random fluctuations with a probability of 99.72% cannot exceed the standard deviation that is accumulated over the previous period by more than three times (i.e., the three-sigma rule). However, when analyzing the value of exchange-traded assets, it turns out that not only do such phenomena exist, but that they are also the main cause of unexpected loss or profit. These phenomena can be regarded as sudden, unpredictable changes in the system of assets that make up an investment portfolio. In other words, as crises of individual assets. To avoid unforeseen losses, such asset states should be monitored and evaluated in the eventual need that the portfolio is re-optimized (rebalanced).
According to the results of the below experiment, which analyzed the prices of 620 exchange-traded assets in the period of 1 January 1980 to 1 June 2016, 710 states of asset crises were detected and analyzed. The main identified features included the following:
- The invariance of asset crises allowed for identifying the phases of the crisis process and modeling changes in the standard deviation of the price fluctuations of a normalized time series during a crisis period;
- The mode value of the ratio of short-term and long-term standard deviations was equal to 2.99, which confirmed the hypothesis of the normality of the distribution of market noise and compliance with the three-sigma rule in non-crisis periods.
Let us assume that, to determine the presence of a crisis, the main method will be to check the short-term standard deviation of the asset price for compliance with the “three-sigma rule”, as shown in Formula (2):
In this case, the variances of the short-term and long-term samples were compared, and they were found to be similar according to a Fisher statistical test [39], as shown in Formula (3):
where is Fisher’s test statistic; are the unbiased sample variances; and is the number of sample units.
Since the boundary of the crisis criterion was clearly defined as three sigmas—and as both samples belong to the same normalized general population—it is possible to modify the criterion to a more simplified form with a unit boundary and standard deviation instead of variance, as is shown in Formula (4):
where is the modified Fisher’s test with a unit boundary; is the short-term standard deviation; and is the accumulated standard deviation.
To apply as an indication of the presence of a crisis, we used the Heaviside function with a simultaneous reduction in to the interval that has a zero boundary corresponding to , as is shown in the Formula (5):
Or as is shown in Formulas (6) and (7):
where C is the indication of the presence of a crisis; is the indication of the absence of a crisis; H is the Heaviside function; is the standard deviation of price fluctuations for the analytical period; and is the accumulated standard deviation.
This modified Fisher’s test will be referred to as a crisis indicator. This indicator has only two values (which are shown in Table 1 and are convenient to use for generating IF-THEN functions): 1 and 0.

Table 1.
Values of the crisis indicator function.
The intensity of the crisis processes may be different for different assets. The relative intensity indicator may reflect the severity of a given crisis. The ratio of the short-term exceedance of a crisis boundary to its height is quite significant, as shown in Formula (8):
Combining this indicator with the crisis indicator, we obtain a value that characterizes the intensity of the crisis in accordance with Table 2, as shown in Formula (9):
where I is the intensity of the crisis; ; H is the Heaviside function; is the standard deviation of price fluctuations for the analytical period; and is the accumulated standard deviation.

Table 2.
Values of the crisis intensity function.
In fact, the intensity indicator I reflects the z-statistics of the short-term deviation that exceeds the accumulated values of asset price fluctuations, thus showing the probability of a crisis for the current state of the asset.
4. Crisis Risk
In the second stage, we introduce the concept of crisis risk. The crisis risk of changes in the asset price is calculated based on a mathematical phase model of the asset crisis, which was obtained as the result of a statistical experiment described below.
According to this model (Figure 7), for the values that are normalized by and which are in the crisis period normalized by its duration t, there is an excess of the short-term standard deviation of the asset above the level . This corresponds to Formula (10):
where is the normalized increment of the short-term deviation during the crisis at time t.
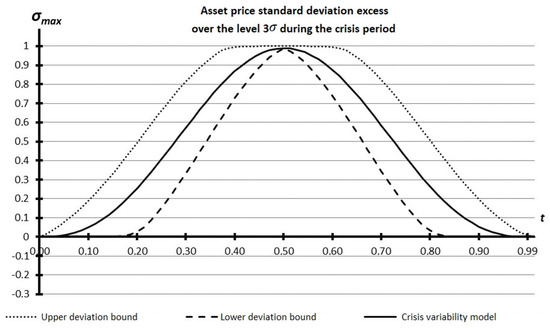
Figure 7.
Crisis variability model .
Accordingly, the upper bound of the risk increment model was calculated using Formula (11):
where is the supremum of the increment of the crisis risk at moment t; is the time frame from the onset of the asset crisis; and is the mean duration of crises for the given asset.
Thus, the risk of a crisis decline in the asset price is calculated according to Formula (12):
where C indicates the existence of an asset crisis; is the non-crisis SD of T; is the highest SD in the course of the i-th crisis; is the time frame from the onset of the asset crisis; is the mean duration of the crises of a given asset; k is the quantity of asset crises that took place in the past; and is Holt’s data decay coefficient.
5. Development of an Econometric Model of the Asset Crisis
To arrange the sequence of experiments and generalize the results obtained, we will draw up a plan of the experimental part for the purposes of formalizing and verifying the econometric model of the crisis.
Plan for the experiment.
Objective: To test the main economic hypotheses.
Method: Statistical analysis of real data.
Experiments:
- Feasibility check of the hypothesis regarding individual asset crises, as well as a definition of the values of the crisis criterion used in the model;
- Feasibility check of the hypothesis regarding the time boundedness of a crisis and its distribution;
- -
- Check the hypothesis regarding crisis duration distribution;
- Feasibility check of the hypothesis regarding the invariance of crises, as well as the phase estimates used in the model;
- Construction of a phase statistical model of the Moscow Exchange asset crisis;
- Test of the phase statistical model of the Moscow Exchange asset crisis;
- Assessment of the quality of the empirical data approximation based on the phase model of the Moscow Exchange asset crisis.
A stratification of the Russian investment assets market is performed, as shown in Table 3. As the main stratified sample for the study, the assets from stratum No. 1 were taken. To achieve the required sample size, statistical data on the value of strategic investment assets in the world and Russian markets were collected. The initial data for the experiments was the time series of the daily closing prices of 620 assets, where at least 7 years was monitored for each. The total sample size was at least 1,000,000 units. Of these, we had the following: 131 Russian assets and 489 foreign assets.

Table 3.
Stratification of the investment asset market.
5.1. Feasibility Check of the Hypothesis Regarding an Individual Asset Crisis, as Well as a Definition of the Values of the Crisis Criterion Used in the Model
The economic rationale of the experiment was as follows: in taking, as a starting point, the axiom of market homogeneity (the axiom of ergodicity) [40], we must accept, as the main property of ergodicity, the repetition of macroeconomic processes (global crises) at the microeconomic level (crises of individual assets). Let us check this statement.
The purpose of the experiment was to test the feasibility of the market state model.
The asset market state evaluation model consisted of five statements, with three statements describing the states such as “growth”, “stagnation”, and “decline” (which do not require a statistical check since their statistical significance corresponds to , i.e., it is trivial). At the same time, the statements about “crisis growth” and “crisis decline” required a feasibility check.
Each statement consists of a trivial part and a feasible part:
- “crisis growth” = “crisis”; “growth”; ;
- “crisis decline” = “crisis”; “decline”; .
Let us check the feasibility of the concept of “crisis” with .
The representativeness of the world’s top 500 financial companies was set according to the Bloomberg index and 131 assets of the Russian MICEX market.
The sample test was of the strategic investment potential (≥7 years).
The sample units were the ratios of a short-term and the cumulative standard deviations averaged over the asset series .
—the average ratio of the cumulative variability of the asset to the short-term variability obeys a certain law of distribution.
—distribution regularities of the average ratio of the cumulative variability of the asset to the short-term variability do not exist.
Rejection tests: test and Student’s t-test.
Experimental conditions: N—general population; n—sample size; —the minimum required sample size for ; —the number of degrees of freedom according to Sturges’ rule; and —the number of degrees of freedom for alpha grouping.
- ;
- Test ;
- Test v t-test ;
- .
Let us perform the grouping with Sturges’ rule [41].
Figure 8 shows the construction of a Sturges histogram.
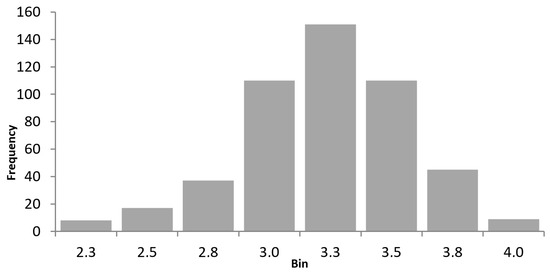
Figure 8.
Sturges histogram.
Let us perform the -grouping. Figure 9 shows the construction of an -histogram.
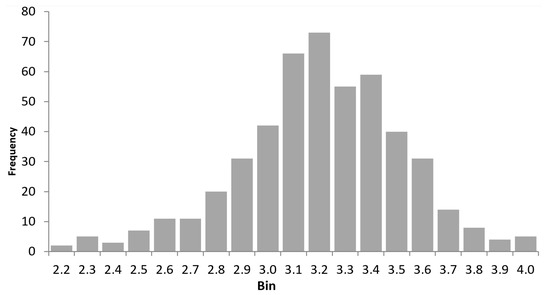
Figure 9.
Alpha histogram.
When considering the histograms, no evidence against the postulated trends was found. was not confirmed intuitively.
We thus carried out a criterion estimation by means of the Sturges Chi-square test for a standard normal distribution:
Given the low power of the criterion, we used the more powerful Test and t-test for a biased normal distribution. Figure 10 shows a graphical representation of the t-test for a biased normal distribution.
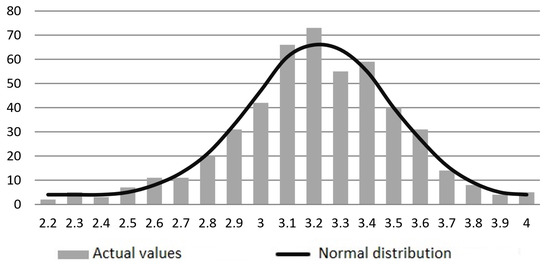
Figure 10.
A t-test for a biased normal distribution.
The rejection was obtained; thus, we accept .
If is accepted, it is necessary to establish the reason for the bias of the distribution to the right. It is because of exchange rules and regulations that asset trading with price fluctuations is halted on most exchanges till the stabilization of the market situation.
Preliminary conclusion: Since is accepted and the reasons for the bias established, we allowed the definition of “crisis” to also include the exceedance of the relation over a certain measure of the central tendency of a standard deviation.
To determine the range of values of the crisis criterion, we conducted a statistical study on the historical values of the ratio of the short-term standard deviation to the cumulative one. Table 4 provides descriptive sampling statistics of the ratio of short-term and cumulative variability for 620 assets over 7 years (more than 1,000,000 sample units) to determine the boundary of the “crisis” state.

Table 4.
Descriptive sample statistics rounded to hundredths.
Using the principle of lowest risk preference, we determined the boundary of the crisis state as the smallest measure of central tendency (MCT) of the ratio of the standard deviations.
Since , such is the mode of distribution, thus coarsening the measure to an integer number of z-values. Therefore, the attribute of “crisis” can be described as .
Conclusions
The expression of the form is statistically significant, and it is a representative of the presence of a “crisis” of the asset.
For an intuitive assessment and for hypothesizing, we constructed graphs of the values of the crisis variability that were normalized by a maximum of 20 randomly selected asset crises, as shown in with Figure 11.
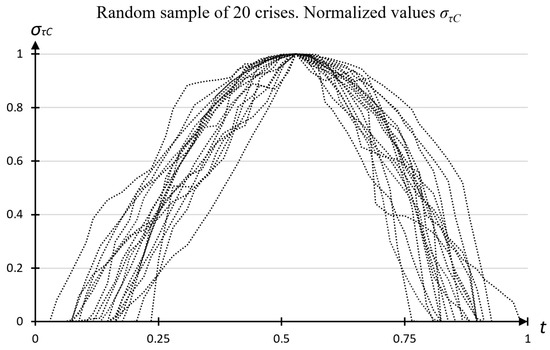
Figure 11.
Visual analysis of the general tendencies of the asset crises.
Let us formulate a number of intuitive hypotheses describing the variance of the exchange-traded assets in times of crisis:
- Crises are bounded by time;
- The duration of crises has general tendencies;
- During their development, crises have at least two phase states.
5.2. Check of the Hypothesis Regarding a Crisis’ Time Boundedness
The economic rationale of the experiment: A crisis can not be endless, sooner or later the market returns to a stable state. Let us check this statement.
5.2.1. The Experiment Objective
To verify the hypothesis regarding the limited duration of the asset crisis defined in Section 5.1, we performed the following:
- The representativeness was a random sample of MICEX assets;
- The sample test was on the short-term strategic investment potential (≥5 years);
- The sample units were the days of the asset crises’ duration;
- —the duration of most crises of MICEX strategic assets is bounded to a certain time period;
- —the duration of most crises of MICEX strategic assets is not bounded by time;
- The dismissal test was the binomial m-test;
- ;
- ;
- .
Let us perform a binomial grouping. Figure 12 shows a binomial histogram.
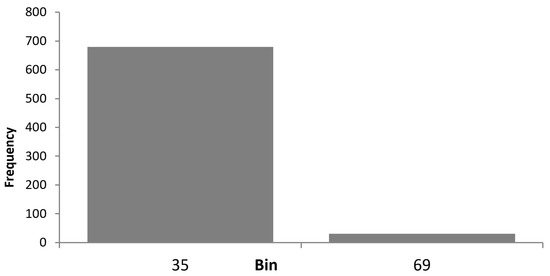
Figure 12.
Binomial histogram.
In the present histogram, the postulated trends were detected, and was not confirmed intuitively.
We carried out the estimation by means of the binomial m-test:
.
The rejection of was obtained; thus, we accept .
5.2.2. Conclusions
The duration of most of the crises of the MICEX strategic assets was bounded to a period of 35 days with .
5.3. Check of the Hypothesis of the Crisis Duration Distribution
The economic rationale of the experiment: Since the duration of the crisis was limited, it may obey some of the laws of distribution. Let us check this statement.
5.3.1. The Purpose of the Experiment
We tested the hypothesis that the duration of the asset crisis obeys a certain law of distribution.
The sample was a random sample of the assets of the Moscow Exchange. The hypotheses regarding the distribution of the duration of crises of strategic assets of the Moscow Exchange were as follows:
- is antimodal;
- is unimodal;
- is bimodal;
- is polymodal;
- The rejection test was Hartigan’s Dip test [42];
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- .
We then performed a grouping with .
Let us construct the histogram. First, we should perform a DIP-test. Figure 13 shows the results from Hartigan’s Dip test for modality.
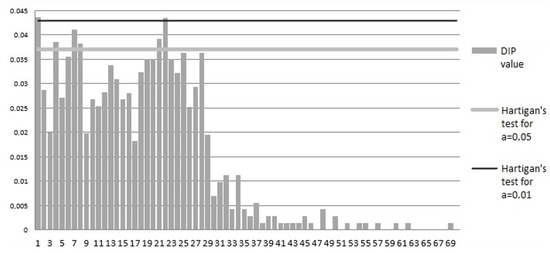
Figure 13.
Hartigan’s Dip test for modality.
We accepted that is a bimodal distribution with .
Let us describe the statistics for a bimodal normal distribution. Figure 14 shows the distribution of the duration of the crises.
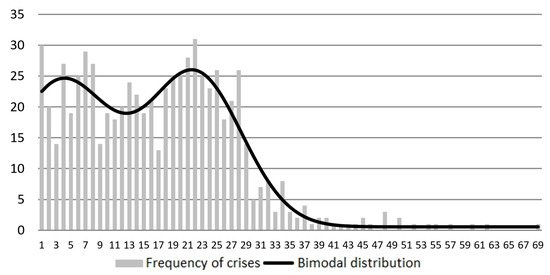
Figure 14.
Bimodal distribution of the duration of the crises.
Let us test and Student’s t-test for this distribution:
5.3.2. Conclusion
The bimodal normal distribution describes the normalized duration of the asset crises, with being at least 0.25, via the statistics of the following form (Table 5):

Table 5.
Statistics on the duration of asset crises.
Thus, the following day’s values can be taken as the respective median values of the duration of crises:
5.4. Check of the Hypothesis Regarding Crisis Invariance
The economic rationale of the experiment: Since the duration of the crisis was limited, and as it obeyed a certain law of distribution, the dynamics of the development of all crises were found to be similar and consisted of several phases. Let us check this statement.
5.4.1. The Experiment Objective
The aim it to verify the hypothesis regarding the existence of phases of crisis variability changes and their identity.
The sample was a random sample of 98 out of a 710 time series of relative values of the standard deviation of assets in crisis periods, and these were normalized by the duration of the crises.
The hypotheses regarding the phases of the crisis variability changes were as follows:
- does not exist;
- do exist, but they are specific for each crisis;
- does exist and obeys a certain law of distribution;
- The test- test was the rejection test;
- ;
- ,
- where is the standard deviation during the crisis;
- is the sample mean of the standard deviation;
- ;
- ,
- where is the standard deviation from the sample mean;
- ;
- ;
- ;
- .
We shall now consider the mean-value and standard-crisis-variability-deviation piecewise linear functions that were normalized by and , as shown in Formulas (13) and (14).
Let us construct and consider the complete histogram for and .
Figure 15 shows the graphs of the crisis variability.
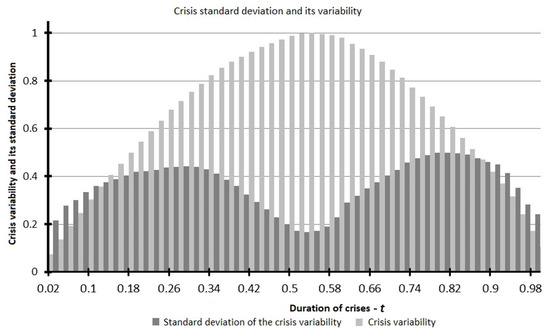
Figure 15.
Mean and standard deviation of the crisis variability.
In the present histogram, the postulated trends were detected, and was not confirmed intuitively.
We next calculated the derivative values .
Then, the rejection of happened.
We next calculated the derivative values and . We then constructed and considered a normalized cumulative histogram of derivative signs and , which are presented in Figure 16.
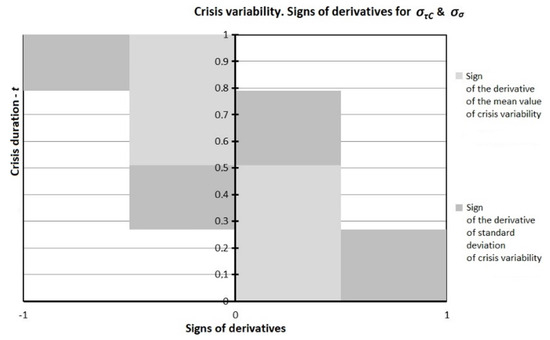
Figure 16.
Normalized cumulative histogram. Derivative signs of the mean and standard deviation of the crisis variability.
In the present histogram, the postulated trends were detected, and was not confirmed intuitively.
Then, the rejection of happened.
If , , then we accept .
5.4.2. Conclusion
The phases of the asset crises variability changes exist and obey a certain law of distribution.
5.5. Construction of a Phase Model of the Crisis
The economic rationale of the experiment: Since the duration of the crisis was limited and obeyed a certain distribution law—and as the dynamics of the development of all crises were found to be similar and consisted of several phases—it was possible to create an approximation model that allowed for predicting both the duration and the risk component in crisis periods. Let us check this statement.
5.5.1. The Purpose of the Experiment
To create a statistically significant phase model of the crisis of the Moscow Exchange asset, as is defined in Section 5.3.
To build the model, we used a sample of 98 maximum-aligned time series of asset variability values in crisis periods that were normalized by value and time with an acceptable error not exceeding 0.025, thus corresponding to for .
When analyzing the model, the main formative factors were the average normalized value of the crisis variability that corresponded to the value and the mean proper standard deviation of the time series variability . Figure 17 shows the normalized input data for the model generation.
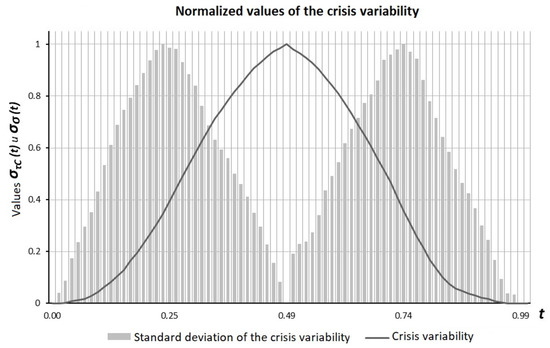
Figure 17.
Normalized input data for the model generation.
Let us assume that, for the construction of a reference function of the form in the case of unbiased phases, the following phase correspondence will be true, as shown in Formula (15):
We represent and in the form of periodic functions, as shown in Formula (16):
When using the generalized reduced gradient method, we approximated the smoothed moving average values of and by the functions of the form and , respectively. Figure 18 shows the approximation of the smoothed averages by periodic functions.
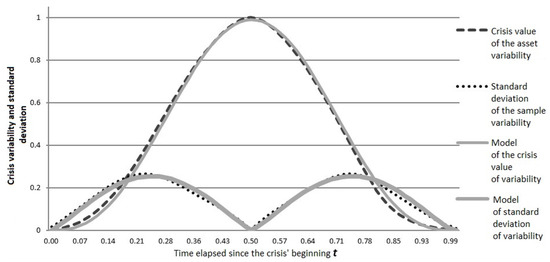
Figure 18.
Approximation of smoothed averages by periodic functions.
Figure 19 shows the range of acceptable values of the model for deviation .
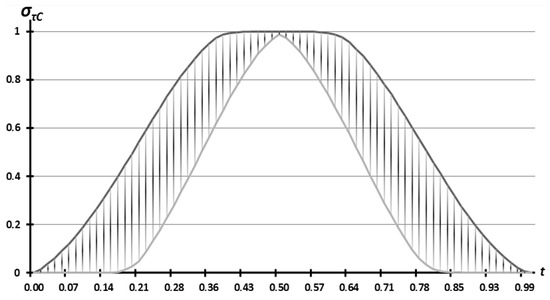
Figure 19.
The range of acceptable values of the model for deviation .
Having identified and , let us describe the main points and phases of the model of the crisis development of the Moscow Exchange strategic asset, as shown in Formulas (18) and (19):
Figure 20 shows the values of the derivatives of .
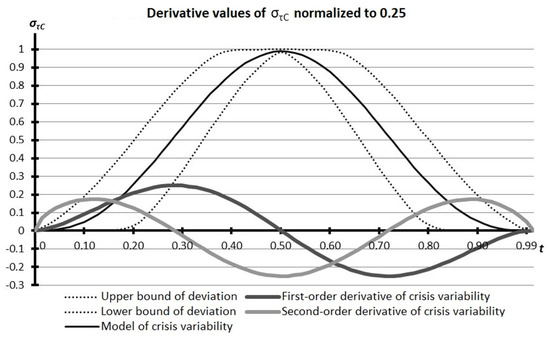
Figure 20.
Values of the derivatives of , which were normalized to 0.25.
Table 6 shows the development phases of the crisis of the Moscow Exchange strategic asset.

Table 6.
Development phases of the Moscow Exchange strategic asset crisis.
5.5.2. Conclusions
A phase model of the development of the crisis of the Moscow Exchange strategic asset was created. Since the creation of the model is based on a non-obvious statement about the correspondence of the form , the model performance should be evaluated analytically for a given .
5.6. Test of the Phase Model of the Asset Crisis
The economic rationale of the experiment: The approximate phase model of the crisis allows for the predicting of the risk components in crisis periods. Let us test this statement on the empirical data.
5.6.1. The Purpose of the Experiment
The aim was to check the quality of the created phase model of the crisis variability of the Moscow Exchange asset.
- The representativeness covered a random sample of short-term standard deviation values in the crisis periods of 31 strategic investment assets of the MICEX;
- The sample units were the 7154 normalized values of the variability exceedance of the crisis time series that was normalized by the duration of the crises of the MICEX assets, which was also normalized by the maximum standard deviation;
- —the quality of the phase model of the crisis was not statistically confirmed;
- —the quality of the phase model of the crisis was sufficient for ;
- The rejection test was the binomial m-test;
- The applicability test of the dismissal test was the accurate binomial test;
- ;
- ;
- .
Let’s perform a binomial grouping by consider it in a histogram. Figure 21 shows the testing of the model.
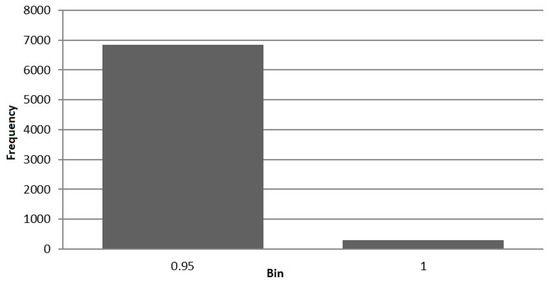
Figure 21.
Success rate of the model testing.
In the present histogram, the postulated trends were detected, and was not confirmed intuitively.
We shall carry out the estimation by means of the binomial m-test:
The rejection of was obtained; thus, we accept .
5.6.2. Conclusions
According to the statistical evaluation, the created phase model of the crisis development of the MICEX strategic asset sufficiently met the requirements of the model quality for a given .
5.7. Evaluation of the Quality of the Approximation of Empirical Data Based on the Phase Model of the Moscow Exchange Asset Crisis
The economic rationale of the experiment: The approximate phase model of the crisis allows for the predicting of the duration of a crisis in crisis periods. Let us test this statement on the empirical data.
5.7.1. The Purpose of the Experiment
The aim was to check the adequacy of the approximation quality of the phase model of the crisis variability during the calculation of the model coefficients.
The representativeness was a sample of the residual, as shown in Formula (20):
where is obtained empirically; is modeled based on the values of a random sample of the 7054 values of the crisis variability of the Moscow Exchange assets.
- —the residuals were homoscedastic and stationary;
- —the residues were not homoscedastic and not stationary;
- The rejection tests used were the White test and F-test;
- ;
- ;
- ,
where F is Fisher’s test; is the table value for ; is the Lagrange multiplier statistic; and is the table value for .
Figure 22 shows a histogram of the residuals.
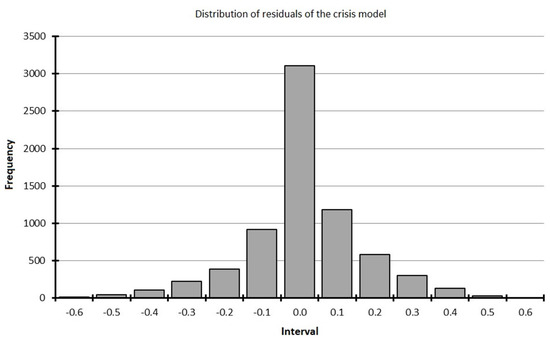
Figure 22.
Distribution of the crisis model residuals.
When considering the histogram, the similarity with the Bessel distribution was revealed, and the postulated trends were detected. was not confirmed intuitively.
We then ran the White test and the F-test as follows:
It was then found that the rejection of did not happen.
Thus, the developed mathematical phase model of asset crisis was constructed with the help of a approximation approach that allows one to predict the development of crisis with an accuracy of , as well as helps with defining the dates of the beginning and end of asset crises. Figure 23 shows an example of a risk forecast on a EUR/RUB currency pair.
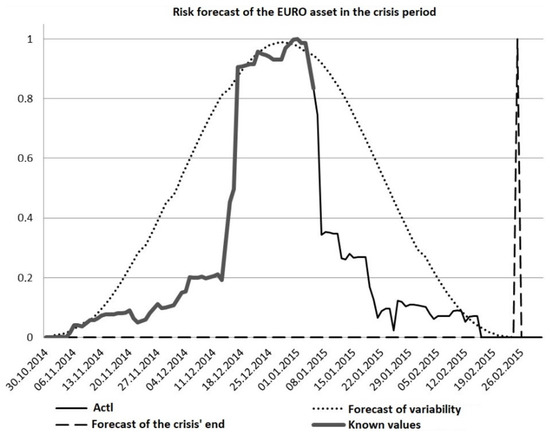
Figure 23.
EUR/RUB risk forecast in the crisis period.
Figure 24 shows an example of a risk forecast on a EUR/RUB currency pair.
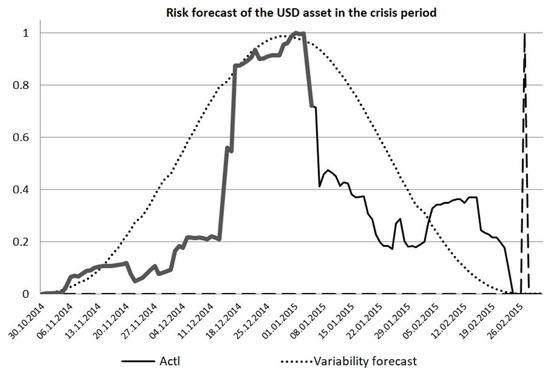
Figure 24.
Risk forecast of a USD/RUB currency pair.
Figure 25 shows an example of a risk forecast on a EUR/RUB currency pair.
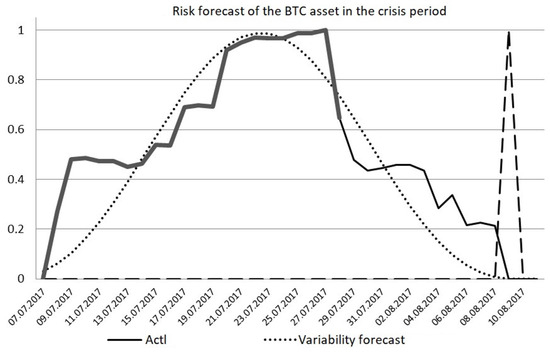
Figure 25.
Bitcoin risk forecast in the crisis period.
Based on the conducted research, it can be concluded that the tendencies to fluctuations in free prices in the stock exchange market have a distinct inclination to a normal distribution, one that is apart from the periods of crisis changes. At the same time, the movements in price during crisis periods are yet more proof of the importance of the three-sigma rule. However, in spite of that, the crisis fluctuations in prices across the market are also normally distributed. In asset crises, four identical phases were identified. These phases not only allowed for predicting possible crisis movements in prices, but they also allowed them to be made with acceptable accuracy after the second phase, which makes it possible to define the ending date of the crisis.
An analysis of a 533 time series when determining the capabilities of the crisis indicator and the range of its application was carried out. Figure 26, Figure 27 and Figure 28 show the graphs of assets with known crisis states.
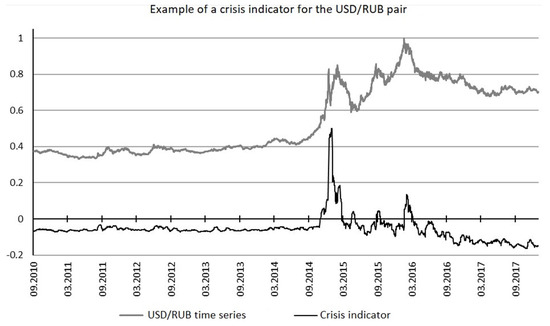
Figure 26.
Indicator-based crisis detection: the case of a USD/RUB currency pair in the time frame of 1 September 2010 till 1 September 2017.
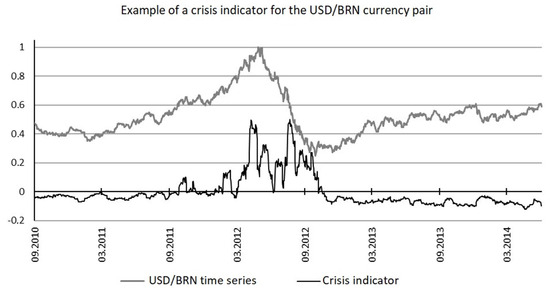
Figure 27.
Indicator-based crisis detection: the case of Brent oil price in the time frame of 1 September 2010 till 1 September 2014.
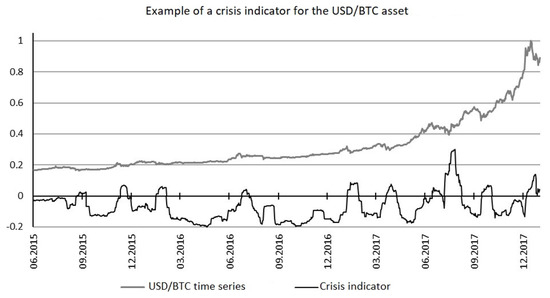
Figure 28.
Indicator-based crisis detection: the case of the BTC cryptocurrency in the time frame of 1 September 2015 till 1 September 2017.
5.7.2. Conclusions
We designed a crisis indicator and a crisis development model that exhibited an ample degree of generality, as well as a level of convincing fidelity regarding the properties aimed at detecting an economic crisis. The designed model was able to achieve a higher effectiveness when compared to the other models due to its validity and statistical capability in making both practical and theoretical predictions of the volatility.
An experiment was conducted to assess the quality of the econometric crisis model on real historical data. The results of the experiment showed the high quality of the model as a crisis detection tool. To identify the crisis phases, it was sufficient to approximate the crisis process by first-order derivatives.
In a statistical analysis of a 620 time series of transnational and Russian investment assets with strategic potential (which had existed for more than 7 years), the hypothesis of crisis invariance was not refuted as follows:
- In terms of the feasibility of the invariant crisis model with , there was a confirmation of the hypothesis regarding the invariance of crises;
- In terms of the invariance of the duration of crises with , there was a confirmation of the hypothesis regarding the duration of crises;
- In terms of the invariance of the crisis phases with , there was a confirmation of the hypothesis regarding the sequence of the crisis phases.
Thus, a method for determining asset crises was developed, and a phase model of the crisis was created.
6. Conclusions
Thus, through the implemented model, we conclude that the tendencies toward fluctuations in the free prices in the stock exchange market have a distinct inclination to a normal distribution, and this is apart from the periods of crisis changes. At the same time, the movements in price during crisis periods are yet more proof of the importance of the three-sigma rule; however, in spite of that, the crisis fluctuations in prices across the market were also found to be normally distributed. In asset crises, four identical phases were identified, which not only allowed for the predicting of possible crisis movements in prices, but they were also made with acceptable accuracy after the second phase, which enabled us to define the ending date of the crisis. As, primarily, an approximation model, the created phase model of crises allows for a determination of the duration of the crisis, after its first phase, with a sufficiently high probability. This also allows for defining its ending date during the second phase of the crisis with a substantial degree of probability. The result of the study was in establishing a functioning mathematical model for forecasting asset risks in times of crisis. As for possible limitations of the current model and thus possible extensions for taking the model further (as well as future research topics), we would like to point out once again that the developed mathematical model of crises was primarily designed to identify and predict the end of asset crises (such as crude oil, gold, stocks, currency pairs, and other tradable assets).
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A

Table A1.
Strategy element weights in relation to the market condition.
Table A1.
Strategy element weights in relation to the market condition.
| Name of the Crisis | Year | Number of Countries Affected by Economic Crises | Number of People Affected by Economic Crises as a Progressive Total |
|---|---|---|---|
| Baronial fiscal crisis | 1258 | 1 | 6090 |
| Default of Edward III | 1340 | 1 | 15,147 |
| Tana Crisis | 1343 | 1 | 6,081,814 |
| Venice Bank Crash | 1346 | 1 | 12,148,480 |
| Bullion Famine | 1392 | 2 | 12,180,569 |
| Great Slump | 1430 | 1 | 12,222,744 |
| Bullion Famine | 1457 | 2 | 12,357,175 |
| Peruvian Silver Crisis | 1492 | 1 | 12,391,460 |
| Overpopulation and agricultural depression | 1550 | 2 | 12,421,425 |
| European Monetary Crisis | 1618 | 1 | 12,437,623 |
| Tulpanomania | 1637 | 1 | 12,480,282 |
| English Revolution | 1640 | 1 | 19,246,949 |
| Great Tobacco Depression | 1703 | 1 | 19,321,905 |
| FR: “Mississippi Bubble”, UK: “South Sea Bubble” | 1720 | 2 | 19,736,091 |
| British Credit Crisis | 1772 | 4 | 19,767,993 |
| Panic of 1785 | 1785 | 1 | 21,528,348 |
| Panic of 1792 | 1792 | 1 | 27,599,777 |
| Atlantic Credit Crisis | 1796 | 2 | 49,999,777 |
| Land Speculation Panic of 1797 | 1797 | 2 | 408,399,777 |
| Danish State Bankruptcy of 1813 | 1813 | 1 | 408,418,917 |
| Post-war famine | 1814 | 2 | |
| Post-Napoleonic depression | 1815 | 1 | 469,318,917 |
| First Great Depression (Panic of 1819) | 1819 | 1 | 487,912,667 |
| Panic of 1825 | 1825 | 1 | 489,604,334 |
| Panic of 1837 | 1837 | 1 | 491,670,306 |
| Panic of 1847 | 1847 | 1 | 492,279,306 |
| Panic of 1857 | 1857 | 1 | 495,254,306 |
| Black Friday of 1866 | 1866 | 1 | 496,006,158 |
| Gold Panic (Black Friday of 1869) | 1869 | 1 | 529,061,714 |
| Panic of 1873; Great Depression of British Agriculture | 1873 | 2 | 551,461,714 |
| Second Great Depression (“Long Depression”?) | 1884 | 1 | 553,920,391 |
| Baring Crisis | 1890 | 1 | 555,612,058 |
| Denver Depression of 1893 and Australian Banking Crisis of 1893 | 1893 | 2 | 591,234,280 |
| Panic of 1896 | 1896 | 1 | 624,289,836 |
| Wall Street Panic of 1901 | 1901 | 1 | 636,189,836 |
| 1907 Bankers’ Panic | 1907 | 1 | 644,453,725 |
| World War I economic impact | 1914 | 5 | 664,239,439 |
| Great Depression in the United Kingdom (the Great Slump) | 1920 | 1 | 665,931,105 |
| Great Britain and the Ruhr Crisis, 1923–1924, and the Hyperinflation Crisis of 1923 | 1923 | 1 | 690,197,772 |
| Scissors Crisis | 1924 | 1 | 962,497,772 |
| Great Depression | 1929 | 1 | 974,397,772 |
| Soviet famine of 1932–33 | 1932 | 1 | 1,004,653,328 |
| Recession of 1937–1938 | 1937 | 1 | 1,016,553,328 |
| World War II economic impact | 1939 | 7 | 1,562,378,328 |
| Post-war famine in the USSR | 1946 | 1 | 1,567,935,471 |
| Recession of 1953 | 1953 | 1 | 1,574,006,899 |
| Eisenhower Recession | 1958 | 1 | 1,585,906,899 |
| Great Chinese Famine | 1960 | 1 | 1,909,131,899 |
| Cuban Missile Crisis economic impact | 1962 | 3 | 2,054,206,899 |
| Latin American Debt Crisis | 1970 | 3 | 2,059,631,899 |
| The Middle East War Crisis | 1972 | 4 | 2,086,756,899 |
| 1973 Oil Embargo Crisis | 1973 | 8 | 2,670,556,899 |
| The Great Inflation and the Latin American Debt Crisis | 1975 | 5 | 2,799,181,899 |
| Second Oil Crisis | 1979 | 1 | 2,817,775,649 |
| Early 1980s recession | 1980 | 4 | 3,482,075,649 |
| Crisis económica en Chile de 1982 | 1982 | 1 | 3,486,450,649 |
| 1983 Israel Bank Stock Crisis | 1983 | 1 | 3,494,150,649 |
| Japanese Asset Price Bubble | 1986 | 1 | 3,506,750,649 |
| Stock Market Crash of 1987 and Black Monday (1987) | 1987 | 1 | 3,804,250,649 |
| Savings and Loan Crisis | 1989 | 1 | 3,878,625,649 |
| Swedish Banking Crisis, Finnish Banking Crisis, and the Early 1990s Recession | 1990 | 7 | 4,311,925,649 |
| August Coup and the India Economic Crisis | 1991 | 2 | 5,833,725,649 |
| The Tequila Crisis and the Venezuelan Banking Crisis of 1994 | 1994 | 2 | 5,849,358,982 |
| The Asian Financial Crisis | 1997 | 2 | 6,067,136,760 |
| The 1998 Russian Financial Crisis, the 1998 Ecuador Financial Crisis, and the Argentine Economic Crisis | 1998 | 3 | 6,254,736,760 |
| The Brazilian Exchange Rate Crisis of 1999 | 1999 | 1 | 6,445,836,760 |
| Recession of the 2000s and the Dot-com Bubble Burst | 2000 | 1 | 7,411,836,760 |
| The 2001 Turkish Economic Crisis | 2001 | 5 | 7,487,436,760 |
| The South American Economic Crisis of 2002 | 2002 | 4 | 7,747,136,760 |
| The Oil Price Shock of 2003 | 2003 | 8 | 8,381,336,760 |
| South America Food Prices Crisis | 2006 | 4 | 8,413,666,073 |
| The United States Subprime Mortgage Crisis | 2007 | 2 | 10,004,066,073 |
| The Global Financial Crisis, the Automotive Industry Crisis, the Icelandic Financial Crisis, the Irish Banking Crisis, the Russian Financial Crisis, the Latvian Financial Crisis, and the Spanish Financial Crisis | 2008 | 10 | 12,281,866,073 |
| The European Sovereign Debt Crisis, the Greek Government Debt Crisis, and the Venezuelan Banking Crisis | 2009 | 3 | 12,706,766,073 |
| The Portuguese Financial Crisis | 2010 | 1 | 12,715,866,073 |
| The United States Debt Ceiling Crisis of 2011 | 2011 | 1 | 13,013,366,073 |
| The European Debt Crisis of 2012 and the Inflation Crisis in Venezuela | 2012 | 2 | 13,429,166,073 |
| Ukrainian Crisis | 2013 | 1 | 13,468,366,073 |
| The Russian Financial Crisis and Brazilian Economic Crisis | 2014 | 16 | 13,931,766,073 |
| The 2015 Chinese Stock Market Crash | 2015 | 1 | 15,224,666,073 |
| Nigeria Contraction | 2016 | 2 | 15,450,066,073 |
| Crisis in Venezuela | 2017 | 1 | 15,475,266,073 |
| The Turkish Currency and Debt Crisis of 2018 | 2018 | 1 | 15,550,866,073 |
| The 2020 Stock Market Crash | 2020 | 84 | 17,013,341,073 |
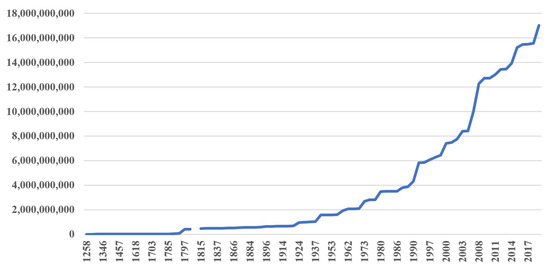
Figure A1.
Number of people affected by economic crises as progressive total.
References
- Marx, K.H. Economic and Philosophical Manuscripts of 1844; Progress Publishers: Moscow, Russia, 1844; p. 333. [Google Scholar]
- Keynes, J.M. The General Theory. The General Theory of Employment, Interest, and Money; Palgrave Macmillan Cham: New York, NY, USA, 2018; p. 404. [Google Scholar] [CrossRef]
- Kirzner, I.M. A Look at Subjectivism, Intelligibility and Economic Understanding: Essays in honor of Ludwig M. Lachmann on his Eightieth Birthday; New York University Press: New York, NY, USA, 1986. [Google Scholar]
- Krugman, P.R. The Return of Depression Economics; W W Norton and Co Inc.: New York, NY, USA, 2000. [Google Scholar]
- Aftalion, A. La realite des surproductions generales: Essai d’une theorie des crises generales et periodiques. Rev. Econ. Polit. 1908, 10, 696–706. [Google Scholar]
- Kondratieff, N.D. The Long Waves in Economic Life. Review 1979, 2, 519–562. [Google Scholar] [CrossRef]
- Mitchell, W.C. Quantitative analysis in economic theory. Am. Econ. Rev. 1925, 15, 1–12. [Google Scholar]
- Rothbard, M.N. America’s Great Depression; Ludwig von Mises Institute: Auburn, AL, USA, 1972. [Google Scholar]
- De Soto, H. The Mystery of Capital: Why Capitalism Triumphs in the West and Fails Everywhere Else. Can. J. Lat. Am. Caribb. Stud. 2002, 27, 172. [Google Scholar]
- Spiethoff, A. Vorbemerkungen zu einer Theorie der Überproduktion: Vortrag, Gehalten am 17. Dezember 1901 in der Staatswissenschaftlichen Vereinigung zu Berlin; Duncker and Humblot: Berlin, Germany, 1902. [Google Scholar]
- Schumpeter, J.A. The Theory of Economic Development; Routledge: London, UK, 2017. [Google Scholar]
- Aftalion, A. The theory of economic cycles based on the capitalistic technique of production. Rev. Econ. Stat. 1927, 9, 165–170. [Google Scholar] [CrossRef]
- Clark, J.M. Business Acceleration and the Law of Demand: A Technical Factor in Economic Cycles. J. Political Econ. 1917, 25, 217–235. [Google Scholar] [CrossRef]
- Harrod, R.F. Notes on trade cycle theory. Econ. J. 1951, 61, 261–275. [Google Scholar] [CrossRef]
- Pigou, A.C. Mr. J. M. Keynes’ General Theory of Employment, Interest and Money. Economica 1936, 3, 115–132. [Google Scholar] [CrossRef]
- Keynes, J.M. Treatise on Money: Pure theory of Money; Harcourt: San Diego, CA, USA, 1930; Volume 3. [Google Scholar]
- Harrod, R.F. Trade Cycle. An Essay; Oxford at the Clarendon Press: Oxford, UK, 1936. [Google Scholar]
- Samuelson, P.A. Interactions between the Multiplier Analysis and the Principle of Acceleration. Rev. Econ. Stat. 1939, 21, 75–78. [Google Scholar] [CrossRef]
- Hicks, J.R. A Contribution to the Theory of the Trade Cycle; Oxford at the Clarendon Press: Oxford, UK, 1950; Volume 126. [Google Scholar]
- Hansen, A.H. Business Cycles and National Income; NYC Norton: Jersey City, NJ, USA, 1951. [Google Scholar]
- Tinbergen, J. Kondratiev cycles and so-called long waves: The early research. Futures 1981, 13, 258–263. [Google Scholar] [CrossRef]
- Krugman, P. Scale Economies, Product Differentiation, and the Pattern of Trade. Am. Econ. Rev. 1980, 70, 950–959. [Google Scholar]
- Cumperayot, P.; Kouwenberg, R. Early warning systems for currency crises: A multivariate extreme value approach. J. Int. Money Financ. 2013, 36, 151–171. [Google Scholar] [CrossRef]
- Jutasompakorn, P.; Brooks, R.; Brown, C.; Treepongkaruna, S. Banking crises: Identifying dates and determinants. J. Int. Financ. Mark. Institutions Money 2014, 32, 150–166. [Google Scholar] [CrossRef]
- Korobeinikov, A. Financial crisis: An attempt of mathematical modelling. Appl. Math. Lett. 2009, 22, 1882–1886. [Google Scholar] [CrossRef]
- Bocola, L.; Bornstein, G.; Dovis, A. Quantitative sovereign default models and the European debt crisis. J. Int. Econ. 2019, 118, 20–30. [Google Scholar] [CrossRef]
- Osiyevskyy, O.; Dewald, J. The pressure cooker: When crisis stimulates explorative business model change intentions. Long Range Plan. 2018, 51, 540–560. [Google Scholar] [CrossRef]
- Rhee, K.J.; Park, K.S. Changes in dividend smoothing after the financial crisis. Econ. Lett. 2018, 172, 37–39. [Google Scholar] [CrossRef]
- Wegener, C.; Kruse, R.; Basse, T. The Walking Debt Crisis. J. Econ. Behav. Organ. 2017, 157, 382–402. [Google Scholar] [CrossRef]
- Hlaing, S.W.; Kakinaka, M. Financial crisis and financial policy reform: Crisis origins and policy dimensions. Eur. J. Political Econ. 2018, 55, 224–243. [Google Scholar] [CrossRef]
- Gao, H.L.; Mei, D.C. The correlation structure in the international stock markets during global financial crisis. Phys. A Stat. Mech. Its Appl. 2019, 534, 122–156. [Google Scholar] [CrossRef]
- Moshirian, F.; Wu, Q. Banking industry volatility and banking crises. J. Int. Financ. Mark. Institutions Money 2009, 19, 351–370. [Google Scholar] [CrossRef]
- Kenourgios, D. On financial contagion and implied market volatility. Int. Rev. Financ. Anal. 2014, 34, 21–30. [Google Scholar] [CrossRef]
- Ross, S. The Arbitrage Theory of Capital Asset Pricing. Handbook of the Fundamentals of Financial Decision Making: Part I; World Scientific: Singapore, 2013; pp. 11–30. [Google Scholar] [CrossRef]
- Ozer-Imer, I.; Ozkan, I. An empirical analysis of currency volatilities during the recent global financial crisis. Econ. Model. 2014, 43, 394–406. [Google Scholar] [CrossRef]
- Garcia-Carranco, S.M.; Bory-Reyes, J.; Balankin, A.S. The crude oil price bubbling and universal scaling dynamics of price volatility. Phys. A Stat. Mech. Its Appl. 2016, 452, 60–68. [Google Scholar] [CrossRef]
- Von Bertalanffy, L. The Theory of Open Systems in Physics and Biology. Science 1950, 111, 23–29. [Google Scholar] [CrossRef] [PubMed]
- Ivanyuk, V. Developing a crisis model based on higher-order moments. Heliyon 2022, 8, e08896. [Google Scholar] [CrossRef] [PubMed]
- Snedecor, G.W.; Cochran, W.G. Statistical Methods, 8th ed.; Iowa State University Press: Ames, IA, USA, 1989. [Google Scholar]
- Tinbergen, J. On a Method of Statistical Business-Cycle Research. A Reply. Econ. J. 1940, 50, 141–154. [Google Scholar] [CrossRef]
- Sturges, H.A. The choice of a class interval. J. Am. Stat. Assoc. 1926, 21, 65–66. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Hartigan, P.M. The Dip Test of Unimodality. Ann. Stat. 1985, 13, 70–84. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).