Statistical Inference for Partially Linear Varying Coefficient Spatial Autoregressive Panel Data Model

Abstract

This paper studies the estimation and inference of a partially linear varying coefficient spatial autoregressive panel data model with fixed effects. By means of the basis function approximations and the instrumental variable methods, we propose a two-stage least squares estimation procedure to estimate the unknown parametric and nonparametric components, and meanwhile study the asymptotic properties of the proposed estimators. Together with an empirical log-likelihood ratio function for the regression parameters, which follows an asymptotic chi-square distribution under some regularity conditions, we can further construct accurate confidence regions for the unknown parameters. Simulation studies show that the finite sample performance of the proposed methods are satisfactory in a wide range of settings. Lastly, when applied to the public capital data, our proposed model can also better reflect the changing characteristics of the US economy compared to the parametric panel data models.

1. Introduction

Spatial econometrics is a branch of econometrics that mainly deals with the interactions of economic units in space, where the space can be in both physical and economic dimensions. Early work on spatial econometrics dates back to [1], when the spatial autoregressive model was first introduced, and since then, it has become an active area thanks to its simplicity in estimation and interpretation. For more details on the traditional spatial autoregressive model, one may refer to [2,3,4], and the references therein. On the other side, however, the parametric structure of the spatial autoregressive model is often subject to the risk of model mis-specification, resulting in modeling bias and even inconsistent estimates. To overcome this shortcoming, nonparametric and semiparametric spatial autoregressive models have also been introduced in the last decade. To name a few, Su and Jin [5] proposed a profile quasi-maximum likelihood estimation approach for a partially linear spatial autoregressive model; Su [6] considered a nonparametric spatial autoregressive model; Malikov and Sun [7] proposed a flexible semiparametric varying coefficient spatial autoregressive model; Sun [8] studied a spatial varying coefficient model with nonparametric spatial weights; and Du et al. [9] developed a partially linear additive spatial autoregressive model and studied the asymptotic properties of the proposed estimators.

Panel data track individual units over time, enabling the estimation of complex models and an extraction of information not possible with cross-sectional or time series data. This two-dimensional information also allows for more comprehensive analysis and inference of panel data ([10,11]). Specifically in spatial econometrics, panel data models are also popular since they take into account the spatial dependence and control of the unobservable heterogeneity. For instance, Lee and Yu ([12]) focused on a spatial autoregressive panel data model with individual fixed effects. Zhang and Shen [13] considered a partially linear spatial autoregressive panel data model with functional coefficients and random effects. Ai and Zhang [14] considered the estimation of a partially specified spatial panel data model with fixed effects. Li [15] proposed a quasi-maximum-likelihood estimation method for a dynamic spatial panel data model. Sun and Malikov [16] studied a varying coefficient spatial autoregressive panel data model with fixed effects.

In this paper, we are interested in the partially linear varying coefficient spatial panel data model with fixed effects, namely,

$$\begin{array}{c}\hfill y_{it}={\lambda }_0\sum _{j=1}^N{w}_{ij}{y}_{jt}+{\mathit{x}}_{it}^{\tau }{\beta }_0+{\mathit{z}}_{it}^{\tau }{\gamma }_0\left(u_{it}\right)+{\alpha }_i+{\epsilon }_{it},i=1,\dots ,N,t=1,\dots ,T,\end{array}$$

(1)

where $y_{it}$ is the response variable, and ${\mathit{x}}_{it}={(x_{it,1},\dots ,x_{it,p})}^{\tau }$, ${\mathit{z}}_{it}={(z_{it,1},\dots ,z_{it,q})}^{\tau }$, and $u_{it}\in [a,b]$ are the associated covariates. In addition, ${\beta }_0={({\beta }_{01},\dots ,{\beta }_{0p})}^{\tau }$ is a p-dimensional vector of unknown parameters, ${\gamma }_0(·)={({\gamma }_{01}(·),\dots ,{\gamma }_{0q}(·))}^{\tau }$ is a q-dimensional vector of unknown functions, and ${\epsilon }_{it}$ is a random error with zero mean and finite variance ${\sigma }^2$. The unobserved individual-specific effect ${\alpha }_i$ is time-invariant to account for the individual’s unobserved ability, which is also allowed to be correlated with covariates ${\mathit{x}}_{it}$, ${\mathit{z}}_{it}$, and $u_{it}$ with an unknown correlation structure; and $w_{ij}$ describes the spatial weight of observation j to i, which can be a decreasing function of the spatial distance between i and j. Lastly, we note that the scalar parameter ${\lambda }_0$ measures the strength of spatial dependence.

Model (1) is a unified and flexible model that includes a variety of existing models as special cases. If ${\gamma }_0\left(u\right)$ does not vary over u, it reduces to a vector of constants so that model (1) becomes the traditional spatial autoregressive panel data model [12]. If $q=1$ and $z_{it}=1$, the model reduces to the partially linear spatial autoregressive model studied by [14]. If ${\mathit{x}}_{it}=0$, the model is given as a varying coefficient spatial autoregressive model. If ${\lambda }_0=0$, model (1) becomes the partially linear varying coefficient panel data model considered in [17]. Moreover, if ${\lambda }_0=0$ and ${\mathit{x}}_{it}=0$, model (1) reduces to the classical varying coefficient panel data model with fixed effects. For further development of this model, one may refer to, for example, [18,19,20].

This paper considers the estimation and empirical likelihood inference for model (1). For panel data models with fixed effects, the individual effects are often viewed as the nuisance parameters. We first tackle the fixed effects issue by applying differencing techniques. We then, from the perspective of computational costs, use B-spline to approximate the nonparametric functions and propose a two-stage least squares estimation method to consistently estimate the unknown parameters. The consistency and asymptotic normality properties of the resulting estimators are established under some mild conditions. Moreover, to construct confidence regions of ${\beta }_0$ in model (1), we also propose an empirical log-likelihood ratio function for the regression parameter and show that it follows, asymptotically, a standard chi-square distribution.

The rest of the paper is organized as follows. Section 2 introduces the two-stage least squares estimation and the empirical likelihood inference for the model. Section 3 provides the regularity conditions and then derives the asymptotic properties of the estimators. Section 4 reports the simulation results for assessing the finite sample performance of the proposed methods. Section 5 demonstrates the usefulness of the proposed methods via a real data analysis. Finally, Section 6 concludes the paper with some future directions, and Section 7 presents the technical results.

2. Model Estimation

Throughout the paper, we assume that N is large and T is finite. We first deal with the fixed effects issue by applying the first difference:

$$\begin{array}{ccc}\hfill y_{it}-y_{i,t-1}& =& {\lambda }_0\sum _{j=1}^N{w}_{ij}(y_{jt}-y_{j,t-1})+({\mathit{x}}_{it}^{\tau }-{\mathit{x}}_{i,t-1}^{\tau }){\beta }_0\hfill \\ \hfill & & +{\mathit{z}}_{it}^{\tau }{\gamma }_0\left(u_{it}\right)-{\mathit{z}}_{i,t-1}^{\tau }{\gamma }_0\left(u_{i,t-1}\right)+{\epsilon }_{it}-{\epsilon }_{i,t-1}.\hfill \end{array}$$

(2)

For the additive structure in ${\mathit{z}}_{it}^{\tau }{\gamma }_0\left(u_{it}\right)-{\mathit{z}}_{i,t-1}^{\tau }{\gamma }_0\left(u_{i,t-1}\right)$, we further assume $E\left({\gamma }_0\left(u_{it}\right)\right)=0$ for the model identification. Let also $∆y_{it}=y_{it}-y_{i,t-1}$, $∆{\mathit{x}}_{it}={\mathit{x}}_{it}-{\mathit{x}}_{i,t-1},$$\zeta ={(1,-1)}^{\tau }$, ${\tilde{\mathit{z}}}_{it}=diag\{{\mathit{z}}_{it},{\mathit{z}}_{i,t-1}\}$, ${\tilde{\gamma }}_0\left(u_{it}\right)={({\gamma }_0{\left(u_{it}\right)}^{\tau },{\gamma }_0{\left(u_{i,t-1}\right)}^{\tau })}^{\tau }$, and $∆{\epsilon }_{it}={\epsilon }_{it}-{\epsilon }_{i,t-1}$. Model (2) can then be written as

$$\begin{array}{ccc}\hfill ∆y_{it}& =& {\lambda }_0\sum _{j=1}^N{w}_{ij}∆y_{jt}+∆{\mathit{x}}_{it}^{\tau }{\beta }_0+{\zeta }^{\tau }{\tilde{\mathit{z}}}_{it}^{\tau }{\tilde{\gamma }}_0\left(u_{it}\right)+∆{\epsilon }_{it}.\hfill \end{array}$$

(3)

Next, we apply the centralized B-spline method to approximate ${\gamma }_0\left(u\right)$. Specifically, let $p^K\left(u\right)={(p_1^{K_1}{\left(u\right)}^{\tau },\dots ,p_q^{K_q}{\left(u\right)}^{\tau })}^{\tau }$ denote a sequence of known basis functions, where $p_l^{K_l}\left(u\right)={(p_{l1}^{K_l}\left(u\right),\dots ,p_{l{K}_l}^{K_l}\left(u\right))}^{\tau }$. For each $l=1,\dots ,q$, there exists some constant ${\theta }_{0l}$ such that ${\gamma }_{0l}\left(u\right)={\left(p_l^{K_l}\left(u\right)\right)}^{\tau }{\theta }_{0l}+{\vartheta }_{0l}\left(u\right)$ with ${\vartheta }_{0l}\left(u\right)$ as the approximation error. For ease of notation, we also define ${\vartheta }_0\left(u\right)={({\vartheta }_{01}\left(u\right),\dots ,{\vartheta }_{0q}\left(u\right))}^{\tau }$ and

$$p\left(u\right)=\left(\begin{array}{ccccccccc}{p}_{11}^{K_1}\left(u\right)& \cdots & p_{1K_1}^{K_1}\left(u\right)& 0& \cdots & 0& 0& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& \cdots & 0& 0& \cdots & 0& p_{q1}^{K_q}\left(u\right)& \cdots & p_{q{K}_q}^{K_q}\left(u\right)\end{array}\right),$$

yielding that

$${\gamma }_0\left(u\right)=p\left(u\right){\theta }_0+{\vartheta }_0\left(u\right),$$

where ${\theta }_0={({\theta }_{01}^{\tau },\dots ,{\theta }_{0q}^{\tau })}^{\tau }$. With the above notations, model (3) can then be expressed as

$$\begin{array}{ccc}\hfill ∆y_{it}& =& {\lambda }_0\sum _{j=1}^N{w}_{ij}∆y_{jt}+∆{\mathit{x}}_{it}^{\tau }{\beta }_0+{\zeta }^{\tau }{\tilde{\mathit{z}}}_{it}^{\tau }\{p_0\left(u_{it}\right){\theta }_0+{({\vartheta }_0{\left(u_{it}\right)}^{\tau },{\vartheta }_0{\left(u_{i,t-1}\right)}^{\tau })}^{\tau }\}+∆{\epsilon }_{it}\hfill \\ \hfill & =& {\lambda }_0\sum _{j=1}^N{w}_{ij}∆y_{jt}+∆{\mathit{x}}_{it}^{\tau }{\beta }_0+q_{it}^{\tau }{\theta }_0+v_{0it}+∆{\epsilon }_{it},\hfill \end{array}$$

(4)

where $p_0\left(u_{it}\right)={(p{\left(u_{it}\right)}^{\tau },p{\left(u_{i,t-1}\right)}^{\tau })}^{\tau }$ is a $2q\times {\sum }_{l=1}^q{K}_l$ matrix, $q_{it}={\left({\zeta }^{\tau }{\tilde{\mathit{z}}}_{it}^{\tau }{p}_0\left(u_{it}\right)\right)}^{\tau }$ is a $\left({\sum }_{l=1}^q{K}_l\right)$-dimensional vector, and $v_{0it}={\zeta }^{\tau }{\tilde{\mathit{z}}}_{it}^{\tau }{({\vartheta }_0{\left(u_{it}\right)}^{\tau },{\vartheta }_0{\left(u_{i,t-1}\right)}^{\tau })}^{\tau }$.

For the sake of descriptive convenience, we denote $∆Y_i={(∆y_{i2},∆y_{i3},\dots ,∆y_{iT})}^{\tau }$ and $∆Y={(∆Y_1^{\tau },∆Y_2^{\tau },\dots ,∆Y_N^{\tau })}^{\tau }$; analogously, $∆X_i$, $∆X$, $Q_i$, $Q,$$V_{0i}$, $V_0$, $∆{\epsilon }_i$ and $∆\epsilon$ can be defined as well. Also let $w_i=(w_{i1},w_{i2},\dots ,w_{iN})$, $W_i=w_i\otimes I_{T-1}$, and $W={(W_1^{\tau },W_2^{\tau },\dots ,W_N^{\tau })}^{\tau }$. We can hence rewrite model (4) as

$$∆Y_i={\lambda }_0{W}_i∆Y+∆X_i{\beta }_0+Q_i{\theta }_0+V_{0i}+∆{\epsilon }_i$$

and

$$\begin{array}{ccc}\hfill ∆Y& =& {\lambda }_{0}W∆Y+∆X{\beta }_0+Q{\theta }_0+V_0+∆\epsilon \hfill \\ \hfill & =& D{\delta }_0+Q{\theta }_0+V_0+∆\epsilon ,\hfill \end{array}$$

(5)

where $D=(W∆Y,∆X)$ and ${\delta }_0={({\lambda }_0,{\beta }_0^{\tau })}^{\tau }.$

Let $S=Q{\left(Q^{\tau }Q\right)}^{-1}{Q}^{\tau }$ denote the projection matrix onto the space spanned by Q. Partialling out the B-spline approximation, we obtain

$$(I-S)∆Y=(I-S)D{\delta }_0+(I-S)V_0+(I-S)∆\epsilon .$$

(6)

To further tackle the endogeneity issue, we apply the two-stage least squares (2SLS) procedure proposed by [21] and obtain the 2SLS estimator of ${\delta }_0$ with

$${\widehat{\delta }}_0={\left\{D^{\tau }(I-S)M(I-S)D\right\}}^{-1}{D}^{\tau }(I-S)M(I-S)∆Y,$$

(7)

where $M=H{\left(H^{\tau }H\right)}^{-1}{H}^{\tau }$ and H is a matrix of instrumental variables. This leads to an estimator of ${\theta }_0$ as

$${\widehat{\theta }}_0={\left(Q^{\tau }Q\right)}^{-1}{Q}^{\tau }(∆Y-D{\widehat{\delta }}_0),$$

and, accordingly, we can also apply ${\widehat{\gamma }}_{0l}\left(u\right)={\left(p_l^{K_l}\left(u\right)\right)}^{\tau }{\widehat{\theta }}_{0l}$ as the 2SLS estimator of ${\gamma }_{0l}\left(u\right)$, $l=1,\dots ,q.$

For the instrumental matrix H, we construct it in a similar way to [13]. Specifically, in the first step, we select the instrumental variables

$$\tilde{H}=(W{(I-\tilde{\lambda }W)}^{-1}(Q\tilde{\theta },∆X),∆X),$$

where $\tilde{\theta }={\left(Q^{\tau }Q\right)}^{-1}{Q}^{\tau }(∆Y-D\tilde{\delta })$ and $\tilde{\delta }={(\tilde{\lambda },{\tilde{\beta }}^{\tau })}^{\tau }={\left\{D^{\tau }(I-S)D\right\}}^{-1}{D}^{\tau }(I-S)∆Y$. In the second step, we use the instrumental variable $\tilde{H}$ to obtain the initial consistent estimators $\overline{\delta }$ and $\overline{\theta }$, and then use them to construct the instrumental variables

$$H=(W{(I-\overline{\lambda }W)}^{-1}(Q\overline{\theta }+∆X\overline{\beta }),∆X).$$

Finally, we use the instrumental variable H to obtain the final estimators ${\widehat{\delta }}_0$ and ${\widehat{\theta }}_0$.

In what follows, we apply the empirical likelihood method to construct the confidence regions of ${\beta }_0$ and ${\lambda }_0$ in model (1). The empirical likelihood method was first introduced by [22], and has now been applied to various regression models ([23,24]). Compared with the two-stage least squares method, an advantage of the empirical likelihood method is that it uses only the data to determine the shape and orientation of confidence regions of ${\beta }_0$ and ${\lambda }_0$. Another advantage is that the empirical likelihood method can construct confidence regions without estimating the asymptotic covariance, which can be rather complicated for the partially linear varying coefficient spatial autoregressive panel data model with fixed effects.

Specifically for model (6), let $∆\tilde{Y}=(I-S)∆Y={(∆{\tilde{Y}}_1^{\tau },\dots ,∆{\tilde{Y}}_N^{\tau })}^{\tau }$ and $\tilde{D}=(I-S)D={({\tilde{D}}_1^{\tau },\dots ,{\tilde{D}}_N^{\tau })}^{\tau }$. If the covariate D is exogenous, then the estimating equation for the parametric components ${\delta }_0$ can be defined as

$$\sum _{i=1}^N{\tilde{D}}_i^{\tau }(∆{\tilde{Y}}_i-{\tilde{D}}_i{\delta }_0)=0.$$

(8)

In practice, however, D is often an endogenous covariate. In this case, the estimating equation defined by (8) cannot obtain a consistent estimator of ${\delta }_0$. To overcome this problem, we propose an adjustment for (8) based on the instrumental variable H, where the key idea is to obtain a linear projection of $\tilde{D}$. From the model $\tilde{D}=H\xi +e,$ the estimator of $\xi$ is known as

$$\widehat{\xi }={\left(H^{\tau }H\right)}^{-1}{H}^{\tau }\tilde{D}.$$

Also letting $\widehat{D}=H\widehat{\xi }={({\widehat{D}}_1^{\tau },\dots ,{\widehat{D}}_N^{\tau })}^{\tau }$, then our adjustment for (8) is given by

$$\sum _{i=1}^N{\widehat{D}}_i^{\tau }(∆{\tilde{Y}}_i-{\tilde{D}}_i{\delta }_0)=0.$$

To define the empirical likelihood ratio, we first treat ${\eta }_i\left({\delta }_0\right)={\widehat{D}}_i^{\tau }(∆{\tilde{Y}}_i-{\tilde{D}}_i{\delta }_0)$ as the auxiliary random vector. Then, by [22], an empirical log-likelihood ratio function for ${\delta }_0$ can be defined as

$$L\left({\delta }_0\right)=-2max\left\{\sum _{i=1}^{N}log\left(N{p}_i\right)|p_i\ge 0,\sum _{i=1}^N{p}_i=1,\sum _{i=1}^N{p}_i{\eta }_i\left({\delta }_0\right)=0\right\},$$

where $p_i$, $i=1,\dots ,N$, are non-negative real numbers. Finally, through the Lagrange multiplier method, we can show that

$$L\left({\delta }_0\right)=2\sum _{i=1}^{N}log[1+{\varphi }^{\tau }{\eta }_i\left({\delta }_0\right)],$$

(9)

where $\varphi$ is a $(p+1)$-dimensional vector that satisfies the equation of

$$\sum _{i=1}^N\frac{{\eta }_i\left({\delta }_0\right)}{1+{\varphi }^{\tau }{\eta }_i\left({\delta }_0\right)}=0.$$

(10)

3. Asymptotic Properties

Let $G_{0it}=z_{it}^{\tau }{\gamma }_0\left(u_{it}\right)$, $∆G_{0it}=G_{0it}-G_{0i,t-1}$, $∆G_{0i}={(∆G_{0i2},∆G_{0i3},\dots ,∆G_{0iT})}^{\tau }$, and $∆G_0={(∆G_{01}^{\tau },∆G_{02}^{\tau },\dots ,∆G_{0N}^{\tau })}^{\tau }$. Define $X_i={(x_{i1},x_{i2},\dots ,x_{iT})}^{\tau }$, and define $Z_i$, $u_i$, and ${\epsilon }_i$ analogously. To derive the asymptotic properties of the proposed estimators, we need the following regularity conditions.

(C1)

$\{(X_i,Z_i,u_i,{\epsilon }_i),i=1,\dots ,N\}$ are independent and identically distributed, and for all $(i,t)$, $E\left[{\epsilon }_{it}\right|X_i,Z_i,u_i,H_i,W]=0,$$E\left({\epsilon }_{it}^2\right|X_i,Z_i,u_i,H_i,W)={\sigma }^2>0$. Moreover, there exists a positive constant $ϵ$ such that $E\left(\right|{\epsilon }_{it}{|}^{2+ϵ})<\infty$, $\underset{i,t}{sup}E\left({\parallel z_{it}\parallel }^{2+ϵ}\right)<\infty$, and $\underset{i,t}{sup}E\left({\parallel x_{it}\parallel }^{2+ϵ}\right)<\infty .$

(C2)

The matrix $I-{\lambda }_{0}W$ is nonsingular with $|{\lambda }_0|<1$, and the row and column sums of the matrices W and ${(I-{\lambda }_{0}W)}^{-1}$ are bounded uniformly in absolute value for any $|{\lambda }_0|<1$. Moreover, for the matrix $C_0=W{(I-{\lambda }_{0}W)}^{-1}$, there exists a constant ${\lambda }_c$ such that ${\lambda }_{c}I-C_0{C}_0^{\prime }$ is positive semidefinite.

(C3)

Let the internal knots of the spline be $s_j$, $j=1,\dots ,K_l$. Also, letting $d_j=s_j-s_{j-1}$ and $d=\underset{1\le j\le K_l}{max}{d}_j$, there exists a constant $M_0$ such that

$$\underset{1\le j\le K_l}{max}\mid d_j-d_{j-1}\mid =o\left(K_l^{-1}\right)\mathrm{and}\frac{d}{\underset{1\le j\le K_l}{min}{d}_j}\le M_0.$$

(C4)

${\gamma }_{0l}\left(u\right)\in C^m[a,b],l=1,\dots ,q,m\ge 2$, where $C^m[a,b]$ denotes the set of functions with the mth bounded continuous derivatives on the interval $[a,b]$.

(C5)

For the knot number $K_l$, it is assumed that $K_1\asymp \cdots \asymp K_q\asymp K$, and $K=O\left(N^{1/(2m+1)}\right)$, where $a_0\asymp b_0$ means that the ratio $a_0/b_0$ is bounded away from zero and infinity.

(C6)

${\mathrm{\Gamma }}^{\tau }\mathrm{\Gamma }/N$ converges in probability to a positive definite matrix $\mathrm{\Pi }$, where ${\mathrm{\Gamma }}^{\tau }=D^{\mathrm{*}\tau }(I-S)M$ and $D^{\mathrm{*}}=(W{(I-{\lambda }_{0}W)}^{-1}(∆X{\beta }_0+∆G_0),∆X)$.

(C7)

For the matrix $D^{\mathrm{*}},$ there exists a constant ${\lambda }_{c^{\mathrm{*}}}$ such that ${\lambda }_{c^{\mathrm{*}}}I-D^{\mathrm{*}}{D}^{\mathrm{*}\tau }$ is positive semidefinite.

(C8)

The density function of $u_{it}$, $f\left(u\right)$, is bounded away from zero and infinity on $[a,b]$. Furthermore, we assume that $f\left(u\right)$ is continuously differentiable on $(a,b)$.

(C9)

Denote $\overline{H}=(I-S)H={({\overline{H}}_1^{\tau },\dots ,{\overline{H}}_N^{\tau })}^{\tau }$ and ${\mathrm{\Sigma }}_i=E(∆{\epsilon }_i∆{\epsilon }_i^{\tau })$. We assume that $\mathrm{\Psi }={lim}_{N\to \infty }E\left(N^{-1}{\sum }_{i=1}^N{\xi }^{\tau }{\overline{H}}_i^{\tau }{\mathrm{\Sigma }}_i{\overline{H}}_i\xi \right)$ is a nonsingular constant matrix.

Condition (C1) or its variant is commonly assumed in the spatial panel data models. It requires the explanatory variables $(x_{it},z_{it},u_{it})$, the instrumental variables H, and the spatial weighting matrix W to be exogenous. Condition (C2) imposes restrictions on the spatial weighting matrix. These restrictions are required in the setting of a spatial autoregressive model ([3,4]). Condition (C3) is a standard condition on the polynomial spline function method ([25]). Condition (C4) ensures that the functions ${\gamma }_{0l}\left(u\right)$ are sufficiently smooth. Condition (C5) is required to achieve the optimal convergence rate of ${\gamma }_{0l}\left(u\right)$. Condition (C6) is required to establish the asymptotic results. Condition (C7) is required to ensure the identifiability of parameters. Condition (C8) is commonly used in the nonparametric literature. And lastly, Condition (C9) is also routinely used in the empirical likelihood inference ([23,26]).

Let $\stackrel{D}{⟶}$ represent the convergence in distribution. The following two theorems derive the asymptotic distribution and the convergence rate of the 2SLS estimators ${\widehat{\delta }}_0$ and $\widehat{\gamma }\left(u\right)$, respectively.

Theorem 1. 

Under conditions (C1)–(C8), we have

$$\sqrt{N}({\widehat{\delta }}_0-{\delta }_0)\stackrel{D}{⟶}\mathcal{N}(0,\mathrm{\Omega }),$$

where $\mathrm{\Omega }={\left({\mathrm{\Gamma }}^{\tau }\mathrm{\Gamma }\right)}^{-1}{\mathrm{\Gamma }}^{\tau }(I-S)\mathrm{\Sigma }(I-S)\mathrm{\Gamma }{\left({\mathrm{\Gamma }}^{\tau }\mathrm{\Gamma }\right)}^{-1}$ and $\mathrm{\Sigma }=diag\{{\mathrm{\Sigma }}_1,\dots ,{\mathrm{\Sigma }}_N\}$.

Theorem 2. 

Under conditions (C1)–(C8), we have

$$\parallel \widehat{\gamma }\left(u\right)-{\gamma }_0{\left(u\right)\parallel }^2=O_p\left(N^{-2m/(2m+1)}\right).$$

Theorem 1 shows that the 2SLS estimator of the parametric component ${\widehat{\delta }}_0$ is $\sqrt{N}$-consistent. Theorem 2 indicates that the 2SLS estimator $\widehat{\gamma }\left(u\right)$ achieves the optimal convergence rate for nonparametric regression with independent and identically distributed data in [27]. In addition, the above two theorems allow us to construct the confidence region for ${\delta }_0$ provided a consistent estimator of the asymptotic covariance $\mathrm{\Omega }$ is obtained. Letting $∆{\widehat{\epsilon }}_i=∆Y_i-{\widehat{\lambda }}_0{W}_i∆Y-∆X_i{\widehat{\beta }}_0-Q_i{\widehat{\theta }}_0$, ${\widehat{\mathrm{\Sigma }}}_i=∆{\widehat{\epsilon }}_i∆{\widehat{\epsilon }}_i^{\tau }$, and $\widehat{\mathrm{\Sigma }}=\mathrm{diag}\{{\widehat{\mathrm{\Sigma }}}_1,\dots ,{\widehat{\mathrm{\Sigma }}}_N\}$, we then propose to estimate $\mathrm{\Omega }$ with

$$\widehat{\mathrm{\Omega }}={\left({\widehat{\mathrm{\Gamma }}}^{\tau }\widehat{\mathrm{\Gamma }}\right)}^{-1}{\widehat{\mathrm{\Gamma }}}^{\tau }(I-S)\widehat{\mathrm{\Sigma }}(I-S)\widehat{\mathrm{\Gamma }}{\left({\widehat{\mathrm{\Gamma }}}^{\tau }\widehat{\mathrm{\Gamma }}\right)}^{-1},$$

where ${\widehat{\mathrm{\Gamma }}}^{\tau }=D^{\tau }(I-S)M$.

Theorem 3. 

Under conditions(C1)– (C8), we have

$$N(\widehat{\mathrm{\Omega }}-\mathrm{\Omega })=o_p\left(1\right).$$

Theorem 3 shows that $\widehat{\mathrm{\Omega }}$ is given as a consistent estimator. Moreover, by Theorem 1 and Slutsky’s theorem, it can be shown that ${\widehat{\mathrm{\Omega }}}^{-1/2}\sqrt{N}({\widehat{\delta }}_0-{\delta }_0)\stackrel{D}{⟶}\mathcal{N}(0,I)$. Hence, the asymptotic $100(1-\alpha )\%$ confidence intervals for ${\delta }_{0k}$ can be constructed as

$${\widehat{\delta }}_{0k}\pm z_{1-\alpha /2}{N}^{-1/2}{\widehat{\mathrm{\Omega }}}_{kk}^{1/2},k=1,\dots ,p+1,$$

where $z_{1-\alpha /2}$ is the $1-\alpha /2$ quantile of the standard normal distribution, and ${\widehat{\mathrm{\Omega }}}_{kk}$ is the kth diagonal element of $\widehat{\mathrm{\Omega }}$.

Next, the following theorem establishes the asymptotic distribution of the empirical log-likelihood ratio function $L\left({\delta }_0\right)$ in (9).

Theorem 4. 

Under conditions (C1)–(C9), if ${\delta }_0$ is the true value of the parameter, then

$$L\left({\delta }_0\right)\stackrel{D}{⟶}{\chi }_{p+1}^2,$$

where ${\chi }_{p+1}^2$ is a standard chi-square distribution with $p+1$ degrees of freedom.

Theorem 4 can be used to construct the empirical likelihood confidence regions for ${\delta }_0$. For any $0<\alpha <1$, an approximate $1-\alpha$ confidence region for ${\delta }_0$ is given by

$$C_{\alpha }\left({\delta }_0\right)=\left\{{\delta }_0\right|L\left({\delta }_0\right)\le {\chi }_{p+1}^2(1-\alpha )\},$$

where ${\chi }_{p+1}^2(1-\alpha )$ is the $1-\alpha$ quantile of the standard chi-square distribution with $p+1$ degrees of freedom.

4. Simulation Study

In this section, we investigate the finite sample performance of the proposed estimation and inference methods with a simulation study. The data are generated from the model

$$y_{it}={\lambda }_0\sum _{j=1}^N{w}_{ij}{y}_{jt}+x_{it,1}{\beta }_1+x_{it,2}{\beta }_2+z_{it}{\gamma }_0\left(u_{it}\right)+{\alpha }_i+{\epsilon }_{it},i=1,\dots ,N,t=1,\dots ,T,$$

where $x_{it,1}\sim \mathcal{N}(0,2.25)$, $x_{it,2}\sim \mathcal{N}(0,1),$$z_{it}\sim \mathcal{N}(0,1.69)$, $u_{it}\sim \mathrm{Uniform}(0,1)$, ${\epsilon }_{it}\sim \mathcal{N}(0,1)$, ${\beta }_1=5$, ${\beta }_2=2$, ${\gamma }_0\left(u_{it}\right)=0.5sin\left(2\pi u_{it}\right)$, ${\alpha }_i={\overline{x}}_{i,1}+{ϵ}_i$ with ${\overline{x}}_{i,1}=T^{-1}{\sum }_{t=1}^T{x}_{it,1}$ and ${ϵ}_i\sim N(0,1)$, and ${\alpha }_1=-{\sum }_{i=2}^N{\alpha }_i.$

Throughout the simulation, we use the centered cubic B-splines as the basis functions. The smoothing parameter K is selected using the generalized cross-validation (GCV) criterion. Similar to [28], we focus on the spatial scenario with a total of R districts, where in each district, there are l members with each neighbor of a member giving equal weight such that $W_0=\left(w_{ij}\right)=I_R\otimes \left(\frac{e_l{e}_l^{\tau }-I_l}{l-1}\right)$, where $e_l$ is an l-dimensional column vector with all elements being 1 and ⊗ is the Kronecker product. In our simulation, the sample sizes are set to be $T=4$ and 6, $N=R\times l$ where $R=30$ and 50, $l=4$ and 8. For comparison, three different values, ${\lambda }_0=0.2$, 0.5, and 0.8, are also considered, where ${\lambda }_0=0.2$ represents weak spatial dependence, ${\lambda }_0=0.5$ represents mild spatial dependence, and ${\lambda }_0=0.8$ represents strong spatial dependence.

We assess the performance of the two-stage least squares estimation by checking the average bias (Bias) and the sample standard deviation (SD) of the parametric components, and assess the varying coefficient function ${\gamma }_0(·)$ by checking the square root of the average squared error (RASE), which is defined as

$$\mathrm{RASE}={\left\{\frac{1}{N_0}\sum _{j=1}^{N_0}{[{\widehat{\gamma }}_0\left(u_j\right)-{\gamma }_0\left(u_j\right)]}^2\right\}}^{1/2},$$

where $\{u_j,j=1,\dots ,N_0\}$ are the regular grid points at which the function ${\widehat{\gamma }}_0\left(u\right)$ is evaluated. In our simulation, $N_0=100$ is used. We carry out 1000 simulations for each setting and then summarize the results in

Table 1. The finite sample performance of the two-stage least squares estimators.

			${\widehat{\mathit{\lambda }}}_0$		${\widehat{\mathit{\beta }}}_1$		${\widehat{\mathit{\beta }}}_2$		${\widehat{\mathit{\gamma }}}_0\left(\mathit{u}\right)$
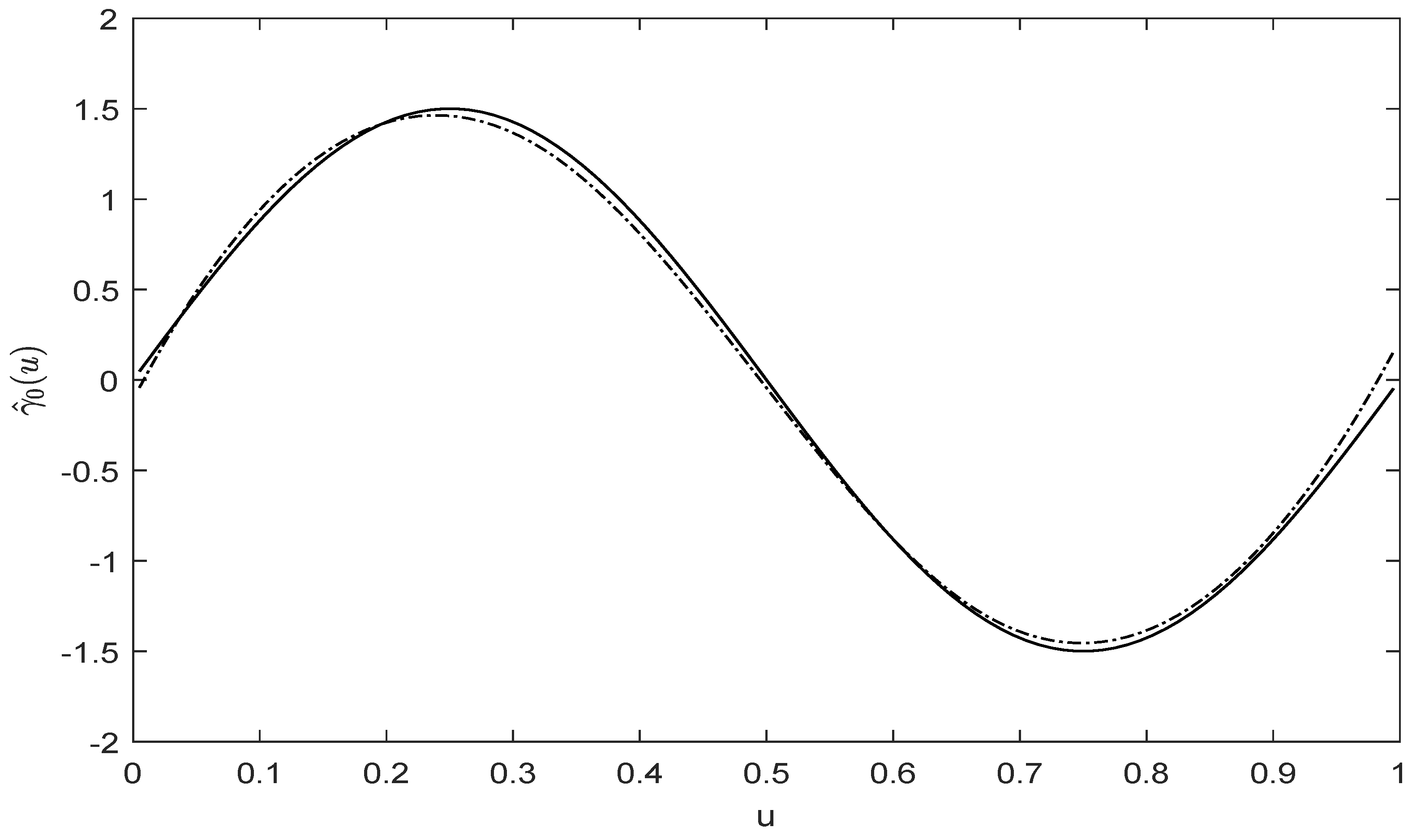
${\mathit{\lambda }}_0$	$(\mathit{R},\mathit{l})$	T	Bias	SD	Bias	SD	Bias	SD	RASE
0.2	$(30,4)$	4	0.0003	0.0077	0.0010	0.0211	−0.0023	0.0264	0.0861
		6	0.0004	0.0067	0.0015	0.0132	0.0031	0.0189	0.0656
	$(30,8)$	4	−0.0001	0.0082	0.0011	0.0113	0.0033	0.0184	0.0615
		6	−0.0002	0.0062	−0.0012	0.0095	0.0034	0.0141	0.0465
	$(50,4)$	4	0.0005	0.0064	−0.0005	0.0132	0.0035	0.0092	0.0682
		6	−0.0001	0.0056	0.0035	0.0099	0.0019	0.0089	0.0523
	$(50,8)$	4	0.0002	0.0060	0.0007	0.0095	0.0022	0.0086	0.0485
		6	−0.0003	0.0047	0.0007	0.0082	−0.0010	0.0075	0.0372
0.5	$(30,4)$	4	−0.0013	0.0050	0.0020	0.0225	0.0004	0.0265	0.0824
		6	0.0002	0.0046	0.0013	0.0141	0.0030	0.0191	0.0656
	$(30,8)$	4	−0.0001	0.0053	0.0011	0.0113	0.0031	0.0181	0.0615
		6	−0.0001	0.0041	−0.0012	0.0096	0.0033	0.0145	0.0466
	$(50,4)$	4	0.0003	0.0044	−0.0008	0.0139	0.0024	0.0094	0.0688
		6	0.0001	0.0032	0.0045	0.0104	0.0002	0.0091	0.0522
	$(50,8)$	4	0.0001	0.0039	0.0007	0.0097	0.0020	0.0086	0.0481
		6	−0.0002	0.0031	0.0005	0.0082	0.0001	0.0079	0.0372
0.8	$(30,4)$	4	−0.0006	0.0022	0.0032	0.0241	0.0008	0.0266	0.0872
		6	0.0001	0.0020	0.0011	0.0145	0.0029	0.0194	0.0665
	$(30,8)$	4	0.0000	0.0021	0.0012	0.0113	0.0033	0.0181	0.0616
		6	0.0002	0.0017	−0.0012	0.0099	0.0013	0.0144	0.0465
	$(50,4)$	4	0.0001	0.0019	−0.0011	0.0151	0.0031	0.0098	0.0682
		6	0.0003	0.0014	0.0046	0.0112	0.0020	0.0094	0.0522
	$(50,8)$	4	0.0001	0.0016	0.0006	0.0103	0.0012	0.0088	0.0485
		6	−0.0001	0.0013	−0.0009	0.0089	0.0005	0.0081	0.0372

and Figure 1. Table 1 lists the average biases and standard deviations of the estimators of ${\lambda }_0$, ${\beta }_1$, and ${\beta }_2$, and the average RASEs of the estimator of ${\gamma }_0(·)$. Figure 1 presents the estimator of ${\gamma }_0(·)$ in a typical sample, which is selected in such a way that its RASE is equal to the median in the 1000 replications.

From Table 1 and Figure 1, we can make a few interesting observations: (i) All the estimators of parameters are close to the true value. (ii) The standard deviations of ${\widehat{\lambda }}_0$, ${\widehat{\beta }}_1$, and ${\widehat{\beta }}_2$ decrease as the sample size increases. (iii) The RASEs of ${\widehat{\gamma }}_0\left(u\right)$ are small for all cases and decrease as the sample size increases, and it can be concluded that the estimate curves fit well to the corresponding true curve, which also coincides with what was discovered from Figure 1. To conclude, the simulation results verify the validity and effectiveness of the proposed estimation procedure.

The second aim of this simulation study is to construct the confidence intervals for the parameters ${\lambda }_0$, ${\beta }_1$, and ${\beta }_2$, respectively. We consider two approaches for comparison, including the empirical likelihood (EL) approach and the normal approximation using the two-stage least squares estimator (2SLS). The average lengths of the confidence intervals and their corresponding empirical coverage probabilities, with a confidence level of $1-\alpha =95\%$, are computed with 1000 simulation runs. The simulation results are presented in

Table 2. The coverage probabilities and average lengths (in parentheses) of the $95\%$ confidence intervals for ${\delta }_0$ using different methods.

			${\widehat{\mathit{\lambda }}}_0$		${\widehat{\mathit{\beta }}}_1$		${\widehat{\mathit{\beta }}}_2$
${\mathit{\lambda }}_0$	$(\mathit{R},\mathit{l})$	T	EL	2SLS	EL	2SLS	EL	2SLS
0.2	(30, 4)	4	0.9320 (0.0219)	0.9240 (0.0264)	0.9310 (0.0727)	0.9270 (0.0753)	0.9350 (0.1185)	0.9280 (0.1296)
		6	0.9360 (0.0211)	0.9270 (0.0263)	0.9340 (0.0624)	0.9310 (0.0652)	0.9390 (0.0814)	0.9310 (0.0908)
	(30, 8)	4	0.9370 (0.0197)	0.9310 (0.0189)	0.9350 (0.0613)	0.9320 (0.0667)	0.9390 (0.0765)	0.9320 (0.0764)
		6	0.9410 (0.0158)	0.9340 (0.0171)	0.9420 (0.0508)	0.9360 (0.0516)	0.9410 (0.0546)	0.9380 (0.0529)
	(50, 4)	4	0.9390 (0.0206)	0.9320 (0.0217)	0.9360 (0.0677)	0.9320 (0.0717)	0.9380 (0.0783)	0.9320 (0.0822)
		6	0.9410 (0.0160)	0.9330 (0.0152)	0.9410 (0.0551)	0.9370 (0.0572)	0.9420 (0.0638)	0.9360 (0.0637)
	(50, 8)	4	0.9450 (0.0145)	0.9390 (0.0151)	0.9440 (0.0438)	0.9410 (0.0496)	0.9450 (0.0588)	0.9400 (0.0607)
		6	0.9480 (0.0139)	0.9440 (0.0148)	0.9520 (0.0332)	0.9450 (0.0375)	0.9510 (0.0579)	0.9450 (0.0594)
0.5	(30, 4)	4	0.9320 (0.0175)	0.9220 (0.0165)	0.9310 (0.0754)	0.9260 (0.0818)	0.9330 (0.1257)	0.9290 (0.1359)
		6	0.9350 (0.0111)	0.9260 (0.0139)	0.9330 (0.0642)	0.9320 (0.0710)	0.9380 (0.0899)	0.9330 (0.1084)
	(30, 8)	4	0.9350 (0.0129)	0.9290 (0.0137)	0.9360 (0.0643)	0.9330 (0.0695)	0.9390 (0.0856)	0.9320 (0.0976)
		6	0.9390 (0.0109)	0.9330 (0.0123)	0.9410 (0.0537)	0.9370 (0.0641)	0.9420 (0.0751)	0.9370 (0.0825)
	(50, 4)	4	0.9390 (0.0116)	0.9340 (0.0136)	0.9350 (0.0706)	0.9320 (0.0742)	0.9370 (0.0875)	0.9310 (0.0922)
		6	0.9420 (0.0096)	0.9370 (0.0105)	0.9410 (0.0551)	0.9360 (0.0612)	0.9420 (0.0779)	0.9350 (0.0793)
	(50, 8)	4	0.9440 (0.0101)	0.9410 (0.0120)	0.9450 (0.0509)	0.9410 (0.0528)	0.9440 (0.0636)	0.9410 (0.0737)
		6	0.9470 (0.0089)	0.9430 (0.0108)	0.9490 (0.0388)	0.9460 (0.0439)	0.9480 (0.0680)	0.9440 (0.0687)
0.8	(30, 4)	4	0.9270 (0.0097)	0.9210 (0.0095)	0.9330 (0.0928)	0.9290 (0.1087)	0.9320 (0.1286)	0.9310 (0.1421)
		6	0.9310 (0.0085)	0.9240 (0.0088)	0.9350 (0.0723)	0.9310 (0.0862)	0.9380 (0.1014)	0.9320 (0.1017)
	(30, 8)	4	0.9330 (0.0072)	0.9280 (0.0093)	0.9350 (0.0653)	0.9320 (0.0729)	0.9380 (0.0896)	0.9330 (0.0934)
		6	0.9360 (0.0066)	0.9310 (0.0078)	0.9390 (0.0508)	0.9360 (0.0571)	0.9410 (0.0813)	0.9360 (0.0869)
	(50, 4)	4	0.9350 (0.0066)	0.9310 (0.0086)	0.9340 (0.0716)	0.9320 (0.0838)	0.9360 (0.0908)	0.9330 (0.0992)
		6	0.9390 (0.0053)	0.9350 (0.0067)	0.9390 (0.0551)	0.9370 (0.0657)	0.9410 (0.0845)	0.9360 (0.0911)
	(50, 8)	4	0.9420 (0.0057)	0.9380 (0.0062)	0.9440 (0.0514)	0.9420 (0.0554)	0.9430 (0.0816)	0.9390 (0.0838)
		6	0.9450 (0.0043)	0.9410 (0.0059)	0.9470 (0.0388)	0.9470 (0.0513)	0.9470 (0.0774)	0.9420 (0.0825)

. It is evident that EL has shorter interval lengths and higher coverage probabilities. This implies that EL performs better than 2SLS in terms of coverage accuracy of the confidence intervals. Lastly, we note that most of the interval lengths decrease and the empirical coverage probabilities increase as the sample size increases.

5. A Real Data Example

In this section, we apply the proposed estimation methods for model (1) to investigate the productivity of public capital in private production based on data for 48 US states observed over 17 years (1970–1986). The public capital data had been considered in [11,29,30,31], and can be downloaded from http://www.mysmu.edu/faculty/zlyang/ (accessed on 1 March 2022). We also note that the previous works were all conducted within the parametric framework, assuming constant elasticities of the specified models across all the states and all the years. Nevertheless, due to changes in policies as well as the change in the economic environment, including the 1973 oil crisis and the 1979 energy crisis, the constant elasticity assumption can be questionable. In addition, the spatial spillover effects are also discussed in the literature. For example, Xu and Yang [32] employed spatial panel data models to capture the possible spatial spillover effects, and they further pointed out that a temporal heterogeneity pattern is observed in the parameter estimation. In view of this, we propose the following partially linear varying coefficient spatial autoregressive panel data model:

$$\begin{array}{ccc}\hfill log\left(y_{it}\right)& =& {\alpha }_i+{\lambda }_0\sum _{j=1}^N{w}_{ij}log\left(y_{jt}\right)+log\left(P{c}_{it}\right){\beta }_1+log\left(L_{it}\right){\beta }_2+Unem{p}_{it}{\beta }_3\hfill \\ \hfill & & +log\left(P{s}_{it}\right){\gamma }_0(t/T)+{\epsilon }_{it},i=1,\dots ,48,t=1,\dots ,17,\hfill \end{array}$$

(11)

where $y_{it}$ denotes the gross state product of state i in year t; ${\alpha }_i$ reflects the unobserved individual fixed effect; $P{c}_{it}$ denotes the public capital including highways and streets, water and sewer facilities, and other public buildings; $L_{it}$ denotes the labor input measured as employment in non-agricultural payrolls; $P{s}_{it}$ is the stock of private capital; and $Unem{p}_{it}$ is the state unemployment rate included to capture business cycle effects. The spatial weight matrix W is specified using a contiguity form, where the $(i,j)$th element is indicated as 1 if the states i and j share a common border, otherwise it is 0. Note that the final W is also row-normalized.

The fitted results are reported in

Table 3. The estimates of the parameters and their $95\%$ confidence intervals.

	Model (11)			Model (12)
	EST	${\mathbf{CI}}_{2\mathbf{SLS}}$	${\mathbf{CI}}_{\mathbf{EL}}$	EST	${\mathbf{CI}}_{2\mathbf{SLS}}$	${\mathbf{CI}}_{\mathbf{EL}}$
${\mathit{\lambda }}_0$	0.0908	[0.0036, 0.1780]	[0.0419, 0.1386]	0.0838	[0.0108, 0.1568]	[0.0346, 0.1318]
${\beta }_1$	−0.0122	[−0.1110, 0.0866]	[−0.1312, 0.1067]	—	—	—
${\beta }_2$	0.8633	[0.7773, 0.9493]	[0.8104, 0.9169]	0.8657	[0.7797, 0.9517]	[0.8122, 0.9197]
${\beta }_3$	−0.0039	[−0.0055,−0.0023]	[−0.0048,−0.0030]	−0.0040	[−0.0056,−0.0025]	[−0.0049,−0.0031]

including the estimates (EST) of the parameters and the $95\%$ confidence intervals (CI). The results in the left panel of Table 3 show that $P{c}_{it}$ does not have a significant effect on the states’ private economic growth. This conclusion is consistent with the finding in [30]. This leads to a reconstructed model as follows:

$$\begin{array}{ccc}\hfill log\left(y_{it}\right)& =& {\alpha }_i+{\lambda }_0\sum _{j=1}^N{w}_{ij}log\left(y_{jt}\right)+log\left(L_{it}\right){\beta }_2+Unem{p}_{it}{\beta }_3\hfill \\ \hfill & & +log\left(P{s}_{it}\right){\gamma }_0(t/T)+{\epsilon }_{it}.\hfill \end{array}$$

(12)

From the right panel of Table 3, we can see that the significance of the spatial coefficient estimate reflects the spatial dependence and confirms the existences of spillover effects between states. Moreover, $L_{it}$ affects the states’ private economic growth positively, and $Unem{p}_{it}$ affects the states’ private economic growth negatively. Further, the fitted varying coefficient function curve is presented in Figure 2. The estimated curve has two inflection points, which approximately correspond to the 1973 oil crisis and the 1979 energy crisis. Figure 2 indicates the fluctuating effects of $P{s}_{it}$ on the states’ private economic growth. In the mid-1970s, the effect of $P{s}_{it}$ on the states’ private economic growth was approximately unchanged, while in the early 1970s and also the mid-1980s, the negative effect of $P{s}_{it}$ on the states’ private economic growth increased rapidly. This demonstrates that the standard applications of parametric panel models may not be valid.

6. Conclusions and Discussion

In this paper, we studied the statistical inference for a partially linear varying coefficient spatial autoregressive panel data model with fixed effects. By means of the basis function approximations and instrumental variable methods, we proposed a two-stage least squares estimation procedure to estimate the unknown parametric and nonparametric components, and meanwhile derived the convergence rate and asymptotic distributions of the estimators under some regularity conditions. We further constructed an empirical log-likelihood ratio function to derive the empirical likelihood confidence regions for the parametric component, which is shown to have an asymptotically correct coverage probability. Simulation studies and real data analysis also demonstrated that the proposed method performs well in the finite sample settings.

Lastly, we note that there are some interesting directions for future research. First, extending the model to a case with spatial errors would be useful yet challenging work. Second, the present paper assumes the spatial matrix W to be predetermined and time-invariant. In practice, however, the spatial structure W may change along with T, especially when it is large. In addition, the spatial coefficient ${\lambda }_0$ may also change with time. These circumstances are outside the scope of the present paper and are left for future research.

7. Proof of the Main Results

To prove the theorems obtained in Section 3, we first present several lemmas. Note that the first three are essentially the same as Corollary 6.21 in [25], Lemma 4.5 in [33], and Lemma A.2 in [34], respectively. For convenience and simplicity, we also express C as a positive constant that may be different at each appearance throughout this section.

Lemma 1. 

Under conditions (C4) and (C5), there exists a constant $C>0$ such that

$$\underset{u\in [a,b]}{sup}|{\gamma }_{0l}\left(u\right)-{\left(p_l^{K_l}\left(u\right)\right)}^{\tau }{\theta }_{0l}|\le C{K}^{-m}.$$

Lemma 2. 

Under condition (C1), there exist two constants $0<c_1<c_2<\infty$ such that

$$(c_1+o_p\left(1\right))\frac{N}{K}\le {\lambda }_{min}^{Q^{\tau }Q}\le {\lambda }_{max}^{Q^{\tau }Q}\le (c_2+o_p\left(1\right))\frac{N}{K}.$$

Lemma 3. 

We denote ${\varsigma }_i,i=1,\dots ,N,$ as independent random variables satisfying $E\left({\varsigma }_i\right)=0$ and $E\left({\varsigma }_i^2\right)<C<\infty$. Then, we have

$$\underset{1\le k\le N}{max}\left|\sum _{i=1}^k{\varsigma }_i\right|=O_p(\sqrt{N}logN).$$

Lemma 4. 

Under conditions (C1)–(C9), if ${\delta }_0$ is the true value of the parameter, we have

$$\frac{1}{\sqrt{N}}\sum _{i=1}^N{\eta }_i\left({\delta }_0\right)\stackrel{D}{⟶}\mathcal{N}(0,\mathrm{\Psi }).$$

Proof. 

We have

$$\begin{array}{ccc}\hfill \frac{1}{\sqrt{N}}\sum _{i=1}^N{\eta }_i\left({\delta }_0\right)& =& \frac{1}{\sqrt{N}}{\widehat{D}}^{\tau }(∆\tilde{Y}-\tilde{D}{\delta }_0)=\frac{1}{\sqrt{N}}{\widehat{D}}^{\tau }(I-S)(∆Y-D{\delta }_0)\hfill \\ \hfill & =& \frac{1}{\sqrt{N}}{\widehat{D}}^{\tau }(I-S)V_0+\frac{1}{\sqrt{N}}{(\widehat{\xi }-\xi )}^{\tau }{H}^{\tau }(I-S)∆\epsilon \hfill \\ \hfill & & +\frac{1}{\sqrt{N}}{\xi }^{\tau }{H}^{\tau }(I-S)∆\epsilon .\hfill \end{array}$$

(13)

By Lemma 1, we have $\parallel V_{0i}\parallel =O\left(K^{-m}\right)$. Also, by [35], we have $\widehat{\xi }=\xi +O_p\left(N^{-1/2}\right).$ Letting $\tilde{\widehat{D}}=(I-S)\widehat{D}=({\tilde{\widehat{D}}}_1,\dots ,{\tilde{\widehat{D}}}_N)$, and invoking condition (C1) and Lemma 3, we can obtain

$$\frac{1}{\sqrt{N}}{\widehat{D}}^{\tau }(I-S)V_0=\frac{1}{\sqrt{N}}\sum _{i=1}^N{\tilde{\widehat{D}}}_i^{\tau }{V}_{0i}=O_p(\frac{1}{\sqrt{N}}·\sqrt{N}logN·K^{-m})=o_p\left(1\right)$$

(14)

and

$$\frac{1}{\sqrt{N}}{(\widehat{\xi }-\xi )}^{\tau }{H}^{\tau }(I-S)∆\epsilon =o_p\left(1\right).$$

(15)

Also let ${\omega }_i={\xi }^{\tau }{\tilde{H}}_i^{\tau }∆{\epsilon }_i$. It is easy to verify that $E\left({\omega }_i\right|H_i,Z_i)=0$ and $Cov\left({\omega }_i\right|H_i,Z_i)={\xi }^{\tau }{\tilde{H}}_i^{\tau }{\mathrm{\Sigma }}_i{\tilde{H}}_i\xi .$ Further, by invoking condition (C9) and by the law of large numbers, we can derive that

$$\frac{1}{N}\sum _{i=1}^N{\xi }^{\tau }{\tilde{H}}_i^{\tau }{\mathrm{\Sigma }}_i{\tilde{H}}_i\xi \stackrel{P}{⟶}\mathrm{\Psi }.$$

(16)

For any given vector $a\in R^{p+1}$ with $a^{\tau }a=1,$ invoking condition (C1), it is easy to show that $E\left(a^{\tau }{\omega }_i\right)=0$ and

$$\underset{i}{sup}E\parallel a^{\tau }{\omega }_i{\parallel }^{2+\delta }\le {\parallel a\parallel }^{2+\delta }\underset{i}{sup}E\parallel {\omega }_i{\parallel }^{2+\delta }\le C\underset{i}{sup}E{\parallel {\omega }_i\parallel }^{2+\delta }<\infty .$$

Hence, $a^{\tau }{\omega }_i$ satisfies the Lyapunov condition for the central limit theorem, yielding that

$$\frac{{\sum }_{i=1}^N{a}^{\tau }{\omega }_i}{{(a^{\tau }{\sum }_{i=1}^{N}Cov\left({\omega }_i\right)a)}^{1/2}}\stackrel{D}{⟶}\mathcal{N}(0,1).$$

(17)

Finally, by (13)–(17), we have

$$\frac{1}{\sqrt{N}}{\xi }^{\tau }{H}^{\tau }(I-S)∆\epsilon =\frac{1}{\sqrt{N}}\sum _{i=1}^N{\xi }^{\tau }{\tilde{H}}_i^{\tau }∆{\epsilon }_i=\frac{1}{\sqrt{N}}\sum _{i=1}^N{\omega }_i\stackrel{D}{⟶}\mathcal{N}(0,\mathrm{\Psi })$$

and

$$\frac{1}{\sqrt{N}}\sum _{i=1}^N{\eta }_i\left({\delta }_0\right)=\frac{1}{N}\sum _{i=1}^N{\omega }_i+o_p\left(1\right)\stackrel{D}{⟶}\mathcal{N}(0,\mathrm{\Psi }).$$

This proves the lemma. □

Lemma 5. 

Under conditions (C1)–(C9), if ${\delta }_0$ is the true value of the parameter, we have

$$\frac{1}{N}\sum _{i=1}^N{\eta }_i\left({\delta }_0\right){\eta }_i{\left({\delta }_0\right)}^{\tau }\stackrel{P}{⟶}\mathrm{\Psi }.$$

Proof. 

Following the same notation as in Lemma 4, we can derive that

$$\frac{1}{N}\sum _{i=1}^N{\eta }_i\left({\delta }_0\right){\eta }_i{\left({\delta }_0\right)}^{\tau }=\frac{1}{N}\sum _{i=1}^N{\omega }_i{\omega }_i^{\tau }+o_p\left(1\right).$$

Further, by a similar argument as that for (16), we have

$$\frac{1}{N}\sum _{i=1}^N{\omega }_i{\omega }_i^{\tau }\stackrel{P}{⟶}\mathrm{\Psi }.$$

This thus proves the lemma. □

Proof of Theorem 1. 

By (5), a simple calculation yields that

$$\begin{array}{ccc}\hfill {\widehat{\delta }}_0-{\delta }_0& =& {\left\{D^{\tau }(I-S)M(I-S)D\right\}}^{-1}{D}^{\tau }(I-S)M(I-S)(D{\delta }_0+Q{\theta }_0+V_0+∆\epsilon )-{\delta }_0\hfill \\ & =& {\left\{D^{\tau }(I-S)M(I-S)D\right\}}^{-1}{D}^{\tau }(I-S)M(I-S)V_0\hfill \\ & & +{\left\{D^{\tau }(I-S)M(I-S)D\right\}}^{-1}{D}^{\tau }(I-S)M(I-S)∆\epsilon .\hfill \end{array}$$

Note also that $D^{\mathrm{*}}=(C_0(∆X{\beta }_0+∆G_0),∆X)$ and

$$D=(W{(I-{\lambda }_{0}W)}^{-1}(∆X{\beta }_0+∆G_0+∆\epsilon ),∆X)=(C_0(∆X{\beta }_0+∆G_0+∆\epsilon ),∆X).$$

Thus, $D=D^{\mathrm{*}}+\mathrm{\Lambda }$, where $\mathrm{\Lambda }=(C_0∆\epsilon ,0)$. Furthermore, we have

$$\begin{array}{ccc}\hfill D^{\tau }(I-S)M(I-S)D& =& {D^{\mathrm{*}}}^{\tau }(I-S)M(I-S)D^{\mathrm{*}}+{\mathrm{\Lambda }}^{\tau }(I-S)M(I-S)\mathrm{\Lambda }\hfill \\ & & +{D^{\mathrm{*}}}^{\tau }(I-S)M(I-S)\mathrm{\Lambda }+{\mathrm{\Lambda }}^{\tau }(I-S)M(I-S)D^{\mathrm{*}}\hfill \\ & =:& R_{11}+R_{12}+R_{13}+R_{14}.\hfill \end{array}$$

It is easy to show that $E(∆\epsilon ∆{\epsilon }^{\tau })={\sigma }^2{I}_N\otimes A$, where $A=2I_{T-1}-J_{T-1}\left(0\right)-J_{T-1}{\left(0\right)}^{\tau }$ is a $(T-1)\times (T-1)$ matrix, and

$$J_{T-1}\left(0\right)={\left(\begin{array}{ccccc}0& 0& 0& \cdots & 0\\ 1& 0& 0& \cdots & 0\\ 0& 1& 0& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& \cdots & 1& 0\end{array}\right)}_{(T-1)\times (T-1)}.$$

Based on Gerschgorin’s disk theorem ([36]), if $\lambda$ is the eigenvalue of A, then $0\le \lambda \le 4$. Thus, there exists a constant ${\lambda }_{max},$ such that $E(∆\epsilon ∆{\epsilon }^{\tau })<{\lambda }_{max}I.$ Further, by condition (C2), we have

$$\begin{array}{ccc}& & E[∆{\epsilon }^{\tau }{C}_0^{\tau }(I-S)M(I-S)C_0∆\epsilon ]\hfill \\ & =& \mathrm{tr}\left\{E[{\left(H^{\tau }H\right)}^{-1/2}{H}^{\tau }(I-S)C_0∆\epsilon ∆{\epsilon }^{\tau }{C}_0^{\tau }(I-S)H{\left(H^{\tau }H\right)}^{-1/2}]\right\}\hfill \\ & \le & {\lambda }_{max}{\lambda }_c\mathrm{tr}\left\{E\left[{\left(H^{\tau }H\right)}^{-1/2}{H}^{\tau }(I-S)H{\left(H^{\tau }H\right)}^{-1/2}\right]\right\}\hfill \\ & \le & {\lambda }_{max}{\lambda }_c\mathrm{tr}\left\{E\left[{\left(H^{\tau }H\right)}^{-1/2}{H}^{\tau }H{\left(H^{\tau }H\right)}^{-1/2}\right]\right\}\hfill \\ & =& O\left(1\right).\hfill \end{array}$$

This shows that

$$∆{\epsilon }^{\tau }{C}_0^{\tau }(I-S)M(I-S)C_0∆\epsilon =O_p\left(1\right),$$

(18)

or, equivalently, $R_{12}=O_p\left(1\right).$ Invoking conditions (C2) and (C7), we have

$$\begin{array}{ccc}\hfill & & E\parallel D^{\mathrm{*}\tau }(I-S)M(I-S)C_0{∆\epsilon \parallel }^2\hfill \\ \hfill & =& \mathrm{tr}\left\{E[D^{\mathrm{*}\tau }(I-S)M(I-S)C_0∆\epsilon ∆{\epsilon }^{\tau }{C}_0^{\tau }(I-S)M(I-S)D^{\mathrm{*}}]\right\}\hfill \\ \hfill & \le & {\lambda }_{max}\mathrm{tr}\left\{E\left[D^{\mathrm{*}\tau }(I-S)M(I-S)C_0{C}_0^{\tau }(I-S)M(I-S)D^{\mathrm{*}}\right]\right\}\hfill \\ \hfill & \le & {\lambda }_{max}{\lambda }_c\mathrm{tr}\left\{E\left[D^{\mathrm{*}\tau }(I-S)M(I-S)M(I-S)D^{\mathrm{*}}\right]\right\}\hfill \\ \hfill & \le & {\lambda }_{max}{\lambda }_c\mathrm{tr}\left\{E\left[{\left(H^{\tau }H\right)}^{-1/2}{H}^{\tau }{D}^{\mathrm{*}}{D}^{\mathrm{*}\tau }H{\left(H^{\tau }H\right)}^{-1/2}\right]\right\}\hfill \\ \hfill & \le & {\lambda }_{max}{\lambda }_c{\lambda }_{c^{\mathrm{*}}}\mathrm{tr}\left\{E\left[{\left(H^{\tau }H\right)}^{-1/2}{H}^{\tau }H{\left(H^{\tau }H\right)}^{-1/2}\right]\right\}\hfill \\ \hfill & =& O\left(1\right).\hfill \end{array}$$

(19)

This implies that $R_{13}=O_p\left(1\right).$ Similarly, it can also be shown that $R_{14}=O_p\left(1\right)$. Taken together, we have

$$D^{\tau }(I-S)M(I-S)D=D^{\mathrm{*}\tau }(I-S)M(I-S)D^{\mathrm{*}}+O_p\left(1\right).$$

(20)

Next, for the term $D^{\tau }(I-S)M(I-S)∆\epsilon$, we note that

$$\begin{array}{ccc}\hfill D^{\tau }(I-S)M(I-S)∆\epsilon & =& D^{\mathrm{*}\tau }(I-S)M(I-S)∆\epsilon +{\mathrm{\Lambda }}^{\tau }(I-S)M(I-S)∆\epsilon \hfill \\ & =:& R_{21}+R_{22}.\hfill \end{array}$$

By a simple calculation, we have

$$\begin{array}{ccc}& & E[∆{\epsilon }^{\tau }(I-S)M(I-S)∆\epsilon ]\hfill \\ & =& \mathrm{tr}\left\{E[{\left(H^{\tau }H\right)}^{-1/2}{H}^{\tau }(I-S)∆\epsilon ∆{\epsilon }^{\tau }(I-S)H{\left(H^{\tau }H\right)}^{-1/2}]\right\}\hfill \\ & \le & {\lambda }_{max}\mathrm{tr}\left\{E\left[{\left(H^{\tau }H\right)}^{-1/2}{H}^{\tau }(I-S)H{\left(H^{\tau }H\right)}^{-1/2}\right]\right\}\hfill \\ & \le & {\lambda }_{max}\mathrm{tr}\left\{E\left[{\left(H^{\tau }H\right)}^{-1/2}{H}^{\tau }H{\left(H^{\tau }H\right)}^{-1/2}\right]\right\}\hfill \\ & =& O\left(1\right).\hfill \end{array}$$

Hence

$$∆{\epsilon }^{\tau }(I-S)M(I-S)∆\epsilon =O_p\left(1\right).$$

(21)

Applying the triangular inequality and invoking (18) and (21), we obtain

$$∆{\epsilon }^{\tau }{C}_0^{\tau }(I-S)M(I-S)∆\epsilon =O_p\left(1\right).$$

That is, $R_{22}=O_p\left(1\right).$ Thus, we have

$$D^{\tau }(I-S)M(I-S)∆\epsilon =D^{\mathrm{*}\tau }(I-S)M(I-S)∆\epsilon +O_p\left(1\right).$$

Lastly, for the term $D^{\tau }(I-S)M(I-S)V_0$, we can represent it as

$$\begin{array}{ccc}\hfill D^{\tau }(I-S)M(I-S)V_0& =& D^{\mathrm{*}\tau }(I-S)M(I-S)V_0+{\mathrm{\Lambda }}^{\tau }(I-S)M(I-S)V_0\hfill \\ & =:& R_{31}+R_{32}.\hfill \end{array}$$

Invoking condition (C7) and Lemma 1, we have

$$\begin{array}{ccc}\hfill E(\parallel R_{31}{\parallel }^2)& =& E\left[\mathrm{tr}\left(V_0^{\tau }(I-S)M(I-S)D^{\mathrm{*}}{D}^{\mathrm{*}\tau }(I-S)M(I-S)V_0\right)\right]\hfill \\ & \le & {\lambda }_{c^{\mathrm{*}}}E\left[\mathrm{tr}\left(V_0^{\tau }(I-S)M(I-S)M(I-S)V_0\right)\right]\hfill \\ & \le & {\lambda }_{c^{\mathrm{*}}}E\left[\mathrm{tr}\left(V_0^{\tau }(I-S)M(I-S)V_0\right)\right]\hfill \\ & \le & {\lambda }_{c^{\mathrm{*}}}E\left[\mathrm{tr}\left(V_0^{\tau }{V}_0\right)\right]\hfill \\ & =& O\left(N{K}^{-2m}\right).\hfill \end{array}$$

This shows that $R_{31}=O_p\left(\sqrt{N}{K}^{-m}\right).$ Similarly, we can have $R_{32}=O_p\left(\sqrt{N}{K}^{-m}\right)$. That is, $D^{\prime }(I-S)M(I-S)V_0=O_p\left(\sqrt{N}{K}^{-m}\right).$

Combining the above results, we can obtain that

$$\begin{array}{ccc}\hfill \sqrt{N}({\widehat{\delta }}_0-{\delta }_0)& =& {\left\{\frac{1}{N}{D}^{\mathrm{*}\tau }(I-S)M(I-S)D^{\mathrm{*}}+O_p\left(N^{-1}\right)\right\}}^{-1}\hfill \\ & & \times \frac{1}{\sqrt{N}}{D}^{\mathrm{*}\tau }(I-S)M(I-S)∆\epsilon +O_p\left(K^{-m}\right)+O_p\left(N^{-1/2}\right).\hfill \end{array}$$

Finally, invoking conditions (C1) and (C6), and using the central limit theorem and Slutsky’s theorem, we have

$$\begin{array}{c}\hfill \sqrt{N}({\widehat{\delta }}_0-{\delta }_0)\stackrel{D}{⟶}\mathcal{N}(0,\mathrm{\Omega }).\end{array}$$

This completes the proof of Theorem 1. □

Proof of Theorem 2. 

By a simple calculation, we have

$$\begin{array}{ccc}\hfill {\widehat{\theta }}_0& =& {\left(Q^{\tau }Q\right)}^{-1}{Q}^{\tau }(∆Y-D{\delta }_0)+{\left(Q^{\tau }Q\right)}^{-1}{Q}^{\tau }D({\delta }_0-\widehat{\delta })\hfill \\ & =& {\theta }_0+{\left(Q^{\tau }Q\right)}^{-1}{Q}^{\tau }∆\epsilon +{\left(Q^{\tau }Q\right)}^{-1}{Q}^{\tau }{V}_0+{\left(Q^{\tau }Q\right)}^{-1}{Q}^{\tau }D({\delta }_0-\widehat{\delta })\hfill \\ & =:& {\theta }_0+R_{41}+R_{42}+R_{43}.\hfill \end{array}$$

For $R_{41}$, by Lemma 2, we have

$$\begin{array}{ccc}\hfill E(\parallel R_{41}{\parallel }^2)& =& E(∆{\epsilon }^{\tau }Q{\left(Q^{\tau }Q\right)}^{-1}{\left(Q^{\tau }Q\right)}^{-1}{Q}^{\tau }∆\epsilon )\hfill \\ & =& O\left(N^{-1}K\right)E\left[\mathrm{tr}\{{\left(Q^{\tau }Q\right)}^{-1/2}{Q}^{\tau }∆\epsilon ∆{\epsilon }^{\tau }Q{\left(Q^{\tau }Q\right)}^{-1/2}\}\right]\hfill \\ & =& O\left(N^{-1}K\right)\mathrm{tr}\left\{E[{\left(Q^{\tau }Q\right)}^{-1/2}{Q}^{\tau }∆\epsilon ∆{\epsilon }^{\tau }Q{\left(Q^{\tau }Q\right)}^{-1/2}]\right\}\hfill \\ & =& O\left(1\right)O\left(N^{-1}K\right)\mathrm{tr}\left\{E\left[{\left(Q^{\tau }Q\right)}^{-1/2}{Q}^{\tau }Q{\left(Q^{\tau }Q\right)}^{-1/2}\right]\right\}\hfill \\ & =& O\left(N^{-1}K\right)E\left[\mathrm{tr}\left\{{\left(Q^{\tau }Q\right)}^{-1/2}{Q}^{\tau }Q{\left(Q^{\tau }Q\right)}^{-1/2}\right\}\right]\hfill \\ & =& O\left(N^{-1}{K}^2\right).\hfill \end{array}$$

This shows that $R_{41}=O_p\left(N^{-1/2}K\right)$. Similarly, by Lemmas 1 and 2, it is easy to show that $R_{42}=O_p\left(K^{-m+1/2}\right)$. Moreover, by Theorem 1 and Lemma 2,

$$\begin{array}{c}\hfill \parallel R_{43}{\parallel }^2={(\widehat{\delta }-{\delta }_0)}^{\tau }{D}^{\tau }Q{\left(Q^{\tau }Q\right)}^{-1}{\left(Q^{\tau }Q\right)}^{-1}{Q}^{\tau }D(\widehat{\delta }-{\delta }_0)=O_p\left(N^{-1}\right).\end{array}$$

or, equivalently, $R_{43}=O_p\left(N^{-1/2}\right)$. Taken together, we have

$$\parallel {\widehat{\theta }}_0-{\theta }_0{\parallel }^2=O_p(N^{-1}{K}^2+K^{-2m+1}+N^{-1})=O_p\left(N^{-1}{K}^2\right).$$

(22)

Furthermore, it is easy to show that

$$\begin{array}{ccc}\hfill \parallel \widehat{\gamma }\left(u\right)-{\gamma }_0{\left(u\right)\parallel }^2& =& \parallel p\left(u\right)({\widehat{\theta }}_0-{\theta }_0)+p\left(u\right){\theta }_0-{\gamma }_0\left(u\right){\parallel }^2\hfill \\ & \le & 2\parallel p\left(u\right)({\widehat{\theta }}_0-{\theta }_0){\parallel }^2+2{\parallel p\left(u\right){\theta }_0-{\gamma }_0\left(u\right)\parallel }^2\hfill \\ & =& 2{({\widehat{\theta }}_0-{\theta }_0)}^{\tau }p{\left(u\right)}^{\tau }p\left(u\right)({\widehat{\theta }}_0-{\theta }_0)+O_p\left(K^{-2m}\right)\hfill \\ & =& O_p\left(K^{-1}\right){({\widehat{\theta }}_0-{\theta }_0)}^{\tau }({\widehat{\theta }}_0-{\theta }_0)+O_p\left(K^{-2m}\right)\hfill \\ & =& O_p(N^{-1}K+K^{-2m})\hfill \\ & =& O_p\left(N^{-2m/(2m+1)}\right).\hfill \end{array}$$

This completes the proof of Theorem 2. □

Proof of Theorem 3. 

Note that

$$N\widehat{\mathrm{\Omega }}={\left(\frac{{\widehat{\mathrm{\Gamma }}}^{\tau }\widehat{\mathrm{\Gamma }}}{N}\right)}^{-1}\frac{{\widehat{\mathrm{\Gamma }}}^{\tau }(I-S)\widehat{\mathrm{\Sigma }}(I-S)\widehat{\mathrm{\Gamma }}}{N}{\left(\frac{{\widehat{\mathrm{\Gamma }}}^{\tau }\widehat{\mathrm{\Gamma }}}{N}\right)}^{-1},$$

$$N\mathrm{\Omega }={\left(\frac{{\mathrm{\Gamma }}^{\tau }\mathrm{\Gamma }}{N}\right)}^{-1}\frac{{\mathrm{\Gamma }}^{\tau }(I-S)\mathrm{\Sigma }(I-S)\mathrm{\Gamma }}{N}{\left(\frac{{\mathrm{\Gamma }}^{\tau }\mathrm{\Gamma }}{N}\right)}^{-1}.$$

Hence, to prove the theorem, we only need to show that

$$\frac{{\widehat{\mathrm{\Gamma }}}^{\tau }\widehat{\mathrm{\Gamma }}}{N}-\frac{{\mathrm{\Gamma }}^{\tau }\mathrm{\Gamma }}{N}=o_p\left(1\right),$$

(23)

$$\frac{{\widehat{\mathrm{\Gamma }}}^{\tau }(I-S)\widehat{\mathrm{\Sigma }}(I-S)\widehat{\mathrm{\Gamma }}}{N}-\frac{{\mathrm{\Gamma }}^{\tau }(I-S)\mathrm{\Sigma }(I-S)\mathrm{\Gamma }}{N}=o_p\left(1\right).$$

(24)

For (23), by $D=D^{\mathrm{*}}+\mathrm{\Lambda }$ and ${\widehat{\mathrm{\Gamma }}}^{\tau }-{\mathrm{\Gamma }}^{\tau }={\mathrm{\Lambda }}^{\tau }(I-S)M$, we have

$$\begin{array}{ccc}\hfill \frac{{\widehat{\mathrm{\Gamma }}}^{\tau }\widehat{\mathrm{\Gamma }}}{N}-\frac{{\mathrm{\Gamma }}^{\tau }\mathrm{\Gamma }}{N}& =& \frac{{(\widehat{\mathrm{\Gamma }}-\mathrm{\Gamma })}^{\tau }(\widehat{\mathrm{\Gamma }}-\mathrm{\Gamma })}{N}+\frac{{\mathrm{\Gamma }}^{\tau }(\widehat{\mathrm{\Gamma }}-\mathrm{\Gamma })}{N}+\frac{{(\widehat{\mathrm{\Gamma }}-\mathrm{\Gamma })}^{\tau }\mathrm{\Gamma }}{N}\hfill \\ & =& \frac{{\mathrm{\Lambda }}^{\tau }(I-S)M(I-S)\mathrm{\Lambda }}{N}+\frac{D^{\mathrm{*}\tau }(I-S)M(I-S)\mathrm{\Lambda }}{N}\hfill \\ & & +\frac{{\mathrm{\Lambda }}^{\tau }(I-S)M(I-S)D^{\mathrm{*}}}{N}\hfill \\ & =:& B_{21}+B_{22}+B_{23}.\hfill \end{array}$$

Futher, from the proof of Theorem 1, it is easy to verify that $B_{21}=O_p\left(N^{-1}\right)$, $B_{22}=O_p\left(N^{-1}\right)$, and $B_{23}=O_p\left(N^{-1}\right)$. Therefore,

$$\frac{{\widehat{\mathrm{\Gamma }}}^{\tau }\widehat{\mathrm{\Gamma }}}{N}-\frac{{\mathrm{\Gamma }}^{\tau }\mathrm{\Gamma }}{N}=O_p\left(N^{-1}\right)+O_p\left(N^{-1}\right)+O_p\left(N^{-1}\right)=o_p\left(1\right).$$

For (24), a simple calculation yields that

$$\begin{array}{ccc}& & \frac{{\widehat{\mathrm{\Gamma }}}^{\tau }(I-S)\widehat{\mathrm{\Sigma }}(I-S)\widehat{\mathrm{\Gamma }}}{N}-\frac{{\mathrm{\Gamma }}^{\tau }(I-S)\mathrm{\Sigma }(I-S)\mathrm{\Gamma }}{N}\hfill \\ & =& \frac{{\widehat{\mathrm{\Gamma }}}^{\tau }(I-S)(\widehat{\mathrm{\Sigma }}-\mathrm{\Sigma })(I-S)\widehat{\mathrm{\Gamma }}}{N}+\frac{{\widehat{\mathrm{\Gamma }}}^{\tau }(I-S)\mathrm{\Sigma }(I-S)\widehat{\mathrm{\Gamma }}}{N}-\frac{{\mathrm{\Gamma }}^{\tau }(I-S)\mathrm{\Sigma }(I-S)\mathrm{\Gamma }}{N}.\hfill \end{array}$$

Note also that

$$\begin{array}{c}\hfill ∆{\widehat{\epsilon }}_i∆{\widehat{\epsilon }}_i^{\tau }-∆{\epsilon }_i∆{\epsilon }_i^{\tau }=(∆{\widehat{\epsilon }}_i-∆{\epsilon }_i){(∆{\widehat{\epsilon }}_i-∆{\epsilon }_i)}^{\tau }+∆{\epsilon }_i{(∆{\widehat{\epsilon }}_i-∆{\epsilon }_i)}^{\tau }+(∆{\widehat{\epsilon }}_i-∆{\epsilon }_i)∆{\epsilon }_i^{\tau }\end{array}$$

and

$$\begin{array}{ccc}\hfill ∆{\widehat{\epsilon }}_i-∆{\epsilon }_i& =& ∆Y_i-D_i{\widehat{\delta }}_0-Q_i{\widehat{\theta }}_0-(∆Y_i-D_i{\delta }_0-Q_i{\theta }_0-V_{0i})\hfill \\ & =& D_i({\delta }_0-{\widehat{\delta }}_0)+Q_i({\theta }_0-{\widehat{\theta }}_0)+V_{0i}.\hfill \end{array}$$

Thus, invoking Lemma 1, Theorem 1, and (22), we have

$$\begin{array}{ccc}& & (∆{\widehat{\epsilon }}_i-∆{\epsilon }_i){(∆{\widehat{\epsilon }}_i-∆{\epsilon }_i)}^{\tau }\hfill \\ & \le & 4D_i({\delta }_0-\widehat{\delta }){({\delta }_0-\widehat{\delta })}^{\tau }{D}_i^{\tau }+4Q_i({\theta }_0-\widehat{\theta }){({\theta }_0-\widehat{\theta })}^{\tau }{Q}_i^{\tau }+4V_{0i}{V}_{0i}^{\tau }\hfill \\ & =& O_p\left(N^{-1}\right)+O_p\left(N^{-1}{K}^2\right)+O_p\left(K^{-2m}\right)=o_p\left(1\right)\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill ∆{\epsilon }_i{(∆{\widehat{\epsilon }}_i-∆{\epsilon }_i)}^{\tau }& =& ∆{\epsilon }_i{({\delta }_0-{\widehat{\delta }}_0)}^{\tau }{D}_i^{\tau }+∆{\epsilon }_i{({\theta }_0-{\widehat{\theta }}_0)}^{\tau }{Q}_i^{\tau }+∆{\epsilon }_i{V}_{0i}^{\tau }\hfill \\ & =& O_p\left(N^{-1/2}\right)+O_p\left(N^{-1/2}K\right)+O_p\left(K^{-m}\right)\hfill \\ & =& o_p\left(1\right).\hfill \end{array}$$

Hence, we obtain

$$∆{\widehat{\epsilon }}_i∆{\widehat{\epsilon }}_i^{\tau }-∆{\epsilon }_i∆{\epsilon }_i^{\tau }=o_p\left(1\right)\mathrm{and}\widehat{\mathrm{\Sigma }}-\mathrm{\Sigma }=o_p\left(1\right).$$

Using condition (C7), similar to the proof of (20), we can obtain that

$$\begin{array}{ccc}\hfill \parallel \frac{{\widehat{\mathrm{\Gamma }}}^{\tau }(I-S)(\widehat{\mathrm{\Sigma }}-\mathrm{\Sigma })(I-S)\widehat{\mathrm{\Gamma }}}{N}\parallel & =& \parallel \frac{D^{\tau }(I-S)M(I-S)(\widehat{\mathrm{\Sigma }}-\mathrm{\Sigma })(I-S)M(I-S)D}{N}\parallel \hfill \\ & =& o_p\left(1\right)\parallel \frac{D^{\tau }(I-S)M(I-S)M(I-S)D}{N}\parallel \hfill \\ & \le & o_p\left(1\right)\parallel \frac{D^{\tau }(I-S)M(I-S)D}{N}\parallel \hfill \\ & =& o_p\left(1\right).\hfill \end{array}$$

Moreover, similar to the proof of (19), it is easy to show that

$$\begin{array}{ccc}& & \frac{{\widehat{\mathrm{\Gamma }}}^{\tau }(I-S)\mathrm{\Sigma }(I-S)\widehat{\mathrm{\Gamma }}}{N}-\frac{{\mathrm{\Gamma }}^{\tau }(I-S)\mathrm{\Sigma }(I-S)\mathrm{\Gamma }}{N}\hfill \\ & =& \frac{{\widehat{\mathrm{\Gamma }}}^{\tau }(I-S)\mathrm{\Sigma }(I-S)(\widehat{\mathrm{\Gamma }}-\mathrm{\Gamma })}{N}-\frac{{(\widehat{\mathrm{\Gamma }}-\mathrm{\Gamma })}^{\tau }(I-S)\mathrm{\Sigma }(I-S)\mathrm{\Gamma }}{N}\hfill \\ & =& \frac{D^{\tau }(I-S)M(I-S)\mathrm{\Sigma }(I-S)M(I-S)\mathrm{\Lambda }}{N}\hfill \\ & & +\frac{{\mathrm{\Lambda }}^{\tau }(I-S)M(I-S)\mathrm{\Sigma }(I-S)M(I-S)D^{\mathrm{*}}}{N}\hfill \\ & =& O_p\left(N^{-1}\right)+O_p\left(N^{-1}\right)\hfill \\ & =& o_p\left(1\right).\hfill \end{array}$$

Taken together, (24) also holds. This completes the proof of Theorem 3. □

Proof of Theorem 4. 

Using a similar argument as in [22], we can obtain

$$\parallel \varphi \parallel =O_p\left(N^{-1/2}\right)$$

and

$$\underset{1\le i\le N}{max}\parallel {\eta }_i\left({\delta }_0\right)\parallel =o_p\left(N^{1/2}\right).$$

Further using the Taylor expansion to $L\left({\delta }_0\right)$, it yields that

$$L\left({\delta }_0\right)=2\sum _{i=1}^{N}log[1+{\varphi }^{\tau }{\eta }_i\left({\delta }_0\right)]=2\sum _{i=1}^N[{\varphi }^{\tau }{\eta }_i\left({\delta }_0\right)-\frac{1}{2}{\left({\varphi }^{\tau }{\eta }_i\left({\delta }_0\right)\right)}^2]+o_p\left(1\right).$$

(25)

In addition, from (10), we have

$$\begin{array}{ccc}\hfill 0& =& \frac{1}{N}\sum _{i=1}^N\frac{{\eta }_i\left({\delta }_0\right)}{1+{\varphi }^{\tau }{\eta }_i\left({\delta }_0\right)}\hfill \\ & =& \frac{1}{N}\sum _{i=1}^N{\eta }_i\left({\delta }_0\right)-\frac{1}{N}\sum _{i=1}^N{\eta }_i\left({\delta }_0\right){\eta }_i{\left({\delta }_0\right)}^{\tau }\varphi +\frac{1}{N}\sum _{i=1}^N\frac{{\eta }_i\left({\delta }_0\right){\left[{\varphi }^{\tau }{\eta }_i\left({\delta }_0\right)\right]}^2}{1+{\varphi }^{\tau }{\eta }_i\left({\delta }_0\right)}.\hfill \end{array}$$

(26)

Note also that

$$\begin{array}{ccc}\hfill \frac{1}{N}\sum _{i=1}^N\frac{\parallel {\eta }_i\left({\delta }_0\right){\parallel }^3{\parallel \varphi \parallel }^2}{|1+{\varphi }^{\tau }{\eta }_i\left({\delta }_0\right)|}& \le & {\parallel \varphi \parallel }^2\underset{1\le i\le N}{max}\parallel {\eta }_i\left({\delta }_0\right)\parallel \frac{1}{N}\sum _{i=1}^N{\parallel {\eta }_i\left({\delta }_0\right)\parallel }^2\hfill \\ & =& O_p\left(N^{-1}\right)o_p\left(N^{1/2}\right)O_p\left(1\right)\hfill \\ & =& o_p\left(N^{-1/2}\right).\hfill \end{array}$$

Then, from (26), it leads to

$$\varphi ={\left[\sum _{i=1}^N{\eta }_i\left({\delta }_0\right){\eta }_i{\left({\delta }_0\right)}^{\tau }\right]}^{-1}\sum _{i=1}^N{\eta }_i\left({\delta }_0\right)+o_p\left(N^{-1/2}\right).$$

(27)

Moreover, from (25) and (27), we have

$$L\left({\delta }_0\right)={\left[\frac{1}{\sqrt{N}}\sum _{i=1}^N{\eta }_i\left({\delta }_0\right)\right]}^{\tau }{\left[\frac{1}{N}\sum _{i=1}^N{\eta }_i\left({\delta }_0\right){\eta }_i{\left({\delta }_0\right)}^{\tau }\right]}^{-1}\left[\frac{1}{\sqrt{N}}\sum _{i=1}^N{\eta }_i\left({\delta }_0\right)\right]+o_p\left(1\right).$$

Finally, invoking Lemmas 4 and 5, the proof of Theorem 4 is complete. □