Hidden Dynamics of a New Jerk-like System with a Smooth Memristor and Applications in Image Encryption
Abstract
:1. Introduction
2. System Description
3. Dynamics Analysis of the New Jerk-like System with a Smooth Memristor
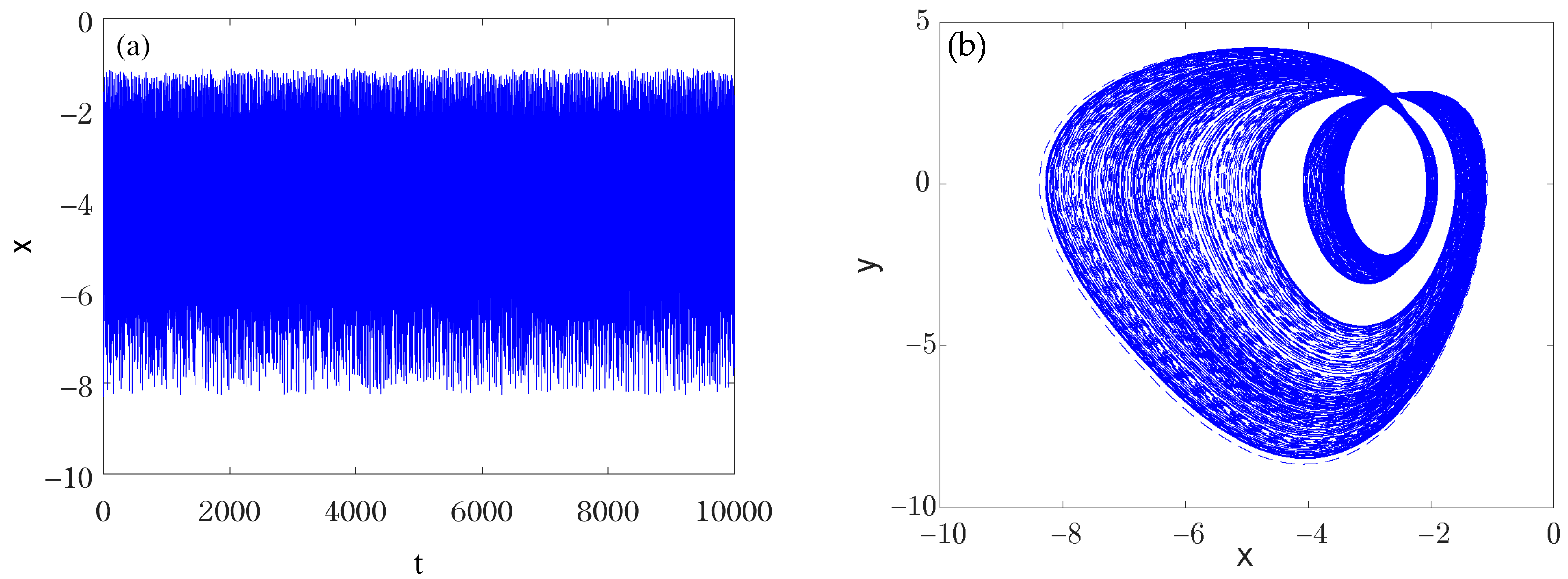
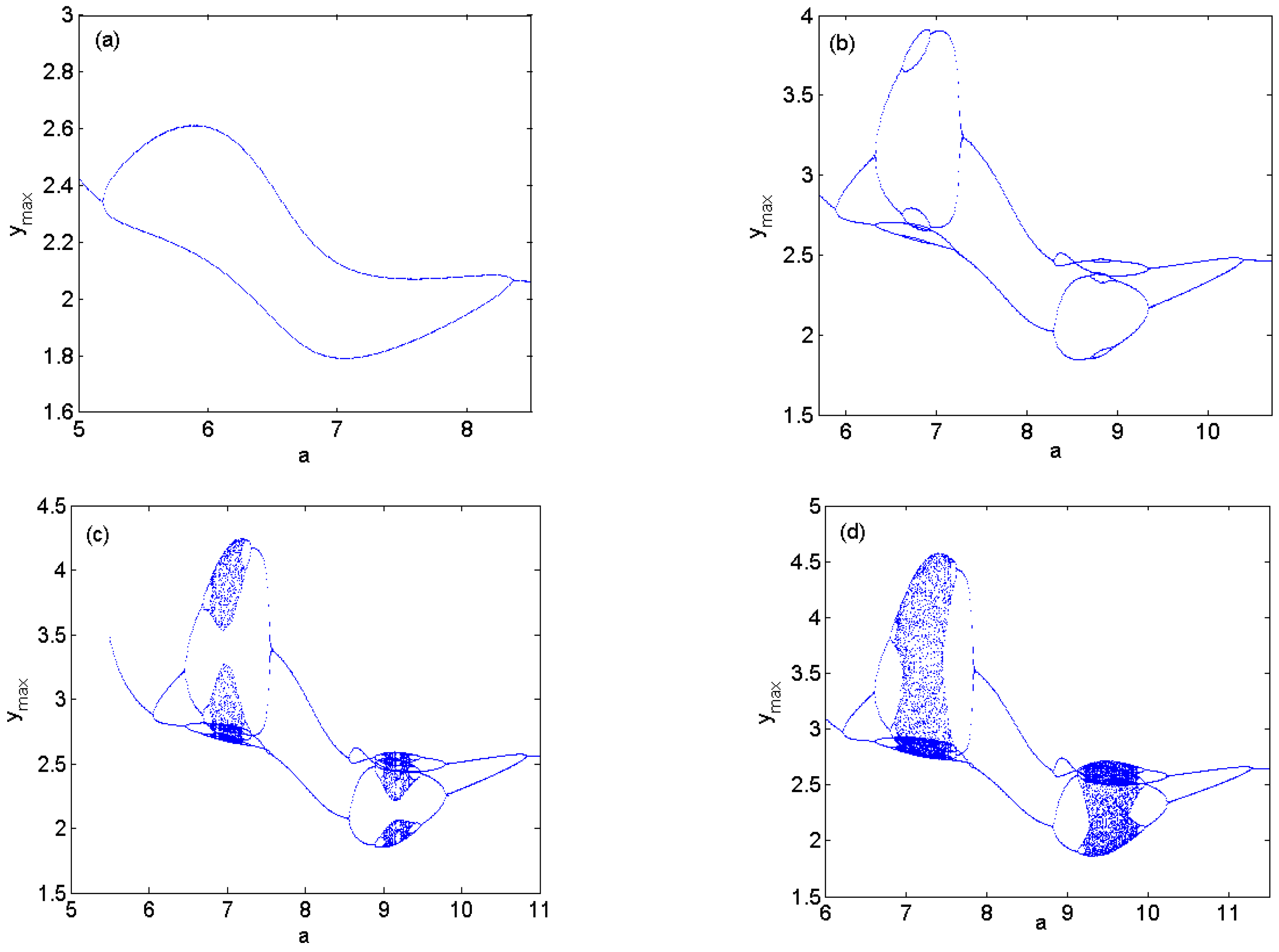
3.1. The Variety of Hidden Dynamics Induced by Parameter Changing
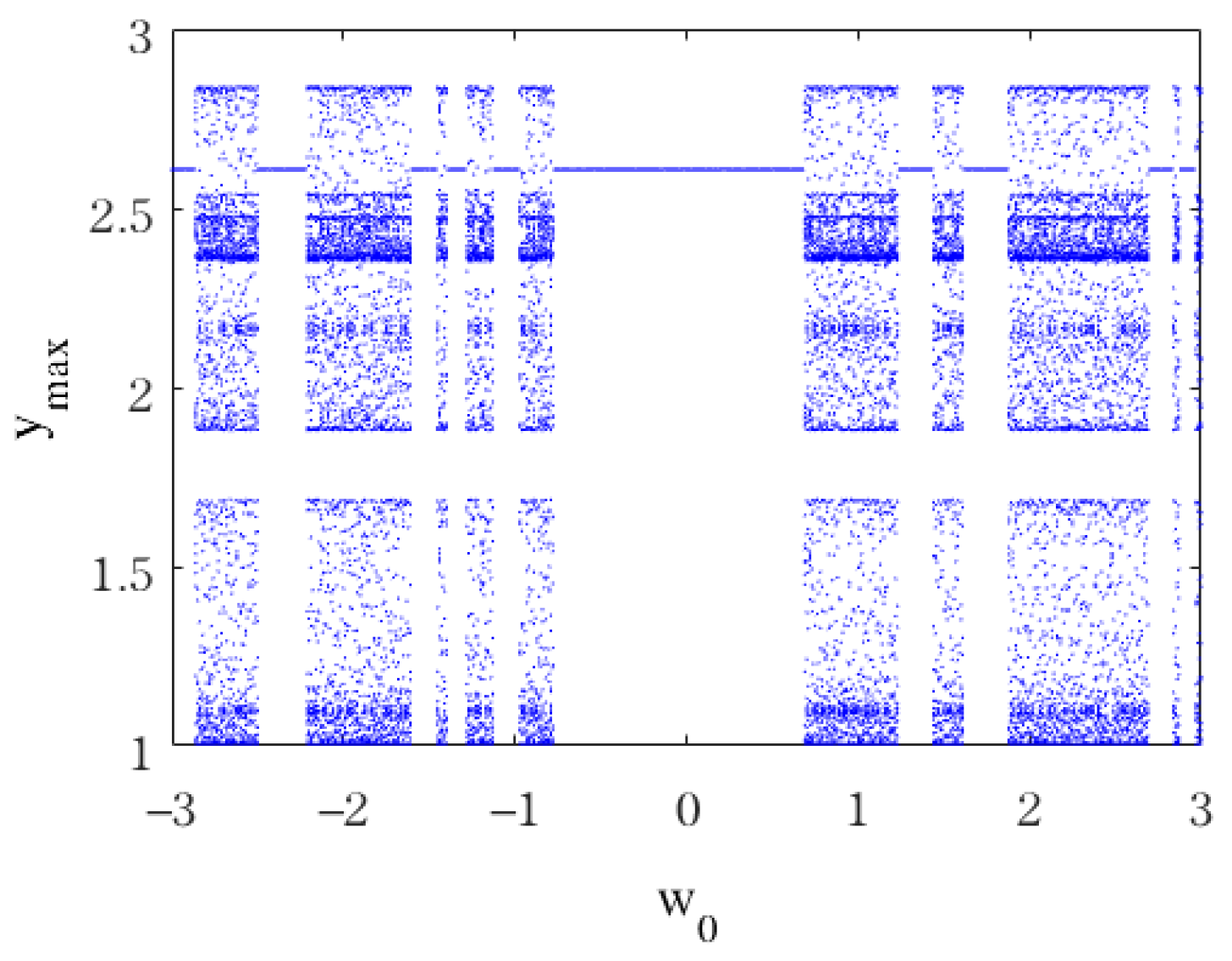
3.2. Hidden Dynamics to Initial Values
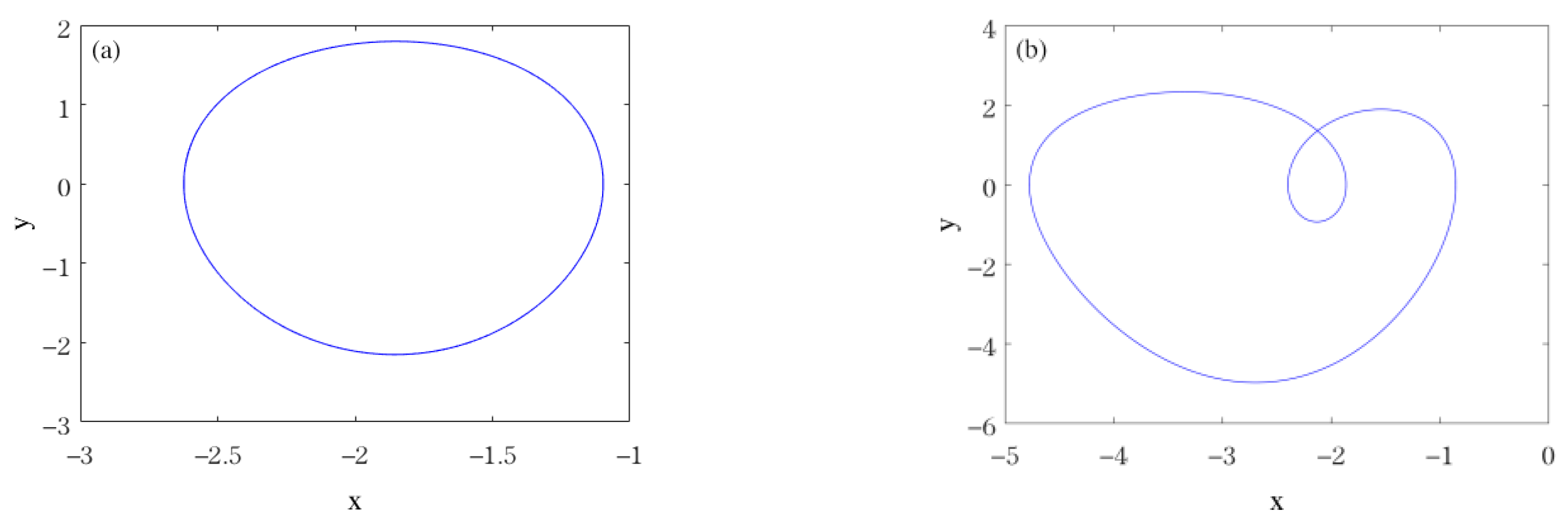
3.3. Offset Boosting of the Hidden Attractors
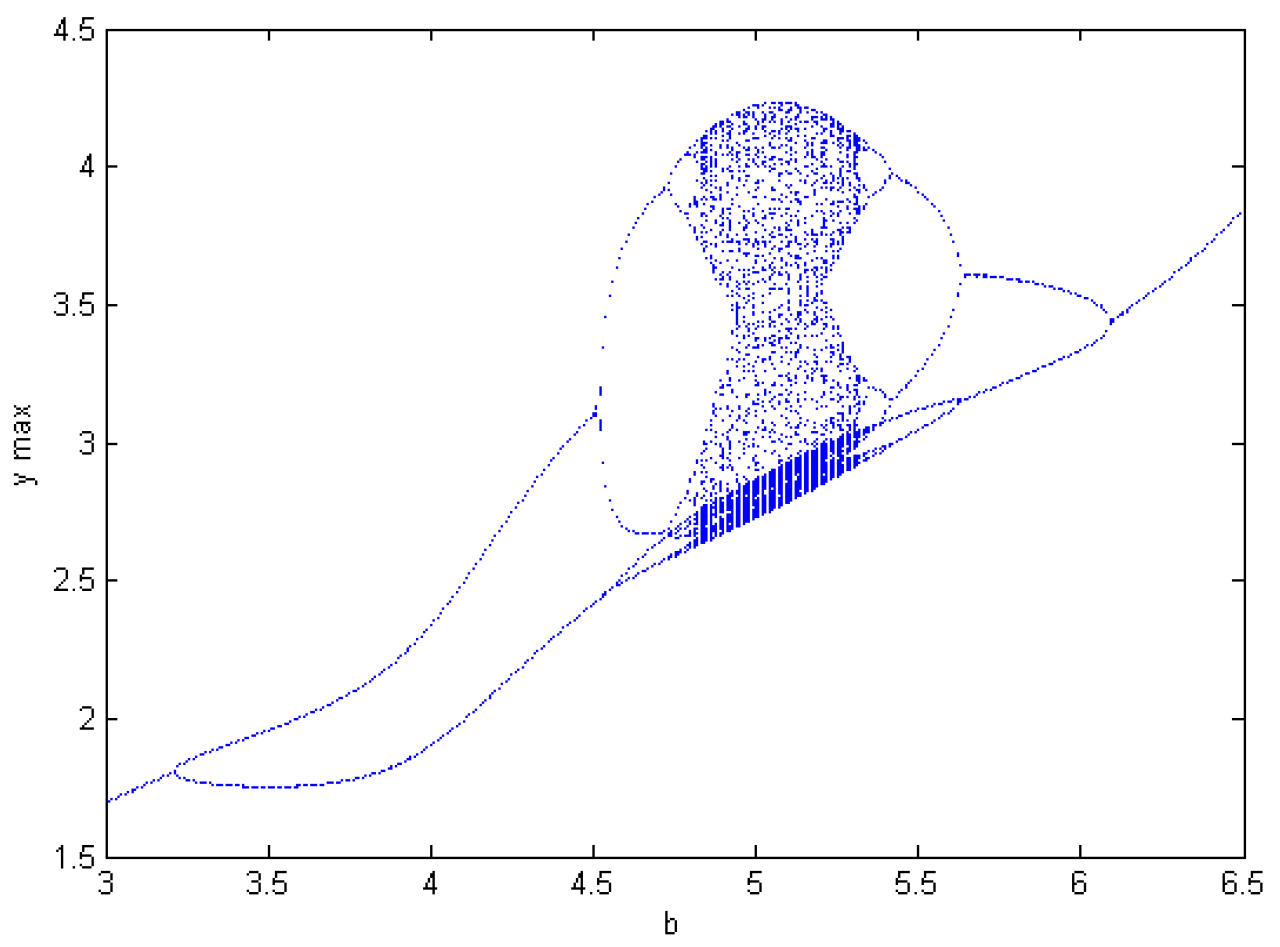
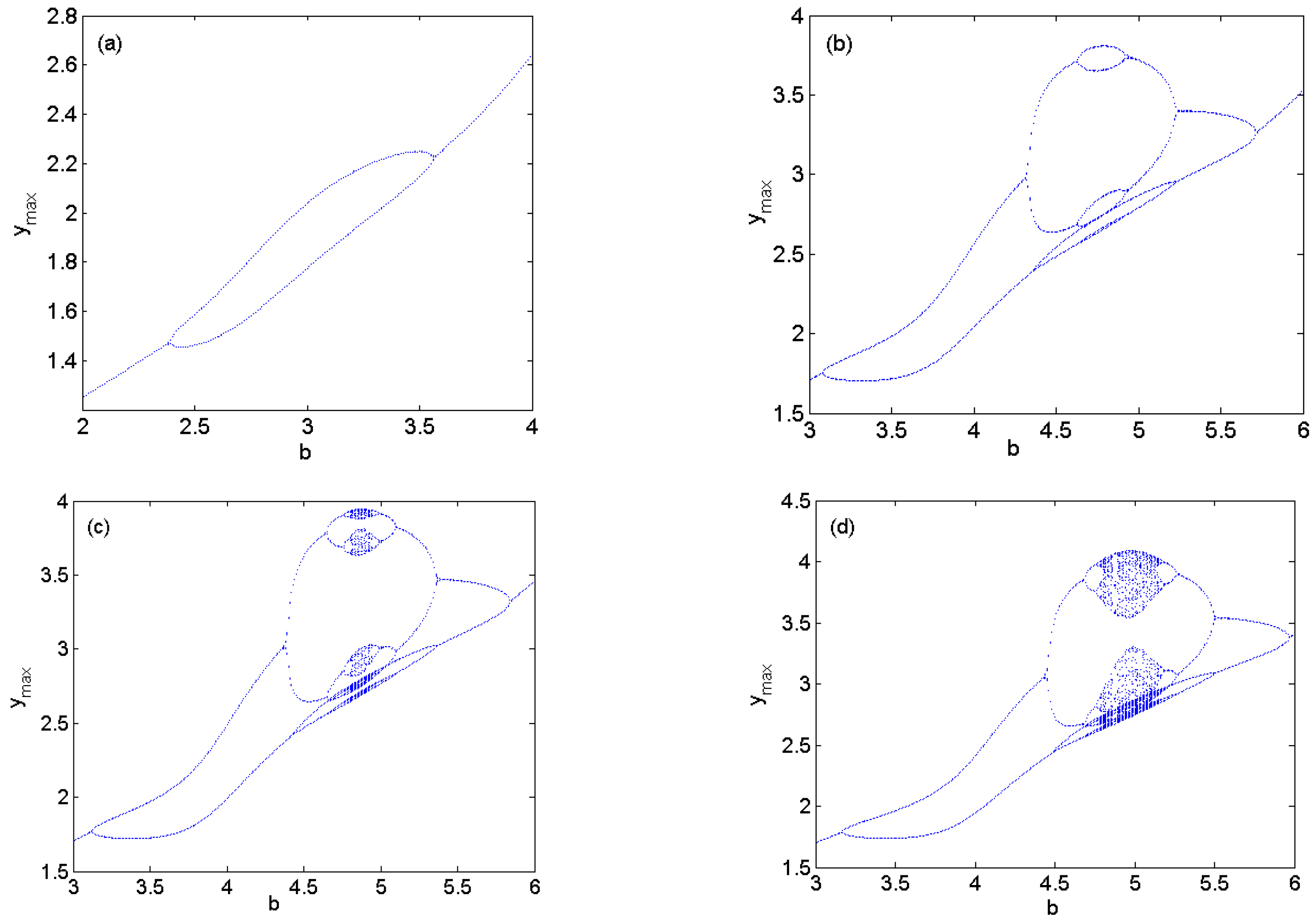
3.4. Antimonotonicity of a Jerk-like System with a Memristor
4. An Image Encryption Algorithm Based on the Jerk-like System with a Smooth Memristor
4.1. Image Encryption Algorithm
4.2. Simulations of the Encryption and Decryption
4.3. Performance Analysis of the Encryption Method Based on the New Jerk-like System with a Memristor
4.3.1. Size of the Key Space
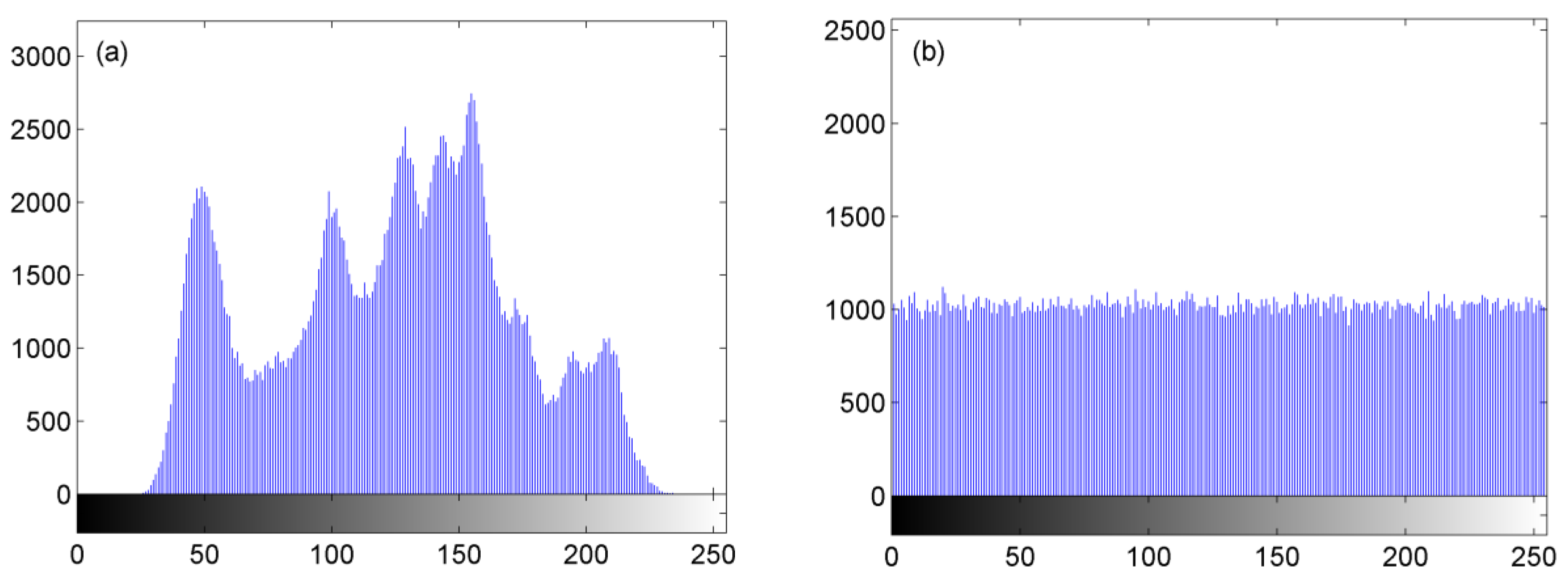
4.3.2. Statistical Feature Analysis
4.3.3. Test of the Key Sensitivity
- Test 1. Change one initial value; for example, let .
- Test 2. Change one system parameter; for example, let .
- Test 3. Change parameter , and let .
- Test 4. Change one memristor parameter , and let .
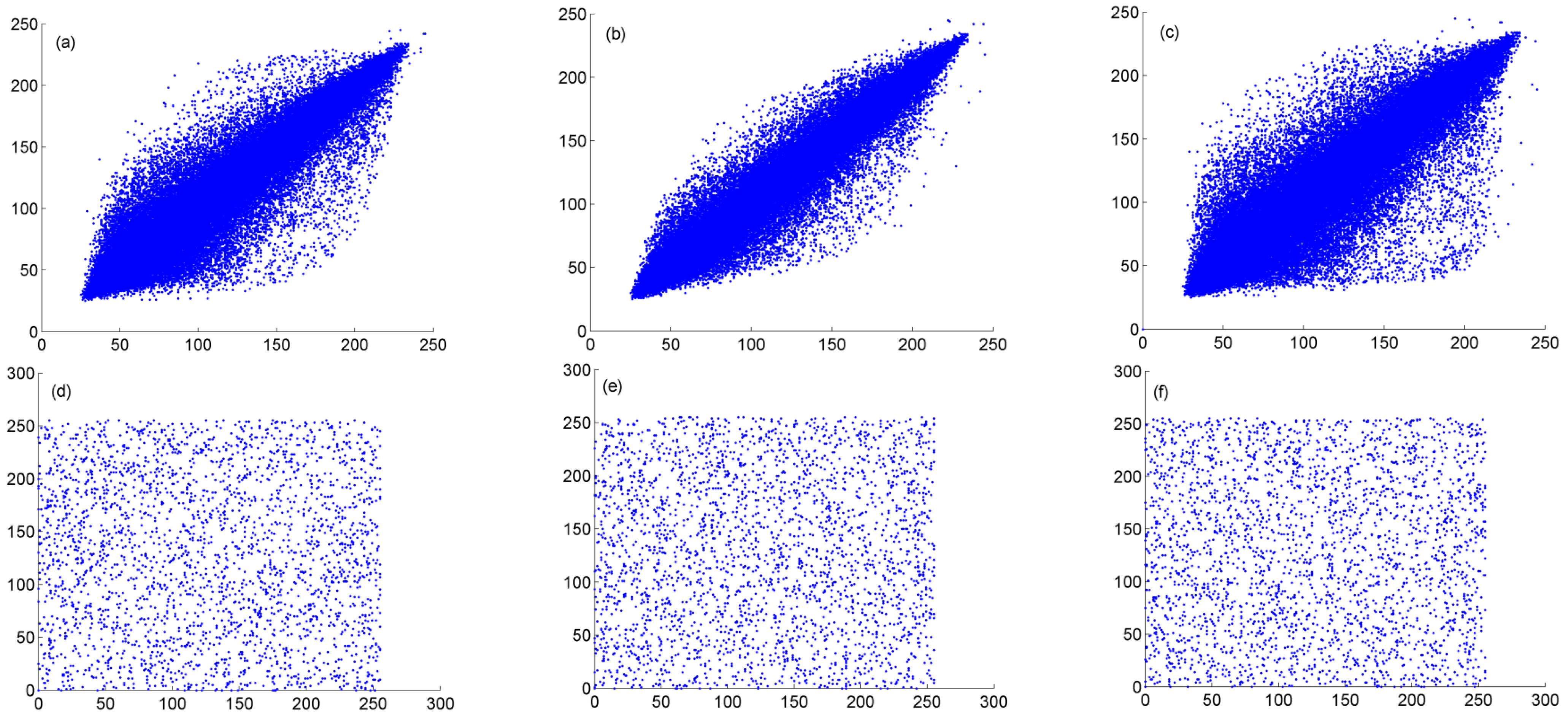
4.3.4. Correlation Analysis between Adjacent Pixels
4.3.5. Analysis of Information Entropy
4.3.6. Analysis of Differential Attack
4.3.7. Analysis of the Robustness
5. Conclusions
- (1)
- System parameters can affect the types of hidden dynamics. The change in parameter can induce various hidden attractors in the new 4D Jerk-like system with a memristor, such as hidden chaotic attractor and hidden period attractors with different periods.
- (2)
- The coexistence of different kinds of hidden attractors can be found. By choosing appropriate system parameters, different kinds of hidden attractors can coexist, such as chaotic attractor and multi-period, period-1 attractor and chaotic attractor, multi-period attractor and period-1 attractor, multi-period attractor and multi-period attractor.
- (3)
- Offset boosting in system (3) is analyzed via transformation. Results suggest that, for the chaotic attractor, period-1 attractor, and period-2 attractor, offset boosting can be realized by altering the boosting controller, while offset boosting of the period-3 attractor and period-4 attractor cannot be gained by changing the boosting controller.
- (4)
- Antimonotonicity has also been demonstrated in the new Jerk-like system with a memristor. Namely, with parameters a or b changing, full Feigenbaum remerging tree appears.
- (5)
- An image encryption algorithm based on the new 4D Jerk-like system with a memristor is designed. By experiments with their analysis and some comparisons with other results, the effectiveness of the proposed encryption method is verified.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lorenz, E.N. Deterministic non-periodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Norouzi, B.; Mirzakuchaki, S. A fast color image encryption algorithm based on hyper-chaotic systems. Nonlinear Dyn. 2014, 78, 995–1015. [Google Scholar] [CrossRef]
- Gokyildirim, A. Circuit realization of the fractional-order Sprott K chaotic system with standard components. Fractal Fract. 2023, 7, 470. [Google Scholar] [CrossRef]
- Inoue, K.; Mao, T.; Okutomi, H.; Umeno, K. An extension of the entropic chaos degree and its positive effect. Jpn. J. Ind. Appl. Math. 2021, 38, 611–624. [Google Scholar] [CrossRef]
- Wang, Y.M.; Leng, X.X.; Zhang, C.K.; Du, B.X. Adaptive fast image encryption algorithm based on three-dimensional chaotic system. Entropy 2023, 25, 1399. [Google Scholar] [CrossRef]
- Beal, A.N. Extracting communication, ranging and test waveforms with regularized timing from the chaotic Lorenz system. Signals 2023, 4, 507–523. [Google Scholar] [CrossRef]
- Takatsuka, K. Quantum chaos in the dynamics of molecules. Entropy 2023, 25, 63. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Vagaitsev, V.I. Hidden attractor in smooth Chua systems. Phys. D 2012, 241, 1482–1486. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Mokaev, T.N. Homoclinic orbits, and self-excited and hidden attractors in a Lorenz-like system describing convective fluid motion. Eur. J. Phys. 2015, 224, 1421–1458. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Mokaev, T.N. Hidden attractor and homoclinic orbit in Lorenz-like system describing convective fluid motion in rotating cavity. Comm. Nonlinear Sci. 2015, 28, 166–174. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Vagaitsev, V.I. Localization of hidden Chua’s attractors. Phys. Lett. A 2011, 375, 2230–2233. [Google Scholar] [CrossRef]
- Vo, T.P.; Shaverdi, Y.; Khalaf, A.J.M.; Alsaadi, F.E.; Hayat, T.; Pham, V.T. A giga-stable oscillator with hidden and self-excited attractors: A megastable oscillator forced by his twin. Entropy 2019, 21, 535. [Google Scholar] [CrossRef] [PubMed]
- Nestor, T.; Dieu, N.J.D.; Jacques, K.; Yves, E.J.; Iliyasu, A.M.; El-Latif, A.A.A. A multidimensional hyperjerk oscillator: Dynamics analysis, analogue and embedded systems implementation, and its application as a cryptosystem. Sensors 2020, 20, 83. [Google Scholar] [CrossRef] [PubMed]
- Lawnik, M.; Moysis, L.; Volos, C. A family of 1D chaotic maps without equilibria. Symmetry 2023, 15, 1311. [Google Scholar] [CrossRef]
- Matouk, A.E.; Abdelhameed, T.N.; Almutairi, D.K.; Abdelkawy, M.A.; Herzallah, M.A.E. Existence of self-excited and hidden attractors in the modified autonomous Van Der Pol- Duffing systems. Mathematics 2023, 11, 591. [Google Scholar] [CrossRef]
- Ahmad, I.; Srisuchinwong, B.; Jamil, M.U. Coexistence of hidden attractors in the smooth cubic Chua’s Circuit with two stable equilibria. Int. J. Bifurc. Chaos 2023, 33, 2330010. [Google Scholar] [CrossRef]
- Liu, M.H.; Yu, S.M. Multi-scroll high-order general Jerk circuits. Acta Phys. Sin.-Chin. Ed. 2006, 55, 5707–5713. [Google Scholar] [CrossRef]
- Vaidyanathan, S. Analysis, control, and synchronization of a 3-D novel Jerk chaotic system with two quadratic nonlinearities. Kyungpook Math. J. 2015, 55, 563–586. [Google Scholar] [CrossRef]
- He, S.B.; Sun, K.H.; Wang, H.H.; Ai, X.X.; Xu, Y.X. Design of n-dimensional multi-scroll Jerk chaotic system and its performances. J. Appl. Anal. Comput. 2016, 6, 1180–1194. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Benkouider, K.; Sambas, A. A new multistable jerk chaotic system, its bifurcation analysis, backstepping control-based synchronization design and circuit simulation. Arch. Control Sci. 2022, 32, 123–152. [Google Scholar] [CrossRef]
- Hu, X.Y.; Sang, B.; Wang, N. The chaotic mechanisms in some jerk systems. AIMS Math. 2022, 7, 15714–15740. [Google Scholar] [CrossRef]
- Kengne, L.K.; Muni, S.S.; Chedjou, J.C.; Kyandoghere, K. Various coexisting attractors, asymmetry analysis and multi-stability control in a 3D memristive jerk system. Eur. Phys. J. Plus 2022, 137, 848. [Google Scholar] [CrossRef]
- Bao, H.; Ding, R.Y.; Hua, M.J.; Wu, H.G.; Chen, B. Initial-condition effects on a two-memristor-based Jerk system. Mathematics 2022, 10, 411. [Google Scholar] [CrossRef]
- Li, F.D.; Zeng, J.R. Multi-scroll attractor and multi-stable dynamics of a three-dimensional Jerk system. Energies 2023, 16, 2494. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, X.L. Dynamics analysis and periodic solution of a 3D Jerk system with hidden attractor. J. Southwest Univ. (Nat. Sci. Ed.) 2017, 39, 1–10. [Google Scholar]
- Vijayakumar, M.D.; Natiq, H.; Leutcho, G.D.; Rajagopal, K.; Jafari, S.; Hussain, I. Hidden and self-excited collective dynamics of a new multistable hyper-Jerk system with unique equilibrium. Int. J. Bifurc. Chaos 2022, 32, 2250063. [Google Scholar] [CrossRef]
- Li, B.X.; Sang, B.; Liu, M.; Hu, X.Y.; Zhang, X.; Wang, N. Some Jerk systems with hidden chaotic dynamics. Int. J. Bifurc. Chaos 2023, 33, 2350069. [Google Scholar] [CrossRef]
- Wang, L.Y. Research progress of the memristor and its application foreground. Electron. Compon. Mater. 2010, 29, 71–74. [Google Scholar]
- Mou, J. Editorial: Advances in memristor and memristor-based applications. Front. Phys. 2022, 10, 1005216. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.C. A simple Jerk-like system without equilibrium: Asymmetric coexisting hidden attractors, bursting oscillation and double full Feigenbaum remerging trees. Chaos Solitons Fractals 2019, 120, 25–40. [Google Scholar] [CrossRef]
- Bao, B.C.; Liu, Z.; Xu, J.P. Dynamical analysis of memristor chaotic oscillator. Acta Phys. Sin.-Chin. Ed. 2010, 59, 3785–3793. [Google Scholar] [CrossRef]
- Sharma, P.R.; Shrimali, M.D.; Prasad, A.; Kuznetsov, N.V.; Leonov, G.A. Controlling dynamics of hidden attractors. Int. J. Bifurc. Chaos 2015, 25, 1550061. [Google Scholar] [CrossRef]
- Dudkowski, D.; Jafari, S.; Kapitaniak, T.; Kuznetsov, N.V.; Leonov, G.A.; Prasad, A. Hidden attractors in dynamical systems. Phys. Rep. 2016, 637, 1–50. [Google Scholar] [CrossRef]
- Li, C.; Wang, X.; Chen, G. Diagnosing multi-stability by offset boosting. Nonlinear Dyn. 2017, 90, 1335–1341. [Google Scholar] [CrossRef]
- Leutcho, G.D.; Kengne, J. A unique chaotic snap system with a smoothly adjustable symmetry and nonlinearity: Chaos, offset-boosting, antimonotonicity, and coexisting multiple attractors. Chaos Soliton. Fract. 2018, 113, 275–293. [Google Scholar] [CrossRef]
- Liu, M.; Sang, B.; Wang, N.; Ahmad, I. Chaotic dynamics by some quadratic Jerk systems. Axioms 2021, 10, 227. [Google Scholar] [CrossRef]
- Zhou, L.; You, Z.Z.; Liang, X.L.; Li, X.W. A memristor-based colpitts oscillator circuit. Mathematics 2023, 10, 4820. [Google Scholar] [CrossRef]
- Guo, Z.G.; Wen, J.J.; Mou, J. Dynamic analysis and DSP implementation of memristor chaotic systems with multiple forms of hidden attractors. Mathematics 2023, 11, 24. [Google Scholar] [CrossRef]
- Dawson, S.P.; Grebogi, C.; Yorke, J.A.; Kan, I.; Ko, C.H. Antimonotonicity: Inevitable reversals of period-doubling cascades. Phys. Lett. A 1992, 162, 249–254. [Google Scholar] [CrossRef]
- Ava, H.; Nicole, M.F. An encryption architecture suitable for on chip integration with sensors. IEEE J. Emerg. Sel. Top. Circuits Syst. 2021, 11, 395–404. [Google Scholar] [CrossRef]
- Kadhim, A.; Khalaf, S. New approach for security chatting in real time. Int. J. Emerg. Trends Technol. Comput. Sci. 2015, 4, 30–36. [Google Scholar]
- Zhang, X.; Seo, S.H.; Wang, C. A lightweight encryption method for privacy protection in surveillance videos. IEEE Access 2018, 6, 18074–18087. [Google Scholar] [CrossRef]
- Alhussan, A.A.; Farhan, A.K.; Abdelhamid, A.A.; El-Kenawy, E.S.M.; Ibrahim, A.; Khafaga, D.S. Optimized ensemble model for wind power forecasting using hybrid whale and dipper-throated optimization algorithms. Front. Energy. Res. 2023, 11, 1174910. [Google Scholar] [CrossRef]
- Zhu, C.X.; Xu, S.Y.; Hu, Y.P.; Sun, K.H. Breaking a novel image encryption scheme based on Brownian motion and PWLCM chaotic system. Nonlinear Dyn. 2015, 79, 1511–1518. [Google Scholar] [CrossRef]
- Wang, J.; Liu, W.Y.; Zhang, S. Adaptive encryption of digital images based on lifting wavelet optimization. Multimed. Tools Appl. 2020, 79, 9363–9386. [Google Scholar] [CrossRef]
- Alhudhaif, A.D.I.; Ahmad, M.; Alkhayyat, A.; Tsafack, N.; Farhan, A.K.; Ahmed, R. Block cipher nonlinear confusion components based on new 5-D hyperchaotic system. IEEE Access 2021, 9, 87686–87696. [Google Scholar] [CrossRef]
- Naif, J.R.; Abdul-majeed, G.H.; Farhan, A.K. Internet of things security using new chaotic system and lightweight AES. J. Al-Qadisiyah Comput. Sci. Math. 2019, 11, 45–52. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S.J. Some basic cryptographic requirements for chaos-based cryptosystem. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zhu, X.Q.; Zhang, Y.Q. An image encryption algorithm based on Josephus traversing and mixed chaotic map. IEEE Access 2018, 6, 23733–23746. [Google Scholar] [CrossRef]









| Parameters | Type of Hidden Attractors | Diagrams |
|---|---|---|
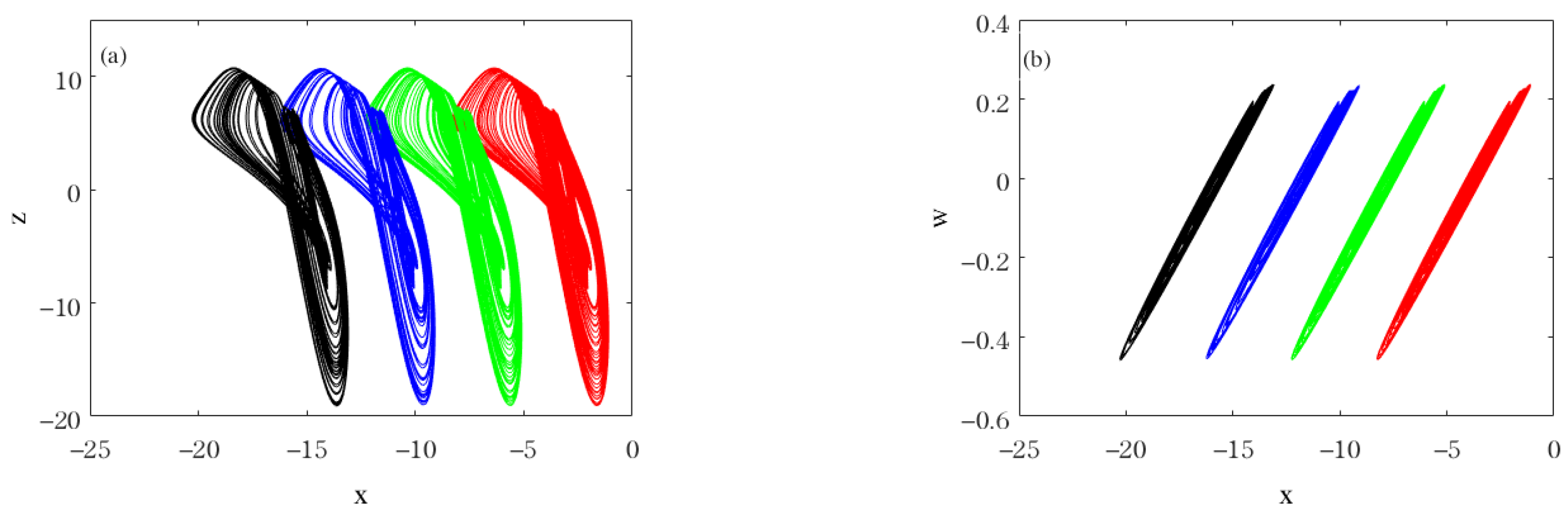
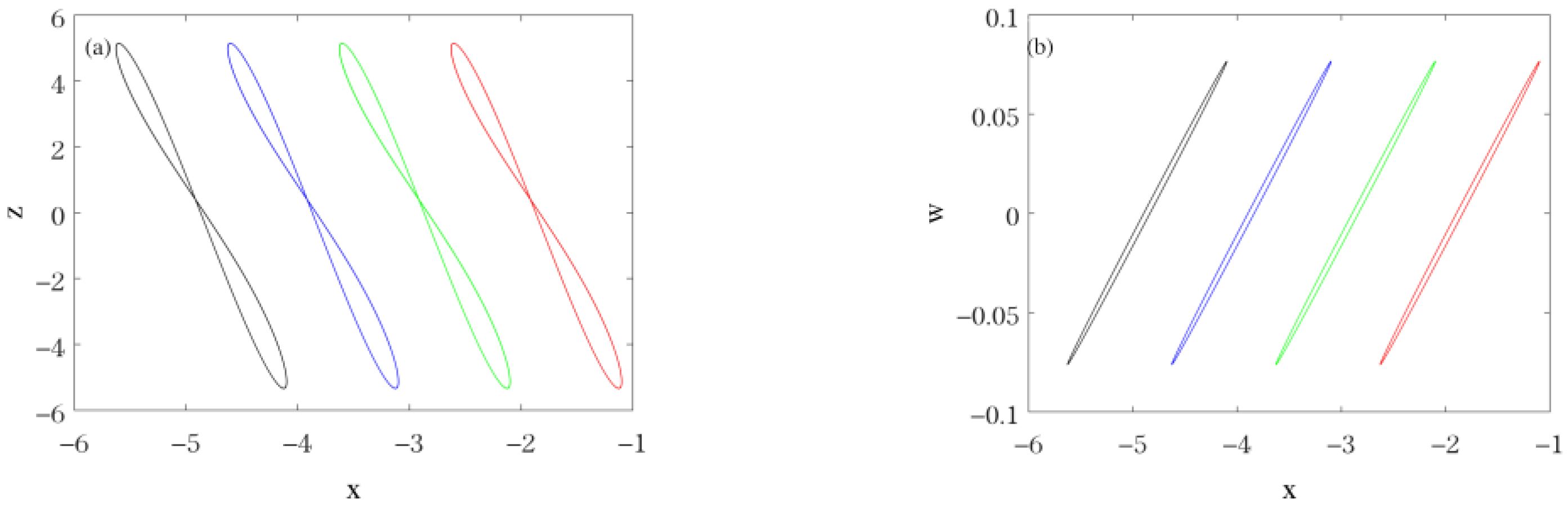
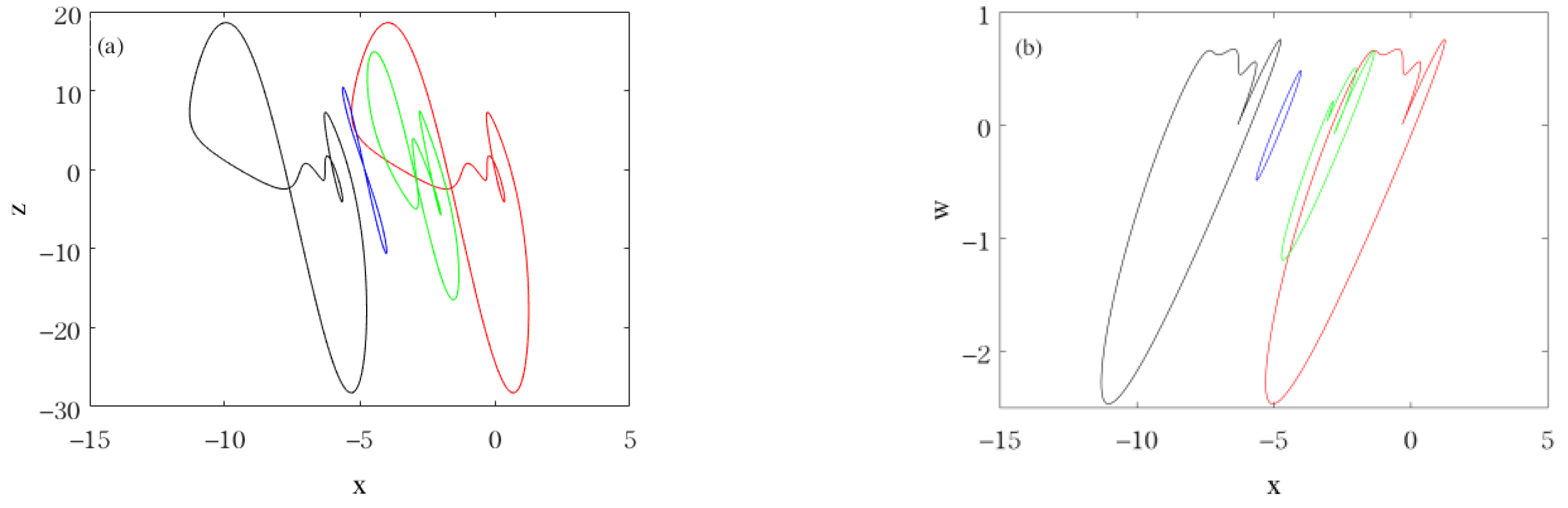
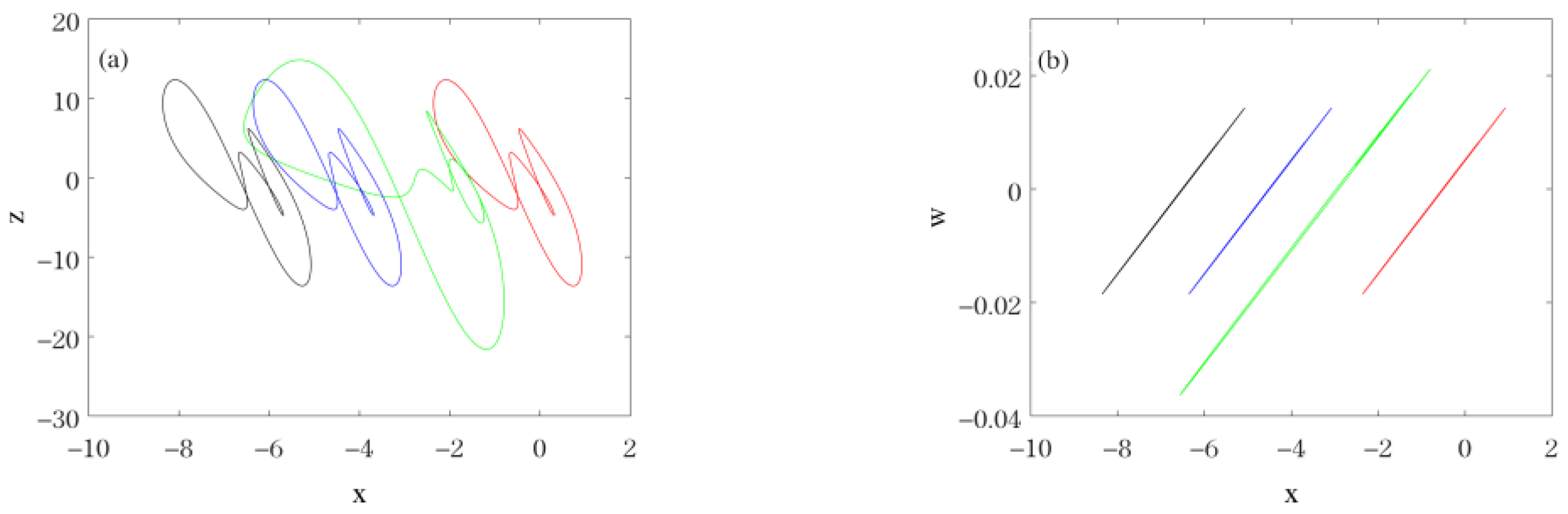
| , , , ,, , | Coexistence of chaotic attractor (red line for initial value (−2, 0, −2, 0)) and periodic-6 attractor (blue line for initial value (−2, 1, −2, 0)). | 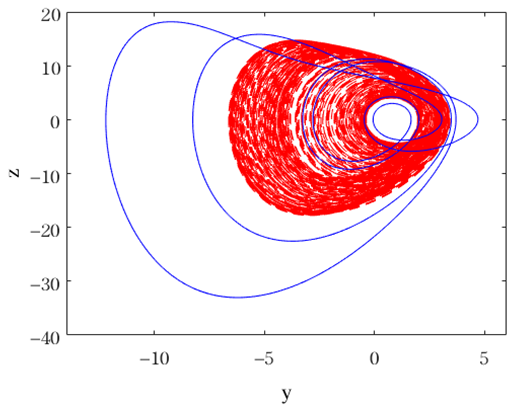 |
| , , , , , , | Coexistence of periodic-1 attractor (red line for initial value (−2, 0, −2, 0)) and chaotic attractor (blue line for initial value (−2, 1, −2, 0)). |  |
| , , , , , , | Coexistence of periodic-4 attractor (red line for initial value (−2, 0, −2, 0)) and periodic-1 attractor (blue line for initial value (−2, 1, −2, 0)). | 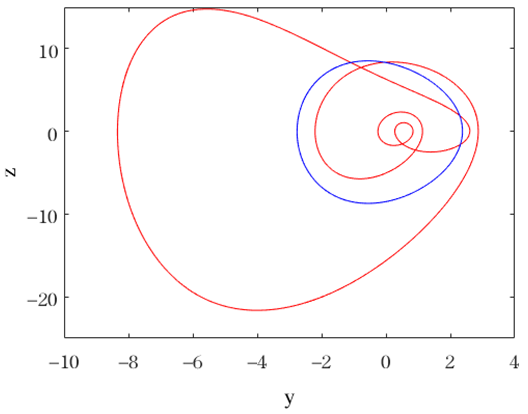 |
| , , , , , , | Coexistence of periodic-3 attractor (red line for initial value (−2, 0, −2, 0)) and periodic-4 attractor (blue line for initial value (−2, 1, −2, 0)). |  |
| Gray Lenna Image | Peppers | Camara Man | Color Lenna Image | |
|---|---|---|---|---|
| Required time | 34 s | 33 s | 32 s | 35 s |
| Test 1 | Test 2 | Test 3 | Test 4 | |
|---|---|---|---|---|
| Percentage difference of cipher image | 99.73% | 99.82% | 99.90% | 99.93% |
| Images | Original Image | Encrypted Image | ||||
|---|---|---|---|---|---|---|
| Horizontal | Vertical | Diagonal | Horizontal | Vertical | Diagonal | |
| Gray Lenna | 0.9604 | 0.9846 | 0.9811 | −0.0220 | −0.0006 | −0.0194 |
| Peppers | 0.9601 | 0.9688 | 0.9502 | 0.0035 | 0.0079 | 0.0008 |
| Camera man | 0.9589 | 0.9712 | 0.9403 | 0.0045 | −0.0056 | 0.0029 |
| Color Lenna | 0.9629 | 0.9879 | 0.9838 | −0.0233 | −0.0002 | −0.0205 |
| Test Images | NPCR | UACI |
|---|---|---|
| Gray Lenna | 99.6194% | 33.4635% |
| Peppers | 99.4936% | 33.3988% |
| Camera man | 99.5738% | 33.4406% |
| Color Lenna | 99.5987% | 33.4589% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhuang, L.; Yu, J.; Jiang, H.; Xu, W.; Shi, X. Hidden Dynamics of a New Jerk-like System with a Smooth Memristor and Applications in Image Encryption. Mathematics 2023, 11, 4613. https://doi.org/10.3390/math11224613
Wang Z, Zhuang L, Yu J, Jiang H, Xu W, Shi X. Hidden Dynamics of a New Jerk-like System with a Smooth Memristor and Applications in Image Encryption. Mathematics. 2023; 11(22):4613. https://doi.org/10.3390/math11224613
Chicago/Turabian StyleWang, Zuolei, Lizhou Zhuang, Jianjiang Yu, Haibo Jiang, Wanjiang Xu, and Xuerong Shi. 2023. "Hidden Dynamics of a New Jerk-like System with a Smooth Memristor and Applications in Image Encryption" Mathematics 11, no. 22: 4613. https://doi.org/10.3390/math11224613





