On Topp-Leone-G Power Series: Saturation in the Hausdorff Sense and Applications

Abstract

This paper discusses the Topp-Leone-G power series class of distributions. The greatest attention is paid to the investigation of intrinsic characteristic “saturation” to the horizontal asymptote in the Hausdorff sense. Some estimates for the value of the Hausdorff distance are obtained. We present a new family of recurrence generated adaptive functions with corresponding applications. The usefulness of the obtained results is demonstrated in a simulation study of some real data sets from the medical sector and insurance. Some suitable software modules within the programming environment CAS MATHEMATICA are proposed.

1. Introduction

One basic and very important practical problem is the construction of adequate, accurate and sufficiently flexible approximation models. In practice, for a given data set, a reliable statistical model can be developed from an appropriate probability distribution. Over the last few years, many authors have derived new compounding distributions by mixing continuous distributions with power series distributions, such as the generalized modified Weibull power series [1], the Gompertz-power series [2], the Inverse Weibull power series [3], the Exponentiated Burr XII power series [4], the Exponentiated generalized power series family [5], the odd power generalized Weibull-G power series [6] and others. In 1950, Albert Noack [7] introduced the family of discrete univariate distributions evolving in power series, although the earliest work on this topic was written by Kosambi (1949) [8]. Let us recall that the probability mass function (pmf), for a random variable distributed as a power series which excludes zero, is given by

$$P(N=n)=\frac{a_n{\theta }^n}{C\left(\theta \right)},n=1,2,\dots$$

where $a_n\ge 0$ depends only on n, $C\left(\theta \right)={\sum }_{n=1}^{\infty }{a}_n{\theta }^n$ and $\theta >0$ is chosen such that $C\left(\theta \right)$ is finite. The power series distributions are discrete and mainly used to model count data. The Topp-Leone is one of the most commonly used distributions. Its generalization, Topp-Leone-G, was proposed by Al-Shomran et al. [9] in 2016. It is very often used as a generator for numerous generalizations with the aim of increasing the versatility of new distributions such as the Topp-Leone generated family [10], the new power Topp-Leone generated family [11], the new Topp-Leone class [12], the Extended Topp-Leone family [13], the alpha power Topp-Leone-G [14] and the new extension of the Topp-Leone family [15].

In 2021, Makubate et al. [16] considered a new class of distributions called the Topp-Leone-G Power Series (TL-GPS). This model is obtained by compounding the Topp-Leone-G distribution with the power series distribution (see also [17]). Note that TL-GPS is an extension of the Topp-Leone power series distribution proposed by Roozegar and Nadarajah [18]. Similar distributions that involve Topp-Leone with power series are the reflected generalized Topp-Leone power series [19], the Topp-Leone generalized exponential Power series [20], the type II exponentiated half-logistic-Topp-Leone-G power series [21], the Exponentiated half Logistic-Topp-Leone-G power series [22] and the type II Topp-Leone-G power series [23].

Definition 1.

Topp-Leone-G Power Series (TL-GPS) distribution is associated with the following general form of CDF function

$$F_{TL-GPS}(t;\theta ,b,\xi )=1-\frac{C\left(\theta S_{TL-G}(t;b,\xi )\right)}{C\left(\theta \right)},$$

(1)

where $C\left(\theta \right)$ is finite, $\theta >0$ and $S_{TL-G(t;b,\xi )}$ is the survival function of Topp-Leone-G that is defined by

$$S_{TL-G}(t;b,\xi )=1-F_{TL-G}(t;b,\xi )=1-{(1-{(1-G(t;\xi ))}^2)}^b$$

(2)

for $b>0$ with the baseline CDF function $G(t;\xi )$ depending on a parameter vector ξ.

Table 1. Sub-classes of Topp-Leone-G Power Series.

Distribution	${\mathbf{a}}_{\mathbf{n}}$	$\mathit{C}\left(\mathit{\theta }\right)$	CDF Function
Topp-Leone-G Poisson	${\displaystyle \frac{1}{n!}}$	$e^{\theta }-1$	${\displaystyle 1-\frac{e^{\theta \left(1-{\left(1-G{(t;\xi )}^2\right)}^b\right)}-1}{e^{\theta }-1}}$
Topp-Leone-G Geometric	1	${\displaystyle \frac{\theta }{1-\theta }}$	${\displaystyle 1-\frac{\left(1-{\left(1-G{(t;\xi )}^2\right)}^b\right)(1-\theta )}{1-\theta \left(1-{\left(1-G{(t;\xi )}^2\right)}^b\right)}}$
Topp-Leone-G Logarithmic	${\displaystyle \frac{1}{n}}$	$-log(1-\theta )$	${\displaystyle 1-\frac{log\left(1-\theta \left(1-{\left(1-G{(t;\xi )}^2\right)}^b\right)\right)}{log(1-\theta )}}$
Topp-Leone-G Binomial	${\displaystyle \left(\genfrac{}{}{0pt}{}{m}{n}\right)}$	${(1+\theta )}^m-1$	${\displaystyle 1-\frac{{\left(1+\theta \left(1-{\left(1-G{(t;\xi )}^2\right)}^b\right)\right)}^m-1}{{(1+\theta )}^m-1}}$

presents some sub-classes of Topp-Leone-G Power Series.

The main aim of this work is investigation of intrinsic characteristic “saturation” to the horizontal asymptote in the Hausdorff sense. This research can be very useful in choosing an appropriate model for approximating specific data and be applicable in various fields such as finance, economics, actuarial sciences, biostatistics and many others. We need a metric for measuring similarity between sigmoidal (cumulative) function and a step function. The Hausdorff distance can be considered as the highest optimal path between these curves as a smaller Hausdorff distance shows a higher closeness.

Definition 2.

The shifted Heaviside step function is defined by

$$h_{t_0}\left(t\right)=\left\{\begin{array}{cc}0\hfill & \mathit{if}t<t_0,\hfill \\ \left[0,1\right]\hfill & \mathit{if}t=t_0,\hfill \\ 1\hfill & \mathit{if}t>t_0.\hfill \end{array}\right.$$

We consider Euclidean space with the maximum norm namely for the points $A=(t_A,x_A)$ and $B=(t_B,x_B)$ in ${\mathbb{R}}^2$ we have $\parallel A-B\parallel =max\left(\right|t_A-t_B|,|x_A-x_B\left|\right)$. Hence we can define the Hausdorff distance [24,25].

Definition 3.

The Hausdorff distance (the H-distance) $\rho (f,g)$ between two interval functions $f,g$ on $\mathrm{\Omega }\subseteq \mathbb{R}$, is the distance between their completed graphs $F\left(f\right)$ and $F\left(g\right)$ considered as closed subsets of $\mathrm{\Omega }\times \mathbb{R}$. More precisely,

$$\rho (f,g)=max\{\underset{A\in F\left(f\right)}{sup}\underset{B\in F\left(g\right)}{inf}\parallel A-B\parallel ,\underset{B\in F\left(g\right)}{sup}\underset{A\in F\left(f\right)}{inf}\parallel A-B\parallel \}.$$

The formal definition of saturation of distribution in Hausdorff sense is proposed by Zaevski and Kyurkchiev [26].

Definition 4.

Let $F(·)$ be the CDF of a distribution with a left–finite domain $[a,b)$, $-\infty <a<b\le \infty$. Its saturation is the Hausdorff distance between the completed graph of $F(·)$ and the curve consisting of two lines – one vertical between the points $(a,0)$ and $(a,1)$ and another horizontal between $(a,1)$ and $(b,F(b\left)\right)$.

Iliev et al. [27] investigated the Hausdorff approximation between the Heaviside step function and Topp -Leone cumulative sigmoids. Similar investigations for some modifications of Topp-Leone and their behavior in the Hausdorff sense can be found in related papers and monographs [28,29,30,31]. Examination of family containing power series distribution is proposed in [32].

The article is structured as follows: In Section 2, our attention is paid to investigation of intrinsic characteristic “saturation” to the horizontal asymptote in the terms of Hausdorff metric. We present in detail approximation analysis for Topp-Leone-Weibull-Poisson (TL-WP). Numerical and real data examples demonstrate the usefulness of obtained theoretical results. Furthermore, family of recurrence generated adaptive functions with corresponding applications is defined in Section 3. We propose a simple dynamic programming module implemented within the programming environment CAS Wolfram Mathematica for computation the Hausdorff distance.

2. Approximation Results

Let us focus on one special case of a Topp-Leone-G Power Series (TL-GPS), namely with a baseline distribution—Weibull and power series distribution—Poisson. We obtain Topp-Leone-Weibull-Poisson (TL-WP) with the CDF function given by

$$F_{TL-WP}(t;\theta ,b,\alpha ,\beta )=1-\frac{e^{\theta \left(1-{\left(1-e^{-2\alpha t^{\beta }}\right)}^b\right)}-1}{e^{\theta }-1},$$

(3)

where $\alpha$, $\beta$, b, $\theta >0$ and $t>0$.

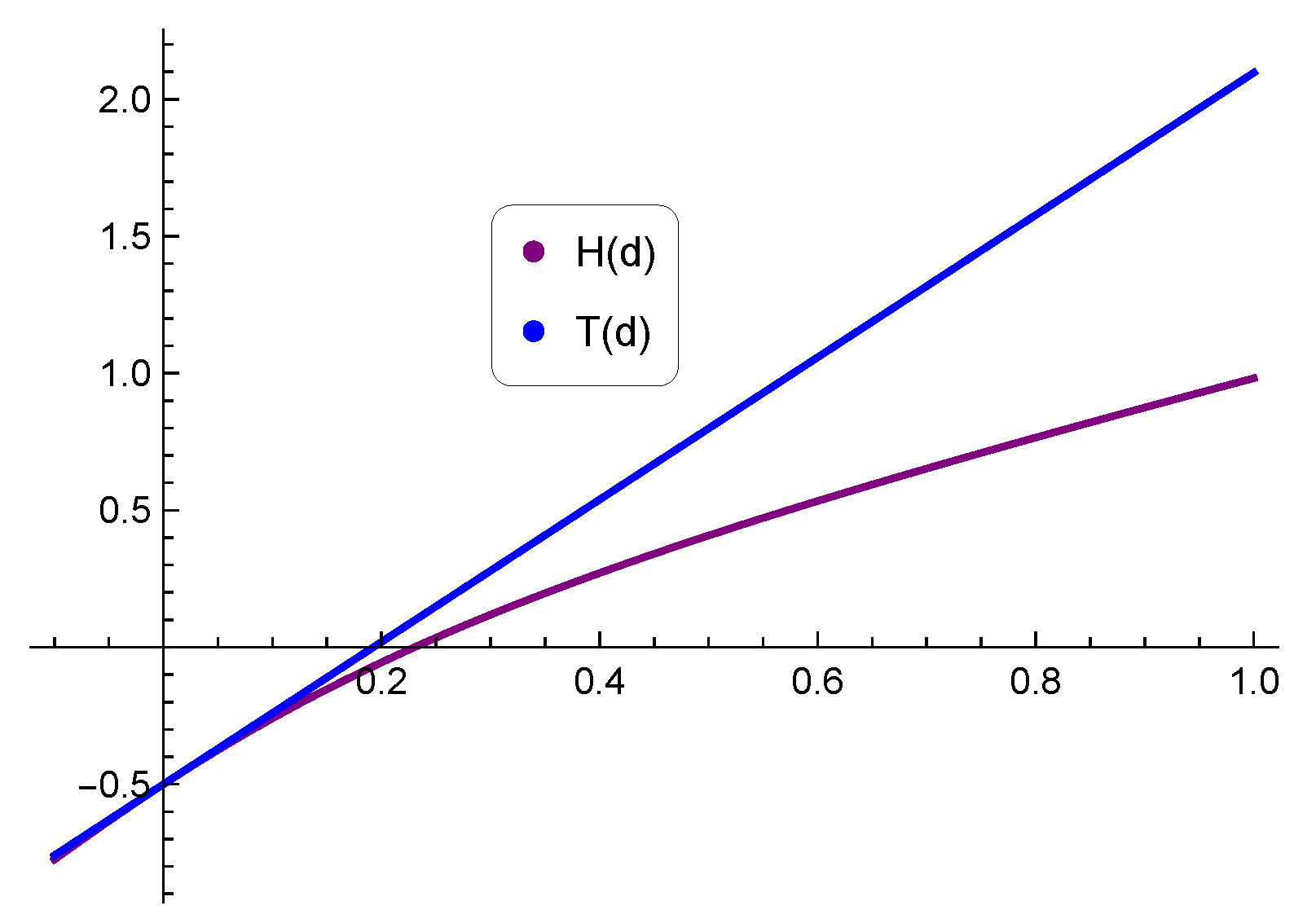
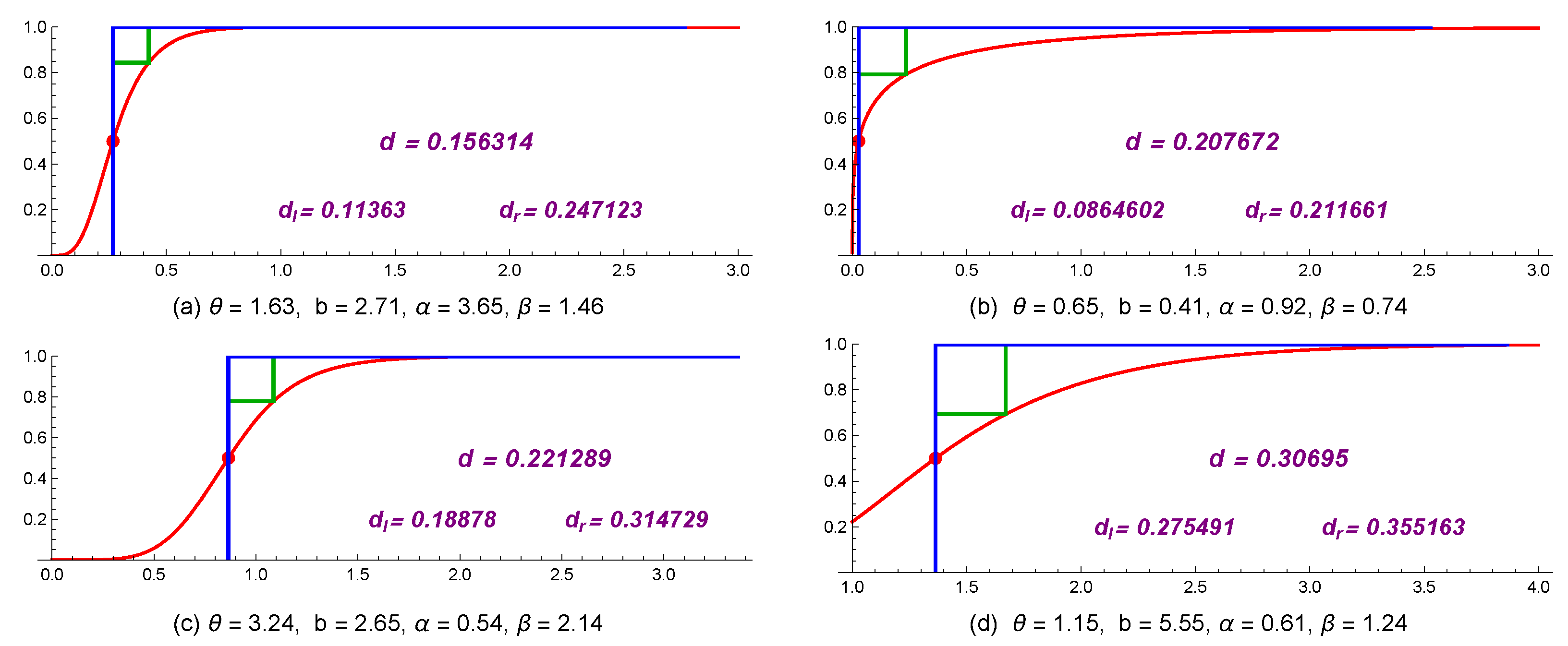
2.1. Hausdorff Approximation

We study the behavior of CDF in the Hausdorff sense and, more precisely, “saturation” to the horizontal asymptote $a=1$. The methodology applied here can be used in a similar way for other special cases of proposed families using different baseline distributions and sub-classes of power series distribution with corresponding approximation problems. In detail, we present an examination of Topp-Leone-Weibull-Poisson CDF functions (3).

According to Definitions (3) and (4), we have that saturation of distribution is the side of the smallest unit square, centered at the point $(0,1)$ touching the graph of the cumulative function. Hence, the Hausdorff distance d between $F_{TL-WP}(t;\theta ,b,\alpha ,\beta )$ and the Heaviside function $h_{t_0}\left(t\right)$ at the “median level” satisfies the following nonlinear equation:

$$F_{TL-WP}(t_0+d;\theta ,b,\alpha ,\beta )=1-d,$$

(4)

where ${\displaystyle F_{TL-WP}(t_0;\theta ,b,\alpha ,\beta )=\frac{1}{2}}$ with

$$t_0=2^{-1/\beta }{\left(-\frac{1}{\alpha }log\left(1-{\left(\frac{\theta -log\left(e^{\theta }+1\right)+log\left(2\right)}{\theta }\right)}^{1/b}\right)\right)}^{1/\beta }.$$

(5)

Note that (4) has a unique root since the function $h\left(d\right)=F(t_0+d)-1+d$ is increasing and continuous.

The next theorem gives some estimates for the saturation in terms of the Hausdorff metric of the TL-GPS CDF function.

Theorem 1.

The Hausdorff distance d between the Heaviside function $h_{t_0}\left(t\right)$ and the CDF function $F_{TL-WP}(t;\theta ,b,\alpha ,\beta )$ defined by (3) satisfies

$$d_l=\frac{1}{2.1A}<d<\frac{ln\left(2.1A\right)}{2.1A}=d_r,$$

where

$$A=1+\frac{b\alpha \beta z{2}^{\frac{1-\beta }{\beta }}\left(e^{\theta }+1\right)\left(u^{-1}-1\right){\left(-\frac{1}{\alpha }log\left(1-u\right)\right)}^{\frac{\beta -1}{\beta }}}{e^{\theta }-1},$$

(6)

with $z=\theta -log\left(e^{\theta }+1\right)+log\left(2\right)$, $u={\left({\displaystyle \frac{z}{\theta }}\right)}^{1/b}$ and $2.1A>e^{1.05}$.

Proof of Theorem 1.

We define function $H\left(d\right)$ by

$$H\left(d\right)=F(t_0+d)-1+d,$$

where the CDF function $F\left(t\right)\equiv F_{TL-WP}(t;\theta ,b,\alpha ,\beta )$ is defined by (3). It is easy to show that $H^{\prime }\left(d\right)>0$, i.e., $H\left(d\right)$, is monotony increasing. Now, we will show that $H\left(d\right)$ can be approximated by

$$T\left(d\right)=-\frac{1}{2}+Ad,$$

where A is defined by (6). From the Taylor expansion, we have

$$H\left(d\right)=F\left(t_0\right)-1+(1+F^{\prime }\left(t_0\right))d+\mathcal{O}\left(d^2\right)=-\frac{1}{2}+(1+F^{\prime }\left(t_0\right))d+\mathcal{O}\left(d^2\right).$$

With simple calculations, we have

$$\begin{array}{ccc}\hfill F^{\prime }\left(t\right)& =& {\left(1-\frac{e^{\theta \left(1-{\left(1-e^{-2\alpha t^{\beta }}\right)}^b\right)}-1}{e^{\theta }-1}\right)}^{\prime }=\frac{-e^{\theta {\left(1-{\left(1-e^{-2\alpha t^{\beta }}\right)}^b\right)}^{\prime }}}{e^{\theta }-1}\hfill \\ & =& \frac{2b\alpha \beta \theta t^{\beta -1}{\left(1-e^{-2\alpha t^{\beta }}\right)}^{b-1}{e}^{\theta \left(1-{\left(1-e^{-2\alpha t^{\beta }}\right)}^b\right)-2\alpha t^{\beta }}}{e^{\theta }-1}\hfill \end{array}$$

Hence, $F^{\prime }\left(t_0\right)=A-1$ for $t_0$ defined by (5). Then, it follows from here that $T\left(d\right)-H\left(d\right)=\mathcal{O}\left(d^2\right)$, so function $T\left(d\right)$ approximates $H\left(d\right)$ for $d\to 0$ with $\mathcal{O}\left(d^2\right)$. In Figure 1, we present the graph of functions $T\left(d\right)$ and $H\left(d\right)$ for fixed values of parameters $\theta =1.63$, $b=2.71$, $\alpha =1.45$ and $\beta =1.06$. Function $T\left(d\right)$ is also monotonically increasing since $T^{\prime }\left(d\right)>0$. If $2.1A>e^{1.05}$, then $T\left(d_l\right)<0$ and $T\left(d_r\right)>0$, which completes the proof. □

Table 2. Values of Hausdorff distance d and its estimations.

$\mathit{\theta }$	b	$\mathit{\alpha }$	$\mathit{\beta }$	${\mathit{d}}_{\mathit{l}}$	d Computed by (4)	${\mathit{d}}_{\mathit{r}}$
0.12	1.31	1.71	8.31	0.096279	0.111481	0.225342
6.15	3.04	1.86	2.44	0.102241	0.130553	0.233152
0.63	2.01	3.05	0.71	0.092198	0.157327	0.219784
1.75	2.33	2.95	1.93	0.127773	0.165547	0.262893
0.75	0.64	1.56	2.14	0.186514	0.222460	0.313204
1.83	4.14	0.75	1.71	0.206195	0.240883	0.325568
0.15	0.98	0.89	0.68	0.235214	0.297660	0.340416
1.25	0.96	0.54	0.36	0.182461	0.307016	0.310406

presents some computational experiments for distinct combinations of distribution parameters $\theta$, b, $\alpha$ and $\beta$. We calculate values of Hausdorff approximation d with its left $d_l$ and right $d_r$ estimations using Theorem 1. Furthermore, some graphical examples are shown in Figure 2.

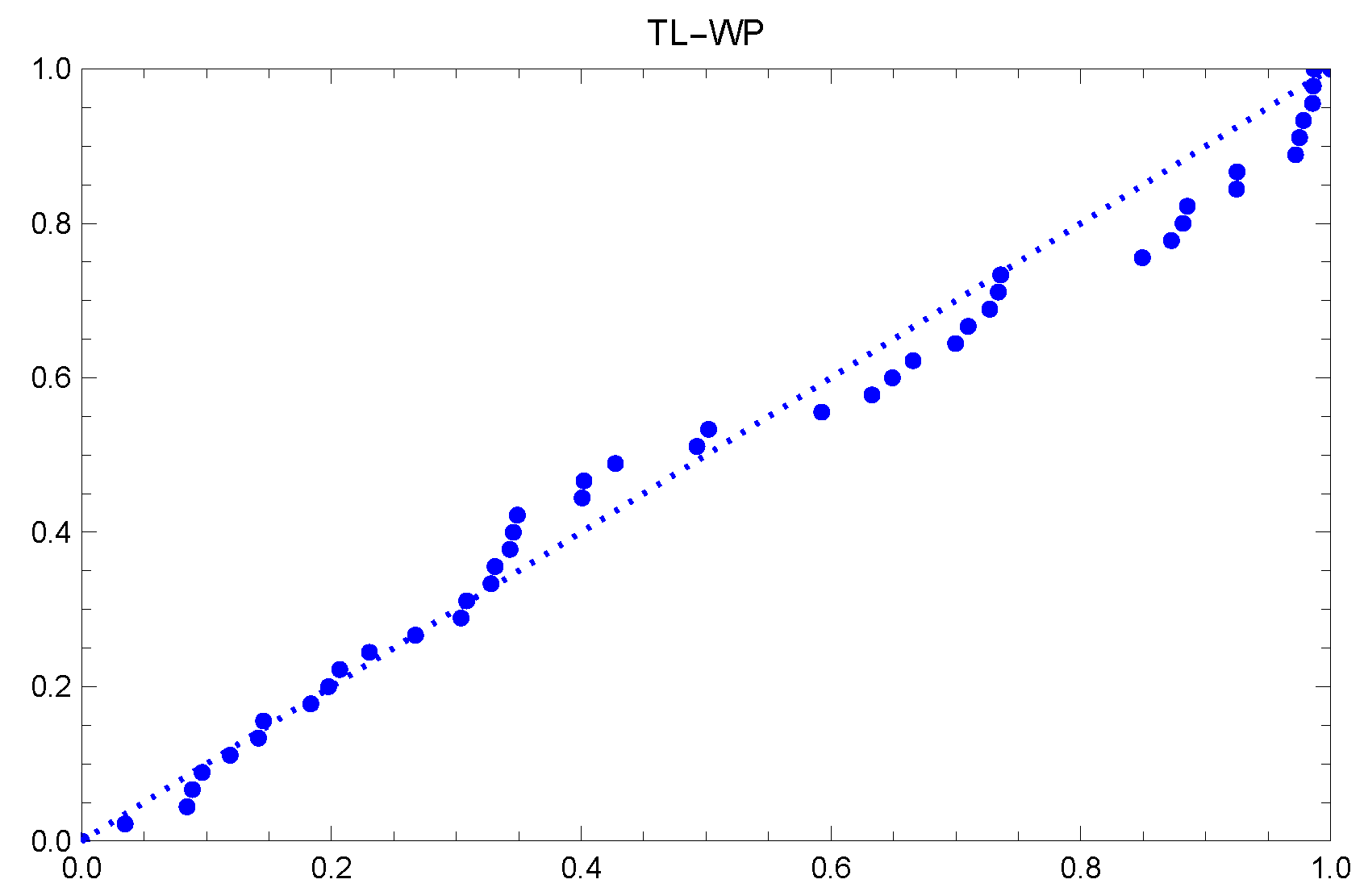
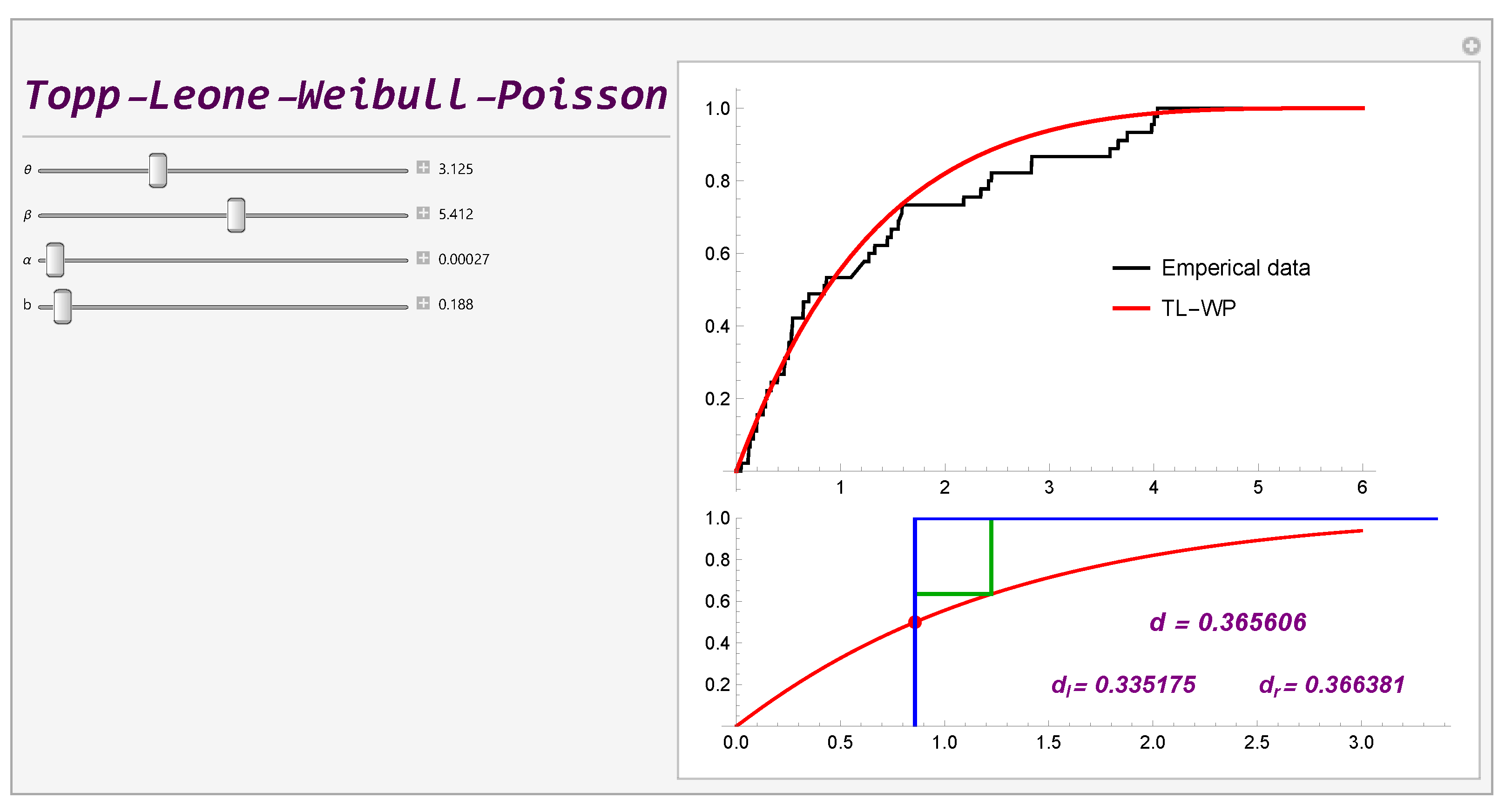
2.2. Some Applications

Let us consider one practical application using modeling data from the medical sector. The data set is a subset of the data corresponding to the survival times (in years) of a group of patients who received chemotherapy alone [33]. The data include the survival times (in years) for 45 patients.

data—chemotherapy
0.047	0.115	0.121	0.132	0.164	0.197	0.203	0.260	0.282	0.296
0.334	0.395	0.458	0.466	0.501	0.507	0.529	0.534	0.540	0.641
0.644	0.696	0.841	0.863	1.099	1.219	1.271	1.326	1.447	1.485
1.553	1.581	1.589	2.178	2.343	2.416	2.444	2.825	2.830	3.578
3.658	3.743	3.978	4.003	4.033

The data—chemotherapy can be approximated with the Topp-Leone-Weibull-Poisson (TL-WP) distribution with corresponding parameters $\theta =3.125$, $\beta =5.412$, $\alpha =0.00027$ and $b=0.188$. This fact is not rejected from standard goodness-of-fit statistical tests. The estimated P-P graphic is displayed in Figure 3.

	Statistic	p-Value
Anderson–Darling	1.20184	0.266033
Cramér–von Mises	0.11562	0.513591
Kolmogorov–Smirnov	0.116999	0.530605
Kuiper	0.168146	0.360015
Pearson ${\chi }^2$	6.33333	0.706149
Watson $U^2$	0.0836651	0.38578

From Theorem 1, for the considered parameters we obtain the values of Hausdorff distance $d=0.365606$ with estimates $d_l=0.335175$ and $d_r=0.366381$, respectively. The obtained result are presented by the dynamic module in Figure 4.

automobile insurance claims
1103	1939	4339	1491	3801	387	1299	326	1789	3310	443
673	6524	1217	1526	109	1279	852	1285	417	1333	3231
493	2201	464	773	4746	2596	1724	2132	1715	879	2467
4631	1856	911	966	789	1115	1716	841	385	1326	450
66	46	419	2315	508	48	34	261	3314	558	86
308	255	467	822	514	3047	298	220	182	61	411
111	381	198	552	28	278	703	535	407	138	193
27	88	318	11	8	38	53	88	49	99	12
123	125	10	77	43	21	382	64	61	42	9
56	44	26	41	44	91	40	509	47	143	59
70	19	153	483	107	93	135	122	62	150	370
48	73	656	172	54	34	143	26	22	116	70
243	462	49	69	157	215	128	46	45	190	90
46	37	91	519	111	44	21	102	25	32	95
64	113	617	511	46	65	0	34	24	71	97
30	11	17	35	15	24	35	0	912	75	5

We continue to investigate applications by considering the automobile insurance claims taken from [34]. The Topp-Leone-Weibull-Poisson (TL-WP) model is applied to this data set (normalized). We obtain the following parameters: $\theta =0.12$, $\beta =0.29$, $\alpha =1.66$ and $b=5.53$. According to the Cramér-von Mises and Pearson ${\chi }^2$ statistical tests, the null hypothesis that the data are distributed according to the TL-WP is not rejected at the 5 percent level. The estimated CDF and the fitted TL-WP distribution as well as the estimated P-P for the automobile insurance claims data set are plotted in Figure 5. We apply Theorem 1 and obtain the saturation $d=0.300044$ with corresponding estimates $d_l=0.225546$ and $d_r=0.33589$.

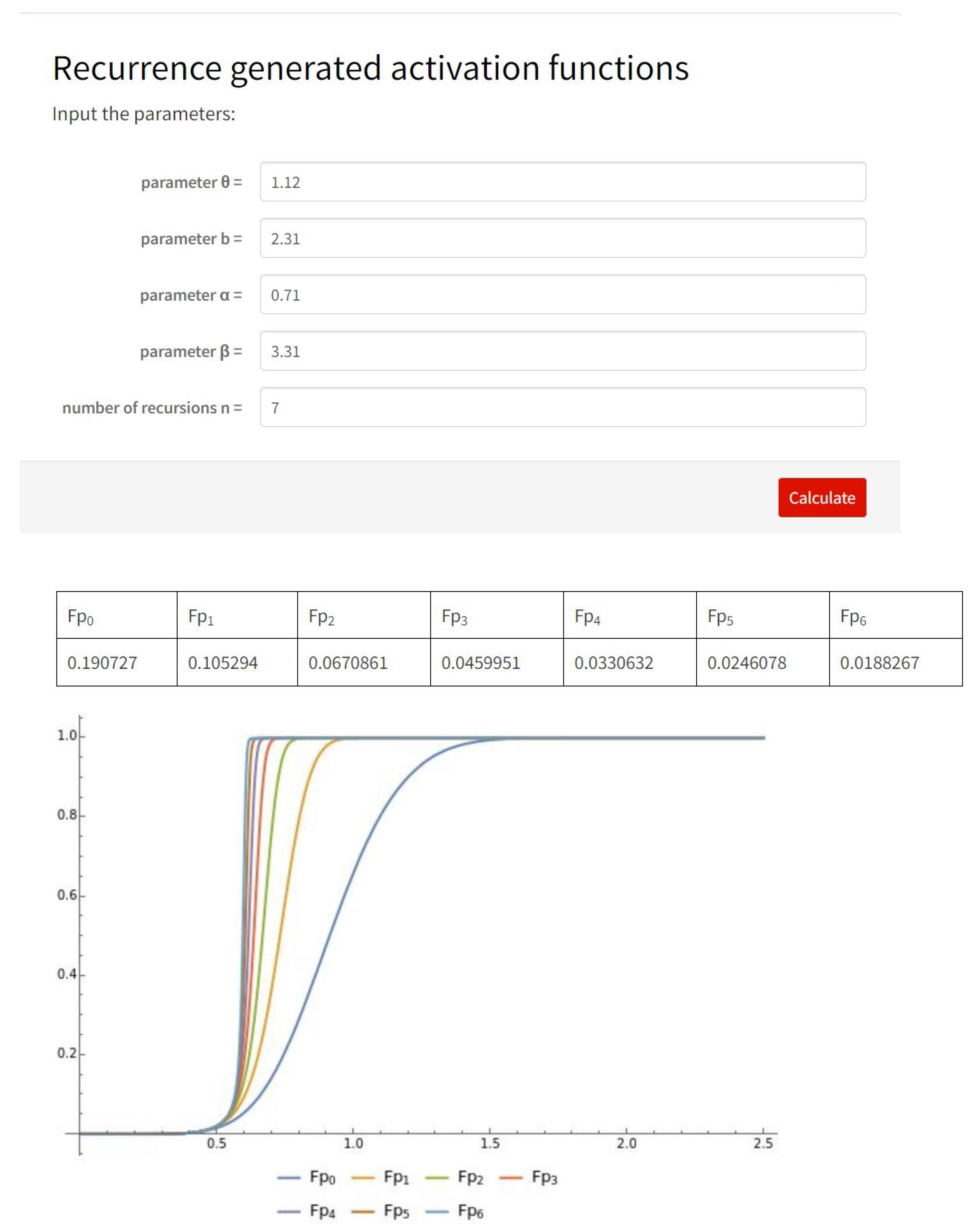
3. Family of Recurrence Generated Activation Functions

We define a family of recurrence generated activation functions based on Topp-Leone-Weibull-Poisson (TL-WP) distribution. Reader can consider a similar recurrence activation function based on TL-GPS distribution with different baseline distribution with relevant approximation models.

$$F_{i+1}\left(t\right)=1-\frac{e^{\theta \left(1-{\left(1-e^{-2\alpha {(t+F_i\left(t\right))}^{\beta }}\right)}^b\right)}-1}{e^{\theta }-1},$$

(7)

where $i=0,1,2,\dots$, with

$$F_0\left(t\right)=1-\frac{e^{\theta \left(1-{\left(1-e^{-2\alpha t^{\beta }}\right)}^b\right)}-1}{e^{\theta }-1};F_0\left(0\right)=0.$$

We can investigate the behavior of the CDF functions $F_i\left(t\right)$, $i=1,2,\dots$ in the Hausdorff sense. Hence, for the Hausdorff distance d we have

$$F_i(t_0+d)=1-d,$$

(8)

where $t_0$ is a positive solution of the equation ${\displaystyle F_i\left(t_0\right)=\frac{1}{2}}$.

The Hausdorff distance d for some combinations of parameters is shown in

Table 3. The Hausdorff distance d computed using (8) for recurrent family (7).

	$\mathit{\theta }=0.17$,	$\mathit{\theta }=2.05$,	$\mathit{\theta }=0.14$,	$\mathit{\theta }=1.83$,
	$\mathit{b}=1.21$	$\mathit{b}=3.04$	$\mathit{b}=0.96$	$\mathit{b}=4.14$
	$\mathbf{\alpha }=\mathbf{1}.\mathbf{81}$,	$\mathbf{\alpha }=\mathbf{2}.\mathbf{86}$,	$\mathbf{\alpha }=\mathbf{0}.\mathbf{68}$,	$\mathbf{\alpha }=\mathbf{0}.\mathbf{75}$,
	$\mathbf{\beta }=\mathbf{6}.\mathbf{29}$	$\mathbf{\beta }=\mathbf{1}.\mathbf{04}$	$\mathbf{\beta }=\mathbf{0}.\mathbf{98}$	$\mathbf{\beta }=\mathbf{1}.\mathbf{71}$
$F_0$	0.133785	0.162163000	0.319380	0.240883
$F_1$	0.061540	0.000221577	0.254825	0.157666
$F_2$	0.034156	0.000150430	0.231841	0.118191
$F_3$	0.020986	0.000150366	0.225110	0.095535
$F_4$	0.013805	0.000150365	0.224923	0.081530

. From here, we see that the Hausdorff distance becomes smaller with how deep we go into the recursion.

We propose a cloud software module implemented in the programming environment Wolfram Cloud for the computation of the Hausdorff distance for recurrence generated adaptive functions from family (7) (see Figure 6). This web (cloud) version of the module only requires browser and internet connection. The user defines the parameters of distribution and the number of recursions. The result is the calculated Hausdorff distance in table view with graphical representation of the generated recurrence adaptive functions.

4. Conclusions

This article is dedicated to an investigation of the characteristics of ”saturation“ in the Hausdorff sense for Topp-Leone-G power series. This research can help scientists in adequate construction and accurate and sufficiently flexible approximation models. We explore in detail the asymptotic behavior of the Hausdorff distance between the Heaviside step function and the Topp-Leone-Weibull-Poisson CDF function. For the considered Hausdorff approximation, some estimates are proved. Suitable numerical examples are shown. Additionally, we present modeling data from the medical sector and insurance. Furthermore, we discuss the application of new families of recurrence generated adaptive functions. The proposed methodology can be successfully applied to other sub-models of Topp-Leone-G power series as well as other commonly used CDFs in practice. Some related results can be found in [35,36,37,38,39]. Several dynamic modules implemented in CAS Wolfram Mathematica are included. A cloud version that only requires a browser and internet connection is offered for some of them. The proposed modules can be upgraded as well as adapted for other distributions and data sets.