Fourier Transform of the Lippmann-Schwinger Equation: Solving Vectorial Electromagnetic Scattering by Arbitrary Shapes

Abstract

In Electromagnetics, the field scattered by an ensemble of particles—of arbitrary size, shape, and material—can be obtained by solving the Lippmann–Schwinger equation. This singular vectorial integral equation is generally formulated in the direct space ${\mathbb{R}}^n$ (typically $n=2$ or $n=3$). In the article, we rigorously computed the Fourier transform of the vectorial Lippmann–Schwinger equation in the space of tempered distributions, ${\mathcal{S}}^{\prime }\left({\mathbb{R}}^3\right)$, splitting it in a singular and a regular contribution. One eventually obtains a simple equation for the scattered field in the Fourier space. This permits to draw an explicit link between the shape of the scatterer and the field through the Fourier Transform of the body indicator function. We compare our results with accurate calculations based on the T-matrix method and find a good agreement.

1. Introduction

The first use of Fourier transform (FT) to describe light scattering might be traced back to the early theories of Kirchhoff or Rayleigh and Sommerfeld [1]. The solution of Helmholtz equation that describes the field diffracted by an aperture in a screen was indeed related to the FT of its shape. Nowadays, solvers based on the Fourier expansion of electromagnetic fields are very efficient to model 1D or 2D periodic gratings [2,3], using the RCWA method [4,5], in close connection with experiments [6,7,8]. For 3D problems, a few results based on the FT of Maxwell equations are available. The calculation of the free space Green tensor [9,10,11,12], or a far-field description of the scattered field for a smooth particle [13], are presented. Using FT, a link between the far field scattered intensity and some geometrical properties of the scatterer (its Gaussian curvature) has been established, e.g., for the Porod’s law [14,15]. In other works, the polarization of electromagnetic waves in complex systems with scatterers was taken into account for an ensemble of point dipoles, e.g., solving the Bethe–Salpeter Equation in Fourier space [16]. However, to compute the vectorial scattered fields in arbitrary 3D geometries, the most popular methods [17], such as finite elements method (FEM) [18] or T-matrix computation [19], e.g., based on an expansion on vectorial spherical harmonics (VSH) [20,21,22], have been developed in real space.

These real space methods are, nevertheless, limited. For example, the memory requirement for FEM is huge when large spatial domains are to be modeled. The convergence of the T-matrix method, computed using the VSH ([17] see 3.1), is still debated [23] when close non-spherical scatterers—whose circumbscribing spheres intersect—are studied. It is therefore still interesting to propose new analytical methods, which is what we shall do in this article.

Budko and co-authors [24,25] made the first move towards a Fourier Transform of the Lippman Schwinger Equation (LSE) for 3D geometries. This work was limited, however, to a scatterer described by Hölder continuous functions, and dealt with the singular part of the LSE only. It shall be interesting to go further and make the FT of the whole LSE. This would permit to (i) relate the field scattered by objects to the Fourier transform of the indicator function (The indicator function—whose value is 1 inside the scatterer(s), 0 outside—is known to be a convenient descriptor of the geometrical properties of the scatterer [14]); to factorize the equation in the Fourier space, instead of dealing with a convolution in real space, and (ii) to solve for the scattered field in fast and convenient way, using tridimensional Fourier transforms [26].

In Section 2, we conduct a rapid review of the regularization procedure that permits us to unambiguously define the Integral equation, see [27,28], and split the kernel in a regular and a singular contribution. Following that, we will detail the calculation of the FT of each part of the equation, see Section 3 and Section 4, in the general case—as long as the scatterer is non-magnetic. For the singular part, see Section 3, we rely on [29] to explicitly express the FT. For the regular part, see Section 4, our approach is based on the work by Grafakos and Teschl [30] regarding the FT of radial (generalized) functions.

We shall gather the results in Section 5 to give the Fourier transform of electromagnetic LSE in ${\mathbb{R}}^3$. Eventually, we give a numerical example, solving the general equation in a few typical cases.

Note that the lengthy proofs and lemma have been gathered in [31].

2. Backgrounds and Purpose

The LS Equation for Electromagnetic Scattering

Stemming directly from the Maxwell equations, the LS equation that describes the field scattered by an arbitrary object in a uniform background is [24,28], in ${\mathbb{R}}^3$,

$$\begin{array}{c}\hfill \mathbf{E}(\mathbf{x},\omega )={\mathbf{E}}_{\mathrm{inc}}(\mathbf{x},\omega )+\left[{k_b}^2+\mathbf{grad}\mathrm{div}\right]{\int }_{{\mathbb{R}}^3}G\left(\parallel \mathbf{x}-{\mathbf{x}}^{\prime }\parallel \right)\chi ({\mathbf{x}}^{\prime },\omega )\mathbf{E}({\mathbf{x}}^{\prime },\omega )\mathrm{d}{\mathbf{x}}^{\prime },\end{array}$$

(1)

where

• $\mathbf{E}$ and ${\mathbf{E}}_{\mathrm{inc}}$ are the total and incident electric field;
• $k_b$ is the wavenumber in the background medium, assumed to be real;
• $\chi$ is the relative difference between scatterer and background complex permittivity: $\chi \left(\mathbf{x}\right):=[\epsilon \left(\mathbf{x}\right)-{\epsilon }_b]/{\epsilon }_b$. The scatterer medium is possibly dispersive—$\chi$ depends on $\omega$—, dissipative —$\chi$ is complex—, and anisotropic—$\chi$ is a $3\times 3$ tensor. In the case of an isotropic medium, $\chi$ boils down to a scalar. If $\epsilon \left(\mathbf{x}\right)$ is constant inside the scatterer, $\chi$ is proportional to the indicator function, and will be denoted like this in the following.
• G is the Green function of Helmholtz equation in vacuum (with $\mathbf{l}:=\mathbf{x}-{\mathbf{x}}^{\prime }$ and $l:=\Vert \mathbf{l}\Vert$).
  Note that if one chooses the $exp(-i\omega t)$ convention for harmonic time evolution (as we do), the outgoing Sommerfeld condition [32] imposes:

  $$\begin{array}{cc}\hfill G\left(l\right)& :=\frac{e^{+i{k}_{b}l}}{4\pi l},\hfill \end{array}$$

  (2)

  so that far enough from the scatterer, the wave behaves as an outgoing spherical wave that carries energy outwards.

As shown in textbooks ([28], p. 36), ([33], chap. 15), the $\mathbf{grad}\mathrm{div}$ operator in Equation (1) cannot be put straightforwardly under the integral sign. However, upon a careful procedure, Equation (1) can be recasted as the singular integral equation

$$\begin{array}{cc}\hfill {\mathbf{E}}_{\mathrm{inc}}(\mathbf{x},\omega )=& \left[\mathbb{I}+\frac{\chi }{3}\right]\mathbf{E}(\mathbf{x},\omega )-\underset{\epsilon \to 0}{lim}{\int }_{{\mathbf{x}}^{\prime }\in {\mathbb{R}}^3\setminus B(\mathbf{x},\epsilon )}{\mathbb{G}}_0\left(\mathbf{x}-{\mathbf{x}}^{\prime }\right)\chi ({\mathbf{x}}^{\prime },\omega )\mathbf{E}({\mathbf{x}}^{\prime },\omega )\mathrm{d}{\mathbf{x}}^{\prime }\hfill \\ \hfill & -{\int }_{{\mathbf{x}}^{\prime }\in {\mathbb{R}}^3}{\mathbb{G}}_1\left(\mathbf{x}-{\mathbf{x}}^{\prime }\right)\chi ({\mathbf{x}}^{\prime },\omega )\mathbf{E}({\mathbf{x}}^{\prime },\omega )\mathrm{d}{\mathbf{x}}^{\prime },\hfill \end{array}$$

(3)

where $\mathbb{I}$ is the unit tensor, ${\mathbb{G}}_0$ and ${\mathbb{G}}_1$ are, respectively, the “singular” part and the “regular” part of the Green tensors (with $\mathbf{l}:=\mathbf{x}-{\mathbf{x}}^{\prime }$ and $l:=\Vert \mathbf{l}\Vert$):

$$\begin{array}{cc}\hfill {\mathbb{G}}_0\left(\mathbf{l}\right)& :=\frac{1}{4\pi l^3}\left(3\mathbb{Q}-\mathbb{I}\right),\\ \hfill {\mathbb{G}}_1\left(\mathbf{l}\right)& :=G_{1I}\left(l\right)\mathbb{I}+G_{1Q}\left(l\right)\mathbb{Q},\end{array}$$

(4)

where

$$\mathbb{Q}:=\frac{\mathbf{l}\left({}^t\mathbf{l}\right)}{l^2}=\frac{1}{l^2}\left(\begin{array}{ccc}{l}_x{l}_x& l_x{l}_y& l_x{l}_z\\ l_y{l}_x& l_y{l}_y& l_y{l}_z\\ l_z{l}_x& l_z{l}_y& l_z{l}_z\end{array}\right),$$

(5)

and

$$\begin{array}{cc}\hfill G_{1I}\left(l\right)& :=\frac{e^{i{k}_{b}l}}{4\pi l^3}\left(-1+i{k}_{b}l-{\left(i{k}_{b}l\right)}^2\right)+\frac{1}{4\pi l^3},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill G_{1Q}\left(l\right)& :=\frac{e^{i{k}_{b}l}}{4\pi l^3}\left(3-3i{k}_{b}l+{\left(i{k}_{b}l\right)}^2\right)-\frac{3}{4\pi l^3}.\hfill \end{array}$$

(7)

Note that in the quasistatic limit, i.e., when $1/k_b$ is much larger than the size of the scatterer, the term with ${\mathbb{G}}_1$ cancels this out and only the principal value that contains ${\mathbb{G}}_0$ contributes.

Equation (3) defines a linear operator whose properties have been studied both in 2D [25] and 3D [24].

Our purpose is to give an explicit formula for the Fourier transform of Equation (3), with the key point being the computation of the Fourier transform of Green tensors ${\mathbb{G}}_0$ and ${\mathbb{G}}_1$. We will proceed in two steps. ${\mathbb{G}}_0$ will be Fourier transformed in a more general way than what has previously been carried out [24], and ${\mathbb{G}}_1$ will be handled using generalized functions theory.

3. Fourier Transform of the Singular Part

The definitions and properties of the Fourier Transform are given in Appendix A. There, we introduce a general notation for the FT, that depends on two parameters a and b, see Equation (A1). In the article, all the calculations are carried using $(a,b)=(1,-1)$. The results in the general case are then given without demonstration so that they can be easily adapted to any definition of the FT.

3.1. General Expression as a Convolution

Let f be an integrable function on the sphere ${\mathbb{S}}^{n-1}$ with mean 0. Following that, the FT can be defined, possibly as a generalized function.

We define accordingly

$$\langle W_f,\phi \rangle :=\underset{\epsilon \to 0}{lim}{\int }_{{\mathbb{R}}^n\setminus B(0,\epsilon )}\frac{f(x/|x\left|\right)}{{\left|x\right|}^n}\phi \left(x\right)\mathrm{d}x,$$

(8)

for $\phi \in \mathcal{S}\left({\mathbb{R}}^d\right)$. It has been shown that $W_f$ is a tempered distribution (see e.g., [34], p. 334),provided that the hypothesis “f has a zero mean over the sphere $\mathbb{S}$” is true (see also [24]). Eventually, the Fourier transform can be found (cf. [34], p. 336). It is the function (i.e., finite) given by:

$$\widehat{W_f}\left(\xi \right)={\int }_{{\mathbb{S}}^{n-1}}f\left(\theta \right)\left(log\frac{1}{|\xi ·\theta |}-\frac{i\pi }{2}\mathrm{sgn}(\xi ·\theta )\right)\mathrm{d}\theta ,$$

(9)

where ${\mathbb{S}}^{n-1}$ is the unit sphere on ${\mathbb{R}}^n$, and $\theta \in {\mathbb{S}}^{n-1}$ is the direction of the vector $x/\left|x\right|$ for $x\in {\mathbb{R}}^n$.

To carry on with the Fourier transform of the singular part, we defined the continuous operator $H_f$ by

$$H_f\left(u\right):=W_{f,1}\star u+W_{f,2}\star u,$$

(10)

where ⋆ represents the convolution, with $u\in {\mathrm{L}}^2$, and

$$\langle W_{f,1},u\rangle :=\underset{\epsilon \to 0}{lim}{\int }_{B(0,1)\setminus B(0,\epsilon )}\frac{f(x/|x\left|\right)}{{\left|x\right|}^n}u\left(x\right)\mathrm{d}x\mathrm{and}{W}_{f,2}:=1_{B{(0,1)}^c}\frac{f(x/|x\left|\right)}{{\left|x\right|}^n},$$

where $B{(0,1)}^c$ is the complementary of the ball of radius 1 in ${\mathbb{R}}^n$.

Besides, we will assume the following hypothesis:

Hypothesis 1.

$\widehat{W_f}$ is bounded.

Remark 1.

As we will see, that will be always the case in our framework.

Theorem 1.

$H_f$ is a continuous operator over the Hilbert space ${\mathrm{L}}^2\left({\mathbb{R}}^n\right)$ with a Fourier transform verifying:

$$\widehat{H_f\left(u\right)}=\widehat{W_f}\widehat{u}\in {\mathrm{L}}^2.$$

(11)

Proof. 

The operator $H_f$ is well-defined since, on one hand, $W_{f,1}$ is a distribution with compact support, u can be assimilated to a tempered distribution (${\mathrm{L}}^2\subset {\mathcal{S}}^{\prime }$) and, on the other hand $W_{f,2}$ and u are in ${\mathrm{L}}^2$.

Additionally, the Fourier transform of $H_f$ is well-defined and

$$\begin{array}{cc}\hfill \widehat{H_f\left(u\right)}& =\widehat{W_{f,1}}\widehat{u}+\widehat{W_{f,2}}\widehat{u}\hfill \\ \hfill & =\widehat{W_f}\widehat{u}\in {\mathrm{L}}^2,\hfill \end{array}$$

since $\widehat{W_f}$ is supposed to be bounded. Then $\overline{\mathcal{F}}\left(\widehat{H_f}\right)\in {\mathrm{L}}^2$, where $\overline{\mathcal{F}}$ denotes the inverse Fourier Transform.

The linear behaviour of $H_f$ is clear and, for the continuity, we have

$$\parallel H_f{\left(u\right)\parallel }_2=\parallel \widehat{H_f\left(u\right)}{\parallel }_2=\parallel \widehat{W_f}\widehat{u}{\parallel }_2\le C\parallel \widehat{u}{\parallel }_2=C{\parallel u\parallel }_2.$$

□

This theorem shows that one can factorize the singular part of the LS equation Equation (3), in the Fourier Domain. Such a factorization was obtained by Budko [24] in the case of a Hölder continuous indicator function. Theorem 1 permits to generalize it to step index profiles (with, e.g., an indicator that is a Heaviside function), for which the function ${\mathbf{x}}^{\prime }\mapsto \chi ({\mathbf{x}}^{\prime },\omega ).\mathbf{E}({\mathbf{x}}^{\prime },\omega )$ is L${}^2$ but not Hölder.

We now have to compute $\widehat{W_f}$.

3.2. Explicit Calculation

In agreement with the definition of ${\mathbb{G}}_0$, let us write each component of f as an homogeneous polynom $P\left(\theta \right)=c{\prod }_{k=1}^n{\theta }_k^{{\alpha }_k}$, where ${\alpha }_k$ are, respectively, even or odd numbers.

First, we can simply say that the part with the log function, in Equation (9), is null if f is an odd function, and the part with the $\mathrm{sgn}$ function is null if f is an even function.

$P\left(\theta \right)$ can be seen as a component of the polyadic tensor of order $s={\sum }_{k=1}^n{\alpha }_k$, whose FT can be deduced from [29].

The obtained results for low order tensors (up to 2) are gathered in the following tables, where $\Psi$ denotes the digamma function. Detail on the calculation of the integrals is provided in Appendix B.2, whereas the general demonstration can be found in [29].

In passing, we note that for polyadic tensors $W_f$, whose components are given in

Table 1. Singular integrals Equation (9) for even and odd tensors.

Tensor Components	Components of ${\mathit{W}}_{\mathit{f}\left(\mathit{\xi }\right)}$
1	$E_0^{{}^{\prime }}$
${\theta }_l$	$O_l=O_1^{{}^{\prime }}{\xi }_l$
${\theta }_l{\theta }_m$	$E_{lm}=E_{11}^{{}^{\prime }}{\xi }_l{\xi }_m+E_{22}^{{}^{\prime }}\left(-{\xi }_l{\xi }_m+{\delta }_{l,m}\right)$

, the Fourier Transformed tensor, $\widehat{W_f}$ are bounded operators, as seen from their components (see Table 1 and

Table 2. Coefficients for the singular integrals of the even and odd tensors.

Tensor Order	Definition of Coefficients	Value
0	$E_0^{{}^{\prime }}\equiv -{\int }_{\partial B(0,1)}log\left(|{\theta }_1^{{}^{\prime }}|\right)\mathrm{d}{\theta }^{{}^{\prime }}$	${\pi }^{n/2}\frac{\Psi (n/2)-\Psi (1/2)}{\Gamma (n/2)}$
1	$O_1^{{}^{\prime }}\equiv -i\pi /{\int }_{{\theta }_1^{{}^{\prime }}>0}{\theta }_1^{{}^{\prime }}\mathrm{d}{\theta }^{{}^{\prime }}$	$-(i\pi /2){\pi }^{\frac{n-1}{2}}\frac{2}{\Gamma \left(\right(n+1)/2)}$
2	$E_{11}^{{}^{\prime }}\equiv -{\int }_{\partial B(0,1)}log\left(|{\theta }_1^{{}^{\prime }}|\right){\theta }_1^{{}^{\prime }}{\theta }_1^{{}^{\prime }}\mathrm{d}{\theta }^{{}^{\prime }}$	${\pi }^{n/2}\frac{1}{2}\frac{\Psi \left(\right(n+2)/2)-\Psi (3/2)}{\Gamma \left(\right(n+2)/2)}$
	$E_{22}^{{}^{\prime }}\equiv -{\int }_{\partial B(0,1)}log\left(|{\theta }_1^{{}^{\prime }}|\right){\theta }_2^{{}^{\prime }}{\theta }_2^{{}^{\prime }}\mathrm{d}{\theta }^{{}^{\prime }}$	${\pi }^{n/2}\frac{1}{2}\frac{\Psi \left(\right(n+2)/2)-\Psi (1/2)}{\Gamma \left(\right(n+2)/2)}$

). This corresponds to our working hypothesis.

3.2.1. The Tridimentional Case, $n=3$

The case of ${\mathbb{R}}^3$ is of particular interest. Let us give some details, using the results:

$${\int }_{{\mathbb{S}}^2}log|{\theta }_1|\mathrm{d}\theta =-4\pi ,{\int }_{{\mathbb{S}}^2}log|{\theta }_1|{\theta }_1^2\mathrm{d}\theta =-\frac{4}{9}\pi ,{\int }_{{\mathbb{S}}^2}log|{\theta }_1|{\theta }_2^2\mathrm{d}\theta =-\frac{16}{9}\pi .$$

From Equation (9), one obtains that, if $f=\eta$ is a polynomial of degree 0,

$$\widehat{W_{\eta }}\left(\xi \right)=4\pi \eta .$$

(12)

Now, if $f\left((x_1,x_2,x_3)\right)=\eta x_i{x}_j$,

$$\widehat{W_f}\left(\xi \right)=-\frac{4\pi }{3}f\left(\xi \right)+\frac{16\pi }{9}\eta {\delta }_{i,j}.$$

(13)

So, if $f\left(l\right)=\frac{1}{4\pi }(3\mathbb{Q}-1)$,

$$\widehat{W_f}\left(\xi \right)=F\left(\tilde{\Theta }\right)=\frac{1}{3}\mathbb{I}-\widehat{\mathbb{Q}},$$

(14)

where $\tilde{\Theta }:=\frac{\xi }{\Vert \xi \Vert }$, and $\widehat{\mathbb{Q}}:=\frac{\xi \left({}^t\xi \right)}{{\Vert \xi \Vert }^2}$. The notation $F\left(\tilde{\Theta }\right)$ is introduced in agreement with [24], to emphasize that, as f is of zero mean on ${\mathbb{S}}^{n-1}$, the Fourier transform of the singular part only depends on $\frac{\xi }{\Vert \xi \Vert }$.

3.2.2. General Notation

Note that we can easily express the result in the general notation, as

$$\widehat{W_f}\left(\xi \right)=F\left(\tilde{\Theta }\right)=c_{a,b}^3\left(\frac{1}{3}\mathbb{I}-\widehat{\mathbb{Q}}\right),$$

(15)

where $c_{a,b}^3$ is defined as

$$c_{a,b}^3={\left(\frac{\left|b\right|}{{\left(2\pi \right)}^{1-a}}\right)}^{\frac{3}{2}}.$$

(16)

4. Fourier Transform of the Regular Part

4.1. Radial Distributions and Grafakos Theorem

As we will see below, in order to compute the FT of the regular part of Equation (3), we shall compute FT of radial distributions, and use specific results on this topic, demonstrated in [30]. Let us first recall some general definitions and properties. Following that, we will limit ourselves to a space dimension $n=3$.

4.1.1. Radial Distributions

While $\mathcal{S}\left({\mathbb{R}}^n\right)$ stands for the space of Schwartz functions on ${\mathbb{R}}^n$, we set:

$$\begin{array}{cc}\hfill & {\mathcal{S}}_{\mathrm{rad}}\left({\mathbb{R}}^n\right)=\{\phi \in \mathcal{S}\left({\mathbb{R}}^n\right):\phi =\phi \circ A,\forall A\in \mathcal{O}\left(n\right)\}\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & {\mathcal{S}}_{\mathrm{rad}}\left(\mathbb{R}\right)={\mathcal{S}}_{\mathrm{even}}\left(\mathbb{R}\right)=\{\phi \in \mathcal{S}\left(\mathbb{R}\right):\phi \left(x\right)=\phi (-x)\}\hfill \end{array}$$

(18)

where $\mathcal{O}\left(n\right)$ is the set of the orthogonal transformations of ${\mathbb{R}}^n$.

We define then the following functions:

$$\begin{array}{cc}\hfill & \left\{\begin{array}{ccc}\hfill \mathcal{S}\left({\mathbb{R}}^n\right)& \to & {\mathcal{S}}_{\mathrm{rad}}\left(\mathbb{R}\right)\hfill \\ \hfill \phi & \mapsto & \left(r\mapsto {\phi }^o\left(r\right):=\frac{1}{{\omega }_{n-1}}{\int }_{{\mathbb{S}}^{n-1}}\phi \left(r\theta \right)\mathrm{d}\theta \right)\hfill \end{array}\right.\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & \left\{\begin{array}{ccc}\hfill {\mathcal{S}}_{\mathrm{rad}}\left(\mathbb{R}\right)& \to & {\mathcal{S}}_{\mathrm{rad}}\left({\mathbb{R}}^n\right)\hfill \\ \hfill \phi & \mapsto & \left(x\mapsto {\phi }^O\left(x\right):=\phi \left(\right|x\left|\right)\right)\hfill \end{array}\right.\hfill \end{array}$$

(20)

(where ${\mathbb{S}}^{n-1}$ is the unit sphere on ${\mathbb{R}}^n$ and ${\omega }_{n-1}$ its surface area; with the convention ${\omega }_0=2$ and ${\phi }^o\left(x\right)=\frac{1}{2}(\phi \left(x\right)+\phi (-x)$, for $\phi \in \mathcal{S}\left(\mathbb{R}\right)$).

Definition 1.

A distribution $u\in {\mathcal{S}}^{\prime }\left({\mathbb{R}}^n\right)$ (with ${\mathcal{S}}^{\prime }\left({\mathbb{R}}^n\right)$ the space of tempered distributions on ${\mathbb{R}}^n$) is called radial if for all $A\in \mathcal{O}\left(n\right)$,

$$u=u\circ A,$$

that is,

$$\langle u,\phi \rangle =\langle u,\phi \circ A\rangle ,$$

for all $\phi \in \mathcal{S}\left({\mathbb{R}}^n\right)$. The set of all radial tempered distributions is denoted by ${\mathcal{S}}_{\mathrm{rad}}^{\prime }\left({\mathbb{R}}^n\right)$.

Proposition 1.

For $u\in {\mathcal{S}}_{\mathrm{rad}}^{\prime }\left({\mathbb{R}}^n\right)$ and $\phi \in \mathcal{S}\left({\mathbb{R}}^n\right)$,

$$\langle u,\phi \rangle =\langle u,{\phi }^{\mathrm{rad}}\rangle ,$$

(21)

where ${\phi }^{\mathrm{rad}}:={\left({\phi }^o\right)}^O$ (i.e., ${\phi }^{\mathrm{rad}}\left(x\right)={\phi }^o\left(\right|x\left|\right)$).

Given a function $\phi :{\mathbb{R}}^n\to \mathbb{R}$ and a fixed $x\in {\mathbb{R}}^n$, ${\phi }^o\left(\right|x\left|\right)$ is then the mean over the sphere of radius $\left|x\right|$ of the function $\phi$ (so, if $\phi$ is already radial, $\phi$ will be of the form $f\left(\right|x\left|\right)$ with $f:\mathbb{R}\to \mathbb{R}$, and we will have directly ${\phi }^o=f$).

Let us define the space

$${\mathcal{R}}_n:=r^{n-1}{\mathcal{S}}_{\mathrm{rad}}\left(\mathbb{R}\right)=\left\{\left(r\mapsto \psi \left(r\right)r^{n-1}\right),\psi \in {\mathcal{S}}_{\mathrm{rad}}\left(\mathbb{R}\right)\right\}.$$

(22)

Remark 2.

${\mathcal{R}}_n$ is a subspace $\mathcal{S}\left(\mathbb{R}\right)$ on which we can use the same topology; we denote its dual (set of the linear continuous functions defined over ${\mathcal{R}}_n$) by ${\mathcal{R}}_n^{\prime }$.

We switched from ${\mathcal{R}}_n^{\prime }$ to radials distributions of ${\mathcal{S}}^{\prime }\left({\mathbb{R}}^n\right)$ as follows:

• if u is radial distribution, we define $u_{\diamond }\in {\mathcal{R}}_n^{\prime }$ by

  $$\langle u_{\diamond },\psi \left(r\right)r^{n-1}\rangle :=\frac{2}{{\omega }_{n-1}}\langle u,{\psi }^O\rangle ,\psi \in {\mathcal{S}}_{\mathrm{rad}}\left(\mathbb{R}\right)$$

  (23)
• if $u_{\diamond }\in {\mathcal{R}}_n^{\prime }$, we define a radial distribution u by

  $$\langle u,\phi \rangle :=\frac{{\omega }_{n-1}}{2}\langle u_{\diamond },{\phi }^o\left(r\right)r^{n-1}\rangle ,\phi \in \mathcal{S}\left({\mathbb{R}}^n\right)$$

  (24)

4.1.2. Grafakos–Teschl Theorem

Theorem 2

([30]). Given $v_1$ in ${\mathcal{S}}^{\prime }\left(\mathbb{R}\right)$, we define a radial distribution $v_k$ on ${\mathbb{R}}^k$ ($k\in {\mathbb{N}}^{*}$) by

$$\langle v_k,\phi \rangle :=\frac{{\omega }_{k-1}}{2}\langle v_1,{\phi }^o\left(r\right)r^{k-1}\rangle ,\phi \in {\mathcal{S}}_{\mathrm{rad}}\left({\mathbb{R}}^k\right)$$

(25)

(if $\phi \in {\mathcal{S}}_{\mathrm{rad}}\left({\mathbb{R}}^n\right)$, then $\phi \left(x\right)={\phi }^o\left(\right|x\left|\right)$).

Let $u^k={\mathcal{F}}_k^{a,b}\left(v_k\right)$. We have then

$$-\frac{{\left(2\pi \right)}^a}{\left|b\right|r}\frac{\mathrm{d}}{\mathrm{d}r}{u}_{\diamond }^n=u_{\diamond }^{n+2}.$$

(26)

In the following, we will limit ourselves to $n=3$.

Besides, instead of using directly the Grafakos–Teschl theorem, we will use the following corollary:

Corollary 1.

Given $v_1$ in ${\mathcal{S}}^{\prime }\left(\mathbb{R}\right)$, we define the radial distribution $v_3$ on ${\mathbb{R}}^3$ by

$$\langle v_3,\phi \rangle :=\frac{{\omega }_2}{2}\langle v_1,{\phi }^o\left(r\right)r^2\rangle ,\phi \in {\mathcal{S}}_{\mathrm{rad}}\left({\mathbb{R}}^3\right)$$

(27)

(if $\phi \in {\mathcal{S}}_{\mathrm{rad}}\left({\mathbb{R}}^n\right)$, then $\phi \left(x\right)={\phi }^o\left(\right|x\left|\right)$). We have then, for all $\phi \in {\mathcal{S}}_{\mathrm{rad}}\left({\mathbb{R}}^3\right)$

$$\langle {\mathcal{F}}_3^{a,b}\left(v_3\right),\phi \rangle =-\frac{{\left(2\pi \right)}^{a+1}}{\left|b\right|}〈r\frac{\mathrm{d}}{\mathrm{d}r}\left({\mathcal{F}}_1^{a,b}\left(v_1\right)\right),{\phi }^o\left(r\right)〉.$$

(28)

Proof. 

With $u^3:={\mathcal{F}}_3^{a,b}\left(v_3\right)$ and $u^1:={\mathcal{F}}_1^{a,b}\left(v_3\right)$ we have

$$\begin{array}{cc}\hfill \langle u^3,\phi \rangle & =\frac{{\omega }_2}{2}\langle u_{\diamond }^3,{\phi }^o\left(r\right)r^2\rangle \mathit{cf}.\left(24\right)\hfill \\ \hfill & =\frac{{\omega }_2}{2}〈-\frac{{\left(2\pi \right)}^a}{\left|b\right|r}\frac{\mathrm{d}}{\mathrm{d}r}{u}^1,{\phi }^o\left(r\right)r^2〉\mathit{cf}.\left(26\right)\hfill \\ \hfill & =-\frac{{\left(2\pi \right)}^{a+1}}{\left|b\right|}〈r\frac{\mathrm{d}}{\mathrm{d}r}\left(u^1\right),{\phi }^o\left(r\right)〉,\hfill \end{array}$$

since ${\omega }_2=4\pi$. □

4.2. Fourier Transform of the Regular Part of $G_{1I}\left(l\right)\mathbb{I}$

Procedure for Computing the FT in ${\mathbb{R}}^3$

We aim at computing the FT of a radial distribution, say $v_3$. We will proceed using Corollary (1), in the following way:

• We need to find a one-dimensional distribution, $v_1$, which verifies

  $$\langle v_3,\phi \rangle =\frac{{\omega }_2}{2}\langle v_1,{\phi }^o\left(r\right)r^2\rangle .$$

  (29)
  (${\omega }_2=4\pi$ being the 1-sphere surface). Note that finding $v_1$ may be, generally speaking, a difficult task.
• One computes the one-dimensional Fourier Transform $u_1:={\widehat{v}}_1$.
• The FT we seek, $u_3:={\widehat{v}}_3$, is then defined by

  $$\langle u_3,\phi \rangle =-{\left(\frac{{\omega }_2}{2}\right)}^2\langle r\frac{\mathrm{d}{u}_1}{\mathrm{d}r},{\phi }^o\left(r\right)\rangle .$$

  (30)
• Note that if $\frac{\mathrm{d}{u}_1}{\mathrm{d}r}=f\left(r\right)$ is not a distribution, but a regular function, one directly writes

  $$u_3=-\pi \frac{f(\parallel l\parallel )}{\parallel l\parallel }.$$

  (31)

In practice, we want to compute the 3D Fourier transform of

$$\begin{array}{c}\hfill l\mapsto a_0\frac{({\mathrm{e}}^{{\mathrm{ik}}_{\mathrm{b}}\mathrm{l}}-1)}{4\pi l^3}+\frac{{\mathrm{e}}^{{\mathrm{ik}}_{\mathrm{b}}\mathrm{l}}}{4\pi l^3}(a_{1}l+a_2{l}^2).\end{array}$$

(32)

And we will later impose, to correspond to the Maxwell equation, that

$$\begin{array}{cc}\hfill a_0& =-1\hfill \\ \hfill a_1& =i{k}_b\hfill \\ \hfill a_2& =k_b^2\hfill \end{array}$$

The idea is thus to reduce the problem to a one dimensional Fourier transform computation. To proceed, we will use Theorem 2. However, this is not sufficient. Indeed, in this theorem, a one-dimensional distribution (denoted by $v_1$) is given and is used to compute the associated (Equation (27)) multidimensional distribution $v_3$. In our work, on the contrary, we start from a multidimensional distribution $v_3$, and $v_1$is not known a priori. To overcome this problem, we will first define (in an heuristic way) a one-dimensional distribution and use Theorem 2 to obtain an associated multidimensional distribution T (using Equation (27)) whose Fourier Transform is established by this very theorem. Finally, to conclude, it remains necessary to prove that the Fourier transform of T is the same as the Fourier transform of $v_3$. The proof relies on a recent result [35]), and we will not elaborate here.

Rewriting Equation (32), in the sense of generalized functions of ${\mathcal{S}}^{\prime }\left(\mathbb{R}\right)$, we define $v_1$ as:

$$\begin{array}{ccc}\hfill v_1\left(r\right)& =& a_0\left[(cos\left(k_{b}r\right)-1)T_{\frac{1}{{\left|r\right|}^3}}+isin\left(k_{b}r\right)T_{\frac{1}{r^3}}\right]+a_1\left[cos\left(k_{b}r\right)T_{\frac{1}{r^2}}+isin\left(k_{b}r\right)T_{\frac{\mathrm{sgn}\left(r\right)}{r^2}}\right]\hfill \\ & +& a_2\left[cos\left(k_{b}r\right)T_{\frac{1}{\left|r\right|}}+isin\left(k_{b}r\right)T_{\frac{1}{r}}\right].\hfill \end{array}$$

(33)

where $T_{\frac{1}{r^n}},T_{\frac{sgn\left(r\right)}{r^2}}$, and $T_{\frac{1}{{\left|r\right|}^n}},$ are the distributions associated to $r\mapsto \frac{1}{r^n}$, $r\mapsto \frac{sgn\left(r\right)}{r^2}$ and $r\mapsto \frac{1}{{\left|r\right|}^n}$, respectively.

We start by computing the one-dimensional Fourier transform of $v_1$.

Using the previous results on the Fourier Transform of distributions ([31], see Sec. I of Supplementary Information), ref. [36] we found, without difficulty:

$$\begin{array}{c}\hfill {\widehat{v}}_1=\sum _{s\in \{-1,0,1\}}\left[\gamma +ln|k-s{k}_b|+i\frac{s\pi }{2}\mathrm{sgn}\left(\mathrm{k}-\mathrm{s}{\mathrm{k}}_{\mathrm{b}}\right)\right]\times \\ \hfill \left[A_2{(k-s{k}_b)}^2+A_1(k-s{k}_b)+A_0\right],\end{array}$$

(34)

with

$$\begin{array}{ccc}\hfill A_0& =& -a_2{s}^2,\hfill \\ \hfill A_1& =& i{a}_{1}s,\hfill \\ \hfill A_2& =& a_0(3s^2-2)/2.\hfill \end{array}$$

(35)

Note that the detailed and rigorous computation is given in an external document for the specific and most important case of $n=3,$ and Maxwell equations. See, in particular, Ref. [31] (Sec. (IV. B) of the main text and Sec. (IV A.) of the Supplementary Information). To compute the FT of the associated 3D distribution $v_3$, according to Corollary 1 (with $a=1$, $b=-1$), we will have to compute the derivative of $\widehat{v_1}$, in the sense of generalized functions.

Using that

$$\frac{d}{dk}\mathrm{sgn}(k-sk{}_b)=2\delta (k-s{k}_b),$$

(36)

and the equalities

$$(k-s{k}_b)\delta (k-s{k}_b)=0,{(k-s{k}_b)}^2\delta (k-s{k}_b)=0,$$

we find that

$$\begin{array}{ccc}\hfill \frac{d{\widehat{v}}_1}{dk}=\sum _{s\in \{-1,0,1\}}& A_2& (1+2\gamma )(k-s{k}_b)+A_1(1+\gamma )+\frac{A_0}{k-s{k}_b}+\hfill \\ & & A_{1}ln|k-s{k}_b|+2A_2(k-s{k}_b)ln|k-s{k}_b|+\hfill \\ & & i\frac{\pi }{2}s\left[2A_0\delta (k-s{k}_b)+(A_1+2A_2(k-s{k}_b))\mathrm{sgn}(\mathrm{k}-{\mathrm{sk}}_{\mathrm{b}})\right].\hfill \end{array}$$

(37)

Computing the sum explicitly, one obtains:

$$\begin{array}{c}\hfill \frac{d{\widehat{v}}_1}{dk}=-a_2\left(T_{\frac{1}{k-k_b}}+T_{\frac{1}{k+k_b}}\right)+a_{0}kln\frac{|k^2-k_b^2|}{k^2}+\left(i{a}_1-a_0{k}_b\right)ln\frac{|k-k_b|}{|k+k_b|}\\ \hfill +i\frac{\pi }{2}[a_0\left[k\mathrm{sgn}\left(\mathrm{k}-{\mathrm{k}}_{\mathrm{b}}\right)-\mathrm{k}\mathrm{sgn}\left(\mathrm{k}+{\mathrm{k}}_{\mathrm{b}}\right)\right]+(i{a}_1-a_0{k}_b)\left[\mathrm{sgn}\left(\mathrm{k}-{\mathrm{k}}_{\mathrm{b}}\right)+\mathrm{sgn}\left(\mathrm{k}+{\mathrm{k}}_{\mathrm{b}}\right)\right]\\ \hfill -2a_2\left(\delta (k-k_b)-\delta (k+k_b)\right)].\end{array}$$

(38)

Then, using Corollary 1, with $a=1$, $b=-1$, $u_3=\widehat{v_3}$ and $u_1=\widehat{v_1}$, we seek ${\widehat{v}}_3$ such as

$$\langle {\widehat{v}}_3,\phi \rangle =-\frac{{\omega }_2^2}{4}〈k\frac{\mathrm{d}}{\mathrm{d}k}{\widehat{v}}_1,{\phi }^o\left(k\right)〉.$$

(39)

By linearity, ${\widehat{v}}_3$ is the sum of the contribution of each term of $k\frac{\mathrm{d}}{\mathrm{d}k}{\widehat{v}}_1$, calculated using Equation (39):

• The contribution of $-a_{2}k\left(T_{\frac{1}{k-k_b}}+T_{\frac{1}{k+k_b}}\right)$ to ${\widehat{v}}_3$ has been calculated, (see [31], Sec. IV. A. 3. of the Supplementary Information), and is

  $$\frac{{\omega }_2}{2}{a}_2{k}_b^{-1}\left[v.p.\left(\frac{1}{k-k_b}\right)-\frac{1}{k+k_b}\right],$$
• Rewriting $a_0{k}^{2}ln\frac{|k^2-k_b^2|}{k^2}=a_0{k}^2\left(ln|k-k_b|+ln|k+k_b|-2ln|k|\right)$, and using ([31], 1. and 2. page 14 of the main text),the contribution of this term to ${\widehat{v}}_3$ is

  $$-\frac{{\omega }_2}{2}{a}_{0}ln\frac{|k^2-k_b^2|}{k^2},$$
• Similarly, the term $\left(i{a}_1-a_0{k}_b\right)kln\frac{|k-k_b|}{|k+k_b|}$ gives a contribution

  $$-\frac{{\omega }_2}{2}\left(i{a}_1-a_0{k}_b\right)G\left(k\right)\mathrm{to}{\widehat{v}}_3,$$
• the term $i\frac{\pi }{2}{a}_{0}k\left[k\mathrm{sgn}\left(\mathrm{k}-{\mathrm{k}}_{\mathrm{b}}\right)-\mathrm{k}\mathrm{sgn}\left(\mathrm{k}+{\mathrm{k}}_{\mathrm{b}}\right)\right]$ gives a contribution, see ([31], 1. page 15 of the main text):

  $$i\pi a_0\frac{{\omega }_2}{2}{\mathbb{1}}_{B(0,k_b)}\left(k\right),$$
• a similar calculation proves that the term $i\frac{\pi }{2}(i{a}_1-a_0{k}_b)k\left[\mathrm{sgn}\left(\mathrm{k}-{\mathrm{k}}_{\mathrm{b}}\right)+\mathrm{sgn}\left(\mathrm{k}+{\mathrm{k}}_{\mathrm{b}}\right)\right]$ gives a contribution

  $$-i\pi \frac{{\omega }_2}{2}(i{a}_1-a_0{k}_b)F\left(k\right),$$
• the term $-i\pi a_{2}k\left(\delta (k-k_b)-\delta (k+k_b)\right)$ gives a contribution, (see [31], 2. page 15 of the main text):

  $$i\pi \frac{a_2}{k_b}\frac{{\omega }_2}{2}\delta \left(\right|k|-k_b),$$

where

$$F\left(k\right)=H\left(\right|k|-k_b)/|k|,\mathrm{and}G\left(k\right)=k^{-1}ln\left|\frac{k-k_b}{k+k_b}\right|,$$

which are both even functions of k.

Using the fact that

$${\widehat{v}}_3={\omega }_2\widehat{G_{1I}},$$

we obtain:

Proposition 2.

The Fourier Transform of the regular part:

$$l\mapsto \frac{e^{i{k}_{b}l}}{4\pi l^3}\left(a_0+a_{1}l+a_2{l}^2\right)-\frac{a_0}{4\pi l^3}$$

is ( with $k=\sqrt{k_x^2+k_y^2+k_z^2}$ )

$$\begin{array}{c}\hfill k\mapsto a_{0}P\left(k\right)+\frac{a_2}{k_b^2}A\left(k\right)-\frac{i{a}_1-a_0{k}_b}{2}\frac{M\left(k\right)}{k},\end{array}$$

(40)

with the definitions:

$$\begin{array}{ccc}\hfill A\left(k\right)& =& \frac{k_b^2}{k^2-k_b^2}+i\frac{\pi }{2}{k}_b\delta \left(\right|k|-k_b),\hfill \end{array}$$

(41)

$$\begin{array}{ccc}\hfill P\left(k\right)& =& -\frac{1}{2}ln\left|\frac{k^2-k_b^2}{k^2}\right|+i\frac{\pi }{2}{\mathbb{1}}_{B(0,k_b)},\hfill \end{array}$$

(42)

$$\begin{array}{ccc}\hfill M\left(k\right)& =& k\left(G\left(k\right)+i\pi F\left(k\right)\right)=ln\left|\frac{k-k_b}{k+k_b}\right|+i\pi H\left(\right|k|-k_b).\hfill \end{array}$$

(43)

4.3. Fourier Transform of the Regular Part of $G_{1Q}\left(l\right)\mathbb{Q}$

We now want to Fourier Transform the tensorial valued function

$$\begin{array}{c}\hfill l\mapsto \left[\frac{e^{i{k}_{b}l}}{4\pi l^3}\left(c_0+c_{1}l+c_2{l}^2\right)-\frac{c_0}{4\pi l^3}\right]\mathbb{Q}.\end{array}$$

(44)

And we will later impose

$$\begin{array}{c}\hfill c_0=3\\ \hfill c_1=-3i{k}_b\\ \hfill c_2=-k_b^2\end{array}$$

Let us define $l\mapsto G_{1Q}\left(l\right)$ with

$$\begin{array}{c}\hfill G_{1Q}\left(l\right)=\left[\frac{e^{i{k}_{b}l}}{4\pi l^3}\left(c_0+c_{1}l+c_2{l}^2\right)-\frac{c_0}{4\pi l^3}\right].\end{array}$$

(45)

Contrary to the previous case, the components of $G_{1Q}\left(l\right)\underline{\underline{Q}}$ do not possess radial symmetry, since they have the form $\frac{l_i{l}_j}{l^2}{G}_{1Q}\left(l\right)$ ($\in {\mathrm{L}}_{\mathrm{loc}}^1\left({\mathbb{R}}^3\right)$): we cannot directly use Corollary 1. Therefore, in order to proceed, we will first build a radial distribution T such that

$$l_i{l}_{j}T=\frac{l_i{l}_j}{l^2}{G}_{1Q}\left(l\right).$$

We will then have (denoting by D the differentiation in the sense of the generalized functions)

$$\mathcal{F}\left(\frac{l_i{l}_j}{l^2}{G}_{1Q}\left(l\right)\right)=\mathcal{F}\left(l_i{l}_{j}T\right)=-D_{k_i}{D}_{k_j}\mathcal{F}\left(T\right).$$

(46)

Heuristically (since the following $\frac{1}{l^2}{G}_{1Q}\left(l\right)$ function is not definite at 0), we have to compute the 3D Fourier transform of $l\mapsto v_1\left(l\right)$ defined with,

$$v_1\left(l\right)=\left[\frac{e^{i{k}_{b}l}-1}{l^5}{c}_0+\frac{e^{i{k}_{b}l}}{l^5}\left(c_{1}l+c_2{l}^2\right)\right],$$

and to use a unidimensional Fourier Transform computation (Corollary 1).

4.3.1. Fourier Transform of $v_1$

Expressing $v_1$ as a generalized function, we obtain:

$$\begin{array}{ccc}\hfill v_1\left(r\right)& =& c_0\left[(cos\left(k_{b}r\right)-1)T_{\frac{1}{{\left|r\right|}^5}}+isin\left(k_{b}r\right)T_{\frac{1}{r^5}}\right]+c_1\left[cos\left(k_{b}r\right)T_{\frac{1}{r^4}}+isin\left(k_{b}r\right)T_{\frac{\mathrm{sgn}\left(r\right)}{r^4}}\right]\hfill \\ & +& c_2\left[cos\left(k_{b}r\right)T_{\frac{1}{{\left|r\right|}^3}}+isin\left(k_{b}r\right)T_{\frac{1}{r^3}}\right].\hfill \end{array}$$

(47)

As in the previous case, we compute the one-dimensional Fourier Transform of $v_1$ in the sense of generalized functions, and obtain:

$$\begin{array}{c}\hfill {\widehat{v}}_1=\frac{-1}{2}\sum _{s\in \{-1,0,1\}}\left[\gamma +ln|k-s{k}_b|+i\frac{s\pi }{2}\mathrm{sgn}\left(\mathrm{k}-\mathrm{s}{\mathrm{k}}_{\mathrm{b}}\right)\right]\times \\ \hfill \left[\frac{C_2}{6}{(k-s{k}_b)}^4+\frac{C_1}{3}{(k-s{k}_b)}^3+C_0{(k-s{k}_b)}^2\right],\end{array}$$

(48)

where the $C_{0,1,2}$ are given by

$$\begin{array}{ccc}\hfill C_0& =& -c_2{s}^2,\hfill \\ \hfill C_1& =& i{c}_{1}s,\hfill \\ \hfill C_2& =& c_0(3s^2-2)/2\hfill \end{array}$$

(49)

Note that the detailed and rigorous computation is given in an external document for the specific case of $n=3,$ and Maxwell equations. See, in particular, [31], Sec. (IV. C) of main text and Sec. (IV B.) of Supplementary Information.

Following that, we need to compute the derivative of these expressions (in the sense of the generalized functions) using the Lemma (II.12), see ([31], p. 13 of Supplementary Information).

We eventually obtain:

$$\begin{array}{ccc}\hfill \frac{d{\widehat{v}}_1}{dk}=-\frac{1}{2}& & \sum _{s\in \{-1,0,1\}}{C}_2(\frac{2}{3}\gamma +\frac{1}{6}){(k-s{k}_b)}^3+C_1(\gamma +\frac{1}{3}){(k-s{k}_b)}^2+C_0(2\gamma +1)(k-s{k}_b)+\hfill \\ & & \left[2C_0(k-s{k}_b)+C_1{(k-s{k}_b)}^2+\frac{2}{3}{C}_2{(k-s{k}_b)}^3\right]ln|k-s{k}_b|+\hfill \\ & & i\frac{\pi }{2}s\left[2C_0(k-s{k}_b)+C_1{(k-s{k}_b)}^2+\frac{2}{3}{C}_2{(k-s{k}_b)}^3\right]\mathrm{sgn}(\mathrm{k}-{\mathrm{sk}}_{\mathrm{b}}).\hfill \end{array}$$

(50)

Rearranging and differentiating, we obtain, using

$$\begin{array}{ccc}\hfill {\eta }_{-1}& =& 4c_2{k}_b+2i{c}_1{k}_b^2-2c_0{k}_b^3/3\hfill \end{array}$$

(51)

$$\begin{array}{ccc}\hfill {\eta }_0& =& 4c_2+4i{c}_1{k}_b-2c_0{k}_b^2\hfill \end{array}$$

(52)

$$\begin{array}{ccc}\hfill {\eta }_1& =& 2i{c}_1-2c_0{k}_b\hfill \end{array}$$

(53)

$$\begin{array}{ccc}\hfill {\eta }_2& =& -2c_0/3\hfill \end{array}$$

(54)

$$\begin{array}{ccc}\hfill -D_{k_i}{D}_{k_j}\left(k^{-1}\frac{d{\widehat{v}}_1}{dk}\right)=& \frac{R_{i,j}}{2}+i\frac{\pi }{2}[-4\frac{c_2}{k_b}\delta \left(\right|k|-k_b)\frac{k_i{k}_j}{k^2}+\hfill & \\ & 2{\eta }_2{\delta }_{i,j}\hfill & \left(\mathrm{if}\right|k|\le k_b)\hfill \\ & (\frac{{\eta }_1}{\left|k\right|}-\frac{{\eta }_{-1}}{{\left|k\right|}^3}){\delta }_{i,j}+(-\frac{{\eta }_1}{\left|k\right|}+3\frac{{\eta }_{-1}}{{\left|k\right|}^3})\frac{k_i{k}_j}{k^2}]\hfill & \left(\mathrm{if}\right|k|\ge k_b)\hfill \end{array}$$

(55)

with

$$\begin{array}{c}\hfill R_{i,j}=\left[\frac{2}{3}{c}_{0}ln\left|\frac{k^2-k_b^2}{k^2}\right|-\frac{{\eta }_{-1}}{k_b{k}^2}+\frac{1}{2}\left({\eta }_{1}k-\frac{{\eta }_{-1}}{k}\right)\frac{1}{k^2}ln\left|\frac{k-k_b}{k+k_b}\right|\right]{\delta }_{i,j}+\\ \hfill \left[-\frac{1}{2}\left({\eta }_{1}k-3\frac{{\eta }_{-1}}{k}\right)\frac{1}{k^2}ln\left|\frac{k-k_b}{k+k_b}\right|+\left(-4c_2\frac{1}{k^2-k_b^2}+\frac{3{\eta }_{-1}}{k_b{k}^2}\right)\right]\frac{k_i{k}_j}{k^2}.\end{array}$$

(56)

Using Equation (46), we obtain, for the $(i,j)$ component:

$$\begin{array}{cc}\hfill \mathcal{F}\left(G_{1Q}\left(l\right){\mathbb{Q}}_{(i,j)}\right)=\left(-\frac{1}{2}\right)\times \left(-D_{k_i}{D}_{k_j}\left(k^{-1}\frac{d{\widehat{v}}_1}{dk}\right)\right)& \\ \hfill =\left[-\frac{c_0}{6}ln\left|\frac{k^2-k_b^2}{k^2}\right|+\frac{{\eta }_{-1}}{4k_b{k}^2}-\frac{1}{8}\left({\eta }_{1}k-\frac{{\eta }_{-1}}{k}\right)\frac{1}{k^2}ln\left|\frac{k-k_b}{k+k_b}\right|\right]{\delta }_{i,j}+& \\ \hfill \left[\frac{1}{8}\left({\eta }_{1}k-3\frac{{\eta }_{-1}}{k}\right)\frac{1}{k^2}ln\left|\frac{k-k_b}{k+k_b}\right|+\left(c_2\frac{1}{k^2-k_b^2}-\frac{3{\eta }_{-1}}{4k_b{k}^2}\right)\right]\frac{k_i{k}_j}{k^2}+\\ \hfill i\frac{\pi }{2}\left[\frac{c_2}{k_b}\delta \left(\left|k\right|-k_b\right)\frac{k_i{k}_j}{k^2}+\left\{\begin{array}{c}-\frac{{\eta }_2}{2}{\delta }_{i,j}\mathrm{if}\left|k\right|<k_b\\ -\frac{1}{4}\left(\frac{{\eta }_1}{\left|k\right|}-\frac{{\eta }_{-1}}{{\left|k\right|}^3}\right){\delta }_{i,j}+\frac{1}{4}\left(\frac{{\eta }_1}{\left|k\right|}-3\frac{{\eta }_{-1}}{{\left|k\right|}^3}\right)\frac{k_i{k}_j}{k^2}\mathrm{if}\left|k\right|>k_b\end{array}\right\}\right].\end{array}$$

(57)

From this, using Equations (40)–(43), we can deduce:

$$\begin{array}{ccc}\hfill \mathcal{F}\left(G_{1I}\left(l\right)\mathbb{I}+G_{1Q}\left(l\right)\mathbb{Q}\right)& =& \left(a_0+\frac{c_0}{3}\right)P\left(k\right)\mathbb{I}+k_b^{-2}A\left(k\right)\left(a_2\mathbb{I}+c_2\widehat{\mathbb{Q}}\right)\hfill \\ \hfill -\frac{i{a}_1-a_0{k}_b}{2}\frac{M\left(k\right)}{k}\mathbb{I}+& & \frac{{\eta }_{-1}}{8}\left(\frac{2}{k_b}+\frac{M\left(k\right)}{k}\right)k^{-2}\left[\mathbb{I}-3\widehat{\mathbb{Q}}\right]\hfill \\ \hfill +\frac{{\eta }_1}{8}\frac{M\left(k\right)}{k}\left[\widehat{\mathbb{Q}}-\mathbb{I}\right].\end{array}$$

(58)

4.3.2. Expression in the General Notation

To express Equation (58) in the general notation for the Fourier Transform, let us first define

$$\begin{array}{c}\hfill {\tilde{a}}_i=\frac{a_i}{k_b^i}\\ \hfill {\tilde{c}}_i=\frac{c_i}{k_b^i}\end{array}$$

The expression in general notation is obtained from Equation (58) replacing, $a_i$ by ${\tilde{a}}_i$, $c_i$ by ${\tilde{c}}_i$, $k_b$ by $k_b/\left|b\right|$, and multiplying the whole expression by $c_{a,b}^3$.

5. Discussion

5.1. Integrability Condition

In order to have a Fourier Transform, the singular part should necessarily be integrable on the unit sphere ${\mathbb{S}}^{n-1}$, which imposes a condition on the zeroth order coefficients only. More precisely, one requires that [24]

$$\begin{array}{c}\hfill {\int }_{{\mathbb{S}}^{n-1}}{\mathbb{G}}_s\mathrm{d}S=0.\end{array}$$

This condition is always satisfied for the odd tensor terms in ${\mathbb{G}}_s$, but for even tensors, up to order 2, one obtains:

$$\begin{array}{c}\hfill {\int }_{{\mathbb{S}}^{n-1}}\left(a_0\mathbb{I}+c_0\mathbb{Q}\right)\mathrm{d}S=0.\end{array}$$

which imposes

$$\begin{array}{c}\hfill c_0=-3a_0,\end{array}$$

which is satisfied by the Maxwell kernel Equation (4).

5.2. At Infinity: Sommerfeld’s Rule

The function $\mathbf{r}\mapsto \mathbf{E}$ should verify some limit condition, which corresponds to scattering by an object in an homogeneous space. Far enough from the scatterer [32], the field $\mathbf{E}$ should have only transverse components, e.g., $\mathbb{Q}E\left(l\right)\underset{l\to +\infty }{⟶}0$. As this should be fulfilled independently of the object shape $\chi$, the kernel should verify $\mathbb{Q}\mathbb{G}\underset{l\to +\infty }{⟶}0$. Noting that $\mathbb{Q}$ is a projector, and assuming that the integrability condition, Section 5.1, is satisfied, this imposes

$$\begin{array}{c}\hfill a_2=-c_2\end{array}$$

Note that this condition is satisfied by the Maxwell kernel Equation (4).

5.3. Electromagnetic Scattering

Considering that, for the Maxwell scattering kernel,

$$\begin{array}{cc}\hfill a_0& =-1c_0=3\hfill \\ \hfill a_1& =i{k}_b{c}_1=-3i{k}_b\hfill \\ \hfill a_2& =k_b^2{c}_2=-k_b^2\hfill \end{array}$$

one obtains ${\eta }_{-1}={\eta }_1=0$.

This leads to the following expression for the FT:

$$\begin{array}{ccc}\hfill \mathcal{F}\left({\mathbb{G}}_1\right)& =& \left(\mathrm{v}.\mathrm{p}.\frac{{k_b}^2}{k^2-{k_b}^2}+i\frac{\pi }{2}{k}_b{\delta }_{S(0,k_b)}\left(k\right)\right)\left[\mathbb{I}-\widehat{\mathbb{Q}}\right],\hfill \end{array}$$

(59)

Using the general Fourier notation defined Equation (A1), we obtain:

$$\begin{array}{ccc}\hfill \mathcal{F}\left({\mathbb{G}}_1\right)& =& c_{a,b}^3{A}_{a,b}\left(k\right)\left[\mathbb{I}-\widehat{\mathbb{Q}}\right],\hfill \end{array}$$

(60)

$$\begin{array}{ccc}\hfill A_{a,b}\left(k\right)& =& \left(\mathrm{v}.\mathrm{p}.\frac{{k_b}^2}{b^2{k}^2-{k_b}^2}+i\frac{\pi }{2}\frac{k_b}{\left|b\right|}{\delta }_{S(0,k_b/|b\left|\right)}\left(k\right)\right),\hfill \end{array}$$

(61)

where $c_{a,b}^3$ is defined by Equation (16).

Finally, we obtain the Fourier Transform of the LS Equation for scattering, using the general Fourier Transform notations as:

$${\widehat{{\mathbf{E}}_{\mathrm{inc}}}}_{(\mathbf{k},\omega )}={\widehat{\mathbf{E}}}_{(\mathbf{k},\omega )}+{\left(\frac{\left|b\right|}{{\left(2\pi \right)}^{a+1}}\right)}^{\frac{3}{2}}\left[A_{a,b}\left(k\right)\left(\widehat{\mathbb{Q}}-\mathbb{I}\right)+\widehat{\mathbb{Q}}\right]\left(\widehat{\chi }\star \widehat{\mathbf{E}}\right),$$

(62)

with $k=\sqrt{k_x^2+k_y^2+k_z^2}$, and $\mathcal{F}\left(\chi \right)$ is, e.g., in the case of an isotropic dielectric, the (3D) Fourier Transform of $(x,y,z;\omega )\mapsto \epsilon (x,y,z;\omega )/{\epsilon }_b\left(\omega \right)-1$, where ${\epsilon }_b\left(\omega \right)$ is the background permittivity. In the anistropic case, both $\chi$ and $\widehat{\chi }$ are 3 × 3 matrix.

For a scattering problem, this equation relates the scattered vectorial quantity to the Fourier transform of the object shape, described analytically by its indicator function.

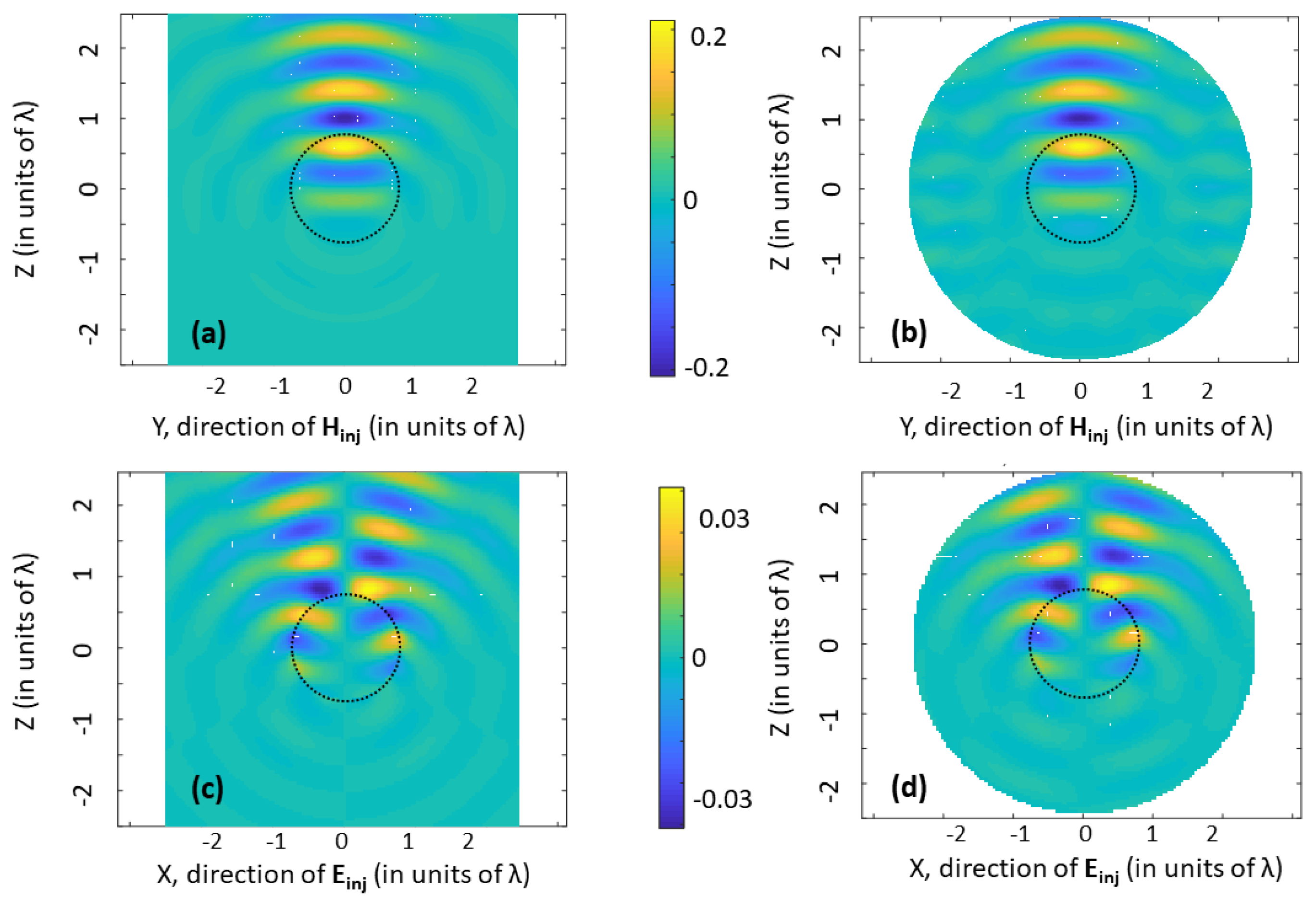
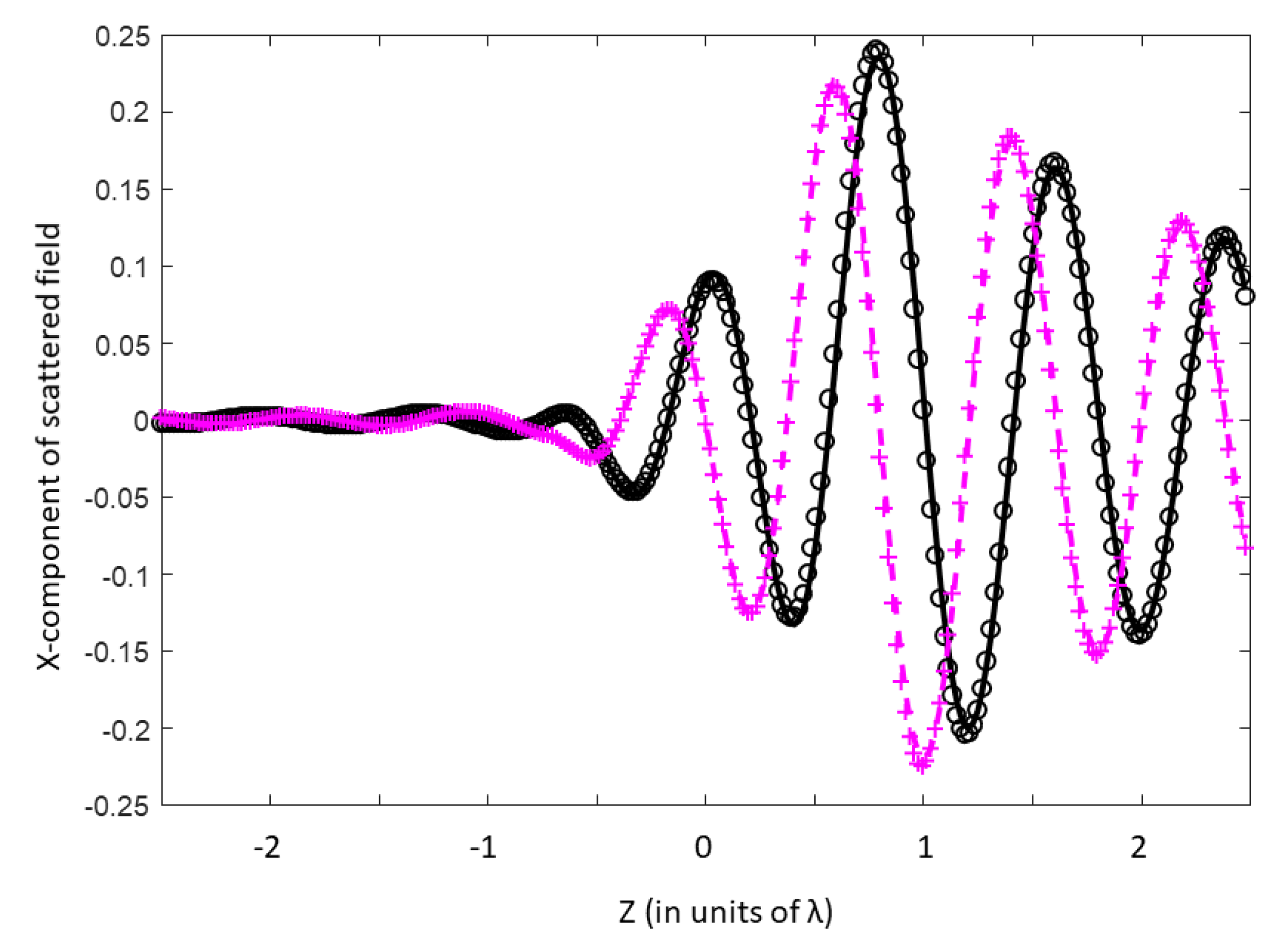
5.3.1. Solution for a Spherical Scatterer, in the Low Contrast Limit

To give an example, we analytically solved Equations (61) and (62). Let us first consider the limit of low index contrast. Note that this corresponds to typical experimental conditions in biophotonics [37,38].

In this case, $\widehat{\chi }\left(\mathbf{k}\right)\ll 1$ in ${\mathbb{R}}^3$, and Equation (62) can be inverted easily to give:

$$\widehat{{\mathbf{E}}_{\mathrm{inc}}}=\widehat{\mathbf{E}}+{\left(\frac{\left|b\right|}{{\left(2\pi \right)}^{a+1}}\right)}^{\frac{3}{2}}\left[A_{a,b}\left(k\right)\left(\widehat{\mathbb{Q}}-\mathbb{I}\right)+\widehat{\mathbb{Q}}\right]\left(\widehat{\chi }\star \widehat{{\mathbf{E}}_{\mathrm{inc}}}\right).$$

(63)

Considering a plane wave excitation, and using, in the following, the notation $\widehat{u}$ for the FT obtained with $a=1,b=-1$ (see Appendix A),

$$\widehat{{\mathbf{E}}_{\mathrm{inc}}}={\left(2\pi \right)}^3{\mathbf{E}}_{\mathbf{o}}\delta (\mathbf{k}-{\mathbf{k}}_{\mathbf{b}}).$$

Then, $\widehat{\chi }\star \widehat{{\mathbf{E}}_{\mathrm{inc}}}={\left(2\pi \right)}^3{\mathbf{E}}_{\mathbf{o}}\widehat{\chi }(\mathbf{k}-{\mathbf{k}}_{\mathbf{b}})$, and the scattered field, defined as ${\mathbf{E}}_{\mathbf{s}}\equiv \mathbf{E}-{\mathbf{E}}_{\mathrm{inc}}$ is given by:

$${\widehat{{\mathbf{E}}_s}}_{(\mathbf{k},\omega )}=-\left[\frac{k_b^2\widehat{\chi }(\mathbf{k}-{\mathbf{k}}_{\mathbf{b}})}{k^2-k_b^2}+i\frac{\pi }{2}{k}_b\delta (k-k_b)\widehat{\chi }(\mathbf{k}-{\mathbf{k}}_{\mathbf{b}})\right]\left(\widehat{\mathbb{Q}}-\mathbb{I}\right){\mathbf{E}}_{\mathbf{o}}-\widehat{\chi }(\mathbf{k}-{\mathbf{k}}_{\mathbf{b}})\widehat{\mathbb{Q}}{\mathbf{E}}_{\mathbf{o}}$$

(64)

This equation gives the analytic solution, in Fourier space, for the (vectorial) field scattered by an arbitrarily shaped scatterer in the regime of small index contrast.

Thanks to, e.g., numerical inverse Fourier Transform, one can obtain the 3D field plots in real space, see Figure 1 and Figure 2, using, for a dielectric sphere of radius $\rho$,

$$\widehat{\chi }\left(\mathbf{k}\right)\equiv \widehat{\chi }(\parallel \mathbf{k}\parallel )=\frac{\epsilon -{\epsilon }_b}{{\epsilon }_b}{j}_1(\parallel \mathbf{k}\parallel \rho )/(\parallel \mathbf{k}\parallel \rho ),$$

where $j_1$ is the spherical Bessel function of order 1. The calculation obtained from Equation (64) is in good agreement with Mie theory—see Figure 1 and Figure 2.

One notice that the injected field has no $\mathbf{z}$ component, and the latter appears in the scattering process, see Figure 1c,d. This effect, though tenuous, is well described by our tensorial approach.

One readily notices that the scattered field is a linear functional of $\chi$, in Equation (64), which is a consequence of the small index contrast hypothesis. In the case of multiple, non-overlapping scatterers, the field would merely be the sum of all individual contributions, stemming from each scatterer.

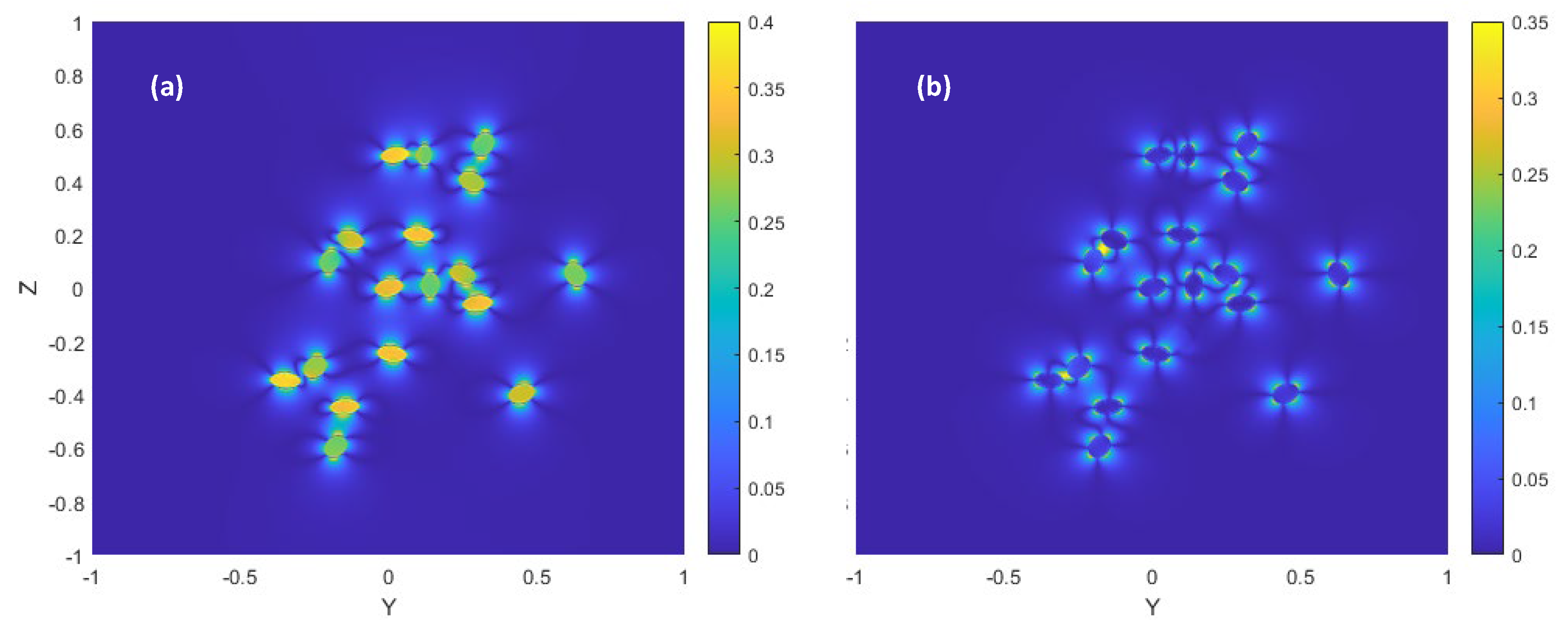
5.3.2. Scattering by an Ensemble of Spheres or Ellipsoids: A Born Expansion

In the case of a large contrast of permittivity between the scatterer and its environment, Equation (62) can be solved using a Born expansion [39]. We proceed here in the Fourier space, rewriting Equation (62) as:

$$\begin{array}{c}\hfill \widehat{\mathbf{E}}={\widehat{\mathbf{E}}}^{\left(\mathbf{0}\right)}+{\widehat{\mathbf{E}}}^{\left(\mathbf{1}\right)}+\cdots ,\end{array}$$

with

${\widehat{\mathbf{E}}}^{\left(\mathbf{0}\right)}={\widehat{\mathbf{E}}}_{\mathrm{inc}}$, and

$${\widehat{\mathbf{E}}}^{(\mathbf{j}+\mathbf{1})}=-\frac{1}{{\left(2\pi \right)}^3}\left[A_{1,-1}\left(k\right)\left(\widehat{\mathbb{Q}}-\mathbb{I}\right)+\widehat{\mathbb{Q}}\right]\left(\widehat{\chi }\star {\widehat{\mathbf{E}}}^{\left(\mathbf{j}\right)}\right).$$

(65)

As an example, we compute the multiple scattering by an ensemble of identical spheres, in the long wavelength limit. To proceed, we now define

$$\widehat{\chi }\left(\mathbf{k}\right)=\frac{\epsilon -{\epsilon }_b}{{\epsilon }_b}{j}_1(\parallel \mathbf{k}\parallel \rho )/(\parallel \mathbf{k}\parallel \rho )\times \sum _{j=0}^{N}exp\left(i\mathbf{k}·{\mathbf{R}}_{\mathbf{j}}\right),$$

where the ${\mathbf{R}}_{\mathbf{j}}$ are vectors of ${\mathbb{R}}^3$. $\chi$ now describes N non-overlapping spheres, placed at ${\mathbf{R}}_{\mathbf{j}}$, and of radius $\rho$.

We remark that when several scatterers, described by ${\left({\chi }_p\right)}_{p\in [1..P]}$, are excited together (e.g., by a plane wave), one can write $\chi ={\sum }_p{\chi }_p$, and express analytically, thanks to Equation (65), all the contributions of the multiple scattering at an order jth of the Born expansion.

In the long wavelength limit, where $A_{1,-1}\left(k\right)=0$, the successive Born expansions can be computed iteratively using Fast Fourier Transform. We have used the following algorithm, based on the fact that $\widehat{\chi }\star {\mathbf{E}}^{\left(\mathbf{j}\right)}$ is the FT of the internal field—the field inside the scatterers—computed at the jth order:

(1)

Knowing ${\mathbf{E}}^{\left(\mathbf{j}\right)}$ in real space, compute the internal field $\chi \left(\mathbf{r}\right).{\mathbf{E}}^{\left(\mathbf{j}\right)}\left(\mathbf{r}\right)$,

(2)

Make a 3D FFT to obtain $\widehat{\chi }\star {\widehat{\mathbf{E}}}^{\left(\mathbf{j}\right)}$ in Fourier space,

(3)

Multiply the result by $\mathbb{Q}$, one obtains ${\widehat{\mathbf{E}}}^{(\mathbf{j}+\mathbf{1})}$,

(4)

Invert the 3D FFT to obtain the field ${\mathbf{E}}^{(\mathbf{j}+\mathbf{1})}$ in real space, inside and outside the scatterers.

(5)

Iterate to step (1), with $j\leftarrow j+1$

One then adds up the orders of Born expansion to obtain the scattered field.

We remark that the first step relies on the internal field only, as $\chi \left(\mathbf{r}\right)=0$ outside the scatterers. Therefore, no specific boundary condition—e.g., perfectly matched layers—is necessary in the real space for this algorithm. However, to avoid the Gibbs effect [40,41], in the implementation of the algorithm, one has to pay attention to the expansion in the Fourier space of the product $\chi \left(\mathbf{r}\right).{\mathbf{E}}^{\left(\mathbf{j}\right)}\left(\mathbf{r}\right)$. As known from previous studies in 1D [2,41] and 2D [42], the unavoidable truncature (due to a finite extent of the numerical Fourier space) can dramatically affect the value of $\widehat{\chi }\star {\widehat{\mathbf{E}}}^{\left(\mathbf{j}\right)}$ that is computed. In the present work, to reconstruct an accurate field profile, we used a specific truncation in the Fourier domain, choosing an apodization function ([43], See Eq. (2)) that permits us to avoid the non-physical Gibbs oscillations. This truncation has been enforced on the Fourier components of $\widehat{\chi }$, at step (2) of the algorithm.

Eventually, our results, see Figure 3, are in good agreement with the standard T-matrix method [20] to compute multiple scattering by an ensemble of spheres in a homogeneous medium. Note that only three spheres among the five we considered are visible on the Y-Z plane cut (X = 0), and only one is visible on the X-Z plane cut (Y = 0). This could permit computing the optical forces that drive the dynamics of a trapped ensemble of glass spheres in a vacuum [44,45,46].

Finally, using the same method, we are able to compute the field scattered by an ensemble of randomly oriented ellipsoid of semi-axes $(a,b,c)$, whose shape can be described analytically in the Fourier space by:

$$\widehat{\chi }\left(\mathbf{k}\right)=\sum _{j=0}^{N}exp\left(i\mathbf{k}·{\mathbf{R}}_{\mathbf{j}}\right)\frac{\epsilon -{\epsilon }_b}{{\epsilon }_b}\frac{j_1\left(\sqrt{\mathbf{k}\mathrm{M}({\varphi }_j,{\theta }_j,{\psi }_j){\mathbf{k}}^{\mathbf{t}}}\right)}{\sqrt{\mathbf{k}\mathrm{M}({\varphi }_j,{\theta }_j,{\psi }_j){\mathbf{k}}^{\mathbf{t}}}},$$

(66)

where $M({\varphi }_j,{\theta }_j,{\psi }_j)$ is the descriptor for the ellipsoid, rotated by the Euler angles ${\varphi }_j$ around X axis, ${\theta }_j$ around Y axis and ${\psi }_j$ around Z axis:

$$\begin{array}{c}\hfill M({\varphi }_j,{\theta }_j,{\psi }_j)=R({\varphi }_j,{\theta }_j,{\psi }_j)\left(\begin{array}{ccc}{a}^2& 0& 0\\ 0& b^2& 0\\ 0& 0& c^2\end{array}\right)R{({\varphi }_j,{\theta }_j,{\psi }_j)}^{-1},\end{array}$$

$R({\varphi }_j,{\theta }_j,{\psi }_j)$ being the associated 3 × 3 Euler rotation matrix.

The result is presented in Figure 4. One can see that the interaction between neighboring scatterers, depending on their orientation, can deeply modify the field locally, e.g., enhance some components of the scattered field that were not present in the injected field.

6. Conclusions

In summary, we studied the Fourier Transformation of the Lippmann–Schwinger equation for electromagnetic scattering. Dealing separately with the singular and the regular part of the equation, we obtained an analytic expression where the role of the scatterer shape is clearly visible. This does not require a periodic geometry, nor the use of perfectly matched layers to adapt the boundary conditions.

We have provided a few numerical examples, using the factorization in Fourier space to solve the equation for simple systems, with low index contrasts, or in the long wavelength limit, in a configuration where multiple scattering occurs.

Perspectives include the possibility to solve, in Fourier space, the Lippmann–Schwinger equation associated with scattering problems in more general cases, taking advantage of recent works to compute fast Fourier Transforms [47]. This could permit, e.g., defining the Quasi-Normal Modes [18,48,49] of a dispersive scattering system. Equation (62) could help, e.g., to obtain a relationship between the scatterer shape and its eigenfunctions (the QNM modes), in particular for the static modes [50], for which $k_b=0$. Field computation could also be carried out in lower dimensional systems, such as structured fibers [51]. Finally, this approach could help us to understand the multiple scattering in an ensemble of particles trapped by light beams using an analytical formalism.