A Novel Simulation-Based Optimization Method for Autonomous Vehicle Path Tracking with Urban Driving Application
Abstract
:1. Introduction
2. Model
2.1. Vehicle Dynamic Model
2.2. PID Controller
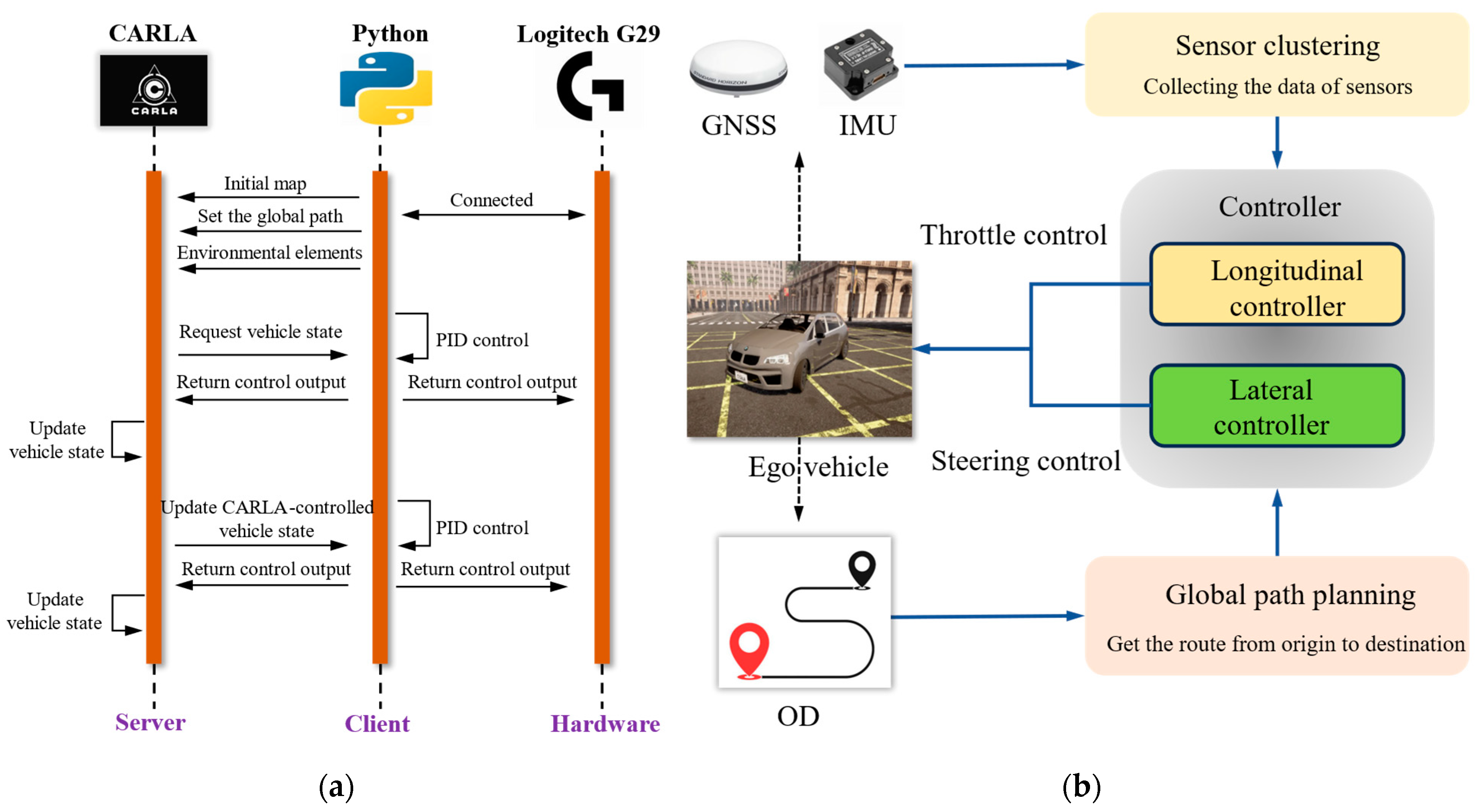
2.3. Simulation Platform
| Algorithm 1: PID control for AV path tracking. |
| Input, #parameters of longitudinal and lateral PID controller # configuration for PID control algorithm |
| Output |
| 1. |
| 2. |
| 3. = 1. |
| 4. == 1 do |
| 6. obtain the vehicle velocity, acceleration, and heading angle using IMU |
| steering angle using Equations (8) and (9) |
| 10. execute the controller output and update the simulation |
| then |
| 13. # track the next reference point |
| 14. End if |
| then |
| 16. Flag = 0 |
| 17. End if |
| then |
| 19. Flag = 0 |
| 20. End if |
| 22. End while |
2.4. PID Parameter Optimization Model
2.4.1. Normalized Dynamic Time Warping
2.4.2. Mean Absolute Lateral Acceleration
3. Methodology
3.1. Efficient Global Optimization
3.1.1. Gaussian Process
3.1.2. Acquisition Function
3.2. Domination-Measure-Based Efficient Global Optimization
| Algorithm 2: Detailed computational process of the proposed DMEGO method. |
| Input of NSGA-II. |
| Output. |
| 1.: Initialization: |
| . |
| . |
| do |
| . |
| for each true objective function . |
| . |
| is determined by . |
| . |
| . |
| can be obtained. |
| 12. End while |
4. Numerical Experiments
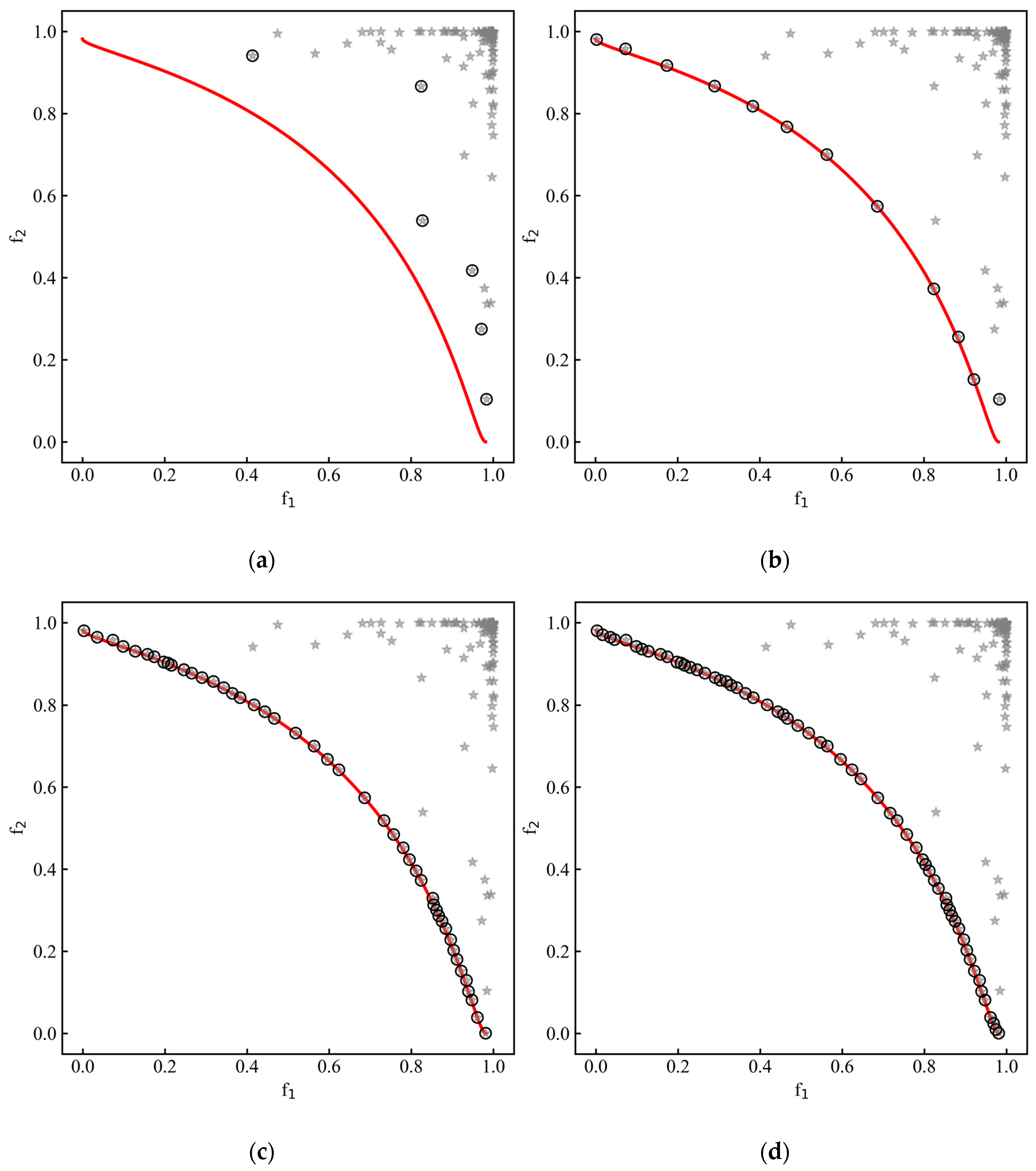
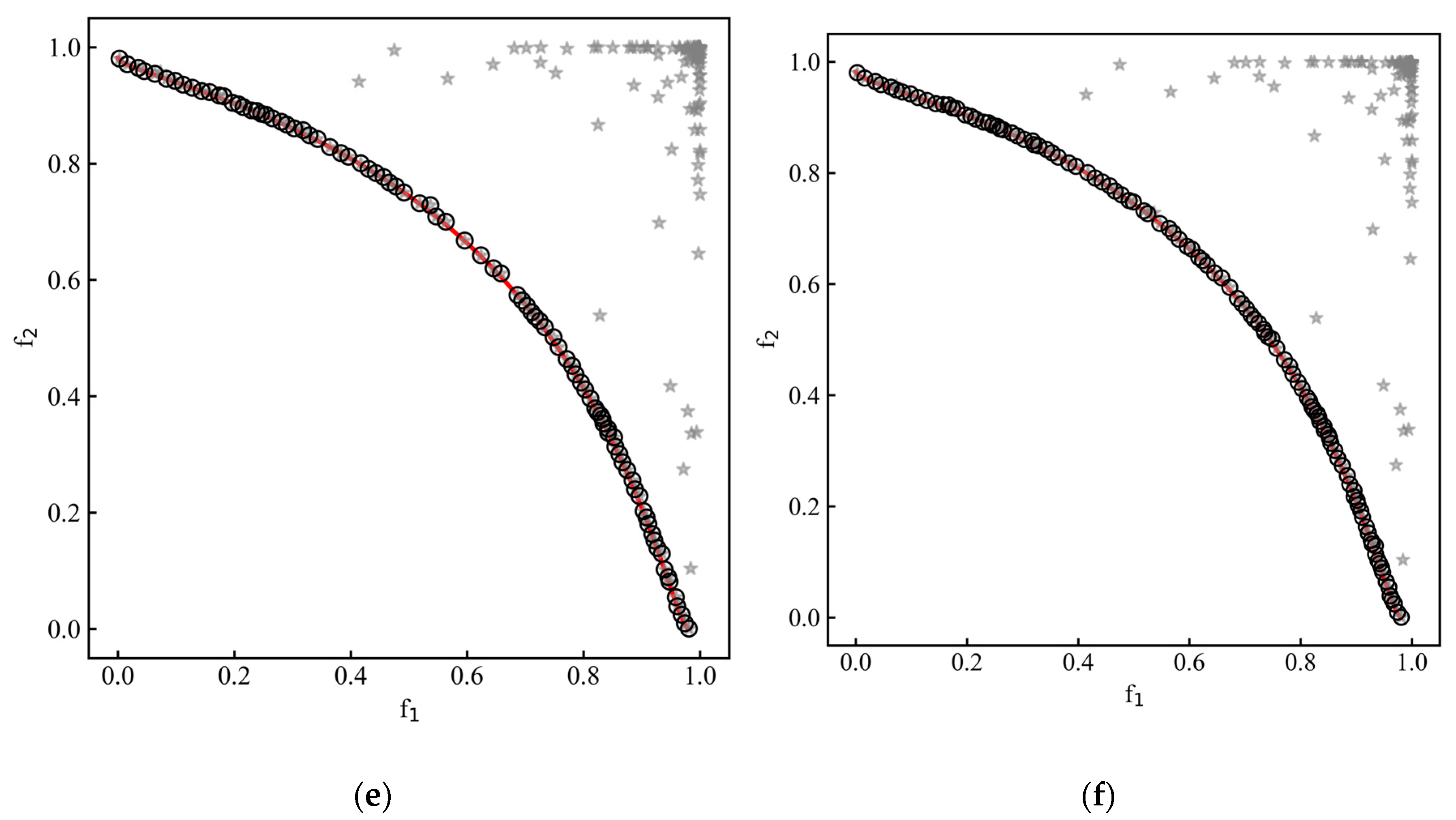
4.1. A Benchmark Test Problem
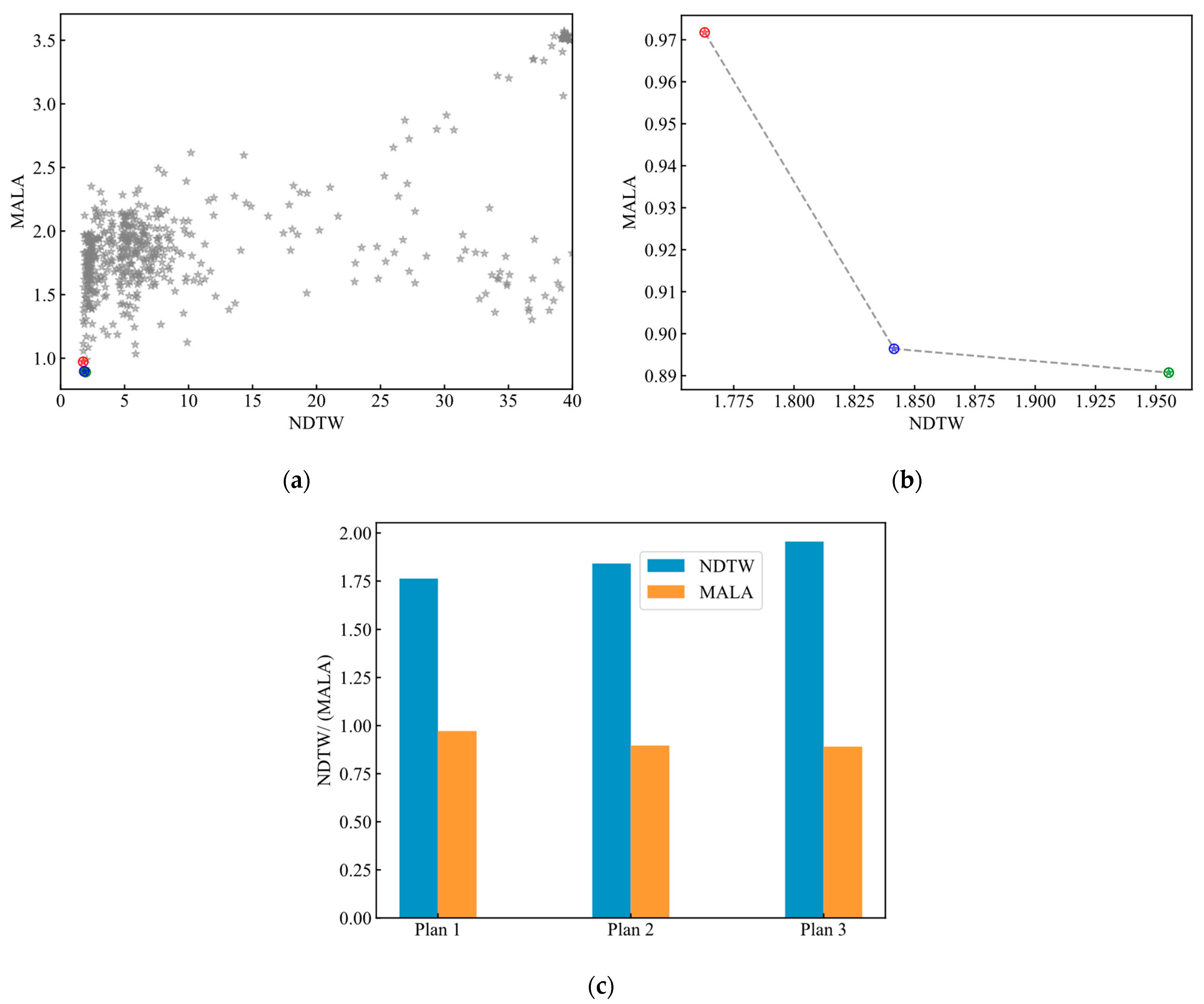
4.2. PID Parameter Optimization Problem Using the DMEGO Method
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Brummelen, J.; O’Brien, M.; Gruyer, D.; Najjaran, H. Autonomous vehicle perception: The technology of today and tomorrow. Transp. Res. Part C Emerg. Technol. 2018, 89, 384–406. [Google Scholar] [CrossRef]
- Gong, B.; Xu, Z.; Wei, R.; Wang, T.; Lin, C.; Gao, P. Reinforcement Learning-Based Lane Change Decision for CAVs in Mixed Traffic Flow under Low Visibility Conditions. Mathematics 2023, 11, 1556. [Google Scholar] [CrossRef]
- Raouf, I.; Khan, A.; Khalid, S.; Sohail, M.; Azad, M.M.; Kim, H.S. Sensor-Based Prognostic Health Management of Advanced Driver Assistance System for Autonomous Vehicles: A Recent Survey. Mathematics 2022, 10, 3233. [Google Scholar] [CrossRef]
- Shang, W.-L.; Zhang, M.; Wu, G.; Yang, L.; Fang, S.; Ochieng, W. Estimation of traffic energy consumption based on macro-micro modelling with sparse data from Connected and Automated Vehicles. Appl. Energy 2023, 351, 121916. [Google Scholar] [CrossRef]
- Rana, M.M.; Hossain, K. Connected and autonomous vehicles and infrastructures: A literature review. Int. J. Pavement Res. Technol. 2023, 16, 264–284. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, J. A Vehicular Edge Computing-Based Architecture and Task Scheduling Scheme for Cooperative Perception in Autonomous Driving. Mathematics 2022, 10, 3328. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Z.; Hua, Q.; Shang, W.L.; Luo, Q.; Yu, K. AI-Empowered Speed Extraction via Port-Like Videos for Vehicular Trajectory Analysis. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4541–4552. [Google Scholar] [CrossRef]
- Schwarting, W.; Alonso-Mora, J.; Rus, D. Planning and decision-making for autonomous vehicles. Annu. Rev. Control Robot. Auton. Syst. 2018, 1, 187–210. [Google Scholar] [CrossRef]
- Kuutti, S.; Bowden, R.; Jin, Y.; Barber, P.; Fallah, S. A survey of deep learning applications to autonomous vehicle control. IEEE Trans. Intell. Transp. Syst. 2020, 22, 712–733. [Google Scholar] [CrossRef]
- Yang, L.; Zhan, J.; Shang, W.L.; Fang, S.; Wu, G.; Zhao, X.; Deveci, M. Multi-Lane Coordinated Control Strategy of Connected and Automated Vehicles for On-Ramp Merging Area Based on Cooperative Game. IEEE Trans. Intell. Transp. Syst. 2023, 24, 13448–13461. [Google Scholar] [CrossRef]
- Bi, H.; Shang, W.L.; Chen, Y.; Yu, K.; Ochieng, W.Y. An Incentive Based Road Traffic Control Mechanism for COVID-19 Pandemic Alike Emergency Preparedness and Response. IEEE Trans. Intell. Transp. Syst. 2022, 23, 25092–25105. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; Nguyen, A.T.; Lauber, J.; Boada, M.J.L.; Boada, B.L. Event-Triggered Robust Path Tracking Control Considering Roll Stability Under Network-Induced Delays for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 1. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Z.; Shen, H.; Wang, J. Robust Adaptive Path-Tracking Control of Autonomous Ground Vehicles With Considerations of Steering System Backlash. IEEE Trans. Intell. Veh. 2022, 7, 315–325. [Google Scholar] [CrossRef]
- Jiang, K.; Hu, C.; Yan, F. Path-following control of autonomous ground vehicles based on input convex neural networks. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 2806–2816. [Google Scholar] [CrossRef]
- Farag, W. Complex trajectory tracking using PID control for autonomous driving. Int. J. Intell. Transp. Syst. Res. 2020, 18, 356–366. [Google Scholar] [CrossRef]
- Lefevre, S.; Carvalho, A.; Borrelli, F. A learning-based framework for velocity control in autonomous driving. IEEE Trans. Autom. Sci. Eng. 2015, 13, 32–42. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, H.; Li, Q.; Li, J.; Zhao, Y. PID trajectory tracking control of autonomous ground vehicle based on genetic algorithm. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 3677–3682. [Google Scholar]
- Al-Mayyahi, A.; Wang, W.; Birch, P. Path tracking of autonomous ground vehicle based on fractional order PID controller optimized by PSO. In Proceedings of the 2015 IEEE 13th International Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 22–24 January 2015; pp. 109–114. [Google Scholar]
- Abajo, M.R.; Sierra-García, J.E.; Santos, M. Evolutive tuning optimization of a PID controller for autonomous path-following robot. In Proceedings of the 16th International Conference on Soft Computing Models in Industrial and Environmental Applications (SOCO 2021), Bilbao, Spain, 22–24 September 2021; pp. 451–460. [Google Scholar]
- Gao, S.; Gao, S.; Pan, W.; Wang, M. Design of Improved PID Controller Based on PSO-GA Hybrid Optimization Algorithm in Vehicle Lateral Control. Stud. Inform. Control 2021, 30, 55–65. [Google Scholar] [CrossRef]
- El Hajjami, L.; Mellouli, E.M.; Berrada, M. Optimal PID control of an autonomous vehicle using Butterfly Optimization Algorithm BOA. In Proceedings of the 4th International Conference on Big Data and Internet of Things, Tangier-Tetuan, Morocco, 23–24 October 2019; pp. 1–5. [Google Scholar]
- Loucif, F.; Kechida, S.; Sebbagh, A. Whale optimizer algorithm to tune PID controller for the trajectory tracking control of robot manipulator. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1. [Google Scholar] [CrossRef]
- Ma’ani, F.A.; Nazaruddin, Y.Y. Optimization of longitudinal control of an autonomous vehicle using flower pollination algorithm based on data-driven approach. Int. J. Sustain. Transp. Technol. 2020, 3, 58–65. [Google Scholar] [CrossRef]
- Nguyen, A.-T.; Reiter, S.; Rigo, P. A review on simulation-based optimization methods applied to building performance analysis. Appl. Energy 2014, 113, 1043–1058. [Google Scholar] [CrossRef]
- Bellamy, H.; Rehim, A.A.; Orhobor, O.I.; King, R. Batched bayesian optimization for drug design in noisy environments. J. Chem. Inf. Model. 2022, 62, 3970–3981. [Google Scholar] [CrossRef]
- Korovina, K.; Xu, S.; Kandasamy, K.; Neiswanger, W.; Poczos, B.; Schneider, J.; Xing, E. Chembo: Bayesian optimization of small organic molecules with synthesizable recommendations. In Proceedings of the Twenty Third International Conference on Artificial Intelligence and Statistics, Online, 26–28 August 2020; pp. 3393–3403. [Google Scholar]
- Zuo, Y.; Qin, M.; Chen, C.; Ye, W.; Li, X.; Luo, J.; Ong, S.P. Accelerating materials discovery with Bayesian optimization and graph deep learning. Mater. Today 2021, 51, 126–135. [Google Scholar] [CrossRef]
- Chen, Y.; Cheng, A.; Zhang, C.; Chen, S.; Ren, Z. Rapid mechanical evaluation of the engine hood based on machine learning. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 345. [Google Scholar] [CrossRef]
- Victoria, A.H.; Maragatham, G. Automatic tuning of hyperparameters using Bayesian optimization. Evol. Syst. 2021, 12, 217–223. [Google Scholar] [CrossRef]
- Močkus, J. On Bayesian methods for seeking the extremum. In Optimization Techniques IFIP Technical Conference; Springer: Berlin/Heidelberg, Germany, 1975; pp. 400–404. [Google Scholar]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Frazier, P.I. Bayesian optimization. In Recent Advances in Optimization and Modeling of Contemporary Problems; Informs: Catonsville, MA, USA, 2018; pp. 255–278. [Google Scholar]
- Hernández-Lobato, J.M.; Hoffman, M.W.; Ghahramani, Z. Predictive entropy search for efficient global optimization of black-box functions. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar]
- Liu, H.; Ong, Y.-S.; Cai, J. A survey of adaptive sampling for global metamodeling in support of simulation-based complex engineering design. Struct. Multidiscip. Optim. 2018, 57, 393–416. [Google Scholar] [CrossRef]
- Desautels, T.; Krause, A.; Burdick, J.W. Parallelizing exploration-exploitation tradeoffs in gaussian process bandit optimization. J. Mach. Learn. Res. 2014, 15, 3873–3923. [Google Scholar]
- González, J.; Dai, Z.; Hennig, P.; Lawrence, N. Batch Bayesian optimization via local penalization. In Proceedings of the 19th International Conference on Artificial Intelligence and Statistics, Cadiz, Spain, 9–11 May 2016; pp. 648–657. [Google Scholar]
- Knowles, J. ParEGO: A hybrid algorithm with on-line landscape approximation for expensive multiobjective optimization problems. IEEE Trans. Evol. Comput. 2006, 10, 50–66. [Google Scholar] [CrossRef]
- Emmerich, M.; Klinkenberg, J.-W. The Computation of the Expected Improvement in Dominated Hypervolume of Pareto Front Approximations; Rapport Technique; Leiden University: Leiden, The Netherlands, 2008; Volume 34, pp. 3–7. [Google Scholar]
- Picheny, V. Multiobjective optimization using Gaussian process emulators via stepwise uncertainty reduction. Stat. Comput. 2015, 25, 1265–1280. [Google Scholar] [CrossRef]
- He, X.; Chen, X.; Xiong, C.; Zhu, Z.; Zhang, L. Optimal Time-Varying Pricing for Toll Roads Under Multiple Objectives: A Simulation-Based Optimization Approach. Transp. Sci. 2016, 51, 412–426. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Dosovitskiy, A.; Ros, G.; Codevilla, F.; Lopez, A.; Koltun, V. CARLA: An open urban driving simulator. In Proceedings of the 1st Annual Conference on Robot Learning, Mountain View, CA, USA, 13–15 November 2017; pp. 1–16. [Google Scholar]
- Wang, S.; Lin, F.; Wang, T.; Zhao, Y.; Zang, L.; Deng, Y. Autonomous Vehicle Path Planning Based on Driver Characteristics Identification and Improved Artificial Potential Field. Actuators 2022, 11, 52. [Google Scholar] [CrossRef]
- Dechter, R.; Pearl, J. Generalized best-first search strategies and the optimality of A. J. ACM 1985, 32, 505–536. [Google Scholar] [CrossRef]
- Tao, Y.; Both, A.; Silveira, R.I.; Buchin, K.; Sijben, S.; Purves, R.S.; Laube, P.; Peng, D.; Toohey, K.; Duckham, M. A comparative analysis of trajectory similarity measures. GIScience Remote Sens. 2021, 58, 643–669. [Google Scholar] [CrossRef]
- Yu, Q.; Luo, Y.; Chen, C.; Chen, S. Trajectory similarity clustering based on multi-feature distance measurement. Appl. Intell. 2019, 49, 2315–2338. [Google Scholar] [CrossRef]
- Taylor, J.; Zhou, X.; Rouphail, N.M.; Porter, R.J. Method for investigating intradriver heterogeneity using vehicle trajectory data: A dynamic time warping approach. Transp. Res. Part B Methodol. 2015, 73, 59–80. [Google Scholar] [CrossRef]
- Wang, S.; Li, L.; Ma, W.; Chen, X. Trajectory analysis for on-demand services: A survey focusing on spatial-temporal demand and supply patterns. Transp. Res. Part C Emerg. Technol. 2019, 108, 74–99. [Google Scholar] [CrossRef]
- Matute-Peaspan, J.A.; Marcano, M.; Diaz, S.; Zubizarreta, A.; Perez, J. Lateral-Acceleration-Based Vehicle-Models-Blending for Automated Driving Controllers. Electronics 2020, 9, 1674. [Google Scholar] [CrossRef]
- Yamakado, M.; Abe, M. An experimentally confirmed driver longitudinal acceleration control model combined with vehicle lateral motion. Veh. Syst. Dyn. 2008, 46, 129–149. [Google Scholar] [CrossRef]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Couckuyt, I.; Deschrijver, D.; Dhaene, T. Fast calculation of multiobjective probability of improvement and expected improvement criteria for Pareto optimization. J. Glob. Optim. 2014, 60, 575–594. [Google Scholar] [CrossRef]
- Zhan, D.; Xing, H. Expected improvement for expensive optimization: A review. J. Glob. Optim. 2020, 78, 507–544. [Google Scholar] [CrossRef]
- Garivier, A.; Moulines, E. On Upper-Confidence Bound Policies for Switching Bandit Problems. In Algorithmic Learning Theory; Springer: Berlin/Heidelberg, Germany, 2011; pp. 174–188. [Google Scholar]
- Hale, J.Q.; Zhu, H.; Zhou, E. Domination Measure: A New Metric for Solving Multiobjective Optimization. INFORMS J. Comput. 2020, 32, 565–581. [Google Scholar] [CrossRef]
- Mete, H.O.; Zabinsky, Z.B. Multiobjective Interacting Particle Algorithm for Global Optimization. INFORMS J. Comput. 2014, 26, 500–513. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Imada, R.; Setoguchi, Y.; Nojima, Y. Reference point specification in inverted generational distance for triangular linear Pareto front. IEEE Trans. Evol. Comput. 2018, 22, 961–975. [Google Scholar] [CrossRef]
- Yan, J.; Li, C.; Wang, Z.; Deng, L.; Sun, D. Diversity Metrics in Multi-objective Optimization: Review and Perspective. In Proceedings of the 2007 IEEE International Conference on Integration Technology, Shenzhen, China, 20–24 March 2007; pp. 553–557. [Google Scholar]
- Fonseca, C.M.; Fleming, P.J. An overview of evolutionary algorithms in multiobjective optimization. Evol. Comput. 1995, 3, 1–16. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]










| Reference | Environment | Various Routes | Road Slope | Weather | Vehicle Type | Bi-Objective | Optimization Algorithm |
|---|---|---|---|---|---|---|---|
| [17] | Mathematical model | ✘ | ✘ | ✘ | ✘ | ✘ | GA |
| [18] | MATLAB | ✘ | ✘ | ✘ | ✘ | ✘ | PSO |
| [19] | Simulink | ✓ | ✘ | ✘ | ✘ | ✘ | GA |
| [20] | MATLAB | ✘ | ✘ | ✘ | ✘ | ✘ | PSO-GA |
| [21] | Simulink | ✘ | ✘ | ✘ | ✘ | ✘ | BOA |
| [22] | Simulink | ✘ | ✘ | ✘ | ✘ | ✘ | WOA |
| [23] | CARLA | ✓ | ✓ | ✘ | ✘ | ✘ | FPA |
| Our work | CARLA | ✓ | ✓ | ✓ | ✓ | ✓ | DMEGO |
| Environmental Perturbations | Examples |
|---|---|
| Town |  |
| Routes | 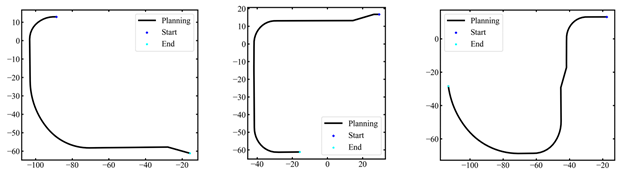 |
| Road slope |  |
| Weather |  |
| Vehicle type |  |
| Method | FEs | NSs | IGD | |
|---|---|---|---|---|
| NSGA-II | 200 | 16 | 0.1039 | 1.2068 |
| ParEGO | 200 | 26 | 0.0333 | 0.8328 |
| BOEGO | 200 | 61 | 0.0183 | 0.8029 |
| DMEGO | 200 | 98 | 0.0047 | 0.5079 |
| Plan 1 | 0.1636 | 2.5338 | 0.4878 | 4.1348 | 7.0627 | 1.9360 |
| Plan 2 | 0.9119 | 1.6485 | 0.2156 | 0.4609 | 3.1066 | 2.1257 |
| Plan 3 | 1.0581 | 1.0931 | 0.5995 | 1.5573 | 6.5103 | 6.7818 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Yu, F. A Novel Simulation-Based Optimization Method for Autonomous Vehicle Path Tracking with Urban Driving Application. Mathematics 2023, 11, 4762. https://doi.org/10.3390/math11234762
Chen Y, Yu F. A Novel Simulation-Based Optimization Method for Autonomous Vehicle Path Tracking with Urban Driving Application. Mathematics. 2023; 11(23):4762. https://doi.org/10.3390/math11234762
Chicago/Turabian StyleChen, Yanzhan, and Fan Yu. 2023. "A Novel Simulation-Based Optimization Method for Autonomous Vehicle Path Tracking with Urban Driving Application" Mathematics 11, no. 23: 4762. https://doi.org/10.3390/math11234762
APA StyleChen, Y., & Yu, F. (2023). A Novel Simulation-Based Optimization Method for Autonomous Vehicle Path Tracking with Urban Driving Application. Mathematics, 11(23), 4762. https://doi.org/10.3390/math11234762







