Modeling of Nonlinear Sea Wave Modulation in the Presence of Ice Coverage
Abstract
:1. Introduction
2. Model Equation
3. Wave Modulation and Attenuation
3.1. Derivation of the Governing Nonlinear Modulation Equation
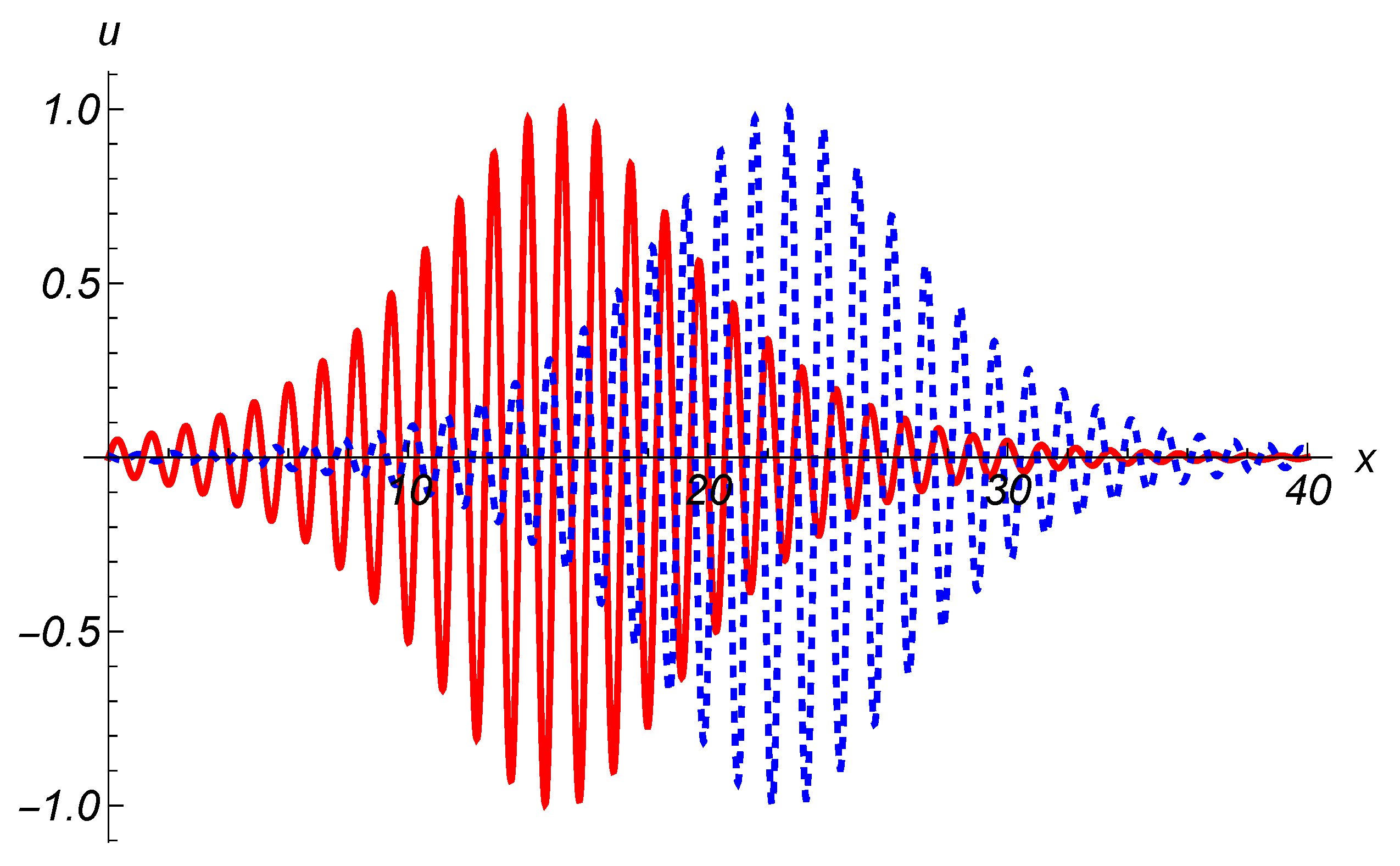
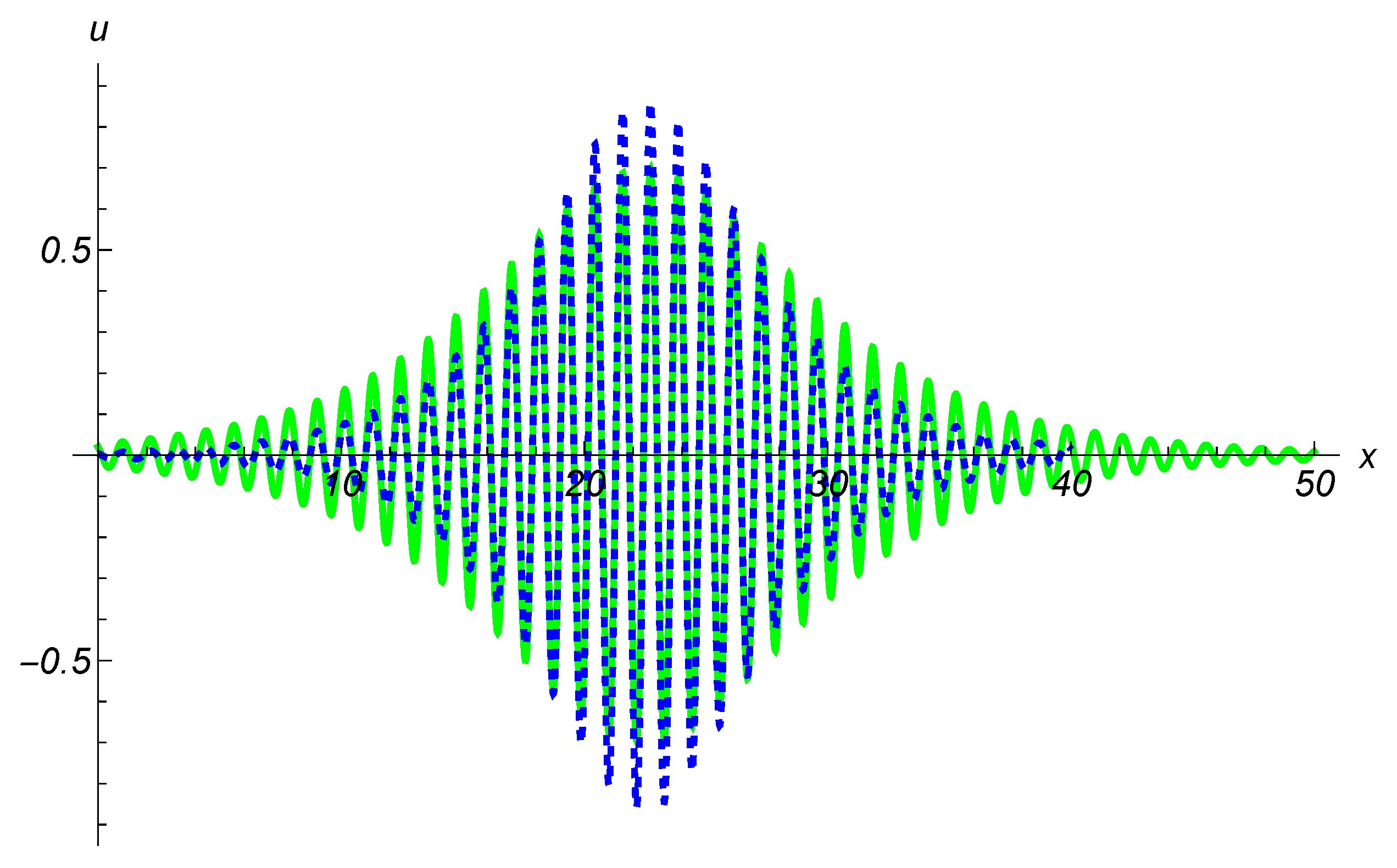
3.2. Attenuation of Modulated Waves
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Meylan, M.H.; Bennetts, L.G.; Mosig, J.E.M.; Rogers, W.E.; Doble, M.J.; Peter, M.A. Dispersion Relations, Power Laws, and Energy Loss for Waves in The Marginal Ice Zone. J. Geophys. Res. Ocean. 2018, 123, 3322–3335. [Google Scholar] [CrossRef]
- Collard, F.; Marié, L.; Nouguier, F.; Kleinherenbrink, M.; Ehlers, F.; Ardhuin, F. Wind-wave attenuation under sea ice in the Arctic: A review of remote sensing capabilities. JGR Ocean. 2022, 127, e2022JC018654. [Google Scholar] [CrossRef]
- Squire, V.A. A fresh look at how ocean waves and sea ice interact. Phil. Trans. R. Soc. A 2018, 376, 20170342. [Google Scholar] [CrossRef]
- Marchenko, A.V. Influence of anisotropic rheology on wave processes in sea ice. Theor. Math. Phys. 2022, 211, 665–678. [Google Scholar] [CrossRef]
- Il’yushin, A.A.; Ogibalov, P.M. A certain generalization of the voigt and maxwell models. Mekhanika Polim. 1966, 2, 190–196. [Google Scholar] [CrossRef]
- Toffoli, A.; Bennetts, L.G.; Meylan, M.H.; Cavaliere, C.; Alberello, A.; Elsnab, J.; Monty, J.P. Sea ice floes dissipate the energy of steep ocean waves. Geophys. Res. Lett. 2015, 42, 8547–8554. [Google Scholar] [CrossRef]
- Stopa, J.E.; Ardhuin, F.; Thomson, J.; Smith, M.M.; Kohout, A.; Doble, M.; Wadhams, P. Wave attenuation through an Arctic marginal ice zone on 12 October 2015. 1. Measurement of wave spectra and ice features from Sentinel 1A. J. Geophys. Ocean. 2018, 123, 3619–3634. [Google Scholar] [CrossRef]
- Wang, R.; Shen, H.H. Gravity waves propagating into an ice-covered ocean: A viscoelastic model. J. Geophys. Res. 2010, 115, C06024. [Google Scholar] [CrossRef]
- Marchenko, A.V. Long waves in a shallow liquid covered with ice. Prikl. Mat. Mekh. 1988, 52, 230. [Google Scholar]
- Il’ichev, A.T.; Marchenko, A.V. Propagation of long nonlinear waves in a heavy liquid covered with ice. Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 1989, 1, 73–79. [Google Scholar]
- Olver, P. Hamiltonian and non-Hamiltonian models for water waves. Lect. Notes Phys. Trends Appl. Pure Math. Mech. 1984, 195, 273–290. [Google Scholar]
- Kochanov, M.B.; Kudryashov, N.A.; Sinelshchikov, L.I. Non-linear waves on shallow water under an ice cover. Higher order expansions. J. Appl. Math. Mech. 2013, 77, 25–32. [Google Scholar] [CrossRef]
- Kolsky, G. Stress Waves in Solids; Dover: New York, NY, USA, 2003. [Google Scholar]
- Akhmediev, N.; Ankirwicz, A. Solitons. Nonlinear Pulses and Beams; Chapman and Hall: London, UK, 1997. [Google Scholar]
- Kodama, Y.; Hasegawa, A. Generation of asymptotically stable optical solitons and suppression of the Gordon-Haus effect. Opt. Lett. 1992, 17, 31–33. [Google Scholar] [CrossRef] [PubMed]
- Lou, S. A Direct Perturbation Method: Nonlinear Schrödinger Equation with Loss. Chin. Phys. Lett. 1999, 16, 659–661. [Google Scholar] [CrossRef]
- Malomed, B.A. Evolution of nonsoliton and “quasi-classical” wavetrains in Nonlinear Schrodinger and Korteweg–de Vries equations with dissipative perturbations. Physica D 1987, 29, 155–172. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Hamiltonians of the Generalized Nonlinear Schrödinger Equations. Mathematics 2023, 11, 2304. [Google Scholar] [CrossRef]
- Porubov, A.V.; Parker, D.F. Some General Periodic Solutions to Coupled Nonlinear Schrödinger Equations. Wave Motion 1999, 29, 97–109. [Google Scholar] [CrossRef]
- Porubov, A.V. Wave modulation in a nonlinear acoustic metamaterial. Int. J. Non-Linear Mech. 2021, 137, 103788. [Google Scholar] [CrossRef]
- Az-Zo’bi, E.; Al-Maaitah, A.F.; Tashtoush, M.A.; Osman, M.S. New generalised cubic–quintic–septic NLSE and its optical solitons. Pramana-J. Phys. 2022, 96, 184. [Google Scholar] [CrossRef]
- Alberello, A.; Părău, E.; Chabchoub, A. The dynamics of unstable waves in sea ice. Sci. Rep. 2023, 13, 13654. [Google Scholar] [CrossRef]
- Alberello, A.; Părău, E. A dissipative Nonlinear Schrödinger model for wave propagation in sea ice. Phys. Fluids 2022, 34, 061702. [Google Scholar] [CrossRef]
- Hunter, J.K.; Scheurle, J. Existence of perturbed solitary wave solutions to a model equation for water waves. Physica D 1988, 32, 253. [Google Scholar] [CrossRef]
- Kawahara, T. Oscillatory Solitary Waves in Dispersive Media. J. Phys. Soc. Jpn. 1972, 33, 260. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Porubov, A.V.; Krivtsov, A.M. Modeling of Nonlinear Sea Wave Modulation in the Presence of Ice Coverage. Mathematics 2023, 11, 4805. https://doi.org/10.3390/math11234805
Porubov AV, Krivtsov AM. Modeling of Nonlinear Sea Wave Modulation in the Presence of Ice Coverage. Mathematics. 2023; 11(23):4805. https://doi.org/10.3390/math11234805
Chicago/Turabian StylePorubov, A. V., and A. M. Krivtsov. 2023. "Modeling of Nonlinear Sea Wave Modulation in the Presence of Ice Coverage" Mathematics 11, no. 23: 4805. https://doi.org/10.3390/math11234805
APA StylePorubov, A. V., & Krivtsov, A. M. (2023). Modeling of Nonlinear Sea Wave Modulation in the Presence of Ice Coverage. Mathematics, 11(23), 4805. https://doi.org/10.3390/math11234805





