Abstract
Conceptual distance refers to the degree of proximity between two concepts within a conceptualization. It is closely related to semantic similarity and relationships, but its measurement strongly depends on the context of the given concepts. DIS-C represents an advancement in the computation of semantic similarity/relationships that is independent of the type of knowledge structure and semantic relations when generating a graph from a knowledge base (ontologies, semantic networks, and hierarchies, among others). This approach determines the semantic similarity between two indirectly connected concepts in an ontology by propagating local distances by applying an algorithm based on the All Pairs Shortest Path (APSP) problem. This process is implemented for each pair of concepts to establish the most effective and efficient paths to connect these concepts. The algorithm identifies the shortest path between concepts, which allows for an inference of the most relevant relationships between them. However, one of the critical issues with this process is computational complexity, combined with the design of APSP algorithms, such as Dijkstra, which is . This paper studies different alternatives to improve the DIS-C approach by adapting approximation algorithms, focusing on Dijkstra, pruned Dijkstra, and sketch-based methods, to compute the conceptual distance according to the need to scale DIS-C to analyze very large graphs; therefore, reducing the related computational complexity is critical. Tests were performed using different datasets to calculate the conceptual distance when using the original version of DIS-C and when using the influence area of nodes. In situations where time optimization is necessary for generating results, using the original DIS-C model is not the optimal method. Therefore, we propose a simplified version of DIS-C to calculate conceptual distances based on centrality estimation. The obtained results for the simple version of DIS-C indicated that the processing time decreased 2.381 times when compared to the original DIS-C version. Additionally, for both versions of DIS-C (normal and simple), the APSP algorithm decreased the computational cost when using a two-hop coverage-based approach.
Keywords:
conceptual distance; shortest path algorithms; accelerated calculation; computational complexity MSC:
68Q25
1. Introduction
The spread of information and communication technologies has significantly increased the amount of available information. Thus, we can decode this information through concepts. Conceptual matching is essential for human and machine reasoning, enabling problem-solving and data-driven inference. Researchers studying the human brain use the term “concept” to describe a unit of meaning stored in memory. The ability to relate concepts and generate knowledge is inherent to humans. Giving computers this capability is a significant advance in computer science.
Transferring the relationship between concepts from the human domain to the computational domain is complex. Sociocultural and language aspects are closely related to the types of concepts acquired by human beings. Determining the similarity between concepts so that a computer can process them is one of the most fundamental and relevant problems in various research fields. Over time, people have explored multiple structures and methods to represent the semantic relationships underlying conceptual distance. The graph is one of the most commonly used abstract data types to represent this information, designed to model connections between people, objects, or entities. Nodes and edges are the two main elements of a graph. Moreover, graphs have specific properties that make them unique and important in different applications.
According to Mejia Sanchez-Bermejo (2013) [1], measuring the conceptual distance and semantic similarity between words has been studied for many years in the fields of linguistic computing and artificial intelligence (AI) because it represents a generic procedure in a wide variety of applications, such as natural language processing, word disambiguation, detection and error correction in text documents, and text classification, among others. Based on psychological assessments, semantic similarity refers to how humans categorize and organize objects or entities [2]. Semantic similarity is a metric determining how closely two terms representing objects from a conceptualization are related. It is determined by analyzing whether the terms share a common meaning [3].
Reducing the computational cost of computing conceptual distances for each pair of concepts in massive graphs will accelerate the evaluation of similarity. As a result, it will have practical benefits and contribute to the development of more efficient applications to solve practical problems, for instance, reducing the computational time required to search for pairs of documents with high semantic similarity in large datasets composed of millions of documents and analyzing the transport network obtained automatically using AI techniques, as described by Chen et al. (2022) [4]. It also extends the understanding of the phenomenon of semantic similarity in computing systems based on conceptual graphs. The research and development of efficient algorithms that reduce computation time by combining approximation or analytical techniques is essential to advance the study of semantic similarity.
In recent years, conceptual graphs generated from ontologies have gained importance. These graphs are strongly connected, where each concept is a vertex, and the two edges represent each relationship (one in each direction). Consequently, it is possible to apply various graph theory search algorithms to study and analyze the relations represented in a conceptual graph. DIS-C Quintero et al. (2019) [5] is a method with which to measure the conceptual distance between concepts. It requires a conversion of a conceptualization into a conceptual graph by calculating the All Pairs Shortest Path (APSP) through the graph. Thus, shortest path algorithms are crucial for solving various optimization problems. The primary purpose of these algorithms is to find the path with the minimum cost or distance between a given pair of vertices in a graph or network. The study of shortest path algorithms and the proposal of different approaches to reduce computational cost have been largely studied, as per the research works proposed by Dreyfus (1969) [6], Gallo and Pallottino (1988) [7], Magzhan and Jani (2013) [8], and Madkour et al. (2017) [9].
Different research works have proposed several techniques and optimizations for efficient, shortest path algorithm performance to handle massive data. Fuhao and Jiping (2009) [10] proposed a novel algorithm using adjacent nodes that was more effective at analyzing networks with massive spatial data. Chakaravarthy et al. (2016) [11] introduced a scalable parallel algorithm that significantly reduces internode communication traffic and achieves high processing rates on large graphs. Yang et al. (2019) [12] focused on routing optimization algorithms based on node-compression in big data environments, addressing the common problem of finding the shortest path in a limited time and the number of connected nodes. Liu et al. (2019) [13] presented a navigation algorithm based on a navigator data structure that effectively navigates the shortest path with high probability in massive complex networks.
On the other hand, research has been developed that generates complex graphs with information that represents vehicle paths or sensor networks, such as the work of Ma et al. (2021) [14]. Li et al. (2023) [15] investigated a massive MIMO uplink system, where a transmitter with two antennas has to upload data in real time to a BS with a more significant number of antennas. Techniques and algorithms are required for high-speed and accurate graph processing in their different forms.
Unfortunately, the shortest path algorithm can propagate local distances to determine the distance between two concepts that are not directly connected by a relation in the ontology. This process is applied to each pair of concepts, allowing semantic proximity to be established. However, these techniques compute such distances at a high computational rate since traditional algorithms, like Dijkstra, have a complexity of , which is disadvantageous for massive graphs. The computational complexity of DIS-C is (using the Floyd–Warshall algorithm); therefore, using techniques such as DIS-C in its original version is inadequate to handle very large graphs directly. This paper proposes the use of other approaches to solve the APSP calculation. The pruned Dijkstra and the Sketch-based algorithms were used in the first approach. Considering that the analysis of the obtained results includes different datasets and that the generated graphs are sparse, a centrality-based strategy is presented to reduce the computational complexity.
The manuscript is organized as follows: Section 2 summarizes the state-of-the-art related to this field. Section 3 presents an analysis of the complexity of the DIS-C algorithm to reference those parts that need to be accurately improved, the algorithms proposed to enhance performance, and the demonstration of its precision and the associated computational complexity. In Section 4, we establish the execution scenarios, which include the total number and type of tests, present the experimental results, and discuss their significance. Finally, Section 5 outlines the conclusion and future work.
2. Related Work
2.1. Semantic Similarity
Conceptual distance is closely related to semantic relationship and semantic similarity. The semantic relationship, on the other hand, is not necessarily conditioned by a taxonomic relationship; in general terms, these relationships are given by any relationship between concepts, such as meronymy, antonymy, functionality, cause-effect, holonymy, hyponymy, hyperonymy, and so on. Moreover, we define conceptual distance as the space that separates two concepts within a conceptualization; in other words, it is the degree of proximity between concepts Quintero et al. (2023) [3]. We can establish a rule that indicates conceptual closeness in terms of how close to 0 (in terms of distance) the assigned value is. However, computing such distances is entirely dependent on the context of the concepts. In order to calculate it, the concepts must first be represented in a model that allows for the expression of the semantic relations and defining the measurement metric from the different underlying structures and representations.
In the network model, ontologies are used to address the problem of formally representing the semantics of information and its relationships Meersman (1999) [16]. The mentioned structures evaluate the conceptual distance between terms. The present work considers the assumption that an ontology can be represented as a strongly connected graph (conceptual graph); in this context, some authors have proposed many approaches to evaluate the closeness between concepts. The contributions of Bondy (1982) [17], West et al. (2001) [18], Bollobás (1998) [19], and Gross et al. (2018) [20] describe the basic concepts, mathematical foundations, and representative problems of graph theory.
On the other hand, since their conception in 2012 by Google [21], knowledge graphs have been the research subject in several articles. This term has been frequently used in academic and business contexts, typically associated with semantic web technologies, linked data, large-scale data analytics, and cloud computing Ehrlinger and Wöß (2016) [22]. The works presented by Fensel et al. (2020) [23] and Ehrlinger and Wöß (2016) [22] focused on reviewing several definitions of a knowledge graph to develop a formal definition. A Knowledge graph describes structured information and can be applied to specific domains such as answering questions, recommending, and retrieving information Zou (2020) [24]. In addition, Pujara et al. (2013) [25] present a method for transforming uncertain extractions about entities and their relationships into a knowledge graph by filtering noise, inferring missing information, and identifying the relevant candidate facts.
In the literature, the authors have identified four groups of methods, models, and techniques for computing semantic similarity: (a) edge counting-based, (b) feature-based, (c) information content-based, and (d) hybrids. In this work, information content-based methods are used to determine semantic similarity based on their direct relationship to the measurement of conceptual distance. The underlying knowledge base provides these methods with a structured representation of terms or concepts connected by semantic relationships. In addition, it proposes an unambiguous semantic measure since it considers the real meaning of the terms Sanchez et al. (2012) [26].
Edge counting-based methods consider an ontology a connected graph, where the nodes are concepts, and the edges are relationships (almost always taxonomic). The number of edges separating two concepts determines the similarity between them. Table 1 summarizes some representative edge counting-based methods. Furthermore, it describes the expression used to calculate the similarity /distance and a summary of the variables involved.

Table 1.
Edge counting-based methods. conceptual distance; similarity between two concepts: a and b.
Feature-based methods are based on the Tversky (1977) [32] similarity model, obtained from set theory, which assesses the similarity between concepts based on their properties, subtracts the common and uncommon features of the terms, and attempts to overcome the limitations of edge count-based measures regarding the fact that taxonomic links in an ontology do not necessarily represent uniform distances; Sanchez et al. (2012) [26]. These types of measurement have the potential to be applied in the calculation of semantic similarity supported by crossed ontological structures. The main limitation is that it requires ontologies or knowledge sources with semantic features, such as dictionaries, and most ontologies rarely contain semantic features other than relations.
The Lesk study [33] proposed the homonymous computing method, which consists of calculating the Lesk measure to disambiguate words in texts. The work presented by Banerjee and Pedersen (2003) [34] is an extension of this and used the terms or synsets provided by WordNet. However, in the modern world, there are multiple sources of information, such as social networks and internet blogs, which provide a large amount of information. For this reason, other works have used different sources of knowledge, such as Wikipedia. In this context, the study of Jiang et al. (2015) [35] evaluated the existing specific methods based on the features, using a formal representation of concepts.
Information content-based approaches improve some of the limitations of edge-counting-based methods. These methods are based on computing information content (IC) and similarity, . Table 2 summarizes the IC-based methods. In addition, this table describes the expressions used to calculate IC and briefly explains the variables involved.

Table 2.
Information content-based methods. similarity; information content.
Hybrid methods combine two or more techniques for calculating semantic similarity. Quintero et al. (2019) [5] proposed the DIS-C method to compute the conceptual distance between two concepts in an ontology based on a fundamental approach that uses the topology of an ontology to compute the weight of relationships between concepts. DIS-C can incorporate various relationships between concepts, such as meronymy, hyponymy, antonymy, functionality, and causality.
The DIS-C method considers the conceptual distance as the space separating two concepts within a conceptualization represented as a directed graph, and it is related to the difference in the information content of the concepts in their definitions. The conceptual structure is irrelevant since the method assigns a distance value to each relationship type and transforms this into a weighted directed graph; as a consequence, DIS-C can be applied to any conceptual structure. The only requirement for the algorithm is that the conceptualization be a 3-tuple of elements , where C is a set of concepts, ℜ is the set of relation types, and R is the set of relationships in the conceptualization. In summary, the method is described through the following steps:
- Assign to each relation as an arbitrary conceptual weight defined in each direction of the relationship.
- A directed and weighted graph (conceptual graph) is created, where the vertices are the concepts contained in the conceptualization, and the edges are the relationships that connect each pair of concepts. Each edge has its counterpart in the opposite direction with a different weighting. Finally, to compute the weighting, the generality of each concept is necessary.
- Calculate the APSP length between each pair of vertices, i.e., diffuse the conceptual distance to all concepts.
2.2. All Pairs Shortest Path Problem (APSP)
Computing the shortest path between each pair of concepts in large graphs is computationally expensive. This type of problem is known in graph theory as “All Pairs Shortest Path” (APSP) [42]. In [5], we used two well-known algorithms: the Floyd–Warshall and Johnson–Dijkstra algorithms. The Floyd–Warshall algorithm is based on transitive Boolean matrix closure [43], with a computational complexity of (n is the number of nodes, and m is the number of edges in the graph). On the other hand, Johnson-Dijkstra has a complexity (using Fibonacci heaps); however, it requires that there be no negative cycle in the graph, and when , the complexity is equal to [44].
When using accelerated matrix multiplication algorithms, the cost is , [45]. Techniques, such as divide and conquer [46], or metaheuristic algorithms [47] are also employed. Another approach is to use new-generation hardware, such as the GPU, to parallelize existing algorithms and reduce runtime [48]. According to Reddy (2016) [49], most algorithms are based on the following two types of computational models:
- Addition comparison model: Assume that the inputs are real weighted graphs, where the only operations allowed on real data are comparison and addition.
- Random access machine (RAM) model: Shortest path algorithms assume that the inputs are weighted graphs of integers manipulated by addition, subtraction, comparison, shift, and various logical operations [50] (the most commonly used model).
Despite the significant interest in the APSP problem, there have only been minor advances in computational complexity over for general graphs based on distance product computation, which is closely related to matrix multiplication. Although subcubic algorithms exist, they only exploit the properties of specific graphs or advantage sparse graphs, so there is no real subcubic combinatorial algorithm. Table 3 describes the algorithms developed with their computational complexity over time, and Figure 1 shows a comparison of the execution time of each algorithm.
Although it is possible to solve the APSP problem in polynomial time, its application in large graphs is not practical. For this reason, it is interesting to analyze heuristic and metaheuristic methods and approximation algorithms with regard to this problem. The clear advantage of this approach is the speed gain, whereas the disadvantage is the accuracy of the computation. In the literature, the authors have employed some relevant investigations into this class of algorithms with regard to the APSP problem: genetic, evolutionary, and optimization algorithms per ant colony.
Attiratanasunthron and Fakcharoenphol (2008) [51] presented a rigorous analysis of the running time of ACO in the shortest path problem. The n-ANT method is inspired by the 1-ANT [52] and AntNet [53] algorithms. Horoba and Sudholt (2009) [54] formalized and optimized the n-ANT algorithm to solve the APSP. The algorithm is a generalization of presented in the same research study. This algorithm decodes the single-source shortest path problem. The computational complexity of is , where is the maximum degree of the graph, l is the maximum number of edges in any shortest path, and .


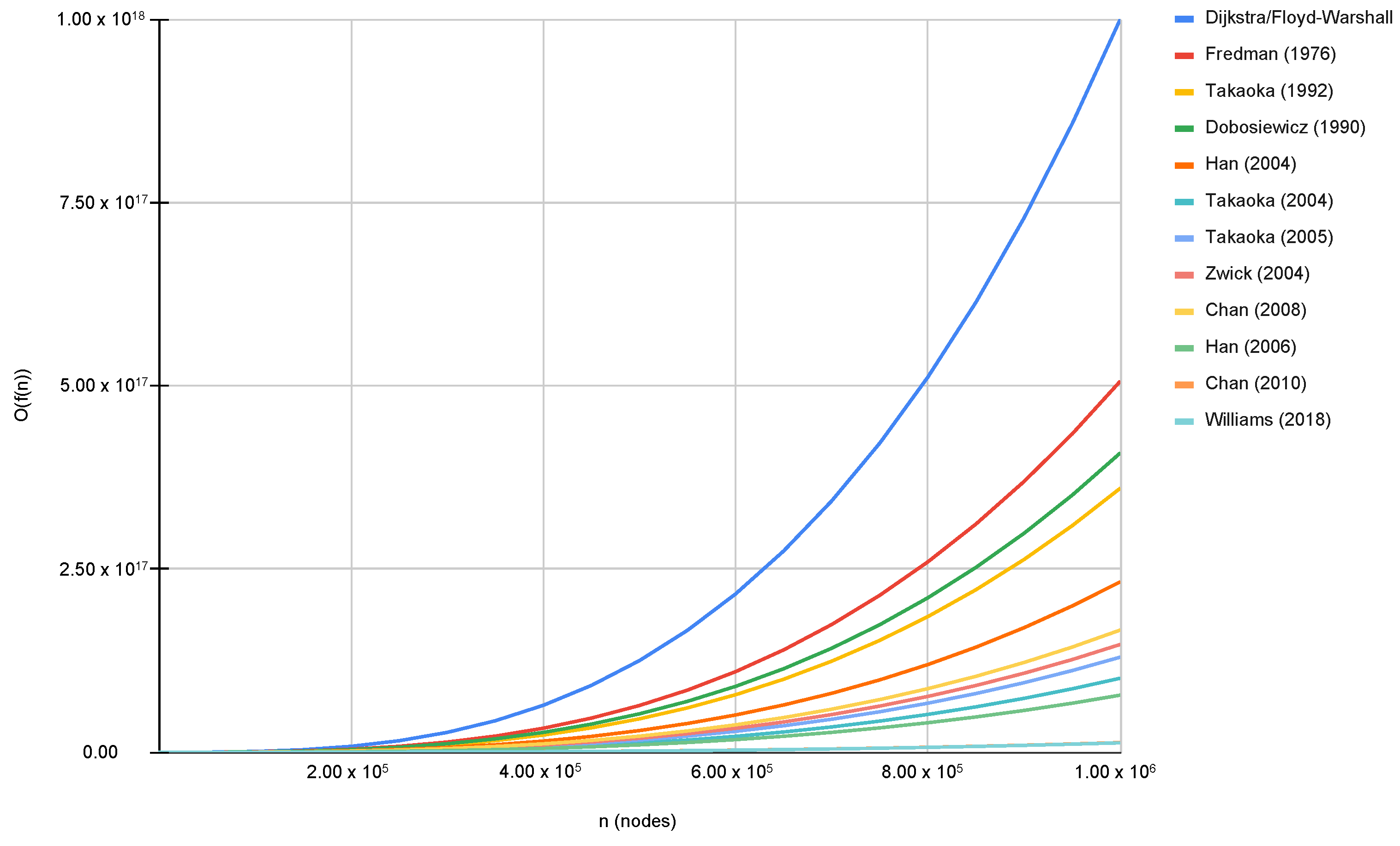

Table 3.
Analytical runtimes for different APSP algorithms.
Table 3.
Analytical runtimes for different APSP algorithms.
| Reference | Year | |
|---|---|---|
| Dijkstra/Floyd–Warshall | 1959/1962 | |
| Fredman (1976) [55] | 1976 | |
| Takaoka (1992) [56] | 1991 | |
| Dobosiewicz (1990) [57] | 1990 | |
| Han (2004) [58] | 2004 | |
| Takaoka (2004) [59] | 2004 | |
| Takaoka (2005) [60] | 2005 | |
| Zwick (2004) [61] | 2004 | |
| Chan (2008) [62] | 2005 | |
| Han (2006) [63] | 2006 | |
| Chan (2010) [64] | 2007 | |
| Williams (2018) [65] | 2014 |

Figure 1.
Comparison between the execution times of the APSP algorithms. This figure shows the number of operations (y-axis) required for each algorithm as the number of nodes increases (x-axis) [55,56,57,58,59,60,61,62,63,64,65].
Figure 1.
Comparison between the execution times of the APSP algorithms. This figure shows the number of operations (y-axis) required for each algorithm as the number of nodes increases (x-axis) [55,56,57,58,59,60,61,62,63,64,65].

On the other hand, Chou et al. (1998) [66] used a hierarchical approach to decompose a network (graph) into several smaller subnets. Therefore, when it is necessary to search for a shorter path, a smaller graph is evaluated. The authors compared the computational complexity between Dijkstra’s algorithm (no error) and two versions of the algorithm called HA: Best HA (best results: 21.5% error) and Nearest HA (the fastest execution instance: 4.68% error). Mohring et al. (2007) [67] presented a similar report that focuses on the shortest path to a single source.
Other research studies that improve the asymptotic limit concerning the are Baswana et al. (2009) [68] and Yuster (2012) [69]. The first applied it to unweighted and undirected graphs and introduced the first algorithm, , to compute the APSP with a 3-approximation, meaning that for each pair of vertices , the distance is less than or equal to , where is the shortest distance of the path. In addition, two algorithms are presented for a 2-approximation, with a complexity of and , and the shortest distance being and , respectively. In both cases, there is a predefined error bound.
Finally, there is the sketch-based approach, which requires two extensive processes. The first is to preprocess, in which the result is a data structure that allows the distance between two nodes to be consulted. This data structure and a distance oracle were introduced in [70]. The second process is related to queries, which is a case of making queries to the oracle, and it returns, in a specified time limit, the result of the shortest distance between two nodes.
In comparison to identical algorithms, these algorithms reduce the time by several orders of magnitude. Das Sarma et al. (2010) [71] is one of the first studies that applied this approach to complex graphs with hundreds of millions of nodes and billions of edges. The description of the algorithm is the following: sample a small number of node sets from the graph, called seed node sets. Then, for each node of the graph, the closest seed within each of these seeds is found. The sketch of a node is the set of the closest seeds and the distance to them. Thus, given a pair of nodes, u and v, the distance between them can be estimated by searching for a common seed in their sketches. However, there are no theoretical guarantees on the degree of optimization of the method for directed graphs. The results showed a better average close to the actual distance when applied to directed graphs.
Wang et al. (2021) [72] focused on finding all the shortest paths in large-scale undirected graphs. The principal difference, regarding the work of Das Sarma et al. (2010) [71], is that Wang et al. (2021) [72] considered the computational complexity needed to perform the preliminary computation. The standard method employed in this problem involves applying a BFS algorithm to the seed node set. It is known that the complexity of BFS is when using an adjacency list or for an adjacency matrix. This complexity is a drawback when processing large graphs. For this reason, they investigated whether it is possible to speed up the preliminary computation using the [73] pruned reference point-labeling technique, i.e., applying a pruned BFS. The specific results of this stage showed linear time in terms of its construction, i.e., . The results indicated a significant improvement, especially in terms of runtime for large graphs.
3. Materials and Methods
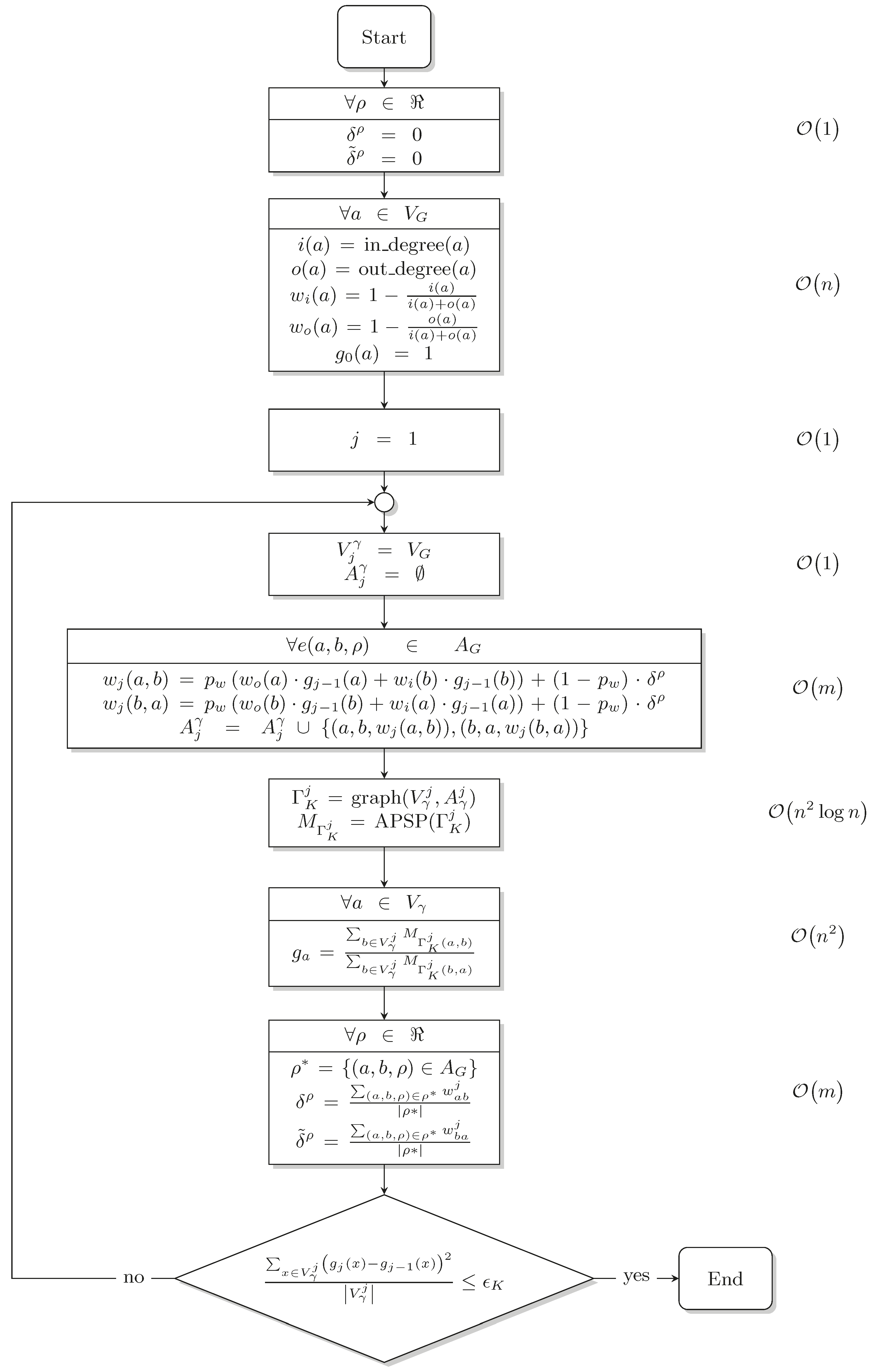
The DIS-C presented by Quintero et al. (2019) [5] uses two algorithms: a basic one, which calculates the conceptual distance within a conceptualization, , and the weights for each relationship type . This algorithm converts the conceptualization K into a graph with and , through which we compute the conceptual distance by calculating the APSP in graph G. The solution described in this paper combines and evaluates several approaches to optimize the APSP. The second algorithm enables automatic weighting, which allows the conceptual distance to be computed automatically without having to provide the weights of the relationship types. Figure 2 shows the flowchart corresponding to the DIS-C algorithm with automatic weighting (where is the entry degree of node a, and is the exit degree of node a; and are the costs of entering and leaving node a, respectively; is the generality of node a; and are the nodes and edges, respectively, of the graph , which is the graph corresponding to the conceptualization K in the j-th iteration. Thus, is the cost of the edge from node a to node b; is a geometric weighting factor. Furthermore, is the APSP distance matrix, and is the set of edges representing the relation . Finally, is the convergence threshold of the algorithm), which will be referred to simply as DIS-C in this paper. Although the DIS-C algorithm consists of several processes, in terms of computational complexity, it is related to the execution of the APSP.
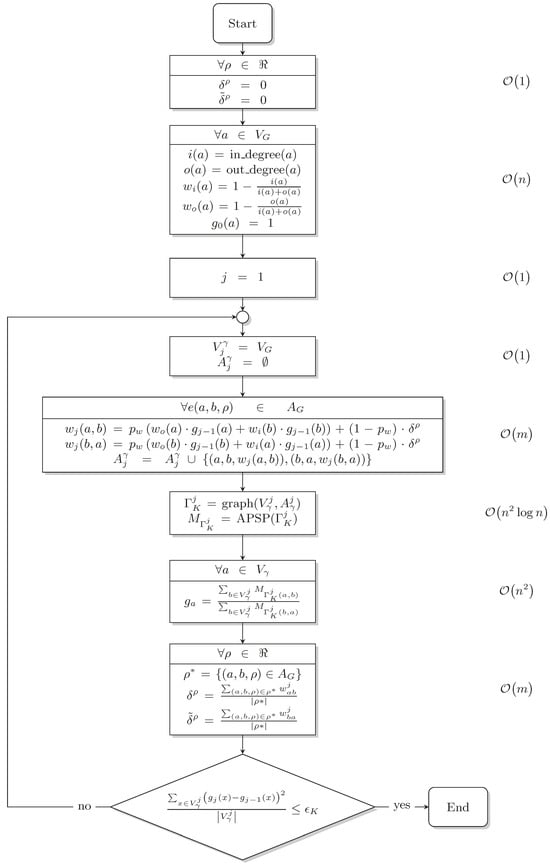
Figure 2.
The DIS-C algorithm flow diagram.
At this stage, we can assume that the computational complexity of the DIS-C algorithm for a conceptualization with n concepts is (A detailed analysis of this topic is presented in [74]).
3.1. The Pruned Dijkstra Algorithm
The algorithm implemented is described in Algorithm 1, and the index construction algorithm is presented in Algorithm 2. Appendix A explains the pruned Dijkstra algorithm. We executed the pruned Dijkstra in the order , and the sequence of vertices is arbitrary but relevant for good algorithm performance. Ideally, starting from the central vertices, many shortest paths will cross them. There are many strategies to order the vertices; one of the most common is based on ordering by centrality. In this work, we choose to order the vertices by the degree of centrality. The graphs generated by the semantic networks behave like networks without scale, where high-degree vertices provide high connectivity to the network. In this way, the shortest path between two vertices is usually through these nodes.
| Algorithm 1: The pruned Dijkstra |
 |
| Algorithm 2: APSP_PDijkstra |
 |
In order to formalize the proposed approach, it must be demonstrated that the algorithm is correct and produces the theoretically proposed result. In order to prove the correctness of the method, it suffices to show that the algorithm computes a two-hop coverage, i.e., for any . This statement is equivalent to proving that, when given any vertex, , all other vertices belong to the input and output coverages of vertex s. Let be the index built without the pruning process; so, it is a two-hop coverage; is the index generated by applying the pruning process. Since there exists a node, , such that , and , the goal is to show that also exists in and .
Theorem 1.
For , and ,
Proof.
Let , assuming there is a path between them, and j be the smallest number, such that , and . It must show that and are contained in and , respectively; that is, . In order to prove that , first consider, for any , in that , where is a path between a and b. Suppose ; through inequality, we obtain the following:
Since and , it contradicts the fact that j is the smallest number. Therefore, for any .
Now, we prove that . Suppose we perform the j-th pruned Dijkstra iteration from node to construct index . Let . Since there is no for , this means that there is no vertex in the i-th pruned Dijkstra iteration that covers the shortest path from to t, and, therefore, . Consequently, vertex t is visited without pruning, and is added.
Finally, suppose we execute the j-th pruned Dijkstra iteration from , but this time, we construct . If s and t are reachable in G, it means that there is a path between and s when considering the input edges or, equivalently, there is . Since we have already proved that for , this means that is a neighbor of s or , and since is the initial vertex of the path , then is the neighbor with the least distance sharing s. In all cases, ; therefore, the node s is visited without pruning (remember that it considers the input edges). Consequently, is added. □
As mentioned earlier, the order in which the nodes are processed affects the performance of the algorithm. Is there an order of execution such that the construction time is minimized? The answer is ’yes’, but finding such an order is challenging. So, there are two approaches: the first is to find the minor nodes that cover all the shortest paths, which is a much bigger problem since it is an instance of the minimum vertex coverage problem, which is NP-hard. The second approach is a parameterized perspective; specifically, the parameter explored is the width of the tree. It also relies on the process of the centroid decomposition of a tree [75]. This approach derives the following lemma; the formal proof is given in [73].
Lemma 1.
Let w be the width of the graph of G. There is a vertex order where the pruned Dijkstra method preprocesses in time, stores an index in space, and answers each query in time.
Considering that this research is not looking for minimum two-hop coverage, using the upper bound of for the algorithm can be considered an inconsistency. However, there is no guarantee that the selected order (degree centrality) is the same as the order required to achieve this computational complexity. We conclude that, according to our implementation, it cannot be faster than that theoretically obtained using the order with which we achieve . This means that there is a lower bound, , in the implementation. In addition, when referring to the Dijkstra algorithm, we can hypothesize that the construction of the coverage using the pruned process, regardless of the order of execution, is much smaller than for the construction of the naive coverage in highly connected graphs, i.e., that .
Thus, we concluded that this lemma indicates an optimal order for processing vertices. Unfortunately, it is extremely complicated to find it.
3.2. The Sketch-Based Algorithms
It is necessary to compute two sketches for each node. The first SKETCH and SKETCH represent the distance from node to the nearest seed and inverse. This is carried out by running the search algorithm two different times, with one employing the input edges and the other using the output edges. We can randomly choose S when considering some criteria to guide the choice; for example, take into account discarding those nodes for which the degree is less than two. Alternatively, the structure of the graph and its specific properties (The strategy for choosing the seed nodes is to emphasize the nodes with the highest value of generality in the conceptual graph; this implies that the most general concepts will be chosen) can be employed. Appendix B provides some complementary aspects of sketch-based algorithms. Algorithm 3 describes the proposed pseudocode for generating the sketches of each node.
| Algorithm 3: Sketches_DIS-C: offline sampling |
 |
For each sample, the closest seed node and its distance are obtained for each node. It is carried out by employing the classic Dijkstra multi-source algorithm. In this form, the seed nodes are computed for each (see Algorithm 4).
| Algorithm 4: Sketches_DIS-C: k sketches offline |
 |
In each iteration, we generate a sketch from an offline sample; therefore, at the end of the algorithm, there will be seeds for each node. The second process of the method is the online one. The calculation of the approximate minimum distance between nodes u and v is carried out by looking at the distance from u and v to any node w that appears in both and . So, we compute the path length from u to v by adding the distance from u to w plus the distance from w to v. The minimum distance is taken if there are two or more shared nodes w. Algorithm 5 shows the proposal to perform this calculation.
| Algorithm 5: Sketches_DIS-C: k sketches online |
 |
Finally, to solve the APSP problem, it is necessary to create another algorithm that is executed for each pair of nodes (Algorithm 6).
| Algorithm 6: Sketches_DIS-C: k sketches online APSP |
 |
In the sketch-based method, there is no accuracy test for general graphs. The method does not guarantee exact node labeling to determine the distance between all vertex pairs.
On the other hand, one of the objectives of this paper is to improve the computational complexity of the original algorithm (which is ). The following theorem demonstrates that the sketch-based method accomplishes this aim.
Theorem 2.
For a set of nodes, , such that the set size is for ; the complexity of the algorithm is .
Proof.
We know that the sketch-based method selects a value, w, based on the number of nodes in the graph, i.e., . Then, given w, subsets of nodes are created for , such that the size of each one is . It follows that . For each element of the subsets, the multi-source Dijkstra algorithm is applied, with the purpose of finding, for all the nodes of G, the closest node of the set. The multi-source Dijkstra has a complexity of ; for each subset of nodes, it is necessary to apply a single execution of Dijkstra algorithm (regardless of the size). Therefore, since there are w subsets of nodes, w Dijkstra processes must be performed from multiple sources, i.e., in total, the complexity is . □
For the implementation employed in this work, we determined w by using the logarithmic function , where . It ensured that . Therefore, for the implementation performed, the method has a complexity of .
4. Results
This section describes the results of the different experiments carried out. In the first section, the performance metrics of the generated graphs are analyzed, and the control algorithm is compared with the proposed one. The second part analyzes the results of the semantic metrics.
4.1. The Datasets
The used datasets contain pairs of words assigned to a numerical value by human evaluation. These sets are divided into two categories: those that measure semantic similarity and those that measure semantic relationship. These sets are described in Table 4.

Table 4.
List of datasets used in the evaluation process.
Thus, this process is executed by a script and, for each dataset, selects a few words, generating the conceptual graph that connects them by applying the DIS-C algorithm to find the conceptual distances. We repeat this process with all word pairs, and finally, all graphs generated from a set of words are merged to obtain a graph with all word pairs in the set. We also apply the DIS-C algorithm to combine the graph that contains the conceptual distances. The purpose of applying DIS-C to those graphs holding a few words is to measure the runtime with different sizes of graphs and, therefore, obtain a significantly larger record.
4.2. Evaluation Metrics
The evaluation metrics used for this research are divided into performance and semantics. The first corresponds to the runtime measurement, which is related to the number of nodes and edges of the graph. The semantic metrics measure the precision in estimating similarity, using the Pearson correlation coefficient (Equation (1)), the Spearman rank correlation coefficient (Equation (2)), and the harmonic score (Equation (3)).
The Pearson correlation compares human similarity vectors and has been widely used to evaluate methods that estimate similarity between words and concepts. The Spearman rank correlation provides an invariant ranking and allows for a comparison of the underlying quality of word similarity measures. Additionally, harmonic scoring that combines Pearson and Spearman correlations to provide a unique weighted score for evaluating word similarity methods has been used. These correlation measurements are essential for evaluating and comparing similarity methods in the literature.
4.3. Generated Graphs and Performance
For each dataset, we generated a graph connecting each pair of words. Later, we computed the corresponding unified graphs. Table 4 shows the size of these graphs. The last row of the table (labeled ‘All’) refers to the union of all graphs; in addition, the algorithms were applied to this graph.
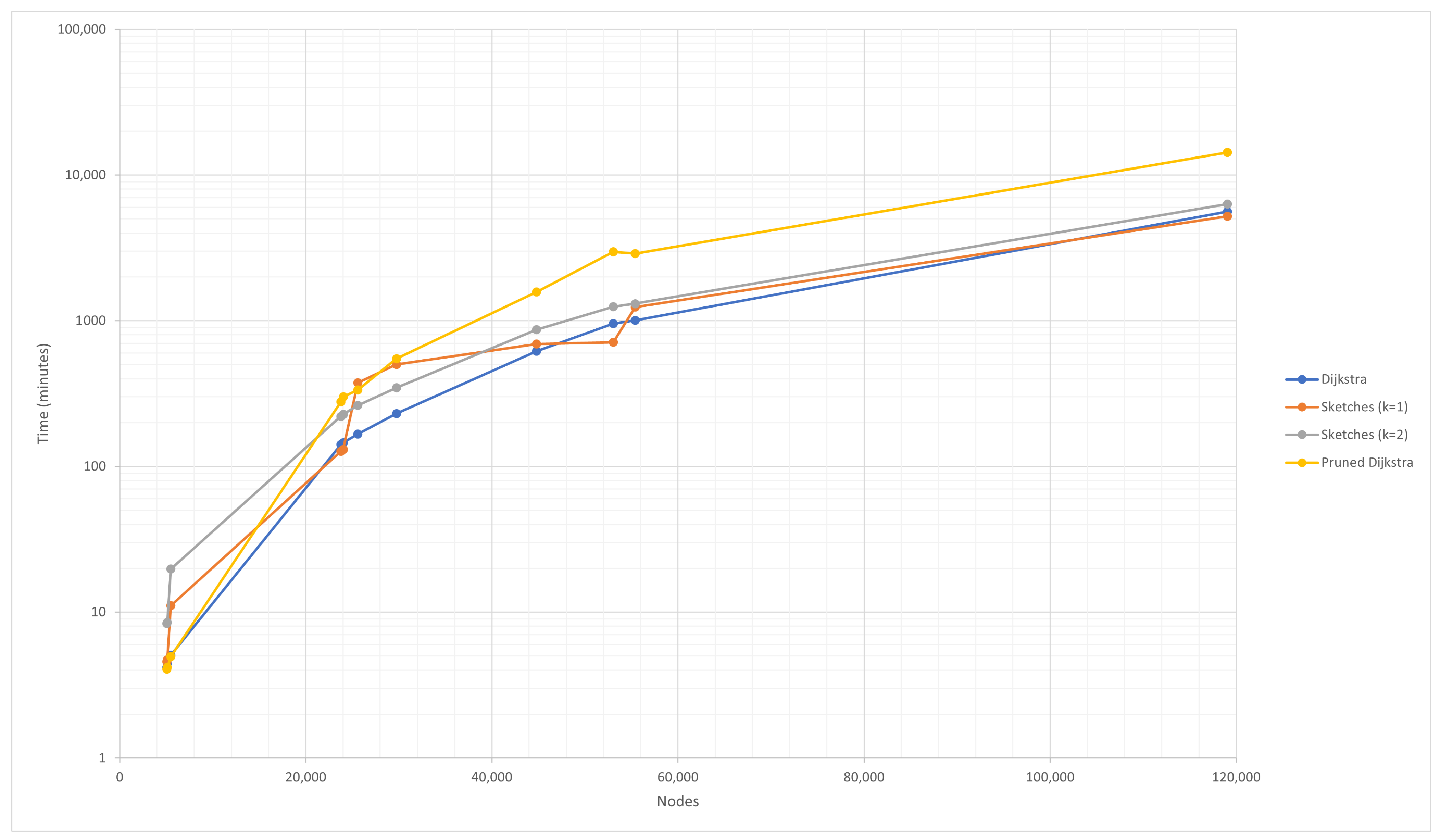
The following is a series of charts on the running time of each proposed algorithm. Figure 3 shows the runtime of the control algorithm, the pruned Dijkstra, and sketch-based algorithms. At specific points, the runtime increases in an “abnormal” way; this is caused by a parameter that differs from the size of the graph; specifically, it is the convergence threshold of the algorithm. It indicates that more iterations are required for this dataset, in particular, the graph structure, to converge with the threshold.
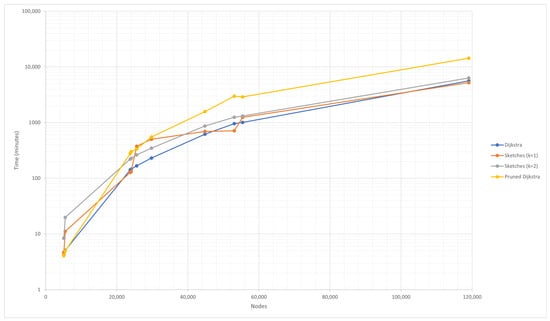
Figure 3.
DIS-C runtime for the Dijkstra, pruned Dijkstra, and sketch-based algorithms.
The convergence threshold is a function of the total generality of the graph, i.e., the sum of all generalities of each node. The total generality of the graph depends on the distance value between each pair of nodes provided by the APSP algorithm; for this reason, the algorithms that obtained the shortest actual distance always reach the convergence threshold in the same number of iterations. In this case, it is the control algorithm and the pruned Dijkstra. On the other hand, the sketch-based algorithm varies the number of iterations to reach the threshold, but in general, it cannot be less than the number achieved by the control algorithm. The reason for this is that the control algorithm determines the precise shortest distances; thus, the total generality of the graph is the smallest possible. The generality of the graph cannot be less than the minimum generality since it is known that the sketch-based algorithm (and any other approximation algorithm) cannot compute a shorter distance than the real one.
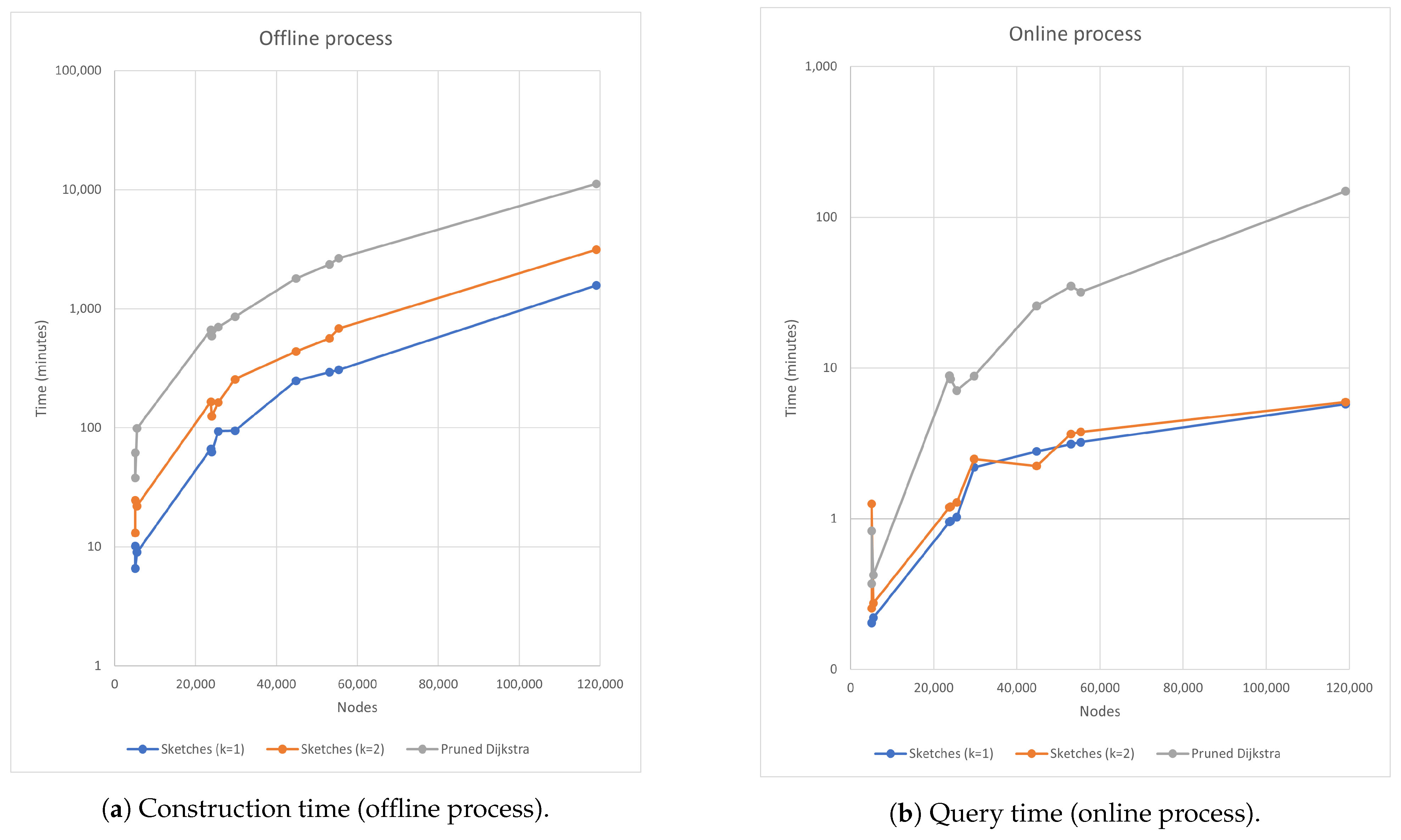
In Figure 3, it is possible to recognize that most of the proposed algorithms have a longer runtime than the control algorithm; this is primarily attributed to graph density; that is, the generated graphs have few edges and can be considered sparse graphs. Notice that only the sketch-based algorithm with is faster than the control algorithm. However, the acceleration is not significant. In order to significantly improve the runtime, it must be reduced by at least one order of magnitude, considering that the runtime in the studied results is measured in days. Since the proposed algorithms are divided into two significant processes (construction and query), the runtimes of these two processes are measured separately. Figure 4 depicts this specific operation.
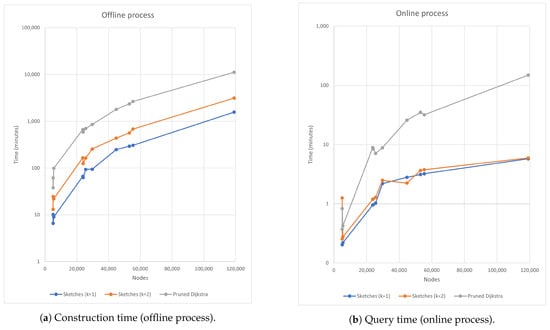
Figure 4.
Comparative offline and online processes using pruned Dijkstra and sketch-based algorithms.
The query time is the most important constraint in the algorithms. When analyzing the complexity of the query process, we found that the complexity of the sketch-based algorithm depends on the size of the coverages, and these are a function of k, so the response when increasing the value of k is predictable, as shown in Figure 4. In the case of the pruned Dijkstra algorithm, the coverage size is huge for more general nodes and decreases as a function of such generality. It induces some nodes to find their shortest distance, which takes longer; this pattern speeds up the overall query time. Although a binary search can be used instead of a linear one, it does not underestimate the quadratic factor inherent in the APSP, the behavior of which is reflected in the results. Considering this inconvenience, we conjecture that graph generality can be computed using only node coverages. This implies that solving the APSP to determine the generality is unnecessary, eliminating the quadratic factor of the APSP.
Based on the previous assumption, a framework for computing generality was established that only considers node coverage because generality was defined as the average of the conceptual distances from concept x to all other concepts, divided by the sum of the average conceptual distances and all concepts in the ontology. In the case of pruned Dijkstra, the more general concepts contain more significant coverage; their influence area is much larger than the less general concepts. This area can be used in a form where the generality of a node depends on itself. The principle of generality is respected by considering the information that other concepts provide for concept x (the distances of the coverage ) and the information that concept x itself provides to its related concepts (the distances of the coverage ). We can consider it as a generality measure based on the extended neighborhood of the nodes represented by their coverages. This is possible because the covers map the topology of the graph. So, we performed the generality computation, as per Equation (4). Henceforth, versions of DIS-C that use this type of generality are denoted as simple.
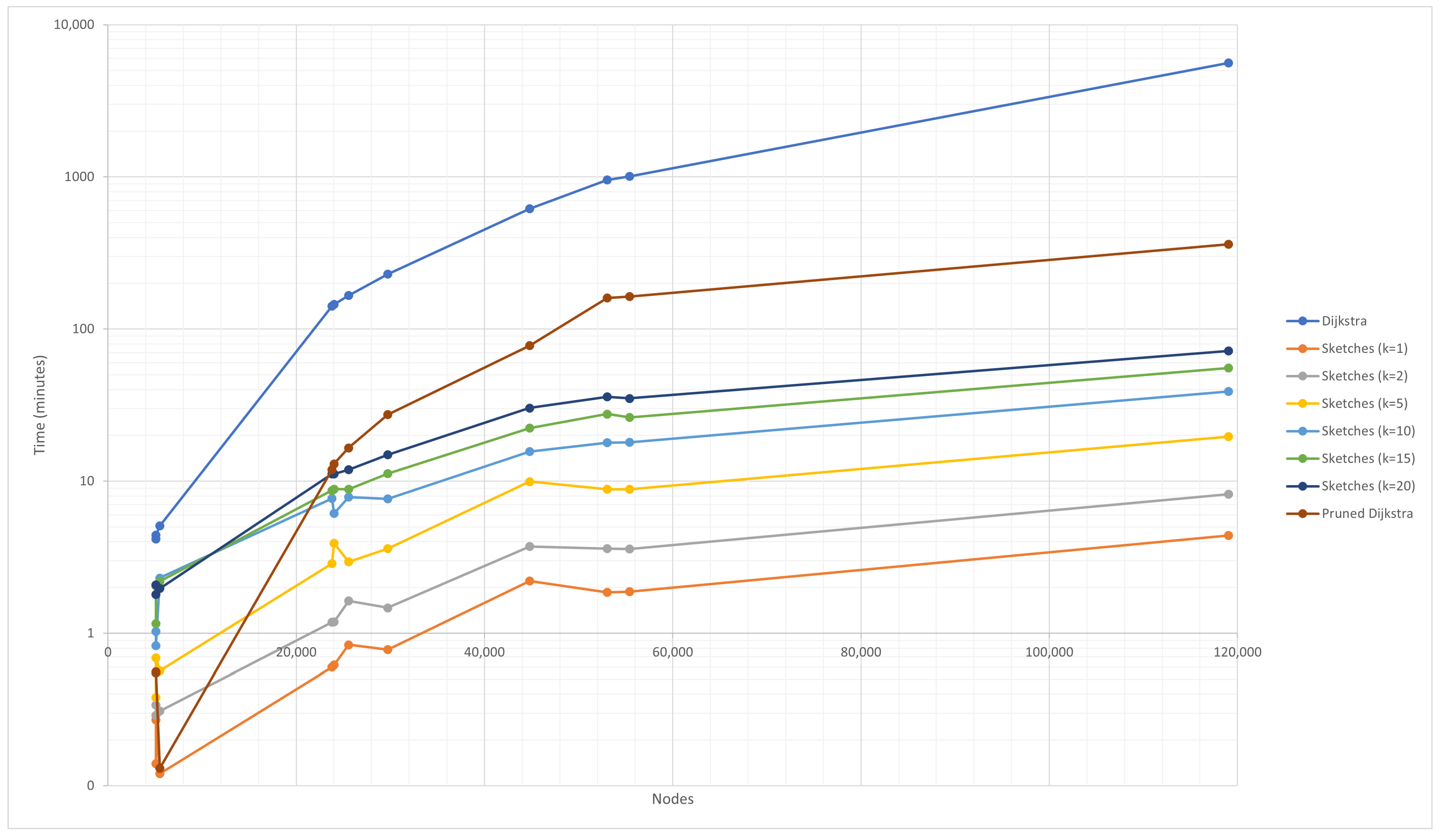
In Figure 5, it is possible to study the total cost of running the simple algorithms in comparison with the others. An evident acceleration is obtained concerning the first versions of the proposed algorithms.
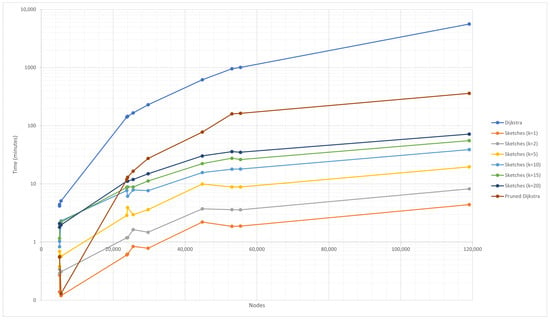
Figure 5.
Simple DIS-C runtime for the following algorithms: Dijkstra, pruned Dijkstra simple, and sketch-based simple.
In the case of the simple pruned Dijkstra algorithm, there is a significant improvement in the runtime, reducing it by an order of magnitude from days to hours for the most extensive graph. In the case of the sketch-based algorithms, there is a more predictive, straight-line relationship with k, i.e., the runtime for is two times lower than for , and so on.
An effective speedup is observed when using the simple version of the algorithms. Similarly, the use of the proposed algorithms in their original form is not recommended in a time-limited context. It is important to emphasize that all algorithms do not use any heuristic; therefore, all are made precise by employing the same input, and the results are obtained consistently. Consequently, a statistically significant analysis does not allow for the detection of differences in the proposed algorithms; in other words, we have the same input, and there is no sensed or monitored data to apply descriptive or inference statistics. The following section examines the usefulness of conceptual distance in practical situations, how much precision is lost in the computation, and whether this is compensated for by the acceleration obtained.
4.4. Conceptual Distance Results
In this section, the results of the conceptual distance obtained in the different datasets evaluated are analyzed, considering the previously proposed metrics. Correlation coefficients are frequently applied in knowledge representation systems; therefore, these coefficients are employed to compare the obtained results with other approaches. Before analyzing the group of datasets, we analyzed the results of a single dataset: MC30. The results of the pruned Dijkstra algorithm correspond directly to the results of the control algorithm because the process obtains the identical shortest distances. The sketch-based algorithm adequately adjusts to the conceptual control distance results; the accuracy of these results depends, essentially, on the value of k; at higher values, the difference from the original results is decreased. This behavior enables us to detect a high correlation with the control algorithm and, in general, with the other versions of the algorithms.
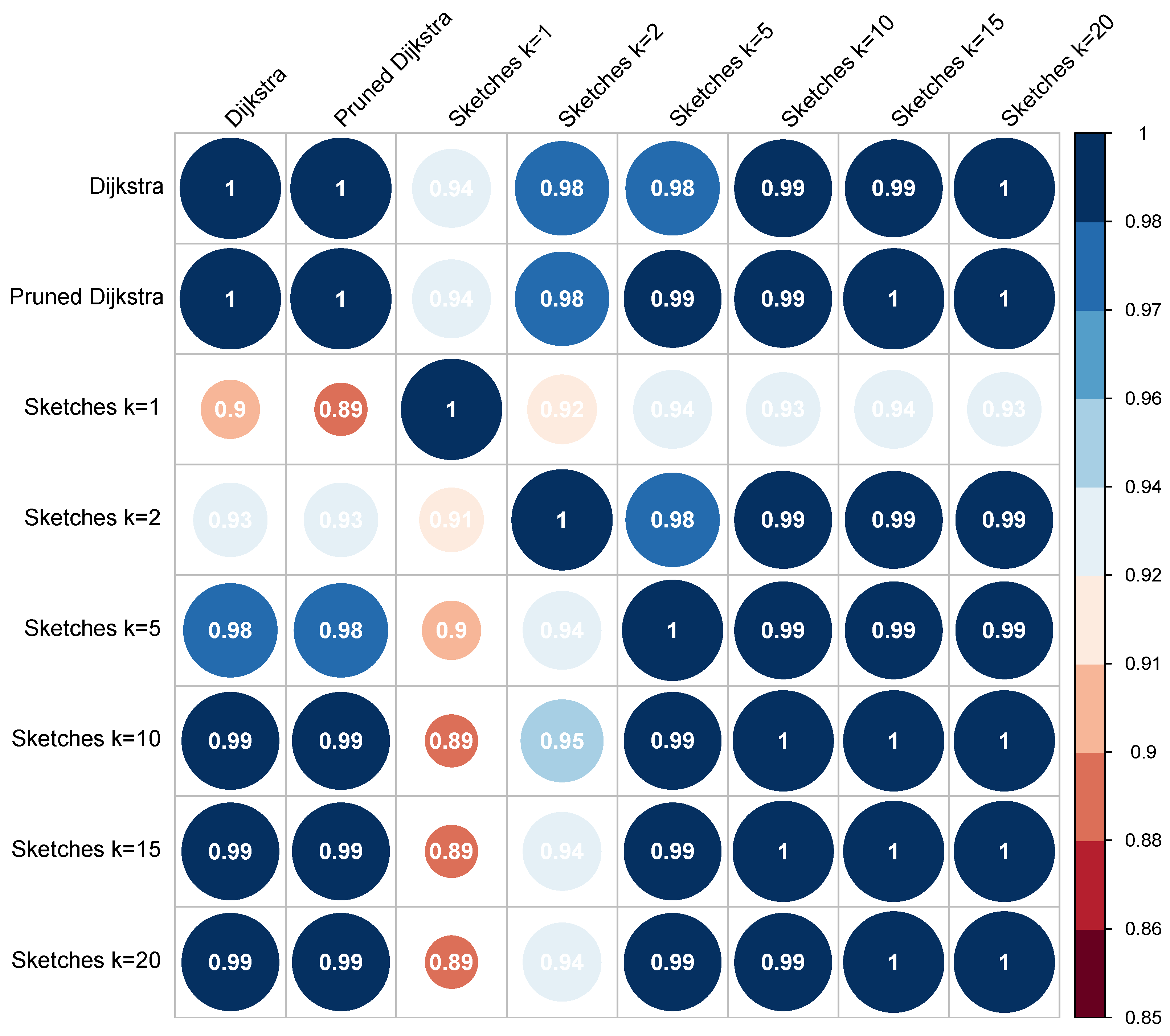
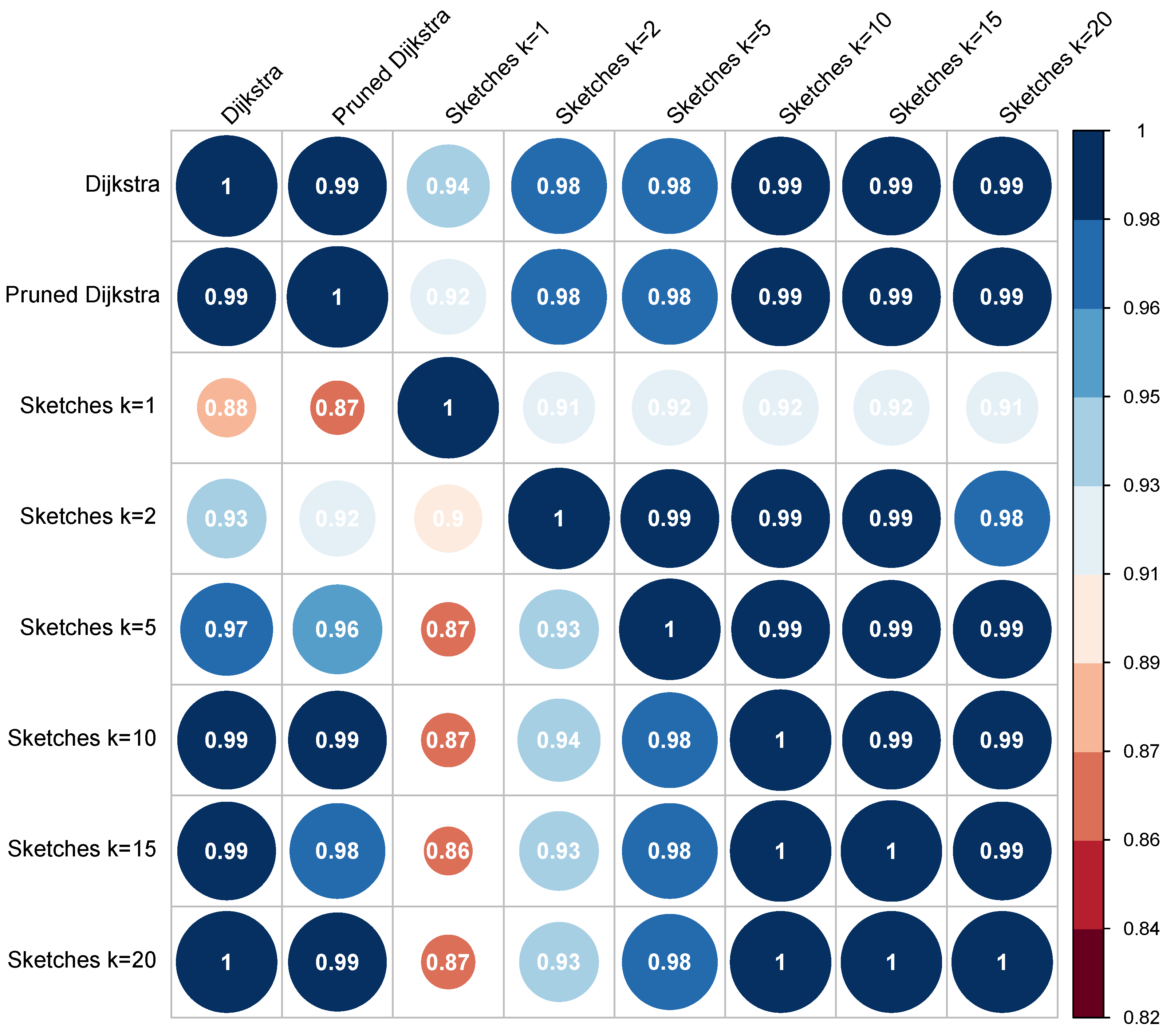
Figure 6 and Figure 7 show the correlation matrix of Person and Spearman, respectively. The upper part of the diagonal represents the correlation between the words in the direction (conceptual distance from the word “a” to the word “b”). In contrast, the lower half of the diagonal is the correlation of . Appendix C provides both the Pearson and Spearman correlation results.
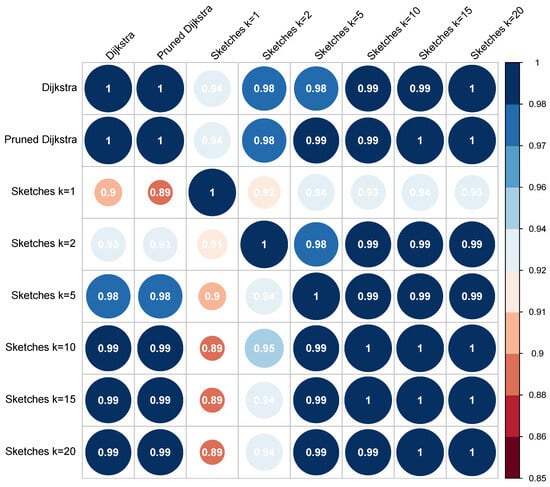
Figure 6.
The Pearson correlation matrix for the MC30 dataset.
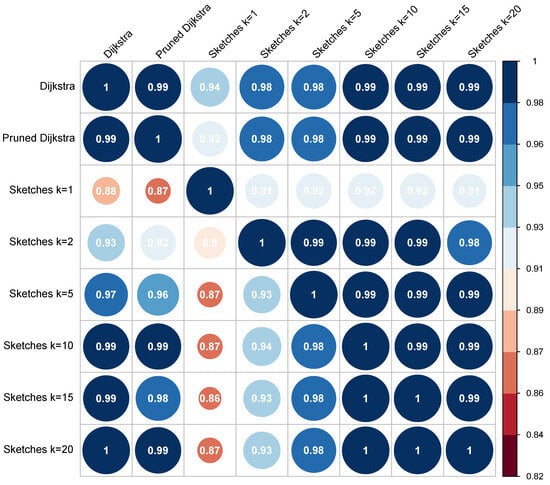
Figure 7.
The Spearman correlation matrix for the MC30 dataset.
The matrices reveal a high correlation for all algorithms. Although the results are excellent in all cases, the correlation values related to the control algorithms are the most relevant for the analysis; these correspond to row 1 and column 1, with values of and , respectively. By correlating the results of each algorithm with the control algorithm, an analysis of the error of each algorithm is implicitly performed. Therefore, as the correlation value is higher in the experiment, the error is decreased, and vice versa, with the advantage of using a metric limited to a specific interval.
In the first case, the lowest correlation value (0.94) corresponds to the sketch-based algorithm with ; however, the correlation increases according to the value of k. The same behavior is replicated in the Spearman matrix and the results of the direction of the concepts. When considering the pruned Dijkstra algorithms, the correlation for the standard version is 1, and for the simple version, it obtained values close to 1 (0.99). These results indicate that the use of the algorithms in the standard or simple version is indifferent because, in both cases, the obtained correlation is very similar or, in some cases, identical.
All the algorithms produced a correlation that was considered high (greater than 0.7). For both types of correlations, the algorithm with the best performance was pruned Dijkstra. The algorithm that produced the lowest correlation was the sketch-based algorithm, with , and values ranging between 0.77 and 0.81; even if they cannot be considered bad results, they show disparity when compared to all the others. If the analysis is focused on the sketch-based algorithms, the pattern observed for the MC30 dataset can be verified, i.e., increasing the value of k also increases the probability of obtaining a better correlation.
Finally, the harmonic values are shown in Table 5; these values unify the performance obtained by both correlations. As mentioned in the previous sections, this table shows that the pruned Dijkstra algorithm achieves the highest correlation values. In contrast, the sketch-based algorithms perform better depending on the given value of its k parameter.

Table 5.
Harmonic values of the correlations.
5. Conclusions and Future Work
This paper investigates the optimization of conceptual distance computation in an ontology using the DIS-C technique. When considering the case of computing conceptual distances by employing a method that solves the APSP problem, both the pruned Dijkstra and the sketch-based algorithms can substitute the Dijkstra algorithm. However, when analyzing the execution times obtained for the test datasets, the use of these two algorithms (pruned Dijkstra and sketch-based) is not recommended for situations where time constraints exist because the growth of the function (which estimates the execution time based on the number of nodes in the graph) is above that obtained by applying the standard Dijkstra algorithm.
Thus, to reduce the computational cost, a simple version of DIS-C was proposed by replacing the use of the APSP as a subprocess for propagating the conceptual distances between all pairs of concepts to compute generality, taking the vertex cover (sometimes referred to as node cover) into account. Based on this simple version, the experiments show that the processing time is up to times faster than the original DIS-C approach. One of the main purposes of this paper was to maintain a reduced loss of precision in distance computation when compared to the original version of DIS-C, with correlation values of . The simple version can be useful in practical applications, and if the highest precision in distance calculation is required, this version using pruned Dijkstra is the best option. Moreover, using the complete topology of a graph to compute the conceptual distance in the DIS-C model is excessive and requires high computational cost. Therefore, we have experimentally demonstrated that the vertex cover is a robust approximation for computing the generality.
On the other hand, if speed is a priority, the simple version of the sketch-based algorithm with moderate values (greater than 1 but less than 20) for the parameter k is a good alternative. We must also consider the size of the conceptualization; for sizes of less than 1000 concepts, the type of algorithm is indifferent, and the use of Dijkstra is a better option since the computation time is not excessive and ensures the calculation, as proposed by the DIS-C model. An interesting way to take advantage of the speed of the sketch-based algorithm with low parameters (less than five) for k is when it is necessary to quickly perform tests on systems using DIS-C or directly when we want to compare the method with others. Implementing the sketch-based approach can provide a reference guide; for example, when good results are obtained with the simple version, it is reasonable to assume that the same results are obtained by executing the original DIS-C approach (when using the Dijkstra algorithm). The previous statement assumes that precision is the most crucial factor and that computation time is not a primary constraint. On the other hand, if time is a limitation, the pruned Dijkstra algorithm can be used as a replacement for Dijkstra, considering its high correlation.
Future work will be oriented toward evaluating the performance of these algorithms on other types of massive graphs, such as knowledge graphs, and analyzing the performance of the simple DIS-C approach with graphics unit processing (GPU) implementations. In addition, new advances in microprocessor architecture design, such as high-performance cores and high-efficiency cores, might be an exciting and suitable alternative to improve performance and computational time. Moreover, additional implementations to test this approach in other application domains involving information theory could be considered to evaluate the effectiveness of the proposed method.
Author Contributions
Conceptualization, R.Q. and E.M.; methodology, G.G. and M.T.-R.; software, E.M. and C.G.S.-M.; validation, R.Q., E.M., and G.G.; formal analysis, M.T.-R. and G.G.; investigation, R.Q. and C.G.S.-M.; resources, M.T.-R.; data curation, G.G.; writing—original draft preparation, R.Q. and C.G.S.-M.; writing—review and editing, M.T.-R. and G.G.; visualization, E.M.; supervision, R.Q.; project administration, C.G.S.-M.; funding acquisition, G.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially sponsored by the Instituto Politécnico Nacional under grants 20231372, 20230901, and 20230655, the Consejo Nacional de Humanidades, Ciencias y Tecnologías and Secretaría de Educación, Ciencia, Tecnología e Innovación de la Ciudad de México (SECTEI/182/2023).
Data Availability Statement
Data are contained within the article.
Acknowledgments
We are thankful to the reviewers for their time and invaluable and constructive feedback, which helped improve the quality of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Pruned Dijkstra
The pruned Dijkstra algorithm is a generalization of the PLL (pruned landmark labeling) method for undirected, weighted graphs [73]. The PLL method is based on the idea of two-hop coverage [86], which is an exact method. It is defined as follows: let be an undirected and weighted graph; for each vertex, , the cover is a set of pairs, , where u is a vertex, and is the distance from u to v in the graph, G. All coverage is denoted as indexed . To compute the distance between the two vertices, s and t, we used the search function (Q), as shown in Equation (A1). L is a two-hop cover of G if for any .
In regard to weighted directed graphs, it is necessary to evaluate two indices; the first, , contains the coverage of all the nodes, considering the incoming edges. The second, , considers the outgoing edges. The procedure for consulting the distances has a simple modification but the idea remains the same. This change is shown in Equation (A2).
A simple solution to build these indices is to employ two executions of the Dijkstra algorithm. Although this method needs to be more obvious and effective, we will explain the details when discussing the next method. Let ; start with an empty index, , where . Suppose Dijkstra is applied to each vertex in the order . After the k-th Dijkstra on a vertex , the distances of are added to the coverages of the vertices reached, where for each with , where is the distance from vertex u to vertex v within the graph, G. It is important to note that the coverages of the vertices reached are not changed, which implies that for each with . Performing this procedure, starting from , gives the same result but takes into account the output edges.
Therefore, and are the final indices contained in . It follows that for any vertex pair, so and are the two-hop covers of G. If s and t are reachable, then and . Creating indices in this form might be more efficient. For this reason, pruning is added to the original method. This technique reduces the search space considerably. In the classic method, a pruned search is performed using the Dijkstra algorithm, processing the vertices in the following order: . Start with a pair of indices, and , and create indices , from and , respectively, using the information obtained by the k-th execution of pruned Dijkstra for vertex .
The pruning process is as follows: Suppose we have the indices and and we execute the pruned Dijkstra from to create a new index . We assume that a vertex, u, with a distance of is visited. If , then we prune u, i.e., not adding both to and any neighbors of u to the priority queue. If the condition is not satisfied, then is added to the cover of u, and Dijkstra is performed as usual. Similar to the original method, for all vertices that were not reached in the k-th execution of the pruned Dijkstra, set and . Finally, and are the terminal indices contained in .
Figure A1 shows an example of the algorithm applied to the graph depicted in the figure, assuming that the order of execution is . The first pruned Dijkstra from vertex 1 visits all other vertices forwards (Figure A2a) and backwards (Figure A2b). In the next iteration from vertex 8 (Figure A2c), when vertex 1 is visited, given that 1, vertex 1 is pruned and neither of its neighbors is visited again; the same occurs in the opposite direction (see Figure A2d). With these two executions, it is possible to cover all the shortest paths, and after executing the process on the remaining vertices, they only refer to themselves.

Figure A1.
Example of a graph for the pruned Dijkstra algorithm.
Figure A1.
Example of a graph for the pruned Dijkstra algorithm.
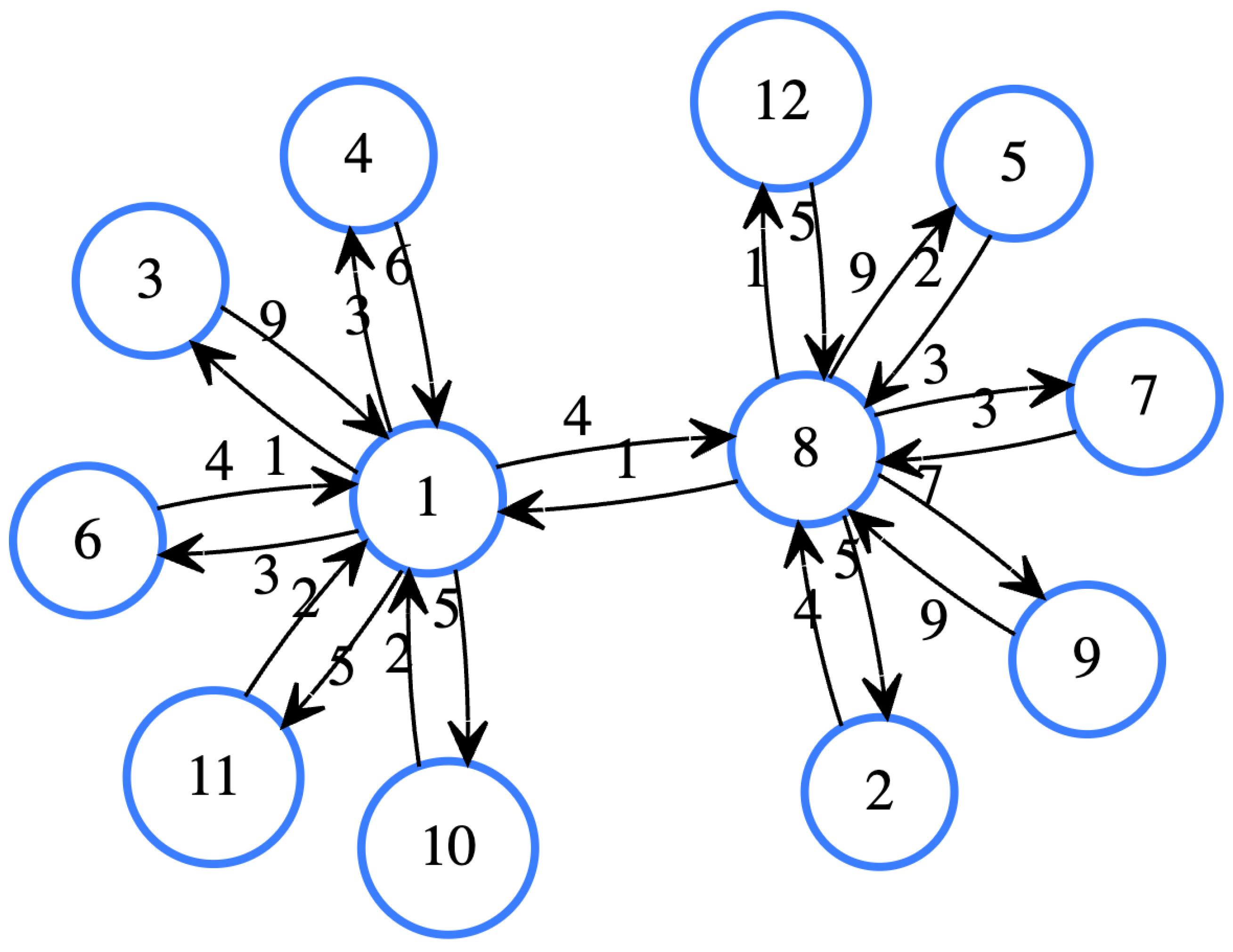
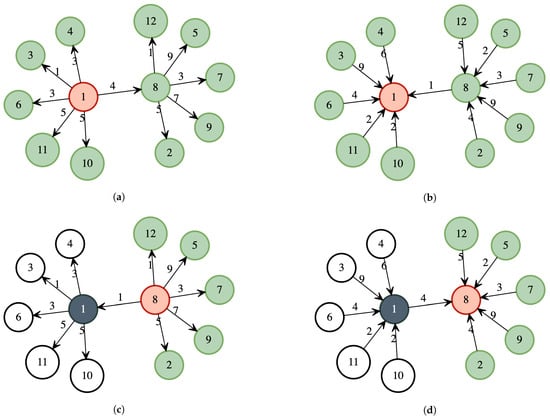
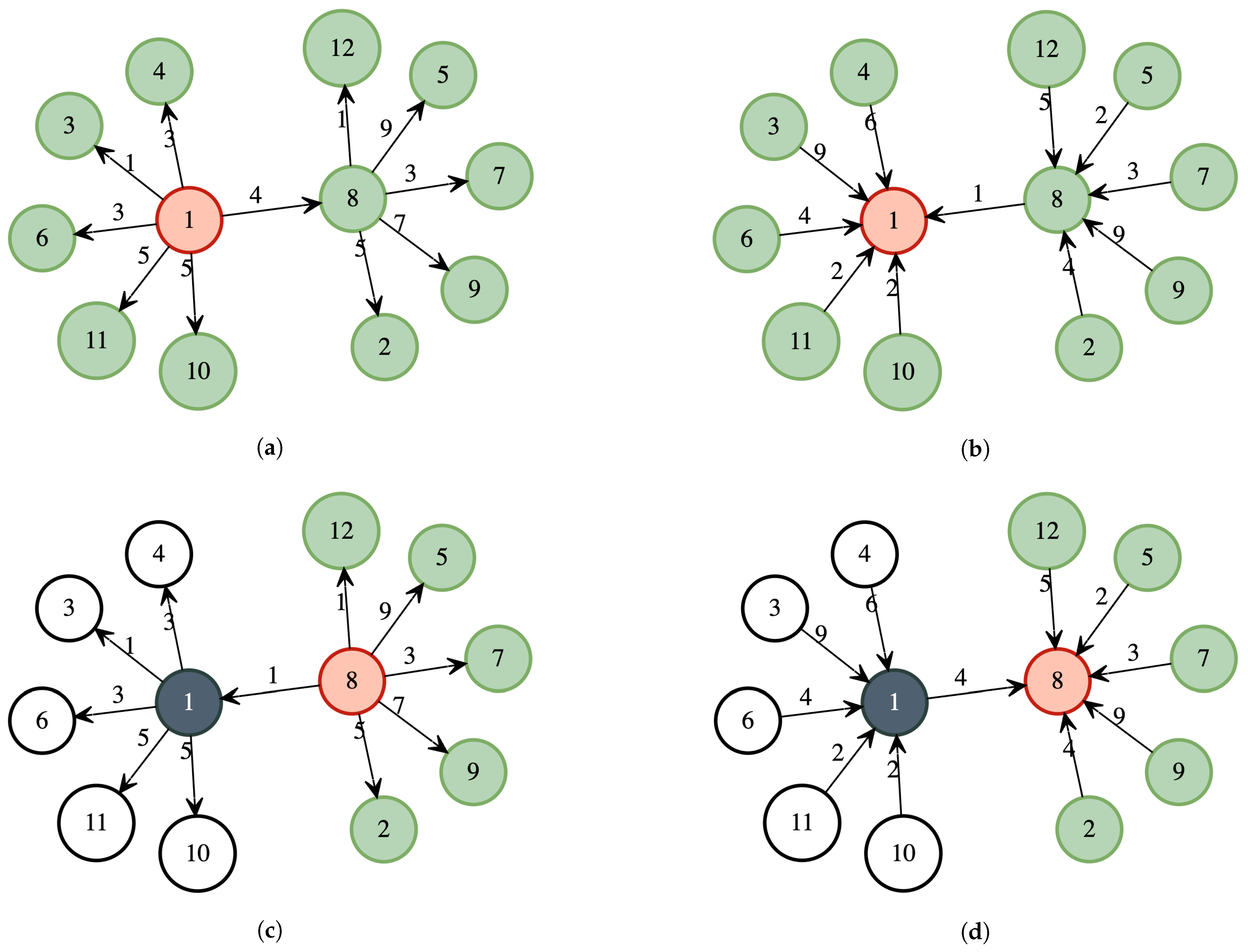
Figure A2.
Example of a pruned Dijkstra. The red vertices denote the execution root, the green vertices represent those visited and added to the coverage, and the gray vertices are the roots. (a) The first pruned Dijkstra from vertex 1 with trailing edges. All vertices are visited. (b) The first pruned Dijkstra from vertex 1 with entry edges. All vertices are visited. (c) The second pruned Dijkstra from vertex 8 with exit edges. Only those adjacent to 8 are visited. (d) The second pruned Dijkstra from vertex 8 with entry edges. Only those adjacent to 8 are visited.
Figure A2.
Example of a pruned Dijkstra. The red vertices denote the execution root, the green vertices represent those visited and added to the coverage, and the gray vertices are the roots. (a) The first pruned Dijkstra from vertex 1 with trailing edges. All vertices are visited. (b) The first pruned Dijkstra from vertex 1 with entry edges. All vertices are visited. (c) The second pruned Dijkstra from vertex 8 with exit edges. Only those adjacent to 8 are visited. (d) The second pruned Dijkstra from vertex 8 with entry edges. Only those adjacent to 8 are visited.
Appendix B. The Sketch-Based Algorithms
Sketch-based algorithms are methods that include two general processes: offline and online. In the offline process, a set of sketches represents the crucial nodes, defined randomly. By considering these sketches, the shortest path to all other vertices is determined. In the online process, the shortest distance between a pair of nodes, , is calculated from the closest common sketch of them.
The offline process consists of sampling sets of the seed vertex, each containing a subset, , of size . For each set, the closest seed, , of each vertex is stored, including its distance; i.e., for every node, u, a sketch of the form SKETCH is created. Therefore, the final size of the sketch for each node is . This technique can be performed using the Dijkstra algorithm. The vertex, , closest to u is denoted as the seed of u. This procedure is repeated k times with different sample sizes. At the end of the k iterations, each node has seeds.
Figure A3 shows an example of the implemented procedure. The graph in Figure A1 is used as a reference. Since there are 12 vertices, the number of seed sets is 3 (), and the size of the sets is 1, 2, and 4, respectively. The vertices in each set are 1 for the first, for the second, and for the last.
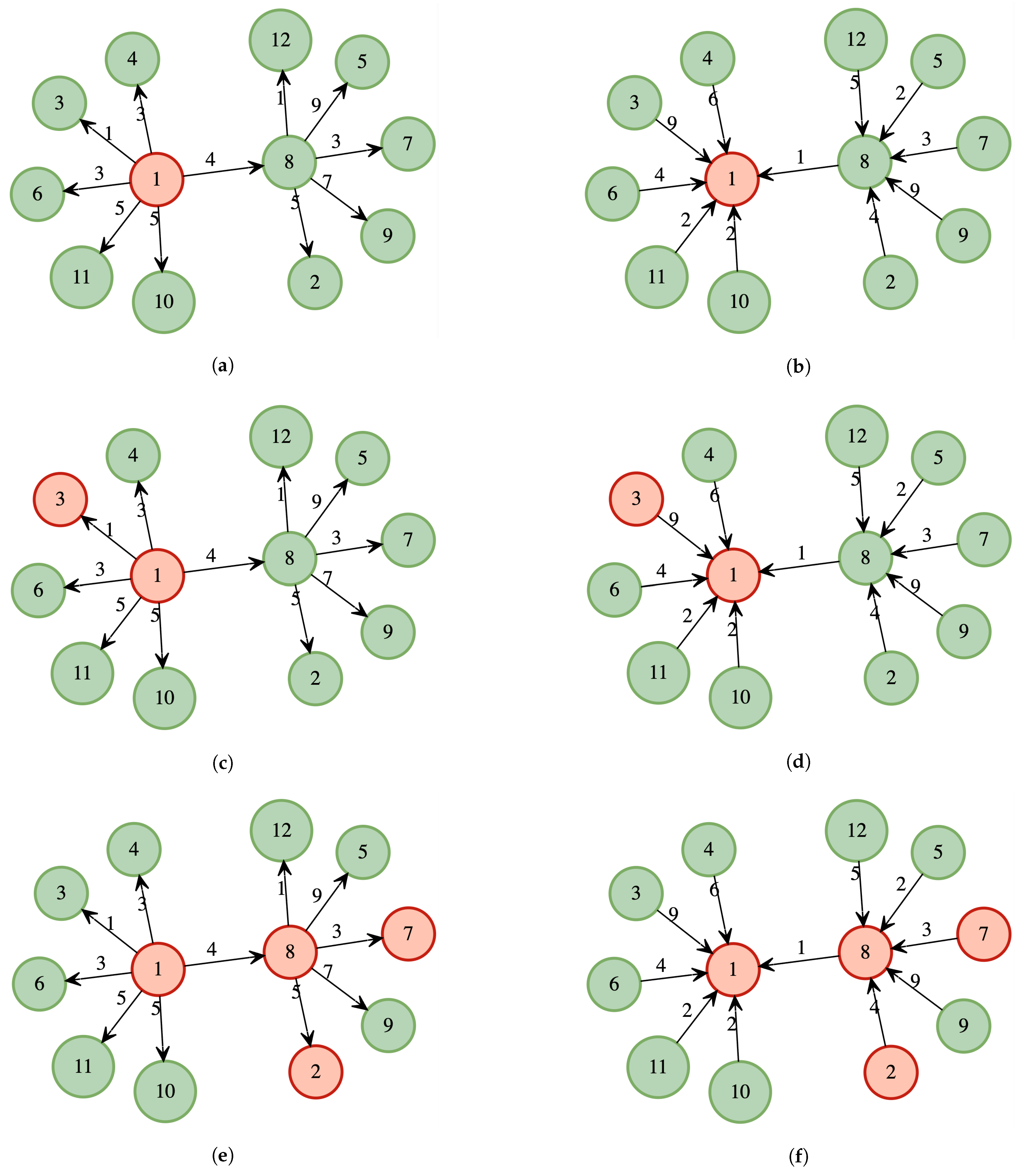
In the first iteration (Figure A3a), all the vertices have vertex 1 in their coverage; this also happens for the input edges (see Figure A3b). In the second iteration (Figure A3c,d), the coverages do not change since vertex 3 does not cover any path shorter than those already covered by vertex 1. Finally, in the last iteration (Figure A3e,f), we have vertex 8 in the seed set; this covers the shortest path of its neighbors, except those that are also in the set; therefore, vertices 5, 12, and 9 will have 8 in their coverage. On the other hand, vertices 2 and 7 are included in their respective coverages.

Figure A3.
Sketch-based algorithm example. The red vertices denote the execution root, and the green ones represent those that are visited. (a) Sketches from set 1 with output edges. All vertices have node 1 in their coverage. (b) Sketches from set 1 with input edges. All vertices have node 1 in their coverage. (c) Sketches from set 2 with output edges. Coverages do not change. (d) Sketches from set 2 with input edges. Coverages do not change. (e) Sketches from set 3 with output edges. 8 is added to the coverage of vertices 5, 9, and 12. (f) Sketches from set 3 with input edges; 8 is added to the coverage of vertices 5, 9, and 12.
Figure A3.
Sketch-based algorithm example. The red vertices denote the execution root, and the green ones represent those that are visited. (a) Sketches from set 1 with output edges. All vertices have node 1 in their coverage. (b) Sketches from set 1 with input edges. All vertices have node 1 in their coverage. (c) Sketches from set 2 with output edges. Coverages do not change. (d) Sketches from set 2 with input edges. Coverages do not change. (e) Sketches from set 3 with output edges. 8 is added to the coverage of vertices 5, 9, and 12. (f) Sketches from set 3 with input edges; 8 is added to the coverage of vertices 5, 9, and 12.
Appendix C. Pearson and Spearman Correlation Results
According to the described experiments, Table A1 and Table A2 describe the results of the Pearson correlation obtained by applying all the algorithms and their configurations to the 11 datasets. In addition, Table A3 and Table A4 show the values of the Spearman correlation.

Table A1.
The Pearson correlation of all datasets in the direction .
Table A1.
The Pearson correlation of all datasets in the direction .
| Algorithm | MC | RG | PS | Agirre | SimLex | MTurk771 | MTurk287 | WSRel | Rel | SCWS | All | Avg. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dijkstra | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Pruned Dijkstra | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.997 | 1.000 |
| Sketches k = 1 | 0.940 | 0.853 | 0.862 | 0.733 | 0.762 | 0.605 | 0.864 | 0.720 | 0.841 | 0.815 | 0.745 | 0.795 |
| Sketches k = 2 | 0.977 | 0.947 | 0.961 | 0.870 | 0.813 | 0.731 | 0.888 | 0.842 | 0.922 | 0.898 | 0.802 | 0.877 |
| Sketches k = 5 | 0.985 | 0.984 | 0.978 | 0.923 | 0.897 | 0.881 | 0.937 | 0.921 | 0.953 | 0.944 | 0.899 | 0.937 |
| Sketches k = 10 | 0.991 | 0.979 | 0.995 | 0.961 | 0.955 | 0.931 | 0.967 | 0.959 | 0.976 | 0.971 | 0.942 | 0.966 |
| Sketches k = 15 | 0.993 | 0.996 | 0.991 | 0.980 | 0.972 | 0.959 | 0.971 | 0.971 | 0.983 | 0.982 | 0.957 | 0.978 |
| Sketches k = 20 | 0.996 | 0.992 | 0.994 | 0.983 | 0.974 | 0.971 | 0.979 | 0.975 | 0.989 | 0.986 | 0.972 | 0.983 |

Table A2.
The Pearson correlation of all datasets in the direction .
Table A2.
The Pearson correlation of all datasets in the direction .
| Algorithm | MC | RG | PS | Agirre | SimLex | MTurk771 | MTurk287 | WSRel | Rel | SCWS | All | Avg. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dijkstra | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Sketches k = 1 | 0.897 | 0.777 | 0.877 | 0.734 | 0.722 | 0.562 | 0.862 | 0.757 | 0.857 | 0.793 | 0.733 | 0.779 |
| Sketches k = 2 | 0.932 | 0.961 | 0.956 | 0.893 | 0.806 | 0.725 | 0.890 | 0.827 | 0.879 | 0.896 | 0.795 | 0.869 |
| Sketches k = 5 | 0.979 | 0.984 | 0.981 | 0.909 | 0.893 | 0.865 | 0.946 | 0.936 | 0.947 | 0.945 | 0.897 | 0.935 |
| Sketches k = 10 | 0.987 | 0.991 | 0.992 | 0.963 | 0.952 | 0.944 | 0.960 | 0.945 | 0.979 | 0.967 | 0.939 | 0.965 |
| Sketches k = 15 | 0.992 | 0.998 | 0.994 | 0.968 | 0.971 | 0.958 | 0.975 | 0.966 | 0.978 | 0.980 | 0.960 | 0.976 |
| Sketches k = 20 | 0.995 | 0.996 | 0.997 | 0.979 | 0.971 | 0.972 | 0.980 | 0.983 | 0.984 | 0.988 | 0.972 | 0.983 |

Table A3.
The Spearman correlation of all datasets in the direction .
Table A3.
The Spearman correlation of all datasets in the direction .
| Algorithm | MC | RG | PS | Agirre | SimLex | MTurk771 | MTurk287 | WSRel | Rel | SCWS | All | Avg. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dijkstra | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Pruned Dijkstra | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.968 | 0.997 |
| Sketches k = 1 | 0.938 | 0.876 | 0.858 | 0.702 | 0.742 | 0.605 | 0.843 | 0.671 | 0.799 | 0.831 | 0.736 | 0.782 |
| Sketches k = 2 | 0.977 | 0.944 | 0.959 | 0.823 | 0.804 | 0.729 | 0.855 | 0.821 | 0.900 | 0.906 | 0.807 | 0.866 |
| Sketches k = 5 | 0.978 | 0.978 | 0.984 | 0.911 | 0.887 | 0.876 | 0.925 | 0.907 | 0.950 | 0.954 | 0.897 | 0.931 |
| Sketches k = 10 | 0.987 | 0.981 | 0.991 | 0.941 | 0.955 | 0.931 | 0.963 | 0.946 | 0.973 | 0.978 | 0.942 | 0.962 |
| Sketches k = 15 | 0.987 | 0.993 | 0.985 | 0.968 | 0.971 | 0.969 | 0.963 | 0.960 | 0.980 | 0.986 | 0.954 | 0.974 |
| Sketches k = 20 | 0.989 | 0.988 | 0.991 | 0.973 | 0.979 | 0.978 | 0.976 | 0.961 | 0.985 | 0.990 | 0.965 | 0.980 |

Table A4.
The Spearman correlation of all datasets in the direction .
Table A4.
The Spearman correlation of all datasets in the direction .
| Algorithm | MC | RG | PS | Agirre | SimLex | MTurk771 | MTurk287 | WSRel | Rel | SCWS | All | Avg. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dijkstra | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Pruned Dijkstra | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.969 | 0.997 |
| Sketches k = 1 | 0.875 | 0.826 | 0.843 | 0.735 | 0.700 | 0.573 | 0.823 | 0.693 | 0.817 | 0.807 | 0.732 | 0.766 |
| Sketches k = 2 | 0.925 | 0.921 | 0.932 | 0.859 | 0.816 | 0.733 | 0.876 | 0.764 | 0.835 | 0.902 | 0.803 | 0.851 |
| Sketches k = 5 | 0.972 | 0.970 | 0.961 | 0.898 | 0.884 | 0.866 | 0.920 | 0.906 | 0.936 | 0.953 | 0.896 | 0.924 |
| Sketches k = 10 | 0.991 | 0.980 | 0.985 | 0.953 | 0.950 | 0.947 | 0.945 | 0.928 | 0.969 | 0.974 | 0.938 | 0.960 |
| Sketches k = 15 | 0.991 | 0.990 | 0.981 | 0.959 | 0.974 | 0.960 | 0.961 | 0.952 | 0.969 | 0.984 | 0.958 | 0.971 |
| Sketches k = 20 | 0.996 | 0.985 | 0.990 | 0.973 | 0.971 | 0.977 | 0.971 | 0.975 | 0.982 | 0.991 | 0.966 | 0.980 |
References
- Mejia Sanchez-Bermejo, A. Similitud Semantica Entre Conceptos de Wikipedia. Bachelor’s Thesis, Universidad Carlos III de Madrid, Getafe, Madrid, Spain, 2013. [Google Scholar]
- Goldstone, R.L. Similarity, interactive activation, and mapping. J. Exp. Psychol. Learn. Mem. Cogn. 1994, 20, 3. [Google Scholar] [CrossRef]
- Quintero, R.; Torres-Ruiz, M.; Saldaña-Pérez, M.; Guzmán Sánchez-Mejorada, C.; Mata-Rivera, F. A Conceptual Graph-Based Method to Compute Information Content. Mathematics 2023, 11, 3972. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Z.; Hua, Q.; Shang, W.L.; Luo, Q.; Yu, K. AI-empowered speed extraction via port-like videos for vehicular trajectory analysis. IEEE Trans. Intell. Transp. Syst. 2022, 24, 4541–4552. [Google Scholar] [CrossRef]
- Quintero, R.; Torres-Ruiz, M.; Menchaca-Méndez, R.; Moreno-Armendariz, M.A.; Guzmán, G.; Moreno-Ibarra, M. DIS-C: Conceptual distance in ontologies, a graph-based approach. Knowl. Inf. Syst. 2019, 59, 33–65. [Google Scholar] [CrossRef]
- Dreyfus, S.E. An appraisal of some shortest-path algorithms. Oper. Res. 1969, 17, 395–412. [Google Scholar] [CrossRef]
- Gallo, G.; Pallottino, S. Shortest path algorithms. Ann. Oper. Res. 1988, 13, 1–79. [Google Scholar] [CrossRef]
- Magzhan, K.; Jani, H.M. A review and evaluations of shortest path algorithms. Int. J. Sci. Technol. Res. 2013, 2, 99–104. [Google Scholar]
- Madkour, A.; Aref, W.G.; Rehman, F.U.; Rahman, M.A.; Basalamah, S. A survey of shortest-path algorithms. arXiv 2017, arXiv:1705.02044. [Google Scholar]
- Zhang, F.; Liu, J. A new shortest path algorithm for massive spatial data based on Dijkstra algorithm. J. LiaoNing Technol. Univ. Sci. Ed. 2009, 28, 554–557. [Google Scholar]
- Chakaravarthy, V.T.; Checconi, F.; Murali, P.; Petrini, F.; Sabharwal, Y. Scalable single source shortest path algorithms for massively parallel systems. IEEE Trans. Parallel Distrib. Syst. 2016, 28, 2031–2045. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Z.; Wang, X.; Hu, Q. Finding the shortest path with vertex constraint over large graphs. Complexity 2019, 2019, 8728245. [Google Scholar] [CrossRef]
- Liu, J.; Pan, Y.; Hu, Q.; Li, A. Navigating a Shortest Path with High Probability in Massive Complex Networks. In Proceedings of the Analysis of Experimental Algorithms: Special Event, SEA2 2019, Kalamata, Greece, 24–29 June 2019; Revised Selected Papers. Springer: Berlin/Heidelberg, Germany, 2019; pp. 82–97. [Google Scholar]
- Ma, X.; Huo, E.; Yu, H.; Li, H. Mining truck platooning patterns through massive trajectory data. Knowl. Based Syst. 2021, 221, 106972. [Google Scholar] [CrossRef]
- Li, S.; Sun, X.; Xiao, Y.H.; Guo, X.; Zhang, J. Noncoherent space-time coding for correlated massive MIMO channel with Riemannian distance. Digit. Signal Process. 2023, 133, 103876. [Google Scholar] [CrossRef]
- Meersman, R.A. Semantic ontology tools in IS design. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1999; pp. 30–45. [Google Scholar] [CrossRef]
- Bondy, J.A. Graph Theory with Applications; Elsevier Science Publishing Co., Inc.: New York, NY, USA, 1982. [Google Scholar]
- West, D.B. Introduction to Graph Theory, 2nd ed.; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Bollobás, B. Modern Fraph Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1998; Volume 184. [Google Scholar]
- Gross, J.L.; Yellen, J.; Anderson, M. Graph Theory and Its Applications; Chapman and Hall/CRC: London, UK, 2018. [Google Scholar]
- Juel Vang, K. Ethics of Google’s Knowledge Graph: Some considerations. J. Inf. Commun. Ethics Soc. 2013, 11, 245–260. [Google Scholar] [CrossRef]
- Ehrlinger, L.; Wöß, W. Towards a definition of knowledge graphs. SEMANTiCS (Posters, Demos, SuCCESS) 2016, 48, 2. [Google Scholar]
- Fensel, D.; Şimşek, U.; Angele, K.; Huaman, E.; Kärle, E.; Panasiuk, O.; Toma, I.; Umbrich, J.; Wahler, A.; Fensel, D.; et al. Introduction: What is a knowledge graph? In Knowledge Graphs: Methodology, Tools and Selected Use Cases; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–10. [Google Scholar]
- Zou, X. A survey on application of knowledge graph. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; Volume 1487, p. 012016. [Google Scholar]
- Pujara, J.; Miao, H.; Getoor, L.; Cohen, W. Knowledge graph identification. In Proceedings of the Semantic Web—ISWC 2013: 12th International Semantic Web Conference, Sydney, NSW, Australia, 21–25 October 2013; Proceedings, Part I 12. Springer: Berlin/Heidelberg, Germany, 2013; pp. 542–557. [Google Scholar]
- Sanchez, D.; Batet, M.; Isern, D.; Valls, A. Ontology-based semantic similarity: A new feature-based approach. Expert Syst. Appl. 2012, 39, 7718–7728. [Google Scholar] [CrossRef]
- Rada, R.; Mili, H.; Bicknell, E.; Blettner, M. Development and application of a metric on semantic nets. IEEE Trans. Syst. Man Cybern. 1989, 19, 17–30. [Google Scholar] [CrossRef]
- Wu, Z.; Palmer, M. Verb semantics and lexical selection. arXiv 1994, arXiv:cmp-lg/9406033. [Google Scholar]
- Hirst, G.; Stonge, D. Lexical Chains as Representations of Context for the Detection and Correction of Malapropisms. Wordnet Electron. Lex. Database 1995, 305, 305–332. [Google Scholar]
- Li, Y.; Bandar, Z.A.; Mclean, D. An approach for measuring semantic similarity between words using multiple information sources. IEEE Trans. Knowl. Data Eng. 2003, 15, 871–882. [Google Scholar] [CrossRef]
- Shenoy, M.K.; Shet, K.; Acharya, U.D. A new similarity measure for taxonomy based on edge counting. Int. J. Web Semant. Technol. 2012, 3, 23. [Google Scholar] [CrossRef]
- Tversky, A. Features of similarity. Psychol. Rev. 1977, 84, 327. [Google Scholar] [CrossRef]
- Lesk, M. Automatic sense disambiguation using machine readable dictionaries: How to tell a pine cone from an ice cream cone. In Proceedings of the 5th Annual International Conference on Systems Documentation, Toronto, ON, Canada, 8–11 June 1986; 1986; pp. 24–26. [Google Scholar]
- Banerjee, S.; Pedersen, T. Extended gloss overlaps as a measure of semantic relatedness. In Proceedings of the 18th International Joint Conference on Artificial Intelligence, IJCAI, Acapulco, Mexico, 9–15 August 2003; Volume 3, pp. 805–810. [Google Scholar]
- Jiang, Y.; Zhang, X.; Tang, Y.; Nie, R. Feature-based approaches to semantic similarity assessment of concepts using Wikipedia. Inf. Process. Manag. 2015, 51, 215–234. [Google Scholar] [CrossRef]
- Resnik, P. Using Information Content to Evaluate Semantic Similarity in a Taxonomy. In Proceedings of the Fourteenth International Joint Conference on Artificial Intelligence, IJCAI, Montreal, QC, Canada, 20–25 August 1995; Volume 1, pp. 449–453. [Google Scholar]
- Jiang, J.J.; Conrath, D.W. Semantic similarity based on corpus statistics and lexical taxonomy. In Proceedings of the 10th Research on Computational Linguistics International Conference, ROCLING X, Taipei, Taiwan, 25–27 August 1997; pp. 19–33. [Google Scholar]
- Gao, J.B.; Zhang, B.W.; Chen, X.H. A WordNet-based semantic similarity measurement combining edge-counting and information content theory. Eng. Appl. Artif. Intell. 2015, 39, 80–88. [Google Scholar] [CrossRef]
- Jiang, Y.; Bai, W.; Zhang, X.; Hu, J. Wikipedia-based information content and semantic similarity computation. Inf. Process. Manag. 2017, 53, 248–265. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, Y.; Gu, J. A New Model of Information Content for Semantic Similarity in WordNet. In Proceedings of the 2008 Second International Conference on Future Generation Communication and Networking Symposia, Sanya, China, 13–15 December 2008; Volume 3, pp. 85–89. [Google Scholar] [CrossRef]
- Sanchez, D.; Batet, M.; Isern, D. Ontology-based information content computation. Knowl. Based Syst. 2011, 24, 297–303. [Google Scholar] [CrossRef]
- Seidel, R. On the All-Pairs-Shortest-Path Problem. In Proceedings of the Twenty-Fourth Annual ACM Symposium on Theory of Computing, STOC’92, New York, NY, USA, 4–6 May 1992; pp. 745–749. [Google Scholar] [CrossRef]
- Warshall, S. A Theorem on Boolean Matrices. J. ACM 1962, 9, 11–12. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, R.; Pandey, V. An Efficient Algorithm for All Pair Shortest Paths. Int. J. Comput. Electr. Eng. 2010, 2, 984–991. [Google Scholar] [CrossRef]
- Zwick, U. All Pairs Shortest Paths Using Bridging Sets and Rectangular Matrix Multiplication. J. ACM 2002, 49, 289–317. [Google Scholar] [CrossRef]
- D’alberto, P.; Nicolau, A. R-Kleene: A high-performance divide-and-conquer algorithm for the all-pair shortest path for densely connected networks. Algorithmica 2007, 47, 203–213. [Google Scholar] [CrossRef]
- Islam, M.T.; Thulasiraman, P.; Thulasiram, R.K. A parallel ant colony optimization algorithm for all-pair routing in MANETs. In Proceedings of the International Parallel and Distributed Processing Symposium, Nice, France, 22–26 May 2003. [Google Scholar]
- Katz, G.J.; Kider, J.T. All-Pairs Shortest-Paths for Large Graphs on the GPU. In Proceedings of the EUROGRAPHICS/ACM SIGGRAPH Conference on Graphics Hardware 2008, Sarajevo, Bosnia and Herzegovina, 20–21 June 2008; pp. 47–55. [Google Scholar]
- Reddy, K.R. A survey of the all-pairs shortest paths problem and its variants in graphs. Acta Univ. Sapientiae Inform. 2016, 8, 16–40. [Google Scholar] [CrossRef]
- Aho, A.V.; Hopcroft, J.E. The Design and Analysis of Computer Algorithms; Pearson Education India: Chennai, India, 1974. [Google Scholar]
- Attiratanasunthron, N.; Fakcharoenphol, J. A running time analysis of an ant colony optimization algorithm for shortest paths in directed acyclic graphs. Inf. Process. Lett. 2008, 105, 88–92. [Google Scholar] [CrossRef]
- Neumann, F.; Witt, C. Runtime analysis of a simple ant colony optimization algorithm. In Proceedings of the International Symposium on Algorithms and Computation, Kolkata, India, 18–20 December 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 618–627. [Google Scholar]
- Di Caro, G.; Dorigo, M. AntNet: Distributed stigmergetic control for communications networks. J. Artif. Intell. Res. 1998, 9, 317–365. [Google Scholar] [CrossRef]
- Horoba, C.; Sudholt, D. Running time analysis of ACO systems for shortest path problems. In Proceedings of the International Workshop on Engineering Stochastic Local Search Algorithms, Brussels, Belgium, 3–4 September 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 76–91. [Google Scholar]
- Fredman, M.L. New bounds on the complexity of the shortest path problem. SIAM J. Comput. 1976, 5, 83–89. [Google Scholar] [CrossRef]
- Takaoka, T. A new upper bound on the complexity of the all pairs shortest path problem. Inf. Process. Lett. 1992, 43, 195–199. [Google Scholar] [CrossRef]
- Dobosiewicz, W. A more efficient algorithm for the min-plus multiplication. Int. J. Comput. Math. 1990, 32, 49–60. [Google Scholar] [CrossRef]
- Han, Y. Improved algorithm for all pairs shortest paths. Inf. Process. Lett. 2004, 91, 245–250. [Google Scholar] [CrossRef]
- Takaoka, T. A faster algorithm for the all-pairs shortest path problem and its application. In Proceedings of the International Computing and Combinatorics Conference, Jeju Island, Republic of Korea, 17–20 August 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 278–289. [Google Scholar]
- Takaoka, T. An O (n3loglogn/logn) time algorithm for the all-pairs shortest path problem. Inf. Process. Lett. 2005, 96, 155–161. [Google Scholar] [CrossRef]
- Zwick, U. A slightly improved sub-cubic algorithm for the all pairs shortest paths problem with real edge lengths. In Proceedings of the International Symposium on Algorithms and Computation, Hong Kong, China, 20–22 December 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 921–932. [Google Scholar]
- Chan, T.M. All-pairs shortest paths with real weights in O (n 3/log n) time. Algorithmica 2008, 50, 236–243. [Google Scholar] [CrossRef]
- Han, Y. An o (n 3 (loglogn/logn) 5/4) time algorithm for all pairs shortest paths. In Proceedings of the European Symposium on Algorithms, Zurich, Switzerland, 11–13 September 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 411–417. [Google Scholar]
- Chan, T.M. More algorithms for all-pairs shortest paths in weighted graphs. SIAM J. Comput. 2010, 39, 2075–2089. [Google Scholar] [CrossRef]
- Williams, R.R. Faster all-pairs shortest paths via circuit complexity. SIAM J. Comput. 2018, 47, 1965–1985. [Google Scholar] [CrossRef]
- Chou, Y.L.; Romeijn, H.E.; Smith, R.L. Approximating shortest paths in large-scale networks with an application to intelligent transportation systems. INFORMS J. Comput. 1998, 10, 163–179. [Google Scholar] [CrossRef]
- Mohring, R.H.; Schilling, H.; Schutz, B.; Wagner, D.; Willhalm, T. Partitioning graphs to speedup Dijkstra’s algorithm. J. Exp. Algorithmics 2007, 11, 2–8. [Google Scholar] [CrossRef]
- Baswana, S.; Goyal, V.; Sen, S. All-pairs nearly 2-approximate shortest paths in O(n2polylogn) time. Theor. Comput. Sci. 2009, 410, 84–93. [Google Scholar] [CrossRef]
- Yuster, R. Approximate shortest paths in weighted graphs. J. Comput. Syst. Sci. 2012, 78, 632–637. [Google Scholar] [CrossRef][Green Version]
- Thorup, M.; Zwick, U. Approximate distance oracles. J. ACM 2005, 52, 1–24. [Google Scholar] [CrossRef]
- Das Sarma, A.; Gollapudi, S.; Najork, M.; Panigrahy, R. A sketch-based distance oracle for web-scale graphs. In Proceedings of the Third ACM International Conference on Web Search and Data Mining, New York, NY, USA, 3–6 February 2010; pp. 401–410. [Google Scholar]
- Wang, Y.; Wang, Q.; Koehler, H.; Lin, Y. Query-by-Sketch: Scaling Shortest Path Graph Queries on Very Large Networks. In Proceedings of the 2021 International Conference on Management of Data, Virtual Event, 20–25 June 2021; pp. 1946–1958. [Google Scholar]
- Akiba, T.; Iwata, Y.; Yoshida, Y. Fast exact shortest-path distance queries on large networks by pruned landmark labeling. In Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data, New York, NY, USA, 22–27 June 2013; pp. 349–360. [Google Scholar]
- Mendiola, E. Algoritmo Para el Cálculo Acelerado de Distancias Conceptuales. Master’s Thesis, Instituto Politécnico Nacional, Mexico City, Mexico, 2022. [Google Scholar]
- Robertson, N.; Seymour, P. Graph minors. III. Planar tree-width. J. Comb. Theory Ser. B 1984, 36, 49–64. [Google Scholar] [CrossRef]
- Miller, G.A.; Charles, W.G. Contextual correlates of semantic similarity. Lang. Cogn. Process. 1991, 6, 1–28. [Google Scholar] [CrossRef]
- Rubenstein, H.; Goodenough, J.B. Contextual correlates of synonymy. Commun. ACM 1965, 8, 627–633. [Google Scholar] [CrossRef]
- Pirro, G. A semantic similarity metric combining features and intrinsic information content. Data Knowl. Eng. 2009, 68, 1289–1308. [Google Scholar] [CrossRef]
- Agirre, E.; Alfonseca, E.; Hall, K.; Kravalova, J.; Pasca, M.; Soroa, A. A Study on Similarity and Relatedness Using Distributional and WordNet-based Approaches. In Proceedings of the Human Language Technologies: The 2009 Annual Conference of the North American Chapter of the Association for Computational Linguistics, Boulder, Colorado, 31 May–5 June 2009; pp. 19–27. Available online: https://aclanthology.org/N09-1003 (accessed on 9 October 2023).
- Hill, F.; Reichart, R.; Korhonen, A. Simlex-999: Evaluating semantic models with (genuine) similarity estimation. Comput. Linguist. 2015, 41, 665–695. [Google Scholar] [CrossRef]
- Halawi, G.; Dror, G.; Gabrilovich, E.; Koren, Y. Large-scale learning of word relatedness with constraints. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 1406–1414. [Google Scholar]
- Radinsky, K.; Agichtein, E.; Gabrilovich, E.; Markovitch, S. A word at a time: Computing word relatedness using temporal semantic analysis. In Proceedings of the 20th International Conference on World Wide Web, Hyderabad, India, 28 March–1 April 2011; pp. 337–346. [Google Scholar]
- Finkelstein, L.; Gabrilovich, E.; Matias, Y.; Rivlin, E.; Solan, Z.; Wolfman, G.; Ruppin, E. Placing search in context: The concept revisited. In Proceedings of the 10th International Conference on World Wide Web, Hong Kong, China, 1–5 May 2001; pp. 406–414. [Google Scholar]
- Szumlanski, S.; Gomez, F.; Sims, V.K. A new set of norms for semantic relatedness measures. In Proceedings of the 51st Annual Meeting of the Association for Computational Linguistics, Sofia, Bulgaria, 4–9 August 2013; Volume 2: Short Papers, pp. 890–895. [Google Scholar]
- Huang, E.H.; Socher, R.; Manning, C.D.; Ng, A.Y. Improving word representations via global context and multiple word prototypes. In Proceedings of the 50th Annual Meeting of the Association for Computational Linguistics, Jeju Island, Republic of Korea, 8–14 July 2012; Volume 1: Long Papers. [Google Scholar]
- Cohen, E.; Halperin, E.; Kaplan, H.; Zwick, U. Reachability and distance queries via 2-hop labels. SIAM J. Comput. 2003, 32, 1338–1355. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).