Fixed/Preassigned-Time Synchronization of Fully Quaternion-Valued Cohen–Grossberg Neural Networks with Generalized Time Delay

Abstract

This article is concerned with fixed-time synchronization and preassigned-time synchronization of Cohen–Grossberg quaternion-valued neural networks with discontinuous activation functions and generalized time-varying delays. Firstly, a dynamic model of Cohen–Grossberg neural networks is introduced in the quaternion field, where the time delay successfully integrates discrete-time delay and proportional delay. Secondly, two types of discontinuous controllers employing the quaternion-valued signum function are designed. Without utilizing the conventional separation technique, by developing a direct analytical approach and using the theory of non-smooth analysis, several adequate criteria are derived to achieve fixed-time synchronization of Cohen–Grossberg neural networks and some more precise convergence times are estimated. To cater to practical requirements, preassigned-time synchronization is also addressed, which shows that the drive-slave networks reach synchronization within a specified time. Finally, two numerical simulations are presented to validate the effectiveness of the designed controllers and criteria.

1. Introduction

In the past few decades, quaternion-valued neural networks (QVNNs) have become increasingly prevalent and have been applied extensively to various fields, including image processing [1], speech recognition [2], robot control [3], and signal processing [4]. Owing to the multi-dimensional inherent properties of quaternions, quaternion neurons exhibit enhanced storage and computational capabilities compared to real-valued and complex-valued neurons. This inherent advantage equips QVNNs with formidable signal processing capabilities. For instance, quaternion neurons have the capability to process color information holistically, unlike real-valued and complex-valued neurons, which handle color space components separately. Consequently, QVNNs naturally handle internal dependencies between color channels [5]. Furthermore, because all parameters in QVNNs are quaternion-valued, they excel in managing rotations and scaling of 3-D vectors [6]. Considering the aforementioned advantages, QVNNs have garnered increasing attention in both practical applications and theoretical analysis, particularly in terms of their dynamic characteristics, such as dissipativity [7,8], stability [9,10,11,12], and synchronization [13,14,15,16].

The synchronization of QVNNs involves attaining consistent states among the quaternion neurons under external control. Nowadays, significant advancements have been achieved in the synchronization of QVNNs. For example, Singh et al. conducted research on the issue of anti-synchronization in quaternion-valued inertial neural networks with unbounded time delays [13]. Zhao et al. discussed the quasi-synchronization of discrete-time fractional-order quaternion-valued memristive neural networks with uncertain parameters and time delays [14]. In their works, synchronization is accomplished over an infinite time frame. However, in numerous practical scenarios, achieving synchronization within a finite time is crucial due to the limited lifespan of organisms or devices. In fact, compared to asymptotic synchronization, finite-time synchronization offers advantages such as accelerated convergence, strengthened robustness, and increased resistance to interference. Given this, Ping et al. [16] investigated finite-time synchronization of QVNNs by employing an improved one-norm and quaternion sign function, along with a well-designed event-triggered controller. It is important to emphasize that the settling time (ST) obtained within a finite-time framework is significantly influenced by the initial states and parameters of the systems.

In many practical scenarios, it is challenging and difficult to measure all initial states. Consequently, defining the ST for finite-time (FNT) synchronization becomes a formidable task. In order to address this challenge, the concept of fixed time (FIT) was introduced and the FIT stability theorem was first proposed in [17], in which the estimate of the ST is improved by eliminating its dependence on initial values. Since then, numerous remarkable research endeavors have emerged, encompassing FIT synchronization of recurrent neural networks [18,19,20], complex-valued neural networks (CVNNs) [21,22,23], and QVNNs [24,25,26,27,28]. In [24,25,26], the FIT synchronization of QVNNs was investigated by decomposing the QVNN model into four real valued neural networks, which resulted in four real-valued controllers being designed. While this method indirectly raises control gain and complicates the viability of control strategies, it underscores the urgency of developing a novel approach that can directly examine neural networks within the quaternion domain.

Except for FIT synchronization, preassigned-time (PET) synchronization is a novel direction achieved by utilizing the enhanced FIT stability outcomes. Unlike FNT and FIT synchronization, the synchronization time of PET synchronization is predetermined to meet practical requirements, making it independent of model parameters and initial conditions. The research on PET synchronization has garnered significant attention among scholars in recent years due to the aforementioned advantages and characteristics. Nevertheless, there remains a scarcity of related research results [29,30]. In [29], a feedback controller and a novel event-triggered controller are designed to discuss the PET synchronization in real-valued networks of piecewise smooth systems. Similarly, in [30], several smooth controllers were designed to facilitate the PET synchronization of real-valued complex networks. It is noteworthy that the majority of existing research results are primarily concentrated within the realm of real numbers, while the research in the quaternion field is in dire need of augmentation. Hence, the research on PET synchronization of QVNNs is of great significance and practical value. Furthermore, it is important to highlight that discontinuous situations are commonplace and unavoidable in real-world problems. However, the existing research outcomes pertaining to QVNNs seldom address these scenarios. Therefore, delving into the behavior of QVNNs with discontinuous activation functions carries substantial theoretical implications and practical relevance.

Drawing from recent research findings, scholars have explored a diverse array of network models. For instance, with the smooth control, the FIT/PAT synchronization was investigated for several types of neural networks, including switched coupled neural networks [31], BAM neural networks [32]. Owing to the strong robustness and generalization capabilities of Cohen–Grossberg neural networks (CGNNs) in data processing, allowing them to better handle the issue of noise interference and unknown data, it has attracted growing attention from scholars due to their significant practical application value. However, it is noteworthy that the research on Cohen–Grossberg quaternion-valued neural networks (CGQVNNs) remains conspicuously absent. Given the wide-ranging potential applications of CGNNs in areas such as pattern recognition, intelligent computing, and signal processing [32,33,34,35,36], a comprehensive examination of CGQVNNs is not only of great practical significance but also holds substantial research value. One of the primary challenges in addressing CGQVNNs lies in determining whether an outer amplification function exists within the quaternion field. If a real-valued amplification function is considered, CGQVNNs do not exhibit significant deviations from prior research outcomes. In addition, if QVNNs are divided into four real valued systems, they will be confronted with increased control costs and higher dimensions of computation. Therefore, how to develop a simpler and more efficient method to explore the FIT/PET synchronization of QVNNs in the quaternion field is an urgent problem to be overcome.

In consideration of the analysis outlined above, the FIT synchronization and PET synchronization of CGQVNNs with generalized time delay and discontinuous activation functions are investigated in this paper by using a measurable selection technique [37,38,39,40] and introducing a direct non-separation analysis framework. The key innovations and contributions of this paper can be succinctly summarized as follows:

(1)

A generalized time delay is introduced into the model of CGQVNNs, which successfully incorporates discrete constant delays [7], discrete time-varying delays [13] and proportional delays [9].

(2)

Compared with previous research on the synchronization issue of QVNNs [27,28], the synchronization problem of CGQVNNs with discontinuous activation functions is investigated for the first time. An effective analytical method is introduced to investigate the FIT synchronization and PET synchronization of CGQVNNs with quaternion-valued amplification function without separation, and high-precision ST is estimated.

(3)

Different from the methods used in [28], the FIT synchronization and PET synchronization of CGQVNNs are discussed through a direct analytical approach. Consequently, several effective quaternion-valued controllers are directly designed for the original CGQVNNs rather than for the four real-valued subsystems obtained by separation, so as to obtain more economical control gains and derive more concise synchronization conditions.

In Section 2, preliminaries are shown. The FIT synchronization and PET synchronization of CGQVNNs are investigated by quaternion-valued controllers in Section 3 and Section 4, respectively. Two numerical examples are provided to validate the theoretical findings presented in Section 5. Finally, Section 6 offers a concise summary of this paper.

Notation 1. 

In this article, $\mathbb{R}$, $\mathbb{Q}$, ${\mathbb{R}}^n$ and ${\mathbb{Q}}^n$ are the set denoting all real numbers, the set of all quaternion numbers, the set of all n-dimensional real column vectors and the set of all n-dimensional quaternion column vectors, respectively. Denote $\mathbb{M}=\{1,2,\cdots n\}$, $ϵ=\{R,I,J,K\}$. For any $\mathbf{z}={\mathbf{z}}^R+i{\mathbf{z}}^I+j{\mathbf{z}}^J+k{\mathbf{z}}^K\in \mathbb{Q}$, $\overline{\mathbf{z}}={\mathbf{z}}^R-i{\mathbf{z}}^I-j{\mathbf{z}}^J-k{\mathbf{z}}^K$, ${|\mathbf{z}|}_1=|{\mathbf{z}}^R|+|{\mathbf{z}}^I|+|{\mathbf{z}}^J|+|{\mathbf{z}}^K|$, ${|\mathbf{z}|}_2=\sqrt{\mathbf{z}\overline{\mathbf{z}}}$. For a discontinuous function $\mathbf{m}(·)={\mathbf{m}}^R(·)+{\mathbf{m}}^I(·)i+{\mathbf{m}}^J(·)j+{\mathbf{m}}^K(·)k$, ${\mathbf{m}}^{ϵ-}\left(\mathbf{x}\right)$ and ${\mathbf{m}}^{ϵ+}\left(\mathbf{x}\right)$ are the left and right limits of $\mathbf{m}(·)$ at point $\mathbf{x}$, respectively. ${\stackrel{`}{\mathbf{m}}}^{ϵ}\left(\mathbf{x}\right)$ and ${\acute{\mathbf{m}}}^{ϵ}\left(\mathbf{x}\right)$ denote as the minimum and the maximum of ${\mathbf{m}}^{ϵ-}\left(\mathbf{x}\right)$ and ${\mathbf{m}}^{ϵ+}\left(\mathbf{x}\right)$. The convex hull is defined as $\overline{co}\left[\mathbf{m}\left(\mathbf{x}\right)\right]=\overline{co}\left[{\mathbf{m}}^R\left(\mathbf{x}\right)\right]+\overline{co}\left[{\mathbf{m}}^I\left(\mathbf{x}\right)\right]i+\overline{co}\left[{\mathbf{m}}^J\left(\mathbf{x}\right)\right]j+\overline{co}\left[{\mathbf{m}}^K\left(\mathbf{x}\right)\right]k=[{\acute{\mathbf{m}}}^R\left(\mathbf{x}\right)$, ${\stackrel{`}{\mathbf{m}}}^R\left(\mathbf{x}\right)]+[{\acute{\mathbf{m}}}^I\left(\mathbf{x}\right)$, ${\stackrel{`}{\mathbf{m}}}^I\left(\mathbf{x}\right)]i+[{\acute{\mathbf{m}}}^J\left(\mathbf{x}\right)$, ${\stackrel{`}{\mathbf{m}}}^J\left(\mathbf{x}\right)]j+[{\acute{\mathbf{m}}}^K\left(\mathbf{x}\right),{\stackrel{`}{\mathbf{m}}}^K\left(\mathbf{x}\right)]k$.

2. Model Description and Preliminaries

In this paper, the following CGQVNN is considered

$$\left\{\begin{array}{cc}\hfill {\displaystyle }& {\displaystyle {\dot{\omega }}_p\left(t\right)=h_p\left({\omega }_p\left(t\right)\right)\left({-a}_p{\omega }_p\left(t\right)+\sum _{q\in \mathbb{M}}{b}_{pq}{\chi }_q\left({\omega }_q\left(t\right)\right)+\sum _{q\in \mathbb{M}}{c}_{pq}{\rho }_q\left({\omega }_q\left(k_{pq}\left(t\right)\right)\right)+{\xi }_p\right),}\hfill \\ \hfill {\displaystyle }& {\omega }_p\left(s\right)={\vartheta }_p\left(s\right),-\varsigma \le s\le 0,p\in \mathbb{M},\hfill \end{array}\right.$$

(1)

where ${\omega }_p\left(t\right)\in \mathbb{Q}$ is the state of the pth unit at time t, $h_p(·)\in \mathbb{Q}$ is an amplification function, $a_p\in \mathbb{Q}$ is the feedback self-connection weight, $b_{pq}$, $c_{pq}\in \mathbb{Q}$ are the connection weights from the q-th neuron to the p-th neuron, ${\chi }_q(·)$ and ${\rho }_q(·):\mathbb{Q}\to \mathbb{Q}$ are discontinuous quaternion activation functions without and with time delay, $k_{pq}\left(t\right)\le t$ is the generalized time delay, ${\xi }_p$ denotes the external input function, ${\vartheta }_p\left(s\right)\in C\left([-\varsigma ,0]\right)$ is the initial state of the network (1), in which $\varsigma =\underset{p,q\in \mathbb{M}}{max}\{|d_{pq}\left(0\right)|\}$. Then, the response system of the system (1) is governed by

$$\left\{\begin{array}{cc}\hfill {\displaystyle }& {\displaystyle {\dot{\zeta }}_p\left(t\right)=h_p\left({\zeta }_p\left(t\right)\right)\left({-a}_p{\zeta }_p\left(t\right)+\sum _{q\in \mathbb{M}}{b}_{pq}{\chi }_q\left({\zeta }_q\left(t\right)\right)+\sum _{q\in \mathbb{M}}{c}_{pq}{\rho }_q\left({\zeta }_q\left(k_{pq}\left(t\right)\right)\right)+{\xi }_p\right)+{\delta }_p\left(t\right),}\hfill \\ \hfill {\displaystyle }& {\zeta }_p\left(s\right)={\upsilon }_p\left(s\right),-\varsigma \le s\le 0,p\in \mathbb{M},\hfill \end{array}\right.$$

(2)

where the parameters in system (2) are the same as system (1), ${\delta }_p\left(t\right)$ is the control input needed to be designed later.

Assumption 1. 

For $p\in \mathbb{M}$, ${\chi }_p$ and ${\rho }_p$ are continuous except on the sets of countable isolate points $\left\{u_r^p\right\}$ and $\left\{v_r^p\right\}$, respectively, and ${\chi }_p^{d-}\left(u_r^p\right)$, ${\chi }_p^{d+}\left(u_r^p\right)$ and ${\rho }_p^{d-}\left(v_r^p\right)$, ${\rho }_p^{d+}\left(v_r^p\right)$ exist. Moreover, there are a finite number of jump points at most for ${\chi }_p$ and ${\rho }_p$ in every bounded compact interval.

Assumption 2. 

For any $p,q\in \mathbb{M}$, $k_{pq}\left(0\right)\le 0$ and there exists a constant ${\tilde{k}}_{pq}>0$ such that

$$0<{\tilde{k}}_{pq}<{\dot{k}}_{pq}\left(t\right)<1.$$

Remark 1. 

Note, that the time delay in the system (1) is a general and unified delay type. Actually, if $k_{pq}\left(t\right)=t-\tau$, the time delay in this article will degenerate into a discrete constant time delay [7]. If $k_{pq}\left(t\right)=t-{\tau }_{pq}\left(t\right)$ with $0\le {\tau }_{pq}\left(t\right)\le \tau$, the time delay in this article will degenerate into a discrete time-varying delay [14]. If $k_{pq}\left(t\right)=k_{q}t$ with $0<k_q<1$, the time delay in this article will reduce to the proportional delay [9]. In other words, the time delay proposed in this paper involves the traditional discrete-time delay and proportional delay.

Definition 1 

([41]). A continuous function vector $\omega \left(t\right)={({\omega }_1\left(t\right),{\omega }_2\left(t\right),\cdots ,{\omega }_n\left(t\right))}^T:[-\varsigma ,T_0)$$\to {\mathbb{Q}}^n$ is called a solution of system (1) on $[-\varsigma ,T_0)$ if

(1) $\omega \left(t\right)$ is absolutely continuous on $[0,T_0)$.

(2) There exist measurable functions $\check{\chi }={({\check{\chi }}_1,\cdots ,{\check{\chi }}_n)}^T:[0,T_0)\to {\mathbb{Q}}^n$ and $\check{\rho }=({\check{\rho }}_1,\cdots ,$${\check{\rho }}_n{)}^T:[0,T_0)\to {\mathbb{Q}}^n$ satisfying ${\check{\chi }}_q\in \overline{co}\left[{\chi }_q\left({\omega }_q\right)\right]$, ${\check{\rho }}_q\in \overline{co}\left[{\rho }_q\left({\omega }_q\right)\right]$, such that

$$\begin{array}{cc}\hfill {\dot{\omega }}_p\left(t\right)=& {\displaystyle h_p\left({\omega }_p\left(t\right)\right)({-a}_p{\omega }_p\left(t\right)+\sum _{q\in \mathbb{M}}{b}_{pq}{\check{\chi }}_q\left(t\right)}\hfill \\ \hfill & {\displaystyle +\sum _{q\in \mathbb{M}}{c}_{pq}{\check{\rho }}_q\left(k_{pq}\left(t\right)\right)+{\xi }_p),p\in \mathbb{M},}\hfill \end{array}$$

(3)

for a.e. $t\in [0,T_0)$.

Similarly, for the response system (2), there exist measurable functions $\widehat{\chi }=({\widehat{\chi }}_1,{\widehat{\chi }}_2,\cdots ,$${\widehat{\chi }}_n{)}^T:[0,T_0)\to {\mathbb{Q}}^n$ and $\widehat{\rho }={({\widehat{\rho }}_1,{\widehat{\rho }}_2,\cdots ,{\widehat{\rho }}_n)}^T:[0,T_0)\to {\mathbb{Q}}^n$ satisfying ${\widehat{\chi }}_q\in \overline{co}\left[{\chi }_q\left({\zeta }_q\right)\right]$, ${\widehat{\rho }}_q\in \overline{co}\left[{\rho }_q\left({\zeta }_q\right)\right]$, such that

$$\begin{array}{cc}\hfill {\dot{\zeta }}_p\left(t\right)=& {\displaystyle h_p\left({\zeta }_p\left(t\right)\right)({-a}_p{\zeta }_p\left(t\right)+\sum _{q\in \mathbb{M}}{b}_{pq}{\widehat{\chi }}_q\left(t\right)}\hfill \\ \hfill & {\displaystyle +\sum _{q\in \mathbb{M}}{c}_{pq}{\widehat{\rho }}_q\left(k_{pq}\left(t\right)\right)+{\xi }_p)+{\delta }_p\left(t\right),p\in \mathbb{M},}\hfill \end{array}$$

(4)

for a.e. $t\in [0,T_0)$.

Define ${\eta }_p\left(t\right)={\zeta }_p\left(t\right)-{\omega }_p\left(t\right)$, $\eta \left(t\right)={({\eta }_1\left(t\right),{\eta }_2\left(t\right),\cdots ,{\eta }_n\left(t\right))}^T$, from systems (3) and (4), the error system can be derived

$$\begin{array}{cc}\hfill {\dot{\eta }}_p\left(t\right)=& {\displaystyle -(h_p\left({\zeta }_p\left(t\right)\right)a_p{\zeta }_p\left(t\right)-h_p\left({\omega }_p\left(t\right)\right)a_p{\omega }_p\left(t\right))}\hfill \\ \hfill & {\displaystyle +\sum _{q\in \mathbb{M}}(h_p\left({\zeta }_p\left(t\right)\right)b_{pq}{\widehat{\chi }}_q\left(t\right)-h_p\left({\omega }_p\left(t\right)\right)b_{pq}{\check{\chi }}_q\left(t\right))}\hfill \\ \hfill & +\sum _{q\in \mathbb{M}}(h_p\left({\zeta }_p\left(t\right)\right)c_{pq}{\widehat{\rho }}_q\left(k_{pq}\left(t\right)\right)-h_p\left({\omega }_p\left(t\right)\right)c_{pq}{\check{\rho }}_q\left(k_{pq}\left(t\right)\right))\hfill \\ \hfill & {\displaystyle +(h_p\left({\zeta }_p\left(t\right)\right)-h_p\left({\omega }_p\left(t\right)\right)){\xi }_p+{\delta }_p\left(t\right),p\in \mathbb{M}.}\hfill \end{array}$$

(5)

Assumption 3. 

For any $p\in \mathbb{M}$, $u,v\in \mathbb{Q}$, functions $h_p(·)$, ${\chi }_p(·)$, ${\rho }_p(·)\in \mathbb{Q}$ satisfy

$$\begin{array}{c}|{\chi }_p\left(u\right)-{\chi }_p{\left(v\right)|}_{\mu }\le l_p^{\mu }{|u-v|}_{\mu }+{\tilde{l}}_p^{\mu },\\ |h_p\left(u\right)-h_p{\left(v\right)|}_{\mu }\le {\tilde{h}}_p^{\mu }{|u-v|}_{\mu },\end{array}$$

where $l_p^{\mu }$, ${\tilde{l}}_p^{\mu }$, ${\tilde{h}}_p^{\mu }>0$, $|{\chi }_p{(·)|}_{\mu }\le L_p^{\mu }$, $|h_p{(·)|}_{\mu }\le H_p^{\mu }$, $|{\rho }_p{(·)|}_{\mu }\le R_p^{\mu }$$(\mu =1,2)$.

Remark 2. 

For several decades, many excellent results were concerned with the real-valued and complex-valued networks with $h_p(·)=1$ [41,42]. However, the theory and methods in these existing works cannot be directly used to investigate CGQVNNs. On the one hand, it is not easy to ensure the monotonicity of the inverse function of $h_p(·)$ if $h_p(·)\in \mathbb{Q}$. On the other hand, it is difficult to construct suitable Lyapunov functions to drive the FIT synchronization of CGQVNN due to the presence of special multiplications of quaternions with non-commutativity. Thus, a new and effective method will be proposed in this paper to deal with these problems.

Definition 2 

([43]). Drive-response CGQVNNs (1) and (2) are said to be FIT synchronized if there exists a number ${\widehat{T}}^{*}\left(\eta \left(s\right)\right)\ge 0$ with $s\in [-\varsigma ,0]$ such that

$$\underset{t\to {\widehat{T}}^{*}\left(\eta \left(s\right)\right)}{lim}{|\eta \left(t\right)|}_{\mu }=0,$$

$${|\eta \left(t\right)|}_{\mu }=0,\forall t\ge {\widehat{T}}^{*}\left(\eta \left(s\right)\right),$$

and there is a positive constant $T_{max}$ such that

$${\widehat{T}}^{*}\left(\eta \left(s\right)\right)\le T_{max},\forall \eta \left(s\right)\in \mathbb{Q},$$

and

$${\eta }_p\left(t\right)={\zeta }_p\left(t\right)-{\omega }_p\left(t\right)={\eta }_p^R\left(t\right)+i{\eta }_p^I\left(t\right)+j{\eta }_p^J\left(t\right)+k{\eta }_p^K\left(t\right).$$

Definition 3. 

Drive-response CGQVNNs (1) and (2) are said to be PET synchronized within the preappointed time $T_{pet}$ if

$$\underset{t\to T_{pet}}{lim}{|\eta \left(t\right)|}_{\mu }=0,$$

$${|\eta \left(t\right)|}_{\mu }=0,\forall t\ge T_{pet},$$

where $T_{pet}>0$ is completely independent of system parameters and initial values.

Definition 4 

([44]). For a quaternion variable $y=y^R+y^{I}i+y^{J}j+y^{K}k\in \mathbb{Q}$, the signum function is defined as

$$\left[y\right]\triangleq \mathrm{sign}\left(y^R\right)+\mathrm{sign}\left(y^I\right)i+\mathrm{sign}\left(y^J\right)j+\mathrm{sign}\left(y^K\right)k.$$

Based on Definition 1, $\forall y\in \mathbb{Q}$, the convex hull of $\left[y\right]$ is defined by

$$\overline{co}\left(\left[y\right]\right)\triangleq \overline{co}\left[\mathrm{sign}\left(y^R\right)\right]+\overline{co}\left[\mathrm{sign}\left(y^I\right)\right]i+\overline{co}\left[\mathrm{sign}\left(y^J\right)\right]j+\overline{co}\left[\mathrm{sign}\left(y^K\right)\right]k,$$

where

$$\overline{co}\left[\mathrm{sign}\left(y^{ϵ}\right)\right]=\left\{\begin{array}{cc}\left\{1\right\},\hfill & y^{ϵ}>0,\hfill \\ [-1,1],\hfill & y^{ϵ}=0,\hfill \\ \{-1\},\hfill & y^{ϵ}<0,\hfill \end{array}\right.$$

and $y^{ϵ}\in \mathbb{R}$.

Lemma 1 

([43]). Assume that there exists a positive definite, regular and radially unbounded function $V\left(\eta \left(t\right)\right):{\mathbb{R}}^n\to \mathbb{R}$ such that

$$\frac{d}{dt}V\left(\eta \left(t\right)\right)\le \upsilon V\left(\eta \left(t\right)\right)-{\sigma }_1{V}^{{\theta }_1}\left(\eta \left(t\right)\right)-{\sigma }_2{V}^{{\theta }_2}\left(\eta \left(t\right)\right),\eta \left(t\right)\in {\mathbb{R}}^n\setminus \left\{\mathbf{0}\right\},$$

where $\upsilon \in \mathbb{R}$, ${\sigma }_1>0$, ${\sigma }_2>0$, $0\le {\theta }_1<1$ and ${\theta }_2>1$, then the following conclusions are true.

(i)

If $0<\upsilon <min\{{\sigma }_1,{\sigma }_2\},$ then $\eta \left(t\right)\equiv 0$ for $t\ge T^{*},$ where

$$\begin{array}{cc}\hfill T^{*}& {\displaystyle =\frac{\pi csc\left(\pi w\right)}{{\sigma }_2({\theta }_2-{\theta }_1)}{\left(\frac{{\sigma }_2}{{\sigma }_1-\upsilon }\right)}^{1-w}I(\frac{{\sigma }_2}{{\sigma }_1+{\sigma }_2-\upsilon },w,1-w)}\hfill \\ \hfill & {\displaystyle +\frac{\pi csc\left(\pi w\right)}{{\sigma }_1({\theta }_2-{\theta }_1)}{\left(\frac{{\sigma }_1}{{\sigma }_2-\upsilon }\right)}^{w}I(\frac{{\sigma }_1}{{\sigma }_1+{\sigma }_2-\upsilon },1-w,w).}\hfill \end{array}$$

(ii)

If $0<\upsilon <2\sqrt{{\sigma }_1{\sigma }_2}$ and ${\theta }_1+{\theta }_2=2,$ then $\eta \left(t\right)\equiv 0$ for $t\ge \tilde{T},$ where

$$\tilde{T}=\frac{2}{\sqrt{\iota }({\theta }_2-1)}(\frac{\pi }{2}+arctan\left(\frac{\upsilon }{\iota }\right)),$$

where $w=(1-{\theta }_1)({\theta }_2-{\theta }_1)$, $\iota =4{\sigma }_1{\sigma }_2-{\upsilon }^2$, the incomplete Beta function ratio $I(r,p,q)$ was given in [43].

Lemma 2 

([43]). If there exist a positive, regular and radially unbounded function $V\left(\eta \left(t\right)\right):{\mathbb{R}}^n\to \mathbb{R}$ and $\upsilon \in \mathbb{R},{\sigma }_1>0,{\sigma }_2>0,0\le {\theta }_1<1,{\theta }_2>1,T_{pet}>0$ such that

$$\frac{d}{dt}V\left(\eta \left(t\right)\right)\le -\frac{\check{T}}{T_{pet}}(-\upsilon V\left(\eta \left(t\right)\right)+{\sigma }_1{V}^{{\theta }_1}\left(\eta \left(t\right)\right)+{\sigma }_2{V}^{{\theta }_2}\left(\eta \left(t\right)\right),\eta \left(t\right)\in {\mathbb{R}}^n\setminus \left\{\mathbf{0}\right\}),$$

then $\eta \left(t\right)\equiv 0$ for $t\ge T_{pet},$ where

$$\check{T}=\left\{\begin{array}{c}{T}^{*},0<\upsilon <min\{{\sigma }_1,{\sigma }_2\},\hfill \\ \tilde{T},0<\upsilon <2\sqrt{{\sigma }_1{\sigma }_2},{\theta }_1+{\theta }_2=2.\hfill \end{array}\right.$$

Lemma 3 

([43]). Assume that $b_p\ge 0$ for $p\in \mathbb{M}$, $0\le {\theta }_1\le 1$ and ${\theta }_2>1$, then

$$\sum _{p\in \mathbb{M}}{b}_p^{{\theta }_1}\ge {(\sum _{p\in \mathbb{M}}{b}_p)}^{{\theta }_1},\sum _{p\in \mathbb{M}}{b}_p^{{\theta }_2}\ge n^{1-{\theta }_2}{(\sum _{p\in \mathbb{M}}{b}_p)}^{{\theta }_2}.$$

Lemma 4 

([44]). For any $b,u\in \mathbb{Q}$, $x\left(t\right):\mathbb{R}\to \mathbb{Q}$, the following properties hold

(1) 

$\overline{\overline{b}}=b$.

(2) 

$b+\overline{b}=2b^R\le {2|b|}_2\le 2{|b|}_1$.

(3) 

$\overline{bu}=\overline{b}\overline{u}$.

(4) 

${\displaystyle \frac{{d|x\left(t\right)|}_1}{dt}=\frac{1}{2}(\overline{\left[x\right(t\left)\right]}\frac{dx\left(t\right)}{dt}+\frac{d\overline{x\left(t\right)}}{dt}\left[x\left(t\right)\right])}$.

Lemma 5 

([41]). For any $r,z,m\in \mathbb{Q}$, one has

(1) 

$(r^R-|r^I|-|r^J|-|r^K{|)|z|}_1\le {\left(\overline{\left[z\right]}rz\right)}^R\le (r^R+|r^I|+|r^J|+|r^K{|)|z|}_1$,

(2) 

$-{|z|}_1{|m|}_1\le {\left(\overline{\left[r\right]}zm\right)}^R\le {|z|}_1{|m|}_1$.

3. Fixed-Time Synchronization

In this section, two different controllers are designed to discuss the FIT synchronization of the CGQVNNs (1) and (2).

For convenience, denote

$${\displaystyle \overline{\lambda }=\underset{p\in \mathbb{M}}{max}\left\{\widehat{h}|a_p{|}_1+{\tilde{h}}_p^1{|\xi |}_1+\sum _{p\in \mathbb{M}}\left({\widehat{h}}_q{l}_p^1|b_{qp}{|}_1+L_q^1{\tilde{h}}_p^1|b_{pq}{|}_1+R_q^1{\tilde{h}}_p^1{|c_{pq}|}_1\right)\right\},}$$

$${\displaystyle \tilde{\lambda }=\underset{p\in \mathbb{M}}{max}\left\{\sum _{q\in \mathbb{M}}\left(2\acute{h}|a_p{|}_2+\acute{h}{l}_p^2|b_{qp}{|}_2+\acute{h}{l}_q^2|b_{pq}{|}_2+2L_p^2{\tilde{h}}_p^2|b_{pq}{|}_2+2R_p^2{\tilde{h}}_p^2{|c_{pq}|}_2\right)\right\},}$$

$$\overline{\alpha }=\underset{p\in \mathbb{M}}{min}\left\{{\alpha }_p\right\},\overline{\beta }=n^{1-{\epsilon }_2}\underset{p\in \mathbb{M}}{min}\left\{{\beta }_p\right\},{\iota }_1=4\overline{\alpha }\overline{\beta }-{\overline{\lambda }}^2,$$

$$\tilde{\alpha }=2^{\frac{{\epsilon }_1+1}{2}}\underset{p\in \mathbb{M}}{min}\left\{{\alpha }_p\right\},\tilde{\beta }=2^{\frac{{\epsilon }_1+1}{2}}{n}^{\frac{1-{\epsilon }_2}{2}}\underset{p\in \mathbb{M}}{min}\left\{{\beta }_p\right\},{\iota }_2=4\tilde{\alpha }\tilde{\beta }-{\tilde{\lambda }}^2,$$

$${\displaystyle {\overline{\lambda }}_1=\underset{p\in \mathbb{M}}{max}\left\{|a_p{|}_1-{\lambda }_p+\sum _{q\in \mathbb{M}}{l}_p^1{|b_{qp}|}_1\right\},{\tilde{\lambda }}_1=\underset{p\in \mathbb{M}}{max}\left\{\sum _{q\in \mathbb{M}}(|a_p{|}_2+l_q^2|b_{pq}{|}_2)\right\},}$$

$${\varpi }_1=(1-{\epsilon }_1)({\epsilon }_2-{\epsilon }_1).$$

Firstly, based on the 1-norm, the control scheme is designed by

$$\begin{array}{cc}\hfill {\delta }_p\left(t\right)=& {\displaystyle -\left[{\eta }_p\left(t\right)\right]\left({\gamma }_p+{\lambda }_p|{\omega }_p{\left(t\right)|}_1+{\alpha }_p|{\eta }_p{\left(t\right)|}_1^{{\epsilon }_1}+{\beta }_p{|{\eta }_p\left(t\right)|}_1^{{\epsilon }_2}\right),}\hfill \end{array}$$

(6)

where ${\alpha }_p$, ${\beta }_p>0$, $0\le {\epsilon }_1<1$, ${\epsilon }_2>1$.

Theorem 1. 

Based on Assumptions 1–3, and the controller (6), if

$$\begin{array}{c}\hfill {\displaystyle \sum _{q\in \mathbb{M}}(|b_{pq}{|}_1{H}_p^1{\tilde{l}}_q^1+2|c_{pq}{|}_1{H}_p^1{R}_q^1)-{\gamma }_p<0,}\end{array}$$

(7)

$$\begin{array}{c}\hfill 2H_p^1-{\lambda }_p<0,\end{array}$$

(8)

then the following results hold.

(1)

If $0<\overline{\lambda }<min\{\overline{\alpha },\overline{\beta }\}$, systems (1) and (2) realize FIT synchronization and the ST is estimated by

$$\begin{array}{cc}\hfill {\widehat{T}}_1& {\displaystyle =\frac{\pi csc(\pi {\varpi }_1)}{\overline{\beta }({\epsilon }_2-{\epsilon }_1)}{(\frac{\overline{\beta }}{\overline{\alpha }-\overline{\lambda }})}^{1-{\varpi }_1}I(\frac{\overline{\beta }}{\overline{\alpha }+\overline{\beta }-\overline{\lambda }},{\varpi }_1,1-{\varpi }_1)}\hfill \\ \hfill & {\displaystyle +\frac{\pi csc(\pi {\varpi }_1)}{\overline{\alpha }({\epsilon }_2-{\epsilon }_1)}{(\frac{\overline{\alpha }}{\overline{\beta }-\overline{\lambda }})}^{{\varpi }_1}I(\frac{\overline{\alpha }}{\overline{\alpha }+\overline{\beta }-\overline{\lambda }},1-{\varpi }_1,{\varpi }_1).}\hfill \end{array}$$

(2)

When ${\epsilon }_1+{\epsilon }_2=2$, $0<\overline{\lambda }<2\sqrt{\overline{\alpha }\overline{\beta }}$, systems (1) and (2) are FIT synchronized and the ST is estimated by

$${\widehat{T}}_2=\frac{2}{\sqrt{{\iota }_1}({\epsilon }_2-1)}(\frac{\pi }{2}+arctan(\frac{\overline{\lambda }}{{\iota }_1})).$$

Proof. 

Consider the Lyapunov function based on 1-norm as follows

$${\displaystyle V_1\left(\widehat{\eta }\left(t\right)\right)=\sum _{p\in \mathbb{M}}{|{\eta }_p\left(t\right)|}_1,}$$

where $\widehat{\eta }\left(t\right)=(|{\eta }_1{\left(t\right)|}_1,|{\eta }_2{\left(t\right)|}_1,\cdots ,|{\eta }_n\left(t\right){{|}_1)}^T\in {\mathbb{R}}^n$.

According to the system (5), one obtains

$$\begin{array}{cc}\hfill D^{+}{V}_1\left(\widehat{\eta }\left(t\right)\right)& {\displaystyle =\frac{1}{2}\sum _{p\in \mathbb{M}}\left(\overline{\left[{\eta }_p\left(t\right)\right]}{D}^{+}{\eta }_p\left(t\right)+D^{+}\overline{{\eta }_p\left(t\right)}\left[{\eta }_p\left(t\right)\right]\right)}\hfill \\ \hfill & {\displaystyle =\frac{1}{2}\sum _{p\in \mathbb{M}}(\overline{\left[{\eta }_p\left(t\right)\right]}(h_p\left({\omega }_p\left(t\right)\right)a_p{\omega }_p\left(t\right)-h_p\left({\zeta }_p\left(t\right)\right)a_p{\zeta }_p\left(t\right))}\hfill \\ \hfill & +\overline{h_p\left({\omega }_p\left(t\right)\right)a_p{\omega }_p\left(t\right)-h_p\left({\zeta }_p\left(t\right)\right)a_p{\zeta }_p\left(t\right)}\left[{\eta }_p\left(t\right)\right])\hfill \\ \hfill & {\displaystyle +\frac{1}{2}\sum _{p\in \mathbb{M}}\sum _{q\in \mathbb{M}}(\overline{\left[{\eta }_p\left(t\right)\right]}{h}_p\left({\zeta }_p\left(t\right)\right)b_{pq}({\widehat{\chi }}_q\left(t\right)-h_p\left({\omega }_p\left(t\right)\right){\check{\chi }}_q\left(t\right))}\hfill \\ \hfill & +\overline{h_p\left({\zeta }_p\left(t\right)\right)b_{pq}{\widehat{\chi }}_q\left(t\right)-h_p\left({\omega }_p\left(t\right)\right)b_{pq}{\check{\chi }}_q\left(t\right)}\left[{\eta }_p\left(t\right)\right])\hfill \\ \hfill & {\displaystyle +\frac{1}{2}\sum _{p\in \mathbb{M}}\sum _{q\in \mathbb{M}}(\overline{\left[{\eta }_p\left(t\right)\right]}{c}_{pq}((h_p({\zeta }_p(t)){\widehat{\rho }}_q(k_{pq}(t))-h_p({\omega }_p(t)){\check{\rho }}_q\left(k_{pq}\left(t\right)\right))}\hfill \\ \hfill & +\overline{h_p\left({\zeta }_p\left(t\right)\right)c_{pq}{\widehat{\rho }}_q\left(k_{pq}\left(t\right)\right)-h_p\left({\omega }_p\left(t\right)\right)c_{pq}{\check{\rho }}_q\left(k_{pq}\left(t\right)\right)}\left[{\eta }_p\left(t\right)\right])\hfill \\ \hfill & {\displaystyle +\frac{1}{2}\sum _{p\in \mathbb{M}}\left(\overline{\left[{\eta }_p\left(t\right)\right]}(h_p\left({\zeta }_p\left(t\right)\right)-h_p\left({\omega }_p\left(t\right)\right)){\xi }_p+\overline{(h_p\left({\zeta }_p\left(t\right)\right)-h_p\left({\omega }_p\left(t\right)\right)){\xi }_p}\left[{\eta }_p\left(t\right)\right]\right)}\hfill \\ \hfill & {\displaystyle -\sum _{p\in \mathbb{M}}{\gamma }_p\left[{\eta }_p\left(t\right)\right]\overline{\left[{\eta }_p\left(t\right)\right]}-\sum _{p\in \mathbb{M}}{\lambda }_p\left[{\eta }_p\left(t\right)\right]\overline{\left[{\eta }_p\left(t\right)\right]}{|{\omega }_p\left(t\right)|}_1}\hfill \\ \hfill & {\displaystyle -\sum _{p\in \mathbb{M}}{\alpha }_p\left[{\eta }_p\left(t\right)\right]\overline{\left[{\eta }_p\left(t\right)\right]}|{\eta }_p{\left(t\right)|}_1^{{\epsilon }_1}-\sum _{p\in \mathbb{M}}{\beta }_p\left[{\eta }_p\left(t\right)\right]\overline{\left[{\eta }_p\left(t\right)\right]}{|{\eta }_p\left(t\right)|}_1^{{\epsilon }_2}.}\hfill \end{array}$$

(9)

According to Assumptions 3 and 4 and Lemmas 4 and 5,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}\sum _{p\in \mathbb{M}}(\overline{\left[{\eta }_p(t)\right]}(h_p({\omega }_p(t))a_p{\omega }_p(t)-h_p({\zeta }_p(t))a_p{\zeta }_p(t))}\hfill \\ \hfill & +\overline{h_p({\omega }_p(t))a_p{\omega }_p(t)-h_p({\zeta }_p(t))a_p{\zeta }_p(t)}\left[{\eta }_p(t)\right])\hfill \\ \hfill & {\displaystyle \le \sum _{p\in \mathbb{M}}{|h_p({\zeta }_p(t))a_p{\zeta }_p(t)-h_p({\omega }_p(t))a_p{\omega }_p(t)|}_1}\hfill \\ \hfill & {\displaystyle \le \sum _{p\in \mathbb{M}}(|h_p({\zeta }_p(t))a_p{\zeta }_p(t)-h_p({\zeta }_p(t))a_p{\omega }_p{(t)|}_1}\hfill \\ \hfill & +|h_p({\zeta }_p(t))a_p{\omega }_p(t)-h_p({\omega }_p(t))a_p{\omega }_p(t){|}_1)\hfill \\ \hfill & {\displaystyle \le \sum _{p\in \mathbb{M}}|a_p{|}_1(|h_p({\zeta }_p(t)){|}_1|{\eta }_p{(t)|}_1+|h_p({\zeta }_p(t))-h_p({\omega }_p(t)){|}_1|{\omega }_p(t){|}_1)}\hfill \\ \hfill & {\displaystyle \le \sum _{p\in \mathbb{M}}|a_p{|}_1(H_p^1|{\eta }_p{(t)|}_1+2H_p^1|{\omega }_p(t){|}_1).}\hfill \end{array}$$

(10)

Similarly,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}\sum _{p\in \mathbb{M}}\sum _{q\in \mathbb{M}}(\overline{\left[{\eta }_p(t)\right]}(h_p({\zeta }_p(t))b_{pq}{\widehat{\chi }}_q(t)-h_p({\omega }_p(t))b_{pq}{\check{\chi }}_q(t))}\hfill \\ \hfill & +\overline{h_p({\zeta }_p(t))b_{pq}{\widehat{\chi }}_q(t)-h_p({\omega }_p(t))b_{pq}{\check{\chi }}_q(t)}\left[{\eta }_p(t)\right])\hfill \\ \hfill & {\displaystyle \le \sum _{p\in \mathbb{M}}\sum _{q\in \mathbb{M}}({|h_p({\zeta }_p(t))b_{pq}({\widehat{\chi }}_q(t)-{\check{\chi }}_q(t))|}_1}\hfill \\ \hfill & +|{\check{\chi }}_q(t)b_{pq}(h_p({\zeta }_p(t))-h_p({\omega }_p(t))){|}_1)\hfill \\ \hfill & {\displaystyle =\sum _{p\in \mathbb{M}}\sum _{q\in \mathbb{M}}(|b_{qp}{|}_1{H}_q^1{l}_p^1+|b_{pq}{|}_1{L}_p^1{\tilde{h}}_p^1)|{\eta }_p{(t)|}_1+{|b_{pq}|}_1{H}_p^1{\tilde{l}}_q^1,}\hfill \end{array}$$

(11)

and

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}\sum _{p\in \mathbb{M}}\sum _{q\in \mathbb{M}}(\overline{\left[{\eta }_p(t)\right]}(h_p({\zeta }_p(t))c_{pq}{\widehat{\rho }}_q(k_{pq}(t))-h_p({\omega }_p(t))c_{pq}{\check{\rho }}_q(k_{pq}(t)))}\hfill \\ \hfill & +\overline{h_p({\zeta }_p(t))c_{pq}{\widehat{\rho }}_q(k_{pq}(t))-h_p({\omega }_p(t))c_{pq}{\check{\rho }}_q(k_{pq}(t))}\left[{\eta }_p(t)\right])\hfill \\ \hfill & {\displaystyle \le \sum _{p\in \mathbb{M}}\sum _{q\in \mathbb{M}}2|c_{pq}{|}_1{H}_p^1{R}_q^1+|c_{pq}{|}_1{R}_q^1{\tilde{h}}_p^1{|{\eta }_p(t)|}_1,}\hfill \end{array}$$

(12)

further,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}\sum _{p\in \mathbb{M}}(\overline{\left[{\eta }_p(t)\right]}(h_p({\zeta }_p(t)){\xi }_p-h_p({\omega }_p(t)){\xi }_p)\overline{(h_p({\zeta }_p(t)){\xi }_p-h_p({\omega }_p(t)){\xi }_p)}\left[{\eta }_p(t)\right])}\hfill \\ \hfill & {\displaystyle \le \sum _{p\in \mathbb{M}}{\tilde{h}}_p^1|{\xi }_p{|}_1{|{\eta }_p(t)|}_1.}\hfill \end{array}$$

(13)

Submitting (10)–(13) into (9),

$$\begin{array}{cc}\hfill D^{+}{V}_1(\widehat{\eta }(t))& {\displaystyle \le \sum _{p\in \mathbb{M}}\left(H_p^1|a_p{|}_1+{\tilde{h}}_p^1{|\xi |}_1+\sum _{q\in \mathbb{M}}(H_p^1{l}_p^1|b_{qp}{|}_1+L_q^1{\tilde{h}}_p^1|b_{pq}{|}_1+R_q^1{\tilde{h}}_p^1|c_{pq}{|}_1)\right){|{\eta }_p(t)|}_1}\hfill \\ \hfill & {\displaystyle +\sum _{p\in \mathbb{M}}(2H_p^1-{\lambda }_p){|{\omega }_p(t)|}_1+\sum _{p\in \mathbb{M}}\left(\sum _{q\in \mathbb{M}}(|b_{pq}{|}_1{\widehat{h}}_p{\tilde{l}}_q^1+2|c_{pq}{|}_1{H}_p^1{R}_q^1)-{\gamma }_p\right)}\hfill \\ \hfill & {\displaystyle -\sum _{p\in \mathbb{M}}{\alpha }_p|{\eta }_p{(t)|}_1^{{\epsilon }_1}-\sum _{p\in \mathbb{M}}{\beta }_p{|{\eta }_p(t)|}_1^{{\epsilon }_2}}\hfill \\ \hfill & {\displaystyle \le \overline{\lambda }\sum _{p\in \mathbb{M}}|{\eta }_p{(t)|}_1-\overline{\alpha }(\sum _{p\in \mathbb{M}}|{\eta }_p{(t)|}_1{)}^{{\epsilon }_1}-\overline{\beta }(\sum _{p\in \mathbb{M}}|{\eta }_p(t){{|}_1)}^{{\epsilon }_2}}\hfill \\ \hfill & =\overline{\lambda }{V}_1(\widehat{\eta }(t))-\overline{\alpha }{V}_1^{{\epsilon }_1}(\widehat{\eta }(t))-\overline{\beta }{V}_1^{{\epsilon }_2}(\widehat{\eta }(t)),\hfill \end{array}$$

where the penultimate inequality is given by conditions (7) and (8).

If $0<\overline{\lambda }<min\{\overline{\alpha },\overline{\beta }\}$, the networks (1) and (2) are FIT synchronized within the time ${\widehat{T}}_1$, which is obtained through Lemma 1. Similarly, the remaining results in Theorem 1 can be readily deduced from Lemma 1. □

Especially, if the amplification function $h_p(·)=1$, system (1) is degenerated to QVNN as follows

$$\begin{array}{c}\hfill {\displaystyle {\dot{\omega }}_p(t)={-a}_p{\omega }_p(t)+\sum _{q\in \mathbb{M}}{b}_{pq}{\chi }_q(t)+\sum _{q\in \mathbb{M}}{c}_{pq}{\rho }_q(k_{pq}(t))+{\xi }_p,p\in \mathbb{M}.}\end{array}$$

(14)

Correspondingly, the response system is degenerated to

$$\begin{array}{c}\hfill {\displaystyle {\dot{\zeta }}_p(t)={-a}_p{\zeta }_p(t)+\sum _{q\in \mathbb{M}}{b}_{pq}{\chi }_q(t)+\sum _{q\in \mathbb{M}}{c}_{pq}{\rho }_q(k_{pq}(t))+{\delta }_p(t)+{\xi }_p,p\in \mathbb{M}.}\end{array}$$

(15)

To realize FIT synchronization, the controller is redesigned by

$$\begin{array}{c}\hfill {\displaystyle {\delta }_p(t)=-\left[{\eta }_p(t)\right]({\gamma }_p+{\alpha }_p|{\eta }_p{(t)|}_1^{{\epsilon }_1}+{\beta }_p|{\eta }_p(t){|}_1^{{\epsilon }_2}),}\end{array}$$

(16)

where ${\alpha }_p$, ${\beta }_p>0$, $0\le {\epsilon }_1<1$, ${\epsilon }_2>1$.

Based on the analysis of Theorem 1, the following corollary can be readily derived.

Corollary 1. 

Based on Assumptions 3 and 4, with controller (16), if

$$\begin{array}{c}\hfill {\displaystyle \sum _{q\in \mathbb{M}}(|b_{pq}{|}_1{\tilde{l}}_q^1+2|c_{pq}{|}_1{R}_q^1)-{\gamma }_p<0,}\end{array}$$

(17)

then the following results are obtained.

(1)

If $0<{\overline{\lambda }}_1<min\{\overline{\alpha },\overline{\beta }\},$ systems (14) and (15) realize FIT synchronization and the ST is estimated by

$$\begin{array}{cc}\hfill {\widehat{T}}_3& {\displaystyle =\frac{\pi csc(\pi {\varpi }_1)}{\overline{\beta }({\epsilon }_2-{\epsilon }_1)}{(\frac{\overline{\beta }}{\overline{\alpha }-{\overline{\lambda }}_1})}^{1-{\varpi }_1}I(\frac{\overline{\beta }}{\overline{\beta }+\overline{\alpha }-{\overline{\lambda }}_1},{\varpi }_1,1-{\varpi }_1)}\hfill \\ \hfill & {\displaystyle +\frac{\pi csc(\pi {\varpi }_1)}{\overline{\alpha }({\epsilon }_2-{\epsilon }_1)}{(\frac{\overline{\alpha }}{\overline{\beta }-{\overline{\lambda }}_1})}^{{\varpi }_1}I(\frac{\overline{\alpha }}{\overline{\beta }+\overline{\alpha }-{\overline{\lambda }}_1},1-{\varpi }_1,{\varpi }_1).}\hfill \end{array}$$

(2)

When ${\epsilon }_1+{\epsilon }_2=2$, $0<{\overline{\lambda }}_1<2\sqrt{\overline{\alpha }\overline{\beta }}$, systems (14) and (15) are FIT synchronized and the ST is estimated by

$${\widehat{T}}_4=\frac{2}{\sqrt{{\iota }_1}({\epsilon }_2-1)}(\frac{\pi }{2}+arctan(\frac{{\overline{\lambda }}_1}{{\iota }_1})).$$

In the following, the FIT synchronization of systems (1) and (2) will be investigated based on 2-norm, the controller is designed as

$$\begin{array}{c}\hfill {\delta }_p(t)=-\left[{\eta }_p(t)\right]({\gamma }_p+{\lambda }_p|{\omega }_p{(t)|}_2+{\alpha }_p|{\eta }_p{(t)|}_2^{{\epsilon }_1}+{\beta }_p|{\eta }_p(t){|}_2^{{\epsilon }_2}),\end{array}$$

(18)

where ${\lambda }_p,{\alpha }_p,{\beta }_p,{\gamma }_p>0$ for any $p\in \mathbb{N}$, and $0\le {\epsilon }_1<1,{\epsilon }_2>1$.

Theorem 2. 

Under Assumptions 1–4 and the controller (18), if

$$\begin{array}{c}\hfill 2H_p^2{|a_p|}_2-{\lambda }_p<0,\end{array}$$

(19)

$$\begin{array}{c}\hfill {\displaystyle \sum _{q\in \mathbb{M}}(H_p^2{\tilde{l}}_q^2|b_{pq}{|}_2+2H_p^2{R}_q^2|c_{pq}{|}_2)-{\gamma }_p<0,}\end{array}$$

(20)

then the following results are obtained.

(1)

If $0<\tilde{\lambda }<min\{\tilde{\alpha },\tilde{\beta }\},$ systems (1) and (2) realize FIT synchronization and the ST is estimated by

$$\begin{array}{cc}\hfill {\widehat{T}}_5& {\displaystyle =\frac{\pi csc(\pi {\varpi }_1)}{\overline{\beta }({\epsilon }_2-{\epsilon }_1)}{(\frac{\tilde{\beta }}{\tilde{\alpha }-\tilde{\lambda }})}^{1-{\varpi }_1}I(\frac{\tilde{\beta }}{\tilde{\alpha }+\tilde{\beta }-\tilde{\lambda }},{\varpi }_1,1-{\varpi }_1)}\hfill \\ \hfill & {\displaystyle +\frac{\pi csc(\pi {\varpi }_1)}{\tilde{\alpha }({\epsilon }_2-{\epsilon }_1)}{(\frac{\tilde{\alpha }}{\tilde{\beta }-\tilde{\lambda }})}^{{\varpi }_1}I(\frac{\tilde{\alpha }}{\tilde{\alpha }+\tilde{\beta }-\tilde{\lambda }},1-{\varpi }_1,{\varpi }_1).}\hfill \end{array}$$

(2)

When ${\epsilon }_1+{\epsilon }_2=2$, $0<\tilde{\lambda }<2\sqrt{\tilde{\alpha }\tilde{\beta }}$, systems (1) and (2) are FIT synchronized and the ST is estimated by

$${\widehat{T}}_6=\frac{2}{\sqrt{{\iota }_2}({\epsilon }_2-1)}(\frac{\pi }{2}+arctan(\frac{\tilde{\lambda }}{{\iota }_2})).$$

Proof. 

Consider the following 2-norm-based Lyapunov function

$${\displaystyle V_2(\tilde{\eta }(t))=\frac{1}{2}\sum _{p\in \mathbb{M}}{|{\eta }_p(t)|}_2^2,}$$

where $\tilde{\eta }(t)=(|{\eta }_1{(t)|}_2,|{\eta }_2{(t)|}_2,\cdots ,|{\eta }_n(t){{|}_2)}^T\in {\mathbb{R}}^n$.

Combining with the error system (5), one has

$$\begin{array}{cc}\hfill D^{+}{V}_2(\tilde{\eta }(t))& {\displaystyle =\frac{1}{2}\sum _{p\in \mathbb{M}}(\overline{{\eta }_p(t)}{D}^{+}{\eta }_p(t)+D^{+}\overline{{\eta }_p(t)}{\eta }_p(t))}\hfill \\ \hfill & {\displaystyle =\frac{1}{2}\sum _{p\in \mathbb{M}}(\overline{{\eta }_p(t)}(h_p({\omega }_p(t))a_p{\omega }_p(t)-h_p({\zeta }_p(t))a_p{\zeta }_p(t))}\hfill \\ \hfill & +\overline{(h_p({\omega }_p(t))a_p{\omega }_p(t)-h_p({\zeta }_p(t))a_p{\zeta }_p(t))}){\eta }_p(t))\hfill \\ \hfill & {\displaystyle +\frac{1}{2}\sum _{p\in \mathbb{M}}\sum _{q\in \mathbb{M}}(\overline{{\eta }_p(t)}(h_p({\zeta }_p(t))b_{pq}{\widehat{\chi }}_q(t)-h_p({\omega }_p(t))b_{pq}{\check{\chi }}_q(t))}\hfill \\ \hfill & +\overline{h_p({\zeta }_p(t))b_{pq}{\widehat{\chi }}_q(t)-h_p({\omega }_p(t))b_{pq}{\check{\chi }}_q(t)}{\eta }_p(t))\hfill \\ \hfill & {\displaystyle +\frac{1}{2}\sum _{p\in \mathbb{M}}\sum _{q\in \mathbb{M}}(\overline{{\eta }_p(t)}(h_p({\zeta }_p(t))c_{pq}{\widehat{\rho }}_q(k_{pq}(t))-h_p({\omega }_p(t))c_{pq}{\check{\rho }}_q(k_{pq}(t)))}\hfill \\ \hfill & +\overline{h_p({\zeta }_p(t))c_{pq}{\widehat{\rho }}_q(k_{pq}(t))-h_p({\omega }_p(t))c_{pq}{\check{\rho }}_q(k_{pq}(t))}{\eta }_p(t))\hfill \\ \hfill & {\displaystyle +\frac{1}{2}\sum _{p\in \mathbb{M}}\left(\overline{{\eta }_p(t)}(h_p({\zeta }_p(t))\xi -h_p({\omega }_p(t))\xi )+\overline{(h_p({\zeta }_p(t))\xi -h_p({\omega }_p(t))\xi )}{\eta }_p(t)\right)}\hfill \\ \hfill & {\displaystyle -\frac{1}{2}\sum _{p\in \mathbb{M}}\sum _{q\in \mathbb{M}}{\gamma }_p(\overline{{\eta }_p(t)}\left[{\eta }_p(t)\right]+{\eta }_p(t)\overline{\left[{\eta }_p(t)\right]})}\hfill \\ \hfill & {\displaystyle -\frac{1}{2}\sum _{p\in \mathbb{M}}{\lambda }_p(\overline{{\eta }_p(t)}\left[{\eta }_p(t)\right]+{\eta }_p(t)\overline{\left[{\eta }_p(t)\right]}){|{\omega }_p(t)|}_2}\hfill \\ \hfill & {\displaystyle -\frac{1}{2}\sum _{p\in \mathbb{M}}{\alpha }_p(\overline{{\eta }_p(t)}\left[{\eta }_p(t)\right]+{\eta }_p(t)\overline{\left[{\eta }_p(t)\right]}){|{\eta }_p(t)|}_2^{{\epsilon }_1}}\hfill \\ \hfill & {\displaystyle -\frac{1}{2}\sum _{p\in \mathbb{M}}{\beta }_p(\overline{{\eta }_p(t)}\left[{\eta }_p(t)\right]+{\eta }_p(t)\overline{\left[{\eta }_p(t)\right]}){|{\eta }_p(t)|}_2^{{\epsilon }_2}.}\hfill \end{array}$$

(21)

Based on Assumptions 3 and 4 and Lemmas 4 and 5, one obtains

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}\sum _{p\in \mathbb{M}}(\overline{{\eta }_p(t)}(h_p({\omega }_p(t))a_p{\omega }_p(t)-h_p({\zeta }_p(t))a_p{\zeta }_p(t))}\hfill \\ \hfill & +\overline{(h_p({\omega }_p(t))a_p{\omega }_p(t)-h_p({\zeta }_p(t))a_p{\zeta }_p(t))}){\eta }_p(t))\hfill \\ \hfill & \le \sum _{p\in \mathbb{M}}|{\eta }_p{(t)|}_2(|h_p({\zeta }_p(t))a_p({\zeta }_p(t)-{\omega }_p(t)){|}_2\hfill \\ \hfill & +|a_p{\omega }_p(t)(h_p({\zeta }_p(t))-h_p({\omega }_p(t))){|}_2)\hfill \\ \hfill & \le \sum _{p\in \mathbb{M}}(H_p^2|a_p{|}_2|{\eta }_p{(t)|}_2^2+2H_p^2|a_p{|}_2|{\omega }_p{(t)|}_2|{\eta }_p(t){|}_2).\hfill \end{array}$$

(22)

Similarly,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}\sum _{p\in \mathbb{M}}\sum _{q\in \mathbb{M}}(\overline{{\eta }_p(t)}(h_p({\zeta }_p(t))b_{pq}{\widehat{\chi }}_q(t)-h_p({\omega }_p(t))b_{pq}{\check{\chi }}_q(t))}\hfill \\ \hfill & +\overline{h_p({\zeta }_p(t))b_{pq}{\widehat{\chi }}_q(t)-h_p({\omega }_p(t))b_{pq}{\check{\chi }}_q(t)}{\eta }_p(t))\hfill \\ \hfill & {\displaystyle \le \sum _{p\in \mathbb{M}}\sum _{q\in \mathbb{M}}\left((\frac{1}{2}\acute{h}{l}_p^2|b_{qp}{|}_2+\frac{1}{2}{H}_p^2{l}_q^2|b_{pq}{|}_2+L_p^2{\tilde{h}}_2|b_{pq}{|}_2)|{\eta }_p{(t)|}_2^2+|b_{pq}{|}_2{H}_p^2{\tilde{l}}_q^2{|{\eta }_p(t)|}_2\right),}\hfill \end{array}$$

(23)

and

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}\sum _{p\in \mathbb{M}}\sum _{q\in \mathbb{M}}(\overline{{\eta }_p(t)}{c}_{pq}(h_p({\zeta }_p(t)){\widehat{\rho }}_q(k_{pq}(t))-h_p({\omega }_p(t)){\check{\rho }}_q(k_{pq}(t)))}\hfill \\ \hfill & +\overline{h_p({\zeta }_p(t))c_{pq}{\widehat{\rho }}_q(k_{pq}(t))-h_p({\omega }_p(t))c_{pq}{\check{\rho }}_q(k_{pq}(t)}{\eta }_p(t))\hfill \\ \hfill & {\displaystyle \le \sum _{p\in \mathbb{M}}\sum _{q\in \mathbb{M}}2H_p^2{R}_q^2|c_{pq}{|}_2|{\eta }_p{(t)|}_2+R_p^2{\tilde{h}}_2|c_{pq}{|}_2{|{\eta }_p(t)|}_2^2.}\hfill \end{array}$$

(24)

Moreover,

$$\begin{array}{cc}\hfill & {\displaystyle -\frac{1}{2}\sum _{p\in \mathbb{M}}{\lambda }_p(\overline{{\eta }_p(t)}\left[{\eta }_p(t)\right]+{\eta }_p(t)\overline{\left[{\eta }_p(t)\right]})|{\omega }_p{(t)|}_2\le -\sum _{p\in \mathbb{M}}{\lambda }_p|{\eta }_p{(t)|}_2{|{\omega }_p(t)|}_2,}\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & {\displaystyle -\frac{1}{2}\sum _{p\in \mathbb{M}}{\gamma }_p(\overline{{\eta }_p(t)}\left[{\eta }_p(t)\right]+{\eta }_p(t)\overline{\left[{\eta }_p(t)\right]})\le -\sum _{p\in \mathbb{M}}{\gamma }_p{|{\eta }_p(t)|}_2,}\hfill \end{array}$$

(26)

$$\begin{array}{c}\hfill {\displaystyle -\frac{1}{2}\sum _{p\in \mathbb{M}}{\alpha }_p(\overline{{\eta }_p(t)}\left[{\eta }_p(t)\right]+{\eta }_p(t)\overline{\left[{\eta }_p(t)\right]})|{\eta }_p{(t)|}_2^{{\epsilon }_1}\le -\tilde{\alpha }(\sum _{p\in \mathbb{M}}\frac{1}{2}|{\eta }_p(t){{|}_2^2)}^{\frac{1+{\epsilon }_1}{2}},}\end{array}$$

(27)

$$\begin{array}{cc}\hfill & {\displaystyle -\frac{1}{2}\sum _{p\in \mathbb{M}}{\beta }_p(\overline{{\eta }_p(t)}\left[{\eta }_p(t)\right]+{\eta }_p(t)\overline{\left[{\eta }_p(t)\right]})|{\eta }_p{(t)|}_2^{{\epsilon }_2}\le -\tilde{\beta }(\sum _{p\in \mathbb{M}}\frac{1}{2}|{\eta }_p(t){{|}_2^2)}^{\frac{1+{\epsilon }_2}{2}}.}\hfill \end{array}$$

(28)

Substitute (22)–(28) into (21),

$$\begin{array}{cc}\hfill D^{+}{V}_2(\tilde{\eta }(t))& {\displaystyle \le \sum _{p\in \mathbb{M}}\sum _{q\in \mathbb{M}}(2H_p^2|a_p{|}_2-{\lambda }_p)|{\omega }_p{(t)|}_2{|{\eta }_p(t)|}_2}\hfill \\ \hfill & {\displaystyle +\sum _{p\in \mathbb{M}}(\sum _{q\in \mathbb{M}}(H_p^2{\tilde{l}}_q^2|b_{pq}{|}_2+2H_p^2{R}_q^2|c_{pq}{|}_2)-{\gamma }_p)|{\eta }_p{(t)|}_2}\hfill \\ \hfill & {\displaystyle +\sum _{p\in \mathbb{M}}\sum _{q\in \mathbb{M}}(H_p^2|a_p{|}_2+\frac{1}{2}{H}_p^2{l}_p^2|b_{qp}{|}_2+\frac{1}{2}{H}_p^2{l}_q^2|b_{pq}{|}_2+L_p^2{\tilde{h}}_2{|b_{pq}|}_2}\hfill \\ \hfill & {\displaystyle +R_p^2{\tilde{h}}_p^2|c_{pq}{|}_2)|{\eta }_p{(t)|}_2^2-\sum _{p\in \mathbb{M}}{\alpha }_p|{\eta }_p{(t)|}_2^{{\epsilon }_1+1}-\sum _{p\in \mathbb{M}}{\beta }_p{|{\eta }_p(t)|}_2^{{\epsilon }_2+1}}\hfill \\ \hfill & \le \tilde{\lambda }{V}_2(\tilde{\eta }(t))-\tilde{\alpha }{V}_2^{{\tilde{\epsilon }}_1}(\tilde{\eta }(t))-\tilde{\beta }{V}_2^{{\tilde{\epsilon }}_2}(\tilde{\eta }(t)).\hfill \end{array}$$

If $0<\tilde{\lambda }<min\{\tilde{\alpha },\tilde{\beta }\}$, then the CGQVNNs (1) and (2) achieve FIT synchronization within the time ${\widehat{T}}_5$. Additionally, the other results presented in Theorem 1 can be straightforwardly derived from Lemma 1. □

To obtain the synchronization criteria of systems (14) and (15) based on 2-norm, the controller is designed as

$$\begin{array}{c}\hfill {\displaystyle {\delta }_p(t)=-\left[{\eta }_p(t)\right]({\gamma }_p+{\alpha }_p|{\eta }_p{(t)|}_2^{{\epsilon }_1}+{\beta }_p|{\eta }_p(t){|}_2^{{\epsilon }_2}),}\end{array}$$

(29)

where ${\gamma }_p$, ${\alpha }_p$, ${\beta }_p>0$, $0\le {\epsilon }_1<1$, ${\epsilon }_2>1$.

According to Theorem 2, the following corollary is easily obtained.

Corollary 2. 

Based on Assumptions 3 and 4, with controller (29), if

$${\displaystyle \sum _{p\in \mathbb{M}}({\tilde{l}}_q^2|b_{pq}{|}_2+2R_q^2|b_{pq}{|}_2)-{\gamma }_p<0,}$$

then the following results are derived.

(1)

If $0<{\tilde{\lambda }}_1<min\{\tilde{\alpha },\tilde{\beta }\},$ systems (14) and (15) can realize FIT synchronization and the ST is estimated by

$$\begin{array}{cc}\hfill {\widehat{T}}_7& {\displaystyle =\frac{\pi csc(\pi {\varpi }_1)}{\overline{\beta }({\epsilon }_2-{\epsilon }_1)}{(\frac{\tilde{\beta }}{\tilde{\alpha }-{\tilde{\lambda }}_1})}^{1-{\varpi }_1}I(\frac{\tilde{\beta }}{\tilde{\alpha }+\tilde{\beta }-{\tilde{\lambda }}_1},{\varpi }_1,1-{\varpi }_1)}\hfill \\ \hfill & {\displaystyle +\frac{\pi csc(\pi {\varpi }_1)}{\tilde{\alpha }({\epsilon }_2-{\epsilon }_1)}{(\frac{\tilde{\alpha }}{\tilde{\beta }-{\tilde{\lambda }}_1})}^{{\varpi }_1}I(\frac{\tilde{\alpha }}{\tilde{\alpha }+\tilde{\beta }-{\tilde{\lambda }}_1},1-{\varpi }_1,{\varpi }_1).}\hfill \end{array}$$

(2)

When ${\epsilon }_1+{\epsilon }_2=2$, $0<\tilde{\lambda }<2\sqrt{\tilde{\alpha }\tilde{\beta }}$, systems (14) and (15) are FIT synchronized and the ST is estimated by

$${\widehat{T}}_8=\frac{2}{\sqrt{{\iota }_2}({\epsilon }_2-1)}(\frac{\pi }{2}+arctan(\frac{\tilde{\lambda }}{{\iota }_2})).$$

Remark 3. 

The FIT synchronization of QVNNs with or without time delay was discussed in [24,25], in which the original QVNN was divided into four real-valued subnetworks. Different from the above theoretical analysis method, a non-separation method is proposed in this paper, which greatly reduces the complexity of the analysis. Besides, several control strategies are designed based on the quaternion-valued sign function to realize the FIT synchronization of CGQVNNs, which can extremely reduce control costs and obtain higher accuracy estimation of ST. Furthermore, the time delay considered in this paper integrates discrete constant delay, discrete time-varying delay and proportional delay, which is more general and widely applicable.

4. Preassigned-Time Synchronization

To achieve the PET synchronization of CGQVNNs (1) and (2), the controller is proposed by

$$\begin{array}{c}\hfill {\displaystyle {\delta }_p(t)=-\frac{\check{T}}{T_{pet}}\left[{\eta }_p(t)\right]({\gamma }_p+{\lambda }_p|{\omega }_p{(t)|}_1+{\alpha }_p|{\eta }_p{(t)|}_1^{{\epsilon }_1}+{\beta }_p|{\eta }_p(t){|}_1^{{\epsilon }_2}),}\end{array}$$

(30)

where ${\gamma }_p,{\lambda }_p,{\alpha }_p,{\beta }_p>0$ for any $p\in \mathbb{N}$, $0\le {\epsilon }_1<1,{\epsilon }_2>1$, and

$$\check{T}=\left\{\begin{array}{c}{\widehat{T}}_1,0<\overline{\lambda }<min\{\overline{\alpha },\overline{\beta }\},\hfill \\ {\widehat{T}}_2,{\epsilon }_1+{\epsilon }_2=2,0<\overline{\lambda }<2\sqrt{\overline{\alpha }\overline{\beta }}.\hfill \end{array}\right.$$

Theorem 3. 

Based on Assumptions 1–3 and the controller (30), if conditions (7) and (8) hold, then the networks (1) and (2) realize PET synchronization within $0<T_{pet}\le \check{T}$.

Proof. 

Similar to the analysis of Theorem 1, one can obtain

$$\begin{array}{cc}\hfill D^{+}{V}_1(\widehat{\eta }(t))& {\displaystyle \le \sum _{p\in \mathbb{M}}(H_p^1|a_p{|}_1+{\tilde{h}}_p^1{|\xi |}_1+\sum _{q\in \mathbb{M}}(H_q^1{l}_p^1|b_{qp}{|}_1+L_q^1{\tilde{h}}_p^1|b_{pq}{|}_1+R_q^1{\tilde{h}}_p^1|c_{pq}{|}_1))|{\eta }_p{(t)|}_1}\hfill \\ \hfill & {\displaystyle +\sum _{p\in \mathbb{M}}(2H_p^1-\frac{\check{T}}{T_{pet}}{\lambda }_p)|{\omega }_p(t){|}_1+\sum _{p\in \mathbb{M}}(\sum _{q\in \mathbb{M}}(|b_{pq}{|}_1{H}_p^1{\tilde{l}}_q^1+2|c_{pq}{|}_1{H}_p^1{R}_q^1)-\frac{\check{T}}{T_{pet}}{\gamma }_p)}\hfill \\ \hfill & {\displaystyle -\sum _{p\in \mathbb{M}}\frac{\check{T}}{T_{pet}}{\alpha }_p|{\eta }_p{(t)|}_1^{{\epsilon }_1}-\sum _{p\in \mathbb{M}}\frac{\check{T}}{T_{pet}}{\beta }_p{|{\eta }_p(t)|}_1^{{\epsilon }_2}}\hfill \\ \hfill & {\displaystyle \le \frac{\check{T}}{T_{pet}}\overline{\lambda }\sum _{p\in \mathbb{M}}|{\eta }_p{(t)|}_1-\frac{\check{T}}{T_{pet}}\overline{\alpha }(\sum _{p\in \mathbb{M}}|{\eta }_p{(t)|}_1{)}^{{\epsilon }_1}-\frac{\check{T}}{T_{pet}}\overline{\beta }(\sum _{p\in \mathbb{M}}|{\eta }_p(t){{|}_1)}^{{\epsilon }_2}}\hfill \\ \hfill & {\displaystyle =\frac{\check{T}}{T_{pet}}(\overline{\lambda }{V}_1(\widehat{\eta }(t))-\overline{\alpha }{V}_1^{{\epsilon }_1}(\widehat{\eta }(t))-\overline{\beta }{V}_1^{{\epsilon }_2}(\widehat{\eta }(t))).}\hfill \end{array}$$

In light of Lemma 2, CGQVNNs (1) and (2) are PET synchronized within $T_{pet}$. □

Corollary 3. 

Based on Assumptions 3 and 4 and the following controller

$${\displaystyle {\delta }_p(t)=-\frac{\breve{T}}{T_{pet}}\left[{\eta }_p(t)\right]({\gamma }_p+{\alpha }_p|{\eta }_p{(t)|}_1^{{\epsilon }_1}+{\beta }_p|{\eta }_p(t){|}_1^{{\epsilon }_2}),}$$

if condition (17) holds, then the networks (14) and (15) achieve PET synchronization within $0<T_{pet}\le \breve{T}$, where ${\gamma }_p,{\alpha }_p,{\beta }_p>0$ for any $p\in \mathbb{N}$, $0\le {\epsilon }_1<1,{\epsilon }_2>1$ and

$$\breve{T}=\left\{\begin{array}{c}{\widehat{T}}_3,0<{\overline{\lambda }}_1<min\{\overline{\alpha },\overline{\beta }\},\hfill \\ {\widehat{T}}_4,0<{\overline{\lambda }}_1<2\sqrt{\overline{\alpha }\overline{\beta }},{\epsilon }_1+{\epsilon }_2=2.\hfill \end{array}\right.$$

Based on 2-norm, the control scheme is designed by

$$\begin{array}{c}\hfill {\displaystyle {\delta }_p(t)=-\frac{\acute{T}}{T_{pet}}\left[{\eta }_p(t)\right]({\gamma }_p+{\lambda }_p|{\omega }_p{(t)|}_2+{\alpha }_p|{\eta }_p{(t)|}_2^{{\epsilon }_1}+{\beta }_p|{\eta }_p(t){|}_2^{{\epsilon }_2}),}\end{array}$$

(31)

where ${\gamma }_p,{\lambda }_p,{\alpha }_p,{\beta }_p>0$ for any $p\in \mathbb{N}$, $0\le {\epsilon }_1<1,{\epsilon }_2>1$, and

$$\acute{T}=\left\{\begin{array}{c}{\widehat{T}}_5,0<\tilde{\lambda }<min\{\tilde{\alpha },\tilde{\beta }\},\hfill \\ {\widehat{T}}_6,0<\tilde{\lambda }<2\sqrt{\tilde{\alpha }\tilde{\beta }},{\epsilon }_1+{\epsilon }_2=2.\hfill \end{array}\right.$$

Theorem 4. 

Based on Assumptions 1–3 and the controller (31), if conditions (19) and (20) hold, then the networks (1) and (2) achieve PET synchronization within $0<T_{pet}\le \acute{T}$.

Similarly, the following corollary can be drawn.

Corollary 4. 

Based on Assumptions 3 and 4 and the following controller

$${\displaystyle {\delta }_p(t)=-\frac{\stackrel{`}{T}}{T_{pet}}\left[{\eta }_p(t)\right]({\gamma }_p+{\alpha }_p|{\eta }_p{(t)|}_1^{{\epsilon }_1}+{\beta }_p|{\eta }_p(t){|}_1^{{\epsilon }_2}),}$$

if condition (17) holds, then the networks (14) and (15) achieve PET synchronization within $0<T_{pet}\le \stackrel{`}{T}$, where ${\gamma }_p,{\alpha }_p,{\beta }_p>0$ for any $p\in \mathbb{N}$, $0\le {\epsilon }_1<1,{\epsilon }_2>1$ and

$$\stackrel{`}{T}=\left\{\begin{array}{c}{\widehat{T}}_7,0<{\tilde{\lambda }}_1<min\{\tilde{\alpha },\tilde{\beta }\},\hfill \\ {\widehat{T}}_8,0<{\tilde{\lambda }}_1<2\sqrt{\tilde{\alpha }\tilde{\beta }},{\epsilon }_1+{\epsilon }_2=2.\hfill \end{array}\right.$$

Remark 4. 

Compared with the results presented in [16,44], the FNT synchronization of CGQVNNs is readily available when ${\beta }_p=0$ in this paper. In [25], the FIT and PET synchronization of QVNNs has been discussed, in which the original QVNNs was decomposed into four real-valued systems and four corresponding controllers were designed. Obviously, this separation method leads to complex and redundant analysis and calculations. Nevertheless, there are limited relevant results available for discussing the FIT and PET synchronization of CGQVNNs using a non-separation method. In Theorems 1–3, three quaternion-valued controllers (18), (6) and (30) are designed, and the FIT and PET synchronization of CGQVNNs under non-separation are completely solved under the non-separation method. In theoretical analysis, only a few common inequalities and real number operations are utilized, which simplifies the analytical process to some extent.

Remark 5. 

In [16], the authors designed an event-triggered controller to realize the FNT synchronization of QVNNs through a non-decomposition method. Inspired by this issue, it is also a challenge to construct event-triggered controllers for the FIT and PET synchronization of CGQVNNs, which will be investigated in the future.

5. Numerical Simulations

In this section, two numerical examples are presented to verify the above theoretical results.

Consider the following CGQVNN with two neurons

$$\begin{array}{cc}{\dot{\omega }}_p(t)=& {\displaystyle h_p({\omega }_p(t))({-a}_p{\omega }_p(t)+\sum _{q=1,2}{b}_{pq}{\chi }_q({\omega }_q(t))}\hfill \\ & {\displaystyle +\sum _{q=1,2}{c}_{pq}{\rho }_q({\omega }_q(k_{pq}(t)))+{\xi }_p),p=1,2,}\hfill \end{array}$$

(32)

in which $a_1=-0.4+0.2i-0.5j-1.3k$, $a_2=-0.3-2.2i+1.1j-0.2k$, ${\chi }_1(\kappa )={\chi }_2(\kappa )=0.1tanh({\kappa }^R)+0.01\mathrm{sign}({\kappa }^R)+i(0.1tanh({\kappa }^I)+0.01\mathrm{sign}({\kappa }^I))+j(0.1tanh({\kappa }^J)+0.01\mathrm{sign}({\kappa }^J))$ $+ k(0.1tanh({\kappa }^K)+0.01\mathrm{sign}({\kappa }^K))$, ${\rho }_1(\kappa )={\rho }_2(\kappa )=0.1cos({\kappa }^R)+0.1\mathrm{sign}({\kappa }^R)+i(0.1cos({\kappa }^I)$ $+ 0.1\mathrm{sign}({\kappa }^I))+ j(0.1cos({\kappa }^J)+0.1\mathrm{sign}({\kappa }^J))+k(0.1cos({\kappa }^K)+0.1\mathrm{sign}({\kappa }^K))$, $h(\kappa )=sin({\kappa }^R)$ $+ 2$ where $\kappa \in \mathbb{Q}$, ${\displaystyle k_{pq}(t)=t-\frac{e^t}{1+e^t}}$, $p,q=1,2$, and

$${(b_{pq})}_{2\times 2}=\left(\begin{array}{cc}-1.6+1.4i+1.2j-2.4k& -0.4+0.6i-0.3j-1.6k\\ 2.5+0.3i-0.2j+0.6k& 2.1+0.4i-0.6j-0.2k\end{array}\right),$$

$${(c_{pq})}_{2\times 2}=\left(\begin{array}{cc}-0.1+0.2i-0.3j+0.6k& 0.8+0.3i-0.5j-0.5k\\ 0.2+0.4i+0.6j-0.2k& 0.6+0.2i-0.3j+0.6k\end{array}\right),$$

$${({\xi }_p)}_{2\times 2}=\left(\begin{array}{cc}2.0+1.5i-1.3j-2.0k& 0\\ 0& 1.2+0.6i-1.6j-0.8k\end{array}\right).$$

The corresponding CGQVNN is given as follows

$$\begin{array}{cc}{\dot{\zeta }}_p(t)=& {\displaystyle h_p({\zeta }_p(t))({-a}_p{\zeta }_p(t)+\sum _{q=1,2}{b}_{pq}{\chi }_q({\zeta }_q(t))}\hfill \\ & {\displaystyle +\sum _{q=1,2}{c}_{pq}{\rho }_q({\zeta }_q(k_{pq}(t)))+{\xi }_p)+{\delta }_p(t),p=1,2.}\hfill \end{array}$$

(33)

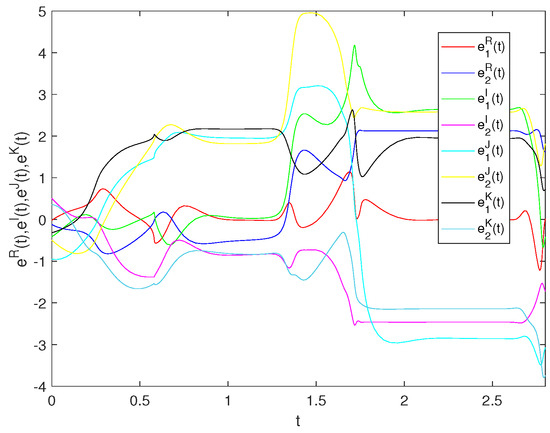
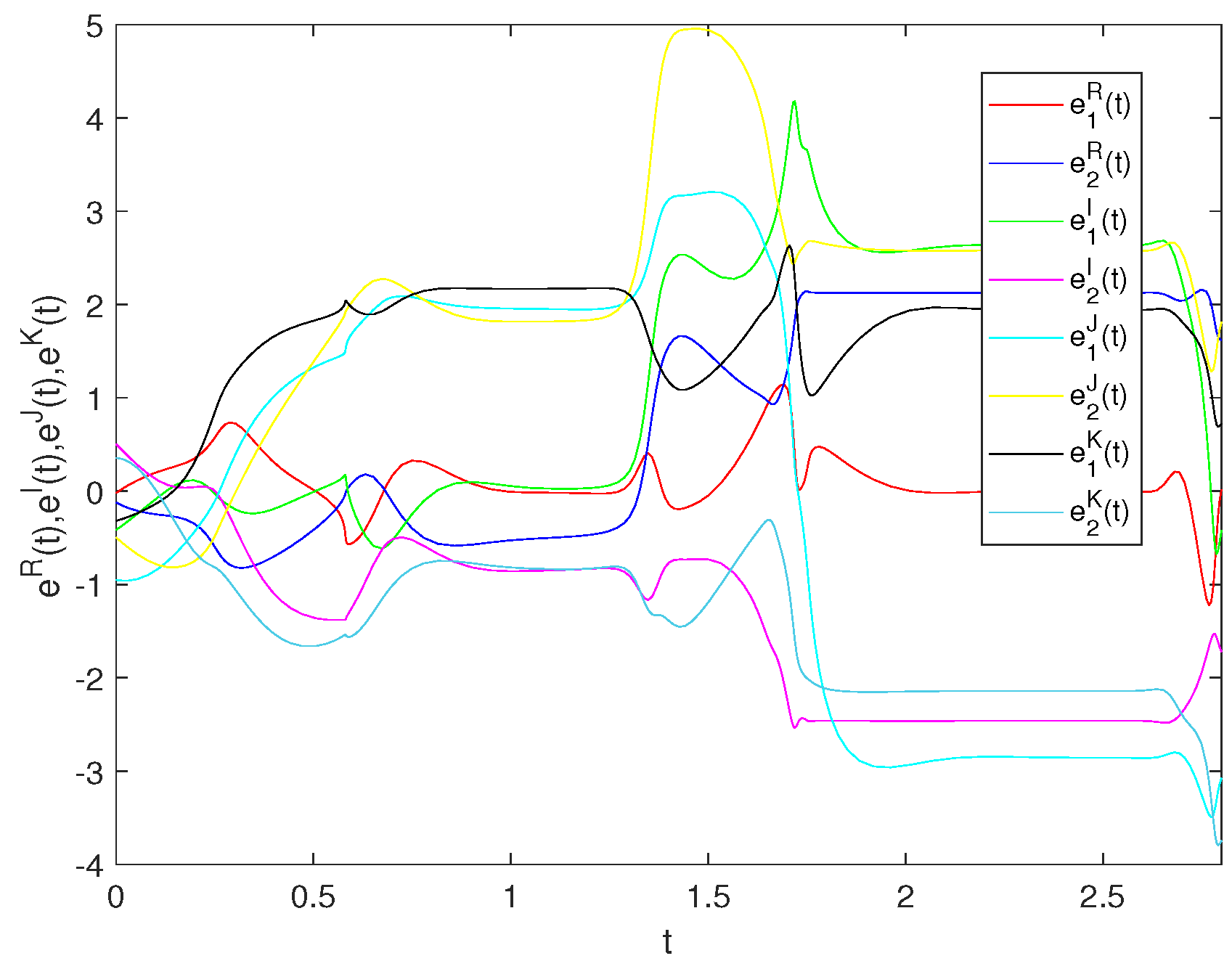
By randomly selecting the initial values, the synchronization error of CGQVNNs (32) and (33) is shown in Figure 1 without control.

Figure 1. Synchronization error of CGQVNNs (32) and (33) without control.

First of all, consider the synchronization of driven-response CGQVNNs (32) and (33) with the controller (8). According to calculation, $l_q^1=1,{\tilde{l}}_q^1=0.08,L_q^1=0.44,R_q^1=0.8$, ${\tilde{h}}_q^1=1,H_q^1=3,$ for any $q=1,2$ and $\overline{\lambda }=22.124$. In (8), select ${\gamma }_1=18.0,{\gamma }_2=14.4$, ${\lambda }_1={\lambda }_2=6.5,\alpha =23.0,\beta =24.0,{\epsilon }_1=0.7,{\epsilon }_2=1.1$. It is not difficult to verify that

$$\begin{array}{c}{\displaystyle 17.5=\sum _{q=1}^2(|b_{1q}{|}_1{H}_1^1{\tilde{l}}_q^1+2|c_{1q}{|}_1{H}_1^1{R}_q^1)<{\gamma }_1=18.0,}\end{array}$$

$$\begin{array}{c}{\displaystyle 13.9=\sum _{q=1}^2(|b_{2q}{|}_1{H}_2^1{\tilde{l}}_q^1+2|c_{2q}{|}_1{H}_2^1{R}_q^1)<{\gamma }_1=14.4,}\end{array}$$

$$\begin{array}{c}6=2H_p^1<{\lambda }_p=6.5,p=1,2,\end{array}$$

$$22.124=\overline{\lambda }<min\{\overline{\alpha },\overline{\beta }\}=22.39.$$

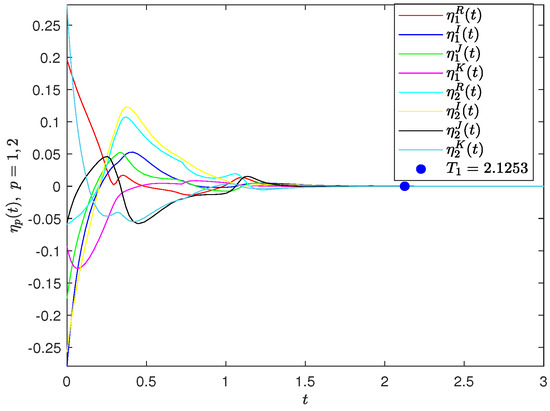
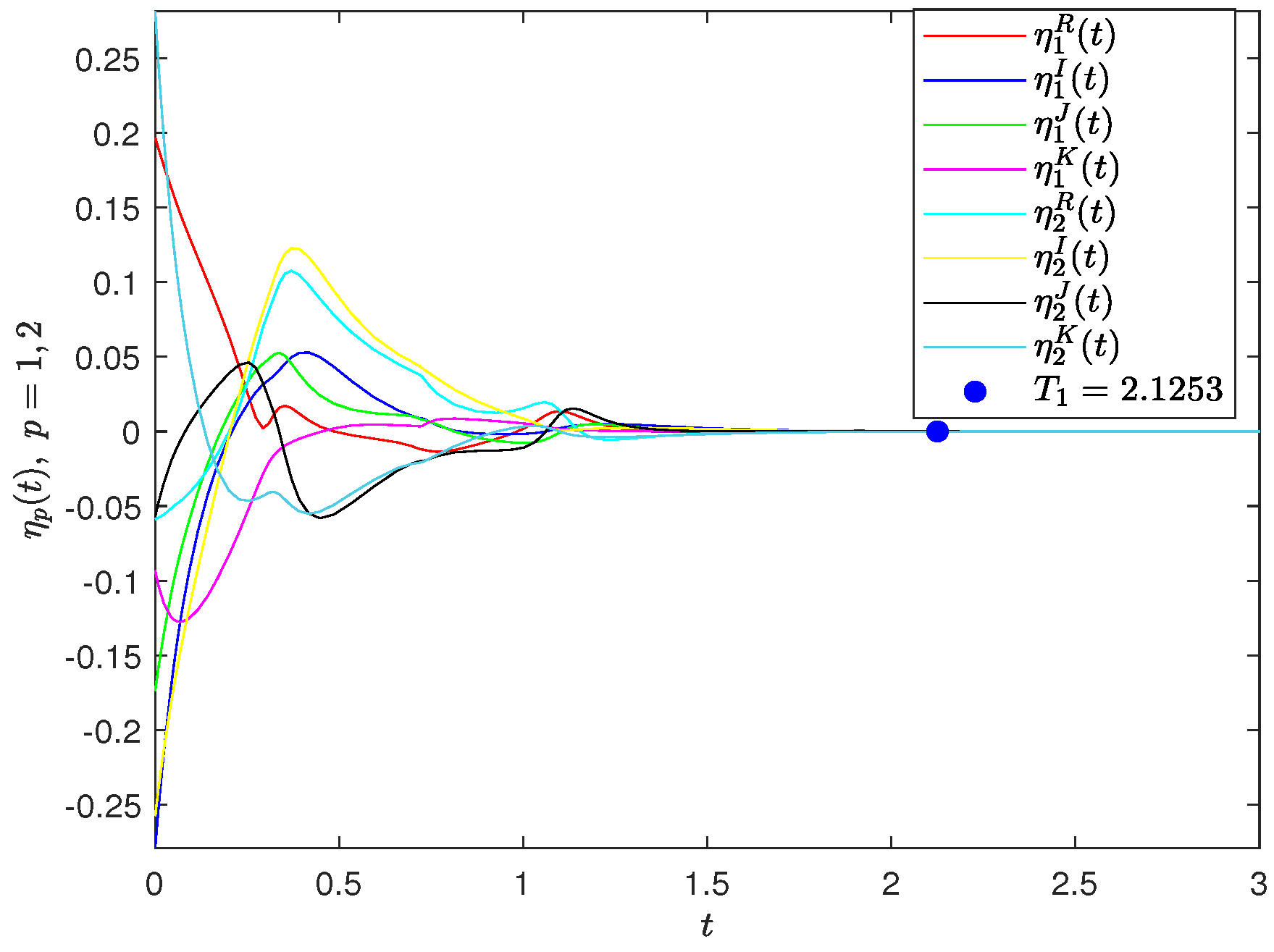
By means of Theorem 1, the driven-response CGQVNNs (32) and (33) achieve FXT synchronization, here the settling time is estimated by ${\widehat{T}}_1=2.1253$. The synchronization result is simulated in Figure 2.

Figure 2. FIT synchronization error of CGQVNNs (32) and (33) under controller (8).

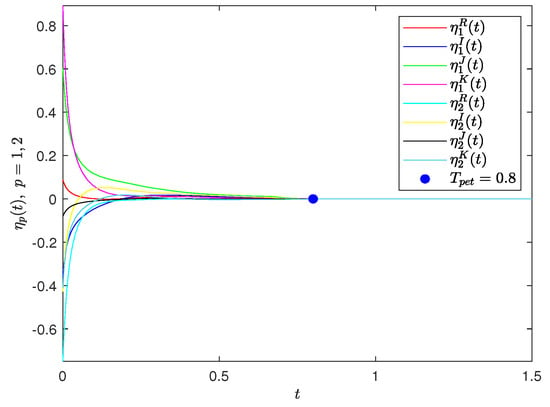
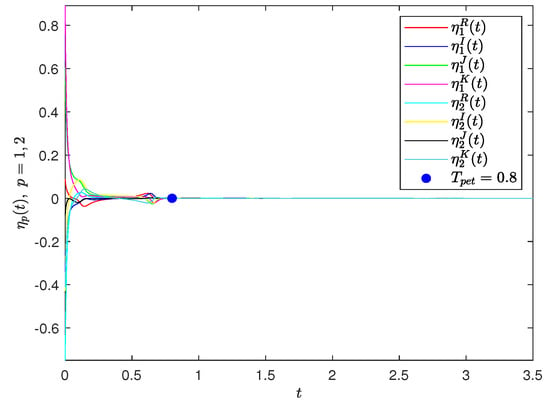
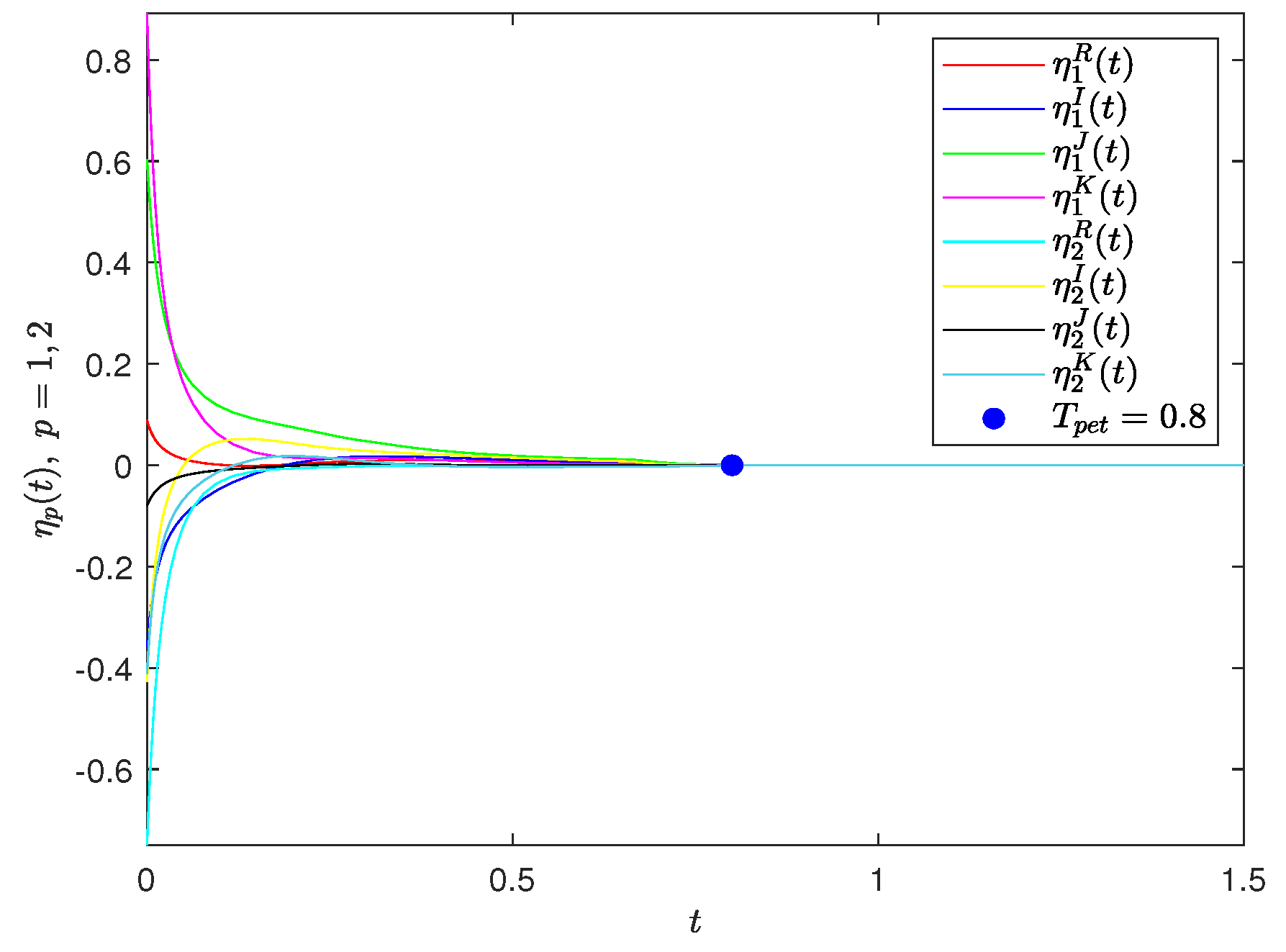
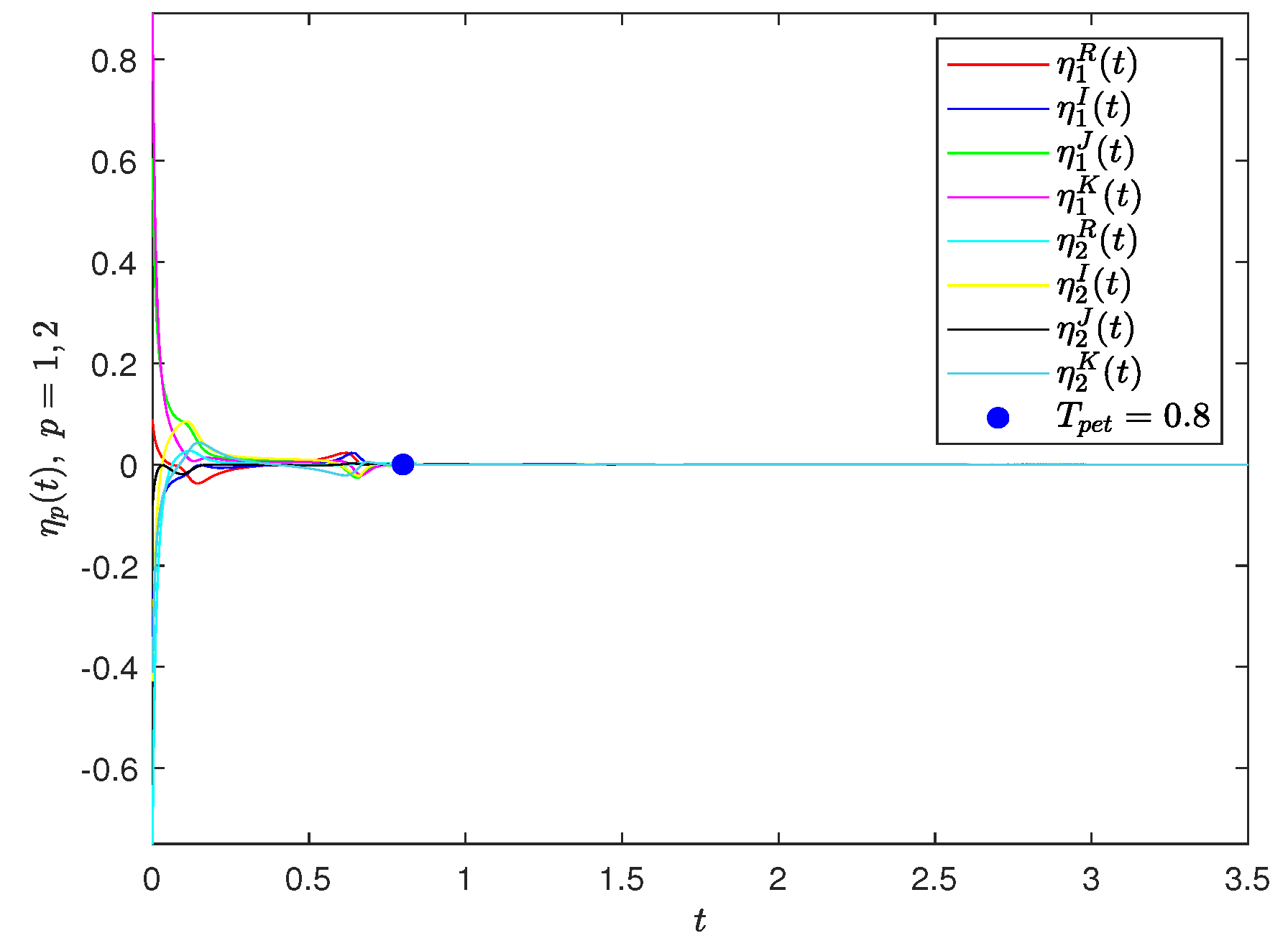
Furthermore, choose $T_{pet}=0.8$ in (38). Under the above-selected parameters, CGQVNNs (32) and (33) reach PET synchronization with $T_{pet}=0.8$ according to Theorem 3, which is demonstrated in Figure 3.

Figure 3. PET synchronization error of CGQVNNs (32) and (33) under controller (8).

Next, let us verify the FIX synchronization of driven-response CGQVNNs (32) and (33) under a 2-norm-based controller (24). By simple calculation, $l_q^2=0.02,{\tilde{l}}_q^2=0.090,$$L_q^2=0.6957,R_q^2=0.4,{\tilde{h}}_q^2=1,H_p^2=3$ for any $q=1,2$ and $\overline{\lambda }=29.02$. In (8), select ${\gamma }_1=11.0,{\gamma }_2=6.0,{\lambda }_1=8.40,{\lambda }_2=15.19,\alpha =15.0,\beta =15.5,{\epsilon }_1=0.7,{\epsilon }_2=1.1$. Thus,

$$\begin{array}{c}8.34=2H_1^2{|a_1|}_2<{\lambda }_p=8.40,\end{array}$$

$$\begin{array}{c}15.18=2H_2^2{|a_2|}_2<{\lambda }_p=15.19,\end{array}$$

$$\begin{array}{c}{\displaystyle 10.28=\sum _{q=1}^2(H_p^2{\tilde{l}}_q^2|b_{1q}{|}_2+2H_p^2{R}_q^2|c_{1q}{|}_2)<{\gamma }_p=11.0,}\end{array}$$

$$\begin{array}{c}{\displaystyle 5.80=\sum _{q=1}^2(H_p^2{\tilde{l}}_q^2|b_{2q}{|}_2+2H_p^2{R}_q^2|c_{2q}{|}_2)<{\gamma }_p=6.0,}\end{array}$$

$$29.02=\tilde{\lambda }<min\{\tilde{\alpha },\tilde{\beta }\}=31.$$

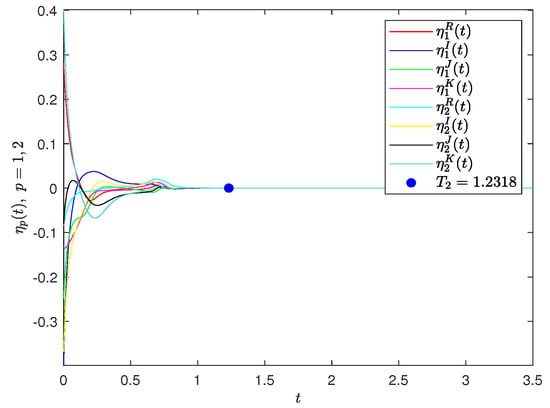
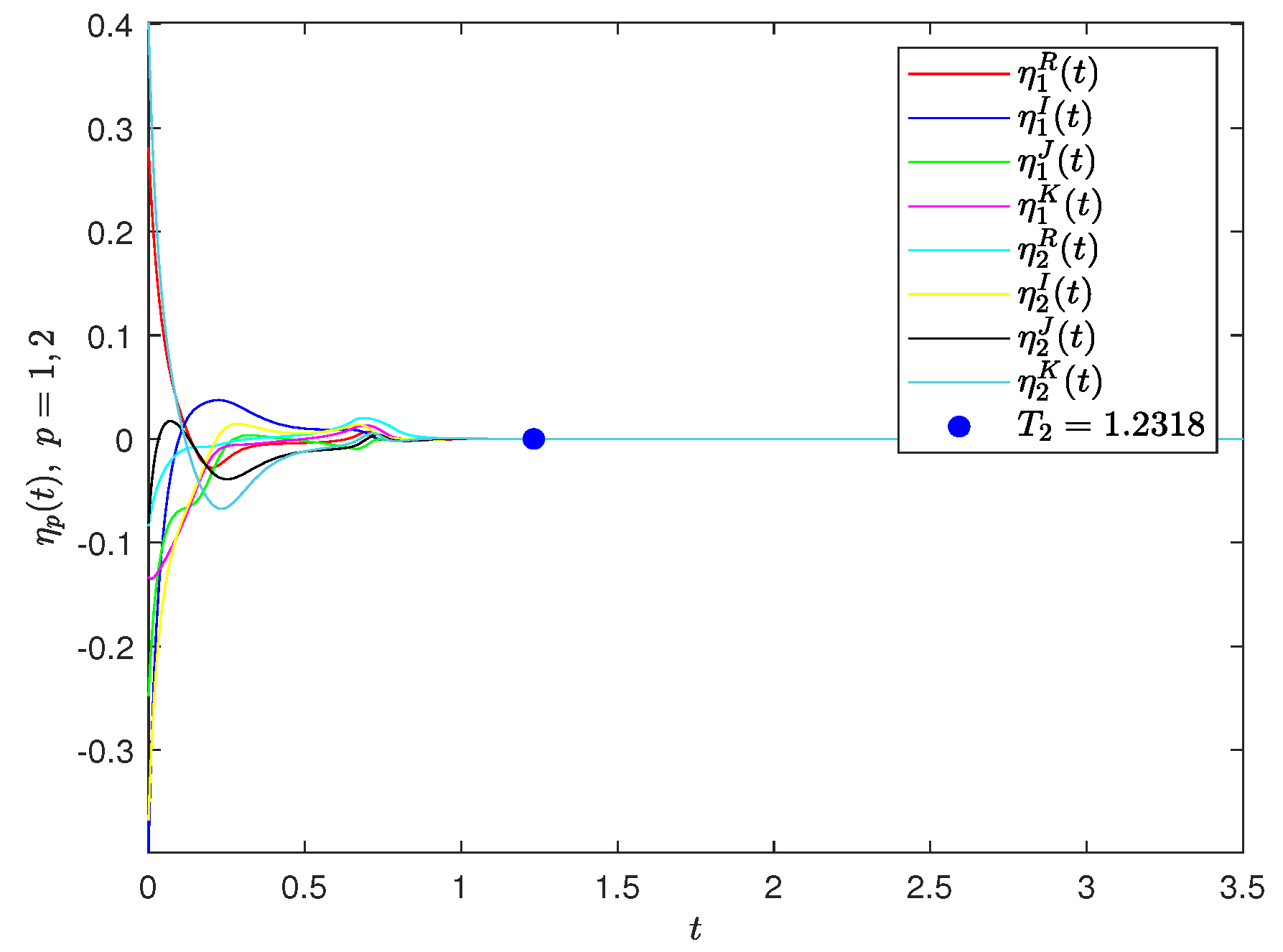
Therefore, CGQVNNs (32) and (33) achieve FIX synchronization based on the controller (24) by using Theorem 2, and the settling time is estimated by ${\widehat{T}}_2=1.2318$. The synchronization result is given in Figure 4.

Figure 4. FIT synchronization error of CGQVNNs (32) and (33) under controller (24).

On the other hand, choose $T_{pet}=0.8$ in (39). Under the above selected parameters, CGQVNNs (32) and (33) reach PET synchronization with $T_{pet}=0.8$ according to Theorem 4, which is shown in Figure 5.

Figure 5. PET synchronization error of CGQVNNs (32) and (33) under controller (39).

6. Conclusions

In this article, the FIT and PET synchronization of CGQVNNs with discontinuous activation functions and generalized time delays have been investigated. In contrast to the previous CGNN models defined in the real-valued or complex-valued domain [34,35,36], the proposed quaternion-valued neural network has stronger storage capacity and is suitable for NNs with discontinuous activation functions. Based on the introduced quaternion-valued symbolic function, two direct control schemes were proposed. At the same time, the criteria of the FIT and the PET synchronization of the CGQVNNs were derived without dividing the quaternion-valued system into real-valued or complex-valued systems. Compared with [24,25], the non-separation method proposed in this paper greatly reduces the computational complexity, and the direct control scheme saves control costs. Finally, two numerical examples were provided to validate the theoretical results.

Considering the control cost, future work will focus on the discussion of FIT or PET synchronization of quaternion-valued NNs by developing a reasonable event-triggered controller, intermittent controller or impulsive controller to reduce the control cost.