Bipartite Consensus Problems for Directed Signed Networks with External Disturbances

Abstract

The intention of this paper is to explore the distributed control issues for directed signed networks in the face of external disturbances under strongly connected topologies. A new class of nonsingular transformations is provided by introducing an output variable, with which the consensus can be equivalently transformed into the output stability regardless of whether the associated signed digraphs are structurally balanced or not. By taking advantage of the standard robust $H_{\infty }$ control theory, the bipartite consensus and state stability results can be built for signed networks under structurally balanced and unbalanced conditions, respectively, in which the desired disturbance rejection performances can also be satisfied. Furthermore, the mathematical expression can be given for the terminal states of signed networks under the influence of external disturbances. In addition, two simulations are presented to verify the correctness of our developed results.

1. Introduction

In the past twenty years, distributed (or coordination) control issues of networked systems are of interest to researchers because of their potential application values in our daily production and life, such as distributed coordination of multi-robots, electric power transmission of smart grids, formation control of aircrafts and so on. Networked systems constitute of multiple interacting agents and interactions among agents, which can complete complex tasks that are difficult for a single agent. If there exist only cooperative interactions among all agents, then these kind of networked systems are termed as unsigned networks (or traditional networks). The main concerns of distributed control of unsigned networks are to design a protocol according to the nearest neighbor information such that all agents can accomplish a common objective under strongly connected topologies [1] and quasi-strongly connected topologies [2], in which consensus is one of the most fundamental problems. Consensus indicates that all agents collaborate with each other such that their terminal states can converge to a common value that may have a relationship with the communication topologies and initial states of agents.

In practice, unsigned networks inevitably suffer from the effect of external disturbances that come from environmental factors, model uncertainties and device aging. The external disturbances may lead to the degradation of performance and even the instability of unsigned networks. Hence, it is necessary to explore how to reduce the detrimental influences of external disturbances and enhance the disturbance rejection abilities of unsigned networks. In the last decade, research in disturbance rejection control has become a focus in the area of distributed control for unsigned networks. Disturbance rejection control problems have been investigated for unsigned networks whose agents are first-order integrator dynamics [3] and second-order integrator dynamics [4], in which the robust $H_{\infty }$ control theory is exploited to analyze the consensus performance of unsigned networks. Moreover, the sufficient conditions have been provided such that all agents can achieve the consensus objective with the desired disturbance rejection performance by employing linear matrix inequality (LMI). Some other robust problems have been investigated by different methods, such as pinning control strategy [5], backstepping control [6], resilient control [7] and disturbance-observer [8]. In addition, disturbance rejection control problems have been generalized to unsigned networks under directed communication topologies and their agents consist of high-order integrator dynamics [9] and general linear dynamics [10]. The distributed control problems have been studied for unsigned networks with communication delays [11,12].

The aforementioned works only concentrate on unsigned networks whose interactions among agents are only cooperative. In actual applications, we can find that both cooperative interactions and antagonistic interactions exist in networked systems due to competition relationships among agents. Different from unsigned networks, these types of network appear from social networks, which contain practical applications in the field of opinion dynamics, political science, economic analysis and crime prevention (see [13,14] for more explanations). For the purposes of describing the interactions among agents, signed digraphs are employed, in which the positive and negative weights of edges can describe the cooperative and antagonistic interactions between any two different agents. In contrast to unsigned networks, these networked systems are termed as signed networks. In the past few years, signed networks have turned into a focus in exploring the distributed control of networked systems. In [15], a fundamental framework has been built for exploring the bipartite consensus of all agents under strongly connected signed digraphs. In order to measure the total difference of all agents, the Laplacian potential has been proposed for signed digraphs in [15]. It is shown that a protocol has been induced from Laplacian potentials such that all agents can achieve the bipartite consensus objective if the structural balance condition is satisfied and otherwise, they can reach the state stability. In this framework, the bipartite consensus problems have further been extended to general signed networks whose topologies and dynamics may be different. In [16], the topology has been considered as quasi-strong connectivity instead of strong connectivity, in which all agents can be divided into two groups: rooted agents and non-rooted agents. The prescribed time interval bipartite consensus problems have been explored in [17], in which the distributed protocol has been designed to ensure the interval bipartite consensus in the prescribed time. With the protocol proposed in [15] being used, all rooted agents can achieve the bipartite consensus objective and all non-rooted agents spread in a interval formed by rooted agents. When the communication topology is switching, the bipartite consensus problems have been studied for signed networks’ nonlinear dynamics [18], in which the sufficient conditions are presented. Furthermore, other collective behaviors have been removed owing to the existence of antagonistic interactions, e.g., modulus consensus under discrete-time dynamics [19] and continuous-time dynamics [20], bipartite formation under nonlinear dynamics [21] and fully distributed control [22], finite-time bipartite consensus with event-triggered method [23] and sliding-mode control [24], bipartite tracking consensus by introducing a virtual leader [25] and pinning control [26], bipartite output consensus with input saturation [27] and nonlinear dynamics [28]. Additionally, bipartite consensus has been studied for signed networks with general linear dynamics [29], input saturation [30], measurement noises [31] and heterogeneous systems [32]. In spite of these plentiful works on signed networks, little work has been produced on the distributed control problems of signed networks in the presence of external disturbances which are inevitable in actual applications.

The goal of this paper is to address the robust consensus problems of directed signed networks under the strongly connected signed digraphs and the effect of external disturbances. The main contributions include the following.

• We introduced an output variable for signed networks. This leads to the consensus issues being converted into the corresponding output stability issues. We focused on the stability instead of consensus, which provide a convenient approach to deal with consensus problems of signed networks. To be specific, for structurally balanced cases, we applied the nonsingular transformation to signed networks, in which a reduced-order system was developed and its output stability reflected the bipartite consensus of signed networks.
• Using the tools of robust $H_{\infty }$ control, we derived the necessary and sufficient conditions to ensure the bipartite consensus (or state stability) objective of directed signed networks under structurally balanced (or unbalanced) conditions. Moreover, the desired disturbance rejection performance was also satisfied.
• When the signed network was structurally balanced, we provided the mathematical expression for the terminal states of all agents. It is worth noting that the terminal states had a relationship with the external disturbances. When considering the structurally unbalanced signed network, the external disturbance had no effect on the terminal values of agents.

The remainder of this paper is arranged as follows. In Section 2, notations and preliminaries used in this paper are provided for signed digraphs. In Section 3, we introduce the problem descriptions for bipartite consensus of signed networks under the influence of external disturbances. We propose the nonsingular transformation for structurally balanced and unbalanced signed networks in Section 4, with which a reduced-order system model can be established. In Section 4, the robust consensus results can be built for signed networks. In Section 5, we give two simulation examples to illustrate the correctness of the developed results. In Section 6, conclusions are provided.

Notations: When considering a positive integer m, we denote ${\mathcal{I}}_n=\{1$, 2, ⋯, $n\}$, $1_n=[1$, 1, ⋯, ${1]}^T\in {\mathbb{R}}^n$, $0_n=[0$, 0, ⋯, ${0]}^T\in {\mathbb{R}}^n$ and $\mathrm{diag}\{d_1$, $d_2$, ⋯, $d_n\}$ as a diagonal matrix whose diagonal elements are $d_1$, $d_2$, ⋯, $d_n$ and non-diagonal elements are zero. When considering $b\in \mathbb{R}$, we denote $\left|a\right|$ as the absolute value of a and $\mathrm{sgn}\left(a\right)$ as the sign of a, i.e.,

$$\mathrm{sgn}\left(a\right)=\left\{\begin{array}{cc}\hfill 1,& a>0\hfill \\ \hfill 0,& a=0\hfill \\ \hfill -1,& a<0.\hfill \end{array}\right.$$

For a vector $x\left(t\right)\in {\mathbb{R}}^n$, we denote $\left|\right|x\left(t\right)\left|\right|$ and ${\left|\right|x\left(t\right)\left|\right|}_2={\left[{\int }_0^{\infty }{x}^T\left(t\right)x\left(t\right)dt\right]}^{1/2}$ as the Euclidean norm and the energy of the vector $x\left(t\right)$, respectively. If ${\left|\right|x\left(t\right)\left|\right|}_2<\infty$ holds, we denote $x\left(t\right)\in {\mathcal{L}}_2$. That is to say, it is a square integral.

2. Preliminaries

A signed network can be modeled as a signed digraph $\mathcal{G}$ that is defined by a triple $\mathcal{G}=(\mathcal{V},\mathcal{E},A)$ with a set $\mathcal{V}=\{v_1,v_2,\cdots ,v_n\}$ of nodes, a set $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}=\{(v_j,v_i):v_i,v_j\in \mathcal{V}\}$ of edges and a matrix $A=\left[a_{ij}\right]\in {\mathbb{R}}^{n\times n}$ adjacency weights. The elements of A satisfy $a_{ij}\ne 0\iff (v_j,v_i)\in \mathcal{E}$ and $a_{ij}=0$, otherwise. The edge $(v_j,v_i)$ indicates a directed link from $v_j$ to $v_i$. That is to say, $v_j$ can send information to $v_j$ and $v_j$ is termed as a neighbor of $v_i$. Moreover, all neighbors of $v_i$ can be denoted as $N\left(i\right)=\{v_j:(v_j,v_i)\in \mathcal{E}\}$. We suppose that the signed digraph $\mathcal{G}$ does not have self-loops, i.e., $a_{ii}=0$, $\forall i\in {\mathcal{I}}_n$. Motivated by [15], we can define the Laplacian matrix L of $\mathcal{G}$ as

$$L=\left[l_{ij}\right]\mathrm{with}{l}_{ij}=\left\{\begin{array}{c}\sum _{h=1}^n\left|a_{ih}\right|,i=h\\ -a_{ij},i\ne j.\end{array}\right.$$

(1)

From [15,16], we can know that the structural balance plays an important role in exploring distributed control problems of signed networks. We give the definition of structural balance in the following.

Definition 1.

A signed digraph $\mathcal{G}$ is said to be structurally balanced if all nodes $\{v_1$, $v_2$, ⋯, $v_n\}$ can be separated into two subsets ${\mathcal{V}}_1$ and ${\mathcal{V}}_2$ satisfying ${\mathcal{V}}_1\cup {\mathcal{V}}_2=\mathcal{V}$ and ${\mathcal{V}}_1\cap {\mathcal{V}}_2=\varnothing$, where $a_{ij}\ge 0$ when $v_i$, $v_j\in {\mathcal{V}}_1$ or $v_i$, $v_j\in {\mathcal{V}}_2$ and $a_{ij}\le 0$ when $v_i\in {\mathcal{V}}_1$, $v_j\in {\mathcal{V}}_2$ or $v_i\in {\mathcal{V}}_2$, $v_j\in {\mathcal{V}}_1$. Otherwise, $\mathcal{G}$ is called structurally unbalanced.

For $\mathcal{G}$, we can induce a corresponding unsigned digraph $\overline{\mathcal{G}}=(\mathcal{V},\mathcal{E},\overline{A})$, in which $\overline{A}=\left|A\right|=\left[\right|a_{ij}\left|\right]\in {\mathbb{R}}^{n\times n}$ holds. According to (1), its Laplacian matrix $\overline{L}$ is provided by

$$\overline{L}=\left[{\overline{l}}_{ij}\right]\mathrm{with}{\overline{l}}_{ij}=\left\{\begin{array}{c}\sum _{h=1}^n\left|a_{ih}\right|,i=h\\ -|a_{ij}|,i\ne j.\end{array}\right.$$

Define a set of all gauge transformations as

$${\mathcal{D}}_n=\{D_n=\mathrm{diag}\{{\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_n\}:{\sigma }_i\in \{-1,1\},i\in {\mathcal{I}}_n\}.$$

It follows from Lemma 1 of [15] that when $\mathcal{G}$ meets a structurally balanced condition, a gauge transformation $D_n$ can be selected from ${\mathcal{D}}_n$ to ensure $\overline{L}=D_{n}L{D}_n$. In addition, removing the ith row and ith column of $D_n$ can construct a new matrix $D_n^i\in {\mathbb{R}}^{(n-1)\times (n-1)}$, $\forall i\in {\mathcal{I}}_n$.

A directed path $\mathcal{P}$ from the initial node $v_i$ to the terminal node $v_j$ is a sequence of edges in $\mathcal{G}$, i.e., $\mathcal{P}=\{(v_i,v_{m_1})$, $(v_{m_1},v_{m_2})$, ⋯, $(v_{m_{k-1}},v_j)\}$ with distinct nodes $v_i$, $v_{m_1}$, $v_{m_2}$, ⋯, $v_{m_{k-1}}$ and $v_j$. The signed digraph $\mathcal{G}$ is strongly connected if there exists a directed path between every different pair of nodes. We assume that the eigenvalues of L are ${\lambda }_1$, ${\lambda }_2$, ⋯, ${\lambda }_n$. If $\mathcal{G}$ is strongly connected, the eigenvalues ${\lambda }_1$, ${\lambda }_2$, ⋯, ${\lambda }_n$ satisfy the following results [15].

(R1)

L has a zero eigenvalue ${\lambda }_1=0$ and $n-1$ eigenvalues ${\lambda }_2$, ${\lambda }_3$, ⋯, ${\lambda }_n$ with positive real parts if and only if $\mathcal{G}$ is structurally balanced.

(R2)

All eigenvalues ${\lambda }_1$, ${\lambda }_2$, ⋯, ${\lambda }_n$ have positive real parts if and only if $\mathcal{G}$ is structurally unbalanced.

3. Problem Description

In this paper, we consider a signed network that consist of n agents, and the communication among agents can be denoted by a signed digraph $\mathcal{G}$ with n nodes. The dynamics of the ith node can be considered as a first-order integrator as follows:

$${\dot{x}}_i\left(t\right)=u_i\left(t\right)+{\omega }_i\left(t\right),\forall i\in {\mathcal{I}}_n$$

(2)

where $x_i\left(t\right)\in \mathbb{R}$ and $u_i\left(t\right)\in \mathbb{R}$ are the information state and control input of the ith node at the time t, and ${\omega }_i\left(t\right)\in \mathbb{R}$ represents the external disturbance suffered by the ith node at the time t. According to [15], the following distributed control protocol is provided by

$$u_i\left(t\right)=\sum _{v_j\in N\left(i\right)}{a}_{ij}[x_j\left(t\right)-\mathrm{sgn}\left(a_{ij}\right)x_i\left(t\right)],\forall i\in {\mathcal{I}}_n.$$

(3)

Define $x\left(t\right)=[x_1\left(t\right)$, $x_2\left(t\right)$, ⋯, $x_n{\left(t\right)]}^T\in {\mathbb{R}}^n$, $u\left(t\right)=[u_1\left(t\right)$, $u_2\left(t\right)$, ⋯, $u_n{\left(t\right)]}^T\in {\mathbb{R}}^n$ and $\omega \left(t\right)=[{\omega }_1\left(t\right)$, ${\omega }_2\left(t\right)$, ⋯, ${\omega }_n{\left(t\right)]}^T\in {\mathbb{R}}^n$ as the state vector, control input vector and external disturbance vector, respectively. By employing the Laplacian matrix L, (2) and (3) can be rewritten as

$$\dot{x}\left(t\right)=-Lx\left(t\right)+\omega \left(t\right).$$

(4)

We say that the bipartite consensus and state stability objective can be achieved for the dynamic system (4) if the following results

(1)

$$\underset{t\to \infty }{lim}\left(|x_i\left(t\right)|-|x_j\left(t\right)|\right)=0,\forall i,j\in {\mathcal{I}}_n;$$

(5)

(2)

$$\underset{t\to \infty }{lim}{x}_i\left(t\right)=0,\forall i\in {\mathcal{I}}_n.$$

(6)

hold, respectively, for any initial state $x_i\left(0\right)$, $\forall i\in {\mathcal{I}}_n$.

In the following, an assumption is provided for the external disturbance $\omega \left(t\right)$.

Assumption 1.

The external disturbance $\omega \left(t\right)$ satisfies the following two conditions:

(C1) 

${\int }_0^{\infty }\omega \left(t\right)dt$ is absolutely convergent;

(C2) 

there exists a constant vector $y\in {\mathbb{R}}^n$ such that

$${\int }_0^{\infty }\omega \left(t\right)dt=y.$$

(7)

Remark 1.

We should point out that Assumption 1 can guarantee that the energy of $\omega \left(t\right)$ is bounded (i.e., $\omega \left(t\right)\in {\mathcal{L}}_2$). However, when the energy of $\omega \left(t\right)$ is bounded, $\omega \left(t\right)$ may not satisfy Assumption 1. These kind of disturbances are relatively common in our daily life, such as a gust of wind, unmodeled dynamics and interfering electromagnetic pulses.

When the external disturbance $\omega \left(t\right)$ does not exist (i.e., $\omega \left(t\right)=0_n$), the system (4) turns into

$$\dot{x}\left(t\right)=-Lx\left(t\right).$$

(8)

For the sake of the following analyses, we provide the consensus results of the system (8) in the following proposition (see [15] for more details).

Proposition 1.

Consider the system (8) whose communication topology is a strongly connected signed digraph $\mathcal{G}$. Then,

(1) 

the bipartite consensus can be achieved for the system (8) if and only if $\mathcal{G}$ is structurally balanced. Moreover, the terminal value $x(\infty )$ is given by

$$x(\infty )=\left({\nu }^{T}x\left(0\right)\right)D_n{1}_n$$

(9)

where $D_n{1}_n$ and ν are the right and left eigenvector of L associated with eigenvalue zero, respectively, and ${\nu }^T{D}_n{1}_n=1$.

(2) 

the state stability can be reached for the system (8) if and only if $\mathcal{G}$ is structurally unbalanced.

From Proposition 1, we can realize the fundamental consensus results of signed networks without external disturbances. It is clear to see that Proposition 1 may be ineffective once there exist external disturbances in signed networks. Obviously, the existence of external disturbances may generate effects on the performance and the terminal value of the system (4). It is reasonable and necessary to require the system (4) to possess the resilience ability when it suffers from the external disturbance $\omega \left(t\right)$. Motivated by these discussions, we investigate how to measure the resilience ability of system (4) subject to $\omega \left(t\right)$ satisfying energy bounded condition (i.e., $\omega \left(t\right)\in {\mathcal{L}}_2$) and further explore the mathematical expression for the terminal value of the system (4).

3.1. Nonsingular Transformation

From the definitions of bipartite consensus (5) and asymptotic stability (i.e., ${lim}_{t\to \infty }{x}_i\left(t\right)=0$ for $\forall i\in {\mathcal{I}}_n$), we can easily see that there exist essential differences between them. According to [3,6,7,9], the stability plays a crucial role in the robust consensus convergence analyses of unsigned networks. Toward this end, we aim to introduce a class of nonsingular transformations for signed networks in this section, which is convenient for the convergence analyses of signed networks.

3.2. Structurally Balanced Case

When $\mathcal{G}$ is structurally balanced, it is imperative to obtain $D_n=\mathrm{diag}\{{\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_n\}\in {\mathcal{D}}_n$ that satisfies $\overline{L}=D_{n}L{D}_n$. For some $j\in {\mathcal{I}}_n$, we introduce a series of states as

$$z_i\left(t\right)=\left\{\begin{array}{cc}{\sigma }_i{x}_i\left(t\right)-{\sigma }_j{x}_j\left(t\right),\hfill & \hfill i<j\\ {\sigma }_{i+1}{x}_{i+1}\left(t\right)-{\sigma }_j{x}_j\left(t\right),\hfill & \hfill i\ge j\end{array}\right.\mathrm{for} \mathrm{each}i\in {\mathcal{I}}_{n-1}.$$

(10)

From (10), we can easily see that the bipartite consensus objective (5) is identical to

$$\underset{t\to \infty }{lim}{z}_i\left(t\right)=0\mathrm{for} \mathrm{each}i\in {\mathcal{I}}_{n-1}.$$

Let us denote $z\left(t\right)={[z_1\left(t\right),z_2\left(t\right),\cdots ,z_{n-1}\left(t\right)]}^T\in {\mathbb{R}}^{n-1}$. With (4), we can induce the following system

$$\left\{\begin{array}{c}\dot{x}\left(t\right)=-Lx\left(t\right)+\omega \left(t\right)\hfill \\ z\left(t\right)=Ex\left(t\right)\hfill \end{array}\right.$$

(11)

where $E\in {\mathbb{R}}^{(n-1)\times n}$ and

$$E=\left\{\begin{array}{cc}[-{\sigma }_1{1}_{n-1},D_n^1],\hfill & j=1\hfill \\ [d_1,\cdots ,d_{j-1},-{\sigma }_j{1}_{n-1},d_j,\cdots ,d_{n-1}],\hfill & 1<j<n\hfill \\ [D_n^n,-{\sigma }_n{1}_{n-1}],\hfill & j=n\hfill \end{array}\right.$$

in which $d_i$, $\forall i\in {\mathcal{I}}_{n-1}$, is the ith column of the matrix $D_n^j$. Thus, the bipartite consensus of the system (4) can be considered as an output stability problem of the system (11) [i.e., ${lim}_{t\to \infty }z\left(t\right)=0_{n-1}$]. For the system (11), we can calculate its transfer function matrix $T_{z\omega }\left(s\right)=E{(sI+L)}^{-1}$ that plays an important role in analysing the consensus performance of the system (11) with respect to the external disturbance $\omega \left(t\right)$.

Since the signed digraph $\mathcal{G}$ is both strongly connected and structurally balanced, there exists a gauge transformation $D_n\in {\mathcal{D}}_n$ such that $\overline{L}=D_{n}L{D}_n$, $L{D}_n{1}_n=0_n$ and $E{D}_n{1}_n=0_{n-1}$ hold. It leads to

$$\left[\begin{array}{c}E\\ EL\\ E{L}^2\\ ⋮\\ E{L}^{n-1}\end{array}\right]D_n{1}_n=0_{n(n-1)}\in {\mathbb{R}}^{n(n-1)}.$$

Hence, we can further deduce

$$\mathrm{rank}\left(\left[\begin{array}{c}E\\ EL\\ E{L}^2\\ ⋮\\ E{L}^{n-1}\end{array}\right]\right)<n$$

that indicates the unobservability of the system (11). However, we should point out that the transfer function matrix $T_{z\omega }\left(s\right)$ reflects the relationship between the external disturbance $\omega \left(t\right)$ and the state variables of (11) that are both controllable and observable. In the following, we aim to select all controllable and observable state variables of (11). Toward this end, we introduce two matrices $F\in {\mathbb{R}}^{n\times (n-1)}$ and $C\in {\mathbb{R}}^{1\times n}$ as follows:

$$F=\left\{\begin{array}{cc}{[0_{n-1},D_n^1]}^T,\hfill & j=1\hfill \\ {[d_1,\cdots ,d_{j-1},0_{n-1},d_j,\cdots ,d_{n-1}]}^T,\hfill & 1<j<n\hfill \\ [D_n^n,0_{n-1}],\hfill & j=n\hfill \end{array}\right.$$

and

$$C=\left\{\begin{array}{cc}[d_j^T,0],\hfill & j<n\hfill \\ [0,0,\cdots ,0,1],\hfill & j=n\hfill \end{array}\right..$$

Let us denote $Q={\left[\begin{array}{cc}{C}^T& E^T\end{array}\right]}^T\in {\mathbb{R}}^{n\times n}$. It can be easily verified that the inverse matrix of Q is provided by $Q^{-1}=\left[\begin{array}{cc}{D}_n{1}_n& F\end{array}\right]$, where $C{D}_n{1}_n=1$, $CF=0_{n-1}^T$, $E{D}_n{1}_n=0_{n-1}$, $EF=I_{n-1}$ and $D_n{1}_{n}C+FE=I_n$. We introduce an auxiliary vector as follows

$$\tilde{x}=x-D_n{1}_{n}C{\int }_0^t\omega \left(\tau \right)d\tau .$$

(12)

Through (11) and (12), we have

$$\left\{\begin{array}{c}\dot{\tilde{x}}\left(t\right)=-L\tilde{x}\left(t\right)+(I_n-D_n{1}_{n}C)\omega \left(t\right)\hfill \\ z\left(t\right)=E\tilde{x}\left(t\right)\hfill \end{array}\right.$$

(13)

in which $L{D}_n{1}_n=0_n$ and $E{D}_n{1}_n=0_{n-1}$ are employed. We define $\widehat{x}\left(t\right)=Q\tilde{x}\left(t\right)$ and $\beta \left(t\right)=C\tilde{x}\left(t\right)$, and can further derive

$$\widehat{x}\left(t\right)=Q\tilde{x}\left(t\right)=\left[\begin{array}{c}C\\ E\end{array}\right]\tilde{x}\left(t\right)=\left[\begin{array}{c}\beta \left(t\right)\\ z\left(t\right)\end{array}\right].$$

(14)

From (13) and (14), it follows

$$\begin{array}{cc}\hfill \left[\begin{array}{c}\dot{\beta }\left(t\right)\\ \dot{z}\left(t\right)\end{array}\right]& =-QL{Q}^{-1}\left[\begin{array}{c}\beta \left(t\right)\\ z\left(t\right)\end{array}\right]+Q(I_n-D_n{1}_{n}C)\omega \left(t\right)\hfill \\ & =-\left[\begin{array}{cc}CL{D}_n{1}_n& CLF\\ EL{D}_n{1}_n& ELF\end{array}\right]\left[\begin{array}{c}\beta \left(t\right)\\ z\left(t\right)\end{array}\right]+\left[\begin{array}{c}0\\ E\omega \left(t\right)\end{array}\right]\hfill \\ & =-\left[\begin{array}{cc}0& CLF\\ 0_{n-1}& ELF\end{array}\right]\left[\begin{array}{c}\beta \left(t\right)\\ z\left(t\right)\end{array}\right]+\left[\begin{array}{c}0\\ E\omega \left(t\right)\end{array}\right]\hfill \end{array}$$

(15)

in which $L{D}_n{1}_n=0_n$ and $E{D}_n{1}_n=0_{n-1}$ are inserted. Since the signed digraph $\mathcal{G}$ is strongly connected and structurally balanced, it follows from Lemma 1 of [15] that the Laplacian matrix L has a zero eigenvalue and $n-1$ eigenvalues with positive real parts. This, together with (15), guarantees that all eigenvalues of $ELF$ contain positive real parts and $-ELF$ is Hurwitz stable. Based on (15), we can induce two subsystems as

$$\dot{\beta }\left(t\right)=-CLFz\left(t\right)$$

(16)

and

$$\dot{z}\left(t\right)=-ELFz\left(t\right)+E\omega \left(t\right).$$

(17)

It can be easily seen from (16) that the convergence of $\beta \left(t\right)$ is only dependent on $z\left(t\right)$ and has no relationship with $\omega \left(t\right)$. For the subsystem (17), we can calculate

$$\mathrm{rank}\left(\left[\begin{array}{cccc}E& -ELFE& \cdots & {(-ELF)}^{n-2}E\end{array}\right]\right)=n-1$$

and

$$\mathrm{rank}\left(\left[\begin{array}{c}{I}_{n-1}\\ -ELF\\ ⋮\\ {(-ELF)}^{n-2}\end{array}\right]\right)=n-1,$$

which implies that the subsystem (17) is both controllable and observable. Moreover, the transfer function matrix $T_{z\omega }\left(s\right)$ of the subsystem (17) satisfies

$$\begin{array}{cc}\hfill T_{z\omega }\left(s\right)& ={(s{I}_{n-1}+ELF)}^{-1}E\hfill \\ \hfill & ={(s{I}_{n-1}+ELF)}^{-1}E(I_n-D_n{1}_{n}C)\hfill \\ \hfill & =E{(s{I}_n+LFE)}^{-1}(I_n-D_n{1}_{n}C)\hfill \\ \hfill & =E{\left[s{I}_n+L(D_n{1}_{n}C+FE)\right]}^{-1}(I_n-D_n{1}_{n}C)\hfill \\ \hfill & =E{(s{I}_n+L)}^{-1}(I_n-D_n{1}_{n}C)\hfill \\ \hfill & =E{(s{I}_n+L)}^{-1}\hfill \end{array}$$

in which we use $E{D}_n{1}_n=0_{n-1}$, $L{D}_n{1}_n=0_n$ and $D_n{1}_{n}C+FE=I_n$. From the above discussions, we can realize that the system (4) and its subsystem (17) have the same transfer function matrix. Therefore, we can investigate the consensus performance of the system (4) by considering its subsystem (17), which provides a method to deal with bipartite consensus problems from the viewpoint of stability.

3.3. Structurally Unbalanced Case

When $\mathcal{G}$ is structurally unbalanced, we directly give an output vector $z\left(t\right)=x\left(t\right)$. Thus,

$$\left\{\begin{array}{c}\dot{x}\left(t\right)=-Lx\left(t\right)+\omega \left(t\right)\hfill \\ z\left(t\right)=x\left(t\right).\hfill \end{array}\right.$$

(18)

Due to the structural unbalance of $\mathcal{G}$, it follows from the result R2 that all eigenvalues ${\lambda }_1$, ${\lambda }_2$, ⋯, ${\lambda }_n$ of L have positive real parts and $\mathrm{rank}\left(L\right)=n$ holds. With $\mathrm{rank}\left(L\right)=n$, we can calculate

$$\mathrm{rank}\left(\left[\begin{array}{cccc}{I}_n& -L& \cdots & {(-L)}^{n-1}\end{array}\right]\right)=n$$

(19)

and

$$\mathrm{rank}\left(\left[\begin{array}{c}{I}_n\\ -L\\ -L^2\\ ⋮\\ -L^{n-1}\end{array}\right]\right)=n.$$

(20)

From (19) and (20), we can realize that the system (18) is not only controllable but also observable.

4. Main Results

In this section, we investigate the convergence performance of directed signed networks in the presence of external disturbances, in which a class of energy-bounded external disturbances is considered. In the following, an induced transfer function matrix norm can be given by

$$\left|\right|T_{z\omega }{\left(s\right)\left|\right|}_{2-2}=\underset{{\left|\right|\omega \left(t\right)\left|\right|}_2\le 1}{sup}{\left|\right|z\left(t\right)\left|\right|}_2$$

It is worthwhile noticing that the induced norm $\left|\right|T_{z\omega }\left(s\right){\left|\right|}_{2-2}$ can also be considered as the $H_{\infty }$ norm of $T_{z\omega }\left(s\right)$. It follows from [33] that

$$\left|\right|T_{z\omega }\left(s\right){\left|\right|}_{2-2}=\underset{\omega \left(t\right)\ne 0_n,\omega \left(t\right)\in {\mathcal{L}}_2}{sup}\frac{{\left|\right|z\left(t\right)\left|\right|}_2}{{\left|\right|\omega \left(t\right)\left|\right|}_2}.$$

(21)

Based on (21), we can further induce ${\left|\right|z\left(t\right)\left|\right|}_2\le \left|\right|T_{z\omega }{\left(s\right)\left|\right|}_{2-2}{\left|\right|\omega \left(t\right)\left|\right|}_2$, which denotes that $\left|\right|T_{z\omega }\left(s\right){\left|\right|}_{2-2}$ can be employed to measure the resilience performance of the signed network (11) or (18) subject to $\omega \left(t\right)\in {\mathcal{L}}_2$. That is to say, by considering the external disturbance $\omega \left(t\right)\in {\mathcal{L}}_2$, we can minimize its detrimental effect on the energy of the output signal $z\left(t\right)$ through investigating $\left|\right|T_{z\omega }\left(s\right){\left|\right|}_{2-2}$.

The following theorem can propose a method to identify whether $\left|\right|T_{z\omega }\left(s\right){\left|\right|}_{2-2}$ satisfies a prescribed performance index or not.

Theorem 1.

Consider the system (4) under a strongly connected signed digraph $\mathcal{G}$, and let the external disturbance $\omega \left(t\right)$ satisfy $\omega \left(t\right)\in {\mathcal{L}}_2$. For a given performance index $\gamma >0$, the following results hold.

(1) 

When $\mathcal{G}$ is structurally balanced, the bipartite consensus objective (5) holds with $\left|\right|T_{z\omega }\left(s\right){\left|\right|}_{2-2}<\gamma$ if and only if there exists a positive definite matrix $P\in {\mathbb{R}}^{(n-1)\times (n-1)}$ satisfying the following matrix inequality:

$$-F^T{L}^T{E}^{T}P-PELF+\frac{1}{{\gamma }^2}PE{E}^{T}P+I_{n-1}<0.$$

(22)

In particular, if the external disturbance $\omega \left(t\right)$ satisfies Assumption 1, then for arbitrary initial state $x\left(0\right)\in {\mathbb{R}}^n$, the terminal value of the system (4) is provided by

$$x(\infty )={\nu }^T\left(x\left(0\right)+y\right)D_n{1}_n$$

(23)

where $D_n{1}_n$ and ν are the right and left eigenvector of L associated with the zero eigenvalue, respectively, and $D_n{1}_n$ and ν satisfy ${\nu }^T{D}_n{1}_n=1$.

(2) 

When $\mathcal{G}$ is structurally unbalanced, the state stability objective (6) holds with $\left|\right|T_{z\omega }\left(s\right){\left|\right|}_{2-2}<\gamma$ if and only if there exists a positive definite matrix $P\in {\mathbb{R}}^{n\times n}$ satisfying the following matrix inequality:

$$-L^{T}P-PL+\frac{1}{{\gamma }^2}{P}^{T}P+I_n<0.$$

(24)

Proof. 

(1) Sufficiency: The proof of sufficiency is divided into the following two steps.

Step 1. We first give the proof of the system (4) achieving the bipartite consensus objective (5). On one hand, owing to all eigenvalues of $ELF$ with positive real parts, we realize that the matrix $-ELF$ is Hurwitz stable. On the other hand, it is important to obtain ${lim}_{t\to \infty }\omega \left(t\right)=0_n$ from $\omega \left(t\right)\in {\mathcal{L}}_2$. This, together with input–to–state stability (ISS), ensures the asymptotic stability of the reduced-order system (17) (i.e., ${lim}_{t\to \infty }z\left(t\right)=0_{n-1}$). Based on (10), we directly develop that the system (4) can accomplish the bipartite consensus objective (5).

Step 2. We explore how to ensure the desired performance $\left|\right|T_{z\omega }\left(s\right){\left|\right|}_{2-2}<\gamma$ under the condition (22). For the matrix inequality (22), we can select a parameter $0<\delta <1$ to guarantee the following matrix inequality:

$$-F^T{L}^T{E}^{T}P-PELF+\frac{1}{{\gamma }^2(1-\delta )}PE{E}^{T}P+I_{n-1}<0.$$

(25)

Using Schur’s complement formula with (25) yields

$$\begin{array}{cc}\hfill & \left[\begin{array}{c}{I}_{n-1}\\ {\mathbf{0}}^T\end{array}\right]\left[\begin{array}{cc}{I}_{n-1}& \mathbf{0}\end{array}\right]+\left[\begin{array}{cc}-F^T{L}^T{E}^{T}P-PELF& PE\\ E^{T}P& -{\gamma }^2(1-\delta )I_n\end{array}\right]<0\hfill \end{array}$$

(26)

where $\mathbf{0}$ is zero matrix whose all elements are zero and its dimension is $(n-1)\times n$. For (26), left multiplying by $\left[\begin{array}{cc}{z}^T\left(t\right)& {\omega }^T\left(t\right)\end{array}\right]$ and right multiplying by $\left[\begin{array}{c}z\left(t\right)\\ \omega \left(t\right)\end{array}\right]$ leads to

$$\begin{array}{c}{z}^T\left(t\right)z\left(t\right)+z^T\left(t\right)P\left[-ELFz\left(t\right)+E\omega \left(t\right)\right]+{\left[-ELFz\left(t\right)+E\omega \left(t\right)\right]}^{T}Pz\left(t\right)\\ -{\gamma }^2(1-\delta ){\omega }^T\left(t\right)\omega \left(t\right)<0.\end{array}$$

(27)

A Lyapunov function candidate is designed as follows:

$$V\left(z\right)=z^T\left(t\right)Pz\left(t\right).$$

Taking the derivation of $V\left(z\right)$ along (17) causes

$$\begin{array}{cc}\hfill \dot{V}\left(z\right)& ={\dot{z}}^T\left(t\right)Pz\left(t\right)+z^T\left(t\right)P\dot{z}\left(t\right)\hfill \\ \hfill & ={\left[-ELFz\left(t\right)+E\omega \left(t\right)\right]}^{T}Pz\left(t\right)+z^T\left(t\right)P\left[-ELFz\left(t\right)+E\omega \left(t\right)\right].\hfill \end{array}$$

With (27), we can further deduce

$$\dot{V}\left(z\right)+z^T\left(t\right)z\left(t\right)<{\gamma }^2(1-\delta ){\omega }^T\left(t\right)\omega \left(t\right).$$

(28)

We integrate (28) on a time interval $[0,T_1]$, $T_1>0$, which leads to

$$\begin{array}{cc}\hfill & z^T\left(T_1\right)Pz\left(T_1\right)+{\int }_0^{T_1}{z}^T\left(t\right)z\left(t\right)dt<{\gamma }^2(1-\delta ){\int }_0^{T_1}{\omega }^T\left(t\right)\omega \left(t\right)dt\hfill \end{array}$$

(29)

where we insert the zero-valued initial condition $z\left(0\right)=0_{n-1}$. Now let $T_1\to \infty$, and we can develop ${lim}_{t\to \infty }z\left(t\right)=0_{n-1}$ because of ${lim}_{t\to \infty }\omega \left(t\right)=0_n$ and the Hurwitz stability of $-ELF$. Therefore, we can rewrite (29) as

$${\left|\right|z\left(t\right)\left|\right|}_2^2<{\gamma }^2{(1-\delta )\left|\right|\omega \left(t\right)\left|\right|}_2^2$$

(30)

when $T_1$ goes towards infinity (i.e., $T_1\to \infty$). From (30), we must derive ${\left|\right|z\left(t\right)\left|\right|}_2{<\gamma \left|\right|\omega \left(t\right)\left|\right|}_2$ and $\left|\right|T_{z\omega }\left(s\right){\left|\right|}_{2-2}<\gamma$. Therefore, the bipartite consensus objective (5) is with $\left|\right|T_{z\omega }\left(s\right){\left|\right|}_{2-2}<\gamma$ when $\mathcal{G}$ is structurally balanced.

Necessity: Since the matrix $-ELF$ is Hurwitz stable and $\left|\right|T_{z\omega }\left(s\right){\left|\right|}_{2-2}<\gamma$ holds, we can obtain

$${\gamma }^2{I}_{n-1}-E^T{(-s{I}_{n-1}+F^T{L}^T{E}^T)}^{-1}{(s{I}_{n-1}+ELF)}^{-1}E>0.$$

(31)

From (31), there must exist a sufficiently small real number $\epsilon >0$ such that

$${\gamma }^2{I}_{n-1}-E^T{(-s{I}_{n-1}-F^T{L}^T{E}^T)}^{-1}{M}_{\epsilon }^T{M}_{\epsilon }{(s{I}_{n-1}-ELF)}^{-1}E>0$$

(32)

where $M_{\epsilon }^T=\left[\begin{array}{cc}{I}_{n-1}& \sqrt{\epsilon }{I}_{n-1}\end{array}\right]$. From (32), it follows that $\left|\right|M_{\epsilon }{(s{I}_{n-1}+ELF)}^{-1}E{\left|\right|}_{2-2}<\gamma$. As a consequence, by Corollary 1 of Chapter 3 in [33], we know that there exists a solution $P\ge 0$ such that

$$-F^T{L}^T{E}^{T}P-PELF+\frac{1}{{\gamma }^2}PE{E}^{T}P+I_{n-1}+\epsilon I_{n-1}=0.$$

(33)

Next, we try to explain the solution P is positive definite. If we denote $M_a^T={\left[\begin{array}{cc}\frac{1}{\gamma }PE& M_{\epsilon }^T\end{array}\right]}^T$, then Equation (33) can be rewritten as

$$-F^T{L}^T{E}^{T}P-PELF=-M_a^T{M}_a.$$

(34)

Due to $\mathrm{rank}\left({\left[M_a^T-{\left(ELF\right)}^T{M}_a^T\cdots {{(-ELF)}^{n-2}}^T{M}_a^T\right]}^T\right)=n-1$, we can deduce that the pair $(-ELF,M_a)$ is observable. This, together with the Hurwitz stability of $-ELF$, guarantees that a positive definite matrix $P>0$ exists such that (33) holds from [34]. With $\epsilon I_{n-1}>0$, we can derive that the Riccati inequality (22) has a unique positive solution $P>0$. The proof of necessity is complete.

Next, we explore the terminal value calculation for the dynamic system (4). The solution of dynamic system (4) can be calculated by

$$x\left(t\right)=e^{-Lt}x\left(0\right)+{\int }_0^t{e}^{-L(t-\tau )}\omega \left(\tau \right)d\tau .$$

(35)

With the structural balance and strong connectivity of $\mathcal{G}$, it follows from Proposition 1 that

$$\underset{t\to \infty }{lim}{e}^{-Lt}x\left(0\right)=\nu x\left(0\right)D_n{1}_n$$

(36)

where $D_n{1}_n$ and $\nu$ are the right and left eigenvectors of L associated with the zero eigenvalue and they satisfy ${\nu }^T{D}_n{1}_n=1$. Next, we calculate ${lim}_{t\to \infty }{\int }_0^t{e}^{-L(t-\tau )}\omega \left(\tau \right)d\tau$. There exists an invertible matrix P such that $J=P^{-1}LP$, where J is the Jordan canonical form of L. We thus can obtain

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim}{\int }_0^t{e}^{-L(t-\tau )}\omega \left(\tau \right)d\tau & =\underset{t\to \infty }{lim}{\int }_0^t{e}^{-PJ{P}^{-1}(t-\tau )}\omega \left(\tau \right)d\tau \hfill \\ \hfill & =P\underset{t\to \infty }{lim}{\int }_0^t{e}^{-J(t-\tau )}{P}^{-1}\omega \left(\tau \right)d\tau .\hfill \end{array}$$

(37)

The Jordan canonical form J can be written as $J=\mathrm{diag}\{0$, $J_2$, $J_3$, ⋯, $J_k\}$ with

$$J_i={\left[\begin{array}{ccccc}{\lambda }_i& 1& 0& \cdots & 0\\ 0& {\lambda }_i& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \cdots & ⋮\\ 0& 0& 0& {\lambda }_i& 1\\ 0& 0& 0& 0& {\lambda }_i\end{array}\right]}_{r_i\times r_i}=N_i+{\lambda }_i{I}_{r_i},i\in \{2,3,\cdots ,n\}$$

where $r_i$ is the algebraic multiplicity of ${\lambda }_i$ and $I_{r_i}\in {\mathbb{R}}^{r_i\times r_i}$ is the unit matrix with dimension $r_i$. It is obvious that $r_2+r_3+\cdots +r_k=n-1$ holds. We can further deduce

$$e^{-J(t-\tau )}={\left[\begin{array}{cccc}1& 0& \cdots & 0\\ 0& e^{-J_2(t-\tau )}& \cdots & 0\\ & & \ddots & \\ 0& 0& \cdots & e^{-J_k(t-\tau )}\end{array}\right]}_{n\times n}.$$

For $e^{-J_i(t-\tau )}$, $\forall i\in \{2,3,\cdots ,n\}$, we have

$$\begin{array}{cc}\hfill e^{-J_i(t-\tau )}& =e^{-({\lambda }_i{I}_{r_i}+N_i)(t-\tau )}\hfill \\ & =e^{-{\lambda }_i{I}_{r_i}(t-\tau )}\times e^{-N_i(t-\tau )}\hfill \end{array}$$

(38)

in which we employ $I_{r_i}{N}_i=N_i{I}_{r_i}$ to develop the second equality. With (38), we can obtain

$$\begin{array}{c}{e}^{-J_i(t-\tau )}=e^{-{\lambda }_i(t-\tau )}\times {\left[\begin{array}{ccccc}1& -(t-\tau )& \frac{{(t-\tau )}^2}{2}& \cdots & \frac{{[-(t-\tau )]}^{r_i-1}}{(r-1)!}\\ 0& 1& -(t-\tau )& \cdots & \frac{{[-(t-\tau )]}^{r_i-2}}{(r-2)!}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & -(t-\tau )\\ 0& 0& 0& \cdots & 1\end{array}\right]}_{r_i\times r_i}.\hfill \end{array}$$

Let us denote $P=[p_1$$p_2$⋯$p_n]$ and $P^{-1}=[q_1$$q_2$⋯$q_n{]}^T$, where the vectors $p_1$ and $q_1$ are the right and left eigenvector for the zero eigenvalue of L, respectively. Thus, the Equation (37) can be written as

$$\begin{array}{cc}\hfill & \underset{t\to \infty }{lim}{\int }_0^t{e}^{-L(t-\tau )}\omega \left(\tau \right)d\tau =\left[\begin{array}{cccc}{p}_1& p_2& \cdots & p_n\end{array}\right]\hfill \\ \hfill & \times \underset{t\to \infty }{lim}{\int }_0^t\left[\begin{array}{cccc}1& & & \\ & e^{-J_2(t-\tau )}& & \\ & & \ddots & \\ & & & e^{-J_k(t-\tau )}\end{array}\right]\left[\begin{array}{c}{q}_1^T\\ q_2^T\\ ⋮\\ q_n^T\end{array}\right]\omega \left(\tau \right)d\tau .\hfill \end{array}$$

(39)

Denote ${\eta }_i\left(\tau \right)=q_i^T\omega \left(\tau \right)\in \mathbb{R}$, $\forall i\in {\mathcal{I}}_n$ and $\eta \left(\tau \right)=\left[\begin{array}{cccc}{\eta }_1\left(\tau \right)& {\eta }_2\left(\tau \right)& \cdots & {\eta }_n\left(\tau \right)\end{array}\right]\in {\mathbb{R}}^n$. We introduce a list of vectors ${\xi }_1\left(\tau \right)={\eta }_1\left(\tau \right)$, ${\xi }_2\left(\tau \right)=[$${\eta }_2\left(\tau \right)$${\eta }_3\left(\tau \right)$⋯${\eta }_{r_2}{\left(\tau \right)]}^T\in {\mathbb{R}}^{r_2}$, ${\xi }_3\left(\tau \right)=[$${\eta }_{r_2+1}\left(\tau \right)$${\eta }_{r_2+2}\left(\tau \right)$⋯${\eta }_{r_3}{\left(\tau \right)]}^T\in {\mathbb{R}}^{r_3}$, ⋯, ${\xi }_k\left(\tau \right)=[$${\eta }_{r_{k-1}+1}\left(\tau \right)$${\eta }_{r_{k-1}+2}\left(\tau \right)$⋯${\eta }_n{\left(\tau \right)]}^T\in {\mathbb{R}}^{r_k}$. We denote ${\xi }_1\left(\tau \right)$, ${\xi }_2\left(\tau \right)$, ⋯, and ${\xi }_k\left(\tau \right)$ as a compact form $\xi \left(\tau \right)=[$${\xi }_1^T\left(\tau \right)$, ${\xi }_2^T\left(\tau \right)$, ⋯, ${\xi }_k^T{\left(\tau \right)]}^T\in {\mathbb{R}}^n$ that satisfies $\xi \left(\tau \right)=\eta \left(\tau \right)$. Thus, the Equation (39) is turned into

$$\begin{array}{c}\underset{t\to \infty }{lim}{\int }_0^t{e}^{-L(t-\tau )}\omega \left(\tau \right)d\tau =\left[\begin{array}{cccc}{p}_1& p_2& \cdots & p_n\end{array}\right]\times \underset{t\to \infty }{lim}{\int }_0^t\left[\begin{array}{c}{\xi }_1\left(\tau \right)\\ e^{-J_2(t-\tau )}{\xi }_2\left(\tau \right)\\ ⋮\\ e^{-J_k(t-\tau )}{\xi }_k\left(\tau \right)\end{array}\right]d\tau .\hfill \end{array}$$

Since the matrix $J_i$, $i\in \{2,3,\cdots ,k\}$ is Hurwitz stable, it follows from [34] that there exist two positive constants ${\alpha }_i$ and ${\beta }_i$ such that

$$\parallel e^{-J_i(t-\tau )}\parallel \le {\alpha }_i{e}^{-{\beta }_i(t-\tau )}.$$

(40)

With (40), we can obtain

$$\begin{array}{cc}\hfill ∥{\int }_0^t{e}^{-J_i(t-\tau )}{\xi }_i\left(\tau \right)d\tau ∥& \le {\int }_0^t\parallel e^{-J_i(t-\tau )}{\xi }_i\left(\tau \right)\parallel d\tau \hfill \\ & \le {\int }_0^t{\alpha }_i{e}^{-{\beta }_i(t-\tau )}\parallel {\xi }_i\left(\tau \right)\parallel d\tau \hfill \\ & =\frac{{\alpha }_i{\int }_0^t{e}^{{\beta }_i\tau }\parallel {\xi }_i\left(\tau \right)\parallel d\tau }{e^{{\beta }_{i}t}}\hfill \end{array}$$

Benefitting from L’Hospital’s Rule, we can induce

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim}\frac{{\alpha }_i{\int }_0^t{e}^{{\beta }_i\tau }\parallel {\xi }_i\left(\tau \right)\parallel d\tau }{e^{{\beta }_{i}t}}& =\underset{t\to \infty }{lim}\frac{{\alpha }_i{e}^{{\beta }_{i}t}\parallel {\xi }_i\left(t\right)\parallel }{{\beta }_i{e}^{{\beta }_{i}t}}\hfill \\ & =\underset{t\to \infty }{lim}\frac{{\alpha }_i}{{\beta }_i}\parallel {\xi }_i\left(t\right)\parallel =0\hfill \end{array}$$

which implies

$$\underset{t\to \infty }{lim}{\int }_0^t{e}^{-J_i(t-\tau )}{\xi }_i\left(\tau \right)d\tau =0_{r_i},i\in \{2,3,\cdots ,k\}.$$

Hence, we can develop

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim}{\int }_0^t{e}^{-L(t-\tau )}\omega \left(\tau \right)d\tau & =[p_1,p_2,\cdots ,p_n]\times \underset{t\to \infty }{lim}{\int }_0^t{e}^{-J(t-\tau )}\left[\begin{array}{c}{q}_1^T\\ q_2^T\\ ⋮\\ q_n^T\end{array}\right]\omega \left(\tau \right)d\tau \hfill \\ & =[p_1,p_2,\cdots ,p_n]\times \underset{t\to \infty }{lim}{\int }_0^t\left[\begin{array}{c}{\xi }_1\left(\tau \right)\\ e^{-J_2(t-\tau )}{\xi }_2\left(\tau \right)\\ ⋮\\ e^{-J_k(t-\tau )}{\xi }_k\left(\tau \right)\end{array}\right]d\tau \hfill \\ & =[p_1,p_2,\cdots ,p_n]\left[\begin{array}{c}{\int }_0^t{q}_1^T\omega \left(t\right)d\tau \\ 0_{r_2}\\ ⋮\\ 0_{r_k}\end{array}\right]=p_1{q}_1^{T}y.\hfill \end{array}$$

(41)

Without loss of generality, we select the vectors $p_1$ and $q_1$ as $p_1=D_n{1}_n$ and $q_1=\nu$. The substitution $p_1=D_n{1}_n$ and $q_1=\nu$ into (41) provides

$$\underset{t\to \infty }{lim}{\int }_0^t{e}^{-L(t-\tau )}\omega \left(\tau \right)d\tau ={\nu }^{T}y{D}_n{1}_n.$$

From (35) and (36), we can immediately develop the mathematical expression (23) for the terminal state of the system (4).

(2) All eigenvalues of L have positive real parts and ${lim}_{t\to \infty }{e}^{-Lt}x\left(0\right)=0_n$ holds. Following the proof of structurally balanced case, we can obtain

$$\underset{t\to \infty }{lim}{\int }_0^t{e}^{-L(t-\tau )}\omega \left(\tau \right)d\tau =0_n.$$

Hence, the system (4) can achieve the state stability when $\mathcal{G}$ is structurally unbalanced. We complete this proof. □

Remark 2.

Motivated by Theorem 1, we can see that the robust distributed control problems can be figured out for signed networks under strongly connected communication topologies, with the existing results of unsigned networks [3] to signed networks. A method is provided to identify whether signed networks can accomplish the bipartite consensus (and, respectively, state stability) objective with the desired performance under structurally balanced (and, respectively, unbalanced) signed digraphs, which is different from the proposed method in [9]. Furthermore, when the existing external disturbances satisfy Assumption 1, we can provide a mathematical expression for calculating the terminal states of all agents. We can further observe that when the signed digraph $\mathcal{G}$ is structurally balanced, the external disturbance can affect the terminal value of all agents. However, when the signed digraph $\mathcal{G}$ is structurally unbalanced, the external disturbance has no influence on the terminal value of agents. It generalizes the existing bipartite consensus results of signed networks [15,16].

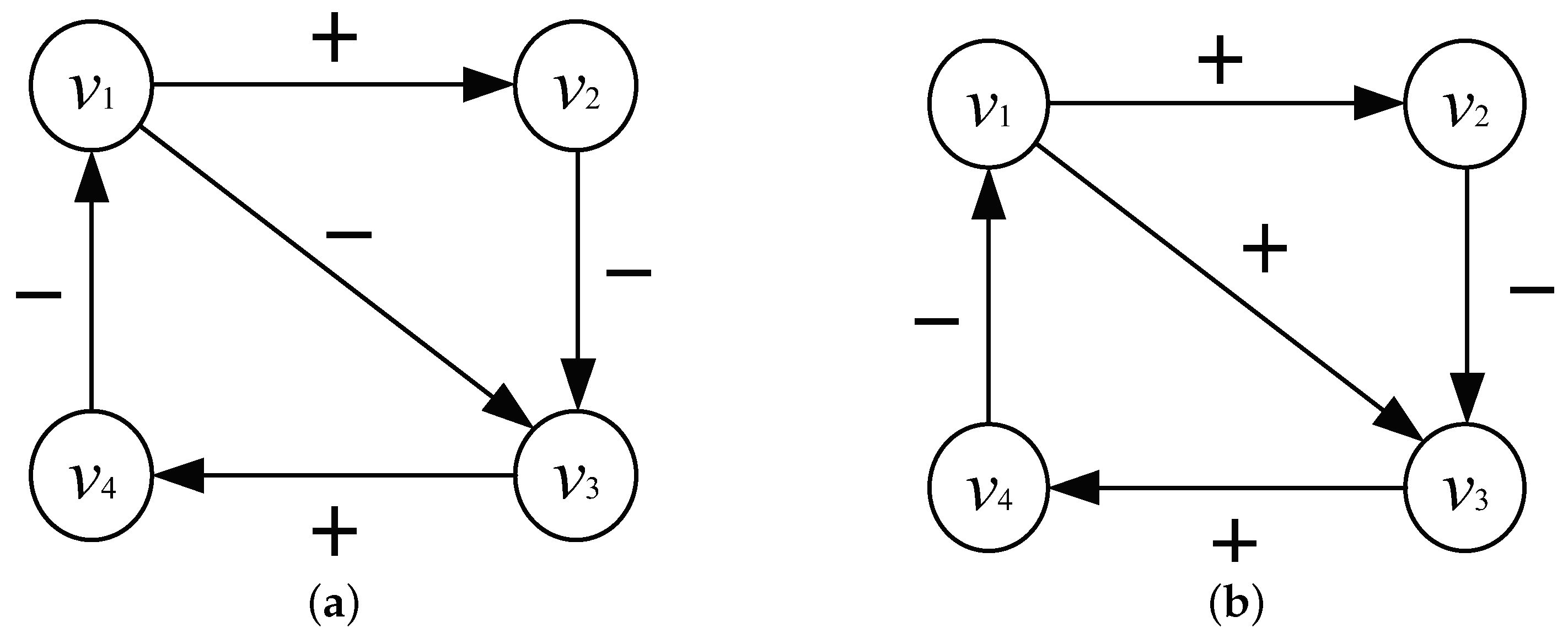
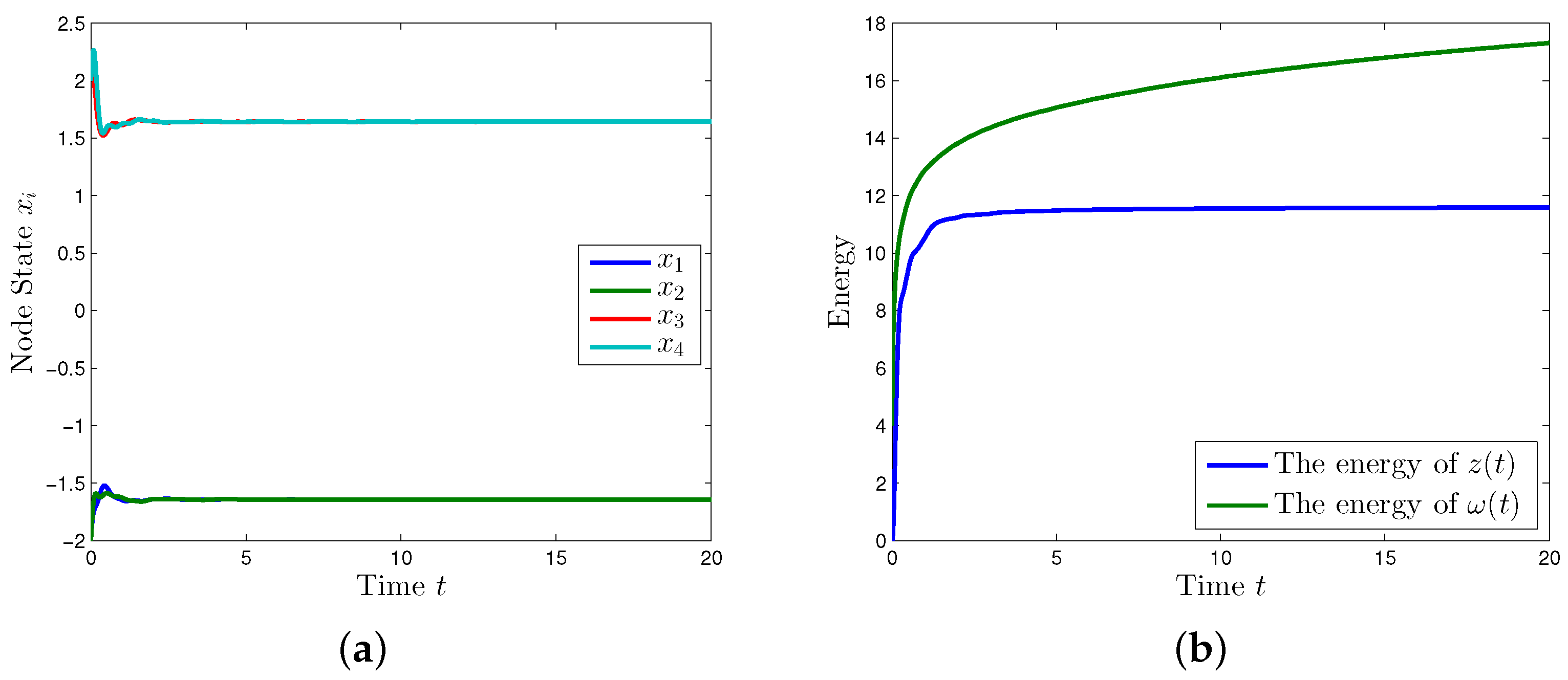
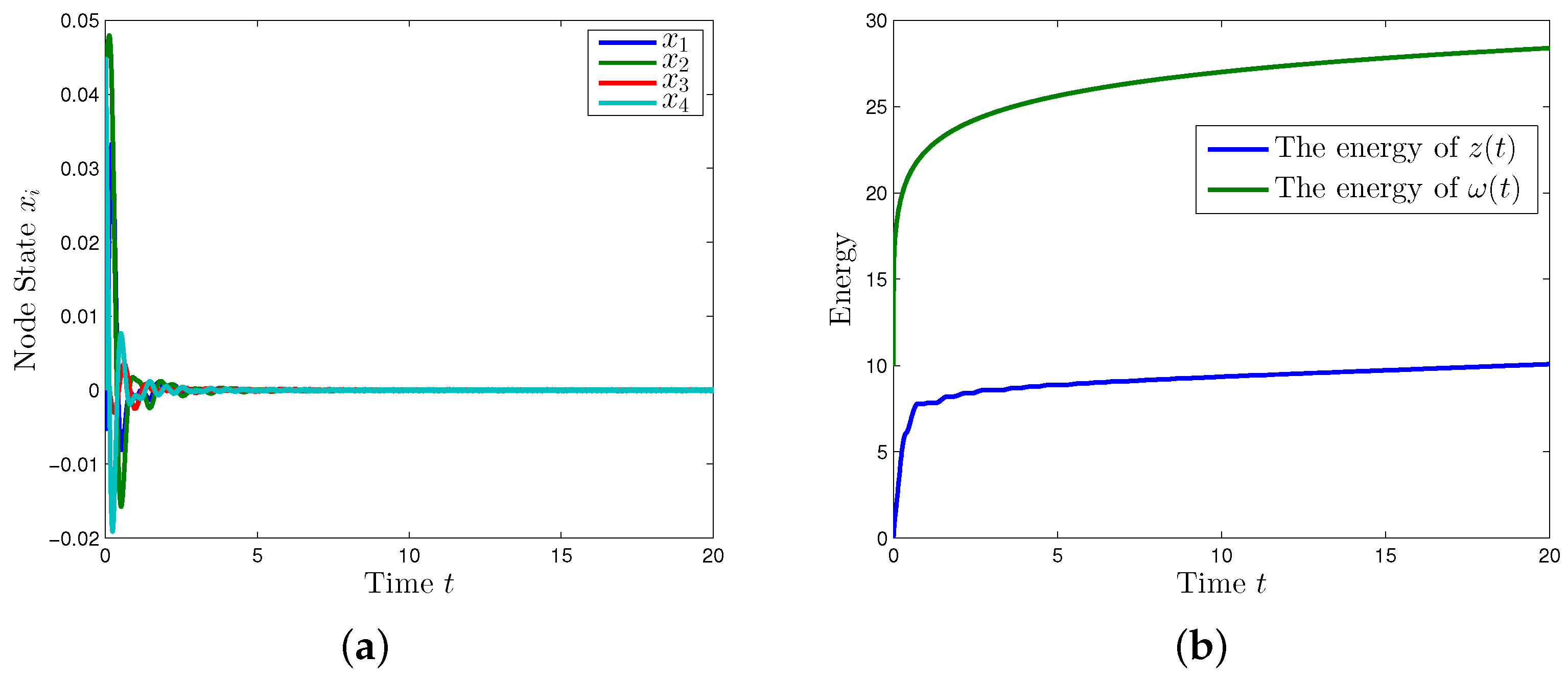
5. Simulation Example

In this section, we introduce two simulation examples to illustrate the validity of the theoretical results. The first example gives the simulation results of signed networks under a structurally balanced case and the second example provides the simulation results of signed networks under a structurally unbalanced case. We consider the system (4) with four nodes labeled from 1 to 4 and their interactions can be described by Figure 1. Moreover, we suppose $\omega \left(t\right)$ existing in the system (4) satisfies

$$\omega \left(t\right)={\left[\begin{array}{cccc}\frac{5}{20t^2+1}cos\left(\pi t\right)& \frac{5}{20t^2+1}cos\left(2\pi t\right)& \frac{5}{20t^2+1}cos\left(3\pi t\right)& \frac{5}{20t^2+1}cos\left(4\pi t\right)\end{array}\right]}^T.$$

It can be easily validated that the external disturbance $\omega \left(t\right)$ is energy bounded (i.e., $\omega \left(t\right)\in {\mathcal{L}}_2$) and ${\int }_0^{\infty }\omega \left(\tau \right)d\tau =[0.8673$$0.4298$$0.2129$${0.1055]}^T$, which satisfies Assumption 1.

Example 1.

We consider the system (4) under a signed digraph ${\mathcal{G}}_1$ in Figure 1. It can easily verify that Figure 1 ${\mathcal{G}}_1$ is both strongly connected and structurally balanced. All nodes can be divided into two groups ${\mathcal{V}}_1=\{v_1,v_2\}$ and ${\mathcal{V}}_2=\{v_3,v_4\}$. The states of $v_1$, $v_2$, $v_3$ and $v_4$ can be denoted by $x_1$, $x_2$, $x_3$ and $x_4$, respectively. Moreover, we can choose the initial state of agents as $x\left(0\right)={\left[\begin{array}{cccc}-2& -2& 2& 2\end{array}\right]}^T$. Without loss of generality, we assume that the desired performance index γ is $\gamma =1$. Note that the desired performance index γ meets if and only if (22) holds. Letting $P=2\times \mathrm{diag}\{1,1,1\}$ and solving the linear matrix inequality (22), we can observ that the weights of edges $(v_4,v_1)$, $(v_1,v_2)$, $(v_2,v_3)$, $(v_3,v_4)$ and $(v_1,v_3)$ are $-5.8226$, $15.7971$, $-11.9896$, $8.6914$ and $-2.7722$, respectively. Since $\omega \left(t\right)$ satisfies Assumption 1, it follows from Theorem 1 that the terminal state of the system (4) is given by

$$x(\infty )={[-1.6434,-1.6434,1.6434,1.6434]}^T.$$

(42)

We plot the state evolution of the system (4) and the energy trajectories of $z\left(t\right)$ and $\omega \left(t\right)$ in Figure 2a and Figure 2b, respectively.

It is obvious from Figure 2a that all nodes can accomplish the bipartite consensus objective (5) whose convergency values satisfy (42). From Figure 2b, it can be found that the consensus performance $\left|\right|T_{z\omega }\left(s\right){\left|\right|}_{2-2}<1$. Obviously, the simulation results of Figure 2a,b are in accordance with Theorem 1.

Example 2.

Consider the communication topology for system (4) described by a signed digraph ${\mathcal{G}}_2$ in Figure 1. Clearly, the signed digraph ${\mathcal{G}}_2$ is both strongly connected and structurally unbalanced, which is different from the signed digraph ${\mathcal{G}}_1$. We pick up the initial state $x\left(0\right)={\left[\begin{array}{cccc}0& 0& 0& 0\end{array}\right]}^T$, the performance index $\gamma =1$ and the positive matrix $P=2\times \mathrm{diag}\{1,1,1,1\}$. We can calculate that the weights of edges $(v_4,v_1)$, $(v_1,v_2)$, $(v_2,v_3)$, $(v_3,v_4)$ and $(v_1,v_3)$ are $-136.3727$, $98.2783$, $-79.2281$, $141.3727$ and $118.6463$, respectively, by taking advantage of the linear matrix inequality (24).

For this case, the simulation of the dynamic behaviors of the system (4) and the stability performance are shown in Figure 3. This figure obviously depicts that the states of nodes converge to zero and the stability performance satisfies $\left|\right|T_{z\omega }\left(s\right){\left|\right|}_{2-2}<1$. We can easily see that the simulation results in Figure 3 are in accordance with Theorem 1.

6. Conclusions

In this paper, we have investigated the distributed robust control problems of directed signed networks in the presence of external disturbances. We have proposed a class of nonsingular transformation for signed networks via introducing an output variable, with which the consensus problems can be equivalently converted into the output stability problems. By employing the tools of robust $H_{\infty }$, we have provided the necessary and sufficient conditions for the bipartite consensus (and, respectively, state stability) of signed networks with the desired disturbance rejection performance under structurally balanced (and, respectively, unbalanced) signed digraphs. Moreover, we have given an alternative approach to calculating the terminal value of signed networks. In addition, two simulation examples have been presented to demonstrate the effectiveness of our derived results.