2. Overview of the Traffic Models with Stochastic Parameters
In [
1,
2] the classification of traffic control strategies is presented in three categories: isolated intersection control; traffic light control through fixed time settings; coordinated and adaptive traffic-dependent signal control. The main development-oriented strategy is the latter, which must take into account the stochastic nature of vehicular traffic flows in an urban environment.
The stochastic behavior of traffic flows was the reason why traffic light parameters were estimated and evaluated by applying simulations in a software environment. An overview of the use of traffic simulation software can be found in [
3,
4]. In [
5], the advantages of a new generation of traffic simulators, which are used for dynamic traffic analysis and the congestion prediction of interconnected road segments, are presented. The use of a traffic simulator in a Web environment is a widely accepted solution that favors its repeated access by a wider audience [
6]. Twenty-nine simulation packages addressing microscopic, macroscopic, mesoscopic, homogeneous, heterogeneous, discrete and continuous flows and traffic models are evaluated in [
7]. Traffic simulation is accepted as a universal tool for evaluating traffic behavior by providing stochastic parameters of traffic flows.
The stochastic components in traffic management are considered through various formal, quantitative and qualitative approaches: fuzzy logic and neural network formalizations [
8,
9,
10]; the application of artificial intelligence solutions [
11]; forecasting traffic flows by time series [
12]; by applying learning technologies [
13,
14]; by supporting meta modeling [
15].
In this work, we aim at the quantification of traffic management defined by analytical models that formalize in a clear way the random nature of the components of traffic behavior. These are mainly the flows that enter a city network and represent management objects. The turning and parking of vehicles inside the roads are also random in nature.
In [
16], the probability of the occurrence of a suitable traffic flow scenario and the delay of a vehicle are calculated. For the set of scenarios, robust timing is estimated that gives the minimum average delay per vehicle for the set of all the traffic scenarios. The optimization problem has a nonlinear objective function that is minimized under a set of linear equalities. The stochastic nature of transport flows is formalized by probabilistic relations for modeling traffic dynamics. In [
17], unknown demands and queuing uncertainty affect the control decisions. In [
18], stochastic travel demands are considered by minimizing the total travel delay over successive time periods. In [
19], a metaheuristic approach is applied to identify a robust plan for fixed-time signals. A robust solution is found among several scenarios of demands. In [
20], a stochastic model predictive control is applied by defining and sequentially solving an optimization problem. It contains chance components from turning and parking vehicles. At each step of the predictive control, the values of the chance parameters are given by algorithmic applications of random generators. The stochastic predictive control model is presented in [
21]. The uncertainty considered relates to the volumes of the traffic flows and the turning ratios of the vehicles in the flow. The uncertainty of traffic demands is formalized in a robust stochastic problem [
22].
In this paper, we aim to quantify the traffic management performed in an optimization problem that contains analytical random connections that describe the stochastic nature of traffic processes in an urban network. The main feature of this research is that it applies probabilistic relations to consider stochastic events in traffic behavior that occur through turning, stopping and the parking of vehicles, events that cannot be formalized in deterministic relations. To define the traffic management optimization problem, we use the well-known store-and-forward model. We formalize the random nature of the traffic through probabilistic inequalities. These inequalities are then approximated as nonlinear algebraic relations. Numerical simulations and the evaluation of this model are performed by applying the model predictive approach. In
Section 3, we present an analysis for analytically incorporating probabilistic relations into an optimization problem for green light duration estimation.
3. Basic Formalization of Traffic Management
Traffic control is aimed at reducing congestion [
23]. Additional goals can be pursued by reducing vehicle emissions [
24]. Mainly, traffic management is carried out through sections of traffic signals. Additions to the supporting traffic light control solutions are used, such as the use of waiting zones [
25], variable speed limits and ramp metering [
26]. The formal model called “store-and-forward” is intensively used to define and solve optimization problems. It originates from the works of [
27]. The model is quite simple and formalizes the analogy with fluid dynamics. The idea of the model is that the traffic of a given section is a linear result of the inflows and outflows. Therefore, it was time for its intensive use to optimize the duration of green lights in urban networks [
28,
29,
30]. The model is successively complicated and applied to green wave optimization [
31]; to the coordination of two-way arterial routes [
32]; to the application of model predictive control [
33,
34].
The theoretical basis of the store-and-forward model is the physical law of conservation: that the outflow in a network must equal the inflow [
35,
36]:
where
and
are the incoming and outgoing flows of vehicles at two consecutive times
t with dimensions (vehicles/time),
Figure 1.
This model is derived from the traffic light optimization case of [
27]. The formal derivation can be illustrated by applying the cellular transmission model [
37]. The continuity of the flows from (1) formally insists on the fulfillment of the equality:
where
is the traffic flow density at time
t and quantified as vehicles per unit distance (vehicles/distance). Replacing the first derivatives by their approximation, it follows:
Given that the density
is equal to the number of vehicles
x at a distance
l,
x =
(.)
l and the flow
q in a time period
T gives the number of vehicles,
x =
Tq(), Relation (3) is modified in (4) and (6):
where T is the duration of the control cycle. Given (1), Equation (4) becomes
The product
represents the vehicles entering the network. Respectively,
gives the number of vehicles that leave the transport network for the end of the control period
T. The store-and-forward model thus reduces to a simple algebraic equality:
saying that the resulting number of vehicles
x(
t + 1) in the transport network is obtained as an algebraic summation of the current value
x(
t) and the difference between the incoming and outgoing vehicles. In particular, the output flow is proportional to the duration of the green light
u (time) and depends on the geometric and structural configuration of the network, denoted as
s (vehicles/per time). Downscaling the network to a single section of the road, the ratio (6) can be interpreted as the number of vehicles that are on a section of the street between two intersections and/or the waiting vehicles in front of a traffic light at a junction, and in discrete form this relation is:
Between two consecutive intersections with traffic lights, there may be additional uncontrolled areas where vehicles can enter/exit or stop/park. Accordingly, except
additional vehicles can enter or leave the main controlled intersection,
Figure 2.
Thus, an additional number of outgoing
and incoming
as well as those of parking and/or stopping
η stochastically influence and affect the total value of vehicles
x. The influence of these factors
,
, η is random and the relation (7) can be formally rewritten as:
but the difference with (7) is that the value of
x becomes stochastic. Accordingly, the control problem that must estimate the duration of the green light
u must take into account that Relation (8) is stochastic. The motivation of this work is based on the existence of stochastic events
,
, η, which cannot be evaluated and formalized with deterministic and formal relations. This is the case of turning, stopping and the parking of vehicles in road sections in an urban network, which are not taken into account for the control of traffic lights in the deterministic case.
In the deterministic case, the optimization problem is defined by the minimization of the objective function up to the green light duration
u and/or
x, given the deterministic Equality (7):
where
x and
u are vectors between the upper and lower bounds. The relation (7) transforms into an inequality. The scale of the transport network and its controlled intersections determine the size of the vectors
u and
x. The objective function
F(
x,
u) can formalize the minimization of the sum of the number of vehicles or the queue lengths for the entire considered network,
[
1], the Total Time Spent and/or the maximization of the output flows
, which formalization is also related to the sum value,
, [
1,
38,
39].
In reality, there is uncertainty not only about the driver’s decision about the formation of the volume value x, but also from the traffic conditions that form the value of the incoming vehicles . The formal description of (8) allows the stochastic component to take into account the stochastic and/or random nature of traffic demands.
As a consequence of (8), the values of
x are also random variables. This insists that the analytic constraint
takes a probabilistic form. This article applies a probabilistic inequality of the form:
which means that the probability that the number of vehicles
x is less than the upper bound
on a road section in the network must be higher than γ, where γ is a confidence level. The Relation (10) is applied in portfolio theory, saying that the probability of losses of an investment x should be lower than the value
and higher than the level of γ [
40]. This relationship in portfolio theory is called Value at Risk (VaR), which is applied to assess the risk of investment decisions.
For the case of traffic control, the probabilistic Relation (10) can be applied as a constraint to the optimization problem or appropriately used as an objective function (this is the case in this study). For the constraint case and considering (10), the optimization problem has the following description:
Problem (11) contains probabilistic dependencies that make it difficult to solve. In [
20], such a class of problems is solved by stochastically generating values of the random variable
ε. Then, a predictive control model approach is applied to solve the discrete dynamic problem (11). However, for actual implementation, only the first element of the optimal solution is applied. Then, a new generation of
ε and a solution of the new problem (11) are performed. An alternative solution to (11) is also demonstrated by a neural network approximation of the probabilistic Relation (10), which is given by training a neural network with historical data.
In [
41], such an optimization problem with probabilistic inequalities was solved by a reduced gradient approach. The gradients are estimated as a combination of the probability of univariate and bivariate normal distributions. The estimators simultaneously estimate the probabilistic bounds and gradients of the objective function for each computational iteration. This computational approach is quite complex and time-consuming.
In [
42], the probabilistic constraint (10) is transformed into a deterministic one. Unfortunately, the applied way of approximating the initial probabilistic constraint to a deterministic one contains many integral components. This makes the resulting nonlinear optimization problem difficult to solve.
The approach taken here is to approximate the probability inequality with a deterministic analytic relation. The approximation is made by using the VaR concept of risk assessment in portfolio investment theory. This approximation allows the resulting deterministic relation to have a quadratic form. This approach allows adding analytical relations that consider stochastic events in traffic behavior that cannot be formalized and taken into account in a deterministic way. Stochastic relations after approximations can be used as additional constraints and/or as an objective function. Our particular solution, which differs from the analysis provided above, is to define a stochastic parameter as an objective function in a traffic light control optimization problem. This allows traffic control to explicitly take into account stochastic changes in traffic behavior.
4. Deterministic Approximation of the Probabilistic Inequality
Without a lack of generalization, we assume that the stochastic values of the number of vehicles on road section
i in the transport network are
, which values have a normal distribution. We assumed a normal distribution of
for physical and engineering reasons. In an urban network environment, the road sections are not that long (this is not the case with the highway), which gives reason to assume that the variance of
will not be higher than the mean value of the
of that section. The physical capacity of a given road section gives us reason for this assumption. This assumption leads to the shapes of the Probability Density Function (PDF) and the Cumulative Density Function (CDF) given in
Figure 3 and
Figure 4.
The following relations are included in the following conclusions derived from the relationship between the CDF and PDF functions.
where
P() is the PDF and
F() is the CDF function.
x is the set of all values that the stochastic variable can take and
is one of those values; γ is the confidence level.
The probabilistic constraint (10) is considered in the form:
The inner inequality of the probability function
P() is multiplied by (−1) to change the direction of the inequality:
The relation (14) is normalized for a stochastic variable with zero mean
and standard deviation equal to 1,
The Relation (14) retains its form, but the values in the PDF are normalized:
Using relation (12), (15) can be rewritten in the form:
or
By multiplying both sides of inequality (16) by the inverse function
, it follows:
The value
is the Z-score of a normalized stochastic function with a normal distribution. This value can be taken from tables [
43]. Taking Relation (12), if the confidence level is
, it means that the probability that the number of vehicles
x is lower than the value
, is supported with a probability of 90%. Accordingly, the probability that the number of vehicles is greater than
x is the value 1
. From [
43], the Z-score value is
. Using the notation
, relation (17) takes the deterministic algebraic form
where
is the predefined value of the number of vehicles that can be accepted on this road section and that participate in the upper bounds of the optimization problem (9), or
x =
. We substitute the probabilistic inequality (18) into (11) and the problem becomes nonlinear deterministic. The graphical interpretation of the dependence (18) is given in
Figure 5. The difference between the mean value
and the normalized volatility
of the stochastic variable
x must be greater than the value
, or
. This means that the stochastic variable must be a value in the set
≤
x ≤ + as shown in
Figure 5.
The probability inequality can be incorporated into the optimization problem in the constraint set as in (11) or in the objective function. The control problem that is defined here uses relation (18) as the optimization objective function. The problem will estimate the duration of green lights u, which will minimize the number of vehicles x at a suitable intersection for the set of values ≤ x ≤ +. Thus, the objective function of the control problem will be the minimization to the arguments u of the sum of vehicles , where the value must be obtained for each junction according to the relation (18).
To incorporate (18) as the objective function of an optimization problem such as (9), the values
and
values must be described as functions of the green light duration
u. Therefore, the optimization problem (11) is transformed into (19) with an objective function according to the probability inequality (18). The optimization problem becomes:
5. A model Predictive Framework for Traffic Light Control
The idea of the predictive control model is to predict the future state of the control system and evaluate the appropriate control influence. In dynamic systems, control is applied only to the first control step. The future state of the system is then estimated again, leading to a new control influence for the next control step. For the optimization problem (19), we will predict the vehicle values at intersections by considering the previous historical values of these vehicle queues. A graphical illustration of this sliding mode control policy is presented in
Figure 6. For this study, the historical period is truncated and the predictions of the number of vehicles are based on their values, which are estimated at the last control step. For the first control step, the predicted control value (
uopt) is for
k = 3,
Figure 6.
Taking into account the historical data, the average values of the vehicles at the intersection and the corresponding volatility are calculated. This makes problem (19) well-defined according to the values of its parameters. The solutions will be implemented. The resulting values of vehicles will be taken into consideration for the new estimations of and . By keeping the same amount of data for the historical period, a sliding policy is implemented to use the more recent historical data.
For this study, the historical period is truncated and the prediction of the number of vehicles is based on their values, which are estimated at the last control step. Formally, this control frame is analytically derived from the following relations:
- -
We assume that at the beginning of the control step, the value of vehicles at an intersection is ;
- -
For the start of the next control step (
k = 1), the number of vehicles
x1 will change according to the store-and-forward relationship (7) or
We take the value of as deterministic, since the stochastic nature of x is considered by relation (18).
The average value of
x for these two data types is:
The volatility of
x is calculated as:
After substituting
from (20) into (21), the analytical relation for the volatility is:
Relations (20) and (22) analytically give the relations
and
. After substituting (20) and (22) into (18), which is the objective function of (19), the stochastic approximation (18) takes the form of a quadratic function to
u:
The optimization problem (19) becomes deterministic with an objective function that formalizes the probabilistic requirement (18) or:
Relations (23) must be described analytically for each intersection of the transport network, which adds additional components to the objective function F(u).
For this study, historical data for mean and volatility estimates are taken for only one previous control step. This short time horizon allows the shortest impacts and changes in traffic requirements to be taken into account. Increasing the history in the control step will change the analytical definition of and against the governing influences u and relations (20) and (21) will be modified accordingly.
Problem (23) can be modified by changing the store-and-forward constraints (7) in such a way that the current number of vehicles at an intersection plus inbounds must be less than the outbound. Thus, formally the control problem will preserve the presence of congestion. The analytical definition of this problem will be modified from (23) as:
Problem (25) contains as an argument only the duration of green light u. The application of the model predictive framework of the model allows the evaluation at each control step the value of the existing vehicles in intersection and a new problem (25) will define the solutions of u for the next control step. The evaluation of can be performed by using the estimated in the store-and-forward relation (7) in a recursive manner for each control step.
6. Stochastic Optimization of Traffic Management in an Urban Environment
The aim of the study is to develop a traffic management model reducing the number of vehicles in sections of the urban transport network, taking into account the stochastic nature of the traffic. The optimization model (25) obtained in the previous
Section 5 is used. The objective function reflects the stochastic nature of the traffic flow and our objective is to minimize the sum of all vehicles in the network and/or waiting at the traffic light at the intersection as functions of the green traffic light duration
u. We consider a real network of intersections in an urban area in Sofia, which is a mixture of areas with residential, business and commercial activities and buildings. The network consists of four intersections and the number of vehicles in the main transport section is
xi,
i = 1,…,15,
Figure 7. Vehicles can go straight or turn left or right at the intersection. The main traffic flow passes through the horizontal street, while the traffic is not intense through the perpendicular streets. This consideration is formalized by multiplying turning vehicles from/to the perpendicular streets by coefficients
l < 1. Right and left turning vehicles are multiplied by
l1 and
l2, respectively. As initial and known values for the model, we use statistics on the street capacity
s, the number of initial vehicles
x0 and the intersection entries
xin.
The objective function of (25) according to (18) can be briefly given as:
and we need to determine the sum of all vehicles
xi,
i = 1,…,15 as functions of
u (
uj,
j = 1,…,8).
6.1. Evaluation of the Number of Vehicles x1(u)
To model the stochastic nature of the traffic, we consider two control cycles for
k = 0 and
k = 1 at the beginning,
Figure 6. When
k = 0, the first value of vehicles is:
The value of
is known (pre-measured). For the next control step:
k = 1, the value of the vehicles is determined according to the store-and-forward model and according to (7) is:
or
To formalize the outgoing flow, we divide it into straight-ahead direction by value
, right-turning vehicles by value
and the corresponding left-turning by value
. The total value of the outflow becomes
. Then, the number of vehicles for the second control cycle according to (28) becomes:
We replace the expression
by
L1 and for simplicity (29) can be represented as:
We have to define both stochastic components of (26):
and
as functions of
u.
Analytical definition of the mean value as a function of u : the mean value
analytically for the case of one historical period is:
The value of
is estimated from (27) and
—from (30). These two components of (31) are given from (27) and (30) and the mean
analytically is:
Analytical definition of volatilityas a function of u: the volatility
for the case of one historical period is:
Next, substituting into (33) the values obtained from (27), (30) and (32) and applying a set of transformations, it follows:
Relations (33) and (34) have to be applied to any relation of the form (6) that will give the analytic components included in the objective function (16). For illustration purposes, these transformations are illustrated for the case of the number of vehicles x1() as a function of the estimated green light .
Determination of the components of the objective function given by x1(
)
We substitute Equation (32) for
and (34) for
in (26):
After processing the above equation, it follows:
Thus, the objective function must have quadratic components and linear component .
6.2. Definition of the Objective Function Components for All Vehicles xi(u), i = 2,…,15
Considering the urban network topology of
Figure 7, the relations for
following the case of (35) are:
The value
depends on the outflows from the second junction,
Figure 7. This outflow from the second intersection depends on the duration of the green light
u3 and the corresponding street capacity
s3 or
s3u3, plus the turning flows from the perpendicular street from the second intersection: (
l1 +
l2)
s4u4. To simplify the notation, we replace the sum of the turning coefficients by
L2 = (
l1 +
l2). This means that the number of vehicles
x3 depends not only on the duration of the green light
u1 at the first intersection, but also on
u3 and
u4 from the second traffic light. The initial value for the control cycle
k = 0 is
,
Figure 6.
Following the store-and-forward model, the vehicles
for the next control cycle
k = 1 will have a value:
The mean value
of vehicles
is given according to relation (32) or:
The corresponding volatility
of vehicles
is given according to (33):
After a set of transformations, it follows:
Using the relations for the mean
from (37) and the volatility
from (38), the value of
takes the analytical form:
Relation (39) gives additional components for the objective function (26) of the optimization problem with quadratic components
and linear components
). These components come from the
vehicles.
Following the network topology in
Figure 7, the expression for vehicles
is analogous to that of
and is of the form:
Relation (40) gives the corresponding quadratic and linear components for the objective function (26) from
.
The length of the queue
depends not only on the duration of the second green traffic light
u3, but also on the traffic coming from the first intersection. At the start of the control loop for
k = 0, the value of
is
. For the next control loop, for
k = 1 the value of
is evaluated using the store-and-forward relation:
For the case according to (31), the mean value
EX of
is given by the ratio:
According to (33), the corresponding volatility
is:
Using the relations for the mean
from (41) and the volatility
from (42), the value of
takes the analytical form
The relation (43) gives the corresponding additional quadratic and linear components for the objective function coming from
.
Through the same formal approach, the relations for the subsequent values of the vehicles are derived, which gives additional quadratic and linear components for the objective function (26) of the optimization problem. The general set of the analytical definition of the critical level of vehicles
for each road section of the urban network is given in the
Appendix A.
6.3. Analytical Description of the Traffic Light Optimization Problem
The objective function of the task is given in the form (25). This refers to the minimization of the sum of all vehicles
xi,
i = 1, …, 15 in the urban network. The values of the number of vehicles are derived analytically, following the ratios (35), (36), (39), (40), (43) and the corresponding ones from the
Appendix A. The sum of the number of vehicles is a non-linear quadratic function, which is represented in (45) in vector form. The constraints of the optimization problem mean that the outgoing traffic flows are required to be greater than the incoming traffic flows for each network junction. The constraints of the optimization problem according to the store-and-forward model are given by following the network topology of
Figure 7 and this gives a set of inequalities:
The last four constraints are relationships between the duration of the green light cycle and the traffic light, where c1, …, c4 are the durations of the traffic light cycle on the control intersections. The yellow light is assumed to have a fixed length of 1/10th of a cycle.
The values of the duration of the green light ui, i = 1, …, 8 according to the stochastic nature of the traffic are estimated from the ratios (35), (36), (39), (40), (44).
The optimization problem can be represented in vector form:
Both the objective function matrices of (45),
Q and
R, have descriptions, given in the
Appendix A. The matrix
Q has eight rows and eight columns, since the control variables of the considered network are
uj,
j = 1, …, 8,
Figure 7:
The matrix elements of (46) are given in the
Appendix A.
The matrix
R from (45) consists of factors of the linear components of
u:
The relevant elements of the
RT matrix are given in the
Appendix A.
The elements of the matrices
A and
b for problem (45) are given in the
Appendix A.
7. Numerical Simulations and Results
The optimization problem (45) is solved in a MATLAB environment with statistical data from a real urban area in Sofia. The solution of this linear-quadratic optimization problem shows a decrease in the values of the vehicles along the sections of the urban network. The dynamic behavior
x1,
x2,
x3 and
x4 for the first junction is given in
Figure 8. The values of
x1,
x2 and
x4 after applying
control solutions for the first control cycle decrease to zero values. The internal transport flow
x3, coming from the second intersection, decreases. Applying this control strategy for several control cycles, the value of
x3 tends to decrease to a zero value,
Figure 8.
Applying the estimated optimal durations of the green lights
for the first control cycle, the corresponding vehicle values for the second and third sections of the network give a further reduction to a zero level of the number of vehicles
x5,
x6,
x7 and
x8,
Figure 9 and
x9,
x10,
x11 and
x12,
Figure 10.
The only car flow that does not support decreasing dynamics is
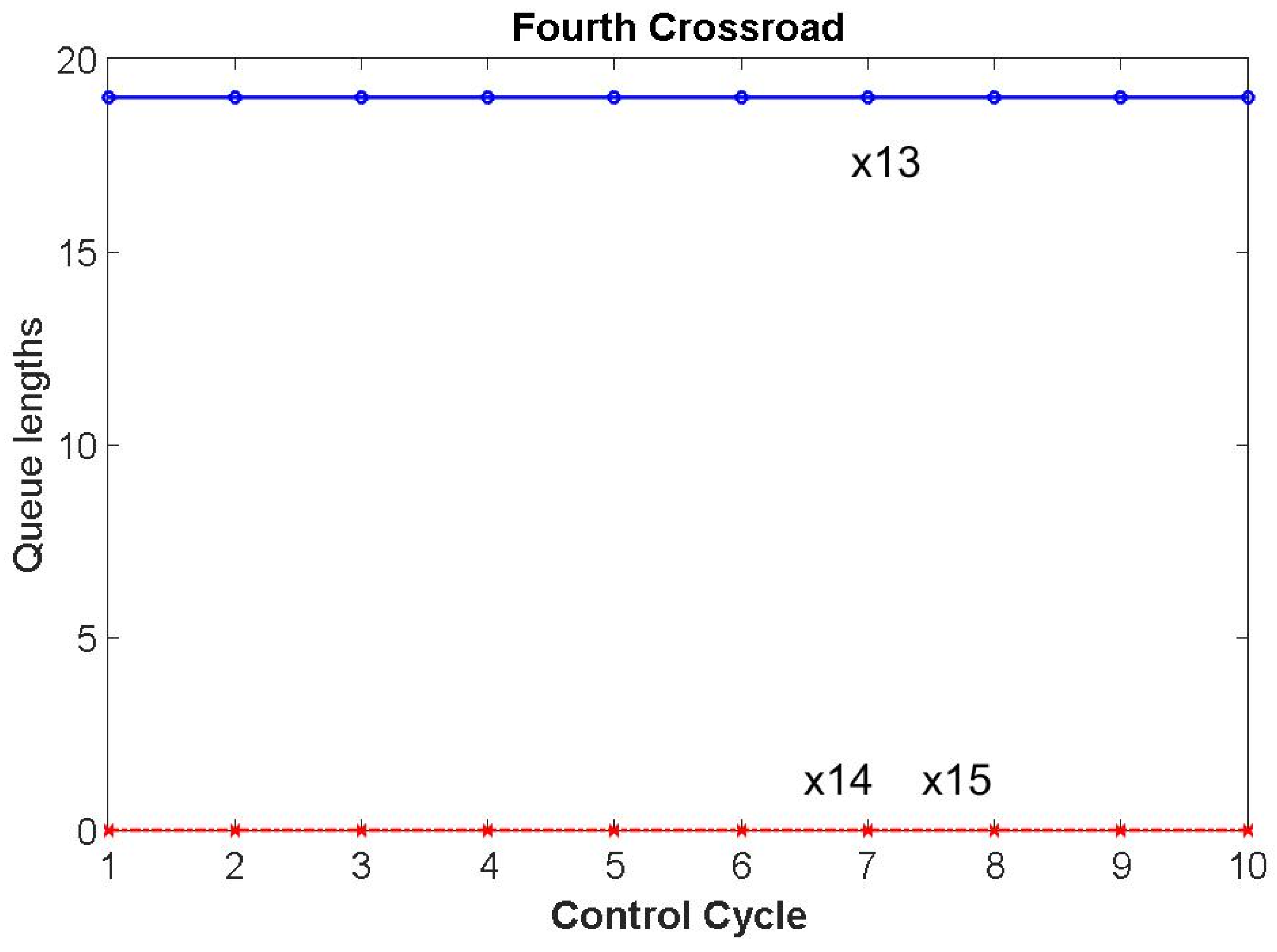
x13,
Figure 11. However, this control keeps its value at a constant level, which is good for minimizing congestion. The traffic authorities should take measures to increase road capacity
s7 to reduce
x13. The remaining vehicle flows
x14 and
x15 also maintain a decreasing character and decrease to zero after the first control cycle,
Figure 11.
The decreasing character of the transport flows for the internal sections of the transport network
x3,
x9 and
x13 are given in
Figure 12, where the control cycles applying task (45) are successively performed.
To evaluate the benefits of the control problem (45), the dynamics of the total number of vehicles in the transport network are also evaluated. The vehicle totals after each control cycle are illustrated in
Figure 13.
It is obvious that this control policy of sequentially applying the solutions to problem (45) leads to a significant reduction of the sum of all queues. This is a useful result for the application of the developed optimization model, which considers probabilistic approximations in its objective function. To evaluate the results obtained from the resulting optimization model for traffic management with probabilistic demands, comparisons are made with the corresponding deterministic optimization problem. The numerical evaluations and comparisons are illustrated in the next section.