Performance Evaluation of a Cloud Datacenter Using CPU Utilization Data

Abstract

Cloud computing and its associated virtualization have already been the most vital architectures in the current computer system design. Due to the popularity and progress of cloud computing in different organizations, performance evaluation of cloud computing is particularly significant, which helps computer designers make plans for the system’s capacity. This paper aims to evaluate the performance of a cloud datacenter Bitbrains, using a queueing model only from CPU utilization data. More precisely, a simple but non-trivial queueing model is used to represent the task processing of each virtual machine (VM) in the cloud, where the input stream is supposed to follow a non-homogeneous Poisson process (NHPP). Then, the parameters of arrival streams for each VM in the cloud are estimated. Furthermore, the superposition of estimated arrivals is applied to represent the CPU behavior of an integrated virtual platform. Finally, the performance of the integrated virtual platform is evaluated based on the superposition of the estimations.

1. Introduction

With the vigorous growth of big data and large-scale data processing, traditional computing models can no longer meet daily computing needs [1]. Cloud computing and its associated virtualization are the most vital architectures for providing cloud services to users, which have become the standard infrastructure for supporting Internet services [2]. In general, cloud computing has a service-oriented architecture, in which services can be categorized into IaaS (Infrastructure-as-a-Service), PaaS (Platform-as-a-Service), and SaaS (Software-as-Service) by the provided layer to clients [3]. Specifically, IaaS provides essential computing, storage, and networking resources on demand. PaaS allows users to access hardware and software computing platforms such as virtualized servers and operating systems over the internet. SaaS provides cloud users access to hosted applications and other hosted services over the internet. In recent decades, many companies have attempted to integrate such servers into a virtual server using PaaS architecture to reduce server management and maintenance costs. For example, Bitbrains is a service provider specializing in hosted services and business computing for enterprises [4]. Clients include many banks (ING), credit card operators (ICS), insurers (Aegon), etc. Bitbrains hosts applications in the solvency domain and examples of its application vendors are Towers Watson and Algorithmics.

PaaS cloud service providers need to gain insight into the relationship between the performance of the cloud service platform and the available resources, not only to meet users’ performance needs but also to fully utilize the infrastructure and resources of the cloud service platform. For cloud service users, performance evaluation quantitatively assesses the various cloud services to ensure that their needs are met. For example, users can conduct quantitative analysis on the same service provided by different cloud service providers through performance evaluation and make the best service selection and decision. Generally, a PaaS cloud computing platform has a vast number of collaborative physical machines, each of which includes multiple virtual machines (VMs). Additionally, performance evaluation of the integrated virtual platform during the design phase of a computer system can help the computer designer plan the system’s capacity [5]. However, with the rapid increase in data, every upgrade to software or hardware (e.g., CPU, memory) comes with high risk and expense [6]. Performance evaluation that evaluates the utility of given upgrades facilitates cost reduction and construction optimization at a datacenter, while erroneous analysis leads to ultimately huge losses. Therefore, it is essential to estimate the system performance from the statistics of existing servers.

Cloud services differ from traditional hosting in three main aspects. First, the cloud provides service on demand; second, cloud services are elastic because users can use the services they want at any given time; third, the cloud provider fully manages the cloud services [7]. Queueing models provide an efficient manner to simulate the behaviors and evaluate the performance of a cloud datacenter. Queueing theory often models web applications as queues and VMs as facility (service) nodes [8]. The parameters of queueing models (e.g., arrivals and service rates) can then be estimated as services arrive in a first-come-first-served (FCFS) manner [9]. Usually, a queueing model can be standardized as $A/B/S/K$, where A and B represent the arrival and service distributions, respectively. S and K are the number of service nodes and queue capacity, respectively. For example, $M/M/1/K$ represents that the arrival and service times follow Poisson and exponential distributions, respectively, and the number of servers and queue length are one and K, respectively. Tasks sent to the cloud datacenter are usually served within a suitable waiting time and will leave the queue when the service is over. However, there remain many challenging issues with queueing models, despite their ability to represent the behavior of cloud datacenters [10]. A cloud center usually has a lot of service nodes. Traditional queueing models rarely consider the system size. Besides, approximation methods are sensitive and inaccurate to the probability distribution of arrival and service times. Furthermore, traditional queueing systems usually observe the inter-arrival times or waiting times to estimate arrival rates for VMs. In a cloud datacenter, task arrivals and wait times are difficult to monitor and collect.

As a solution, our previous work [11] proposed an approach to estimate the arrival intensity of computer systems only from CPU utilization data. CPU utilization data is one of the most commonly used statistics to monitor CPU behavior during task execution. Most operating systems have the function to calculate CPU utilization by default. Besides, the CPU behavior of an existing server was modeled by an $M_t/M/1/K$ queueing system, where the arrival stream is according to a non-homogeneous Poisson process (NHPP), and the service time obeys an exponential distribution. NHPP is the best-known generalization of the Poisson process in that the arrival intensity is given as a function of time t [12]. Therefore, an NHPP can better approximate the arrival process of the tasks accurately than a homogeneous Poisson process (HPP) [13]. For the Poisson process, the renewal process is the partial sum process associated with independent random variables with an exponential law [14]. An alternative way to avoid the independently and identically distributed requirement is the Markovian arrival process (MAP) [15].

To reasonably plan the cloud computing platform and improve its performance, we aim to evaluate the performance of Bitbrains cloud servers in a PaaS architecture in this paper. More precisely, we use an $M_t/M/1/K$ queueing model to represent the CPU behavior of each VM, which can dynamically calculate the task arrival rate at different times. In addition, because the arrivals and waiting times of tasks in computer systems are difficult to monitor and collect, we estimate the arrival intensity of each VM in the cloud datacenter from the CPU utilization data. Finally, the performance of the integrated virtual platform is evaluated by applying the superposition technique of NHPPs. The main contributions are organized as follows:

• Performance evaluation of a cloud server: It is non-trivial and significant to evaluate the performance of a cloud datacenter (i.e., Bitbrains) to meet user performance needs and make full use of the resources of the PaaS cloud service platform.
• Parameter estimation for a queueing model subject to NHPP arrival using CPU utilization data: An NHPP is used as the arrival process of the queueing model, which can dynamically calculate the task arrival rate at different times. Additionally, we use CPU utilization to estimate the parameters because of the unobservability of the task arrival process and waiting times of the computer system. CPU utilization is the most commonly used statistic, but task arrival and service processes are not visible.
• Flexibility and scalability for performance evaluation: any queuing model based on utilization data can be solved using our approach. In addition, our model can be combined with distributed computing to further improve the capability of performance evaluation.

The remainder of the paper is as follows. The related research works are reviewed in Section 2. In Section 3, the cloud datacenter system (i.e., Bitbrains) is first introduced in detail. Then, the EM algorithm-based parameter estimation method is proposed. In Section 4, we first estimate the parameters (i.e., arrival intensity function) of the $M_t/M/1/K$ queueing model. Then, we evaluate the performance of the Bitbrains using only CPU utilization data. Finally, the paper is concluded in Section 5.

2. Literature Review

In recent years, data has exploded with the rapid growth of computers and the Internet. As one of the solutions to cope with the era of big data, cloud computing has gained wide attention and application. It is an extremely worthwhile task to evaluate the performance of cloud computing platforms. For cloud computing platform designers, performance evaluation can help them decide the size of system memory, the number of CPUs, etc. For cloud computing providers, performance evaluation can help them allocate facilities and resources appropriately. For users, it can help them choose the right provider.

2.1. Queueing Models as Solutions

However, only a small part of the work involves the performance evaluation of cloud computing data centers, and many researchers prefer to evaluate the performance evaluation of cloud computing centers using queuing models [16,17,18,19,20]. Moreover, most of the literature estimates the parameters of the queuing model by collecting data such as queue lengths or waiting times. For example, Thiruvaiyaru et al. [16] collected queue length data and estimated parameters from an $M/M/1$ queueing model. Ross et al. [19] collected queue length data at successive time points and estimated the parameters of an $M/M/c$ queuing system. Then, they generated density-dependent transition rates for Markov processes by placing the arrival rates in the same order as the number of servers. Liu et al. [20] calculated the queue lengths using the number of vehicles in the queueing system and proposed a real-time length estimation method through the probed vehicles. Unlike queue length data, waiting time data is another commonly used data that can be used to estimate the parameters of queueing models. Waiting times contain partial information about inter-arrivals and service times. Basawa et al. [17] collected waiting times of n successive customers from $M/M/1$ and $M/E_k/1$, respectively. Fischer et al. [18] used the Laplace transform method to approximate the distribution of waiting times and then estimated the parameters of an $M/G/1$ queueing model. For performance evaluation of cloud computing systems, Khazaei et al. [10] modeled a cloud center as an $M/G/m/m$ queuing system. They used a combination of a transformation-based analytical model and an embedded Markov chain model to obtain a complete probability distribution of response times and the number of tasks. Finally, they evaluated the performance of the system.

However, for observable queuing systems, the collection of queue lengths and waiting times consumes much time. For non-observable queuing, data such as queue lengths and waiting times, which can visually reflect queue information, are difficult to collect. For example, the arrival time, time interval, and waiting time of two successive tasks are not observable in a cloud computing system.

CPU utilization data is one of the most common statistics used to monitor CPU behavior during task execution. Most operating systems have the function to calculate CPU utilization by default. However, unlike queue lengths and waiting times, CPU utilization is utilization data. In other words, CPU monitoring is not continuous but at certain time intervals. Therefore, CPU utilization data belongs to incomplete data, which increases the difficulty of the parameter estimation of a queueing model. Moreover, the utilization data does not reflect the queue information intuitively like the queue lengths but reflects its information implicitly. For example, a high CPU utilization indicates that many tasks are waiting to be processed in a queue or that the current task is taking a long time to process. Therefore, it is more challenging to estimate parameters and evaluate performance from CPU utilization data. To the best of our knowledge, there are no other papers on queueing parameter evaluation based on utilization data other than our proposed [11,15].

2.2. Non-Homogeneous Poisson Process

Most works prefer to assume the arrival process of tasks as a homogeneous Poisson process (HPP) with a constant arrival rate. However, a Poisson arrival process is not a good choice in practice. For example, cloud computing datacenter visits are generally characterized by higher working hours than evenings and higher weekdays than weekends. The arrival process of tasks usually varies dynamically with time, i.e., it is a non-homogeneous Poisson process (NHPP) [12]. In general, queuing systems based on NHPP arrivals are more difficult to estimate parameters than HPP-based systems. Rothkopf and Oren [21] proposed an approximate method to estimate a dynamically varying arrival process of a queuing system. Heyman and Whitt [22] modeled an $M_t/G/c$ queuing system to deal with the non-simultaneous arrival process of asymptotic behavior. They defined an intensity function $\lambda \left(t\right)$ to represent the time-varying Poisson arrival rate. In addition, Green et al. [23] evaluated the performance of a queuing system with the NHPP arrival process and exponential service times. Pant et al. [24] assumed a $M_t/M/1$ queuing system in which customers arrive at the system with a sinusoidal arrival intensity function $\lambda \left(t\right)$.

2.3. Parameter Estimation of Queueing Models

The maximum likelihood estimates (MLE) is the most commonly used estimation method of queueing models [25,26,27]. Wang et al. [26] proposed an $M/M/R/N$ queueing model, which had R multiple severs in the queue. They estimated the HPP arrival rate and service time to obey the exponential distribution using MLE. Amit et al. [27] collected the number of customers in an $M/M/1$ queueing system, and then estimated the traffic intensity by MLE. We have stated above that CPU utilization data is different from observable data and belongs to incomplete data. Therefore, a statistical inference technique for evaluating the performance of incomplete data is required. Expectation maximization (EM) [28] is a useful algorithm that can iteratively compute partial data with MLE. The EM algorithm is powerful for stochastic models with multiple parameters. An EM algorithm generally has two steps (i.e., the expectation step and the maximization step, respectively). MLE iteratively computes the expectation step and the maximization step iteratively and then stops iterating until the loss function converges. Wu [29] verified the convergence of the EM algorithm theoretically. They proposed that the MLE of the EM sequence can converge to a unique value in the case that the likelihood function is unimodal and differentiable. Rydén [30] estimated the parameters of a queueing model with Markov Modulated Poisson Process (MMPP) using MLE via an EM algorithm. Similarly, Basawa et al. [31] estimated the parameters of an $GI/G/1$ queueing system using an EM algorithm from waiting times. Okamura et al. [32] defined group data and tried to estimate arrival and processing rates of a queueing system with an Markovian arrival process (MAP) using an EM algorithm-based approach.

In this paper, we propose a novel statistical inference technique for incomplete data to evaluate the performance of cloud datacenters. Empirically, the task arrival process in a datacenter often exhibits a cyclical and recurring nature. The cycle of this process can be in the form of a day, a week, a year or other units. For example, datacenter access is greater during business hours than early mornings and evenings. Weekday accesses will also be larger than weekend accesses. Therefore, we model each virtual machine (VM) of a cloud datacenter as an $M_t/M/1/K$ queueing system. An NHPP can better represent this cyclic characteristic. Then, we estimate parameters only from CPU utilization data using the EM algorithm. In a cloud datacenter, CPU utilization is the most commonly used statistic to monitor the behavior of each VM. Because any computer operating system can calculate CPU utilization by default, we do not need to spend time collecting information such as queue length and waiting times in the queuing system.

3. Methodology

In this section, we first briefly introduce the Bitbrains cloud datacenter. The system behavior can be modeled by an $M_t/M/1/K$ queueing model. Then, we define utilization data formally and approximate the NHPP to a series of HPPs. Finally, the details of the MLE optimization method based on an EM algorithm are described.

3.1. Bitbrains Cloud Datacenter

Bitbrains is a service provider that specializes in managed hosting and business computation for enterprises [33]. One of the typical applications of Bitbrains is for financial reporting, which is used predominately at the end of financial quarters. The workloads of Bitbrains are master-worker models, where the workers are used to calculate Monte Carlo simulations [34]. For example, a customer would request a cluster of computing nodes to run such simulations. The request is accompanied by the requirements as follows. First, data transmission between the customer and the datacenter through a secure channel, computing nodes rented as VM in the datacenter to provide predictable performance, and high availability for running critical business simulations.

Bitbrains uses the standard VMware provisioning mechanisms to manage computing resources, such as dynamic resource scheduling and storage dynamic resource scheduling. In general, Bitbrains consist of three types of VMs: management servers, application servers, and computing nodes. The management servers can be used for the daily operation of customer environments. Application servers are used as database servers, web servers, and head nodes. Computing nodes are mainly used to compute and simulate financial risk assessment. CPU utilization data of Bitbrains used in this work were collected between August and September 2013 two traces, which are described in

Table 1. Workload traces of the Bitbrains cloud datacenter.

Name of Trace	#VMs	Period of Data Collection	Storage Technology	Memory Size (GB)	Cores
fastStorage	1250	1 month	SAN	17,729	4057
Rnd	500	3 months	NAS and SAN	5485	1444
Total	1750			23,214	5501

.

3.2. Collection of CPU Utilization Data

CPU utilization is the most commonly used statistic to monitor the behavior of each VM in the cloud datacenter Bitbrains. We define CPU utilization in each time interval of each VM in the cloud datacenter Bitbrains as $\mathrm{\Delta }t$. CPU utilization can be considered as the ratio of the busy time to the total time of one monitoring. The busy time is given by the cumulative time in which the server is processing a task. For each fixed time interval, a computer system or VM calculates the time fraction as utilization. Parameter estimation from utilization data is more challenging than other related work. Based on the behavior of the CPU utilization data, we assume that the utilization within a time interval consists of an unobserved time and a successive observed time, respectively. Furthermore, since the CPU cannot be monitored during an unobserved period, we can only collect CPU utilization data during an observed period. For the CPU, each observation period is short (only a few milliseconds), so there is at most one change from busy to idle or idle to busy during each observation period. Formally, let $t_u$ and $t_o$ be the lengths of the unobserved and observed periods of each time interval, respectively. $B_t$ and $I_t$ are the lengths of busy and idle times in time slot t. According to the above assumptions, CPU utilization for one-time interval $t_u+t_o$ can be defined as follows:

$$u=B_{t_o}/(B_{t_o}+I_{t_o}),$$

(1)

where u indicates the CPU utilization for one-time interval, $B_{t_o}$ and $I_{t_o}$ represent the lengths of busy and idle times in t, respectively, and $t_o\ll t_u$.

3.3. System Behavior as the $M_t/M/1/K$ Queueing Model

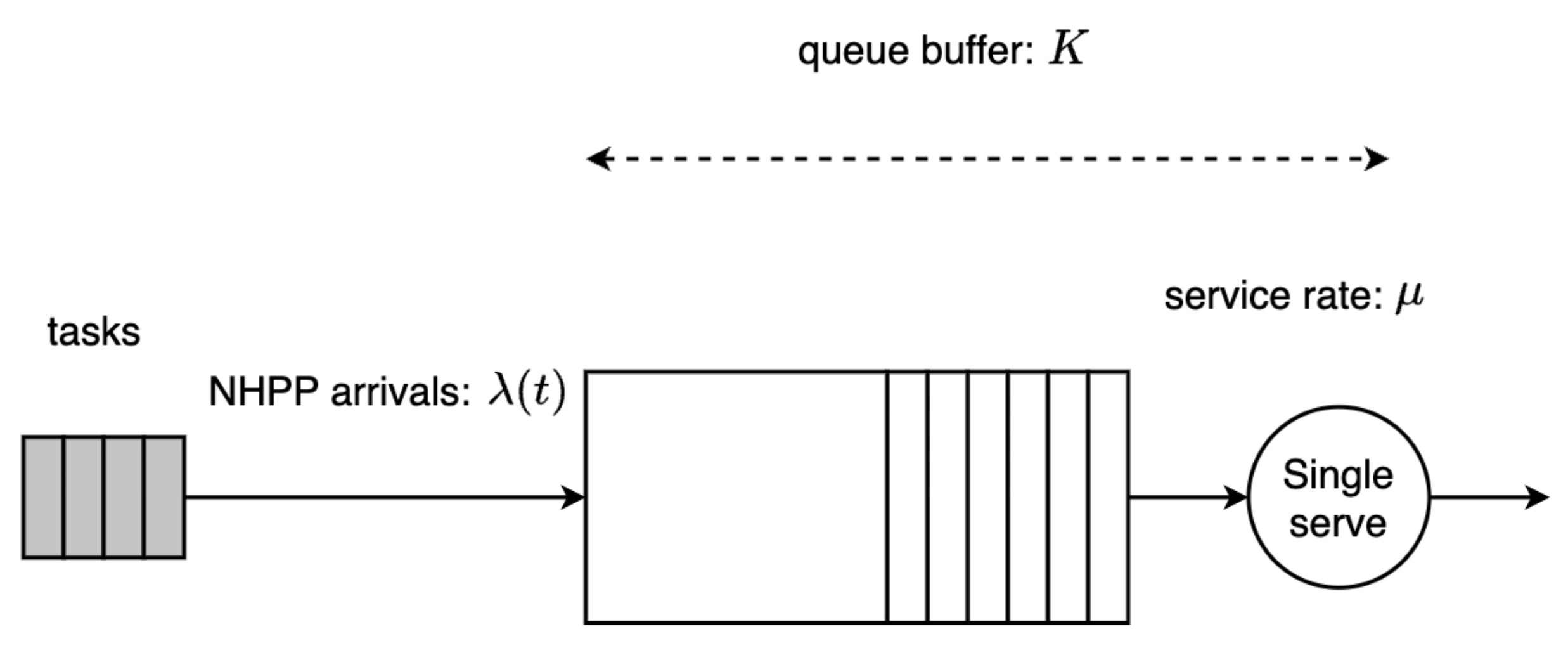
First, users send the task requests that need to process by Bitbrains. Then, Bitbrains allocates computing resources for each task. Note that user tasks are independent of each other. When the CPU of the VM is idle, the first assigned task can be sent directly to the CPU for processing, or it needs to wait in the buffer of size K. For the VM with a buffer size of K, the arriving tasks that exceed K cannot enter the buffer for processing. Additionally, the waited tasks in the buffer will be processed by the CPU. The served task will leave the VM once finished.

Therefore, the system behavior of Bitbrains can be represented by the queueing model: web applications are often modeled as queues, and VMs are modeled as service nodes. We assume that the arrivals obey an NHPP with the intensity function is $\lambda \left(t\right)$. Service time is according to exponential distribution whose rate is $\mu$. As shown in Figure 1, the system can be modeled by an $M_t/M/1/K$ queueing model.

In queueing theory, we usually use a continuous time Markov chain (CTMC) to formalize the behavior of a queueing model. For the $M_t/M/1/K$ queueing model, the infinitesimal generator matrix of the CTMC can be expressed as follows:

$$\begin{array}{c}\hfill \mathbf{Q}\left(t\right)=\left(\begin{array}{cccc}-\lambda \left(t\right)& \lambda \left(t\right)& & \\ \mu & -(\mu +\lambda (t\left)\right)& \lambda \left(t\right)\\ & \ddots & \ddots & \\ & & \mu & -\mu \end{array}\right)\end{array}$$

(2)

3.4. Approximate NHPP as a Series of HPPs

The time dynamics $\lambda \left(t\right)$ of an NHPP, often called time intensity, is a function of time t, which is hardly estimated. Usually, the arrival process of an NHPP can be regarded as a series of independent HPPs. To simplify the model and estimation, the intensity function $\lambda \left(t\right)$ of an NHPP can be approximated by a series of HPPs. Specifically, assume that the total time for utilization data collection is T. T can be divided into n ($n\ge 1$) same periods, and each divided time interval can be represented by $\mathrm{\Delta }t$. In practice, a large value of n is chosen. The n HPPs can be approximated as an NHPP with the intensity of $\lambda \left(t\right)$. At the ith ($1\le i\le n$) time interval, the arrival tasks obey the HPP with the arrival rate being a constant of ${\lambda }_i$. The approximated piecewise constant function of NHPP is shown as

$$\lambda \left(t\right)=\left\{\begin{array}{ccc}{\lambda }_1\hfill & & (0\le t\le \mathrm{\Delta }t)\hfill \\ {\lambda }_2\hfill & & (\mathrm{\Delta }t<t\le 2\mathrm{\Delta }t)\hfill \\ ⋮& & ⋮\\ {\lambda }_n\hfill & & \left(\right(n-1)\mathrm{\Delta }t<t\le T)\hfill \end{array}\right.$$

(3)

3.5. Parameter Estimation of the $M_t/M/1/K$ Queueing Model

According to Equation (3), the infinitesimal generator matrix of Equation (2) can be modified to n independent infinitesimal generator matrices, and the ith matrix can be denoted by ${\mathit{Q}}_i$ ($1\le i\le n$). ${\mathit{Q}}_i^0$ is defined as the ith infinitesimal generator matrix with CPU states that transfer from idle to idle or from busy to busy. ${\mathit{Q}}_i^0$ is denoted by

$${\mathit{Q}}_i^0=\left(\begin{array}{cc}-{\lambda }_i& \\ & \begin{array}{cccc}-(\mu +{\lambda }_i)& {\lambda }_i& & \\ & & \ddots & \ddots & \\ & & & \mu & -\mu \end{array}\end{array}\right).$$

(4)

Similarly, ${\mathit{Q}}_i^1$ is defined as the ith infinitesimal generator matrix with CPU states that transfer from idle to busy or from busy to idle. ${\mathit{Q}}_i^0$ is represented as follows.

$${\mathbf{Q}}_i^1=\left(\begin{array}{cc}& {\lambda }_i\\ \mu & \mathit{O}\end{array}\right),$$

(5)

where $\mathit{O}$ is zero matrix and,

$$\begin{array}{c}\hfill {\mathit{Q}}_i={\mathit{Q}}_i^0+{\mathit{Q}}_i^1.\end{array}$$

(6)

Define utilization as $\mathcal{D}=({\mathcal{D}}_1,{\mathcal{D}}_2,\dots ,{\mathcal{D}}_n)$. The utilization data in i-th period $\mathrm{\Delta }t$ is defined as ${\mathcal{D}}_i=(u_i^1,u_i^2,\dots ,u_i^k)$, $0\le u_i^j\le 1$. Then the likelihood function can be formulated from utilization data by using MLE, as shown below:

$$\begin{array}{cc}\hfill & \mathrm{L}({\lambda }_1,\cdots ,{\lambda }_n;\mathcal{D})=\mathit{p}{\mathrm{L}}_1({\lambda }_1;{\mathcal{D}}_1)\cdots {\mathrm{L}}_n({\lambda }_n;{\mathcal{D}}_n)\mathbf{1},\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & {\mathrm{L}}_i({\lambda }_i;{\mathcal{D}}_i)={\mathcal{L}}_i\left(u_i^1\right)\cdots {\mathcal{L}}_i\left(u_i^k\right),\hfill \end{array}$$

(8)

With Equations (4)–(6), the items of Equation (8) can be expressed as

$$\begin{array}{}\mathrm{(9)}& \begin{array}{cc}\hfill & {\mathcal{L}}_i\left(u\right)=exp\left({\mathit{Q}}_i{t}_u\right){\mathbf{\Lambda }}_{0}exp\left({\mathit{Q}}_i^0(1-u)t_o\right){\mathit{Q}}_i^{1}exp\left({\mathit{Q}}_i^{0}u{t}_o\right)\hfill \\ \hfill & +exp\left({\mathit{Q}}_i{t}_u\right){\mathbf{\Lambda }}_{1}exp\left({\mathit{Q}}_i^{0}u{t}_o\right){\mathit{Q}}_i^{1}exp\left({\mathit{Q}}_i^0(1-u)t_o\right),\hfill \\ \hfill & \mathrm{if} 0<u<1,\hfill \end{array}\hfill \mathrm{(10)}& \begin{array}{cc}\hfill & {\mathcal{L}}_i\left(u\right)=exp\left({\mathit{Q}}_i{t}_u\right){\mathbf{\Lambda }}_{0}exp\left({\mathit{Q}}_i^0{t}_o\right),\mathrm{if} u=0,\hfill \end{array}\mathrm{(11)}& \begin{array}{cc}\hfill & {\mathcal{L}}_i\left(u\right)=exp\left({\mathit{Q}}_i{t}_u\right){\mathbf{\Lambda }}_{1}exp\left({\mathit{Q}}_i^0{t}_o\right),\mathrm{if} u=1,\hfill \end{array}\end{array}$$

where $\mathit{p}$ is the initial probability vector. Also ${\mathbf{\Lambda }}_0$ and ${\mathbf{\Lambda }}_1$ are $(K+1)$-by-$(K+1)$ block matrices;

$$\begin{array}{cccc}\hfill {\mathbf{\Lambda }}_0& =\left(\begin{array}{cccc}1& & & \\ & 0& & \\ & & \ddots & \\ & & & 0\end{array}\right),\hfill & \hfill {\mathbf{\Lambda }}_1& =\left(\begin{array}{cccc}0& & & \\ & 1& & \\ & & \ddots & \\ & & & 1\end{array}\right).\hfill \end{array}$$

(12)

3.6. EM Algorithm for CPU Utilization Data

An EM algorithm is an effective machine learning algorithm that can be used for parameter estimation of queueing models with incomplete data. We have stated that CPU utilization data belongs to incomplete data and assumed that the utilization within a time interval consists of an unobserved time and a successive observed time, respectively. Since data could be collected only during observed time, we try to use the EM algorithm to estimate the parameters. An EM algorithm aims to find the MLE for the $M_t/M/1/K$ queueing model from incomplete observation. The two steps of an EM algorithm is demonstrated as follows:

• Expectation step: The expected log-likelihood function is calculated using the posterior probabilities of the hidden variables. The equation is calculated as follows:

  $$\begin{array}{c}\hfill \mathrm{E}[logp(\mathcal{D},\mathcal{U};{\mathit{\theta }}^{\prime })],\end{array}$$

  (13)

  where $\mathcal{D}$ and $\mathcal{U}$ are the observed and missing data in an unobserved time interval, respectively. The ${\mathit{\theta }}^{\prime }$ is a vector of parameters to be estimated.
• Maximization step: The parameter $\mathit{\theta }$ is updated by maximizing the expected log-likelihood function found in the expectation step. The equation is shown below:

  $$\begin{array}{c}\hfill \mathit{\theta }=arg\; max\mathrm{E}[logp(\mathcal{D},\mathcal{U};{\mathit{\theta }}^{\prime })],\end{array}$$

  (14)

Then, the parameter estimates from the maximization step are used as the initial parameters in the next expectation step to determine the distribution of the latent variables. Finally, the optimal parameters can be obtained by iterating these two steps several epochs until convergence. The EM algorithm can represent the arrival rate ${\lambda }_{i,j}$ by

$$\begin{array}{c}\hfill {\lambda }_{i,j}=\frac{\mathrm{E}\left[N_{i,j}\right]}{\mathrm{E}\left[S_i\right]}=\frac{\mathrm{E}[N_{i,j}^{\mathit{U}}+N_{i,j}^{\mathit{O}}\mid \mathcal{D}]}{\mathrm{E}[S_i^{\mathit{U}}+S_i^{\mathit{O}}\mid \mathcal{D}]},\end{array}$$

(15)

where ${\lambda }_{i,j}$ is the arrival rate from i state to j state, $N_{i,j}$ is the number of transition from state i to state j, $S_i$ is the sojourn time in state i, $N_{i,j}^{\mathit{U}}$ is the number of transition from state i to state j at unobserved time period, $N_{i,j}^{\mathit{O}}$ is the number of transition from state i to state j at observed time period, $S_i^{\mathit{U}}$ is the sojourn time in state i at unobserved period and $S_i^{\mathit{O}}$ is the sojourn time in state i at observed period.

3.7. The Number of Time Intervals

n is is the total number of the divided time intervals in data collection time of T. n is a hyperparameter of the proposed approach. Different n determines different models. If n is too small, the estimated intensity function does not reflect the non-homogeneity property. For example, $n=1$ means that the NHPP is simplified to an HPP, while if n is too large, the estimated intensity function overreacts to small fluctuations, resulting in an overfitting phenomenon. To choose an appropriate n, we use the Akaike Information Criterion (AIC) [35] to quantify the goodness of the models. Note that a smaller AIC indicates a better fit of the model. Therefore, we choose the n when the AIC takes the minimum value. The formula is shown as follows:

$$\begin{array}{c}\hfill AIC=-2LLF+2(♯\mathrm{of}\mathrm{parameters}),\end{array}$$

(16)

where LLF denotes the maximum value of the log-likelihood function.

3.8. Superposition of Arrival Intensities

In the PaaS environment, the cloud server of Bitbrains provides computer platforms (e.g., CPUs) as a service by using a hardware virtualization technique. Therefore, the arrival process for the non-virtual CPU can be estimated by a superposition of the arrival process of virtual servers. Formally, define ${\lambda }^i\left(t\right)(i=1,\dots ,m)$ as the arrival intensity of NHPP for the i-th virtualized platform. Since the CPU task arrival processes for virtualized platforms can be regarded as independent stochastic processes, the CPU task arrival process in the PaaS is given by

$$\begin{array}{c}\hfill {\lambda }^{all}\left(t\right)=\sum _{i=1}^m{\lambda }^i\left(t\right).\end{array}$$

(17)

The procedure for the parameter estimation of the $M_t/M/1/K$ is summarized as in Algorithm 1.

Algorithm 1 Parameter estimation procedure for the $M_t/M/1/K$ model

Step 1: Divide the total time interval $[0,T]$ into n fixed periods: $$\begin{array}{c}\hfill 0=t_0<t_1<·<t_n=T;t_i=i\mathrm{\Delta }t\end{array}$$ Step 2: Approximate $\lambda \left(t\right)$ as a piecewise intensity function: $$\begin{array}{c}\hfill \lambda \left(t\right)\approx {\lambda }_i,(t_{i-1}<t\le t_i)\end{array}$$ Step 3: Determine parameters by maximizing the LLF: $$\begin{array}{c}\hfill (\widehat{{\lambda }_1},\dots ,\widehat{{\lambda }_n})=\underset{{\lambda }_1,\dots ,{\lambda }_n}{argmax}\log \mathrm{L}({\lambda }_1,\dots ,{\lambda }_n;\mathcal{D})\end{array}$$ Step 4: Select the optimal model by minimizing AIC: $$\begin{array}{c}\hfill \mathrm{AIC}=-2(\log -\mathrm{likelihood}-n)\end{array}$$ Step 5: Evaluate performance of the cloud datacenter (e.g., average response time).

Finally, we evaluate the performance of the integrated platform by using the estimated parameters, such as the arrival intensity and service rate.

4. Results

We randomly select five VMs from the $Rnd$ trace of Bitbrains and estimate their arrival intensities of $M_t/M/1/K$ queueing model from CPU utilization data. Then, we evaluate the average response time of the superposed platform. The service rate of the exponential distribution is set as $\mu =3$. Buffer size of the $M_t/M/1/K$ queueing model is set as $K=20$. Because Bitbrains monitors CPU utilization every $0.3$ s, we fix the unobserved and observed time length to $t_u=0.29$ s and $t_o=0.01$ s, respectively.

Figure 2 demonstrates CPU utilization data collected from five VMs. The CPU utilization collected from VM 1, VM 2, and VM 3 is dense. Their CPU utilization values vary drastically in the interval [0, 0.2], [0, 0.02], and [0, 0.1]. Compared with VM 1, VM 2, and VM 3, the CPU utilization data collected from VM 4 and VM 5 are more sparse, with their utilization data varying in the interval [0, 0.1]. Moreover, the five sets of data seem to have a certain periodicity, which is one of the reasons we choose the NHPP as the arrival stream of Bitbrains.

4.1. Results of Parameter Estimation

To get the optimal value of n, the AIC values are calculated.

Table 2. AIC values of the NHPP models with $n=1,2,\dots ,20$ for the five VMs.

n	VM 1		VM 2		VM 3		VM 4		VM 5
	LLF	AIC	LLF	AIC	LLF	AIC	LLF	AIC	LLF	AIC
1	3723.04	7448.08	2213.02	4428.04	3975.99	7953.98	−592.64	1187.28	3977.81	7957.62
2	3724.93	7453.86	2258.62	4521.24	3975.99	7955.98	−568.31	1140.62	3977.81	7959.62
3	3727.64	7461.28	2252.30	4510.60	3976.78	7959.56	−543.53	1093.06	3978.60	7963.20
4	3728.80	7465.60	2259.45	4526.90	3975.99	7959.98	−511.13	1030.26	3977.81	7963.62
5	3730.77	7471.54	2259.37	4528.74	3975.99	7961.98	−490.91	991.82	3977.81	7965.62
6	3731.20	7474.40	2258.76	4529.52	3974.40	7960.80	−493.50	999.00	3976.22	7964.44
7	3733.26	7480.52	2260.99	4535.98	3974.40	7962.80	−498.08	1010.2	3976.22	7966.44
8	3736.95	7489.90	2261.39	4538.78	3975.99	7967.98	−510.05	1036.1	3977.81	7971.62
9	3735.16	7488.32	2261.14	4540.28	3972.01	7962.02	−498.33	1014.7	3973.83	7965.66
10	3741.32	7502.64	2262.18	4544.36	3975.99	7971.98	−450.52	921.04	3977.81	7975.62
11	3741.63	7505.26	2270.92	4563.84	3979.96	7981.92	−440.00	902.00	3981.78	7985.56
12	3728.69	7481.38	2256.75	4537.50	3969.62	7963.24	−440.40	904.80	3971.44	7966.88
13	3727.72	7481.44	2262.06	4550.12	3969.62	7965.24	−457.46	940.92	3971.44	7968.88
14	3733.88	7495.76	2261.93	4551.86	3974.40	7976.80	−463.62	955.24	3976.22	7980.44
15	3735.56	7501.12	2263.24	4556.48	3972.01	7974.02	−456.38	942.76	3973.83	7977.66
16	3740.05	7512.10	2258.22	4548.44	3969.62	7971.24	−458.24	948.48	3971.44	7974.88
17	3749.15	7532.30	2265.31	4564.62	3974.40	7982.80	−432.36	898.72	3976.22	7986.44
18	3755.99	7547.98	2268.34	4572.68	3979.17	7994.34	−440.88	917.76	3980.99	7997.98
19	3753.52	7545.04	2263.81	4565.62	3973.60	7985.20	−424.02	886.04	−3975.42	7988.84
20	3759.30	7558.60	2266.39	4572.78	3975.99	7991.98	−429.57	899.14	3977.81	7995.62

exhibits the AIC values, where $n=1,2,\dots ,20$ for the five VMs. From the table, the optimal number of the time intervals of the five VMs can be obtained when the values of AIC are the smallest (i.e., 7448.08 for VM 1, 4428.04 for VM 2, 7953.98 for VM 3, 886.04 for VM 4, and 7957.62 for VM 5). The optimal number of the n are $n_1=1,n_2=1,n_3=1,n_4=19$, and $n_5=1$ for the five VMs. The five estimated intensity functions are demonstrated in Figure 3.

From Figure 3, we can find that the task arrival rates for VM1, VM2, VM3, and VM5 are $3.60,3.08,3.72$, and $0.43$. In other words, the four VMs obey four HPPs, not the NHPPs. Furthermore, since the AIC of VM 4 is smallest when $n=19$, the NHPP arrivals of VM 4 can be approximated as 19 HPPs with different arrival rates, and the arrival rate is reached to the maximum in the 17th time interval. In summary, the estimated arrival rate from the CPU utilization of VM 3 is the largest and the arrival process obeys an HPP, while the estimated arrival rate from VM 4 is the smallest and the arrival obeys an NHPP.

4.2. Results of Performance Evaluation

Finally, we evaluate performance in the scenario of the integrated systems using the estimated arrival rates and intensity function. According to Equation (17), we can calculate the integrated arrival intensity function ${\lambda }^{all}\left(t\right)$. Using ${\lambda }^{all}\left(t\right)$, we can simulate arrival streams whose arrival intensity obeys ${\lambda }^{all}\left(t\right)$. Thus, we can get the arrival time of each task in the arrival stream. Then, by simulating processing times that obey an exponential distribution, we can similarly simulate the CPU processing time for each task. Finally, using the arrival time and processing time, we can calculate the average response time of the arrival stream. The algorithm is shown in Algorithm 2.

Algorithm 2 Performance evaluation for the $M_t/M/1/K$ model

Step 1: Calculate the intensity function ${\lambda }^{all}\left(t\right)$ of the integrated system, which obeys NHPP according to Equation (17): $$\begin{array}{c}\hfill {\lambda }^{all}\left(t\right)=\sum _{i=1}^m{\lambda }^i\left(t\right).\end{array}$$ Step 2: Simulate the arrival times ($t_{arr}$) whose arrival intensity obeys ${\lambda }^{all}\left(t\right)$: $$\begin{array}{c}\hfill \mathrm{Simulated}\mathrm{arrival}\mathrm{times}:t_{arr}^1,t_{arr}^2,\cdots ,t_{arr}^{1000}.\end{array}$$ Step 3: Simulate the service time ($t_{ser}$) for an exponential distribution with service rate $\mu$: $$\begin{array}{c}\hfill \mathrm{Simulated}\mathrm{service}\mathrm{times}:t_{ser}^1,t_{ser}^2,\cdots ,t_{ser}^{1000}.\end{array}$$ Step 4: Calculate the average response time ($T_{res}$).

Table 3. An example of the calculation of response times.

Process	Arrival Time (${\mathit{t}}_{\mathit{arr}}$)	Service Time (${\mathit{t}}_{\mathit{ser}}$)	Response Time (${\mathit{t}}_{\mathit{res}}$)
P1	0 ms	8 ms	0 ms
P2	1 ms	7 ms	7 ms
P3	2 ms	10 ms	13 ms

shows an example of the calculation of response times. During the processing of the first arrival (P1), P2 has to wait for 8 ms before it can be processed. In addition, the arrival time of P2 is 1 ms. Therefore, the response time of P2 is $8-1=7$ ms. Similarly, the arrival of P3 has to keep waiting until P1 and P2 are served (i.e., after $8+7=15$ ms). Since the arrival time of P3 is 2 ms, the response time of P3 is $15-2=13$ ms.

We conduct ten loops and calculate the average response times. The average response times of the superposition of the five VMs are evaluated by changing the service rate from $\mu =10$ to $\mu =30$. The results are given in

Table 4. Average response times of the $M_t/M/1/K$ queueing model.

$\mathbf{Service}\mathbf{Rate}\mathit{\mu }$	${\mathit{T}}_{\mathit{res}}\left(\mathit{s}\right)$	$\mathbf{Service}\mathbf{Rate}\mathit{\mu }$	${\mathit{T}}_{\mathit{res}}\left(\mathit{s}\right)$
11	12.680	21	0.196
12	8.127	22	0.168
13	4.904	23	0.150
14	3.057	24	0.156
15	1.687	25	0.116
16	0.815	26	0.113
17	0.621	27	0.103
18	0.554	28	0.105
19	0.311	29	0.089
20	0.354	30	0.085

. Furthermore, to make the response times more intuitive, we make the the results of Table 4 into Figure 4.

When the service rate is small ($\mu \le 15$), the average response times of the integrated system tend to be very large ($T_{res}\ge 1.687$ s). With the increase of service rate ($\mu \ge 16$), the effect of $\mu$ on the average response times becomes smaller. In other words, as a designer of a cloud computing platform, at least 16 CPUs need to be designed to meet user requirements. As a cloud computing provider, 16 CPUs are good enough to provide cloud computing services. Therefore, 16 CPUs can be allocated to all users in the interval of [0, T]. As a user of a cloud computing, we can choose an appropriate number of CPUs to balance performance and cost.

5. Conclusions

In this paper, we have modeled the behavior of five VMs of Bitbrains by using an $M_t/M/1/K$ queueing model. In particular, the model parameters were estimated by approximating an NHPP using a series of discrete HPPs and the MLE with EM algorithm. The performance of the integrated virtual platform was evaluated based on the superposition of the estimations of five VMs.

However, our proposed approach have a main limitation. In general, a cloud data center contains a large number of physical machines and virtual machines. For each virtual machine, the arrival and service rates of the tasks can be calculated independently. Therefore, the parameters of each virtual machine can be estimated in a distributed manner. However, due to hardware limitations, we cannot compute the parameters of each virtual machine. In this paper, we estimated the parameters for five VMs.

In the future, we would like to address the above limitation first. We would like to evaluate all the arrival processes of the VMs in Bitbrians in a distributed manner offline. Due to the fundamental weaknesses of an EM algorithm, the iterative convergence process is time-consuming. Therefore, we would choose a faster iterator, such as the Adam, for the parameter estimation. Finally, the performance of the whole cloud computing platform can be evaluated, which is meaningful for the cloud service providers and users.

In addition, a $MAP/M/1/K$ assumption will be considered to estimate the arrival rates and evaluate the system performance. As a generalization of an NHPP, a MAP takes account of the dependency between consecutive arrivals and is often used to model complex, bursty, and correlated traffic streams. Therefore, we would like to concentrate on the MAP parameter estimation of quasi-birth-death queueing systems using utilization data.