Accurate Approximation of the Matrix Hyperbolic Cosine Using Bernoulli Polynomials

Abstract

This paper presents three different alternatives to evaluate the matrix hyperbolic cosine using Bernoulli matrix polynomials, comparing them from the point of view of accuracy and computational complexity. The first two alternatives are derived from two different Bernoulli series expansions of the matrix hyperbolic cosine, while the third one is based on the approximation of the matrix exponential by means of Bernoulli matrix polynomials. We carry out an analysis of the absolute and relative forward errors incurred in the approximations, deriving corresponding suitable values for the matrix polynomial degree and the scaling factor to be used. Finally, we use a comprehensive matrix testbed to perform a thorough comparison of the alternative approximations, also taking into account other current state-of-the-art approaches. The most accurate and efficient options are identified as results.

1. Introduction

Due to their use in many engineering and scientific applications, the numerical computation of matrix functions has received remarkable and growing attention in recent years. For instance, the efficient evaluation of matrix functions is part of reduced-order models [1] and (pp. 275–303 in [2]), image denoising [3] and graph neural networks [4], among other applications.

The field of approximation theory for matrix functions is quite extensive (see, e.g., the corresponding chapters of [5]). The best-known methods are based on rational or polynomial approximations, or on different matrix decomposition techniques (e.g., Schur).

Among the different matrix functions, the hyperbolic ones must be highlighted. A set of state-of-the-art algorithms developed by the authors to calculate matrix hyperbolic sine and cosine functions can be found in [6,7,8,9,10]. Very recent generalizations of these matrix functions can also be found in references [11,12]. Among many others fields, hyperbolic sine and cosine functions are applied in the study of communicability analysis in complex networks [13,14] or to construct the exact series solution of coupled hyperbolic systems [15,16]. Additionally, algorithms for the matrix inverse hyperbolic cosine and sine are included in [17], while methods for computing the action of the hyperbolic cosine or sine of a matrix on a vector are provided in [18,19].

On the other hand, different numerical methods have been recently proposed for the effective calculation of the matrix hyperbolic tangent function [20]. This matrix function is used, for example, to give an analytical solution of the radiative transfer equation [21], in the heat transference field [22,23], in the study of symplectic systems [24,25], in graph theory [26] and in the development of special types of exponential integrators [27,28].

In addition, the generalizations of some well-known classical special functions into matrix frameworks are important both from the theoretical and applied points of view. These new extensions (Laguerre, Hermite, Chebyshev, Jacobi matrix polynomials, etc.) have proved to be very useful in various fields, such as physics, engineering, statistics and telecommunications. Recently, Bernoulli polynomials $B_n\left(x\right)$, which are defined in [29] as the coefficients of the generating function

$$g(x,t)=\frac{t{e}^{tx}}{e^t-1}=\sum _{n\ge 0}\frac{B_n\left(x\right)}{n!}{t}^n,\left|t\right|<2\pi ,$$

(1)

and which have the explicit expression for $B_n\left(x\right)$

$$B_n\left(x\right)=\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right){\mathcal{B}}_k{x}^{n-k},$$

(2)

where the Bernoulli numbers are defined by ${\mathcal{B}}_n=B_n\left(0\right)$, satisfying the explicit recurrence

$${\displaystyle {\mathcal{B}}_0=1,{\mathcal{B}}_n=-\sum _{k=0}^{n-1}\left(\genfrac{}{}{0pt}{}{n}{k}\right)\frac{{\mathcal{B}}_k}{n+1-k},n\ge 1,}$$

(3)

were generalized to the matrix framework in [30]. Excluding ${\mathcal{B}}_1=-0.5$, all Bernoulli numbers ${\mathcal{B}}_n$, with n being an odd number, are null (see Appendix A, Remark A1, for the deduction of formula (3)).

For a matrix $A\in {\mathbb{C}}^{r\times r}$, the n-th Bernoulli matrix polynomial is defined by the expression

$$B_n\left(A\right)=\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right){\mathcal{B}}_k{A}^{n-k}.$$

(4)

For these matrix polynomials, we have the following series expansion of the matrix exponential function:

$$e^{At}=\left(\frac{e^t-1}{t}\right)\sum _{n\ge 0}\frac{B_n\left(A\right)t^n}{n!},\left|t\right|<2\pi .$$

(5)

To obtain practical approximations of the matrix exponential function using expression (5), we use the scaling and squaring technique [31,32]. This method is based on the well-known property of

$$e^A={\left(e^{A{2}^{-s}}\right)}^{2^s},$$

(6)

where $s\ge 0$ is an integer, called the scaling factor, to be determined in order to reduce the norm of matrix A appropriately. Let us take m as the approximation polynomial degree to be used. Then, from (5), using $t=1$, we have

$$e^{A{2}^{-s}}\approx \left(e-1\right)\sum _{n=0}^m\frac{B_n\left(A{2}^{-s}\right)}{n!}.$$

(7)

Once approximation (7) is computed, s squaring steps must be carried out to reverse the scaling effect to finally obtain $e^A$. As an objective of this work, an algorithm (described in Section 2) was developed to determine the most appropriate values of m and s.

The use of expansion (5) to approximate the matrix exponential function with good results of precision and computational cost can be found in [30]. For a matrix $A\in {\mathbb{C}}^{r\times r}$, using expression (5), we obtain (see Appendix A, Remark A2)

$$cosh\left(A\right)=sinh\left(1\right)\sum _{n\ge 0}\frac{B_{2n}\left(A\right)}{\left(2n\right)!}+\left(cosh\left(1\right)-1\right)\sum _{n\ge 0}\frac{B_{2n+1}\left(A\right)}{(2n+1)!}.$$

(8)

Notice that unlike what happens when considering hyperbolic cosine series expansions using Taylor or Hermite polynomials, all Bernoulli polynomials are needed in the development of $cosh\left(A\right)$ (and not just the even-numbered). However, this also possible by operating to obtain an alternative approximation to the matrix hyperbolic cosine where only polynomials of even degree appear, as follows (see Appendix A, Remark A3):

$$cosh\left(A\right)=sinh\left(1\right)\sum _{n\ge 0}\frac{2^{2n}{B}_{2n}\left(\frac{1}{2}(A+I)\right)}{\left(2n\right)!}.$$

(9)

Currently, few methods addressing the effective computation of the matrix hyperbolic cosine for matrices of non-trivial size are available in the literature, such as those appearing, e.g., in graph theory [14]. For instance, the work [33] (which presents the available software, according to the authors, for the computation of matrix functions) indicates only two codes for the computation of the matrix hyperbolic cosine (MATLAB’s funm function, based on the Schur–Parlett algorithm for general functions [34], and thfm, included in GNU Octave’s extra package linear-algebra and based on the computation of the matrix exponential function by means of expm).

Therefore, the main objective, and the novelty, of this work is to address that need for methods by designing, implementing and evaluating different algorithms for the computation of the matrix hyperbolic cosine by means of Bernoulli polynomials. Some of the methods proposed are based on approximations (8) and (9), and others are based on the computation of the matrix exponential using Bernoulli polynomials.

Hereafter, we denote, with ${\mathbb{C}}^{r\times r}$, the set of all complex square matrices of order r, as mentioned above, and with I, the identity matrix. Additionally, a matrix polynomial of degree m, for $A\in {\mathbb{C}}^{r\times r}$, is given by the expression $P_m\left(A\right)=p_{0}I+p_{1}A+\cdots +p_{m-1}{A}^{m-1}+p_m{A}^m$, where coefficients $p_i,0\le i\le m$, are complex numbers. The result of rounding a real number x to the nearest integer greater than or equal to x is denoted with $⌈x⌉$. Additionally, the result of rounding x to the nearest integer less than or equal to x is represented by $⌊x⌋$. Finally, matrix norm $∥·∥$ represents any subordinate matrix norm. In particular, ${∥·∥}_2$ stands for the traditional 2-norm.

The paper is organized as follows: In Section 2, three algorithms that compute the matrix hyperbolic cosine function are described. They are based either on the previous Bernoulli series expansions or on the theoretical definition of the matrix hyperbolic cosine in terms of the matrix exponential, which also derives from its series expansion based on Bernoulli polynomials. After the appropriate implementation of all these algorithms in their respective MATLAB codes, Section 3 presents an exhaustive comparison among all of them in order to choose the most appropriate one. For this purpose, numerous experiments were carried out, where their numerical and computational performance were evaluated against a widely heterogeneous testbed composed of three types of matrices. Finally, conclusions are given in Section 4.

2. The Proposed Algorithms

2.1. Algorithms Based on the Bernoulli Series of the Matrix Hyperbolic Cosine

By truncating series (8), one obtains the $m-$th order Bernoulli approximation to the matrix hyperbolic cosine (we assume that m is even for simplicity of exposition)

$$cosh\left(A\right)\approx P_m\left(A\right)=sinh\left(1\right)\sum _{n=0}^{m/2}\frac{B_{2n}\left(A\right)}{\left(2n\right)!}+\left(cosh\left(1\right)-1\right)\sum _{n=0}^{m/2-1}\frac{B_{2n+1}\left(A\right)}{(2n+1)!},$$

(10)

where polynomial $P_m$ can be expressed as

$$P_m\left(A\right)=\sum _{k=0}^m{p}_k^{\left(m\right)}{A}^k.$$

Similarly, by truncating series (9), the second alternative $m-$th order Bernoulli approximation to our target matrix function is obtained as

$$cosh\left(A\right)\approx sinh\left(1\right)\sum _{n=0}^{m/2}\frac{2^{2n}{B}_{2n}\left(\frac{1}{2}(A+I)\right)}{\left(2n\right)!},$$

(11)

which is a polynomial of order m with all odd-order terms being equal to zero. Thus, by defining $\overline{A}:=A^2$, we obtain a polynomial ${\overline{P}}_{\overline{m}}$ of order $\overline{m}=m/2$.

$$cosh\left(A\right)\approx {\overline{P}}_{\overline{m}}\left(\overline{A}\right)=\sum _{k=0}^{\overline{m}}{\overline{p}}_k^{\left(\overline{m}\right)}{\overline{A}}^k,$$

(12)

where $p_k^{\left(m\right)}$ and ${\overline{p}}_k^{\left(\overline{m}\right)}$ are coefficients dependent on order m and on the truncated series considered, respectively. These Bernoulli polynomial coefficients become more and more similar to those of the Taylor series as degree m of the polynomial increases. In the case of the polynomial from (12), the coefficients converge to the even-order coefficients of the Taylor series (with the odd-order coefficients being zero).

Algorithms 1 and 2 are related to the hyperbolic cosine computation of a matrix A using formulation (10) or (11), where the scaling and squaring technique is considered. In Line 1 of Algorithm 1 (Line 2 of Algorithm 2), the most appropriate values corresponding to order $m=m_k$ of the approximation polynomial and scaling parameter s are found out, attempting to reduce the norm of matrix A and calculate $cosh\left(A\right)$ as accurately as possible. That will be discussed in Section 2.3.

Next, in Line 2 of Algorithm 1 (Line 3 of Algorithm 2), matrix A is properly scaled, and in the following line, polynomial $P_{m_k}\left(A\right)$ or ${\overline{P}}_{m_k}\left(A\right)$ must be efficiently computed using methods such as those described in [35,36]. In our implementations, the Paterson–Stockmeyer method [35] was employed. In this procedure, assuming that polynomial order $m_k$ is chosen from the set

$$\mathbb{M}=\left\{m_1,m_2,\cdots \right\}=\left\{1,2,4,6,9,12,16,20,25,30,36,42,49,56,64,\cdots \right\},$$

powers $A^i$, $2\le i\le q$, must be calculated, where $q=⌈\sqrt{m_k}⌉$ or $q=\lfloor \sqrt{m_k}\rfloor$ is an integer divisor of $m_k$. With these matrix powers $A^i$, we can efficiently compute $P_{m_k}\left(A\right)$ as

$$\begin{array}{cc}\hfill P_{m_k}\left(A\right)& =\hfill \\ \hfill \left(\right((p_{m_k}{A}^q& +p_{m_k-1}{A}^{q-1}+p_{m_k-2}{A}^{q-2}+\cdots +p_{m_k-q+1}A+p_{m_k-q}I)A^q\hfill \\ \hfill & +p_{m_k-q-1}{A}^{q-1}+p_{m_k-q-2}{A}^{q-2}+\cdots +p_{m_k-2q+1}A+p_{m_k-2q}I)A^q\hfill \\ \hfill & +p_{m_k-2q-1}{A}^{q-1}+p_{m_k-2q-2}{A}^{q-2}+\cdots +p_{m_k-3q+1}A+p_{m_k-3q}I)A^q\hfill \\ \hfill & \cdots \hfill \\ \hfill & +p_{q-1}{A}^{q-1}+p_{q-2}{A}^{q-2}+\cdots +p_{1}A+p_{0}I,\hfill \end{array}$$

(13)

where k matrix products are involved.

Finally, in Lines 4–6 of Algorithm 1 (Lines 5–7 of Algorithm 2), $cosh\left(A\right)$ is appropriately recovered by repeatedly using the double-angle formula $cosh\left(2A\right)=2{cosh}^2\left(A\right)-I$.

Algorithm 1: Given a matrix $A\in {\mathbb{C}}^{r\times r}$, a minimum order $m_{lower}\in \mathbb{M}$ and a maximum order $m_{upper}\in \mathbb{M}$, this algorithm computes $C=cosh\left(A\right)$ with the Bernoulli series (10)

1 Select suitable values of $m_k\in \mathbb{M}$, $m_{lower}\le m_k\le m_{upper}$, and $s\in \mathbb{N}\cup \left\{0\right\}$ for the Bernoulli approximation (10) of $cosh\left(2^{-s}A\right)$ (see Section 2.3) 2 $A=2^{-s}A$ 3  $C=P_{m_k}\left(A\right)$ /*$\phantom{(}$ Compute $P_{m_k}\left(A\right)$ in (10) by (13)$\phantom{(}$ */ 4  for $i=1$ to s do /*$\phantom{(}$ Recover $cosh\left(A\right)$$\phantom{(}$ */ 5   $C=2C^2-I$ 6 end

Algorithm 2: Given a matrix $A\in {\mathbb{C}}^{r\times r}$, a minimum order $m_{lower}\in \mathbb{M}$ and a maximum order $m_{upper}\in \mathbb{M}$, this algorithm computes $C=cosh\left(A\right)$ with the Bernoulli series (11)

1 $\overline{A}=A^2$ 2 Select suitable values of $m_k\in \mathbb{M}$, $m_{lower}\le m_k\le m_{upper}$, and $s\in \mathbb{N}\cup \left\{0\right\}$, to approximate $cosh\left(2^{-s}A\right)$ using ${\overline{P}}_m\left(4^{-s}\overline{A}\right)$ (see Section 2.3) 3 $A=4^{-s}\overline{A}$ 4  $C={\overline{P}}_{m_k}\left(A\right)$ /*$\phantom{(}$ Compute ${\overline{P}}_{m_k}\left(A\right)$ in (12) by (13)$\phantom{(}$ */ 5  for $i=1$ to s do /*$\phantom{(}$ Recover $cosh\left(A\right)$$\phantom{(}$ */ 6   $C=2C^2-I$ 7 end

2.2. Algorithm Based on the Bernoulli Series of the Matrix Exponential

Another way to approximate the matrix hyperbolic cosine is by means of Algorithm 3, which uses the formula

$$cosh\left(A\right)=\frac{e^A+e^{-A}}{2},$$

(14)

and computes the matrix exponential by means of ([30] Algorithm 1), although in this paper, we use forward error analysis, as in the previous section, instead of the backward error used in [30].

Algorithm 3: Given a matrix $A\in {\mathbb{C}}^{r\times r}$, a minimum order $m_{lower}\in \mathbb{M}$ and a maximum order $m_{upper}\in \mathbb{M}$, this algorithm computes $C=cosh\left(A\right)$ with the Bernoulli series of the matrix exponential using the formula $cosh\left(A\right)=\frac{e^A+e^{-A}}{2}$

1 Select suitable values of $m_k\in \mathbb{M}$, $m_{lower}\le m_k\le m_{upper}$, and $s\in \mathbb{N}\cup \left\{0\right\}$ for the Bernoulli approximation of $e^{2^{-s}A}$ (see Section 2.3) 2 $A=2^{-s}A$ 3  $E_1={\tilde{P}}_{m_k}\left(A\right)$ and $E_2={\tilde{P}}_{m_k}(-A)$ by using (8) from [30] and (13) 4 for $i=1$ to s do /*$\phantom{(}$ Recover $e^A$ and $e^{-A}$$\phantom{(}$ */ 5   $E_1=E_1^2$ 6   $E_2=E_2^2$ 7 end 8 $C=\frac{E_1+E_2}{2}$

In Line 1, Algorithm 3 selects the suitable values of $m_k\in \mathbb{M}$ and $s\in \mathbb{N}\cup \left\{0\right\}$, according to Section 2.3, for computing the Bernoulli approximation to the matrix exponential using the scaling and squaring procedure. Once the norm of matrix A is reduced in Line 2 of Algorithm 3, then $E_1={\tilde{P}}_{m_k}\left(2^{-s}A\right)$ and $E_2={\tilde{P}}_{m_k}(-2^{-s}A)$ are calculated in Line 3, where ${\tilde{P}}_{m_k}$ is a polynomial approximation to the matrix exponential function by means of Bernoulli matrix polynomials, according to (8) from [30]. The evaluation of ${\tilde{P}}_{m_k}$ is performed using the Paterson–Stockmeyer method (13). Next, in Lines 4–7 of Algorithm 3, $e^A$ and $e^{-A}$ are recovered. Finally, $cosh\left(A\right)$ is computed in Line 8.

2.3. Selecting the Order of Polynomials and the Scaling Factor

The computation of scaling factor s and order m of the Bernoulli approximation in the previous three algorithms is based on the absolute or relative forward error, presented next. We first consider approximation polynomial $P_m$ derived from (10). Let m be a large enough value such that coefficients $p_i^{\left(m\right)}$ of Bernoulli approximation $P_m\left(A\right)$ from (10) to $cosh\left(A\right)$ are practically identical to those of the Taylor approximation. Then, the absolute forward error when computing $P_m\left(A\right)$ can be calculated and bounded as follows:

$$E_{af}\left(P_m\left(A\right)\right)=∥cosh\left(A\right)-P_m\left(A\right)∥\approx ∥\sum _{i>m}^{}{a}_i{A}^i∥,$$

(15)

where ${\displaystyle \sum _{i>m}}{a}_i{A}^i$ is the absolute forward error series of the Taylor approximation of order m.

Let $h_m\left(x\right)={\displaystyle \sum _{i>m}}{a}_i{x}^i$ and ${\tilde{h}}_m\left(x\right)={\displaystyle \sum _{i>m}}\left|a_i\right|x^i$. If Theorem 1.1 from [37] is applied, then

$$E_{af}\left(P_m\left(A\right)\right)\approx ∥h_m\left(A\right)∥\le {\tilde{h}}_m\left({\alpha }_m\right),$$

where

$${\alpha }_m=max\left\{{∥A^i∥}^{1/i}:i=m+1,m+2,\cdots ,2m+1\right\}.$$

Let

$${\Theta }_m=max\left\{\theta \ge 0:\sum _{i>m}\left|a_i\right|{\theta }^i\le u\right\},$$

(16)

where $u=2^{-53}$ is the unit roundoff in IEEE double-precision arithmetic.

If

$${\alpha }_m<{\Theta }_m,$$

(17)

then we have

$$E_{af}\left(P_m\left(A\right)\right)\approx ∥h_m\left(A\right)∥⩽{\tilde{h}}_m\left({\alpha }_m\right)⩽{\tilde{h}}_m\left({\Theta }_m\right)⩽u.$$

(18)

and scaling parameter s is 0.

However, if (17) is not fulfilled, then the smallest value of s, such that $2^{-s}{\alpha }_m<{\Theta }_m$, must be determined. In this case, we obtain

$$E_{af}\left(P_m\left(2^{-s}A\right)\right)\approx ∥h_m\left(2^{-s}A\right)∥⩽{\tilde{h}}_m\left(2^{-s}{\alpha }_m\right)⩽{\tilde{h}}_m\left({\Theta }_m\right)⩽u.$$

(19)

On the other hand, if $cosh\left(A\right)$ is also invertible and, once again, m is a sufficiently large value such that terms $p_i^{\left(m\right)}$ of Bernoulli approximation $P_m\left(A\right)$ to our goal matrix function are equivalent to those of the Taylor one, then the relative forward error corresponding to this approximation can be computed and bounded in the following way:

$$\begin{array}{c}{E}_{rf}\left(P_m\left(A\right)\right)=∥cosh{\left(A\right)}^{-1}\left(cosh\left(A\right)-P_m\left(A\right)\right)∥=\\ =∥I-cosh{\left(A\right)}^{-1}{P}_m\left(A\right)∥\approx ∥{\displaystyle \sum _{i>m}}{b}_i{A}^i∥,\end{array}$$

where ${\displaystyle \sum _{i>m}}{b}_i{A}^i$ is the relative forward error series of the Taylor approximation of order m.

Similarly to the case of the absolute forward error, let $g_m\left(x\right)={\displaystyle \sum _{i>m}}{b}_i{x}^i$ and ${\tilde{g}}_m\left(x\right)={\displaystyle \sum _{i>m}}\left|b_i\right|x^i$. Then, from ([37] Theorem 1.1), we have

$$E_{rf}\left(P_m\left(A\right)\right)\approx ∥g_m\left(A\right)∥\le {\tilde{g}}_m\left({\alpha }_m\right).$$

Let ${\widehat{\Theta }}_m$ be

$${\widehat{\Theta }}_m=max\left\{\theta \ge 0:\sum _{i>m}\left|b_i\right|{\theta }^i\le u\right\}.$$

(20)

If the condition

$${\alpha }_m<{\widehat{\Theta }}_m,$$

(21)

holds, then we have

$$E_{rf}\left(P_m\left(A\right)\right)\approx ∥g_m\left(A\right)∥⩽{\tilde{g}}_m\left({\alpha }_m\right)⩽{\tilde{g}}_m\left({\widehat{\Theta }}_m\right)⩽u.$$

(22)

Conversely, if (21) is not verified, then the smallest value of s, such that $2^{-s}{\alpha }_m<{\widehat{\Theta }}_m$, is established. In this case, we obtain

$$E_{rf}\left(P_m\left(2^{-s}A\right)\right)\approx ∥g_m\left(2^{-s}A\right)∥⩽{\tilde{g}}_m\left(2^{-s}{\alpha }_m\right)⩽{\tilde{g}}_m\left({\widehat{\Theta }}_m\right)⩽u.$$

(23)

The values of ${\Theta }_{m_k}$ and ${\widehat{\Theta }}_{m_k}$, $m_k\in \mathbb{M}$, for $E_{af}\left(P_{m_k}\left(A\right)\right)$ and $E_{rf}\left(P_{m_k}\left(A\right)\right)$, respectively, were computed using MATLAB Symbolic Math Toolbox. All of them appear in

Table 1. Values of ${\Theta }_{m_k}$ and ${\widehat{\Theta }}_{m_k}$, $m_k\in \mathbb{M}$, for $E_{af}\left(P_{m_k}\left(A\right)\right)$ and $E_{rf}\left(P_{m_k}\left(A\right)\right)$, respectively.

${\mathit{m}}_{\mathit{k}}$	${\mathbf{\Theta }}_{{\mathit{m}}_{\mathit{k}}}$	${\widehat{\mathbf{\Theta }}}_{{\mathit{m}}_{\mathit{k}}}$
1	$1.4901161193847656\times {10}^{-8}$	$1.4901161193847656\times {10}^{-8}$
2	$2.2719845183149197\times {10}^{-4}$	$2.2719845056098161\times {10}^{-4}$
4	$6.5633223103254337\times {10}^{-3}$	$6.5633004324626544\times {10}^{-3}$
6	$3.8138663224761025\times {10}^{-2}$	$3.8135350033771671\times {10}^{-2}$
9	$1.1495105955344324\times {10}^{-1}$	$1.1487736634745561\times {10}^{-1}$
12	$4.3834831618193604\times {10}^{-1}$	$4.3534267124176623\times {10}^{-1}$
16	$9.8107632446570958\times {10}^{-1}$	$9.5208962937681607\times {10}^{-1}$
20	$1.7042776030289366\times {10}^0$	$1.5057818246088250\times {10}^0$
25	$2.5674905431377995\times {10}^0$	$1.6432017599233490\times {10}^0$
30	$4.0560126128455938\times {10}^0$	$1.7809320553510379\times {10}^0$
36	$5.7109000664700984\times {10}^0$	$1.9262789521867196\times {10}^0$
42	$7.4825284953464246\times {10}^0$	$2.0820807241460830\times {10}^0$
49	$9.3385619211370852\times {10}^0$	$2.2421030188466875\times {10}^0$
56	$1.19081054947739435\times {10}^1$	$2.4876517018759325\times {10}^0$
64	$1.45559420698812616\times {10}^1$	$2.7461075372183124\times {10}^0$

.

An analogous study was carried out for Bernoulli approximation $cosh\left(A\right)\approx {\overline{P}}_{\overline{m}}\left(\overline{A}\right)$ from (12). In this case, we assume that $\overline{m}$ is a large enough value such that coefficients ${\overline{p}}_k^{\left(\overline{m}\right)}$ of polynomial ${\overline{P}}_{\overline{m}}$ are practically identical to the corresponding even-order coefficients of the Taylor approximation to $cosh\left(A\right)$, while the odd-order coefficients are zero. Then, the absolute forward error is

$$E_{af}\left({\overline{P}}_{\overline{m}}\left(\overline{A}\right)\right)=∥cosh\left(A\right)-{\overline{P}}_{\overline{m}}\left(\overline{A}\right)∥\approx ∥\sum _{i>2\overline{m}}{a}_i{A}^i∥=∥\sum _{i>\overline{m}}{\overline{a}}_i{\overline{A}}^i∥,$$

where $\overline{A}=A^2$, coefficients $a_i$ are from (15) and ${\overline{a}}_i=a_{2i}$. Similarly, the relative forward error is

$$E_{rf}\left({\overline{P}}_{\overline{m}}\left(\overline{A}\right)\right)=∥cosh{\left(A\right)}^{-1}\left(cosh\left(A\right)-{\overline{P}}_{\overline{m}}\left(\overline{A}\right)\right)∥\approx ∥\sum _{i>\overline{m}}^{}{b}_{2i}{\overline{A}}^i∥\approx ∥\sum _{i>\overline{m}}^{}{\overline{b}}_i{\overline{A}}^i∥,$$

where ${\overline{b}}_i=b_{2i}$.

Let ${\Theta }_{P_m}$ and ${\widehat{\Theta }}_{P_m}$ be the values of ${\Theta }_m$ and ${\widehat{\Theta }}_m$ for polynomial $P_m$ as defined in (16) and (20), respectively. We can analogously define the corresponding values for polynomial ${\overline{P}}_{\overline{m}}$, ${\Theta }_{{\overline{P}}_{\overline{m}}}$ and ${\widehat{\Theta }}_{{\overline{P}}_{\overline{m}}}$, and it is easy to see that ${\Theta }_{{\overline{P}}_{\overline{m}}}={\Theta }_{P_{2\overline{m}}}^2,{\widehat{\Theta }}_{{\overline{P}}_{\overline{m}}}={\widehat{\Theta }}_{P_{2\overline{m}}}^2$.

If the inequation ${\alpha }_{\overline{m}}<{\Theta }_{{\overline{P}}_{\overline{m}}}$ or ${\alpha }_{\overline{m}}<{\widehat{\Theta }}_{{\overline{P}}_{\overline{m}}}$ is not satisfied, then the smallest value of s is calculated such that $4^{-s}{\alpha }_{\overline{m}}<{\Theta }_{{\overline{P}}_{\overline{m}}}$ or $4^{-s}{\alpha }_{\overline{m}}<{\widehat{\Theta }}_{{\overline{P}}_{\overline{m}}}$, respectively, for absolute or relative forward error, where

$${\alpha }_{\overline{m}}=max\left\{{∥{\overline{A}}^i∥}^{1/i}:i=\overline{m}+1,\overline{m}+2,\cdots ,2\overline{m}+1\right\}.$$

The values of ${\Theta }_{{\overline{m}}_k}\equiv {\Theta }_{{\overline{P}}_{{\overline{m}}_k}}$ and ${\widehat{\Theta }}_{{\overline{m}}_k}\equiv {\widehat{\Theta }}_{{\overline{P}}_{{\overline{m}}_k}}$ are listed in

Table 2. Values of ${\Theta }_{{\overline{m}}_k}$ and ${\widehat{\mathbf{\Theta }}}_{{\overline{m}}_k}$, ${\overline{m}}_k\in \mathbb{M}$, for $E_{af}\left({\overline{P}}_{{\overline{m}}_k}\left(\overline{A}\right)\right)$ and $E_{rf}\left({\overline{P}}_{{\overline{m}}_k}\left(\overline{A}\right)\right)$, respectively, for Series (12).

${\overline{\mathit{m}}}_{\mathit{k}}$	${\mathbf{\Theta }}_{{\overline{\mathit{m}}}_{\mathit{k}}}$	${\widehat{\mathbf{\Theta }}}_{{\overline{\mathit{m}}}_{\mathit{k}}}$
1	$5.1619136514626776\times {10}^{-8}$	$5.1619135937310811\times {10}^{-8}$
2	$4.3077199749215582\times {10}^{-5}$	$4.3076912566764470\times {10}^{-5}$
4	$1.3213746092459254\times {10}^{-2}$	$1.3196809298927527\times {10}^{-2}$
6	$1.9214924629953856\times {10}^{-1}$	$1.8952324140391652\times {10}^{-1}$
9	$1.7498015129635465\times {10}^0$	$1.5605489459377038\times {10}^0$
12	$6.5920076891020321\times {10}^0$	$2.7025357197364501\times {10}^0$
16	$2.10870186062700462\times {10}^1$	$3.3425537406235706\times {10}^0$
20	$4.73520019672591133\times {10}^1$	$4.1166704209376803\times {10}^0$
25	$9.94413296329754246\times {10}^1$	$5.3203288339799650\times {10}^0$
30	$1.74869078212905435\times {10}^2$	$6.8352932849387500\times {10}^0$
36	$2.979204830753341753\times {10}^2$	$9.1455271414679480\times {10}^0$
42	$4.576519665452191248\times {10}^2$	$1.20985467228657093\times {10}^1$
49	$6.913637319746218282\times {10}^2$	$1.65236965866542853\times {10}^1$
56	$9.767604294039372235\times {10}^2$	$2.22163895347595428\times {10}^1$
64	$1.3667813478651733021\times {10}^3$	$3.05920634266714515\times {10}^1$

.

Finally, absolute and relative forward error series were also taken into account for the approximation of the matrix exponential in Algorithm 3 using matrix polynomial ${\tilde{P}}_m$.

Table 3. Values of ${\Theta }_{m_k}$ and ${\widehat{\Theta }}_{m_k}$, $m_k\in \mathbb{M}$, for the forward absolute and relative errors, $E_{af}\left(P_{m_k}\left(A\right)\right)$ and $E_{rf}\left(P_{m_k}\left(A\right)\right)$, of the exponential matrix.

${\mathit{m}}_{\mathit{k}}$	${\mathbf{\Theta }}_{{\mathit{m}}_{\mathit{k}}}$	${\widehat{\mathbf{\Theta }}}_{{\mathit{m}}_{\mathit{k}}}$
1	$1.4901161156840223\times {10}^{-8}$	$1.4901161119832789\times {10}^{-8}$
2	$8.7334702258487179\times {10}^{-6}$	$8.7334575136353609\times {10}^{-6}$
4	$1.6783942982781048\times {10}^{-3}$	$1.6780188443217515\times {10}^{-3}$
6	$1.7764527083684662\times {10}^{-2}$	$1.7730821996540237\times {10}^{-2}$
9	$1.1483174747739708\times {10}^{-1}$	$1.1376892457878242\times {10}^{-1}$
12	$3.3521368782861483\times {10}^{-1}$	$3.2805420180372574\times {10}^{-1}$
16	$8.2460319163860885\times {10}^{-1}$	$7.9127401766002403\times {10}^{-1}$
20	$1.5041473223951629\times {10}^0$	$1.4150704475615321\times {10}^0$
25	$2.5585766884181380\times {10}^0$	$2.3536427669894273\times {10}^0$
30	$3.7810696269831392\times {10}^0$	$3.4118771725567707\times {10}^0$
36	$5.4064650937902918\times {10}^0$	$4.7855459552778310\times {10}^0$
42	$7.1556200904384877\times {10}^0$	$6.2345518738859917\times {10}^0$
49	$9.3073843996022152\times {10}^0$	$7.9882499230847923\times {10}^0$
56	$1.1545348315212191\times {10}^1$	$9.7882040407606592\times {10}^0$
64	$1.4179107337111319\times {10}^1$	$1.1884024795730356\times {10}^1$

collects the corresponding values of ${\Theta }_{m_k}$ and ${\widehat{\Theta }}_{m_k}$ for $E_{af}\left({\tilde{P}}_{m_k}\left(A\right)\right)$ and $E_{rf}\left({\tilde{P}}_{m_k}\left(A\right)\right)$.

Taking into account the precomputed values of ${\Theta }_{m_k}$ and ${\widehat{\Theta }}_{m_k}$ of Table 1, Table 2 and Table 3, Algorithm 4 computes the most appropriate values of polynomial order m and scaling parameter s. In fact, Algorithm 4 is an improvement on [38]’s Algorithm 4, where it is explained in further detail. The main difference with respect to [38] is that the new code can be used to determine the values of m and s independently of the nature of the error, covering relative, absolute, forward and backward errors. This is accommodated by means of Line 8 in Algorithm 4, which takes into account that the first non-zero term occupies position $m_i$, for the relative backward error series, or $m_i+1$, for the absolute/relative forward or absolute backward error ones. Moreover, the new code is valid for matrix functions such as exponential, cosine and hyperbolic cosine by simply varying the corresponding values of ${\Theta }_m$, always according to the type of error considered. For simplicity, in Algorithm 4, we use $\Theta$ to refer to $\Theta$ or $\widehat{\Theta }$ of the corresponding polynomial, depending on the type of error considered, and we also use the following notation:

$${\alpha }_i\equiv {\alpha }_{m_i},{\Theta }_i\equiv {\Theta }_{m_i}.$$

Additionally, ${\alpha }_m$ is approximated as ${\alpha }_m\approx {\parallel A^m\parallel }^{1/m}$, as justified in [38]. In line 18, $p_{m_i}$ is the highest-order coefficient of the approximating polynomial.

Algorithm 4: Given a matrix $A\in {\mathbb{C}}^{r\times r}$, a minimum order $m_{lower}\in \mathbb{M}$ and a maximum order $m_{upper}\in \mathbb{M}$, this algorithm provides an order $m\in \mathbb{M}$, $m_{lower}\le m\le m_{upper}$, a scaling factor s and the necessary powers of A to compute $cosh\left(A\right)$ or $exp\left(A\right)$

1 $A_1=A$; $i=lower$; $f=0$ 2 for $j=2$ to $\lceil \sqrt{m_i}\rceil$do 3   $A_j=A_{j-1}A$ 4 end 5 while $f=0$ and $i\le upper$ do 6   $v=\sqrt{m_i}$; $j=⌈v⌉$ 7   if $j>v$ then $A_j=A_{j-1}A$ 8   Compute $a_i\approx ∥A^k∥$ from $A^j$, and maybe from A /*$\phantom{(}$$k=m_i$ (relative backward error) or $k=m_i+1$ (absolute / relative forward error or absolute backward error)$\phantom{(}$ */ 9   ${\alpha }_i=\sqrt[k]{a_i}$ 10   if ${\alpha }_i<{\Theta }_i$ then $f=1$ 11   else $i=i+1$ 12 end 13 if $f=1$ then $s=0$ 14 else 15   $i=upper$ 16   $s=max\left(0,⌈f_s{log}_2({\alpha }_i/{\Theta }_i)⌉\right)$ /* $\phantom{(}$$f_s=1$ for Algorithms 1 and 3, $f_s=0.5$ for Algorithm 2 $\phantom{(}$ */ 17   while $f=0$ do 18     if $s>0$ and $|p_{m_i}|a_i{r}^{(1-s)m_i}<u$ then $s=s-1$ /* $\phantom{(}$$r=2$ (Algorithms 1 or 3) or $r=4$ (Algorithm 2) $\phantom{(}$ */ 19     else $f=1$ 20   end 21 end 22 $m=m_i$

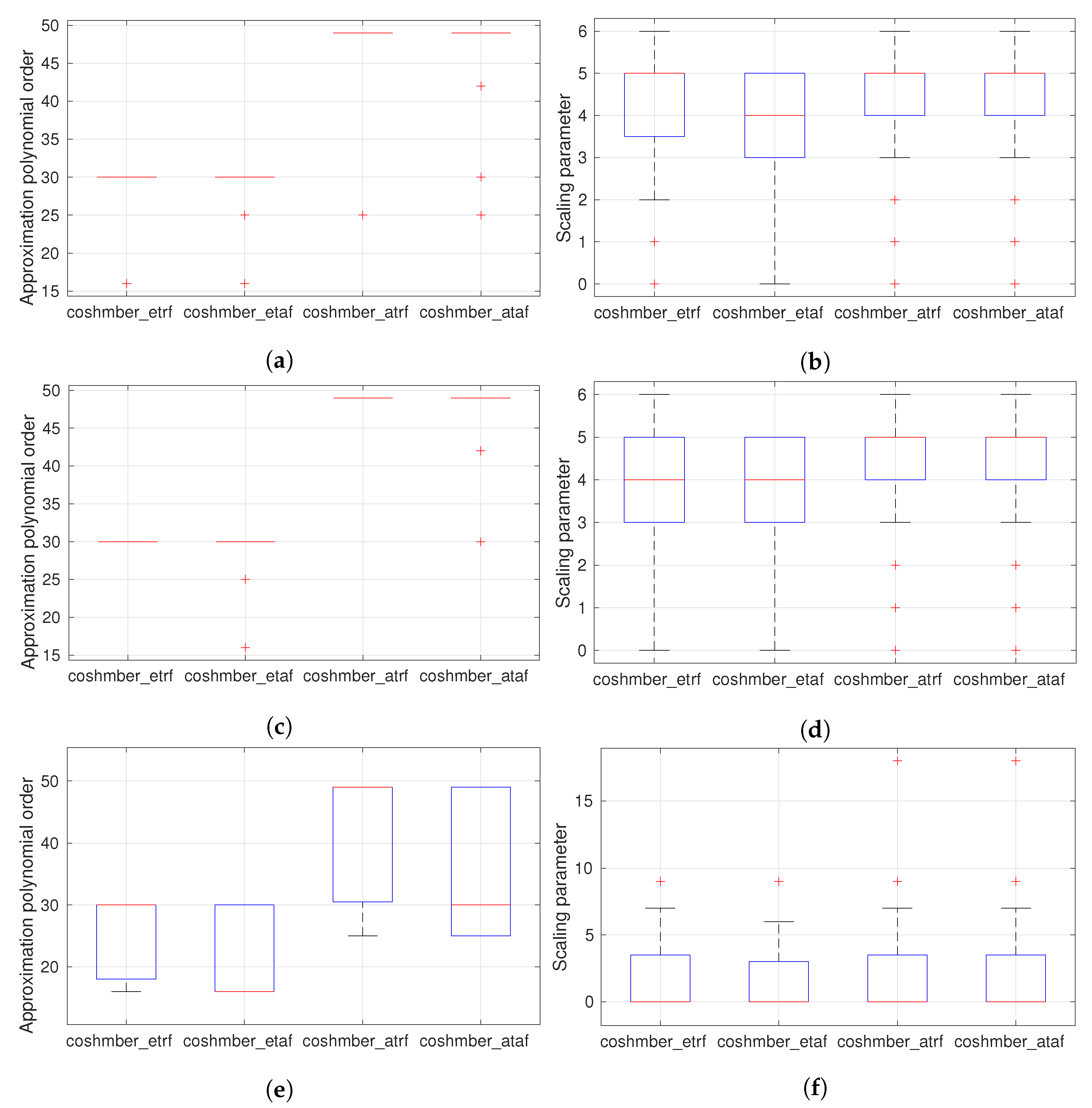
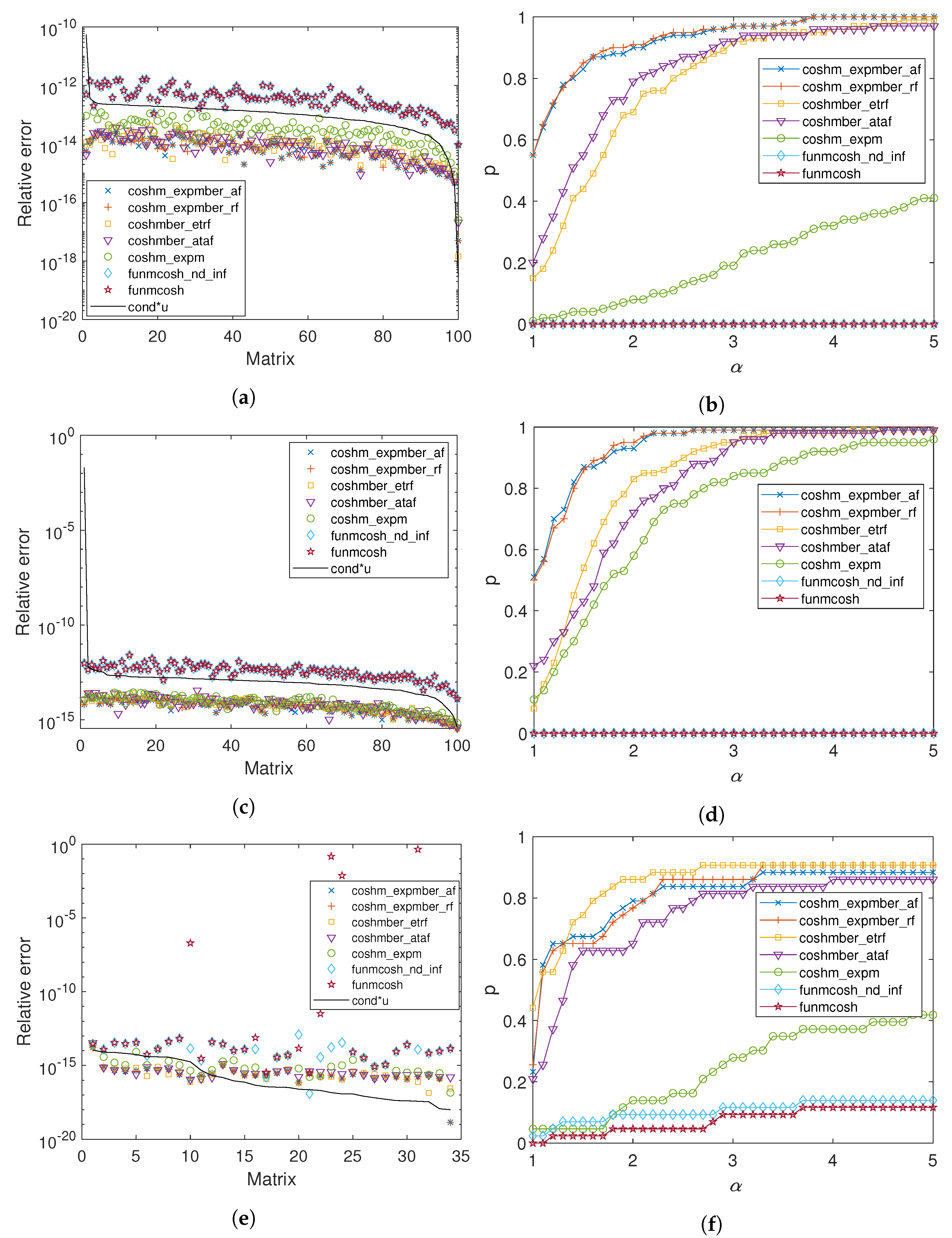
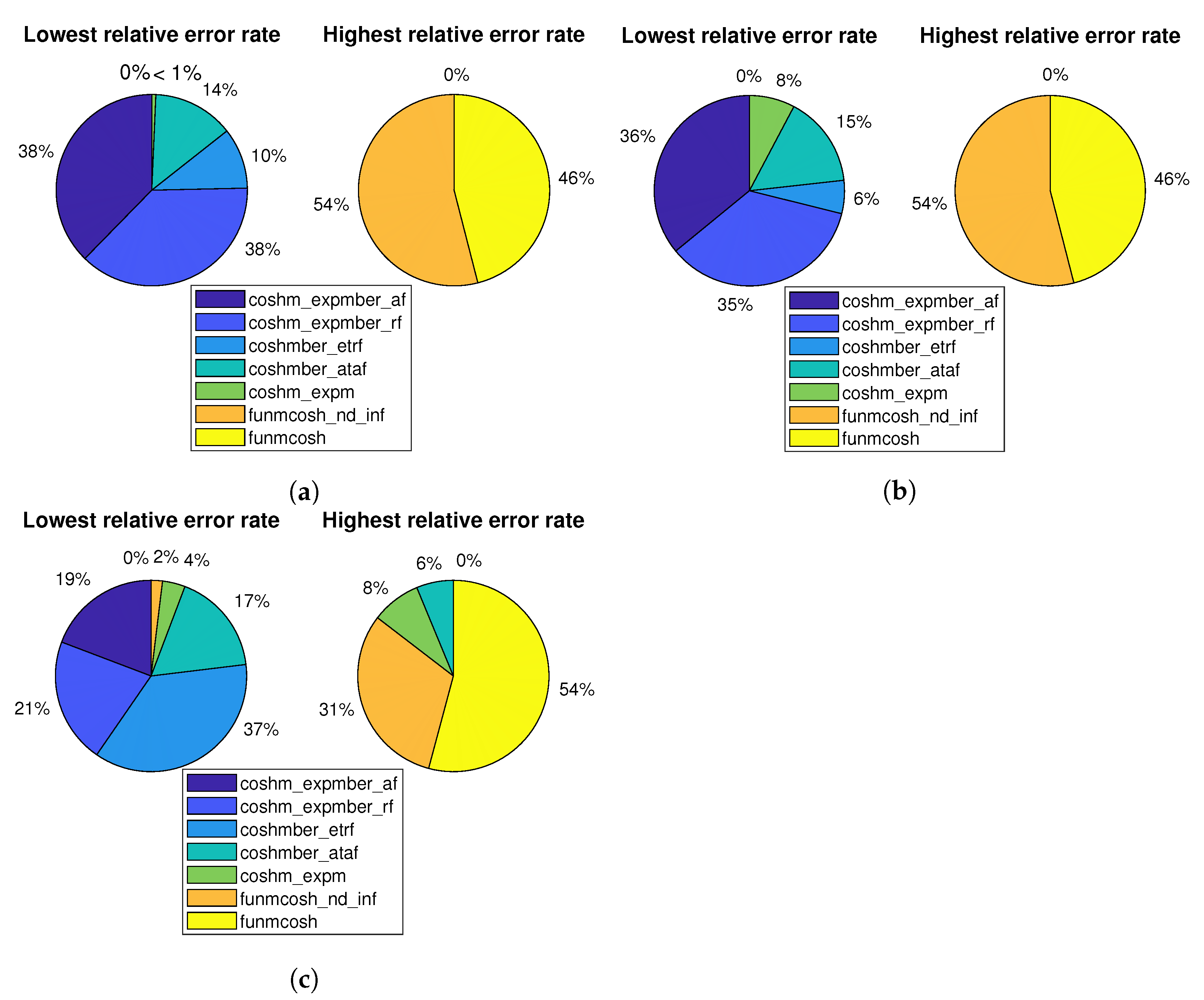
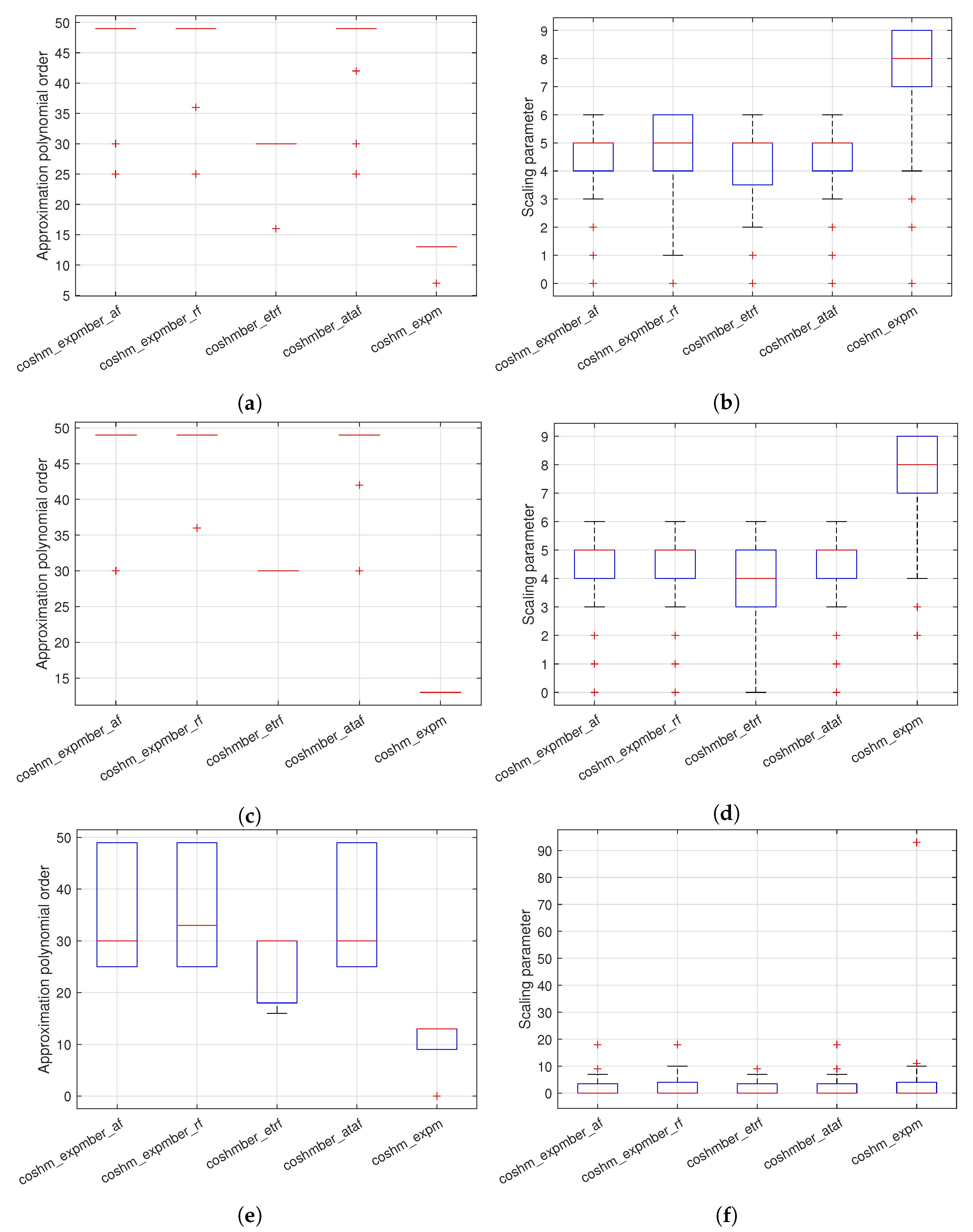
3. Computational Experiments

In this section, a whole set of experiments carried out in order to compare the numerical and computational performance of the proposed algorithms are presented. For this purpose, the following codes, implemented in MATLAB programming language, were evaluated:

• coshmber_ataf and coshmber_atrf: They correspond to the coding of Algorithm 1, using the absolute or relative forward error, respectively. Polynomial degree m takes values from the set $\left\{25,30,36,42,49\right\}$.
• coshmber_etaf and coshmber_etrf: They are implementations of Algorithm 2, after considering the absolute or relative forward error. The values of $m\in \left\{16,20,25,30\right\}$.
• coshm_expmber_af and coshm_expmber_rf: These functions include the implementation of Algorithm 3, where the absolute or relative forward error is correspondingly taken into account. Again, the values of $m\in \left\{25,30,36,42,49\right\}$.
• coshm_expm: This code also employs formula (14), but alternatively to the above ones (coshm_expmber_af and coshm_expmber_rf), the matrix exponential is computed by means of the code of MATLAB built-in function expm. Recall that function expm works out the matrix exponential combining the scaling and squaring technique with the Padé approximation [32,39].
• funmcosh: It consists of a short function that invokes the MATLAB built-in function funm to compute the matrix hyperbolic cosine. Function funm employs a Schur decomposition with reordering and blocking, and a block recurrence of Parlett [34]. It supports the matrix cosine, sine, hyperbolic cosine and hyperbolic sine. The derivatives of the matrix function to be approximated are also needed and computed.
• funmcosh_nd_inf: As in the previous case, it is just a simple code that calls function funm_nd_inf, implemented in [40], to calculate the hyperbolic cosine. More specifically, function funm_nd_inf is based on a multi-precision Schur–Parlett algorithm ([40] Algorithm 5.1) that does not require the matrix function derivatives. As blocking parameter $\delta$ is set to ∞ (no blocking), the whole Schur factor T is computed by [40]’s Algorithm 4.1.
  It is worth noting that, although function funm_nd, which is also implemented in [40] and which employs a value of $\delta =0.1$, could have been used instead of function funm_nd_inf, the latter was finally chosen because it provided more accurate results in the different numerical experiments performed.

In the subsequent computational experiments, the following three sets of matrices were selected in an attempt to provide a test battery as numerically heterogeneous as possible. The “exact" value of the matrix hyperbolic cosine function was computed by means of MATLAB Symbolic Math Toolbox and the vpa (variable-precision floating-point arithmetic) function with 256 significant digits:

• Set 1: A total of 100 diagonalizable square complex matrices of order 128, generated as $A=V·D·V^{-1}$. V is an orthogonal matrix such that $V=H/\sqrt{n}$, with H being a Hadamard matrix and n its number of rows or columns, while D is a random diagonal matrix with complex eigenvalues. The 2-norm of the matrices varied from 0.1 to 350. The “exact" matrix hyperbolic cosine was computed as $cosh\left(A\right)=V·cosh\left(D\right)·V^T$ using the vpa function.
• Set 2: A total of 100 non-diagonalizable square complex matrices of size 128 and generated as $A=V·J·V^{-1}$. V is a matrix determined in exactly the same way as in the case of the previous set. However, J is a Jordan matrix with complex eigenvalues whose modules are less than five and with random algebraic multiplicity from 1 to 3. The 2-norm varied from 3.76 to 339.11. The matrix hyperbolic cosine was also “exactly" computed by means of the vpa function as $cosh\left(A\right)=V·cosh\left(J\right)·V^{-1}$.
• Set 3: A total of 72 square matrices of dimension 128, 52 of which are from Matrix Computation Toolbox (MCT) [41] and 20 from Eigtool MATLAB Package (EMP) [42]. Unfortunately, only 44 of these matrices (36 of MCT and 8 of EMP) could be successfully employed. The remaining matrices had to be excluded owing to the following reasons:

  -

  Their “exact" solution could not be computed: matrices 4, 5, 10, 16, 17, 18, 21, 25, 26, 35, 40, 42, 43, 44 and 49 from MCT and matrices 1, 5, 6, 7, 9 and 15 from EMP.

  -

  The relative error made by all the codes was too high due to their ill conditioning: matrix 2 from MCT and matrices 3 and 10 from EMP.

  -

  They were repetitive (already present in MCT): matrices 8, 11, 13 and 16 from EMP.

  The “exact" calculation of the hyperbolic cosine of these matrices was performed in the following way:

  -

  First, from initial matrix A and by means of the eig MATLAB function, a diagonal matrix D of eigenvalues and a matrix V whose columns were the corresponding eigenvectors were provided, such that $A=V·D·V^{-1}$. Thus, matrix $C_1=V·cosh\left(D\right)·V^{-1}$ was worked out.

  -

  Second, matrix $C_2=cosh\left(A\right)$ was computed as the approximation to the hyperbolic cosine of matrix A through the scaling and squaring algorithm and Taylor polynomials using the vpa function.

  -

  Finally, matrix $C_1$ was accepted as the “exact" solution in the calculation of the hyperbolic cosine of A if it was satisfied that

  $$\frac{{∥C_1-C_2∥}_2}{{∥C_1∥}_2}\le u.$$

  Otherwise, matrix A was not part of the matrices of set 3.

All the executions were carried out on a Microsoft Windows 11 x64 PC equipped with an Intel Core i7-12700H processor and 32 GB of RAM, using MATLAB R2021b.

Henceforth, the normwise relative error made by each of the methods in the hyperbolic cosine computation for each test matrix was one of the key aspects to consider when comparing their goodness. This normwise relative error was obtained as follows:

$$\mathrm{E}\mathrm{r}\left(\mathrm{A}\right)=\frac{\parallel cosh\left(A\right)-\widetilde{cosh}{\left(A\right)\parallel }_2}{{∥cosh\left(A\right)∥}_2},$$

where $cosh\left(A\right)$ corresponds to the exact solution and $\widetilde{cosh}\left(A\right)$ corresponds to the calculated one.

 Experiment 1. 

In this experiment, we compared the codes corresponding to Algorithms 1 and 2 (coshmber_ataf, coshmber_atrf, coshmber_etaf and coshmber_etrf) using the three matrix sets.

Figure 1a,c,e show the normwise relative errors of the matrix hyperbolic cosine computed with those codes, with the solid line representing the value of $k_{cosh}u$, where $k_{cosh}$ is the estimated condition number of the matrix hyperbolic cosine function, obtained using function funm_condest1 from Higham’s Matrix Function Toolbox [5,43], and $u=2^{-53}$ is the unit roundoff error. Thus, the solid line is an indication of the expected relative error. The results show the stability of the methods, especially when applied to the matrices of sets 1 and 2, for which the relative error remained below the solid line. Although the results were more irregular for the third matrix set, the error values were small in all cases. We can also see in Figure 1e that coshmber_etaf produced the highest error for a considerable number of matrices of set 3.

It should be noted that nine matrices of the third set are excluded from Figure 1e because their estimated condition number $k_{cosh}$ was too high. The same is also performed in Figure 4e, which is referenced later. These matrices were number 6, 7, 12, 15, 23, 36, 39, 50 and 51 from MCT.

Figure 1b,d,f present performance profiles comparing the accuracy of the codes on the different matrix sets. For a given value $\alpha$ on the x-axis, the value of p on the y-axis is the proportion of matrices for which the considered code had a relative error lower than or equal to $\alpha$ times the smallest relative error of all the codes for the matrix. Performance plots are explained in detail in [5] (section 10.5) and are quite accepted. The different accuracy of the methods on matrices of the third set was very apparent, as can be seen in Figure 1f, where code coshmber_etrf clearly outperformed the other methods, while as anticipated above, coshmber_etaf was the least accurate alternative. The remaining two codes were very similar in terms of accuracy. For sets 1 and 2, the differences were less important, although we can see that coshmber_etrf was also on top for lower values of $\alpha$ for the second set and for higher values of $\alpha$ for the first set, confirming it as the most accurate option. It can also be seen that coshmber_etaf was the least accurate option for the first set and was also below the other codes for high values of $\alpha$ for the second set.

Figure 2 shows the proportion of matrices, in each set, for which each code provided the lowest/highest error. It confirms that coshmber_etrf was the most accurate option, especially taking into account sets 3 and 2, while coshmber_etaf was the least accurate option for the first set. It also shows that coshmber_atrf and coshmber_ataf were very similar in terms of accuracy, although the latter seemed to be slightly better.

Table 4. Experiment 1: Number of matrix products for all the matrices in a set for each code.

Code	Set 1	Set 2	Set 3
coshmber_etrf	1306	1303	424
coshmber_etaf	1276	1273	388
coshmber_atrf	1638	1637	563
coshmber_ataf	1622	1623	527

considers the computational costs, in terms of number of matrix products for all the matrices within a set, of the different codes in experiment 1. We can see that the codes based on Algorithm 2, which use polynomials containing even-order terms only, required a lower number of products.

As a conclusion of experiment 1, coshmber_etrf was identified as the most accurate code and also as one of the most efficient. It was certainly much more accurate than coshmber_etaf, which is also based on Algorithm 2. With respect to the two the codes based on Algorithm 1, they were very similar in terms of accuracy and computational cost, although coshmber_ataf seemed to be slightly better in both respects.

For completeness, Figure 3 presents box plots of the values of parameters m and s selected by Algorithm 4 for the tests of experiment 1. In each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th percentile ($q_1$) and the 75th percentile ($q_3$), respectively. The whiskers extend to the most extreme data points in the interval of $[q_1-1.5\times (q_3-q_1),q_3+1.5(q_3-q_1)]$, while the values outside of the interval were considered outliers and are marked with a ’+’ symbol. Figure 3 shows that the order m of the polynomials used by coshmber_etrf and coshmber_etaf, corresponding to expression (12), was lower than that of the other two codes, corresponding to expression (10). We can also see that for sets 1 and 2, m took the same value within a given method almost always ($m=30$ for coshmber_etrf and coshmber_etaf and $m=49$ for the other two methods). The values of s were similar for all the methods, although slightly lower for coshmber_etrf and coshmber_etaf, especially in set 2.

 Experiment 2. 

In this experiment, we took the best code identified in the previous experiment (coshmber_etrf) together with the best code based on Algorithm 1 (coshmber_ataf) and compared them with functions coshm_expmber_af and coshm_expmber_rf, corresponding to Algorithm 3, and with other options based on state-of-the-art approaches, such as functions coshm_expm, funmcosh_nd_inf and funmcosh. Matrix 4 from EMP was excluded from the third matrix set in this experiment, because funmcosh could not compute its hyperbolic cosine.

Similarly to Experiment 1, Figure 4a,c,e show the normwise relative errors of the different codes, together with the value of $k_{cosh}u$ given by the solid line. We can see that funmcosh and funmcosh_nd_inf produced considerably larger errors than the other codes. This was especially true for some matrices of the third set, where the result produced by funmcosh was very inaccurate. The other codes presented good stability, with errors below the solid line for sets 1 and 2 and not far from that line for set 3.

In Figure 4b,d,f, we can see the performance plots for the different codes. It is clear that funmcosh and funmcosh_nd_inf were the options with the worst performance for any matrix set, as indicated by the lower values of the profile in the three figures. The next worst one was coshm_expm. We can also see that coshm_expmber_af and coshm_expmber_rf were the best options for matrix sets 1 and 2, while for the third set, coshmber_etrf was the best option, followed by the two previous codes.

Figure 5 shows the proportion of matrices in each set for which each code provided the lowest/highest error. It confirms that coshm_expmber_af and coshm_expmber_rf were the best options for matrix sets 1 and 2, while coshmber_etrf was the best option for the third matrix set. It also shows that funmcosh and funmcosh_nd_inf performed the worst.

Table 5. Experiment 2: Number of matrix products for all the matrices in a set for each code.

Code	Set 1	Set 2	Set 3
coshm_expmber_af	2649	2651	776
coshm_expmber_rf	2697	2693	790
coshmber_etrf	1306	1303	411
coshmber_ataf	1622	1623	497
coshm_expm	2894	2891	645
funmcosh_nd_inf	1433	1433	616
funmcosh	1400–2233	1400–2233	602–917

considers the computational costs, in terms of number of matrix products for all the matrices in each set, of the different codes in this experiment. It should be clarified that, although function coshm_expm uses the code of function expm, some modifications were performed to avoid repeating computations common to the exponentials of A and $-A$. In particular, the Schur decomposition, and the computation of the scaling parameters and the order of the Padé approximant were performed only once.

Function funmcosh does not perform matrix products, being based instead on the Schur–Parlett algorithm with a computational cost between $28n^3$ and $\frac{1}{3}{n}^4$ flops [34]. Similarly and according to [40], the cost of function funm_nd_inf, and consequently of function funmcosh_nd_inf, consists of $28n^3$ flops using the desired precision plus $\frac{2}{3}{n}^3$ flops using higher precision. In our case, where $n=128$, this can be respectively translated to a number of matrix products between 14 and $22.33$ for funmcosh and $14.33$ for funmcosh_nd_inf, assuming that the cost of a matrix product is $2n^3$ flops. As we can see, coshmber_etrf was the code with the lowest computational cost, while coshm_expm and the two codes based on Algorithm 3 were the most demanding ones, requiring approximately twice the number of matrix products of coshmber_etrf. This comes from the fact that the codes based on Algorithm 3 and function coshm_expm need to evaluate the matrix exponential twice.

Figure 6 presents box plots for order m of the polynomials and scaling parameter s selected by Algorithm 4 in each of the codes of the experiment, except for funmcosh and funmcosh_nd_inf, for which the parameters were not available. We can see that coshm_expm generally used lower polynomial orders and higher scaling parameters than the other codes. Among those other codes, coshm_expm used lower orders, while the value of s was similar for all them.

In summary, we can conclude that codes coshm_expmber_rf, coshm_expmber_af and coshmber_etrf are the most accurate ones, clearly outperforming options based on existing approaches, such as funmcosh, funmcosh_nd_inf or coshm_expm. Code coshmber_etrf is also the best option from the point of view of computational cost.

4. Conclusions

In this work, we propose and analyze three different algorithms to approximate the matrix hyperbolic cosine by means of Bernoulli polynomials. Two of the proposed approximations come from different Bernoulli series expansions of the matrix hyperbolic cosine. One of them consists of both even- and odd-order terms, while the other contains only even-order terms. The third proposed approximation comes from the approximation of the matrix exponential using Bernoulli matrix polynomials.

The selection of polynomial order m and scale parameter s is performed by means of Algorithm 4, which is an extension of [38]’s Algorithm 4 to consider any type of error, either absolute or relative, forward or backward. Algorithm 4 uses precomputed values of ${\Theta }_m$ as inputs. These values are provided in this paper for the different polynomial approximations and for absolute and relative forward error types.

By combining the three different approximation algorithms with the two error types (absolute or relative), we obtained six different computing codes to approximate the matrix hyperbolic cosine. These codes were compared using a comprehensive testbed of matrices with different characteristics. We also compared the codes with reference methods based on current state-of-the-art approaches.

From the point of view of accuracy, codes coshm_expmber_rf and coshm_expmber_af (corresponding to Algorithm 3 with relative and absolute forward error, respectively), and coshmber_etrf (based on Algorithm 2 with relative error) emerged as the best options. All of them clearly outperformed the alternatives, such as funmcosh, funmcosh_nd_inf and coshm_expm, based on state-of-the-art methods. In terms of computational cost, the number of matrix products of codes coshm_expmber_rf and coshm_expmber_af approximately doubled that of the less demanding option, coshmber_etrf. Thus, coshmber_etrf is a good option for applications where the computational cost is an important consideration.