Implementation and Performance Analysis of Kalman Filters with Consistency Validation
Abstract
1. Introduction
2. The Kalman Filters and Suboptimal Filters
2.1. Discrete Kalman Filter
2.2. Continuous Kalman Filter
2.3. Suboptimal Filters: Estimators with a General Gain
- (1)
- with or
- (2)
- with or
3. Discrete Kalman Filter from Discretization of Continuous Kalman Filter
4. Illustrative Examples and Discussion
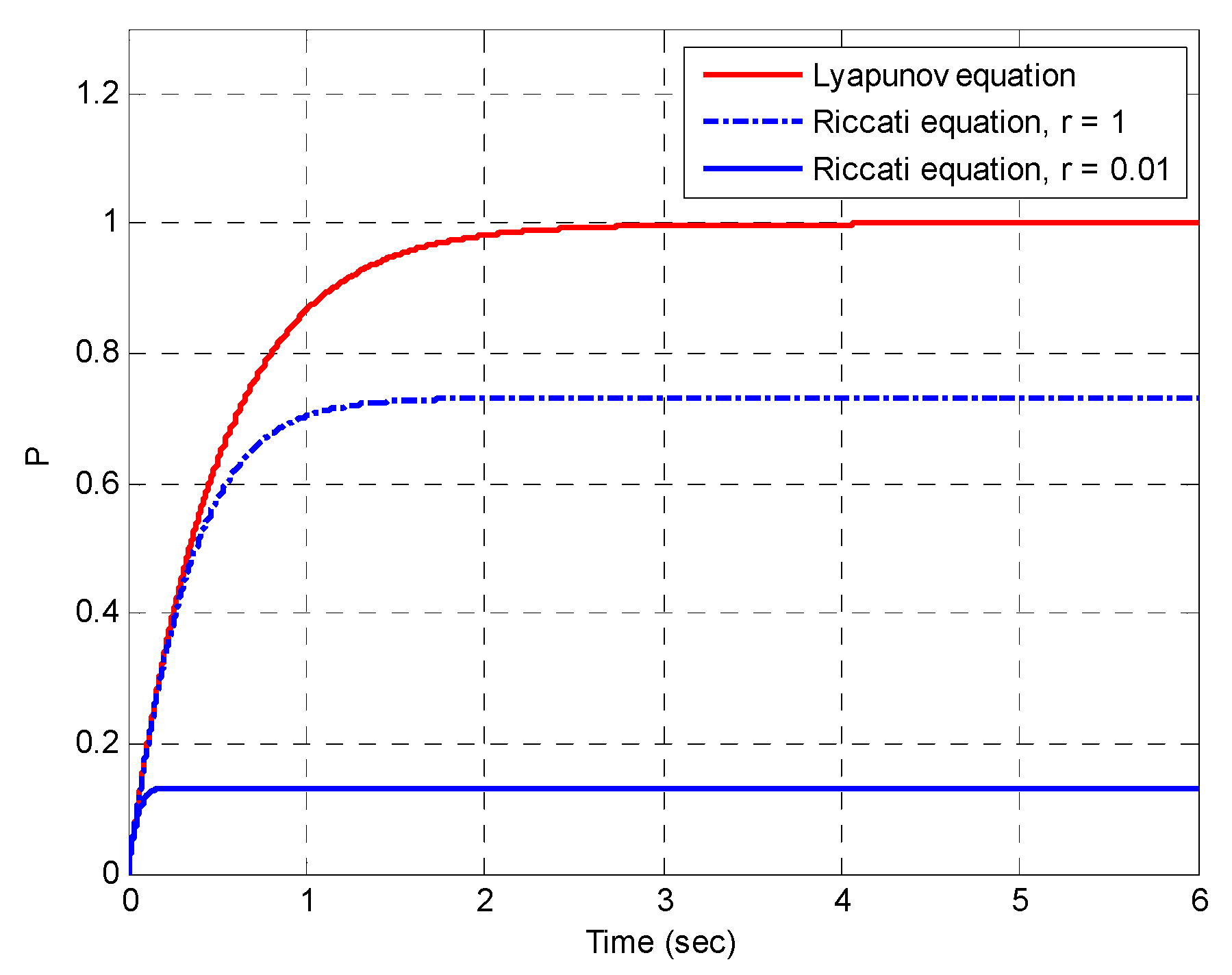
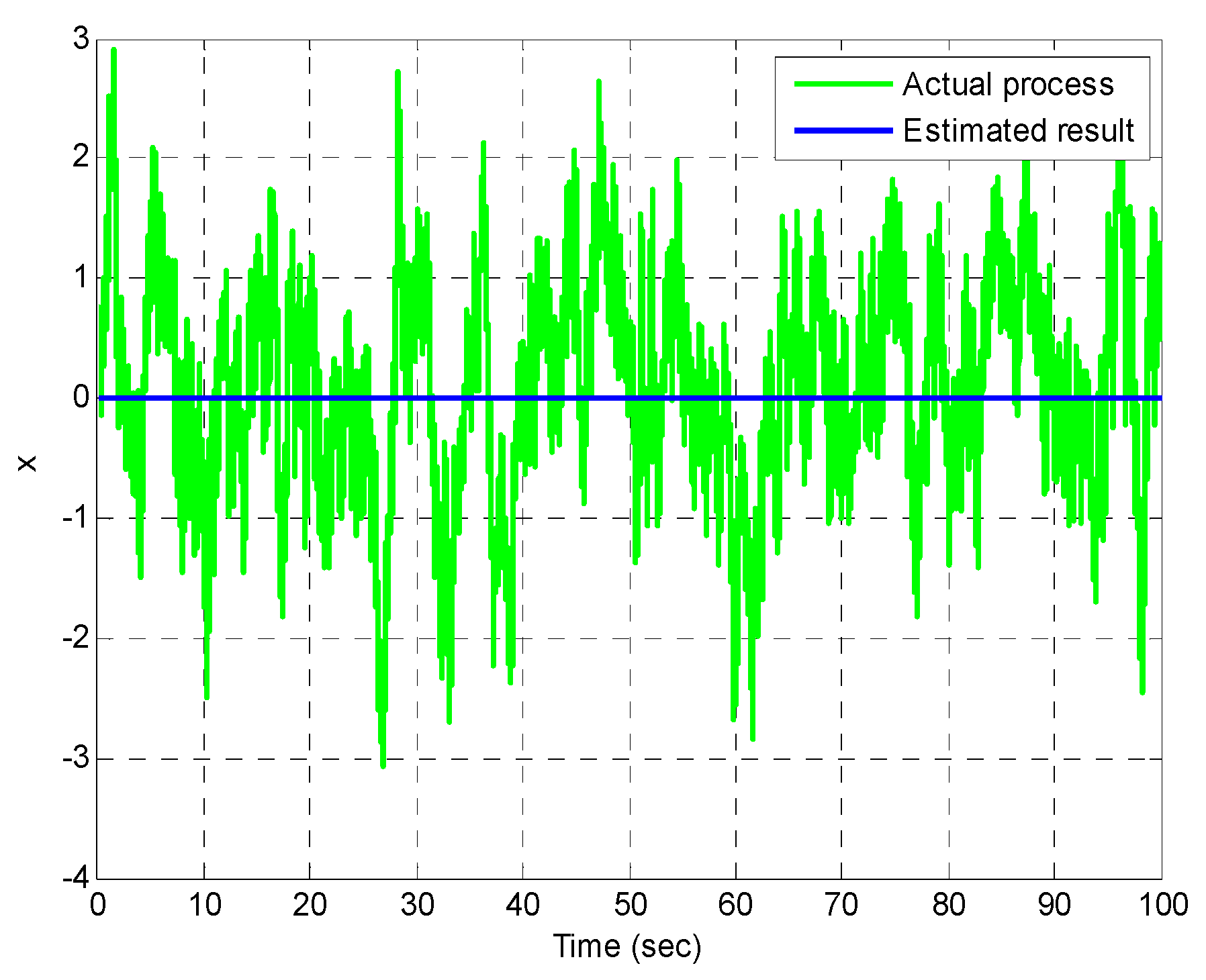
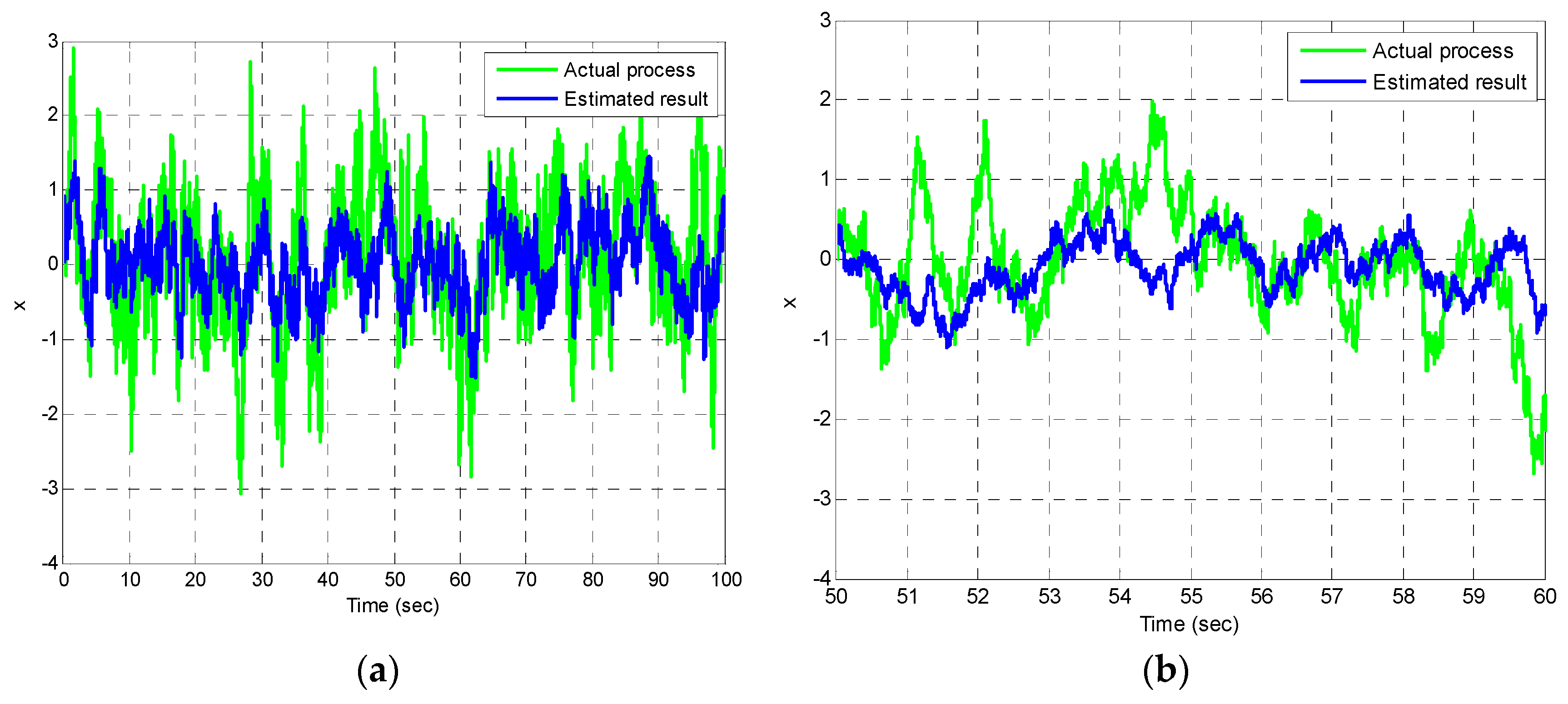
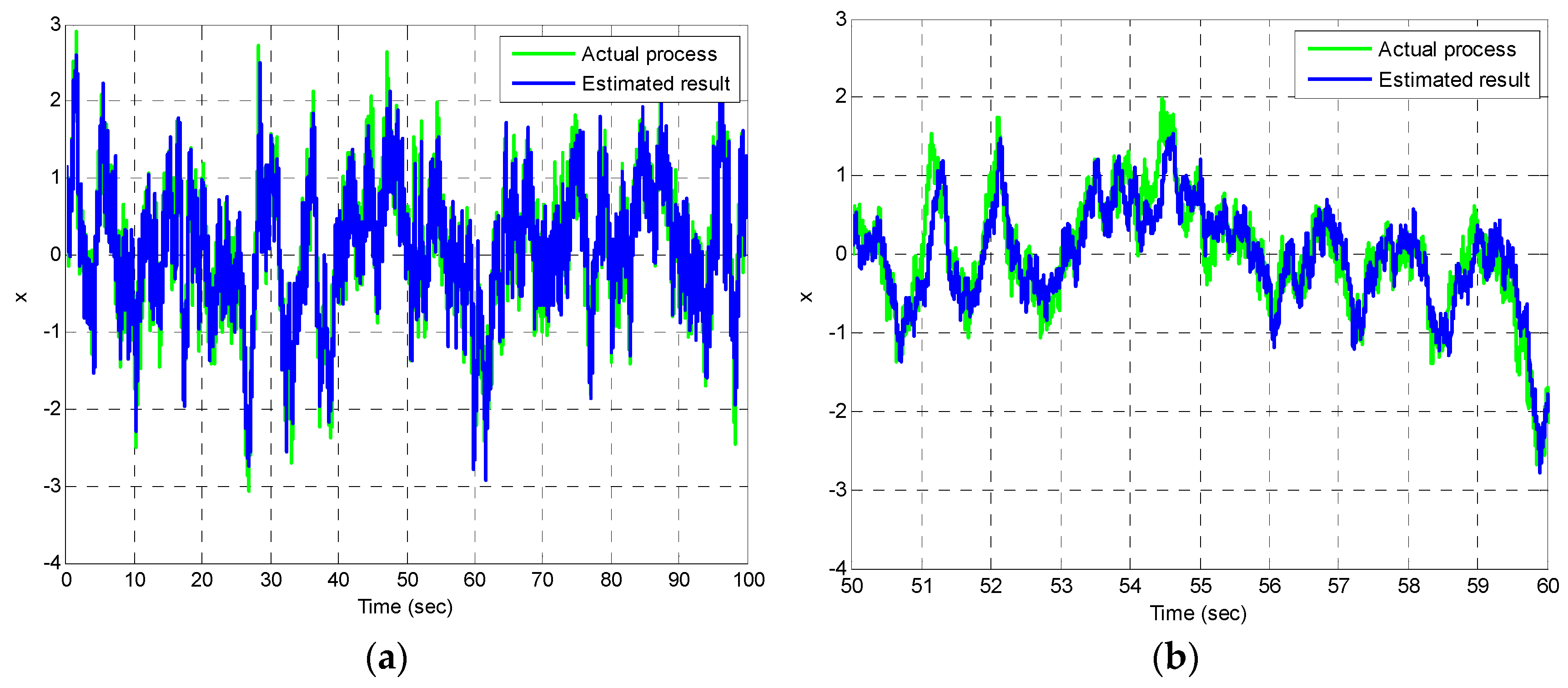
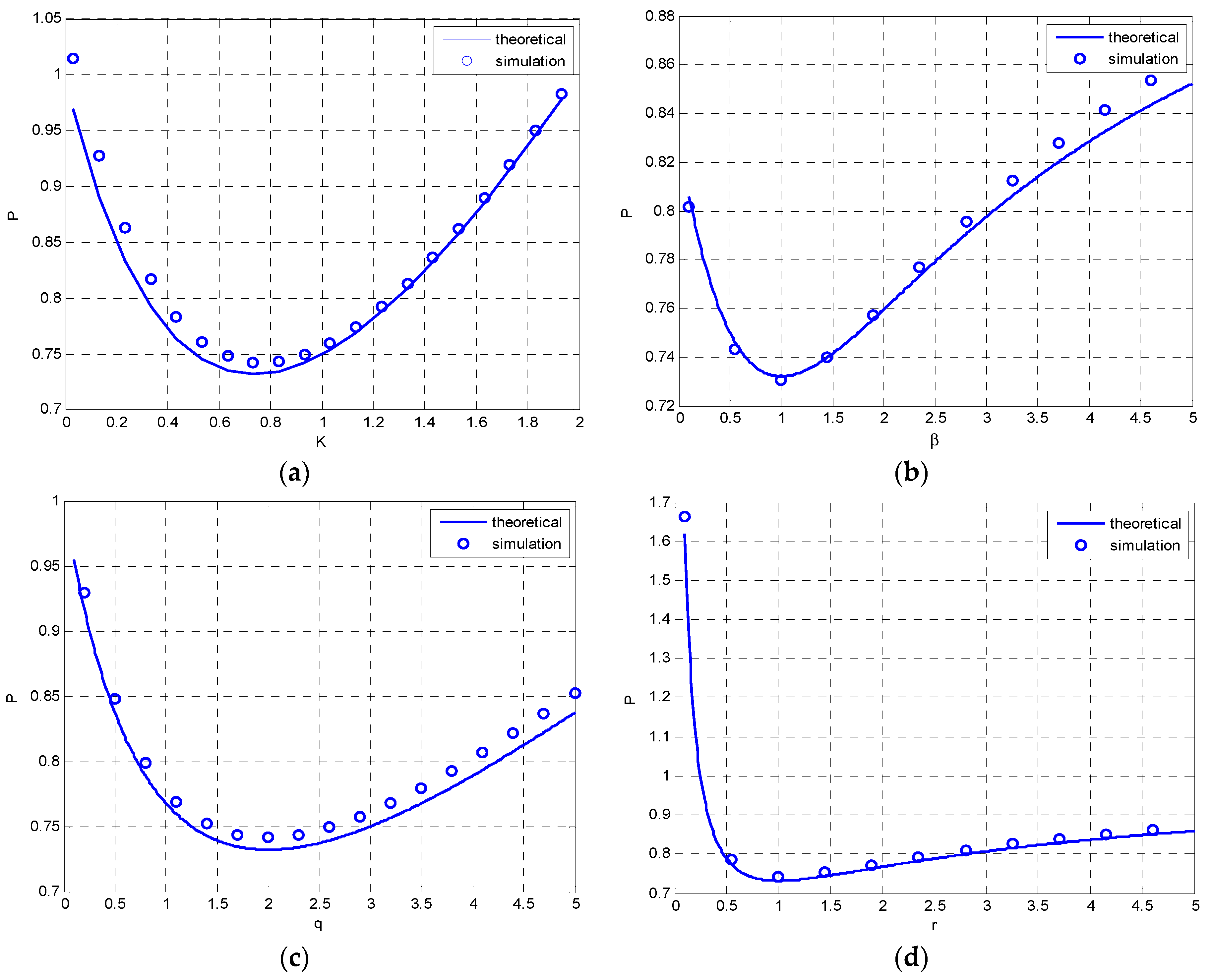
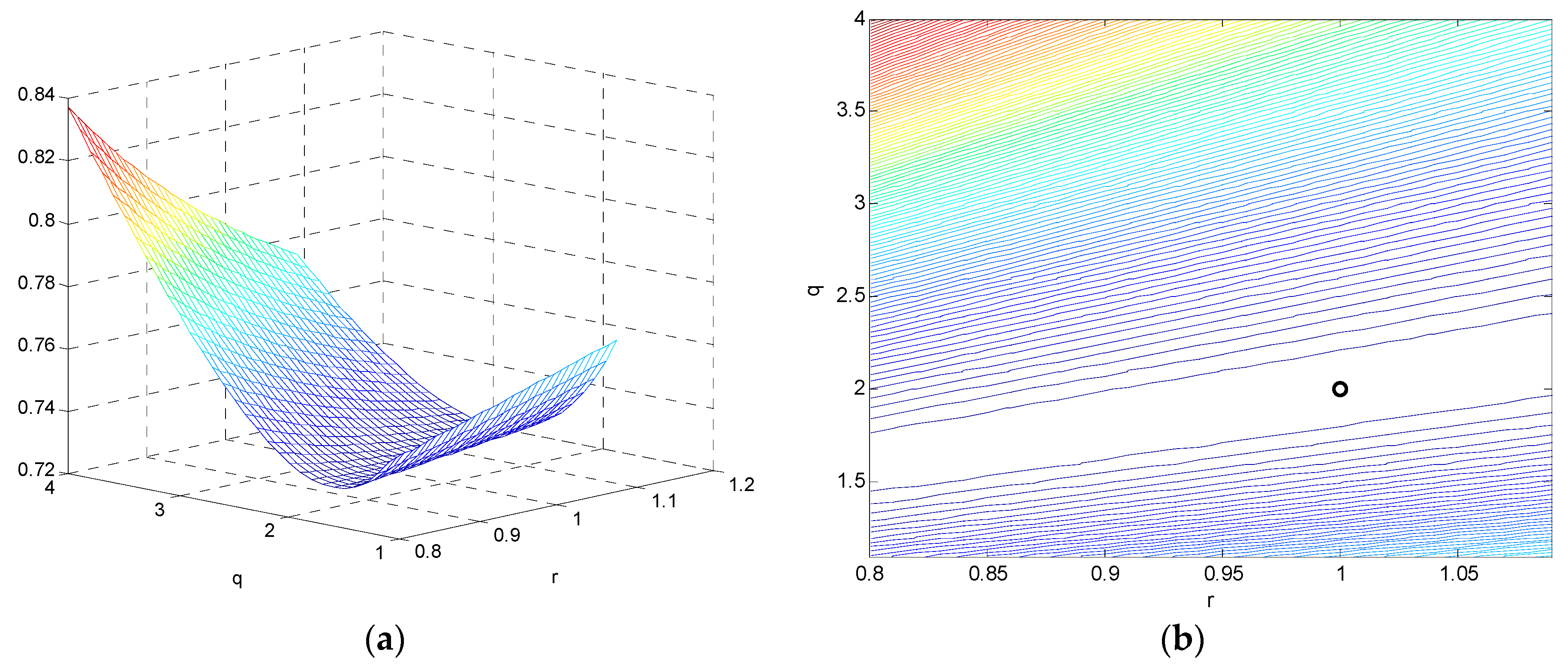
4.1. Example 1: The Scalar Gauss-Markov Process
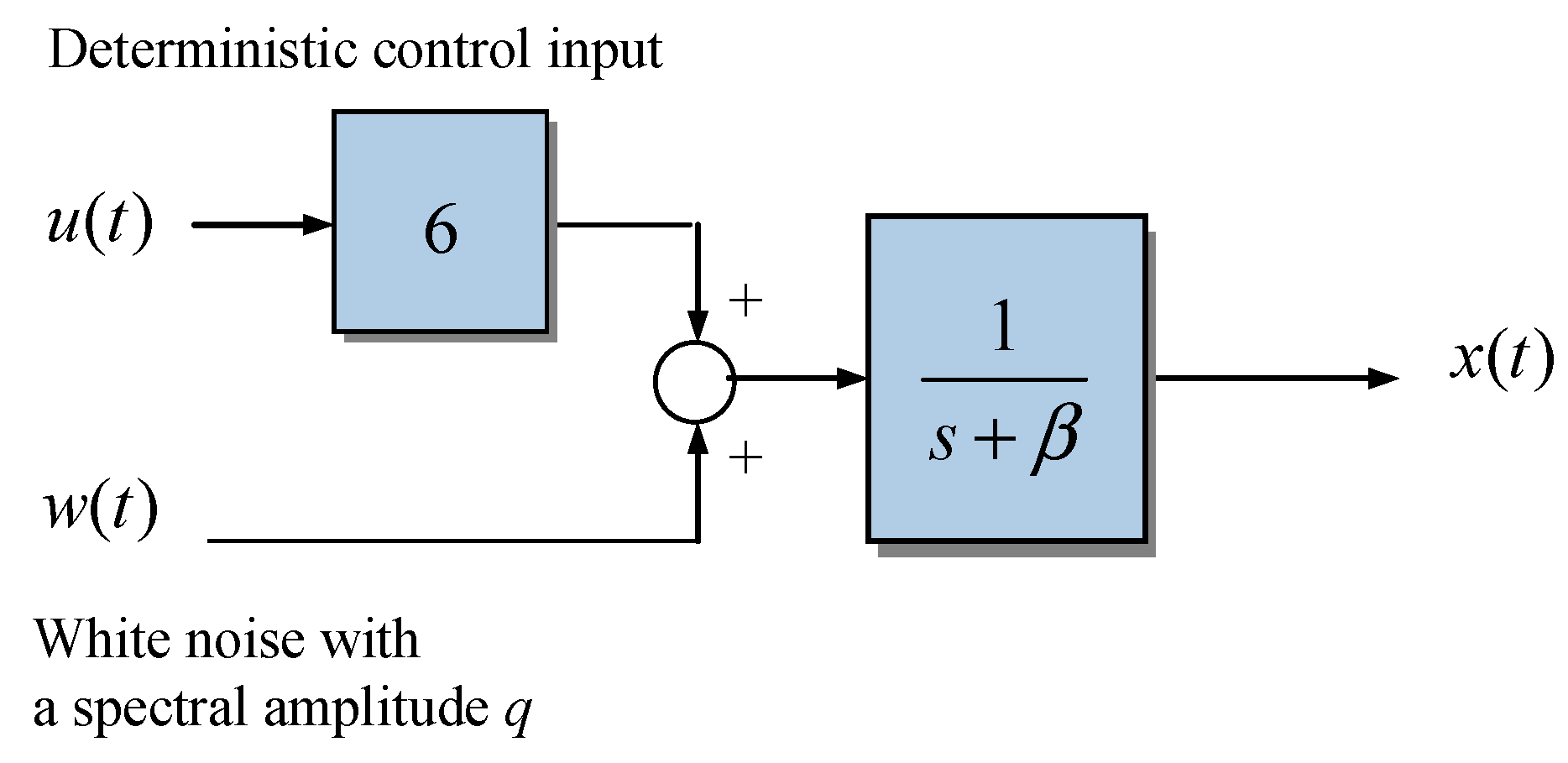
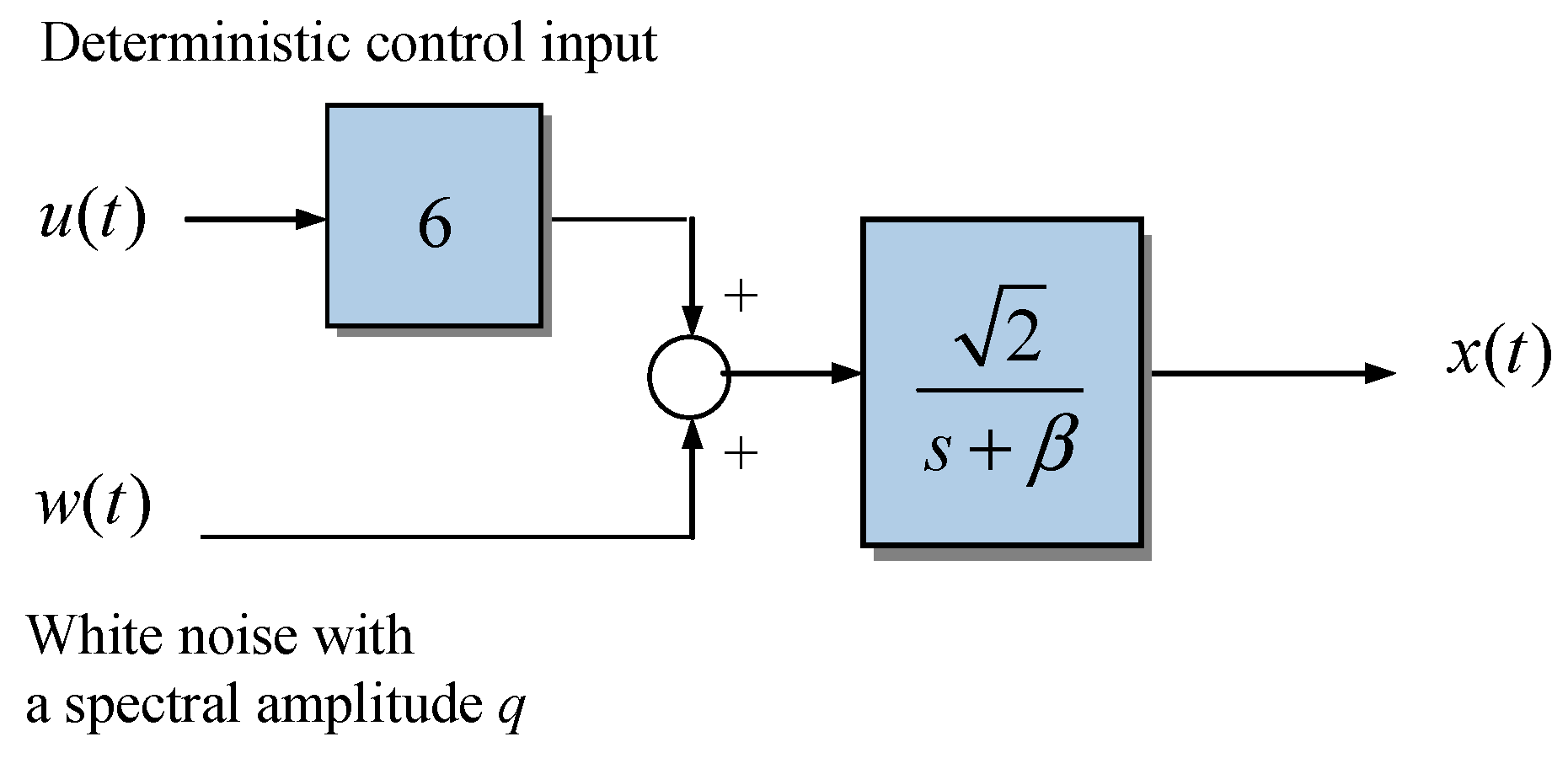
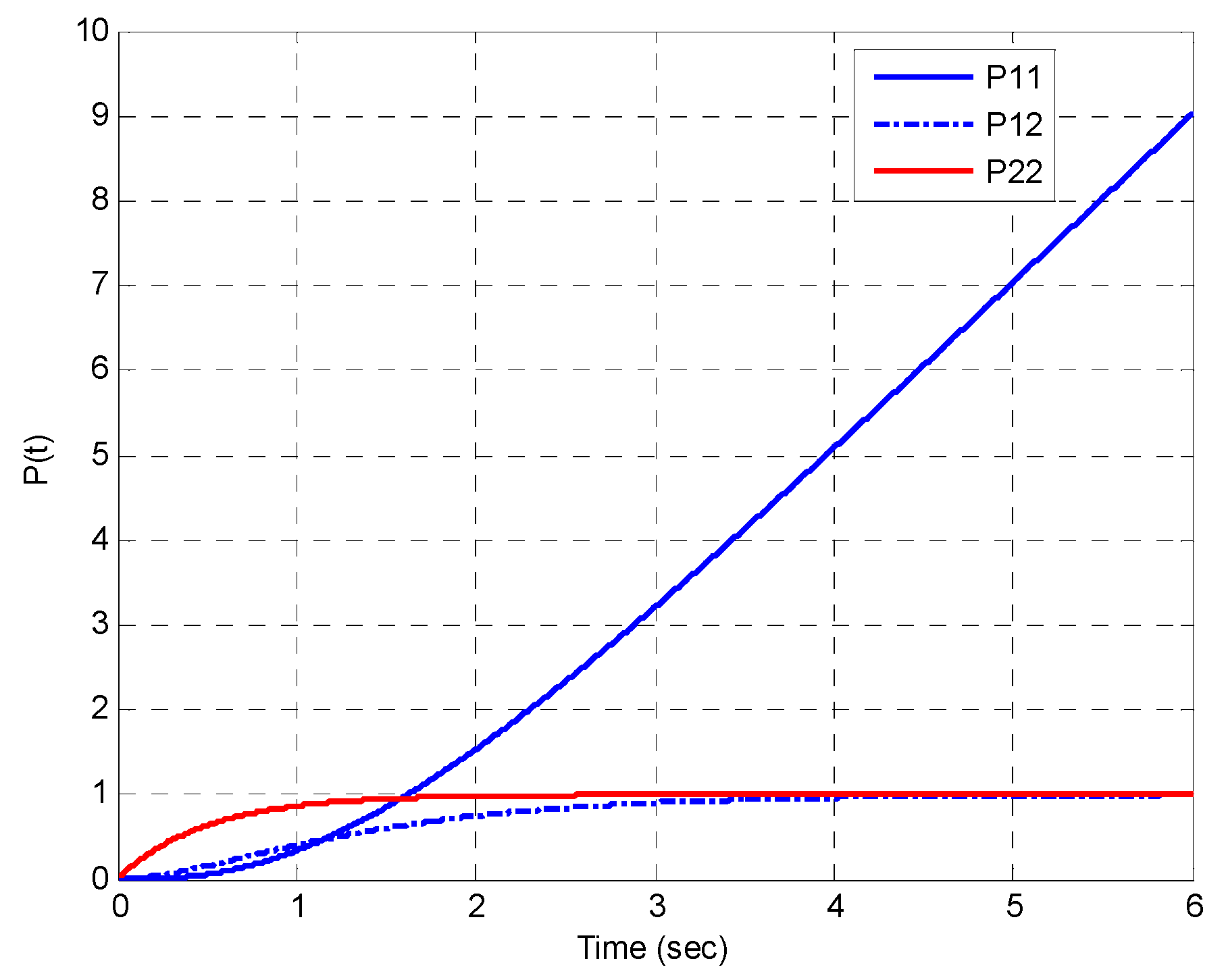
4.2. Example 2: An Additional Deterministic Control Input Is Introduced
4.3. Example 3: A Larger Gain Is Applied to the System
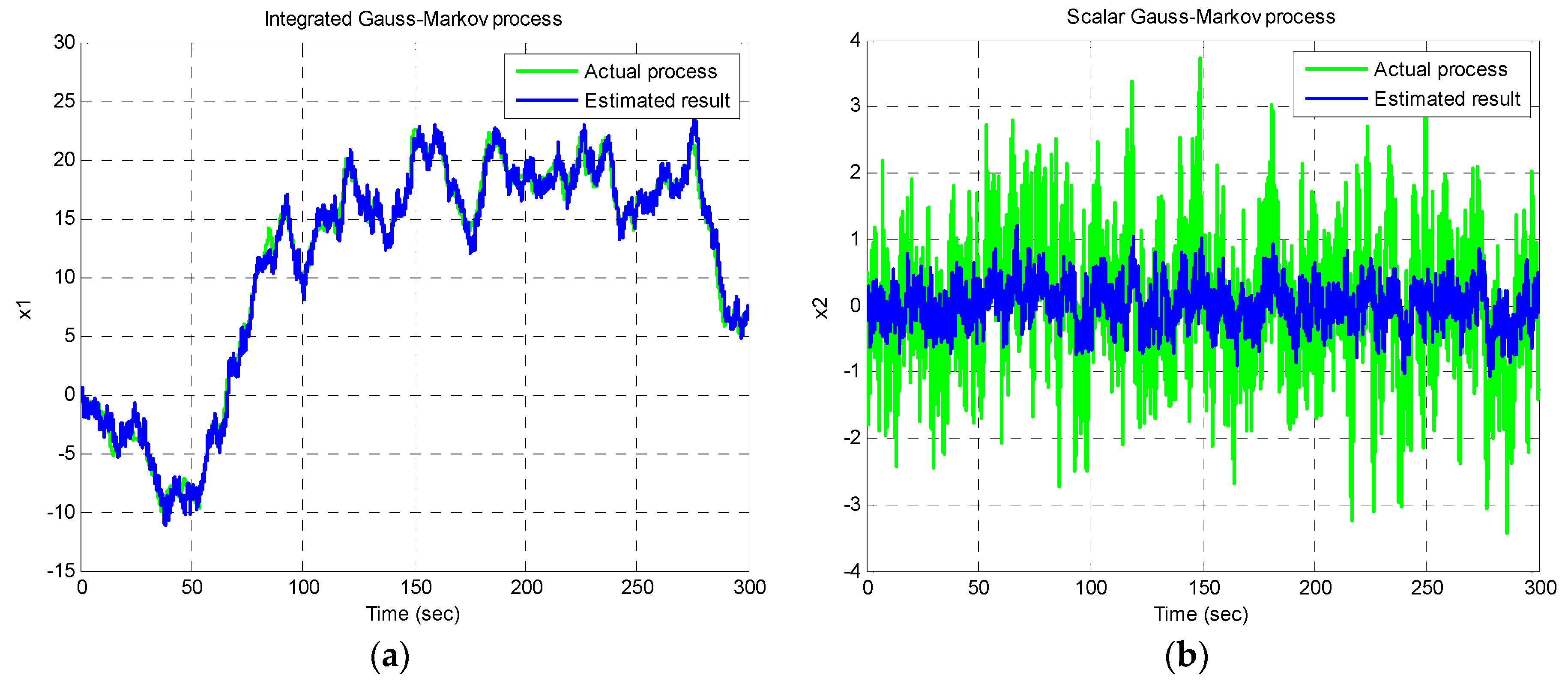
4.4. Example 4: The Integrated Gauss-Markov Process
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. Trans. ASME—J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Brown, R.G.; Hwang, P.Y.C. Introduction to Random Signals and Applied Kalman Filtering; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Gelb, A. Applied Optimal Estimation; M.I.T. Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Grewal, M.S.; Andrews, A.P. Kalman Filtering, Theory and Practice Using MATLAB, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Lewis, F.L. Optimal Estimation; John Wiley & Sons, Inc.: New York, NY, USA, 1986. [Google Scholar]
- Lewis, F.L.; Xie, L.; Popa, D. Optimal and Robust Estimation, with an Introduction to Stochastic Control Theory, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Maybeck, S.P. Stochastic Models, Estimation, and Control; Academic Press: New York, NY, USA, 1978; Volume 1. [Google Scholar]
- Zhu, J.; Chang, X.; Zhang, X.; Su, Y.; Long, X. A Novel Method for the Reconstruction of Road Profiles from Measured Vehicle Responses Based on the Kalman Filter Method. CMES-Comput. Model. Eng. Sci. 2022, 130, 1719–1735. [Google Scholar] [CrossRef]
- Zhao, S.; Jiang, C.; Zhang, Z.; Long, X. Robust Remaining Useful Life Estimation Based on an Improved Unscented Kalman Filtering Method. CMES-Comput. Model. Eng. Sci. 2020, 123, 1151–1173. [Google Scholar] [CrossRef]
- Xu, B.; Bai, L.; Chen, K.; Tian, L. A resource saving FPGA implementation approach to fractional Kalman filter. IET Control Theory Appl. 2022, 16, 1352–1363. [Google Scholar] [CrossRef]
- Won, J.H.; Dötterböck, D.; Eissfeller, B. Performance comparison of different forms of Kalman filter approaches for a vector-based GNSS signal tracking loop. Navigation 2010, 57, 185–199. [Google Scholar] [CrossRef]
- Zhang, J.H.; Li, P.; Jin, C.C.; Zhang, W.A.; Liu, S. A novel adaptive Kalman filtering approach to human motion tracking with magnetic-inertial sensors. IEEE Trans. Ind. Electron. 2019, 67, 8659–8669. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Z.Y.; Xie, R.R. Quadratic extended Kalman filter approach for GPS/INS integration. Aerosp. Sci. Technol. 2006, 10, 709–713. [Google Scholar] [CrossRef]
- Wiltshire, R.A.; Ledwich, G.; O’Shea, P. A Kalman filtering approach to rapidly detecting modal changes in power systems. IEEE Trans. Power Syst. 2007, 22, 1698–1706. [Google Scholar] [CrossRef]
- Jwo, D.J. Remarks on the Kalman filtering simulation and verification. Appl. Math. Comput. 2007, 186, 159–174. [Google Scholar] [CrossRef]
- Kwan, C.M.; Lewis, F.L. A note on Kalman filtering. IEEE Trans. Educ. 1999, 42, 225–228. [Google Scholar] [CrossRef]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; Technical Report TR 95-041; University of North Carolina, Department of Computer Science: Chapel Hill, NC, USA, 2006; Available online: https://www.cs.unc.edu/~welch/media/pdf/kalman_intro.pdf (accessed on 30 July 2010).
- Rhudy, M.B.; Salguero, R.A.; Holappa, K. A Kalman filtering tutorial for undergraduate students. Int. J. Comput. Sci. Eng. Surv. 2017, 8, 1–18. [Google Scholar] [CrossRef]
- Love, A.; Aburdene, M.; Zarrouk, R.W. Teaching Kalman filters to undergraduate students. In Proceedings of the 2001 American Society for Engineering Education Annual Conference & Exposition, Albuquerque, NM, USA, 24–27 June 2001; pp. 6.950.1–6.950.19. [Google Scholar]
- Song, T.L.; Ahn, J.Y.; Park, C. Suboptimal filter design with pseudomeasurements for target tracking. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 28–39. [Google Scholar] [CrossRef]
- Sun, S. Multi-sensor weighted fusion suboptimal filtering for systems with multiple time delayed measurements. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; Volume 1, pp. 1617–1620. [Google Scholar]
- Fronckova, K.; Prazak, P. Possibilities of Using Kalman Filters in Indoor Localization. Mathematics 2020, 8, 1564. [Google Scholar] [CrossRef]
- Correa-Caicedo, P.J.; Rostro-González, H.; Rodriguez-Licea, M.A.; Gutiérrez-Frías, Ó.O.; Herrera-Ramírez, C.A.; Méndez-Gurrola, I.I.; Cano-Lara, M.; Barranco-Gutiérrez, A.I. GPS Data Correction Based on Fuzzy Logic for Tracking Land Vehicles. Mathematics 2021, 9, 2818. [Google Scholar] [CrossRef]
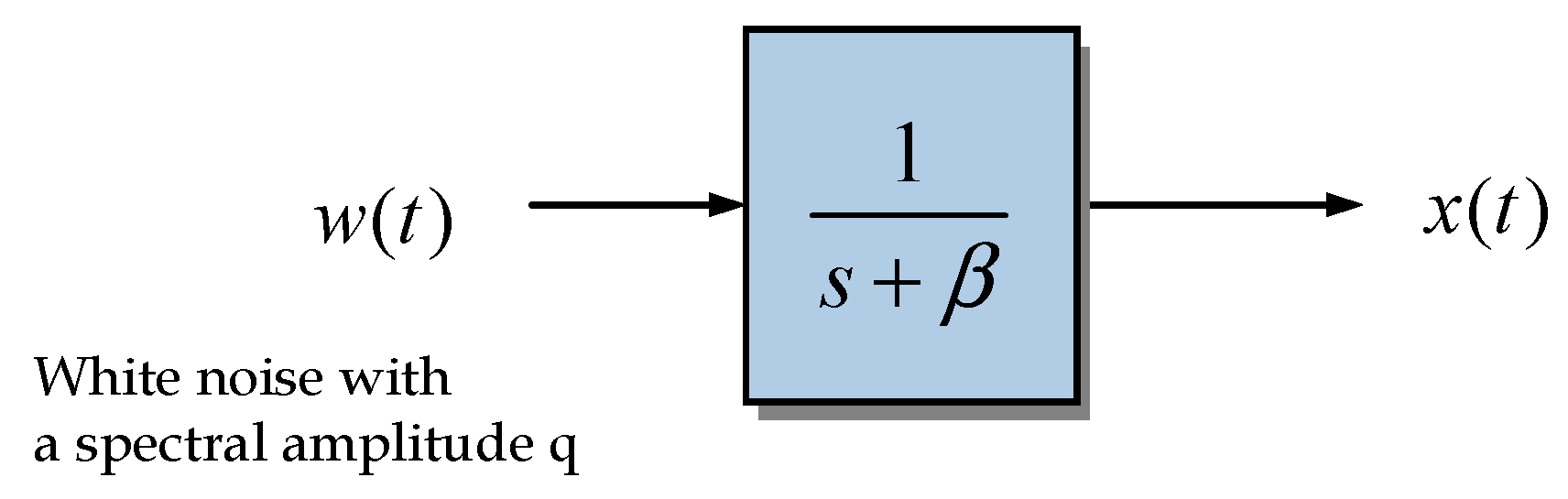






| Initialization: Initialize State Vector and State Covariance Matrix |
|---|
| Time update |
| (1) State propagation |
| (2) Error covariance propagation |
or |
| Measurement update |
| (3) Kalman gain matrix evaluation |
| (4) State estimate update |
| (5) Error covariance update |
| Initialization: Initialize State Vector and State Covariance Matrix |
|---|
| (1) Solve the error covariance propagation by the matrix Riccati equation for P, which is symmetric positive-definite. |
| (2) Calculation of Kalman gain matrix |
| (3) State estimate update |
| Examples | System Models | Highlights of Important Issues |
|---|---|---|
| 1 | A standard scalar Gauss-Markov process |
|
| 2 | Larger deterministic control input: an additional deterministic control input is introduced. |
|
| 3 | Larger random input: a larger gain is applied to the scalar Gauss-Markov process |
|
| 4 | Integrated Gauss-Markov process |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jwo, D.-J.; Biswal, A. Implementation and Performance Analysis of Kalman Filters with Consistency Validation. Mathematics 2023, 11, 521. https://doi.org/10.3390/math11030521
Jwo D-J, Biswal A. Implementation and Performance Analysis of Kalman Filters with Consistency Validation. Mathematics. 2023; 11(3):521. https://doi.org/10.3390/math11030521
Chicago/Turabian StyleJwo, Dah-Jing, and Amita Biswal. 2023. "Implementation and Performance Analysis of Kalman Filters with Consistency Validation" Mathematics 11, no. 3: 521. https://doi.org/10.3390/math11030521
APA StyleJwo, D.-J., & Biswal, A. (2023). Implementation and Performance Analysis of Kalman Filters with Consistency Validation. Mathematics, 11(3), 521. https://doi.org/10.3390/math11030521








