Four-Parameter Weibull Distribution with Lower and Upper Limits Applicable in Reliability Studies and Materials Testing
Abstract
:1. Introduction
- If t represents time measured, for example, in seconds, then, the physical unit of the α parameter is s–β in the Kies modification and in the Phani modification (for fracture toughness measured in MPa m0.5, the unit is even more complicated). The parameters with such dubious units cannot have any meaningful interpretation. In the (W4) CDF, all quantities have the same unit (s, MPa m0.5, etc.).
- The simplification for t0 << t << t∞ leads to
2. Examples of W4 CDF Applications in Reliability Studies
- no bathtub-shaped HR is obtained for the (W2) and (W3min) CDFs,
- the bathtub-shaped HR is obtained for the (W3max) CDF when β < 1 (see [4]),
- the bathtub-shaped HR is obtained for the (W4) CDF also when β > 1 (the limit is given by Equation (18)).
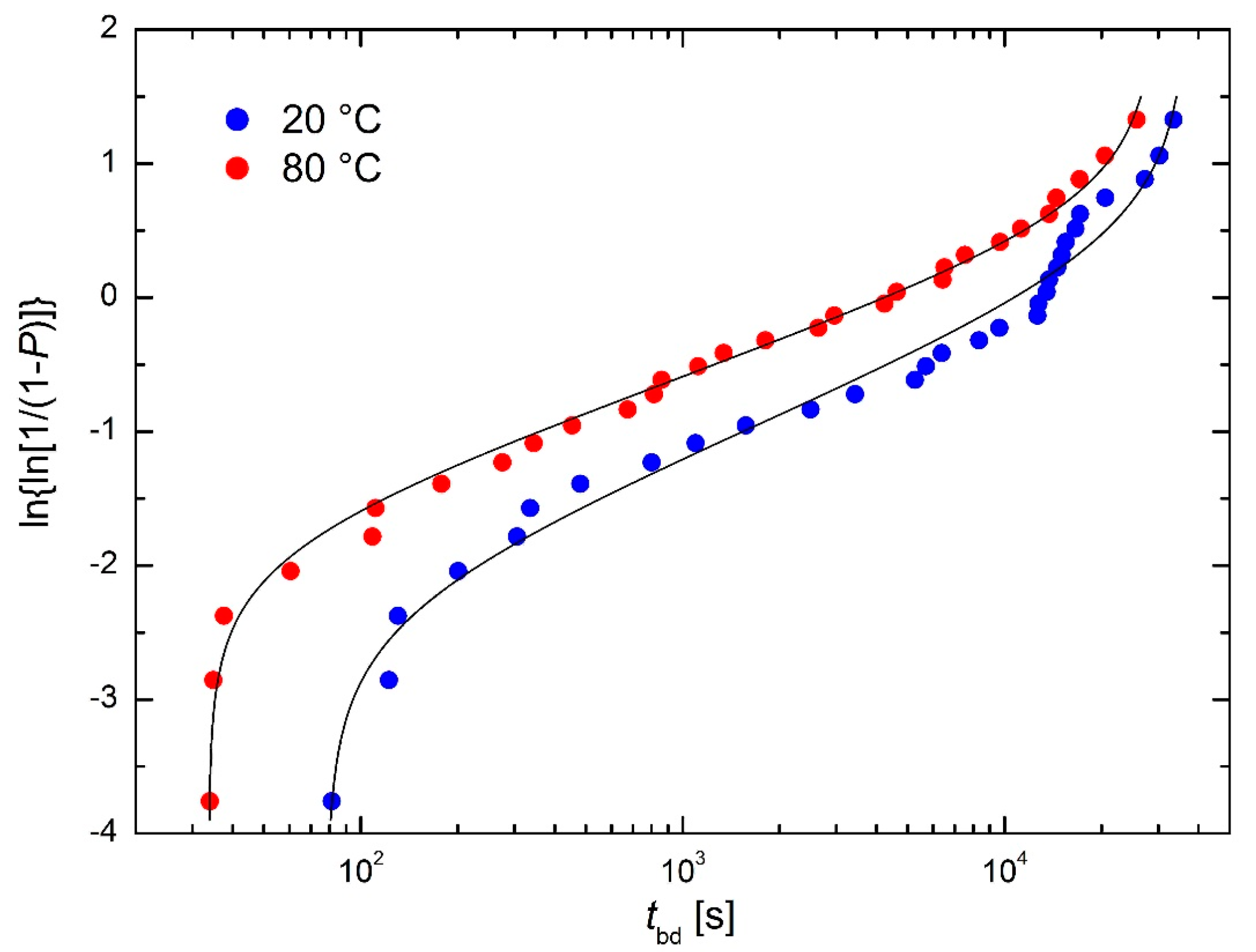
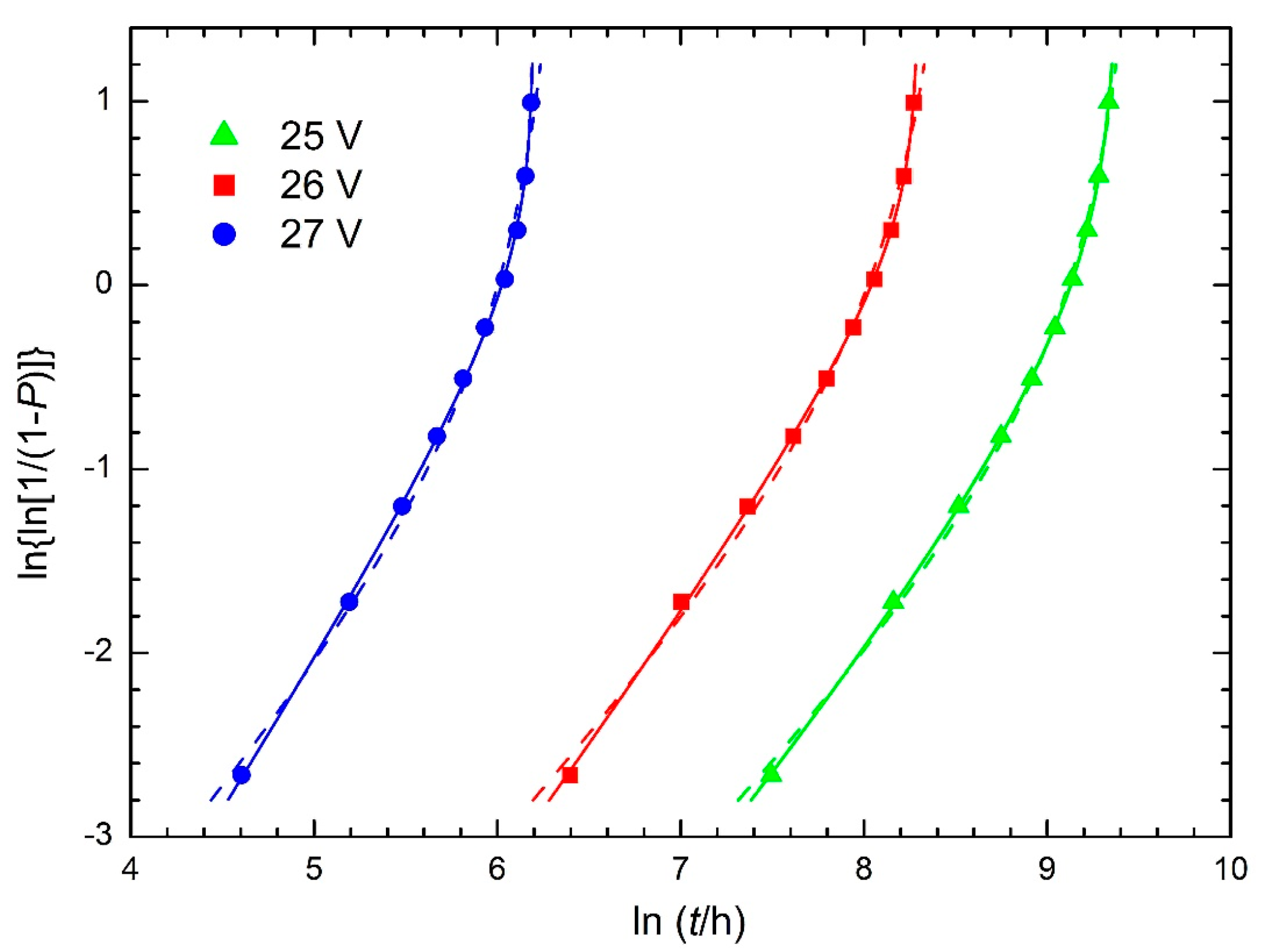
2.1. Time-to-Breakdown of Hf-Doped Ta2O5 Capacitors
- straight-line plot means constant HR,
- concavely curved plot means increasing HR,
- convexly curved plot means decreasing HR,
- twice-curved S-shaped plot means bathtub-shaped HR.
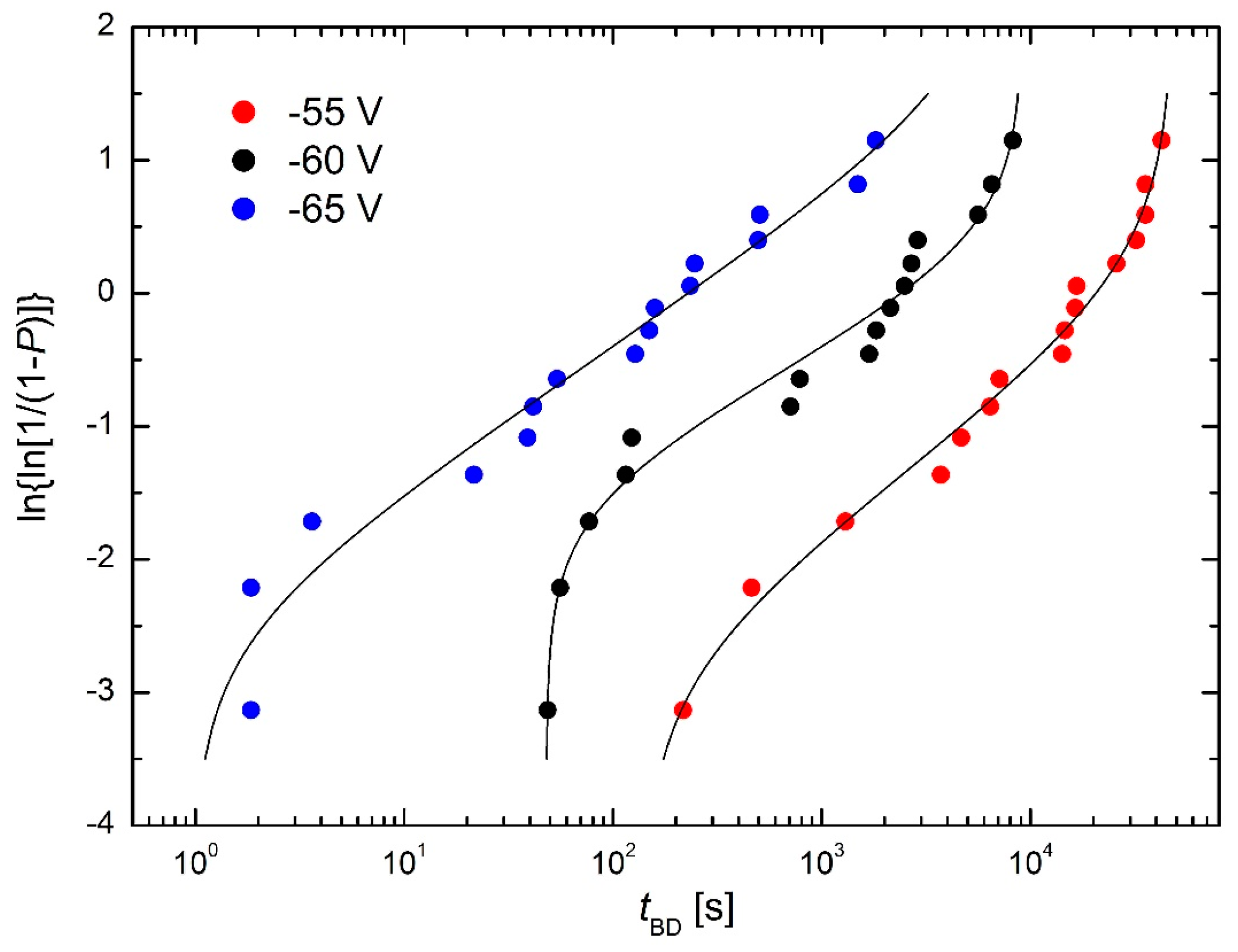
2.2. Reliability of AlGaN/GaN HEMTS
2.3. Reliability of Multilayer Ceramic Piezoelectric Actuators
3. Examples of W4 CDF Applications in Material Testing
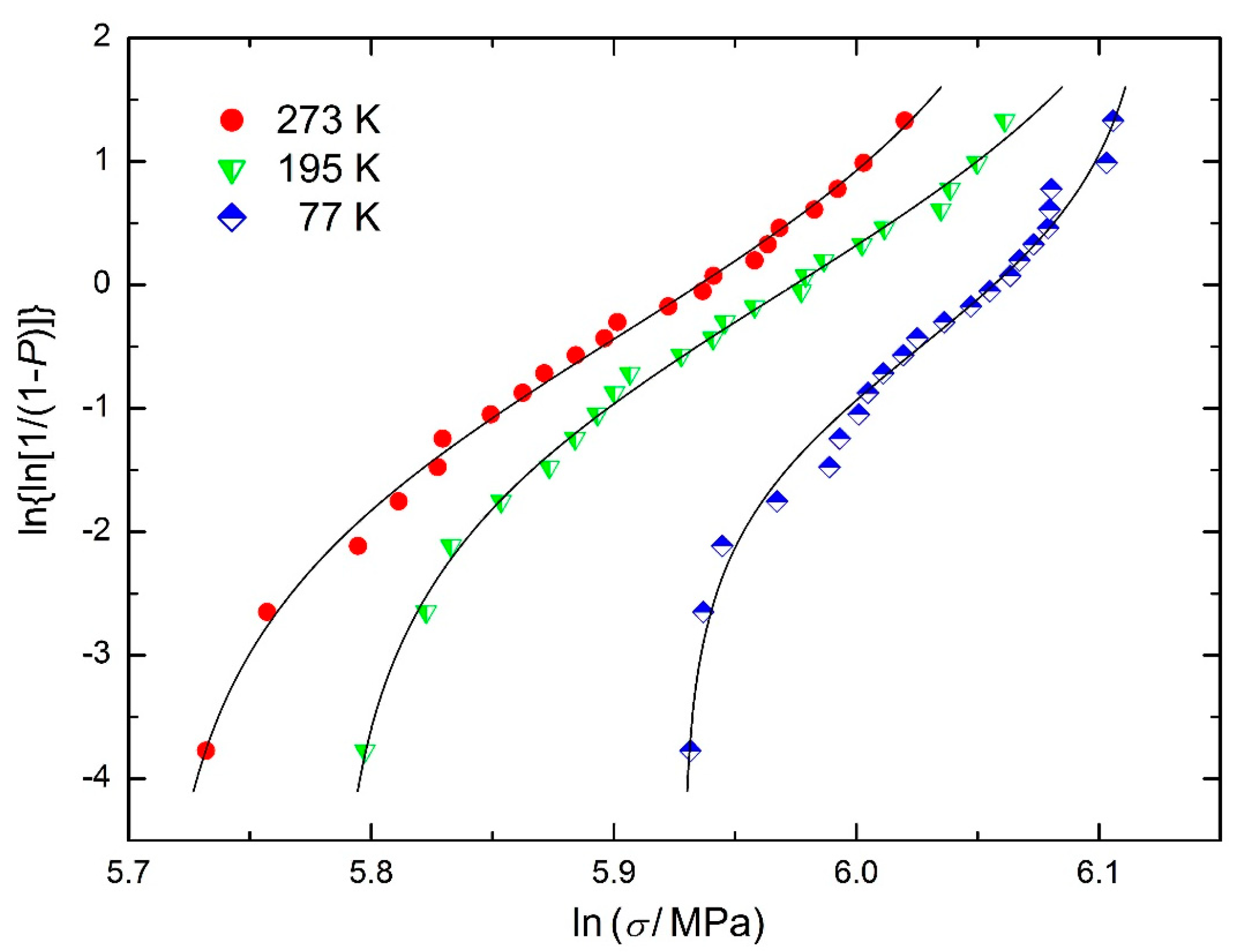
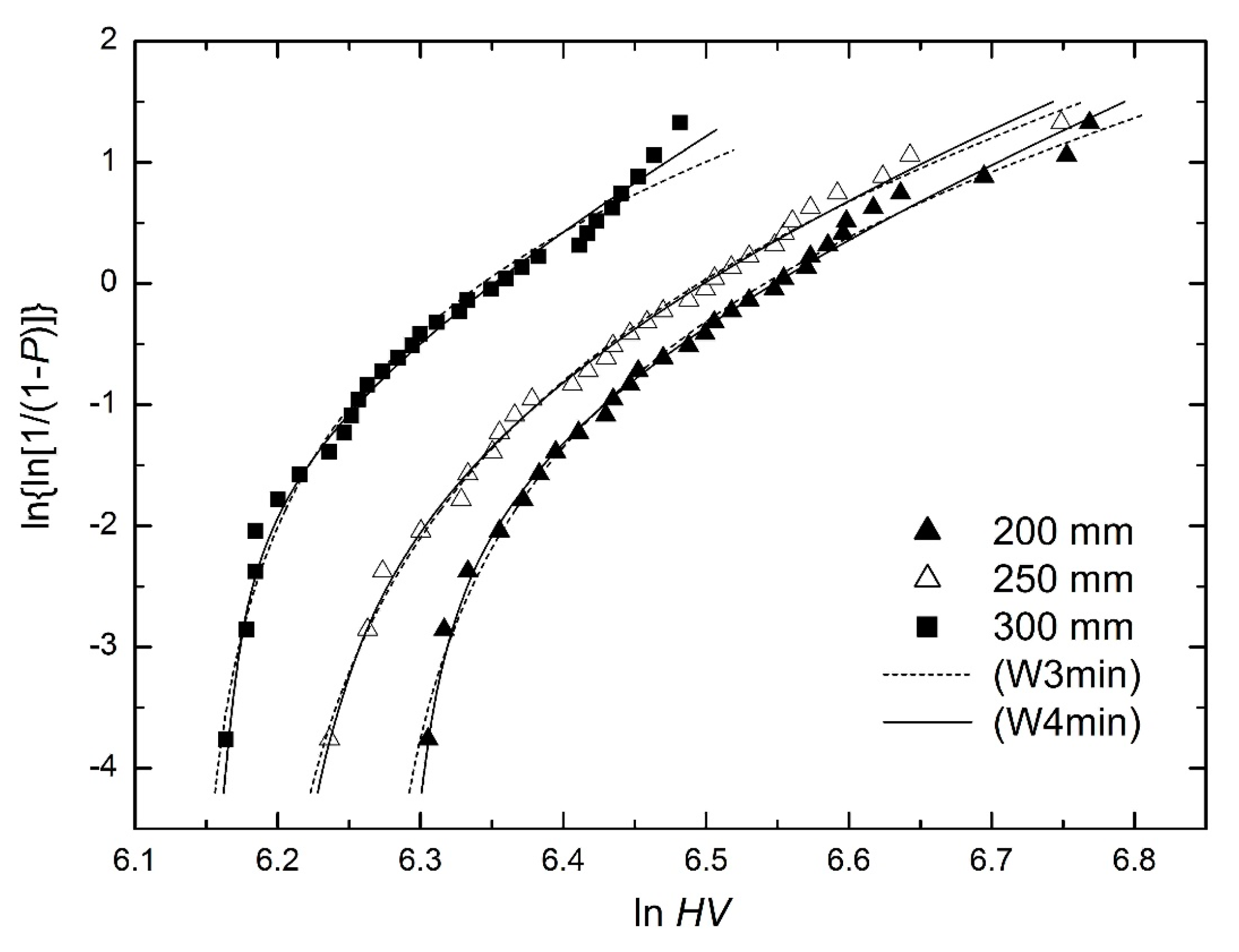
3.1. Flexural Strength of Aluminum Nitride Ceramics
3.2. Tensile Strength of Coated SiC Fibres
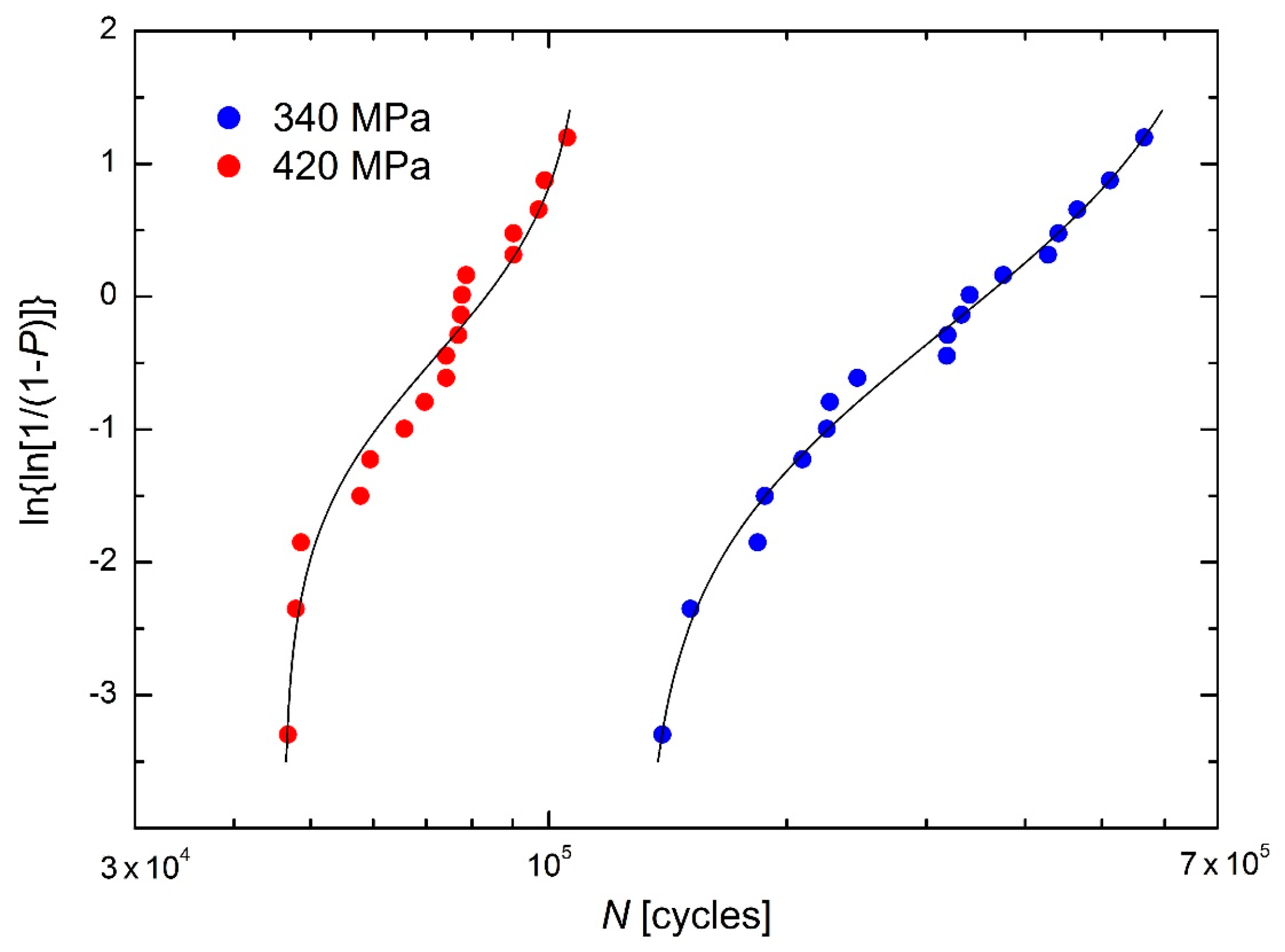
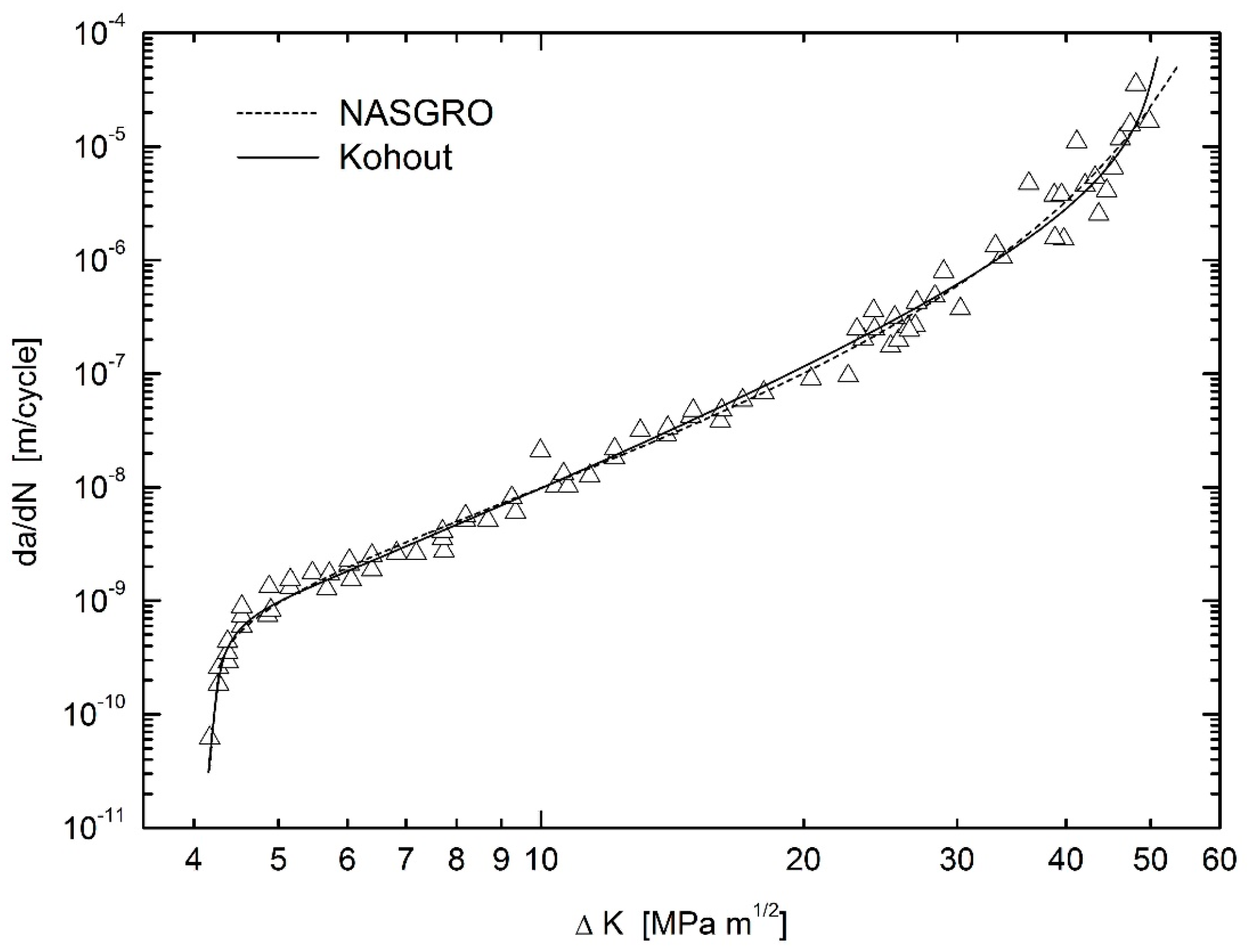
3.3. Fatigue of FeE 460 Steel
3.4. Flexural Fatigue of Concrete
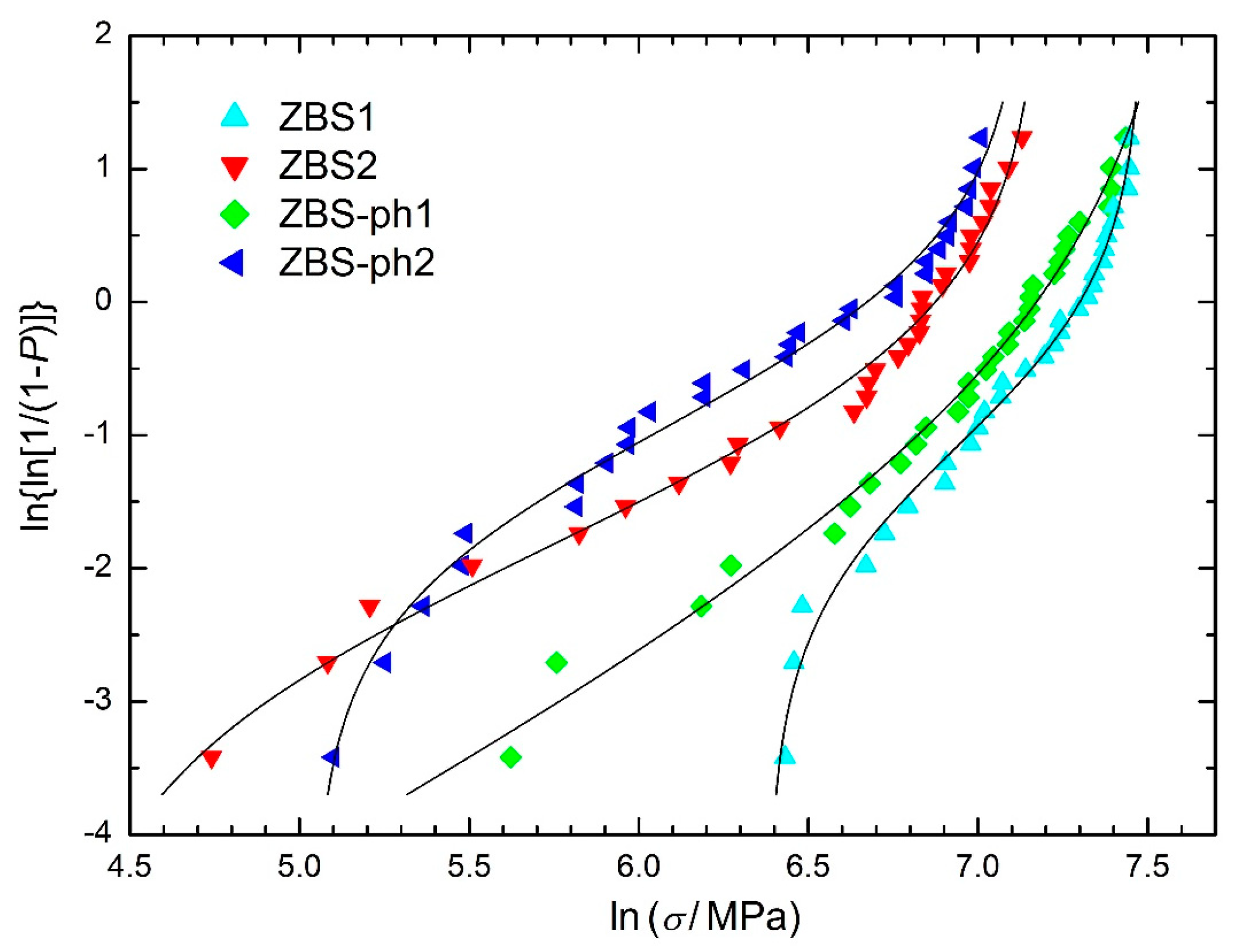
3.5. Surface Defects of a Sandblasted Glass
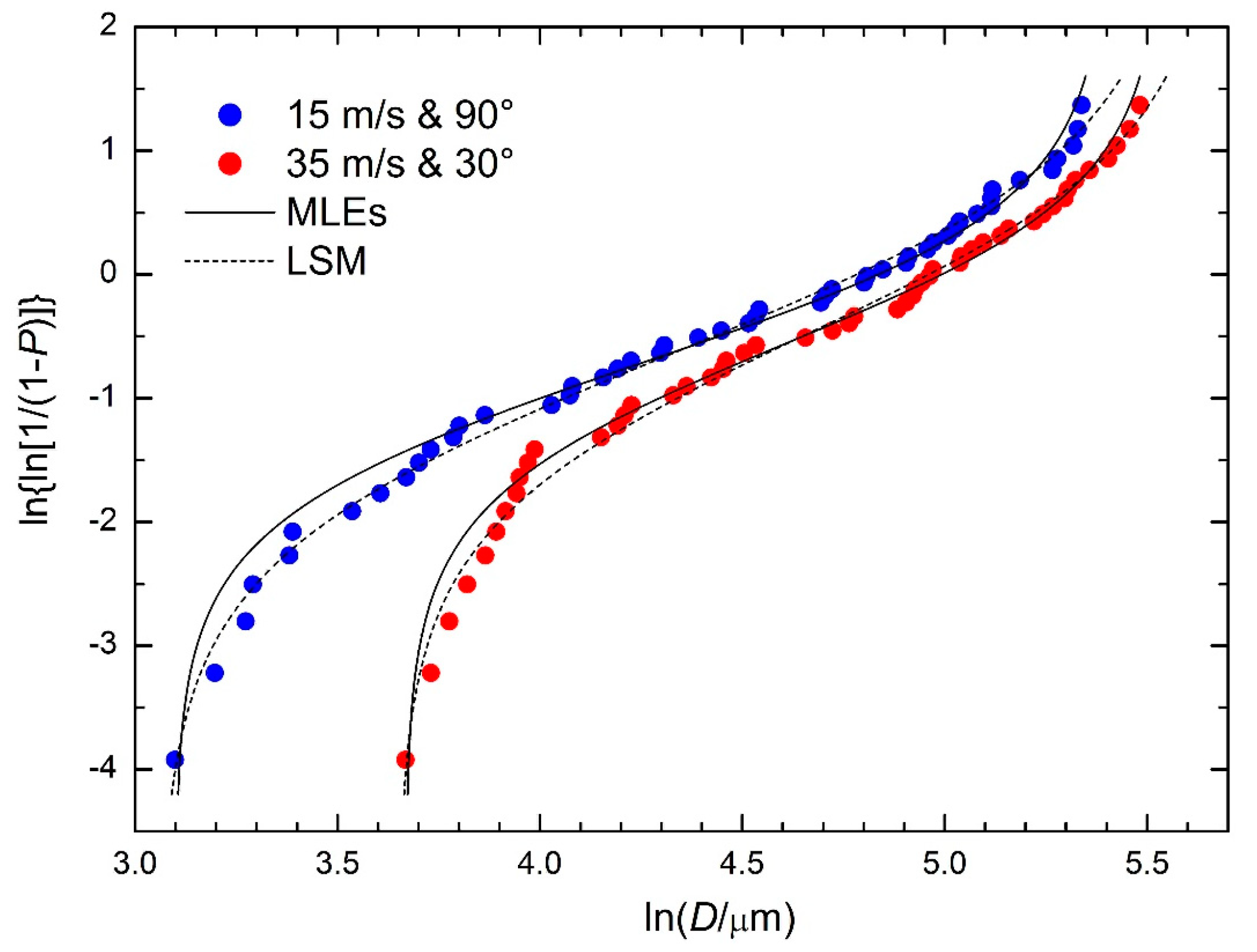
4. Distribution Parameters Determined by MLEs
5. CDF with a Greater Number of Parameters
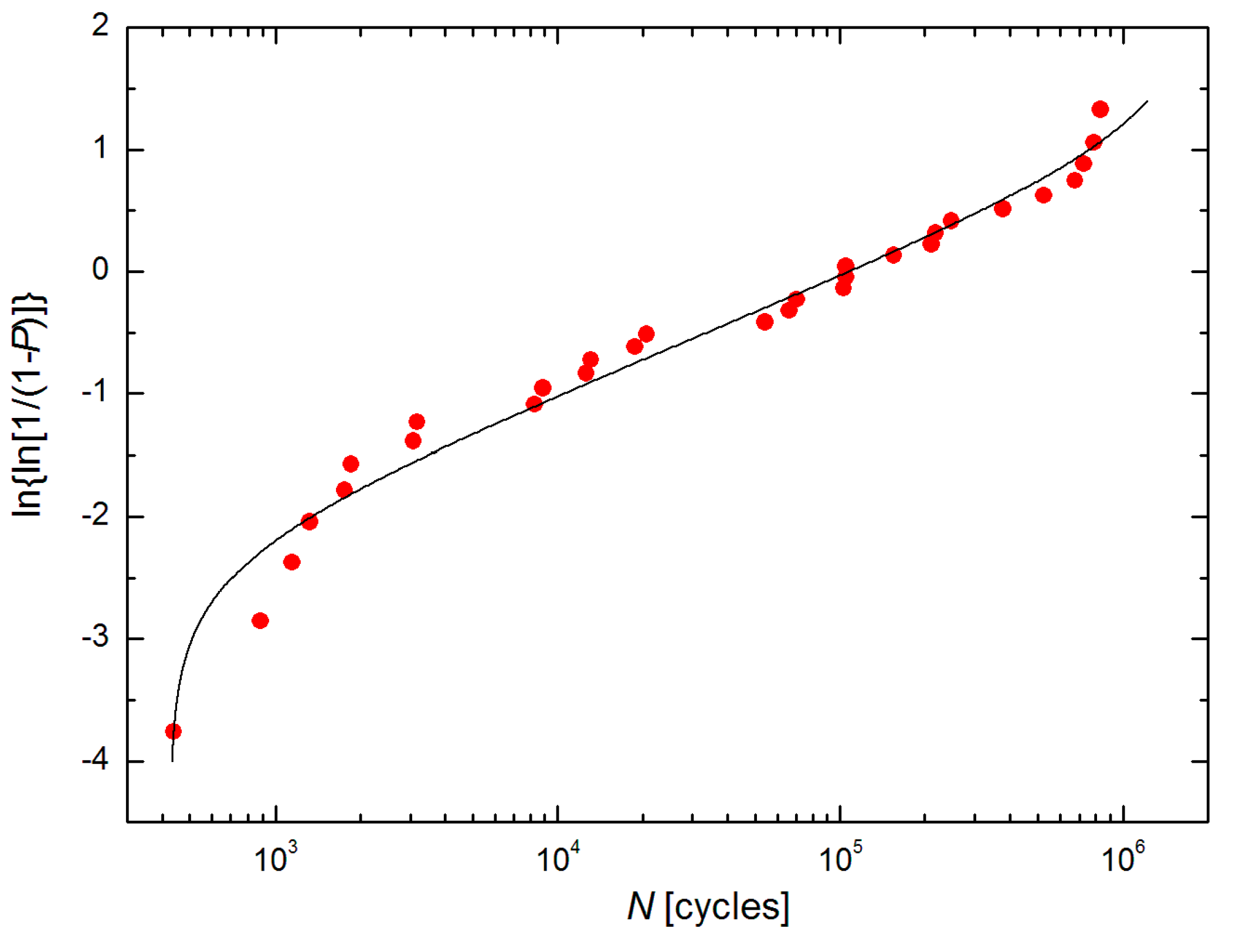
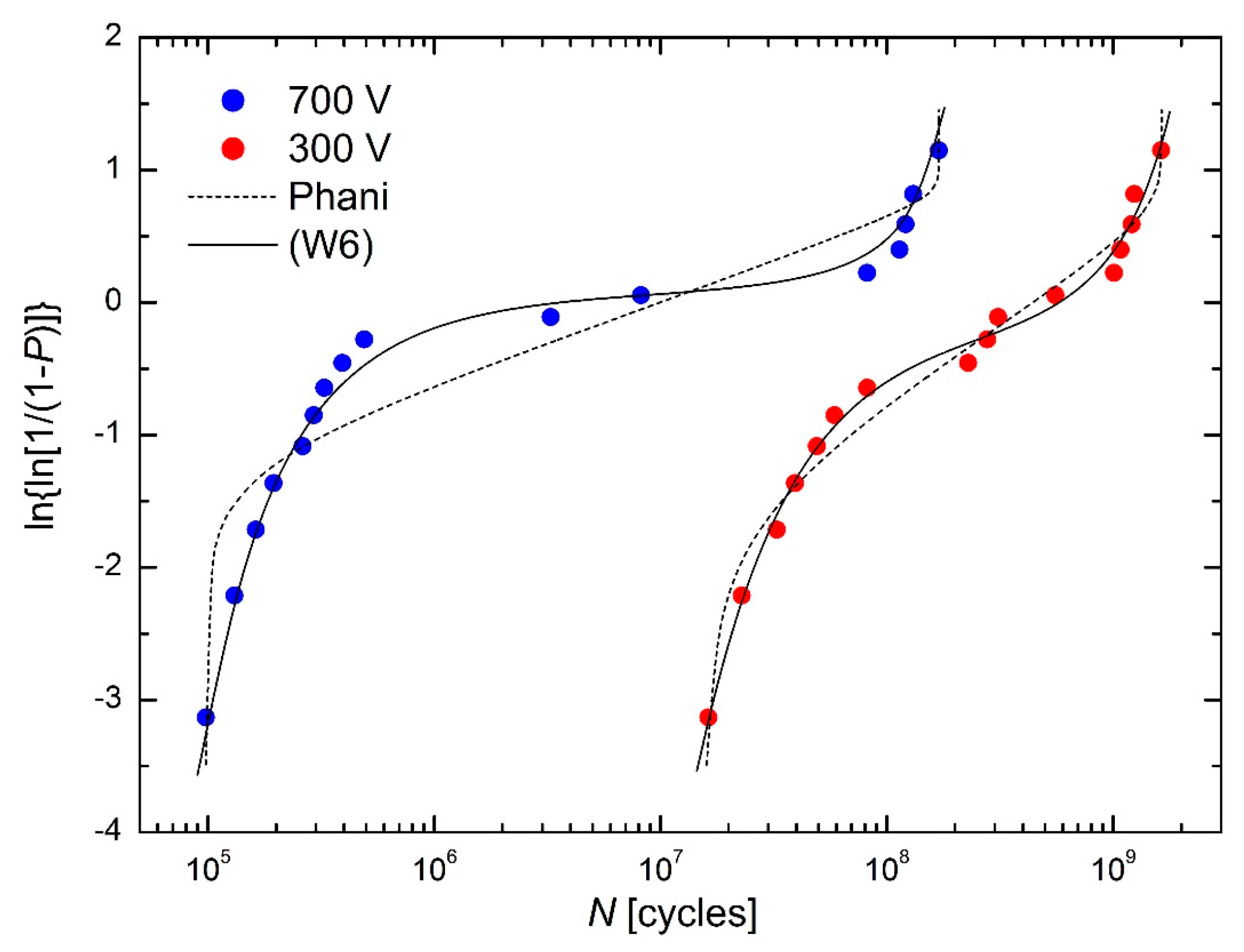
- using the (W4) CDF was fully unstable; therefore, the firmly given values N0 = 9.79 × 104 cycles (closely below the minimum number of cycles) and N∞ = 1.71 × 108 cycles (closely above the maximum number of cycles) had to be used (see Figure 6),
- using the Phani CDF was stable, but the fit was not acceptable (see the left dashed line in Figure 13),
- using the (W6) CDF was stable, and the fit was fully acceptable (see the left solid line in Figure 13).
- to better fit generally,
- to better fit all parts of the Weibull plot,
- to smaller curvature of the part of the curve with small curvature (almost a straight-line part, see upper parts of solid lines),
- to bigger curvature of the arc of the curve (see lower parts of solid lines),
- to a higher value of the t0 parameter.
6. Discussion
6.1. Modular form of the (W6) CDF
6.2. Upper and Lower Limitations of Data Sets in Reliability Studies and Material Testing
- the third curve (from the left) in Figure 8, which is significantly curved only once and not the (W4), but the (W3max) CDF is suitable in this case.
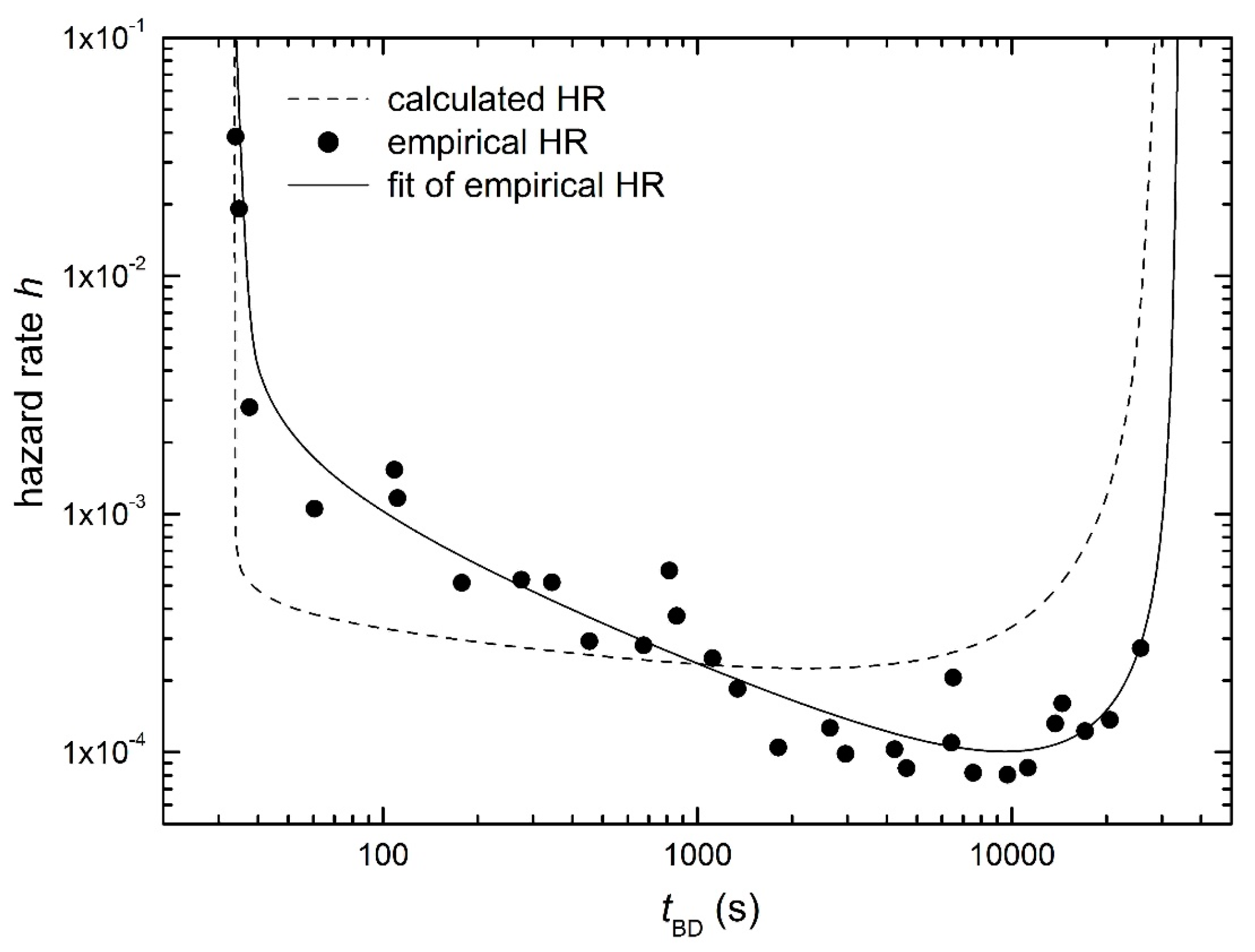
6.3. Bathtub-Shaped Hazard Rate Curve
6.4. Optimum Number of Distribution Parameters
- when the coefficient of determination noticeably increases or, equivalently, the residual sum of squares noticeably decreases,
- when the relative standard deviations of the regression parameters do not reach tens of a percent (or more),
- when the maximum likelihood value noticeably increases.
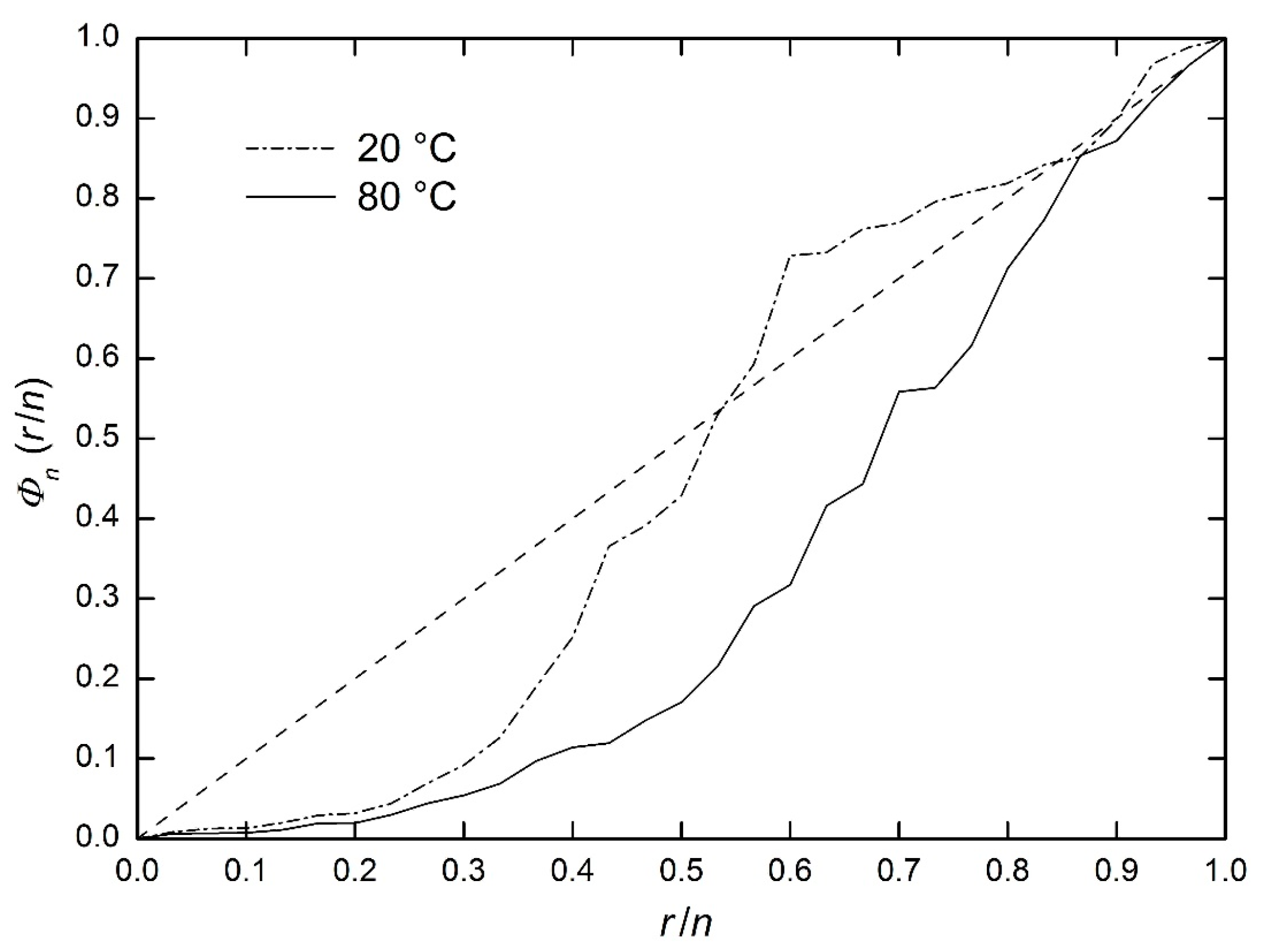
6.5. Curvature of the Weibull Plots
6.6. Other Authors’ CDFs with More Parameters
6.7. Final Comment
7. Conclusions
- The Weibull plots, which are somehow curved, are usually fitted with several straight lines. The concavely–convexly curved Weibull plots can be successfully fitted with the regression function described by Equation (W4) containing the lower limit t0 and the upper limit t∞ of the independent variable. This equation can be especially useful in reliability studies and material testing.
- In the field of reliability, the t0 and t∞ parameters can be called minimum and maximum lifetime (time to failure, time-to-breakdown, etc.). In material testing, they can be called minimum and maximum strength (fracture toughness, defect size, etc.). In the fatigue of materials, the t∞ parameter can mean the number of cycles to fracture.
- The hazard rate curves corresponding to the (W4) CDF are bathtub-shaped (with the minimum hazard rate for the tmin = (1 + β) t0/2 + (1 − β) t∞/2 value) not only for β < 1 (as in the case of the (W3max) CDF) but also for the greater values of the β parameter. Their limitation depends on the t∞/t0 ratio.
- In most cases of reliability studies described by the (W4) CDF, the values of the β parameter are small enough (especially if they are determined using the MLEs) to obtain bathtub-shaped hazard rate curves. In material testing, higher values of the β parameter are more usual, but here, the hazard rate has no specific significance.
- It turns out that there seems to be a certain border area between the decreasing HR and the bathtub-shaped HR, where different criteria (hazard rate dependence versus TTT plot) give different qualitative results (whether the decreasing or the bath-tub shaped HR).
- In the cases of data sets, when longer straight parts of their Weibull plots convert into sharper arcs, the CDFs with the higher number of parameters can be successfully used: (W4max) instead of (W3max), (W4min) instead of (W3min), and (W6) instead of (W4). It is valid, especially for big data sets with limited dispersion.
- All presented CDFs are fully consistent with the (W2) CDF describing the straight-line Weibull plot. The Kies modification, as published, is not consistent with the (W2) CDF but can be rewritten into a fully consistent form, which is fully equivalent to the (W4) CDF. The Phani modification with five parameters is not consistent with the (W2) CDF. It represents a certain intermediate stage between the (W4) and (W6) CDFs and usually does not lead to a noticeably better fit than the (W4) CDF. Its application is questionable.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weibull, W. A Statistical Distribution Function of Wide Applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Weibull, W. A Statistical Theory of the Strength of Materials; Generalstabens litografiska anstalts förlag: Stockholm, Sweden, 1939. [Google Scholar]
- Benard, A.; Bos-Levenbach, E.C. Het uitzetten van waarnemingen op waarschijnlijkdeids-papier (The Plotting of Observations on Probability Paper). Stat. Neerl. 1953, 7, 163–173. [Google Scholar] [CrossRef] [Green Version]
- Kohout, J. Three-parameter Weibull distribution with upper limit applicable in reliability studies and materials testing. Microelectron. Reliab. 2022, 137, 114769. [Google Scholar] [CrossRef]
- Wu, B.; Ni, N.; Fan, X.; Zhao, X.; Xiao, P.; Guo, F. Strength degradation of SiC fibers with a porous ZrB2-SiC coating: Role of the coating porous structure. J. Eur. Ceram. Soc. 2019, 40, 961–971. [Google Scholar] [CrossRef]
- Kies, J.A. The Strength of Glass; Report No. 5093; Naval Research Laboratory: Washington, DC, USA, 1958. [Google Scholar]
- Phani, K.K. A new modified Weibull distribution function. J. Am. Ceram. Soc. 1987, 70, 182–184. [Google Scholar] [CrossRef]
- Atanassova, E.; Novkovski, N.; Spassov, D.; Paskaleva, A.; Skeparovski, A. Time-dependent-dielectric-breakdown characteristics of Hf-doped Ta2O5/SiO2 stack. Microelectron. Reliab. 2014, 54, 381–387. [Google Scholar] [CrossRef]
- Aarset, M.V. How to Identify a Bathtub Hazard Rate. IEEE Trans. Reliab. 1987, 36, 106–108. [Google Scholar] [CrossRef]
- Marcon, D.; Meneghesso, G.; Wu, T.; Stoffels, S.; Meneghini, M.; Zanoni, E.; Decoutere, S. Reliability Analysis of Permanent Degradations on AlGaN/GaN HEMTs. IEEE Trans. Electron. Devices 2013, 60, 3132–3141. [Google Scholar] [CrossRef]
- Jung-Hyuk Koh, Tae-geun Kim, Reliability of Pb(Mg, Nb)O3-Pb(Zr, Ti)O3 multilayer ceramic piezoelectric actuators by Weibull method. Microelectron. Reliab. 2006, 46, 183–188. [CrossRef]
- Wei, S.; Xie, Z.; Xue, W.; Yi, Z.; Chen, J.; Cheng, L. Strengthening mechanism of aluminum nitride ceramics from 293 to 77 K. Mater. Lett. 2014, 119, 32–34. [Google Scholar] [CrossRef]
- Haibach, E.; de Back, J.; Lieurade, H.P.; Olivier, R.; Rinaldi, F.; Simon, P. Fatigue Investigation of Typical Welded Joints in Steel FeE 460 as Compared to FeE 355 (Final Report); Office for Official Publications of the European Communities: Luxembourg, 1979; Available online: https://op.europa.eu/cs/publication-detail/-/publication/abc108c7-e101-4e94-a58e-71a08af10a96/language-en (accessed on 7 December 2022).
- Kasu, S.R.; Deb, S.; Mitra, N.; Muppireddy, R.A.; Kusam, S.R. Influence of aggregate size on flexural fatigue response of concrete. Constr. Build. Mater. 2019, 229, 116922. [Google Scholar] [CrossRef]
- Barka, B.; Faci, A.; Bouaouadja, N.; Bousbaa, C.; Benachour, D.; Fatmi, M. Influence of the velocity and impact angle on the distribution of the surface defects of a sandblasted glass. Int. J. Appl. Glass Sci. 2018, 9, 471–479. [Google Scholar] [CrossRef]
- Gan, J.A.; Berndt, C.C. Effects of standoff distance on porosity, phase distribution and mechanical properties of plasma sprayed Nd–Fe–B coatings. Surf. Coat. Technol. 2013, 216, 127–138. [Google Scholar] [CrossRef]
- EN 62506:2013; Methods for Product Accelerated Testing (IEC 62506:2013). European Standardization Organization: Brussels, Belgium, 2013.
- Forman, R.G.; Shivakumar, V.; Mettu, S.R.; Newman, J.C. Fatigue Crack Growth Computer Program ‘NASGRO’ Version 3.0; Reference Manual JSC-22267B, NASA/Lyndon B; Johnson Space Center: Houston, TX, USA, 2000. [Google Scholar]
- Kohout, J. A new function describing fatigue crack growth curves. Int. J. Fatigue 1999, 21, 813–821. [Google Scholar] [CrossRef]
- Bartosiewicz, L.; Krause, A.R.; Kovacs, B.; Putatunda, S.K. Fatigue Crack Growth Behavior of Austempered Ductile Cast Iron. AFS Trans. 1992, 100, 135–142. [Google Scholar]
- Sun, C.T.; Jin, Z.-H. Fracture Mechanics; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Zeng, H.; Tian, L.; Chen, Q. Five and four-parameter lifetime distributions for bathtub-shaped failure rate using Perks mortality equation. Reliab. Eng. Syst. Saf. 2016, 152, 307–315. [Google Scholar] [CrossRef]
- Perks, W. On some experiments in the graduation of mortality statistics. J. Inst. Actuar. 1932, 63, 12–57. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Beghriche, A.; Zeghdoudi, H.; Raman, V.; Chouia, S. New polynomial exponential distribution: Properties and applications. Stat. Transit. New Ser. 2022, 23, 95–112. [Google Scholar] [CrossRef]
- Gulzar, M.; Meriem, B.; Gemeay, A.M.; Almetwally, E.M.; Zeghdoudi, H.; Alshawarbeh, E.; Abdulrahman, A.T.; El-Raouf, M.M.A. Hussam, E. The Power XLindley Distribution: Statistical Inference, Fuzzy Reliability, and COVID-19 Application. J. Funct. Spaces 2022, 2022, 9094078. [Google Scholar]
- Metiri, F.; Zeghdoudi, H.; Ezzebsa, A. On the Characterisation of X-Lindley Distribution by Truncated Moments: Properties and Application. Oper. Res. Decis. 2022, 32, 97–109. [Google Scholar]


| Equation | η [s] | β | t0 [s] | t∞ [s] | tmin [s] | h(tmin) [s−1] | βmax |
|---|---|---|---|---|---|---|---|
| (W4) | 4941 | 0.849 | 33.75 | 29,204 | 2232 | 2.247 × 10−4 | 1.002 |
| (17) | 4722 | 0.437 | 34.08 | 33,863 | 9549 | 1.005 × 10−4 | 1.002 |
| Method → | MLEs | LSM | ||
|---|---|---|---|---|
| conditions | parameter | Equations (24) and (25) | a = 0 (Equation (4)) | a = 0.5 (Equation (3)) |
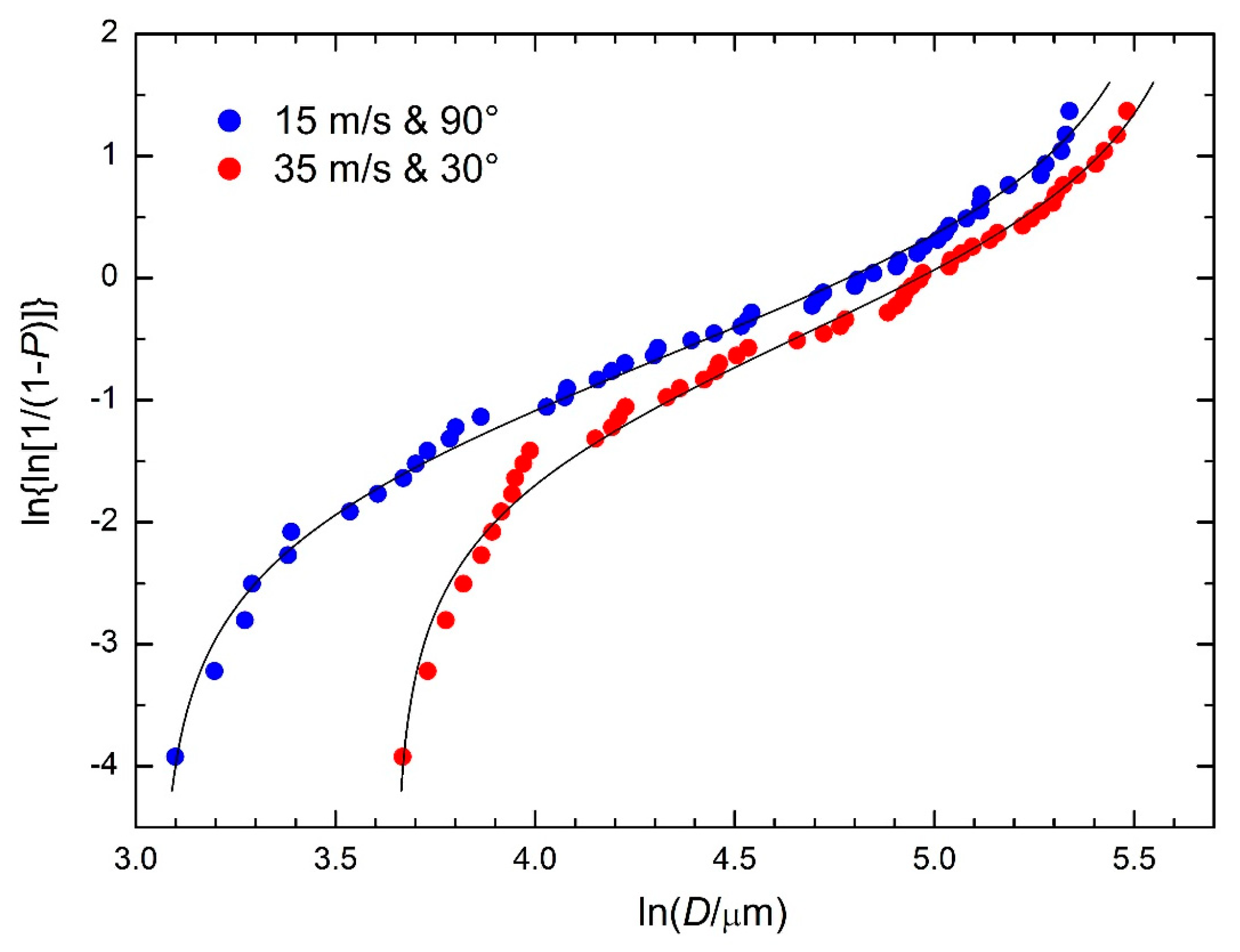
| 15 m/s and 90° | η [μm] | 243.8 | 177.9 | 174.0 |
| β [-] | 0.576 | 0.748 | 0.804 | |
| D0 [μm] | 22.2 | 21.4 | 21.8 | |
| D∞ [μm] | 220.7 | 266.7 | 264.5 | |
| 35 m/s and 30° | η [μm] | 260.1 | 205.1 | 202.0 |
| β [-] | 0.590 | 0.724 | 0.751 | |
| D0 [μm] | 39.2 | 38.5 | 38.8 | |
| D∞ [μm] | 253.3 | 290.7 | 288.8 | |
| Equation | Parameters | 300 V | 700 V |
|---|---|---|---|
| (W4) ≡ Kies [6] | 4 | 0.454 | 1.872 |
| (12) or (27) ≡ Phani [7] | 5 | 0.387 | 1.679 |
| (W6) | 6 | 0.131 | 0.155 |
| Quantity | S | t0 [HV] | ||||
|---|---|---|---|---|---|---|
| Distance [mm] | 200 | 250 | 300 | 200 | 250 | 300 |
| (W3min) | 0.2994 | 0.2264 | 0.7570 | 526 | 483 | 465 |
| (W4min) | 0.2120 | 0.1974 | 0.4112 | 542 | 497 | 474 |
| Quantity | S | t∞ [h] | ||||
|---|---|---|---|---|---|---|
| Voltage [V] | 25 | 26 | 27 | 25 | 26 | 27 |
| (W3min) | 0.02192 | 0.05284 | 0.07469 | 13482 | 4976 | 585 |
| (W4min) | 0.00059 | 0.00314 | 0.00308 | 11900 | 3999 | 491 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kohout, J. Four-Parameter Weibull Distribution with Lower and Upper Limits Applicable in Reliability Studies and Materials Testing. Mathematics 2023, 11, 544. https://doi.org/10.3390/math11030544
Kohout J. Four-Parameter Weibull Distribution with Lower and Upper Limits Applicable in Reliability Studies and Materials Testing. Mathematics. 2023; 11(3):544. https://doi.org/10.3390/math11030544
Chicago/Turabian StyleKohout, Jan. 2023. "Four-Parameter Weibull Distribution with Lower and Upper Limits Applicable in Reliability Studies and Materials Testing" Mathematics 11, no. 3: 544. https://doi.org/10.3390/math11030544






