Hotelling T2 Control Chart for Detecting Changes in Mortality Models Based on Machine-Learning Decision Tree
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mortality Modelling
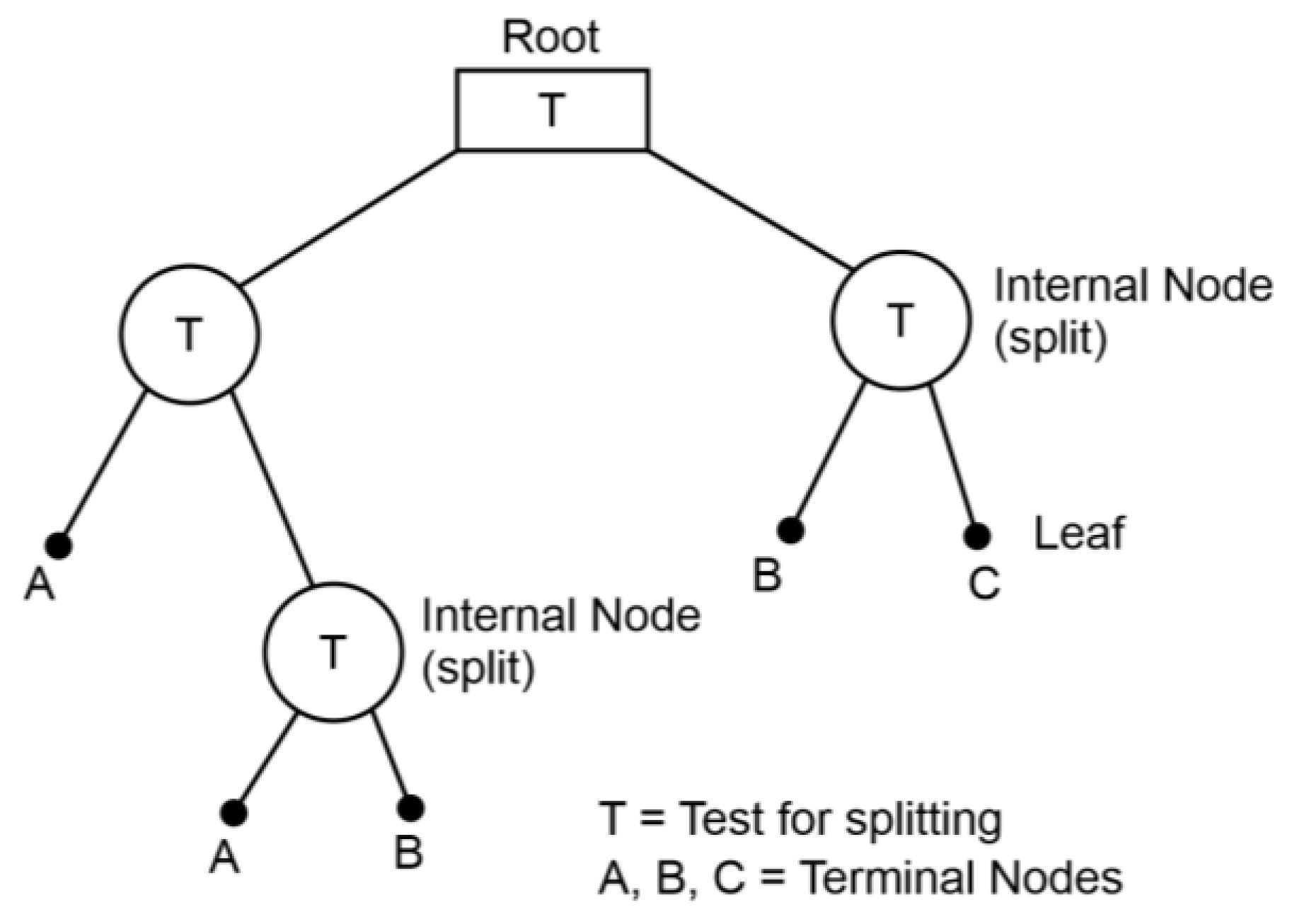
2.2. The Use of Machine Learning in the Models
2.3. Externally Studentized Deviance
2.4. Hotelling T2 Control Chart
3. Implementation: Mortality Modelling
3.1. Fitting Lee–Carter Model
3.2. Fitting LC, RH, and CBD Models
4. Analysis of the Multivariate Control Chart
4.1. Hotelling T2 Control Chart
4.2. Decomposition of The Residuals to Explore Specific Age Groups
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cox, P.R. Demography; Cambridge University Press: Cambridge, MA, USA, 1976. [Google Scholar]
- Embrechts, P.; Wüthrich, M.V. Recent challenges in actuarial science. Annu. Rev. Stat. Its Appl. 2022, 9, 119–140. [Google Scholar] [CrossRef]
- Zili, A.H.A.; Kharis, S.A.A.; Lestari, D. Peramalan tingkat kematian Indonesia akibat COVID-19 menggunakan model ARIMA. J. Indones. Sos. Sains 2021, 2, 1–8. [Google Scholar] [CrossRef]
- Gompertz, B. XXIV. On the nature of the function expressive of the law of human mortality, and on a new mode of deter-mining the value of life contingencies. In a letter to Francis Baily, Esq. FRS & c. Philos. Trans. R. Soc. Lond. 1825, 115, 513–583. [Google Scholar]
- de Moivre, A. Annuities upon Lives, or, the Valuation of Annuities upon Any Number of Lives, as Also, of Reversions: To Which Is Added, an Appendix Concerning the Expectations of Life, and Probabilities of Survivorship; Oxford University: London, UK, 1731. [Google Scholar]
- Weibull, W. A Statistical Theory of the Strength of Materials; Generalstabens Litografiska Anstalts Förlag: Stockholm, Sweden, 1939. [Google Scholar]
- Luy, M.; di Giulio, P.; di Lego, V.; Lazarevič, P.; Sauerberg, M. Life expectancy: Frequently used, but hardly understood. Gerontology 2020, 66, 95–104. [Google Scholar] [CrossRef]
- Díaz-Rojo, G.; Debón, A.; Mosquera, J. Multivariate control chart and Lee–Carter models to study mortality changes. Mathematics 2020, 8, 2093. [Google Scholar] [CrossRef]
- García-Bustos, S.; Cárdenas-Escobar, N.; Debón, A.; Pincay, C. A control chart based on Pearson residuals for a negative binomial regression: Application to infant mortality data. Int. J. Qual. Reliab. Manag. 2021, 39, 2378–2399. [Google Scholar] [CrossRef]
- AKoetsier; de Keizer, N.; de Jonge, E.; Cook, D.; Peek, N. Performance of risk-adjusted control charts to monitor in-hospital mortality of intensive care unit patients: A simulation study. Crit. Care Med. 2012, 40, 1799–1807. [Google Scholar] [CrossRef]
- Felix-Cardoso, J.; Vasconcelos, H.; Rodrigues, P.; Cruz-Correia, R. Excess mortality during COVID-19 in five European countries and a critique of mortality data analysis. MedRxiv 2020. [Google Scholar] [CrossRef]
- Deprez, P.; Shevchenko, P.; Wüthrich, M.V. Machine learning techniques for mortality modeling. Eur. Actuar. J. 2017, 7, 337–352. [Google Scholar] [CrossRef]
- Lee, R.D.; Carter, L.R. Modeling and Forecasting U. S. Mortality. J. Am. Stat. Assoc. 1992, 87, 659. [Google Scholar] [CrossRef]
- Renshaw, A.; Haberman, S. A Cohort-Based Extension to the Lee–Carter Model for Mortality Reduction factors. Insur. Math. Econ. 2006, 38, 556–570. [Google Scholar] [CrossRef]
- Haberman, S.; Renshaw, A. A comparative study of parametric mortality projection models. Insur. Math. Econ. 2011, 48, 35–55. [Google Scholar] [CrossRef] [Green Version]
- Cairns, A.J.G.; Blake, D.; Dowd, K. A Two-Factor Model for Stochastic Mortality with Parameter Uncertainty: Theory and Calibration. J. Risk Insur. 2006, 73, 687–718. [Google Scholar] [CrossRef]
- Hong, W.H.; Yap, J.; Selvachandran, G.; Thong, P.; Son, L.H. Forecasting mortality rates using hybrid Lee–Carter model, artificial neural network and random forest. Complex Intell. Syst. 2021, 7, 163–189. [Google Scholar] [CrossRef]
- Levantesi, S.; Pizzorusso, V. Application of Machine Learning to Mortality Modeling and Forecasting. Risks 2019, 7, 26. [Google Scholar] [CrossRef] [Green Version]
- Morgan, J. Classification and Regression Tree Analysis; Boston University: Boston, MA, USA, 2014; Volume 298. [Google Scholar]
- Loh, W.-Y. Fifty years of classification and regression trees. Int. Stat. Rev. 2014, 82, 329–348. [Google Scholar] [CrossRef] [Green Version]
- Coelho, E.; Nunes, L.C. Forecasting mortality in the event of a structural change. J. R. Stat. Soc. Ser. A Stat. Soc. 2011, 174, 713–736. [Google Scholar] [CrossRef]
- Debón, A.; Montes, F.; Puig, F. Modelling and forecasting mortality in Spain. Eur. J. Oper. Res. 2008, 189, 624–637. [Google Scholar] [CrossRef] [Green Version]
- Renshaw, A.; Haberman, S. On simulation-based approaches to risk measurement in mortality with specific reference to Poisson Lee–Carter modelling. Insur. Math. Econ. 2008, 42, 797–816. [Google Scholar] [CrossRef] [Green Version]
- Villegas, A.; Kaishev, V.; Millossovich, P. StMoMo: An R package for stochastic mortality modelling. In Proceedings of the 7th Australasian Actuarial Education and Research Symposium, Queensland, Australia, 3 December 2015. [Google Scholar]
- Hotelling, H. Techniques of Statistical Analysis. In Chapter Multivariate Quality Control Illustrated by the Testing of Sample Bombsights; McGraw-Hill: New York, NY, USA, 1947; pp. 113–184. [Google Scholar]
- Tracy, N.D.; Young, J.C.; Mason, R.L. Multivariate Control Charts for Individual Observations. J. Qual. Technol. 1992, 24, 88–95. [Google Scholar] [CrossRef]
- Urdinola, B.P.; Torres, F.; Velasco, J.A. Latin American Human Mortality Database. 2022. Available online: www.lamortalidad.org (accessed on 23 October 2022).
- Turner, H.; Firth, D. Generalized Nonlinear Models in R: An Overview of the Gnm Package; University of Warwick: Coventry, UK, 2007. [Google Scholar]
- Adebón; Martínez-Ruiz, F.; Montes, F. A geostatistical approach for dynamic life tables: The effect of mortality on re-maining lifetime and annuities. Insur. Math. Econ. 2010, 47, 327–336. [Google Scholar]
- Jdanov, D.A.; Jasilionis, D.; Shkolnikov, V.; Barbieri, M. Human Mortality Database; Max Planck Institute for Demographic Research: Rostock, Germany; University of California: Berkeley, CA, USA; French Institute for Demographic Studies: Paris, France, 2019. [Google Scholar]







| Model | |||
|---|---|---|---|
| LC1 | LC2 | ||
| Deviance | Female | 872549.4 | 1614.1 |
| Male | 627047.6 | 14261.2 | |
| MSE | Female | 1968.57 | 370.71 |
| Male | 2500.44 | 532.95 | |
| MAPE | Female | 0.42938 | 0.06283 |
| Male | 0.37023 | 0.08015 |
| Model before DT | Model after DT | ||||||
|---|---|---|---|---|---|---|---|
| LC | RH | CBD | LC | RH | CBD | ||
| MSE | Female | 1,015,645 | 142,174 | 14,369,727 | 112,582 | 36,499 | 1,461,146 |
| Male | 716,095 | 265,295 | 15,412,708 | 94,242 | 62,945 | 1,278,129 | |
| MAPE | Female | 0.1634 | 0.0625 | 0.4363 | 0.0639 | 0.0437 | 0.1679 |
| Male | 0.0968 | 0.0646 | 0.3596 | 0.0504 | 0.0409 | 0.1697 | |
| Sex | Year | T2 Values 1 |
|---|---|---|
| Female | 1991 2015 | 24.84 25.86 |
| Male | 1991 1996 2001 2003 | 26.81 25.89 26.96 25.76 |
| Age Group | Female | Male | ||||
|---|---|---|---|---|---|---|
| 1991 | 2015 | 1991 | 1996 | 2001 | 2003 | |
| 0–1 | 3.70 * | 0.83 | 3.87 * | 3.89 * | 3.09 * | 0.27 |
| 1–4 | 1.20 | 0.85 | 1.00 | 0.99 | 0.24 | 2.33 |
| 5–9 | 0.07 | 1.28 | 0.14 | 0.50 | 0.57 | 0.18 |
| 10–14 | 1.56 | 0.41 | 3.09 * | 4.89 * | 0.40 | 0.27 |
| 15–19 | 0.57 | 0.87 | 0.61 | 1.03 | 0.76 | 0.10 |
| 20–24 | 0.93 | 1.40 | 0.06 | 2.13 | 1.39 | 1.28 |
| 25–29 | 0.61 | 3.89 * | 1.28 | 1.33 | 0.40 | 1.56 |
| 30–34 | 0.18 | 0.38 | 0.41 | 0.44 | 0.07 | 1.36 |
| 35–39 | 0.91 | 0.39 | 0.39 | 0.56 | 0.83 | 0.80 |
| 40–44 | 0.18 | 2.96 * | 1.75 | 0.69 | 3.86 * | 0.71 |
| 45–49 | 1.96 | 1.29 | 0.59 | 0.83 | 0.02 | 5.08 * |
| 50–54 | 1.71 | 1.27 | 0.01 | 1.61 | 1.42 | 5.31 * |
| 55–59 | 0.56 | 0.24 | 0.17 | 0.62 | 1.11 | 0.20 |
| 60–64 | 1.53 | 0.54 | 0.09 | 0.40 | 0.04 | 0.59 |
| 65–69 | 1.18 | 0.76 | 1.21 | 0.25 | 0.34 | 0.33 |
| 70–74 | 3.23 * | 1.95 | 2.79 * | 0.42 | 0.82 | 2.63 * |
| 75–79 | 0.06 | 0.78 | 1.21 | 0.58 | 1.44 | 0.95 |
| 80–84 | 0.68 | 0.25 | 3.18 * | 0.54 | 0.45 | 0.68 |
| 85+ | 3.74 * | 0.19 | 2.46 * | 3.47 * | 0.48 | 2.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rakhmawan, S.A.; Omar, M.H.; Riaz, M.; Abbas, N. Hotelling T2 Control Chart for Detecting Changes in Mortality Models Based on Machine-Learning Decision Tree. Mathematics 2023, 11, 566. https://doi.org/10.3390/math11030566
Rakhmawan SA, Omar MH, Riaz M, Abbas N. Hotelling T2 Control Chart for Detecting Changes in Mortality Models Based on Machine-Learning Decision Tree. Mathematics. 2023; 11(3):566. https://doi.org/10.3390/math11030566
Chicago/Turabian StyleRakhmawan, Suryo Adi, M. Hafidz Omar, Muhammad Riaz, and Nasir Abbas. 2023. "Hotelling T2 Control Chart for Detecting Changes in Mortality Models Based on Machine-Learning Decision Tree" Mathematics 11, no. 3: 566. https://doi.org/10.3390/math11030566
APA StyleRakhmawan, S. A., Omar, M. H., Riaz, M., & Abbas, N. (2023). Hotelling T2 Control Chart for Detecting Changes in Mortality Models Based on Machine-Learning Decision Tree. Mathematics, 11(3), 566. https://doi.org/10.3390/math11030566






