Deterioration Control Decision Support System for the Retailer during Availability of Trade Credit and Shortages

Abstract

The deterioration rate is a significant aspect of perishable goods. Since perishable items will always deteriorate, there are effective methods for reducing the rate of deterioration. Furthermore, in the existing inventory control literature, the deterioration rate is often viewed as an exogenous component. Keeping this problem in mind, this article develops the perishable inventory control system from the retailer’s perspective in which: (i) the deterioration rate is a controllable factor and suggests a new fresh quality technology (FQT) indicator, (ii) demand is determined by the perishable product’s quality, that is controlled by its rate of deterioration, (iii) the credit duration is predefined, and (iv) shortages are expected. The key goal is to demonstrate that there is an ideal quantity of the order that minimizes the retailer’s overall cost in terms of cycle time and deterioration rate. Finally, theoretical results are validated by solving two numerical illustrations and conducting a sensitivity analysis of the main factors resulting from the following managerial implications: (i) if the range of deterioration is between zero and one then the retailer should invest in the preservation factor to preserve the perishable product and if greater than one the retailer should not invest in the preservation factor, (ii) credit period significantly reduces the total cost. Hence, this trade credit strategy is more beneficial to the model.

1. Introduction

In real-world scenarios, the deterioration of products is a big issue in every business segment. As perishable goods transit through a supply chain, they deteriorate at different rates. Farming products such as fruits, vegetables, and meat are examples of perishable products. Uncontrolled deterioration results in a large amount of spoiling waste. The loss ratio due to the deterioration of fresh produce is as high as 30% in many countries [1]. In China, the annual loss of agricultural products amounts to more than USD 43 billion, which is equivalent to the production output of 0.1 billion hectares of cultivated land (China Economic Information Daily 2016). Recent advanced technologies such as the freshness preservation effort (FPE) [2], fresh-keeping effort (FKE) investment strategies, and a fresh product supply chain (FSC) system [3] have resulted in the development of emerging innovations that may be utilized efficiently to assess and control the rate of deterioration [4]. In general, the rate of deterioration (DR) calculates the proportion of perishable items that are unusable due to decay or expiry [5]. For illustration, fresh vegetables have a different DR depending on the storage climate and handling techniques. Furthermore, the rate of deterioration of the most perishable items remains constant under constant environmental conditions but begins to fluctuate when storing temperature and humidity change. Because a perishable product’s deterioration rate is proportional to its quality, it has a significant impact on sales [3]. The availability of fresh goods on display affects sales at the point of purchase [2]. Due to the general significant visual aspects of the farming quality of the product and stock, the consumption trend and, as a result, inventory management of agricultural products differs from those for other perishable goods.

Since a perishable item’s rate of deterioration may be reduced by proper handling and storage environments, it should be evaluated as a decision parameter when circumstances permit. As a result, the appropriate inventory strategy can be controlled using both freshness-dependent demand and deterioration control information. Hence, to support deterioration rate management, this article suggests a unique fresh quality technology (FQT) parameter. Investing in suitable technology and manpower to furnish needed storage and handling conditions, on the other hand, loss of farming goods due to a lower rate of deterioration. The reduced degradation rate of farming goods justifies the high investment cost for effective inventory management. Although loss prevention is an important aim in farming product inventory control, economic concerns are a primary focus for real-world retail decision making. Therefore, in this model, deterioration rate is controllable and considered as a decision variable with the effort of freshness technologies and quality.

In this modern dynamic and competitive business context, trade credit policy becomes one of the most appropriate and efficient strategies to enhance demand and control commodities. If a supplier offers a retailer to pay for products later without incurring interest costs, the retailer is more inclined to purchase commodities. Therefore, the supplier provides the retailer with a specific time to make the payment. This type of business finance in which the retailer is permitted to purchase goods and pay the supplier afterward is identified as a trade credit policy [6]. Many companies use this strategy to increase sales and attract more customers. In addition, when a product’s demand frequently increases because of the quality and freshness but the product is unavailable for a sustained duration, shortages arise. Therefore, this article permits the partially backlogged shortages when the cycle time comes to an end and also considers the upstream credit period in which the supplier offers a retailer a mutual credit time so that the retailer can pay the balance at a later scheduled date; this realistic scenario forms the basis of this study.

1.1. Aim of This Study

The objective of this research is to go into a new realm such as the field of inventory management for agricultural products. The following important interesting and significant questions are examined in this research:

• What is the need for controlling deterioration rate using fresh quality technology and effort according to a cost factor?
• Why does the deterioration rate always consider the ideal rate if the deterioration rate is between 0 and 1?
• Why must the optimal rate of deterioration and preservation factor be in the interval $\left[1,+\propto \right)$?
• How does a strategy of trade credit affect a retailer’s productivity and profitability?
• When should a retailer have to place a back order to escape stock-outs?
• If this model were implemented in reality, what would the managerial implications be?

1.2. Contribution

Perishable products have high and varying deterioration rates when passing through their logistics systems. Agri-fresh products are a typical example of perishable products that include fresh fruits, fresh vegetables, and fresh meat. This article models the perishable inventory decision support system [7] with deterioration-controlled/freshness-dependent demand, and quality indication. Additionally, the allowable shortages condition, trade credit policy, and controllable deterioration rate are used to analyze the dynamics with various scalable parameters. We analytically model this scenario and perform sensitivity analysis to generate associated managerial implications. The most significant contributions are summarized below:

• This study develops a perishable inventory system in which deterioration rate is considered as a decision parameter and investigates its impact on perishable quality control parameters.
• The rate of deterioration is controlled using the fresh quality technique and effort as a cost factor.
• The demand depends on the deterioration and quality of the perishable product.
• Quality is defined as the time integration of the original and deteriorating quality. For illustration, a farming product with a reduced deterioration rate, which appears fresh and has much more available stock, will generate higher demand.
• Trade credit policy and its impact on the overall cost of the retailer.
• Partially backlogged shortages are permitted.

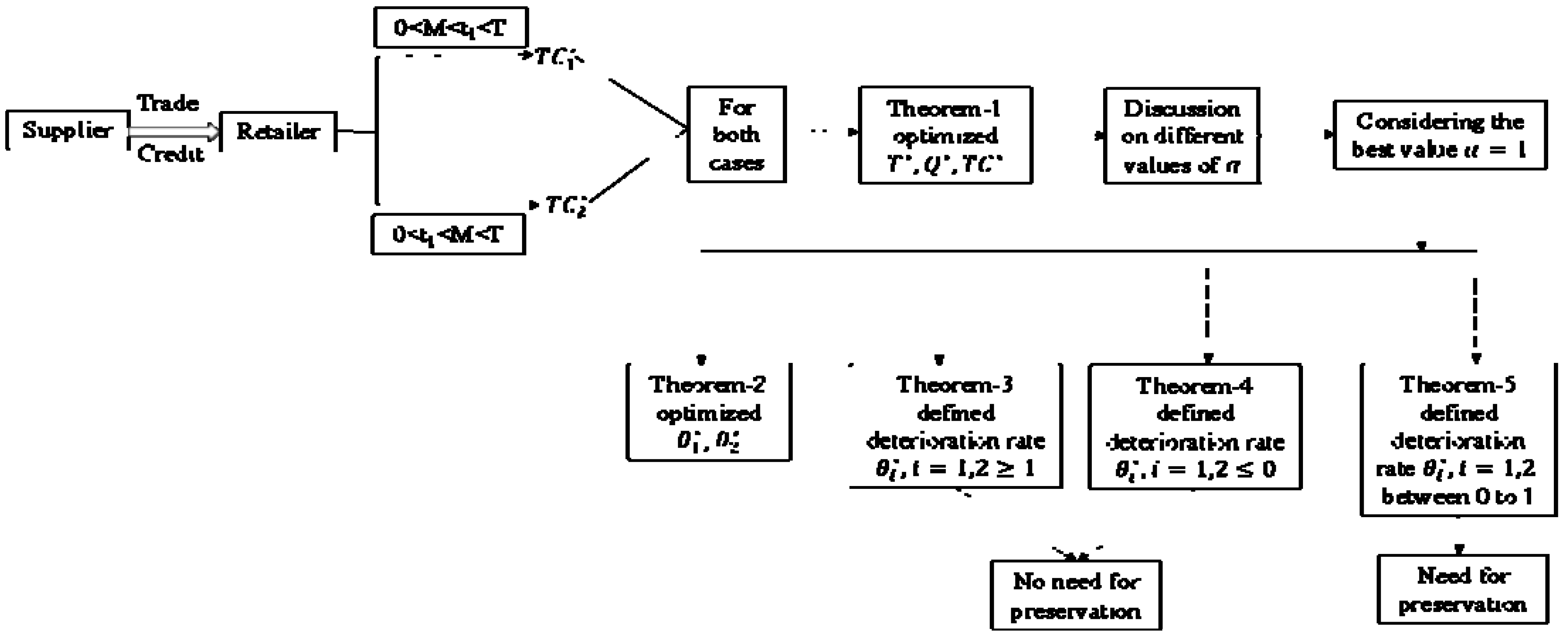
1.3. Flow of the Paper

The remaining portion of this article is discussed as follows: Section 2 is the existing review of the literature. In Section 3, the notation and assumptions are discussed. Section 4 creates a mathematical model for various upstream trade credit scenarios to minimize the overall cost of the retailer. After that, Section 5 contains the numerical study, the sensitivity analysis for the key parameters, and managerial implications for the retailer. Finally, Section 6 moderates the conclusion and future prospects for this article.

2. Literature Review

In this part, a review of the literature on product demand, deterioration, and trade credit policy in inventory models is used to highlight gaps in the area and demonstrate how prior works have contributed to this research. The first segment focuses on the literature on modeling techniques with demand, the second focuses on models with deteriorating items, and the third focuses on trade credit.

2.1. Literature Review on Inventory Models under Various Types of Demand

The most essential aspect of a business and enterprise is demand. The various forms of demand have been explored by researchers over the past few years. As a result, the researchers have taken into account various kinds of demand and developed inventory models. In this way, [8] represents a model for advertisement-dependent demand with a single-layered trade credit policy system. In [9], the authors prepared a mathematical model under the exponentially declining demand by using the concept of an allowable shortage. An economic order quantity (EOQ) model under time-linked quadratic demand with constant deterioration was introduced by [10]. Further, the perishable commodities inventory model with the preservation tool and price reduction problem under the stock- and price-dependent demand is explained by [11]. An EOQ model under the ramp demand for deteriorating products has been discussed in [12]. In recent times, a model with the consideration of shortages under the time and selling price-dependent demand has been established in [13]. An inventory model with a nonlinear stock-dependent demand for non-instantaneously deterioration is developed in [14]. After this, the role of trapezoidal demand in the inventory model for sustainable operations of fixed lifetime products is discussed in [15]. This study extends the work of [2], which proposed a controllable deterioration rate linked model for the deterioration-dependent demand. There is very little research that depends on the relationship between deterioration and demand. The contribution of this study is that the demand is completely reliant on the deterioration rate.

2.2. Literature Review on Inventory Models under Deteriorating Inventories

Since managing deteriorating inventory affects so many businesses, academics have published several articles to address the related difficulties in reality. Hence, the rate of deterioration is an important factor for describing the essential characteristics of perishable goods. Several products have a deteriorating nature over time such as fresh fruits and vegetables, milk, juice, any dairy product, etc. The retailer aims to control the amount of deterioration and stimulate demand. Therefore, the researchers took this into account and established models to reduce the rate of deterioration. The review of a perishable inventory since 2001 is reflected in [5]. Further, in [16], an inventory model under the quadratic demand by applying a maximum fixed lifetime deterioration rate is extended. A model with shortages for the constant deteriorating goods was derived by [17,18]. Furthermore, in [19], a mathematical model in which the rate of deterioration is non-instantaneous and demand is motivated by the price and stock of the product is derived. An inventory model for continuously deteriorating goods with the scheme of payment in advance was formulated by [20]. Later, a stock model for the time-dependent decline products under the demand which is sensitive to both time and price was determined by [21]. A model for controllable deterioration rate was developed by [22,23]. Further, the most significant contributions in this study were elaborated upon by [2] who established a controllable deterioration rate linked model. In [24], a concept related to the Weibull deterioration rate over the finite time perspective was established. Recently, the inventory model with green-level-dependent demand with constant deterioration has been derived in [25]. After this, [26] and others have contributed notable contributions to this field of research. Therefore, all of the researchers considered the various types of deterioration but this article focuses on the controllable deterioration rate of the perishable products.

2.3. Literature Review on Inventory Models under Trade Credit Policy

Many stock models are developed that assume payment is paid at the moment the order amount is received. However, in reality, the payment of purchase cost differs between the following: (i) payment on delivery received [27], (ii) acceptable partial payment delay, (iii) a partial deposit payment [28], and (iv) partial advance payment and allowing partial payment delay [29]. For example, a mathematical model for deteriorating products under a single-layered trade credit strategy is elaborated upon in [30]. Further, a stock model for time-dependent deteriorating goods under the two-layered partial trade credit scheme is developed in [31]. In [32], the impact of carbon emission of a supply chain under the two-layered trade credit policy is established. In addition, the partial backlogged shortages and multi-layered trade credit model are discussed in [33]. Additionally, a mathematical model under the price- and advertisement-dependent demand for a single-layered trade credit system was calculated in [34]. In this way, a stock model with two-layered trade credit and dynamic demand is incorporated in [35]. Lately, a model under the price-sensitive demand with investment in preservation equipment and single-layered trade credit policy has been created in [36]. Other inventory models include a trade credit strategy provided by [37,38,39]. Recently, the inventory model with partial linked-to-order upstream trade credit and downstream full trade credit has been developed by [40]. Moreover,

Table 1. An overview of similar studies on the EOQ model.

Source	Demand	Deterioration	Shortages	Trade Credit
[12]	Ramp type	Constant	Yes	Yes
[31]	Constant	No	Yes	Yes
[35]	Constant	Constant	Yes	Yes
[2]	Deterioration-dependent	Controllable deterioration	No	No
[22]	Price- and stock-dependent	Controllable deterioration	Yes	No
[24]	Constant	Weibull deterioration	Yes	No

provides a concise description of the existing literature relevant to the proposed model.

2.4. Gap Identification

According to the literature survey and Table 1, several studies have worked on different combinations but the uniqueness of this research is that all of the combinations such as deterioration-dependent demand, controllable deterioration, allowable shortages, and trade credit policy which were previously not considered in any articles are examined. The work of [2] established an inventory model for the controllable rate of deterioration. In this model, they only focused on the deterioration of the perishable product. In contrast to [2], this article considers the fresh quality technology (FQT), trade credit policy, and allowable shortages. Furthermore, in the literature, many authors used different techniques to control the deterioration rate. The items deteriorate in nature as shown in [16]. To control the rate of deterioration, the authors developed some technologies such as freshness preservation effort (FPE) [2], fresh-keeping effort (FKE) investment strategies, and a fresh product supply chain (FSC) system [3], as well as the freshness-keeping effort of third-party logistics service providers (TPLSPs) [41]. This study significantly derives the relation between the fresh quality technology (FQT) indicator and the deterioration rate which is the novelty of this work.

3. Notation and Assumptions

Assumptions

The inventory system only applies to a single item.

The indicator of fresh quality technology (FQT) is $\gamma =\frac{h_{\theta }}{h_c}$, where $h_{\theta }$ denotes the controllable marginal cost of holding with preservation and $h_c$ is the maximum cost of holding including preservation which denotes the highest-level effort of $h_{\theta }$. Additionally, $0<h_{\theta }<h_c$ and when $h_{\theta }\to h_c$ the deterioration rate is minimized [2].

The higher the FQT indicator $\gamma$, the less the degradation rate of perishable food, resulting in fresh items for longer periods. In [1], the impact of FQT on quality such as a power function was represented. Since the rate of deterioration and quality of farming products move in different paths, this article assumes that the controllable deterioration rate is defined as:

$$\theta =1-{\gamma }^{\frac{1}{\alpha }}$$

(1)

The FQT indicator $\gamma$ and the controlled marginal cost are expressed in the following equations:

$$\gamma ={\left(1-\theta \right)}^{\alpha }$$

(2)

$$h_{\theta }=h_c{\left(1-\theta \right)}^{\alpha }$$

(3)

According to Equation (2), decreasing the degradation rate, in general, implies a rise in the amount of freshness technology expense. When the deterioration rate is minimized, i.e., $\theta \to 0$, the FQT indicator $\gamma \to 1$ and $h_{\theta }$ becomes close to $h_c$. Likewise, when $\theta \to 1$, the FQT indicator $\gamma \to 0$ and $h_{\theta }$ becomes close to 0.

This article presumes that demand is determined by the perishable product’s quality, which is determined by the rate of deterioration. This hypothesis is premised on the reality that when two products are provided at the same price, retailers are more interested in choosing the freshest product available. Customers’ interest in purchasing fresh farming items is also influenced by shelf product availability since more visible stock generates a higher demand. Therefore, motivated by this reality, the demand rate is defined as

$$D\left(\theta \right)=D_0-\beta \theta$$

(4)

where $D_0$ is the constant demand, $\beta$ is a demand-on-quality variable, and $D\left(\theta \right)=0$ when $D_0-\beta \theta \le 0$ [2].

Consumers determine the quality of the product based on the rate of deterioration. For illustration, customers are aware that when spots emerge on a banana, the rate of deterioration is sure to increase. Likewise, if yellowing occurs on a calabrese top, the rate of deterioration rises. Additionally, users can check the quality of packaged farmed commodities from the displayed stock, which is the deterioration rate’s direct time integration. As a consequence, the deterioration rate may be directly utilized to reflect demand.

The credit duration of $M$ years is given by a supplier to a retailer. During the interval of time $\left[0,M\right]$, the retailer will earn interest $I_e$ on sold items and will be charged interest $I_c$ for unsold items throughout the interval $\left[M,T\right]$.

The proportion of partially backlogged shortages is represented by $\varsigma \left(t\right)$, which is a decreasing function that is also differentiable with respect to time $t$.

For the negative inventory, the sum of the exponential partial backlogging is identified as $e^{-\varsigma \left(T-t\right)}$, where $\varsigma >0$ is the backlogging parameter and $\left(T-t\right)$ is the waiting time for the next replacement.

There is no waiting period and the replenishment rate is infinite.

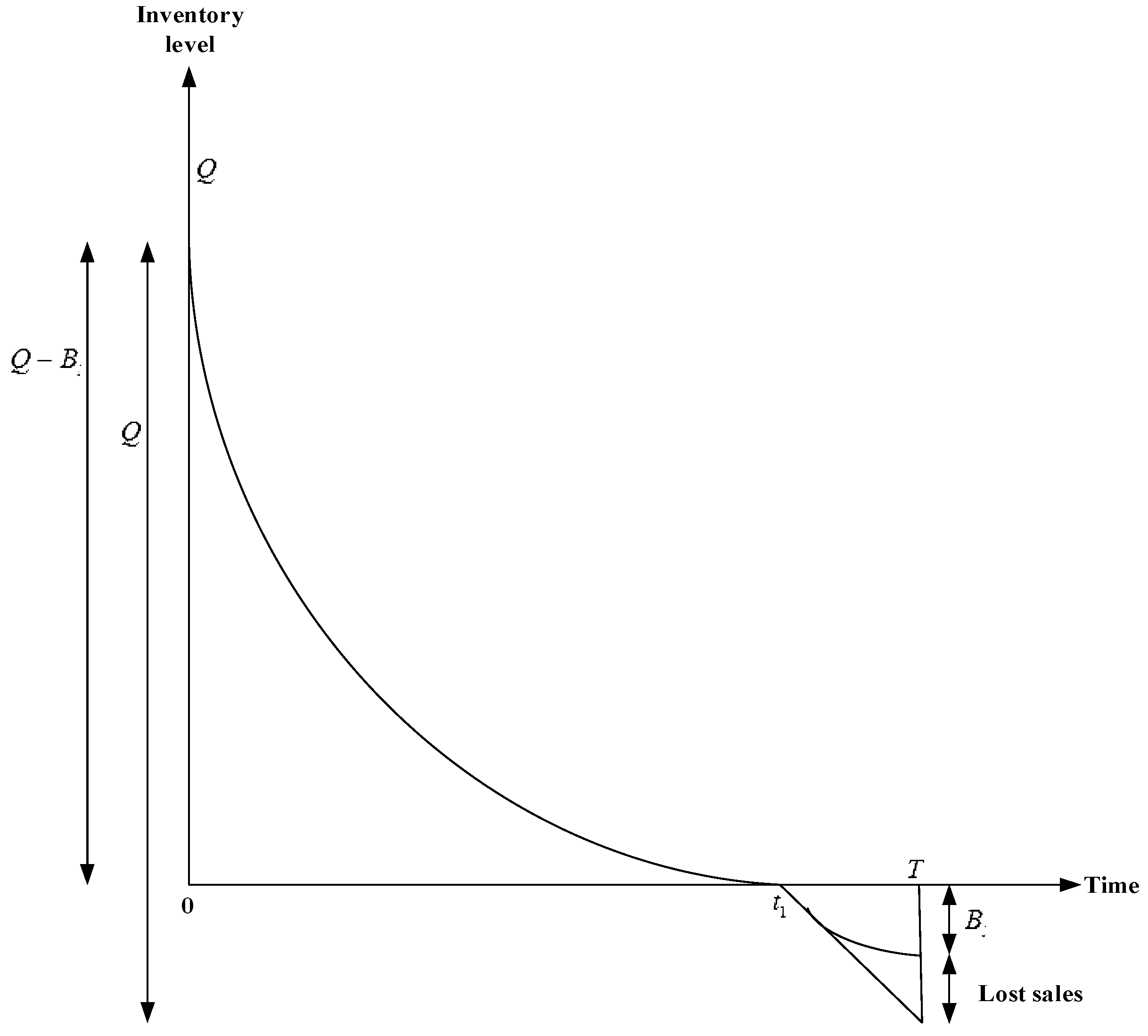
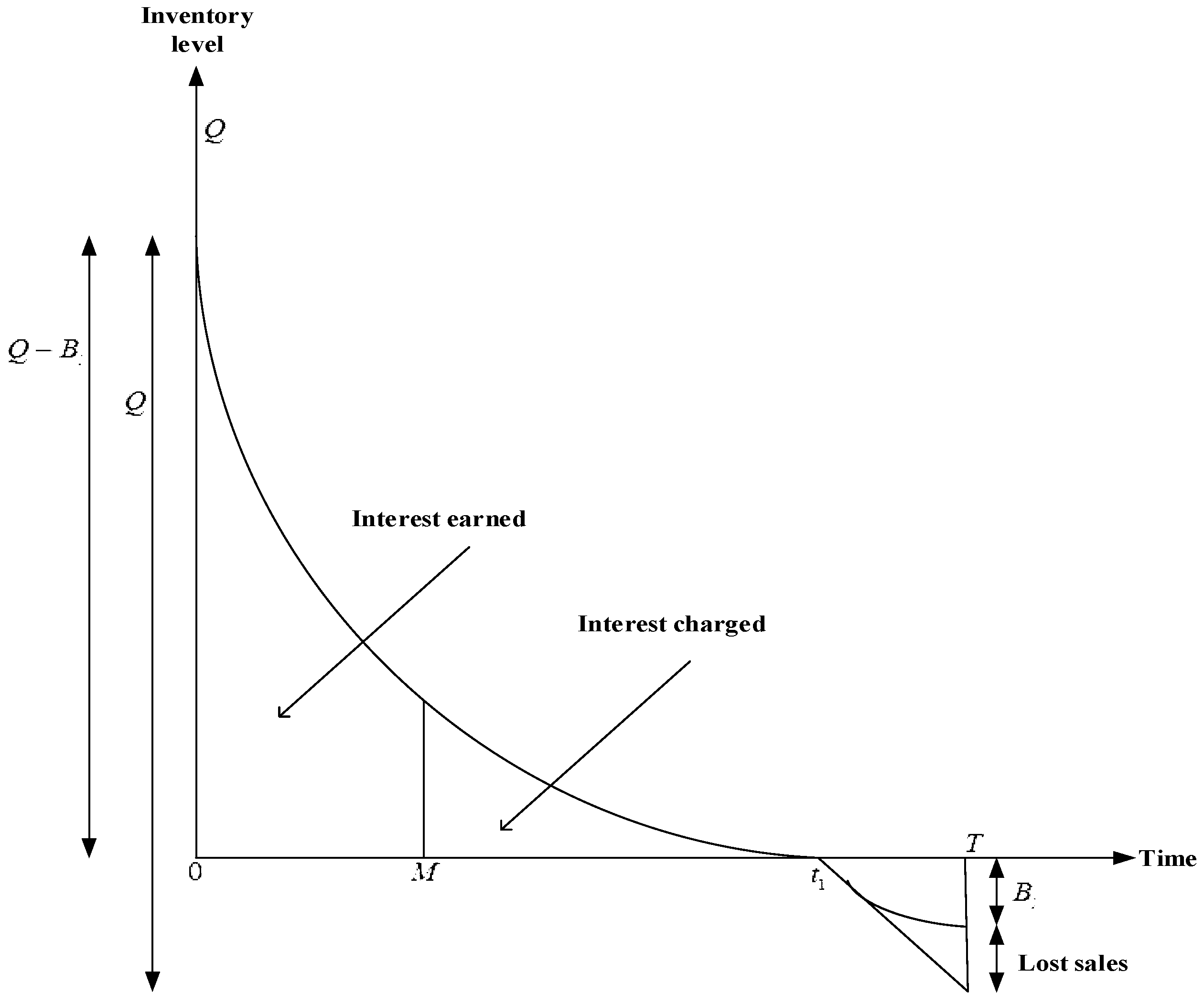
4. Mathematical Model

The mathematical model for perishable products with exponentially partially backlogged shortages under the demand based on the deterioration is presented in this section. Additionally, per cycle time the level of inventory drops according to both the deterioration rate and demand for the product. Furthermore, the graph of the level of inventory against cycle time $T$ is represented in Figure 1.

Now, because of the deterioration-dependent rate of demand, the level of inventory decreases in time $\left[0,t_1\right]$ and the inventory level vanishes at a time $t_1$. Thus, the level of inventory during the time $\left[0,t_1\right]$ can be obtained as

$$\frac{d{I}_1\left(t\right)}{dt}=-\theta I_1\left(t\right)-D(\theta ), 0\le t\le t_1$$

(5)

Under the boundary condition $I_1\left(t_1\right)=0$, the stock level at any time $t\in \left[0,t_1\right]$ from Equation (5) can be obtained as

$$I_1\left(t\right)=\frac{D_0-\beta \theta }{\theta }\left[e^{\theta \left(T-t\right)}-1\right], 0\le t\le t_1$$

(6)

Next, at a time $t=t_1$, the inventory level vanishes, resulting in shortages of the structure that increase exponentially $e^{-\varsigma \left(T-t\right)},\varsigma >0$ with the $T-t$ wait time until the next shipment arrives in the system. Additionally, the maximum shortages level might be attained at the time $t=T$ as indicated by $B_l$. Therefore, the level of inventory during the interval $\left[t_1,T\right]$ can be evaluated as follows:

$$\frac{d{I}_2\left(t\right)}{dt}=D\left(\theta \right)e^{-\varsigma \left(T-t\right)}, t_1\le t\le T$$

(7)

As per the boundary condition $I_2\left(t_1\right)=0$, the level of stock at any time $t\in \left[t_1,T\right]$ from Equation (7) is:

$$I_2\left(t\right)=\frac{D_0-\beta \theta }{\varsigma }\left(e^{-\varsigma \left(T-t\right)}-e^{-\varsigma \left(T-t_1\right)}\right)$$

(8)

Additionally, another boundary condition $I_2\left(T\right)=B_l$ gives

$$B_l=B_l\left(T\right)=\frac{D_0-\beta \theta }{\varsigma }\left(1-e^{-\varsigma \left(T-t_1\right)}\right)$$

(9)

Since $I_1\left(0\right)=Q-B_l$, as per the replenishment time $T$, the order quantity is obtained via Equations (6) and (9).

$$\begin{array}{c}Q-B_l=\frac{D_0-\beta \theta }{\theta }\left[e^{\theta T}-1\right]\hfill \\ Q=B_l+\frac{D_0-\beta \theta }{\theta }\left[e^{\theta T}-1\right]\hfill \\ Q=\left(D_0-\beta \theta \right)\left(\frac{\left(1-e^{-\varsigma \left(T-t_1\right)}\right)}{\varsigma }+\frac{\left(e^{\theta T}-1\right)}{\theta }\right)\hfill \end{array}$$

(10)

Next, the amount of sales that are lost at a time $t\in \left[t_1,T\right]$ is derived as:

$$\begin{array}{c}{N}_l\left(t\right)=\underset{t_1}{\overset{t}{\int }}D\left(\theta \right)\left(1-e^{-\varsigma \left(T-t\right)}\right)dt, t_1\le t\le T\hfill \\ N_l\left(t\right)=\frac{\left(D_0-\beta \theta \right)\left(\varsigma \left(t-t_1\right)+e^{-\varsigma \left(T-t_1\right)}-e^{-\varsigma \left(T-t\right)}\right)}{\varsigma }\hfill \end{array}.$$

(11)

Now, in this model, a supplier provides goods to a retailer with allowable payment delay which is the trade credit policy. The interest received, interest charge, and total cost function are analyzed and also optimize the deterioration rate as follows in various circumstances:

Case (I): $\left(0<M<t_1\right)$

During this situation, the credit phase arises before the inventory vanishes in the system which means a supplier allots a period of credit $M$ to a retailer before a time $t_1$. Throughout the time $\left[0,M\right]$, the retailer receives interest on the profit earned through sustaining shortages in the preceding cycle (see Figure 2).

Hence, the earned interest by a retailer can be estimated as:

$$\begin{gathered} I{E}_1=S{I}_e\underset{0}{\overset{M}{\int }}tD\left(\theta \right)dt+S{I}_e\underset{0}{\overset{M}{\int }}{B}_l\left(T\right)dt \\ I{E}_1=S{I}_e\left(D_0-\beta \theta \right)M\left[\frac{1}{2}M+\frac{\left(1-e^{-\varsigma \left(T-t_1\right)}\right)}{\varsigma }\right] \end{gathered}$$

(12)

The retailer earns interest throughout the interval $\left[0,M\right]$, but after the credit time $M$ a retailer charges for the interest on unsold goods in the time period $\left[M,t_1\right]$. Therefore, the interest charge of a retailer can be calculated as:

$$\begin{gathered} I{C}_1=P{I}_c\underset{M}{\overset{t_1}{\int }}{I}_1\left(t\right)dt \\ I{C}_1=P{I}_c\left(\frac{D_0-\beta \theta }{\theta }\right)\left(\frac{-e^{T\theta -t_1\theta }+e^{-M\theta +T\theta }}{\theta }-t_1+M\right) \end{gathered}$$

(13)

Case (II): $\left(0<t_1<M\right)$

In this situation, the credit period occurs after the inventory vanishes in the system which means a supplier provides a credit period $M$ to a retailer after a time $t=t_1$. So, all the products received from the supplier were sold on credit by the retailer throughout the time $\left[0,M\right]$. Thus, the interest charged to a retailer was zero (i.e., $I{C}_2=0$) in the system. The retailer only receives interest on sold products throughout the time $\left[0,M\right]$ and also earns interest on additional inventory throughout the interval $\left[t_1,M\right]$ (see Figure 3).

As an outcome, the earned interest by a retailer is calculated as:

$$\begin{gathered} I{E}_2=S{I}_e\underset{0}{\overset{t_1}{\int }}tD\left(\theta \right)dt+S{I}_e\underset{0}{\overset{M}{\int }}{B}_l\left(T\right)dt+S{I}_{e}D\left(\theta \right)\left(M-t_1\right)t_1 \\ I{E}_2=\frac{1}{2}S{I}_e\left(D_0-\beta \theta \right)t_1^2+\frac{S{I}_e\left(1-e^{-\varsigma \left(T-t_1\right)}\right)\left(D_0-\beta \theta \right)M}{\varsigma }+S{I}_e\left(M-t_1\right)\left(D_0-\beta \theta \right)t_1 \end{gathered}$$

(14)

$$I{C}_2=0$$

(15)

Now, the total cost components per cycle time $T$ are identified as:

• Cost of ordering per order: $OC=K$
• Cost of holding per unit per unit time: $HC=\left[h+h_c{\left(1-\theta \right)}^{\alpha }\right]\underset{0}{\overset{t_1}{\int }}{I}_1\left(t\right)dt$$=\frac{\left[h+h_c{\left(1-\theta \right)}^{\alpha }\right]\left(D_0-\beta \theta \right)\left(e^{\theta T}-e^{\theta \left(T-t_1\right)}-t_1\theta \right)}{{\theta }^2}$
• Cost of deterioration per cycle time $T$: $DC=c_p\left(Q-\underset{0}{\overset{t_1}{\int }}D\left(\theta \right)dt\right)$$=c_p\left(D_0-\beta \theta \right)\left(\frac{1-e^{-\varsigma \left(-Ta+T\right)}}{\varsigma }+\frac{e^{\theta T}}{\theta }-1-t_1\right)$
• Cost of backlogging per unit: $BC=c_b\underset{t_1}{\overset{T}{\int }}{I}_2\left(t\right)dt$$=\frac{c_b\left(D_0-\beta \theta \right)\left(-e^{-\varsigma \left(T-t_1\right)}\left(\varsigma T-\varsigma t_1+1\right)-1\right)}{{\varsigma }^2}$
• Cost of lost sales per cycle time $T$: $\mathrm{LC}=c_{0}D\left(\theta \right)\underset{t_1}{\overset{T}{\int }}\left(1-e^{-\varsigma \left(T-t\right)}\right)dt$$=\frac{c_0\left(D_0-\beta \theta \right)\left(\varsigma \left(T-t_1\right)+e^{-\varsigma \left(T-t_1\right)}-1\right)}{\varsigma }$

Hence, the total cost function per cycle time $T$ of a retailer is stated as

$$\begin{gathered} T{C}_i\left(T,\theta \right)=\frac{1}{T}\left(OC+HC+DC+BC+LC+I{C}_i-I{E}_i\right); i=1,2 \\ T{C}_i\left(T,\theta \right)=\{\begin{array}{l}T{C}_1\left(T,\theta \right) \mathrm{if} 0<M<t_1<T\\ T{C}_2\left(T,\theta \right) \mathrm{if} 0<t_1<M<T\end{array} \end{gathered}$$

(16)

in which

$$\begin{gathered} T{C}_1=\frac{1}{T}\left(\begin{array}{l}K+\frac{\left(h+h_c{\left(1-\theta \right)}^{\alpha }\right)\left(D_0-\beta \theta \right)\left(-e^{\theta \left(T-t_1\right)}-t_1\theta +e^{\theta T}\right)}{{\theta }^2}\\ +c_p\left(D_0-\beta \theta \right)\left(\frac{1-e^{-\varsigma \left(-Ta+T\right)}}{\varsigma }+\frac{e^{\theta T}}{\theta }-1-t_1\right)\\ +\frac{c_b\left(D_0-\beta \theta \right)\left(-e^{-\varsigma \left(T-t_1\right)}\left(\varsigma T-\varsigma t_1+1\right)-1\right)}{{\varsigma }^2}\\ +\frac{c_0\left(D_0-\beta \theta \right)\left(\varsigma \left(T-t_1\right)+e^{-\varsigma \left(T-t_1\right)}-1\right)}{\varsigma }\\ +P{I}_c\left(\frac{D_0-\beta \theta }{\theta }\right)\left(\frac{-e^{T\theta -t_1\theta }+e^{-M\theta +T\theta }}{\theta }-t_1+M\right)\\ -S{I}_e\left(D_0-\beta \theta \right)M\left(\frac{1}{2}M+\frac{\left(1-e^{-\varsigma \left(T-t_1\right)}\right)}{\varsigma }\right)\end{array}\right) \\ T{C}_1\left(T,\theta \right)=\frac{1}{T}\left(K+\left(D_0-\beta \theta \right)\left(\begin{array}{l}\frac{\left(h+h_c{\left(1-\theta \right)}^{\alpha }\right)\left(\left(1+\theta T+\frac{{\theta }^2{T}^2}{2}\right)-aT\theta -e^{-Ta\theta +T\theta }\right)}{{\theta }^2}\\ -c_b\left(e^{-\varsigma \left(-Ta+T\right)}\left(T\left(1-a\right)\varsigma +1\right)-1\right)\\ +\left(\frac{1-e^{-\varsigma \left(-Ta+T\right)}}{\varsigma }\right)\left(c_p-S{I}_{e}M-c_0\right)\\ +c_{p}T\left(1-a+\frac{\theta T}{2}\right)+c_{0}T\left(1-a\right)-\frac{1}{2}S{I}_e{M}^2\\ +\frac{P{I}_c}{\theta }\left(\frac{-e^{-Ta\theta +T\theta }+e^{-M\theta +T\theta }}{\theta }-aT+M\right)\end{array}\right)\right) \end{gathered}$$

(17)

and

$$\begin{gathered} T{C}_2=\frac{1}{T}\left(\begin{array}{l}K+\frac{\left(h+h_c{\left(1-\theta \right)}^{\alpha }\right)\left(D_0-\beta \theta \right)\left(-e^{\theta \left(T-t_1\right)}-t_1\theta +e^{\theta T}\right)}{{\theta }^2}\\ +c_p\left(D_0-\beta \theta \right)\left(\frac{1-e^{-\varsigma \left(-Ta+T\right)}}{\varsigma }+\frac{e^{\theta T}}{\theta }-1-t_1\right)\\ +\frac{c_b\left(D_0-\beta \theta \right)\left(-e^{-\varsigma \left(T-t_1\right)}\left(\varsigma T-\varsigma t_1+1\right)-1\right)}{{\varsigma }^2}\\ +\frac{c_0\left(D_0-\beta \theta \right)\left(\varsigma \left(T-t_1\right)+e^{-\varsigma \left(T-t_1\right)}-1\right)}{\varsigma }\\ -S{I}_e\left(D_0-\beta \theta \right)\left(\frac{1}{2}{t}_1{}^2+\frac{M\left(1-e^{-\varsigma \left(T-t_1\right)}\right)}{\varsigma }+\left(M-t_1\right)t_1\right)\end{array}\right) \\ T{C}_2\left(T,\theta \right)=\frac{1}{T}\left(K+\left(D_0-\beta \theta \right)\left(\begin{array}{l}\frac{\left(h+h_c{\left(1-\theta \right)}^{\alpha }\right)\left(\begin{array}{l}\left(1+\theta T+\frac{{\theta }^2{T}^2}{2}\right)\\ -aT\theta -e^{-Ta\theta +T\theta }\end{array}\right)}{{\theta }^2}\\ -c_b\left(e^{-\varsigma \left(-Ta+T\right)}\left(T\left(1-a\right)\varsigma +1\right)-1\right)\\ +\left(\frac{1-e^{-\varsigma \left(-Ta+T\right)}}{\varsigma }\right)\left(c_p-S{I}_{e}M-c_0\right)\\ +c_{p}T\left(1-a+\frac{\theta T}{2}\right)+c_{0}T\left(1-a\right)\\ -S{I}_{e}aT\left(M-\frac{aT}{2}\right)\end{array}\right)\right) \end{gathered}$$

(18)

After converting the exponential forms into the linear forms in the function of total cost, the first derivative with respect to $T$ and $\theta$ for both cases can be evaluated as:

$$\frac{\partial T{C}_1\left(T,\theta \right)}{\partial T}=\frac{1}{2}\left(D_0-\beta \theta \right)\left(\begin{array}{l}2a^2{c}_b+h+h_c{\left(1-\theta \right)}^{\alpha }-4c_{b}a\\ +2c_b+c_p\theta +\frac{M^2{I}_{e}S}{2T^2}\end{array}\right)-\frac{K}{T^2}=0$$

(19)

$$\frac{\partial T{C}_2\left(T,\theta \right)}{\partial T}=\frac{1}{2}\left(D_0-\beta \theta \right)\left(\begin{array}{l}{I}_{e}S{a}^2+2a^2{c}_b+h+h_c{\left(1-\theta \right)}^{\alpha }\\ +4c_{b}a+2c_b+c_p\theta \end{array}\right)-\frac{K}{T^2}=0$$

(20)

$$\frac{\partial T{C}_1\left(T,\theta \right)}{\partial \theta }=\frac{1}{2T}\left(\begin{array}{l}-\left(D_0-\beta \theta \right){\left(1-\theta \right)}^{\alpha -1}{T}^2{h}_c\alpha -2M{I}_{e}ST\beta \left(a-1\right)\\ -2T^2\beta c_b{\left(a-1\right)}^2+S{I}_e\beta M^2-{\left(1-\theta \right)}^{\alpha }{T}^2\beta h_c\\ -2T^2\beta c_p\theta +T^2{c}_p{D}_0-T^2\beta h+4T\beta c_p\left(a-1\right)\end{array}\right)=0$$

(21)

$$\frac{\partial T{C}_2\left(T,\theta \right)}{\partial \theta }=\left(\begin{array}{l}-\frac{1}{2}{\left(1-\theta \right)}^{\alpha -1}T\alpha h_c\left(D_0-\beta \theta \right)-\frac{1}{2}{I}_{e}ST{a}^2\beta \\ -T\beta c_b{\left(a-1\right)}^2+M{I}_{e}S\beta -\frac{1}{2}{\left(1-\theta \right)}^{\alpha }T\beta h_c\\ -T\beta c_p\theta -\frac{1}{2}T\beta h+\frac{1}{2}T{c}_p{D}_0+2\beta c_p\left(a-1\right)\end{array}\right)=0$$

(22)

Theorem 1: 

For any given$\theta$defined in the interval$\left(0,1\right)$we have:

Case (I) $\left(0<M<t_1\right)$: the total cost $T{C}_1\left(T,\theta \right)$ in Equation (19) is convex in $T$ and achieves its global minimum with regard to

$$T_1^{*}=\sqrt{\frac{\left(M^{2}S{I}_e\left(D_0-\beta \theta \right)-2K\right)}{\left(\beta \theta -D_0\right)\left(2c_b{\left(a-1\right)}^2+h_c{\left(1-\theta \right)}^{\alpha }+c_p\theta +h\right)}}$$

(23)

the optimal order quantity

$$Q_1^{*}=\left(a-2\right)\sqrt{\frac{\left(\beta \theta -D_0\right)\left(M^{2}S{I}_e\left(\beta \theta -D_0\right)+2K\right)}{\left(2c_b{\left(a-1\right)}^2+h_c{\left(1-\theta \right)}^{\alpha }+c_p\theta +h\right)}}$$

(24)

and optimum minimum cost

$$T{C}_1^{*}=\frac{\sqrt{\frac{K\left(\beta \theta -D_0\right)}{\left(E_1+h_c{\left(1-\theta \right)}^{\alpha }+c_p\theta \right)}}\left(\begin{array}{l}{X}_1\left(2c_p{h}_c{\left(1-\theta \right)}^{\alpha }+E_2+2c_p^2\theta \right)\\ +E_3+M{I}_{e}S{c}_p\theta +M{I}_{e}S{h}_c{\left(1-\theta \right)}^{\alpha }\end{array}\right)}{\sqrt{\frac{K\left(E_1+h_c{\left(1-\theta \right)}^{\alpha }+c_p\theta \right)}{\left(\beta \theta -D_0\right)}}}$$

(25)

where $X_1=\left(a-1\right)$, $E_1=I_{e}S{a}^2+2c_b{\left(a+1\right)}^2+h$, $E_2=2c_{p}h+2I_{e}S{c}_p{a}^2$, and $E_3=2M{I}_{e}S{c}_b{\left(a+1\right)}^2+4c_p{c}_b{\left(a-1\right)}^3+M{I}_e{}^2{S}^2{a}^2+M{I}_{e}Sh$ in Equation (25).

Case (II) $\left(0<t_1<M\right)$: the total cost $T{C}_2\left(T,\theta \right)$ in Equation (20) is convex in $T$ and achieves its global minimum with regard to

$$T_2^{*}=\sqrt{\frac{2K}{\left(D_0-\beta \theta \right)\left(I_{e}S{a}^2+2c_b{\left(a+1\right)}^2+h_c{\left(1-\theta \right)}^{\alpha }+c_p\theta +h\right)}}$$

(26)

the optimal order quantity

$$Q_2^{*}=\left(a-2\right)\sqrt{\frac{2K\left(D_0-\beta \theta \right)}{\left(I_{e}S{a}^2+2c_b{\left(a+1\right)}^2+h_c{\left(1-\theta \right)}^{\alpha }+c_p\theta +h\right)}}$$

(27)

and the optimum minimum cost

$$T{C}_2^{*}=\left(\left(D_0-\beta \theta \right)X_1{E}_4\left(\frac{\begin{array}{l}\left(\beta \theta -D_0\right)\left(2K{c}_p\theta +2K{\left(1-\theta \right)}^{\alpha }{h}_c+E_5\right)\\ +X_1{}^2\left(\begin{array}{l}2M^2{I}_{e}S{D}_0{}^2{c}_b-2M^2{I}_{e}S{\beta }^2{\theta }^2{c}_b\\ -4M^2{I}_{e}S\beta \theta D_0{c}_b\end{array}\right)\\ +\left(D_0{}^2+{\beta }^2{\theta }^2\right)\left(M^2{I}_{e}Sh+M^2{I}_{e}S{h}_c{\left(1-\theta \right)}^{\alpha }\right)\\ -2M^2{I}_{e}S\beta c_p{\theta }^2{D}_0+M^2{I}_{e}S{\beta }^2{c}_p{\theta }^3\\ -2M^2{I}_{e}S\beta \theta D_0{h}_c{\left(1-\theta \right)}^{\alpha }+\theta E_6\end{array}}{\sqrt{\begin{array}{l}\left(D_0-\beta \theta \right)\left(2c_b{\left(a-1\right)}^2+h+h_c{\left(1-\theta \right)}^{\alpha }+c_p\theta \right)\\ \left(M^{2}S{I}_e\left(\beta \theta -D_0\right)+2K\right)\end{array}}}\right)\right)$$

(28)

where $X_1=\left(a-1\right)$, $E_4=\left(M{I}_{e}S-2c_p\right)$, $E_5=4K{a}^2{c}_b+4K{c}_b+2Kh-8aK{c}_b$, and $E_6=\left(M^2{I}_{e}S{c}_p{D}_0{}^2-2M^2{I}_{e}S\beta h{D}_0\right)$ in Equation (28).

Proof: 

See Appendix A. □

Discussion on the Different $\alpha$ Values

The rate of deterioration $\theta =1-{\gamma }^{\frac{1}{\alpha }}$ is controlled by two factors which are fresh quality technology indicator $\gamma$ and the deterioration rate preservation factor $\alpha$. For the different farmed items, the rate of deterioration will not be the same under identical storage conditions and the same preservation effort due to their different natural perishability characteristics. If the ideal rate of deterioration is known, then the FQT for managing the deterioration rate can be obtained via Equation (2).

Now, the discussion on the different $\alpha$ values is explained below.

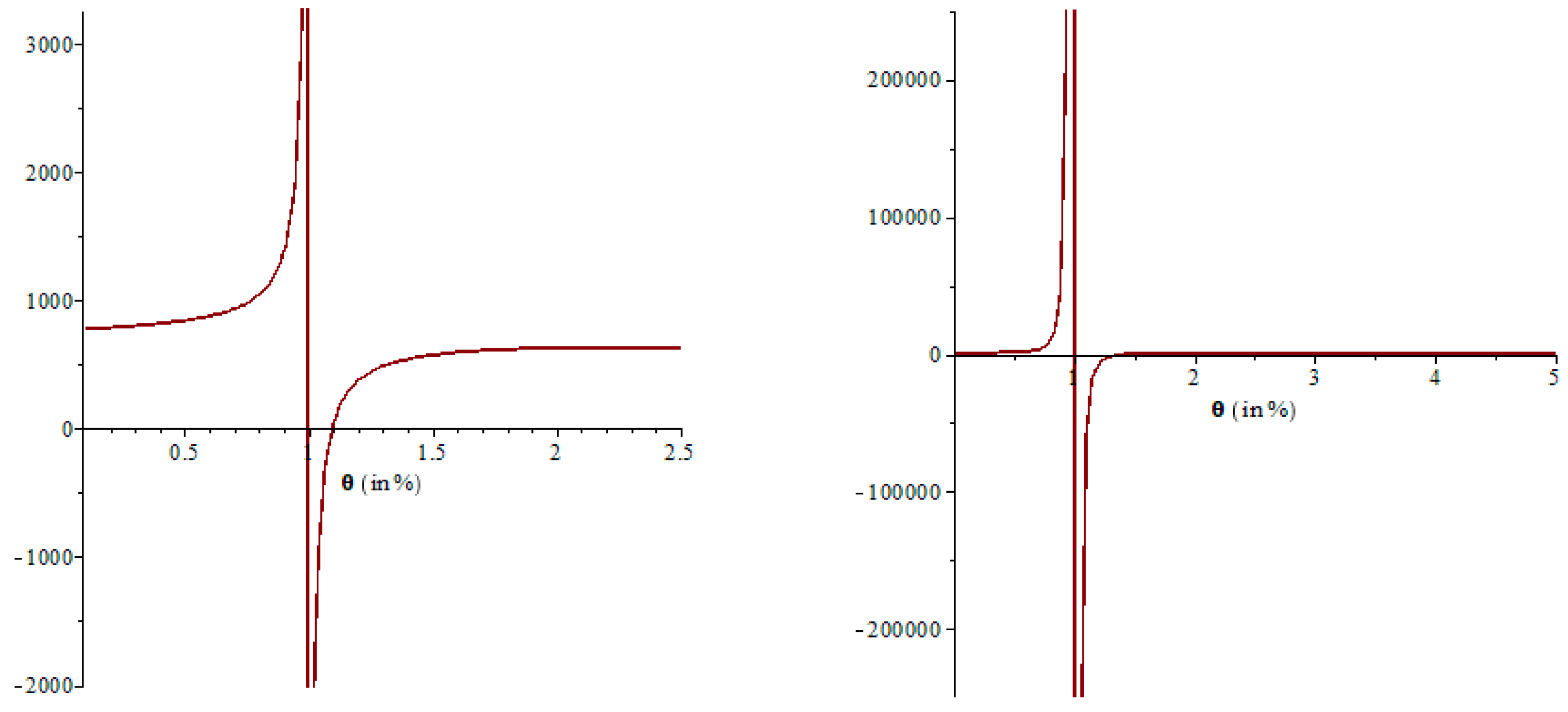
• When $\alpha =0$ then $\frac{1}{\alpha }$ becomes infinite which is not possible and the equation $\theta =1-{\gamma }^{\frac{1}{\alpha }}$ is not solvable. Therefore, $\alpha =0$ is not conceivable.
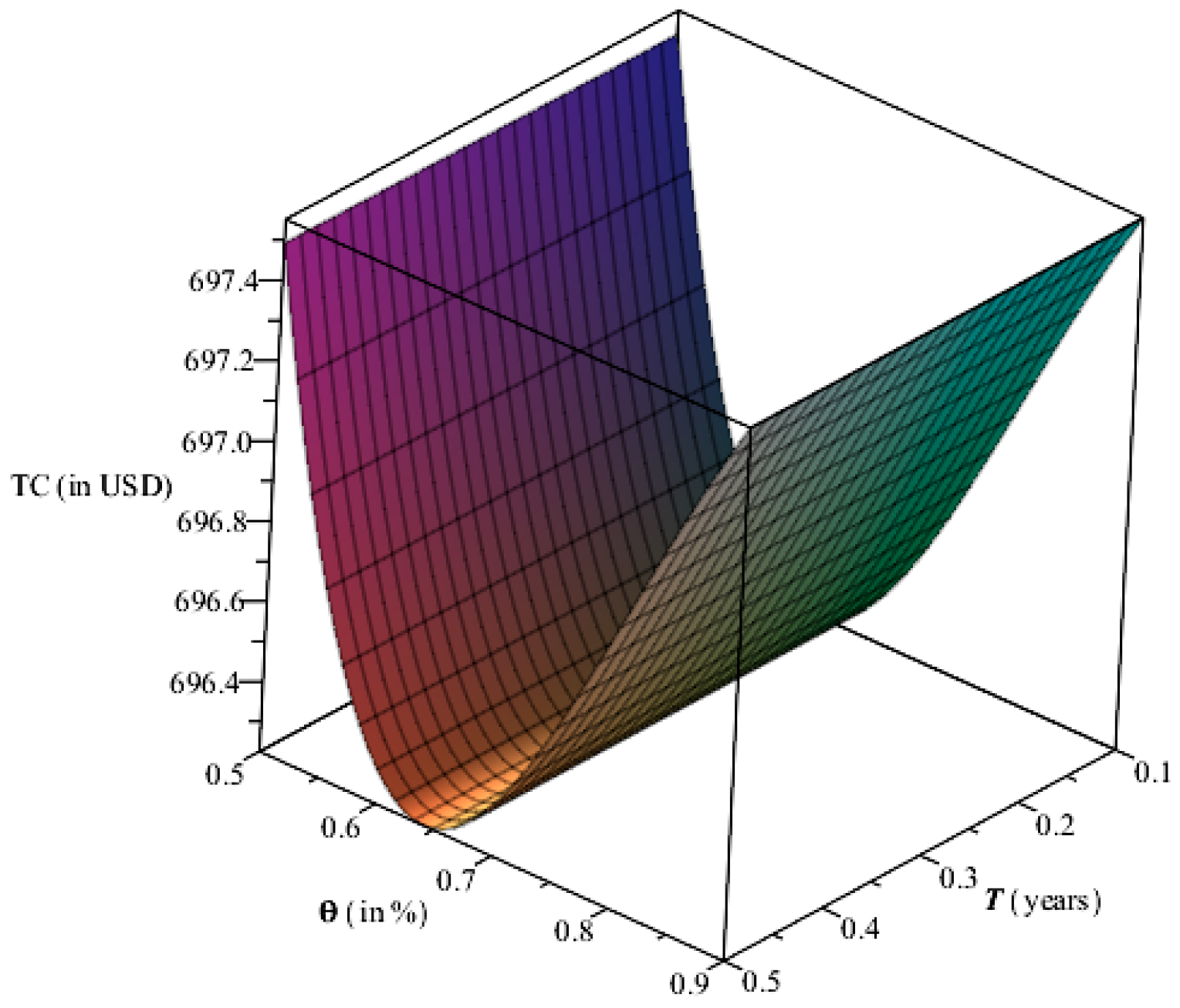
• When $\alpha <1$, then from Figure 4 it is observed that $\theta$ is not in the optimal range. Therefore, $\alpha <1$ is also not considered.
• When $0<\alpha <1$, it is noticed that deterioration rates for various items vary even when they are kept at the same freshness level. For various goods, the relationship coefficient between $\theta$ and $\alpha$ takes on different values. For illustration, with the same FQT and preservation cost, the rate of deterioration is different for oranges and grapes.

  Table 2. Rate of deterioration for different values of $\alpha$ .

  $\mathit{\alpha }$	…	$\frac{1}{3}$	$\frac{1}{2}$	1	2	3	…
  $\theta$	…	0.963	0.84	0.6	0.367	0.263	…

  shows this, where $\alpha$ is as in Equation (1) and the FQT indicator $\gamma$ is set to 0.4.

From Table 2, it is reflected that the higher the rate of $\alpha$, the lower the rate of deterioration. If the value $\alpha$ is smaller than the product, then it is more susceptible to deterioration. As a result, $0<\alpha <1$ signifies situations during which perishable qualities are more significant than when $\alpha =1$.

4.

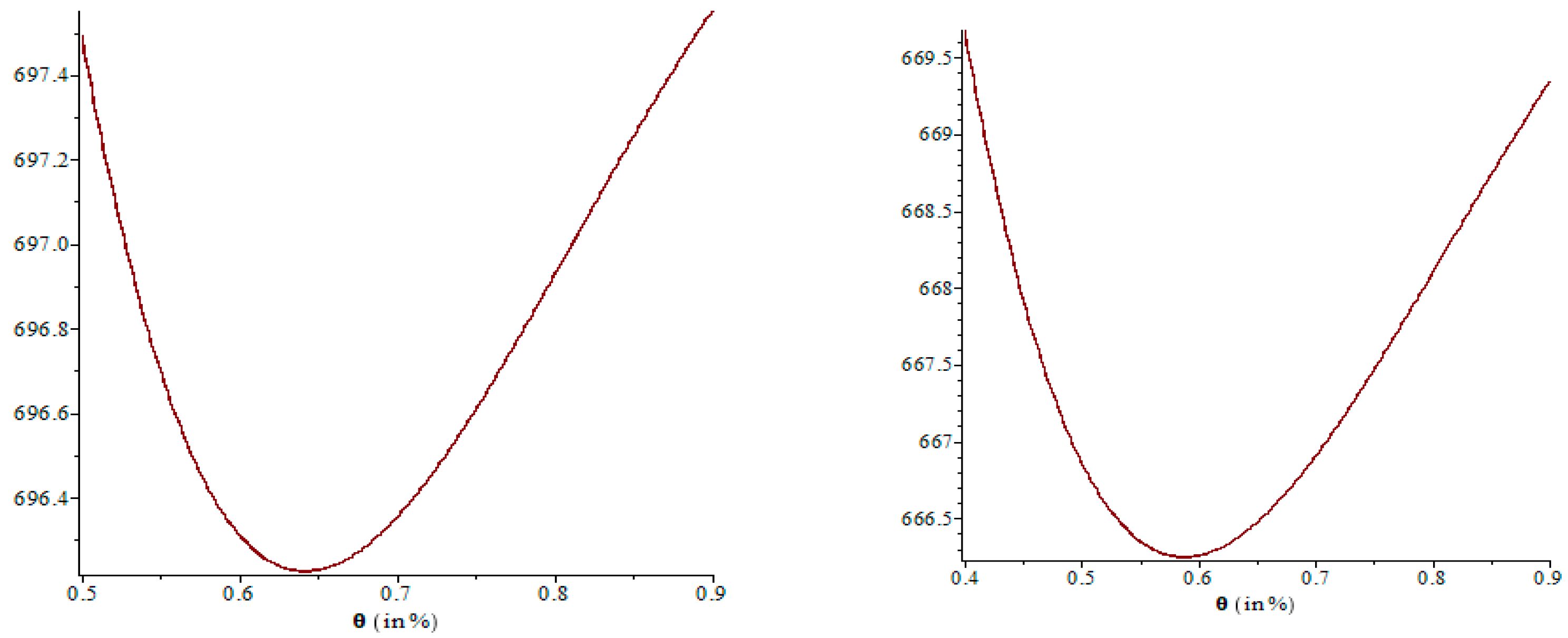
When $\alpha \ge 1$: from Figure 5 it is observed that the conceivable value $\alpha$ is greater or equal to 1. To verify that Equation (1) and other equations based on Equation (1) are reliable against changes in $\alpha$ values, the range $\alpha$ might be restricted to $\left[1,+\propto \right)$. Therefore, in this model, the optimal rate of deterioration is discussed only for $\alpha =1$ and $\alpha >1$. Furthermore, this portion concludes some managerial outcomes.

𝛼 = 1: Steps to make a decision

The second derivative of total cost function with respect to $\theta$ for Case (I) $0<M<t_1$ is

$$\frac{{\partial }^{2}T{C}_1\left(T,\theta \right)}{\partial {\theta }^2}=\frac{T}{2}\left(\left(D_0-\beta \theta \right)\left(\alpha -1\right)\left({\left(1-\theta \right)}^{\alpha -2}\alpha h_c\right)+2{\left(1-\theta \right)}^{\alpha -1}\alpha \beta h_c-2\beta c_p\right)$$

(29)

It is difficult to identify the nature of the second derivative equation so when $\alpha =1$ the derivative becomes

$$\frac{{\partial }^{2}T{C}_1\left(T,\theta \right)}{\partial {\theta }^2}=T\beta \left(h_c-c_p\right)$$

(30)

Additionally, it is the same for Case (II): $0<t_1<M$

$$\frac{{\partial }^{2}T{C}_2\left(T,\theta \right)}{\partial {\theta }^2}=\frac{T}{2}\left(\left(D_0-\beta \theta \right)\left(\alpha -1\right)\left({\left(1-\theta \right)}^{\alpha -2}\alpha h_c\right)+2{\left(1-\theta \right)}^{\alpha -1}\alpha \beta h_c-2\beta c_p\right)$$

(31)

and at $\alpha =1$ the second derivative becomes

$$\frac{{\partial }^{2}T{C}_2\left(T,\theta \right)}{\partial {\theta }^2}=T\beta \left(h_c-c_p\right)$$

(32)

Now, Equations (30) and (32) allow for a simpler evaluation of the optimum solution.

Theorem 2: 

For the first case $\left(0<M<t_1\right)$ when $\alpha =1$ and $c_p>h_c$ , the value of $\theta$ (noted as ${\theta }_1^{*}$ ) is

$${\theta }_1^{*}=\frac{D_0}{2\beta }-\frac{\left(h+h_c\right)}{2\left(c_p-h_c\right)}+\frac{\left(a-1\right)\left(2c_p-MS{I}_e\right)}{T\left(c_p-h_c\right)}-\frac{c_b{\left(a-1\right)}^2}{\left(c_p-h_c\right)}+\frac{M^{2}S{I}_e}{2T^2\left(c_p-h_c\right)}$$

(33)

and the total cost function $T{C}_1\left(T,\theta \right)$ follows a saddle face, and for the case $\left(0<t_1<M\right)$ when $\alpha =1$ and $c_p>h_c$ , the value of $\theta$ (noted as ${\theta }_2^{*}$ ) is

$${\theta }_2^{*}=\frac{D_0}{2\beta }-\frac{\left(h+h_c\right)}{2\left(c_p-h_c\right)}-\frac{c_b{\left(a-1\right)}^2}{\left(c_p-h_c\right)}+\frac{2c_p\left(a-1\right)}{T\left(c_p-h_c\right)}-\frac{S{a}^2{I}_e}{2\left(c_p-h_c\right)}+\frac{MS{I}_e}{T\left(c_p-h_c\right)}$$

(34)

and the total cost function $T{C}_2\left(T,\theta \right)$ follows a saddle face.

Proof: 

See Appendix B. □

Theorem 3: 

For the case $\left(0<M<t_1\right)$ when ${\theta }_1^{*}\ge 1$ , the optimum rate of deterioration tends to be 0, the equivalent optimum cycle time is $T_1^{*}=\sqrt{\frac{\left(2K-M^{2}S{I}_e{D}_0\right)}{D_0\left(2c_b{\left(a-1\right)}^2+h_c+h\right)}}$, and the optimum quantity of the order is $Q_1^{*}=\left(a-2\right)\sqrt{\frac{D_0\left(M^{2}S{I}_e{D}_0-2K\right)}{\left(2c_b{\left(a-1\right)}^2+h_c+h\right)}}$, and for the case $\left(0<t_1<M\right)$ when ${\theta }_2^{*}\ge 1$, the optimum deterioration rate tends to be 0, the equivalent optimum cycle time is $T_2^{*}=\sqrt{\frac{2K}{D_0\left(I_{e}S{a}^2+2c_b{\left(a+1\right)}^2+h_c+h\right)}}$, and the optimum order quantity is $Q_2^{*}=\left(a-2\right)\sqrt{\frac{2K{D}_0}{\left(I_{e}S{a}^2+2c_b{\left(a+1\right)}^2+h_c+h\right)}}$.

Proof: 

See Appendix C. □

Theorem 4: 

For the case $\left(0<M<t_1\right)$ when ${\theta }_1^{*}\le 0$, the optimal rate of deterioration tends to be 1, the equivalent optimal cycle time is $T_1^{*}=\sqrt{\frac{\left(M^{2}S{I}_e\left(D_0-\beta \right)-2K\right)}{\left(\beta -D_0\right)\left(2c_b{\left(a-1\right)}^2+c_p+h\right)}}$, and the optimum order quantity is defined as $Q_1^{*}=\left(a-2\right)\sqrt{\frac{\left(\beta -D_0\right)\left(M^{2}S{I}_e\left(\beta -D_0\right)+2K\right)}{\left(2c_b{\left(a-1\right)}^2+c_p+h\right)}}$, and for the case $\left(0<t_1<M\right)$ when ${\theta }_2^{*}\le 0$, the optimum rate of deterioration tends to be 1, an equivalent optimal cycle time is $T_2^{*}=\sqrt{\frac{2K}{\left(D_0-\beta \right)\left(I_{e}S{a}^2+2c_b{\left(a+1\right)}^2+c_p+h\right)}}$ , and the optimum order quantity is $Q_2^{*}=\left(a-2\right)\sqrt{\frac{2K\left(D_0-\beta \right)}{\left(I_{e}S{a}^2+2c_b{\left(a+1\right)}^2+c_p+h\right)}}$.

Proof: 

See Appendix D. □

The expressions of $T_i^{*}$ and $Q_i^{*},i=1,2$ in Theorems 3 and 4 are similar to each other. The main difference between them is that in Theorem 3 there is no term for the deterioration cost and in Theorem 4 there is no term related to the marginal holding cost. Theorem 3 concludes that retailers should give full efforts to preserving the product to attain minimum deterioration and that this is applicable to high-value perishable products. Theorem 4 specifies that retailers should not try to preserve the product and that this is applicable to low-price products.

Now, for Theorem 5, values X's, Y's, Z's, and W's are shown in

Table 3. Values of X's, Y's, Z's, and W's.

$\begin{array}{l}\left(a-1\right)=X_1\\ \left(a-2\right)=X_2\\ \left(c_p-h_c\right)=X_3\\ \left(h+h_c\right)=X_4\\ \left(h^2+h_c{}^2\right)=X_5\\ \left(2M^3{S}^2\beta I_e{}^2-4M^{2}S\beta c_p{I}_e\right)=Y_1\\ \left(4K-M^{2}S{I}_e{D}_0\right)=Y_2\\ M^2{S}^2\beta I_e{}^2=Y_3\\ \left(2MS\beta I_e-4\beta c_p\right)=Y_4\\ M^{2}S\beta I_e=Y_5\\ \left({\beta }^{2}h{c}_b+{\beta }^2{h}_c{c}_b+\beta c_p{D}_0{c}_b-\beta c_b{D}_0{h}_c\right)=Y_6\\ \left(-M^3{S}^2{\beta }^2{I}_e{}^2+2M^{2}S{c}_p{\beta }^2{I}_e\right)=Y_7\\ \left(\beta h{D}_0+\beta h_c{D}_0\right)=Y_8\\ \left(-{\beta }^2{X}_5-D_0{}^2{X}_3{}^2-4{\beta }^2{c}_b{}^2{X}_1{}^4-2{\beta }^{2}h{h}_c\right)=Y_9\\ \left(M^2{S}^2{\beta }^2{I}_e{}^2-4MS{\beta }^2{c}_p{I}_e+4{\beta }^2{c}_p^2\right)=Y_{10}\end{array}$

$\begin{array}{l}\left({\beta }^2{c}_b{h}_c-\beta c_p{D}_0{c}_b+\beta D_0{c}_b{h}_c+{\beta }^{2}h{c}_b\right)=Z_1\\ \left(-6M^{2}S\beta I_e{D}_0+8K\beta \right)=Z_2\\ \beta D_0\left(c_{p}h-h_c{}^2\right)=Z_3\\ {\beta }^{2}h{h}_c=Z_4\\ \left(S{a}^2\beta I_e+2\beta c_b{X}_1{}^2+\beta X_4+D_0{X}_3\right)=Z_5\\ \left(-S{a}^2\beta I_e-2\beta c_b{X}_1{}^2-\beta X_4-D_0{X}_3\right)=-Z_5\\ 4\beta c_p{X}_1+2MS\beta I_e=Z_6\\ \left(-2S{\beta }^{2}h{I}_e{a}^2-4{\beta }^2{c}_b{X}_1{}^2-2\beta D_0{X}_3\right)=Z_7\\ \left(-2S\beta D_0{I}_e{a}^2-4\beta D_0{c}_b{X}_1{}^2\right)=Z_8\\ \left(D_0{}^2{X}_3{}^2-{\beta }^2{X}_4{}^2\right)=Z_9\\ 16MS{\beta }^2{c}_p{I}_e{X}_1+4M^2{S}^2{\beta }^2{I}_e{}^2+16{\beta }^2{c}_p^2{X}_1{}^2=Z_{10}\\ -2S{a}^2{\beta }^2{I}_e{D}_0+4\beta D_0{c}_b{X}_1{}^2-2\beta D_0{h}_c+8K\beta =W_1\\ 2S{a}^2{\beta }^2{I}_e+4{\beta }^2{c}_b{X}_1{}^2+4{\beta }^2=W_2\\ 2\beta D_0\left(h_c{}^2+c_{p}h\right)=W_3\\ \left(S^2{a}^4{\beta }^2{I}_e{}^2+4S{\beta }^2{I}_e{c}_b{\left(a{X}_1\right)}^2+4{\beta }^2{c}_b{}^2{X}_1{}^4\right)=W_4\end{array}$

:

Theorem 5: 

For the case $\left(0<M<t_1\right)$ when $0<{\theta }_1^{*}<1$:

• ${\theta }_1^{*}$ and $Q_{11}^{*}$ are not the global optimal solutions, where $Q_{11}^{*}=\frac{\frac{1}{2}\left(\sqrt{2}\beta T^2{X}_2\sqrt{\frac{1}{X_3{}^2\beta T^6}\left(\begin{array}{l}\left(-T{X}_1{Y}_1+T^2{X}_3{Y}_2-2M^2{T}^{2}S\beta I_e{c}_b{X}_1{}^2-M^2{T}^{2}S\beta I_e{X}_4+Y_3\right)\\ \left(-T{X}_1{Y}_4-2T^2\beta c_b{X}_1{}^2+Y_5-T^2\beta X_4-T^2{D}_0{X}_3\right)\end{array}\right)}\right)}{\left(-T{X}_1{Y}_4+2T^2\beta c_b{X}_1{}^2+Y_5-T^2\beta X_4+T^2{D}_0{X}_3\right)}$ is and the value of $Q_1^{*}$ is at $\theta ={\theta }_1^{*}$.
• ${\gamma }^{*}\to 0$ or ${\gamma }^{*}\to 1$

For case $\left(0<t_1<M\right)$ when $0<{\theta }_2^{*}<1$:

• ${\theta }_2^{*}$ and $Q_{22}^{*}$ are not the global optimal solutions, where $Q_{22}^{*}=\frac{\left(\sqrt{2}\beta T{X}_2\sqrt{\frac{K\left(-T{Z}_5+Z_6\right)}{X_3\beta T^2}}\right)}{T{Z}_5+Z_6}$ is the value of $Q_2^{*}$ at $\theta ={\theta }_2^{*}$.
• ${\gamma }^{*}\to 0$ or ${\gamma }^{*}\to 1$

Proof: 

See Appendix E. □

Theorem 5 reflects the situation that falls in between the two extreme conditions. Based on their current management conditions, the enterprise can select the appropriate management technique. Theorem 5 concludes that when $0<{\theta }_i^{*}<1 ;i=1,2$ there are some points where the overall cost attains its extreme at the specific value of $Q \mathrm{or} T$. The total cost rises with the increasing rate of deterioration when $0<{\theta }_i^{*}<1 ;i=1,2$ and the total cost decreases with the increasing rate of deterioration when $\theta >{\theta }_i^{*};i=1,2$. Therefore, for Case (I) except for when ${\theta }_1^{*}=\frac{D_0}{2\beta }-\frac{\left(h+h_c\right)}{2\left(c_p-h_c\right)}+\frac{\left(a-1\right)\left(2c_p-MS{I}_e\right)}{T\left(c_p-h_c\right)}-\frac{c_b{\left(a-1\right)}^2}{\left(c_p-h_c\right)}+\frac{M^{2}S{I}_e}{2T^2\left(c_p-h_c\right)}$, at two different $\theta$ there should be two equivalent overall costs. For Case (II) except for the value of ${\theta }_2^{*}=\frac{D_0}{2\beta }-\frac{\left(h+h_c\right)}{2\left(c_p-h_c\right)}-\frac{c_b{\left(a-1\right)}^2}{\left(c_p-h_c\right)}+\frac{2c_p\left(a-1\right)}{T\left(c_p-h_c\right)}-\frac{S{a}^2{I}_e}{2\left(c_p-h_c\right)}+\frac{MS{I}_e}{T\left(c_p-h_c\right)}$, at two different $\theta$ there should be two equivalent overall costs. This suggests that under the same controlled-cost conditions, a retailer may sometimes decrease waste.

As a result, when $\alpha =1$ and $c_p>h_c$, the optimal deterioration rate that minimizes the total cost implies ${\gamma }^{*}\to \{\begin{array}{l}1 {\theta }_1 \mathrm{or} {\theta }_2\ge 1\\ 1 \mathrm{or} 0 0<{\theta }_1 \mathrm{or} {\theta }_2<1\\ 0 {\theta }_1 \mathrm{or} {\theta }_2\le 0\end{array}$.

The previously stated results can help to improve a retailer’s ability to make relevant decisions. There are three steps to finding the decision.

First step: Correlate the cost of purchase $c_p$ with the maximum cost of holding $h_c$ which is relevant to keeping the product fresh.

Second step: If $c_p>h_c$, analyze the rate of ${\theta }_i^{*}$ for $i=1,2$. If ${\theta }_i^{*}\ge 1$, the optimal value of the fresh quality technology indicator $\gamma$ moves towards 1; if ${\theta }_i^{*}\le 0$, the optimal value of fresh quality technology indicator $\gamma$ attempts 0; when $0<{\theta }_i^{*}<1$, follow the third step.

Third step: This step consists of determining the overall cost when $\theta \to 0 \mathrm{or} \theta \to 1$, and the lower value is selected by the retailer.

When the optimal FQT indicator attains 0 for both cases, the optimal cycle time is $T_1^{*}=\sqrt{\frac{\left(M^{2}S{I}_e\left(D_0-\beta \right)-2K\right)}{\left(\beta -D_0\right)\left(2c_b{\left(a-1\right)}^2+c_p+h\right)}}$ and $T_2^{*}=\sqrt{\frac{2K}{\left(D_0-\beta \right)\left(I_{e}S{a}^2+2c_b{\left(a+1\right)}^2+c_p+h\right)}}$, and the optimal order quantities are $Q_1^{*}=\left(a-2\right)\sqrt{\frac{\left(\beta -D_0\right)\left(M^{2}S{I}_e\left(\beta -D_0\right)+2K\right)}{\left(2c_b{\left(a-1\right)}^2+c_p+h\right)}}$ and $Q_2^{*}=\left(a-2\right)\sqrt{\frac{2K\left(D_0-\beta \right)}{\left(I_{e}S{a}^2+2c_b{\left(a+1\right)}^2+c_p+h\right)}}$.

Additionally, the minimum total cost functions are $T{C}_1^{*}=\frac{\sqrt{\frac{K\left(\beta -D_0\right)}{\left(E_1+c_p\right)}}\left(X_1\left(E_2+2c_p^2\right)+E_3\right)}{\sqrt{\frac{K\left(E_1+c_p\right)}{\left(\beta -D_0\right)}}}$ and $T{C}_2^{*}=\left(\left(D_0-\beta \right)X_1{E}_4\left(\frac{\begin{array}{l}\left(\beta -D_0\right)\left(2K{c}_p+E_5\right)\\ +X_1{}^2\left(2M^2{I}_{e}S{D}_0{}^2{c}_b-2M^2{I}_{e}S{\beta }^2{c}_b-4M^2{I}_{e}S\beta D_0{c}_b\right)\\ +\left(D_0{}^2+{\beta }^2\right)\left(M^2{I}_{e}Sh\right)+E_6-2M^2{I}_{e}S\beta c_p{D}_0+M^2{I}_{e}S{\beta }^2{c}_p\end{array}}{\sqrt{\left(D_0-\beta \right)\left(2c_b{\left(a-1\right)}^2+h+c_p\right)\left(M^{2}S{I}_e\left(\beta -D_0\right)+2K\right)}}\right)\right)$.

Furthermore, when the optimal FQT indicator attains 1, for both cases the optimal order quantities are $Q_1^{*}=\left(a-2\right)\sqrt{\frac{D_0\left(M^{2}S{I}_e{D}_0-2K\right)}{\left(2c_b{\left(a-1\right)}^2+h_c+h\right)}}$ and $Q_2^{*}=\left(a-2\right)\sqrt{\frac{2K{D}_0}{\left(I_{e}S{a}^2+2c_b{\left(a+1\right)}^2+h_c+h\right)}}$, the cycle times are $T_1^{*}=\sqrt{\frac{\left(2K-M^{2}S{I}_e{D}_0\right)}{D_0\left(2c_b{\left(a-1\right)}^2+h_c+h\right)}},$ and $T_2^{*}=\sqrt{\frac{2K}{D_0\left(I_{e}S{a}^2+2c_b{\left(a+1\right)}^2+h_c+h\right)}}$, and the minimum total costs are $T{C}_1^{*}=\frac{\sqrt{\frac{K{D}_0}{\left(E_1+h_c\right)}}\left(X_1\left(2c_p{h}_c+E_2\right)+E_3+M{I}_{e}S{h}_0\right)}{\sqrt{\frac{K\left(E_1+h_c\right)}{D_0}}},$ and $T{C}_2^{*}=\left(\left(D_0\right)X_1{E}_4\left(\frac{\left(-D_0\right)\left(2K{h}_c+E_5\right)+X_1{}^2\left(2M^2{I}_{e}S{D}_0{}^2{c}_b\right)+\left(D_0{}^2\right)\left(M^2{I}_{e}Sh+M^2{I}_{e}S{h}_c\right)}{\sqrt{\left(D_0\right)\left(2c_b{\left(a-1\right)}^2+h+h_c\right)\left(M^{2}S{I}_e\left(-D_0\right)+2K\right)}}\right)\right)$.

As an outcome, Figure 6 shows the decision support system for the retailer.

5. Numerical Study and Sensitivity Analysis

5.1. Numerical Study

This model is applicable to perishable products such as fresh foods, dairy products, and some bakery items. To authenticate this model, two numerical examples are presented for both of the cases of trade credit policy. The comparable parameters’ values are extended from [2] to adapt the prototype.

Illustration 1: For Case I $\left(0<M<t_1<T\right)$ 

Let $\alpha =4,$ $D_0=100 \mathrm{units}/\mathrm{year},$ $K=40 \mathrm{USD}/\mathrm{order},$ $\beta =15,$ $c_b=0.6 \mathrm{USD}/\mathrm{unit} \mathrm{time},$ $a=0.8,$ $c_p=10/\mathrm{units},$ $\varsigma =0.7,$ $I_e=0.1/\mathrm{USD}/\mathrm{year},$ $c_0=0.6 \mathrm{USD}/\mathrm{unit} \mathrm{time},$ $h=10/\mathrm{unit}/\mathrm{unit} \mathrm{time},$ $S=30 \mathrm{USD}/\mathrm{unit},$ $h_c=8/\mathrm{unit}/\mathrm{unit} \mathrm{time},$ $M=0.1 \mathrm{years},$ $I_c=0.12/\mathrm{USD}/\mathrm{year},$ $P=20 \mathrm{USD}/\mathrm{unit}$.

After solving this system, the optimum evaluates of decision variables are $T^{*}=0.219 \mathrm{years}$, ${\theta }^{*}=0.64$, and total cost per cycle $T{C}_1{}^{*}\left(T,\theta \right)=696.23 \mathrm{USD}$; the initial optimal quantity of order $Q^{*}=25.17 \mathrm{units}$ including the backorder quantity $B_l^{*}=4 \mathrm{units}$. Additionally, $t_1{}^{*}=aT=0.175 \mathrm{years}$, and ${\gamma }^{*}=0.016$.

The characteristic of convexity for the overall cost function $T{C}_1^{*}\left(T,\theta \right)$ is obtained in Figure 7.

Illustration 2: For Case II $\left(0<t_1<M<T\right)$ 

Use a similar set of statistics as with Illustration 1, with the exception of  $M=0.2 \mathrm{years}$.The optimal evaluates of decision variables are $T^{*}=0.224 \mathrm{years}$ and ${\theta }^{*}=0.58$, the total cost per cycle $T{C}_2{}^{*}\left(T,\theta \right)=666.24 \mathrm{USD}$, and the initial optimal quantity of order $Q^{*}=25.92 \mathrm{units}$ including backorder quantity $B_l^{*}=4 \mathrm{units}$. Additionally, $t_1{}^{*}=aT=0.179 \mathrm{years}$, and ${\gamma }^{*}=0.028$.

The convexity tendency of the overall cost function $T{C}_2{}^{*}\left(T,\theta \right)$ is determined in Figure 8.

5.2. Sensitivity Analysis

In this section, sensitivity analysis is performed on Illustration 2 and shows a variation in decision variables by varying parameters of inventory values up to $-20\%, -10\%, 10\%, \mathrm{and} 20\%$.

The following observations are obtained from

Table 4. Sensitivity analysis.

Parameters	Values	$\begin{array}{l} \mathit{T} \\ \left(\mathbf{in} \mathbf{Years}\right)\end{array}$	$\begin{array}{l} \mathit{\theta }\\ \left(\mathbf{in} \%\right)\end{array}$	$\begin{array}{l} \mathit{Q} \\ \left(\mathbf{in} \mathbf{Units}\right)\end{array}$	$\begin{array}{l} {\mathit{t}}_1 \\ \left(\mathbf{in} \mathbf{Years}\right)\end{array}$	$\begin{array}{l} \mathit{T}\mathit{C}\\ \left(\mathbf{in} \mathbf{USD}\right)\end{array}$	$\begin{array}{l} \mathit{\gamma }\\ \left(\mathbf{in} \%\right)\end{array}$
$\alpha$	3.2	0.220	0.70	25.16	0.176	667.84	0.021
	3.6	0.222	0.64	25.57	0.178	667.05	0.026
	4.4	0.226	0.55	26.23	0.181	665.45	0.031
	4.8	0.228	0.51	26.49	0.182	664.68	0.033
$D_0$	80	0.236	0.66	23.94	0.189	606.97	0.011
	90	0.236	0.66	24.14	0.189	611.95	0.014
	110	0.214	0.55	27.45	0.171	719.16	0.041
	120	0.205	0.52	28.84	0.164	771.01	0.051
$K$	32	0.166	0.65	22.73	0.159	628.49	0.015
	36	0.212	0.61	24.39	0.170	647.94	0.023
	44	0.236	0.57	27.36	0.189	683.61	0.034
	48	0.247	0.56	28.73	0.198	700.17	0.039
$\beta$	12	0.225	0.49	26.61	0.180	674.78	0.066
	13.5	0.225	0.53	26.33	0.180	670.71	0.048
	16.5	0.222	0.69	25.15	0.178	661.14	0.009
	18	4.847	4.42	9.24	3.877	41019.31	136.543
$c_p$	8	0.216	1.21	23.64	0.172	584.01	0.002
	9	0.210	1.24	22.89	0.162	618.44	0.003
	11	0.196	1.34	21.00	0.157	712.13	0.013
	12	0.190	1.38	20.22	0.152	754.20	0.020
$h$	8	0.240	0.55	27.85	0.192	645.88	0.043
	9	0.232	0.57	26.85	0.185	656.24	0.036
	11	0.222	0.60	25.66	0.178	669.17	0.026
	12	0.212	0.65	24.24	0.169	685.23	0.016
$h_c$	6.4	0.226	0.55	26.21	0.181	665.69	0.043
	7.2	0.226	0.57	26.01	0.180	666.06	0.033
	8.8	0.206	1.14	22.61	0.164	669.83	0.0005
	9.6	0.206	1.15	22.59	0.164	669.83	0.0005
$M$	0.16	0.224	0.60	25.84	0.179	677.14	0.025
	0.18	0.224	0.60	25.88	0.179	671.70	0.027
	0.22	0.225	0.58	25.96	0.180	660.79	0.031
	0.24	0.225	0.57	26.00	0.180	655.33	0.033
$I_e$	0.08	0.227	0.59	26.21	0.182	673.20	0.028
	0.09	0.226	0.59	26.06	0.181	669.73	0.028
	0.11	0.223	0.59	25.79	0.179	662.75	0.030
	0.12	0.222	0.59	25.69	0.178	660.30	0.030
$S$	24	0.227	0.59	26.21	0.182	673.20	0.028
	27	0.226	0.59	26.06	0.181	669.73	0.028
	33	0.223	0.59	25.79	0.179	662.75	0.030
	36	0.222	0.59	25.69	0.178	660.30	0.030

:

• When the rate of deterioration preservation factor $\left(\alpha \right)$ increases, the FQT indicator $\left(\gamma \right)$, cycle time $\left(T\right)$, quantity of order $\left(Q\right)$, and the time considered for inventory level to drop to zero $\left(t_1\right)$ increase slowly while the deterioration rate $\left(\theta \right)$ decreases slowly. However, total cost $\left(TC\right)$ decreases gradually.
• There is a negative effect of fixed demand rate $\left(D_0\right)$ on total cost $\left(TC\right)$ and FQT indicator $\left(\gamma \right)$. They all are increased rapidly. Further, order quantity $\left(Q\right)$ increases slowly, and cycle time $\left(T\right)$, deterioration rate $\left(\theta \right)$, and time considered for inventory level to drop to zero $\left(t_1\right)$ decrease slowly.
• If ordering cost $\left(K\right)$ increases, the deterioration rate $\left(\theta \right)$ decreases slowly while order quantity $\left(Q\right)$ and time considered for inventory level to drop to zero $\left(t_1\right)$ increase slowly. However, total cost $\left(TC\right)$, FQT indicator $\left(\gamma \right)$, and cycle time $\left(T\right)$ increase rapidly.
• Change in the parameter’s sales price $\left(S\right)$ and interest earned $\left(I_e\right)$, total cost $\left(TC\right)$, the time considered for inventory level to drop to zero $\left(t_1\right)$, cycle time $\left(T\right)$, order quantity $\left(Q\right)$, and FQT indicator $\left(\gamma \right)$ decrease slowly. However, there are no changes in the rate of deterioration $\left(\theta \right)$.
• As the demand-on-quantity variable $\left(\beta \right)$ changes, cycle time $\left(T\right)$, total cost $\left(TC\right)$, order quantity $\left(Q\right)$, and the time considered for inventory level to drop to zero $\left(t_1\right)$ decrease slowly, whereas the FQT indicator $\left(\gamma \right)$ decreases rapidly and the deterioration rate $\left(\theta \right)$ increases rapidly.
• The FQT indicator $\left(\gamma \right)$ increases slowly and total cost $\left(TC\right)$ decreases rapidly. Further, cycle time $\left(T\right)$, order quantity $\left(Q\right)$, the time considered for inventory level to drop to zero $\left(t_1\right)$, and deterioration rate $\left(\theta \right)$ decrease slowly whenever the upstream trade credit period $\left(M\right)$ changes.
• As the holding parameter $\left(h\right)$ increases, quantity of order $\left(Q\right)$ decreases slowly and total cost $\left(TC\right)$ decreases rapidly. On the other hand, cycle time $\left(T\right)$, the time considered for the stock level to drop to zero $\left(t_1\right)$, and FQT indicator $\left(\gamma \right)$ decrease rapidly and the rate of deterioration $\left(\theta \right)$ increases slowly.
• As the cost of procurement $\left(c_p\right)$ varies, the deterioration rate $\left(\theta \right)$ increases slowly, while cycle time $\left(T\right)$, order quantity $\left(Q\right)$, and time considered for inventory level to drop to zero $\left(t_1\right)$ decrease slowly. Furthermore, total cost $\left(TC\right)$ increases rapidly and the FQT indicator $\left(\gamma \right)$ increases slowly; after that, it increases rapidly.
• The cycle time $\left(T\right)$ and time considered for level of inventory to drop to zero $\left(t_1\right)$ decrease slowly, the total cost $\left(TC\right)$ increases rapidly, and then both become constant. However, order quantity $\left(Q\right)$ decreases slowly, the deterioration rate $\left(\theta \right)$ increases slowly, and FQT indicator $\left(\gamma \right)$ decreases rapidly when the maximum cost of holding parameter $\left(h_c\right)$ fluctuates.

5.3. Managerial Implications

• A retailer should take a long credit period from the supplier to receive more benefits since the credit period significantly reduces the total cost per cycle time rapidly while the cycle time drops slowly.
• Based on Theorem 3, a retailer should not invest in the preservation factor because the rate of deterioration is ${\theta }_i\ge 1;i=1,2$ which implies that the product fully deteriorates. So, there is no need to preserve and increase the total cost. For example, if all of the tomatoes, lemons, bread, flowers, and other perishable items fully deteriorate then the retailer should not invest to sustain that kind of product.
• According to Theorem 4, if ${\theta }_i\ge 1;i=1,2$ then the retailer should not invest in preservation because the product is non-deteriorating. For example, if dry inventory, coffee powder, tea powder, etc., have zero deterioration rate then the retailer should not invest in the preservation factor to raise the cost.
• According to Theorem 5, if the range of deterioration is $0<{\theta }_i<1;i=1,2$ then the retailer should invest in the preservation factor to preserve the perishable product and fulfill the demand of consumers. Dairy products, cooked leftovers, vegetables, fruits, and so on need a preservation and temperature environment according to their freshness. So, if the product is not fully deteriorated or non-deteriorating then the retailer should invest in the preservation factor because the demand is quality-dependent on the perishable product.
• As Table 4 shows, the retailer should decrease the cost of holding parameter, reduce the ordering cost, focus on the quality of the perishable product, and adjust the sales price to generate more revenue and less expenditure.
• If the rate of deterioration is low and demand is high, the retailer should buy additional inventory before the shortages occur. If the flowers are fresh, retailers will buy them, and demand will rise gradually. Therefore, before all of the flowers are sold, the retailer should order more flowers.
• To achieve the optimal rate of deterioration, the value of the rate of the deterioration preservation factor $\alpha$ must be restricted $\left[1,\propto \right)$. If the value of the rate of the deterioration preservation factor is less than 1, the optimal deterioration rate increases, implying a rise in the overall cost of a retailer. (See Table 2).

6. Conclusions

This study is inspired by a farmed product deterioration problem faced by a supplier selling vegetables or fresh fruits to a retailer, in which retailers are more willing to purchase at a given fixed price for better quality, less deteriorated, and more storable perishable items. This study is premised on prior research on perishable inventory control by investigating deterioration rate as a decision parameter and its consequences for perishable quality control indicators, associated customer demands, and a variable operational cost. In addition, this article assumes that demand is influenced by quality deterioration over a certain period. This work also assumes that the rate of deterioration can be controlled using FQT and effort as cost factors. In addition, the supplier offers its retailer a mutually acceptable trade credit. This advantages both the retailer and the supplier. Additionally, shortages are allowed. Furthermore, considering controlled deterioration/freshness-dependent demand, product quality indication, and manageable DR to analyze its dynamic behavior with several parameters including trade credit under allowable partially backlogged shortages, this EOQ model is a theoretical extension and an example of innovation with practical interpretations and implementations. This study has analytically analyzed this situation and conducted sensitivity analysis to develop managerial consequences.

Finally, this research concludes that the retailer should invest in the preservation factor when the rate of deterioration of the perishable product is between 0 and 1. If the rate of deterioration is 0, then the product is non-deteriorating and the retailer does not need to invest in the FQT indicator. Similarly, for the deterioration rate of 1 whereby the product already deteriorates, there is no need to spend on preservation. The value of the deterioration rate preservation factor must be in the interval of $\left[1,\propto \right)$ to obtain the optimum value of the deterioration rate as proved in the model. The retailer should order the inventory before the shortages occur in the system and the retailer should use the trade credit policy to minimize the total cost and earn more profit per cycle time. In addition, this model includes the correlation between the fresh quality indicator and the deterioration rate.

This approach is used in all areas that deal with the deterioration and quality of perishable goods, for example, fresh food items, frozen food items, fresh flowers, dairy products, seafood, cooked foods, fresh vegetables and fruits, etc., but this inventory model is derived under the following limitations:

• This model discussed the relation between the fresh quality technology (FQT) indicator and controllable rate of deterioration. However, preservation technology was not applied to reduce the rate of deterioration. Additionally, the fluctuating rate of deterioration and the functional relationship between the rate of deterioration and the quality indicator are not considered in this model.
• The proposed inventory model is developed with deterioration-dependent demand. This can be expanded for different kinds of demand such as fuzzy demand as shown in [43], freshness-dependent demand as discussed in [44], etc.
• This study allows for a one-layered trade credit policy and partially backlogged shortages. In spite of this, one can consider a two-layered trade credit policy and fully backlogged shortages as shown in [45].