Existence of Self-Excited and Hidden Attractors in the Modified Autonomous Van Der Pol-Duffing Systems
Abstract
:1. Introduction
2. Preliminaries
3. The MAVPD Systems
4. Discussion on Hopf Bifurcation in the MAVPD Systems
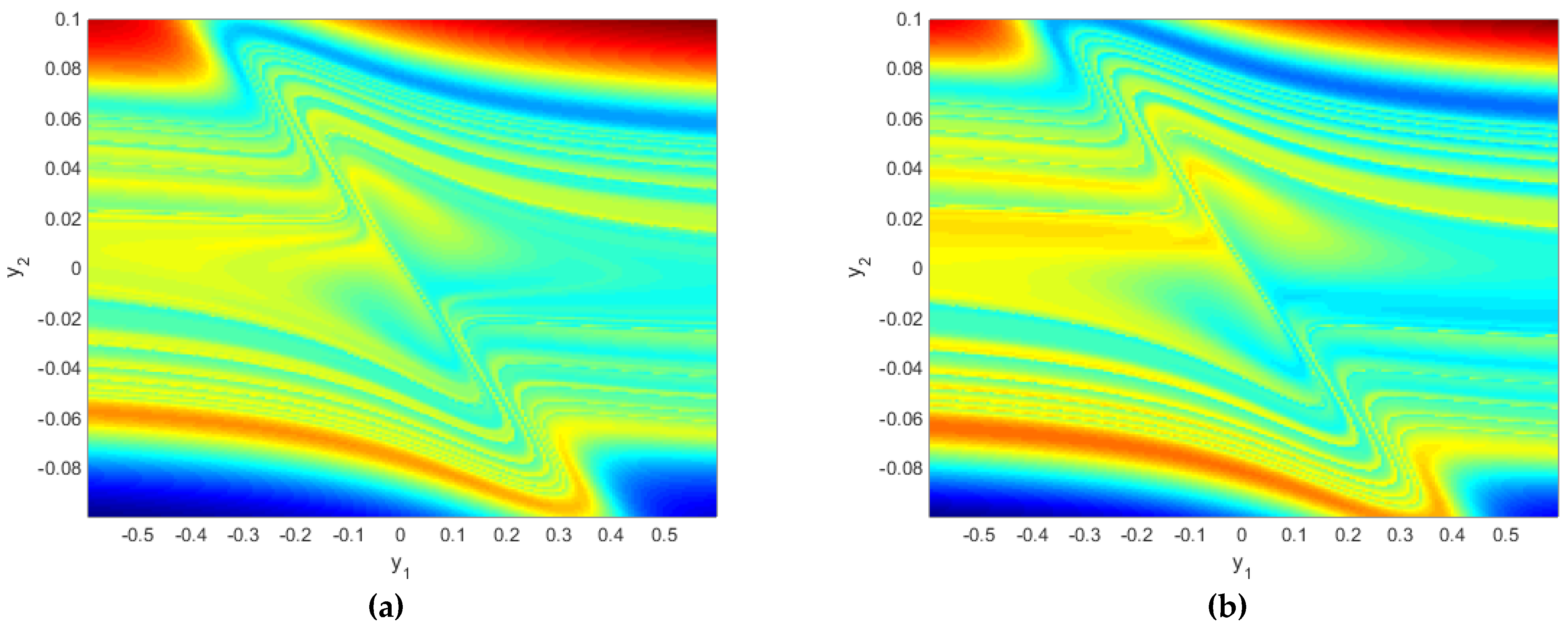
5. Hidden Oscillation Localization
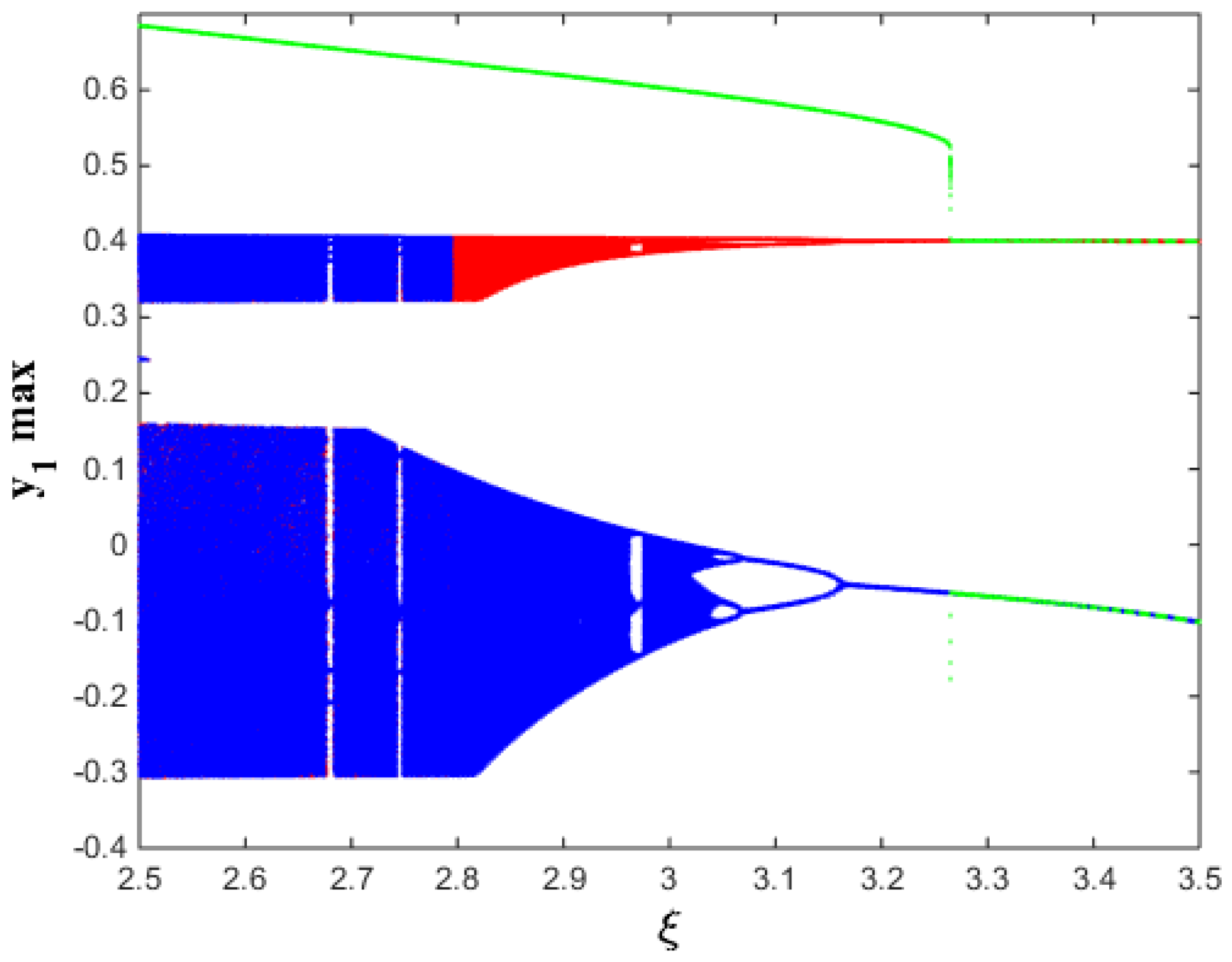
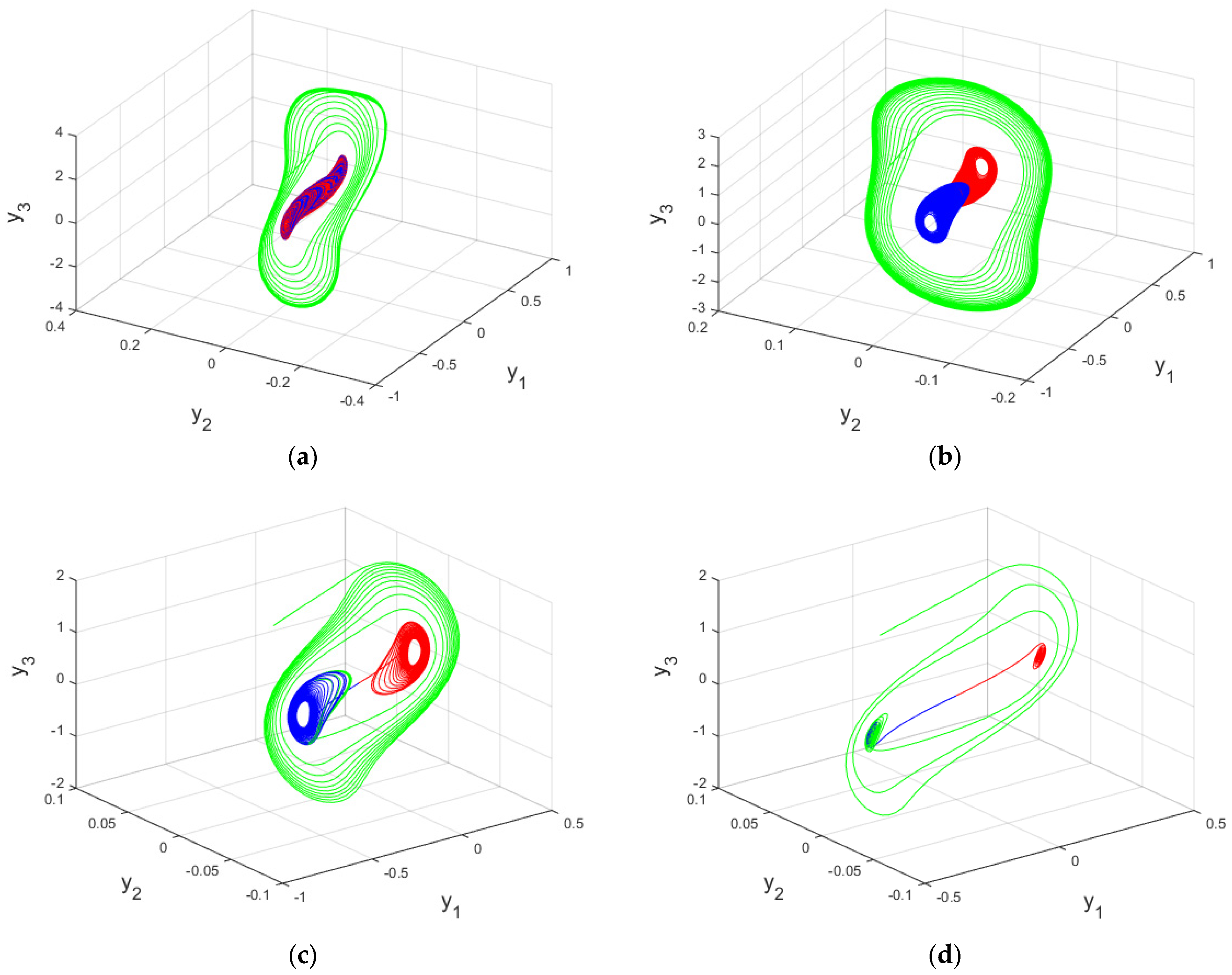
6. Existence of Self-Excited and Hidden Attractors in the Integer-Order MAVPD System
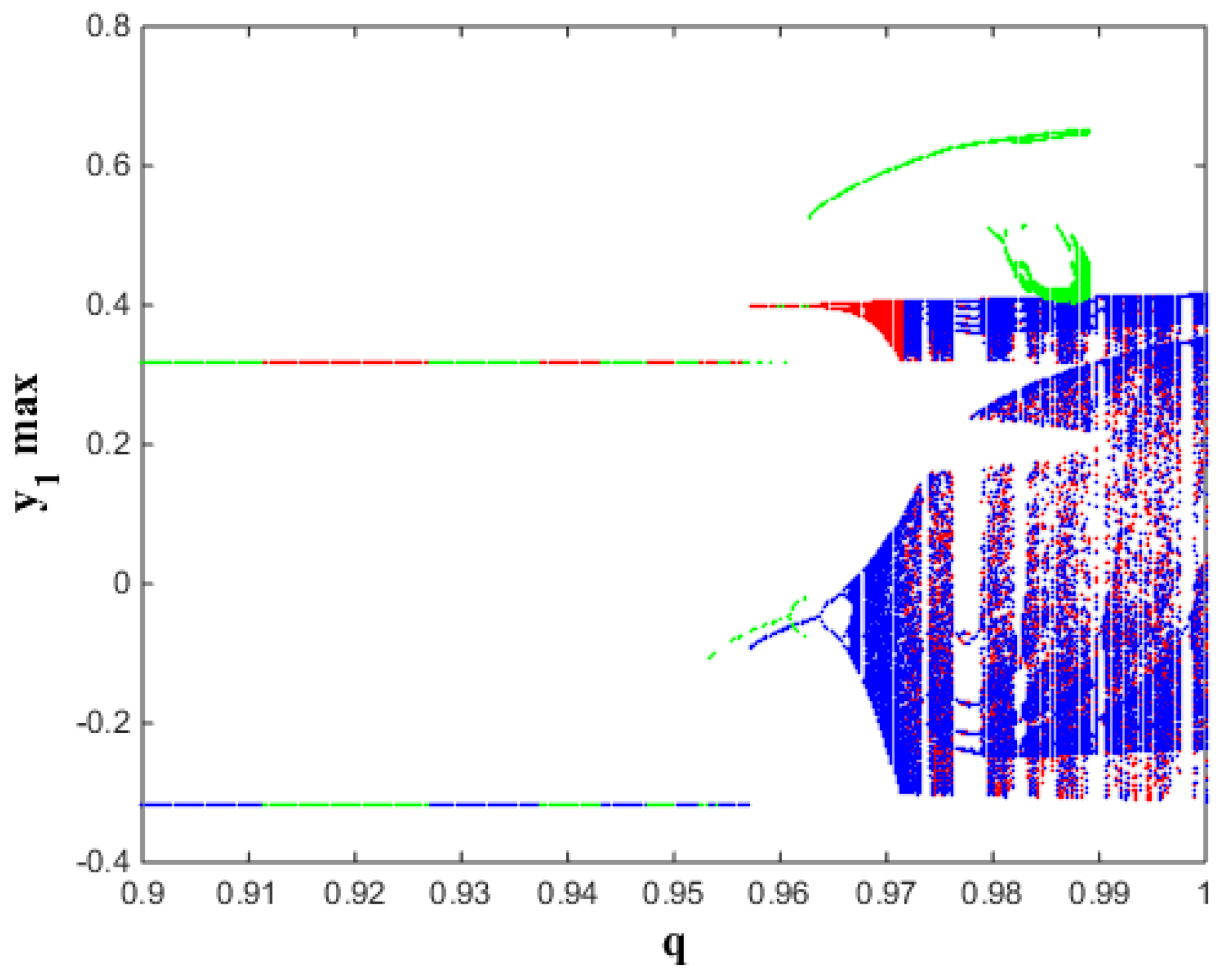
7. Existence of Self-Excited and Hidden Attractors in the Fractional-Order MAVPD System
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Guerra, R.; Montesinos-García, J.J.; Flores-Flores, J.P. Encryption and Decryption Algorithms for Plain Text and Images Using Fractional Calculus; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Abbas, S.; Nazar, M.; Nisa, Z.U.; Amjad, M.; El Din, S.M.; Alanzi, A.M. Heat and mass transfer analysis of MHD Jeffrey fluid over a vertical plate with CPC fractional derivative. Symmetry 2022, 14, 2491. [Google Scholar] [CrossRef]
- Kumar, A.; Alzaid, S.S.; Alkahtani, B.S.T.; Kumar, S. Complex dynamic behaviour of food web model with generalized fractional operator. Mathematics 2022, 10, 1702. [Google Scholar] [CrossRef]
- Zenkour, A.; Abouelregal, A. Fractional thermoelasticity model of a 2D problem of mode-I crack in a fibre-reinforced thermal environment. J. Appl. Comput. Mech. 2019, 5, 269–280. [Google Scholar]
- Abouelregal, A.; Ahmad, H. A modified thermoelastic fractional heat conduction model with a single lag and two different fractional orders. J. Appl. Comput. Mech. 2021, 7, 1676–1686. [Google Scholar]
- Ahmed, E.; Elgazzar, A.S. On fractional order differential equations model for non-local epidemics. Phys. A 2007, 379, 607–614. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, R.; Cattani, C.; Samet, B. Chaotic behaviour of fractional predator-prey dynamical system. Chaos Solitons Fractals 2020, 135, 109811. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A. Fractional-order diffusion-wave equation. Int. J. Theor. Phys. 1996, 35, 311–322. [Google Scholar] [CrossRef]
- Hilfer, R. (Ed.) Applications of Fractional Calculus in Physics; World Scientific: Upper Saddle River, NJ, USA, 2000. [Google Scholar] [CrossRef]
- Henriques, M.; Valério, D.; Gordo, P.; Melicio, R. Fractional-order colour image processing. Mathematics 2021, 9, 457. [Google Scholar] [CrossRef]
- Laskin, N. Fractional market dynamics. Phys. A 2000, 287, 482–492. [Google Scholar] [CrossRef]
- Matouk, A.E.; Agiza, H.N. Bifurcations, chaos and synchronization in ADVP circuit with parallel resistor. J. Math. Anal. Appl. 2008, 341, 259–269. [Google Scholar] [CrossRef]
- Fan, Q.-J. Horseshoe in a modified Van der Pol–Duffing circuit. Appl. Math. Comput. 2009, 210, 436–440. [Google Scholar] [CrossRef]
- Braga, D.C.; Mello, L.F.; Messias, M. Bifurcation analysis of a Van der Pol-Duffing circuit with parallel resistor. Math. Probl. Eng. 2009, 2009, 149563. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Li, Z. Controlling chaos based on the modified ADVP Model. In Proceedings of the 2009 International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC 2009), Hangzhou, China, 26–27 August 2009; Volume 1, pp. 40–43. [Google Scholar]
- Wang, L.; Li, Z. Measurement the frequency of weak sinusoidal signal based on the genetic algorithm. In Proceedings of the 2010 Sixth International Conference on Natural Computation (ICNC 2010), Yantai, China, 10–12 August 2010; pp. 3597–3600. [Google Scholar] [CrossRef]
- Zhao, H.; Lin, Y.; Dai, Y. Hidden attractors and dynamics of a general autonomous van der Pol–Duffing oscillator. Int. J. Bifurc. Chaos 2014, 24, 1450080. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; Matouk, A.E.; Elsaid, A.; Nour, H.M.; Elsonbaty, A. Nonlinear dynamics of a modified autonomous van der Pol–Duffing chaotic circuit. Electron. J. Math. Anal. Appl. 2014, 2, 199–213. [Google Scholar]
- Cai, P.; Tang, J.-S.; Li, Z.-B. Analysis and controlling of Hopf bifurcation for chaotic Van der Pol–Duffing system. Math. Comput. Appl. 2014, 19, 184–193. [Google Scholar] [CrossRef]
- Zhou, L.-Q.; Zhao, Z.-M.; Huang, D.-G.; Chen, F.-Q. Local dynamics of autonomous Van Der Pol–Duffing circuit system containing parallel resistor. In Proceedings of the 2017 3rd International Conference on Applied Mechanics and Mechanical Automation (AMMA 2017), Phuket, Thailand, 6–7 August 2017; pp. 10–14. [Google Scholar]
- Han, X.; Xia, F.; Ji, P.; Bi, Q.; Kurths, J. Hopf-bifurcation-delay-induced bursting patterns in a modified circuit system. Commun. Nonlinear Sci. Numer. Simul. 2016, 36, 517–527. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, X.; Jiang, W.; Ding, H.; Chen, L.; Bi, Q. Bursting oscillations induced by multiple coexisting attractors in a modified 3D van der Pol-Duffing system. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106806. [Google Scholar] [CrossRef]
- Matouk, A.E. Chaos, feedback control and synchronization of a fractional-order modified autonomous Van der Pol-Duffing circuit. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 975–986. [Google Scholar] [CrossRef]
- Matouk, A.E. Chaos synchronization of a fractional-order modified Van der Pol-Duffing system via new linear control, backstepping control and Takagi-Sugeno fuzzy approaches. Complexity 2016, 21, 116–124. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Vagaitsev, V.I. Hidden attractor in smooth Chua systems. Phys. D 2012, 241, 1482–1486. [Google Scholar] [CrossRef]
- Danca, M.-F. Hidden chaotic attractors in fractional-order systems. Nonlinear Dyn. 2017, 89, 577–586. [Google Scholar] [CrossRef] [Green Version]
- Almatroud, A.O.; Matouk, A.E.; Mohammed, W.W.; Iqbal, N.; Alshammari, S. Self-excited and hidden chaotic attractors in Matouk’s hyperchaotic systems. Discret. Dyn. Nat. Soc. 2022, 2022, 6458027. [Google Scholar] [CrossRef]
- Matouk, A.E. Chaotic attractors that exist only in fractional-order case. J. Adv. Res. 2022; in press. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent-II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. In Proceedings of the Computational Engineering in Systems and Application Multi-Conference, IMACS, IEEE-SMC Proceedings, Lille, France, 9–12 July 1996; Volume 1, pp. 963–968. [Google Scholar]
- Matouk, A.E. Stability conditions, hyperchaos and control in a novel fractional order hyperchaotic system. Phys. Lett. A 2009, 373, 2166–2173. [Google Scholar] [CrossRef]
- Matouk, A.E.; Khan, I. Complex dynamics and control of a novel physical model using nonlocal fractional differential operator with singular kernel. J. Adv. Res. 2020, 24, 463–474. [Google Scholar] [CrossRef]
- Hilbert, D. Mathematical problems. Bull. Am. Math. Soc. 1901, 8, 437–479. [Google Scholar] [CrossRef] [Green Version]
- Bautin, N.N. On the number of limit cycles generated on varying the coefficients from a focus or centre type equilibrium state. Dokl. Akad. Nauk. SSSR 1939, 24, 668–671. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef] [Green Version]
- Tavazoei, M.S. A note on fractional-order derivatives of periodic functions. Automatica 2010, 46, 945–948. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V. Analytical numerical methods for investigation of hidden oscillations in nonlinear control systems. IFAC Proc. Vol. 2011, 44, 2494–2505. [Google Scholar] [CrossRef]
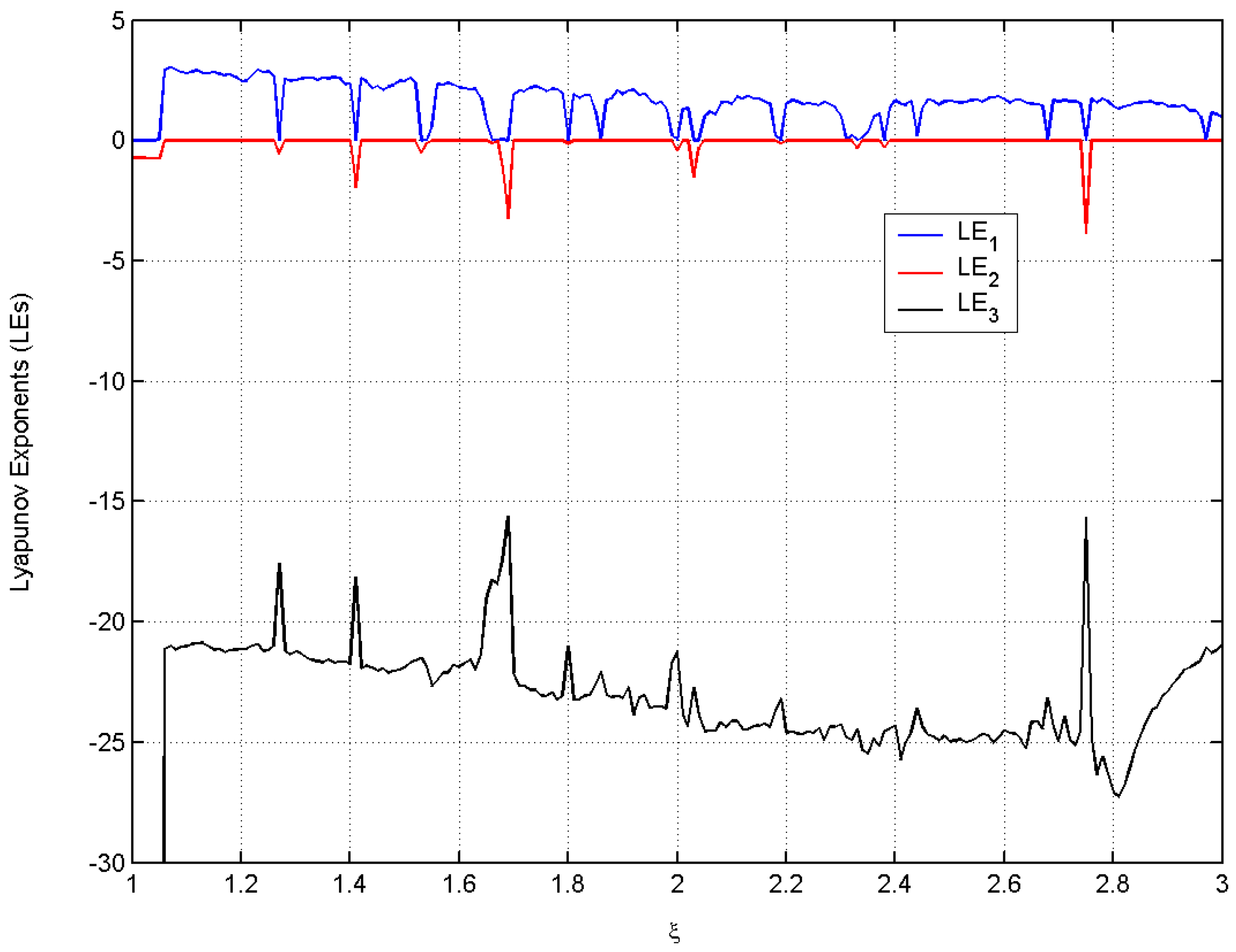
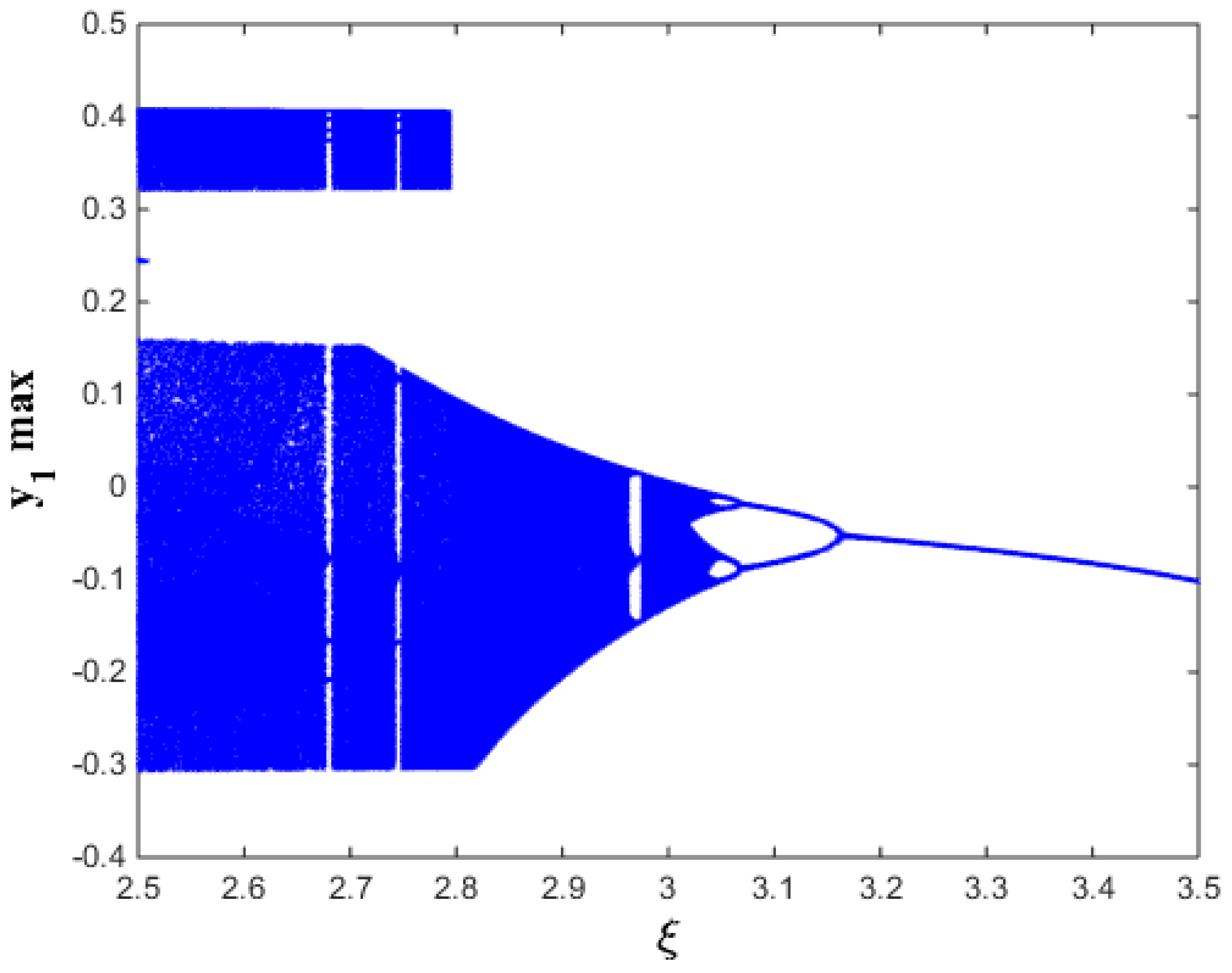
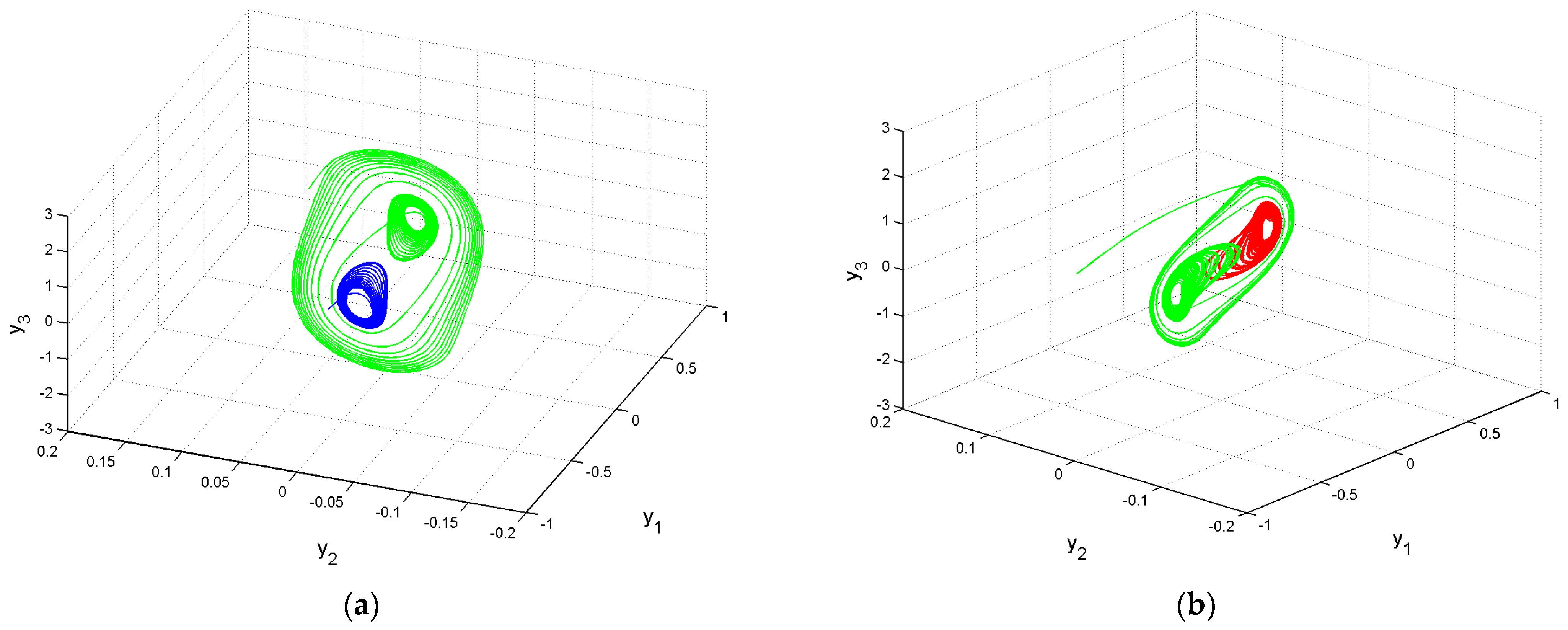

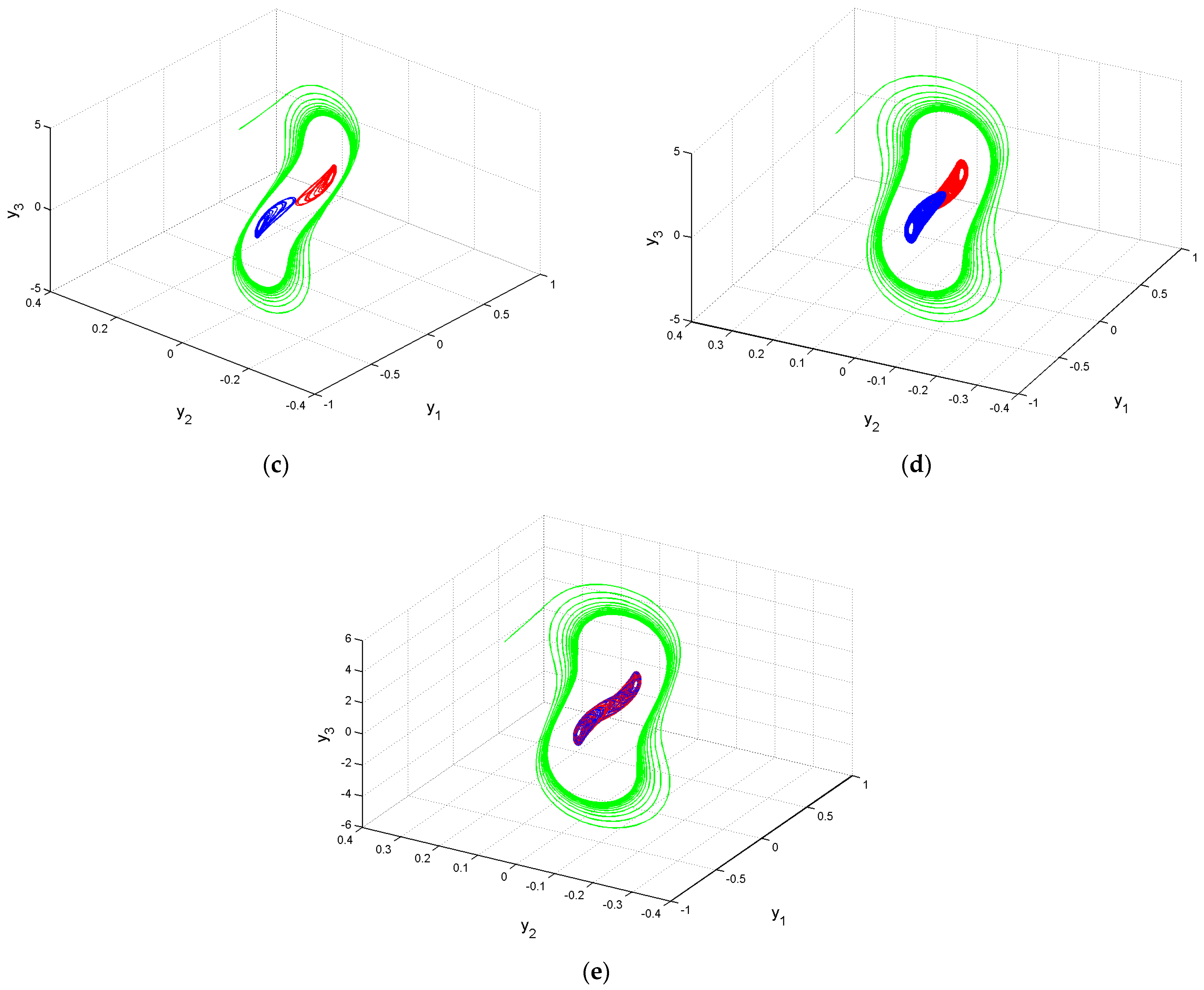
| Bifurcation Parameter | Initial Conditions | ||
|---|---|---|---|
| 10.2344 | 0.1136 | ||
| 18.6143 | 0.8951 | ||
| 18.6261 | 0.9096 | ||
| 18.6711 | 0.9723 | ||
| 18.7228 | 1.0636 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matouk, A.E.; Abdelhameed, T.N.; Almutairi, D.K.; Abdelkawy, M.A.; Herzallah, M.A.E. Existence of Self-Excited and Hidden Attractors in the Modified Autonomous Van Der Pol-Duffing Systems. Mathematics 2023, 11, 591. https://doi.org/10.3390/math11030591
Matouk AE, Abdelhameed TN, Almutairi DK, Abdelkawy MA, Herzallah MAE. Existence of Self-Excited and Hidden Attractors in the Modified Autonomous Van Der Pol-Duffing Systems. Mathematics. 2023; 11(3):591. https://doi.org/10.3390/math11030591
Chicago/Turabian StyleMatouk, A. E., T. N. Abdelhameed, D. K. Almutairi, M. A. Abdelkawy, and M. A. E. Herzallah. 2023. "Existence of Self-Excited and Hidden Attractors in the Modified Autonomous Van Der Pol-Duffing Systems" Mathematics 11, no. 3: 591. https://doi.org/10.3390/math11030591
APA StyleMatouk, A. E., Abdelhameed, T. N., Almutairi, D. K., Abdelkawy, M. A., & Herzallah, M. A. E. (2023). Existence of Self-Excited and Hidden Attractors in the Modified Autonomous Van Der Pol-Duffing Systems. Mathematics, 11(3), 591. https://doi.org/10.3390/math11030591






