A Hybrid Marine Predator Sine Cosine Algorithm for Parameter Selection of Hybrid Active Power Filter

Abstract

Power quality issues are handled very well by filter technologies. In recent years, the advancement of hybrid active power filters (HAPF) has been enhanced due to ease of control and flexibility as compared to other filter technologies. These filters are a beneficial asset for a power producer that requires a smooth filtered output of power. However, the design of these filters is a daunting task to perform. Often, metaheuristic algorithms are employed for dealing with this nonlinear optimization problem. In this work, a new hybrid metaheuristic algorithm (Marine Predator Algorithm and Sine Cosine Algorithm) has been proposed for selecting the best parameters for HAPF. The comparison of different algorithms for obtaining the HAPF parameters is also performed to show case efficacy of the proposed hybrid algorithm. It can be concluded that the proposed algorithm produces robust results and can be a potential tool for estimating the HAPF parameters. The confirmation of the performance of the proposed algorithm is conducted with the results of fitness statistical results, boxplots, and different numerical analyses.

1. Introduction

Power quality issues are a major drawback for power system networks due to increasing load demand, uses of non-linear loads, etc. New semiconductor technologies are implemented in power systems to provide high efficiency, considerable flexibility, and controllability. Unfortunately, the non-sinusoidal current that is drawn by these devices has a negative impact on power quality, a crucial qualitative indication for both the electric utility provider and the end customer. Nonlinear loads are often characterized by harmonic current sources and harmonic voltage sources, two different forms of harmonic sources. The degradation of the load’s power factor (PF), a rise in transmission-line losses, and a consequent decrease in the effectiveness of the transmission network are all anticipated as non-linear loads become more prevalent. In distribution networks, harmonic distortion levels noticeably increase [1].

Harmonics are removed from the power system network using passive power filters (PPF), active power filters (APF), and hybrid active power filters (HAPF). PPF’s inability to adapt the compensation features in response to dynamic changes in nonlinear loads is a drawback. Additionally, special caution must be used when using inductor (L) or capacitor (C) values with small permissible design tolerances because even minor changes to these values can alter the filter’s resonant frequency [2]. These drawbacks of PPF are overcome by an APF, which is typically composed of a three-phase pulse width modulated (PWM) voltage source inverter. A voltage source inverter, as opposed to a current-source inverter, is typically employed in an active filter due to the former’s superior efficiency, lower cost, and smaller size [3]. The series active filter serves as a harmonic isolator, whereas the shunt active filter serves as a harmonic compensator by injecting current that is out of phase with the distortion components present in the line current [3]. The converters must have a high-power rating if APF is the only component used in the circuit. As a result, the large size and cost of a solo active filter have been addressed by the development of HAPF, which combines components of both active and passive filters. A passive power filter (PPF) is a widely accepted real application; due to the many associated advantages of HAPF, implementation of HAPF is considered more widely. HAPF and PPF design are studied with the application of different optimization techniques and research investigations. Some of the noteworthy applications are Particle Swarm Optimization (PSO), Sequential Quadratic Programming (SQP), Hybrid DE ([4,5,6]), and application of the Bacterial Foraging Algorithm. However, design of HAPF with the application of recent metaheuristics is still a potential and unexplored area [7].

The main cause behind this, is complexity in modelling is due to high optimal gains. These gains can be tuned with the help of the trial-and-error method. Complexity increases due to the fact that both load and sources introduce harmonics. References [8,9] showcase HAPF design strategies without incorporating nonlinearity in the source.

Moreover, it should be pointed out that meta-heuristic algorithms make a major contribution in the design of the different types of filters. Cupertino presented an innovative optimization technique for the suggested model; the performance of the system was significantly improved using a Genetic Algorithm (GA) to optimize the effective parameters of a parallel active power filter [10,11]. To overcome the problems of sizing for passive filters, Rachid et al. [12] used the ant colony optimization (ACO) techniques and attained adequate results. Aside from this, from Jian et al. [13] focused on the GA-based metaheuristic application for a switch harmonic filter and showed in the results that switching harmonics can be easily mitigated by the proposed innovative technique. For HAPF design, Tiwari et al. [14] applied the ACO optimization algorithm and achieved suitable results.

Nevertheless, despite a lot of surveys, there are exiguous studies on meta-heuristic algorithms for HAPF design rather than PPF and APF. Many researchers have used different optimization techniques in the optimal solution of HAPF. Consequently, Biswas et al. [15] proposed an algorithm based on differential evolution (DE) to optimize the parameters of HAPF design. In the reference [16], total voltage harmonic distortion and current harmonic distortion have been incorporated in a composite objective function with the aim to minimize total harmonic pollution. From the literature, it is concluded that the filter design problem is a complex problem. Hence, in that work, the author presented a new version of TLBO for completing the design part. The algorithm is called Hierarchical Teaching–Learning Based-Optimization (HTLBO). The algorithm is based on the exploration and exploitation balance of the teaching and learning phase. Some more noteworthy applications have been reported in references [17,18,19].

1.1. Meta-Heuristic Optimization Techniques for Real Applications

Metaheuristic methods have been implemented with real world engineering problems due to following reasons:

• The structure of the algorithms is very easy and adaptive; hence it can be molded according to the problem.
• The derivative-free structure of these algorithms makes them applicable on discrete functions and even those that are not differentiable.
• Ease of hybridization; due to the simple structure, further experiments are possible for determining more accurate results and better convergence.

During the last two years, several approaches have been reported on real life applications that encompass the above mentioned virtues of metaheuristic algorithms. A few examples of real applications, found in terms of power harmonic components, are identification in reference [20]. Another application, robot path finding detection, has been solved with the help of the recently published metaheuristic Whale Optimization Algorithm (WOA) [21]. Simulations are performed for executing the bidding strategies with the help of the Ant Lion Optimizer (ALO) algorithm [22]. Likewise, a few hybrid algorithms have been reported in the references [23,24,25,26,27,28,29,30]. In these hybrid algorithms, two algorithms are fused in order to utilize the capabilities of optimization properties of both algorithms as one solution. Furthermore, in recent years, several new metaheuristic algorithms have been proposed, taking inspiration from the nature inspired processes, mathematical processes, and physical laws. Reference [31] presented an application of weighted mean square algorithm. Further, the implementation and the applications of these algorithms are visible in references [32,33,34,35,36,37,38,39,40]. From these approaches, it is clear that metaheuristic algorithms are widely accepted algorithms, and they can be applied in real-life challenging problems. This becomes the primary motivation for employing metaheuristics in this estimation problem.

Further, the design of HAPF and PPF is a challenging task to perform. In recent years, this optimization problem has been solved with many optimizers. To name a few, a multi objective framework has been proposed in reference [40] for constructing large-scale filters with the application of Hybrid Differential Evolution (HDE). A similar approach has been solved with mixed integer distributed ant colony optimization [41]. Bacterial foraging, as well as the Harris Hawks Optimizer algorithm, have been employed in references [42] and [43], respectively. An approach based on Feasible Sequential Quadratic Programming was introduced in reference [44]. The Power Quality Compensation technique using a universal power conditioner has been applied with the addition of a shunt filter in the system in reference [45]. To optimize the HAPF’s parameters, Biswas et al. [15] presented L-SHADE as a single objective function. In comparison, it considerably raised the likelihood of discovering the ideal solution and enhanced harmonic compensation performance. The proposed L-SHADE has been successful in finding the optimal parameters to reduce harmonic pollution; however, because of the solution space’s local optima, it still has low average performance. Therefore, based on objective function, we conduct research to enhance parameter extraction performance. To track the purpose of tracking several targets using various solar-powered unmanned aerial vehicles (SUVs) in an urban setting, Wu [46] developed adaptive GOA (AGOA) for trajectory optimization. Afshin et al. [47] created the Marine Predator Algorithm (MPA), a population-based meta-heuristic algorithm based on predatory behavior that can be influenced by marine predators such as sharks, sunfish, monitor lizards, swordfish, equine fishes, etc. MPA showed very competitive results and offers several benefits, including fewer parameters, straightforward settings, straightforward implementation, and precise calculation. This optimization approach has been used to achieve the best parameter selection for HAPF.

Another recently created meta-heuristic algorithm that can address a number of real-world engineering problems is the Sine Cosine Algorithm (SCA), which was first put forth by Mirjalili in 2016 [48]. SCA participates in the MPA algorithm in this study to enhance the MPA algorithm’s performance. The SCA implements a sine-cosine mechanism (SCM) that allows the example to follow either a sine or a cosine trajectory at random. When opposed to the MPA method, the SCA algorithm has a higher exploration ability because these two trajectories allow people to look either toward or away from the example. In view of the following discussion, the major contributions of this work are as follows:

• An optimization routine has been proposed and developed for parameter estimation of HAPF.
• A hybrid algorithm based on the implementation of the sine cosine equations of the SCA algorithm has been incorporated in the second phase of MPA. Evaluation of the performance of the proposed change has been conducted with the help of different test cases.
• The evaluation of the filter performance has been performed with the help of harmonic pollution, fitness function values, and objective function values of an optimization run.

1.2. Paper Structure

The remaining part of this manuscript has been organized as follows: In Section 2, basic details of hybrid filter technologies are depicted. In Section 3, problem formulation has been explained and development of the optimization routine has been shown. In Section 4, development of proposed MPA-SCA has been explained and basic details of MPA and SCA have also been discussed. In Section 5, numerical results are explained. Last but not the least, all major contributions of the work have been presented and future scope of the work is also discussed in conclusion section.

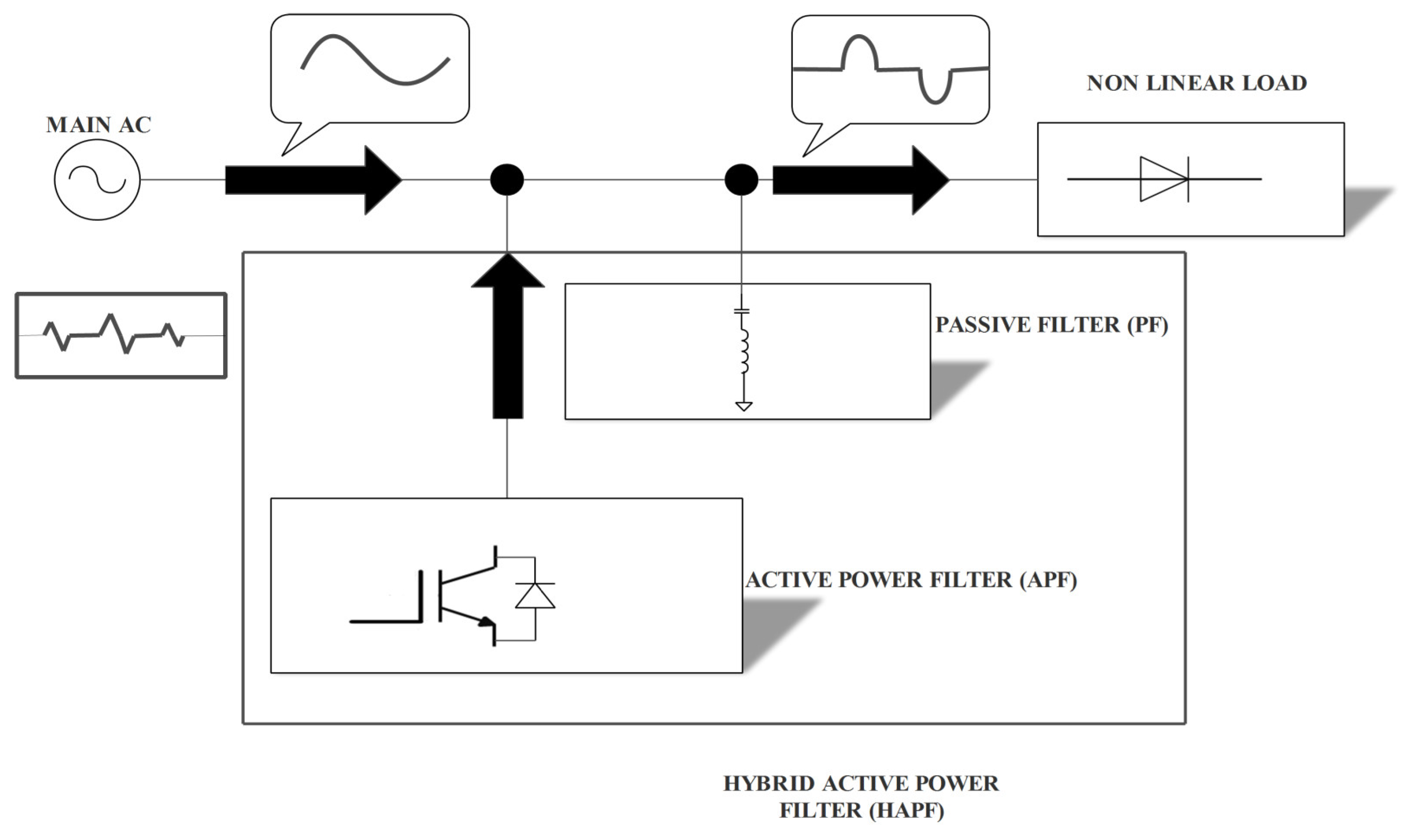
2. Hybrid Active Power Filter

To cover up the shortcoming of active and passive filters, HAPF was developed to mitigate both the voltage and current harmonics. A hybrid power filter’s structure is available in both series and parallel. HAPF combines the benefits of APF and PPF. The two most popular topologies of HAPF have been deeply studied in the literature [8,9,10]. Figure 1 shows the basic configuration of HAPF, consisting of a PF, APF, AC source, and a non-linear load.

The HAPF combines an active shunt power filter and a shunt passive filter. The APF rule entails recognizing all harmonic components and distinguishing the elements inherent in the other harmonic elements that are transformed into the resulting reference currents [17].

To obtain the benefits from the hybrid filters, different configurations have been carried, out which are:

✧

Series Active Power Filter with Shunt Power Filter;

✧

Shunt Active Power Filter and Shunt Power Filter Configuration;

✧

Active Power Filter in series with Shunt Power Filter.

2.1. Series APF and Shunt PF

Figure 2 shows the combination of the series APF and shunt PF. The series APF is connected through a transformer which is used to serve the low impedance for the lower frequency component, whilst the shunt-connected PF served the low impedance for the high frequency component. Therefore, this combination has the benefit of reducing both voltage and current harmonics.

2.2. Shunt APF and Shunt PF

The order of the frequencies the APF filters out determines the power rating of the device. As a result, an APF employed to filter out low order harmonics has a low power rating, smaller and less expensive. The design of this filter combination follows this rationale. The shunt-connected passive filter is intended to filter out higher order harmonics, whilst the shunt-connected APF is designed to filter out low order current harmonics. Figure 3 depicts the filter topology’s circuit architecture. The main drawback of this filter arrangement is that it is unsuitable for conditions of fluctuating loading, since only one precise preset harmonic can be tuned in the passive filter.

2.3. APF in Series with Shunt PF

The filter configuration of APF in series with shunt PF is shown in Figure 4. Active power filters provide the necessary DC link voltage for harmonic correction. The stress on the power electronic switches found in the APF is decreased by the passive filter, which maintains the voltage of the grid’s basic component. High to medium voltage ranges employ this design.

3. Problem Formulation

3.1. Circuit Analysis

There are two most important HAPF topologies in the electrical power system. The architecture details of APF in series with shunt PF and the combination of series APF along with shunt PF are shown in Figure 5 and Figure 6, respectively. In Figure 5, the active power filter improves the passive filter’s performance by injecting a harmonic current and cancelling the load harmonics. For reducing the voltage rating of the APF, the fundamental source voltage is applied to the shunt passive filter. In Figure 6, the series APF provides high impedance by supplying the harmonics and forces the harmonic current through passive filters, thus permitting them to reduce the APF’s current rating. In the configuration of “APF in series with shunt passive filter”, the point of common coupling (PCC) represents that other linear loads are connected in the structure. APF and non-linear loads are also connected at the PCC. According to the requirements of the system, a set of tuned filters consisting of inductive and capacitive reactance respectively are connected to APF in series. These are shown by $x_l$ and $x_c$ in both the configurations.

The single-phase equivalent circuit at fundamental frequency is commonly used for the HAPF topologies. In Figure 7, script ‘1′ indicates the parameter value at fundamental frequency. It can be observed from the single-phase equivalent circuit for “APF in series with shunt passive filter” and “combined series APF and shunt passive filter”, which are shown in Figure 8 and Figure 9, respectively, that harmonics frequencies differ for both configurations. The reason behind this difference is that the position of the active power filter and its response to the supply harmonics is also different [18]. The active power filter plays a vital role in harmonic mitigation, as it injects voltage harmonic at the terminal. This injected voltage harmonic is proportional to the harmonic components of the supply current. Hence, a linear relationship between these two can be characterized as $v_{af}=k{i}_{sh}$. This equation contains a proportionality constant (k) that is filter gain. At fundamental frequency, this provides a zero impedance. From here, it is implied that active filter components act as a virtual harmonic resistor that provides zero impedance at fundamental frequency [19]. This work enumerates the optimization of three best parameters, i.e., k,$x_l$, and $x_c$, with the structure consisting of source and load, which are non-linearities. Source harmonic voltage and current non-linearities are accounted in $v_{sh}$ and $i_{sh}$, respectively, and those of loads are in $v_{lh}$ $a\mathrm{nd} i_{lh}$.

Utility supply voltage and nonlinear load are expressed by the Thevenin voltage source and harmonic current source, respectively, presented as:

$$v_s(t)={\displaystyle {\sum }_h{v}_{sh}(t)}$$

(1)

$$i_l(t)={\displaystyle {\sum }_h{i}_{lh}(t)}$$

(2)

Source impedance of the h-th harmonics is:

$$z_{sh}=r_{sh}+j{x}_{sh}$$

(3)

Load impedance of the h-th harmonics is:

$$z_{lh}=r_{lh}+j{x}_{lh}$$

(4)

The load admittance of the circuit is:

$$y_{lh}=g_{lh}-j{b}_{lh}$$

(5)

At higher level harmonic, i.e., ‘h ≥ 2’, after analyzing the equivalent circuit of Figure 5 for the series realization of the filter topology, the following relationship is identified between voltage and current of load and supply end, respectively:

$$i_{sh}=\frac{a+jb}{c+jd}$$

(6)

$$v_{lh}=\frac{e+jf}{c+jd}$$

(7)

At higher level harmonic i.e., ‘h ≥ 2’, after analyzing the equivalent circuit of Figure 4 for the series realization of the filter topology, the following relationship is identified between the voltage and current of load and supply end, respectively:

$$v_{lh}=\frac{e+jf}{c+j{d}^{\prime }}$$

(8)

$$v_{lh}=\frac{e+j{f}^{\prime }}{c+jd\prime }$$

(9)

where

$$a=v_{sh}{r}_{lh}-i_{lh}{x}_{lh}\left(h_{xl}-\frac{x_c}{h}\right)$$

(10)

$$b=v_{sh}\left(x_{lh}+h{x}_l-\frac{x_c}{h}\right)+i_{lh}{r}_{lh}\left(h_{xL}-\frac{x_c}{h}\right)$$

(11)

$$c=r_{tlh}+k{r}_{lh}-\left(x_{lh}+x_{sh}\right)\left(h_{xl}-\frac{x_c}{h}\right)$$

(12)

$$r_{tlh}=r_{sh}{r}_{lh}-x_{sh}{x}_{lh}$$

(13)

$$d=x_{tlh}+k{x}_{lh}-\left(r_{lh}+r_{sh}\right)\left(h_{xl}-\frac{x_c}{h}\right)$$

(14)

$$x_{tlh}=r_{lh}{x}_{sh}-r_{sh}{x}_{lh}$$

(15)

$$e=v_{sh}\left[k{r}_{lh}-x_{lh}\left(h{x}_l-\frac{x_c}{h}\right)\right]+i_{lh}{x}_{tlh}\left(h_{xl}-\frac{x_c}{h}\right)$$

(16)

$$f=v_{sh}\left[k{x}_{lh}+r_{lh}\left(h{x}_l-\frac{x_c}{h}\right)\right]-i_{lh}{r}_{tlh}\left(h_{xl}-\frac{x_c}{h}\right)$$

(17)

$$d^{\prime }=x_{tlh}+k{x}_{lh}+\left(k+r_{lh}+r_{sh}\right)\left(h_{Xxl}-\frac{x_c}{h}\right)$$

(18)

$$f^{\prime }=v_{sh}\left[k{x}_{lh}+\left(k+r_{lh}\right)\left(h{x}_l-\frac{x_c}{h}\right)\right]-i_{lh}{r}_{tlh}\left(h_{xl}-\frac{x_c}{h}\right)$$

(19)

It can be observed from the equations that the compensated utility supply harmonic current is inverse to gain k. Usually in active filter configuration, this phenomenon is identified as obstructing the resistor that suppresses the harmonic current generated by the nonlinearity of the source. Consequently, for the harmonic current, this acts as a damping resistor. This diminishes the resonance between the shunt and passive filter and source impedance. The following mathematical expression showcases the compensated load displacement factor and pf represents compensated load power factor.

$$dpf=\frac{p_{l1}}{v_{l1}{i}_{s1}}=\frac{g_{l1}{v}_{l1}}{i_{s1}}$$

(20)

$$pf=\frac{p_l}{v_l{i}_s}=\frac{g_{l1}{v}_{l1}+{\displaystyle {\sum }_{h\ge 2}{g}_{lh}{v}_{lh}^2}}{\sqrt{\left(i_{s1}^2+{\displaystyle {\sum }_{h\ge 2}{i}_{sh}^2}\right)\left(v_{l1}^2+{\displaystyle {\sum }_{h\ge 2}{v}_{lh}^2}\right)}}$$

(21)

In subscript ‘1’ the transmission loss formula is expressed as:

$$p_{loss}=i_{s1}^2+r_{s1}+{\displaystyle {\sum }_{h\ge 2}{i}_{sh}^2{r}_{sh}}$$

(22)

Transmission efficiency can be calculated by:

$$\eta =\frac{p_l}{p_l+i_{s1}^2+r_{s1}+{\displaystyle {\sum }_{h\ge 2}{i}_{sh}^2{r}_{sh}}}$$

(23)

Further, the expression for voltage (compensated) and utility supply current (compensated) can be represented by following expressions.

$$Vthd=\frac{\sqrt{{\displaystyle {\sum }_{h\ge 2}{v}_{lh}^2}}}{v_{l1}}$$

(24)

$$Ithd=\frac{\sqrt{{\displaystyle {\sum }_{h\ge 2}{i}_{lh}^2}}}{i_{s1}}$$

(25)

Finally, we can calculate the harmonic pollution through below formula as follows:

$$hp=\sqrt{Vth{d}^2+Ith{d}^2}$$

(26)

3.2. Fitness Function for Filter Design

To minimize the harmonic pollution, three parameters are considered for the optimization process: $k,x_c,x_l$ for HAPF design. The range of these parameters can be manifested as:

$$\left\{\begin{array}{l}0\le k\le 20\\ 0\le x_c\le 20\\ 0\le x_l\le 1\end{array}\right\}$$

(27)

It is worth mentioning here that these three parameters, namely filter gain and composing inductance and capacitance values, have an impact on filter performance. When designing the filter, the guidelines of IEEE Standard 519-2014 are adhered to. These are based on a system voltage level and system short circuit ratio. The allowable ranges for Vthd and Ithd are, respectively, as follows:

$$\left\{\begin{array}{l}Vthd\le Vth{d}_{\lim }\\ Ithd\le Ith{d}_{\lim }\end{array}\right\}$$

(28)

Where Equation (28) defines the limitation on as $Vth{d}_{\lim }$ and, similarly, the limitation of current can be designated as $Ith{d}_{\lim }$. These limitations are strictly adhering to the guidelines of IEEE 519-2014. On the basis of these representations, i.e., (Equations (27) and (28)), following expression is taken as an objective function:

$$h{p}_{app}=abs\left(Vth{d}_{\lim }-Vthd\right)+abs\left(Ith{d}_{\lim }-Ithd\right)$$

(29)

When solving for this optimization process, the individual harmonic is optimized with the help of following expression:

$$\mathrm{Maximize} ‘h{p}_{app}’ \mathrm{subject} \mathrm{to} pf=p{f}_{goal}\pm \epsilon$$

(30)

where $p{f}_{goal}$ represents the power factor that we want to achieve and is set to 95% for this proposed work. In the above equation, a small error value $\epsilon$ is established to smooth the iterative process and its value is set to 1%. It is further investigated that the objective function input ‘$-h{p}_{app}$’ is minimized. Moreover, for evaluating the value of objective functions by this algorithm, all the harmonics levels are within the limitations. If harmonics levels are not meeting the limitations, experimental data are rejected, and the value of the objective function will be set to a high value, such as 100. Hence, with the use of a single objective function, the suppression of harmonic pollution is addressed in this work. Here, the nonlinearity of the source and load are is taken for investigation.

4. Development of MPA-SCA

In this section, development steps of MPA-SCA have been explained. For better understanding, basic parent algorithms are also incorporated in the paper.

4.1. Marine Predators Algorithm

The Marine Predators Algorithm (MPA) is a metaheuristic optimization technique that draws its inspiration from nature. It adheres to the natural laws that regulate the best foraging strategy and encounter rates between predators and prey in marine ecosystems. Brownian and Lévy steps are used by the MPA to imitate how predators behave when attacking their prey. Predators employ these steps to find their prey. The Lévy and Brownian movements, which are widely used in ocean predators’ foraging strategies, as well as the optimal encounter rate policy in the biological interaction between predators and prey, are the main sources of inspiration for MPA. In addition, because of the surrounding environmental problems, the predators spend 80% of their time looking for prey in the neighborhood and the remaining 20% in other habitats. The algorithm has a strong capacity to resist becoming stuck in local optima thanks to a technique known as fish aggregating devices (FADs). When predators and prey interact biologically, the best encounter rate policy depends on the movements that each predator and prey make, as well as their relative velocities. For environments with little prey concentration, marine predators adopt the Lévy method, while in environments with lots of prey, they use Brownian mobility. While moving across several habitats throughout the course of their existence, they exhibit the same proportions of Lévy and Brownian movements. They alter their behavior in an effort to locate places with a different distribution of prey due to environmental influences, whether they are natural or human caused. Predators are designed to employ Lévy distribution especially when their prey is following the movement in the fashion of Brownian or Lévy motion at a low velocity ratio (v = 0.1). The best (optimal) strategy for a predator is to follow the path suggested by Brownian motion in the unit velocity ratio (v = 1) if the prey moves with Lévy trajectories. Depending on the system size, more possibilities may occur and predator and prey can act or experimented with different distributions. The predator remains still at a high-velocity ratio (v = 10), as this is the most suitable option to grab a prey in stochastic environment. In this instance, the prey is either travelling using Brownian or Lévy motions, and they make use of their sharp memories to keep track of both their friends and the best places to go foraging.

Further, it is worth mentioning here that MPA is based on these two motions, hence, there is an acute need for understanding the philosophy of these random walk models comprising of (i) Brownian and (ii) Lévy motion before explaining the steps of the suggested algorithm.

(i)

Brownian Motion

Using a normal (Gaussian) distribution with a zero mean (μ = 0) and unit variance (σ² = 1), the probability function defining the step length for the typical Brownian motion is used to obtain the step length. The following describes the controlling Probability Density Function (PDF) at point x for this motion:

$$F_b=\left(x;\mu ,\sigma \right)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{x-{\mu }^2}{2{\sigma }^2}\right)=\frac{1}{\sqrt{2\pi }}\exp \left(-\frac{x^2}{2}\right)$$

(31)

(ii)

Lévy Flight

Using a probability function specified by the Lévy distribution (power law tail), Lévy flight is a sort of random walk in which the step sizes are determined.

$$L\left(X_j\right)\approx {\left|x_j\right|}^{1-\alpha }$$

(32)

where,$x_j$ denotes the flight length and 1 < α ≤ 2 denotes the power law exponent.

Based on the definitions, the framework of the algorithm can be understood as follows:

The MPA algorithm starts with the initial population cast with the help of normal distribution of the random numbers between upper and lower bounds or corresponding variables. This proposition can further be written as per following equation:

$$X_0=X_{\min }+rand\left(X_{\max }-X_{\min }\right)$$

(33)

where, X_min and X_max denote the lower and upper limit of control variables, respectively, and the rand is a random value in the range of (0, 1). Elite matrix becomes a subset of the solution that possesses fittest solution. The dimension of the matrix consists of a number of search agents and problem dimensions. For this problem, three variables are there, and no. of search agents considered is 50.

$$Elite=\left(\begin{array}{ccc}{X}_{1.1}^{1E}& X_{1.2}^{1E}\cdots & X_{1.d}^{1E}\\ \begin{array}{l}{X}_{2.1}^{1E}\\ ⋮\end{array}& \begin{array}{l}{X}_{2.2}^{1E}\cdots \\ ⋮\end{array}& \begin{array}{l}{X}_{2.1}^{1E}\\ ⋮\end{array}\\ X_{n.1}^{1E}& X_{n.2}^{1E}\cdots & X_{n.d}^{1E}\end{array}\right)$$

(34)

where $\overrightarrow{X}{}^{1E}$ represents the top predator vector, n is the number of search agents, and d is the number of dimensions. The philosophy of MPA says that both predator and prey act as search agents, as they both look for food. Hence, updating the elite matrix is considered with the help of a weakly fit replacement.

Another representative matrix of MPA is called the prey matrix. This matrix is an auxiliary matrix that helps in updating the process of the elite matrix. An initialization process enables this matrix. Predators update their position with the help of this matrix. Further, the fittest matrix is constructed and designated as elite. This matrix is represented as:

$$Prey=\left(\begin{array}{ccc}{X}^p{}_{1,1}& X^p{}_{1,2}\cdots & X^p{}_{1,d}\\ \begin{array}{l}{X}^p{}_{2,1}\\ ⋮\end{array}& \begin{array}{l}{X}^p{}_{2,2}\cdots \\ ⋮\end{array}& \begin{array}{l}{X}^p{}_{2,d}\\ ⋮\end{array}\\ X^p{}_{n,1}& X^p{}_{n,2}\cdots & X^p{}_{n,d}\end{array}\right)$$

(35)

where, X_i,j represents the jth dimension of ith prey. The entire optimization process is mainly dependent on the above-specified two matrices.

The MPA optimization process can be categorized into three main phases.

Phase 1: This phase is applicable for up to one third of the iteration process. In this phase, it has been assumed that predator velocity is lower than prey. Additionally, the velocity ratio is quite a bit higher. This fact ensures the exploration of the search space. During this phase, the velocity ratio is higher than 10. Hence, the weak stagnation in the movement of the predator is observed. The representative expressions for this phase are as follows:

$$\mathrm{While}Iter<\frac{1}{3}Max\_Iter$$

$$\begin{gathered} \overrightarrow{Stepsiz{e}_1}=\overrightarrow{{\lambda }_B}\otimes \left(\overrightarrow{Elit{e}_1}-\overrightarrow{{\lambda }_B}\otimes \overrightarrow{Pre{y}_1}\right) \\ \overrightarrow{Pre{y}_1}=\overrightarrow{Pre{y}_1}+P.\overrightarrow{R}\otimes \overrightarrow{Stepsiz{e}_1} \end{gathered}$$

(36)

Where $\overrightarrow{{\lambda }_B}$ is a vector containing random numbers based on normal distribution representing the Brownian motion.

Phase 2: during this phase, balance between exploration and exploitation decides the convergence of the algorithm. For exploitation, prey is responsible, and predator is responsible for exploration. Based on the rule, in the unit velocity ratio (v ≈ 1), as discussed, prey follows a random walk through Lévy; accordingly, the predator decides on the strategy to move in Brownian motion.

$$While\frac{1}{3}Max\_Iter<Iter<\frac{2}{3}Max\_Iter$$

For the first half of the population

$$\begin{gathered} {\overrightarrow{Stepsize}}_1=\overrightarrow{{\lambda }_L}\otimes \left(\overrightarrow{Elit{e}_1}-\overrightarrow{{\lambda }_L}\otimes \overrightarrow{Pre{y}_1}\right) i=1,\dots ,n/2 \\ \overrightarrow{Pre{y}_1}=\overrightarrow{Pre{y}_1}+P.\overrightarrow{R}\otimes \overrightarrow{Stepsiz{e}_1} \end{gathered}$$

(37)

where $\overrightarrow{{\lambda }_L}$ is a vector of random numbers based on Lévy distribution representing Lévy movement.

Phase 3: In this phase, predator is moving faster than the prey, which is mostly associated with high exploitation capability. In a low velocity ratio (v = 0.1), the best strategy for the predator is Lévy.

$$\mathit{While}Iter>\frac{2}{3}Max\_Iter$$

$${\overrightarrow{Stepsize}}_1=\overrightarrow{R_L}\otimes \left(\overrightarrow{R_L}\otimes \overrightarrow{Elit{e}_1}-\overrightarrow{\mathrm{Pr}e{y}_1}\right)i=1,\dots ,n$$

(38)

$$\overrightarrow{\mathrm{Pr}e{y}_1}=\overrightarrow{Elit{e}_1}+P.CF\otimes \overrightarrow{Stepsiz{e}_1}$$

For more details on this algorithm, readers are directed to the original paper.

4.2. Sine Cosine Algorithm

The SCA is also a recently developed meta-heuristic algorithm, proposed by Seyedali Mirjalili in 2016, which can resolve a variety of practical engineering problems. Based on a mathematical framework primarily derived with the help of the sine and cosine rule, SCA shifts various initial random solutions to the feasible potential zone of convergence. Additionally, SCA employs variables that possess random and adaptive behavior to relocate the bad solutions into a feasible zone with the ease. For these reasons, this algorithm has been widely used. The SCA employs two basic algorithms for search: the first algorithm is a population search strategy and second one is a local search strategy. These two strategies are responsible for global exploration and local exploitation. The wide applicability of SCA is due to its simple, hassle free, and adaptive structure. The algorithm has been hybridized with many other algorithms for effective numerical optimization. Due to these features, SCA is successfully applied to solve different optimization problems, such as scheduling, feature selection, classification, economic power dispatch planning, benchmark functions, and power energy.

Without loss of generality, the candidate solutions in SCA are formulated as a matrix:

$$X=\left(\begin{array}{ccc}{x}_{(1,1)}& x_{(1,2)}\cdots & x_{(1,d)}\\ \begin{array}{l}{x}_{(2,1)}\\ ⋮\end{array}& \begin{array}{l}{x}_{(2,2)}\cdots \\ ⋮\end{array}& \begin{array}{l}{x}_{(2,d)}\\ ⋮\end{array}\\ x_{(n,1)}& x_{(n,2)}\cdots & x_{(n,d)}\end{array}\right)$$

(39)

where the row vector is represented per the following entries $X_n=\left[x_{n,1}, x_{n,2}, \dots , x_{n,d}\right]$. Similar to other optimization algorithms, the initialization process contains the formation of this matrix that includes size (N × d). Further, the position update expressions are based on the evaluation of trigonometric functions with encoding steps. For updating the positions in the algorithm, sine and cosine functions are employed and the expressions for the same can be represented by following:

$$Y_i^{t+1}=Y_i^t+r_1\times \sin \left(r_2\right)\times \left|r_3{j}_i^t-Y_i^t\right|$$

(40)

$$Y_i^{t+1}=Y_i^t+r_1\times \cos \left(r_2\right)\times \left|r_3{j}_i^t-Y_i^t\right|$$

(41)

where $Y_i^t$ is the position of the current solution in i-th dimension at t-th iteration. Further, the randomness is added with the incorporation for $r_1$/$r_2$/$r_3$. Expressions (40) and (41) represent the position update to reach the desired destination point in the i-th dimension. Further, the update equation employs absolute values of the differences only. For the implementation of SCA expressions, (40) and (41) are combined with the use of random probability:

$$Y_i^{t+1}=\{Y_i^t+m_1\times \sin \left(r_2\right)\times \left|r_3{j}_i^t-Y_i^t\right|$$

(42)

$$Y_i^{t+1}=\{Y_i^t+m_1\times \cos \left(r_2\right)\times \left|r_3{j}_i^t-Y_i^t\right|$$

(43)

where $j_i^t$ denotes the local best solution obtained so far, random number r₂ is between [0, 2π]. Hence, with the incorporation of the sine and cosine rule, the search direction is aggregated towards the global best solution. Random number r₃ is distributed between [0, 2] and random number r₄ acts as a probability switch for employing the sine or cosine function in the position update phase. Further, the bridging is provided with the help of a monotonically decreasing linear function, m₁. This number decreases with the increment in iterative count increasing.

$$m_1=a-t\ast \frac{a}{T_{\max }}$$

(44)

The expression for this bridging is showcased with the help of expression (44). Here, a is a constant. The current iteration of the iterative process is designated as t and T_max is the max iteration count that decides the stopping criterion for the optimization process. As described earlier, the balancing between the exploration and exploitation phases is conducted with the help of m₁. Success of the optimization process heavily depends upon this parameter.

4.3. Proposed Hybrid MPA-SCA

The proposed Hybrid MPA-SCA algorithm is employed to estimate three parameters (filter gain, capacitance, and inductance) from the above-mentioned HAPF topologies. For the estimation process, APF in series with the passive shunt filter (series topology) and combined series APF and shunt passive filter (parallel topology) are considered.

As reported in many applications, alone, MPA and SCA both are capable of handling optimization issues with ease and great efficacy as compared to other meta-heuristic algorithms. Since both algorithms have different internal mechanisms to deal with diverse problems, as well as for certain issues, these algorithms suffer from stagnation and local minima entrapment. Therefore, significant modifications are required in the parent algorithms to identify the best designing parameters of various filter topologies. The following are the main reasons behind the alteration of the original algorithm:

• During phase 2 of algorithm, there is a high probability of stagnation in the local minima due to the fact that the exploration phase is not finished in order to reach the intermediate stage; the same is true of the exploitation phase, also at the intermediate stage. Hence, the simple rule update may yield some infeasible solutions in this case that may result in local minima stagnation.
• Hence, a modified update rule is proposed for prey that is based on the sine cosine adaptation of the algorithm. A probability factor is defined as sine and cosine values inspired from the position update of the SCA algorithm. Further, the representative expression for this adaption may be given as:

$$\begin{array}{l}\gamma =rand(\cos (rand))\\ if\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\gamma \ge 0.5\\ \overrightarrow{\mathrm{Pr}e{y}_1}=\overrightarrow{\mathrm{Pr}e{y}_1}+P.\overrightarrow{R}\otimes \overrightarrow{Stepsiz{e}_1}\times \cos (\gamma )\\ else\\ \overrightarrow{\mathrm{Pr}e{y}_1}=\overrightarrow{\mathrm{Pr}e{y}_1}+P.\overrightarrow{R}\otimes \overrightarrow{Stepsiz{e}_1}\times \sin (\gamma )\end{array}$$

(45)

With this update rule, the update equation is enhanced. The proposed mechanism is embedded in the algorithm and the updated algorithm is named the MPA-SCA algorithm.

Discussion: The proposed rule has more significance, as, based on research conducted on the bridging mechanism of the metaheuristics, it may be concluded that this bridging has an ample effect on the state of convergence of the algorithm, as well as the stagnation of the local minima entrapment conditions. Further, the proposed hybrid version of the algorithm will be evaluated on the basis of solution quality obtained and the filter designs it yields. Different from the conventional approach, the metaheuristics are not here evaluated on the standard benchmark function, as already, such research has been carried out by the researchers. Hence, the following section presents an analysis of the results and discusses the implications of the proposed modification on the performance of the algorithm. The flow of the proposed algorithm has been depicted in Algorithm 1.

Algorithm 1 Pseudo code: Proposed MPA-SCA Algorithms
Step 1.	Initialize search agents (Prey) populations i = 1..., n
Step 2.	While Termination Criterion Does not meet (Calculate the fitness and different matrices described in expressions (34) and (35)
Step 3.	If Iter < Max_Iter/3
	Update prey based on Equation (36)
Step 4.	Else if Max_Iter/3 < Iter < 2 ∗ Max_Iter/3
	For the updation of the populations into two folds (i = 1..., n)
	Update prey based on Equation (45)
Step 5.	Else if Iter > 2 ∗ Max_Iter/3
	Update prey based on Equation (38)
End (if)
	Accomplish memory saving and Elite update
	Applying FADs’ effect and update
End while

5. Analysis of Experimental Results

In this section, the application of diverse metaheuristic algorithms for designing the parameters of the hybrid active–passive filter is presented. For comparison, all algorithms are bound to run for 30 times. The stopping criterion of the algorithm is considered as the exhaustion of the maximum no. of iterations. The maximum no. of iterations for this optimization process has been kept as 500. The following algorithms are considered for the evaluation (

Table 1. Details of Participating Algorithms.

Name of Algorithm	Major Characteristics of the Algorithm	Category
Grey Wolf Optimization [49]	Based on the hunting of the grey wolf	Nature Inspired Algorithm (Behavior)
Sine Cosine Algorithm [48]	Based on trigonometric rules of position update	Swarm Intelligence-Based Algorithm inspired by mathematical functions
Chaotic Marine Predator Algorithm (CMPA) [50]	Based on the behavior of the food searching strategy of marine predators	Nature Inspired Algorithm (Behavior)
Whale Optimization Algorithm and its advanced version (Augmented Whale Optimization Algorithm (AWOA)) [51,52]	Hunting strategy of whales through bubble netting	Nature Inspired Algorithm (Behavior)
Harris Hawk Optimization Algorithm [53]	Attacking strategy on rabbit	Nature Inspired Algorithm (Behavior)
Crow Search Algorithm [54]	Behavior of crow and position update on the basis of the sharp memory of the crows	Nature Inspired Algorithm (Behavior)
Enhanced Chaotic Grasshopper Optimization Algorithm [55]	Based on the life cycle and movement strategy of grasshoppers	Nature Inspired Algorithm (Behavior)
Marine Predators Algorithm [47]	Based on the hunting of marine predators	Nature Inspired Algorithm
Flower Pollination Algorithm [56]	Based on the pollination	Nature Inspired Algorithm (Process)
Multi Verse Optimizer [57]	Based on the physical laws of multi verse	Physics

):

Analysis of Harmonic Pollution: As discussed in problem formulation, the experiments have been conducted for the analysis of harmonic pollution of the iterative process with the help of the calculation of statistical attributes such as:

• Mean value of HP obtained from Optimization run;
• Standard Deviation value of HP obtained from Optimization run;
• Maximum value or worst value of HP obtained from Optimization run;
• Minimum value of best value of HP obtained from Optimization run.

For all the participating algorithms, these four parameters are calculated and tabulated in

Table 2. Harmonic Pollution (HP) Statistics for Four Topologies of Series structure.

Topology-1 (Series)					Topology-2 (Series)
Algorithm	HP-Statistical Attributes				Algorithm	HP-Statistical Attributes
	Max	Min	Mean	SD		Max	Min	Mean	SD
MPA-SCA	0.235824	0.235824	0.235824	1.43 × 10−10	MPA-SCA	2.752029	2.752029	2.752029	4.27 × 10−9
MPA	0.235824	0.235824	0.235824	1.83 × 10−10	MPA	2.752029	2.752029	2.752029	8.31 × 10−9
SCA	1.44814	0.235049	0.44804	0.454965	SCA	2.970749	2.705925	2.744592	0.044462
GWO	0.492863	0.235761	0.244709	0.046871	GWO	2.758108	2.737616	2.750605	0.004665
WOA	0.457229	0.235761	0.283102	0.059442	WOA	2.791659	2.728764	2.763505	0.014736
MVO	0.493802	0.235761	0.330901	0.125682	MVO	13.44247	2.743669	3.156759	1.944584
CSA	0.493003	0.235812	0.407311	0.123236	CSA	2.952725	2.720597	2.871241	0.10131
FPA	0.235939	0.235776	0.235832	3.71 × 10−5	FPA	2.752787	2.751169	2.75196	3.59 × 10−4
HHO	0.801755	0.235947	0.400669	0.137242	HHO	2.978814	2.700313	2.871331	0.098372
CMPA	0.55539	0.248702	0.35613	0.075584	CMPA	2.989874	2.672063	2.77443	0.077334
ECGOA	0.893207	0.248887	0.54476	0.17253	ECGOA	3.175558	2.740154	2.957158	0.085101
AWOA	0.493	0.23578	0.392561	0.125776	AWOA	2.952504	2.697139	2.872817	0.100804
Topology-3 (Series)					Topology-4 (Series)
Algorithm	HP-Statistical Attributes				Algorithm	HP-Statistical Attributes
	Max	Min	Mean	SD		Max	Min	Mean	SD
MPA-SCA	5.671945	5.671945	5.671945	1.04 × 10−9	MPA-SCA	6.339927	6.339927	6.339927	3.29 × 10−10
MPA	5.671945	5.671945	5.671945	1.76 × 10−9	MPA	6.339927	6.339927	6.339927	4.18 × 10−10
SCA	5.905161	5.672844	5.704757	0.047126	SCA	347.0379	6.340298	19.98467	62.95686
GWO	17.12968	5.66159	6.130355	2.079862	GWO	35.94208	1.934139	10.05672	9.321973
WOA	80.8472	4.160479	10.6829	15.31928	WOA	39.8214	3.989967	13.81374	9.676749
MVO	33.15487	3.338734	9.65829	6.478725	MVO	351.0236	4.612612	25.65877	62.25545
CSA	5.88795	5.751216	5.88339	0.024964	CSA	33.66454	6.33993	11.81966	8.529696
FPA	5.887968	5.671899	5.687382	5.45 × 10−2	FPA	30.42419	6.326296	7.234712	4.38
HHO	71.96283	5.672535	12.17002	15.35204	HHO	1555.804	6.351692	67.16096	281.8028
CMPA	6.115478	5.762231	5.950431	0.086461	CMPA	48.26047	6.437116	9.105037	9.147228
ECGOA	31.96992	5.963248	11.83319	8.181191	ECGOA	50.68444	6.153766	13.20195	9.400668
AWOA	5.887949	5.887947	5.887948	4.63 × 10−7	AWOA	39.90043	4.197232	12.26866	9.577424

and

Table 3. Harmonic Pollution (HP) Statistics for Four Topologies of Parallel structure.

Topology-1 (Parallel)					Topology-2 (Parallel)
Algorithm	HP-Statistical Attributes				Algorithm	HP-Statistical Attributes
	Max	Min	Mean	SD		Max	Min	Mean	SD
MPA-SCA	0.227358	0.227358	0.227358	2.71 × 10−10	MPA-SCA	2.754218	2.754218	2.754218	3.16 × 10−9
MPA	0.227358	0.227358	0.227358	2.88 × 10−10	MPA	2.754218	2.754218	2.754218	4.55 × 10−9
SCA	1.540463	0.226645	0.561062	0.550442	SCA	2.852008	2.694887	2.760584	0.036992
GWO	0.458854	0.227309	0.235344	0.042215	GWO	23.22957	2.744314	3.436385	3.738339
WOA	1.538521	0.22731	0.305256	0.239995	WOA	2.827789	2.712834	2.763879	0.02347
MVO	0.45924	0.227338	0.304952	0.110742	MVO	2.94992	2.74116	2.799505	0.082647
CSA	0.45881	0.227343	0.382775	0.109506	CSA	2.949172	2.731838	2.888504	0.090862
FPA	0.22763	0.22732	0.227376	6.30 × 10−5	FPA	2.756777	2.753395	2.754264	5.76 × 10−4
HHO	0.986941	0.227813	0.411603	0.150028	HHO	3.00042	2.689728	2.86761	0.10087
CMPA	0.633684	0.228126	0.329684	0.102188	CMPA	2.997078	2.684481	2.773105	0.073081
ECGOA	0.785555	0.233648	0.46482	0.115018	ECGOA	3.262607	2.762591	2.970238	0.125936
AWOA	0.458804	0.227332	0.404935	0.099306	AWOA	2.949219	2.710616	2.880074	0.094219
Topology-3 (Parallel)					Topology-4 (Parallel)
Algorithm	HP-Statistical Attributes				Algorithm	HP-Statistical Attributes
	Max	Min	Mean	SD		Max	Min	Mean	SD
MPA-SCA	5.680787	5.680787	5.680787	8.33 × 10−10	MPA-SCA	6.491804	6.491804	6.491804	1.70 × 10−9
MPA	5.680787	5.680787	5.680787	1.18 × 10−9	MPA	6.951745	6.491804	6.881109	1.91 × 10−9
SCA	18.75719	5.67968	6.139192	2.383221	SCA	27.84881	6.496107	8.047248	5.139513
GWO	75.03596	3.179032	9.035578	13.67917	GWO	30.01716	3.180714	7.99458	5.090187
WOA	20.50213	3.948563	6.541731	3.219661	WOA	118.6962	3.380581	13.27721	20.54415
MVO	22.83762	3.932113	7.665998	3.904528	MVO	30.5377	6.145469	10.48941	5.77847
CSA	5.906084	5.680802	5.887405	0.057728	CSA	81.42312	3.830066	13.52468	14.94403
FPA	5.9061	5.680749	5.704009	6.85 × 10−2	FPA	9.496073	5.172203	6.654876	6.19 × 10−1
HHO	40.19606	4.177925	8.15946	7.418736	HHO	97.94805	3.023637	13.24849	17.41042
CMPA	6.113927	5.754902	5.961314	0.10126	CMPA	18.15076	1.005695	7.413693	3.031412
ECGOA	39.81213	4.31944	12.06873	9.537644	ECGOA	28.14325	3.145787	10.11361	4.744195
AWOA	5.906083	5.680789	5.898572	4.11 × 10−2	AWOA	24.45016	1.620379	8.214011	4.259875

for series and parallel structure, respectively.

The following points emerged from this analysis:

• As far as the standard deviation values for Topology (1–4) obtained for series structure are observed, it can be concluded that these values are minimum for the proposed MPA-SCA. It is also worth mentioning here that other attributes are also quite comparable with standard algorithms. Hence, low values of obtained standard deviation indicate the superiority of the algorithm over other opponents. A similar trend is also observed in the parallel topology structure, where the standard deviation values are optimal for the proposed algorithm. The significant values are indicated in boldface.
• It is important to mention here that some algorithms perform pessimistically when dealing with this optimization problem, such as, for instance, for series structure (MVO for Topology-2, WOA, MVO, HHO, and ECGOA for Topology-3, SCA, GWO, WOA, MVO, CSA, FPA, HHO, CMPA, ECGOA, and AWOA provides high standard deviation values for HP. These values indicate that algorithms are not compatible with the optimization problem and can also provide some ambiguous results in some cases. Similarly, for parallel topology, GWO, HHO, and ECGOA provide pessimistic results for Topology-3, and WOA, CSA, and HHO provide a high value of standard deviation while solving the optimization for parallel Topology-4.

It Is always advisable to conduct statistical significance tests with the algorithms in order to validate the optimization performance. Hence, a statistical significance test has been conducted for evaluation of the performance of the proposed algorithm. MPA-SCA is statistically compared with other algorithms by considering the 5% level of significance. The details of the test are given below in

Table 4. Description of Statistical Significance Test.

Name of Test	Calculated Parameter	Details
Wilcoxon Rank sum Test	p-Values and H- Values	If the p-value of the compared algorithms is greater than 0.05 then no difference exists between algorithms. H-values = 0
		If the p-value of the compared algorithms is less than 0.05 then a significant difference exists between algorithms. H-values = 1

:

On the basis of the given conditions, each participating algorithm is compared with the other and the table is prepared.

Table 5. Statistical Significance of the Rank-sum test.

Topology	Topology-1 (Series)		Topology-2 (Series)		Topology-3 (Series)		Topology-4 (Series)
Parameter	p-Value	H-Value	p-Value	H-Value	p-Value	H-Value	p-Value	H-Value
SCA	1.72 × 10−12	1	6.46 × 10−12	1.00	3.02 × 10−11	1	3.01 × 10−11	1
GWO	1.72 × 10−12	1	6.46 × 10−12	1.00	3.02 × 10−11	1	2.52 × 10−11	1
WOA	1.72 × 10−12	1	6.46 × 10−12	1.00	2.98 × 10−11	1	1.44 × 10−11	1
MVO	1.72 × 10−12	1	6.46 × 10−12	1.00	2.40 × 10−11	1	7.88 × 10−12	1
CSA	1.72 × 10−12	1	6.46 × 10−12	1.00	3.02 × 10−11	1	2.52 × 10−11	1
FPA	1.72 × 10−12	1	6.46 × 10−12	1.00	3.02 × 10−11	1	3.02 × 10−11	1
HHO	1.72 × 10−12	1	6.46 × 10−12	1.00	2.95 × 10−11	1	9.40 × 10−12	1
CMPA	1.72 × 10−12	1	6.46 × 10−12	1.00	3.02 × 10−11	1	3.02 × 10−11	1
ECGOA	1.72 × 10−12	1	6.46 × 10−12	1.00	2.26 × 10−11	1	1.21 × 10−12	1
AWOA	1.72 × 10−12	1	6.46 × 10−12	1.00	3.02 × 10−11	1	1.44 × 10−11	1
MPA	1	0	0.807846738	0	0.153667235	0	0.8766349	0
Topology	Topology-1 (Parallel)		Topology-2 (Parallel)		Topology-3 (Parallel)		Topology-4 (Parallel)
Parameter	p-Value	H-Value	p-Value	H-Value	p-Value	H-Value	p-Value	H-Value
SCA	1.55 × 10−11	1	2.25 × 10−11	1	3.02 × 10−11	1	3.01 × 10−11	1
GWO	1.55 × 10−11	1	2.25 × 10−11	1	3.01 × 10−11	1	2.95 × 10−11	1
WOA	1.55 × 10−11	1	2.25 × 10−11	1	3.01 × 10−11	1	6.48 × 10−12	1
MVO	1.55 × 10−11	1	2.25 × 10−11	1	2.80 × 10−11	1	2.37 × 10−12	1
CSA	1.55 × 10−11	1	2.25 × 10−11	1	3.02 × 10−11	1	3.16 × 10−12	1
FPA	1.55 × 10−11	1	2.25 × 10−11	1	3.02 × 10−11	1	3.01 × 10−11	1
HHO	1.55 × 10−11	1	2.25 × 10−11	1	2.95 × 10−11	1	4.11 × 10−12	1
CMPA	1.55 × 10−11	1	2.25 × 10−11	1	3.02 × 10−11	1	2.92 × 10−11	1
ECGOA	1.55 × 10−11	1	2.25 × 10−11	1	5.22 × 10−12	1	1.21 × 10−12	1
AWOA	1.55 × 10−11	1	2.25 × 10−11	1	3.02 × 10−11	1	1.27 × 10−11	1
MPA	0.178795323	0	0.527602679	0	0.096262831	0	0.559230536	0

shows the results of this statistical significance test and evaluates the performance of the algorithm on the basis of this significance.

From the p-value analysis it can be observed that except the parent MPA, the algorithm shows a significant difference with other algorithms, as the p-values are less than 0.05 and the corresponding entries for H-values are equal to 1. On the other hand, comparing MPA the H-values along with p-values shows competitive performance. Hence, on the basis of the obtained low standard deviation value, it can be said that the proposed MPA-SCA can be a better choice for handling an optimization problem such as this.

5.1. Boxplot Analysis

For proving the efficacy of the algorithm, boxplots are often employed. Boxplots of designs are exhibited in this section. These plots exhibit the ability of the algorithm to find the solution in a narrow range. By observing the shape of the boxplots, it may be concluded that:

• The algorithm yields positive results and that are too in narrow range.
• The algorithm exhibits very competitive performance when compared with other opponents.

Figure 10 and Figure 11 exhibit the data distribution characteristics of the optimization process. It appears that the optimization process is more accurate when it is solved with proposed MPA-SCA. From this result, it is concluded that the narrow characteristic of the boxplot reveals an exciting virtue of the proposed algorithm for solving such types of problems.

5.2. Execution Time Analysis

For proving the efficacy of the algorithm, an execution time analysis has been conducted and it is observed that the proposed MPA-SCA has a faster convergence compared with other algorithms. Here, the execution time of one run of all cases has been reported for each algorithm for every test case. The experiment has been conducted on an AMD Ryzen 5 3450U with a Radeon Vega Mobile Gfx 2.10 GHz machine. It is observed that MPA-SCA yields the first run with 0.22 (CPU-time), MPA (0.234), SCA (0.41), GWO (0.35), WOA (0.26), MVO (0.277), CSA (0.289), FPA (0.32), HHO (0.22), CMPA (0.43), ECGOA (0.42), and AWOA (0.42). It is worth mentioning here that the algorithms that are having chaotic loops in the mechanism are taking a long time to convergence; hence, these are declared as computationally complex algorithms. However, it has been observed that the proposed MPA-SCA has promising results, as it has an optimal time for one run as compared to other algorithms. Hence, it can be concluded that the proposed algorithm is not only computationally less complex but also yields accurate results. To showcase the same fact, in the next subsection, fitness value analysis has been presented.

5.3. Fitness Function Value Analysis

In this section, fitness function values are depicted with the help of calculations of statistical attributes, such as best, worst, mean, and standard deviation values.

Depiction of the results in terms of fitness function values are showcased in

Table 6. Analysis of Fitness Function Values.

Series	Parameters	MPA-SCA	MPA	SCA	GWO	WOA	MVO	CSA	FPA	HHO	CMPA	ECGOA	AWOA
Topology-1	Max	−9.67504	−9.67504	−8.16102	−9.32006	−9.36947	−9.31952	−9.32079	−9.67498	−8.89561	−9.199	−8.77154	−9.32079
	Min	−9.67504	−9.67504	−9.67158	−9.67498	−9.67497	−9.6749	−9.67504	−9.67504	−9.675	−9.65748	−9.64865	−9.67504
	Mean	−9.67504	−9.67504	−9.38097	−9.66256	−9.60957	−9.54405	−9.43878	−9.67503	−9.44708	−9.41425	−9.22929	−9.45405
	SD	3.29 × 10−16	3.30 × 10−16	0.555189	0.06469	0.082034	0.17304	0.169725	1.37 × 10−5	0.189851	0.123635	0.236657	0.171987
Topology-2	Max	−6.78502	−6.78502	−6.21413	−6.23222	−6.23221	100	−6.46302	−6.78499	−6.42416	−6.34147	−5.74773	−6.46302
	Min	−6.78502	−6.78502	−6.77016	−6.7849	−6.78501	−6.785	−6.78502	−6.78502	−6.78462	−6.734	−6.76511	−6.78502
	Mean	−6.78502	−6.78502	−6.4368	−6.76611	−6.75875	−3.14964	−6.58266	−6.78501	−6.5785	−6.5598	−6.33637	−6.5731
	SD	1.18 × 10−15	5.05 × 10−15	0.252263	0.100836	0.100855	19.48234	0.156784	6.68 × 10−6	0.151291	0.11008	0.219109	0.152814
Topology-3	Max	−2.08504	−2.08504	−1.69757	100	100	100	−1.7655	−1.76547	100	−1.30849	100	−1.7655
	Min	−2.08504	−2.08504	−2.07437	−2.08404	−2.08426	−2.08427	−1.92316	−2.08456	−2.08388	−1.75493	−1.50652	−1.7655
	Mean	−2.08504	−2.08504	−1.97135	4.839298	15.09655	42.30153	−1.77076	−2.06077	18.56314	−1.53463	46.7119	−1.7655
	SD	2.01 × 10−9	5.80 × 10−9	0.085572	25.86796	38.61987	51.31849	0.028785	0.080298	41.41502	0.0997	50.70806	8.94 × 10−7
Topology-4	Max	−1.10197	−1.10197	1	1	1	1	1	1	1	1	1	1
	Min	−1.10197	−1.10197	−1.08501	−1.10147	−1.10021	−1.10044	−1.10196	−1.07419	−1.08285	−0.87559	1	−1.10195
	Mean	−1.10197	−1.10197	−0.80406	−0.24807	0.273946	0.542432	−0.14476	−0.76916	0.524989	0.072894	1	0.299951
	SD	1.87 × 10−9	9.83 × 10−10	0.614464	1.036617	0.984738	0.859799	1.032489	0.419199	0.811663	0.468885	0	0.968612

. Graphical representation of the results is shown in Figure 12 and Figure 13 for both structures. In the light of following discussion, the application of this filter can be seen with the power conditioning devices mentioned in references [45,58,59].

5.4. Total Harmonic Distortion Analysis

For evaluating the performance of proposed filter design approach, THD analysis of the MPA-SCA has been showcased in this section.

Table 7. Evaluation of the Proposed Filter through THD Analysis.

Series	ITHD (%)	VTHD (%)	Parallel	ITHD (%)	VTHD (%)
Toplogy-1	0.12497	0.19999	Toplogy-1	0.12044	0.19284
Topology-2	2.67705	0.54400	Topology-2	2.70840	0.50027
Topology-3	4.60850	3.30646	Topology-3	4.615498	3.31187624
Topology-4	4.9987	3.89803	Topology-4	4.9869	4.1404734

shows the results of THD calculation of current and voltage values obtained after the outfitting of proposed MPA-SCA filter. It is observed that for all configurations the values of obtained are less than 5% for all cases. Hence, configuration of the filter obtained with the help of the proposed algorithm can be accepted for industrial implementation.

The following points emerged from this analysis:

• It is observed that THD values of voltage are quite a bit higher for series Topology-3 and 4 and corresponding values of current THDs are also comparatively high. Since these values are less than threshold value 5. It can be said that further improvement is possible.
• For parallel topology, THD values of voltage and currents are high for Topology-3 and 4. It is also worth mentioning here that these values come in the acceptable range, as per reference [60].
• Here, the THD has been computed in the presence of [5,7,11,13] harmonic contamination. This composition has been taken for creating a real-life scenario in industrial processes. However, the acceptable THD values show that the proposed modification and implementation of the filter is successful for all evaluated cases.

6. Conclusions

The mitigation technologies pertaining to power harmonics are important in emerging scenarios. The paper presented an approach for integrating two distinct algorithms in one through a hybridization fusion process in position update. Further, the applicability of the algorithm is tested over different cases of industrial power plants. Analysis of the algorithm’s performance has been conducted with the help of convergence characteristics, box plot analysis, and fitness function value analysis. From the analysis, it can be concluded that the proposed algorithm provides better results as compared to other algorithms and can be used as a potential tool for mitigating the harmonics.

• A proposal of a hybrid algorithm is put forward in the manuscript. Two strong metaheuristics, MPA and SCA, are fused with each other to utilize the inherent properties of each one in a hybrid structure.
• Further, the application of the proposed MPA-SCA has been explored in the application of designing hybrid filters of series and parallel topologies. While observing the response of the proposed framework, it is concluded that the parameter estimation process of the proposed metaheuristic is strong and robust.
• The harmonic pollution obtained from the process also shows a constant growth and is stable compared to other algorithms. Finally, the statistical significance, along with data distribution analysis, show that the proposed modifications are profound for the parameter estimation process of the filter.

Due to the involvement of trigonometric operators, for some hard optimization problems, entrapment in local minima can be observed. Hence, involving chaotic loops in the position update phase may be addressed in further versions of the work.